Torque Limit-Based Inertial Control of a DFIG for Rapid Frequency Stabilization

With the increasing penetration of renewable energy generation, the frequency stability of a power grid can be significantly threatened. A doubly-fed induction generator (DFIG) participates in the frequency support of a power grid by releasing kinetic energy (KE) to boost the frequency nadir (FN). However, during rotor speed restoration, it is difficult to counterbalance the size of a second frequency drop (SFD) and the rotor speed recovery duration. This paper proposes an improved torque limit-based inertial control (TLBIC) to raise the FN by releasing less kinetic energy while guaranteeing rapid frequency stabilization with reduced SFD. To this end, when detecting a disturbance, the DFIG enhances the active reference power to the torque limit, and then the active power reduces smoothly based on an exponential function until the maximum power point tracking (MPPT) curve is met, and the rotor speed reverts to the initialization operating condition along the MPPT curve. A simulation system model with various wind power penetrations is established in EMTP-RV. Results show that the proposed scheme boosts the FN at a high level with less KE and guarantees rapid frequency stabilization.

Introduction

Recently, wind power generation has developed rapidly due to the shortage of fossil fuel and worsening environmental situations. Doubly-fed induction generators (DFIGs) are widely applied in the field of wind power because of the relatively low price, decoupling control operation of the active power and reactive power, maximum power point tracking (MPPT) control, deloading operation, and other advanced control strategies (Bao et al., 2020; Xiong et al., 2020). In addition, DFIGs are connected to the grid by power electronic converters, which decouple the rotor speed of the wind turbine from the system frequency. Consequently, DFIGs are unable to sustain the system frequency (Yang et al., 2022; Yang et al., 2021; Xiong et al., 2021a). With the increasing penetration level of wind power, the power system will face significant challenges in system frequency stability. Therefore, more and more attention has been paid to DFIG active frequency support (Wang and Tomsovic, 2018; Xiong et al., 2021b).

DFIGs supply inertial control using additional control strategies. In Kheshti et al. (2019), the most characteristic inertial control can be roughly divided into two types: virtual inertial control (PD control) (Morren et al., 2006; Fernandez et al., 2008; Lee et al., 2016; Van de Vyver et al., 2016; Li et al., 2017; Hu and Wu, 2019; Peng et al., 2020) and stepwise inertial control (Ullah et al., 2008; Lao, 2021). PD control emulates the inertia response and primary frequency response of synchronous generations (SGs) to provide a frequency response. Compared with PD control, stepwise inertial control can supply a rapid frequency response due to the operating characteristics of a DFIG (Kheshti et al., 2019). However, after DFIGs participate in frequency regulation by releasing rotor kinetic energy, the rotor speed will deviate from the optimal state corresponding to MPPT operation. Therefore, the rotor speed needs to regain the optimal state considering the economic benefits of the wind farm, but the speed recovery is accompanied by power mutation, which trend to cause a significant SFD (Xiong et al., 2021c).

In Hafiz and Abdennour (2015), the active power is designed as a slope function. Even though this scheme lessens the SFD to a certain extent, but it delays the rotor speed recovery. Furthermore, the parameters of this function in different scenarios need to be reset. In order to recover the rotor speed, a constant power reference is addressed (Kang et al., 2016a; Kang et al., 2016b). However, the tradeoff between the depth of an SFD and the rotor speed restoration is difficult to achieve. The study of Xu and Xu (2017) suggests a constant accelerating power reference based on the mechanical power curve, which realizes the smooth recovery of the rotor speed. Nevertheless, the mechanical power curve is difficult to acquire and SFD still exists due to the sudden power drop. The authors of (Lao, 2021) suggested a frequency regulation strategy based on logistic regression function, which realizes smooth rotor speed recovery. However, the function used in this strategy is too complex, and too many parameters need to be defined, which brings difficulties to engineering applications. To compensate for the energy required for rotor speed recovery, a coordinated frequency control strategy for the wind turbine and SG is addressed (Xu et al., 2018). The rotor speed recovery can be realized with reduced SFD by adjusting the primary frequency modulation parameters of the SG. However, for a large-scale power system with high wind power penetrations, this strategy is not economical to regain the rotor speed. In Wu et al. (2017), a frequency control strategy based on the energy storage system is suggested, which realizes the rapid speed recovery while eliminating the SFD. However, the overall operation and maintenance cost of the power system increases due to the high cost of the energy storage system.

To approach the above issues, this paper addresses an improved torque limit-based inertial control (TLBIC) scheme to raise the FN by releasing less rotational energy while guaranteeing rapid frequency stabilization with reduced SFD. To this end, when detecting a disturbance, the power reference of the DFIG increases to the torque limit. Afterward, the power reference decreases smoothly based on an exponential function until it the maximum power point tracking (MPPT) curve is met, and then the rotor speed reverts to the initialization operating condition along the MPPT curve. In addition, DFIGs are assumed to work in MPPT mode prior to frequency disturbance. The benefits of the proposed TLBIC scheme are verified under various wind power penetrations and wind speed conditions based on an EMTP-RV simulator.

Modeling of a Doubly-Fed Induction Generator

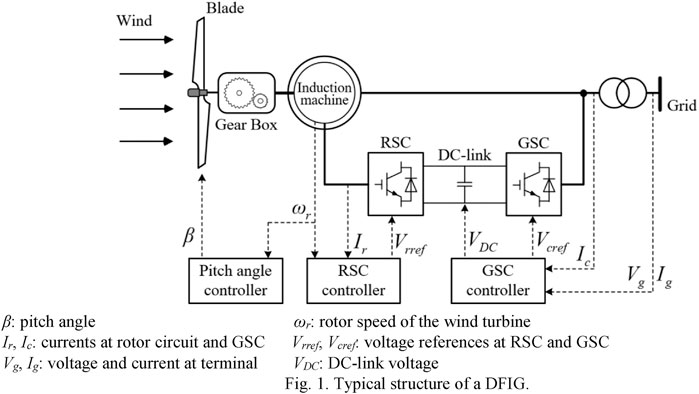
This section mainly introduces the typical structure of a DFIG, as illustrated in Figure 1 which includes a wind turbine model, two-mass shaft model, and DFIG controllers.

FIGURE 1

FIGURE 1. Typical structure of a DFIG.

Wind Turbine Model

The mechanical input power captured by a wind turbine from moving air is represented as:

$P_m=\frac{1}{2}{c}_P(\lambda ,\beta )\rho A{v}_w^3=\frac{1}{2}{c}_P(\lambda ,\beta )\rho \pi R^2{v}_w^3(1)$

where c_p represents the power coefficient; λ and β are the tip-speed ratio and pitch angle, respectively; ρ is the air density; A indicates the swept area by blade; R means the blade length and v_w means the wind velocity.

As in (Kang et al., 2016a; Kang et al., 2016b), c_p employed in Eq. 1 can be represented as:

$c_P(\lambda ,\beta )=0.645\{0.00912\lambda +\frac{-5-0.4(2.5+\beta )+116{\lambda }_i}{e^{21{\lambda }_i}}\}(2)$

where

${\lambda }_i=\frac{1}{\lambda +0.08(2.5+\beta )}-\frac{0.035}{1+{(2.5+\beta )}^3}(3)$

and λ is given as:

$\lambda =\frac{{\omega }_{r}R}{v_w}.(4)$

where ω_r represents the rotor speed of the generator.

For capturing more wind energy resources, the DFIG usually works in MPPT operation. As in Fernandez et al. (2008), the MPPT operation power reference, P_MPPT, is expressed as:

$P_{MPPT}=\frac{1}{2}{c}_{P,\max }\rho \pi R^2{\left(\frac{{\omega }_{r}R}{{\lambda }_{opt}}\right)}^3=k{\omega }_r^3(5)$

where c_{p, max} is a maximum value of c_p when β = 0°, λ = λ_opt and set to 0.5 in this paper; λ_opt is the optimal λ of the wind turbine to capture the maximum wind energy and set to 9.95 in this paper; k is a calculation of the characteristic parameters of the wind turbine and set to 0.512 in this paper.

Two-Mass Shaft Model

This paper uses a two-mass shaft model to express the mechanical dynamics between the wind turbine and induction generator, the model can be represented as Eqs 6–9 in (Boukhezzar and Siguerdidjane, 2011).

$J_t\frac{d{\mathit{\omega }}_t}{dt}=T_m-T_L(6)$

$J_g\frac{d{\mathit{\omega }}_r}{dt}=T_H-T_{em}(7)$

$T_L=K\theta +D({\mathit{\omega }}_t-{\mathit{\omega }}_L)(8)$

$N=\frac{T_L}{T_H}=\frac{{\mathit{\omega }}_r}{{\mathit{\omega }}_L}(9)$

where J_t and J_g are the inertia constants of the wind turbine and generator, respectively; T_m and T_em are the mechanical torque, electrical torque of the wind turbine and generator, respectively; ω_t is the rotor speed of the wind turbine; T_L and T_H are the torques of the low-speed and the high-speed shafts, respectively; ω_L is the rotor speed of the low-speed shaft; K is the spring constant; D is the damping constant; θ is the torsional twist; N is the gear ratio.

β: pitch angle ω_r: rotor speed of the wind turbine.

I_r, I_c: currents at rotor circuit and GSC V_rref, V_cref: voltage references at RSC and GSC.

V_g, I_g: voltage and current at terminal V_DC: DC-link voltage.

Control System of a DFIG

The control system consists of a pitch angle controller, a rotor-side controller (RSC) and grid-side controller (GSC). The pitch angle controller adjusts the pitch angle according to the current wind speed to ensure the maximum of DFIG output power on the premise of the stable operation. An RSC realizes active and reactive power decoupling control and MPPT control of the DFIG. The GSC is mainly responsible for maintaining the DC-link voltage.

When the wind turbine output power is abnormally excessive or rapidly increased, the rapid change of the torque is inevitable. Especially in severe cases, severer mechanical torsion may damage the wind turbine. In order to protect the mechanical structure of the wind turbine and ensure the safe operation, the output power should meet Kang et al. (2016a)

$P_{em}\le P_{T\lim }=T_{\lim }{\mathit{\omega }}_r(10)$

where P_em is the electromagnetic output power; P_Tlim is the maximum reference power based on torque limit; T_lim indicates the torque limit of the wind turbine and set to 0.88 p. u. in this paper.

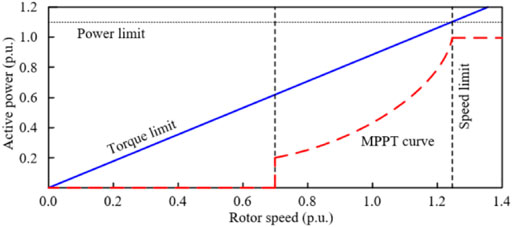
Furthermore, the maximum power is 1.10 p. u., the minimum rotor speed is 0.70 p. u., and the maximum rotor speed is 1.25 p. u. as in Yang et al. (2018) (Figure 2).

FIGURE 2

FIGURE 2. Power characteristic curve of a DFIG.

Analysis the Inertial Control of a DFIG on the Dynamic System Frequency

When the DFIG implements the inertial control, the relationship between the active power variation (ΔP_IC) and the rotor speed of the DFIG can be represented as:

$\mathrm{\Delta }{\mathit{P}}_{\mathit{IC}}={\mathit{J}}_{\mathit{DFIG}}{\mathit{\omega }}_{\mathit{r}}\raisebox{1ex}{$\mathit{d}{\mathit{\omega }}_{\mathit{r}}$}\!\left/ \!\raisebox{-1ex}{$\mathit{dt}$}\right.(11)$

where J_DFIG means the moment of inertia of the DFIG.

According to the definition of the inertia constant of the SG, the inertia constant of the DFIG (H_DFIG) can be expressed as:

${\mathit{H}}_{\mathit{DFIG}}=\raisebox{1ex}{${\mathit{J}}_{\mathit{DFIG}}{\mathit{\omega }}_n^2$}\!\left/ \!\raisebox{-1ex}{$\mathit{2}{\mathit{S}}_{\mathit{DFIG}}$}\right.(12)$

where ω_n and S_DFIG indicate the rated rotor speed and rated capacity of the DFIG, respectively.

Rearranging Eq. 11 and converting it to a per unit (p.u.) system, the expression of Eq. 11 can be modified as in Eq. 13

$\mathrm{\Delta }{P}_{IC\_pu}=2H_{DFIG}{\mathit{\omega }}_{pu}\frac{d{\mathit{\omega }}_{pu}}{dt}(13)$

where ΔP_{IC_pu} and ω_pu are ΔP_IC and the rotor speed of the DFIG in p. u., respectively.

By integrating both sides of Eqs 13, 14 is obtained

$\mathrm{\Delta }{E}_{pu}=H_{DFIG}\left[{\mathit{\omega }}_{pu}^2\left(t_1\right)-{\mathit{\omega }}_{pu}^2\left(t_0\right)\right](14)$

where ΔE_pu is the released kinetic energy of the DFIG in p. u. during the inertia response, ω_pu(t₁) and ω_pu(t₀) are the rotor speed of the DFIG at t₁ and t₀ in p. u., respectively.

As in Miao et al. (2015), since the system frequency in p. u. is the same as ω_pu, ω_pu in Eq. 14 is replaced by the frequency in p. u., thus, the expression of Eq. 14 can be modified as:

${\mathit{f}}_{pu}\left(t_1\right)=\sqrt{\frac{\mathrm{\Delta }{E}_{pu}}{H_{DFIG}}\mathit{+}{\mathit{f}}_{pu}^2\left(t_0\right)}(15)$

where f_pu(t₁) and f_pu(t₀) are the system frequency at t₁ and t₀ in p. u., respectively.

Therefore, the frequency deviation, Δf_pu = f_pu(t₁)—f_pu(t₀), is given by Eq. 16:

$\mathrm{\Delta }{\mathit{f}}_{pu}=-{\mathit{f}}_{pu}\left(t_0\right)+\sqrt{\frac{\mathrm{\Delta }{E}_{pu}}{H_{DFIG}}\mathit{+}{\mathit{f}}_{pu}^2\left(t_0\right)}(16)$

As shown in Eq. 16, it is evidenced that the DFIG can support the system frequency by inertia response. The large ΔE_pu can reduce the system frequency deviation so as to boost the FN.

Torque Limit-Based Inertial Control of a DFIG

After the KE stored in rotor is released to support the system frequency, the rotor speed will deviate from the initial operation state, and even cause the wind turbine stalling. Furthermore, the rotor speed recovery trends to cause a significant SFD due to the reduction on the output power. In order to effectively heighten the FN without a stalling and recover the rotor speed with reduced SFD, the inertial control strategy of the DFIG should be carefully designed.

The following section briefly introduces the characteristics of the conventional TLBIC scheme of (Kang et al., 2016a). Thereafter, the proposed TLBIC scheme is described in detailed in the second part of this section.

Conventional Torque Limit-based Inertial Control Scheme of a DFIG.

To improve the FN without causing the wind turbine stalling, the process of the TLBIC contains two periods: period of supporting the system frequency (A-B-C trajectory) and period of recovering rotor speed of the wind turbine (C-C’-D-A trajectory) (Figure 3A).

FIGURE 3

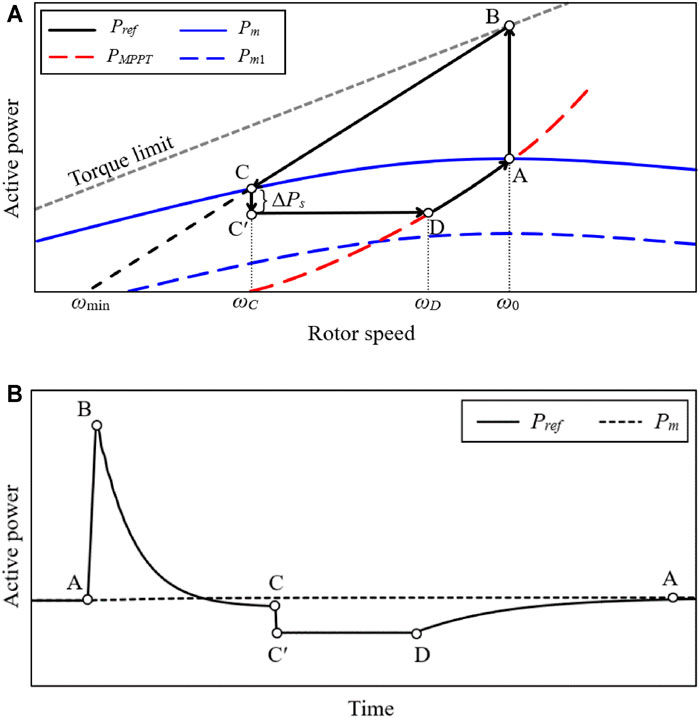
FIGURE 3. Operational features of the conventional TLBIC scheme: (A) Power trajectory in the ω_r domain; (B) Active power in the time domain.

Period of Supporting the System Frequency

As shown in A-B-C trajectory of Figure 3A, the DFIG operates at MPPT mode prior to a disturbance, which corresponds to Point A. Upon detecting a disturbance, the power reference of a DFIG instantly increases to Point B (which is the torque limit) along Line A-B so as to boost the FN effectively. To avoid the wind turbine stalling, the reference power P_ref decreases along Point B to Point C. During the period of supporting the system frequency, the reference power P_ref, is given by:

$P_{ref}\mathit{=}{\mathit{P}}_{MPPT}\left({\mathit{\omega }}_{\min }\right)+\frac{P_{T\lim }\left({\mathit{\omega }}_0\right)-{\mathit{P}}_{MPPT}\left({\mathit{\omega }}_{\min }\right)}{{\mathit{\omega }}_0-{\mathit{\omega }}_{\min }}({\mathit{\omega }}_r-{\mathit{\omega }}_{\min })(17)$

where ω_min is the minimum rotor speed; ω₀ is the rotor speed prior to a disturbance; P_MPPT(ω_min) and P_MPPT(ω₀) are the value of P_MPPT at ω_min and ω₀, respectively; P_Tlim(ω₀) is the maximum power corresponding to torque limit at ω₀.

Since P_ref is greater than the input mechanical power P_m, ω_r decreases continuously based on the swing equation. Besides, as described in Eq. 17, the power reference P_ref is a linear function of ω_r, the active power output will decrease along the Line B-C with ω_r (see B-C trajectory in Figure 3A). When P_ref becomes equal to P_m at Point C, the rotor speed converges to ω_C. Accordingly, ω_C is higher than the minimum speed limit ω_min, so that this strategy effectively avoids the stalling of the wind turbine.

Period of Recovering Rotor Speed of the Wind Turbine

As in (Kang et al., 2016a), if ω_r satisfies the following condition, ω_r converges.

$\left|\mathit{\omega }(t+T)-\mathit{\omega }\left(t\right)\right|\le 3.45\times {10}^{-7}\text{p}\text{.u}\text{.}(18)$

where T is the sampling interval of ω_r.

At Point C, the active power P_ref(ω_C) instantly reduces ΔP_s to Point Cʹ so as to recover ω_r, and keep the value until the MPPT curve is met. At Point D, P_ref is switched to P_MPPT. Afterwards, ω_r returns from Point D to Point A by the action of the MPPT curve. P_ref for C-Cʹ-D stage can be expressed as in Eq. 19.

$P_{ref}\mathit{=}{\mathit{P}}_{ref}\left({\mathit{\omega }}_C\right)-\mathrm{\Delta }{\mathit{P}}_{\mathit{s}}(19)$

where ΔP_s is a constant.

As displayed in Figure 3B, since the condition Eq. 18 is difficult to achieve. Accordingly, this period of ω_r convergence remains for a long time and leads to a waste of the KE which is unnecessary. In addition, to accelerate ω_r recovery, a large ΔP_s is desirable. However, too large ΔP_s may result in a severe SFD undoubtedly. Therefore, it is difficult to counterbalance the size of an SFD and the rotor speed recovery duration.

Proposed Torque Limit-based Inertial Control Scheme of a DFIG

To approach the above issues of the conventional TLBIC scheme, a proposed TLBIC scheme is carried out in this study.

The proposed TLBIC scheme aims to 1) improve the FN at a high level with less released kinetic energy and 2) ensure the frequency stabilization with reduced SFD. To this end, P_ref is represented as in Eq. 20, as shown in Figure 4B.

$P_{ref}\left(t\right)=P_{T\lim }\left({\mathit{\omega }}_0\right)\times \frac{1}{{\exp }^{\left[\mathit{\alpha }(t-t_0)\right]}}\begin{array}{c}\end{array}\begin{array}{c}\end{array}t\ge t_0(20)$

where α is the frequency control parameter; t₀ is the moment of disturbance occurrence.

FIGURE 4

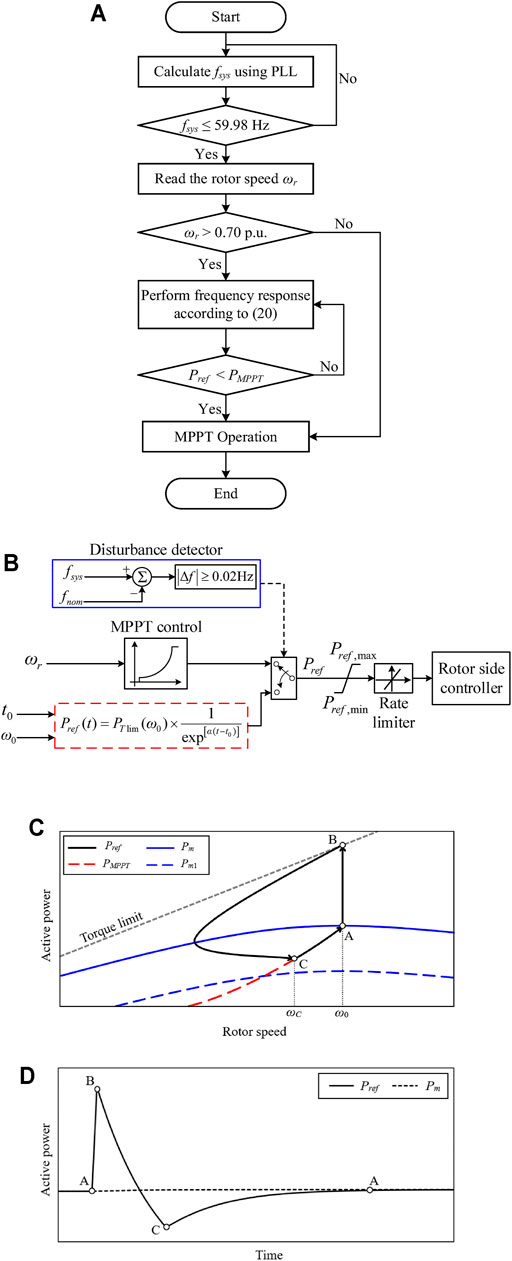
FIGURE 4. Operational features of the proposed TLBIC scheme: (A) Flowchart of the proposed TLBIC scheme; (B) Block diagram of the proposed TLBIC scheme; (C) Power trajectory in the ω_r domain; (D) Active power in the time domain.

The flowchart and the power operation features of the proposed TLBIC scheme are presented in Figures 4A,C, respectively. As the conventional TLBIC scheme, the proposed reference power increases instantly from P_MPPT(ω₀) to P_Tlim(ω₀) at t₀ (see A-B trajectory in Figure 4C), so as to provide short-term frequency response. Different from the conventional reference power (which is a function of ω_r), the proposed reference power is a function of the time. As time goes on, P_ref continues to decrease smoothly until the MPPT curve is met (see B-C trajectory in Figure 4C). At Point C, P_ref equals P_m and ω_r converges to ω_C. Afterwards, P_ref of the DFIG switches to P_MPPT, and the rotor speed returns to the initial state along the P_MPPT curve for optimum power production (see C-A trajectory in Figure 4C).

Compared with the conventional TLBIC scheme, the proposed TLBIC scheme is more manageable, which can control the output active power at the initial period of the frequency response by adjusting α. In addition, the proposed TLBIC scheme starts the restoration of ω_r earlier without the period of ω_r convergence and avoids the release of unnecessary KE. As shown in Figure 4D; Eq. 20, with the assistance of time-varying power function, P_ref decreases smoothly with time and switches to MPPT mode without an active power mutation, which effectively ensures frequency stabilization.

It is quite important to remark that the setting of α in Eq. 20: a small α is instrumental in rapid ω_r restoration. However, a small α is not benefit to release the rotating KE and boost the FN; On the contrary, a large α could rise the FN effectively, but it delays ω_r recovery and causes a severe SFD. Therefore, the setting of α is critically important. Besides, P_ref should be limited by an active power rate limiter and a maximum power limiter.

Modeling of Simulation System

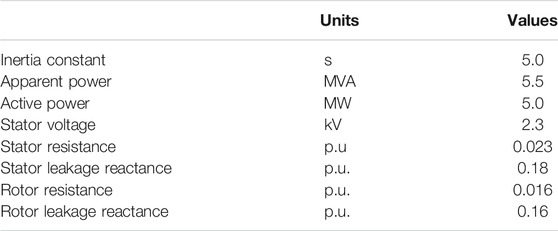
Simulations on various wind power penetrations and wind speed conditions are conducted in EMTP-RV simulator to demonstrate the effectiveness of the proposed TLBIC scheme. As displayed in Figure 5, the model system consists of one aggregated DFIG-based wind farm, six synchronous generators, a 350-MW asynchronous motor, and a 240-MW static load. The main parameters of the DFIG are shown in Table 1.

FIGURE 5

FIGURE 5. Model system with an aggregated wind farm.

TABLE 1

TABLE 1. Parameters of the DFIG.

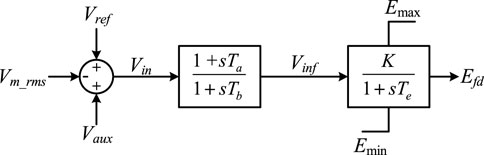
As in (Byerly et al., 1973), all synchronous generators use the IEEEG1 governor and SEXS exciter. The classical configurations of the IEEEG1 model (type B) and SEXS exciter are displayed in Figure 6, 7, respectively. Note that the secondary frequency response is not implemented in this study, thus the frequency will not eventually return to the acceptable range.

FIGURE 6

FIGURE 6. IEEEG1 model (type B).

FIGURE 7

FIGURE 7. SEXS exciter.

Case Studies

In this section, the performances of the proposed scheme under the scenarios by varying the wind power penetration levels of 30 and 40% are verified. Moreover, the average wind speed is set to 8.0 m/s and a stochastic wind speed model is employed in this study. As a disturbance, SG₄ which generates 150 MW prior to a disturbance is tripped at 40.0 s.

The following several subsections will compare the performances of the proposed scheme with the conventional scheme and MPPT operation in terms of the system frequency nadir, second frequency drop, starting time of rotor speed recovery, and released kinetic energy, respectively.

The released kinetic energy ΔE_rel in this paper is defined as:

$\mathrm{\Delta }{E}_{rel}=H_{DFIG}({\mathit{\omega }}_0^2-{\mathit{\omega }}_C^2)(21)$

Case 1: Wind Power Penetration = 30% and Wind Speed = 8 m/s

Figure 8 shows the simulation results for case 1, in which the wind power penetration level is 30% and wind speed condition is 8.0 m/s. In addition, ΔP_s for the conventional scheme is set to 0.05 p. u., as suggested in (GB/T19963, 2011), and the KE available from the wind turbine is 1.708 s.

FIGURE 8

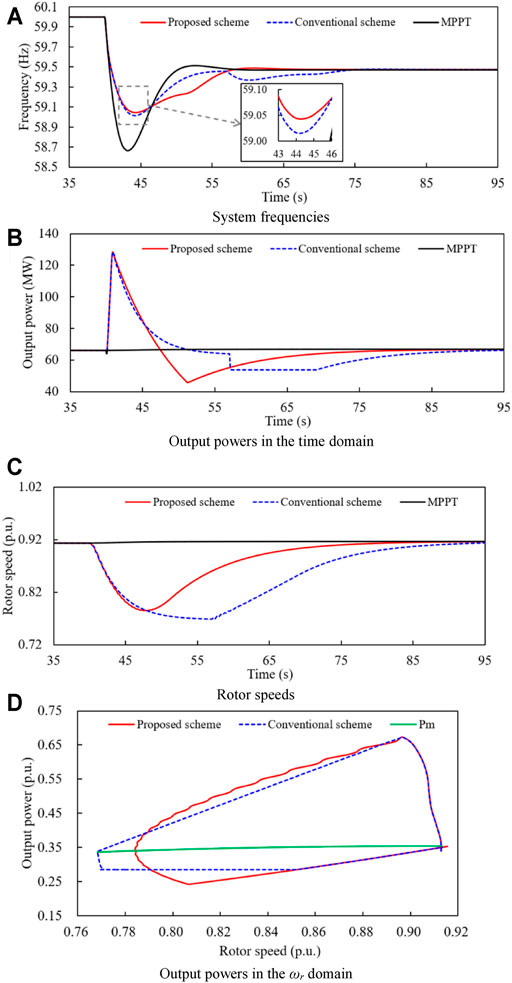
FIGURE 8. Simulation results for case 1. (A) System frequencies. (B) Output powers in the time domain. (C) Rotor speeds. (D) Output powers in the ωr domain.

Since SG₄ is offline at t = 40 s, the system active power is out-off-balanced so that the frequency drops. As shown in Figure 8A, the frequency nadirs of the proposed TLBIC scheme, conventional TLBIC scheme, and MPPT control are 59.043, 59.014, and 58.665 Hz, respectively. When the DFIG operates at MPPT mode, it does not participate in system frequency response including inertia response and governor response, thus, its active power output and rotor speed remain unchanged. In addition, compared with the conventional strategy, the FN of the proposed TLBIC strategy is slightly boosted by 0.029 Hz. This is mainly because α is set to 0.1 so that the active power of the proposed TLBIC scheme is larger in the initial period of the inertial response (Figure 8D).

Figure 8C displays the rotor speeds of case 1, ω_r in the proposed TLBIC strategy drops faster and decreases to 0.784 p. u. at 47.6 s, and then gradually returns to ω₀. Due to the slow rotor speed convergence, ω_r in the conventional TLBIC scheme converges to 0.768 p. u. at 57.0 s. Consequently, the proposed TLBIC scheme begins the restoration of the rotor speed earlier than the conventional TLBIC scheme by 9.4 s. Moreover, the KE released from the wind turbine during the inertial response in the proposed TLBIC scheme is 1.085 s, while the released KE in the conventional TLBIC scheme is 1.209 s (Table 2). The reason for this phenomenon is that ω_C is more in the proposed TLBIC scheme.

TABLE 2

TABLE 2. Simulation results for all cases.

In order to recover ω_r, the conventional scheme instantly reduces the output power by 10 MW at 57 s to accelerate the recovery of ω_r, which causes a severe SFD of 0.632 Hz (Figures 8A,B). In contrast, the proposed reference power P_ref decreases smoothly with time by Eq. 20, which effectively ensures the rapid rotor recovery and frequency stabilization without a fluctuation, as shown in Figure 8A.

Case 2: Wind Power Penetration = 40% and Wind Speed = 8 m/s

Figure 9 shows the simulation results for case 2, in which the wind power penetration level is more than it is in case 1 by 10%.

FIGURE 9

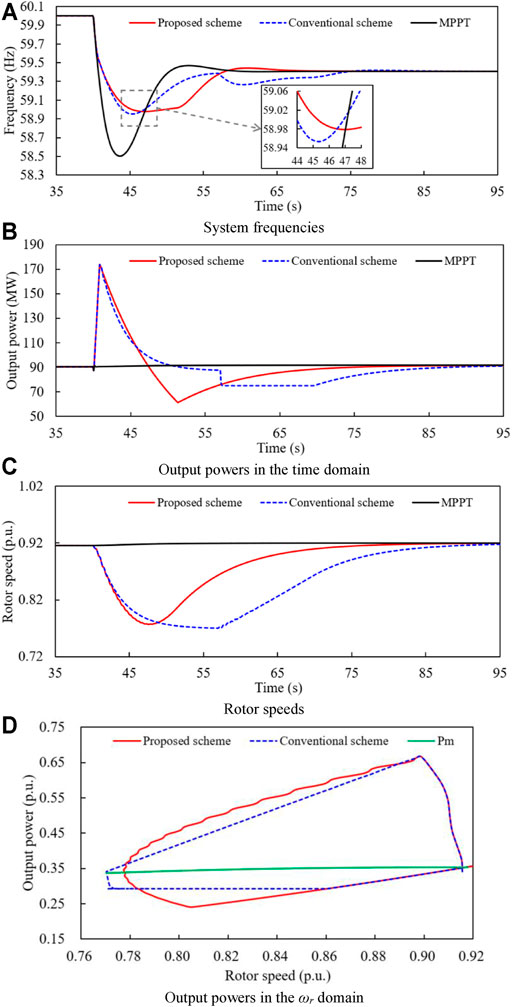
FIGURE 9. Simulation results for case 2. (A) System frequencies. (B) Output powers in the time domain. (C) Rotor speeds. (D) Output powers in the ωr domain.

As illustrated in Figure 9A, the FN of the MPPT operation is 58.501 Hz, which is lower than that of case 1 by 0.164 Hz obviously. This mainly suffers from the higher wind power penetration. Furthermore, the frequency nadirs of the proposed and conventional TLBIC strategy are 58.977 Hz, 58.953 Hz, respectively. Compared with the conventional TLBIC scheme, the FN of the proposed TLBIC scheme is improved by 0.024 Hz due to the setting of α in Eq. 20. In addition, the system frequencies for the proposed and conventional TLBIC strategy reach the steady state at 68.0 and 85.0 s, respectively.

ω_r in the proposed and conventional TLBIC scheme start the restoration at 47.6 and 57.0 s, respectively. Moreover, a significant SFD occurs at 60.3 s in the conventional TLBIC scheme while there is no frequency fluctuation in the proposed TLBIC scheme during the restoration of ω_r. The size of the SFD for the conventional TLBIC scheme is 0.735 Hz, which is larger than that in case 1 by 0.103 Hz because of a bigger ΔP_s.

Table 2 presents the simulation results for case 2, the released KE in the proposed and conventional TLBIC scheme are 1.167 and 1.221 s, respectively. Obviously, the released KE of the proposed TLBIC scheme is less.

Simulation results of the above two cases clearly illustrate that the proposed TLBIC strategy can heighten the FN at a high level with less KE while guaranteeing the fast frequency stabilization under high wind power penetrations.

The above two cases have demonstrated the benefits of the proposed TLBIC strategy under constant wind speed. Whereas, considering the wind velocities are variable in a realistic scenario, the availability of the proposed TLBIC strategy will be investigated on a stochastic wind speed model in the following section.

Case 3: Wind Power Penetration = 30% and Random Wind Speed Condition

The stochastic wind speed model is presented in Figure 10A. As displayed in Figure 10B, the frequency nadirs of the proposed TLBIC scheme, conventional TLBIC scheme, and MPPT control occur at 44.2, 43.7 and 43.2 s and are 59.043, 59.014, and 58.665 Hz, respectively, and the frequency nadirs of three control schemes is all lower than those of case 1 due to the influence of the wind speed drop (Figure 10A). Moreover, the system frequencies for the proposed and conventional TLBIC scheme reach the steady state at 62.0 and 72.0 s, respectively.

FIGURE 10

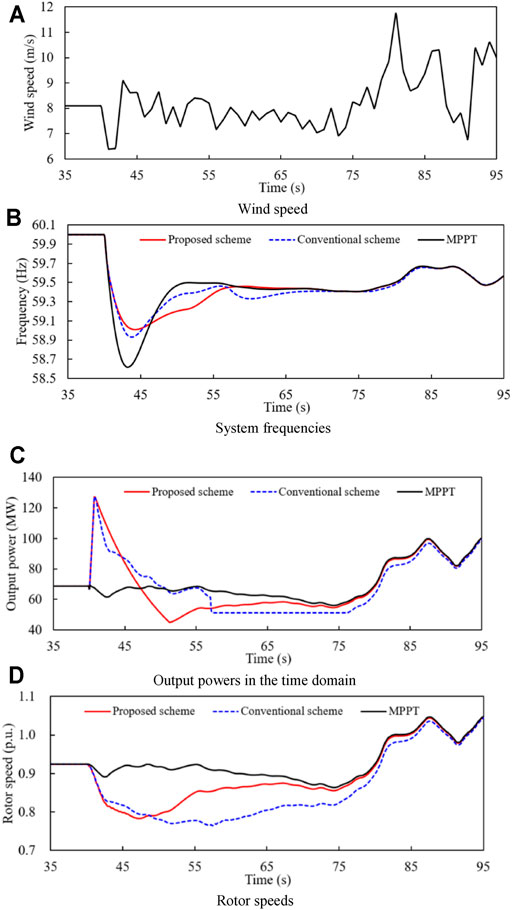
FIGURE 10. Simulation results for case 3. (A) Wind speed. (B) System frequencies. (C) Output powers in the time domain. (D) Rotor speeds.

Since the DFIG output power is closely related to the wind speed, the output power raise at 73 s with the increase of the wind speed (Figures 10A,C). As displayed in Table 2, ω_r of the proposed TLBIC scheme starts the recovery at 47.1 s which is earlier than that of the conventional TLBIC scheme by 10.3 s. Furthermore, the released KE during the frequency response in the proposed and conventional TLBIC scheme are 1.203 and 1.350 s, respectively.

Simulation results displayed in case 3 also demonstrate that the advantages and effectiveness of the proposed TLBIC scheme. Even though in a stochastic wind speed, the proposed TLBIC scheme still heightens the FN at a high level with less KE while guaranteeing the rapid frequency stabilization with reduced SFD.

Conclusion

This study suggests an optimized inertial control of a DFIG for heightening the FN at a high level with less KE and guaranteeing the fast frequency stabilization under high wind power penetrations with reduced SFD. To this end, when detecting a disturbance, the active power of the DFIG increases to the torque limit so that enough rotor kinetic energy is released into the power grid, and then the power reference smoothly reduces until the MPPT curve is met. Afterwards, the rotor speed reverts to the initialization along the MPPT curve without a frequency fluctuation.

Simulation results on various wind penetrations and wind velocities significantly demonstrate that the proposed TLBIC scheme shows better performances during the frequency response over the conventional TLBIC scheme: 1) during the period of supporting the system frequency, the proposed TLBIC strategy heightens the FN at a high level with less released KE; 2) during the period of recovering the rotor speed, the proposed TLBIC scheme guarantees the rapid frequency stabilization with reduced SFD effectively. Consequently, the optimized scheme can provide an effective approach for reducing the waste of the KE and balancing the depth of the SFD and the duration of rotor speed restoration.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher. Requests to access the datasets should be directed to HW, wanghongmei@ntu.edu.cn.

Author Contributions

YX contributed to the conception and design of the proposed strategy. All authors wrote and edited the manuscript.

Funding

This work was supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (20KJB470026).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, W., Ding, L., and Liu, Z. (2020). Analytically derived fixed termination time for stepwise inertial control of wind turbines—Part I: Analytical derivation. Inter. J. Elect. Power Energ. Sys 121, 1–10. doi:10.1016/j.ijepes.2020.106120

CrossRef Full Text | Google Scholar

Boukhezzar, B., and Siguerdidjane, H. Nonlinear control of a variable speed wind turbine using a two-mass model. IEEE Trans. Energ. Convers. 26 (1), 149–161. Mar. 2011.

Google Scholar

Byerly, R. T., Aanstad, O., and Berry, D. H. (1973). Dynamic models for steam and hydro turbines in power system studies. IEEE Trans. Power App. Syst. 92 (6), 1904–1915.

Google Scholar

Fernandez, L. M., Garcia, C. A., and Jurado, F. (2008). Comparative study on the performance of control systems for doubly fed induction generator (DFIG) wind turbines operating with power regulation. Energy 33 (9), 1438–1452. doi:10.1016/j.energy.2008.05.006

CrossRef Full Text | Google Scholar

GB/T19963 (2011). Technical Rule for Connecting to Power System. China.

Google Scholar

Hafiz, F., and Abdennour, A. (2015). Optimal use of kinetic energy for the inertial support from variable speed wind turbines. Renew. Energ. 80, 629–643. doi:10.1016/j.renene.2015.02.051

CrossRef Full Text | Google Scholar

Hu, Y.-L., and Wu, Y.-K. (2019). Approximation to frequency control capability of a DFIG-based wind farm using a simple linear gain droop control. IEEE Trans. Ind. Applicat. 55 (3), 2300–2309. doi:10.1109/tia.2018.2886993

CrossRef Full Text | Google Scholar

Kang, M., Kim, K., and Muljadi, E. (2016). Frequency control support of a doubly-fed induction generator based on the torque limit. IEEE Trans. Power Syst. 31 (6), 4574–4583. doi:10.1109/tpwrs.2015.2514240

CrossRef Full Text | Google Scholar

Kang, M., Muljadi, E., Hur, K., and Kang, Y. C. (2016). Stable adaptive inertial control of a doubly-fed induction generator. IEEE Trans. Smart Grid 7 (6), 2971–2979.

CrossRef Full Text | Google Scholar

Kheshti, M., Ding, L., Nayeripour, M., Wang, X., and Terzijia, V. (2019). Active power support of wind turbines for grid frequency events using a reliable power reference scheme. Renew. Energ. 139, 1421–1454. doi:10.1016/j.renene.2019.03.016

CrossRef Full Text | Google Scholar

Lao, H. (2021). Innovated inertia control of DFIG with dynamic rotor speed recovery. CSEE J. Power Energ. Syst.

Google Scholar

Lee, J., Jang, G., Muljadi, E., Blaabjerg, F., Chen, Z., and Cheol Kang, Y. (2016). Stable short-term frequency support using adaptive gains for a DFIG-based wind power plant. IEEE Trans. Energ. Convers. 31 (3), 1068–1079. doi:10.1109/tec.2016.2532366

CrossRef Full Text | Google Scholar

Li, Y., Xu, Z., and Wong, K. P. (2017). Advanced control strategies of PMSG-based wind turbines for system inertia support. IEEE Trans. Power Syst. 32 (4), 3027–3037. doi:10.1109/tpwrs.2016.2616171

CrossRef Full Text | Google Scholar

Miao, L., Wen, J., Xie, H., Yue, C., and Lee, W.-J. (2015). Coordinated Control Strategy of Wind Turbine Generator and Energy Storage Equipment for Frequency Support. IEEE Trans. Ind. Applicat. 51 (4), 2732–2742. doi:10.1109/tia.2015.2394435

CrossRef Full Text | Google Scholar

Morren, J., Pierik, J., and de Haan, S. W. H. (2006). Inertial response of variable speed wind turbines. Electric Power Syst. Res. 76 (11), 980–987. doi:10.1016/j.epsr.2005.12.002

CrossRef Full Text | Google Scholar

Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2020). Two-Stage Variable Proportion Coefficient Based Frequency Support of Grid-Connected DFIG-WTs. IEEE Trans. Power Syst. 35 (2), 962–974. doi:10.1109/tpwrs.2019.2943520

CrossRef Full Text | Google Scholar

Ullah, N. R., Thiringer, T., and Karlsson, D. (2008). Temporary Primary Frequency Control Support by Variable Speed Wind Turbines- Potential and Applications. IEEE Trans. Power Syst. 23 (2), 601–612. doi:10.1109/tpwrs.2008.920076

CrossRef Full Text | Google Scholar

Van de Vyver, J., De Kooning, J. D. M., Meersman, B., Vandevelde, L., and Vandoorn, T. L. (2016). Droop control as an alternative inertial response strategy for the synthetic inertia on wind turbines. IEEE Trans. Power Syst. 31 (2), 1129–1138. doi:10.1109/tpwrs.2015.2417758

CrossRef Full Text | Google Scholar

Wang, S., and Tomsovic, K. (2018). A novel active power control framework for wind turbine generators to improve frequency response. IEEE Trans. Power Syst. 33 (6), 6579–6589. doi:10.1109/tpwrs.2018.2829748

CrossRef Full Text | Google Scholar

Wu, Y.-K., Yang, W. H., and Hu, Y. L. Frequency regulation at a wind farm using a timing–varying inertia and droop controls. IEEE Trans. Ind. Appl. 55 (1), 213–2224. Jan./Feb. 2019.

Google Scholar

Wu, Z., Gao, D. W., Zhang, H., Yan, S., and Wang, X. (2017). Coordinated control strategy of battery energy storage system and PMSG-WTG to enhance system frequency regulation capability. IEEE Trans. Sustain. Energ. 8 (3), 1330–1343. doi:10.1109/tste.2017.2679716

CrossRef Full Text | Google Scholar

Xiong, L., Liu, L., Liu, X., and Liu, Y. (2021). Frequency Trajectory Planning Based Strategy for Improving Frequency Stability of Droop-Controlled Inverter Based Standalone Power Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 11 (1), 176–187. doi:10.1109/jetcas.2021.3052006

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, Y., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: a review. CSEE J. Power Energ. Syst. (Early Access), 1–18.

Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid Power Compensation-Based Frequency Response Strategy for Low-Inertia Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4), 4500–4513. doi:10.1109/jestpe.2020.3032063

CrossRef Full Text | Google Scholar

Xiong, Y., Yao, W., and Fen, J. (2021). Two-level combined control scheme of VSC-HVDC integrated off shore wind farms for onshore system frequency support. IEEE Trans. Power Syst. 36 (1), 781–792.

Google Scholar

Xu, G., Liu, F., Hu, J., and Bi, T. (2018). Coordination of wind turbines and synchronous generators for system frequency control. Renew. Energ. 129, 225–236. doi:10.1016/j.renene.2018.05.104

CrossRef Full Text | Google Scholar

Xu, G., and Xu, L. (2017). Improved use of WT kinetic energy for system frequency support. IET Renew. Power Generation 11 (8), 1094–1100. doi:10.1049/iet-rpg.2016.0183

CrossRef Full Text | Google Scholar

Yang, D., Jin, Z., Zheng, T., Jin, E., Zhang, X., and Hua, L. (2021). Frequency Control Scheme with Dynamic Droop Characteristics of a DFIG for Mitigating the Frequency Fluctuations. Int. Trans. Ele ctr. Energ. Syst. 33 (11), 1–11.

Google Scholar

Yang, D., Jin, Z., Zheng, T., and Jin, E. (2022). An adaptive droop control strategy with smooth rotor speed recovery capability for type III wind turbine generators. Int. J. Electr. Power Energ. Syst. 135, 107532. doi:10.1016/j.ijepes.2021.107532

CrossRef Full Text | Google Scholar

Yang, D., Kim, J., Kang, Y. C., Muljadi, E., Zhang, N., Hong, J., et al. (2018). Temporary frequency support of a DFIG for high wind power penetration. IEEE Trans. Power Syst. 33 (3), 3428–3437. doi:10.1109/tpwrs.2018.2810841

CrossRef Full Text | Google Scholar