Measurement and Thermodynamic Modeling for CO2 Solubility in the N-(2-Hydroxyethyl) Piperazine + Water System

Amine scrubbing is the most important technique for capturing CO₂. The cyclic diamine N-(2-Hydroxyethyl)-piperazine (HEPZ), a derivative of piperazine, with good mutual solubility in aqueous solution, a low melting point, and a high boiling point, has the potential to replace PZ as an activator added in the mixed amine system to capture CO₂. In this study, the solubility of CO₂ in aqueous HEPZ solutions was determined for three HEPZ concentrations and four temperatures. The VLE data for HEPZ-H₂O were obtained using a gas–liquid double circulation kettle at pressure 30–100 kPa, and the thermodynamic model for the HEPZ-H₂O-CO₂ system was built in Aspen Plus based on the electrolytic non-random two-liquid (ENRTL) activity model. The physical parameters for HEPZ and the interaction parameters for ENRTL, along with reaction constants of carbamate reactions, were regressed. Using the thermodynamic model, the CO₂ cyclic capacity, speciation with loading, and heat of reaction for the CO₂ capture system by the aqueous HEPZ solution are predicted and analyzed.

Introduction

Power generation by burning fossil fuels is the most important source of greenhouse gas emissions that cause global climate change (Anderson, 2016). Carbon capture and storage (CCS), as the process of capturing CO₂ from flue gas from conventional coal-fired power plants, is the direct method to curb global warming (Plasynski et al., 2009). Amine scrubbing has been successfully and widely used in ammonia production as well as natural gas processing and is considered to be the most promising technology for industrialization of capture and separation of CO₂ from flue gas generated by coal-fired power plants (Rochelle, 2009). The industrial applications’ challenges for amine scrubbing are the high energy consumption and huge size of separation equipment and heat exchange equipment as well as cost, which attributes to the flue gas’ large flow rate as well as its low CO₂ partial pressure. Therefore, the development of new solvents and high-efficiency separation equipment and the enhancement of technological processes have been extensively studied to reduce the cost of capture. Developing new amines with outstanding properties is the most important method to reduce renewable energy and cost (Feron and Hendriks, 2005).

Good-performance absorbents can greatly reduce the operating cost of the capture process and generally need to have the following properties (Liang et al., 2015): the cyclic capacity is high, the reaction kinetics is fast, the heat of absorption is relatively low, the resistance to oxidative and thermal degradation is high, and the corrosivity, volatility, viscosity, and cost are low. The high CO₂ cyclic capacity can reduce the solution’s circulation flow rate, thereby reducing the power of the pump and the energy consumption of the reboiler. The fast absorption kinetics reduces the size of the absorbers and strippers and also the maximal achievable rich loading, thereby reducing operating costs. The relatively low heat of absorption can help reduce the regeneration duty. The resistance to oxidative as well as thermal degradation is correlated with the quantity of solvent make-up as well as byproduct emissions to environment and volatility to the quantity of amine loss as well as emission. The low-viscosity solvents enhance mass and heat transfer, thus reducing the amount of packing and the size of the heat exchanger. Different amines have different molecular structures and absorption mechanisms, resulting in different absorption characteristics. There is a fast reaction rate, a low CO₂ cyclic capacity, and a high absorption heat for the primary and secondary amines (Rinker et al., 2000). On the contrary, tertiary amines and steric-hindered amines have a high CO₂ cyclic capacity, a slow absorption rate, and a low absorption heat (Dubois and Thomas, 2012). A mixed-amine system—mixed solvent of amines with different reaction mechanisms—combines the advantages of two alcohol amine solutions: a high CO₂ cyclic capacity, a low heat of absorption, and a fast absorption rate. Activators are usually added to steric-hindered amines or tertiary amines to increase the absorption rate. Monoethanolamine (MEA) and piperazine (PZ) are the most commonly used activators, and related mixed amine systems have been extensively studied (Aronu et al., 2011; Choi et al., 2009; Dash et al., 2011; Mandal et al., 2001; Puxty and Rowland, 2011; Sakwattanapong et al., 2009).

The disadvantage of PZ as an activator is its low boiling point and high melting point. It is easy to crystallize at low temperatures and cannot be configured with higher-concentration solutions, which reduces the absorption. Its boiling point of 146°C is within the range of 120–160°C, the maximum working temperature of the device, so it is easy to volatilize at high temperatures, increasing the amount of amine loss and emission in large-scale carbon capture deployment. PZ derivatives have a similar molecular structure with PZ and in recent years have also been used to study their activation properties in mixed-amine solvents (Choi et al., 2016; Li et al., 2014a; Li et al., 2014b; Li et al., 2013; Yuan et al., 2017). Rochelle’s group from the University of Texas had studied about the absorption kinetics of PZ derivatives for CO₂ capture (Chen and Rochelle, 2011). Our group’s previous study (Li et al., 2014b) measured the cyclic capacity of these PZ derivatives and calculated the heat of CO₂ absorption by using the simplified Gibbs–Helmholtz equation. According to Chen and Rochelle’s research, the screening results indicate that there is a lower heat-of-CO₂ absorption and an equal absorption rate as well as a higher cyclic capacity in 1-methylpiperazine (1MPZ) than in PZ. However, 1MPZ has greater volatility than MEA and PZ (Mandal et al., 2001). The high volatility is usually a problem for commercial use. Among all derivatives of PZ, N-(2-Hydroxyethyl) piperazine (HEPZ) has the highest boiling point of 246°C, a melting point of −38.5°C, and better water solubility and thermal stability than PZ. The chemical structure of HEPZ is shown in Figure 1. HEPZ can withstand higher temperatures and configure higher-concentration solutions in industrial applications, which show the potential of HEPZ to replace PZ as an activator. Since no literature studied the absorption performance of the HEPZ aqueous solution and mixed-amine system with HEPZ, there is a need to measure the relevant experimental data.

FIGURE 1

FIGURE 1. Chemical structure of HEPZ, PZ, and MEA.

This study studied the HEPZ aqueous solution for CO₂ capture, aiming to develop a rigorous thermodynamic model of HEPZ/CO₂/H₂O to accurately calculate the energy consumption during the capturing and then represent all relevant thermodynamic properties, such as vapor–liquid equilibrium (VLE), chemical reaction equilibrium, and heat capacity, which are important elements for the process simulation as well as optimization of CO₂ capture. First, the gas–liquid double-circulation kettle was used to measure the VLE data for HEPZ/H₂O at negative pressure and normal pressure, and the CO₂ solubility data of HEPZ aqueous solutions with three concentrations (5 wt%, 15 wt%, and 30 wt%) as well as four temperatures (313.15, 343.15, 373.15, and 393.15 K) were measured using a stainless-steel reactor, which are necessary data for an accurate thermodynamic model. Data from the literature, such as heat capacity, saturated vapor pressure, etc., and the experimental data of this study were regressed to obtain the missing physical property parameters as well as interaction parameters of the model. Therefore, in this study, the activity coefficient model of electrolyte non-random double liquid (ENRTL) is adopted, which has been successfully used in the $MEA/C{O}_2/H_{2}O$system (Hessen et al., 2010; Zhang and Chen, 2011), PZ/CO₂/H₂O system (Frailie et al., 2011), and AMP/PZ/CO₂/H₂O system (Li et al., 2014a). The results calculated by the model in this study agreed with experimental data, and at the same time, the composition, cyclic capacity, and heat of absorption of the HEPZ aqueous system are predicted and analyzed by the model as well.

Experiment

Materials

In this study, the chemicals and their information are shown in the Supplementary Material. All chemicals were used without further purification. MEA was used for validation of experimental methods. Deionized water was used to prepare the aqueous solutions, and the amine solutions in this study are all liquid at room temperature.

Vapor–Liquid Equilibrium

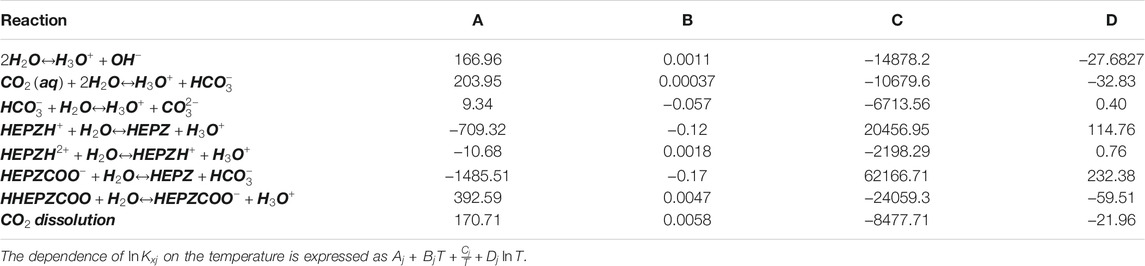
In this study, a customized gas–liquid double-circulation device made of glass was adopted to determine the VLE data of the HEPZ aqueous solution. The working principle is gas–liquid dual circulation. The two circulating pumps are used to forcefully circulate the gas and liquid parts at the same time so that the gas and liquid phases are fully contacted and the time to balance is shortened. The equilibrium temperature can be accurately measured, and partial condensation is very small. The construction of the gas–liquid double-circulation device is shown in Figure 2.

FIGURE 2

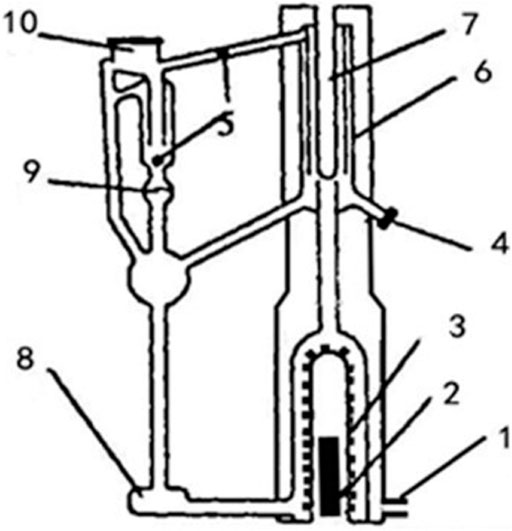
FIGURE 2. Gas–liquid double-circulation device: 1. vacuum pump, 2. heating rods, 3. boiling chamber, 4. liquid-phase sampling port, 5. vapor-phase sampling port, 6. balance cell, 7. temperature measuring cell, 8. magneton, 9. cock, 10. condensation pipe and pressure control system.

The device is made of glass. The solution is pumped into the boiling chamber from the reagent inlet at the bottom of the equipment and heated to boiling using the heating rod. The outer-side air of the boiling chamber is evacuated using a vacuum pump to vacuum for heat preservation. The boiling solution is flushed to the liquid sampling port by bubbles, and the thermometer put in the temperature-measuring cell candetermine the temperature of the boiling liquid phase in order to obtain the boiling point, which is stable after reaching boiling. The vapor enters the condensing tube and flows back to the gas sampling port after condensing; we closed the cock to hold the condensate, which is a sample of the gas phase. After opening the cock, the condensate and reagent are stirred using a magnet and continued to be heated to boil. The entire equipment is connected to an external pressure control device, which is brought to a certain negative pressure using a vacuum pump, achieving the control of the equipment pressure. Therefore, the equipment can obtain VLE data at different pressures. After the solution is boiled, the liquid and vapor phase samples are collected, and the concentration of each phase solution is measured using an Abbe refractometer. This equipment used in this study can measure the boiling point of a certain concentration of the solution and the vapor–liquid composition after boiling at a certain negative pressure or atmospheric pressure. The construction and the operation principle of the Abbe refractometer are provided in the Supplementary Material.

The main sources of error of the device are as follows: the sampling time after boiling is difficult to determine, and the accuracy of the pressure control device is limited; the fluctuation is about $\pm$0.2 kPa. The uncertainty of the thermometer used in this study is ±0.2°C. The color of some solutions turns yellow at high temperature. There will be a certain error in the analysis of the refractometer.

CO₂ Solubility

According to Dong et al. (2010), CO₂ solubility has been measured in the stainless-steel reactor. The apparatus contains four 400 cm³ stainless-steel equilibrium cells (they have an identical structure with the one shown in Dong’s research) that were designed to operate at a temperature as high as 130°C and a pressure as high as 1 MPa, a 500 cm³ stainless-steel gas container with a temperature transducer and a pressure transducer on the top, and CO₂ and $N_2$ tanks.

The key part of the device is the gas–liquid balance reactor, and the temperature in the gas and liquid phases was controlled using a heating jacket and then determined by two temperature transducers, whose accuracy was 0.1 K. A stirring paddle equipped in the kettle is driven by the external motor to generate magnetic force and drive the solution inside of the sealed kettle. The overall pressure was determined by a pressure transducer (JYB-KO-HAA, Kunlunhaian Co.), whose accuracy was about 0.5%. Meanwhile, the same temperature and pressure transducers were adopted by the CO₂ gas container, which is used to obtain the total amount of CO₂ that was introduced into the reactor by recording the pressure difference before and after each injection. Due to the simple structure of the gas chamber, the actual volume can be directly calibrated by the drainage method. However, the internal structure of the reactor is complicated and cannot be directly measured by the drainage method. Its actual volume is calibrated by the gas pressure difference method after measuring the volume of the CO₂ gas chamber. At the beginning of each experiment, the reactor cell is washed by the remaining air through N₂, and then, the aqueous amine solution with a volume of 100 cm³ is injected into the cell. Meanwhile, the temperature of the reactor was set at the experiment temperature. Later, CO₂ was injected to the cell, and 10 h was provided for the absorption equilibrium after every injection.

The partial pressure of CO₂ was obtained by determining the increase in the total pressure compared to the initial value after an injection of CO₂, and it was assumed that the partial pressure of N₂ and H₂O was constant in each experiment. Using the Peng–Robinson (PR) cubic equation, the exact quantity at the gas phase was judged by three factors, including volume, pressure, and temperature (Peng and Robinson, 1976). Then, the dissolved CO₂ concentration was expressed by CO₂ loading with mole CO₂/mole amine. The loading uncertainty was 8%, which was determined by the uncertainty of pressure, temperature, and volume, which were 0.5%, 0.1, and 0.5%, respectively. The uncertainty of CO₂ partial pressure was estimated as 2%, and the details are shown in the study by Dong et al. (2010).

Validation of Experimental Methods

MEA/H₂O/CO₂, a well-known and widely studied system, was selected to verify the experimental methods. The CO₂ solubility for the MEA solution has been measured in a vapor–liquid equalizer, as described in the study by Dong et al. (2010). In Dong et al.’s study, only the data at 313 K were verified. In order to verify the accuracy of experimental equipment in a wider temperature range, the same equipment was used to measure the CO₂ solubility for 30 wt% MEA at 313.15 and 393.15 K. The experimental results are highly correlated with Lee et al. (1976)’s data and shown in Supplementary Material, but the CO₂ pressure at a temperature of 313.15 K is slightly higher than the data from the literature, which is in line with the results of Dong et al. (2010).

To validate the gas–liquid double-circulation device for measurements, vapor–liquid equilibrium data for ethanol were measured at 293.15 K and 101.3 kPa. Then, these data were compared to those obtained from the literature. Data from this study agreed with the data from the study by Kurihara et al. (1993), as shown in Supplementary Material, validating the experimental method. The measurement accuracy of the Abbe refractometer is $\pm 0.0001$ nD.

Thermodynamic Systems

Physical dissolution and chemical absorption happen in the process of CO₂ captured by amine solution, so physical equilibrium and chemical equilibrium need to be considered. There are a variety of intermolecular interactions in the loaded solution, including the interactions between molecules, between molecules and ions, and between ions, making the solution deviate from the ideal state. It is necessary to introduce an activity coefficient model for correction. The relative theories of physical equilibrium, chemical equilibrium, and activity coefficient that need to be considered in establishing a thermodynamic model are introduced in this section.

Physical Equilibrium

In a vapor–liquid equilibrium system, the activity of the components during the liquid phase is the same as the fugacity during the gas phase. For the components of amines and water, which use pure substances as the reference state, the formula of equilibrium can be expressed as

$y_i{\varnothing }_{i}P=x_i{\gamma }_i{P}_i^s.(1)$

For the component CO₂ using the infinite dilution state as the reference state, which is amine and CO₂, the equilibrium formula is as follows:

$y_i{\varnothing }_{i}P=x_i{\gamma }_i^{\ast }H,(2)$

where $y_i$ represents the mole fraction of component $i$ at the gas phase, ${\varnothing }_i$ represents the fugacity coefficient of component $i$ at the gas stage, $P$ represents the total pressure at the system temperature, $P_i^s$ represents the vapor pressure of component $i$ at the system temperature, $x_i$ represents the mole fraction of component $i$ at the liquid stage, ${\gamma }_i^{\ast }$ represents the asymmetric activity coefficient of $i$ in water, and $H_i$ represents Henry’s constant of $i$ in water at the system temperature and vapor pressure of water.

The dependence of the Henry constant on temperature can be expressed as

$\ln H_i=A_i+\frac{B_i}{T\left(K\right)}+C_i\ln T\left(K\right)+D_{i}T\left(K\right).(3)$

The Redlich–Kwong (RK) equation of the state model was used to describe the gas phase. The Henry constant of CO₂ in water was taken from the study by Chen et al. (1979).

Chemical Absorption

Chemical absorption reaction equations in the loaded HEPZ solution are as follows:

$2H_{2}O\leftrightarrow H_3{O}^{+}+O{H}^{-},(4)$

$C{O}_2\left(aq\right)+2H_{2}O\leftrightarrow H_3{O}^{+}+HC{O}_3^{-},(5)$

$HC{O}_3^{-}+H_{2}O\leftrightarrow H_3{O}^{+}+C{O}_3^{2-},(6)$

$HEPZ{H}^{+}+H_{2}O\leftrightarrow HEPZ+H_3{O}^{+},(7)$

$HEPZ{H}_2^{2+}+H_{2}O\leftrightarrow HEPZ{H}^{+}+H_3{O}^{+},(8)$

$HEPZCO{O}^{-}+H_{2}O\leftrightarrow HEPZ+HC{O}_3^{-},(9)$

$HHEPZCOO+H_{2}O\leftrightarrow HEPZCO{O}^{-}+H_3{O}^{+}.(10)$

All the reaction equilibrium constants of the reactions mentioned above can be obtained from the standard-state Gibbs free energies of the equations’ chemicals. The calculation equation is as follows:

$K_j=\text{exp}\left(-\frac{\Delta G_j^0}{RT}\right),(11)$

where $K_j$ represents the chemical equilibrium constant of reaction $j$, $R$ represents the universal gas constant, $T$ represents the temperature, and $\Delta G_j^0$ represents the reference state Gibbs energy change of reaction $j$. Knowing the standard Gibbs free energy, the standard enthalpy of each component’s formation, and the heat capacity in the reference state in the reaction equilibrium equation, the equilibrium constant of each reaction can be calculated. For reactions four to six, the equilibrium constants from the previous studies were usually consistent with the concentrations based on the molality. However, in this study, the model is on the basis of the mole fraction. Therefore, the equilibrium constants were converted by the method mentioned in the study by Li et al. (2014a).

Protonation reactions 7 and 8 produced new ions $HEPZ{H}^{+}$ and $HEPZ{H}_2^{2+}$ in solution, which are absent in the ion database of Aspen. Therefore, the standard-state thermodynamic properties of $HEPZ{H}^{+}$ and $HEPZ{H}_2^{2+}$ are lacked in Aspen and need to be manually adjusted to fit the $pKa$ values from the study by Hamborg and Versteeg (2009). For $HEPZCO{O}^{-}$ and $HEPZCOOH$, the standard-state thermodynamic properties are regressed from $C{O}_2$ solubility data obtained in this study. Using the thermodynamic properties of the products and the reactants, the equilibrium constants of all reactions can be obtained.

Activity Coefficient

Referring to 3.2, a series of reactions will take place in the loaded HEPZ solution, and multiple ions were produced in the process. The interaction between ions causes the liquid system to gradually deviate from the ideal state. It needs to introduce a coefficient model with accurate activity for calculations and simulation. In this study, the activity coefficients for binary interactions in the unloaded amine solution were calculated by the NRTL model, but those for the molecule–molecule binary, molecule–ion pair binary, and ion pair–ion pair binary in the loaded amine solution were calculated by the ENRTL model. The dependence of binary parameters on the temperature can be expressed as

${\tau }_{ij}=a_{ij}+\frac{b_{ij}}{T},(12)$

where $ij$ can be molecule–molecule, molecule–ion pair, ion–molecule pair, or ion pair–ion pair. Meanwhile, the binary parameter $a_{ij}$ is 0.3 for the molecule–molecule interaction, 0.2 for the molecular–ion pair interaction, and 0 for the ion pair–ion pair interaction, and the default values for both ion pair–ion pair and molecule–molecule binary parameters are 0. The default value of the molecule–ion pair binary parameters $a_{ij}$ is (8, −4) when the molecule is H₂O; otherwise, the default values are set at 8 and −15. The default values for $b_{ij}$ are 0.

Results of Modeling

All data and their range and resource used for regression are listed in Table 1.

TABLE 1

TABLE 1. Data used for regression.

N-(2-Hydroxyethyl) Piperazine

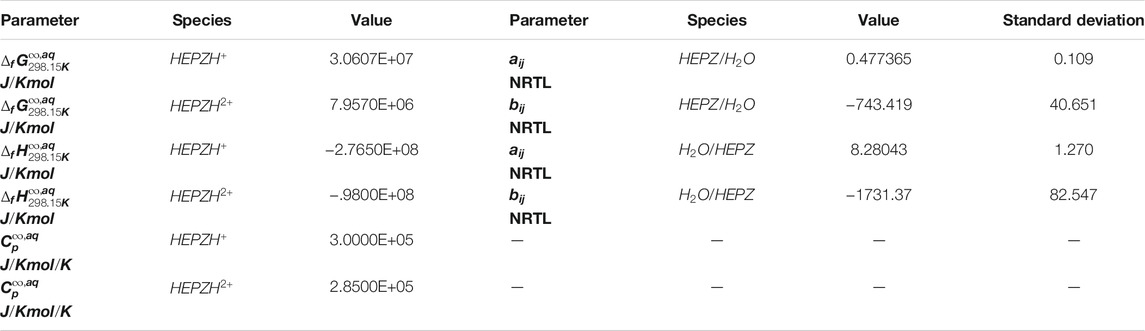
The heat capacity data of HEPZ obtained from the study by Poozesh et al. (2013), Tagiuri (2019) were regressed to acquire the ideal gas heat capacity constants ($C_p^{ig}$), and Antoine’s constants were from the database of Aspen; the value and standard deviation are listed in Table 2. Most of the parameters’ standard deviations shown in Table 1 are far smaller than those contained therein. The heat capacity calculated by the model was in good agreement with the value from experimental data, and the average relative deviation was 0.09% for the heat capacity.

TABLE 2

TABLE 2. Parameters regressed for HEPZ and their deviations.

The dependence of Antoine’s constants on the temperature is expressed as $A+ \frac{B}{T}+C\ln T+D{T}^2$, but for $C_p^{ig}$, it is $A+BT+ C{T}^2 +D{T}^3$. Numbers 1–4 correspond to the letters A–D, respectively.

N-(2-Hydroxyethyl) Piperazine + H₂O

The data from experiments and the literature were regressed in this model, including excess enthalpy, the VLE data acquired in this study, and heat capacity (Poozesh et al., 2013; Tagiuri, 2019) for the mixed solution of HEPZ/H₂O. The $pKa$ values were obtained by regression through manual adjustment of the standard-state properties of $HEPZ{H}^{+}$ and $HEPZ{H}^{2+}$. The regressed parameters along with their standard deviations are shown in Table 3.

TABLE 3

TABLE 3. Parameters regressed for HEPZ/H₂O and their deviations ($\alpha = 0.3$).

In this study, VLE data at 30 kPa, 40 kPa, 55 kPa, 70 kPa, and 85 kPa and the atmosphere pressure of 101 kPa were measured. Because the viscosity of the high-concentration solution of HEPZ is too large, it is not convenient for experimental measurements. The mass fraction range of HEPZ in this experiment is 0.1–0.75. Figure 3 shows the data obtained by the experimental measurement and the data calculated by the model. The upper line and points represent for the mole fraction of HEPZ at the gas phase ($y_{HEPZ}$), and the lower ones stand for the mole fraction of HEPZ at the liquid phase ($x_{HEPZ}$). Because the solution will turn yellow at high temperature, there will be certain errors in the analysis with a refractometer. Besides, the boiling point of HEPZ is much higher than that of H₂O, and the concentration of HEPZ in the gas phase distilled from the HEPZ solution in this study is very low, resulting in a larger measurement error. The average relative deviation of the VLE data $x_{HEPZ}$/$y_{HEPZ}$ of HEPZ at negative pressure is 1.66%/70.9%, 1.26%/57.7%, 0.294%/46.7%, 0.0519%/8.17%, and 0.529%/153%, respectively. The average relative deviation of the VLE data $x_{HEPZ}$/$y_{HEPZ}$ of HEPZ at atmosphere pressure is 0.760%/57.2%.

FIGURE 3

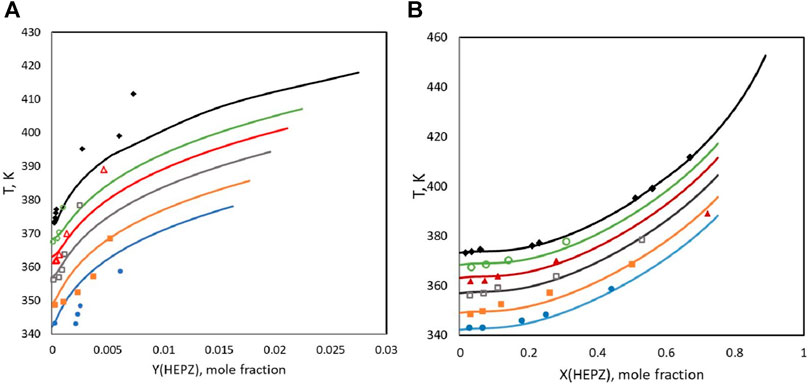
FIGURE 3. VLE data for HEPZ/H₂O at 30 kPa, 40 kPa, 55 kPa, 70 kPa, 85 kPa, and 101 kPa. (A) Gas-phase data; (B) liquid-phase data: lines, Aspen results: blue, 30 kPa; yellow: 40 kPa; gray: 55 kPa; red: 70 kPa; green: 85 kPa; and black: 101 kPa; points, this study: ●, 30 kPa; ■, 40 kPa; □, 55 kPa; ▲, 70 kPa; ○, 85 kPa; and ◆: 101 kPa.

HEPZ has two dissociation constants pKa₁ and pKa₂, which are regressed by the manual adjustment of the standard-state properties of $HEPZ{H}^{+}$ and $HEPZ{H}^{2+}$, with the standard formation Gibbs Free Energy at 298.15 K ${\Delta }_f{G}_{298.15K}^{\infty ,aq}$, the standard enthalpy of formation at 298.15 K ${\Delta }_f{H}_{298.15K}^{\infty ,aq}$, and the infinite dilution state heat capacity parameter at 298.15 K $C_p^{\infty ,aq}$. The non-randomness factor $\alpha$ was a fixed value (0.3), and the results of these properties are listed in Table 3. The average value of the relative deviation between the pKa₁ and pKa₂ data from the study by Hamborg and Versteeg (2009) and Aspen is 0.01%.

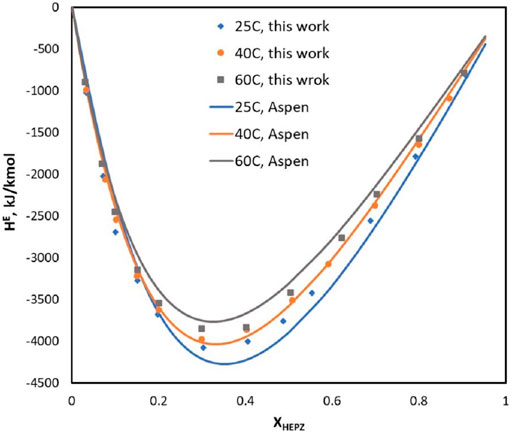
Poozesh et al. (2015) and Tagiuri (2019) measured the heat capacity values for HEPZ/H₂O at various temperatures ranging from 303 to 353 K, and the mole fraction of HEPZ ranges from 0.1 to 0.9. In Figure 4, the calculated value of the model is compared with the measured value of the literature. In the high-concentration area, Figure 5 shows that there is a good correlation between the value calculated by Aspen and the experiment values. However, in the area of low concentration, the experiment values increase as T increases, and the calculated values do not show the same trend. The average relative deviation of all points is 0.0235%. The excess enthalpy of HEPZ/H₂O calculated by Aspen is shown in Figure 5, and the average value of the relative deviation for excess enthalpy regression was 8.57%.

FIGURE 4

FIGURE 4. Heat capacity values for HEPZ/H₂O (lines: Aspen, this study; points: ●: $x=0.1002$; ●: $x=0.2006$; ●: $x=0.3$; ●: $x=0.4044$; ●: $x=0.5$; ●: $x=0.6012$; ●: $x=0.7$; ●: $x=0.8$; and ●: $x=0.9$).

FIGURE 5

FIGURE 5. Excess enthalpy of HEPZ/H₂O.

N-(2-Hydroxyethyl) Piperazine/H₂O/CO₂

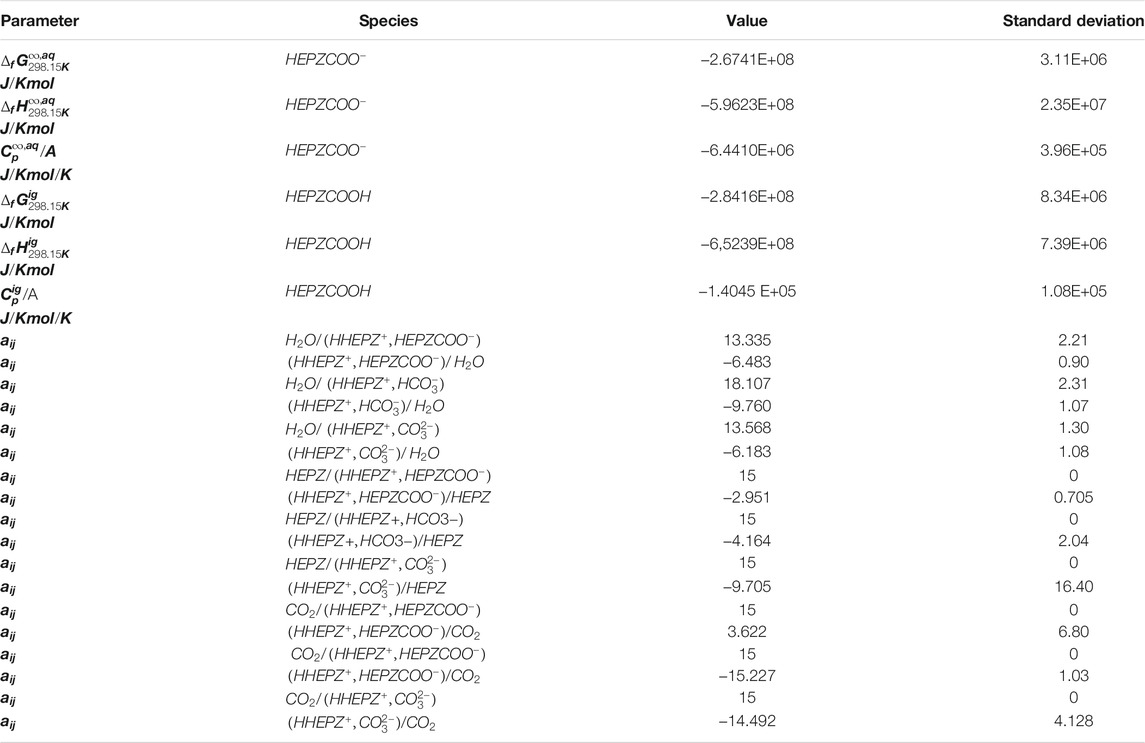
CO₂ solubility data were measured by the method in 2.3, and then, they were regressed to acquire the ENRTL parameters as well as the standard-state properties ${\Delta }_f{G}_{298.15K}^{\infty ,aq}$, ${\Delta }_f{H}_{298.15K}^{\infty ,aq}$, and $C_p^{\infty ,aq}$ for $HEPZCO{O}^{-}$ and ${\Delta }_f{G}_{298.15K}^{ig}$, ${\Delta }_f{H}_{298.15K}^{ig}$, and $C_p^{ig}$ for $HEPZCOOH$. The non-randomness factor $\alpha$ was a fixed value (0.2). The results of the regression are shown in Table 4. The experimental data as well as the calculation results obtained by the model are shown in Figure 6. The experimental data were calculated by the model, and the mean relative deviation of the regression for 5 wt% HEPZ in Figure 6A is 13.35%, and it is 9.79% for 15 wt% HEPZ in Figure 6B and 14.98% for 30 wt% HEPZ in Figure 6C.

TABLE 4

TABLE 4. Parameters regressed for HEPZ/H₂O/CO₂ and their deviations ($\alpha = 0.2$).

FIGURE 6

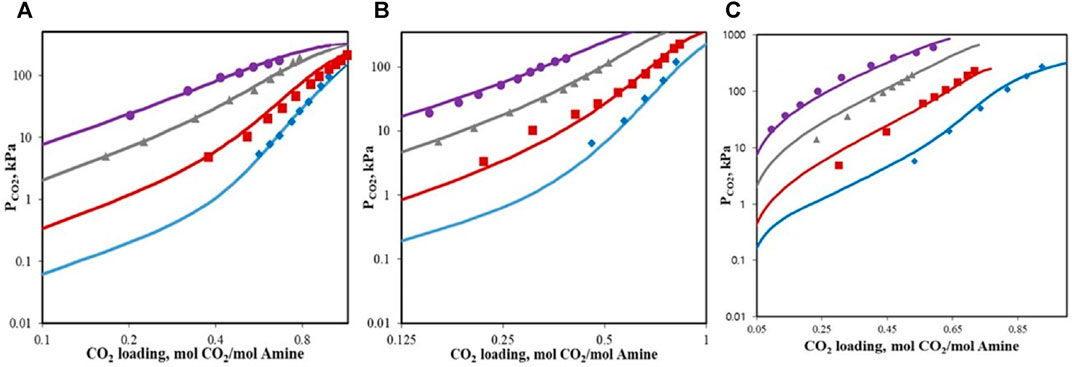
FIGURE 6. (A) CO₂ solubility into 5 wt% HEPZ/H₂O (lines, model results; points, this study: ◆, 313.15 K; ■, 343.15 K; ▲, 373.15 K; and ●, 393.15 K); (B) CO₂ solubility into 15 wt% HEPZ/H₂O (lines, model results; points, this study: ◆, 313.15 K; ■, 343.15 K; ▲, 373.15 K; and ●, 393.15 K); (C) CO₂ solubility into 30 wt% HEPZ/H₂O (lines, model results; points, this study: ◆, 313.15 K; ■, 343.15 K; ▲, 373.15 K; and ●, 393.15 K).

Cyclic Capacity

Circulating capacity is an important property to characterize the properties of amines, and there are two ways to calculate cyclic capacity. When considering a CO₂ removal rate of 90% in the absorber, one way (way 1) is defining lean loading as the CO₂ loading when the partial pressure of CO₂ is 1 kPa at a temperature of 313.15 K, and the rich loading of CO₂ partial pressure is 10 kPa. Meanwhile, cyclic capacity represents the difference between the rich and lean loadings with the unit of $g$ of CO₂/kg of the solvent.

However, in the actual operation of the absorption tower, the absorption tower is not at a constant temperature, and at the bottom of the tower, the rich loading is determined by the equilibrium partial pressure of CO₂ in the flue gas as well as the temperature of the liquid. Also, the lean loading is defined by the desorption tower and not by the equilibrium partial pressure of CO₂ in the top gas of the absorption tower. The other way (way 2) to calculate cyclic capacity is defining lean loading as the $C{O}_2$ loading when the partial pressure of $C{O}_2$ is 15 $kPa$at 393.15 $K$ and rich loading as 15 $kPa$ of $C{O}_2$ partial pressure at 313.15$K$. All results are shown in Table 5.

TABLE 5

TABLE 5. Cyclic capacity for 5 wt%, 15 wt%, and 30 wt% HEPZ solutions by way 1 and way 2.

Speciation

Figure 7 shows the speciation data for 5 wt%, 15 wt%, and 30 wt% HEPZ solutions at a temperature of 313.15 K forecast by the model. For 5 wt% and 15 wt% HEPZ solutions, when the loading is 0–0.5, most of the CO₂ absorbed is converted into $C{O}_3^{2-}$ and $HEPZCO{O}^{-}$, and the other is converted into $HC{O}_3^{-}$; most HEPZ is converted into $HEPZ{H}^{+}$. At the loading of 0.5–1, the main reactants are CO₂, HEPZ, and $HEPZ{H}^{+}$, and some $HEPZCO{O}^{-}$ and $C{O}_3^{2-}$ are also consumed to generate $HC{O}_3^{-}$ and $HHEPZCOO$. For the 30 wt% HEPZ solutions, when the loading is lower than 0.3, HEPZ is consumed and converted to $HEPZ{H}^{+}$, $HEPZCO{O}^{-}$, $C{O}_3^{2-}$, and $HHEPZCOO$, and the important products are $HEPZ{H}^{+}$ and $HEPZCO{O}^{-}$. At a loading of 0.3–0.7, $HEPZCO{O}^{-}$ becomes a reactant which is converted to $HHEPZCOO$. At a greater loading, the proportion of $C{O}_3^{2-}$ and $HEPZ{H}^{+}$ continues to increase, and the proportion of $HEPZ$ and $HEPZCO{O}^{-}$ decreases, showing the CO₂ absorbed mainly converted to $C{O}_3^{2-}$. It is because the solution is more alkaline in this loading range, which is consistent with the theoretical analysis. As the concentration of HEPZ increases, the $HC{O}_3^{-}$ produced by the reaction gradually decreases.

FIGURE 7

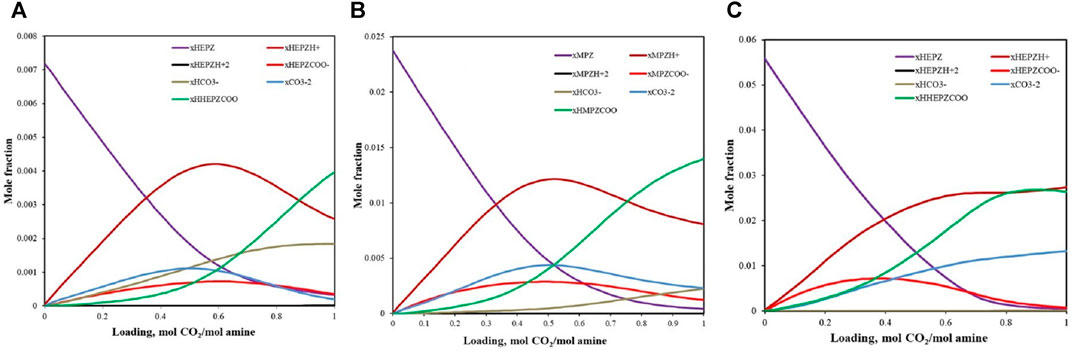
FIGURE 7. Speciation for CO₂ absorbed into 5 wt% (A), 15 wt% (B), and 30 wt% (C) HEPZ/H₂O solutions at 313.15 K.

Reaction Equilibrium Constant and Heat of Reaction

With the activity coefficient as well as mole fraction of species in the 30 wt% HEPZ solutions at different temperatures calculated by the Aspen model, the equilibrium constants of the reactions in the system can be obtained as a function of temperature as follows:

$K_{xj}={\displaystyle \prod _i{{\displaystyle \left(x_i{\gamma }_i\right)}}^{v_{ij}}},(13)$

where $x$ represents the $K_{xj}$ on the basis of the mole fraction, $j$ represents reaction numbers 1–7, ${\gamma }_i$ is the activity coefficient of component $i$, $x_i$ represents the mole fraction of component $i$, and $v_{ij}$ represents the stoichiometric coefficient of component $i$ in reaction $j$. The parameters of the $\ln K_{xj}-T$ curve calculated by Aspen through regression are shown in Table 6.

TABLE 6

TABLE 6. Parameters of equations for reaction equilibrium constants.

The overall differential heat of reaction $\Delta H_{r, overall}$ is the sum of the heat contributions $\Delta H_{r, j}$ obtained from each of the seven reactions occurring in the solution, which are mentioned in $3.1$, and in this study, there is one more reaction that was considered to denote the dissolution equilibrium of $C{O}_2$ from the gas phase to the liquid phase:

$C{O}_2\left(gas\right)\leftrightarrow C{O}_2\left(aq\right).(14)$

Heat of Absorption Meanwhile, the heat of CO₂ physical dissolution $\Delta H_{dissolution}$ also contributes to $\Delta H_{r, overall}$, given by

$\Delta H_{r, overall}={\displaystyle \sum _{j=1}^7\Delta {\xi }_j\Delta H_{r, j}}+\Delta H_{dissolution},(15)$

where $\Delta {\xi }_j$ represents the reaction degree of the key component of reaction $j$ when absorbing 1 mole CO₂, which can be calculated by the incremental change of the key component when 1 mole CO₂ is absorbed.

$\Delta {\xi }_1=\frac{\Delta n_{O{H}^{-}}}{\Delta n_{C{O}_2}^{\ast }},(16)$

$\Delta {\xi }_2=1-\frac{\Delta n_{C{O}_2}}{\Delta n_{C{O}_2}^{\ast }},(17)$

$\Delta {\xi }_3=\frac{\Delta n_{C{O}_3^{2-}}}{\Delta n_{C{O}_2}^{\ast }},(18)$

$\Delta {\xi }_4=-\frac{\Delta n_{HEPZ{H}^{+}}+\Delta n_{HEPZ{H}^{2+}}}{\Delta n_{C{O}_2}^{\ast }},(19)$

$\Delta {\xi }_5=-\frac{\Delta n_{HEPZ{H}^{2+}}}{\Delta n_{C{O}_2}^{\ast }},(20)$

$\Delta {\xi }_6=-\frac{\Delta n_{HEPZCO{O}^{-}}+\Delta n_{HHEPZCOO}}{\Delta n_{C{O}_2}^{\ast }},(21)$

$\Delta {\xi }_7=-\frac{\Delta n_{HHEPZCOO}}{\Delta n_{C{O}_2}^{\ast }},(22)$

where $\Delta n_i$ represents the changes of the number of moles of component $i$ and $\Delta n_{C{O}_2}^{\ast }$ represents the total moles of CO₂ that were absorbed to improve the content of CO₂ from one loading to a higher one. The Van’t Hoff equation can be adopted to calculate the heat contributions $\Delta H_{r, j}$ from each of the seven reactions, given as follows:

$\Delta H_{r, j}=R{T}^2{\left(\frac{\partial \ln K_{xj}}{\partial T}\right)}_p=R(-C_j+D_{j}T+B_j{T}^2),(23)$

where the equation parameters of $\ln K_{xj}$ are listed in Table 6, and the equation for $\Delta H_{dissolution}$ is

$\Delta H_{dissolution}=R(8477.71-21.9574T+0.00578075T^2).(24)$

As this study did not take into account the species interaction, only the heat of physical dissolution and the chemical reaction heat were considered, but the excess enthalpy was not. $\Delta H_{r, overall}$ is calculated for analyzing the contribution of reactions to the heat of absorption, and the values of $\Delta H_{r, j}$ at a temperature of 313.15 K are 52.53, 3.63, 10.58, 27.49, 21.71, −47.20, and 48.9$0 kJ/mol$, and $j$equals 1–7. The physical heat of CO₂ dissolution $\Delta H_{dissolution}$ is −18 $kJ/mol$at a temperature of 313.15 K. The total differential chemical reaction heat as well as the heat released by the seven reactions and the heat from CO₂ dissolution in 30 wt% HEPZ solution are shown in Figure 8. This part aims to carry out a discussion on the contribution of reactions to the total absorption heat, and Eq 17 only calculates the heat of physical dissolution, the chemical reaction heat, and the excess enthalpy, so the results are lower than the actual heat of absorption.

FIGURE 8

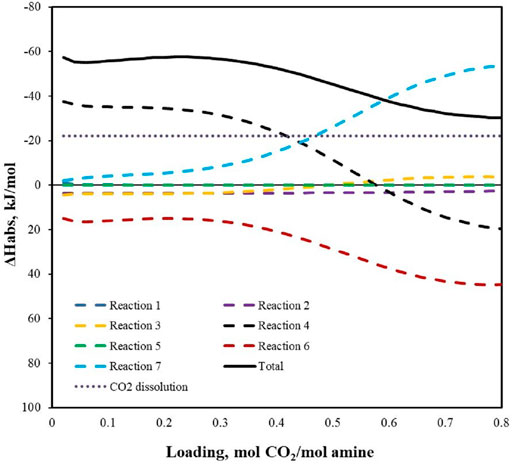
FIGURE 8. Differential heat of reaction in 30 wt% HEPZ at 313.15 K (—: total differential chemical reaction heat; ┅: heat of each reaction).

Conclusion

In this study, CO₂ solubility was measured using the stainless-steel reactor for HEPZ aqueous solutions with three concentrations (5 wt%, 15 wt%, and 30 wt%) and four temperatures. Then, the VLE data for HEPZ/H₂O were acquired using a gas–liquid double-circulation kettle at negative pressures (30 pKa, 40 pKa, 55 pKa, 70 pKa, and 85 pKa) and atmosphere pressure, within various mole fractions. The e-NRTL model as well as the sequential regression method were adopted to successfully develop a rigorous thermodynamic model for HEPZ/CO₂/H₂O in Aspen Plus. The missing physical parameters for HEPZ and the amine ions and the physical properties of interactions of NRTL as well as ENRTL were regressed from data acquired from this study and the literature. Based on the data from this study and the corresponding literature, the missing physical parameters of HEPZ, the standard state characteristics of amine ions, the interaction parameters of the non-random two-liquid model (NRTL), and ENRTL were regressed, including vapor pressure as well as heat capacity $C_p$ of HEPZ, vapor–liquid equilibrium (VLE), heat capacity of mixture aqueous solutions, pKa data for HEPZ/H₂O, and CO₂ solubility data for HEPZ/CO₂/H₂O. All calculated results agreed with the data obtained from experiments andCarbon capture and storage (CCS), as the process of capturing CO the literature.

The composition, cyclic capacity, and heat of absorption of the HEPZ aqueous system were predicted and analyzed by the model. Then, the heat of absorption reduced dramatically when the loading became higher. Meanwhile, the concentration of HEPZ indicated a negative impact on the absorption heat within the whole studied loading range, while the temperature showed a positive impact on the absorption heat, and the higher the temperature, the more obvious the tendency of the heat of absorption to decrease due to the load increase. The cyclic capacity increases as the concentration of HEPZ increases. Besides, the activity coefficient of all the species became larger when the concentration went higher. At a low loading, the main productors are $HEPZ{H}^{+}$ and $HEPZCO{O}^{-}$. At a greater loading, $HEPZCO{O}^{-}$ is converted to $HHEPZCOO$. As the concentration of HEPZ increases, the $HC{O}_3^{-}$ produced by the reaction gradually decreases.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

SL measured CO₂ solubility and wrote the whole manuscript. Jianyou measured vapor–liquid equilibria for HEPZ + water. JC revised the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors JC.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge the financial support from the National Natural Science Foundation of China (No. 21978145) and the National Science and Technology Support Program of China (No. 2015BAC04B01).

Supplementary Material

The Supplementary Material for this article can be found online at https://www.frontiersin.org/articles/10.3389/fenrg.2021.785039/full#supplementary-material

References

Anderson, S. (2016). Authentic Learning. Libr. J. 141 (9), 28–32. doi:10.4135/9781483392868.n5

CrossRef Full Text | Google Scholar

Aronu, U. E., Hoff, K. A., and Svendsen, H. F. (2011). CO2 Capture Solvent Selection by Combined Absorption-Desorption Analysis. Chem. Eng. Res. Des. 89 (8a), 1197–1203. doi:10.1016/j.cherd.2011.01.007

CrossRef Full Text | Google Scholar

Chen, C.-C., Britt, H. I., Boston, J. F., and Evans, L. B. (1979). Extension and Application of the Pitzer Equation for Vapor-Liquid Equilibrium of Aqueous Electrolyte Systems with Molecular Solutes. Aiche J. 25 (5), 820–831. doi:10.1002/aic.690250510

CrossRef Full Text | Google Scholar

Chen, X., and Rochelle, G. T. (2011). Aqueous Piperazine Derivatives for CO2 Capture: Accurate Screening by a Wetted wall Column. Chem. Eng. Res. Des. 89 (9), 1693–1710. doi:10.1016/j.cherd.2011.04.002

CrossRef Full Text | Google Scholar

Choi, J. H., Kim, Y. E., Nam, S. C., Yun, S. H., Yoon, Y. I., and Lee, J.-H. (2016). CO2 Absorption Characteristics of a Piperazine Derivative with Primary, Secondary, and Tertiary Amino Groups. Korean J. Chem. Eng. 33 (11), 3222–3230. doi:10.1007/s11814-016-0180-9

CrossRef Full Text | Google Scholar

Choi, W.-J., Seo, J.-B., Jang, S.-Y., Jung, J.-H., and Oh, K.-J. (2009). Removal Characteristics of CO2 Using Aqueous MEA/AMP Solutions in the Absorption and Regeneration Process. J. Environ. Sci. 21 (7), 907–913. doi:10.1016/S1001-0742(08)62360-8

CrossRef Full Text | Google Scholar

Dash, S. K., Samanta, A., Nath Samanta, A., and Bandyopadhyay, S. S. (2011). Absorption of Carbon Dioxide in Piperazine Activated Concentrated Aqueous 2-Amino-2-Methyl-1-Propanol Solvent. Chem. Eng. Sci. 66 (14), 3223–3233. doi:10.1016/j.ces.2011.02.028

CrossRef Full Text | Google Scholar

Dong, L., Chen, J., and Gao, G. (2010). Solubility of Carbon Dioxide in Aqueous Solutions of 3-Amino-1-Propanol. J. Chem. Eng. Data 55 (2), 1030–1034. doi:10.1021/je900492a

CrossRef Full Text | Google Scholar

Dubois, L., and Thomas, D. (2012). Screening of Aqueous Amine-Based Solvents for Postcombustion CO2 Capture by Chemical Absorption. Chem. Eng. Technol. 35 (3), 513–524. doi:10.1002/ceat.201100523

CrossRef Full Text | Google Scholar

Feron, P. H. M., and Hendriks, C. A. (2005). CO2Capture Process Principles and Costs. Oil Gas Sci. Technol. - Rev. IFP 60 (3), 451–459. doi:10.2516/ogst:2005027

CrossRef Full Text | Google Scholar

Frailie, P., Plaza, J., Van Wagener, D., and Rochelle, G. T. (2011). Modeling Piperazine Thermodynamics. Energ. Proced. 4, 35–42. doi:10.1016/j.egypro.2011.01.020

CrossRef Full Text | Google Scholar

Hamborg, E. S., and Versteeg, G. F. (2009). Dissociation Constants and Thermodynamic Properties of Alkanolamines. Energ. Proced. 1 (11), 1213–1218. doi:10.1016/j.egypro.2009.01.159

CrossRef Full Text | Google Scholar

Hessen, E. T., Haug-Warberg, T., and Svendsen, H. F. (2010). The Refined E-NRTL Model Applied to CO2-H2O-alkanolamine Systems. Chem. Eng. Sci. 65 (11), 3638–3648. doi:10.1016/j.ces.2010.03.010

CrossRef Full Text | Google Scholar

Kurihara, K., Nakamichi, M., and Kojima, K. (1993). Isobaric Vapor-Liquid Equilibria for Methanol + Ethanol + Water and the Three Constituent Binary Systems. J. Chem. Eng. Data 38 (3), 446–449. doi:10.1021/je00011a031

CrossRef Full Text | Google Scholar

Lee, J. I., Otto, F. D., and Mather, A. E. (1976). Equilibrium between Carbon-Dioxide and Aqueous Monoethanolamine Solutions. J. Appl. Chem. Biotechnol. 26 (10), 541–549.

Google Scholar

Li, H., Frailie, P. T., Rochelle, G. T., and Chen, J. (2014a). Thermodynamic Modeling of piperazine/2-aminomethylpropanol/CO2/water. Chem. Eng. Sci. 117, 331–341. doi:10.1016/j.ces.2014.06.026

CrossRef Full Text | Google Scholar

Li, H., Moullec, Y. L., Lu, J., Chen, J., Marcos, J. C. V., and Chen, G. (2014b). Solubility and Energy Analysis for CO 2 Absorption in Piperazine Derivatives and Their Mixtures. Int. J. Greenhouse Gas Control. 31, 25–32. doi:10.1016/j.ijggc.2014.09.012

CrossRef Full Text | Google Scholar

Li, L., Li, H., Namjoshi, O., Du, Y., and Rochelle, G. T. (2013). Absorption Rates and CO2 Solubility in New Piperazine Blends. Energ. Proced. 37 (37), 370–385. doi:10.1016/j.egypro.2013.05.122

CrossRef Full Text | Google Scholar

Liang, Z., Rongwong, W., Liu, H., Fu, K., Gao, H., Cao, F., et al. (2015). Recent Progress and New Developments in post-combustion Carbon-Capture Technology with Amine Based Solvents. Int. J. Greenhouse Gas Control. 40, 26–54. doi:10.1016/j.ijggc.2015.06.017

CrossRef Full Text | Google Scholar

Mandal, B. P., Guha, M., Biswas, A. K., and Bandyopadhyay, S. S. (2001). Removal of Carbon Dioxide by Absorption in Mixed Amines: Modelling of Absorption in Aqueous MDEA/MEA and AMP/MEA Solutions. Chem. Eng. Sci. 56 (21-22), 6217–6224. doi:10.1016/S0009-2509(01)00279-2

CrossRef Full Text | Google Scholar

Peng, D.-Y., and Robinson, D. B. (1976). A New Two-Constant Equation of State. Ind. Eng. Chem. Fund. 15 (1), 59–64. doi:10.1021/i160057a011

CrossRef Full Text | Google Scholar

Plasynski, S. I., Litynski, J. T., McIlvried, H. G., and Srivastava, R. D. (2009). Progress and New Developments in Carbon Capture and Storage. Crit. Rev. Plant Sci. 28 (3), 123–138. doi:10.1080/07352680902776440

CrossRef Full Text | Google Scholar

Poozesh, S., Rayer, A. V., and Henni, A. (2015). Molar Excess Enthalpy (HmE) for Systems of Aqueous Piperazine Derivatives. J. Chem. Thermodynamics 90, 242–250. doi:10.1016/j.jct.2015.06.006

CrossRef Full Text | Google Scholar

Poozesh, S., Rayer, A. V., and Henni, A. (2013). Molar Heat Capacity (Cp) of Aqueous Cyclic Amine Solutions from (298.15 to 353.15) K. J. Chem. Eng. Data 58 (7), 1989–2000. doi:10.1021/je400178k

CrossRef Full Text | Google Scholar

Puxty, G., and Rowland, R. (2011). Modeling CO2 Mass Transfer in Amine Mixtures: PZ-AMP and PZ-MDEA. Environ. Sci. Technol. 45 (6), 2398–2405. doi:10.1021/es1022784

PubMed Abstract | CrossRef Full Text | Google Scholar

Rinker, E. B., Ashour, S. S., and Sandall, O. C. (2000). Absorption of Carbon Dioxide into Aqueous Blends of Diethanolamine and Methyldiethanolamine. Ind. Eng. Chem. Res. 39 (11), 4346–4356. doi:10.1021/ie990850r

CrossRef Full Text | Google Scholar

Rochelle, G. T. (2009). Amine Scrubbing for CO 2 Capture. Science 325 (5948), 1652–1654. doi:10.1126/science.1176731

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakwattanapong, R., Aroonwilas, A., and Veawab, A. (2009). Reaction Rate of CO2 in Aqueous MEA-AMP Solution: Experiment and Modeling. Energ. Proced. 1 (11), 217–224. doi:10.1016/j.egypro.2009.01.031

CrossRef Full Text | Google Scholar

Tagiuri, A. M. (2019). Studies of Solubility of CO2 in Ionic Liquids, Kinetics, and Heat of Reactions of CO2 in Promising Cyclic Amines. PhD thesis. University of Regina. Available at: https://ourspace.uregina.ca/handle/10294/8969.

Google Scholar

Yuan, Y., Sherman, B., and Rochelle, G. T. (2017). Effects of Viscosity on CO2 Absorption in Aqueous Piperazine/2-Methylpiperazine. Energ. Proced. 114, 2103–2120. doi:10.1016/j.egypro.2017.03.1345

CrossRef Full Text | Google Scholar

Zhang, Y., and Chen, C.-C. (2011). Thermodynamic Modeling for CO2 Absorption in Aqueous MDEA Solution with Electrolyte NRTL Model. Ind. Eng. Chem. Res. 50 (1), 163–175. doi:10.1021/ie1006855

CrossRef Full Text | Google Scholar