Short-Lived Interfaces in Energy Materials

1 Introduction

Energy storage is pivotal for a swift implementation of a renewable energy economy, but still awaits a technically and economically feasible large scale solution. Primary physical parameter used to assess the suitability of a specific technology is the total amount of stored energy, e.g., energy storage density. Secondary parameter is the kinetics, i.e., the minimum time to extract the energy, often expressed by the power density. The latter is defined by the specific physical and chemical processes. In this review, we discuss the corresponding parameters along three archetypal examples of different energy storage technologies highlighted in Figure 1.

FIGURE 1

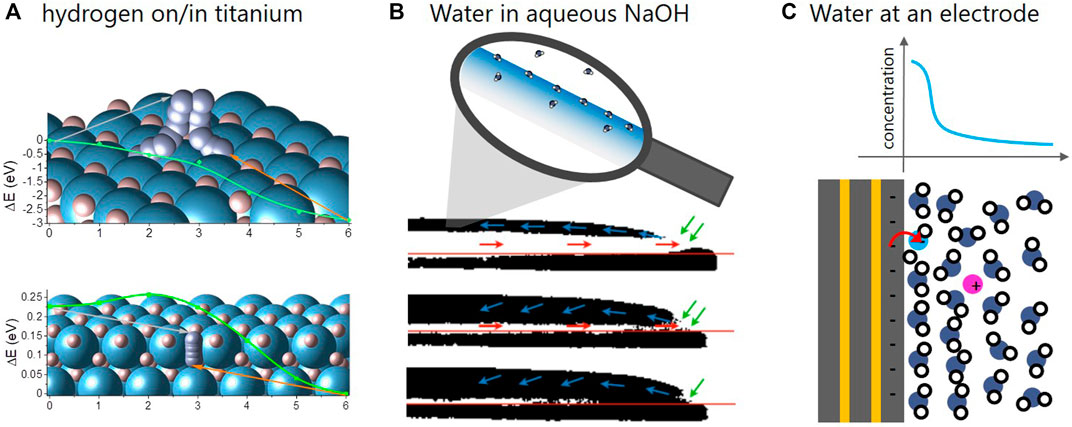
FIGURE 1. Schemes of the archetypal energy storage/conversion systems, in which short-lived interfaces play an important role. (A): Hydrogen dissociation/recombination (top) and surface-subsurface hopping (bottom) on Ti [adapted from Billeter et al. (2021)]. The y-axis is the energy of hydrogen molecule and atom, respectively, while the x-axis is the reaction coordinate describing the pathway of the molecule and atom. (B): Water absorption into aqueous NaOH visualized by neutron imaging [adapted from Fumey et al. (2022)]. Highly concentrated aqueous NaOH absorbs water vapor. The process was made visible by neutron imaging showing the absorbed H₂O in the original NaOD-D₂O droplet in black and white, respectively. (C): Scheme of electrode-electrolyte interface during water splitting [adapted from Sambalova et al. (2021)]. A specific analysis method based on magneto-optics was developed to probe the water/OH⁻ gradient in the vicinity of the electrode.

Although fundamentally different, the chosen systems are similar in that all processes are governed by molecular reactions taking place at an interface. In metal hydrides, stored hydrogen is split/recombined at the surface of the metal hydrides before it diffuses through the solid (Borgschulte et al., 2006). The power density of heat storage is determined by the water uptake kinetics in liquid sorbents, which is limited both by diffusion as well as surface phenomena (Fumey et al., 2020). And electrochemical conversion relies on the efficiency of the electrocatalytic reactions at the electrode-electrolyte interface. Needless to say that the improvement of these interface reactions gained great attention by scientists, resulting in huge effort dedicated to research and development of new catalysts. There are limitations of this approach, though: referring to catalysts for electrochemical CO₂ reduction, Chan, 2020 provokes with the following statement: “To date, I am not aware of a new catalyst with intrinsic activity towards C₂ products that unequivocally exceeds that of Cu foil.” This statement should be discussed in the light of the great achievements, which have recently been made in this field: the father of the electrochemical CO₂ conversion Hori et al., 1987 reports current densities of around 5 mA cm⁻² with a Faraday efficiency of around 20% percent towards C₂H₄ using a copper foil. Recently, current densities as high as 750 mA cm⁻² with a Faraday efficiency above 60% using polycrystalline copper surfaces were achieved by Dinh et al., 2018, i.e., with basically the same electrocatalyst as used by Hori et al., 1987. The secret to this great success lies in a sophisticated design of the electrochemical interface, i.e., the controlled transport of reactants and products from and to the active Cu sites (Dinh et al., 2018; Nesbitt et al., 2020); while the phenomena on the molecular level at the interface play a minor role only.

The question arises, whether this approach is similarly successful in other areas of energy storage, and what is its limitation. In a simplified way, one may argue that the ultimate limit is the fundamental turnover frequency (TOF) of the catalyst, namely of its active sites (“intrinsic catalytic activity”). However, there are systems, in which the TOF depends on the applied conditions (see, e.g., Borgschulte et al., 2013). This, in turn, can be used to tailor the interface properties. Alternatively, one may circumvent a rate-limiting interface to improve the overall kinetics. In any case, an improvement relies on the knowledge of interface structure on the microscopic as well as macroscopic dimension. Despite the clarity of the goal, analysis of such interfaces is challenging, in particular, if they are impermanent. In this review, we will summarize the state-of-the-art of three archetypal energy storage/conversion systems with respect to the importance of the underlying active interface, conceptualize the chosen approaches, address the analytical challenges that need to be overcome, and give an outlook for future research and development.

2 Interfaces in Energy Conversion and Storage

A renewable energy scenario must consider the renewable primary energy input as well as the demand and consumption pathways. The latter are mechanical work, electricity, and heat. The sun delivers light and heat, and only indirectly mechanical work (wind, precipitation, waves). This means that most of the incoming energy must be converted to the desired forms of energy. Although heat appears to be readily available, there is a mismatch between the availability and the demand peaks. This seasonal energy variation is a challenge in general, in particular at higher latitudes of earth’s hemispheres (Mulder, 2014). Energy storage is thus inevitable. The debate about which forms of energy storage are most suitable is ongoing. A description of them is beyond the scope of this review (see, e.g., Züttel et al., 2010). Great potential is seen in converting solar light into hydrogen either directly (photo-catalytic or photo-electrochemical energy conversion (Reece et al., 2011; Berardi et al., 2014; Dogutan and Nocera, 2019), or indirectly via photovoltaics and water electrolysis (Züttel et al., 2010; Jacobsson, 2018). Water electrolysis in alkaline electrolyzers is an established technology with very high conversion efficiencies without using precious metals (Ni, Fe; see, e.g., Zeng and Zhang, 2010; Phillips and Dunnill, 2016). We discuss the ingenious design of the electrochemical cell (“zero-gap geometry”) in subsection 2.3. The underlying physical principle is based on the approach “improving the dynamic interface”. This approach has been shown to be equally successful in heat storage in aqueous sodium hydroxide solution (Fumey et al., 2020; Fumey et al., 2022), and is discussed in detail in subsection 2.2. Hydrogen as an energy carrier requires safe and efficient storage strategy, which is still an obstacle for its widespread introduction (Andersson and Grönkvist, 2019). Hydrogen storage in metal hydrides is a promising solution to this problem (e.g., Schlapbach and Züttel, 2001; Yang et al., 2010; Modi and Aguey-Zinsou, 2021). From a didactic point of view, it is the simplest model system to demonstrate the importance of “short-lived interfaces” for kinetics and its quantitative description. We thus start with this system.

2.1 Hydrogen Sorption in Metal Hydrides

The qualitative picture of hydrogen sorption in (transition) metal hydrides is relatively simple and thus allows an in-depth modeling of the kinetics. During hydrogen absorption in metal hydrides there are two main steps involved (Schlapbach, 1992; Fukai, 2005): the dissociation of the hydrogen molecule and the transport of the chemisorbed hydrogen towards the subsurface and adjacent diffusion in the bulk (see Figure 2).

FIGURE 2

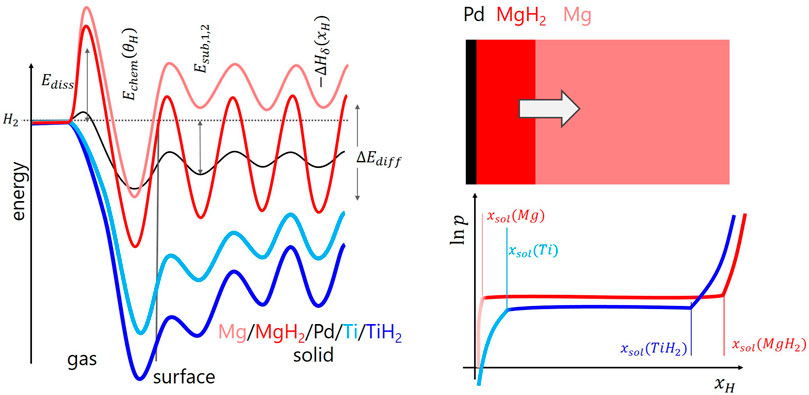
FIGURE 2. Left graph: characteristic solid-gas interaction steps pictured by the dependence of the potential energy on the distance z from the surface for Mg, MgH₂, Pd, Ti, and TiH₂ [adapted from Refs. Fukai (2005); Borgschulte et al. (2006); Billeter et al. (2021)]. Top right shows a simplified model of the hydrogenation of a Mg thin film capped with a catalyst. Bottom right is the sketch of the pressure-composition isotherms of Mg and Ti. See text for details.

Since physisorption of gas molecules on surfaces requires no activation energy and the impingement rate of H₂ onto the surface is high, the gas phase can be assumed to be in equilibrium with the physisorbed state. Furthermore, the heat of formation ΔH_phys is very small and the molecule remains in its entity. This step is thus neglected in most cases. For chemisorption, the hydrogen molecule has to dissociate (see, e.g., for Ti Figure 1A), and for that it has to overcome a dissociation barrier of 0 ≤ E_diss < 2 eV which, in most cases, e.g. in case of Mg, is high (Figure 2), and only few materials such as Ti and Pd have negligible E_diss. The hydrogen atoms are then in practically all relevant cases strongly chemisorbed (Fukai, 2005; Borgschulte et al., 2006; Billeter et al., 2021). Figure 2 emphasizes the importance of “catalysis” in hydrogen storage and hydrogen permeable membranes: the static surface barrier E_diss is the main barrier for hydrogen uptake in promising materials such as Mg, and reducing it by adding a “catalyst” such as Pd or Ti without a significant E_diss on the surface of the storage material is straightforward.

Hydrogen storage in metal hydrides relies on hydrogen sorption in the bulk of the metal/alloy. The prerequisite for hydrogen storage is the hopping of hydrogen chemisorbed on the surface into a subsurface sites (Figure 1A), and adjacent layers. After two to three monolayers, the potential-energy surface is bulk-like (Figure 2), i.e., hoping between layers corresponds to bulk diffusion in the metal/alloy from minimum to minimum in the potential-energy surface. This corresponds to the heat of solution (−ΔH_sol) governed by the activation energy of diffusion ΔE_diff. However, relevant amount of hydrogen is absorbed in the hydride phase only (e.g., in TiH₂, MgH₂). The physics is usually discussed along so-called pressure composition isotherms, sketched in Figure 2. At low pressures, hydrogen is dissolved up to a maximum concentration x_sol(M). At this concentration, it is energetically beneficial to form the hydride phase, which grows on expense of the solubility phase, until reaching again a single phase at x_sol(MH₂). It is worth noting here that hydrogen uptake is thus inherently linked to the formation and annihilation of (short-lived) interfaces.

The details of these interfaces define growth of the phases and thus eventually hydrogen uptake kinetics (Førde et al., 2007; Lai et al., 2019), and are beyond the scope of this work. We refer to Fukai (2005), Schlapbach (1992) and others. Some key features may be listed: changes into a new phase are associated with modifications of the surface potential energy. For Ti going from the α-phase to the δ-phase, the changes are moderate as the heat of solution (ΔH_sol) is similarly negative as is the heat of hydride formation (compare light and dark blue curves in Figure 2). The activation energies of diffusion do not differ markedly either (Billeter et al., 2021). This leads to relatively high boundary solubility both for the hydrogen as well as vacancy solubility in the solid solution and hydride phase, respectively. Hydrogen uptake kinetics is thus mainly determined by transport phenomena, i.e., diffusion. The situation is different in the hydrogen - magnesium system. The heat of solution in Mg is positive and thus x_sol is extremely small. This leads to very marked interfaces. Furthermore, diffusion of hydrogen requires the availability of empty sites. They exist in TiH₂, as also the hydride vacancy solubility is high, but hardly in MgH₂ (Töpler et al., 1982; Uchida et al., 2015). This results in the formation of a blocking layer on the surface of a Mg layer (grain) upon hydrogenation (Zhdanov et al., 1993; see Figure 2).

Eventually, the motivation for elucidating the mechanism of hydrogen sorption in metal hydrides lies in improvement of the kinetics by development of a fast hydrogen storage material (Lai et al., 2019).¹ The line of thought is well explained on the example of MgH₂. Earth-abundant and cheap, MgH₂ has been recognized as a promising material, and although the equilibrium thermodynamics of this material are suboptimal (Zhou et al., 2021a), much research has been performed on its kinetics (see, e.g., Sun et al., 2020). The surface of Mg and MgH₂ grains as smallest unit in a technical hydrogen storage material is usually covered by oxides, drastically reducing the dissociation kinetics (see, e.g., Friedrichs et al., 2006; Borgschulte et al., 2008; Lai et al., 2019). Metal particles with low dissociation barrier and fast hydrogen diffusion such as Pd (Zhdanov et al., 1993) and TiH₂ (Zhang et al., 2019; Zhou et al., 2021b) are attached to the metal hydride to lower the static interface. Many other materials than Pd and Ti have been found to be active catalyst (Sun et al., 2020). However, removing the rate-limiting step at the surface, means that the rate limiting step occurs at the inner layers. Zhdanov et al., 1993 found that the hydride blocking layer slows down the hydrogenation kinetics markedly. The velocity of this moving (dynamic) interface depends on the diffusion of hydrogen in the hydride layer, which is much slower than in α − Mg (Töpler et al., 1982; Uchida et al., 2015).

One solution to reducing the effect of the blocking layer is to improve the hydrogen diffusion in it by additives (Hao and Sholl, 2008; Koteski et al., 2015). However, various trials were not very effective. Using thermodynamic conditions, under which the blocking layer is not formed (Zhdanov et al., 1993; Uchida et al., 2015), is possible, but unpractical. Alternatively, the bulk material is broken up into small grains by, e.g., ball milling (Zaluski et al., 1997; Lai et al., 2019). If the grains are below a critical size, the blocking layer cannot be formed. Additives added during ball-milling prevent grain growth during hydrogen cycling (Aguey-Zinsou et al., 2006), and facilitate hydrogen dissociation and hydrogen transport along the grain boundaries (Barkhordarian et al., 2006; Lai et al., 2019).

Using alloys instead of pure metals is an established concept to tailor thermodynamics for efficient hydrogen storage (Fukai, 2005; Schlapbach, 1992). Alternatively, composites can be used to optimize the heat of reaction (Reilly and Wiswall, 1967; Bösenberg et al., 2007). In general, various so-called complex metal hydride systems are composites at least in one hydrogenation state (Frankcombe, 2012; Orimo et al., 2007; Ikeda et al., 2021), complicating the description of sorption kinetics and underlying morphology changes.

2.2 Water Absorption Into Aqueous NaOH

The supply of the heat demand of buildings located at high latitudes with renewable energy is challenging, as for about quarter of the year the energy must come from stored energy (Pinel et al., 2011; Shah et al., 2018). Liquid sorption heat storage is a promising technology, providing loss-free storage over time, high energy density, and relatively low cost (Hadorn, 2008). The concept is based on a sorption heat pump equipped with liquid sorbent and sorbate storage. Typical hygroscopic fluids studied are aqueous solutions of lithium bromide, lithium chloride, calcium chloride, and sodium hydroxide (Zhang et al., 2014; Weber and Dorer, 2008), with sodium hydroxide showing superior potential with respect to high energy density and low material price (Fumey et al., 2017). Recently, functional storage systems became available. These reach performance values near to the anticipated and required temperature swing, power- and energy density (Fumey et al., 2022). The reason for this is not of technical nature, but due to the detrimental relation between power- and energy density. It is special for this kind of energy storage, and thus worth to illuminate in greater detail.

The water vapor pressure p of the aqueous sodium hydroxide solution is concentration and temperature-dependent. An increase in the water vapor pressure or a decrease in the solution temperature leads to absorption of water, thus increasing water concentration c at the gas-liquid interface. A decrease in the water vapor pressure triggers the reversed process. The resulting chemical current density of water molecules j (molar flux $\dot{M}$ per area A) is linked to the resulting heat flow $\dot{q}$ via the heat of water absorption ΔH (Fumey et al., 2020):

$\dot{M}=A\cdot j=\dot{q}\cdot {\left(\mathrm{\Delta }H\right)}^{-1}(1)$

If this process takes place in a mass and heat exchanger (Figure 3), the heat flux will not lead to a significant increase of the temperature (assuming that the heat removal is sufficient and that the applied water vapor pressure is a step-like function, i.e., constant after initial increase/decrease). For heat release, the vapor pressure is increased (Figure 3A, C). The solution with low water concentration is water enriched from c_low to c_high while passing the mass- and heat exchanger. The maximum water concentration c_high depends on T_l and on the kinetics: Δc^h > Δc^s, where the indices h, and s stand for high and slow kinetics. However, the concentration difference defines the total storage density, which now depends on the kinetics. During heat absorption (i.e., high T = T_u, Figure 3B, D), the process is reversed, but exhibits the same detrimental relation between kinetics and storage density. For slow kinetics, we start already at a lower maximum concentration $c_{high}^s$ giving a smaller maximum temperature swing ΔT = T_u − T_l. This is in contrast to, e.g., energy storage in batteries. Here, the voltage (corresponds to the temperature swing in thermal energy storage) may be reduced at high current densities/slow kinetics, but the terminal voltage is generally not affected.

FIGURE 3

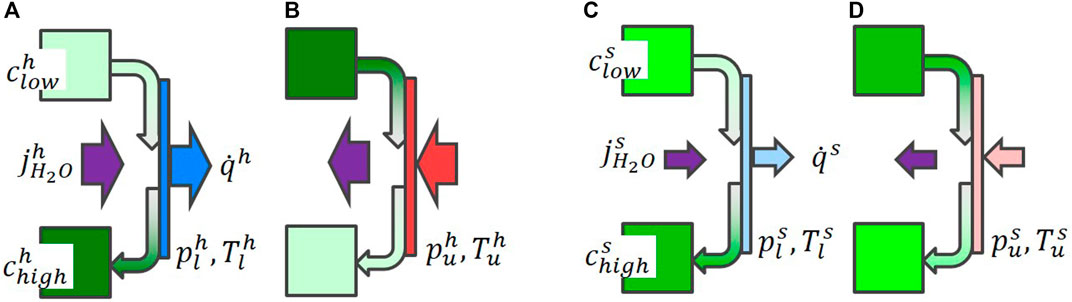
FIGURE 3. Scheme illustrating the heat storage in aqueous NaOH. Two reservoirs with low and high water concentrations c_low, c_high are connected via a heat and mass exchanger. For heat release [schemes (A), C)], water vapor is absorbed $(j_{H_{2}O})$ at the water vapor pressure p and temperature T, generating heat $(\dot{q})$ and increasing the water concentration; for heat uptake [schemes (B, D)], water desorbs and thereby cools the liquid. The indices h and s denote fast and slow kinetics. The final concentrations and thus the total amount of heat stored/released depends on the kinetics.

Because of the importance of kinetics in thermal energy storage, Fumey et al., 2020 studied the gas-liquid interface under operation conditions. For this, a confocal Raman setup was designed allowing the temporally and spatially resolved measurement of the water concentration upon absorption/desorption. The measurement brought to the fore that the measured water gradient is well fitted to solutions of 2nd Ficks law using the literature diffusion coefficient of water in aqueous NaOH. This means that diffusion is rate-limiting. From a scientific point of view, this is a satisfying result. However, it is the most difficult outcome from an applied perspective: the intrinsic diffusion coefficient of H₂O in aqueous NaOH cannot be easily altered. Furthermore, the diffusion gradient extends over 100–200 μm. The thickness of the floating aqueous NaOH is much thicker, but cannot be thinned markedly due to the low viscosity of aqueous NaOH (Smith, 1956; Kim et al., 1996; Li et al., 2016). An improvement of the performance of a mass and heat exchanger by lowering the diffusion barrier seemed to be unpromising.

In addition to mass transport on a microscopic scale, mass transport occurs on a macroscopic scale via convection (Fujita, 1993; Li et al., 2016). Neutron imaging gave indication that this convection can be induced by buoyancy (Fumey et al., 2022, see Figure 1B). With appropriate design, the convection flux provides continuously fresh NaOH solution to the gas-liquid interface. Based on these observations, Fumey et al. (2022) constructed a mass and heat exchanger with an area specific power of 1.28 kWm⁻² with an extrapolated thermal energy storage density of 243 kWh m⁻³, near to the theoretical limit of 360 kWhm⁻³. This solution may be generalized by the approach “separation of interface and mass transport”: at the interface, reaction is fast; to guarantee fast uptake into the bulk, the material at the interface is transported by convection (Figure 1B).

An open research question is, whether the Marangoni-effect plays a role in the increase of the convection [for basics of the Marangoni effect we refer to Leal (2007)]. However, the effect is based on a gradient of the surface tension, e.g., generated by a point source (Roché et al., 2014). This gradient may exist in heat and mass exchanger under certain conditions. However, under steady state conditions, the influence of the surface gradient can be considered to be small.

2.3 Short-Lived Interfaces in Electrochemical Energy Conversion

Alkaline water electrolysis is an established technology, which has been optimized over 100 years (see, e.g., Zeng and Zhang, 2010; Phillips and Dunnill, 2016). Accordingly, there is not much room for further optimization. However, various technical challenges have been successfully overcome over the course of development. These challenges are common in electrochemical conversion associated with the evolution of gases. Having a closer look may thus help optimizing other electrochemical reactions, such as CO₂ reduction.

In liquid alkaline electrolysis, the desired high current densities translate into a relatively large pH gradient between the electrodes. At the oxygen evolution electrode

$4O{H}^{-}\to O_2+2H_{2}O+4e^{-}(2)$

OH⁻ is consumed and water produced, while water is consumed and OH⁻ produced at the hydrogen evolution electrode:

$4H_{2}O+4e^{-}\to 2H_2+4O{H}^{-}(3)$

This gradient adds to the overpotentials from electro-catalysis at the electrodes. To lower it, the distance between the electrode (“gap”) d should be as small as possible (Figure 4), because the electrolyte resistance R₀ increases with it:

$R_0={\rho }_0\left(c_{OH}\right)\frac{d}{A}(4)$

A is the electrode surface; ρ₀(c_OH) is the resistivity of the electrolyte, which depends on its pH (concentration of OH⁻). However, in addition to the ion transport, the formed hydrogen and oxygen bubbles have to be removed as quickly as possible, because they block the ion transport. Tobias (1959) proposed Bruggemann’s equation

$\rho /{\rho }_0={\left(1-v\right)}^{-3/2}(5)$

to correlate the bubble induced resistivity ρ/ρ₀ to gas void fraction v in electrolytic cells. The gas void fraction is closely related to the number and size of the bubbles, which depend on a number of parameters such as pressure, temperature, and surface tension of electrolyte and electrode. In practice, the distribution is determined experimentally. The important fact is that the void- (simplified bubble-) concentration decreases, if the volume, i.e., the gap between the electrode increases. Figure 4 shows some empirical results of the bubble induced resistivity R/R₀, with R₀ the resistance of the electrolyte without bubbles (Hine and Murakami, 1980). The resistance increases with applied current, as it is the origin of the produced bubbles; however, the main effect is the gap: the resistivity increases extremely for gaps smaller than 0.5 cm [Figure 4, from Hine and Murakami (1980)]. The behavior is reciprocal to the behavior of electrolyte resistance R₀ with distance (Eq. 4), and apparently only a bad compromise is possible.

FIGURE 4

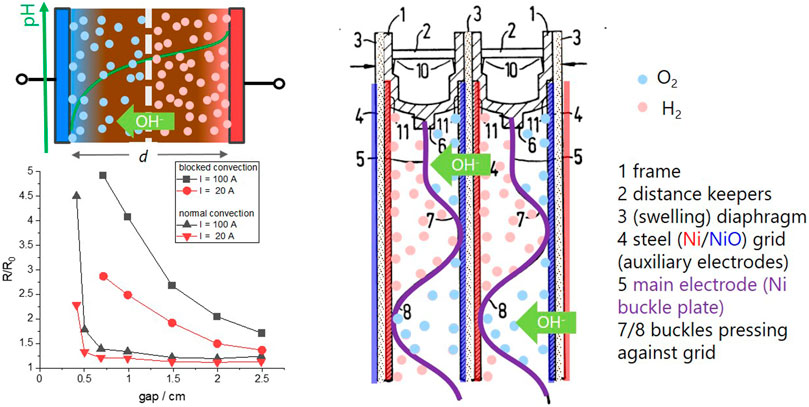
FIGURE 4. Left: simple sketch of an electrolyzer with bubbles formed between the electrodes (top). The bottom graph shows the normalized bubble resistivity of a model electrolyzer with normal convection and blocked convection as a function of the electrode gap (from Hine and Murakami (1980)). Right: technical drawing of the bipolar electrodes in an alkaline zero-gap electrolyzer (adapted from Zdansky (1977)).

To solve this challenge, Zdansky invented the so-called “zero-gap” geometry (Zdansky, 1959): he reduced the gap to basically zero, i.e., to the minimum distance defined by the obligatory porous diaphragm, which prevents a mixing of hydrogen and oxygen gas. As the electrode meshes (or grids) touch the diaphragm, the bubbles cannot be formed between the electrodes, and thus do not block the ion current in the electrolyte. Instead, they are formed at the other side of the meshes, where there is enough space to purge the bubbles away by the flow of the electrolyte (see the bipolar configuration of a zero-gap alkaline electrolyzer in Figure 4). At the same time, the electrolyte resistance R₀ is minimized given a diaphragm with proper porosity/tortuosity is used (Ju et al., 2018).

This 60 year old design has become the standard in alkaline (liquid) electrolyzers with only minor further improvements mainly addressing materials properties of the diaphragm and electrodes (Zeng and Zhang, 2010; Phillips and Dunnill, 2016; Ju et al., 2018). Some new concepts are the so-called hybrid electrolyzers with a gas diffusion electrode as anode and a conventional immersed porous cathode (Koj et al., 2019).

Apart from the bubble resistivity, Zdansky (1959) reports an improvement of the diffusion layer properties in zero-gap electrolyzers. On the other hand, a recent publication challenges this statement arguing that the electrode area facing the diaphragm is not active, a depletion of OH⁻ ions in the vicinity of the electrodes occurs, and the supersaturation of the electrodes increases the equilibrium potential at elevated current densities (Haverkort and Rajaei, 2021).

Inherent to electrochemistry is the dependence of the reaction on external parameters such as applied potential. The potential determines the electron transfer reaction, and with it the species and number of adsorbed molecules. If ions, i.e., charged species, are involved, the corresponding electric field will determine the gradient built up (Figure 1C, see discussion above). Can the species be influenced by other external fields as well? Recently, a markedly increased electrochemical efficiency of the oxygen evolution reaction in water splitting was achieved by applying a uniform magnetic field to the oxygen evolution electrode Garcés-Pineda et al., 2019. Magnetic enhancement was observed also for the hydrogen evolution reaction at different electrodes Zhou et al., 2020; Lin et al., 2012. The effect is surprising, if one considers only spin-spin interactions at the interface as the origin of the effect. Typical magnetic energies are orders of magnitude lower than chemical energies (energy of spin-spin interactions $<\mu$J mol⁻¹, Steiner and Ulrich, 1989). Using magneto-optical spectroscopy, Sambalova et al., 2021 demonstrated that the effect on hydrogen evolution can at least partially be traced back to the magnetic properties of the species near to the electrode (OH⁻ and H₂O). The thermodynamic force f_mag induced by a homogeneous magnetic field is restricted to the interface with a steep gradient of the susceptibility χ:

$f_{mag}=-\frac{\partial }{\partial x}{\mu }_{mag}=-\frac{1}{2{\mu }_0}{B}^2\cdot \frac{\partial \chi }{\partial x}(6)$

The susceptibility of an alkaline solution depends on the concentration of OH⁻ ions, i.e., the effect depends on the pH-gradient as a result of the electrochemical double layer (EDL) built up during electrolysis.

Apart from demonstrating the impact of a magnetic field on the EDL, the authors report a time dependence of the effect indicating a redistribution of ions as a response to the thermodynamic force. This effect can be utilized: modulating the external fields can alter the overall reaction mechanism. In so-called pulse-electrolysis (Liu et al., 2021), the time to accumulate a certain coverage of intermediates and/or products and corresponding changes of the electrode-electrolyte interface is used to enhance efficiency of the water splitting reaction (Vincent et al., 2018) as well as to control the selectivity of the products in electrochemical CO₂ reduction (Kumar et al., 2016). It is too early to assess the success of these ideas in practical applications; however, they are a beautiful demonstration of “short-lived interfaces for energy conversion”.

2.4 Concepts to Improve Interfaces in Energy Materials

Aim of this review is to conceptualize how to overcome kinetic barriers from interfaces in energy materials/systems. The various different concepts used to overcome the kinetic barriers may be simplified by:

1. removing the static interface

2. improving the static interface

3. removing the dynamic interface

4. improving the dynamic interface

A static interface is often the surface such as the oxide skin on MgH₂ blocking hydrogen dissociation and transport. Its removal [concept 1)] is only a theoretical option, as there are always contaminants in technical hydrogen (Delmelle et al. (2014)). Concept 2) is the only option. An electrode surface is a static interface with function. Thus, it cannot be removed [concept 1)], and its performance must be optimized [concept 2)]. The surface of liquids is a static interface, too, but there is no kinetic barrier at least for water uptake in aqueous NaOH.

With the surface removed or properly optimized, other reaction steps may be rate-limiting. We focus here on the dynamic (“short-lived”) interfaces being built only under certain circumstances. This makes analysis difficult, because they only exist under operando conditions (see subsection 2.5). However, already knowing their existence is helpful. Basically, the same concepts as for the static interface may be applied.

To explain the relevance of interfaces in hydrogenation reactions, we chose the well studied example of MgH₂, because discussion of the effectiveness of additives is often led only along their sorption rate enhancement. This results in a multitude of often contradicting papers, simply because an additive improving the static interface may not help to reduce the barrier of the dynamic one. The case MgH₂ is well studied, in contrast to hydrogen sorption kinetics in NaAlH₄. In particular the role of additives such as TiH_x as a hydrogenation catalyst in Al + NaH to form NaAlH₄ remains elusive (Bogdanović and Schwickardi, 1997; Frankcombe, 2012). There is consensus that the effective catalysts affect the static interface, i.e., they enable hydrogen dissociation and recombination (concept 1). The additional properties that make catalysts such as Ti better than classical hydrogenation catalysts, such as Pd, is not fully understood (Frankcombe, 2012). Reducing the dynamic interface by improving the transport of alane species has been suggested (concept 4, here called zipper model, see Marashdeh et al., 2007), although experimental evidence is lacking. The difficulty of complex hydrides is the formation of at least two solid phases during decomposition, which generates additional short-lived interfaces with mass transport of hydrogen and even metal atoms. Here, a fast interface reaction has been identified as prerequisite for the functioning of reactive hydride composites (Kato et al., 2012; Ali et al., 2021). Further research is needed for deeper insight into the dynamic interfaces during formation and decomposition.

The diffusion layer built upon water uptake in aqueous NaOH is not a sharp interface on a microscopic scale. As the system boundaries are much larger, it is the rate-limiting interface on a macroscopic scale. Both concepts (3 and 4) have been tested in the past: improving diffusion by additives (concept 4), and removing the interface by separating interface reaction and mass transport by introducing convection (concept 3).

The dynamic interface in electrochemistry is by far the most complex one. Although known since 100 years, research focuses on the improvement of the static interface by, e.g., developing electrocatalysts, while the dynamic interface is neglected probably due to the apparently simple measures to overcome it. Simple measures such as “stirring” to eliminate the impact of the diffusion (concept 3) are established techniques in analytical research (“rotating disc electrode”, see Baur (2007)). Similar to the case water uptake in a liquid, the challenge lies in the development of a design, where this idea is implemented into the confined and optimized technical device. The Zdansky “zero-gap” electrolyzer is a compelling example for this. The introductory example of electro-chemical CO₂ reduction to ethylene highlights concept 4): one can make use of the interface to control the mass transport of reactants to the interface (Nesbitt et al., 2020). The electro-chemical double layer (Figure 1C) is an interesting hybrid interface: it is always there (i.e., it is static), but depends on external parameters (i.e., it is dynamic) posing both a challenge for fundamental analysis as well as technical improvements.

In this review, we omitted the discussion of battery systems as important electro-chemical energy storage systems. The reason for this is not that short-lived interfaces do not exist here. On the contrary, the concept is directly applicable to nickel - metal hydride batteries with hydrogen diffusion processes in the metal hydride (Feng and Northwood, 2004), and the critical electrode-electrolyte interface (Han et al., 1999). Similar processes are relevant in Li-ion batteries as well (e.g., Li-ion diffusion, see Zhu and Wang, 2010). However, additional topics such as the stability of electrolyte, electrode, and interfaces are challenges in battery research (see, e.g., Xiao et al., 2020), which go beyond the scope of this review.

2.5 Analysis of Short-Lived Interfaces

Most statements on the existence of specific rate-limiting steps are made on the basis of kinetic measurements, e.g., hydrogen sorption kinetics (Førde et al., 2007; Zhou et al., 2021a; Lai et al., 2019; heat exchange kinetics (Zhang et al., 2014), current—voltage relationships, impedance spectroscopy and their modelling (Dau and Pasquini, 2019; Mukouyama and Nakanishi, 2020). There is an uncertainty of the interface models, if solely gained from a kinetic analysis. Direct proof of the corresponding dynamic interface is required to unambiguously assign the best kinetic model.

Hydrogen sorption kinetics in MgH₂ is an archetypal example. First hints of a dynamic interface built up during hydrogenation (“blocking layer”) date back to Stampfer et al. (1960), with indications substantiating using kinetic analyses by Rudman (1979) and Zhdanov et al. (1993). Convincing evidence was then provided by the visualisation of the hydrogen distribution using the N15-method (Rydén et al., 1989). It is worth mentioning that the proof relies on thin Mg films capped with Pd to remove the static interface barrier (i.e., successful realization of concept 1). Furthermore, hydrogen diffusion is slow and can be quenched by cooling allowing the use of the post-mortem nuclear N15-method. These boundary conditions cannot always be met. Below we give an overview of the state-of-the-art analysis methods and future developments with particular emphasis on operando methods.

Perhaps the most direct method of probing a surface is photoelectron spectroscopy. As it is an established technique, we refer to the various books and reviews describing the potential of the method (Briggs and Seah, 1983; Hüfner, 2003). In a nutshell: X-ray photoelectron spectroscopy and related techniques reveal qualitative and quantitative elemental composition of a surface. The small mean free path length of photoelectrons limits the information depth to few monolayers, and restricts the analysis to ultra-high vacuum environments. New developments extend the information depth up to around 10 nm, allowing to probe buried interface even when using laboratory apparatus using hard X-rays (Regoutz et al., 2018; Sambalova et al., 2020, see also Figure 5A, B). Sophisticated engineering pushed the maximum allowed gas pressure up to the bars range (near ambient pressure photoelectron spectroscopy, see, e.g., Knudsen et al., 2016; Roy et al., 2018; Amann et al., 2019; Novotny et al., 2020).

FIGURE 5

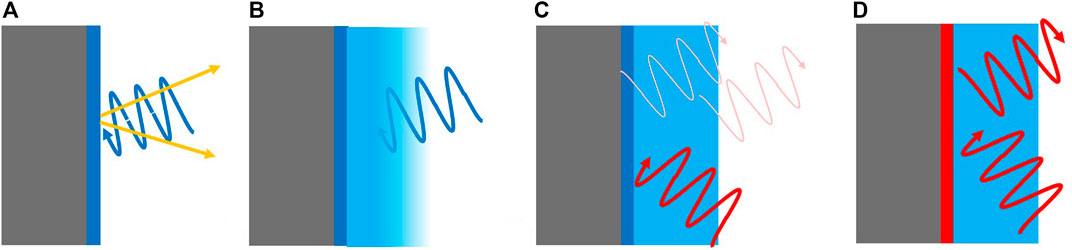
FIGURE 5. (A) Typical surface science analysis: nm mean free path length of electrons (yellow arrows, waves stand for photons) guarantees surface sensitivity. (B) Short mean free path length (of electrons and/or photons) impedes the analysis of buried interfaces. (C) Unrestricted mean free path length allows the measurement of buried interfaces, but spatial resolution is usually limited. (D) resonant interaction of the probe beam with the interface scales the spatial resolution down to the interface region.

The direct measurement of the ion gradients in the electrolyte in the vicinity of the interface is extremely challenging (Zaera, 2012), because the water layers above it absorb (photo-)electrons (Figure 5B). Recent technical developments (see refs. above) have made it possible to probe water and a spectator molecule (pyrazine) in an alkaline electrolyte in the vicinity of an electrode by photoelectron spectroscopy (Favaro et al., 2016). The results verify the shape of the potential in the EDL with nanometer resolution as function of applied potential and electrolyte concentration in a beautiful way, as predicted by the established theoretical framework (Helmholtz/Debye theory of the EDL, see, e.g., Devanathan and Tilak, 1965).

Other analysis techniques utilize photons to circumvent the challenges associated with electrons (e.g., X-ray absorption spectroscopy, de Groot, 2001; Newton and Dent, 2013; Nachtegaal et al., 2017). An established optical technique is diffusive reflectance infrared Fourier transform spectroscopy (DRIFTS Terreni et al., 2020; Negahdar et al., 2020). In general, operando investigations using probes with small mean free path lengths are usually limited to changes of the surface of materials, or adsorbates on it (Li and Gong, 2020).

Probing technical electrode/electrolyte interfaces such as in measurement of electro-chemical gradients on a mesoscopic length scale is difficult with photoemission spectroscopy (Figure 5B). Here optical methods such as spatially resolved Raman spectroscopy similar to the one described in section 2.2 have high potential. Visible light is hardly absorbed by typical electrolytes, and Raman spectroscopy is sensitive to molecular vibrations such as OH and ${\mathrm{C}\mathrm{O}}_3^{2-}$. Lu et al. (2020) applied the method to probe the pH gradient and CO₂—OH⁻ neutralization reaction near to a CO₂ reduction electrode. They find that the ${\mathrm{H}\mathrm{C}\mathrm{O}}_3^{-}$ concentration profile extends a distance of 120 μm into the electrolyte at zero current. The pH gradient layer narrows with increasing CO₂ reduction current densities. These findings are highly relevant for the development of novel electrochemical CO₂ electrolyzers (Nesbitt et al., 2020). However, the space resolution of confocal Raman spectroscopy and related optical microscopy methods is of the order of 200 nm (Sil and Umapathy, 2014) limited by the Abbe-limit (see also Figure 5C). If sub-micrometer resolution is sufficient, Raman microscopy and generally optical methods are powerful tools to visualise particularly dynamic phenomena (hydrogen sorption: Borgschulte et al., 2010; Duan et al., 2018, diffusion gradients in liquids: Fumey et al., 2020; Lu et al., 2020), particularly because of the good time resolution. New developments push the resolution limits down to 20 nm using scanning near field optical microscopy (Karst et al., 2020). The latter study highlights the importance of spatial resolution by differentiating the hydrogen dynamics in small grains from the one in macroscopic behavior: the nm-sized grains transform individually, i.e., the hydrogen sorption kinetics does not follow a continuous diffusion as may be drawn from macroscopic observations with micrometer resolution.

To enhance the interface sensitivity in optical spectroscopy, resonance effects can be exploited, e.g., in surface plasmon enhanced Raman spectroscopy. Here, the surface enhances locally (nm range) the signal intensity (Dieringer et al., 2006). This means that although excitation and collection take place on a much larger scale, the measured signal can be associated to the adjacent interface layers (Figure 5D); e.g., to the EDL in the vicinity of a hydrogen evolution electrode (Yonezawa et al., 2017). The same principle applies to second-harmonic and sum-frequency generation spectroscopy (Shen, 1989), which have been employed in catalysis (Roiaz et al., 2016), surface characterization of liquids (Yamaguchi et al., 2012), electrochemical interfaces (Rey and Dlott, 2017).

Electron microscopy has traditionally been the method with highest spatial resolution. Surfaces and interfaces can be investigated with atomic resolution (e.g., de Graaf et al., 2020). Due to the high energies of the electrons used, operando conditions are possible, allowing the measurement of pressure composition isotherms of individual palladium nano-particles (Baldi et al., 2014).

Still, the operando, i.e., time resolved measurement under reaction conditions of elemental distribution over a wide range with nm precision is an open research question. Nuclear methods such as the above mentioned N15-nuclear resonance analysis can measure the hydrogen concentration in thin films with a typical depth resolution of 5–10 nm, over a depth of several microns (Lanford et al., 1976; Wilde and Fukutani, 2008; Wilde and Fukutani, 2014)). A related nuclear method is elastic recoil detection (ERD, Barbour and Doyle, 1995). Nuclear methods are in general very well suited for depth profiling, such as neutron imaging. The spatial resolution of neutron imaging is only in the micrometer range (Morgano et al., 2018), but its great advantages are the time resolution (Zboray and Trtik, 2018) and the compatibility to the harsh conditions as is relevant in catalysis (Terreni et al., 2018), heat storage (Fumey et al., 2022), and fuel cells (Boillat et al., 2017; Minnaar et al., 2020).

Finally, we would like to emphasise the importance of simultaneously good time and space resolution for the analysis of dynamic interfaces. Figure 6 shows a times series of neutron radiography images of water absorption into Ni-loaded zeolite beads [from Terreni et al. (2018)]. The time resolution of 1 min is (here) given by the time required to take an image with an appropriate signal to noise ratio. The spatial resolution was approximately 50 μm. However, this value is misleading, because it was measured on a static interface (at the bead’s outer surface). The interface of interest moves while the camera accumulates counts, here with a maximum velocity of around 80 μm per min. Thus, the “dynamic” spatial resolution deteriorates to more than double the static value. Terreni et al. (2018) repeated the measurements at higher temperatures, where the diffusion of water in zeolites is faster, and the total uptake smaller than at lower temperatures. The latter worsens the contrast ratio, and thus the signal to noise ratio, both effects impeding the measurement of meaningful diffusion gradients at higher temperatures.

FIGURE 6

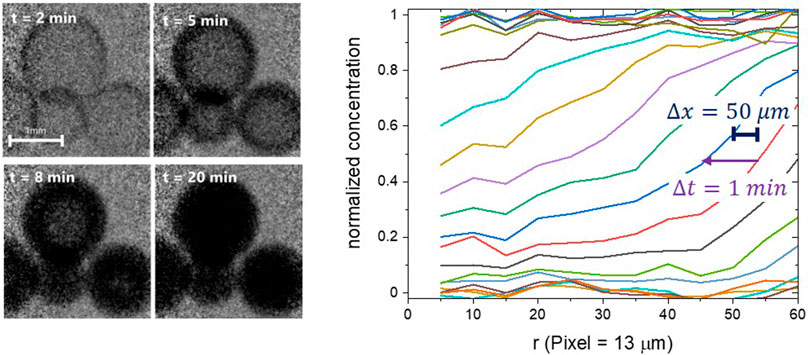
FIGURE 6. Left: times series of neutron radiography images of water absorption into Ni-loaded zeolite beads at 50°C [from Terreni et al. (2018)]. Right: normalized radial water concentration extracted from the times series. The spatial resolution was approximately 50 μm, with the time resolution of 1 min. The true gradient can be expected to be much steeper.

3 Conclusion

In this review, we discuss the kinetics of chemical energy storage/conversion systems alongside the concept of static and dynamic interfaces as rate-limiting steps. The review omits the importance of physical and chemical properties of energy materials, which may be found elsewhere. However, having identified the rate-limiting interface, the appropriate materials science should be applied to overcome them. In particular, a static interface must be treated differently from a dynamic one. At this point, material science comes back into play.

In detail, we give an overview of static and dynamic interfaces in hydrogen storage, sorption based thermal energy storage, electrochemical water splitting and electrochemical CO₂ reduction. We show successful examples, both historical and very recent ones, of how to lower the detrimental effect that stem from these interfaces. Emphasis is laid on the description of analysis methods suitable to probe static and dynamic interfaces.

The given examples are not exhaustive: similar effects of static and dynamic interfaces are expected to occur in other electrochemical applications such as fuel-cells (PEM-electrolyzers), batteries, etc.

In this review, we omit the description of numerical simulations for further insights into short-lived interfaces in energy materials due to practical reasons. Without doubt, theoretical approaches can bridge cases, which are difficult to access experimentally, and are important to generalize the usually specific technical systems.

Author Contributions

AB is the originator of the conceptual design, all authors contributed to writing of the manuscript, and reviewed and commented on it.

Funding

Financial support from the Swiss National Science Foundation (grant Nos. 172662 and 182987) is greatly acknowledged. Additional funding from the UZH-UFSP program LightChEC was received. This research work is financially supported by the Swiss Innovation Agency Innosuisse grant Nr. 1155002545 and is part of the Swiss Competence Centre for Energy Research SCCER HaE. Supplementary funding is received from the Swiss Federal Office of Energy SFOE grant Nr. SI/501605-01 in the frame of the IEA SHC Task 58/ECES Annex 33 participation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Additional technical measures may be needed, such as tank design taking into account heat transfer, chemical and mechanical stress, etc., which we omit here.

References

Aguey-Zinsou, K.-F., Ares Fernandez, J. R., Klassen, T., and Bormann, R. (2006). Using mgo to Improve the (de)Hydriding Properties of Magnesium. Mater. Res. Bull. 41, 1118–1126. doi:10.1016/j.materresbull.2005.11.011

CrossRef Full Text | Google Scholar

Ali, N. A., Sazelee, N. A., and Ismail, M. (2021). An Overview of Reactive Hydride Composite (RHC) for Solid-State Hydrogen Storage Materials. Int. J. Hydrogen Energ. 46, 31674–31698. doi:10.1016/j.ijhydene.2021.07.058

CrossRef Full Text | Google Scholar

Amann, P., Degerman, D., Lee, M.-T., Alexander, J. D., Shipilin, M., Wang, H.-Y., et al. (2019). A High-Pressure X-ray Photoelectron Spectroscopy Instrument for Studies of Industrially Relevant Catalytic Reactions at Pressures of Several Bars. Rev. Scientific Instr. 90, 103102. doi:10.1063/1.5109321

CrossRef Full Text | Google Scholar

Andersson, J., and Grönkvist, S. (2019). Large-Scale Storage of Hydrogen. Int. J. Hydrogen Energ. 44, 11901–11919. doi:10.1016/j.ijhydene.2019.03.063

CrossRef Full Text | Google Scholar

Baldi, A., Narayan, T. C., Koh, A. L., and Dionne, J. A. (2014). In Situ detection of Hydrogen-Induced Phase Transitions in Individual Palladium Nanocrystals. Nat. Mater. 13, 1143–1148. doi:10.1038/nmat4086

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbour, J. C., and Doyle, B. (1995). in Handbook of Modern Ion Beam Materials Analysis. Editors J. Tesmer, and M. Nastasi (Pittsburgh, PA: Materials Research Society).

Google Scholar

Barkhordarian, G., Klassen, T., and Bormann, R. (2006). Kinetic Investigation of the Effect of Milling Time on the Hydrogen Sorption Reaction of Magnesium Catalyzed With Different Nb2O5 Contents. J. Alloys Compounds. 407, 249–255. doi:10.1016/j.jallcom.2005.05.037

CrossRef Full Text | Google Scholar

Baur, J. E. (2007). “Diffusion Coefficients,” in Handbook of Electrochemistry. Editor C. G. Zoski (Amsterdam: Elsevier), 829–848. doi:10.1016/B978-044451958-0.50036-7

CrossRef Full Text | Google Scholar

Berardi, S., Drouet, S., Francàs, L., Gimbert-Suriñach, C., Guttentag, M., Richmond, C., et al. (2014). Molecular Artificial Photosynthesis. Chem. Soc. Rev. 43, 7501–7519. doi:10.1039/C3CS60405E

PubMed Abstract | CrossRef Full Text | Google Scholar

Billeter, E., Lodziana, Z., and Borgschulte, A. (2021). Surface Properties of the Hydrogen - Titanium System. J. Phys. Chem. C. 125 (45), 25339–25349. doi:10.1021/acs.jpcc.1c08635

CrossRef Full Text | Google Scholar

Bogdanović, B., and Schwickardi, M. (1997). Ti-Doped Alkali Metal Aluminium Hydrides as Potential Novel Reversible Hydrogen Storage Materials. J. Alloys Compounds. 253-254, 1–9. doi:10.1016/S0925-8388(96)03049-6

CrossRef Full Text | Google Scholar

Boillat, P., Lehmann, E. H., Trtik, P., and Cochet, M. (2017). Neutron Imaging of Fuel Cells - Recent Trends and Future Prospects. Curr. Opin. Electrochemistry. 5, 3–10. doi:10.1016/j.coelec.2017.07.012

CrossRef Full Text | Google Scholar

Borgschulte, A., Bielmann, M., Züttel, A., Barkhordarian, G., Dornheim, M., and Bormann, R. (2008). Hydrogen Dissociation on Oxide Covered MgH2 by Catalytically Active Vacancies. Appl. Surf. Sci. 254, 2377–2384. doi:10.1016/j.apsusc.2007.09.069

CrossRef Full Text | Google Scholar

Borgschulte, A., Gallandat, N., Probst, B., Suter, R., Callini, E., Ferri, D., et al. (2013). Sorption Enhanced CO2 Methanation. Phys. Chem. Chem. Phys. 15, 9620–9625. doi:10.1039/C3CP51408K

PubMed Abstract | CrossRef Full Text | Google Scholar

Borgschulte, A., Gremaud, R., Łodziana, Z., and Züttel, A. (2010). Hydrogen Tracer Diffusion in LiBH4 Measured by Spatially Resolved Raman Spectroscopy. Phys. Chem. Chem. Phys. 12, 5061–5066. doi:10.1039/C000229A

PubMed Abstract | CrossRef Full Text | Google Scholar

Borgschulte, A., Westerwaal, R., Rector, J., Schreuders, H., Dam, B., and Griessen, R. (2006). Catalytic Activity of Noble Metals Promoting Hydrogen Uptake. J. Catal. 239, 263–271. doi:10.1016/j.jcat.2006.01.031

CrossRef Full Text | Google Scholar

Bösenberg, U., Doppiu, S., Mosegaard, L., Barkhordarian, G., Eigen, N., Borgschulte, A., et al. (2007). Hydrogen Sorption Properties of MgH2-LiBH4 Composites. Acta Materialia. 55, 3951–3958. doi:10.1016/j.actamat.2007.03.010

CrossRef Full Text | Google Scholar

Briggs, D., and Seah, M. P. (1983). Practical Surface Analysis by Auger and X-ray Photoelectron Spectroscopy. Chichester: John Wiley & Sons.

Google Scholar

Chan, K. (2020). A Few Basic Concepts in Electrochemical Carbon Dioxide Reduction. Nat. Commun. 11, 5954. doi:10.1038/s41467-020-19369-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Dau, H., and Pasquini, C. (2019). Modelling the (Essential) Role of Proton Transport by Electrolyte Bases for Electrochemical Water Oxidation at Near-Neutral Ph. Inorganics. 7, 20. doi:10.3390/inorganics7020020

CrossRef Full Text | Google Scholar

de Graaf, S., Momand, J., Mitterbauer, C., Lazar, S., and Kooi, B. J. (2020). Resolving Hydrogen Atoms at Metal-Metal Hydride Interfaces. Sci. Adv. 6, eaay4312. doi:10.1126/sciadv.aay4312

PubMed Abstract | CrossRef Full Text | Google Scholar

de Groot, F. (2001). High-Resolution X-ray Emission and X-ray Absorption Spectroscopy. Chem. Rev. 101, 1779–1808. doi:10.1021/cr9900681

PubMed Abstract | CrossRef Full Text | Google Scholar

Delmelle, R., Gehrig, J. C., Borgschulte, A., and Züttel, A. (2014). Reactivity Enhancement of Oxide Skins in Reversible Ti-Doped NaAlH4. AIP Adv. 4, 127130. doi:10.1063/1.4904428

CrossRef Full Text | Google Scholar

Devanathan, M. A. V., and Tilak, B. V. K. S. R. A. (1965). The Structure of the Electrical Double Layer at the Metal-Solution Interface. Chem. Rev. 65, 635–684. doi:10.1021/cr60238a002

CrossRef Full Text | Google Scholar

Dieringer, J. A., McFarland, A. D., Shah, N. C., Stuart, D. A., Whitney, A. V., Yonzon, C. R., et al. (2006). Introductory Lecture : Surface Enhanced Raman Spectroscopy: New Materials, Concepts, Characterization Tools, and Applications. Faraday Discuss. 132, 9–26. doi:10.1039/B513431P

PubMed Abstract | CrossRef Full Text | Google Scholar

Dinh, C.-T., Burdyny, T., Kibria, M. G., Seifitokaldani, A., Gabardo, C. M., García de Arquer, F. P., et al. (2018). CO2 Electroreduction to Ethylene via Hydroxide-Mediated Copper Catalysis at an Abrupt Interface. Science. 360, 783–787. doi:10.1126/science.aas9100

PubMed Abstract | CrossRef Full Text | Google Scholar

Dogutan, D. K., and Nocera, D. G. (2019). Artificial Photosynthesis at Efficiencies Greatly Exceeding That of Natural Photosynthesis. Acc. Chem. Res. 52, 3143–3148. doi:10.1021/acs.accounts.9b00380

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, X., Griessen, R., Wijngaarden, R. J., Kamin, S., and Liu, N. (2018). Self-Recording and Manipulation of Fast Long-Range Hydrogen Diffusion in Quasifree Magnesium. Phys. Rev. Mater. 2, 085802. doi:10.1103/PhysRevMaterials.2.085802

CrossRef Full Text | Google Scholar

Favaro, M., Jeong, B., Ross, P. N., Yano, J., Hussain, Z., Liu, Z., et al. (2016). Unravelling the Electrochemical Double Layer by Direct Probing of the Solid/liquid Interface. Nat. Commun. 7, 12695. doi:10.1038/ncomms12695

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, F., and Northwood, D. O. (2004). Hydrogen Diffusion in the Anode of Ni/mh Secondary Batteries. J. Power Sourc. 136, 346–350. doi:10.1016/j.jpowsour.2004.03.015

CrossRef Full Text | Google Scholar

Forde, T., Maehlen, J., Yartys, V., Lototsky, M., and Uchida, H. (2007). Influence of Intrinsic Hydrogenation/Dehydrogenation Kinetics on the Dynamic Behaviour of Metal Hydrides: A Semi-Empirical Model and its Verification. Int. J. Hydrogen Energ. 32, 1041–1049. doi:10.1016/j.ijhydene.2006.07.015

CrossRef Full Text | Google Scholar

Frankcombe, T. J. (2012). Proposed Mechanisms for the Catalytic Activity of Ti in NaAlH4. Chem. Rev. 112, 2164–2178. doi:10.1021/cr2001838

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedrichs, O., Sánchez-López, J. C., López-Cartes, C., Dornheim, M., Klassen, T., Bormann, R., et al. (2006). Chemical and Microstructural Study of the Oxygen Passivation Behaviour of Nanocrystalline Mg and MgH2. Appl. Surf. Sci. 252, 2334–2345. doi:10.1016/j.apsusc.2005.04.018

CrossRef Full Text | Google Scholar

Fujita, T. (1993). Falling Liquid Films in Absorption Machines. Int. J. Refrigeration 16, 282–294. doi:10.1016/0140-7007(93)90081-I

CrossRef Full Text | Google Scholar

Fukai, Y. (2005). The Metal-Hydrogen System: Basic Bulk Properties. 2nd rev. and updated ed. Berlin: Springer.

Google Scholar

Fumey, B., Baldini, L., and Borgschulte, A. (2020). Water Transport in Aqueous Sodium Hydroxide Films for Liquid Sorption Heat Storage. Energy Technol. 8, 2000187. doi:10.1002/ente.202000187

CrossRef Full Text | Google Scholar

Fumey, B., Borgschulte, A., Stoller, S., Fricker, R., Knechtle, R., Kaestner, A., et al. (2022). Enhanced Gas-Liquid Absorption through Natural Convection Studied by Neutron Imaging. Int. J. Heat Mass Transfer. 182, 121967. doi:10.1016/j.ijheatmasstransfer.2021.121967

CrossRef Full Text | Google Scholar

Fumey, B., Weber, R., and Baldini, L. (2017). Liquid Sorption Heat Storage - A Proof of Concept Based on Lab Measurements With a Novel Spiral Fined Heat and Mass Exchanger Design. Appl. Energ. 200, 215–225. doi:10.1016/j.apenergy.2017.05.056

CrossRef Full Text | Google Scholar

Garcés-Pineda, F., Blasco-Ahicart, M., and Nieto-Castro, D. (2019). Direct Magnetic Enhancement of Electrocatalytic Water Oxidation in Alkaline media. Nat. Energ. 4, 519–525. doi:10.1038/s41560-019-0404-4

CrossRef Full Text | Google Scholar

Hadorn, J. C. (2008). Thermal Energy Storage for Solar and Low Energy Buildings – State of the Art. Lleida: Servei de Publicacions (UDL).

Google Scholar

Han, J., Feng, F., Geng, M., Buxbaum, R., and Northwood, D. O. (1999). Electrochemical Characteristics of the Interface Between the Metal Hydride Electrode and Electrolyte for an Advanced Nickel/Metal Hydride Battery. J. Power Sourc. 80, 39–45. doi:10.1016/S0378-7753(98)00250-X

CrossRef Full Text | Google Scholar

Hao, S., and Sholl, D. S. (2008). Hydrogen Diffusion in MgH2 and NaMgH3 via Concerted Motions of Charged Defects. Appl. Phys. Lett. 93, 251901. doi:10.1063/1.3046737

CrossRef Full Text | Google Scholar

Haverkort, J. W., and Rajaei, H. (2021). Voltage Losses in Zero-gap Alkaline Water Electrolysis. J. Power Sourc. 497, 229864. doi:10.1016/j.jpowsour.2021.229864

CrossRef Full Text | Google Scholar

Hine, F., and Murakami, K. (1980). Bubble Effects on the Solution IR Drop in a Vertical Electrolyzer under Free and Forced Convection. J. Electrochem. Soc. 127, 292–297. doi:10.1149/1.2129658

CrossRef Full Text | Google Scholar

Hori, Y., Murata, A., Takahashi, R., and Suzuki, S. (1987). Electroreduction of Carbon Monoxide to Methane and Ethylene at a Copper Electrode in Aqueous Solutions at Ambient Temperature and Pressure. J. Am. Chem. Soc. 109, 5022–5023. doi:10.1021/ja00250a044

CrossRef Full Text | Google Scholar

Hüfner, S. (2003). Photoelectron Spectroscopy: Principles and Applications. Berlin, Heidelberg: Springer. doi:10.1007/978-3-662-09280-4_1

CrossRef Full Text | Google Scholar

Ikeda, K., Fujisaki, F., Otomo, T., Ohshita, H., Honda, T., Kawamata, T., et al. (2021). Generating Mechanism of Catalytic Effect for Hydrogen Absorption/Desorption Reactions in NaAlH4-TiCl3. Appl. Sci. 11, 8349. doi:10.3390/app11188349

CrossRef Full Text | Google Scholar

Jacobsson, T. J. (2018). Photoelectrochemical Water Splitting: an Idea Heading towards Obsolescence? Energy Environ. Sci. 11, 1977–1979. doi:10.1039/C8EE00772A

CrossRef Full Text | Google Scholar

Ju, W., Heinz, M. V. F., Pusterla, L., Hofer, M., Fumey, B., Castiglioni, R., et al. (2018). Lab-Scale Alkaline Water Electrolyzer for Bridging Material Fundamentals With Realistic Operation. ACS Sustainable Chem. Eng. 6, 4829–4837. doi:10.1021/acssuschemeng.7b04173

CrossRef Full Text | Google Scholar

Karst, J., Sterl, F., Linnenbank, H., Weiss, T., Hentschel, M., and Giessen, H. (2020). Watching In Situ the Hydrogen Diffusion Dynamics in Magnesium on the Nanoscale. Sci. Adv. 6, eaaz0566. doi:10.1126/sciadv.aaz0566

PubMed Abstract | CrossRef Full Text | Google Scholar

Kato, S., Borgschulte, A., Bielmann, M., and Züttel, A. (2012). Interface Reactions and Stability of a Hydride Composite (NaBH4 + MgH2). Phys. Chem. Chem. Phys. 14, 8360–8368. doi:10.1039/C2CP23491B

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, K. J., Berman, N. S., and Wood, B. D. (1996). The Interfacial Turbulence in Falling Film Absorption: Effects of Additives. Int. J. Refrigeration. 19, 322–330. doi:10.1016/S0140-7007(96)00025-4

CrossRef Full Text | Google Scholar

Knudsen, J., Andersen, J. N., and Schnadt, J. (2016). A Versatile Instrument for Ambient Pressure X-ray Photoelectron Spectroscopy: The Lund Cell Approach. Surf. Sci. 646, 160–169. doi:10.1016/j.susc.2015.10.038

CrossRef Full Text | Google Scholar

Koj, M., Qian, J., and Turek, T. (2019). Novel Alkaline Water Electrolysis With Nickel-Iron Gas Diffusion Electrode for Oxygen Evolution. Int. J. Hydrogen Energ. 44, 29862–29875. doi:10.1016/j.ijhydene.2019.09.122

CrossRef Full Text | Google Scholar

Koteski, V., Belošević-Čavor, J., Batalović, K., Radaković, J., and Umićević, A. (2015). Hydrogen Diffusion in MgH2 Doped With Ti, Mn and Fe. RSC Adv. 5, 34894–34899. doi:10.1039/C5RA04168F

CrossRef Full Text | Google Scholar

Kumar, B., Brian, J. P., Atla, V., Kumari, S., Bertram, K. A., White, R. T., et al. (2016). Controlling the Product Syngas H2:CO Ratio through Pulsed-Bias Electrochemical Reduction of CO2 on Copper. ACS Catal. 6, 4739–4745. doi:10.1021/acscatal.6b00857

CrossRef Full Text | Google Scholar

Lai, Q., Sun, Y., Wang, T., Modi, P., Cazorla, C., Demirci, U. B., et al. (2019). How to Design Hydrogen Storage Materials? Fundamentals, Synthesis, and Storage Tanks. Adv. Sustainable Syst. 3, 1900043. doi:10.1002/adsu.201900043

CrossRef Full Text | Google Scholar

Lanford, W. A., Trautvetter, H. P., Ziegler, J. F., and Keller, J. (1976). New Precision Technique for Measuring the Concentration Versus Depth of Hydrogen in Solids. Appl. Phys. Lett. 28, 566–568. doi:10.1063/1.88826

CrossRef Full Text | Google Scholar

Leal, L. (2007). Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge: Cambridge University Press.

Google Scholar

Li, J., and Gong, J. (2020). Operando Characterization Techniques for Electrocatalysis. Energ. Environ. Sci. 13, 3748–3779. doi:10.1039/D0EE01706J

CrossRef Full Text | Google Scholar

Li, M., Lu, Y., Zhang, S., and Xiao, Y. (2016). A Numerical Study of Effects of Counter-current Gas Flow Rate on Local Hydrodynamic Characteristics of Falling Films over Horizontal Tubes. Desalination. 383, 68–80. doi:10.1016/j.desal.2016.01.016

CrossRef Full Text | Google Scholar

Lin, M.-Y., Hourng, L.-W., and Kuo, C.-W. (2012). The Effect of Magnetic Force on Hydrogen Production Efficiency in Water Electrolysis. Int. J. Hydrogen Energ. 37, 1311–1320. doi:10.1016/j.ijhydene.2011.10.024

CrossRef Full Text | Google Scholar

Liu, T., Wang, J., Yang, X., and Gong, M. (2021). A Review of Pulse Electrolysis for Efficient Energy Conversion and Chemical Production. J. Energ. Chem. 59, 69–82. doi:10.1016/j.jechem.2020.10.027

CrossRef Full Text | Google Scholar

Lu, X., Zhu, C., Wu, Z., Xuan, J., Francisco, J. S., and Wang, H. (2020). In Situ Observation of the pH Gradient Near the Gas Diffusion Electrode of CO2 Reduction in Alkaline Electrolyte. J. Am. Chem. Soc. 142, 15438–15444. doi:10.1021/jacs.0c06779

PubMed Abstract | CrossRef Full Text | Google Scholar

Marashdeh, A., Olsen, R. A., Løvvik, O. M., and Kroes, G.-J. (2007). Naalh4 Clusters With Two Titanium Atoms Added. J. Phys. Chem. C. 111, 8206–8213. doi:10.1021/jp067083b

CrossRef Full Text | Google Scholar

Minnaar, C., De Beer, F., and Bessarabov, D. (2020). Current Density Distribution of Electrolyzer Flow fields: In Situ Current Mapping and Neutron Radiography. Energy Fuels. 34, 1014–1023. doi:10.1021/acs.energyfuels.9b03814

CrossRef Full Text | Google Scholar

Modi, P., and Aguey-Zinsou, K.-F. (2021). Room Temperature Metal Hydrides for Stationary and Heat Storage Applications: A Review. Front. Energ. Res. 9, 616115. doi:10.3389/fenrg.2021.616115

CrossRef Full Text | Google Scholar

Morgano, M., Trtik, P., Meyer, M., Lehmann, E. H., Hovind, J., and Strobl, M. (2018). Unlocking High Spatial Resolution in Neutron Imaging through an Add-On Fibre Optics Taper. Opt. Express. 26, 1809–1816. doi:10.1364/OE.26.001809

PubMed Abstract | CrossRef Full Text | Google Scholar

Mukouyama, Y., and Nakanishi, S. (2020). An Ordinary Differential Equation Model for Simulating Local-Ph Change at Electrochemical Interfaces. Front. Energ. Res. 8, 298. doi:10.3389/fenrg.2020.582284

CrossRef Full Text | Google Scholar

Mulder, F. M. (2014). Implications of Diurnal and Seasonal Variations in Renewable Energy Generation for Large Scale Energy Storage. J. Renew. Sustainable Energ. 6, 033105. doi:10.1063/1.4874845

CrossRef Full Text | Google Scholar

Nachtegaal, M., Hartfelder, U., and van Bokhoven, J. (2017). Operando Research in Heterogeneous Catalysis. Cham: Springer International Publishing. doi:10.1007/978-3-319-44439-0

CrossRef Full Text | Google Scholar

Negahdar, L., Parlett, C. M. A., Isaacs, M. A., Beale, A. M., Wilson, K., and Lee, A. F. (2020). Shining Light on the Solid-Liquid Interface: In Situ/Operando Monitoring of Surface Catalysis. Catal. Sci. Technol. 10, 5362–5385. doi:10.1039/D0CY00555J

CrossRef Full Text | Google Scholar

Nesbitt, N. T., Burdyny, T., Simonson, H., Salvatore, D., Bohra, D., Kas, R., et al. (2020). Liquid-Solid Boundaries Dominate Activity of CO2 Reduction on Gas-Diffusion Electrodes. ACS Catal. 10, 14093–14106. doi:10.1021/acscatal.0c03319

CrossRef Full Text | Google Scholar

Newton, M. A., and Dent, A. J. (2013). “Energy-Dispersive EXAFS: Principles and Application in Heterogeneous Catalysis,” in SituCharacterization of Heterogeneous Catalysts (New Jersey: John Wiley & Sons), 75–119. chap. Energy-Dispersive EXAFS: Principles and Application in Heterogeneous Catalysis. doi:10.1002/9781118355923.ch3

CrossRef Full Text | Google Scholar

Novotny, Z., Aegerter, D., Comini, N., Tobler, B., Artiglia, L., Maier, U., et al. (2020). Probing the Solid-Liquid Interface With Tender X Rays: A New Ambient-Pressure X-ray Photoelectron Spectroscopy Endstation at the Swiss Light Source. Rev. Scientific Instr. 91, 023103. doi:10.1063/1.5128600

CrossRef Full Text | Google Scholar

Orimo, S.-i., Nakamori, Y., Eliseo, J. R., Züttel, A., and Jensen, C. M. (2007). Complex Hydrides for Hydrogen Storage. Chem. Rev. 107, 4111–4132. doi:10.1021/cr0501846

PubMed Abstract | CrossRef Full Text | Google Scholar

Phillips, R., and Dunnill, C. W. (2016). Zero gap Alkaline Electrolysis Cell Design for Renewable Energy Storage as Hydrogen Gas. RSC Adv. 6, 100643–100651. doi:10.1039/C6RA22242K

CrossRef Full Text | Google Scholar

Pinel, P., Cruickshank, C. A., Beausoleil-Morrison, I., and Wills, A. (2011). A Review of Available Methods for Seasonal Storage of Solar thermal Energy in Residential Applications. Renew. Sustainable Energ. Rev. 15, 3341–3359. doi:10.1016/j.rser.2011.04.013

CrossRef Full Text | Google Scholar

Reece, S. Y., Hamel, J. A., Sung, K., Jarvi, T. D., Esswein, A. J., Pijpers, J. J., et al. (2011). Wireless Solar Water Splitting Using Silicon-Based Semiconductors and Earth-Abundant Catalysts. Science 334, 645–648. doi:10.1126/science.1209816

PubMed Abstract | CrossRef Full Text | Google Scholar

Regoutz, A., Mascheck, M., Wiell, T., Eriksson, S. K., Liljenberg, C., Tetzner, K., et al. (2018). A Novel Laboratory-Based Hard X-ray Photoelectron Spectroscopy System. Rev. Scientific Instr. 89, 073105. doi:10.1063/1.5039829

CrossRef Full Text | Google Scholar

Reilly, J. J., and Wiswall, R. H. (1967). Reaction of Hydrogen With Alloys of Magnesium and Copper. Inorg. Chem. 6, 2220–2223. doi:10.1021/ic50058a020

CrossRef Full Text | Google Scholar

Rey, N. G., and Dlott, D. D. (2017). Studies of Electrochemical Interfaces by Broadband Sum Frequency Generation. J. Electroanalytical Chem. 800, 114–125. doi:10.1016/j.jelechem.2016.12.023

CrossRef Full Text | Google Scholar

Roché, M., Li, Z., Griffiths, I. M., Le Roux, S., Cantat, I., Saint-Jalmes, A., et al. (2014). Marangoni Flow of Soluble Amphiphiles. Phys. Rev. Lett. 112, 208302. doi:10.1103/PhysRevLett.112.208302

CrossRef Full Text | Google Scholar

Roiaz, M., Monachino, E., Dri, C., Greiner, M., Knop-Gericke, A., Schlögl, R., et al. (2016). Reverse Water-Gas Shift or Sabatier Methanation on Ni(110)? Stable Surface Species at Near-Ambient Pressure. J. Am. Chem. Soc. 138, 4146–4154. doi:10.1021/jacs.5b13366

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, K., Artiglia, L., and van Bokhoven, J. A. (2018). Ambient Pressure Photoelectron Spectroscopy: Opportunities in Catalysis From Solids to Liquids and Introducing Time Resolution. ChemCatChem. 10, 666–682. doi:10.1002/cctc.201701522

CrossRef Full Text | Google Scholar

Rudman, P. S. (1979). Hydrogen‐diffusion‐rate‐limited Hydriding and Dehydriding Kinetics. J. Appl. Phys. 50, 7195–7199. doi:10.1063/1.325831

CrossRef Full Text | Google Scholar

Rydén, J., Hjörvarsson, B., Ericsson, T., Karlsson, E., Krozer, A., and Kasemo, B. (1989). Unusual Kinetics of Hydride Formation in Mg-Pd Sandwiches, Studied by Hydrogen Profiling and Quartz Crystal Microbalance Measurements. J. Less Common Met. 152, 295–309. doi:10.1016/0022-5088(89)90097-0

CrossRef Full Text | Google Scholar

Sambalova, O., Billeter, E., Mann, J., Miyayama, T., Burnat, D., Heel, A., et al. (2020). Hard and Soft X‐ray Photoelectron Spectroscopy for Selective Probing of Surface and Bulk Chemical Compositions in a Perovskite‐type Ni Catalyst. Surf Interf. Anal 52, 811–817. doi:10.1002/sia.6843

CrossRef Full Text | Google Scholar

Sambalova, O., Billeter, E., Yildirim, O., Sterzi, A., Bleiner, D., and Borgschulte, A. (2021). Magnetic Field Enhancement of Electrochemical Hydrogen Evolution Reaction Probed by Magneto-Optics. Int. J. Hydrogen Energ. 46, 3346–3353. doi:10.1016/j.ijhydene.2020.10.210

CrossRef Full Text | Google Scholar

Schlapbach, L., and Züttel, A. (2001). Hydrogen-Storage Materials for Mobile Applications. Nature. 414, 353–358. doi:10.1038/35104634

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlapbach, L. (1992). “Surface Properties and Activation,” in Hydrogen in Intermetallic Compounds II. Editor L. Schlapbach (Berlin: Springer-Verlag). doi:10.1007/3-540-54668-5_9

CrossRef Full Text | Google Scholar

Shah, S. K., Aye, L., and Rismanchi, B. (2018). Seasonal thermal Energy Storage System for Cold Climate Zones: A Review of Recent Developments. Renew. Sustainable Energ. Rev. 97, 38–49. doi:10.1016/j.rser.2018.08.025

CrossRef Full Text | Google Scholar

Shen, Y. R. (1989). Surface Properties Probed by Second-Harmonic and Sum-Frequency Generation. Nature. 337, 519–525. doi:10.1038/337519a0

CrossRef Full Text | Google Scholar

Sil, S., and Umapathy, S. (2014). Raman Spectroscopy Explores Molecular Structural Signatures of Hidden Materials in Depth: Universal Multiple Angle Raman Spectroscopy. Sci. Rep. 4, 5308. doi:10.1038/srep05308

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, G. (1956). Problems Pertaining to the Dehydration of Sodium Hydroxide by Volatilization of Water.(Oak Ridge, Tennessee: Oak Ridge National Laboratory, Metallurgy Division and Union Carbide Nuclear Company and U.S. Atomic Energy Commission).

Google Scholar

Stampfer, J. F., Holley, C. E., and Suttle, J. F. (1960). The Magnesium-Hydrogen System1-3. J. Am. Chem. Soc. 82, 3504–3508. doi:10.1021/ja01499a006

CrossRef Full Text | Google Scholar

Steiner, U. E., and Ulrich, T. (1989). Magnetic Field Effects in Chemical Kinetics and Related Phenomena. Chem. Rev. 89, 51–147. doi:10.1021/cr00091a003

CrossRef Full Text | Google Scholar

Sun, Z., Lu, X., Nyahuma, F. M., Yan, N., Xiao, J., Su, S., et al. (2020). Enhancing Hydrogen Storage Properties of MgH2 by Transition Metals and Carbon Materials: A Brief Review. Front. Chem. 8, 552. doi:10.3389/fchem.2020.00552

PubMed Abstract | CrossRef Full Text | Google Scholar

Terreni, J., Sambalova, O., Borgschulte, A., Rudić, S., Parker, S. F., and Ramirez-Cuesta, A. J. (2020). Volatile Hydrogen Intermediates of CO2 Methanation by Inelastic Neutron Scattering. Catalysts. 10, 433. doi:10.3390/catal10040433

CrossRef Full Text | Google Scholar

Terreni, J., Trottmann, M., Delmelle, R., Heel, A., Trtik, P., Lehmann, E. H., et al. (2018). Observing Chemical Reactions by Time-Resolved High-Resolution Neutron Imaging. J. Phys. Chem. C. 122, 23574–23581. doi:10.1021/acs.jpcc.8b07321

CrossRef Full Text | Google Scholar

Tobias, C. W. (1959). Effect of Gas Evolution on Current Distribution and Ohmic Resistance in Electrolyzers. J. Electrochem. Soc. 106, 833. doi:10.1149/1.2427506

CrossRef Full Text | Google Scholar

Töpler, J., Buchner, H., Säufferer, H., Knorr, K., and Prandl, W. (1982). Measurements of the Diffusion of Hydrogen Atoms in Magnesium and Mg₂Ni by Neutron Scattering. J. Less Common Met. 88, 397–404. doi:10.1016/0022-5088(82)90248-X

CrossRef Full Text | Google Scholar

Uchida, H. T., Wagner, S., Hamm, M., Kürschner, J., Kirchheim, R., Hjörvarsson, B., et al. (2015). Absorption Kinetics and Hydride Formation in Magnesium Films: Effect of Driving Force Revisited. Acta Materialia. 85, 279–289. doi:10.1016/j.actamat.2014.11.031

CrossRef Full Text | Google Scholar

Vincent, I., Choi, B., Nakoji, M., Ishizuka, M., Tsutsumi, K., and Tsutsumi, A. (2018). Pulsed Current Water Splitting Electrochemical Cycle for Hydrogen Production. Int. J. Hydrogen Energ. 43, 10240–10248. doi:10.1016/j.ijhydene.2018.04.087

CrossRef Full Text | Google Scholar

Weber, R., and Dorer, V. (2008). Long-term Heat Storage With NaOH. Vacuum. 82, 708–716. doi:10.1016/j.vacuum.2007.10.018

CrossRef Full Text | Google Scholar

Wilde, M., and Fukutani, K. (2014). Hydrogen Detection Near Surfaces and Shallow Interfaces With Resonant Nuclear Reaction Analysis. Surf. Sci. Rep. 69, 196–295. doi:10.1016/j.surfrep.2014.08.002

CrossRef Full Text | Google Scholar

Wilde, M., and Fukutani, K. (2008). Penetration Mechanisms of Surface-Adsorbed Hydrogen Atoms into Bulk Metals: Experiment and Model. Phys. Rev. B. 78, 115411. doi:10.1103/PhysRevB.78.115411

CrossRef Full Text | Google Scholar

Xiao, Y., Wang, Y., Bo, S.-H., Kim, J. C., Miara, L. J., and Ceder, G. (2020). Understanding Interface Stability in Solid-State Batteries. Nat. Rev. Mater. 5, 105–126. doi:10.1038/s41578-019-0157-5

CrossRef Full Text | Google Scholar

Yamaguchi, S., Kundu, A., Sen, P., and Tahara, T. (2012). Communication: Quantitative Estimate of the Water Surface Ph Using Heterodyne-Detected Electronic Sum Frequency Generation. J. Chem. Phys. 137, 151101. doi:10.1063/1.4758805

CrossRef Full Text | Google Scholar

Yang, J., Sudik, A., Wolverton, C., and Siegel, D. J. (2010). High Capacity Hydrogenstorage Materials: Attributes for Automotive Applications and Techniques for Materials Discovery. Chem. Soc. Rev. 39, 656–675. doi:10.1039/b802882f

PubMed Abstract | CrossRef Full Text | Google Scholar

Yonezawa, Y., Minamimoto, H., Nagasawa, F., Takase, M., Yasuda, S., and Murakoshi, K. (2017). In-Situ Electrochemical Surface-Enhanced Raman Scattering Observation of Molecules Accelerating the Hydrogen Evolution Reaction. J. Electroanalytical Chem. 800, 7–12. doi:10.1016/j.jelechem.2017.04.049

CrossRef Full Text | Google Scholar

Zaera, F. (2012). Probing Liquid/Solid Interfaces at the Molecular Level. Chem. Rev. 112, 2920–2986. doi:10.1021/cr2002068

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaluski, L., Zaluska, A., and Ström-Olsen, J. O. (1997). Nanocrystalline Metal Hydrides. J. Alloys Compounds. 253-254, 70–79. doi:10.1016/S0925-8388(96)02985-4

CrossRef Full Text | Google Scholar

Zboray, R., and Trtik, P. (2018). 800 Fps Neutron Radiography of Air-Water Two-Phase Flow. MethodsX. 5, 96, 102. doi:10.1016/j.mex.2018.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Zdansky, E. A. (1959). Elektrolyseur für die Wasserzersetzung (Swiss Patent: CH000000341483). Bern.

Google Scholar

Zdansky, E. A. (1977). Wasserelektrolyseur (German Disclosure Document: DE000002600344). Bern.

Google Scholar

Zeng, K., and Zhang, D. (2010). Recent Progress in Alkaline Water Electrolysis for Hydrogen Production and Applications. Prog. Energ. Combustion Sci. 36, 307–326. doi:10.1016/j.pecs.2009.11.002

CrossRef Full Text | Google Scholar

Zhang, L., Lu, X., Ji, L., Yan, N., Sun, Z., and Zhu, X. (2019). Catalytic Effect of Facile Synthesized TiH1.971 Nanoparticles on the Hydrogen Storage Properties of MgH2. Nanomaterials. 9, 1370. doi:10.3390/nano9101370

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Li, M., Shi, W., Wang, B., and Li, X. (2014). Experimental Investigation on Charging and Discharging Performance of Absorption Thermal Energy Storage System. Energ. Convers. Management. 85, 425–434. doi:10.1016/j.enconman.2014.05.100

CrossRef Full Text | Google Scholar

Zhdanov, V. P., Krozer, A., and Kasemo, B. (1993). Kinetics of First-Order Phase Transitions Initiated by Diffusion of Particles From the Surface into the Bulk. Phys. Rev. B. 47, 11044–11048. doi:10.1103/PhysRevB.47.11044

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, C., Gao, Y., Bowman, R. C., Zhang, J., Liu, H., Sun, P., et al. (2021a). A High Throughput Dynamic Method for Characterizing Thermodynamic Properties of Catalyzed Magnesium Hydrides by Thermogravimetric Analysis. Phys. Chem. Chem. Phys. 23, 15374–15383. doi:10.1039/D1CP02498A

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, C., Zhang, J., Bowman, R. C., and Fang, Z. Z. (2021b). Roles of Ti-Based Catalysts on Magnesium Hydride and its Hydrogen Storage Properties. Inorganics. 9, 36. doi:10.3390/inorganics9050036

CrossRef Full Text | Google Scholar

Zhou, W., Chen, M., Guo, M., Hong, A., Yu, T., Luo, X., et al. (2020). Magnetic Enhancement for Hydrogen Evolution Reaction on Ferromagnetic MoS2 Catalyst. Nano Lett. 20, 2923–2930. doi:10.1021/acs.nanolett.0c00845

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., and Wang, C. (2010). Galvanostatic Intermittent Titration Technique for Phase-Transformation Electrodes. J. Phys. Chem. C. 114, 2830–2841. doi:10.1021/jp9113333

CrossRef Full Text | Google Scholar

Züttel, A., Remhof, A., Borgschulte, A., and Friedrichs, O. (2010). Hydrogen: the Future Energy Carrier. Phil. Trans. R. Soc. A. 368, 3329–3342. doi:10.1098/rsta.2010.0113

CrossRef Full Text | Google Scholar