Neutronics Perturbation Calculation Method Study of Solid Breeder Tritium Breeding Blanket for TBR Enhancement

Tritium breeding blanket (TBB) is an essential component in a fusion reactor, which has functions of tritium breeding, energy generation, and neutron shielding. Tritium breeding ratio (TBR) is a key parameter to evaluate whether the TBB could produce enough tritium to achieve the tritium self-sufficiency (TBR >1) for fusion reactor. Current codes or software are hard to meet the requirements of high efficiency, high resolution, and high automation for neutronic optimization of TBB. In this article, the application of the density perturbation calculation on a solid breeder TBB was first performed. Then, the method of the geometry perturbation calculation based on the virtual density theory was studied. Results and comparison analysis indicate that the 1st + 2nd-order neutronic perturbation calculations (including the density perturbation and the geometry perturbation) results are consistent with the transport results under a perturbation of −15% to +15%. It is proven to be valid to use the perturbation calculation for rapid TBR enhancement study of the solid breeder TBB.

Introduction

The tritium breeding blanket (TBB) is an essential component to achieve the tritium production, energy generation, and extraction in the fusion reactor. The solid breeder TBB is an important alternative for a demonstration fusion reactor (DEMO) or a fusion power plant. The tritium self-sufficiency is a significant goal, and the tritium breeding ratio (TBR) is a key parameter to evaluate whether the TBB can produce enough tritium to achieve the tritium self-sufficiency for fusion reactor, which could be calculated as follows: (Wan et al., 2017; Zhuang et al., 2019).

$\text{TBR}=\frac{{\displaystyle \iint \left[N_{{}^6\text{L}\text{i}}{\sigma }_{{}^6\text{L}\text{i}\left(n,\alpha \right)}\left(\overrightarrow{r},E\right)+N_{{}^7\text{L}\text{i}}{\sigma }_{{}^7\text{L}\text{i}\left(n,a\right)}\left(\overrightarrow{r},E\right)\right]}\cdot \varphi \left(\overrightarrow{r},E,t\right)dEd\overrightarrow{r}}{S_{\mathit{plasma}}}.(1)$

N⁶_Li and N⁷_Li are the atom densities of 6Li and 7Li separately, σ⁶_Li and σ⁷_Li are the cross sections of (n, T) reaction of 6Li and 7Li separately, Φ(r, E, t) is the neutron flux distribution, S_plasma is the generation rate of fusion neutron in plasma. In brief, TBR represents the average atom number of tritium produced in TBB for every fusion neutron consumed.

However, the TBR of the fusion reactor will be impacted by a number of factors, including the geometries (the opening ports to install the corresponding heating and diagnostic equipment [Cao et al., 2021], and a heterogeneous model of the blanket [Qu et al., 2020]), materials (type, density, enrichment), nuclear libraries (uncertainty), and neutron transport codes (uncertainty). Meanwhile, the tritium losses occur during the fuel cycle because of the tritium decay, leakage, extraction, and retention, which is a considerable challenge to the tritium self-sufficiency. Therefore, a higher TBR is needed. Taking the above facts into account, the TBR design goal of a fusion reactor is set as 1.15 (Fischer et al., 2005).

Consequently, neutronic optimization study toward the solid breeder TBB is imperative in blanket design, which is a process to enhance the TBR (by means of density and geometric adjustments) as much as possible on the basis of engineering feasibilities (Qu et al., 2021). The current neutronic optimization methods are based on multiple neutronic transport calculation. Monte-Carlo codes MCNP-4C based on FENDL-3.2 are selected for the neutronic transport calculation and optimization for the solid breeder TBB (Forster and Godfrey, 1985). However, the following concerns will be arisen:

(1) As for the neutronic optimization for a typical solid breeder TBB module, multiple neutronic transport calculation will lead to a considerable amount of computation and a low efficiency. However, this method could not be adopted for the neutronic optimization for the whole solid breeder TBBs of a fusion reactor. (2) Small density or geometric adjustments will be performed in the neutronic optimization, and there will be an extremely little change for the TBR. This has the same order magnitude with the standard deviation of Monte-Carlo codes. As a response, accurate change results of TBR may not be obtained through multiple neutronic transport calculation.

The above two concerns can be effectively avoided by using the neutronic perturbation calculation instead. The variation of the neutron flux can be obtained by solving the neutronic perturbation equation based on the neutron flux before adjustments in the condition that no significant distortion of the neutron flux distribution occurs. Currently, the perturbation calculation is widely used in the neutronic analysis and design of fission reactors.

In this article, the verification of the density perturbation calculation on the solid breeder TBB was first performed. Then, the method of the geometry perturbation calculation was studied and verified. The work can provide a solid foundation for the rapid neutronic optimization of the solid breeder TBB.

Neutronics Model

A helium-cooled ceramic breeder (HCCB) TBB typical module based on the latest design of China Fusion Engineering Test Reactor (CFETR) HCCB blanket (Wang et al., 2019; Qu et al., 2020) (shown as Figure 1) was selected for the neutronic analysis and the verification of the density perturbation calculation. The toroidal width and poloidal length of the blanket module are both 120 cm, and the radial thickness is 80 cm (2.5 cm for first wall (FW), 56.5 cm for breeding zone, 14 cm for manifold, and 7 cm for back plate). The tungsten armor with 3 mm in radial before the FW is omitted in this article. The poloidal length of caps is the same as that of the FW thickness.

FIGURE 1

FIGURE 1. CAD model of the CFETR HCCB blanket typical module.

CLF-1 steel was selected as the structure material, Li₄SiO₄ (the enrichment of 6Li is 90%) as the tritium breeder, and beryllium as the neutron multiplier in the pebble bed regions. The packing fractions for the Li₄SiO₄ and Be pebble beds were assumed to be 62% and 80%, respectively. The whole breeding zone was divided into nine regions in radial: five regions for the tritium breeding, four regions for the neutron multiplication, and there are eight cooling plates (CPs), which provide cooling function and structural support for the blanket box. The initial radial dimensions of the blanket module are summarized in Table 1.

TABLE 1

TABLE 1. The initial radial dimensions of the blanket module.

Based on the HCCB CAD model, the homogeneous neutronic model was produced for 3D transport calculation, shown as Figure 2. In the homogeneous model, different materials of the breeding blanket were mixed according to their volume fractions in each functional region. Reflecting boundaries were applied, including both the toroidal and poloidal directions. In radial direction, reflecting boundary was also adopted in the surface near plasma, and free boundary was adopted in the outer surface of the back plate. A general neutron source of a Gaussian fusion energy spectrum was added in the front of the FW.

FIGURE 2

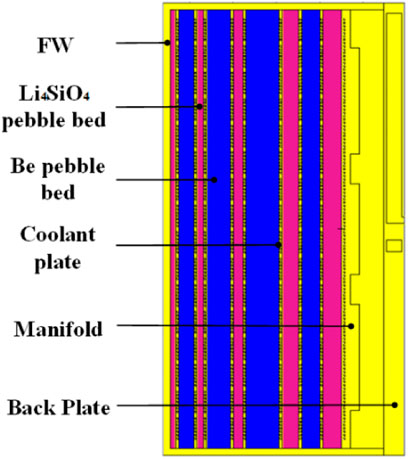
FIGURE 2. 3D neutronic model of the HCCB TBB (Qu et al., 2020).

Methods

Perturbation Theory

The perturbation theory could be adopted for the cases that there is no obvious change of neutron flux distribution for a specific neutronic system before and after a perturbation. Based on the neutron flux distribution before the perturbation, the neutron flux distribution after the perturbation could be obtained by solving the neutron adjoined equation (shown as Eq. 2).

$\begin{array}{c}-\frac{1}{v}\frac{\partial {\varphi }^{\ast }}{\partial t}-\Omega \cdot \nabla {\varphi }^{\ast }+\Sigma {\varphi }^{\ast }-{\displaystyle {\int }_0^{\infty }d{E}^{\prime }{\displaystyle {\int }_{{\Omega }^{\text{'}}}{\Sigma }_s\left(r;E,\Omega \to E\prime ,\Omega \prime \right)}}{\varphi }^{\ast }\left(r,E^{\prime },{\Omega }^{\prime },t\right)d{\Omega }^{\prime },\\ =\frac{v{\Sigma }_f\left(r,E\right)}{4\pi }{\displaystyle {\int }_0^{\infty }d{E}^{\prime }}{\displaystyle {\int }_{{\Omega }^{\text{'}}}\chi \left(E^{\text{'}}\right){\varphi }^{\ast }\left(r^{\prime },E^{\prime },{\Omega }^{\prime },t\right)}d{\Omega }^{\prime }.\end{array}(2)$

Φ fnlowast(r, E, t) is the adjoined neutron flux which is the distribution of neutron value.

The perturbation calculation has been widely used in reactor physics calculation for fission reactors, including the core Doppler coefficient calculation, the differential value calculation of control rods, coolant cavitation value calculation, and so on. The type of perturbation includes density perturbation, cross-section perturbation, temperature perturbation, and so on.

The perturbation theory could also be put to use for the rapid calculation of neutron flux distribution of the solid breeder TBB of fusion reactors. As for a density perturbation, the TBR could be rapidly calculated through Eq. 1 based on the perturbation calculation. As for a geometric perturbation, the TBR could be rapidly calculated through the following flowchart (shown as Figure 3).

FIGURE 3

FIGURE 3. Flowchart of TBR calculation with a geometric perturbation of the solid breeder TBB.

Virtual Density Theory

The density perturbation calculation for the change of the TBR on the TBB was verified. Comprehensively, the study for the geometry perturbation calculation for the change of the TBR on the TBB based on the virtual density theory could be performed (Hess et al., 1998).

According to the expression for isotropic deformation calculation based on the virtual density theory, the equivalent coefficient can be calculated as follows:

$\epsilon =\frac{N_2-N_1}{N_1}=\frac{{\kappa }_d{\kappa }_l{N}_1-N_1}{N_1}={\kappa }_d{\kappa }_l-1.(3)$

ε is the equivalent coefficient of a specific kind of material that indicates the rate of change of atom density (shown as the following formula); N₁ is the atom density before the deformation, and N₂ is the equivalent atom density; κ_d is the density change coefficient; κ_l is the linear scale change coefficient; δ_N and δ_ρ are the variation of the atom density and mass density of the specific material, separately.

$\epsilon =\frac{\delta N}{N}=\frac{\delta \rho }{\rho }.(4)$

According to the isotropic expansion case of a sphere, the density change coefficient and the linear scale change coefficient are expressed as follows:

${\kappa }_d=\frac{1}{f^3}.(5)$

${\kappa }_l=f,(6)$

f is the change coefficient of radium. If f = 1.01, the radium will be increased by 1%. Thus, the equivalent coefficient of an isotropic expansion case can be calculated as follows:

$\epsilon ={\kappa }_d{\kappa }_l-1=\frac{1}{f^2}-1.(7)$

As for the geometry adjustment (radial expansion or compression of each tritium breeder region or the neutron multiplier region for the HCCB TBB) of the TBB for the neutronic optimization, it is not an isotropic deformation case but an anisotropic deformation one.

In this article, the CFETR HCCB TBB typical module with a sandwich-like breeder zone was also selected for the geometry perturbation method study. According to Figure 1, both the tritium breeder regions and neutron multiplier regions are rectangular solids, which can be described with the radial thickness, toroidal width, and poloidal length. The toroidal width and poloidal length keep as constant during the neutronic optimization and the geometry adjustment for the neutronic optimization can be regarded as the radial expansion or compression case. In this case, there will be a change for the radial thickness (κ_d = f) and the density change (κ_l = 1/f) in a specific region, so the radial equivalent coefficient can be calculated as follows:

${\epsilon }_r=\frac{f}{f}-1=0.(8)$

Meanwhile, there is no change in the toroidal width and the poloidal length (d_o = 1) and a reduction in the density (κ_l = 1/f); consequently, the toroidal and poloidal equivalent coefficient can be calculated as follows:

${\epsilon }_t={\epsilon }_p=\frac{1}{f}-1.(9)$

Figure 4 shows the local layout of the HCCB TBB before and after the geometric adjustment. The local layout model consists of the tritium breeder regions, CPs, and neutron multiplier regions. The total radial thickness of the local layout model is assumed to be constant during the geometry adjustment. According to the local layout, l^CP is the radial thickness of the CP, which is also be assumed to be a constant during the neutronic optimization. l₁^Li4SiO4 and l₂^Li4SiO4 are the radial thickness of the tritium breeder region before and after the geometry adjustment, separately, and Δl is the increment of the tritium breeding region. Correspondingly, l₁^Be and l₂^Be are the radial thickness of the neutron multiplier region before and after the geometry adjustment, separately, and Δl is the decrement of the Be region. ρ₁^Li4SiO4 and ρ₁^Be are the densities of the tritium breeder region and the neutron multiplier region before the geometry adjustment separately, and ρ₂^Li4SiO4 and ρ₂^Be are the densities of the tritium breeder region and the neutron multiplier region after the geometry adjustment. The equivalent coefficients of the tritium breeder region and the neutron multiplier region can be calculated as follows:

${\epsilon }^{{\mathit{Li}}_4{\mathit{SiO}}_4}=\frac{1}{f}-1=\frac{-\Delta l}{l_1^{{\mathit{Li}}_4{\mathit{SiO}}_4}+\Delta l},(10)$

${\epsilon }^{\mathit{Be}}=\frac{1}{f}-1=\frac{\Delta l}{l_1^{\mathit{Be}}-\Delta l}.(11)$

FIGURE 4

FIGURE 4. Local layout of the HCCB TBB before (middle) and after (bottom) the geometry adjustment.

The equivalent density change of these two regions can be calculated as follows:

$\delta {\rho }^{{\text{Li}}_4{\text{SiO}}_4}=\frac{-\Delta l\cdot {\rho }_1^{{\text{Li}}_4{\text{SiO}}_4}}{l_1^{{\text{Li}}_4{\text{SiO}}_4}+\Delta l}=\frac{-\Delta l\cdot {\rho }_1^{{\text{Li}}_4{\text{SiO}}_4}}{l_2^{{\text{Li}}_4{\text{SiO}}_4}},(12)$

$\delta {\rho }^{\mathit{Be}}=\frac{\Delta l\cdot {\rho }_1^{\mathit{Be}}}{l_1^{\mathit{Be}}-\Delta l}=\frac{\Delta l\cdot {\rho }_1^{\mathit{Be}}}{l_2^{\mathit{Be}}}.(13)$

ε^Li4SiO4 and ε^Be are the equivalent coefficients of the tritium breeder region and the neutron multiplier region, respectively. δρ^Li4SiO4 and δρ^Be are the equivalent density change of the tritium breeder region and the neutron multiplier, individually.

Then, the conclusions are made from the local layout model to the HCCB TBB typical model, which can be shown as Figure 5.

FIGURE 5

FIGURE 5. Layout of the HCCB TBB typical module.

In the HCCB TBB typical module with the sandwich-like breeder zone, there are m tritium breeder regions, n neutron multiplier regions, and k CPs (k = m + n − 1). Before the geometry adjustment, the radial thickness and the density of each tritium breeder region are expressed by l_i^Li4SiO4 and ρ_i^Li4SiO4 (i = 1,2 … m), respectively. The radial thickness and the density of each neutron multiplier region are defined as l_j^Be and ρ_j^Be (j = 1,2 … n), separately. After the geometry adjustment, the change of the radial thickness and the change of the density of each tritium breeder region are Δl_i^Li4SiO4 and Δρ_i^Li4SiO4 (i = 1,2 … m), individually. The change of the radial thickness and the change of the density of each neutron multiplier region are Δl_j^Be and Δρ_j^Be (j = 1,2 … n). The total radial thickness of the breeder zone of the TBB remains unchanged (shown as the following equation).

${\displaystyle \sum _{i=1}^m\Delta l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}}+{\displaystyle \sum _{j=1}^n\Delta l_j^{\mathit{Be}}}=0.(14)$

Based on the conclusions above, the equivalent coefficients and equivalent change of the density of each tritium breeder region and neutron multiplier region can be calculated as follows:

${\epsilon }_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}=\frac{-\Delta l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}}{l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}+\Delta l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}}\left(i=\mathrm{1,2}\cdots m\right),(15)$

${\epsilon }_j^{\mathit{Be}}=\frac{-\Delta l_j^{\mathit{Be}}}{l_j^{\mathit{Be}}+\Delta l_j^{\mathit{Be}}}\left(j=\mathrm{1,2}\cdots n\right).(16)$

$\delta {\rho }_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}=\frac{-\Delta l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}\cdot {\rho }_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}}{l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}+\Delta l_i^{{\mathit{Li}}_4{\mathit{SiO}}_4}}\left(i=\mathrm{1,2}\cdots m\right),(17)$

$\delta {\rho }_j^{\mathit{Be}}=\frac{-\Delta l_j^{\mathit{Be}}\cdot {\rho }_j^{\mathit{Be}}}{l_j^{\mathit{Be}}+\Delta l_j^{\mathit{Be}}}\left(j=\mathrm{1,2}\cdots n\right).(18)$

Verification

Density Perturbation

The neutronic perturbation calculation for the change of the TBR and nuclear heat of each part on the TBB of three cases was performed, and the details of the three cases are listed in Table 2 (Mckinney and Iverson, 1996; Schnabel et al., 2021). Ten percent is selected for the interval of density perturbation (5% is selected for the TBR comparison under case 1).

TABLE 2

TABLE 2. Details of the three cases for the neutronic perturbation calculation.

Two kinds of the results were calculated for comparison: the transport results, and the 1st + 2nd order of the neutronic perturbation results. The TBR comparison of the HCCB TBB of cases 1, 2, and 3 are shown as Figure 6. The nuclear heat comparison (F6 tally results are compared) is shown as Figure 7. The curve of relative bias is also shown in each figure (in red). Regions of each relative bias band are marked with different colors. The variation of TBR and F6 calculated by transport code and perturbation method under each case is shown as Figure 8 and Figure 9 individually. The MC transport results were regarded as the reference. In this article, 1E7 particles are simulated, and some variance reduction techniques (such as weight windows, forced collision, energy splitting, and roulette) are used in the MCNP-4C calculation. In this way, the Monte-Carlo relative deviation could reduce to ∼0.01%. Therefore, the change of TBB neutronics performances were large enough (an order of magnitude larger) compared with the standard deviation of MCNP-4C code, and the perturbation problem could be verified using the MC method.

FIGURE 6

FIGURE 6. Curves of the TBR versus the density perturbation of the HCCB TBB under each case.

FIGURE 7

FIGURE 7. Curves of the F6 versus the density perturbation of the HCCB TBB under each case.

FIGURE 8

FIGURE 8. Curves of variation of TBR versus the density perturbation rate under each case.

FIGURE 9

FIGURE 9. Curves of the variation of F6 versus the density perturbation rate under each case.

Analysis toward the above results indicates that the 1st + 2nd order of the neutronic perturbation calculation results (including TBR and nuclear heat) is consistent with the transport results under a density perturbation of -15% to +15% under each case (with a relative bias <0.2%). Meanwhile, the neutronic perturbation calculation is much faster than the transport calculation (the efficiency could be improved by more than 100 times in conservative estimating). Therefore, the perturbation calculation can be a substitute for the transport calculation, which will be a better choice for the rapid neutronic optimization for the TBB.

Geometric Perturbation

The CFETR HCCB TBB typical module was chosen for the verification of the geometry perturbation calculation. Geometry adjustments toward the CFETR HCCB TBB of five cases were performed, and the radial adjustment of each region of the HCCB TBB typical module of each case are listed in Table 3. Case 0 is the initial scheme of the CFETR HCCB TBB, which the radial lengths of each region can be found in Table 1. The maximum geometry adjustment of all regions is less than 15% (case 5 in Li-1 region). According to the virtual density theory, the equivalent mass densities of each tritium breeder region and neutron multiplier region can be summarized in Table 4.

TABLE 3

TABLE 3. Radial geometry adjustment of each region of the HCCB TBB typical module for each case.

TABLE 4

TABLE 4. Equivalent mass densities of each region under each case.

Three methods (methods A, B, and C) were used for the neutronic calculation for the HCCB TBB. The model with the geometry adjustment (shown in Table 3) of each case was adopted, and 3D neutronic transport calculation was performed in method A; 3D neutronic transport calculation based on the model with the equivalent density adjustment (shown in Table 4) of each case was made in method B; 3D neutronic transport calculation of the initial scheme was performed, and perturbation calculation (the 1st + 2nd order) based on the virtual density theory of each case was made in model C. The neutron flux of each region calculated by methods A and B is listed and compared in Table 5 (the tritium breeding region) and Table 6 (the neutron multiplier region), separately. According to the design parameters of CFETR phase II, a fusion power of 1.5 GW was assumed, based on which a neutron wall load of 1.69 MW/m² was adopted in the calculations for a single TBB module (Cao et al., 2021). The TBRs calculated by using the three methods are listed in Table 7. The MCNP-4C code was adopted for the 3D neutronic and perturbation calculation based on FENDL-3.2. All the results calculated by method A are regarded as the references. The analysis and conclusions can be portrayed as follows:

(1) Relative deviations that the neutron flux of each region and the TBR are listed in Tables 5, 6, 7, separately for using methods A and B generally showing an increasing trend as the radial geometry variation of each region goes up.

(2) The closer the specific region is to plasma, the larger the relative deviation of the neutron flux is.

(3) The maximum relative deviation of the neutron flux is less than 1.5% in the vast majority of cases.

(4) The maximum relative deviation of the TBR between methods A and B is less than or equal to 0.51%. However, the deviation is no more than 0.2% in the case that the perturbation rate is less than 15%, which showed a good coincidence with the transport results and fully met the requirements for TBB neutronics optimization. The TBR calculated by method C is almost identical to that obtained by method B, but it is much faster in terms of efficiency.

TABLE 5

TABLE 5. Variation of the neutron flux of each tritium breeding region calculated by each method of each case.

TABLE 6

TABLE 6. Variation of the neutron flux of each neutron multiplier region calculated by each method of each case.

TABLE 7

TABLE 7. Variation of the TBR calculated by each method of each case.

Therefore, the geometry perturbation calculation can be adopted for the solid breeder TBB of the fusion reactor for the rapid neutronic optimization based on the virtual density theory.

Conclusion

In this article, the verification of the density perturbation calculation on the solid TBB was first performed. Then, method of the geometry perturbation calculation based on the virtual density theory was studied. Results indicate that the neutronic perturbation calculation, including the density perturbation and the geometry perturbation, has been proven to be valid for the rapid TBR enhancement of the solid TBB.

The Monte Carlo transport calculation results in this article could meet the requirements of neutronics optimization of TBB, and a detailed test of the effects of perturbation calculations by deterministic calculations will be mentioned in a future study (Zheng et al., 2017; Wang, 2019).

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

SQ: Methodology, Software, Writing—original draft. QC: Visualization, Validation. FZ: Validation. XD: Supervision. XRW: Supervision. XYW: Writing—Reviewing and Editing.

Funding

The work at Southwestern Institute of Physics (SWIP) is supported by the National Natural Science Foundation of China Number 11905046, China ITER HCCB TBS project Number CGB-TBM-HCCB, National Key R&D Program of China Number 2017YFE0300601 and Talent Project of SWIP Number 202001XWCXRC013.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Acknowledge to the KIT (Karlsruhe Institute of Technology) for the development of McCAD code.

References

Cao, Q., Wang, X., Wu, X., Yin, M., Qu, S., Zhao, F., et al. (2021). Neutronics And Shielding Design Of Cfetr Hccb Blanket. Fusion Eng. Des. 172 (3), 112918. doi:10.1016/j.fusengdes.2021.112918

CrossRef Full Text | Google Scholar

Fischer, U., Pereslavtsev, P., and Hermsmeyer, S. (2005). Neutronic Design Optimisation of Modular HCPB Blankets for Fusion Power Reactors. Fusion Eng. Des. 75-79 (0), 751–757. doi:10.1016/j.fusengdes.2005.06.222

CrossRef Full Text | Google Scholar

Forster, R. A., and Godfrey, T. N. K., 1985 “MCNP- A General Monte-Carlo Code for Neutrons and Photon Transport.” In Proceedings of the Joint Los Alamos National Laboratory. 240 33–55. April 1985.France.

Google Scholar

Hess, A. K., Mckinney, G. W., Hendricks, J. S., and Carter, L. L.. (1998). Verification of the MCNP (TM) Perturbation Correction Feature for Cross-Section Dependent Tallies[J]. Office of Scientific & Technical Information Technical Reports. United states. doi:10.2172/1197

CrossRef Full Text | Google Scholar

Mckinney, G. W., and Iverson, J. L. (1996). Verification of the MCNP{trademark Perturbation Technique[J]. office of scientific & technical information technical reportsUnited states. doi:10.2172/221051

CrossRef Full Text | Google Scholar

Qu, S., Cao, Q., Duan, X., Wang, X., Li, Z., and Wang, X. (2020). Neutronics Effects of Homogeneous Model on Solid Breeder Blanket of CFETR. Fusion Eng. Des. 160, 111825. doi:10.1016/j.fusengdes.2020.111825

CrossRef Full Text | Google Scholar

Qu, S., Cao, Q., Duan, X., Wang, X., and Wang, X. (2021). Study on Multiphysics Coupling and Automatic Neutronic Optimization for Solid Tritium Breeding Blanket of Fusion Reactor. Energies 14 (17), 5442. Sep. 2021. doi:10.3390/en14175442

CrossRef Full Text | Google Scholar

Schnabel, G., Capote, R., and Trkov, A. (2021). Fusion Evaluated Nuclear Data Library-FENDL-3.2. Available at: https://www-nds.iaea.org/fendl/.

Google Scholar

Wan, Y. X., Li, J. G., Liu, Y., Wang, X., Chan, V., and Chen, C. (2017). Overview of the Present Progress and Activities on the CFETR. Nucl. Fusion 57, 10. doi:10.1088/1741-4326/aa686a

CrossRef Full Text | Google Scholar

Wang, X. Y. (2019). Development Status of Helium Cooled Ceramic Breeder Tritium Breeding Blanket (HCCB TBB) in China [R]. Budapest Hungary.

Google Scholar

Wang, X. Y., Feng, K. M., Chen, Y. J., Zhang, L., Feng, Y., and Wu, X. H. (2019). Current Design And R&D Progress Of Cn Hccb Tbs. ” Nucl. Fusion. 59(7). 10.1088/1741-4326/ab0c32.

Google Scholar

Zheng, Y., Xiao, Y., and Wu, H., (2017). Application of the Virtual Density Theory in Fast Reactor Analysis Based on the Neutron Transport Calculation. Nucl. Eng. Des. 320, 200–206. doi:10.1016/j.nucengdes.2017.05.020

CrossRef Full Text | Google Scholar

Zhuang, G., Li, G. Q., Li, J. G., Wan, Y. X., Liu, Y., and Wang, X. (2019). Progress of the CFETR Design. ” Nucl. Fusion. 59(11) 112010. 10.1088/1741-4326/ab0e27.

CrossRef Full Text | Google Scholar