Research on a New Single-End Fault Location Method for Single-Phase Grounding Faults of Transmission Lines Through Transition Resistance

A single-end fault location method for single-phase nonmetallic grounding faults of transmission lines in a double terminal system is studied and proposed. First, the reason for the poor accuracy of the single-end fault location method in case of single-phase nonmetallic grounding faults is analyzed theoretically, and the necessary conditions for the single-end accurate fault location are put forward. Second, under the necessary conditions of the single-end accurate fault location, according to the topology of fault component networks, the calculation method of the single-end accurate fault location of transmission lines in a double terminal system is studied. Moreover, the influence of line capacitance is considered in this fault location method, and a simple expression for calculating the fault distance is obtained. Finally, the transmission line with a single-phase nonmetallic grounding fault is modeled in PSCAD; therefore, the correctness and the ability against transition resistance of the new single-end fault location method are verified by simulation.

Introduction

In the operation of power systems, most faults occur in transmission lines; therefore, timely repair after line faults is the key to ensure the reliability of power supply. Accurate fault location can quickly locate the fault point, effectively reduce the burden of line inspection, and speed up the restoration of power supply. According to the source of fault information, the existing fault location methods for transmission line can be classified into two main types: the double-end fault location and the single-end fault location. In principle, the double-end fault location can eliminate the influence of transition resistance, which results in the advantages of a simple algorithm and high positioning accuracy; however, there also exist limitations such as data transmission depends on communication and some algorithms need data synchronization. However, the single-end fault location has the advantages of no communication impact and no need of data synchronization, which means the single-end fault location is of irreplaceable value in certain cases of power grids. According to the principle of fault location, the single-end fault location can be divided into the traveling wave method and the impedance method. The single-end fault location method using line impedance to calculate fault distance is widely used in power systems. However, in case of a fault with the existence of transition resistance, the single-end fault location method using the impedance method cannot directly calculate the fault distance in principle, which causes the poor accuracy of the single-end fault location in a nonmetallic fault; thus, the existence of transition resistance has become the biggest problem affecting the accuracy of the single-end fault location method. Therefore, it is of great practical value to theoretically analyze the reasons for the poor accuracy of the single-end fault location in the presence of transition resistance, find the necessary conditions for the single-end accurate fault location, and study and propose a new single-end accurate fault location method (Apostolopoulos and Korres, 2011; Bains and Zadeh, 2015; Fei et al., 2015; Ghorbani and Mehrjerdi, 2020; Kawady and Stenzel, 2003; Li et al., 2020; Wang and Chen, 2021; Wang et al., 2021; Xu and Zhang, 2015).

Experts around the world have done some research on the single-end fault location method in case of nonmetallic grounding faults in transmission lines. He et al. (2018) proposed an improved single-end fault location method which makes use of the electrical quantity at one end and the single-end fault location results at the other end so as to improve the accuracy of the fault location. However, this method depends on communication technology and needs to compare the location information at both ends of the line. Aboshady et al. (2019) proposed a fault location method based on single-end impedance and broadband frequency analysis. In this method, the fault is regarded as a high-frequency component voltage source injected into the system so as to solve the influence of transition resistance. Moreover, using the third-order Taylor expansion of the transmission line equation, a third-order polynomial about the fault distance x is obtained at the fault point, and the fault distance x is calculated by iterative solution. However, when the fault distance x is solved by iteration, it is not proved that the iterative algorithm must be convergent from the mathematical principle. Jia et al. (2013) proposed a single-end fault location method based on impedance measurement, which includes iterative estimation of voltage before a fault and the least square curve fitting. The algorithm provides fast and accurate fault location by comparing the calculated line reactance between the fault point and the measurement point with the known line reactance. However, the algorithm does not consider the influence of line capacitance on fault location and thus cannot be applied to the lines with large capacitance parameters. Patynowski et al. (2015) proposed a fault location method based on synchronized phasor. The solution includes three algorithms for different fault types. These algorithms calculate by using synchronized information to solve the problem of the large ranging error for fault location when there exists transition resistance. However, due to the use of synchronized phasor, additional clock synchronization of data through Ethernet or radio is required; that is, the fault location algorithm will depend on communication. Bains et al. (2017) proposed an improved fault location algorithm based on the impedance method for double circuit transmission lines. The algorithm eliminates the transition resistance by constructing the KVL equation of double circuit lines in a fault negative-sequence network and obtains the equation containing the fault distance. However, the algorithm cannot eliminate the influence of the negative-sequence internal impedance of the opposite system. When the negative-sequence internal impedance of the opposite system changes greatly, the accuracy of the algorithm will be reduced. Taheri et al. (2020) proposed a fault location algorithm based on a fault sequence component network for series capacitor–compensated transmission lines. The algorithm reads the data at the speed of 1 kHz, uses the formula to solve 61 fault distances in the generated 61 data windows, then eliminates the fault location results with low probability of occurrence, and takes the harmonic average of the remaining ranging results as the final fault location results. However, when the algorithm produces the final fault location results, it depends on the selection of eliminated data and cannot directly calculate the fault location results accurately.

The above references do not indicate the fundamental reason why the single-end fault location method cannot calculate the accurate fault distance when there exists transition resistance. Therefore, based on the analysis of existing methods, this work first studies the necessary conditions for the single-end accurate fault location method in case of the single-phase grounding fault through transition resistance of transmission lines. Second, based on the necessary conditions of the single-end accurate fault location and the equivalent circuit structure of the fault component network, a new method is studied in order to realize the single-end accurate fault location in the presence of transition resistance, and the influence of line capacitance on fault location is also considered. Finally, the correctness and the ability against transition resistance of the proposed new method are verified by simulation.

The Principle of Single-End Fault Location and the Necessary Conditions for Accurate Ranging

The schematic diagram of single-phase nonmetallic grounding fault of the double terminal system transmission line studied in this work is shown in Supplementary Figure S1. There are an M-side equivalent system and an N-side equivalent system on both sides of the transmission line. Take the electrical quantity at the M-side as an example for single-end fault location, and the set point m as the electrical quantity measurement point. The total length of the line is l km, and A-phase grounding fault passing through the transition resistance $R_{\text{g}}$ occurs on the line at the point that is x km away from the M-side system.

Among them, $Z_{\text{s}}$is the unit self-impedance per kilometer of the line. There is a coupling relationship between lines, which is represented by the coupled wave line in the figure, and the unit mutual impedance per kilometer of lines is set as $Z_{\text{m}}$.

${\dot{U}}_{\text{MA}},{\dot{U}}_{\text{MB}},{\dot{U}}_{\text{MC}}$ and ${\dot{U}}_{\text{NA}},{\dot{U}}_{\text{NB}},{\dot{U}}_{\text{NC}}$ are the voltages of the three phases A, B, and C, respectively, of the M-side and N-side systems. $Z_{\text{M}1}$and $Z_{\text{N}1}$ are the respective positive-sequence internal impedance of the M-side and N-side systems, and the zero-sequence internal impedance of the M-side and N-side systems is, respectively, set as $Z_{\text{M0}}$ and $Z_{\text{N0}}$. If the neutral point equivalent ground impedance $Z_{\text{Mg}}$ and $Z_{\text{Ng}}$ of the M-side and N-side systems shown in Supplementary Figure S1 are used to reflect the zero-sequence impedance of the M-side and N-side systems, the calculation method will be as shown in (Eq. 1) and (Eq. 2).

$Z_{\text{Mg}}=\frac{Z_{\text{M0}}-Z_{\text{M}1}}{3},(1)$

$Z_{\text{Ng}}=\frac{Z_{\text{N0}}-Z_{\text{N}1}}{3}.(2)$

In order to eliminate the influence of load currents under fault conditions, the fault component is used to study the fault location method (Zhang et al., 2006). The fault component network in the additional fault state in case of A-phase nonmetallic grounding faults is established by fault state decomposition, as shown in Supplementary Figure S2.Here, $\Delta {\dot{U}}_{\text{m}i}$and $\Delta {\dot{I}}_{\text{m}i}$ (i = A, B, C) are, respectively, the voltage change and the current change at the measuring point after faults. According to the superposition theorem satisfied by the linear circuit, the expressions are shown in (Eq. 3) and (Eq. 4), respectively.

$\{\begin{array}{l}\Delta {\dot{U}}_{\text{mA}}={\dot{U}}_{\text{mAf}}-{\dot{U}}_{\text{mA}}\\ \Delta {\dot{U}}_{\text{mB}}={\dot{U}}_{\text{mBf}}-{\dot{U}}_{\text{mB}}\\ \Delta {\dot{U}}_{\text{mC}}={\dot{U}}_{\text{mCf}}-{\dot{U}}_{\text{mC}}\end{array},(3)$

$\{\begin{array}{l}\Delta {\dot{I}}_{\text{mA}}={\dot{I}}_{\text{mAf}}-{\dot{I}}_{\text{mA}}\\ \Delta {\dot{I}}_{\text{mB}}={\dot{I}}_{\text{mBf}}-{\dot{I}}_{\text{mB}}\\ \Delta {\dot{I}}_{\text{mC}}={\dot{I}}_{\text{mCf}}-{\dot{I}}_{\text{mC}}\end{array},(4)$

where ${\dot{U}}_{\text{m}i\text{f}}$and ${\dot{U}}_{\text{m}i}$ are the measured voltages of phase i at the measuring point m, respectively, after and before the fault; ${\dot{I}}_{\text{m}i\text{f}}$and ${\dot{I}}_{\text{m}i}$ are the measured currents of phase i at the measuring point m, respectively, after and before the fault (i = A, B, C). Since the electrical quantity at the point m before and after the fault can be measured, the voltage change and current change are known. At the same time, it can be found from Supplementary Figure S2 that the B-phase line is connected in parallel with the C-phase line, so the voltage at both ends of the B-phase line and the C-phase line is equal. Since the parameters of the B-phase line and the C-phase line are the same, the current flowing through the B-phase and C-phase lines should also be equal, that is, the current and voltage relationships shown in (Eq. 5) and (Eq. 6) should be satisfied.

$\Delta {\dot{I}}_{\text{mB}}=\Delta {\dot{I}}_{\text{mC}},(5)$

$\Delta {\dot{U}}_{\text{mB}}=\Delta {\dot{U}}_{\text{mC}}.(6)$

In this study, only the steady-state fault component is applied in the calculation process. Therefore, the grounding fault branch with transition resistance can be equivalent to a power frequency constant current source ${\dot{I}}_{\text{f}}$, with its current direction being from the fault grounding point to the fault component network, and ${\dot{U}}_{I\text{f}}$ is the voltage on both sides of the constant current source. By combining the three grounding points in Supplementary Figure S2 into one grounding point, the equivalent circuit of the fault component network can be obtained, as shown in Supplementary Figure S3. Here, ${\dot{I}}_{\text{NA}}$ is the A-phase current from the fault point to the system on side N, and ${\dot{I}}_{\text{N}}$ is the current flowing through the equivalent ground impedance of the neutral point of the N-side system. It can be seen from Supplementary Figure S3 that there are four meshes in the equivalent simplified circuit. According to the mesh current law, four independent loop current equations can be listed in theory. Therefore, four independent circuits l₁ = b₁b₃b₆, l₂ = b₂b₃b₆, l₃ = b₄b₆, and l₄ = b₅b₆ are selected as follows to write the loop current equation, as shown in (Eq. 7).

$\{\begin{array}{c}{\dot{U}}_{I\text{f}}={\dot{I}}_{\text{f}}{Z}_{\text{s}}l-({\dot{I}}_{\text{f}}{Z}_{\text{s}}+\Delta {\dot{I}}_{\text{mA}}{Z}_{\text{s}}+\Delta {\dot{I}}_{\text{mB}}{Z}_{\text{m}}+\Delta {\dot{I}}_{\text{mC}}{Z}_{\text{m}})x+({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{mA}})Z_{\text{N}1}+({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}})Z_{\text{Ng}}\\ +(\Delta {\dot{I}}_{\text{mA}}{Z}_{\text{s}}+\Delta {\dot{I}}_{\text{mB}}{Z}_{\text{m}}+\Delta {\dot{I}}_{\text{mC}}{Z}_{\text{m}})l①\\ \Delta {\dot{U}}_{\text{mA}}={\dot{I}}_{\text{f}}{Z}_{\text{s}}(l-x)+({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{mA}})Z_{\text{N}1}+({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}})Z_{\text{Ng}}+(\Delta {\dot{I}}_{\text{mA}}{Z}_{\text{s}}+\Delta {\dot{I}}_{\text{mB}}{Z}_{\text{m}}+\Delta {\dot{I}}_{\text{mC}}{Z}_{\text{m}})l②\\ \Delta {\dot{U}}_{\text{mB}}={\dot{I}}_{\text{f}}{Z}_{\text{m}}(l-x)+\Delta {\dot{I}}_{\text{mB}}{Z}_{\text{N}1}+({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}})Z_{\text{Ng}}+(\Delta {\dot{I}}_{\text{mA}}{Z}_{\text{m}}+\Delta {\dot{I}}_{\text{mB}}{Z}_{\text{s}}+\Delta {\dot{I}}_{\text{mC}}{Z}_{\text{m}})l③\\ \Delta {\dot{U}}_{\text{mC}}={\dot{I}}_{\text{f}}{Z}_{\text{m}}(l-x)+\Delta {\dot{I}}_{m\text{C}}{Z}_{\text{N}1}+({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}})Z_{\text{Ng}}+(\Delta {\dot{I}}_{\text{mA}}{Z}_{\text{m}}+\Delta {\dot{I}}_{\text{mB}}{Z}_{\text{m}}+\Delta {\dot{I}}_{\text{mC}}{Z}_{\text{s}}\end{array}.④(7)$

By observing the equations shown in (Eq. 7) and combining the current voltage relationship between phase B and phase C shown in (Eq. 5) and (Eq. 6), it can be found that Eq. 3 is linearly related to Eq. 4. This shows that although the equivalent circuit diagram contains four meshes, due to the particularity of parameters, it can only write three independent loop current equations. The equations contain five unknown quantities: ${\dot{U}}_{I\text{f}}$ is the voltage on both sides of the constant current source; ${\dot{I}}_{\text{f}}$ is the current of the constant current source; $Z_{\text{N}1}$ is the positive-sequence internal impedance of the system on side N; $Z_{\text{Ng}}$ is the equivalent ground impedance of the neutral point of the system on side N; and x is the fault distance.

According to the theory of solving equations in mathematics, the fault distance x cannot be solved because the number of unknown quantities is more than the number of independent equations, which is the fundamental reason why the single-end fault location method cannot achieve accurate fault location in the case of single-phase nonmetallic grounding faults.

It can be seen that if you want to use the single terminal quantity for accurate calculation of fault distances in case of single-phase nonmetallic grounding faults, you also need to know two of the four unknown quantities ${\dot{U}}_{I\text{f}}$, ${\dot{I}}_{\text{f}}$, $Z_{\text{N}1}$, and $Z_{\text{Ng}}$. This is not only a necessary condition for solving the equation group (Eq. 7) but also a necessary condition for the single-end accurate fault location. Since the unknown quantities ${\dot{U}}_{I\text{f}}$ and ${\dot{I}}_{\text{f}}$ are related to the fault type and fault location, they cannot be estimated. Therefore, only when the positive-sequence internal impedance $Z_{\text{N}1}$ and the neutral point equivalent ground impedance $Z_{\text{Ng}}$ of the N-side system are obtained, the accurate solution of the fault distance x can be realized theoretically.

According to the operation knowledge of power systems, the positive-sequence internal impedance $Z_{\text{N}1}$ of the N-side system is related to the operation mode of the system, and the neutral point equivalent ground impedance $Z_{\text{Ng}}$ of the N-side system is related to the grounding of transformer neutral points under different operation modes of the system. In the actual operation process, the operation state of the system will not change frequently, so the method of obtaining the impedance values of variables $Z_{\text{N}1}$ and $Z_{\text{Ng}}$ according to the system operation state before a fault is feasible. That is, when the normal operation and operation mode of the system change, the internal impedance of the N-side system can be sent to the ranging device to participate in the calculation of the fault distance x as a known parameter. Through the above analysis, from the theoretical level, the necessary condition for the single-end accurate fault location is to know the positive-sequence internal impedance $Z_{\text{N}1}$ and the neutral point equivalent ground impedance $Z_{\text{Ng}}$ of the N-side system.

Single-End Accurate Fault Location Method

Single-End Accurate Fault Location Method Without Considering Line Capacitance

It can be seen from the analysis in Section 1 that when the necessary conditions for the single-end accurate fault location are met, that is, when the positive-sequence internal impedance $Z_{\text{N}1}$ and the neutral point equivalent ground impedance $Z_{\text{Ng}}$ of the N-side system are known, the fault distance x can be accurately solved by the single-end fault location method. Therefore, this section will deduce the single-end fault location formula on the premise of knowing the internal impedance of the N-side system.

Eqs 2–4 in the equation group shown in (Eq. 7) constitute the phasor equation of the three-phase ABC. Therefore, the phasor equation can be converted into a sequence equation by using the phase sequence transformation formula (Yi et al., 2005) shown in (Eq. 8).

$\left[\begin{array}{l}{\dot{F}}_1\\ {\dot{F}}_2\\ {\dot{F}}_0\end{array}\right]=\frac{1}{3}\left[\begin{array}{ccc}1& a& a^2\\ 1& a^2& a\\ 1& 1& 1\end{array}\right]\left[\begin{array}{l}{\dot{F}}_{\text{A}}\\ {\dot{F}}_{\text{B}}\\ {\dot{F}}_{\text{C}}\end{array}\right],(8)$

where ${\dot{F}}_1$, ${\dot{F}}_2$, and ${\dot{F}}_0$, respectively, represent the positive-sequence, negative-sequence, and zero-sequence components, and ${\dot{F}}_{\text{A}}$, ${\dot{F}}_{\text{B}}$, and ${\dot{F}}_{\text{C}}$, respectively, represent phasor components of phase A, phase B, and phase C, and $a=-0.5+0.866i$.

Through the processing of phase sequence transformation formulas, the equation group composed of a positive-sequence equation and a zero-sequence equation can be obtained, as shown in (Eq. 9).

$\{\begin{array}{l}\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}{Z}_{\text{s}}l+\Delta {\dot{I}}_{\text{m}1}{Z}_{\text{m}}l-{\dot{I}}_{\text{f}}(l-x)(Z_{\text{s}}-Z_{\text{m}})-Z_{\text{N}1}({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{m}1})=0\\ \Delta {\dot{U}}_{\text{m}0}-\Delta {\dot{I}}_{\text{m0}}{Z}_{\text{s}}l-2\Delta {\dot{I}}_{\text{m0}}{Z}_{\text{m}}l-{\dot{I}}_{\text{f}}(l-x)(Z_{\text{s}}+2Z_{\text{m}})-Z_{\text{N0}}\left({\dot{I}}_{\text{f}}+\Delta {\dot{I}}_{\text{m0}}\right)=0\end{array}.(9)$

Meanwhile, the relationship between the unit positive-sequence impedance $Z_{l1}$ or the unit zero-sequence impedance $Z_{l0}$ of the line and the unit self-impedance as well as the mutual impedance of the line satisfies the equation shown in (Eq. 10):

$\{\begin{array}{l}{Z}_{l1}=Z_{\text{s}}-Z_{\text{m}}\\ Z_{l0}=Z_{\text{s}}+2Z_{\text{m}}\end{array}.(10)$

By introducing (Eq. 10) into (Eq. 9), the equations shown in (Eq. 11) can be obtained:

$\{\begin{array}{c}\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}(Z_{l1}l+Z_{\text{N}1})-{\dot{I}}_{\text{f}}(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{\text{f}}{Z}_{l1}x=0\\ \Delta {\dot{U}}_{\text{m0}}-\Delta {\dot{I}}_{\text{m0}}(Z_{l0}l+Z_{\text{N0}})-{\dot{I}}_{\text{f}}(Z_{l0}l+Z_{\text{N0}})+{\dot{I}}_{\text{f}}{Z}_{l0}x=0\end{array}.(11)$

The expression of ${\dot{I}}_{\text{f}}$ can be obtained from the positive order equation in (Eq. 11), as shown in (Eq. 12):

${\dot{I}}_{\text{f}}=\frac{\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}(Z_{l1}l+Z_{\text{N}1})}{Z_{\text{N}1}+Z_{l1}(l-x)}.(12)$

Next, (Eq. 12) is brought into the zero-sequence equation in (Eq. 11) and simplified to obtain the expression of the fault distance x, as shown in (Eq. 13):

$x=\frac{k_1-k_2}{k_3-k_4},(13)$

where the expression of the parameters k₁–k₄ is shown in (Eq. 14):

$\{\begin{array}{c}{k}_1=(Z_{\text{N}1}+Z_{l1}l)(\Delta {\dot{U}}_{\text{m}0}-\Delta {\dot{I}}_{\text{m0}}{Z}_{l0}l-\Delta {\dot{I}}_{\text{m0}}{Z}_{\text{N0}})\\ k_2=(Z_{\text{N0}}+Z_{l0}l)(\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}{Z}_{l1}l-\Delta {\dot{I}}_{\text{m}1}{Z}_{\text{N}1})\\ k_3=Z_{l1}(\Delta {\dot{U}}_{\text{m0}}-\Delta {\dot{I}}_{\text{m0}}{Z}_{l0}l-\Delta {\dot{I}}_{\text{m0}}{Z}_{\text{N0}})\\ k_4=Z_{l0}(\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}{Z}_{l1}l-\Delta {\dot{I}}_{\text{m}1}{Z}_{\text{N}1})\end{array}.(14)$

It can be seen from (Eq. 13) that the voltage and current of the positive sequence and zero sequence in the equation can be obtained by the phase sequence transformation from the voltage and current variations of each phase measured at the measuring point. The total length l of the line, the positive-sequence impedance $Z_{l1}$, and the zero-sequence impedance $Z_{l0}$ per unit length of the line can be measured when the transmission line is put into operation. As a necessary condition for solving the fault distance, the variables $Z_{\text{N}1}$ and $Z_{\text{N0}}$ need to be sent to the ranging device by the N-side system.

Through the above analysis, it can be seen that under different fault conditions, the parameters k₁–k₄ in (Eq. 13) are known quantities in the plural form; thus, the solution of the fault distance x is actually the ratio obtained by dividing two known plural numbers. Due to certain measurement and calculation errors, the fault distance x obtained by plural division is generally in the plural form. Therefore, the modulus of the fault distance x in the plural form is taken as the final ranging result, as shown in (Eq. 15).

$x=\left|\frac{k_1-k_2}{k_3-k_4}\right|.(15)$

In the fault distance calculation formula (Eq. 15) obtained according to the above derivation processes, the capacitance parameters of the transmission line are not considered. When the capacitance parameters of the transmission line are small, the ranging error is very slight, and the above equation can be established. However, when the capacitance parameters of the transmission line are large in case of selecting the cable as the transmission line, the accuracy of the fault distance calculated by (Eq. 15) may be poor. Therefore, the single-end fault location method considering the transmission line capacitance parameters is studied as follows.

Single-End Accurate Fault Location Method Considering Line Capacitance

Since the capacitance parameters of overhead lines are small, it is not necessary to consider the line capacitance for overhead transmission lines; however, for cable lines, the phase-to-ground capacitance parameters are large and contain no phase-to-phase capacitance. Therefore, only when the cable is used as the transmission line, the influence of the phase-to-ground capacitance for the single-end fault location method needs to be considered.

The transmission system equivalent model consistent with Supplementary Figure S1 is adopted. When considering the phase-to-ground capacitance of the cable transmission line, the $\text{π}$-type equivalent model of the transmission line is adopted, and the equivalent circuit diagram in case of the A-phase nonmetallic grounding fault is shown in Supplementary Figure S4.

As shown in Supplementary Figure S4, $C_l$ represents the phase-to-ground capacitance per unit length of the cable transmission line, and the value of the phase-to-ground capacitance of the line after $\text{π}$-type equivalence is shown in the figure, and the definitions of other physical quantities in Supplementary Figure S1 remain unchanged. The current generated on the equivalent phase-to-ground capacitance of the cable transmission line is shown in equation (Eq. 16), where $\omega$ is the angular frequency.

$\{\begin{array}{c}{\dot{I}}_{C\text{MA}}=\frac{1}{2}\Delta {\dot{U}}_{\text{mA}}i\omega C_{l}l\\ {\dot{I}}_{C\text{NA}}=\frac{1}{2}\left[\Delta {\dot{U}}_{\text{mA}}-(\Delta {\dot{I}}_{\text{mA}}-{\dot{I}}_{C\text{MA}})Z_{\text{s}}x-(\Delta {\dot{I}}_{\text{mA}}+{\dot{I}}_{\text{f}}-{\dot{I}}_{C\text{MA}})Z_{\text{s}}(l-x)\right]i\omega C_{l}l\\ {\dot{I}}_{C\text{MB}}=\frac{1}{2}\Delta {\dot{U}}_{\text{mB}}i\omega C_{l}l\\ {\dot{I}}_{C\text{NB}}=\frac{1}{2}\left[\Delta {\dot{U}}_{\text{mB}}-(\Delta {\dot{I}}_{\text{mB}}-{\dot{I}}_{C\text{MB}})Z_{\text{s}}l\right]i\omega C_{l}l\\ {\dot{I}}_{C\text{MC}}=\frac{1}{2}\Delta {\dot{U}}_{\text{mC}}i\omega C_{l}l\\ {\dot{I}}_{C\text{NC}}=\frac{1}{2}\left[\Delta {\dot{U}}_{\text{mC}}-(\Delta {\dot{I}}_{\text{mC}}-{\dot{I}}_{C\text{MC}})Z_{\text{s}}l\right]i\omega C_{l}l\end{array}\text{.}(16)$

As shown in (Eq. 16), it can be seen that the cable transmission line will generate six phase-to-ground capacitive currents after $\text{π}$-type equivalence. Except the capacitive current ${\dot{I}}_{C\text{NA}}$ on the A-phase cable transmission line on the N-side, the other phase-to-ground capacitive currents can be calculated by using the line parameters and measured quantities in (Eq. 16). Since the phase-to-ground capacitive current ${\dot{I}}_{C\text{NA}}$ contains variables ${\dot{I}}_{\text{f}}$ and x, it cannot be obtained only by cable line parameters and measurements. Therefore, it is necessary to use (Eq. 12) and (Eq. 15) in Section 2.1 to solve the values of ${\dot{I}}_{\text{f}}$ and x when the line capacitance is not considered and bring them into (Eq. 16) as approximate accurate values to obtain the value of the phase-to-ground capacitive current ${\dot{I}}_{C\text{NA}}$. Through the above solution process, the 6 phase-to-ground capacitive current values thus can be obtained.

According to the circuit equivalence method in Section 1, the equivalent circuit of fault component network when considering the phase-to-ground capacitance of the cable transmission line is shown in Supplementary Figure S5.

According to the experience in writing equations in Section 1, the circuits l₁ = b₂b₃b₆, l₂ = b₄b₆, and l₃ = b₅b₆ are selected to write the loop current equation in the form of the three-phase ABC phasor, as shown in (Eq. 17).

$\{\begin{array}{c}\Delta {\dot{U}}_{\text{mA}}=(\Delta {\dot{I}}_{\text{mA}}-{\dot{I}}_{C\text{MA}})Z_{\text{s}}x+(\Delta {\dot{I}}_{\text{mA}}+{\dot{I}}_{\text{f}}-{\dot{I}}_{C\text{MA}})Z_{\text{s}}(l-x)+(\Delta {\dot{I}}_{\text{mB}}-{\dot{I}}_{C\text{MB}})Z_{\text{m}}l+(\Delta {\dot{I}}_{\text{mC}}-{\dot{I}}_{C\text{MC}})Z_{\text{m}}l+(\Delta {\dot{I}}_{\text{mA}}+{\dot{I}}_{\text{f}}-{\dot{I}}_{C\text{MA}}-{\dot{I}}_{C\text{NA}})Z_{\text{N}1}\\ +(\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}}+{\dot{I}}_{\text{f}}-{\displaystyle \sum {\dot{I}}_C})Z_{\text{Ng}}①\\ \Delta {\dot{U}}_{\text{mB}}=(\Delta {\dot{I}}_{\text{mB}}-{\dot{I}}_{C\text{MB}})Z_{\text{s}}l+(\Delta {\dot{I}}_{\text{mA}}-{\dot{I}}_{C\text{MA}})Z_{\text{m}}x+(\Delta {\dot{I}}_{\text{mA}}+{\dot{I}}_{\text{f}}-{\dot{I}}_{C\text{MA}})Z_{\text{m}}(l-x)+(\Delta {\dot{I}}_{\text{mC}}-{\dot{I}}_{C\text{MC}})Z_{\text{m}}l+(\Delta {\dot{I}}_{\text{mB}}-{\dot{I}}_{C\text{MB}}-{\dot{I}}_{C\text{NB}})Z_{\text{N}1}\\ +(\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}}+{\dot{I}}_{\text{f}}-{\displaystyle \sum {\dot{I}}_C})Z_{\text{Ng}}②\\ \Delta {\dot{U}}_{\text{mC}}=(\Delta {\dot{I}}_{\text{mC}}-{\dot{I}}_{C\text{MC}})Z_{\text{s}}l+(\Delta {\dot{I}}_{\text{mA}}-{\dot{I}}_{C\text{MA}})Z_{\text{m}}x+(\Delta {\dot{I}}_{\text{mA}}+{\dot{I}}_{\text{f}}-{\dot{I}}_{C\text{MA}})Z_{\text{m}}(l-x)+(\Delta {\dot{I}}_{\text{mB}}-{\dot{I}}_{C\text{MB}})Z_{\text{m}}l+(\Delta {\dot{I}}_{\text{mC}}-{\dot{I}}_{C\text{MC}}-{\dot{I}}_{C\text{NC}})Z_{\text{N}1}\\ +(\Delta {\dot{I}}_{\text{mA}}+\Delta {\dot{I}}_{\text{mB}}+\Delta {\dot{I}}_{\text{mC}}+{\dot{I}}_{\text{f}}-{\displaystyle \sum {\dot{I}}_C})Z_{\text{Ng}}\end{array},③(17)$

where ${\displaystyle \sum {\dot{I}}_C}$ is the sum of the 6 phase-to-ground capacitive currents generated after $\text{π}$-type equivalence of the cable transmission line, as shown in (Eq. 18).

${\displaystyle \sum {\dot{I}}_C}={\dot{I}}_{C\text{MA}}+{\dot{I}}_{C\text{NA}}+{\dot{I}}_{C\text{MB}}+{\dot{I}}_{C\text{NB}}+{\dot{I}}_{C\text{MC}}+{\dot{I}}_{C\text{NC}}.(18)$

Similarly, according to the phase sequence transformation formula shown in (Eq. 8) and the line impedance relationship shown in (Eq. 10), the equations composed of the positive-sequence and zero-sequence equations can be obtained from (Eq. 17), as shown in (Eq. 19).

$\{\begin{array}{c}\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{C\text{M}1}(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{C\text{N}1}{Z}_{\text{N}1}-{\dot{I}}_{\text{f}}(Z_{l1}(l-x)+Z_{\text{N}1})=0\\ \Delta {\dot{U}}_{\text{m0}}-\Delta {\dot{I}}_{\text{m0}}(Z_{l0}l+Z_{\text{N0}})+{\dot{I}}_{C\text{M0}}(Z_{l0}l+Z_{\text{N0}})+{\dot{I}}_{C\text{N0}}{Z}_{\text{N0}}-{\dot{I}}_{\text{f}}(Z_{l0}(l-x)+Z_{\text{N0}})=0\end{array},(19)$

where ${\dot{I}}_{C\text{M}1}$ and ${\dot{I}}_{C\text{M0}}$ as well as ${\dot{I}}_{C\text{N}1}$ and ${\dot{I}}_{C\text{N0}}$ are the positive-sequence and zero-sequence phase-to-ground capacitive currents, respectively, at the M-side as well as at the N-side, and their expressions are shown in (Eq. 20):

$\{\begin{array}{l}{\dot{I}}_{C\text{M}1}={\dot{I}}_{C\text{MA}}+a{\dot{I}}_{C\text{MB}}+a^2{\dot{I}}_{C\text{MC}}\\ {\dot{I}}_{C\text{M0}}={\dot{I}}_{C\text{MA}}+{\dot{I}}_{C\text{MB}}+{\dot{I}}_{C\text{MC}}\\ {\dot{I}}_{C\text{N}1}={\dot{I}}_{C\text{NA}}+a{\dot{I}}_{C\text{NB}}+a^2{\dot{I}}_{C\text{NC}}\\ {\dot{I}}_{C\text{N0}}={\dot{I}}_{C\text{NA}}+{\dot{I}}_{C\text{NB}}+{\dot{I}}_{C\text{NC}}\end{array}.(20)$

The expression of ${\dot{I}}_{\text{f}}$ can be obtained from the positive order equation in (Eq. 19), as shown in (Eq. 21):

${\dot{I}}_{\text{f}}=\frac{\Delta {\dot{U}}_{\text{m}1}-\Delta {\dot{I}}_{\text{m}1}(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{C\text{M}1}(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{C\text{N}1}{Z}_{\text{N}1}}{(Z_{l1}(l-x)+Z_{\text{N}1})}.(21)$

Next, (Eq. 21) is brought into the zero-sequence equation in (Eq. 19) and then simplified to obtain the expression of the fault distance x, as shown in (Eq. 22).

$x=\frac{h_1-h_2}{h_3-h_4},(22)$

where the expression of parameters h₁–h₄ is shown in (Eq. 23):

$\{\begin{array}{c}{h}_1=(Z_{\text{N}1}+Z_{l1}l)\left[\Delta {\dot{U}}_{\text{m0}}-(\Delta {\dot{I}}_{\text{m}0}-{\dot{I}}_{C\text{M0}})(Z_{l0}l+Z_{\text{N0}})+{\dot{I}}_{C\text{N0}}{Z}_{\text{N0}}\right]\\ h_2=(Z_{\text{N0}}+Z_{l0}l)\left[\Delta {\dot{U}}_{\text{m}1}-(\Delta {\dot{I}}_{\text{m}1}-{\dot{I}}_{C\text{M}1})(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{C\text{N}1}{Z}_{\text{N}1}\right]\\ h_3=Z_{l1}\left[\Delta {\dot{U}}_{\text{m0}}-(\Delta {\dot{I}}_{\text{m}0}-{\dot{I}}_{C\text{M0}})(Z_{l0}l+Z_{\text{N0}})+{\dot{I}}_{C\text{N0}}{Z}_{\text{N0}}\right]\\ h_4=Z_{l0}\left[\Delta {\dot{U}}_{\text{m}1}-(\Delta {\dot{I}}_{\text{m}1}-{\dot{I}}_{C\text{M}1})(Z_{l1}l+Z_{\text{N}1})+{\dot{I}}_{C\text{N}1}{Z}_{\text{N}1}\right]\end{array}.(23)$

It can be seen that all variables in the equation are known quantities through (Eq. 22) and the analysis in Section 2.1; thus, the known quantities with all of the parameters h₁–h₄ being in plural forms can be obtained under different fault conditions. Similarly, the fault distance x can be obtained after taking the modulus value, as shown in (Eq. 24):

$x=\left|\frac{h_1-h_2}{h_3-h_4}\right|.(24)$

When calculating the phase-to-ground capacitive current ${\dot{I}}_{C\text{NA}}$, there is an error in theory since the values of ${\dot{I}}_{\text{f}}$ and x are used in the case that the line capacitance is not considered in Section 2.1; therefore, the method of multiple iterations should be used to reduce the error. However, the method of only correcting once is adopted instead of multiple iterative calculations in order to reduce the amount of calculation and improve the ranging speed, and the calculation method of only correcting once can fully meet the accuracy requirements of ranging results according to the subsequent simulation results.

Simulation Verification of Single-End Fault Location Method

In this study, the PSCAD simulation software is used to verify the fault location method, and the respective power parameters of the M-side and N-side of the three-phase symmetrical system are set, as shown in Table 1.

TABLE 1

TABLE 1. Power parameters of the M-side and N-side.

A double terminal system, as shown in Supplementary Figure S1, is built in PSCAD, and the overhead line model and cable model are, respectively, selected as the transmission lines so as to verify the proposed single-end accurate fault location method.

First, the transmission line is set as an overhead line with a total length of 300 km, the Bergeron model is adopted, and the line parameters are input by geometric parameters. The parameter values of the unit positive-sequence impedance $Z_{l1}$, the unit zero-sequence impedance $Z_{l0}$, and the unit phase-to-ground capacitance $C_l$ of the overhead line generated at 50 Hz by the line constant program are shown in (Eq. 25):

$\{\begin{array}{c}{Z}_{l1}=0.00601+0.16445i\left(\Omega \text{/kM}\right)\\ Z_{l0}=0.11221+0.53648i\left(\Omega \text{/kM}\right)\\ C_l=5.78949\times {10}^{-8}\left(\text{F/kM}\right)\end{array}.(25)$

Next, the transmission line is replaced with a cable, the total length of the line is set as 50 km, the Bergeron model is adopted, and the line parameters with geometric parameters are input. The respective parameter values of the unit positive-sequence impedance $Z_{l1}$, the unit zero-sequence impedance $Z_{l0}$, and the unit phase-to-ground capacitance of the cable line at 50 Hz generated by the line constant program are shown in (Eq. 26):

$\{\begin{array}{c}{Z}_{l1}=0.01952+0.074656i\left(\Omega \text{/kM}\right)\\ Z_{l0}=0.01949+0.074671i\left(\Omega \text{/kM}\right)\\ C_l=1.60984\times {10}^{-7}\left(\text{F/kM}\right)\end{array}.(26)$

The A-phase nonmetallic grounding faults are set at distances of 50, 150, and 250 km from the overhead transmission line to the M-side system and at distances of 10, 25, and 40 km from the cable transmission line to the M-side system, with transition resistances of 100$\Omega$, 200$\Omega$, and 300$\Omega$, respectively.

According to the measured data of the measuring point, the three-phase voltage and current variations of the M-side can be obtained under different fault distances and transition resistances. Combined with the line parameters of overhead lines and cables, the fault distance x is calculated by, respectively, using the ranging formula (Eq. 15) without considering the capacitance and the ranging (Eq. 24) considering the capacitance to verify the correctness of the single-end accurate fault location method. The calculation formulas for defining the absolute error $e_{\text{a}}$ and the relative error $e_{\text{r}}$ are shown in (Eq. 29):

$\{\begin{array}{l}{e}_{\text{a}}=x_{\text{c}}-x_{\text{a}}\\ e_{\text{r}}=\frac{e_{\text{a}}}{l}\times 100\%\end{array},(29)$

where $x_{\text{c}}$ is the calculated fault distance solved by the ranging formula, $x_{\text{a}}$ is the actual fault distance, and l is the total length of the transmission line.

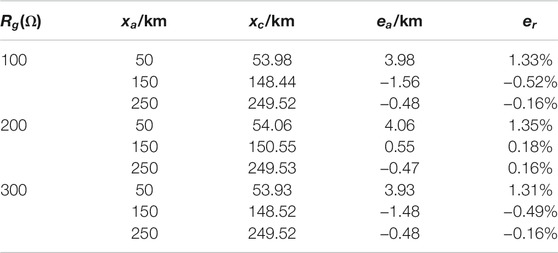
For overhead transmission lines, the fault distances and error rates obtained under different transition resistances and different actual fault positions can be calculated by using the ranging formula (Eq. 15) without considering the capacitance of the overhead lines, as shown in Table 2.

TABLE 2

TABLE 2. Error table for calculation of overhead line fault distance.

It can be seen from Table 2 that the maximum relative error of the ranging results is 1.33% because the capacitance parameters of the overhead line model are small; thus, the ranging results calculated by using the ranging formula (Eq. 15) without considering the capacitance of the overhead line can be of great accuracy. This shows that the ranging formula (Eq. 15) is correct and of great accuracy with a strong ability against transition resistances when the transmission line capacitance is small.

We also simulate overhead transmission lines with different line lengths from 200 to 500 km. According to the simulation results, the fault location formula (Eq. 15) without considering the line capacitance parameters can achieve accurate location within the range of line length not exceeding 400 km. Although the fault location accuracy decreases with the increase in the line length, the relative errors of all fault location results are within 2%. The correction effect of the fault location (Eq. 24) considering line capacitance is not obvious when the length of the overhead line exceeds 200 km, and with the increase in the line length, the accuracy of the location result of (Eq. 24) is even lower than that of (Eq. 15). Because the line model is the $\text{π}$-type equivalent lumped parameter model, the distribution parameter effect is more obvious when the line length is long, and that is the reason why the fault location error of (Eq. 24) grows larger and larger with the increase in the line length.

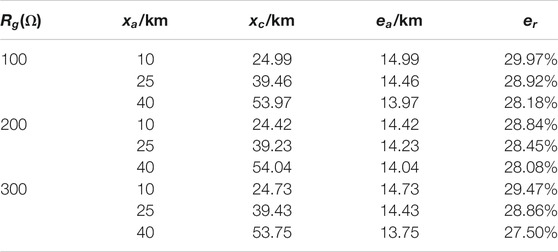
For cable transmission lines, the fault distances and error rates are calculated by using the ranging formula (Eq. 15) without considering the cable line capacitance. The fault distances and error rates are shown in Table 3 under different transition resistances and different actual fault positions.

TABLE 3

TABLE 3. Error table for calculation of cable line fault distance.

It can be seen from Table 3 that the maximum relative error of the ranging results is 29.97%, which is due to the large phase-to-ground capacitance parameters of the cable line model and the calculation by using the ranging formula (Eq. 15) without considering the cable line capacitance parameters. Therefore, the influence of the capacitance current must be considered when the capacitance parameter of the transmission line is large. In this case, the error of the ranging formula (Eq. 15) is significant.

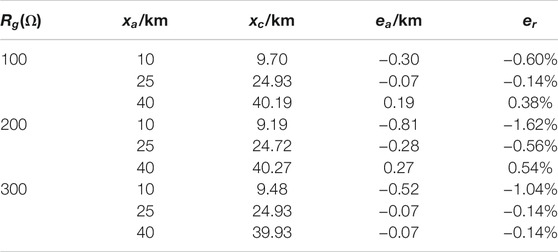
For cable transmission lines, the fault distances and error rates are calculated by using the ranging formula (Eq. 24) considering the phase-to-ground capacitance of cable lines. The fault distances and error rates are shown in Table 4 under different transition resistances and different actual fault positions.

TABLE 4

TABLE 4. Error table for calculation of cable line fault distance.

It can be seen from Table 4 that the maximum relative error of ranging results is reduced from 29.97% to −1.62%; that is, the accuracy of ranging results has been greatly improved after considering the phase-to-ground capacitance of the cable line. This shows that when the phase-to-ground capacitance of the transmission line itself is large, the fault distance needs to be calculated by using the ranging formula (Eq. 24) considering the phase-to-ground capacitance, which can effectively improve the ranging accuracy with a strong ability against transition resistances.

We also simulate cable lines with different line lengths from 50 to 100 km. According to the simulation results, the fault location results of (Eq. 15) without considering the line capacitance parameters have large fault location errors for the cable line under the above length range. The fault location results of (Eq. 24) considering the line capacitance can accurately locate the fault when the cable line is no more than 100 km. The relative errors of all fault location results are within 2%.

Conclusion

This work studies a new method of the single-end fault location for single-phase grounding faults of the transmission lines passing through transition resistances, puts forward the necessary conditions and the accurate location method of the single-end accurate fault location, and solves the problem of poor accuracy of the single-end fault location in principle. The simulation results show that the single-end accurate fault location method proposed in this study really has sufficient accuracy and a strong ability against transition resistances, and the advantages are as follows:

1) This study deeply analyzes the single-end fault location method as well as the reasons for the low accuracy of the single-end fault location from the principle level and creatively puts forward the necessary conditions for the single-end accurate fault location method. That is, the positive-sequence internal impedance $Z_{\text{N}1}$ and the neutral point equivalent impedance to ground $Z_{\text{Ng}}$ of the N-side system shall be known.

2) By using the $\text{π}$-type equivalent model of the transmission line, the ranging formula without considering the line capacitance parameters is modified, the influence of the transmission line capacitance parameters on the ranging results is effectively solved, and the ranging accuracy of the single-end fault location method for the cable lines is improved.

3) The phasor equations are transformed into positive-sequence and zero-sequence equations using the phase sequence transformation formula. A simple single-end accurate fault location formula with certain duality law is obtained with the use of the simplified calculation, which improves the practicability of this ranging method.

4) The fault location formula (Eq. 15) without considering the line capacitance parameters should be used for overhead line fault location. The fault location (Eq. 24) considering line capacitance should be used for cable line fault location.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

BoL contributed technical ideas; LS was responsible for the specific implementation of the technical scheme; WW provided technical support for the study; BiL provided technical support for the study; and XC provided technical support for the study.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.772345/full#supplementary-material

References

Aboshady, F. M., Thomas, D. W. P., and Sumner, M. (2019). A New Single End Wideband Impedance Based Fault Location Scheme for Distribution Systems. Electric Power Syst. Res. 173 (AUG), 263–270. doi:10.1016/j.epsr.2019.04.034

CrossRef Full Text | Google Scholar

Apostolopoulos, C. A., and Korres, G. N. (2011). A Novel Fault-Location Algorithm for Double-Circuit Transmission Lines without Utilizing Line Parameters. IEEE Trans. Power Deliv. 26 (3), 1467–1478. doi:10.1109/tpwrd.2010.2102777

CrossRef Full Text | Google Scholar

Bains, T. S., Sidhu, T. S., and Xu, Z. (2017). Impedance-based Fault Location Algorithm for Ground Faults in Series Capacitor Compensated Transmission Lines[J]. IEEE Transactions on Power Delivery, 1.

Google Scholar

Bains, T., and Zadeh, M. (2015). Supplementary Impedance-Based Fault-Location Algorithm for Series-Compensated Lines[J]. IEEE Trans. Power Deliv. 31 (1), 1.

Google Scholar

Fei, X., Dong, X., and Wang, B. (2015). A Novel Single-Ended Fault Location Scheme and Applications Considering Secondary Circuit Transfer characteristics[C]. Power & Energy Society General MeetingIEEE.

Google Scholar

Ghorbani, A., and Mehrjerdi, H. (2020). Accurate Fault Location Algorithm for Shunt-Compensated Double Circuit Transmission Lines Using Single End Data[J]. Int. J. Electr. Power Energ. Syst., 116. doi:10.1016/j.ijepes.2019.105515

CrossRef Full Text | Google Scholar

He, X., Zhao, Y., and Shi, S. (2018). Modified Single-Ended Fault Location Method for Single-Phase-To-Ground Faults in T-Connected line[C]. 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2). IEEE.

Google Scholar

Jia, K., Thomas, D., and Sumner, M. (2013). A New Single-Ended Fault-Location Scheme for Utilization in an Integrated Power System. IEEE Trans. Power Deliv. 28 (1), 38–46. doi:10.1109/tpwrd.2012.2215346

CrossRef Full Text | Google Scholar

Kawady, T., and Stenzel, (2003). A Practical Fault Location Approach for Double Circuit Transmission Lines Using Single End data[J]. Power Delivery. IEEE Transactions on.

Google Scholar

Li, P., Wei, X, and Yin, X. (2020). A Specialized System-On-Chip Based Distance Protection for Distribution Grids with Inverter Interfaced Distributed Generation [J]. Front. Energ. Res. 12, 8. doi:10.3389/fenrg.2020.614292

CrossRef Full Text | Google Scholar

Patynowski, D., Cardenas, J., and Menendez, D. (2015). Fault Locator Approach for High-Impedance Grounded or Ungrounded Distribution Systems Using Synchrophasors[C]IEEE. College Station, TX: Conference for Protective Relay Engineers, 302–310.

Google Scholar

Taheri, R., Eslami, M., and Damchi, Y. (2020). Single-end Current-Based Algorithm for Fault Location in Series Capacitor Compensated Transmission Lines. Int. J. Electr. Power Energ. Syst. 123, 106254. doi:10.1016/j.ijepes.2020.106254

CrossRef Full Text | Google Scholar

Wang, C., An, J., and Mu, G. (2021). Power System Network Topology Identification Based on Knowledge Graph and Graph Neural Network [J]. Front. Energ. Res. 2, 8. doi:10.3389/fenrg.2020.613331

CrossRef Full Text | Google Scholar

Wang, Y., and Chen, N. (2021). Fault Location Scheme for Abnormal Grounding Point in Isolated Ground Wire of Large-Scale Clean Energy Transmission [J]. Front. Energ. Res. 7, 9. doi:10.3389/fenrg.2021.702245

CrossRef Full Text | Google Scholar

Xu, Z., and Zhang, Z. (2015). What Accuracy Can We Expect from the Single-Ended Fault locator?[C]. Conference for Protective Relay EngineersIEEE, 690–716.

Google Scholar

Yi, C., Jiang, P., Wan, Q., and Gao, S. (2005). Power System analysis[M], 7. Bei Jing: CHINA ELECTRIC POWER PRESS, 144–146.

Google Scholar

Zhang, G., Wang, C., and Yang, M. (2006). Single Ended Fault Location Method for Distribution Network Based on Fault Component[J]. Power Syst. Prot. Control. 34 (012), 6–9.

Google Scholar