Numerical Investigation of Pool Boiling Under Ocean Conditions with Lattice Boltzmann Simulation. Part Ⅰ: Heaving Condition

Pool boiling is the heat-transfer mechanism of many heat exchangers inside ocean nuclear power plants working under the complex marine circumstances. Also, ocean conditions will create a new acceleration field other than gravity for the fluid, which induces some unique thermal–hydraulic characteristics. In this study, pool boiling under heaving conditions is numerically simulated using multiple relaxation time phase change lattice Boltzmann method. Firstly, the simulated results under static condition have been validated with recognized empirical equations, such as Rohsenow’s correlation at nucleate boiling, Zuber’s model, and Kandlikar’s model about critical heat flux (CHF). Then, pool boiling patterns, the boiling curve of time-averaged heat flux, transient heat flux, and heaving effects on different pool boiling regions are investigated. The results show that pool boiling curves of time-averaged heat flux between heaving conditions and static conditions with middle superheat degrees are similar. Heat transfer under heaving conditions at low superheat is somewhat enhanced, and it is weakened at high superheat, which leads to a slightly smaller critical heat flux with larger superheat compared with that under static conditions. Moreover, distinct fluctuation of the transient heat flux of pool boiling under heaving conditions is found for all boiling regimes. Furthermore, the heaving condition shows both positive and negative effects on pool boiling heat transfer at high-gravity and low-gravity regions, respectively. Besides, both the larger heaving height and shorter period time bring out more violent heaving motion and make a greater impact on pool boiling heat transfer.

Introduction

Marine applications, such as ocean nuclear power plants (ONPPs), power propulsion of ships, offshore small modular reactors, floating liquefied natural gas (FLNG) platforms, and seawater desalination apparatuses, have been developed by a great leap forward in these years with the large-scale exploitation and utilization of ocean resources (Yan, 2017; Wang et al., 2019; Tian et al., 2020). Unlike the land-based condition, ocean applications would be affected by marine motions, which are caused by wind forces, tides, and ocean currents. The marine motion would induce additional inertial forces on the system and thus change the thermal–hydraulic characteristics of the energy and power plants. Also, the additional inertia forces introduced by rotational movement could be divided into normal inertial force, tangential inertial force, and additional Coriolis force (Yan, 2017) as follows:

${\mathbf{F}}_{\text{in}}=-\text{m}\left({\mathbf{a}}_{\text{n}}+{\mathbf{a}}_{\text{t}}+{\mathbf{a}}_{\text{co}}\right),(1)$

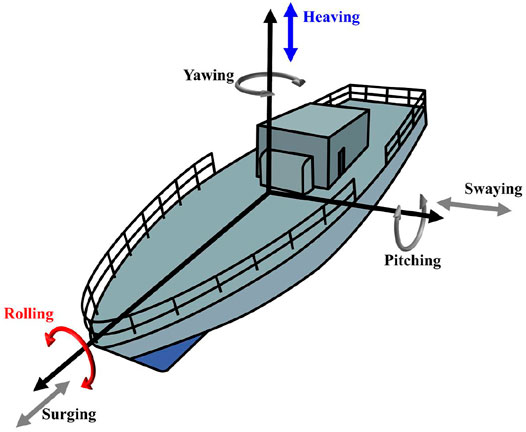
where F_in is the additional inertia force, a_n is the normal acceleration, a_t is the tangential acceleration, and a_co is the Coriolis acceleration; also, translational motions will bring out additional forces along the corresponding direction. For research convenience, marine motions are generally decomposed to three translational motions (heaving, swaying, and surging) and three rotational motions (rolling, pitching, and yawing) (Wang et al., 2019), which are illustrated in Figure 1. Among these, heaving and rolling conditions are most commonly encountered, which will induce one kind of inertial force parallel to gravity and three kinds of inertial forces, respectively, and their effects on the work fluid inside the marine applications would produce unique thermal–hydraulic characteristics, which will be studied in this study series with Part Ⅰ focused on heaving conditions and Part Ⅱ (Zou et al., 2021) concentrated on rolling conditions.

FIGURE 1

FIGURE 1. Six degrees of freedom about marine motions.

In recent decades, studies about thermal–hydraulic characteristics of marine applications under heaving conditions have been focused on flow circulation or flow boiling (Tian et al., 2020), which were mainly applied to the marine reactors (O'Rourke, 2010). These investigations have included critical heat flux (CHF), heat-transfer coefficient (HTC), bubble behaviors, flow patterns, flow instability, and pressure drop. Among these studies, CHF, HTC, and bubble behaviors could be referenced for the research of pool boiling mechanisms under heaving conditions. Most studies have shown that heaving motion could decrease CHF of flow boiling. In early 1966, Isshiki (1966) found that CHF decreased linearly with the increase of heaving acceleration, and Otsuji and Kurosawa (1982) got a similar result that heaving motion reduced CHF because of long bubble slugs causing the dry-out of the liquid film. Then, Ishida et al. (1990) pointed out that the CHF ratio was proportional to the 1/4th power of the gravitational acceleration ratio in their model and verification experiment of flow boiling under heaving conditions. Hwang et al. (2011) simulated CHF under heaving conditions using commercial codes, and the results showed that the CHF was much lower than that under static conditions because of gravity acceleration oscillation and the decrease of mass flow rate. Gui et al. (2020) theoretically investigated CHF characteristics in a narrow rectangular channel by considering the additional forces due to heaving and rolling motions, and it was shown that the CHF decreased because of inlet flow oscillation. Liu et al. (2018) developed a combining model investigating the CHF and the flow instability in ocean motion and found that heaving motion had little effect on CHF.

As for HTC and bubble behaviors of boiling under ocean conditions, almost all works were focused on the rolling condition, and thus, investigations about effects of heaving conditions were scarce. Xi et al. (2015) theoretically computed that the time-averaged HTC was reduced under heaving conditions compared to that under a static state. Recently, Hong et al. (Ishida et al., 1990) acquired the bubble departure size in forced convective flow under static and heaving conditions, and they found that the bubble departure diameter increased by increasing the heaving acceleration. The additional inertial force caused by heaving motion has been always parallel to gravity force, which would lead to the bubbles withstanding the high gravity and low gravity states. The study of Macro et al. (Di Marco and Grassi, 2002) about pool boiling under different gravitational accelerations showed that bubbles became smaller at high gravity, and they grew bigger at low gravity. Similar results could also be found in the simulation by Ma et al. (2017) and experiments by Raj et al. (2010). Besides, the gravity influences on CHF have also been studied in previous research studies (Raj et al., 2010; Ma et al., 2017; Fang et al., 2019), and the results showed that higher gravity within a certain range could increase CHF.

Relatively few studies have been published on pool boiling under ocean conditions, especially the investigations under heaving motion. Actually, many marine heat exchangers adopted pool boiling (Yu, 2020), and their unique thermal–hydraulic characteristics under complex ocean conditions would need to be uncovered. The lattice Boltzmann method is a mesoscopic numerical method potential on multiphase flow and phase transition (Huang et al., 2019; Huang et al., 2021). Recently, simulations using the lattice Boltzmann method (LBM) about pool boiling have been a hot topic (Cheng et al., 2014; Li et al., 2016), and it is very effective to incorporate the inertial forces caused by ocean conditions. Among multiphase models of LBM, pseudo-potential LBM and phase field LBM have been applied to phase change heat transfer (boiling, evaporation, and condensation). Zhang and Chen (2003) took the first LBM simulation of nucleate boiling using the pseudo-potential model with a new scheme of the force term. Later, Hazi and Markus (2009) developed a pseudo-potential LBM phase change model based on a local balance law for entropy by introducing a source term to the temperature equation, which applied the equation of state (EOS) to drive spontaneous phase change without artificial hypothesis, and this treatment has been intensively adopted. Subsequently, Gong and Cheng (2012) proposed an improved phase change source term and obtained the whole pool boiling curve (Gong and Cheng, 2015). Besides, Li et al. (2015) developed a hybrid thermal pseudo-potential LBM model by taking a finite-difference scheme to compute the temperature field and investigate the effects of surface wettability on boiling heat transfer. On the other hand, Dong et al. (2009), Safari et al. (2013), and Tanaka et al. (2011) devised their phase change model from the category of phase field LBM, respectively. With the help of these theoretical models’ development, LBM simulations of phase change heat transfer have ushered in the explosive growth. During these studies, a pseudo-potential model has been most widely used because of its high efficiency, and the whole boiling curve including natural convection, nucleate boiling, CHF, and film boiling was investigated, together with the bubble behaviors of nucleation, growth, coalescence, and departure (Gong and Cheng, 2015; Li et al., 2015). This method could also be used to simulate boiling heat transfer under marine conditions by taking into account the inertial forces.

In this study, pseudo-potential LBM is adopted to study pool boiling under heaving conditions. In the Model Description Section, we discuss briefly the model used in this study and the strategy of including the inertia force. Then, the computation setup and boundary conditions are given, and the model is validated with recognized empirical equations of pool boiling under static conditions in the Computation Setup, Boundary Conditions, and Model Validation Section. Moreover, results and discussion are implemented in the Results and Discussion Section, where the mechanism of pool boiling under heaving conditions is shown, with conclusions drawn in the Concluding Remarks Section. Besides, it is noteworthy that the methodology and results in this study serve a reference for the investigation of pool boiling under rolling conditions in Part Ⅱ of this study series (Zou et al., 2021), which provides a comprehensive study of pool boing under complex marine conditions together.

Model Description

MRT Pseudo-potential Multiphase LBM

The evolution equation of LBM with the MRT collision operator is given by the following (D'Humières et al., 2002):

$\mathbf{f}\left(\mathbf{x}+{\mathbf{e}}_i{\delta }_t,t+{\delta }_t\right)-\mathbf{f}\left(\mathbf{x},t\right)=-\mathbf{\Lambda }\left(\mathbf{f}\left(\mathbf{x},t\right)-{\mathbf{f}}^{eq}\left(\mathbf{x},t\right)\right)+{\delta }_t\mathbf{\Gamma }\overline{\mathbf{F}}\left(\mathbf{x},t\right),(2)$

where f_i (x, t) is the discrete density distribution function at position x and time t with particle velocity e_i, Λ = M⁻¹SM is the collision matrix, S is a non-negative diagonal matrix relevant to the relaxation time given by $\mathbf{S}=\mathbf{diag}\left({\tau }_{\rho }^{-1},{\tau }_e^{-1},{\tau }_{\epsilon }^{-1},{\tau }_j^{-1},{\tau }_q^{-1},{\tau }_j^{-1},{\tau }_q^{-1},{\tau }_{\upsilon }^{-1},{\tau }_{\upsilon }^{-1}\right),$ and M is an orthogonal transformation matrix (D'Humières et al., 2002). In this study, S = diag (1.0, 1.1, 1.2, 1.0, 1.0, 1.0, 1.0, τ_v⁻¹, τ_v⁻¹). Γ = M⁻¹(I-S/2)M is the collision matrix for forces. The relaxation time τ_v is related to fluid kinematic viscosity with τ_υ = υ/(c_s²δ_t) + 0.5, and the density distribution function f is projected into the moment space with M, m = Mf, and m^eq = Mf^eq, in which m^eq is defined as follows:

${\mathbf{m}}^{\mathbf{eq}}=\rho {(1,-2+3|\mathbf{u}{|}^2,1-3|\mathbf{u}{|}^2,u_x,-u_x,u_y,-u_y,u_x^2-u_y^2,u_x{u}_{\text{y}})}^{\mathbf{T}}.(3)$

The detailed collision and streaming processes in Eq. 2 are executed as

$\begin{array}{l}\mathbf{m}\prime =\mathbf{m}-\mathbf{S}(\mathbf{m}-{\mathbf{m}}^{eq})+{\delta }_t(\mathbf{I}-\mathbf{S}/2)\mathbf{M}\overline{\mathbf{F}},\\ \mathbf{f}\prime ={\mathbf{M}}^{-1}\mathbf{m}\prime ,\\ \mathbf{f}(\mathbf{x}+{\mathbf{e}}_i{\delta }_t,t+{\delta }_t)=\mathbf{f}\prime (\mathbf{x},t).\end{array}(4)$

The last term F̅ in Eq. 2 is the discrete force implemented into LBM, and the method proposed by Guo et al. (2002) is adopted in MRT as

$\overline{F_i}(\mathbf{x},t)={\omega }_i\left[\frac{\mathbf{F}\cdot {\mathbf{e}}_i}{c_s^2}+\frac{\mathbf{vF}:({\mathbf{e}}_i{\mathbf{e}}_i-{\mathbf{c}}_s^2\mathbf{I})}{c_s^4}\right],(5)$

where ω_i is the weighting coefficient with ω₀ = 4/9, ω_1-4 = 1/9, and ω_5-8 = 1/36; c_s is lattice sound speed given by c_s² = c²/3 in the D2Q9 model with c = δ_x/δ_t being the lattice speed; and v is the real fluid velocity. The discrete lattice velocity vectors e_i are given by the following:

${\mathbf{e}}_i=\left[\begin{array}{ccccccccc}0& 1& 0& -1& 0& 1& -1& -1& 1\\ 0& 0& 1& 0& -1& 1& 1& -1& -1\end{array}\right].(6)$

Moreover, F is the total force, including inter-particle force F_int, fluid–solid interaction force F_s, gravitational force F_g, and inertial force F_h caused by heaving motion.

$\mathbf{F}={\mathbf{F}}_{int}+{\mathbf{F}}_s+{\mathbf{F}}_g+{\mathbf{F}}_h.(7)$

The inter-particle interaction force F_int is given as

${\mathbf{F}}_{int}=-\beta \phi \left(\mathbf{x}\right){\displaystyle \sum _{i}G\left(\mathbf{x}+{\mathbf{e}}_i\delta t\right)\phi \left(\mathbf{x}+{\mathbf{e}}_i\delta t\right){\mathbf{e}}_i-\frac{1-\beta }{2}{\displaystyle \sum _{i}G\left(\mathbf{x}+{\mathbf{e}}_i\delta t\right){\phi }^2\left(\mathbf{x}+{\mathbf{e}}_i\delta t\right){\mathbf{e}}_i}},(8)$

where β = 1.16 is a weighting factor depending on the equation of state used; it is chosen with simulation tests on Maxwell reconstruction in the equation of state (Gong and Cheng, 2017). G (x + e_iδt) denotes the interaction strength of the fluid, which is defined as

$G(\mathbf{x}+{\mathbf{e}}_i\delta t)=\{\begin{array}{l}{g}_1=2G,\left|{\mathbf{e}}_i\right|=1\\ g_2=0.5G,\left|{\mathbf{e}}_i\right|=\sqrt{2}\\ 0,otherwise\end{array}.(9)$

φ(x) is the effective density computed as

$\phi \left(\mathbf{x}\right)=\sqrt{\frac{2\left(p-\rho c_s^2\right)}{c_{0}G}},(10)$

where c₀ = 6 in the D2Q9 model and p is the pressure calculated with the equation of state. Here, the Peng–Robinson equation of state (PR EOS) is adopted, which is given as

$\begin{array}{l}p=\frac{\rho RT}{1-b\rho }-\frac{a{\rho }^2\gamma \left(T\right)}{1+2b\rho -b^2{\rho }^2},\\ \gamma \left(T\right)={\left[1+\left(0.37464+1.54226w-0.26992w^2\right)\left(1-\sqrt{T/T_c}\right)\right]}^2,\end{array}(11)$

where $a=0.45724R^2{T}_c^2/p_c$, $b=0.0778R{T}_c/p_c$, T_c is the critical temperature, p_c is the critical pressure, ρ_c is the critical density, R is the gas constant, and w is the acentric factor. In this simulation, a = 2/49, b = 2/21, R = 1, and w = 0.344 are chosen.

The fluid–solid interaction force F_s is calculated as

${\mathbf{F}}_s=-G_s\rho \left(\mathbf{x}\right){\displaystyle \sum _i{\omega }_{i}s(\mathbf{x}+{\mathbf{e}}_i\delta t){\mathbf{e}}_i},(12)$

where G_s is the parameter denoting the fluid–solid interaction strength, and s(x) is a binary function (with s(x) = 1 for solid and s(x) = 0 for fluid).

The gravitational force is defined as

${\mathbf{F}}_g=\rho \left(\mathbf{x}\right)\mathbf{g},(13)$

where g is the gravitational acceleration.

The macroscopic density ρ and velocity u of the fluid are given as

$\begin{array}{l}\rho ={\displaystyle \sum _i{f}_i},\\ \mathbf{u}=\frac{1}{\rho }{\displaystyle \sum _i{f}_i{\mathbf{e}}_i.}\end{array}(14)$

The real fluid velocity v is computed as

$\mathbf{v}=\mathbf{u}+\frac{\delta t}{2\rho }\mathbf{F}.(15)$

Energy Equation Model

The evolution equation of the temperature distribution function is given by the following (Gong and Cheng, 2012):

$g_i(\mathbf{x}+{\mathbf{e}}_i\delta t,t+\delta t)-g_i(\mathbf{x},t)=-\frac{1}{{\tau }_T}\left(g_i(\mathbf{x},t)-g_i^{eq}(\mathbf{x},t)\right)+{\omega }_i\varphi \delta t,(16)$

where τ_T is the relaxation time related to thermal diffusivity α with τ_T = α/(c_s²δ_t) + 0.5 and g_i^eq (x, t) is the equilibrium distribution function for temperature, which is given as

$g_i^{eq}={\omega }_{i}T\left[1+\frac{{\mathbf{e}}_i\cdot \mathbf{v}}{c_s^2}+\frac{{({\mathbf{e}}_i\cdot \mathbf{v})}^2}{2c_s^4}-\frac{{\mathbf{v}}^2}{2c_s^2}\right].(17)$

Here, we can take v = 0 to simulate heat conduction inside the solid.

The source term ϕ resulting from phase change is defined as follows (Zhang and Cheng, 2017):

$\varphi =T\left(\nabla \cdot \mathbf{v}\right)\left[1-\frac{1}{\rho c_v}{\left(\frac{\partial p}{\partial T}\right)}_{\rho }\right]+\left[\frac{1}{\rho c_v}\nabla \cdot \left(k\nabla T\right)-\nabla \cdot \left(\frac{k}{\rho c_p}\nabla T\right)\right].(18)$

The temperature is calculated as

$T={\displaystyle \sum _i{g}_i}.(19)$

Inertial Force Under Heaving Motion

Heaving motions are shown in Figure 2, and extra inertial acceleration can be figured out with the change of heaving displacement h, which has sine relationship with time,

$\begin{array}{l}h=h_m\sin \left(2\pi \frac{t}{t_p}\right),\\ a_h=\frac{d^{2}h}{d{t}^2}=-h_m{\left(\frac{2\pi }{t_p}\right)}^2\sin \left(2\pi \frac{t}{t_p}\right),\end{array}(20)$

where h_m is the maximum heaving height, t_p is the heaving period, and a_h is the heaving acceleration. h_m = 1900δ_x and t_p = 100000δ_t are adopted in this study without otherwise specified, and the maximum value of a_h is 0.5g. It should be noted that the simulation is based on the inertial system under heaving motion, and the direction of additional inertial force is opposite to the heaving acceleration, which is determined as

${\mathbf{F}}_h=-m{\mathbf{a}}_h.(21)$

FIGURE 2

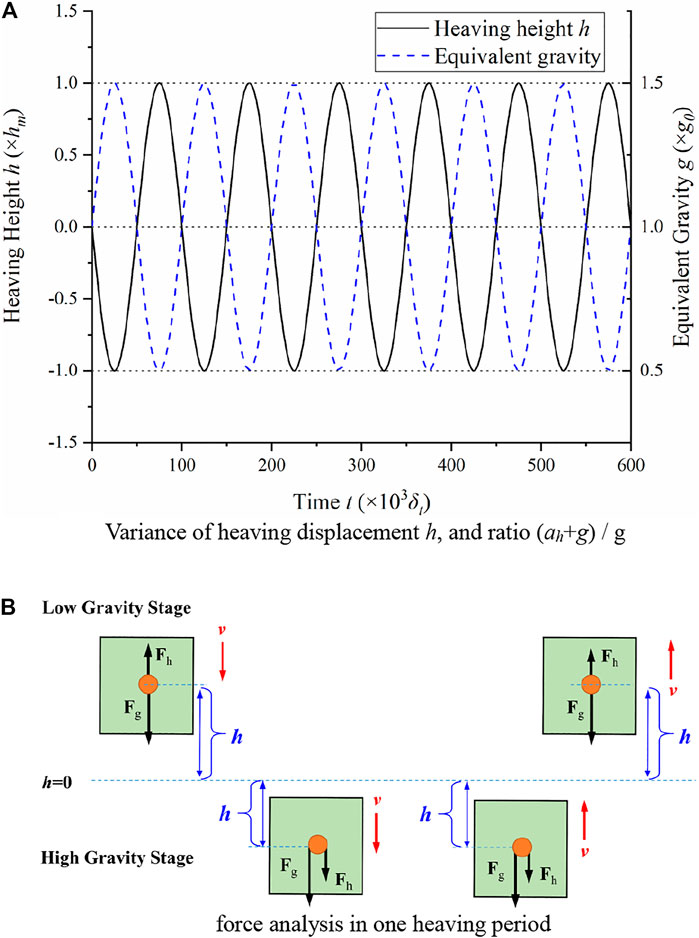
FIGURE 2. Schematic diagram of heaving motion and force analysis. (A) Variance of heaving displacement h and ratio (a_h + g)/g. (B) Force analysis in one heaving period.

Computation Setup, Boundary Conditions, and Model Validation

In this section, we will first introduce the computation setup and boundary conditions. Then, the model is validated with the Laplace law and heat-transfer curve with recognized empirical equations of pool boiling under static conditions.

Computation Setup and Boundary Conditions

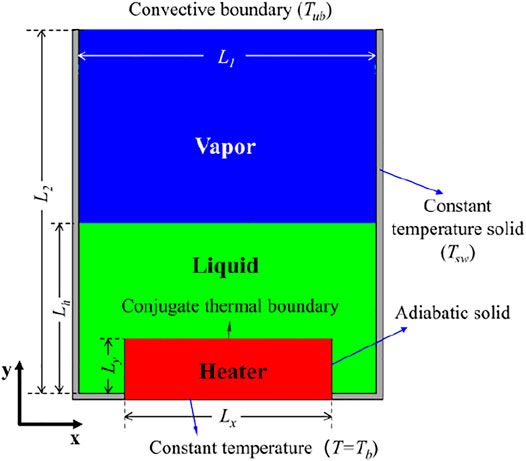
The 2D computation domain shown in Figure 3 is an 800 × 1,000 lattice region (corresponding to L₁ × L₂ = 16.5l₀ × 20.6l₀, where l₀ is the capillary length), which was found to be able to ensure accuracy through grid dependency checking. The liquid (below L_h = 400) is heated in an adiabatic solid container with a heater (L_x × L_y = 600 × 100) placed downside, and the top of the container is open. Some researchers have studied the influence of liquid height on pool boiling and found that the liquid level at 5l₀ is enough for studying HTC and CHF (Pioro et al., 2004), and the liquid level of 6.2l₀ is adopted in this study.

FIGURE 3

FIGURE 3. Schematic diagram of computation domains and boundary conditions.

The computation is initialized with the saturated liquid and vapor at T₀ = 0.8T_c with property parameters as given in Table 1. The kinematic viscosity ν and thermal diffusivity α will directly influence relation time, so the values are obtained with some simulation tests based on a reasonable Pr = ν/α. Then, the dynamic viscosity is calculated with μ = ραPr. On the other hand, when the thermal conductivity ratio k_l/k_v is determined, c_p,l/c_p,v can be calculated by α = k/ρc_p. Latent heat of vaporization h_fg = 0.4392 is calculated with the method proposed by Liu and Cheng (2013). The physical parameters ζ (including υ, α, c_p, and c_v) of the fluid in the interface regime are computed by linear interpolation as

$\zeta ={\zeta }_l\frac{\rho -{\rho }_v}{{\rho }_l-{\rho }_v}+{\zeta }_v\frac{{\rho }_l-\rho }{{\rho }_l-{\rho }_v}.(22)$

TABLE 1

TABLE 1. Property parameters adopted in this study.

The convective boundary (Lou et al., 2013) is applied on the upper boundary, and a constant wall temperature T_sw = T₀ is adopted on the left and right sides. A heater is placed in the center of the bottom, with physical parameters given as (ρc_p)_s = 23.6 and α_s = 4, corresponding to k_s/k_l = 80 and k_s/k_v = 1,360. The heater temperature downside is fixed at T_b with the other position being adiabatic. Besides, the conjugate thermal boundary is adopted on the heater surface as follows (Li et al., 2014):

$\begin{array}{l}{g}_{\overline{i}}\left({\mathbf{x}}_l,t+\delta t\right)=\frac{1-\xi }{1+\xi }{g}_i\left({\mathbf{x}}_l,t+\delta t\right)+\frac{2\xi }{1+\xi }{g}_{\overline{i}}\left({\mathbf{x}}_s,t+\delta t\right),\\ g_i\left({\mathbf{x}}_s,t+\delta t\right)=-\frac{1-\xi }{1+\xi }{g}_{\overline{i}}\left({\mathbf{x}}_s,t+\delta t\right)+\frac{2}{1+\xi }{g}_i\left({\mathbf{x}}_l,t+\delta t\right),\end{array}(23)$

where $\overline{i}$ is the opposite direction to i. The thermal mass ratio of the solid and fluid is defined as $\xi ={\left(\rho c_p\right)}_s/{\left(\rho c_p\right)}_f$.

Model Validation

Validation of the Model With the Laplace Law

Consider first the problem of the formation of a stationary bubble with a radius r in a saturated liquid. The pressure jump Δp across the bubble interface depends on the Laplace law as

$\Delta p=p_{in}-p_{out}=\frac{\sigma }{r},(24)$

where p_in and p_out represent the pressure inside and outside the bubble, respectively, and σ is the surface tension. Figure 4A shows the coexistence of a stationary bubble (blue color) with radius r = 40 surrounded by its saturated liquid (red color) at T_s = 0.8T_c in a 200 × 200 domain with period boundaries on all borders. As presented in Figure 4B, by changing the initial radius of the bubble, the simulated pressure jump Δp is proportional to 1/r, which is in good agreement with the Laplace law, and the surface tension is obtained as σ = 0.2454.

FIGURE 4

FIGURE 4. (A) Coexistence of a bubble surrounded by the saturated liquid at 0.8T_c. (B) Fitting curve of Laplace’s law with surface tension σ = 0.2454.

Simulation of Pool Boiling Under Static Conditions and Validated With Empirical Equations

To analyze bubble scale process, characteristic parameters are chosen as follows (Son et al., 1999; Gong and Cheng, 2017):

$l_0=\sqrt{\frac{{\sigma }_{lv}}{g({\rho }_l-{\rho }_v)}},u_0=\sqrt{g{l}_0},t_0=\frac{l_0}{u_0},(25)$

where l₀ is the capillary length and u₀ and t₀ are, respectively, the characteristic velocity and time.

The corresponding dimensionless parameters are then defined as l^* = l/l₀, t^* = t/t₀, and the dimensionless wall superheat is defined as the Jakob number,

$Ja=c_{p,l}\left(T_w-T_{sat}\right)/h_{fg}.(26)$

Moreover, the dimensionless time-averaged heat flux $q\prime$ is defined as follows (Ma and Cheng, 2019):

$q\prime =\frac{q}{q_{bo}}=\frac{1}{q_{bo}{L}_x\Delta t}{\displaystyle {\int }_0^{\Delta t}\left[{\displaystyle {\int }_{L_x}-k_s{\left(\frac{\partial T}{\partial y}\right)}_{y=0}}dx\right]dt},(27)$

where L_x is the heater length, Δt is the evolution time of pool boiling, and q_bo is the reference boiling heat flux with q_bo = μ_lh_fg/l₀.

The boiling curves with time-averaged heat flux $q\prime$ calculated during the heaving period t_p (40,000–140,000δ_t) is shown in Figure 5A. For the nucleate boiling region, the Rohsenow’s correlation (Rohsenow, 1951) is used for comparison,

$\frac{c_{p,l}\Delta T}{h_{fg}}=c_{sf}{\left(\frac{q/A}{{\mu }_l{h}_{fg}}\sqrt{\frac{\sigma }{g({\rho }_l-{\rho }_v)}}{C}_l^{-1}\right)}^{0.33}{\mathrm{Pr}}_l^{1.7},(28)$

where c_sf is an experimental coefficient. C_l = l₀^real/l₀^LB is the length scale factor between LB simulation and reality, and C_l = 3.89 × 10⁻⁵ is calculated in this study. The red dashed line in Figure 5A is the curve of Rohsenow’s model with c_sf = 0.0059, and c_sf is between 0.00225 and 0.027 for fluid–heating surface combinations in the literature (Holman, 2010). The simulation result fits well with Rohsenow’s correlation.

FIGURE 5

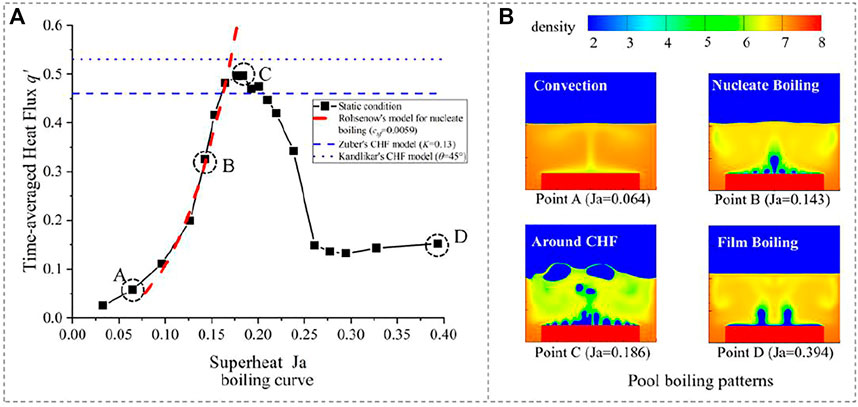
FIGURE 5. (A) Pool boiling curve under static conditions validated with recognized empirical equations. (B) Pool boiling patterns with typical bubbles’ evolution.

The simulated critical heat flux (CHF) is compared with the CHF model proposed by Zuber (Zuber, 1959), which is given by the following:

$Q_{CHF}=K{\rho }_v{h}_{fg}{\left[\frac{\sigma \left({\rho }_l-{\rho }_v\right)g}{{\rho }_v^2}\right]}^{0.25},(29)$

where K = 0.12 to 0.157 and K = 0.13 is adopted for comparing (shown as the horizontal dashed line on the top in Figure 5A). The simulated CHF is 8.0% higher than Zuber’s model. Moreover, it should be mentioned that in Kandlikar’s CHF model (Kandlikar, 2001), K is calculated from the contact angle as

$K=\frac{1+\cos \theta }{16}{\left[\frac{2}{\pi }+\frac{\pi }{4}\left(1+\cos \theta \right)\right]}^{0.5},(30)$

In this study, the contact angle of the surface is 45°, and the simulated CHF agrees very well with Kandlikar’s CHF model.

Pool boiling patterns with typical bubbles’ evolution during different boiling regimes under static conditions are presented in Figure 5B. It is shown that there is no bubble nucleation on the heater in the natural convection regime where the heat flux is low. As the wall superheat (Ja) increases, bubbles start to nucleate on the wall and grow or merge to a size big enough to departure from the surface. The heat flux in the nucleate boiling regime increases with a higher slope as shown in Figure 5A. Then, vigorous bubbles’ coalescence causes the occurrence of local dry-out, and the heat flux reaches the maximum value at Ja = 0.186. After CHF, it enters into the transition boiling regime where a larger vapor film patch covers the heater, and the boiling heat flux decreases by increasing wall superheat. Furthermore, as the wall superheat goes to Ja = 0.3, the boiling pattern changes to film boiling where a stable vapor film with two vapor column forms on the surface and restrains the liquid supplementing to the hot surface.

Results and Discussion

In this section, the pool boiling heat-transfer curve of time-averaged heat flux between heaving conditions and static conditions is first computed. Then, heat-transfer characteristics of pool boiling under heaving conditions are given, including pool boiling patterns at different regimes, the fluctuation of transient heat flux, and the effects of heaving effects on pool boiling at different boiling regions.

Pool Boiling Patterns Under Heaving Conditions

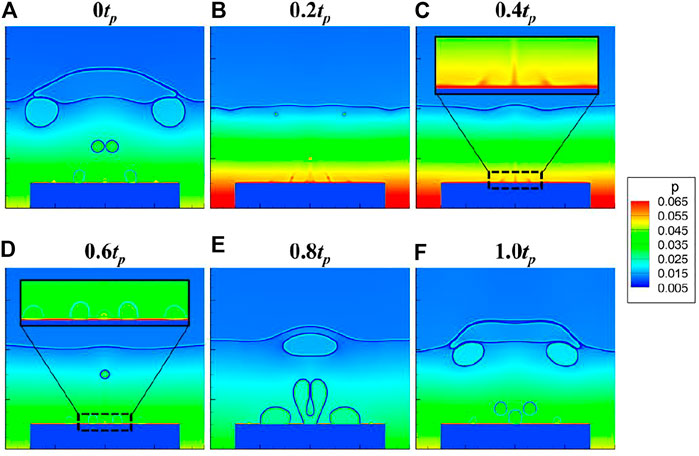
After the above verification of the model with empirical equations under static conditions, pool boiling under heaving conditions is simulated in this section with a heaving period of 100000δ_t with a maximum additional inertial acceleration of 0.5g₀. Representative pool boiling patterns during one stable heaving period (t = 3 × 10⁵δ_t ∼ 4 × 10⁵δ_t) are presented in Figure 6. At the nucleate boiling regime as shown in Figure 6A, bubbles are observed to have a normal size at the beginning; then, they become smaller at the half supergravity period from 0t_p to 0.5t_p. Then, it enters the half low-gravity period from 0.5t_p to 1.0t_p, and bubbles return to the normal size and keep growing bigger for low gravity. According to the analysis given by Friz (1935), the departure diameter of bubbles is proportional to g^−0.5, which is also validated in other simulations (Gong and Cheng, 2012; Fang et al., 2017; Li et al., 2017). Therefore, high gravity leads to small bubbles, and low gravity brings out large bubbles, which has been experimentally observed (Di Marco and Grassi, 2002; Raj et al., 2010), and it is consistent with this simulation result.

FIGURE 6

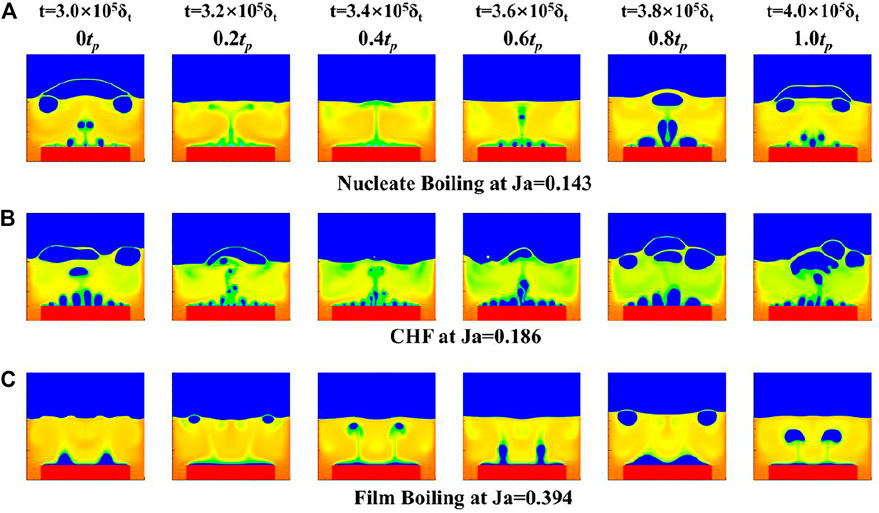
FIGURE 6. Pool boiling patterns under heaving conditions: (A) nucleate boiling regime, (B) CHF, and (C) film boiling regime.

The results for pool boiling at CHF under heaving conditions as presented in Figure 6B are similar to that at the nucleate boiling regime. More bubbles exist because of higher superheat, and the bubbles also undergo the cycles of smaller sizes at the half supergravity period and bigger sizes at the other half low-gravity period. As for film boiling regime in Figure 6C, the change of bubble size is also alike, and it needs to be noticed that the shape of the vapor film is much influenced by the heaving motion.

Comparison of the Boiling Curve Between Heaving Conditions and Static Conditions

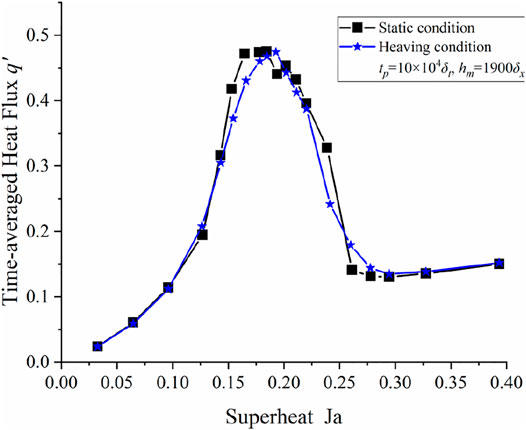
In this section, we take heaving period t_p = 10 × 10⁴δ_t and maximum heaving height h_m = 1900δ_x. The boiling curve with the time-averaged heat flux during the heaving period t_p (40,000–140,000δ_t) is presented in Figure 7, which includes the whole boiling regimes of natural convection, nucleate boiling, CHF, and film boiling. It is shown that the heaving effects have a very slight effect on the time-averaged heat flux. At convection and film boiling regions, the time-averaged heat flux curves between heaving and static conditions may almost coincide with each other because of the perfect periodicity of heaving motion. As for the nucleate boiling region and CHF under heaving motion, heat transfer at low superheat is somewhat enhanced, and it is weakened at high superheat, which leads to slightly smaller CHF with larger superheat compared with that under static conditions. This result is attributed to the combined effects of heaving motion on bubble detachment and coalescence. Detachment of isolated bubbles at low superheat is improved by heaving motion, which increases the time-averaged heat flux. On the other hand, there are times when low gravity appears under heaving conditions, the bubbles are bigger with the lower buoyancy, and more bubbles stay and merge on the surface. Also, coalescence of bubbles at high superheat is drastic under heaving conditions, and rewetting of the liquid to the heater surface is hindered, which leads to a somewhat lower CHF. The effects of heaving motion on the whole boiling curve under different boiling regimes will be analyzed as follows.

FIGURE 7

FIGURE 7. Pool boiling curves under static and heaving conditions.

Transient Heat Flux at the Convection Regime Under Heaving Conditions

It is shown in Figure 7 that heaving motion has a slight effect on the time-average heat flux of pool boiling because of its periodic nature, and this phenomenon will be analyzed based on the variance of transient heat flux $q_t\prime$, which is defined as

$q_t\prime =\frac{q_t}{q_{bo}}=\frac{1}{q_{bo}{L}_x}{\displaystyle {\int }_{L_x}-k_s{\left(\frac{\partial T}{\partial y}\right)}_{y=0}}dx.(31)$

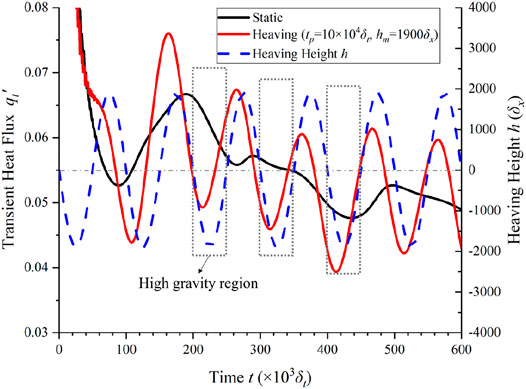
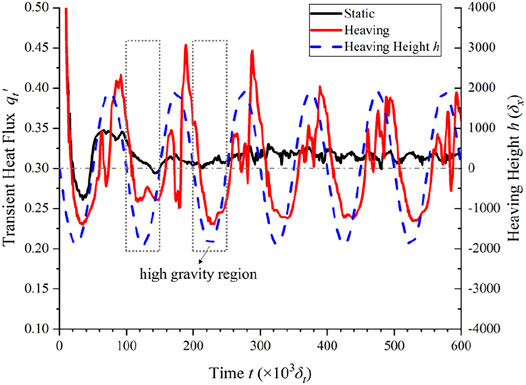
The transient heat flux at the convection regime is given in Figure 8. It can be found that the transient heat flux fluctuates with time periodically under heaving conditions. The gray stippled line is plotted with heaving height h = 0, and the gray dashed line marks the high-gravity region. By comparing the curve of heaving height h and transient heat flux under heaving conditions, we find that after it comes to the high-gravity stage, the heat flux rises, and when it enters the low-gravity region, the transient heat flux starts to decrease. The peaks of transient heat flux always appear after it comes to the low-gravity region, and the valley will be found after it becomes high gravity. In other words, the heat flux will be minimum shortly after the containers fall to the average height (h = 0) and will be maximum after the containers rise to the average height. The phase offset between transient heat flux at convection and heaving motion is caused by the inertia of liquid flow. On the other hand, transient heat flux under static conditions will be no obvious pattern, and its variance range is much lower.

FIGURE 8

FIGURE 8. Transient heat flux at the convection regime with Ja = 0.065.

In order to explain the effects of heaving motion on transient heat flux, graphs of velocity vector and pressure field are given in Figure 9, which shows the moments at h = 0. From t = 0t_p to 0.5t_p, it undergoes a high-gravity process and the convection velocity increases at increasing pressure field, and thus, the transient heat flux rises. On the other hand, during the half period at low gravity from t = 0.5t_p to 1.0t_p, the convection velocity decreases at decreasing pressure field, and thus, the transient heat flux goes down. Since the convection cycle is caused by gravity and density difference, the transient heat flux increases at the half high-gravity period because of convection promotion and vice versa at the half low-gravity period.

FIGURE 9

FIGURE 9. Velocity vector and pressure field at the convection regime under heaving conditions.

Transient Heat Flux at the Nucleate Boiling Regime Under Heaving Conditions

The transient heat flux at the nucleate boiling regime is plotted in Figure 10. The gray dashed line marked the high-gravity region. At this regime, the heat flux is mainly influenced by bubble nucleation and liquid convection. At the high-gravity region, the liquid pressure is high, which leads to difficult bubble nucleation. On the other hand, the buoyancy is large and the liquid convection is strong. It is interesting to observe that the variation of transient heat flux is a little more hysteretic than that at the convection region. The peaks of transient heat flux are always in the low-gravity region, shortly after the system rises to its maximum position. Accordingly, the valley of the transient heat flux is at the high-gravity period. It should be noted that the transient heat flux and heaving motion keep relatively good synchronization.

FIGURE 10

FIGURE 10. Transient heat flux at the nucleate boiling regime with Ja = 0.143.

From Figure 11, it can be concluded that large gravity leads to high pressure in the liquid, and the nucleation is impeded, so the heat flux is low at the high-gravity region. On the contrary, more bubbles and bigger bubbles are generated at the low-gravity region, corresponding to a high heat flux. Because the nucleation and growth of bubbles need time, the peak will be later than the moment with minimum gravity and finally will be found to be just before the containers rise to the average height (h = 0 for here).

FIGURE 11

FIGURE 11. Pressure field at the convection regime under heaving conditions.

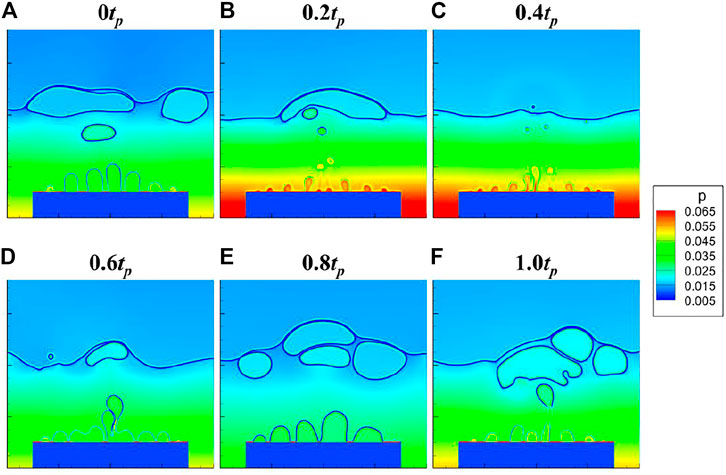
Transient Heat Flux at CHF Under Heaving Conditions

The transient heat flux at CHF fluctuates violently under static conditions, as shown in Figure 12A, and it is noisy. And as seen in Figure 12B, the transient heat flux at CHF under heaving condition is different from that in nucleate boiling regime, because the peaks coincide with the high-gravity region. Analyzing the bubbles’ behavior in Figure 13, it is found that the superheat at CHF is always very high and bubble nucleation is strong all the time at this moment. On the other hand, since the bubbles are small at the high-gravity region, the water rewetting is easier and less area is occupied by vapor, so it corresponds to the peak of heat flux at the high-gravity region. Besides, the pressure gradient is larger with higher gravity, and the bubble’s buoyancy is improved, so the heat flux is higher with easier bubble departure. On the contrary, when the gravity is low, more area is occupied by vapor and the bubble’s departure is also influenced, and the heat flux is low.

FIGURE 12

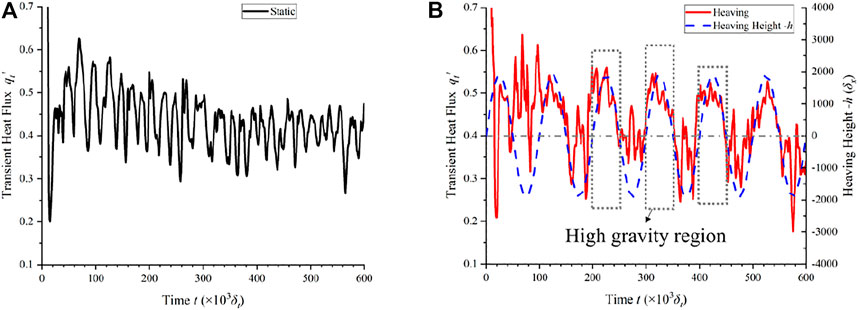
FIGURE 12. Transient heat flux around CHF with Ja = 0.186: (A) static condition, and (B) heaving condition. (negative heaving height −h is used here for better observation).

FIGURE 13

FIGURE 13. Pressure field around CHF under heaving conditions.

Transient Heat Flux at the Film Boiling Regime Under Heaving Conditions

At the film boiling regime, the fluctuation of transient heat flux is more regular, as shown in Figure 14, since the bubble behavior is periodic at this moment. The peaks represent the bubble’s departure from the vapor film, and since bubbles grow very regularly at film boiling, there exist many small peaks in the transient heat flux. Moreover, the fluctuation of transient heat flux under heaving conditions is larger at the low-gravity region and smaller at the high-gravity region. The reason is different-size bubbles’ departure will leave vapor films of different thicknesses.

FIGURE 14

FIGURE 14. Transient heat flux at the film boiling regime with Ja = 0.394.

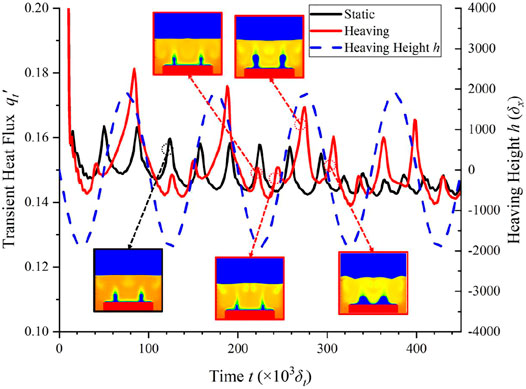
Effects of Heaving Parameters

The influence of heaving parameters on nucleate boiling is studied, and the transient heat flux curves are given in Figure 15, where four conditions are simulated with two different heaving height and two different heaving period. Figures on the same row have the same heaving height (Figures 15A–D), and these on the same column have the same heaving period (Figures 15A–D). It can be found that both larger heaving height and shorter period time bring out more violent heaving motion, and the fluctuation amplitude will be larger. Besides, the fluctuation period of heat flux is the same with the heaving height, which can also be reflected by comparing Figures 15A,C with Figures 15B,D. It needs to be noticed that the valley may be very deep for short heaving period time as seen in Figure 15B, because more and larger bubbles burst to nucleate and grow, and then vapor films form on the heater surface temporarily.

FIGURE 15

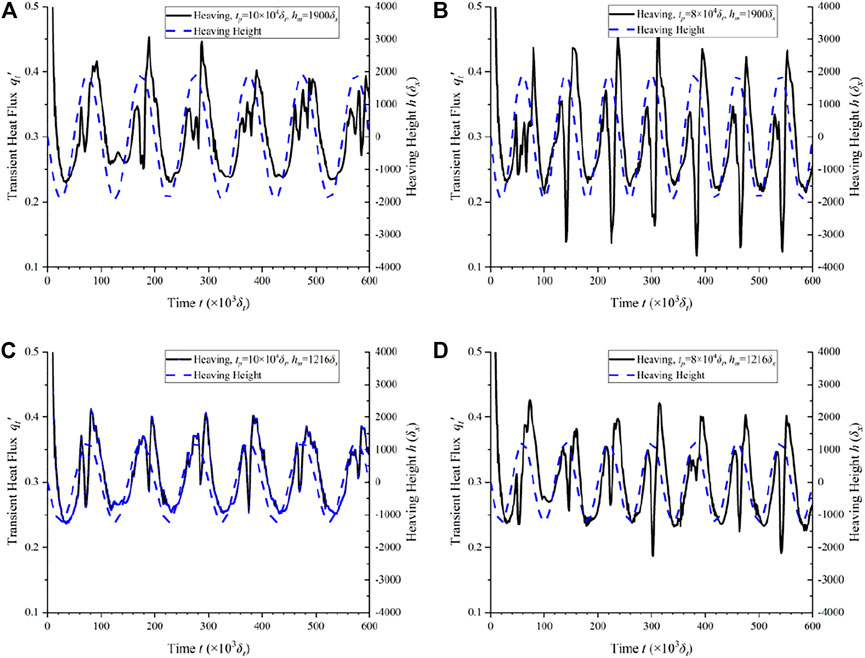
FIGURE 15. Transient heat flux with different heaving parameters at the nucleate boiling regime (Ja = 0.143). (A) Heaving period t_p = 10 × 10⁴δ_t, maximum heaving height h_m = 1900δ_x, (B) t_p = 8 × 10⁴δ_t, h_m = 1900δ_x, (C) t_p = 10 × 10⁴δ_t, h_m = 1216δ_x, and (D) t_p = 8 × 10⁴δ_t, h_m = 1216δ_x.

Concluding Remarks

In this study, lattice Boltzmann simulations of pool boiling under heaving conditions are performed. First, the simulated boiling curve under static conditions has been validated with Rohsenow’s correlation for nucleate boiling, Zuber’s model, and Kandlikar’s model for CHF. Then, heat-transfer characteristics and bubble behaviors of pool boiling under heaving conditions are investigated, and the differences with that under static conditions have been analyzed. Moreover, heaving effects on bubble behaviors and heat transfer at different pool boiling regions are studied. The following conclusions can be drawn from this study:

1) Pool boiling under heaving condition will go through periods of high gravity and low gravity, which leads to unique bubble behaviors of nucleation, growth, coalescence, and departure. Moreover, pool boiling heat transfer under heaving condition is somewhat enhanced at low superheat, and it is weakened at high superheat, which leads to slightly smaller CHF with larger superheat compared with that under static condition.

2) The variance of transient heat flux under heaving conditions is directly related with bubble behaviors, and its fluctuation is very distinct. The transient heat flux and heaving motion keep good synchronization for all pool boiling regimes (convection, nucleate boiling, CHF, and film boiling), and their phase offset is different according to pool boiling intensity and bubble behaviors under large-gravity or low-gravity stages. On the contrary, the transient heat flux of pool boiling under static conditions is relatively chaotic.

3) Large gravity under heaving motion leads to high pressure in the liquid, and bubble nucleation is impeded. On the contrary, more bubbles and bigger bubbles are generated at the low-gravity region, corresponding to a high heat flux.

4) Both a larger heaving height and a shorter period time generate more violent heaving motion, and the fluctuation amplitude of transient heat flux for pool boiling will be larger. Besides, the valley of transient heat flux may be very deep for a short heaving period time.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

QZ: methodology, validation, formal analysis, and writing—original draft. XL: conceptualization, writing—review and editing, supervision, and funding acquisition. YH: formal analysis and investigation. YC: validation and investigation. PL: validation.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 51806155).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Cheng, P., Quan, X., Gong, S., Liu, X., and Yang, L. (2014). Recent Analytical and Numerical Studies on Phase-Change Heat Transfer. Advances in Heat Transfer. 46. 187–248. doi:10.1016/bs.aiht.2014.08.004

CrossRef Full Text | Google Scholar

D'Humières, D., Ginzburg, I., Krafczyk, M., Lallemand, P., and Luo, L. S. (2002). Multiple-relaxation-time Lattice Boltzmann Models in Three Dimensions. Philos. Trans. A. Math. Phys. Eng. Sci. 360, 437–451. doi:10.1098/rsta.2001.0955

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Marco, P., and Grassi, W. (2002). Motivation and Results of a Long-Term Research on Pool Boiling Heat Transfer in Low Gravity. Int. J. Therm. Sci. 41 (7), 567–585. doi:10.1016/s1290-0729(02)01351-0

CrossRef Full Text | Google Scholar

Dong, Z., Li, W., and Song, Y. (2009). Lattice Boltzmann Simulation of Growth and Deformation for a Rising Vapor Bubble through Superheated Liquid. Numer. Heat Transfer, A: Appl. 55 (4), 381–400. doi:10.1080/10407780902720718

CrossRef Full Text | Google Scholar

Fang, W.-Z., Chen, L., Kang, Q.-J., and Tao, W.-Q. (2017). Lattice Boltzmann Modeling of Pool Boiling with Large Liquid-Gas Density Ratio. Int. J. Therm. Sci. 114, 172–183. doi:10.1016/j.ijthermalsci.2016.12.017

CrossRef Full Text | Google Scholar

Fang, X., Zheng, L., He, Y., Li, G., Bi, M., Yang, B., et al. (2019). Experimental Study of Pool Boiling Critical Heat Flux on Thin Wires under Various Gravities. Microgravity Sci. Technol. 31 (4), 339–345. doi:10.1007/s12217-019-9688-z

CrossRef Full Text | Google Scholar

Friz, W. (1935). Maximum Volume of Vapor Bubbles. Physic. Zeitschz. 36, 379–354.

Google Scholar

Gong, S., and Cheng, P. (2012). A Lattice Boltzmann Method for Simulation of Liquid–Vapor Phase-Change Heat Transfer. Int. J. Heat Mass Transfer 55 (17-18), 4923–4927. doi:10.1016/j.ijheatmasstransfer.2012.04.037

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2015). Lattice Boltzmann Simulations for Surface Wettability Effects in Saturated Pool Boiling Heat Transfer. Int. J. Heat Mass Transfer 85, 635–646. doi:10.1016/j.ijheatmasstransfer.2015.02.008

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2017). Direct Numerical Simulations of Pool Boiling Curves Including Heater's thermal Responses and the Effect of Vapor Phase's thermal Conductivity. Int. Commun. Heat Mass Transfer 87, 61–71. doi:10.1016/j.icheatmasstransfer.2017.06.023

CrossRef Full Text | Google Scholar

Gui, M., Tian, W., Wu, D., Su, G. H., and Qiu, S. (2020). Study on CHF Characteristics in Narrow Rectangular Channel under Complex Motion Condition. Appl. Therm. Eng. 166, 114629. doi:10.1016/j.applthermaleng.2019.114629

CrossRef Full Text | Google Scholar

Guo, Z., Zheng, C., and Shi, B. (2002). Discrete Lattice Effects on the Forcing Term in the Lattice Boltzmann Method. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 65 (4), 046308. doi:10.1103/PhysRevE.65.046308

PubMed Abstract | CrossRef Full Text | Google Scholar

Hazi, G., and Markus, A. (2009). On the Bubble Departure Diameter and Release Frequency Based on Numerical Simulation Results. Int. J. Heat Mass Transfer 52 (5-6), 1472–1480. doi:10.1016/j.ijheatmasstransfer.2008.09.003

CrossRef Full Text | Google Scholar

Holman, J. P. (2010). Heat Transfer. New York: McGraw Hill Higher Education.

Google Scholar

Huang, R., Wu, H., and Adams, N. A. (2019). Lattice Boltzmann Model with Self-Tuning Equation of State for Multiphase Flows. Phys. Rev. E 99 (2), 023303. doi:10.1103/PhysRevE.99.023303

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, R., Wu, H., and Adams, N. A. (2021). Mesoscopic Lattice Boltzmann Modeling of the Liquid-Vapor Phase Transition. Phys. Rev. Lett. 126 (24), 244501. doi:10.1103/physrevlett.126.244501

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, J.-S., Kim, J.-W., Nam, H.-U., and Park, G.-C. (2011). Assessment of MARS Code for Predicting Critical Heat Flux under Heaving Conditions. Nucl. Techn. 176 (2), 260–273. doi:10.13182/nt11-a13300

CrossRef Full Text | Google Scholar

Ishida, I., Kusunoki, T., Murata, H., Yokomura, T., Kobayashi, M., and Nariai, H. (1990). Thermal-hydraulic Behavior of a marine Reactor during Oscillations. Nucl. Eng. Des. 120 (2-3), 213–225. doi:10.1016/0029-5493(90)90374-7

CrossRef Full Text | Google Scholar

Isshiki, N. (1966). Effects of Heaving and Listing upon Thermo-Hydraulic Performance and Critical Heat Flux of Water-Cooled marine Reactors. Nucl. Eng. Des. 4 (2), 138–162. doi:10.1016/0029-5493(66)90088-4

CrossRef Full Text | Google Scholar

Kandlikar, S. G. (2001). A Theoretical Model to Predict Pool Boiling CHF Incorporating Effects of Contact Angle and Orientation. J. Heat Transfer 123 (6), 1071–1079. doi:10.1115/1.1409265

CrossRef Full Text | Google Scholar

Li, L., Chen, C., Mei, R., and Klausner, J. F. (2014). Conjugate Heat and Mass Transfer in the Lattice Boltzmann Equation Method. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 89 (4), 043308. doi:10.1103/PhysRevE.89.043308

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Kang, Q. J., Francois, M. M., He, Y. L., and Luo, K. H. (2015). Lattice Boltzmann Modeling of Boiling Heat Transfer: the Boiling Curve and the Effects of Wettability. Int. J. Heat Mass Transfer 85, 787–796. doi:10.1016/j.ijheatmasstransfer.2015.01.136

CrossRef Full Text | Google Scholar

Li, Q., Luo, K. H., Kang, Q. J., He, Y. L., Chen, Q., and Liu, Q. (2016). Lattice Boltzmann Methods for Multiphase Flow and Phase-Change Heat Transfer. Prog. Energ. Combust. Sci. 52, 62–105. doi:10.1016/j.pecs.2015.10.001

CrossRef Full Text | Google Scholar

Li, Q., Zhou, P., and Yan, H. J. (2017). Improved thermal Lattice Boltzmann Model for Simulation of Liquid-Vapor Phase Change. Phys. Rev. E 96 (6), 063303. doi:10.1103/PhysRevE.96.063303

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., and Cheng, P. (2013). Lattice Boltzmann Simulation of Steady Laminar Film Condensation on a Vertical Hydrophilic Subcooled Flat Plate. Int. J. Heat Mass Transfer 62, 507–514. doi:10.1016/j.ijheatmasstransfer.2013.03.002

CrossRef Full Text | Google Scholar

Liu, D., Tian, W., Xi, M., Chen, R., Qiu, S., and Su, G. H. (2018). Study on Safety Boundary of Flow Instability and CHF for Parallel Channels in Motion. Nucl. Eng. Des. 335, 219–230. doi:10.1016/j.nucengdes.2018.05.024

CrossRef Full Text | Google Scholar

Lou, Q., Guo, Z., and Shi, B. (2013). Evaluation of Outflow Boundary Conditions for Two-phase Lattice Boltzmann Equation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 87 (6), 063301. doi:10.1103/PhysRevE.87.063301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, X., and Cheng, P. (2019). 3D Simulations of Pool Boiling above Smooth Horizontal Heated Surfaces by a Phase-Change Lattice Boltzmann Method. Int. J. Heat Mass Transfer 131, 1095–1108. doi:10.1016/j.ijheatmasstransfer.2018.11.103

CrossRef Full Text | Google Scholar

Ma, X., Cheng, P., Gong, S., and Quan, X. (2017). Mesoscale Simulations of Saturated Pool Boiling Heat Transfer under Microgravity Conditions. Int. J. Heat Mass Transfer 114, 453–457. doi:10.1016/j.ijheatmasstransfer.2017.06.019

CrossRef Full Text | Google Scholar

O'Rourke, R. (2010). Navy Nuclear-Powered Surface Ships: Background, Issues, and Options for Congress. In: Congressional Research Service. United States: Diane Publishing.

Google Scholar

Otsuji, T., and Kurosawa, A. (1982). Critical Heat Flux of Forced Convection Boiling in an Oscillating Acceleration Field - I. General Trends. Nucl. Eng. Des. 71 (1), 15–26. doi:10.1016/0029-5493(82)90165-0

CrossRef Full Text | Google Scholar

Pioro, I. L., Rohsenow, W., and Doerffer, S. S. (2004). Nucleate Pool-Boiling Heat Transfer. I: Review of Parametric Effects of Boiling Surface. Int. J. Heat Mass Transfer 47 (23), 5033–5044. doi:10.1016/j.ijheatmasstransfer.2004.06.019

CrossRef Full Text | Google Scholar

Raj, R., Kim, J., and McQuillen, J. (2010). Gravity Scaling Parameter for Pool Boiling Heat Transfer. J. Heat Transfer 132 (9), 091502. doi:10.1115/1.4001632

CrossRef Full Text | Google Scholar

Rohsenow, W. M. (1951). A Method of Correlating Heat Transfer Data for Surface Boiling of Liquids. Trans. Asme 74, 969–976.

Google Scholar

Safari, H., Rahimian, M. H., and Krafczyk, M. (2013). Extended Lattice Boltzmann Method for Numerical Simulation of thermal Phase Change in Two-phase Fluid Flow. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 88 (1), 013304. doi:10.1103/PhysRevE.88.013304

PubMed Abstract | CrossRef Full Text | Google Scholar

Son, G., Dhir, V. K., and Ramanujapu, N. (1999). Dynamics and Heat Transfer Associated with a Single Bubble during Nucleate Boiling on a Horizontal Surface. J. Heat Transfer 121 (3), 623–631. doi:10.1115/1.2826025

CrossRef Full Text | Google Scholar

Tanaka, Y., Yoshino, M., and Hirata, T. (2011). Lattice Boltzmann Simulation of Nucleate Pool Boiling in Saturated Liquid. Commun. Comput. Phys. 9 (5), 1347–1361. doi:10.4208/cicp.141109.161210s

CrossRef Full Text | Google Scholar

Tian, Z., Gu, B., Zhang, Y., and Gao, W. (2020). Flow Boiling Heat Transfer under marine Motions: A Comprehensive Review. Ann. Nucl. Energ. 143, 107455. doi:10.1016/j.anucene.2020.107455

CrossRef Full Text | Google Scholar

Wang, S., Yang, B., Zhou, Z., and Long, J. (2019). Review on thermal-hydraulic Characteristics of Nuclear Reactors under Ocean Conditions. Nucl. Sci. Eng. 193 (1-2), 14–32. doi:10.1080/00295639.2018.1512791

CrossRef Full Text | Google Scholar

Xi, M., Wu, Y., Tian, W., Su, G. H., and Qiu, S. (2015). The Influence of Ocean Conditions on thermal-hydraulic Characteristics of a Passive Residual Heat Removal System. Prog. Nucl. Energ. 85, 573–587. doi:10.1016/j.pnucene.2015.08.010

CrossRef Full Text | Google Scholar

Yan, B. H. (2017). Review of the Nuclear Reactor thermal Hydraulic Research in Ocean Motions. Nucl. Eng. Des. 313, 370–385. doi:10.1016/j.nucengdes.2016.12.041

CrossRef Full Text | Google Scholar

Yu, J. (2020). Marine Nuclear Power Technology. Shanghai: Shanghai Jiao Tong University Press. doi:10.1007/978-981-15-2894-1

CrossRef Full Text | Google Scholar

Zhang, R., and Chen, H. (2003). Lattice Boltzmann Method for Simulations of Liquid-Vapor thermal Flows. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 67 (6), 066711. doi:10.1103/PhysRevE.67.066711

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., and Cheng, P. (2017). Mesoscale Simulations of Boiling Curves and Boiling Hysteresis under Constant wall Temperature and Constant Heat Flux Conditions. Int. J. Heat Mass Transfer 110, 319–329. doi:10.1016/j.ijheatmasstransfer.2017.03.039

CrossRef Full Text | Google Scholar

Zou, Q., Liu, L., Hu, Y., Chang, Y., and Yang, R. (2021). Numerical Investigation of Pool Boiling Under Ocean Condition with Lattice Boltzmann Simulation. Part Ⅱ: Rolling Condition. Front. Energy Res. 9, 668. doi:10.3389/fenrg.2021.771781

CrossRef Full Text | Google Scholar

Zuber, N. (1959). Hydrodynamic Aspects of Boiling Heat Transfer (Thesis), United States Atomic Energy Commission. Los Angeles, CA: University of California.

CrossRef Full Text | Google Scholar

Nomenclature

a Parameter in the PR equation of state

a_Co Coriolis acceleration

a_h Heaving acceleration

a_n Normal acceleration

a_t Tangential acceleration

b Parameter in the PR equation of state

c₀ Coefficient used in effective density calculation

c_s Lattice sound speed (m s⁻¹)

c_v Specific heat at constant volume (kJ kg⁻¹ K⁻¹)

c_p Specific heat at constant pressure (kJ kg⁻¹ K⁻¹)

c_sf Experimental coefficient

C_l Length scale factor

e Lattice velocity vector (m s⁻¹)

f Density distribution function

F⃖ Discrete force

F Actual body force

F_h Additional forces introduced by heaving motion

g_a Temperature distribution function Gravity

g Gravity vector (N m⁻²) Gravity

G Interaction strength function

h Heaving displacement

h_m Maximum heaving amplitude

h_fg Latent heat of vaporization

Ja Jacob number, dimensionless superheat

k Thermal conductivity (W m⁻¹ K⁻¹)

K Experimental coefficient

l₀ Capillary length

l^* Dimensionless length

L₁ Length of the calculation domain

L₂ Height of the calculation domain

L_h Initial height of the water level

L_x Length of the heater

L_y Height of the heater

m Density distribution function in moment space

M Orthogonal transformation matrix

p Pressure (Pa)

Pr Prandtl number

q Heat flux (W/m²)

q’ Dimensionless heat flux

q_bo Reference boiling heat flux

r Radius of the bubble Position vector of the fluid particle pointed from the rotation axis

R Gas constant (kJ kg⁻¹ K⁻¹)

S Diagonal matrix related to relaxation time

t Time

t₀ Characteristic time

t^* Dimensionless time

t_p Heaving period

T Temperature(K)

T_s Saturation temperature (K)

T_w Wall temperature (K)

u₀ Characteristic velocity

u Velocity vector (m s⁻¹)

v Actual fluid velocity vector

w Acentric factor of the fluid

x Position vector

Greek symbol

α Thermal diffusivity

β Weighting factor

β^* Angular acceleration

δx Lattice spacing

δt Lattice time step

Λ Collision matrix

Γ Collision matrix for forces

μ Dynamic viscosity

ν Kinematic viscosity (m⁻²s)

ω Weighting factor

ω^* Angular velocity

φ Effective density

ϕ Phase change source term

ρ Density (kg m⁻³)

σ Surface tension (N m⁻¹)

τ Relaxation time

ξ Thermal mass ratio of solid and fluid

Subscripts or Superscripts

c Critical state

eq Equilibrium

g Gravity

i Discrete velocity direction

int Interaction

l Liquid

n Centripetal

s Solid

t Tangential

v Vapor