Wind Speed Distributions Used in Wind Energy Assessment: A Review

With economic development and population growth, energy demand has shown an upward trend. Renewable energy is inexhaustible and causes little pollution, which has broad prospects for development. In recent years, wind energy has been developed as an essential renewable energy source. The use of wind power is very environmentally friendly and plays a critical role in economic growth. Assessing the characteristics and potential of wind energy is the first step in the effective development of wind energy. The wind speed distribution at a specific location determines the available wind energy. This paper reviews the wind speed distribution models used for wind energy assessment, and they are applicable to different wind regimes. All potential wind speed distribution models should be considered for modeling wind speed data at a particular site. Previous studies have selected several parameter estimation methods and evaluation criteria to estimate model parameters and evaluate the goodness-of-fit. This paper discusses their advantages and disadvantages. The characteristics of wind speed distribution are constantly varying geographically and temporally. Wind energy assessment should consider local geographical elements, such as local climate, topography, and thermal properties difference between the land and the sea, and focus on long-term variations in wind characteristics.

Introduction

Energy is a necessary material basis for the survival and development of human society. In recent years, the energy crisis has become a worldwide problem faced by humankind. With the continuous growth of the population and the rapid development of the global economy, energy demand is also increasing. Traditional fossil fuels (such as coal, oil, natural gas, etc.) have been widely used in almost all areas of daily life. However, fossil fuel reserves are limited. Fossil fuels gradually formed in nature over millions of years may be entirely exhausted by humans within a few hundred years (Baz et al., 2021). In addition, the carbon in fossil fuels is transformed into carbon dioxide, which increases the concentration of carbon dioxide in the atmosphere, leading to aggravation of the greenhouse effect, changing the global climate, and breaking the ecological balance (Arenas-López and Badaoui, 2020). As people gradually realize the importance and urgency of environmental protection, energy conservation, emission reduction, and sustainable development, renewable energy has become the primary energy source required for future social development and has broad potential demands. Wind energy is one of the potential renewable energy sources that can be used for commercial purposes. Many countries take wind power development to improve the energy structure and protect the ecological environment. Wind energy also plays a vital role in economic growth, creating more employment opportunities, and promoting the development of science and technology (Liu et al., 2019; Kandpal and Dhingra, 2021). Wind energy has recently attracted widespread attention in the power generation industry (Jansen et al., 2020). Global wind-generated power has increased significantly from 2012 to 2017 (Figure 1) (World Bank, 2017).

FIGURE 1

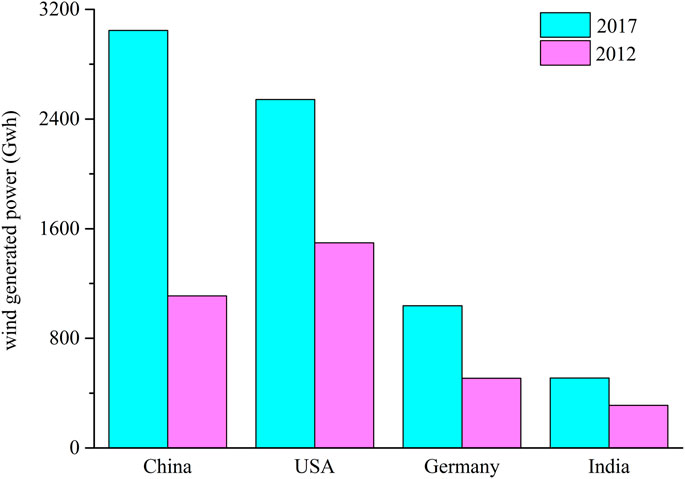
FIGURE 1. Changes in wind energy output from 2012 to 2017 in the four countries with the highest wind power generation (China, the United States, Germany, and India).

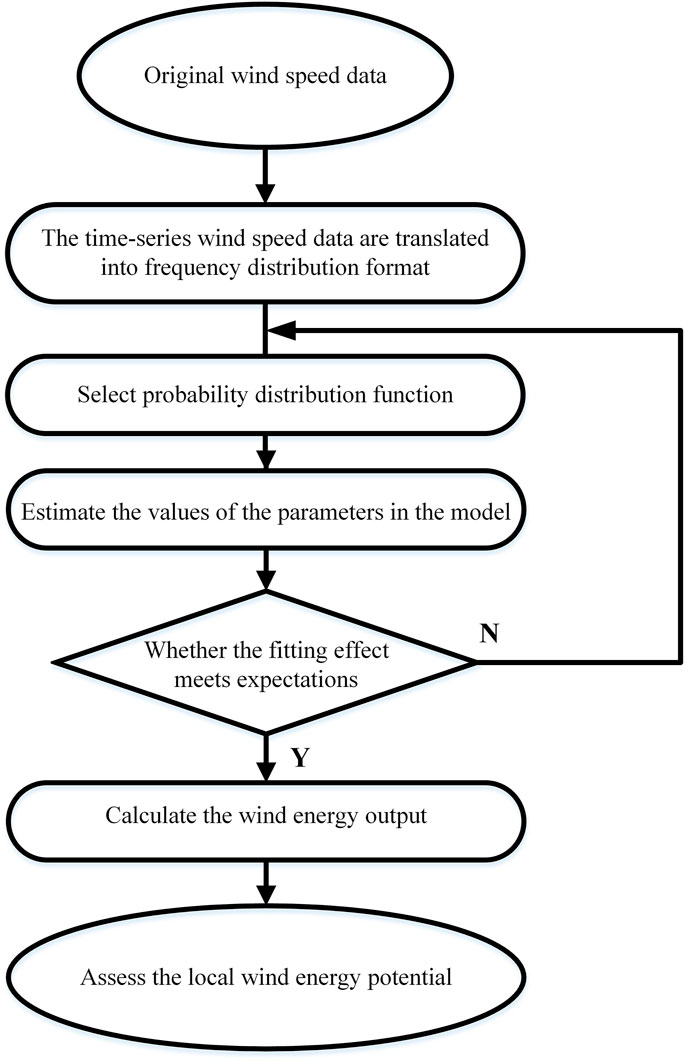
At present, to meet the increasing electricity demand, researchers have focused on improving the efficiency of wind power generation (Chen and Blaabjerg, 2009). Assessing the characteristics and potential of wind energy is the first step in the effective development of wind energy. Wind energy resource assessment is an essential part of the feasibility analysis of wind farm projects. Whether the assessment is reasonable directly impacts the cost of power generation and economic benefits (Mauritzen, 2020). The wind speed distribution at a specific location determines the available wind energy and the performance of the energy conversion system. Therefore, to reduce the uncertainty of wind energy output estimation, it is necessary to accurately understand the distribution characteristics of wind speed (Celik, 2003). Two methods are generally used to determine the wind speed distribution: 1) the time series method (Morales et al., 2010; Katikas et al., 2021) and 2) the statistical analysis method (Ouarda et al., 2016; Elie Bertrand et al., 2020). The result obtained by the time series method may be more accurate because it is based on the original wind speed data. However, with an enormous amount of data, the processing process of the time series method is more complicated. When there is a lack of long-term wind speed data, it is more feasible to use statistical analysis to explain the behavior and characteristics of historical wind speed data and estimate the wind energy output. The statistical analysis method uses limited parameters to characterize wind speed distribution, which is efficient and straightforward. The process of statistical analysis to assess the potential of wind energy is shown in Figure 2. It is crucial to determine the most suitable probability density function (pdf) for historical wind speed data (Alavi et al., 2016a). The most widely used pdf in wind speed modeling is the Weibull distribution (Petković et al., 2014; Wais, 2017a; Sarkar et al., 2019). In recent years, researchers have considered several pdfs to find the most accurate model for the wind energy assessment of a particular site (Lo Brano et al., 2011; Ouarda et al., 2015; Jia et al., 2020; Wang et al., 2021). After determining the pdf, the value of each parameter in the function should be estimated. The commonly used parameter estimation methods mainly include the maximum likelihood method (Miao et al., 2019), the least squares method (Jung and Schindler, 2017), the moment method (Li and Miao, 2021), and the power density method (Akdağ and Dinler, 2009). Previous studies used different goodness-of-fit criteria to evaluate the accuracy of the model. Commonly used criteria include the coefficient of determination (ul Haq et al., 2020), the root mean square error (Guarienti et al., 2020), the Kolmogorov-Smirnov test statistic (Ouarda and Charron, 2018), the Anderson-Darling test statistic (Soukissian, 2013), and the chi-square test statistic (Wang et al., 2016).

FIGURE 2

FIGURE 2. The process of evaluating local wind energy potential based on original wind speed data.

Although the research of wind speed distribution has pursued the unified modeling of existing wind regimes, previous studies have not proposed a model that can provide a sufficient description at any site. Correspondingly, different parameter estimation methods and goodness-of-fit criteria have advantages and disadvantages, which bring difficulties to wind energy potential assessment. This paper reviews wind speed models, parameter estimation methods, and goodness-of-fit criteria and briefly discusses the advantages and disadvantages. The aim is to analyze the reasons for the differences in the fitting effects of models in different geographical locations and time scales.

Wind Speed Distribution Models

The kinetic energy contained in the airflow is converted into electrical energy by the wind turbines. The wind speed presents a positively skewed distribution with statistical characteristics. However, wind power has randomness, volatility, and intermittent characteristics, making the output power of wind farms fluctuate considerably. Several probability distribution models have been widely used in wind farm analysis, planning, design, construction, and operation. Wind speed distribution models can be roughly divided into two classes: parametric distribution models and nonparametric distribution models.

Parametric Distribution Models

The theoretical average output can be calculated as follows (Masseran, 2015):

$\overline{P}=\underset{0}{\overset{\infty }{{\displaystyle \int }}}\frac{1}{2}\rho v^{3}f\left(v\right)\text{d}v,(1)$

Where $\overline{P}$ is the theoretical average wind energy output, $v$ is the observed wind speed, and $f\left(v\right)$ is the pdf of wind speed.

The observed average output can be calculated as follows：

$\overline{P_o}=\frac{1}{2}\rho {\overline{v}}^3,(2)$

Where $\overline{P_o}$ is the observed average wind energy output, $\overline{v }$ is the observed mean wind speed.

Energy prevision bias is the percentage error between the theoretical average output and the observed average output:

$\phi =\left|\frac{\overline{P}-\overline{P_o}}{\overline{P_o}}\right|\times 100\%.(3)$

The estimation of wind power mainly depends on the $f\left(v\right)$. Therefore, selecting an appropriate pdf can provide more accurate energy potential results and reduce energy prevision bias.

Weibull Distribution

The Weibull distribution was promoted by the Swedish physicist Weibull (Weibull, 1951), and it has been used in various fields, such as physics, materials science, geography, medicine, economics, etc. The pdf of the two-parameter Weibull distribution is:

$f\left(x\right)=\frac{k}{\alpha }{\left(\frac{x}{\alpha }\right)}^{k-1}\text{exp}\left[-{\left(\frac{x}{\alpha }\right)}^k\right],(4)$

where $\alpha$ is the scale parameter, which controls the abscissa scale of the data distribution; $k$ is the shape parameter of the Weibull distribution, which determines the width of the data distribution. The two-parameter Weibull distribution has a simple form, high flexibility, and efficient computing parameters, making it the most popular and famous wind speed distribution model. The Weibull distribution has significant advantages, especially in areas dominated by temperate depressions (Harris and Cook, 2014). For example, Bilir et al. (2015) used a two-parameter Weibull distribution to evaluate wind energy resources near Ankara, the capital of Turkey. Shu et al. (2015) used a two-parameter Weibull model to characterize the wind speed distribution in Hong Kong. In addition, the Weibull distribution has also been applied to the estimation of the performance of the automatic wind power generation system (Celik, 2006), the simulation and prediction of the wind speed time series (Kaplan and Temiz, 2017), the wind turbine failure analysis (Jin et al., 2021), etc. Nevertheless, the two-parameter Weibull distribution is not suitable for all wind regimes in nature. Previous studies have shown that the two-parameter Weibull distribution is less effective in fitting low wind speeds, especially for wind speed data with considerable null wind probability (Akgül et al., 2016). The two-parameter Weibull distribution cannot determine the actual null wind probability, so null wind speed data needs to be removed before fitting, making it impossible to characterize the existing wind regimes.

A three-parameter Weibull distribution is proposed for wind energy evaluation as an alternative probability distribution for the two-parameter Weibull distribution (Montoya et al., 2019):

$f\left(x\right)=\frac{k}{\alpha }{\left(\frac{x-\mu }{\alpha }\right)}^{k-1}\text{exp}\left[-{\left(\frac{x-\mu }{\alpha }\right)}^k\right],(5)$

where $\mu$ is the location parameter, which represents the minimum wind speed. The three-parameter Weibull distribution can estimate the probability of null wind speed and give greater weight to low wind speeds. Wais (2017b) showed that the accuracy of the two-parameter Weibull distribution is higher in estimating wind power output only when the null wind speed is insignificant. Otherwise, the relative error of the three-parameter Weibull distribution is minor. However, adding a location parameter may lead to the negative values of the pdf, which requires artificial control of the lower limit of the three-parameter Weibull distribution to avoid negative wind speed. In addition, compared with the two-parameter Weibull distribution, the three-parameter Weibull distribution cannot achieve the same high value at high wind speeds. Since wind power has a cubic relationship with the wind speed, although the three-parameter Weibull function fits the wind speed better at some sites, it does not necessarily mean that it estimates the output more accurately.

When the shape parameter of the two-parameter Weibull distribution is equal to 2, the Rayleigh distribution is formed:

$f\left(x\right)=\frac{x}{{\alpha }^2}\text{exp}\left[-\frac{1}{2}{\left(\frac{x}{\alpha }\right)}^2\right].(6)$

Rayleigh distribution is used to model wind speed and evaluate the standard performance of wind turbines (Saleh et al., 2012; Valencia Ochoa et al., 2019). Compared with the Weibull distribution, because the Rayleigh distribution contains only one parameter, it is more convenient to use, and its parameters are easier to estimate. However, the Rayleigh distribution is based on the assumption that the long-term mean wind vector is zero. The vector of wind prevailing at sea, such as trade wind, deviates significantly from zero, making the applicability of the Rayleigh distribution to sea winds relatively limited (Perrin et al., 2006).

Extreme Value Distribution

Previous studies have shown that extreme wind speeds have almost no effect on the parameter values of the Weibull distribution (Wang et al., 2015). Once the wind speed exceeds the threshold, the Weibull model is no longer applicable. There are obvious errors in the maximum annual wind speed distribution and the return period estimated by the Weibull model, which affects the risk assessment of extreme winds (Perrin et al., 2006). A practical alternative is to use extreme value distributions.

Extreme value distributions used for wind speed modeling include the Gumbel distribution, the inverse Weibull distribution, and the generalized extreme value distribution. The pdf of the Gumbel distribution is as follows:

$f\left(x\right)=\frac{1}{\alpha }\text{exp}\left[-\frac{x-\mu }{\alpha }-\text{exp}\left(\frac{x-\mu }{\alpha }\right)\right],(7)$

where $\alpha$ is the scale parameter, and $\mu$ is the location parameter.

The pdf of the inverse Weibull distribution is as follows:

$f\left(x\right)=\frac{k}{\alpha }{\left(\frac{\alpha }{x}\right)}^{k+1}\text{exp}\left[-{\left(\frac{\alpha }{x}\right)}^k\right],(8)$

where $\alpha$ is the scale parameter, and $k$ is the shape parameter.

The pdf of the generalized extreme value distribution is shown as follows:

$f\left(x\right)=\frac{1}{\alpha }{\left[1-\frac{k}{\alpha }\left(x-\mu \right)\right]}^{\frac{1}{k}-1}-\text{exp}\left\{-{\left[1-\frac{k}{\alpha }\left(x-\mu \right)\right]}^{\frac{1}{k}}\right\},(9)$

where $\alpha$ is the scale parameter, $k$ is the shape parameter, and $\mu$ is the location parameter.

Gumbel distribution and inverse Weibull distribution are subsets of the generalized extreme value distribution. The extreme value distribution is a heavy-tailed distribution whose right tail is thicker than the Weibull distribution. Therefore, the extreme value distribution is more accurate when estimating the occurrence probability of extreme wind speeds. However, due to the lack of historical extreme wind speed data, the traditional extreme value distribution can only estimate the annual maximum wind speed distribution and does not consider the monthly or daily extreme winds, thus reducing the reliability of quantifying extreme events (Torrielli et al., 2013). In addition, studies generally believe that there is a threshold wind speed, and the extreme value distribution is not suitable for modeling below the threshold wind speed. However, the estimation results of threshold wind speed are pretty different, so the applicable range of extreme value distribution is unclear, making it difficult to determine the most suitable type of extreme value distribution (Kang et al., 2015).

Gamma Distribution

Gamma distribution is also one of the distributions widely used in wind speed distribution modeling (Aries et al., 2018). The two-parameter gamma distribution is also called the Pearson Type III distribution:

$f\left(x\right)=\frac{{\alpha }^k}{\text{Γ}\left(\text{k}\right)}{x}^{k-1}\text{exp}\left(-\alpha x\right),(10)$

where $\alpha$ is the scale parameter, and $k$ is the shape parameter.

If the logarithm of a random variable conforms to the gamma distribution, the random variable follows the Log Pearson type III distribution:

$f\left(x\right)={\left[ln\left(x\right)-\mu \right]}^{k-1}\frac{1}{\text{Γ}\left(\text{k}\right){\alpha }^k}\text{exp}\left[-\frac{ln\left(x\right)-\mu }{\alpha }\right],(11)$

where $\alpha$ is the scale parameter, $k$ is the shape parameter, and $\mu$ is the location parameter.

The random variable that obeys the Gamma distribution takes the reciprocal to get the inverse Gamma distribution, also known as the Pearson type IV distribution (Masseran, 2015):

$f\left(x\right)=\frac{{\alpha }^k}{\text{Γ}\left(\text{k}\right)}{x}^{-k-1}\text{exp}\left(-\frac{\alpha }{x}\right),(12)$

where $\alpha$ is the scale parameter, and $k$ is the shape parameter.

The above distributions are subsets of the generalized Gamma distribution. The generalized Gamma distribution is one of the earliest probability distribution models applied to wind speed modeling (Guedes et al., 2020), and its pdf is shown as follows:

$f\left(x\right)=\frac{k{\left(x-\mu \right)}^{kh-1}}{{\alpha }^{kh}\text{Γ}\left(h\right)}\text{exp}\left\{-{\left[\frac{\left(x-\mu \right)}{\alpha }\right]}^k\right\},(13)$

where $\alpha$ is the scale parameter, $k$ and $h$ are shape parameters, and $\mu$ is the location parameter. The generalized Gamma distribution adds a shape parameter, which significantly improves the flexibility of the model. When the value of $h$ is equal to 1, it is transformed into a Weibull distribution. When the value of $h$ is equal to 2, it is transformed into a generalized normal distribution. When the value of $k$ is equal to 1, it is transformed into a Gamma distribution. When the value of $h$ tends to infinity, it is transformed into a lognormal distribution (Alavi et al., 2016b):

$f\left(x\right)=\frac{1}{x\alpha \sqrt{2\pi }}\text{exp}\left\{-\frac{{\left[ln\left(x\right)-\mu \right]}^2}{2{\alpha }^2}\right\},(14)$

where $\alpha$ is the standard deviation of the logarithm of the random variable, and $\mu$ is the mean of the logarithm of the random variable.

Kiss and Jánosi (2008) proposed that the fitting effect of the generalized Gamma distribution is significantly better than that of the Weibull distribution, especially for high wind speeds, and is suitable for regions with different underlying surfaces and climatic conditions in Europe. Sarkar et al. (2017) proposed that the fitting effect of the Gamma distribution and the Weibull distribution are close, and the Gamma distribution can be used as an alternative model for the Weibull distribution in low ranges. However, the analytical expression of the wind power density function derived from the Gamma distribution is complicated, and the analytical expressions of the mean, variance, skewness, and kurtosis of the wind power density function cannot be determined, which affects the efficiency of wind energy potential assessment (Samal, 2021). Therefore, to simplify the calculation process, the Gamma distribution cannot be the first choice for the wind speed distribution model.

Multi-Parameter Probability Distribution

Several probability distribution models containing more than three parameters have been proposed to characterize the wind speed distribution to pursue higher fitting accuracy. Commonly used multi-parameter probability distributions include the four-parameter Burr distribution, Johnson SB distribution, Kappa distribution, and the five-parameter Wakeby distribution. The pdf of Burr distribution is as follows:

$f\left(x\right)=\frac{hk{\left(\frac{x-\mu }{\alpha }\right)}^{hk-1}}{\alpha {\left[1+{\left(\frac{x-\mu }{\alpha }\right)}^h\right]}^{k+1}},(15)$

where $\alpha$ is the scale parameter, $k$ and $h$ are shape parameters, and $\mu$ is the location parameter.

The pdf of Johnson SB distribution is shown as follows:

$f\left(x\right)=\frac{\alpha k}{\sqrt{2\pi }\left(x-\mu \right)\left(\mu +\alpha -x\right)}\text{exp}\left[-\frac{h+kln{\left(\frac{x-\mu }{\mu +\alpha -x}\right)}^2}{2}\right],(16)$

where $\alpha$ is the scale parameter, $k$ and $h$ are shape parameters, and $\mu$ is the location parameter.

The pdf of Kappa distribution is shown as follows:

$f\left(x\right)=\frac{1}{\alpha }{\left[1-\frac{k\left(x-\mu \right)}{\alpha }\right]}^{\frac{1}{k-1}}{\left[F\left(x\right)\right]}^{1-h},(17)$

where $\alpha$ is the scale parameter, $k$ and $h$ are the shape parameters, and $\mu$ is the location parameter. $F\left(x\right)$ is the cumulative distribution function (cdf) of the Kappa distribution.

The pdf of Wakeby distribution is as follows:

$f\left(x\right)={\left\{\alpha {\left[1-F\left(x\right)\right]}^{\gamma -1}+k{\left[1-F\left(x\right)\right]}^{-h-1}\right\}}^{-1}.(18)$

$F^{-1}\left(x\right)=\mu +\frac{\alpha }{\gamma }\left[1-{\left(1-F\right)}^{\gamma }\right]-\frac{k}{h}\left[1-{\left(1-F\right)}^{-h}\right],(19)$

where $\alpha$ and $k$ are scale parameters, $\gamma$ and $h$ are shape parameters, and $\mu$ is the location parameter.

Lo Brano et al. (2011) proposed that the Burr distribution provides high fitting accuracy for wind speed data in southern Italy. The results of Jung and Schindler (2017) showed that Wakeby distribution and Kappa distribution are suitable choices for onshore and offshore wind speed distribution models, respectively. Soukissian (2013) proposed that Johnson SB fits the wind speed data measured in the Mediterranean Sea well. Because the multi-parameter probability distribution contains more parameters, it is more flexible, more adaptable, and has higher fitting accuracy, which reduces the error of wind energy estimation. However, compared with the two-parameter or three-parameter probability distribution models, its complexity is also greatly improved. Therefore, if the multi-parameter probability distribution model does not significantly improve the estimation accuracy, it is not recommended to prioritize this type of model in most cases.

Mixture Distributions

The above models are all single wind speed distributions. The single distribution cannot describe complex wind regimes, especially the wind speed distribution with bimodal or multimodal characteristics (Santos et al., 2021). Therefore, previous studies tend to use mixture distributions to assess the wind energy potential under complex wind regimes. The pdf of the mixture distributions are as follows:

$f\left(x\right)={\displaystyle \sum _{i=1}^a{\text{ω}}_i{f}_i\left(x\right)},(20)$

$\alpha$ is the number of mixtures, ${\text{ω}}_i$ is the weight of each single distribution model, and $f_i\left(x\right)$ is the pdf of different single distributions.

Generally, for special wind regimes, the fitting effect of mixture distributions is better than that of single wind speed distributions. Carta and Ramírez (2007) used a two-component mixture Weibull distribution to describe the wind regimes at weather stations in Spain. Ouarda et al. (2015) proposed that mixed distributions, such as mixed Weibull and Gamma distributions, fit bimodal wind speed regimes better than single distributions. However, there are still some difficulties in using mixture distributions appropriately. Firstly, it is difficult to determine which one or several single distribution models are used to construct a mixed distribution. The fitting effects of mixed distributions constructed from different single wind speed distributions are significantly different (Hu et al., 2016). Secondly, the optimal number of single distributions to form a mixture distribution cannot be calculated, and the researcher often subjectively determines it (Ouarda and Charron, 2018). In addition, the parameter estimation process of the mixture distribution is more complicated, which leads to over-parameterization. Therefore, the use of mixture distributions has limitations.

Nonparametric Distribution Model

Although parametric distributions have certain advantages in wind speed modeling, choosing a qualified distribution is still challenging. The theoretical probability distribution model may not describe the actual wind regimes, and the estimated parameter values may not pass statistical tests (Xu et al., 2015). The nonparametric model does not need to make any assumptions about the theoretical distribution of wind speed, nor does it need to estimate the parameters of any distribution. Its parameters can be automatically learned from the historical data (Qin et al., 2011). Commonly used nonparametric models include kernel density estimation (KDE) and maximum entropy principle (MEP).

Kernel Density Estimation

KDE can get the pdf from the sample data:

$f\left(\alpha \right)=\frac{1}{nh}{\displaystyle \sum _{i=1}^{n}K\left(a\right)},(21)$

where $n$ is the number of samples, $h$ is the bandwidth, $K\left(\alpha \right)$ is the kernel function, and $\alpha$ is the relative difference between the estimated value and the sample value:

$\alpha =\frac{x-x_i}{h},(22)$

where $x$ is the observed value, and $x_i$ is the estimated value. There are several kernel functions used to construct KDE functions, among which the most widely used is the Gaussian kernel function:

$K\left(\alpha \right)=\frac{1}{\sqrt{2\pi }}\text{exp}\left[-\frac{{\left(x-x_i\right)}^2}{2h^2}\right].(23)$

KDE models have substantial flexibility and stability. Han et al. (2019) used wind speed data from a total of 698 wind stations across China, and the test results showed that the effect of the KDE model is better than that of the Weibull distribution and other 18 commonly used parametric distribution models. The fitting results of historical wind speed data from four wind sites in central China showed that KDE has higher accuracy (Han et al., 2018). KDE model needs to select an appropriate bandwidth. Otherwise, there will be over-fitting or under-fitting, which will significantly affect the estimated value. Although several methods for selecting bandwidth, determining the best bandwidth is still challenging (Tenreiro, 2011).

Maximum Entropy Principle

The content of MEP theory is that under some constraints, the distribution model should reach the maximum remaining uncertainty (i.e., maximum entropy):

$\max S=-\underset{a}{\overset{b}{{\displaystyle \int }}}f\left(x\right)\text{lnf}\left(x\right)\text{d}x,(24)$

where $S$ is the Shannon’s entropy. $f\left(x\right)$ is the pdf of wind speed, $a$ is the minimum of wind speed, and $b$ is the maximum of wind speed. The constraints are as follows:

$\underset{a}{\overset{b}{{\displaystyle \int }}}f\left(x\right)\text{d}x=1.(25)$

$\underset{a}{\overset{b}{{\displaystyle \int }}}{x}^{n}f\left(x\right)\text{d}x=m_n,(26)$

where $m_n$ is the $n$-th order statistical moment:

$m_n=\frac{1}{N}{\displaystyle \sum _{n=1}^N{x}^n},(27)$

where $N$ is the number of samples. Through Lagrangian multiplier method, the expression of pdf can be obtained:

$f\left(x\right)=\text{exp}\left({\beta }_0+{\displaystyle \sum _{i=1}^T{\beta }_i{x}^i}\right),(28)$

where ${\beta }_0, {\beta }_1,\dots , {\beta }_T$ is the Lagrange multipliers, and $T$ is the maximum of $n$.

MEP has strong flexibility and can describe complex wind regimes with a large proportion of null wind and a bimodal distribution (Zhou et al., 2010). In some cases, MEP can more accurately characterize the wind speed distribution than parametric distributions, and the estimation error of wind power density is minor (Chellali et al., 2012). However, MEP has limitations in some cases, such as the difficulty of selecting constraint conditions (Zhang et al., 2014).

Parameter Estimation Method

Particular parameters define all single distribution models and mixed models. Determining the best value of the parameter has a significant impact on the effect of models in fitting wind speed data. Previous studies have used different methods to estimate the parameters of the wind speed distribution models, but calculating the best value of the parameters is still a challenging task.

Maximum Likelihood Method

MLM needs first to construct a likelihood function or a log-likelihood function and then seek the parameter value that makes the function reach the maximum value. MLM estimates the parameter values of the probability distribution through numerical iteration, and the most commonly used method is Newton’s method (Tosunoğlu, 2018). The maximum likelihood estimator is asymptotically unbiased, consistent, and asymptotically effective, and it can reach the minimum variance. In addition, MLM can estimate sample variance to construct confidence intervals and perform hypothesis testing, suitable for analyzing wind speed data in the form of time series (Ramírez and Carta, 2005). However, MLM is more sensitive to the initial value. When the upper and lower limits of the parameters are unknown, its effect is poor (Flynn, 2006). The numerical iterative method requires a large amount of calculation, especially when estimating the parameters of a multi-parameter model or a mixture model, the efficiency of MLM is low (Seo et al., 2019). Some studies have applied improved MLM, called the alternative maximum likelihood method (AMLM), to modeling wind speed distribution (Akdağ and Güler, 2015). AMLM is based on the idea of linearizing the nonlinear term in the likelihood equation through Taylor series expansion and derives the parameter estimator in a non-iterative manner. MLM and AMLM are often used to estimate the shape parameter and scale parameter of the Weibull distribution. Previous studies have shown that the accuracy of the two methods will show differences due to the different geographical locations of wind speed observations (Chaurasiya et al., 2018).

Least Squares Method

LSM is known as the graphic method. The parameter value estimated by LSM minimizes the sum of squares of the deviations between the empirical cdf and the cdf of the model

$\text{Min} S\left(V_{\text{max}};\phi \right)=\text{Min}\left\{{\displaystyle \sum }_{i=1}^N{\left[P_i-F\left(V_{\text{max},i};\phi \right)\right]}^2\right\},(29)$

where $\phi$ is a vector containing the parameters of the pdf. Divide the observed values into $N$ intervals: $0-V_1$, $V_1-V_2$…, $V_{N-1}-V_N$. $V_{max}$ is the maximum value in each interval, $P_i$ is the empirical cdf, and $F$ is the cdf of the model:

$F\left(x\right)=\underset{0}{\overset{x}{{\displaystyle \int }}}f\left(x\right).(30)$

Some studies have proposed that the accuracy and robustness of LSM are lower than other parameter estimation methods, which may be related to the error in the definition of the cdf (Chang, 2011). Deep et al. (2020) used the modified LSM for parameter estimation, and the results show that its effect is not inferior to other methods. LSM needs to linearize the objective function, and the logarithmic transformation is the basis of LSM. The cdf of the Weibull and Rayleigh distributions contains the exponential term, which is easy to perform the logarithmic transformation, so it is more suitable to use LSM to estimate its parameters. However, linearization of Lognormal and Gamma distribution is more complicated, making LSM unsuitable for these two models (Alrashidi et al., 2020).

The Method of Moments

The first step of MOM is generally to calculate the first four moments of a random variable:

$\overline{x}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{x}_i.(31)$

$s=\sqrt{\frac{1}{n-1}}{\displaystyle \sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2.(32)$

$g=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(\frac{x_i-\overline{x}}{s}\right)}^3.(33)$

$w=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(\frac{x_i-\overline{x}}{s}\right)}^4,(34)$

where $\overline{x}$, $s$, $g$, $w$ are the mean, standard deviation, skewness, and kurtosis of the wind speed series respectively; $n$ is the length of the wind series; $x_i$ is the wind speed of the $i$-th time step. The second step of MOM is to make the sample moments equal to the population moments. MOM is simpler and more accurate than other parameter estimation methods, especially for multi-parameter distributions such as Johnson SB distribution and Wakeby distribution (Liu et al., 2015). But MOM estimator is skewed and unstable and cannot reach the minimum variance (Carta et al., 2009).

Some studies have proposed the linear moment estimation method (LMOM) for parameter estimation based on MOM. LMOM needs to calculate the probability weighted moments:

$b_0=\frac{1}{Z}{\displaystyle \sum _{z=1}^Z{x}_z}.(35)$

$b_r=\frac{1}{Z}{\displaystyle \sum _{z=r+1}^Z\frac{\left(z-1\right)\left(z-2\right)\dots (z-r)}{\left(Z-1\right)\left(Z-2\right)\dots (Z-r)}{x}_z}, (36)$

where $b_r$ is the $r$-th order probability weighted moment ($r>0$). Then the first five linear moments can be calculated:

$\{\begin{array}{c}{a}_1=b_0\\ a_2=2b_1-b_0\\ a_3=6b_2-6b_1+b_0\\ a_4=20b_3-30b_2+12b_1-b_0\\ a_5=70b_4-140b_3+90b_2-20b_1+b_0\end{array}.(37)$

LMOM estimator is unbiased, it is more stable for samples with abnormal data, and better results will be obtained with a smaller sample size (Soukissian and Tsalis, 2018). However, LMOM, like MOM, cannot fully utilize all the valid information in the sample. When other parameter estimation methods are difficult to calculate parameters, MOM and LMOM are effective alternative methods.

Power Density Method

Akdağ and Dinler (2009) proposed a new method for calculating the shape and scale parameters of the Weibull distribution. The relationship between the scale parameter $\alpha$ of the Weibull distribution and the average wind speed $\overline{V}$ is:

$\alpha =\frac{\overline{V}}{\Gamma \left(1+\frac{1}{k}\right)}.(38)$

From Eqs 1, 28:

$\frac{\overline{V^3}}{{\left(\overline{V}\right)}^3}=\frac{\Gamma \left(1+\frac{3}{k}\right)}{\Gamma {\left(1+\frac{1}{k}\right)}^3},(39)$

where $\overline{V^3}$ is the average value of the wind speed cube, $\frac{\overline{V^3}}{{\left(\overline{V}\right)}^3}$ is recorded as the energy pattern factor ($E_p$), and the value of $E_p$ at a particular site is generally regarded as a fixed value, ranging from 1.4 to 4.4. Therefore, the shape parameter $k$ of the Weibull distribution can be calculated by:

$k=1+\frac{3.69}{{\left(E_p\right)}^2}.(40)$

As long as the average wind speed value is obtained, PDM is applicable and does not require complete historical wind speed data. PDM does not need to calculate complicated iterative equations, so the numerical solution of the parameters can be obtained easily. In addition, the wind power density can be directly estimated by this method. The results of Shu et al. (2015) showed that the accuracy of PDM is not worse than other traditional parameter estimation methods. However, PDM is currently only suitable for estimating the parameters of the Weibull distribution. Other probability distribution models may not be able to derive the power density expression from Eq. 1, or the expression may be too complicated to perform the next step. Therefore, the scope of the application of PDM is minimal.

Goodness-of-Fit Criteria

After the distribution model and the parameter values are determined, it is necessary to evaluate the goodness-of-fit of the model. The goodness-of-fit criteria reflect how well the selected model fits the wind speed data so that the applicability of the model to the sample can be evaluated. Choosing different goodness-of-fit criteria may lead to different results.

Coefficient of Determination (${\mathit{R}}^2$)

$R^2$ is one of the most widely used goodness-of-fit criteria. It is a metric for estimating the consistency between the distribution model and the observed data.$R^2$ is expressed as the square of the correlation coefficient between the observed value and the estimated value:

$R^2=1-\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-x_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}},(41)$

$y_i$ is the $i$-th observed data, $\overline{y}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{y}_i$, $x_i$ is the $i$-th estimated value, and $n$ is the number of samples.

There are several commonly used variants of $R^2$. The first is $R_{PP}^2$, which refers to $R^2$ associated with P-P plot:

$R_{PP}^2=1-\frac{{\displaystyle \sum _{i=1}^n{\left(F_i-{\widehat{F}}_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(F_i-\overline{F}\right)}^2}},(42)$

where $F_i$ is the empirical cumulative probability of the measured data in the $i$-th wind speed interval, $\overline{F}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{F}_i$, ${\widehat{F}}_i$ is the estimated cumulative probability of the $i$-th wind speed interval.

The second variant is $R_{PP}^2$, which refers to $R^2$ associated with the Q-Q plot:

$R_{QQ}^2=1-\frac{{\displaystyle \sum _{i=1}^n{\left(p_i-{\widehat{p}}_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(p_i-\overline{p}\right)}^2}},(43)$

where $p_i$ is the probability of the measured data in the $i$-th wind speed interval, ${\widehat{p}}_i$ is the estimated probability of the $i$-th wind speed interval, ${\widehat{p}}_i=F^{-1}\left(F_i\right)$, $\overline{p}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{p}_i$.

The third variation is the adjusted coefficient of determination ($R_a^2$):

$R_a^2=1-\left(1-R^2\right)\frac{N-1}{N-d},(44)$

where $N$ is the number of samples, and $d$ is the number of parameters in the probability distribution model.

The closer the value of $R^2$ and its variants to 1, the better the fitting effect of the model. Among them, $R^2$ has the simplest structure and is easier to use. However, $R^2$ cannot fully reflect the fitting effect of the theoretical distribution, and it is not appropriate to use $R^2$ alone to evaluate the model (Hossain et al., 2014). The definition of $R_{PP}^2$ is related to the cdf, and the gradient of the cdf reaches the maximum when the random variable takes the middle value, so the middle part of the distribution has a more significant influence on the value of $R_{PP}^2$. $R_{QQ}^2$ is more sensitive to the maximum gradient of the inverse cumulative distribution function, which corresponds to the tail of the distribution. The plotting position of the Weibull distribution provides an unbiased estimate of the cumulative probability, so $R_{PP}^2$ is usually preferred to evaluate the fitting effect of the Weibull distribution (Akdağ et al., 2010). $R_a^2$ provides penalties for multi-parameter models and avoids overfitting. When the gap between $N$ and $d$ is large, $R_a^2\approx R^2$, indicating that $R_a^2$ is not suitable for wind speed data with a large sample size. Dividing the wind speed data into a histogram can significantly improve the applicability of $R_a^2$.

Root Mean Square Error ($\mathit{RMSE}$)

$RMSE$ determines the accuracy of the model through the item-by-item comparison between the observed probability and the estimated probability. RMSE usually has two forms, $RMS{E}_{PP}$ which is similar to $R_{PP}^2$ and $RMS{E}_{QQ}$ which is similar to $R_{QQ}^2$:

$RMS{E}_{PP}={\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(F_i-{\widehat{F}}_i\right)}^2\right]}^{\frac{1}{2}}.(45)$

$RMS{E}_{QQ}={\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(p_i-{\widehat{p}}_i\right)}^2\right]}^{\frac{1}{2}}.(46)$

The closer the $RMSE$ value is to 0, the better the fitting effect of the selected model. $RMSE$ is usually used together with $R^2$ as a criterion for evaluating the goodness-of-fit of the model. However, $RMSE$ is more sensitive to abnormal data. If a specific wind speed data deviates greatly from the expected value, the error caused by it is more prominent. It is not appropriate to use $RMSE$ to evaluate the goodness of the model in fitting short-term wind speed data. In addition, unlike $R^2$, the value of $RMSE$ is related to the selected probability distribution model, so $RMSE$ cannot be used to compare the goodness-of-fit of different models to the same set of wind speed data.

Kolmogorov-Smirnov Test and Anderson-Darling Test

The KS and AD tests are used to determine whether a given probability distribution model is suitable for a set of wind speed observation data. They are also used to compare the goodness-of-fit of different models to the same set of data. Both the KS and AD tests compare the empirical cumulative probability with the estimated cumulative probability distribution. Specifically, the KS test calculates the maximum difference between the two:

$KS=\text{max}\left|F_i-{\widehat{F}}_i\right|.(47)$

The KS test is an accurate nonparametric test suitable for a continuous distribution. It is more sensitive to the middle part of the distribution.

AD test is improved based on KS test:

$AD=\left\{-n-{\displaystyle \sum }_{i=1}^n\frac{2i-1}{n}\left[ln\left({\widehat{F}}_i\right)+ln\left(1-{\widehat{F}}_{n-i+1}\right)\right]\right\}.(48)$

The AD test is related to the weight function and is more sensitive to the tail of the distribution. Both the KS and AD tests have a critical value. If these two test statistics are lower than the critical value, the assumed distribution is accepted. The critical value of the KS test is independent of the selected model, and the critical value of the AD test varies with the model, so the AD test is more accurate (Saeed et al., 2021).

Chi-Square Test (χ2)

χ2 can verify whether the measured wind speed data frequency is consistent with the frequency obtained from the assumed model. It is often used to compare the goodness-of-fit of different models. The chi-square test needs to divide the observation data into several groups, and the frequency of each group is expressed in the form of histograms. Then calculate the test statistics:

$\chi 2={\displaystyle \sum _{i=1}^T\frac{{\left(O_i-E_i\right)}^2}{E_i}},(49)$

where, $O_i$ is the observed frequency of the $i$-th group, $E_i$ is the estimated frequency of the $i$-th group, calculated by the following equation:

$E_i=n\left[F\left(v_i\right)-F\left(v_{i-1}\right)\right],(50)$

$v_i$ and $v_{i-1}$ are the upper and lower bounds of the wind speed of the $i$-th group, respectively.

If the value of $\text{χ}2$ is greater than the critical value, the assumed model is rejected. Similar to the AD test, the critical value of the chi-square test depends on the selected probability distribution model. Since the frequency histogram is used, the chi-square test is less affected by a single observation. However, the chi-square test results show significant differences under different class intervals, and the selection of class intervals is usually subjectively determined, limiting its applicability (Mert and KarakuŞ, 2015).

Discussion

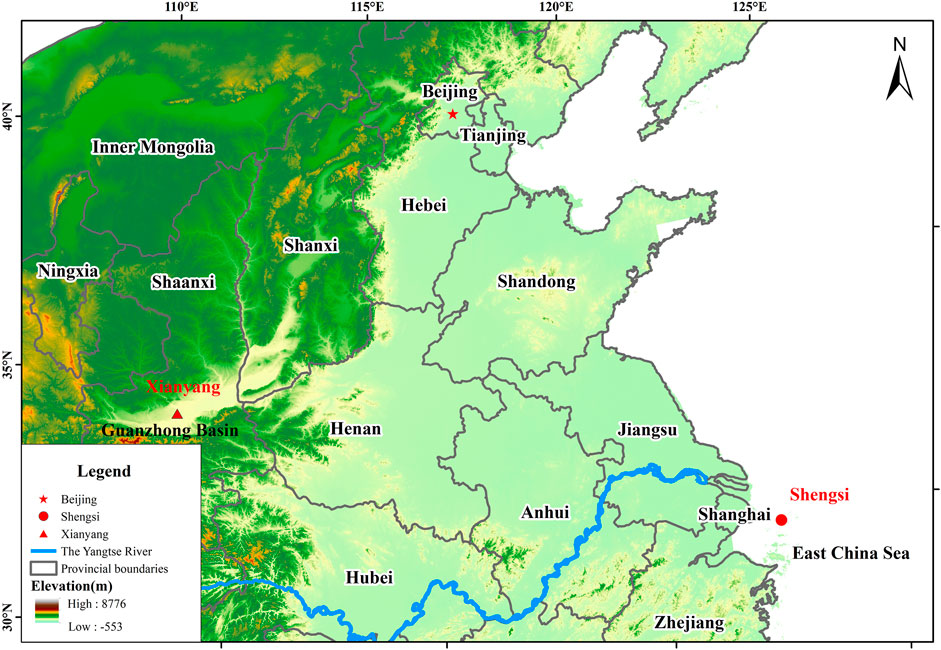
The fitting effect of the wind speed distribution model usually varies according to the location of different sites (Ouarda et al., 2016). This section uses a case study to compare the fitting effects of the two-parameter Weibull distribution and the three-parameter Weibull distribution at different sites. Two sites are selected in this study. Shengsi is located in the southeast of the Yangtze River estuary and is an island on the East China Sea. Xianyang is a city located in the Guanzhong Basin, surrounded by mountains (Figure 3). Table 1 introduces the altitude, geographic coordinates, period of record, maximum wind speed, and the probability of null wind speed of the two sites. The wind speed data are obtained from the Integrated Surface Database of the National Centers for Environmental Information (www.ncei.noaa.gov/maps/hourly/). The resolution of wind speed data is 1 m/s, and it is recorded every three hours. Previous studies have shown that the wind direction has almost no influence on the wind energy output, and the output of each direction is not distinguished (Kiss and Jánosi, 2008). Therefore, this case study uses wind speed data aggregated from all directions.

FIGURE 3

FIGURE 3. The geographical location of shengsi and Xianyang.

TABLE 1

TABLE 1. The altitude, geographic coordinates, period of record, maximum wind speed, and the probability of null wind speed of the two sites in Shengsi and Xianyang.

The two-parameter Weibull distribution and the three-parameter Weibull distribution are used to fit the wind speed observation data of the two sites, respectively. To ensure that the fitting effects are comparable, the Least Squares Method is used to estimate the parameter values, and$R^2$ is used as the goodness-of-fit criteria. Figure 4 shows the fitting curves of the two distributions. In Shengsi, the fitting curves of the two distributions basically coincide. However, in Xianyang, the three-parameter Weibull distribution obtains a more accurate estimation of the probability of null wind speed by adjusting the value of the location parameter $\mu$, while the two-parameter Weibull distribution underestimates the low wind speed probability. By comparing the value of $R^2$ (Table 2), it can be concluded that the two distributions have basically the same fitting effect on the wind speed data of Shengsi, but the fitting effect of the three-parameter Weibull distribution is better than that of the two-parameter Weibull distribution in Xianyang. Considering that the two-parameter Weibull distribution has more flexibility and its parameters are easier to estimate, it is recommended to use the two-parameter Weibull distribution to evaluate the wind energy in Shengsi. However, for Xianyang, where low wind speeds account for a large proportion, it is more suitable to use the three-parameter Weibull distribution to fit wind speed data.

FIGURE 4

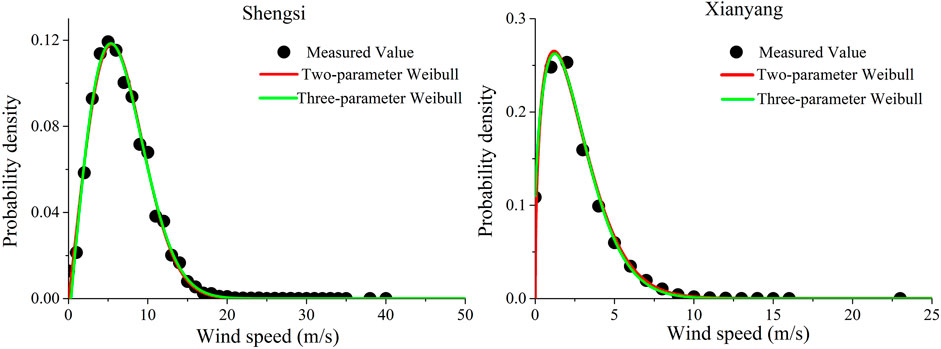
FIGURE 4. Fitting curves of two-parameter Weibull distribution and three-parameter Weibull distribution at Shengsi and Xianyang sites.

TABLE 2

TABLE 2. Estimated parameter values and $R^2$ values of the two sites.

The wind speed distribution characteristics of different sites determine the applicability of the models. Shengsi is located in the coastal area of eastern China, where there is a thermal difference between land and sea, coupled with the influence of the East Asian monsoon and tropical storms, resulting in strong winds throughout the year. Xianyang is located in the inland area, affected by the continental climate, causing a large proportion of null wind. In addition, the topography also affects the characteristics of wind speed distribution (Kim and Lim, 2017). The mountains around Xianyang block the airflow movement, while the terrain of Shengsi is flat, and the airflow is less obstructed.

For a specific site, the wind speed distribution may have different characteristics over time. Xiao et al. (2021) proposed that the wind speed in the Badain Jaran Desert in China reached the highest in April, followed by November, which was much higher than the wind speed in other months. Usta and Kantar (2012) proposed that the statistical characteristics of monthly, seasonal, and yearly wind speed data, such as mean, variance, skewness, and kurtosis, are significantly different. Therefore, the optimal wind speed distribution model under different time scales of wind speed data may be different. Some studies have conducted wind energy assessments on longer time scales. Gao et al. (2018) proposed that climate warming has led to a gradual decline in the long-term wind energy potential of the Indian Ocean, which will affect the economic income of wind farms. Shu et al. (2015) proposed that long-term temperature variations will lead to variations in wind characteristics, which will change the energy output. However, on the one hand, the trend of climate change is very complex and has not been fully understood, making it difficult to predict long-term variations in wind characteristics. On the other hand, the location of wind farms is often determined only by wind speed observation data within 1–2 years or even less (Chen and Blaabjerg, 2009). If the wind energy potential of the area decreases year by year due to rising temperatures, the output of wind farms may not meet expectations. Therefore, wind energy assessment should consider the impact of long-term climate change rather than focusing only on the current output of the site.

Conclusion

Previous studies have proposed a variety of probability distribution models for the modeling of wind speed distribution. In different sites, the models have shown particular applicability, but a specific model has not been found to have the best fitting effect on the wind speed data recorded at all sites. In addition, the selection of parameter estimation methods and the setting of goodness-of-fit test statistics are not unified. They have their advantages and disadvantages and are suitable for different observation data and wind speed distribution models. Therefore, all potential wind speed distribution models should be considered for selecting the wind speed distribution model for a particular site. According to the chosen model and the characteristics of the wind speed observation data, the parameter estimation method and the goodness-of-fit test statistics are determined.

Wind characteristics determine the wind energy output of a wind farm. The characteristics of wind speed distribution are constantly varying geographically and temporally. The wind characteristics at different locations are affected by various geographical elements, such as local climate, topography, and thermal properties difference between the land and the sea. The variations in these geographical elements make the applicability of a model in different regions may change significantly. The wind speed distribution in different months, seasons, and years may have different characteristics for a specific site. Long-term variations in wind characteristics are a topic of great concern because they will lead to gradual variations in wind energy potential and affect the economic benefits of wind farms. We suggest that wind energy assessment consider the long-term variations in local wind characteristics instead of just focusing on the current energy output.

Author Contributions

SH contributed to conceptualization. DZ contributed to funding acquisition. XN contributed to methodology. HQ contributed to formal analysis. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (grant numbers 41871008, 41930641, 41871011, and 41571008).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akdağ, S. A., Bagiorgas, H. S., and Mihalakakou, G. (2010). Use of Two-Component Weibull Mixtures in the Analysis of Wind Speed in the Eastern Mediterranean. Appl. Energ. 87 (8), 2566–2573. doi:10.1016/j.apenergy.2010.02.033

CrossRef Full Text | Google Scholar

Akdağ, S. A., and Dinler, A. (2009). A New Method to Estimate Weibull Parameters for Wind Energy Applications. Energy Convers. Manag. 50 (7), 1761–1766. doi:10.1016/j.enconman.2009.03.020

CrossRef Full Text | Google Scholar

Akdağ, S. A., and Güler, Ö. (2015). A Novel Energy Pattern Factor Method for Wind Speed Distribution Parameter Estimation. Energ. Convers. Manag. 106, 1124–1133. doi:10.1016/j.enconman.2015.10.042

CrossRef Full Text | Google Scholar

Akgül, F. G., Şenoğlu, B., and Arslan, T. (2016). An Alternative Distribution to Weibull for Modeling the Wind Speed Data: Inverse Weibull Distribution. Energ. Convers. Manag. 114, 234–240. doi:10.1016/j.enconman.2016.02.026

CrossRef Full Text | Google Scholar

Alavi, O., Mohammadi, K., and Mostafaeipour, A. (2016a). Evaluating the Suitability of Wind Speed Probability Distribution Models: A Case of Study of East and Southeast Parts of Iran. Energ. Convers. Manag. 119, 101–108. doi:10.1016/j.enconman.2016.04.039

CrossRef Full Text | Google Scholar

Alavi, O., Sedaghat, A., and Mostafaeipour, A. (2016b). Sensitivity Analysis of Different Wind Speed Distribution Models with Actual and Truncated Wind Data: A Case Study for Kerman, Iran. Energ. Convers. Manag. 120, 51–61. doi:10.1016/j.enconman.2016.04.078

CrossRef Full Text | Google Scholar

Alrashidi, M., Rahman, S., and Pipattanasomporn, M. (2020). Metaheuristic Optimization Algorithms to Estimate Statistical Distribution Parameters for Characterizing Wind Speeds. Renew. Energ. 149, 664–681. doi:10.1016/j.renene.2019.12.048

CrossRef Full Text | Google Scholar

Arenas-López, J. P., and Badaoui, M. (2020). A Fokker–Planck Equation Based Approach for Modelling Wind Speed and its Power Output. Energ. Convers. Manag. 222, 113152. doi:10.1016/j.enconman.2020.113152

CrossRef Full Text | Google Scholar

Aries, N., Boudia, S. M., and Ounis, H. (2018). Deep Assessment of Wind Speed Distribution Models: A Case Study of Four Sites in Algeria. Energ. Convers. Manag. 155, 78–90. doi:10.1016/j.enconman.2017.10.082

CrossRef Full Text | Google Scholar

Baz, K., Cheng, J., Xu, D., Abbas, K., Ali, I., Ali, H., et al. (2021). Asymmetric Impact of Fossil Fuel and Renewable Energy Consumption on Economic Growth: A Nonlinear Technique. Energy 226, 120357. doi:10.1016/j.energy.2021.120357

CrossRef Full Text | Google Scholar

Bilir, L., İmir, M., Devrim, Y., and Albostan, A. (2015). An Investigation on Wind Energy Potential and Small Scale Wind Turbine Performance at İncek Region – Ankara, Turkey. Energ. Convers. Manag. 103, 910–923. doi:10.1016/j.enconman.2015.07.017

CrossRef Full Text | Google Scholar

Carta, J. A., and Ramírez, P. (2007). Analysis of Two-Component Mixture Weibull Statistics for Estimation of Wind Speed Distributions. Renew. Energ. 32 (3), 518–531. doi:10.1016/j.renene.2006.05.005

CrossRef Full Text | Google Scholar

Carta, J. A., Ramírez, P., and Velázquez, S. (2009). A Review of Wind Speed Probability Distributions Used in Wind Energy Analysis. Renew. Sustain. Energ. Rev 13 (5), 933–955. doi:10.1016/j.rser.2008.05.005

CrossRef Full Text | Google Scholar

Celik, A. N. (2006). A Simplified Model for Estimating Yearly Wind Fraction in Hybrid-Wind Energy Systems. Renew. Energ. 31 (1), 105–118. doi:10.1016/j.renene.2005.03.006

CrossRef Full Text | Google Scholar

Celik, A. N. (2003). Energy Output Estimation for Small-Scale Wind Power Generators Using Weibull-Representative Wind Data. J. Wind Eng. Ind. Aerod 91 (5), 693–707. doi:10.1016/s0167-6105(02)00471-3

CrossRef Full Text | Google Scholar

Chang, T. P. (2011). Performance Comparison of Six Numerical Methods in Estimating Weibull Parameters for Wind Energy Application. Appl. Energ. 88 (1), 272–282. doi:10.1016/j.apenergy.2010.06.018

CrossRef Full Text | Google Scholar

Chaurasiya, P. K., Ahmed, S., and Warudkar, V. (2018). Study of Different Parameters Estimation Methods of Weibull Distribution to Determine Wind Power Density Using Ground Based Doppler SODAR Instrument. ALEX ENG. J. 57 (4), 2299–2311. doi:10.1016/j.aej.2017.08.008

CrossRef Full Text | Google Scholar

Chellali, F., Khellaf, A., Belouchrani, A., and Khanniche, R. (2012). A Comparison between Wind Speed Distributions Derived from the Maximum Entropy Principle and Weibull Distribution. Case of Study; Six Regions of Algeria. Renew. Sustain. Energ. Rev 16 (1), 379–385. doi:10.1016/j.rser.2011.08.002

CrossRef Full Text | Google Scholar

Chen, Z., and Blaabjerg, F. (2009). Wind Farm—A Power Source in Future Power Systems. Renew. Sustain. Energ. Rev 13 (6-7), 1288–1300. doi:10.1016/j.rser.2008.09.010

CrossRef Full Text | Google Scholar

Deep, S., Sarkar, A., Ghawat, M., and Rajak, M. K. (2020). Estimation of the Wind Energy Potential for Coastal Locations in India Using the Weibull Model. Renew. Energ. 161, 319–339. doi:10.1016/j.renene.2020.07.054

CrossRef Full Text | Google Scholar

Elie Bertrand, K. S., Abraham, K., and Lucien, M. A. (2020). Sustainable Energy through Wind Speed and Power Density Analysis in Ambam, South Region of Cameroon. Front Energ. Res 8, 176. doi:10.3389/fenrg.2020.00176

CrossRef Full Text | Google Scholar

Flynn, M. R. (2006). Fitting Human Exposure Data with the Johnson S(B) Distribution. J. Expo. Sci. Environ. Epidemiol. 16 (1), 56–62. doi:10.1038/sj.jea.7500437

CrossRef Full Text | Google Scholar

Gao, M., Ding, Y., Song, S., Lu, X., Chen, X., and McElroy, M. B. (2018). Secular Decrease of Wind Power Potential in India Associated with Warming in the Indian Ocean. Sci. Adv. 4 (12), eaat5256. doi:10.1126/sciadv.aat5256

PubMed Abstract | CrossRef Full Text | Google Scholar

Guarienti, J. A., Kaufmann Almeida, A., Menegati Neto, A., de Oliveira Ferreira, A. R., Ottonelli, J. P., and Kaufmann de Almeida, I. (2020). Performance Analysis of Numerical Methods for Determining Weibull Distribution Parameters Applied to Wind Speed in Mato Grosso Do Sul, Brazil. Sustain. Energ. Techn 42, 100854. doi:10.1016/j.seta.2020.100854

CrossRef Full Text | Google Scholar

Guedes, K. S., de Andrade, C. F., Rocha, P. A. C., Mangueira, R. d. S., and de Moura, E. P. (2020). Performance Analysis of Metaheuristic Optimization Algorithms in Estimating the Parameters of Several Wind Speed Distributions. Appl. Energ. 268, 114952. doi:10.1016/j.apenergy.2020.114952

CrossRef Full Text | Google Scholar

Han, Q., Hao, Z., Hu, T., and Chu, F. (2018). Non-parametric Models for Joint Probabilistic Distributions of Wind Speed and Direction Data. Renew. Energ. 126, 1032–1042. doi:10.1016/j.renene.2018.04.026

CrossRef Full Text | Google Scholar

Han, Q., Ma, S., Wang, T., and Chu, F. (2019). Kernel Density Estimation Model for Wind Speed Probability Distribution with Applicability to Wind Energy Assessment in China. Renew. Sustain. Energ. Rev 115, 109387. doi:10.1016/j.rser.2019.109387

CrossRef Full Text | Google Scholar

Harris, R. I., and Cook, N. J. (2014). The Parent Wind Speed Distribution: Why Weibull?. J. Wind Eng. Ind. Aerod 131, 72–87. doi:10.1016/j.jweia.2014.05.005

CrossRef Full Text | Google Scholar

Hossain, J., Sharma, S., and Kishore, V. V. N. (2014). Multi-peak Gaussian Fit Applicability to Wind Speed Distribution. Renew. Sustain. Energ. Rev 34, 483–490. doi:10.1016/j.rser.2014.03.026

CrossRef Full Text | Google Scholar

Hu, Q., Wang, Y., Xie, Z., Zhu, P., and Yu, D. (2016). On Estimating Uncertainty of Wind Energy with Mixture of Distributions. Energy 112, 935–962. doi:10.1016/j.energy.2016.06.112

CrossRef Full Text | Google Scholar

Jansen, M., Staffell, I., Kitzing, L., Quoilin, S., Wiggelinkhuizen, E., Bulder, B., et al. (2020). Offshore Wind Competitiveness in Mature Markets without Subsidy. Nat. Energ. 5 (8), 614–622. doi:10.1038/s41560-020-0661-2

CrossRef Full Text | Google Scholar

Jia, J., Yan, Z., Peng, X., and An, X. (2020). A New Distribution for Modeling the Wind Speed Data in Inner Mongolia of China. Renew. Energ. 162, 1979–1991. doi:10.1016/j.renene.2020.10.019

CrossRef Full Text | Google Scholar

Jin, X., Chen, Y., Wang, L., Han, H., and Chen, P. (2021). Failure Prediction, Monitoring and Diagnosis Methods for Slewing Bearings of Large-Scale Wind Turbine: A Review. Measurement 172, 108855. doi:10.1016/j.measurement.2020.108855

CrossRef Full Text | Google Scholar

Jung, C., and Schindler, D. (2017). Global Comparison of the Goodness-Of-Fit of Wind Speed Distributions. Energy Convers. Manag 133, 216–234. doi:10.1016/j.enconman.2016.12.006

CrossRef Full Text | Google Scholar

Kandpal, D., and Dhingra, T. (2021). Migrating to Reverse Auction Mechanisms in Wind Energy Sector: Status and Challenges. Energ Policy 156, 112352. doi:10.1016/j.enpol.2021.112352

CrossRef Full Text | Google Scholar

Kang, D., Ko, K., and Huh, J. (2015). Determination of Extreme Wind Values Using the Gumbel Distribution. Energy 86, 51–58. doi:10.1016/j.energy.2015.03.126

CrossRef Full Text | Google Scholar

Kaplan, O., and Temiz, M. (2017). A Novel Method Based on Weibull Distribution for Short-Term Wind Speed Prediction. Int. J. Hydrogen Energ 42 (28), 17793–17800. doi:10.1016/j.ijhydene.2017.03.006

CrossRef Full Text | Google Scholar

Katikas, L., Dimitriadis, P., Koutsoyiannis, D., Kontos, T., and Kyriakidis, P. (2021). A Stochastic Simulation Scheme for the Long-Term Persistence, Heavy-Tailed and Double Periodic Behavior of Observational and Reanalysis Wind Time-Series. Appl. Energ. 295, 116873. doi:10.1016/j.apenergy.2021.116873

CrossRef Full Text | Google Scholar

Kim, Y., and Lim, H. (2017). Effect of Island Topography and Surface Roughness on the Estimation of Annual Energy Production of Offshore Wind Farms. Renew. Energ. 103, 106–114. doi:10.1016/j.renene.2016.11.020

CrossRef Full Text | Google Scholar

Kiss, P., and Jánosi, I. M. (2008). Comprehensive Empirical Analysis of ERA-40 Surface Wind Speed Distribution over Europe. Energ. Convers. Manag. 49 (8), 2142–2151. doi:10.1016/j.enconman.2008.02.003

CrossRef Full Text | Google Scholar

Li, D., and Miao, S. (2021). Fitting the Wind Speed Probability Distribution with Maxwell and Power Maxwell Distributions: A Case Study of North Dakota Sites. Sustain. Energ. Techn 47, 101446. doi:10.1016/j.seta.2021.101446

CrossRef Full Text | Google Scholar

Liu, G., Zhou, J., Jia, B., He, F., Yang, Y., and Sun, N. (2019). Advance Short-Term Wind Energy Quality Assessment Based on Instantaneous Standard Deviation and Variogram of Wind Speed by a Hybrid Method. Appl. Energ. 238, 643–667. doi:10.1016/j.apenergy.2019.01.105

CrossRef Full Text | Google Scholar

Liu, M., Li, W., Billinton, R., Wang, C., and Yu, J. (2015). Modeling Tidal Current Speed Using a Wakeby Distribution. Electr. Pow Syst. Res. 127, 240–248. doi:10.1016/j.epsr.2015.06.014

CrossRef Full Text | Google Scholar

Lo Brano, V., Orioli, A., Ciulla, G., and Culotta, S. (2011). Quality of Wind Speed Fitting Distributions for the Urban Area of Palermo, Italy. Renew. Energ. 36 (3), 1026–1039. doi:10.1016/j.renene.2010.09.009

CrossRef Full Text | Google Scholar

Masseran, N. (2015). Evaluating Wind Power Density Models and Their Statistical Properties. Energy 84, 533–541. doi:10.1016/j.energy.2015.03.018

CrossRef Full Text | Google Scholar

Mauritzen, J. (2020). Will the Locals Benefit? Energ Policy 142. doi:10.1016/j.enpol.2020.111489

CrossRef Full Text | Google Scholar

Mert, İ., and KarakuŞ, C. (2015). A Statistical Analysis of Wind Speed Data Using Burr, Generalized Gamma, and Weibull Distributions in Antakya, Turkey. Turk J. Electr. Eng. Co 23, 1571–1586. doi:10.3906/elk-1402-66

CrossRef Full Text | Google Scholar

Miao, S., Gu, Y., Li, D., and Li, H. (2019). Determining Suitable Region Wind Speed Probability Distribution Using Optimal Score-Radar Map. Energ. Convers. Manag. 183, 590–603. doi:10.1016/j.enconman.2019.01.001

CrossRef Full Text | Google Scholar

Montoya, J. A., Díaz-Francés, E., and P, G. F. (2019). Estimation of the Reliability Parameter for Three-Parameter Weibull Models. Appl. Math. Model. 67, 621–633. doi:10.1016/j.apm.2018.11.043

CrossRef Full Text | Google Scholar

Morales, J. M., Mínguez, R., and Conejo, A. J. (2010). A Methodology to Generate Statistically Dependent Wind Speed Scenarios. Appl. Energ. 87 (3), 843–855. doi:10.1016/j.apenergy.2009.09.022

CrossRef Full Text | Google Scholar

Ouarda, T. B. M. J., Charron, C., and Chebana, F. (2016). Review of Criteria for the Selection of Probability Distributions for Wind Speed Data and Introduction of the Moment and L-Moment Ratio Diagram Methods, with a Case Study. Energ. Convers. Manag. 124, 247–265. doi:10.1016/j.enconman.2016.07.012

CrossRef Full Text | Google Scholar

Ouarda, T. B. M. J., and Charron, C. (2018). On the Mixture of Wind Speed Distribution in a Nordic Region. Energ. Convers. Manag. 174, 33–44. doi:10.1016/j.enconman.2018.08.007

CrossRef Full Text | Google Scholar

Ouarda, T. B. M. J., Charron, C., Shin, J. Y., Marpu, P. R., Al-Mandoos, A. H., Al-Tamimi, M. H., et al. (2015). Probability Distributions of Wind Speed in the UAE. Energ. Convers. Manag. 93, 414–434. doi:10.1016/j.enconman.2015.01.036

CrossRef Full Text | Google Scholar

Perrin, O., Rootzén, H., and Taesler, R. (2006). A Discussion of Statistical Methods Used to Estimate Extreme Wind Speeds. Theor. Appl. Climatol 85 (3-4), 203–215. doi:10.1007/s00704-005-0187-3

CrossRef Full Text | Google Scholar

Petković, D., Shamshirband, S., Anuar, N. B., Saboohi, H., Abdul Wahab, A. W., Protić, M., et al. (2014). An Appraisal of Wind Speed Distribution Prediction by Soft Computing Methodologies: A Comparative Study. Energ. Convers. Manag. 84, 133–139. doi:10.1016/j.enconman.2014.04.010

CrossRef Full Text | Google Scholar

Qin, Z., Li, W., and Xiong, X. (2011). Estimating Wind Speed Probability Distribution Using Kernel Density Method. Electr. Pow Syst. Res. 81 (12), 2139–2146. doi:10.1016/j.epsr.2011.08.009

CrossRef Full Text | Google Scholar

Ramírez, P., and Carta, J. A. (2005). Influence of the Data Sampling Interval in the Estimation of the Parameters of the Weibull Wind Speed Probability Density Distribution: a Case Study. Energ. Convers. Manag. 46 (15-16), 2419–2438. doi:10.1016/j.enconman.2004.11.004

CrossRef Full Text | Google Scholar

Saeed, M. A., Ahmed, Z., and Zhang, W. (2021). Optimal Approach for Wind Resource Assessment Using Kolmogorov–Smirnov Statistic: A Case Study for Large-Scale Wind Farm in Pakistan. Renew. Energ. 168, 1229–1248. doi:10.1016/j.renene.2021.01.008

CrossRef Full Text | Google Scholar

Saleh, H., Abou El-Azm Aly, A., and Abdel-Hady, S. (2012). Assessment of Different Methods Used to Estimate Weibull Distribution Parameters for Wind Speed in Zafarana Wind Farm, Suez Gulf, Egypt. Energy 44 (1), 710–719. doi:10.1016/j.energy.2012.05.021

CrossRef Full Text | Google Scholar

Samal, R. K. (2021). Assessment of Wind Energy Potential Using Reanalysis Data: A Comparison with Mast Measurements. J. Clean. Prod. 313, 127933. doi:10.1016/j.jclepro.2021.127933

CrossRef Full Text | Google Scholar

Santos, F. S. d., Nascimento, K. K. F. d., Jale, J. d. S., Stosic, T., Marinho, M. H. N., and Ferreira, T. A. E. (2021). Mixture Distribution and Multifractal Analysis Applied to Wind Speed in the Brazilian Northeast Region. Chaos Soliton Fract 144, 110651. doi:10.1016/j.chaos.2021.110651

CrossRef Full Text | Google Scholar

Sarkar, A., Deep, S., Datta, D., Vijaywargiya, A., Roy, R., and Phanikanth, V. S. (2019). Weibull and Generalized Extreme Value Distributions for Wind Speed Data Analysis of Some Locations in India. Ksce J. Civ Eng. 23 (8), 3476–3492. doi:10.1007/s12205-019-1538-4

CrossRef Full Text | Google Scholar

Sarkar, A., Gugliani, G., and Deep, S. (2017). Weibull Model for Wind Speed Data Analysis of Different Locations in India. Ksce J. Civ Eng. 21 (7), 2764–2776. doi:10.1007/s12205-017-0538-5

CrossRef Full Text | Google Scholar

Seo, S., Oh, S.-D., and Kwak, H.-Y. (2019). Wind Turbine Power Curve Modeling Using Maximum Likelihood Estimation Method. Renew. Energ. 136, 1164–1169. doi:10.1016/j.renene.2018.09.087

CrossRef Full Text | Google Scholar

Shu, Z. R., Li, Q. S., and Chan, P. W. (2015). Statistical Analysis of Wind Characteristics and Wind Energy Potential in Hong Kong. Energ. Convers. Manag. 101, 644–657. doi:10.1016/j.enconman.2015.05.070

CrossRef Full Text | Google Scholar

Soukissian, T. H., and Tsalis, C. (2018). Effects of Parameter Estimation Method and Sample Size in Metocean Design Conditions. Ocean Eng. 169, 19–37. doi:10.1016/j.oceaneng.2018.09.017

CrossRef Full Text | Google Scholar

Soukissian, T. (2013). Use of Multi-Parameter Distributions for Offshore Wind Speed Modeling: The Johnson SB Distribution. Appl. Energ. 111, 982–1000. doi:10.1016/j.apenergy.2013.06.050

CrossRef Full Text | Google Scholar

Tenreiro, C. (2011). Fourier Series-Based Direct Plug-In Bandwidth Selectors for Kernel Density Estimation. J. Nonparametr Stat. 23, 533–545. doi:10.1080/10485252.2010.537337

CrossRef Full Text | Google Scholar

Torrielli, A., Repetto, M. P., and Solari, G. (2013). Extreme Wind Speeds from Long-Term Synthetic Records. J. Wind Eng. Ind. Aerod 115, 22–38. doi:10.1016/j.jweia.2012.12.008

CrossRef Full Text | Google Scholar

Tosunoğlu, F. (2018). Accurate Estimation of T Year Extreme Wind Speeds by Considering Different Model Selection Criterions and Different Parameter Estimation Methods. Energy 162, 813–824. doi:10.1016/j.energy.2018.08.074

CrossRef Full Text | Google Scholar

ul Haq, M. A., Rao, G. S., Albassam, M., and Aslam, M. (2020). Marshall–Olkin Power Lomax Distribution for Modeling of Wind Speed Data. Energy Rep 6, 1118–1123. doi:10.1016/j.egyr.2020.04.033

CrossRef Full Text | Google Scholar

Usta, I., and Kantar, Y. M. (2012). Analysis of Some Flexible Families of Distributions for Estimation of Wind Speed Distributions. Appl. Energ. 89 (1), 355–367. doi:10.1016/j.apenergy.2011.07.045

CrossRef Full Text | Google Scholar

Valencia Ochoa, G., Núñez Alvarez, J., and Vanegas Chamorro, M. (2019). Data Set on Wind Speed, Wind Direction and Wind Probability Distributions in Puerto Bolivar - Colombia. Data Brief 27, 104753. doi:10.1016/j.dib.2019.104753

PubMed Abstract | CrossRef Full Text | Google Scholar

Wais, P. (2017a). A Review of Weibull Functions in Wind Sector. Renew. Sustain. Energ. Rev 70, 1099–1107. doi:10.1016/j.rser.2016.12.014

CrossRef Full Text | Google Scholar

Wais, P. (2017b). Two and Three-Parameter Weibull Distribution in Available Wind Power Analysis. Renew. Energ. 103, 15–29. doi:10.1016/j.renene.2016.10.041

CrossRef Full Text | Google Scholar

Wang, J., Hu, J., and Ma, K. (2016). Wind Speed Probability Distribution Estimation and Wind Energy Assessment. Renew. Sustain. Energ. Rev 60, 881–899. doi:10.1016/j.rser.2016.01.057

CrossRef Full Text | Google Scholar

Wang, J., Qin, S., Jin, S., and Wu, J. (2015). Estimation Methods Review and Analysis of Offshore Extreme Wind Speeds and Wind Energy Resources. Renew. Sustain. Energ. Rev 42, 26–42. doi:10.1016/j.rser.2014.09.042

CrossRef Full Text | Google Scholar

Wang, Y., Li, Y., Zou, R., and Song, D. (2021). Bayesian Infinite Mixture Models for Wind Speed Distribution Estimation. Energ. Convers. Manag. 236, 113946. doi:10.1016/j.enconman.2021.113946

CrossRef Full Text | Google Scholar

Weibull, W. (1951). A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 18, 293–297. doi:10.1115/1.4010337

CrossRef Full Text | Google Scholar

World Bank, (2017). Renewable Electricity Output 2017.

Google Scholar

Xiao, N., Dong, Z., Xiao, S., Wang, J., and Liu, Z. (2021). An Improved Approach to Estimate Sand-Driving Winds. J. Clean. Prod. 285, 124820. doi:10.1016/j.jclepro.2020.124820

CrossRef Full Text | Google Scholar

Xu, X., Yan, Z., and Xu, S. (2015). Estimating Wind Speed Probability Distribution by Diffusion-Based Kernel Density Method. Electr. Pow Syst. Res. 121, 28–37. doi:10.1016/j.epsr.2014.11.029

CrossRef Full Text | Google Scholar

Zhang, H., Yu, Y.-J., and Liu, Z.-Y. (2014). Study on the Maximum Entropy Principle Applied to the Annual Wind Speed Probability Distribution: A Case Study for Observations of Intertidal Zone Anemometer Towers of Rudong in East China Sea. Appl. Energ. 114, 931–938. doi:10.1016/j.apenergy.2013.07.040

CrossRef Full Text | Google Scholar

Zhou, J., Erdem, E., Li, G., and Shi, J. (2010). Comprehensive Evaluation of Wind Speed Distribution Models: A Case Study for North Dakota Sites. Energ. Convers. Manag. 51 (7), 1449–1458. doi:10.1016/j.enconman.2010.01.020

CrossRef Full Text | Google Scholar