Refinements of Pin-Based Pointwise Energy Slowing-Down Method for Resonance Self-Shielding Calculation-II: Verifications

Introduction

The resonance treatment (or resonance self-shielding calculation) is an essential and challenging process to solve the multigroup neutron transport equation that requires the effective multigroup cross sections (XSs). The equivalence theory is one of the resonance treatment methods which have an ultimate purpose to accurately predict the effective multigroup XSs (Knott et al., 2010; Stamm’ler and Abbate, 1983). The equivalence theory, in the literal sense, is to create a homogeneous system (infinite dilution system) that is equivalent to a heterogeneous system by utilizing background XSs. The equivalence theory has been widely used by providing a reasonable solution with a short computation time, as standard resonance treatment method, and has been adopted by conventional codes such as CASMO (Rhodes et al., 2006a), WIMS (Powney and Newton, 2004), and APOLLO (Knott et al., 2010). However, there have been several fundamental approximations which impede its accuracy. The clumsy problem results from not considering a spatial effect of the resonance self-shielding by subdivided regions in the fuel pellet. In other words, a fuel pellet is assumed as a medium. Other important approximations are the resonance interference effect and the scattering source approximation. In order to reduce the error caused from the approximations, many studies have been conducted in the equivalence theory field. To consider the self-shielding effect for subdivided regions in the fuel pellet, the spatially dependent Dancoff method (SDDM) (Matsumoto et al., 2005) calculates the coefficients of the rational approximation incorporating the Dancoff factor for the fuel pellet as a medium and applies a weighting function for the spatial self-shielding for each subdivided region in the fuel pellet using the Stoke–Weiss method (Stoker and Weiss, 1996). SDDM adopts the Dancoff correction with the black limit approximation based on Stamm’ler correction (Stamm’ler and Abbate, 1983). In black limit approximation, the resonance material is the perfect neutron absorber. In contrast, the spatially dependent gray resonance self-shielding method (SDGM) (Koike et al., 2012) improves the coefficients in the rational approximation by considering gray resonance. In a similar manner, the spatially dependent resonance self-shielding method (SDSS) is implemented in CASMO5 (Ferrer and Hykes, 2019). SDGM and SDSS use the Stoke–Weiss method to compute the fuel escape probability for subdivided regions in the isolated fuel, and both methods consider gray resonance with optimum rational approximation (Rhodes et al., 2006b; Choi et al., 2015).

Another error source of the equivalence-based methods is the approximation of the scattering source with narrow or intermediate resonance approximation. The scattering source approximation is caused by the overestimation of the ²³⁸U effective XS (Choi et al., 2021; Choi et al., 2017). Some studies have addressed the issue (Powney and Newton, 2004; Yamamoto et al., 2011; Zhang et al., 2015) but still require drastic improvements.

A new resonance treatment method was also developed to overcome limitations of the equivalence theory (Choi et al., 2017). The new method utilizes the pointwise energy XSs to solve the slowing-down equation based on a subdivided fuel pellet and a fictitious moderator region, which is called the pin-based pointwise energy slowing-down method (PSM) (Choi et al., 2021; Choi et al., 2017; Choi, 2022). Solving the pointwise energy slowing-down addresses two main issues in the equivalence theory, namely, the resonance scattering and the resonance interference effect. Another advantage of the PSM is what does not use the resonance integral (RI) table. PSM allows to calculate the effective XS for the nonuniform material compositions and temperature profiles in the fuel pellet. The accuracy of the effective XSs calculated shows good agreements with the effective XSs calculated by Monte Carlo calculation.

In the accompanying paper (Choi, 2022), PSM was reviewed and PSM-CPM, the refined method of PSM with collision probability method (CPM), was introduced. PSMs (PSM and PSM-CPM) are verified with a few of light-water (LWR) reactor problems with the uniform material composition and temperature profile. PSM generates the table of the collision probability as a function of the total XS for the isolated fuel pellet before slowing-down calculation, where it is assumed that the total XS of all the subdivided regions in the fuel pellet is constant. In this case, the average total XS in the entire fuel pellet is used in the lookup of the collision probability. Because PSM-CPM calculates the collision probability in the isolated fuel pellet solving the pointwise slowing-down equation, different total XSs in each subdivided region with the nonuniform material compositions or temperature profiles are explicitly considered. When the fuel is burned and the thermal hydraulic feedback is involved with the neutron transport calculation, the nonuniformity of the material compositions and temperature profiles in the fuel pellet appears. In this case, PSM-CPM is an alternative option to calculate the collision probability of subdivided regions in the isolated fuel pellet under the nonuniform material composition and temperature profile. With the development of PSM, there have been the resonance self-shielding methods which adopt the ultra-fine-group (UFG) method to solve the slowing-down equation (Liu et al., 2015; Zhang et al., 2018). Along with this study, the nonuniformity problem has also been the central issue by many studies which have addressed the difficulties of rigorously predicting the effective XSs by the nonuniformity of the material compositions or temperature profiles (Liu et al., 2015; Zhang et al., 2018; Li, 2020; Zhang et al., 2020). There have also been cutting-edge approaches on treating the nonuniformity in the resonance self-shielding calculation using the machine learning technique (Qin et al., 2020a; Qin et al., 2020b).

In this paper, PSM and PSM-CPM (PSMs) are reviewed, and comparative analyses are presented extensively with various test cases with the condition of nonuniform material compositions and temperature profiles. The purpose of comparative analysis is to present the limitation of PSM as well as the accuracy of PSMs representing the effect depending on how to calculate the collision probability in the isolated fuel pellet. Test cases for the accuracy assessments consist of various conditions of the geometry, material distribution, temperature profile, and burnup. A total of five sections are presented with the problem descriptions and the results. In each section, the detailed XS and reaction rate comparison is presented to show the accuracy of PSMs, in which it is also compared with the results of the conventional equivalence theory methods.

Methods

Conventional Equivalence Theory Methods

The equivalence theory is derived with the transport equation with collision probabilities for the two-region problem and with the scattering source approximation with the intermediate resonance (IR) approximation as follows:

${\displaystyle {\sum }_{t,F}\left(E\right){\varphi }_F}\left(E\right)V_F=P_{FF}\left(E\right)V_F{Q}_{s,F}\left(E\right)+P_{MF}\left(E\right)V_M{Q}_{s,M}\left(E\right)(1)$

where

$\{\begin{array}{c}{Q}_{s,F}\left(E\right)={\displaystyle \sum _{r\in F}{N}^r\left({\lambda }^r{\sigma }_p^r\frac{1}{E}+\left(1-{\lambda }^r\right){\sigma }_s^r\left(E\right){\varphi }_F\left(E\right)\right)}\\ Q_{s,M}\left(E\right)={\displaystyle \sum _{r\in M}{N}^r\left({\lambda }^r{\sigma }_p^r\frac{1}{E}\right)}\end{array}(2)$

$F$ is the index of the fuel pellet; $M$ is the index of moderator; ${\displaystyle {\sum }_{t,F}\left(E\right)}$ is the total XS of fuel; ${\varphi }_F\left(E\right)$ is the flux in fuel; $V_F$ is the volume of the fuel pellet, $P_{FF}\left(E\right)$ is the fuel-to-fuel collision probability; $P_{MF}\left(E\right)$ is the collision probability from $M$ to $F$; $N^r$ is the number density of the nuclide $r$; ${\sigma }_s^r\left(E\right)$ is the scattering XS of the nuclide $r$; ${\lambda }^r$ is the IR parameter; and ${\Sigma }_p^r$ is the potential XS of the nuclide $r$.

Equation 1 is rewritten by using the approximated scattering source and the reciprocity theorem in Eq. 4 as follows:

${\displaystyle {\sum }_{t,F}\left(E\right){\varphi }_F}\left(E\right)=P_{FF}\left(E\right)\left[{\lambda }_F{\Sigma }_{p,F}\frac{1}{E}+\left(1-{\lambda }_F\right){\Sigma }_{s,F}\left(E\right){\varphi }_F\left(E\right)\right]+P_{FM}\left(E\right){\displaystyle {\sum }_{t,F}\left(E\right)}{V}_F\frac{1}{E}(3)$

where ${\lambda }_X{\Sigma }_{p,X}={\displaystyle \sum _{r\in X}{\lambda }^r{N}^r{\sigma }_p^r},\left(X=F\mathrm{or}M\right)$, and the reciprocity theorem is

$P_{FM}\left(E\right){\displaystyle {\sum }_{t,F}\left(E\right)}{V}_F=P_{MF}\left(E\right){\Sigma }_{t,M}{V}_M\approx P_{MF}\left(E\right){\lambda }_M{\Sigma }_{p,M}{V}_M(4)$

Then, the fuel-to-fuel collision probability is approximated by the rational equation as follows:

$P_{FF}\left(E\right)=1-P_{FM}\left(E\right)={\displaystyle \sum _{n=1}^N\frac{{\beta }_n{\Sigma }_{t,F}\left(E\right)}{{\Sigma }_{t,F}\left(E\right)+{\alpha }_n{\Sigma }_e}}(5)$

where $N$ is the number of rational expressions; ${\alpha }_n$ and ${\beta }_n$ are the coefficients of the nth rational term for the fuel rod; and ${\Sigma }_e$ is the escape XS of the fuel rod (Knott et al., 2010).

It should be noted that the subscript $F$ is not indicated in $a_n$, ${\beta }_n$, and ${\Sigma }_e$ for simplification, even though the parameters are for the fuel rod. When the multi-term rational approximation is used, the total flux is approximated as a linear combination of the nth fluxes. By substituting Eq. 5 into Eq. 3 with the approximation, the flux is

${\varphi }_F\left(E\right)={\displaystyle \sum _{n=1}^N{\beta }_n{\varphi }_{F,n}\left(E\right)}={\displaystyle \sum _{n=1}^N{\beta }_n\frac{{\lambda }_F{\Sigma }_{p,F}+{\alpha }_n{\Sigma }_e}{{\Sigma }_{a,F}\left(E\right)+{\lambda }_F{\Sigma }_{rs,F}\left(E\right)+{\lambda }_F{\Sigma }_{p,F}+{\alpha }_n{\Sigma }_e}}\frac{1}{E}(6)$

where ${\Sigma }_{rs,F}\left(E\right)$ is the resonance scattering XS of the fuel.

In the equivalence theory, it is assumed that the fuel contains only one resonant nuclide and only the nuclide has the absorption XS. Therefore, ${\Sigma }_{a,F}\left(E\right)$ and ${\Sigma }_{rs,F}\left(E\right)$ are assumed to be both macroscopic XSs of the fuel and the resonant nuclide $r$ (i.e., ${\Sigma }_{a,F}\left(E\right)=N^r{\sigma }_a^r\left(E\right)$). The flux in the fuel is rewritten as Eq. 7 by dividing the numerator and denominator by the number density of the target nuclide $r$, and Eq. 7 is presented as the lethargy form.

${\varphi }_F\left(u\right)={\displaystyle \sum _{n=1}^N{\beta }_n\frac{{\sigma }_{b,n}^r}{{\sigma }_a^r\left(u\right)+{\sigma }_{b,n}^r}}(7)$

where ${\sigma }_a^r\left(E\right)$ is the absorption XS of the nuclide $r$; ${\lambda }^r{\sigma }_{rs}^r\left(E\right)$ is the resonance scattering XS multiplied by the IR parameter of the nuclide $r$; and ${\sigma }_{b,n}^r$ is the nth term background XS of the nuclide $r$ and is defined as follows:

${\sigma }_{b,n}^r=\frac{1}{N^r}\left({\lambda }_F{\Sigma }_{p,F}+{\alpha }_n{\Sigma }_e\right)(8)$

The resonance scattering XS in Eq. 7 is usually dropped for simplicity. The effective multigroup XS is calculated as a ratio of the reaction rate to the flux integrated over the energy range. Therefore, the multigroup XS for the reaction $x$ is calculated as follows:

${\sigma }_{x,g}^r=\frac{{\displaystyle {\int }_{\Delta u_g}{\sigma }_x^r\left(u\right){\varphi }_F\left(u\right)du}}{{\displaystyle {\int }_{\Delta u_g}{\varphi }_F\left(u\right)du}}=\frac{{\displaystyle {\int }_{\Delta u_g}{\sigma }_x^r\left(u\right){\displaystyle \sum _{n=1}^N{\beta }_n\frac{{\sigma }_{b,n}}{{\sigma }_a^r\left(u\right)+{\sigma }_{b,n}}}du}}{{\displaystyle {\int }_{\Delta u_g}{\displaystyle \sum _{n=1}^N{\beta }_n\frac{{\sigma }_{b,n}}{{\sigma }_a\left(u\right)+{\sigma }_{b,n}}}du}}=\frac{{\displaystyle \sum _{n=1}^N{\beta }_{n,g}{\sigma }_{x,n,g}^r{\varphi }_{n,g}}}{{\displaystyle \sum _{n=1}^N{\beta }_{n,g}{\varphi }_{n,g}}}(9)$

where

${\sigma }_{x,n,g}^r={\sigma }_{x,g}^r\left({\sigma }_{b,n,g}^r\right)x=a,s,f(10)$

${\varphi }_{n,g}={\varphi }_g\left({\sigma }_{b,n,g}^r\right)=\frac{{\sigma }_{b,n,g}^r}{{\sigma }_{a,n,g}^r+{\sigma }_{b,n,g}^r}(11)$

${\sigma }_{b,n,g}^r=\frac{1}{N^r}\left({\displaystyle \sum _r{\lambda }_g^r{N}^r{\sigma }_p^r}+{\alpha }_{n,g}{\Sigma }_e\right)(12)$

Actually, the IR parameter has energy dependency because every resonance has a different width. Therefore, the energy-integrated IR parameter ${\lambda }_g^r$ has energy group dependency. The multigroup parameters such as ${\alpha }_{n,g}$, ${\beta }_{n,g}$, and ${\sigma }_{b,n,g}^r$ also have energy group dependency.

There are various calculation methods for the coefficients of the first flight collision probability shown in Eq. 5. The enhanced neutron current method (Yamamoto, 2008) and gray resonance treatment method (Koike et al., 2012) solve the fixed-source transport equation without the resonance scattering XS, as follows:

$\Omega \cdot \nabla {\psi }_g\left(v,\Omega \right)+\left[{\Sigma }_{a,g}^{\ast }\left(v\right)+{\lambda }_g{\Sigma }_p\left(v\right)\right]{\psi }_g\left(v,\Omega \right)=\frac{1}{4\pi }{\lambda }_g{\Sigma }_p\left(v\right)(13)$

where ${\psi }_g\left(v,\Omega \right)$ is the angular flux for the position $v$ and angle $\Omega$, and ${\Sigma }_{x,g}^{\ast }\left(v\right)$ is the approximated XS of the reaction $x$.

In the enhanced neutron current method, the total XS or the absorption XS are assumed to be infinite, and the Dancoff factor is calculated from the total reaction rate of the fuel region. The Dancoff factor can be used in the calculation of the rational approximation with Wigner’s one-term or Carlvik’s two-term method (Knott et al., 2010). In the gray resonance treatment method, the fuel flux is calculated with several discrete values of the fuel XSs, and then the rational approximation is calculated through the least square fitting process to the fuel flux. In their methods, the resonance scattering XS was omitted, but Eq. 13 can be easily rewritten with the resonance scattering XS as follows:

$\Omega \cdot \nabla {\psi }_g\left(v,\Omega \right)+\left[{\Sigma }_{a,g}^{\ast }\left(v\right)+{\lambda }_g{\Sigma }_{rs,g}^{\ast }\left(v\right)+{\lambda }_g{\Sigma }_p\left(v\right)\right]{\psi }_g\left(v,\Omega \right)=\frac{1}{4\pi }{\lambda }_g{\Sigma }_p\left(v\right)(14)$

There are several existing methods for spatial self-shielding calculation inside a fuel pellet with the equivalence theory. In this study, recent methods such as SDGM and SDSS as mentioned in Introduction section are not considered as the comparable methods. In the Distributed Resonance Integral (DRI) method (Xu et al., 2009), the legacy method implemented in CASMO-5, the average effective XS of the fuel pellet is calculated with a single region, and then an empirical radial distribution function is applied. The function is generated from Monte Carlo calculations, for the ²³⁸U resonance integral (Xu et al., 2009). Matsumoto developed the SDDM (Matsumoto et al., 2005) based on the idea of Stoker–Weiss (Stoker and Weiss, 1996). SDDM calculates the coefficients of the rational approximation using the Dancoff factor for the fuel pellet with a single region and applies a weighting function for the spatial self-shielding inside the fuel pellet. Both the DRI method and the SDDM can consider the radial self-shielding effect inside the fuel pellet and calculate the spatially dependent multigroup XSs. However, both methods have the following two drawbacks. First, the methods use the multi-term rational approximation (Carlvik’s two-term) and the effective XSs come from the XS lookup table using the multiple background XSs. Second, the methods use the resonance parameters or the effective XSs calculated for the fuel pellet with a single region. In the DRI method, the corrected effective XS is normalized as follows:

${\displaystyle \sum _{i\in F}{N}_i^{U238}{V}_i{\sigma }_{a,i,g}^{U238}}={\displaystyle \sum _{i\in F}{N}_i^{U238}{V}_i{\overline{\sigma }}_{a,g}^{U238}}(15)$

where $N_i^{U238}$ is the number density of ²³⁸U in a subdivided region $i$; ${\overline{\sigma }}_{a,g}^{U238}$ is the average absorption XS of ²³⁸U; and ${\sigma }_{a,i,g}^{U238}$ is the corrected absorption XS of ²³⁸U in a subdivided $i$ with the empirical correction factor $w_i$. as

${\sigma }_{a,i,g}^{\mathrm{U}238}=w_i{\overline{\sigma }}_{a,g}^{\mathrm{U}238}(16)$

If the averaged ²³⁸U absorption XS is not calculated properly, the distributed absorption XS still has bias in the averaged XS. SDDM calculates the effective XS of a subdivided region $i$ using the coefficients of rational approximation for averaged fuel as follows:

${\sigma }_{x,i,g}^r=\frac{{\displaystyle \sum _{m=1}^4{F}_{i,m}{\displaystyle \sum _{n=1}^N{\beta }_{n,g}R{I}_{x,g}^r\left({\sigma }_{b,i,n,m,g}^r\right)}}}{1-{\displaystyle \sum _{m=1}^4{F}_{i,m}{\displaystyle \sum _{n=1}^N{\beta }_{n,g}\frac{R{I}_{a,g}^r\left({\sigma }_{b,i,n,m,g}^r\right)}{{\sigma }_{b,i,n,m,g}^r}}}}(17)$

where $F_{i,m}$ is the weighting function, and ${\sigma }_{b,i,n,m,g}^r$ is the background XS defined as

${\sigma }_{b,i,n,m,g}^r=\frac{1}{N^r}\left({\displaystyle \sum _r{\lambda }_g^r{N}^r{\sigma }_p^r}+{\alpha }_{n,g}{\Sigma }_{e,i,m}\right)(18)$

where ${\Sigma }_{e,i,m}$ is the escape XS of a subdivided region $i$ and the shape $m$.

The fuel-to-fuel collision probability generated for the fuel pellet with a single region has a significant error because of the scattering source distribution inside the fuel. Therefore, SDDM also has the same problem as long as ${\alpha }_{n,g}$ and ${\beta }_{n,g}$ are calculated for the fuel lump.

Pin-Based Pointwise Energy Slowing-Down Method

For a subdivided region in the fuel pellet and a nonfuel region, the pointwise energy slowing-down equations can be reformulated by ignoring the fission source and inelastic scattering source and using the reciprocity relation as follows:

${\varphi }_i\left(u\right)={\displaystyle \sum _{j\in F}\frac{P_{ij}\left(u\right)}{{\Sigma }_{t,j}\left(u\right)}{Q}_{s,j}\left(u\right)}+\frac{P_{iM}\left(u\right)}{{\Sigma }_{p,M}}{Q}_{s,M}\left(u\right),i\in F(19)$

${\varphi }_M\left(u\right)={\displaystyle \sum _{i\in F}\frac{P_{Mi}\left(u\right)}{{\Sigma }_{t,i}\left(u\right)}{Q}_{s,i}\left(u\right)}+\frac{P_{MM}\left(u\right)}{{\Sigma }_{p,M}}{Q}_{s,M}\left(u\right)(20)$

where $i$ and $j$ are the indexes of the subdivided regions of the fuel pellet; $F$ and $M$ are the fuel pellet and the nonfuel region, respectively.

PSMs (PSM and PSM-CPM) calculate $P_{ij}\left(u\right)$, $P_{iM}\left(u\right)$, $P_{Mi}\left(u\right)$, and $P_{MM}\left(u\right)$ to obtain the fluxes and scattering sources shown in Eq. 19 and 20 by solving the neutron slowing-down equations with a fixed source at high energy.

A two-step approach is used to calculate the collision probabilities. In the first step, the collision probabilities of the subdivided regions in the isolated fuel pellet are calculated. The collision probability of the isolated fuel pellet is denoted as $P_{ij}^{iso}$. In the PSM (not PSM-CPM), ${\widehat{P}}_{ij}^{iso}$ is tabulated as a function of the total XS of the fuel pellet before solving slowing-down equations, and then $P_{ij}^{iso}$ is interpolated from the ${\widehat{P}}_{ij}^{iso}$ table. In this tabulation, the total XS of fuel is assumed to be constant for the entire fuel pellet. The assumption of the constant material composition and temperature in the fuel pellet is not exact for the burned fuel and nonuniform temperature profile. In this case, the total XS of the entire fuel pellet for interpolating $P_{ij}^{iso}$ at certain energy is replaced by the average total XS of the entire fuel pellet. This is the fundamental inconsistency for calculating the collision probability of the isolated fuel in PSM. The validity of the assumption and the effect of the effective XS by the theoretical inconsistency have been addressed in studies (Liu et al., 2015; Zhang et al., 2018; Zhang et al., 2020).

On the other hand, PSM-CPM calculates $P_{ij}^{iso}$ by using the CPM solvers for all energy points during solving of slowing-down equations without the assumption in that of PSM. Depending on how to calculate $P_{ij}^{iso}$, the distinction is made between PSM and PSM-CPM. Introducing the ${\widehat{P}}_{ij}^{iso}$ table can lead to an error in computing the collision probability even though it can reduce significant calculation time. In particular, the annular type of fuel pellet which has an extreme variation of total XSs in each subdivided region is caused by the significant error.

In PSMs (i.e., PSM and PSM-CPM), Carlvik’s two-term rational approximation in the equivalence theory is incorporated to correct the shadowing effect from neighboring fuel rods and structural materials. Since $P_{ij}^{iso}$ is calculated in an isolated fuel rod, a correction is required to consider the shadowing effect properly.

The shadowing effect correction factor, which adjusts the fuel escape probability of isolated fuel pin to consider the shadowing effect, is defined as a ratio of the fuel escape probabilities of two systems as follows:

${\eta }_i\left(u\right)\approx {\eta }_F\left(u\right)=\frac{P_{e,F}\left(u\right)}{P_{e,F}^{iso}\left(u\right)}(21)$

where $P_{e,F}^{iso}$ is the fuel escape probability of an isolated fuel pin and $P_{e,F}$ is that of the fuel pin in the lattice.

The shadowing effect correction factor is multiplied to the fuel escape probability in each subdivided region of the fuel pellets as follows:

$P_{iM}\left(u\right)=P_{e,i}\left(u\right)={\eta }_i\left(u\right)P_{e,i}^{iso}\left(u\right)(22)$

where

$P_{iM}^{iso}\left(u\right)=P_{e,i}^{iso}\left(u\right)=1-{\displaystyle \sum _{j\in F}{P}_{ij}^{iso}\left(u\right)}(23)$

It is assumed that the subdivided regions of the fuel pellet have the same shadowing effect. The collision probability is then normalized to consider the changes in the fuel escape probability as follows:

$P_{ij}\left(u\right)=P_{ij}^{iso}\left(u\right)\frac{1-P_{e,i}\left(u\right)}{1-P_{e,i}^{iso}\left(u\right)}(24)$

The collision probabilities from the non-fuel region are written as follows:

$P_{Mi}\left(u\right)=\frac{P_{iM}\left(u\right){\Sigma }_{t,i}\left(u\right)V_i}{{\Sigma }_{p,M}{V}_M}(25)$

$P_{MM}\left(u\right)=1-{\displaystyle \sum _{i\in F}{P}_{Mi}\left(u\right)}=1-{\displaystyle \sum _{i\in F}\frac{P_{iM}\left(u\right){\Sigma }_{t,i}\left(u\right)V_i}{{\Sigma }_{p,M}{V}_M}}(26)$

Finally, all the collision probabilities and escape probabilities are derived to solve the slowing-down equations in Eqs. 19, 20.

Accuracy Assessment

Various LWR problems are solved to verify the accuracy of the PSMs. Table 1 presents a summary of test cases and methods used in the verifications. The test cases include various conditions of the geometry (i.e., pin-cell and FA), material distribution (i.e., uniform and nonuniform), temperature profile (i.e., pin-cell and FA), and burnup (i.e., fresh fuel and burned fuel). The methods used in the comparisons are as follows:

1) EQ: the conventional equivalence theory

2) DRI: the distributed resonance integral method used in CASMO-5 (Xu et al., 2009)

3) SDDM: the spatially dependent Dancoff method used in PARAGON (Matsumoto et al., 2005)

4) MCXS: simulation with tallied multigroup XSs using the MCNP6 code

5) PSM: the pin-based pointwise slowing-down method with the ${\widehat{P}}_{ij}^{iso}$ table (Choi et al., 2017)

6) PSM-CPM: the pin-based pointwise slowing-down method with the CPM (Choi, 2022)

TABLE 1

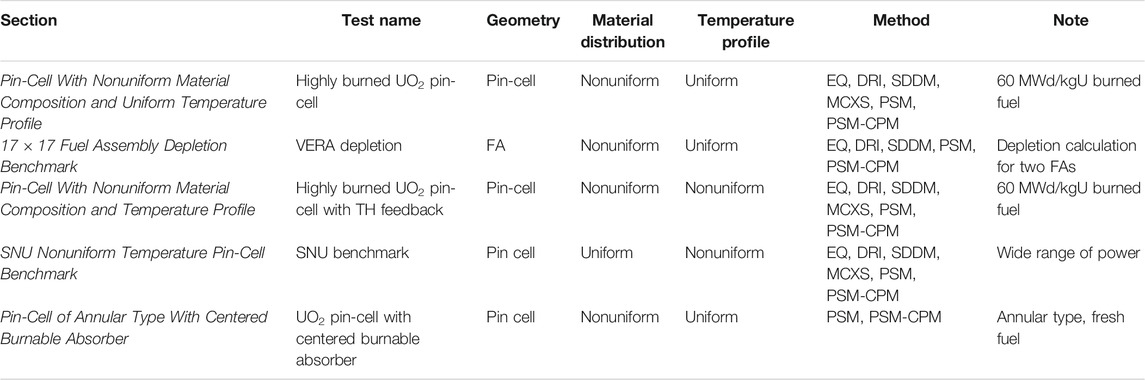
TABLE 1. Summary of test cases (Choi et al., 2021).

MCXS means the multigroup transport simulation with multigroup absorption and nu*fission XSs calculated from the continuous energy Monte Carlo code (i.e., MCNP6 (Goorley et al., 2012)). (n, 2n) and (n, 3n) XSs are also tallied to calculate absorption XSs for the simulation. The scattering matrix is not tallied from the MCNP6, because MCNP6 cannot calculate the multigroup scattering XS matrix. From the perspective of the resonance self-shielding calculation, the first purpose is to calculate the exact multigroup XSs. However, the multigroup simulation cannot completely reproduce the continuous energy solution, even though the exact multigroup XS is used in the simulation. Using the exact multigroup XS does not guarantee that the reaction rate is exact. There are still many error sources in the multigroup calculations (e.g., anisotropy, angular dependency of the multigroup XSs). This problem has not been clearly solved. Some studies tried to apply an artificial correction factor (i.e., SPH method) to reproduce the continuous energy solution (SUGIMURA and Yamamoto, 2007; Joo et al., 2009). The SPH method is not applied in this work because of the following reasons. First, the SPH method still cannot completely reproduce the continuous energy solution because the SPH factor is generated with a local continuous energy solution (i.e., pin cell). Second, the source from the continuous energy solution is assumed to be same as the source in the multigroup calculation during the SPH iteration. Third, the SPH factor is only applied in the resonance energy range. How to preserve the continuous energy reaction rate is still an open problem. Fortunately, the error in the reaction rate is not significant if the exact multigroup XS is used (see Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile, 17 × 17 Fuel Assembly Depletion Benchmark and Pin-Cell With Nonuniform Material Composition and Temperature Profile sections).

All the methods listed above are implemented in the STREAM code to compare the accuracy of the methods in the following sections. It should be noted that the results in this work do not mean that the CASMO-5 and PARAGON codes are the same as those of DRI and SDDM. There may be many unpublished methods used in the vendor codes. In other words, the resonance self-shielding methods of CASMO-5 and PARAGON are not completely the same as the STREAM code with DRI and SDDM, respectively. Although the overall theories are the same as that of the STREAM code, the detailed implementations may be different. For example, a vendor code uses an empirical correction factor to correct the fuel escape probabilities (SUGIMURA and Yamamoto, 2007), but the detailed values of the correction factor are not shown. In addition, some codes adjust the resonance integral table to obtain an accurate result (Koike et al., 2012). In treating the resonance interference effect, the Bondarenko iteration is usually used in the equivalence theory. However, some codes try to consider the resonance interference effect in the process, which generates the multigroup XS library by solving the slowing-down equations with typical mixed fuel materials (Koike et al., 2012). Some codes use many energy groups (e.g., ∼300 groups) to reduce the error from the resonance interference effect (Knott et al., 2010). As discussed above, the detailed methods implemented in lattice physics codes are slightly different from the basic equivalence theory. Most of the methods are empirical corrections applied to fit the results to the Monte Carlo solution or experimental data. It is difficult to compare the methods consistently, because the information of the empirical corrections is insufficient and there are excessively various modified methods to implement. Therefore, the theoretical methods are implemented in the STREAM code to compare with the PSMs. DRI is also one of the empirical corrections, but there are sufficient descriptions to implement. There is no empirical correction (except DRI) in the STREAM code and the STREAM libraries.

In solving LWR problems, various parameters are compared to examine the accuracy and the calculation efficiency of the PSMs. In some problems (Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile, 17 × 17 Fuel Assembly Depletion Benchmark, and Pin-Cell With Nonuniform Material Composition and Temperature Profile sections), the multigroup reaction rates are compared to examine the accuracy of the resonance self-shielding methods in detail. The eigenvalue represents the global condition of the problem. The eigenvalue can agree well with the reference solution, owing to error cancellation of some local errors in the reaction rates. Therefore, it is important to compare the reaction rates and the XSs. The difference in k-inf can be reconstructed with the difference of the absorption and fission reaction rates as follows:

$\begin{array}{l}d{k}_{\inf }=k_{\mathrm{STREAM}}-k_{\text{Ref}\text{.}}=d\left(\frac{P}{A}\right)=\frac{AdP-PdA}{A^2}\\ =dP-PdA={\displaystyle \sum _{r,i,g}\Delta P_{r,i,g}}-P_{\mathrm{STREAM}}{\displaystyle \sum _{r,i,g}{A}_{r,i,g}}\end{array},(27)$

where $d{k}_{\inf }$ is the difference in k-inf between k-inf from the STREAM code ($k_{STREAM}$) and MCNP6 ($k_{\mathrm{Ref}.}$); $P$ is the sum of the neutron production rate, which is identical to the nu*fission rates; $A$ is the sum of absorption rates; $r$ is the index of the region; $i$ is the index of the nuclide; $g$ is the index of the energy group; $\Delta P_{r,i,g}$ is the difference in the production rate in region $r$, nuclide $i$, and group $g$; and $\Delta A_{r,i,g}$ is the difference in the absorption rate in region $r$, nuclide $i$, and group $g$.

The sum of the absorption rates from both STREAM and MCNP6 are normalized to unity. Therefore, there is no $A$ in the second line of Eq. 27. From the normalization, $P_{r,i,g}$ and $-P_{\mathrm{STREAM}}{A}_{r,i,g}$ mean contribution of k-inf in elements $r$, $i$, and $g$ from the production rate and absorption rate, respectively. $\Delta P_{r,i,g}$ means the contribution to the difference in k-inf from the difference in the production rates of elements $r$, $i$, and $g$. In the same context, $-P_{\mathrm{STREAM}}\Delta A_{r,i,g}$ is the contribution to the difference in k-inf from the difference in the absorption rates. The sum of $\Delta P_{r,i,g}$ and $-P_{\mathrm{STREAM}}\Delta A_{r,i,g}$ is the total contribution to the difference in k-inf from the two reactions. From the equations, it is convenient to calculate which elements make the significant differences from the perspective of the eigenvalue.

Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile

The burned pin-cell problem was designed to examine the accuracy of PSMs for the pin-cell with the nonuniform material composition in the fuel pellet. When the collision probability is calculated, PSM uses one more approximation, which is that the material composition is constant in the fuel pellet, as described in an accompanying paper (Choi, 2022). PSM-CPM was developed as a rigorous version of PSM. PSM-CPM uses a more rigorous method to calculate the collision probabilities in the subregions of the pellet. The 3.1-wt.% UO₂ pin cell was burned up to 60 MWd/kgHM with an initial power density of 40 W/gHM. The discharge burnup of the fuel assembly in the actual reactor design was approximately 45 MWd/kgHM. The problem has more difficult conditions in terms of the heterogeneous material distributions. The materials used in the problem are as follows: 3.1 wt% UO₂ fuel, air gap, Zircaloy-4 cladding, and H₂O moderator with 1,300 ppm boron. The geometries of the pin-cell are the fuel pellet of outer radius 0.4096 cm; the cladding of inner radius 0.4180 cm; the cladding of thickness 0.057 cm; the gap placed between the fuel pellet and the cladding; and the pin-pitch of 1.26 cm.

The depletion calculation was performed with the STREAM code using PSM. In the calculation, the fuel pellet was divided into 15 subregions of equal volume. The depletion calculation was performed for the individual subregions. Therefore, the material compositions of the submehes are different from each other after the depletion. The STREAM code uses a depletion chain with 1,304 nuclides. Among the nuclides, 393 nuclides have neutron XS data. In order to reduce the calculation time in generating the reference solution, the 160 most important nuclides were selected in terms of the eigenvalue, and the modified pin-cell model was constructed. The difference in the eigenvalue between the original model and the modified model was less than 10 pcm. Figure 1 shows the temperature profile and the distribution of the material composition in the fuel pellet. The MCNP6 and STREAM codes solved the modified problem, and the results from the codes were compared.

FIGURE 1

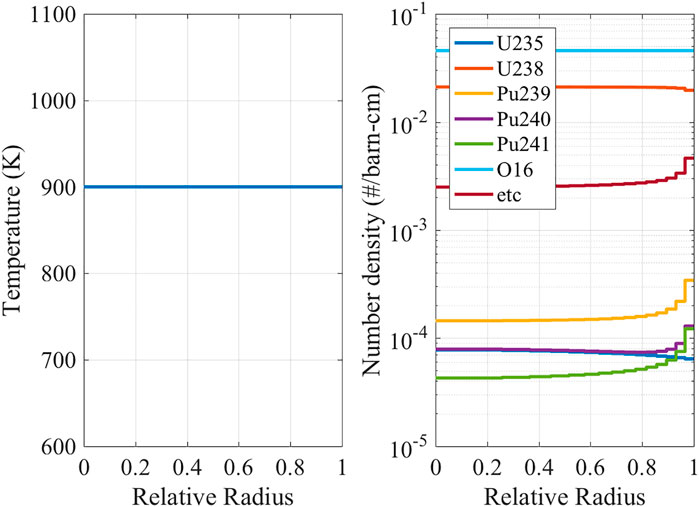
FIGURE 1. Temperature profile and number densities (60 MWd/kg burned fuel pin-cell) (Choi et al., 2021).

The k-inf results are compared in Table 2. PSM-CPM is used in this comparison in addition to PSM. EQ, DRI, and SDDM have differences of the order of 400 pcm in k-inf. MCXS, PSM, and PSM-CPM show more accurate results, with differences in k-inf of the order of 100 pcm. There is a difference of 27 pcm in k-inf between PSM and PSM-CPM. In order to compare the results in detail, the nuclide-wise reaction rates are compared in Table 3. In the nuclide-wise reaction rate comparison, various actinides and the fission products cause differences in the reaction rates. Among the actinides, ²³⁹Pu and ²³⁸U are the major error sources. With EQ, DRI, and SDDM, differences of 100–200 pcm occur from ²³⁹Pu and ²³⁸U. PSM-CPM calculates the reaction rates of ²³⁹Pu and ²³⁸U with differences of less than 30 pcm. Various fission products cause significant differences in the reaction rate for EQ, DRI, and SDDM. ¹⁵⁰Sm causes differences of the order of 90 pcm in the reaction rate for the three methods. However, PSM and PSM-CPM calculate quite accurate reaction rates of ¹⁵⁰Sm, with differences of 1 pcm.

TABLE 2

TABLE 2. k-inf and difference (60 MWd/kg burned fuel pin-cell) (Choi et al., 2021).

TABLE 3

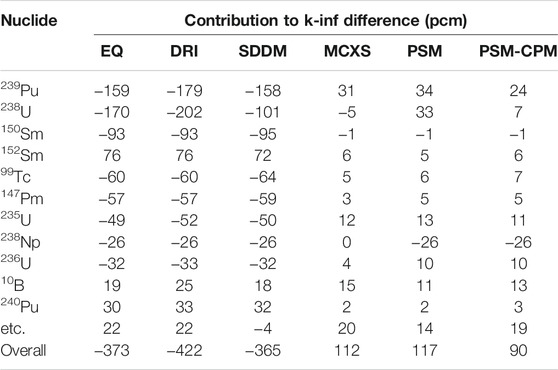
TABLE 3. Nuclide-wise contribution to k-inf difference (60 MWd/kg burned fuel pin-cell) (Choi et al., 2021).

Supplementary Figure S1 [contribution to the k-inf difference for ²³⁹Pu in all regions (Burned UO₂ pin-cell) (Choi et al., 2021)] shows the group-wise reaction rate comparison results for ²³⁹Pu. There are significant differences in the reaction rate of ²³⁹Pu with EQ, DRI, and SDDM. In particular, differences of 30–40 pcm occur in Groups 25 and 29. The significant differences are successfully reduced by PSM and PSM-CPM. In Groups 25 and 29, the differences of the reaction rates are less than 5 pcm.

In Supplementary Figure S2 [comparison of absorption and nu*fission reaction rates for ²³⁹Pu in resonance energy groups (Burned UO₂ pin-cell) (Choi et al., 2021)] and Supplementary Figure S3 (comparison of absorption XS and reaction rate for ²³⁹Pu in Group 29 (Burned UO₂ pin-cell) (Choi et al., 2021)), the region-wise reaction rates are compared. The reaction rates in the resonance energy ranges are integrated and compared in Supplementary Figure S2. It is shown that the magnitude of the reaction rates from EQ, DRI, and SDDM tends to be underestimated for both the absorption and production rates. DRI and SDDM do not show noticeable improvement in the reaction rate compared to that of EQ. PSM and PSM-CPM calculate more accurate reaction rates in the fuel pellet. The absorption XSs and reaction rates in Group 29 are compared in Supplementary Figure S3. The absorption XSs from EQ, DRI, and SDDM are underestimated by 15%. The underestimated absorption XS causes underestimated absorption rates. A similar bias occurs in the production rates. PSM and PSM-CPM show greatly improved results. The differences in the reaction rates from PSM and PSM-CPM are negligible.

Supplementary Figure S4 [contribution to the k-inf difference for ²³⁸U in all regions (Burned UO₂ pin-cell) (Choi et al., 2021)] shows the group-wise reaction rate comparison for ²³⁸U. The reaction rates of ²³⁸U with EQ, DRI, and SDDM are significantly different from the reference, causing differences of the order of 100 pcm in Groups 26 and 27. PSM and PSM-CPM have differences of less than 30 pcm in these groups. Supplementary Figure S5 [comparison of absorption XS and reaction rate for ²³⁸U in Group 27 (burned UO₂ pin-cell) (Choi et al., 2021)] shows the region-wise absorption XSs and reaction rates. The absorption XSs in the inner regions are significantly overestimated by EQ and DRI. SDDM has more accurate absorption XSs. However, the differences are still significant. The difference in the absorption XSs with PSM and PSM-CPM are quite accurate. There are no noticeable differences in the absorption XSs. There are differences of 10–30 pcm in the absorption reaction rates of the outermost region from MCXS, PSM, and PSM-CPM.

Supplementary Figure S6 [contribution to k-inf difference for ¹⁵⁰Sm in all regions (burned UO₂ pin-cell) (Choi et al., 2021)] shows the comparison of the group-wise reaction rate of ¹⁵⁰Sm. In order to calculate accurate multigroup XSs of the fission products, it is important to consider the resonance interference effect as well as the fuel escape probability. Resonant nuclides (i.e., ²³⁸U) have relatively more contributions to the multigroup XSs of the fission products. In Group 27, differences of more than 90 pcm in the reaction rates occur with EQ, DRI, and SDDM. In the region-wise comparison for Group 27, there are significant differences in the XSs and the reaction rates from the three methods {see Supplementary Figure S7 (comparison of absorption XS and reaction rate for ¹⁵⁰Sm in group 27 (burned UO₂ pin cell) (Choi et al., 2021)]}. The major source of the differences is the resonance interference effect. This should be considered with the detailed pointwise XSs and flux distributions because the positions of the resonance peaks have very significant impacts on the interference effect. However, the Bondarenko iteration method in the conventional equivalence theory considers the resonance interference effect in the multigroup parameters. PSM and PSM-CPM solve the pointwise energy equations with the fuel material with mixed nuclides, such that the resonance interference effect is considered spontaneously. There is no noticeable difference in the XSs and reaction rates.

From the verification with the burned pin-cell problem, it is concluded that PSM and PSM-CPM calculate considerably accurate multigroup XSs and reaction rates. PSM and PSM-CPM always exhibit superior results to those of EQ, DRI, and SDDM. EQ, DRI, and SDDM exhibit significant differences in the XSs and the reaction rates of actinides and the fission products. Because PSM and PSM-CPM solve the pointwise energy slowing-down equations on the fly, the resonance interference effect can be accurately considered. Therefore, high accuracy can be achieved with PSM and PSM-CPM for the highly burned pin-cell problem.

17 × 17 Fuel Assembly Depletion Benchmark

The depletion problems were solved to verify the accuracy of the XS for the depletion calculation. Because the reaction rates are used in the depletion calculation, it is important to calculate the accurate multigroup XS and reaction rates to achieve high accuracy in the final solution. Two types of FA problems were solved, as shown in Table 4. Problem A is the normal UO₂ FA without any burnable poison. Twenty-four gadolinia fuel rods are used in problem B. The two FAs were burned with a power density of 40 W/g. The final burnup is 60 MWd/kgHM. The verification problems came from the VERA depletion benchmark (Kim, 2015). Problems A and B are identical to problems 2C and 2P in the VERA depletion benchmark, respectively.

TABLE 4

TABLE 4. Description for fuel assembly depletion problems (Choi et al., 2021).

The reference data were generated by the SERPENT2 Monte Carlo code (Leppänen, 2015). The STREAM and SERPENT codes utilized a common recoverable energy per fission (which is usually called kappa) to be compared consistently. STREAM and SERPENT2 used their data for the depletion chain, decay, and yield. SERPENT2 uses more than 3,000 nuclides in the depletion chain. SERPENT2 uses an algorithm to determine the nuclides in the depletion chain depending on the problem. STREAM uses 1,304 nuclides in the depletion chain. The fuel pellet was divided into 15 subregions, such that each pellet had 15 different depletion zones. In order to obtain reliable results, sufficiently many depletion steps must be used in the depletion calculation. In the STREAM and SERPENT2 calculations, 40 steps are used for both the UO₂ FA without poison and the FA with Pyrex. Forty steps are sufficient to calculate the converged k-inf for both codes. With the SERPENT code, more than 300 steps are needed to obtain fully converged solutions for the FA with the 24 gadolinia fuel rods. STREAM uses quadratic depletion methods to reduce the discretization error (Lee et al., 2013). With the quadratic depletion method (Lee et al., 2013), STREAM can yield a converged solution within 40–50 depletion steps. The FA depletion problems were solved with rigorous mesh divisions and the number of time steps. The obtained results are shown in Figures 2, 3.

FIGURE 2

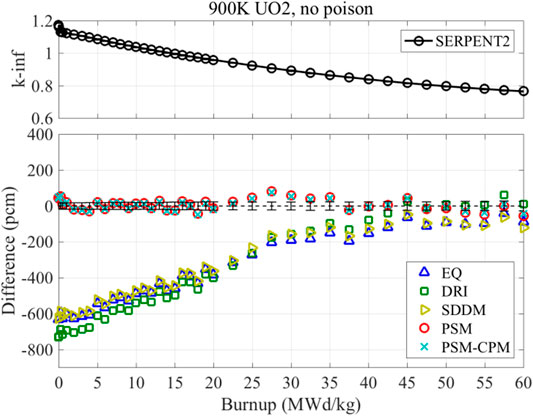
FIGURE 2. Analysis result of 17 × 17 fuel assembly without poison (Choi et al., 2021).

FIGURE 3

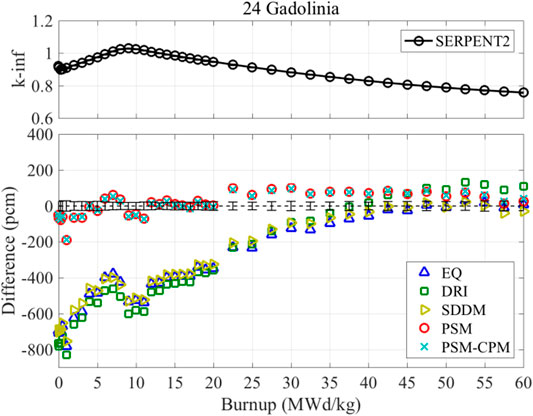
FIGURE 3. Analysis result of 17 × 17 fuel assembly with 24 gadolinia fuel rods (Choi et al., 2021).

EQ, DRI, and SDDM have significant bias in k-inf as a function of the burnup. The initial k-inf is underestimated by 600 pcm. The difference in k-inf decreases as the burnup increases. In the comparisons of the reaction rates in the previous sections, ²³⁸U absorption reaction rates are significantly overestimated by the three methods, leading to a negative contribution to the difference in k-inf. Therefore, the number density of ²³⁹Pu is overestimated with the three methods. This is the major reason for the trends in k-inf. PSM and PSM-CPM show very accurate and consistent results of k-inf. The differences in k-inf are of the order of 100 pcm from 0 to 60 MWd/kgHM burnup. It is important to note that the difference between PSM and PSM-CPM is less than 10 pcm for all the depletion steps in the two FA problems. It is noted that PSM has bias when the nonuniform temperature profile is used. However, the nonuniform material compositions do not cause a noticeable bias in the results of PSM.

Although STREAM and SERPENT2 use common kappa data, they still use many different data and libraries for the depletion calculations. Therefore, the error from the use of different data is included in the comparisons. It is difficult to say how much difference in k-inf is caused by the difference in the depletion libraries. Because the depletion results with PSM and PSM-CPM show very good agreement with that of SERPENT2, it is expected that the error is not significant. A more detailed examination is necessary.

From the verification with the depletion problem, it is confirmed that PSM and PSM-CPM calculate accurate and consistent results for the depletion. To obtain high accuracy in the depletion calculation, it is important to calculate accurate reaction rates for every single nuclide. The resonance interference treatment is also important because many resonant nuclides are mixed together. Although the material compositions are not uniform in the fuel pellet, PSM calculates very close results to PSM-CPM. The difference between PSM and PSM-CPM is less than 10 pcm.

Pin-Cell With Nonuniform Material Composition and Temperature Profile

In Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile and 17 × 17 Fuel Assembly Depletion Benchmark sections, the verification problem had nonuniform material compositions in the fuel pellets. In this section, both the material composition and temperature profiles are nonuniform. Currently, the whole-core transport calculation with multiphysics coupling is one of the main issues. If the TH feedback calculation is coupled, the fuel pellet has a nonuniform temperature profile. Obviously, the temperature has an impact on the XSs. PSM approximates the constant pointwise energy XS in the fuel pellet in computing the collision probability. Therefore, the approximation cannot work with the nonuniform temperature profile. Because of this issue, PSM-CPM is also developed to eliminate the approximation. Both methods are verified with the highly burned UO₂ pin-cell problem with the temperature profile. An identical pin-cell to that in Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile section is used in the verification. However, the depletion calculation is performed with the TH feedback. The parameters used in the TH feedback are described as follows: inlet temperature of 565 K, mass flux of 3,706 kg/m²⋅s, initial power density of 40 W/gHM, and height of 380 cm.

Similarly to the pin-cell problem in Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile section, the 160 most important nuclides of the fuel were selected, and the new modified pin-cell problem was made to reduce the calculation time elapsed in generating the reference solution. Figure 4 shows the temperature profile and the material distribution in the fuel pellet. The STREAM code with the different methods and the MCNP6 code were used in the modified pin-cell problem for the verification.

FIGURE 4

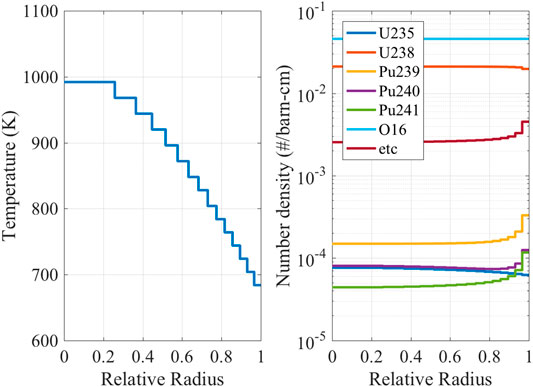
FIGURE 4. Temperature profile and number densities (60 MWd/kg burned fuel pin-cell with TH feedback) (Choi et al., 2021).

Here, some remarks on generating the reference solution are offered. The original MCNP6 data library is given for temperatures with 300-K intervals. Therefore, it is necessary to generate the ACE library for all the temperatures of interest. In order to obtain an accurate reference solution, the ACE library for MCNP6 was generated for all temperatures in the problem. The MAKXSF program in the MCNP6 code package was used to generate the S($\alpha$, $\beta$) data of hydrogen in light water. One may use the LEAPR module in the NJOY code to generate the S($\alpha$, $\beta$) data for the temperature (Kahler et al., 2012), which is not given in ENDF. However, it was concluded that MAKXSF can generate more reasonable S($\alpha$, $\beta$) data in terms of the trend of k-inf versus the temperature.

The STREAM code performs linear interpolation to calculate the XSs of any temperature of interest. The temperature interval of the pointwise energy XS library is approximately 100 K between 293.6 and 1800 K. The 100-K interval is sufficient to calculate an accurate multigroup XS from the pointwise energy slowing-down calculation. The interval for the multigroup XS library is also 100 K.

The results for k-inf and the nuclide-wise reaction rate comparison are shown in Tables 5, 6, respectively. The results are very similar to the results in the Pin-Cell With Nonuniform Material Composition and Uniform Temperature Profile section. EQ, DRI, and SDDM show differences of the order of 300 pcm in k-inf, whereas PSM and PSM calculate k-inf with differences of the order of 100 pcm. In the nuclide-wise comparison, EQ, DRI, and SDDM have significant differences in the various actinide and fission products. PSM and PSM-CPM show good agreement in the nuclide-wise reaction rate. The maximum difference is less than 40 pcm. The difference between PSM and PSM-CPM is not noticeable.

TABLE 5

TABLE 5. k-inf and difference (60 MWd/kg burned fuel pin-cell with TH feedback) (Choi et al., 2021).

TABLE 6

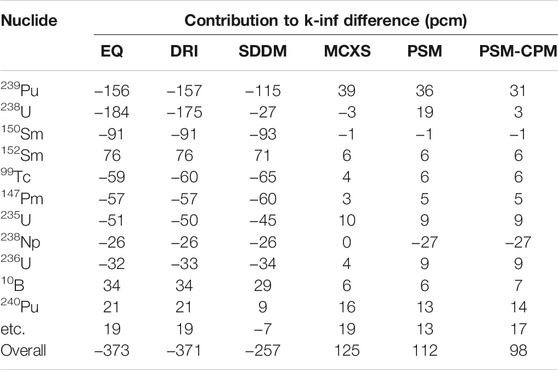
TABLE 6. Nuclide-wise contribution to k-inf difference (60 MWd/kg burned fuel pin-cell with TH feedback) (Choi et al., 2021).

Supplementary Figure S8 [contribution to k-inf difference for ²³⁹Pu in all regions (burned UO₂ pin-cell with TH feedback) (Choi et al., 2021)] shows the comparison of the reaction rate of ²³⁹Pu. EQ, DRI, and SDDM have significant differences in the reaction in Groups 25, 27, and 29. PSM and PSM-CPM have differences of less than 5 pcm in the reactions of the groups. In the region-wise comparison {see Supplementary Figure S9 [comparison of absorption XS and reaction rate for ²³⁹Pu in Group 29 (burned UO₂ pin-cell with TH feedback) (Choi et al., 2021)]}, the absorption is accurately calculated with PSM and PSM-CPM, whereas there are differences of the order of 15% in the XSs with EQ, DRI, and SDDM. There is a slight difference in the XSs from PSM and PSM-CPM. In comparison to PSM-CPM, PSM calculates slightly smaller XSs in the inner regions and larger XSs in the outer regions. The XSs from PSM are slightly tilted compared to those of PSM-CPM. The difference is less than 0.5%.

Supplementary Figure S10 (contribution to k-inf difference for ²³⁸U in all regions [burned UO₂ pin-cell with TH feedback) (Choi et al., 2021)] shows the comparison of the group-wise reaction rates of ²³⁸U. EQ, DRI, and SDDM have differences of the order of 100 pcm in Groups 26 and 27. PSM and PSM-CPM have differences of less than 30 pcm in the reaction rates in these groups. The difference between the PSM and PSM-CPM is not noticeable. In Supplementary Figure S11 [comparison of absorption XS and reaction rate for ²³⁸U in Group 27 (burned UO₂ pin-cell with TH feedback) (Choi et al., 2021)], the region-wise XSs and the reaction rates of ²³⁸U are compared. PSM-CPM calculates quite an accurate multigroup XS. The differences in the XSs are less than 1% in all the subregions of the pellet. Similarly to the comparison with ²³⁹Pu, the XSs from PSM are slightly tilted compared to those from PSM-CPM. In comparing with PSM-CPM, PSM calculates overestimated XSs in the inner regions and underestimated XSs in the outer regions.

From the verification with the burned pin cell with the nonuniform temperature profile, it is verified that PSM and PSM-CPM calculate the accurate multigroup XSs and the reaction rates. PSM-CPM show reasonable accuracy for the problem with the nonuniform temperature profile and material distributions. However, PSM has a slight in–out tilt in the XS compared to that of PSM-CPM. The nonuniform temperature profile causes a bias in PSM. The reason for the bias will be discussed in the next section with a more significantly nonuniform temperature profile.

SNU Nonuniform Temperature Pin-Cell Benchmark

A research team in Seoul National University (SNU) developed a nonuniform fuel temperature benchmark (Jung et al., 2016) to examine the accuracy of the subgroup method of the pin-cell problem with a nonuniform temperature profile. The benchmark includes 14 pin-cell problems with the seven different power levels and two sets of temperature profiles (i.e., uniform and nonuniform temperature profiles). The materials used in the problem are as follows: 3 wt% UO₂ fuel, air gap, natural zirconium cladding, and H₂O moderator. The fuel pellet is divided into five subregions of equal volume.

There are a set of temperature profiles, as shown in Figure 5. The profiles are given for the difference power levels from 50 to 200%. The 100% power level corresponds to full-power operation. In case of uniform temperature profiles, an average temperature for the fuel region is given for difference power levels. More detailed specifications are available elsewhere (Jung et al., 2016). The reference solution was generated using MCNP6. The default scattering kernel (i.e., SVT) was used in the calculation. For a consistent comparison, the STREAM code also used the SVT upscattering correction to treat the resonance upscattering effect. Although five subregions were used in the fuel pellet in the benchmark, each subregion was divided into three regions to examine the information in more detail. Therefore, 15 subregions were used in the calculation using the MCNP6 and STREAM codes.

FIGURE 5

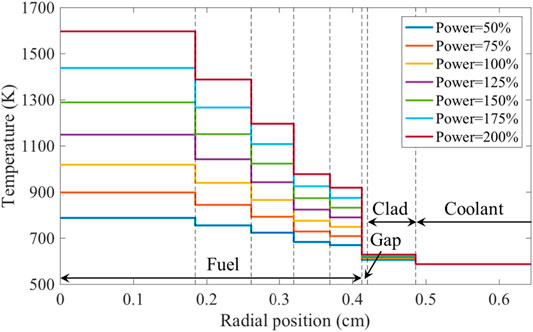
FIGURE 5. Temperature profiles of nonuniform temperature cases (SNU benchmark) (Choi et al., 2021).

The pin-cell problems in the benchmark were solved with the different methods, and the obtained reactivities are compared in Figure 6. The reactivities and the differences are plotted as functions of the average temperature of the fuel pellet. EQ, DRI, and SDDM show the significantly underestimated reactivities. Differences of approximately 500 pcm are observed in the results. The reactivities are biased as a function of the average fuel temperature. PSM and PSM-CPM calculate the reactivities with differences of less than 100 pcm for all the cases. There is no noticeable bias in the results with PSM-CPM. The results with MCXS are similar to those with PSM-CPM. In the nonuniform cases, PSM shows a slightly biased reactivity. As the power increases, the reactivity with PSM is underestimated. In order to examine the temperature bias, the fuel temperature coefficient (FTC) was calculated. The FTC was calculated with least-square fitting to the reactivities versus the average fuel temperatures, and the results are shown in Table 7.

FIGURE 6

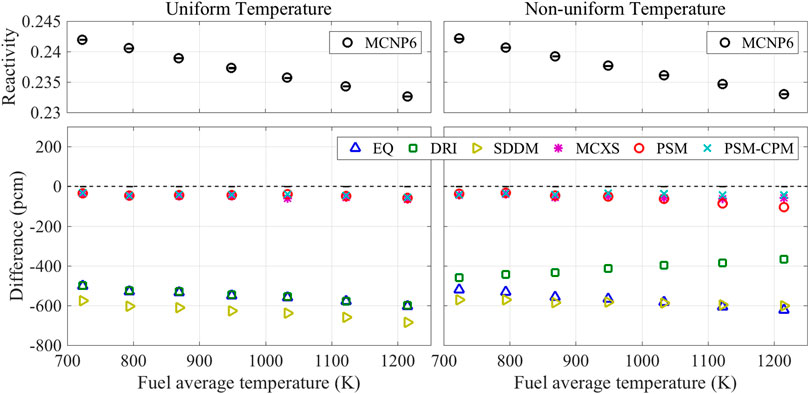
FIGURE 6. Comparison of reactivity (SNU benchmark) (Choi et al., 2021).

TABLE 7

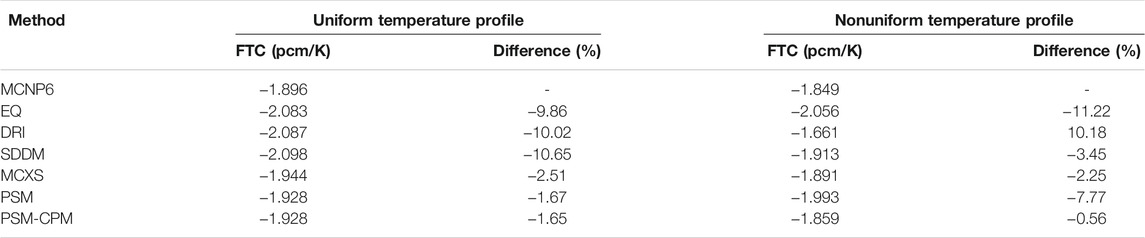
TABLE 7. Fuel temperature coefficients (SNU benchmark) (Choi et al., 2021).

There are significant differences in the FTCs with the EQ, DRI, and SDDM. For the cases with the uniform temperature profile, the three methods have differences of the order of 10% in the FTCs. If the nonuniform temperature profile is used, the three methods still have quite significant differences in the FTCs. The FTCs with DRI and SDDM are not consistent for the two profiles. The differences in the FTCs with DRI change from −10.02% to 10.18% when the temperature profile is changed. The differences in the FTCs with SDDM change from −10.65% to −3.45%. The FTC with PSM is quite accurate, with a difference of 1.67% if the uniform temperature profile is used. However, PSM has a difference of 7.77% in the FTC for the problem with the nonuniform temperature profile. PSM shows a significant bias in the FTC. However, PSM-CPM shows consistent and accurate results for both temperature profiles. The differences in the FTCs are 1.65% and 0.56% for each profile.

In order to examine the bias in the FTC, the detailed reaction rates are compared for the problem with 200% power and the nonuniform temperature profile. Supplementary Figure S12 [contribution to k-inf difference for ²³⁸U in all regions (200% power nonuniform temperature case) (Choi et al., 2021)] shows the group-wise comparison of the reaction rates. PSM and PSM-CPM show relatively accurate results in the reaction rates of the resonance energy groups. There are differences of 5–30 pcm in k-inf between PSM and PSM-CPM. In Supplementary Figure S13 [comparison of absorption XS for ²³⁸U in Group 29 (200% power nonuniform temperature case) (Choi et al., 2021)], the region-wise absorption XSs and the reaction rates in Group 29 are compared, respectively. The absorption XSs with PSM are tilted along the radial direction. The XSs in the inner regions are overestimated, whereas the XSs in the outer regions are underestimated. The maximum difference in the XS with PSM is 9%. However, PSM-CPM shows negligible differences in the XSs.

The differences in the XSs between PSM and PSM-CPM are caused by their methods of calculating the collision probabilities. PSM calculates the average total XS and then interpolates the collision probability from the ${\widehat{P}}_{ij}^{iso}$ table using the average pointwise energy total XS.

Figure 7 shows the macroscopic pointwise energy total XSs and the ratio of the XSs in each region to the average XS in the pellet between 4 and 27.7 eV. When the temperature increases, the overall resonance XSs increase. In calculating the collision probability with PSM, the resonance XSs in the inner regions are underestimated. With the underestimated XSs, PSM overestimates the fuel escape probabilities in the inner regions and then overestimates the scattering sources from the moderator. Finally, the reaction rates of the resonance are overestimated, and therefore the multigroup XSs are overestimated in the inner regions. The reaction rates in the outer regions are underestimated because of the overestimated fuel escape probabilities. Therefore, the multigroup XS is underestimated in the outer regions.

FIGURE 7

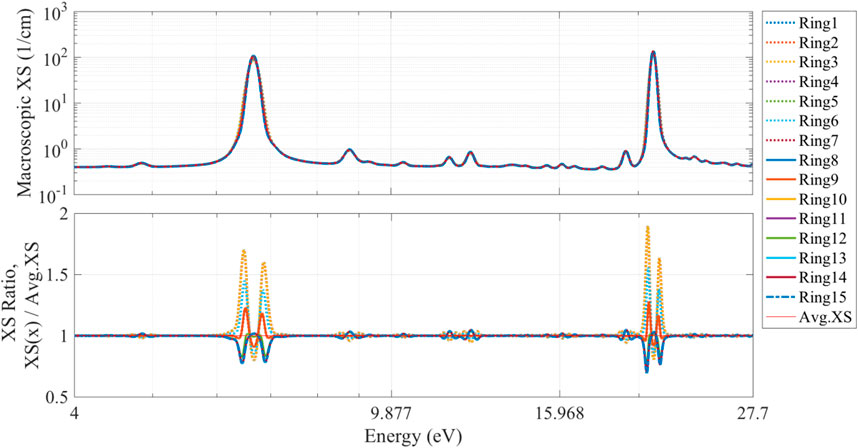
FIGURE 7. Macroscopic total XSs in fuel pellet (200% power nonuniform temperature case) (Choi et al., 2021).

From the verification with the SNU benchmark, it is concluded that accurate k-inf values can be calculated with PSM and PSM-CPM. For the pin cell with 200% power, PSM has a bias in calculating the FTC for the problems with the nonuniform temperature profile. PSM calculates tilted multigroup XSs in the fuel pellet because of the approximation in calculating the collision probability. It is verified that PSM-CPM can consider the nonuniform temperature profile accurately because the approximation is not used in the PSM-CPM. The FTCs, multigroup XSs, and reaction rates from PSM-CPM are very accurate compared to the reference solutions.

Pin-Cell of Annular Type With Centered Burnable Absorber

The pin-cell problem was virtually designed to examine the accuracy of PSM-CPM for the pin cell with the extremely nonuniform material composition in the fuel pellet. The problem has most difficult conditions in terms of the heterogeneous material distributions. The materials used in the problem are as follows: Gd₂O₃ burnable absorber, coated molybdenum (Mo) alloys cladding, UO₂ fuel, air gap, Zirlo cladding, and H₂O moderator. The geometries of the pin cell are: the absorber of outer radius 0.065 cm; the Mo cladding of outer radius 0.070 cm; the UO₂ fuel of inner radius 0.075 cm; the UO₂ fuel of outer radius 0.4096 cm; the Zirlo cladding of inner radius 0.4178 cm; the Zirlo of outer radius 0.4750 cm; the gaps filled with the air placed between fuel and both claddings; and the pin pitch of 1.26 cm.

The UO₂ region in the fuel pellet was divided into 11 subregions of equal outer radius. The reference was calculated by MCS Monte Carlo code (Lee et al., 2020). The results from the codes were compared.

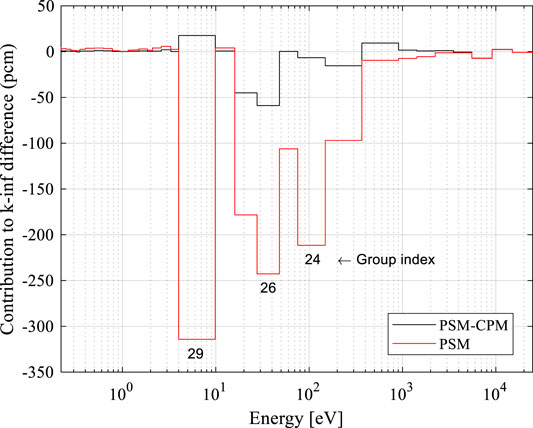
The k-inf results are compared in Table 8. PSM has a significant difference of −2,609 pcm in k-inf. PSM-CPM shows an accurate result, with a difference in k-inf of -58 pcm.

TABLE 8

TABLE 8. k-inf and difference (annular fuel pin cell).

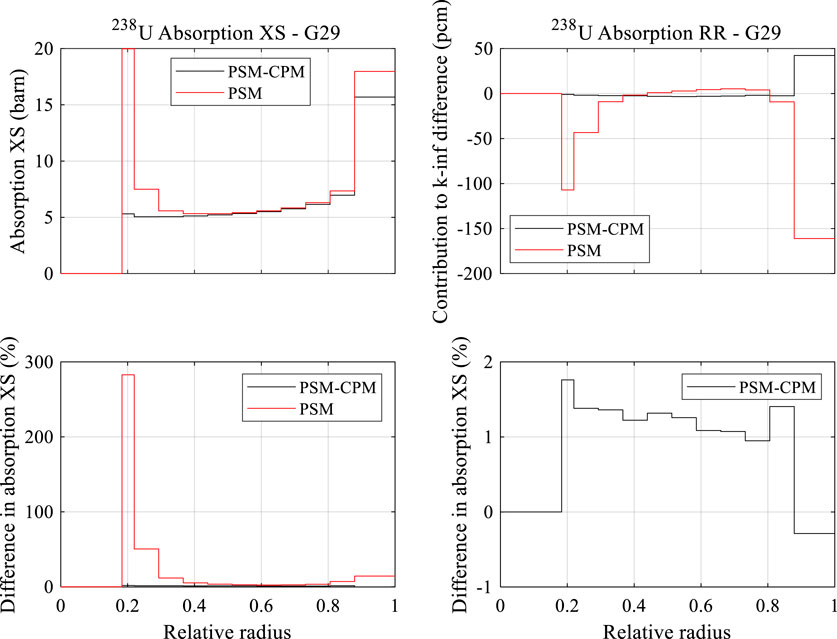
Figure 8 shows the group-wise reaction rate comparison for ²³⁸U in the resonance region. The reaction rates of ²³⁸U with PSM are significantly different from the reference, causing a difference in the order of 300 pcm in Group 29. PSM-CPMs show very accurate results in the reaction rates of the resonance energy groups. Figure 9 shows the region-wise absorption XSs and reaction rates. The absorption XSs in the inner UO₂ regions are significantly overestimated by PSM. The difference in the absorption XSs with PSM-CPM are quite accurately less than 2% of relative error compared to the reference. There are differences of 100–150 pcm in the absorption reaction rates of the outermost and inner region from PSM. However, there is a difference of less than 50 pcm in that of the outermost region from PSM-CPM.

FIGURE 8

FIGURE 8. Contribution to k-inf difference for ²³⁸U in the resonance region.

FIGURE 9

FIGURE 9. Comparison of absorption XS and reaction rate for ²³⁸U in Group 29 (Annular pin-cell).

The major source of the differences is how they calculate the collision probability for the isolated fuel pellet. This problem has extreme stiffness of total XS distribution due to the centered burnable absorber in the fuel pellet. In the case of PSM which assumes that total XS is constant in the fuel pellet, it should cause an error. For general LWR problems in the previous sections, the assumption in PSM has not introduced significant errors and has shown the same level of accuracy as compared to PSM-CPM. However, PSM should not be an option in such a problem that the total XS has varied with a large difference in the fuel pellet. It is noted that both PSM and PSM-CPM use Carlvik’s two-term rational approximation to calculate the collision probability in the fuel pellet in the lattice. It is assumed that the shadowing effect is not significantly different for the individual subregions of the fuel pellet. The effect by the assumption is one of the issues that need to be further investigated.

From the verification with the annular pin-cell problem which has a burnable absorber in the center region of the fuel pellet, it is concluded that PSM-CPM calculates considerably accurate multigroup XSs and reaction rates. PSM exhibits significant differences in the XSs and the reaction rates of ²³⁸U. Because PSM-CPMs solve the pointwise energy slowing-down equations calculating the collision probability corresponding to the variation of the material compositions and the temperature profiles, high accuracy can be achieved even for the highly stiff pin-cell problem.

Conclusion

PSM has been briefly reviewed, and a PSM-CPM that is refined with respect to the way to calculate the collision probability in the isolated fuel pellet is introduced. PSM-CPM calculates the collision probability during solving of the pointwise slowing-down equation, but PSM uses pre-tabulated collision probability as a function of the total XS for a fuel pellet lump and indices of subdivided regions. Then, the collision probability is interpolated during the slowing-down calculation. The discrepancy in the effective XSs caused by the assumption in PSM is investigated through the comparative analysis. The comparative analysis is performed compared to legacy equivalence theory methods such as SDDM and DRI with various LWR problems, which have uniform and nonuniform material compositions and temperature profiles in the fuel pellets. By combination with various conditions (geometry, material composition distribution, temperature profile in the fuel pellet, and burnup), various test cases have represented problems under possible conditions in the LWR design.

First, the accuracy of PSMs (PSM and PSM-CPM) has been examined with the burned pin-cell problem that has the nonuniform material composition in the fuel pellet. This test has demonstrated that PSMs calculate the accurate multigroup XSs and reaction rates and show superior accuracy than that of conventional methods.

Second, the accuracy of PSMs and conventional methods is tested with the depletion problems. The accuracy of the depletion calculation is directly related to the accuracy of the reaction rates for every single nuclide with the burnup. When the material composition is not uniform in the fuel pellets, PSM showed a result with a difference of less than 10 pcm from PSM-CPM. It showed that the accuracy of PSM-CPM under nonuniformity of material composition by the depletion does not demonstrate a noticeable difference in PSM.

Third, PSMs have been verified with test cases which have nonuniform material composition and temperature profiles in the fuel pellet. The condition represents the effect of the TH feedback and the depletion in the fuel pellet. For the highly burned UO₂ pin-cell problem with a nonuniform temperature profile, the accuracy of PSMs has been verified with the comparisons of multigroup XSs and the reaction rates with the reference solutions. However, the XS from PSM has shown a slight in–out tilt compared to that of PSM-CPM.

Fourth, a bias in PSM, as mentioned above, has been investigated by solving the SNU benchmark which includes the pin-cell problems with the nonuniform temperature profile. It was demonstrated that PSMs show great accuracy in the calculation of the eigenvalue. PSM has a bias in calculating the FTC for the pin cell with a two times higher-power level than that in full-power operation. PSM calculates tilted multigroup XSs in the fuel pellet due to the approximation in calculating the collision probability. However, it is verified that PSM-CPM eliminates the approximation of PSM, giving the result of accurate FTCs, multigroup XSs, and reaction rates.

Finally, the annular pin-cell problem which has a burnable absorber in the center region of the fuel pellet has been tested with PSMs. PSM showed significant differences in the eigenvalue and XSs. However, it was clearly demonstrated that PSM-CPM achieves high accuracy in the calculation of XSs and reaction rates for the problem that has a highly stiff distribution in terms of the XS in the fuel pellet.

More improvement in the computational efficiency of PSM-CPM and the verifications with the up-to-date resonance self-shielding methods based on the equivalence theory, the subgroup method, and the UFG method will be performed in the future work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

WK and SC contributed to verifications. WK wrote the first draft of the manuscript. SC and WK wrote sections of the manuscript. SC reviewed and edited the manuscript. DL supervised all the activity for the manuscript. All authors contributed to the manuscript revision and read and approved the submitted version.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the government of Korea (MSIT). (No.NRF-2019M2D2A1A03058371). This work was partially supported by Korea Institute of Energy Technology Evaluation and Planning(KETEP) grant funded by the Korea government (MOTIE) (20206510100040).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.765865/full#supplementary-material.

References

Choi, S., Lee, C., and Lee, D. (2017). Resonance Treatment Using Pin-Based Pointwise Energy Slowing-Down Method, Ulsan: Republic of Korea. J. Comput. Phys. 330, 134–155. doi:10.1016/j.jcp.2016.11.007

CrossRef Full Text | Google Scholar

Choi, S., Lee, H., Hong, S. G., and Lee, D. (2015). Resonance Self-Shielding Methodology of New Neutron Transport Code STREAM. J. Nucl. Sci. Tech. 52, 1133–1150. doi:10.1080/00223131.2014.993738

CrossRef Full Text | Google Scholar

Choi, S., Kim, W., and Lee, D. (2021). Refinements of Pin-based Pointwise Energy Slowing-down Method for Resonance Self-shielding Calculation-I: Theory. Front. Energ. Res.

Google Scholar

Choi, S. (2022). Refinements of Pin-Based Pointwise Energy Slowing-Down Method for Resonance Self-Shielding Calculation-I: Theory. Front. Energ. Res.

Google Scholar

Ferrer, R., and Hykes, J. (2019). Development of A Spatially-dependent Resonance Self-Shielding Method in Casmo5, M&C 2019. Portland: OR.

Google Scholar

Goorley, T., James, M., Booth, T., Brown, F., Bull, J., Cox, L. J., et al. (2012). Initial MCNP6 Release Overview. Nucl. Tech. 180, 298–315. doi:10.13182/NT11-135

CrossRef Full Text | Google Scholar

Joo, H. G., Kim, G. Y., and Pogosbekyan, L. (2009). Subgroup Weight Generation Based on Shielded Pin-Cell Cross Section Conservation. Ann. Nucl. Energ. 36, 859–868. doi:10.1016/j.anucene.2009.03.017

CrossRef Full Text | Google Scholar

Jung, Y. S., Lim, C. H., and Joo, H. G. (2016). Temperature Dependent Subgroup Formulation with Number Density Adjustment for Direct Whole Core Power Reactor Calculation. Ann. Nucl. Energ. 96, 249–263. doi:10.1016/j.anucene.2016.06.001

CrossRef Full Text | Google Scholar

Kahler, A. C., MacFarlane, R. E., Muir, D. W., and Boicourt, R. M. (2012). The NJOY Nuclear Data Processing System. Version 2012. Los Alamos: New Mexico National Laboratory. LA-UR-12-27079.

Google Scholar

Kim, K. S. (2015). Specification for the VERA Depletion Benchmark Suite. Oak Ridge: United States National Laboratory. CASL-X-2015-1014-000.

Google Scholar

Knott, D., and Yamamoto, A. (2010). “Lattice Physics Computations,” in Handbook of Nuclear Engineering. Editor D. G. Cacuci (Boston, MA: Springer US), 913–1239. doi:10.1007/978-0-387-98149-9_9

CrossRef Full Text | Google Scholar

Koike, H., Yamaji, K., Kirimura, K., Sato, D., Matsumoto, H., and Yamamoto, A. (2012). Advanced Resonance Self-Shielding Method for gray Resonance Treatment in Lattice Physics Code GALAXY. J. Nucl. Sci. Tech. 49, 725–747. doi:10.1080/00223131.2012.693885

CrossRef Full Text | Google Scholar

Lee, D., Rhodes, J., and Smith, K. (2013). Quadratic Depletion Method for Gadolinium Isotopes in CASMO-5. Nucl. Sci. Eng. 174, 79–86. doi:10.13182/NSE12-20

CrossRef Full Text | Google Scholar

Lee, H., Kim, W., Zhang, P., Lemaire, M., Khassenov, A., Yu, J., et al. (2020). MCS - A Monte Carlo Particle Transport Code for Large-Scale Power Reactor Analysis. Ann. Nucl. Energ. 139, 107276. doi:10.1016/j.anucene.2019.107276

CrossRef Full Text | Google Scholar

Leppänen, J. (2015). Serpent – a Continuous-Energy Monte Carlo Reactor Physics Burnup Calculation Code. Espoo: VTT Technical Research Centre of Finland.

Google Scholar

Li, J. (2020).Multi-ring Subgroup Method in Characterising Highly Self-Shielded Gadolinia Burnable Poison Pins for the UK EPR Nuclear Fuel Assembly. In International Conference on Computing. New York, NY: Electronics & Communications Engineering, 196–200. doi:10.1109/iCCECE49321.2020.9231157

CrossRef Full Text | Google Scholar

Liu, Y., Martin, W., Williams, M., and Kim, K.-S. (2015). A Full-Core Resonance Self-Shielding Method Using a Continuous-Energy Quasi-One-Dimensional Slowing-Down Solution that Accounts for Temperature-dependent Fuel Subregions and Resonance Interference. Nucl. Sci. Eng. 180 (3), 247–272. doi:10.13182/nse14-65

CrossRef Full Text | Google Scholar

Matsumoto, H., Ouisloumen, M., and Takeda, T. (2005). Development of Spatially Dependent Resonance Shielding Method. J. Nucl. Sci. Tech. 42, 688–694. doi:10.1080/18811248.2004.9726438

CrossRef Full Text | Google Scholar

Powney, D. J., and Newton, T. D. (2004). Overview of the WIMS 9 Resonance Treatment. Serco Assur. Dorchester, ANSWERS/WIMS/TR. 26.

Google Scholar

Qin, S., Zhang, Q., Liang, L., Zhao, Q., Zhang, Z., Wu, H., et al. (2020). Fitting-based Resonance Database Method for Resonance Self-Shielding Calculations of Large-Scale Task Considering Depletion and Intra-pin Distribution. Ann. Nucl. Energ. 139, 107247. doi:10.1016/j.anucene.2019.107247

CrossRef Full Text | Google Scholar

Qin, S., Zhang, Q., Zhang, J., Liang, L., Zhao, Q., Wu, H., et al. (2020). Application of Deep Neural Network for Generating Resonance Self-Shielded Cross-Section. Ann. Nucl. Energ. 149, 107785. doi:10.1016/j.anucene.2020.107785

CrossRef Full Text | Google Scholar

Rhodes, J., Smith, K., and Lee, D. (2006). Vancouver, BC: Canada, 10–14.CASMO-5 Development and ApplicationsProc. Int. Conf. on Advances in Nuclear Analysis and Simulation (PHYSOR 2006)September

Google Scholar

Rhodes, J., Smith, K., and Lee, D. (2006). CASMO-5 Development and Applications, PHYSOR-2006. Vancouver, BC: Canada.

Google Scholar

Stamm'ler, R. J. J., and Abbate, M. J. (1983). Methods of Steady-State Reactor Physics in Nuclear Design. London: Academic Press.

Google Scholar

Stoker, C. C., and Weiss, Z. J. (1996). Spatially Dependent Resonance Cross Sections in a Fuel Rod. Ann. Nucl. Energ. 23, 765–778. doi:10.1016/0306-4549(95)00074-7

CrossRef Full Text | Google Scholar

Sugimura, N., and Yamamoto, A. (2007). Resonance Treatment Based on Ultra-fine-group Spectrum Calculation in the AEGIS Code. J. Nucl. Sci. Tech. 44, 958–966. doi:10.1080/18811248.2007.9711335

CrossRef Full Text | Google Scholar

Xu, Z., Rhodes, J., and Smith, K. (2009). Casmo-5 versus Mcnp-5 Benchmark of Radial Power Profile in A Fuel Pin. Lagrange Park, IL: M&C 2009.

Google Scholar

Yamamoto, A., Endo, T., and Koike, H. (2011). Improved Derivation of Multigroup Effective Cross Section for Heterogeneous System by Equivalence Theory. Nucl. Sci. Eng. 168, 75–92. doi:10.13182/NSE10-50

CrossRef Full Text | Google Scholar

Yamamoto, A. (2008). Evaluation of Background Cross Section for Heterogeneous and Complicated Geometry by the Enhanced Neutron Current Method. J. Nucl. Sci. Tech. 45, 1287–1292. doi:10.1080/18811248.2008.9711916

CrossRef Full Text | Google Scholar

Zhang, Q., Jiang, R., Zhao, Q., Cao, L., and Wu, H. (2018). Accurate Resonance Absorption Calculation for Fuel Pins with Non-uniform Intra-pellet Temperature Profile Based on ultra-fine-group Slowing-Down Calculations. Ann. Nucl. Energ. 120, 392–401. doi:10.1016/j.anucene.2018.06.005

CrossRef Full Text | Google Scholar

Zhang, Q., Shuai, Q., Zhao, Q., Liang, L., Wu, H., and Cao, L. (2020). Improvements on the Method of ultra-fine-group Slowing-Down Solution Coupled with Method of Characteristics on Irregular Geometries. Ann. Nucl. Energ. 136, 1070171–1107017.15. doi:10.1016/j.anucene.2019.107017

CrossRef Full Text | Google Scholar

Zhang, Q., Wu, H., Cao, L., and Zheng, Y. (2015). An Improved Resonance Self-Shielding Calculation Method Based on Equivalence Theory. Nucl. Sci. Eng. 179, 233–252. doi:10.13182/NSE13-108

CrossRef Full Text | Google Scholar