Optimization and H∞ Performance Analysis for Load Frequency Control of Power Systems With Time-Varying Delays

With the development and expansion of the power grid, the load frequency control (LFC) scheme receives sensor signals and outputs control signals through an open communication network with a mass of data and extensive information exchange, which may introduce constant, and time-varying delays. This paper considers the optimization and H_∞ performance problem for LFC of power systems with time-varying delays. Some improved criteria for guaranteeing the stability and H_∞ performance of the closed-loop system with unknown external load disturbances via the Lyapunov stability theory application. An unique delay-dependent proportional-integral (PI) controller and an optimized PI controller are designed for a specified H_∞ performance index and set, respectively. The criteria proposed in this paper are based on linear matrix inequalities (LMIs), which can be easily solved by the MATLAB LMI-Toolbox. Finally, in case studies, the effectiveness of our method is demonstrated.

1 Introduction

LFC strategy is equipped to guarantee the power grid frequency, an important index of power quality, stability (de A. F. Mello et al., 2020). With the development and expansion of the power grid, the dedicated independent communication network has been unable to meet the operation of the power grid (Khalil and Swee Peng, 2018). Recently, LFC scheme transmits sensor and control signals based on an open communication network, where random delays and data packets will be introduced into the LFC scheme (Shen et al., 2021). These network factors may cause the LFC system performance degradation and even instability. Thus, it is necessary to study the influence of time-varying delays on performance of the LFC system in an open communication network.

The network controlled LFC system involves two main cases of time-varying delays: 1) the communication time-varying delay from the control center to the governor (Ramakrishnan and Ray, 2015; Yang et al., 2018; Chen et al., 2020; Manikandan and Kokil, 2020), where delay-dependent stability analysis and controller design are investigated by using single delay to model all time delays; 2) In fact, not only the communication time-varying delay from the control center to the governor but also from the sensor to the control center (Jiang et al., 2012; Xu et al., 2017; Shen et al., 2019a), where general delay-dependent stability analysis is studied by using additive time-varying delays to model two different time delays. In a word, the LFC scheme with communication channels can be treated as a typical delayed system. For the stability analysis of the system, it is significance to seek the maximum allowable time delay upper bounds to guarantee the stability of the power system based on LFC scheme, which has attracted more and more scholars’ attention (Ali et al., 2020; del Giudice et al., 2021; Ladygin et al., 2020; Baykov et al., 2019). The stability conditions and controller design are obtained mainly by the Lyapunov stability theory. For further reducing the conservatism of stability criteria, two updates are in progress. On the one hand, the Lyapunov-Krasovskii functional (LKFs) are improved via some novel approaches. Duan et al. (2019a); Duan et al. (2020a); Hua et al. (2021) constructed new LKFs by using the delay decomposition method. The LKFs were modified in Duan et al. (2016); Duan et al. (2017); Scopus et al. (2020); Gholami (2021) by intruducing some multiple integral items. Duan et al. (2020b) augmented the LKF with some augmented vectors. On the other hand, the upper bounds of the derivatives of the LKFs are estimated using some novel tight inequality techniques. Jensen inequality and B-L inequality were proposed in Gu (2000) and Seuret and Gouaisbaut (2015), respectively, where a tight upper bound of the derivative of the LKFs was obtained. Zhang et al. (2017a); Duan et al. (2018); Duan et al. (2019b); Feng et al. (2020); Kwon and Lee (2021) reduced the conservatism of the stability criterion via some relaxed integral inequality techniques. Recently, a novel negative definite inequality equivalent transformation lemma was proposed in Fúlvia et al. (2020), which improved the degree of freedom for solving the LMI in the main theorem without introducing extra conservatism. Thus, there is still room to further reduce the conservatism of stability criteria for the LFC power system along with the update of stability methods for general time-delayed systems.

Moreover, the growing power system based on network control leads to the complexity and uncertainty. Many important control algorithms, such as robust control (Shayeghi et al., 2008), genetic algorithm (Rerkpreedapong et al., 2003), sliding mode control (Vrdoljak et al., 2010) and H_∞ control (Dey et al., 2012; Shen et al., 2021), are used to ensure the operation stability and disturbance rejection capability of large-scale power systems. However, in many studies, especially in controller design, the influence of time delays, especially time-varying delays, is ignored. Based on the above discussion, the H_∞ LFC problem of power systems with time-varyig delays and load disturbances is studied in this paper. The contributions of this paper can be summarized as follows:

• H_∞ performance problem for the LFC power systems with time-varying delays is considered in this paper, where fixed and optimized controller gains for an given H_∞ performance index γ and an performance index set [γ₁, γ₂] are respectively proposed;

• An augmented LKF combining delay-dependent non-integral terms with some single-integral terms under different time-varying delay subintervals are constructed, which reduces the conservatism caused by the LKF structure;

• A novel negative definite inequality equivalent transformation lemma proposed in (Fúlvia et al., 2020) is used to transform the nonlinear inequality to the LMI equivalently, which can be easily solved by the MATLAB LMI-Toolbox.

This paper is organized as follows. Section 2 gives the models of LFC schemes; Section 3 provides stability assessment and H_∞ controller design for the LFC system. Section 4 shows cases studies. Conclusions are drawn in Section 5.

Notation: Throughout this paper, the notations are standard. ${\mathbb{R}}^n$ denotes the n-dimensional Euclidean space; ${\mathbb{R}}^{n\times m}$ is the set of all n × m real matrices; For $P\in {\mathbb{R}}^{n\times n}$, P > 0 (respectively, P < 0) mean that P is a positive (respectively, negative) definite matrix. $\text{diag}\left\{a_1,a_2,\dots ,a_n\right\}$ denotes an n-order diagonal matrix with diagonal elements a₁, a₂, …, a_n. e_i (i = 0, 1, …, m) are block entry matrices. For example, $e_2=\left[0I\underset{m-2}{\underbrace{0\cdots 0}}\right]$. For a real matrix B and two real symmetric matrices A and C of appropriate dimensions, $\left[\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill *\hfill & \hfill C\hfill \end{array}\right]$ denotes a real symmetric matrix, where * denotes the entries implied by symmetry. Sym{A} = A+ A^T.

2 System Description and Problem Preliminaries

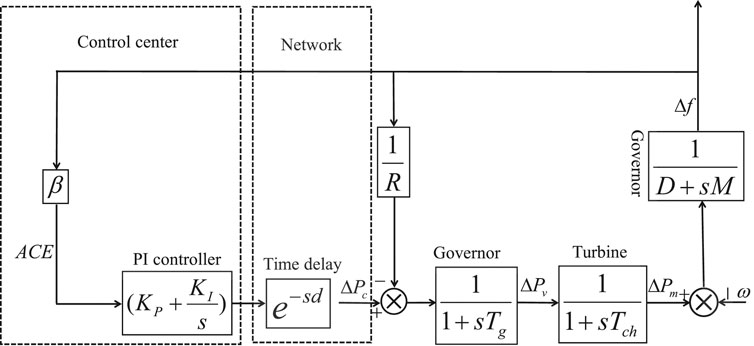
In this section, the model of one-area power system equipped with PI controllers and taking into account the time-varying communication delays is given. The basic diagram of the simplified LFC of one-area power system is shown in Figure 1, where e^−sd is time delay, arising during the control signal sent from the control center to the governor.

FIGURE 1

FIGURE 1. The basic diagram of the simplified LFC of one-area power system.

According the LFC system as shown in (Bevrani, 2014) and Figure 1, the common LFC scheme model of one-area can be expressed as follows:

$\left\{\begin{array}{c}\dot{\stackrel{̄}{x}}(t)=\bar{A}\bar{x}(t)+\bar{B}\mathrm{\Delta }{P}_c(t)+\bar{F}\bar{\omega }(t),\hfill \\ \bar{y}(t)=\bar{C}\bar{x}(t),\hfill \end{array}\right.(1)$

where

$\begin{array}{ll}\hfill \bar{x}(t)=& \left[\begin{array}{c}\hfill \mathrm{\Delta }f(t)\hfill \\ \hfill \mathrm{\Delta }{P}_m(t)\hfill \\ \hfill \mathrm{\Delta }{P}_v(t)\hfill \end{array}\right],\bar{y}(t)=ACE(t),\bar{A}=\left[\begin{array}{ccc}\hfill -\frac{D}{M}\hfill & \hfill \frac{1}{M}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{1}{T_{ch}}\hfill & \hfill \frac{1}{T_{ch}}\hfill \\ \hfill -\frac{1}{R{T}_g}\hfill & \hfill 0\hfill & \hfill -\frac{1}{T_g}\hfill \end{array}\right],\hfill \\ \hfill & \bar{B}=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill \frac{1}{T_g}\hfill \end{array}\right],\bar{F}=\left[\begin{array}{c}\hfill -\frac{1}{M}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\bar{C}=\left[\beta 00\right]\hfill \end{array}$

and explanations of some terms are shown in Table 1. The following PI controller is used as the LFC scheme:

$u(t)=-K_{P}ACE(t)-K_I\int ACE(t)dt.(2)$

Due to the existence of the time-varying delay, in the feedback channel, the following is obtained

$\mathrm{\Delta }{P}_C(t)=u(t-h(t)),ACE(t)=\beta \mathrm{\Delta }f(t),(3)$

where h(t) represents the time-varying delay, and 0 ≤ h(t) ≤ h, $\mid \dot{h}(t)\mid \le \mu$ with h and μ being positive constants.

TABLE 1

TABLE 1. Explanation of terminologies.

By defining virtual state and measurement output vector as y(t) = col{ACE(t), ∫ACE(t)dt} and x(t) = col{Δf(t), ΔP_m(t), ΔP_v(t), ∫ACE(t)dt}, K = [K_P K_I], the closed-loop LFC system can be expressed as the following linear system with time-varying delays:

$\left\{\begin{array}{c}\dot{x}(t)=Ax(t)+BKCx(t-h(t))+F\omega (t),\hfill \\ y(t)=Cx(t),\hfill \\ x(t)=\varphi (t),t\in [-h,0],\hfill \end{array}\right.(4)$

where ϕ(t) denotes its initial condition which is a vector continuous function of t∈[−h, 0] and the system parameters are listed in the following form

$A=\left[\begin{array}{cccc}\hfill -\frac{D}{M}\hfill & \hfill \frac{1}{M}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{1}{T_{ch}}\hfill & \hfill \frac{1}{T_{ch}}\hfill & \hfill 0\hfill \\ \hfill -\frac{1}{R{T}_g}\hfill & \hfill 0\hfill & \hfill -\frac{1}{T_g}\hfill & \hfill 0\hfill \\ \hfill \beta \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],B=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -\frac{1}{T_g}\hfill \\ \hfill 0\hfill \end{array}\right],C=\left[\begin{array}{cccc}\hfill \beta \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],F=\left[\begin{array}{c}\hfill -\frac{1}{M}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right].$

A definition and some lemmas need to be displayed here before we proceed with the next step of calculation and discussion.

Definition 1 (Shen et al., 2019b) the system is considered to be asymptotically stable and meets the H_∞ performance index γ if the following conditions are met.

• The system is asymptotically stable when the disturbance input is not taken into account (i.e., ω(t) ≡ 0).

• For any nonzero disturbance, given a positive scalar γ, the following inequality is satisfied under zero initial conditions (x(t) = 0, t ∈ [− d, 0]):

$\mathrm{\Omega }={\int }_0^{\infty }\left[y^T(\alpha )y(\alpha )-{\gamma }^2{\omega }^T(\alpha )\omega (\alpha )\right]d\alpha \le 0.(5)$

Lemma 1(Seuret and Gouaisbaut, 2015). For a positive definite matrix R and differentiable function x in $[a,b]\to {\mathbb{R}}^n$, the followings hold

${\int }_a^b{\dot{x}}^T(s)R\dot{x}(s)ds\ge \frac{1}{b-a}{\omega }^T\mathcal{R}\omega ,$

where $\mathcal{R}=\text{diag}\{R,3R,5R\}$, ω = col{ω₁, ω₂, ω₃} with ω₁ = x(b) − x(a), ${\omega }_2=x(b)+x(a)-\frac{2}{b-a}{\int }_a^{b}x(s)ds$, ${\omega }_3={\omega }_1-\frac{6}{b-a}{\int }_a^{b}x(s)ds+\frac{12}{{(b-a)}^2}{\int }_a^b(b-s)x(s)ds$.

Lemma 2(Zhang et al., 2017b). For positive definite matrices R₁, $R_2\in {\mathbb{R}}^{n\times n}$, vectors v₁, $v_2\in {\mathbb{R}}^n$ and a scalar α ∈ [0, 1], if there exist symmetric matrices $X_1,X_2\in {\mathbb{R}}^{n\times n}$ and any matrices $S_1,S_2\in {\mathbb{R}}^{n\times n}$ such that

$\left[\begin{array}{cc}\hfill R_1-X_1\hfill & \hfill S_1\hfill \\ \hfill \ast \hfill & \hfill R_1\hfill \end{array}\right]\ge 0,\left[\begin{array}{cc}\hfill R_2-X_2\hfill & \hfill S_2\hfill \\ \hfill \ast \hfill & \hfill R_2\hfill \end{array}\right]\ge 0,$

the following inequality holds

$\frac{1}{\alpha }{v}_1^T{R}_1{v}_1+\frac{1}{1-\alpha }{v}_2^T{R}_2{v}_2\ge v_1^T[R_1+(1-\alpha )X_1]v_1+v_2^T[R_2+\alpha X_2]v_2+2v_1^T[\alpha S_1+(1-\alpha )S_2]v_2.$

Lemma 3(Fúlvia et al., 2020). Let symmetric matrices A₀, A₁, $A_2\in {\mathbb{R}}^{m\times m}$ and a vector $\zeta \in {\mathbb{R}}^m$. Then, the following inequality

${\zeta }^T(h_t^2{A}_2+h_t{A}_1+A_0)\zeta <0$

holds for all h_t ∈ [0, h] if and only if there exist a positive definite matrix $D\in {\mathbb{R}}^{m\times m}$ and a skew-symmetric matrix $G\in {\mathbb{R}}^{k\times k}$ such that

$\left[\begin{array}{cc}\hfill A_0\hfill & \hfill \frac{1}{2}{A}_1\hfill \\ \hfill \ast \hfill & \hfill A_2\hfill \end{array}\right]<{\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill -D\hfill & \hfill G\hfill \\ \hfill \ast \hfill & \hfill D\hfill \end{array}\right]\left[\begin{array}{c}\hfill C\hfill \\ \hfill J\hfill \end{array}\right],$

where $C=\left[\frac{h}{2}I0\right]$ and $J=\left[\frac{h}{2}I-I\right]$.

3 Main Results

In order to make the calculation process more concise, some expressions are given in advance as below

$\begin{array}{ll}\hfill h_t=& h(t),{\bar{h}}_t=h-h(t),h_d=1-\dot{h}(t),\hfill \\ \hfill {\eta }_0(t)=& \text{col}\left\{x(t),x(t-h_t),x(t-h)\right\},\hfill \\ \hfill {\eta }_1(t)=& \text{col}\left\{x(t),x(t-h_t),{\int }_{t-h_t}^{t}x(s)ds\right\},\hfill \\ \hfill {\eta }_2(t)=& \text{col}\left\{x(t-h_t),x(t-h),{\int }_{t-h}^{t-h_t}x(s)ds\right\},\hfill \\ \hfill {\eta }_3(t,s)=& \text{col}\left\{\dot{x}(s),x(s),{\eta }_0(t),{\int }_s^{t}x(\theta )d\theta ,{\int }_{t-h_t}^{s}x(\theta )d\theta ,{\int }_{t-h}^{t-h_t}x(\theta )d\theta \right\},\hfill \\ \hfill {\eta }_4(t,s)=& \text{col}\left\{\dot{x}(s),x(s),{\eta }_0(t),{\int }_s^{t-h_t}x(\theta )d\theta ,{\int }_{t-h_t}^{t}x(\theta )d\theta ,{\int }_{t-h}^{s}x(\theta )d\theta \right\},\hfill \end{array}$

$\begin{array}{ll}\hfill {\rho }_1(t)=& {\int }_{t-h}^{t-h_t}\frac{x(s)}{{\bar{h}}_t},{\rho }_2(t)={\int }_{t-h}^{t-h_t}\frac{(t-h_t-s)x(s)}{{\bar{h}}_t^2},\hfill \\ \hfill {\rho }_3(t)=& {\int }_{t-h_t}^t\frac{x(s)}{h_t},{\rho }_4(t)={\int }_{t-h_t}^t\frac{(t-s)x(s)}{h_t^2},\hfill \\ \hfill \xi (t)=& \text{col}\left\{x(t),x(t-h_t),x(t-h),\dot{x}(t),\dot{x}(t-h_t),\dot{x}(t-h),{\rho }_1(t),{\rho }_2(t),{\rho }_3(t),{\rho }_4(t),\omega (t)\right\}.\hfill \end{array}$

3.1 H_∞ Performance Analysis

Theorem 1 Given positive scalars h, μ, ɛ_j and γ, system (4) is stable and meets the H_∞ performance index γ, if there exist positive definite matrices $S_{i2}\in {\mathbb{R}}^{3n\times 3n}$, $Q_i\in {\mathbb{R}}^{8n\times 8n}$, $R_i\in {\mathbb{R}}^{n\times n}$, ${\mathcal{D}}_i\in {\mathbb{R}}^{(10n+1)\times (10n+1)}$, symmetric matrices $S_{i1},X_i\in {\mathbb{R}}^{3n\times 3n}$, skew-symmetric matrices ${\mathcal{G}}_i\in {\mathbb{R}}^{(10n+1)\times (10n+1)}$, any matrices $Y_i\in {\mathbb{R}}^{3n\times 3n}$, (i = 1, 2; j = 1, 2, 3), $U\in {\mathbb{R}}^{n\times n}$, such that the following matrix inequalities hold for ${\dot{h}}_t\triangleq {\mu }_i\in \{-\mu ,\mu \}$.

$\begin{array}{l}\hfill h{S}_{i1}+S_{i2}>0,\end{array}(6)$

$\begin{array}{ll}\hfill \left[\begin{array}{cc}\hfill {\bar{R}}_i-X_i\hfill & \hfill Y_i\hfill \\ \hfill \ast \hfill & \hfill {\bar{R}}_i\hfill \end{array}\right]>& 0,\hfill \end{array}(7)$

$\begin{array}{ll}\hfill \left[\begin{array}{cc}\hfill {\mathrm{\Omega }}_0({\mu }_i)\hfill & \hfill \frac{1}{2}{\mathrm{\Omega }}_1({\mu }_i)\hfill \\ \hfill \ast \hfill & \hfill {\mathrm{\Omega }}_2({\mu }_i)\hfill \end{array}\right]-{\left[\begin{array}{c}\hfill \mathcal{C}\hfill \\ \hfill \mathcal{J}\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill -{\mathcal{D}}_i\hfill & \hfill {\mathcal{G}}_i\hfill \\ \hfill \ast \hfill & \hfill {\mathcal{D}}_i\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathcal{C}\hfill \\ \hfill \mathcal{J}\hfill \end{array}\right]<& 0,\hfill \end{array}(8)$

where the notations of other symbols and matrices can be found in Appendix A. Thus, the controller gain matrix calculated by

$K={(UB)}^{+}{K}_0,(9)$

where the generalized inverse of (UB) is expressed as (UB)⁺.

Proof Construct an LKF candidate as

$V(t)=V_1(t)+V_2(t)+V_3(t)(10)$

with

$\begin{array}{ll}\hfill V_1(t)=& {\eta }_1^T(t)S_1(t){\eta }_1(t)+{\eta }_2^T(t)S_2(t){\eta }_2(t),\hfill \\ \hfill V_2(t)=& {\int }_{t-h_t}^t{\eta }_3^T(t,s)Q_1{\eta }_3(t,s)ds+{\int }_{t-h}^{t-h_t}{\eta }_4^T(t,s)Q_2{\eta }_4(t,s)ds\hfill \\ \hfill V_3(t)=& h{\int }_{t-h}^{t-h_t}(h-t+s){\dot{x}}^T(s)R_1\dot{x}(s)ds+h{\int }_{t-h_t}^t(h-t+s){\dot{x}}^T(s)R_2\dot{x}(s)ds,\hfill \end{array}$

where S₁(t) = h_tS₁₁ + S₁₂ and $S_2(t)={\bar{h}}_t{S}_{21}+S_{22}$.Calculating the derivative of V(t), we can obtain the following formulas

$\begin{array}{ll}\hfill {\dot{V}}_1(t)=& 2{\dot{\eta }}_1^T(t)S_1(t){\eta }_1(t)+{\eta }_1^T(t){\dot{S}}_1(t){\eta }_1(t)\hfill \\ \hfill & +2{\dot{\eta }}_2^T(t)S_2(t){\eta }_2(t)+{\eta }_2^T(t){\dot{S}}_2(t){\eta }_2(t)\hfill \\ \hfill =& 2{\xi }^T(t){\mathrm{\Delta }}_{13}^T(h_t{S}_{11}+S_{12})({\mathrm{\Delta }}_{11}+h_t{\mathrm{\Delta }}_{12})\xi (t)\hfill \\ \hfill & +{\xi }^T(t){({\mathrm{\Delta }}_{11}+h_t{\mathrm{\Delta }}_{12})}^T{\dot{h}}_t{S}_{11}({\mathrm{\Delta }}_{11}+h_t{\mathrm{\Delta }}_{12})\xi (t)\hfill \\ \hfill & +2{\xi }^T(t){\mathrm{\Delta }}_{23}^T({\bar{h}}_t{S}_{21}+S_{22})({\mathrm{\Delta }}_{21}+h_t{\mathrm{\Delta }}_{22})\xi (t)\hfill \\ \hfill & -{\xi }^T(t){({\mathrm{\Delta }}_{21}+h_t{\mathrm{\Delta }}_{22})}^T{\dot{h}}_t{S}_{21}({\mathrm{\Delta }}_{21}+h_t{\mathrm{\Delta }}_{22})\xi (t),\hfill \end{array}(11)$

$\begin{array}{ll}\hfill {\dot{V}}_2(t)=& {\eta }_1^T(t,t)Q_1{\eta }_1(t,t)-{\eta }_2^T(t,t-h_1)Q_2{\eta }_2(t,t-h_1)\hfill \\ \hfill & -h_{1d}{\eta }_1^T(t,t-h_t)Q_1{\eta }_1(t,t-h_t)\hfill \\ \hfill & +h_{1d}{\eta }_2^T(t,t-h_t)Q_2{\eta }_2(t,t-h_t)\hfill \\ \hfill & +2{\int }_{t-h_t}^t{\eta }_1^T(t,s)Q_1\frac{\partial }{\partial t}{\eta }_1(t,s)ds\hfill \\ \hfill & +2{\int }_{t-h}^{t-h_t}{\eta }_2^T(t,s)Q_2\frac{\partial }{\partial t}{\eta }_2(t,s)ds\hfill \\ \hfill =& {\xi }^T(t)\left[{({\mathrm{\Delta }}_{31}+h_t{\mathrm{\Delta }}_{32})}^T{Q}_1({\mathrm{\Delta }}_{31}+h_t{\mathrm{\Delta }}_{32})\right.\hfill \\ \hfill & \left.-{({\mathrm{\Delta }}_{41}+h_t{\mathrm{\Delta }}_{42})}^T{Q}_2({\mathrm{\Delta }}_{41}+h_t{\mathrm{\Delta }}_{42})\right]\xi (t)\hfill \\ \hfill & -h_{1d}{\xi }^T(t)\left[{({\mathrm{\Delta }}_{33}+h_t{\mathrm{\Delta }}_{34})}^T{Q}_1({\mathrm{\Delta }}_{33}+h_t{\mathrm{\Delta }}_{34})\right.\hfill \\ \hfill & \left.-{({\mathrm{\Delta }}_{43}+h_t{\mathrm{\Delta }}_{44})}^T{Q}_2({\mathrm{\Delta }}_{43}+h_t{\mathrm{\Delta }}_{44})\right]\xi (t)\hfill \\ \hfill & +2{\xi }^T(t)\left[{({\mathrm{\Delta }}_{10}+h_t{\mathrm{\Delta }}_{11}+h_t^2{\mathrm{\Delta }}_{12})}^T{Q}_1{\mathrm{\Lambda }}_1\right.\hfill \\ \hfill & \left.+{({\mathrm{\Lambda }}_{20}+h_t{\mathrm{\Lambda }}_{21}+h_t^2{\mathrm{\Lambda }}_{22})}^T{Q}_2{\mathrm{\Lambda }}_2\right]\xi (t),\hfill \end{array}(12)$

$\begin{array}{ll}\hfill {\dot{V}}_3(t)=& h^2{\dot{x}}^T(t)R_2\dot{x}(t)+h{h}_d{\bar{h}}_t{\dot{x}}^T(t-h_t)(R_1-R_2)\dot{x}(t-h_t)\hfill \\ \hfill & -h\left({\int }_{t-h}^{t-h_t}{\dot{x}}^T(s)R_1\dot{x}(s)ds+{\int }_{t-h_t}^t{\dot{x}}^T(s)R_2\dot{x}(s)ds\right).\hfill \end{array}(13)$

According to R_i > 0, (i = 1, 2), letting $\beta =\frac{h_t}{h}$, it follows from Lemmas 1 and 2 that

$\begin{array}{ll}\hfill -h\left({\int }_{t-h}^{t-h_t}{\dot{x}}^T(s)R_1\dot{x}(s)ds\right.& \left.+{\int }_{t-h_t}^t{\dot{x}}^T(s)R_2\dot{x}(s)ds\right)\hfill \\ \hfill \le & -\frac{1}{\beta }{\xi }^T(t){\Gamma }_1^T{\bar{R}}_1{\Gamma }_1\xi (t)-\frac{1}{1-\beta }{\xi }^T(t){\Gamma }_2^T{\bar{R}}_2{\Gamma }_2\xi (t)\hfill \\ \hfill \le & -{\xi }^T(t)\left[{\Gamma }_1^T({\bar{R}}_1+\beta X_1){\Gamma }_1+2{\Gamma }_1^T[(1-\beta )Y_1+\beta Y_2]{\Gamma }_2\right.\hfill \\ \hfill & \left.+{\Gamma }_2^T[{\bar{R}}_2+(1-\beta )X_2]{\Gamma }_2\right]\xi (t).\hfill \end{array}$

For an appropriately matrix $U\in {\mathbb{R}}^{n\times n}$, $\chi =[1\cdots 1]\in {\mathbb{R}}^n$, ɛ_i > 0, (i = 1, 2, 3), we can get

$\begin{array}{ll}\hfill 0=& 2\left[x^T(t)x^T(t-h_t){\dot{x}}^T(t){\omega }^T(t)\right]\text{col}\{U,{\epsilon }_{1}U,{\epsilon }_{2}U,{\epsilon }_3\chi U\}\times \hfill \\ \hfill & \left[Ax(t)+BKCx(t-h_t)+F\omega (t)-\dot{x}(t)\right]=2{\xi }^T(t){\mathrm{\Delta }}_0^T\{U\}{\mathrm{\Pi }}_0\xi (t).\hfill \end{array}(15)$

Finally, from the above derivation (11)–(15) and definition 1, we have

$\begin{array}{ll}\hfill \mathrm{\Xi }=& \dot{V}(t)+y^T(t)y(t)-{\gamma }^2{\omega }^T(t)\omega (t)\hfill \\ \hfill \le & {\xi }^T(t)\left[{\mathrm{\Omega }}_0({\dot{h}}_t)+h_t{\mathrm{\Omega }}_1({\dot{h}}_t)+h_t^2{\mathrm{\Omega }}_2({\dot{h}}_t)\right]\xi (t).\hfill \end{array}(16)$

According to Lemma 3, the LMI (8) implies that Ξ < 0. Due to 0 < t < ∞, associating with (5), it has

$V(\infty )-V(0)+{\int }_0^{\infty }{y}^T(s)y(s)ds-{\gamma }^2{\int }_0^{\infty }{\omega }^T(s)\omega (s)ds<0.(17)$

Since V(∞) > 0, V(0) ≡ 0, then

${\int }_0^{\infty }{y}^T(s)y(s)ds-{\gamma }^2{\int }_0^{\infty }{\omega }^T(s)\omega (s)ds\le 0,(18)$

which can guarantee that system (4) meets the H_∞ performance index. This completes the proof.

3.2 Optimization of the Controller Gain

Obviously, the matrix inequalities in Theorem 3.1 are LMIs, which can be easily solved by the MATLAB LMI-Toolbox. That is, for a given H_∞ performance index γ, the acquisition of the controller gain K can be processed simply by the convex optimization algorithm described as follows:

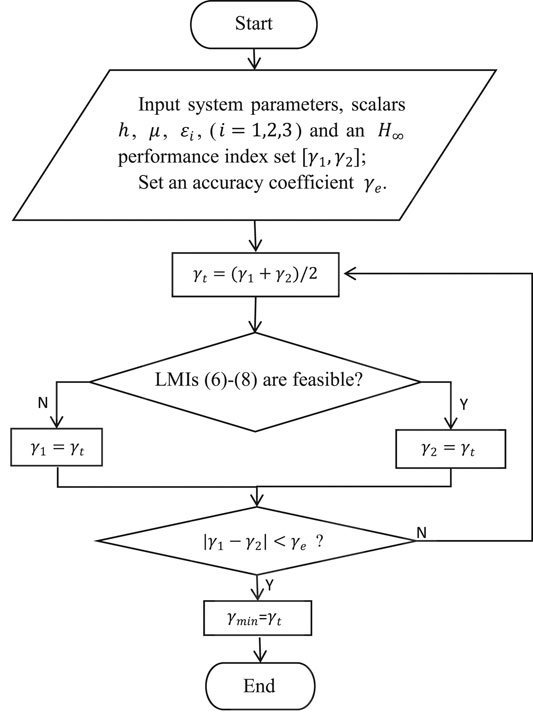
For a given H_∞ performance index set [γ₁, γ₂], the controller gain K can be optimized via the binary search technique shown in Figure 2. Algorithm 2 is used to further illustrate the method.

FIGURE 2

FIGURE 2. Binary search optimization for solving optimal performance index.

Optimization of the Controller Gain.

Input: System parameters, scalars h, μ, ɛ_i, (i = 1, 2, 3), H_∞ performance index set [γ₁, γ₂] and an accuracy coefficient γ_e.

Output: The controller gain K.

1:  Construct LMIs (6)–(8);

2:  Set γ_t = γ₂, Count = 0;

3:  Run the LMI solver to solve the LMIs (6)–(8);

4:  if LMIs (6)–8) are feasible, then proceed to the step 7;

5:  else

6:  if Count = 0, then cannot find a suitable solution,

end algorithm;

else go to step 8;

end if

end if

7:  Set Count = 1 and solve the controller gain K by using

8:  γ₁ = γ_t;

9:  if |γ₁ − γ₂| < γ_e, then go to step 12;

10:  else γ_t = |γ₁ + γ₂|/2, and reverse back to step 3;

11:  end if

12:  Return K.

3.3 Delay-Dependent Stability Criterion for One-Area System

Remark 1 When dealing with unknown external load disturbances in power systems, it can be modeled as a nonlinear perturbation in the current and delayed state vectors (Ramakrishnan and Ray, 2015):

$Fw(t)=g(x(t),x(t-h(t)))(19)$

meets the following condition

$\Vert g(\cdot )\Vert \le \epsilon \Vert x(t)\Vert +\theta \Vert x(t-h(t))\Vert ,(20)$

where ɛ and θ are known non-negative scalars. A more generalized form of the condition is adopted, as follows:

$g^T(\cdot )g(\cdot )\le {\epsilon }^2{x}^T(t)M^{T}Mx(t)+{\theta }^2{x}^T(t-h(t))N^{T}Nx(t-h(t)),(21)$

where M and N are known constant matrices with appropriate dimensions. The non-negative scalars ɛ, θ and matrices M, N can be used to quantify the impact of load disturbances on power systems.

Corollary 1 Given positive scalars h, μ, ɛ, θ and λ system (4) is asymptotically stable, if there exist positive definite matrices $S_{i2},Q_i\in {\mathbb{R}}^{3n\times 3n}$, $R_i\in {\mathbb{R}}^{n\times n}$, ${\mathcal{D}}_i,{\mathcal{G}}_i\in {\mathbb{R}}^{11n\times 11n}$, symmetric matrices $S_{i1},X_i\in {\mathbb{R}}^{3n\times 3n}$, any matrices $Y_i\in {\mathbb{R}}^{3n\times 3n}$, (i = 1, 2; j = 1, 2, 3), $\tilde{U}\in {\mathbb{R}}^{4n\times n}$, such that LMIs (6), (7) and the following LMIs hold for ${\dot{h}}_t\triangleq {\mu }_i\in \{-\mu ,\mu \}$.

$\left[\begin{array}{cc}\hfill {\tilde{\mathrm{\Omega }}}_{10}({\mu }_i)\hfill & \hfill \frac{1}{2}{\mathrm{\Omega }}_{11}({\mu }_i)\hfill \\ \hfill *\hfill & \hfill {\mathrm{\Omega }}_{21}({\mu }_i)\hfill \end{array}\right]-{\left[\begin{array}{c}\hfill \mathcal{C}\hfill \\ \hfill \mathcal{J}\hfill \end{array}\right]}^T\left[\begin{array}{cc}\hfill -{\mathcal{D}}_i\hfill & \hfill {\mathcal{G}}_i\hfill \\ \hfill \ast \hfill & \hfill {\mathcal{D}}_i\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathcal{C}\hfill \\ \hfill \mathcal{J}\hfill \end{array}\right]<0(22)$

with

$\begin{array}{ll}\hfill {\tilde{\mathrm{\Omega }}}_0({\mu }_i)=& \text{Sym}\left\{{\mathrm{\Delta }}_{13}^T{S}_{12}{\mathrm{\Delta }}_{11}+{\mathrm{\Delta }}_{23}^T(h{S}_{21}+S_{22}){\mathrm{\Delta }}_{21}+{\mathrm{\Lambda }}_{10}^T{Q}_1{\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_{20}^T{Q}_2{\mathrm{\Lambda }}_2\right\}+{\dot{h}}_t{\mathrm{\Delta }}_{11}^T{S}_{11}{\mathrm{\Delta }}_{11}\hfill \\ \hfill & -{\dot{h}}_t{\mathrm{\Delta }}_{21}^T{S}_{21}{\mathrm{\Delta }}_{21}+{\mathrm{\Delta }}_{31}^T{Q}_1{\mathrm{\Delta }}_{31}-{\mathrm{\Delta }}_{41}^T{Q}_2{\mathrm{\Delta }}_{41}-h_d{\mathrm{\Delta }}_{33}^T{Q}_1{\mathrm{\Delta }}_{33}+h_d{\mathrm{\Delta }}_{43}^T{Q}_2{\mathrm{\Delta }}_{43}\hfill \\ \hfill & +e_4^T(h^2{R}_2)e_4+h^2{h}_d{e}_5^T(R_1-R_2)e_5+{\Gamma }_1^T{\bar{R}}_1{\Gamma }_1+{\Gamma }_2^T({\bar{R}}_2+X_2){\Gamma }_2\hfill \\ \hfill & +\text{Sym}\{{\Gamma }_1^T{Y}_1{\Gamma }_2\}+\text{Sym}\{{\mathrm{\Delta }}_0^T\tilde{U}{\mathrm{\Pi }}_0\}+\lambda {\theta }^2{e}_1^T{N}^{T}N{e}_1+\lambda {\epsilon }^2{e}_2^T\lambda {\epsilon }^2{M}^{T}M{e}_2-e_{11}^T\lambda I{e}_{11}\hfill \end{array}$

and other symbols see Theorem 1.

Proof The proof process of Corollary 1 is similar to Theorem 1, so it is omitted here.

Remark 2 Compared with the literature (Ramakrishnan and Ray, 2015; Yang et al., 2017; Jiao et al., 2021), the results in this paper reduce the conservatism via the augmented LKF application. The LKF proposed in this paper contains more information of the time-varying delay and the coupling information between the state variables and the delay than the literature (Ramakrishnan and Ray, 2015; Yang et al., 2017; Jiao et al., 2021), which reduces the conservatism caused by the LKF structure.

4 Case Studies

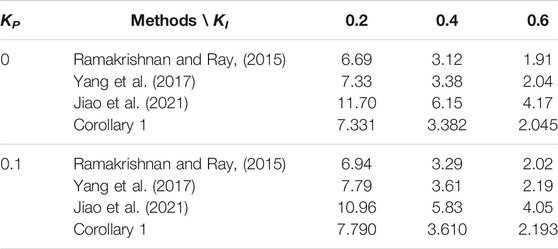
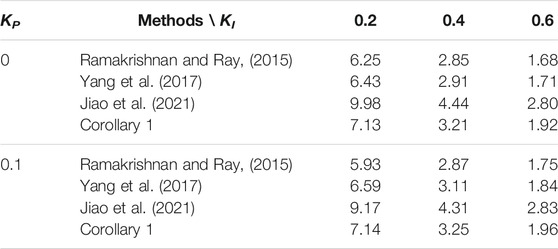
In this section, firstly, the effectiveness of the delay-dependent stability criterion for one-area LFC system proposed in this paper is shown. For given different K_P and K_I values, the maximum allowable time-delay upper bound values (MAUB) can be obtained by solving the LMIs in Corollary 1 via Matlab LMI-Toolbox. The LFC system parameters are described as Table 2 (Jiang et al., 2012), one-area LFC systems will be discussed and comparatively analyzed in the following subsections.

TABLE 2

TABLE 2. Parameters of one-area LFC system.

4.1 Conservativeness Comparison

In order to compare with the existing results, Table 3 and Table 4 give the MAUB values of the case of given K_P and K_I values, ɛ = 0, θ = 0, M = N = 0.1I₄, $|\dot{h}(t)|\le 0$ or $|\dot{h}(t)|\le 0.9$. From these tables, we can observe the results of Corollary 1 are less conservative than those of (Ramakrishnan and Ray, 2015; Yang et al., 2017). And the MAUB increases as K_P increases whereas for a fixed K_I value, and the MAUB decreases as K_I increases whereas for a fixed K_P value.

TABLE 3

TABLE 3. MAUBs h for μ = 0 under one-area LFC system.

TABLE 4

TABLE 4. MAUBs h for μ = 0.9 under one-area LFC system.

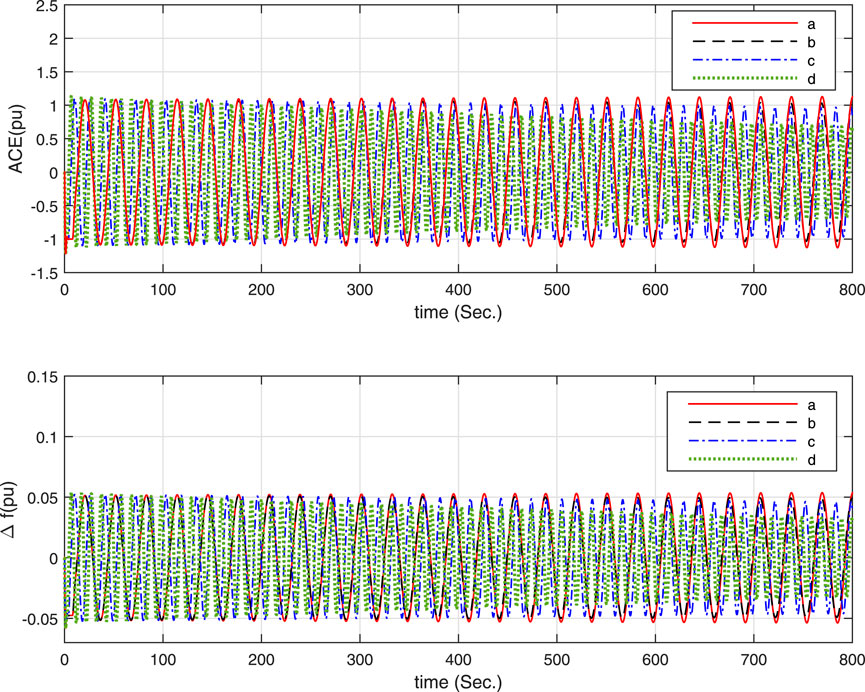
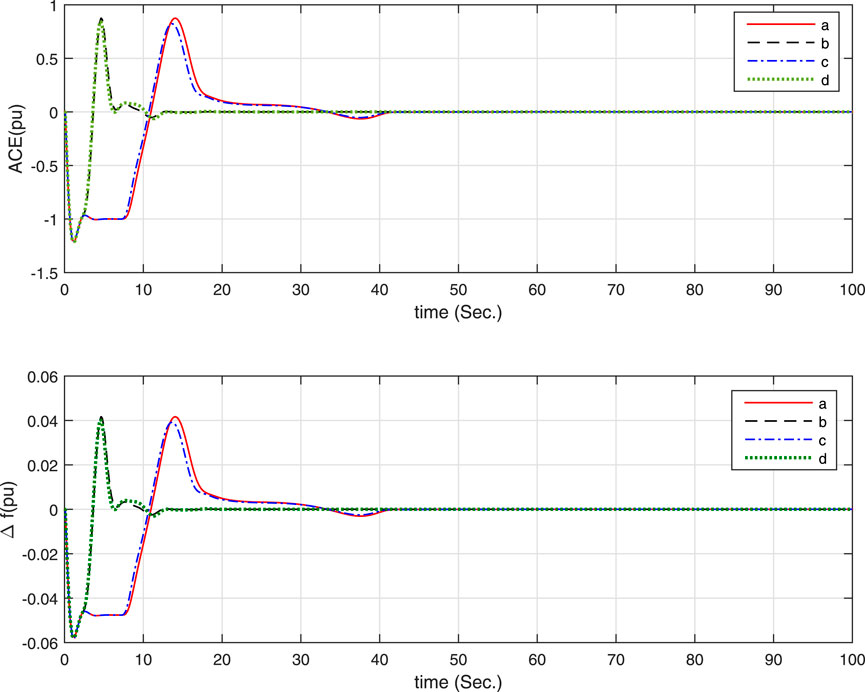
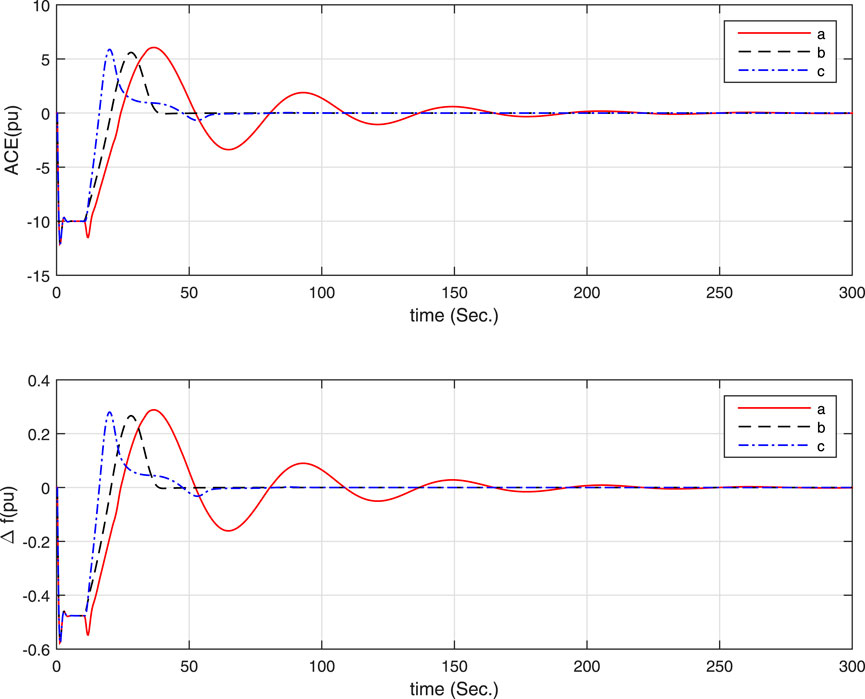
Simple simulations are carried out under an increase step load of 0.1 pu happening at 1s and the following assumptions. The simulation results are shown in Figures 3, 4, in which the LFC has achieve its objective and the control system is stable. In addition, according to the red curve a of Figure 3, the LFC system closes to critical stability with h(t) = 7.8, K_P = 0.1 and K_I = 0.2, while Corollary 1 in this paper obtains the MAUB h = 7.790. Thus, the delay-dependent stability criterion proposed in this paper is effective in estimating the upper bound of the maximum allowable time delay.

• For Figure 3, different K_I and fixed K_P = 0.1 and μ = 0:

a. K_I = 0.2, h(t) = 7.8;

b. K_I = 0.2, h(t) = 7.79;

c. K_I = 0.4, h(t) = 3.61;

d. K_I = 0.6, h(t) = 2.193;

• For Figure 4, different K_P, K_I fixed μ = 0.9:

a. K_P = 0, K_I = 0.2, $h(t)=\frac{7.13}{2}sin\left(\frac{1.8}{7.13}t\right)+\frac{7.13}{2}$;

b. K_P = 0, K_P = 0.6, $h(t)=\frac{1.92}{2}sin\left(\frac{1.8}{1.92}t\right)+\frac{1.92}{2}$;

c. K_P = 0.1, K_I = 0.2, $h(t)=\frac{7.14}{2}sin\left(\frac{1.8}{7.14}t\right)+\frac{7.14}{2}$;

d. K_P = 0.1, K_I = 0.6, $h(t)=\frac{1.96}{2}sin\left(\frac{1.8}{1.96}t\right)+\frac{1.96}{2}$.

FIGURE 3

FIGURE 3. Frequency deviation and control error responses of one-area LFC scheme under μ = 0.

FIGURE 4

FIGURE 4. Frequency deviation and control error responses of one-area LFC scheme under μ = 0.9.

4.2 Optimization and H_∞ Performance Discussion

In this subsection, much attention is focused on the following two aspects.

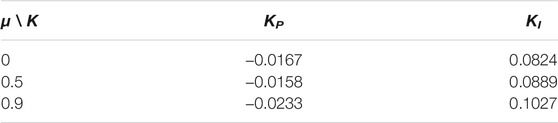
1) Design of the Controller: the MAUB is preset as 10 s and h(t) is considered as constant (μ = 0) and time-varying delay (μ = 0.9), respectively. For a given H_∞ performance index γ = 0.4, the controller gains can be obtained in Table 5 by referring to the process given in Algorithm 1;

2) Optimization of the Controller: the MAUB is preset as 10 s and h(t) is considered as constant (μ = 0) and time-varying delay (μ = 0.9), respectively. For a given H_∞ performance index set [0, 100] and γ_e = 0.5, the controller gains can be obtained in Table 6 by referring to the process given in Algorithm 2.

TABLE 5

TABLE 5. Controller gains for h = 10 under different μ.

TABLE 6

TABLE 6. Controller gains for h = 10 under different μ.

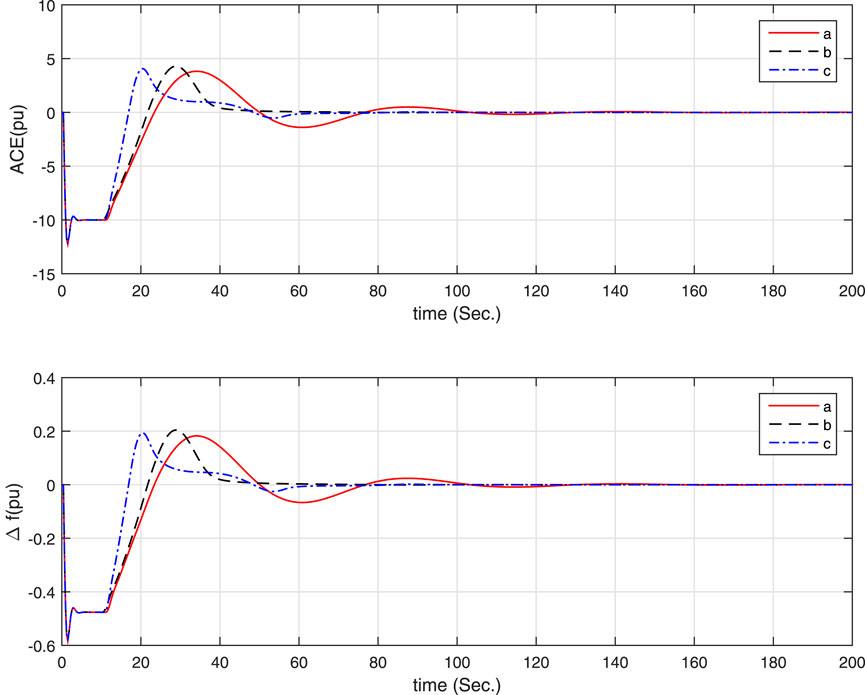
Simple simulations are carried out under an increase step load of 0.1 pu happening at 1s and the following assumptions. The simulation results are shown in Figures 5, 6, in which the LFC has achieve its objective. This scenario suggests that, the use of optimized controller has the merit of improving the performance of the LFC system in terms of its transient response characteristics as well as disturbance rejection capabilities over the tuned local PI controllers acting alone in the system.

• For Figure 5, h = 10 and γ = 0.4:

a. K_P = − 0.0167, K_P = 0.0824, h(t) = 8;

b. K_P = − 0.0158, K_P = 0.0889, $h(t)=\frac{10}{2}sin\left(\frac{1}{10}t\right)+\frac{10}{2}$;

c. K_P = − 0.0233, K_P = 0.1027, $h(t)=\frac{10}{2}sin\left(\frac{1.8}{10}t\right)+\frac{10}{2}$;

• For Figure 6, h = 10:

a. K_P = − 0.0175, K_P = 0.0857, h(t) = 8, γ = 0.3;

b. K_P = − 0.0194, K_P = 0.1008, $h(t)=\frac{10}{2}sin\left(\frac{1}{10}t\right)+\frac{10}{2}$, γ = 0.37;

c. K_P = − 0.0237, K_P = 0.1191, $h(t)=\frac{10}{2}sin\left(\frac{1.8}{10}t\right)+\frac{10}{2}$, γ = 0.37.

FIGURE 5

FIGURE 5. Frequency deviation and control error responses of one-area LFC scheme under γ = 0.4.

FIGURE 6

FIGURE 6. Frequency deviation and control error responses of one-area LFC scheme under γ = 0.37.

5 Conclusion

This paper focus on optimization and H_∞ performance problem for LFC of power systems with time-varying delays. For the one-area LFC systems with single communication delays, stability criteria are obtained via Lyapunov stability theory application. Firstly, the one-area LFC system is described as linear systems with time-varying delays and load disturbances; Secondly, a modified LKF is constructed, which contains more coupling information between time-varying delays and state variables than some previous published results to further reduce the conservativeness of the stability criterion; Thirdly, an unique delay-dependent PI controller and an optimized PI controller are designed for a specified H_∞ performance index and set, respectively. Finally, the effectiveness of the proposed method is illustrated by comparison and discussion in numerical examples, which shows that the use of optimized controller has the merit of improving the performance of the LFC system in terms of its transient response characteristics as well as disturbance rejection capabilities over the tuned local PI controllers acting alone in the system. However, the improvement of stability results is in the cost of increasing computational complexity. The derivation method of the stability criterion presented in this paper can be extended to multi-area LFC system, which is one of our further main topics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, methodology, KS and WD; data curation, software, YL; writingoriginal draft, KS; writingreview and editing, JC. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported partly by the Guangdong higher education innovation strong school project under Grant no. 2018KQNCX296, the Technology Research Plan of Guangzhou under Grant no. 202002030230, the Industry University Research Cooperation Project of Jiangsu Province under Grant no. BY2020649, the NSF of Yancheng Biological Engineering Higher Vocational and Technical School under Grant no. x202104 and the Yellow Sea Rookie of Yancheng Institute of Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.762480/full#supplementary-material

References

Ali, D., Mohammad, M., Zeinolabedin, M., and Lieven, V. (2020). A Novel Technique for Load Frequency Control of Multi-Area Power Systems. Energies 13, 2125. doi:10.3390/en13092125

CrossRef Full Text | Google Scholar

Baykov, D. V., Gulyaev, I. V., Inshakov, A. P., and Teplukhov, D. Y. (2019). Simulation Modeling of an Induction Motor Drive Controlled by an Array Frequency Converter. Russ. Electr. Engin. 90, 485–490. doi:10.3103/s1068371219070034

CrossRef Full Text | Google Scholar

Bevrani, H. (2014). Robust Power System Frequency Control. Springer.

Google Scholar

Chen, B.-Y., Shangguan, X.-C., Jin, L., and Li, D.-Y. (2020). An Improved Stability Criterion for Load Frequency Control of Power Systems with Time-Varying Delays. Energies 13, 2101. doi:10.3390/en13082101

CrossRef Full Text | Google Scholar

de A. F. Mello, F. R., Apostolopoulou, D., and Alonso, E. (2020). Cost Efficient Distributed Load Frequency Control in Power Systems. IFAC-PapersOnLine 53, 8037–8042. doi:10.1016/j.ifacol.2020.12.2236

CrossRef Full Text | Google Scholar

del Giudice, D., Brambilla, A., Grillo, S., and Bizzarri, F. (2021). Effects of Inertia, Load Damping and Dead-Bands on Frequency Histograms and Frequency Control of Power Systems. Int. J. Electr. Power Energ. Syst. 129, 106842. doi:10.1016/j.ijepes.2021.106842

CrossRef Full Text | Google Scholar

Dey, R., Ghosh, S., Ray, G., and Rakshit, A. (2012). H∞ Load Frequency Control of Interconnected Power Systems with Communication Delays. Int. J. Electr. Power Energ. Syst. 42, 672–684. doi:10.1016/j.ijepes.2012.03.035

CrossRef Full Text | Google Scholar

Duan, W., Du, B., Li, Y., Shen, C., Zhu, X., Li, X., et al. (2018). Improved Sufficient LMI Conditions for the Robust Stability of Time-delayed Neutral-type Lur'e Systems. Int. J. Control. Autom. Syst. 16, 2343–2353. doi:10.1007/s12555-018-0138-2

CrossRef Full Text | Google Scholar

Duan, W., Fu, X., and Liu, Z. (2017). “Improved robust stability criteria for time-delay Lur’e system. Int. J. Control Automation Syst. 19, 1–12. doi:10.1002/asjc.1339

CrossRef Full Text | Google Scholar

Duan, W., Fu, X., and Yang, X. (2016). “Further results on the robust stability for neutral-type Lur’e system with mixed delays and sector-bounded nonlinearities. Int. J. Control Automation Syst. 14, 1–9. doi:10.1007/s12555-014-0547-9

CrossRef Full Text | Google Scholar

Duan, W., Li, Y., and Chen, J. (2020a). An Enhanced Stability Criterion for Linear Time-Delayed Systems via New Lyapunov-Krasovskii Functionals. Adv. Difference Equations 2020, 37–57. doi:10.1186/s13662-019-2439-z

CrossRef Full Text | Google Scholar

Duan, W., Li, Y., and Chen, J. (2019). Further Stability Analysis for Time-Delayed Neural Networks Based on an Augmented Lyapunov Functional. IEEE Access 7, 104655–104666. doi:10.1109/access.2019.2931714

CrossRef Full Text | Google Scholar

Duan, W., Li, Y., and Chen, J. (2019). New results on stability analysis of uncertain neutral-type Lur’e systems derived from a modified Lyapunov-Krasovskii functional. Complexity 2019, 1–20. doi:10.1155/2019/1706264

CrossRef Full Text | Google Scholar

Duan, W., Li, Y., Sun, Y., Chen, J., and Yang, X. (2020). Enhanced master-slave synchronization criteria for chaotic Lur'e systems based on time-delayed feedback control. Mathematics Comput. Simulation 177, 276–294. doi:10.1016/j.matcom.2020.04.010

CrossRef Full Text | Google Scholar

Feng, W., Luo, F., Duan, W., Li, Y., and Chen, J. (2020). An Improved Stability Criterion for Linear Time-Varying Delay Systems. Automatika 61, 229–237. doi:10.1080/00051144.2019.1706885

CrossRef Full Text | Google Scholar

Fúlvia, S., de, O., and Fernando, O. (2020). Further Refinements in Stability Conditions for Time-Varying Delay Systems. Appl. Maths. Comput. 369, 124866.

Google Scholar

Gholami, Y. (2021). Existence and Global Asymptotic Stability Criteria for Nonlinear Neutral-type Neural Networks Involving Multiple Time Delays Using a Quadratic-Integral Lyapunov Functional. Adv. Differ. Equ 2021, 112. doi:10.1186/s13662-021-03274-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, K. (2000). “An Integral Inequality in the Stability Problem of Time-Delay Systems,” in Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, December 12–15, 2000.

Google Scholar

Hua, C., Qiu, Y., Wang, Y., and Guan, X. (2021). An Augmented Delays-dependent Region Partitioning Approach for Recurrent Neural Networks with Multiple Time-Varying Delays. Neurocomputing 423, 248–254. doi:10.1016/j.neucom.2020.10.047

CrossRef Full Text | Google Scholar

Jiang, L., Yao, W., Wu, Q. H., Wen, J. Y., and Cheng, S. J. (2012). Delay-dependent Stability for Load Frequency Control with Constant and Time-Varying Delays. IEEE Trans. Power Syst. 27, 932–941. doi:10.1109/tpwrs.2011.2172821

CrossRef Full Text | Google Scholar

Jiao, S., Xia, J., Wang, Z., Chen, X., Wang, J., and Shen, H. (2021). An Improved Result on Stability Analysis of Delayed Load Frequency Control Power Systems. Int. J. Control. Autom. Syst. 19, 1633–1639. doi:10.1007/s12555-019-1063-8

CrossRef Full Text | Google Scholar

Khalil, A., and Swee Peng, A. (2018). An Accurate Method for Delay Margin Computation for Power System Stability. Energies 11, 3466. doi:10.3390/en11123466

CrossRef Full Text | Google Scholar

Kwon, N. K., and Lee, S. Y. (2021). An Affine Integral Inequality of an Arbitrary Degree for Stability Analysis of Linear Systems with Time-Varying Delays. IEEE Access 9, 51958–51969. doi:10.1109/access.2021.3070149

CrossRef Full Text | Google Scholar

Ladygin, A. N., Bogachenko, D. D., and Kholin, V. V. (2020). Efficient Control of Induction Motor Current in a Frequency-Controlled Electric Drive. Russ. Electr. Engin. 91, 362–367. doi:10.3103/s106837122006005x

CrossRef Full Text | Google Scholar

Manikandan, S., and Kokil, P. (2020). Stability Analysis of Load Frequency Control System with Constant Communication Delays. IFAC-PapersOnLine 53, 338–343. doi:10.1016/j.ifacol.2020.06.057

CrossRef Full Text | Google Scholar

Ramakrishnan, K., and Ray, G. (2015). Stability Criteria for Nonlinearly Perturbed Load Frequency Systems with Time-Delay. IEEE J. Emerg. Sel. Top. Circuits Syst. 5, 383–392. doi:10.1109/jetcas.2015.2462031

CrossRef Full Text | Google Scholar

Rerkpreedapong, D., Hasanovic, A., and Feliachi, A. (2003). Robust Load Frequency Control Using Genetic Algorithms and Linear Matrix Inequalities. IEEE Trans. Power Syst. 18, 855–861. doi:10.1109/tpwrs.2003.811005

CrossRef Full Text | Google Scholar

Scopus, P., Tian, Y., and Wang, Z. (2020). Stability Analysis for Delayed Neural Networks Based on the Augmented Lyapunov-Krasovskii Functional with Delay-product-type and Multiple Integral Terms. Neurocomputing 410, 295–303.

CrossRef Full Text | Google Scholar

Seuret, A., and Gouaisbaut, F. (2015). Hierarchy of LMI Conditions for the Stability Analysis of Time-Delay Systems. Syst. Control. Lett. 81, 1–7. doi:10.1016/j.sysconle.2015.03.007

CrossRef Full Text | Google Scholar

Shayeghi, H., Jalili, A., and Shayanfar, H. A. (2008). A Robust Mixed H2/H∞ Based LFC of a Deregulated Power System Including SMES. Energ. Convers. Manage. 49, 2656–2668. doi:10.1016/j.enconman.2008.04.006

CrossRef Full Text | Google Scholar

Shen, C., Li, Y., Zhu, X., and Duan, W. (2019). Improved Stability Criteria for Linear Systems with Two Additive Time-Varying Delays via a Novel Lyapunov Functional. J. Comput. Appl. Maths. 363, 312–324.

Google Scholar

Shen, H., Jiao, S., Park, J. H., and Sreeram, V. (2021). An Improved Result on $H_{\infty }$ Load Frequency Control for Power Systems with Time Delays. IEEE Syst. J. 15, 3238–3248. doi:10.1109/JSYST.2020.3014936

CrossRef Full Text | Google Scholar

Shen, H., Xing, M., Huo, S., Wu, Z.-G., and Park, J. H. (2019). Finite-time H∞ Asynchronous State Estimation for Discrete-Time Fuzzy Markov Jump Neural Networks with Uncertain Measurements. Fuzzy Sets Syst. 356, 113–128. doi:10.1016/j.fss.2018.01.017

CrossRef Full Text | Google Scholar

Vrdoljak, K., Perić, N., and Petrović, I. (2010). Sliding Mode Based Load-Frequency Control in Power Systems. Electric Power Syst. Res. 80, 514–527. doi:10.1016/j.epsr.2009.10.026

CrossRef Full Text | Google Scholar

Xu, H.-T., Zhang, C.-K., Jiang, L., and Smith, J. (2017). Stability Analysis of Linear Systems with Two Additive Time-Varying Delays via Delay-product-type Lyapunov Functional. Appl. Math. Model. 45, 955–964. doi:10.1016/j.apm.2017.01.032

CrossRef Full Text | Google Scholar

Yang, F., He, J., and Wang, D. (2018). New Stability Criteria of Delayed Load Frequency Control Systems via Infinite-Series-Based Inequality. IEEE Trans. Ind. Inf. 14, 231–240. doi:10.1109/tii.2017.2751510

CrossRef Full Text | Google Scholar

Yang, F., He, J., and Wang, J. (2017). “Novel Stability Analysis of Delayed LFC Power Systems by Infinite-Series-Based Integral Inequality,” in Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, August 27–30, 2017, 1384–1389. doi:10.1109/ccta.2017.8062652

CrossRef Full Text | Google Scholar

Zhang, C.-K., He, Y., Jiang, L., and Wu, M. (2017). Notes on Stability of Time-Delay Systems: Bounding Inequalities and Augmented Lyapunov-Krasovskii Functionals. IEEE Trans. Automat. Contr. 62, 5331–5336. doi:10.1109/tac.2016.2635381

CrossRef Full Text | Google Scholar

Zhang, X.-M., Han, Q.-L., Seuret, A., and Gouaisbaut, F. (2017). An Improved Reciprocally Convex Inequality and an Augmented Lyapunov-Krasovskii Functional for Stability of Linear Systems with Time-Varying Delay. Automatica 84, 221–226. doi:10.1016/j.automatica.2017.04.048

CrossRef Full Text | Google Scholar

Appendix A

Notations of other symbols and matrices for Theorem 1:

$\begin{array}{ll}\hfill {\mathrm{\Delta }}_0=& \text{col}\{e_1,e_2,e_4,e_{11}\},{\mathrm{\Pi }}_0=A{e}_1+BKC{e}_2+F{e}_{11}-e_4,\hfill \\ \hfill \bar{U}=& \text{col}\{U,{\epsilon }_{1}U,{\epsilon }_{2}U,{\epsilon }_3\chi U\},\hfill \\ \hfill {\mathrm{\Delta }}_{11}=& \text{col}\{e_1,e_2,e_0\},{\mathrm{\Delta }}_{12}=\text{col}\{e_0,e_0,e_9\},{\mathrm{\Delta }}_{13}=\text{col}\{e_4,h_d{e}_2,e_1-h_d{e}_2\},\hfill \\ \hfill {\mathrm{\Delta }}_{21}=& \text{col}\{e_2,e_3,h{e}_7\},{\mathrm{\Delta }}_{22}=\text{col}\{e_0,e_0,-e_7\},{\mathrm{\Delta }}_{23}=\text{col}\{h_d{e}_5,e_6,h_d{e}_2-e_3\},\hfill \\ \hfill {\mathrm{\Delta }}_{31}=& \text{col}\{e_4,e_1,e_1,e_2,e_3,e_0,e_0,h{e}_7\},{\mathrm{\Delta }}_{32}=\text{col}\{e_0,e_0,e_0,e_0,e_0,e_0,e_9,-e_7\},\hfill \\ \hfill {\mathrm{\Delta }}_{33}=& \text{col}\{e_5,e_2,e_1,e_2,e_3,e_0,e_0,h{e}_7\},{\mathrm{\Delta }}_{34}=\text{col}\{e_0,e_0,e_0,e_0,e_0,e_9,e_0,-e_7\},\hfill \\ \hfill {\mathrm{\Delta }}_{41}=& \text{col}\{e_6,e_3,e_1,e_2,e_3,h{e}_7,e_0,e_0\},{\mathrm{\Delta }}_{42}=\text{col}\{e_0,e_0,e_0,e_0,e_0,-e_7,e_9,e_0\},\hfill \\ \hfill {\mathrm{\Delta }}_{43}=& \text{col}\{e_5,e_2,e_1,e_2,e_3,e_0,e_0,h{e}_7\},{\mathrm{\Delta }}_{44}=\text{col}\{e_0,e_0,e_0,e_0,e_0,e_0,e_9,-e_7\},\hfill \\ \hfill {\mathrm{\Lambda }}_{10}=& \text{col}\{e_1-e_2,e_0,e_0,e_0,e_0,e_0,e_0,e_0\},\hfill \\ \hfill {\mathrm{\Lambda }}_{11}=& \text{col}\{e_0,e_9,e_1,e_2,e_3,e_0,e_0,h{e}_7\},\hfill \\ \hfill {\mathrm{\Lambda }}_{12}=& \text{col}\{e_0,e_0,e_0,e_0,e_0,e_9-e_{10},e_{10},-e_7\},\hfill \\ \hfill {\mathrm{\Lambda }}_{20}=& \text{col}\{e_2-e_3,h{e}_7,h{e}_1,h{e}_2,h{e}_3,h^2(e_7-e_8),e_0,h^2{e}_8\},\hfill \\ \hfill {\mathrm{\Lambda }}_{21}=& \text{col}\{e_0,-e_7,-e_1,-e_2,-e_3,-2h(e_7-e_8),h{e}_9,-2h{e}_8\},\hfill \\ \hfill {\mathrm{\Lambda }}_{22}=& \text{col}\{e_0,e_0,e_0,e_0,e_0,e_8-e_7,-e_9,e_8\},\hfill \\ \hfill {\mathrm{\Lambda }}_1=& \text{col}\{e_0,e_0,e_4,h_d{e}_5,e_6,e_1,-h_d{e}_2,h_d{e}_2-e_3\},\hfill \\ \hfill {\mathrm{\Lambda }}_2=& \text{col}\{e_0,e_0,e_4,h_d{e}_5,e_6,h_d{e}_2,e_1-h_d{e}_2,-e_3\},\hfill \\ \hfill {\Gamma }_1=& \text{col}\{e_2-e_3,e_2+e_3-2e_7,e_2-e_3+6e_7+12e_8\},\hfill \\ \hfill {\Gamma }_2=& \text{col}\{e_1-e_2,e_1+e_2-2e_9,e_1-e_2+6e_9+12e_{10}\},\hfill \\ \hfill \mathcal{C}=& \left[\frac{h}{2}I0\right],\mathcal{J}=\left[\frac{h}{2}I-I\right],{\bar{R}}_i=\text{diag}\{R_i,3R_i,5R_i\},K_0=UBK,\hfill \\ \hfill {\mathrm{\Omega }}_0({\mu }_i)=& \text{Sym}\left\{{\mathrm{\Delta }}_{13}^T{S}_{12}{\mathrm{\Delta }}_{11}+{\mathrm{\Delta }}_{23}^T(h{S}_{21}+S_{22}){\mathrm{\Delta }}_{21}+{\mathrm{\Lambda }}_{10}^T{Q}_1{\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_{20}^T{Q}_2{\mathrm{\Lambda }}_2\right\}+{\dot{h}}_t{\mathrm{\Delta }}_{11}^T{S}_{11}{\mathrm{\Delta }}_{11}\hfill \\ \hfill & -{\dot{h}}_t{\mathrm{\Delta }}_{21}^T{S}_{21}{\mathrm{\Delta }}_{21}+{\mathrm{\Delta }}_{31}^T{Q}_1{\mathrm{\Delta }}_{31}-{\mathrm{\Delta }}_{41}^T{Q}_2{\mathrm{\Delta }}_{41}-h_d{\mathrm{\Delta }}_{33}^T{Q}_1{\mathrm{\Delta }}_{33}+h_d{\mathrm{\Delta }}_{43}^T{Q}_2{\mathrm{\Delta }}_{43}\hfill \\ \hfill & +e_4^T(h^2{R}_2)e_4+h^2{h}_d{e}_5^T(R_1-R_2)e_5+{\Gamma }_1^T{\bar{R}}_1{\Gamma }_1+{\Gamma }_2^T({\bar{R}}_2+X_2){\Gamma }_2\hfill \\ \hfill & +\text{Sym}\{{\Gamma }_1^T{Y}_1{\Gamma }_2\}+\text{Sym}\{{\mathrm{\Delta }}_0^T\bar{U}{\mathrm{\Pi }}_0\}+e_1^T{C}^{T}C{e}_1-e_{11}^T{\gamma }^{2}I{e}_{11},\hfill \\ \hfill {\mathrm{\Omega }}_1({\mu }_i)=& \text{Sym}\left\{{\mathrm{\Delta }}_{13}^T{S}_{11}{\mathrm{\Delta }}_{11}+{\mathrm{\Delta }}_{13}^T{S}_{12}{\mathrm{\Delta }}_{12}+{\dot{h}}_t{\mathrm{\Delta }}_{11}^T{S}_{11}{\mathrm{\Delta }}_{12}+{\mathrm{\Delta }}_{23}^T(h{S}_{21}+S_{22}){\mathrm{\Delta }}_{22}\right.\hfill \\ \hfill & \left.-{\mathrm{\Delta }}_{23}^T{S}_{21}{\mathrm{\Delta }}_{21}-{\dot{h}}_t{\mathrm{\Delta }}_{22}^T{S}_{21}{\mathrm{\Delta }}_{21}+{\mathrm{\Lambda }}_{11}^T{Q}_1{\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_{21}^T{Q}_2{\mathrm{\Lambda }}_2\right\}+{\mathrm{\Delta }}_{32}^T{Q}_1{\mathrm{\Delta }}_{32}\hfill \\ \hfill & -{\mathrm{\Delta }}_{42}^T{Q}_2{\mathrm{\Delta }}_{42}-{\dot{h}}_t{\mathrm{\Delta }}_{34}^T{Q}_1{\mathrm{\Delta }}_{34}+h_d{\mathrm{\Delta }}_{44}^T{Q}_2{\mathrm{\Delta }}_{44}-h{h}_d{e}_5^T(R_1-R_2)e_5\hfill \\ \hfill & -\frac{1}{h}[{\Gamma }_1^T{X}_1{\Gamma }_1-{\Gamma }_2^T{X}_2{\Gamma }_2]+\frac{1}{h}\text{Sym}\{{\Gamma }_1^T(Y_1-Y_2){\Gamma }_2\},\hfill \\ \hfill {\mathrm{\Omega }}_2({\mu }_i)=& \text{Sym}\left\{{\mathrm{\Delta }}_{13}^T{S}_{11}{\mathrm{\Delta }}_{12}-{\mathrm{\Delta }}_{23}^T{S}_{21}{\mathrm{\Delta }}_{22}+{\mathrm{\Lambda }}_{12}^T{Q}_1{\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_{22}^T{Q}_2{\mathrm{\Lambda }}_2\right\}\hfill \\ \hfill & +{\dot{h}}_t{\mathrm{\Delta }}_{12}^T{S}_{11}{\mathrm{\Delta }}_{12}-{\dot{h}}_t{\mathrm{\Delta }}_{22}^T{S}_{21}{\mathrm{\Delta }}_{22}+{\mathrm{\Delta }}_{32}^T{Q}_1{\mathrm{\Delta }}_{32}\hfill \\ \hfill & -{\mathrm{\Delta }}_{42}^T{Q}_2{\mathrm{\Delta }}_{42}-h_d{\mathrm{\Delta }}_{34}^T{Q}_1{\mathrm{\Delta }}_{34}+h_d{\mathrm{\Delta }}_{44}^T{Q}_2{\mathrm{\Delta }}_{44},\hfill \end{array}$