- School of Materials and Metallurgy, Guizhou University, Guiyang, China
Various reactors with different sizes have been widely used for the production of titanium sponge in the Kroll process. But the further commercialization of the forced heat transfer design of the Kroll reactor is limited by lack of standard parameter to evaluate its convective heat transfer characteristics. This work proposes to evaluate and compare the Kroll reactor with the dimensionless Nusselt number. The results shown that the heat transfer coefficients for both surfaces increase with the volume flow rate of cooling air for each dimensionless temperature, and the heat transfer coefficients of the external surface of the reactor are higher than that of the internal surface of the heater. And new correlations regarding the Nusselt number between the cooling air and the external surface of the reactor or the internal surface of the heater are obtained based on experimental data, while the characteristics of the cooling air, equipment and operation parameters are considered.
Introduction
The Kroll process is the most widely preferred industrial choice in titanium chain (Nakamura et al., 2017; Gao et al., 2018; Roux et al., 2019), even if it was of archaic, costly and energy-intensive (Wang et al., 2018b). Some of the major technological breakthroughs and equipment improvements in respect of titanium sponge production relating to the Kroll process have been achieved in the past decades (Gao et al., 2018), and the production cost has been significantly brought down (Zhang et al., 2016). However, further improvement is limited due to the insufficient theoretical understanding of the titanium sponge production (Wang et al., 2018a; Wang W. et al., 2020). For example, several efforts toward energy conservation were reported in the literature, but their commercial application is limited owning to technical or economic constraints (Wang and Wu, 2017). Currently, it’s necessary to further decrease the energy consumption and improve energy efficiency of the Kroll process (Krauter et al., 2018).
In response to the problems of the titanium sponge production discussed above, we had exploited a waste thermal energy recovery system with forced heat transfer design to enhance the surface heat dissipation of the Kroll reactor (Figure 1A) (Wang et al., 2017a), and to reduce the carbon emission. The result showed that there was a growth rate of about only 5.00% in the heat transfer rate in a vertical annular duct of the Kroll reactor, while the feeding rate of titanium tetrachloride increases significantly of about 9.61%. Therefore, the forced convective heat transfer system as currently designed was hence expected to reduce the electrical power consumption by improving the production efficiency (shorten the production cycle), rather than by recycling waste thermal energy in the subsequent recovery system (Wang et al., 2017b). It is no doubt that the forced convective heat transfer design lowered the cost and improved the energy efficiency. However, the quantification and comparison of the heat transfer characteristics of the Kroll reactor with different sizes is difficult due to the lack of a standard method. For example, one previous work evaluated the heat transfer coefficient only based on the cooling air mass flow rate (Wang et al., 2017a). The result could not be compared with other works which study the Kroll reactor with a different size.

FIGURE 1. System for: (A) enhancing heat transfer and recovering waste thermal energy for the Kroll equipment (Wang et al., 2017b) and (B) the experimental apparatus and measurements.
This works proposes a dimensionless Nusselt number as a general approach for quantifying and comparing the heat transfer characteristics of the vertical annular duct for the different Kroll reactor. And the Nusselt number has not been used for evaluating the heat transfer characteristics of the Kroll reactor in titanium sponge production. The establishment of this standard is expected to push the commercialization of the forced heat transfer design and optimizing the efficiency of the titanium sponge production process.
Experimental Apparatus and Procedure
The detailed structure of the Kroll equipment in titanium sponge production and the vertical annular duct named air-cooling zone had been depicted in our previously published works (Wang et al., 2017a; Wang et al., 2017b), and the reducer unit capacity is 12 tons per batch. Therefore, the apparatus and measurements are only represented briefly in the present experiment. The external diameter of the Kroll reactor is dext = 2264 mm and the internal diameter of the heater is dint = 2690 mm that would surround a concentric vertical annular duct for the Kroll equipment, which is outlined in Figure 1B with the present measurements. The thickness of the air-cooling zone is Dh/2 = 213 mm, and the length is l = 1192 mm. There are nine groups of the inlet and the outlet for the cooling air (Wang et al., 2017a). Both the roughness of the external surface and that of the internal surface are ignored.
The cooling air inlet temperatures, tin, and outlet temperatures, tout, are measured by standard thermocouples (type K, Class II) and collected by the analog I/O module (type ADAM-4018+, 16-channel, 0–1370.0°C). The thermocouples for measuring cooling air inlet temperatures are numbered Row I and that for measuring cooling air outlet temperatures are numbered Row II. The accuracy of the analog I/O module is better than ±0.10% full-scale. The temperature of the TiCl4-Mg system in the Kroll reactor, tc, is extracted from the DCS control system with an accuracy of ±2.0°C. The volume flow rate of cooling air, qV, is measured by a hot-wire anemometer (0.0056 to 0.1405°m3/s, HHF-SD1) with an accuracy of ±1.00% full-scale stated by manufacturer. The measurements for the temperatures and the volume flow rate of cooling air are all installed near the center of the inlets or outlets. The external surface temperature of the reactor, text, and internal surface temperature of the heater, tint, are measured by a non-contact infrared thermometer (−50–1370°C, DT-8869H) with an accuracy of ±1.50% full-scale.
The air inlet temperature and the air outlet temperature are the average value of nine measurements, respectively. The air volume flow rate is the sum value of nine measurements. All available experimental data for the natural and the forced convective heat transfer are listed in the Supplementary Tables S1, S2 in the Supplementary Material, respectively.
Technological Notes
To determine the heat transfer characteristics of the cooling air in both the natural convection and forced convection in the vertical annular duct of the Kroll equipment, the complex heat transfer coefficient and the Nusselt number that due to convection and radiation are analyzed. Experiments and measurements are conducted with stable production process. We firstly analyzed the convective heat transfer characteristics of the cooling air in the vertical annular duct of the Kroll equipment, and a new set of the heat transfer correlations were established by considering the characteristics of cooling air, equipment and operation parameters. In the vertical annular duct, the cooling air absorbs thermal energy from the external surface of the reactor and the internal surface of the heater by convective and radiant heat transfer,
Where Q is the heat transfer rate due to convection and radiation, h is the complex heat transfer coefficient, A is the heat transfer area, Δt is the logarithmic temperature difference (Wang et al., 2017a), and d is the internal diameter of the heater or the external diameter of the reactor. The subscripts, int and ext, represent the internal surface of the heater and the external surface of the reactor, respectively. The enthalpy energy change of cooling air is calculated by:
Where tin and tout are the inlet and the outlet temperatures of cooling air, qV is the volume flow rate, ρ and cp are the density and the specific heat capacity of cooling air, respectively. Then, the Nusselt number is expressed as (Liu et al., 2019; Wang B. et al., 2020):
Where Dh is the characteristic length and λ is the thermal conductivity of cooling air. It could be expected that the Nusselt number is the function of the Rayleigh number for natural convective heat transfer or the function of the Reynolds number and the Prandtl number for forced convective heat transfer, while the physical and the geometrical characteristics would be summarized into dimensionless parameters as follows (Wang B. et al., 2020):
Where Ra is the Rayleigh number, Re is the Reynolds number, Pr is the Prandtl number, and Ct is the dimensionless temperature. These dimensionless parameters are defined as (Cheng et al., 2019; Chai et al., 2020):
Where g is the gravitational acceleration, μ is the viscosity of cooling air, Ts is the temperature of the heat transfer surface in the Kelvin scale.
Results and Disscussions
The complex heat transfer coefficients of the natural convection and the forced convection for both heat transfer surfaces are illustrated in Figure 2, respectively. Measurements and calculations reveal that the heat transfer coefficients increase linearly with the volume flow rate of the cooling air for each dimensionless temperature. In the case of natural convective heat transfer, as shown in Figures 2A,B, higher temperature differences between the cooling air and heat transfer surfaces would lead to a higher volume flow rate of cooling air and higher heat transfer rate. It would be observed that a higher volume flow rate of the cooling air is correlated with a greater heat transfer rate. Besides, the Rayleigh numbers have a positive correlation with the Nusselt numbers for both heat transfer surfaces, as shown in Figure 3. And the Nusselt number increased obviously with the Rayleigh number. Hence, it is possible to improve the heat transfer performance of the air-cooling zone by using a forced convection scheme. For natural convective heat transfer (Figures 2A,B), it is clear that the heat transfer coefficient of the external surface of the reactor is about 3.50 times that of the internal surface of the heater for each dimensionless temperature. Hence, the heat transfer rate of the external surface of the reactor maybe close to 80.00% of the total heat transfer rate. That is, the performance of the vertical annular air-cooling zone of the Kroll equipment is mainly determined by heat transfer between the cooling air and the external surface of the reactor in the case of natural convection.
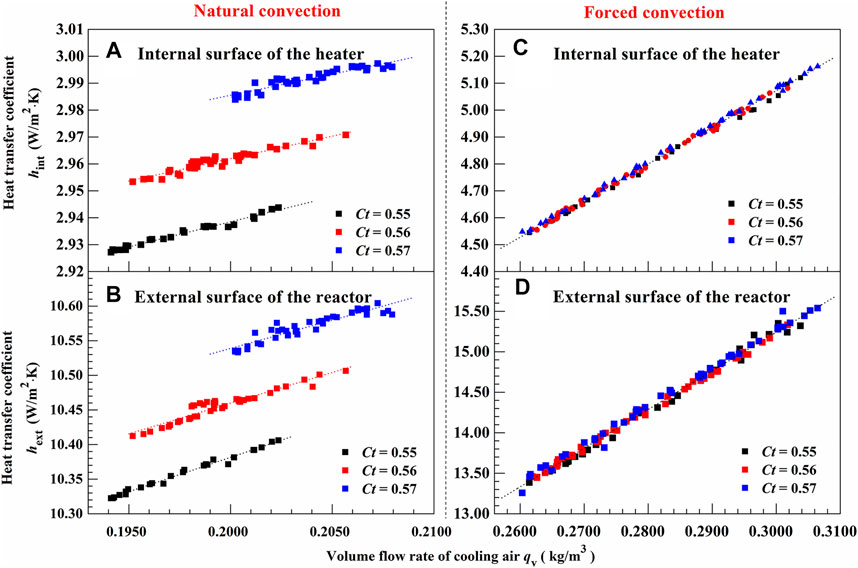
FIGURE 2. Complex mean heat transfer coefficients of the natural convection and the forced convection.
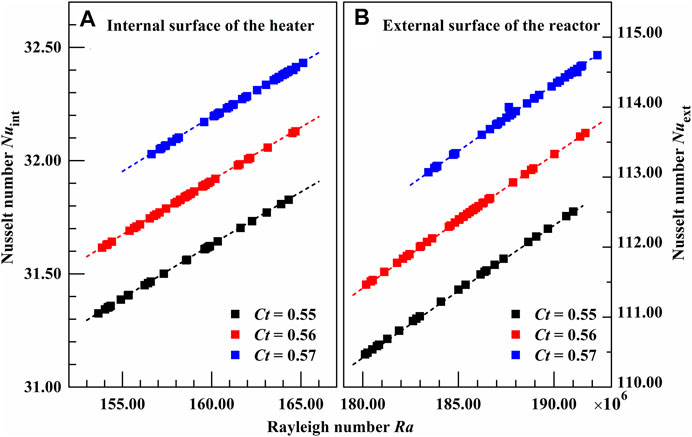
FIGURE 3. Relationship between Nusselt number and relative dimensionless parameters of the natural convection.
Besides the air volume flow rate, a higher dimensionless temperature Ct results in a greater heat transfer coefficient for the natural convection, as shown in Figures 2A,B. It is understandable that the natural convection in the vertical annular air-cooling zone is driven by the temperature difference between the cooling air and the TiCl4-Mg system in the Kroll reactor. Thus, the Nusselt number also increases with the dimensionless temperature, as shown in Figure 3. The Rayleigh number and the dimensionless temperature show important effects on the heat transfer in the natural convection case. Thus, the physical and the geometrical characteristics could be summarized into dimensionless parameters as follows:
The external surface of the reactor:
The internal surface of the heater:
The Eq. 11 could be used as the criteria for evaluating the performance of the natural convection in the vertical annular air-cooling zone of the Kroll equipment for titanium sponge production. The parameters used include the characteristics of the cooling air, equipment and operation parameters.
In the case of forced convective heat transfer, as shown in Figures 2C,D, the complex heat transfer coefficients for both the external and internal surfaces are investigated. Note that the heat transfer coefficients increase linearly with volume flow rate of the cooling air for all dimensionless temperatures. It would be observed that a higher volume flow rate of the cooling air results in a greater heat transfer rate during forced convection. Thus, the Nusselt numbers for both heat transfer surfaces increase obviously with the Reynolds number, as shown in Figure 4.
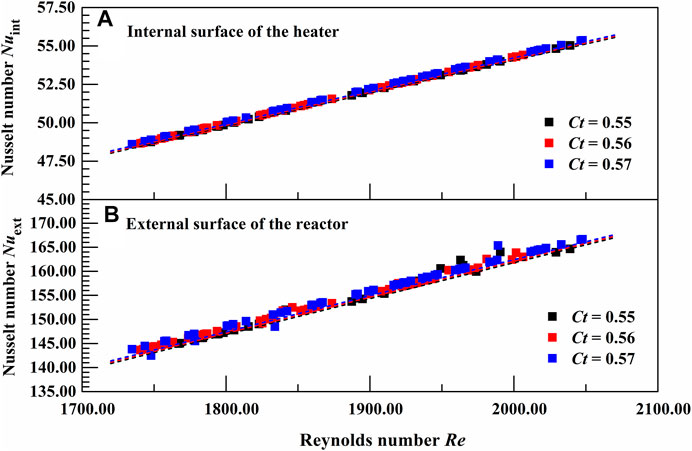
FIGURE 4. Relationship between Nusselt number and relative dimensionless parameters of the forced convection.
However, the heat transfer coefficient of the external surface of the reactor is only about 3.00 times that of the internal surface of the heater for all dimensionless temperatures. The heat transfer rate of the external surface of the reactor accounts for about 76.00% of the total heat transfer rate. That is, the performance of the vertical annular air-cooling zone of the Kroll equipment is still mainly determined by the heat transfer between the cooling air and the external surface of the reactor in the case of forced convection.
The purpose of the forced convection in the vertical annular duct of the Kroll equipment is to enhance the heat transfer of the TiCl4-Mg system. The heat transfer coefficients for both heat transfer surfaces are nearly independent with the dimensionless temperature, and so do the Nusselt numbers. Thus, the physical and the geometrical characteristics would be summarized into dimensionless parameters as follows:
The external surface of the reactor:
The internal surface of the heater:
The Eq. 12 could be a design criterion of the forced convection in the vertical annular air-cooling zone of the Kroll equipment for titanium sponge production, while the characteristics of the cooling air, equipment and operation parameters are considered.
Conclusion
In summary for quantifying the heat transfer characteristics for the Kroll equipment used in titanium sponge production, this work proposes to calculate the Nusselt numbers based on parameters including the cooling air, equipment and operation. and the heat transfer coefficients for both the external surface of the reactor and the internal surface of the heater are also investigated. The main findings of this study can be listed as follows:
1) The heat transfer coefficients for both surfaces increase with the volume flow rate of cooling air for each dimensionless temperature.
2) The heat transfer coefficients of the external surface of the reactor are higher than that of the internal surface of the heater.
3) The dimensionless temperature has an important effect on the Nusselt number in the natural convective heat transfer, except for the forced convection.
4) New correlations regarding the Nusselt number between the cooling air and the external surface of the reactor or the internal surface of the heater are obtained based on experimental data, while the characteristics of the cooling air, equipment and operation parameters are considered.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
WW: conceptualization; data curation; formal analysis; methodology; writing-original draft; project administration. FW: supervision; writing-review and editing.
Funding
The authors acknowledge the financial support received from the Science and Technology Foundation of Guizhou Province (grant number QKHJC-ZK 2021-YB261), the National Natural Science Foundation of China (grant number 51874108), and the Talent Projects of Guizhou University and the Education Department of Guizhou Province (grant number GDPY 2019-20, GDRJHZ 2019-14, and QJHKYZ 2021-097).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to Qiang Liang and Lvguo Zhang of Zunyi Titanium Co., Ltd. for their valuable discussions and experimental batches supply throughout this work. One of the authors, WW, is grateful to Professor Xiang Ge of Guizhou University for his valuable advice. And all co-authors thank the reviewers for the valuable comments and suggestions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.759781/full#supplementary-material
References
Chai, X., Liu, X., Xiong, J., and Cheng, X. (2020). Numerical Investigation of Turbulent Heat Transfer Properties at Low Prandtl Number. Front. Energ. Res. 8, 112. doi:10.3389/fenrg.2020.00112
Cheng, H., Yanlin, A. B., Wang, J., and Zhao, J. (2019). Diameter Effect on the Wall Temperature Behaviors During Supercritical Water Heat Transfer Deterioration in Circular Tubes and Annular Channels. Front. Energ. Res. 7, 73. doi:10.3389/fenrg.2019.00073
Gao, F., Nie, Z., Yang, D., Sun, B., Liu, Y., Gong, X., et al. (2018). Environmental Impacts Analysis of Titanium Sponge Production Using Kroll Process in China. J. Clean. Prod. 174, 771–779. doi:10.1016/j.jclepro.2017.09.240
Krauter, N., Eckert, S., Gundrum, T., Stefani, F., Wondrak, T., Frick, P., et al. (2018). Inductive System for Reliable Magnesium Level Detection in a Titanium Reduction Reactor. Metall. Materi Trans. B. 49 (4), 2089–2096. doi:10.1007/s11663-018-1291-y
Liu, Z., Yue, Y., She, L., and Fan, G. (2019). Numerical Analysis of Turbulent Flow and Heat Transfer in Internally Finned Tubes. Front. Energ. Res. 7, 64. doi:10.3389/fenrg.2019.00064
Nakamura, K., Iida, T., Nakamura, N., and Araike, T. (2017). Titanium Sponge Production Method by Kroll Process at OTC. Mater. Trans. 58 (3), 319–321. doi:10.2320/matertrans.MK201634
Roux, R. N., Van der Lingen, E., and Botha, A. P. (2019). A Systematic Literature Review on the Titanium Metal Product Value Chain. Sajie 30 (3), 115–133. doi:10.7166/30-3-2233
Wang, B., Chen, B., Ke, B., Wang, G., Li, R., Wen, J., et al. (2020a). Analysis of the Flow Characteristics of the Liquid Film on the Wall Surface of the Corrugated Plate Dryer Based on PSD Method: A Short Communication. Front. Energ. Res. 8, 215. doi:10.3389/fenrg.2020.00215
Wang, W., and Wu, F. (2017). Exergy Destruction Analysis of Heat Exchanger in Waste Heat Recovery System in Kroll Process. Ijex 22 (1), 89–101. doi:10.1504/IJEX.2017.10001122
Wang, W., Wu, F., and Jin, H. (2017a). Enhancement and Performance Evaluation for Heat Transfer of Air Cooling Zone for Reduction System of Sponge Titanium. Heat Mass. Transfer 53 (2), 465–473. doi:10.1007/s00231-016-1836-z
Wang, W., Wu, F., and Jin, H. (2020b). Gaseous P-V-T Property Measurements for Titanium Tetrachloride from 873.0 to 1173.0 K and Low Pressure of 34.05 kPa. ACS Omega 5 (30), 18573–18578. doi:10.1021/acsomega.0c00667
Wang, W., Wu, F., and Yu, Q. (2017b). Feasibility Study for Recovering Waste Heat in Reduction System of Kroll Process: Energy Analysis and Economic Valuation. Russ. J. Non-ferrous Met. 58 (3), 258–268. doi:10.3103/S1067821217030208
Wang, W., Wu, F., Yu, Q., and Jin, H. (2018a). Experimental Investigation of Titanium Tetrachloride in Pool Boiling Heat Transfer. Int. J. Heat Mass Transfer 122, 1308–1312. doi:10.1016/j.ijheatmasstransfer.2018.02.051
Wang, W., Wu, F., Yu, Q., and Jin, H. (2018b). Interfacial Liquid-Vapor Phase Change and Entropy Generation in Pool Boiling Experiment for Titanium Tetrachloride. J. Therm. Anal. Calorim. 133 (3), 1571–1578. doi:10.1007/s10973-018-7203-1
Keywords: dimensionless temperature, heat transfer coefficient, nusselt number, convective heat transfer, titanium sponge
Citation: Wang W and Wu F (2021) Quantifying Heat Transfer Characteristics of the Kroll Reactor in Titanium Sponge Production. Front. Energy Res. 9:759781. doi: 10.3389/fenrg.2021.759781
Received: 17 August 2021; Accepted: 16 September 2021;
Published: 30 September 2021.
Edited by:
Zongliang Zuo, Qingdao University of Technology, ChinaReviewed by:
Kun Wang, Northeastern University, ChinaZhen Yao, Guizhou Normal University, China
Mengqi Wei, Jiangsu Provincial Academy of Environmental Science, China
Copyright © 2021 Wang and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenhao Wang, d2h3YW5nQGd6dS5lZHUuY24=
 Wenhao Wang
Wenhao Wang Fuzhong Wu
Fuzhong Wu