Control Method for PEMFC Using Improved Deep Deterministic Policy Gradient Algorithm

A data-driven PEMFC output voltage control method is proposed. Moreover, an Improved deep deterministic policy gradient algorithm is proposed for this method. The algorithm introduces three techniques: Clipped multiple Q-learning, policy delay update, and policy smoothing to improve the robustness of the control policy. In this algorithm, the hydrogen controller is treated as an agent, which is pre-trained to fully interact with the environment and obtain the optimal control policy. The effectiveness of the proposed algorithm is demonstrated experimentally.

Introduction

Fuel Cell is the fourth type of power generation technology after hydroelectric, thermal and nuclear power generation. It converts chemical energy stored in fuel and oxidizer directly into electricity through electrode reactions in an isothermal environment (Yang et al., 2021a; Yang et al., 2021b). As a new type of chemical power source, the fuel cell generation process is not a direct combustion of fuel compared to thermal power generation, the power generation efficiency is not limited by the Carnot cycle and the emission of harmful substances is extremely low(Yang et al., 2020; Yang et al., 2018). Its energy conversion rate is as high as 80 %, and its actual efficiency is double that of an ordinary internal combustion engine (Bougrine et al., 2013) The fuel cell is therefore a new power source with high efficiency and clean features, combining new technologies in energy, chemicals, materials and automatic control (Yang et al., 2019a; Yang et al., 2021c).

However, as the PEMFC system is a complex system with multiple inputs and outputs, nonlinear, approximately east, with random disturbances, time-varying and high order (Yang et al., 2019b; Li and Yu, 2021a), it is difficult to achieve satisfactory control results with traditional PID control (Li et al., 2021). In order to obtain accurate and fast response results, various advanced control strategies have been applied in the research of PEMFC output control strategies. (Zhang et al., 2019; Li and Yu, 2021b; Zhang et al., 2021).

In recent years, scholars at home and abroad have done a lot of research on the control of PEMFC, which is mainly divided into the following categories:

1) Model-based control methods (Wang and Kim, 2014): including internal model control (IMC) (Danzer et al., 2008), model predictive control (MPC) (Kim, 2010), model-based adaptive control (Zhang et al., 2008), nonlinear model predictive control (NMPC) (Park and Gajic, 2014), model multivariable control (nonlinear multivariable control) (Talj et al., 2009), time delay control (Liu et al., 2016), generalized model control (Damour et al., 2014), etc.

2) Sliding mode control. Some higher order sliding mode control methods have also been applied to PEMFC, (Ou et al., 2015) such as first order sliding mode control, higher order super twisted sliding mode control and (Chen et al., 2018) higher order sliding mode control with an observer.

3) PID and its improvement algorithms. Some improved algorithms on the PID algorithm have also been used extensively, for example, neural PID controller (Zhao et al., 2020), fuzzy PID control (Sun et al., 2018), and algorithm combining PID and fuzzy controller (Ou et al., 2017), feedback linearization controller, and reference fractional order PID (FOPID) controller.

4) Adaptive control. Some adaptive control has also been applied to PEMFC control, such as data-driven adaptive controller, an adaptive control based on parameter identification, and adaptive pole search controller.

5) Compound control. There are also some compound controllers, for example, PID-neural network control, interval type II fuzzy (Fuzzy)-PID control, fuzzy adaptive PID control.

The existing research problems are:

1) There is no model -free control algorithm that can effectively adapt to the non-linear characteristics of PEMFC.

2) No optimal algorithm with adaptive capabilities and low computational effort.

For this reason, model-free controllers with strong adaptive capabilities are more suitable for such systems.

A data-driven PEMFC output voltage control method is proposed. Moreover, an Improved deep deterministic policy gradient algorithm is proposed for this method. The algorithm introduces three techniques: double Q learning, policy delay update, and policy smoothing to improve the robustness of the control policy. In this algorithm, the hydrogen controller is treated as an agent, which is pre-trained to fully interact with the environment and obtain the optimal control policy. The effectiveness of the proposed algorithm is demonstrated experimentally.

The innovations in this paper are.

1) A data-driven PEMFC output voltage control method is proposed.

2) An Improved deep deterministic policy gradient algorithm is proposed.

The remainder of this paper comprises the following sections: the PEMFC model is demonstrated in PEMFC Model, and the proposed algorithm is described in Proposed Method; the experimental results are analysed and discussed in Case Studies, and the findings in this paper are summarised in Conclusion.

PEMFC Model

PEMFC Output Voltage

The dynamic model of the PEMFC has been refined from the electrochemical model. Ideally, the voltage released at full reaction is 1.229 V. The actual potential decreases due to irreversible losses, which in practice are also known as polarization overvoltage. In the power generation process of a PEMFC, polarization overvoltage is mainly manifested as activation overvoltage, ohmic overvoltage and concentration overvoltage. Therefore, in the actual power generation process, the individual voltage is inevitably less than the ideal standard electric potential due to the polarization overvoltage. In addition to the factors such as temperature, pressure and current density, chemical and material factors such as electrode material and electrolyte can also influence the polarization or overvoltage of the electrodes.

$V_{\text{cell }}=E-{\eta }_{\text{act }}-{\eta }_{\text{ohm }}-{\eta }_{\text{con }}(1)$

For a fuel cell stack consisting of N single cells connected in series, the output voltage V can be expressed as

$V=N{V}_{\text{cell }}(2)$

Ohmic Voltage Overvoltage

The ohmic polarization overvoltage is mainly caused by the equivalent membrane impedance of the proton exchange membrane to the transfer of protons and the impedance of the electrodes and current collectors to the transfer of electrons. Based on the Amphlett model, the PEMFC ohmic overvoltage mainly includes the voltage drop caused by the impedance of the two parts of the PEMFC. These two parts of impedance, one part is the equivalent membrane impedance of the proton membrane, The other part is the resistance that prevents protons from passing through the proton membrane which is usually a constant. According to the resistivity theorem, the equivalent membrane impedance R_m can be obtained by the following formula:

$R_M=\frac{{\rho }_{M}B}{A}(3)$

In the formula, ${\rho }_{\left(M\right)}$ is the resistivity of the proton membrane to the electron flow $(\Omega \cdot \left(\text{cm}\right)),B$ is the thickness of the proton exchange membrane. ${\rho }_M$ can be obtained by the following formula.

${\rho }_M=\frac{181.6[1+0.03\left(\frac{I}{A}\right)+0.062\left(\frac{T}{303}\right){\left(fracIA\right)}^{25}}{\left[\lambda -0.634-3\left(\frac{I}{A}\right)\right]\exp \left[4.18\left(\frac{T-303}{T}\right)\right]}(4)$

Empirically, the internal resistance of the battery is

$R_{\text{int}}=0.01605-3.5\times {10}^{-5}T+8\times {10}^{-5}i(5)$

Ohmic polarization overvoltage can be expressed as:

${\eta }_{\text{ohm }}=I{R}_{\text{int }}=I\left(R_{\text{m}}+R_{\text{c}}\right)(6)$

Activation Overvoltage

Activation overvoltage is the deviation of an electrode’s potential from its equilibrium potential due to a delay in its electrochemical reaction. The activation polarization overvoltage of the cathode can be obtained

$V_{\text{ux }t,c}=\frac{RT}{{\alpha }_{c}Fn}(\ln [nF{K}_c^0\exp \left(-\frac{\Delta G}{RT}\right)\times {\left(C_{i_2}\right)}^{\left(1-{\alpha }_i\right)}{\left(C_{H_2}\right)}^{\left(1-{\alpha }_c\right)}{\left(C_{H_{2}o}\right)}^{{\alpha }_{\iota }}]-\ln I)(7)$

Anode activation polarization overvoltage:

$V_{at,a}=-\frac{\Delta G}{2F}+\frac{RT}{2F}\ln \left(4FA{K}_a^0{C}_{H_2}\right)-\frac{RT}{2F}\ln I(8)$

The total activation polarization overvoltage is the sum of the anode activation overvoltage and the cathode activation overvoltage, expressed as:

${\eta }_{\text{act}}={\xi }_1+{\xi }_{2}T+{\xi }_{3}T\ln c\left({\text{O}}_2\right)+{\xi }_{4}T\ln I(9)$

$c\left({\text{O}}_2\right)$is the concentration of dissolved oxygen at the cathode catalyst interface which is calculated as follows:

$c\left({\text{O}}_2\right)=P_{{\text{O}}_2}/5.08\times {10}^6\exp \left(-498/T\right)(10)$

Thermodynamic Electric Potential

According to the empirical formula for the PEMFC, the thermodynamic electric potential can be obtained as follows:

$E=\frac{\Delta G}{2F}+\frac{\Delta S}{2F}\left(T-T_{\text{ref}}\right)+\frac{RT}{2F}\left(\ln p_{{\text{H}}_2}+\frac{1}{2}\ln p_{0_2}\right)(11)$

PEMFC can directly convert chemical energy into electrical energy. The chemical energy release of a fuel cell can be calculated by the change of the Gibbs self-burning energy $\left(\Delta g_{\left(f\right)}\right)$. The Gibbs self-burning energy is usually used to calculate the externally available energy, for basic chemical reaction formula of hydrogen/oxygen reaction PEMFC is:

$H_2+\frac{1}{2}{O}_2-H_{2}O(12)$

The corresponding change in Gibbs’ self-reliance is:

$\text{Δ}{g}_f=g_{f, products }-g_{f, reactan is }={\left(g_f\right)}_{H_{2}O}-{\left(g_f\right)}_{H_2}-{\left(g_f\right)}_{O_2}(13)$

The changed Gibbs self-burning energy is a function of temperature and pressure:

$\Delta g_f=\Delta g_f^0-\overline{R}{T}_{fc}\ln \left[\frac{p_{H_2}{p}_{O_2}^{\frac{1}{2}}}{p_{H_{2}O}}\right](14)$

We can deduce the voltage of the fuel cell:

$E=\frac{-\Delta g_f}{2F}=\frac{-\Delta g_f^0}{2F}+\frac{R{T}_{fc}}{2F}\ln \left[\frac{p_{H_2}{p}_{O_2}^{\frac{1}{2}}}{p_{H_{2}O}}\right](15)$

When specific values are brought in, the equation can be transformed into

$E=1.229-0.85\times {10}^{-3}\left(T-298.15\right)+4.3085\times {10}^{-5}T\left(\ln p_{{\text{H}}_2}+\ln p_{0_2}/2\right)(16)$

Dense Differential Polarization Overvoltage

Concentration overvoltage is a phenomenon caused by the deviation of the electrode potential from the equilibrium potential due to the difference between the concentration of ions in the solution at the electrode interface layer and the concentration of the body solution in the electrolytic bath, which can be expressed as:

${\eta }_{\text{con}}=-\beta \ln \left(J/J_{\max }\right)(17)$

Dynamic and Capacitive Characteristics of the Double Layer Charge

The phenomenon of a “double layer of charge” in a proton exchange membrane fuel cell is particularly important for the dynamics of the PEMFC. On the surface of the electrode electrons are collected and on the surface of the electrolyte hydrogen ions are collected. Between them there is a potential difference in which charge and energy are stored, which acts as an equivalent capacitance. This “smoothest out” the voltage loss across the equivalent resistance and results in a very realistic dynamic model of the PEMFC. Therefore, when modelling the dynamics of the PEMFC, a capacitance is added to the electrochemical model. This “equivalent capacitance” is able to better represent this effect by smoothing the output voltage response of the fuel cell as the current changes, with a transition time.

In Figure 1, the polarization voltage across _Rd is$V_{\text{d}},$ given by the differential equation for the voltage change of a single cell as

$\text{d}{V}_{\text{d}}/\text{d}t=I/C-V_{\text{d}}/R_{\text{d}}C(18)$

$V_d=i{R}_d={\eta }_{act}+{\eta }_{con}(19)$

Thus, the voltage of the stack can be expressed as:

$V_{st}=n{V}_{\text{cell }}=n\left[E-I\left(R_{act}+R_{\text{con }}+R_{\text{ohm }}\right)\right]=n\left(E-I{R}_{\text{equ }}\right)(20)$

The output power and efficiency of the stack can therefore be expressed as:

$P_{st}=I\cdot V_{st}\eta =V_{\text{cell }}\cdot I/E\cdot I=V_{\text{cell }}/E(21)$

FIGURE 1

FIGURE 1. Results of case.

Proposed Method

DDPG

The DDPG method fuses deep neural networks with Deterministic Policy Gradients (DPG) algorithms and uses actor -critic a framework as the basic architecture for the algorithm. The actor network is used to update the policy and the critic network is used to approximate the state action value function. The use a non-linear neural network as an approximator. Inspired by the algorithm, DQN solve this problem by setting up a target actor network and a target critic network, as well as an experience replay mechanism. Instead of DQN directly copying the current network to the target network, DDPG updates the target network in a “soft” way, ensuring that each parameter update is small, thus achieving a stable training effect.

$\begin{array}{l}{\theta }^{Q^{\prime }}\leftarrow \tau {\theta }^Q+(1-\tau ){\theta }^{Q^{\prime }}\\ {\theta }^{{\mu }^{\prime }}\leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}\end{array}(22)$

In DDPG, the objective function is defined as a sum with discounted rewards

$J\left({\theta }^{\mu }\right)={\text{E}}_{{\theta }^{\mu }}\left[r_1+\gamma r_2+\gamma r_3+\cdots \right](23)$

$L\left({\theta }^Q\right)=\frac{1}{N}{\displaystyle \sum _i{\left(y_i-Q\left(s_i,a_i|{\theta }^Q\right)\right)}^2}(24)$

Of which

$y_i=r_i+\gamma Q^{\prime }\left(s_{i+1},\mu \left(s_{i+1}|{\theta }^{{\mu }^{\prime }}\right)|{\theta }^{\alpha }\right)(25)$

The actor network parameters are updated by means of a chain derivative rule for the objective function:

${{\nabla }_{{\theta }^a}J\left({\theta }^{\mu }\right)\approx \frac{1}{N}{\displaystyle \sum _i{\nabla }_a}Q\left(s,a|{\theta }^{\mathrm{\varrho }}\right)|}_{s=s,a=\mu \left(x\right)}{{\nabla }_{{\theta }^a}\mu \left(s|{\theta }^{\mu }\right)|}_{s_j}(26)$

To address the problem of under-exploration caused by actors mapping states to deterministic actions in the DPG approach, the DDPG algorithm generates temporal correlated noise through the Ornstein-Uhlenbeck (OU) process to improve the exploration capability of the algorithm under deterministic strategies.

DDPG uses an empirical replay mechanism based on random sampling but suffers from Q-value overestimation.

The IDDPG algorithm uses two critics. The target value formula is as follows:

$y_t=r\left(s_t,a_t\right)+\gamma {\min }_{i=\mathrm{1,2}}{Q}_{{\theta }_t}\left(s_{t+1},{\pi }_{{\varphi }^{\prime }}\left(s_{t+1}\right)+\epsilon \right)(27)$

Case Studies

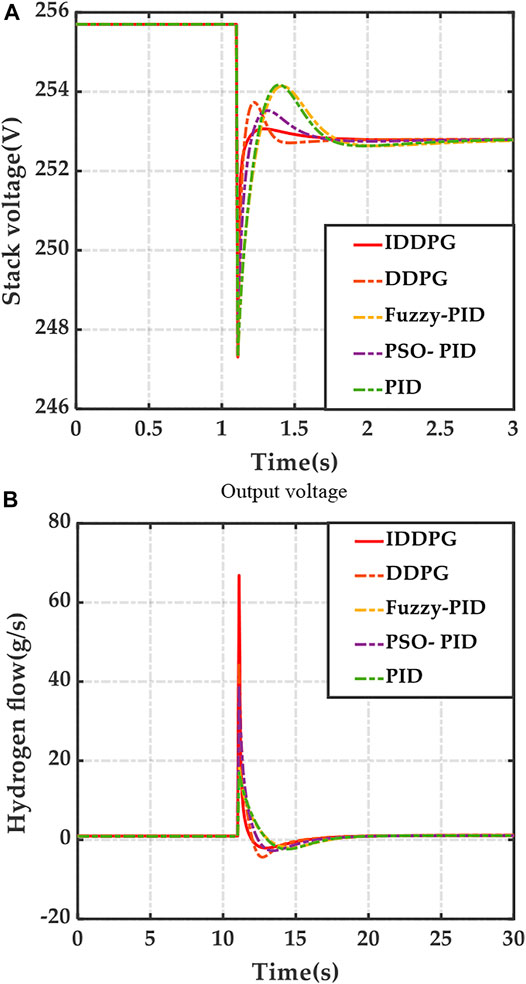
The DDPG control strategy, fuzzy PID controller (Fuzzy-PID), PSO optimized fuzzy PID controller (PSO- PID), and PID are introduced in this paper as comparative examples. The load variation makes the step disturbance at 1 s. The load current magnitude appears from 100 A with load disturbance and rises to 127 A. The results are shown in Figures 1A,B.

1 According to Figures 1A,B-, the IDDPG algorithm improves the robustness of the algorithm because it uses advanced techniques to solve the Q overestimation problem in conventional deep reinforcement learning algorithms. In contrast, the DDPG algorithm does not use an effective strategy to improve the robustness of the algorithm, so the algorithm tends to fall into local optima, making the final control strategy sub-optimal and not robust. In addition, the other algorithms do not have better optimal control capability and have difficulty in adapting to the non-linear characteristics of the PEMFC, therefore, their output voltage control performance is low.

2 For Fuzzy-based algorithms, their performance is mostly better than Optimized-based algorithms due to their ability to automatically adjust coefficients, but the simplicity of the Fuzzy rule makes them less accurate.

Optimized-based algorithms are not adaptive and robust due to the inability to adjust the coefficients in real time, which ultimately leads to overshooting and instability of the output voltage.

In summary: In Case 1, the IDDPG algorithm has better static and dynamic performance and is able to control the output voltage effectively.

Conclusion

A data-driven PEMFC output voltage control method is proposed. An improved deep deterministic policy gradient algorithm is proposed for this method, which introduces three techniques: Clipped multiple Q-learning, policy delay update and policy smoothing to improve the robustness of the control policy. In this algorithm, the hydrogen controller is treated as an agent, which is pre-trained to fully interact with the environment and obtain the optimal control policy. The effectiveness of the proposed algorithm is experimentally demonstrated.

The IDDPG algorithm has a short response time, a fast response time, good dynamic and static performance indicators, enabling timely and effective output voltage control.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

JL: conceptualization, methodology, software, data curation, writing- original draft preparation, visualization, investigation, software, validation. YL: Writing- Reviewing and editing. TY: Supervision.

Funding

This work was jointly supported by National Natural Science Foundation of China (U2066212).

Conflict of Interest

Author Y Li was employed by the company China Electric Power Research Institute.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bougrine, M. D., Benalia, A., and Benbouzid, M. H. (2013). “Nonlinear Adaptive Sliding Mode Control of a Powertrain Supplying Fuel Cell Hybrid Vehicle,” in 3rd International Conference on Systems and Control (Algiers, Algeria: IEEE), 714–719. doi:10.1109/icosc.2013.6750938

CrossRef Full Text | Google Scholar

Chen, J., Liu, Z., Wang, F., Ouyang, Q., and Su, H. (2018). Optimal Oxygen Excess Ratio Control for PEM Fuel Cells. IEEE Trans. Contr. Syst. Technol. 26, 1711–1721. doi:10.1109/TCST.2017.2723343

CrossRef Full Text | Google Scholar

Damour, C., Benne, M., Lebreton, C., Deseure, J., and Grondin-Perez, B. (2014). Real-time Implementation of a Neural Model-Based Self-Tuning PID Strategy for Oxygen Stoichiometry Control in PEM Fuel Cell. Int. J. Hydrogen Energ. 39, 12819–12825. doi:10.1016/j.ijhydene.2014.06.039

CrossRef Full Text | Google Scholar

Danzer, M. A., Wilhelm, J., Aschemann, H., and Hofer, E. P. (2008). Model-based Control of Cathode Pressure and Oxygen Excess Ratio of a PEM Fuel Cell System. J. Power Sourc. 176, 515–522. doi:10.1016/j.jpowsour.2007.08.049

CrossRef Full Text | Google Scholar

Kim, Y.-B. (2010). Improving Dynamic Performance of Proton-Exchange Membrane Fuel Cell System Using Time Delay Control. J. Power Sourc. 195, 6329–6341. doi:10.1016/j.jpowsour.2010.04.042

CrossRef Full Text | Google Scholar

Li, J., and Yu, T. (2021a). A New Adaptive Controller Based on Distributed Deep Reinforcement Learning for PEMFC Air Supply System. Energ. Rep. 7, 1267–1279. doi:10.1016/j.egyr.2021.02.043

CrossRef Full Text | Google Scholar

Li, J., and Yu, T. (2021b). Distributed Deep Reinforcement Learning for Optimal Voltage Control of PEMFC. IET Renew. Power Generation 15, 2778–2798. doi:10.1049/rpg2.12202

CrossRef Full Text | Google Scholar

Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021). Efficient Experience Replay Based Deep Deterministic Policy Gradient for AGC Dispatch in Integrated Energy System. Appl. Energ. 285, 116386. doi:10.1016/j.apenergy.2020.116386

CrossRef Full Text | Google Scholar

Liu, J., Luo, W., Yang, X., and Wu, L. (2016). Robust Model-Based Fault Diagnosis for PEM Fuel Cell Air-Feed System. IEEE Trans. Ind. Electron. 63, 3261–3270. doi:10.1109/TIE.2016.2535118

CrossRef Full Text | Google Scholar

Ou, K., Wang, Y.-X., and Kim, Y.-B. (2017). Performance Optimization for Open-Cathode Fuel Cell Systems with Overheating Protection and Air Starvation Prevention. Fuel Cells 17, 299–307. doi:10.1002/fuce.201600181

CrossRef Full Text | Google Scholar

Ou, K., Wang, Y.-X., Li, Z.-Z., Shen, Y.-D., and Xuan, D.-J. (2015). Feedforward Fuzzy-PID Control for Air Flow Regulation of PEM Fuel Cell System. Int. J. Hydrogen Energ. 40, 11686–11695. doi:10.1016/j.ijhydene.2015.04.080

CrossRef Full Text | Google Scholar

Park, G., and Gajic, Z. (2014). A Simple Sliding Mode Controller of a Fifth-Order Nonlinear PEM Fuel Cell Model. IEEE Trans. Energ. Convers. 29, 65–71. doi:10.1109/TEC.2013.2288064

CrossRef Full Text | Google Scholar

Sun, L., Shen, J., Hua, Q., and Lee, K. Y. (2018). Data-driven Oxygen Excess Ratio Control for Proton Exchange Membrane Fuel Cell. Appl. Energ. 231, 866–875. doi:10.1016/j.apenergy.2018.09.036

CrossRef Full Text | Google Scholar

Talj, R. J., Hissel, D., Ortega, R., Becherif, M., and Hilairet, M. (2010). Experimental Validation of a PEM Fuel-Cell Reduced-Order Model and a Moto-Compressor Higher Order Sliding-Mode Control. IEEE Trans. Ind. Electron. 57, 1906–1913. doi:10.1109/TIE.2009.2029588

CrossRef Full Text | Google Scholar

Wang, Y.-X., and Kim, Y.-B. (2014). Real-time Control for Air Excess Ratio of a PEM Fuel Cell System. Ieee/asme Trans. Mechatron. 19, 852–861. doi:10.1109/TMECH.2013.2262054

CrossRef Full Text | Google Scholar

Yang, B., Li, D., Zeng, C., Chen, Y., Guo, Z., Wang, J., et al. (2021a). Parameter Extraction of PEMFC via Bayesian Regularization Neural Network Based Meta-Heuristic Algorithms. Energy 228, 120592. doi:10.1016/j.energy.2021.120592

CrossRef Full Text | Google Scholar

Yang, B., Swe, T., Chen, Y., Zeng, C., Shu, H., Li, X., et al. (2021b). Energy Cooperation between Myanmar and China under One Belt One Road: Current State, Challenges and Perspectives. Energy 215, 119130. doi:10.1016/j.energy.2020.119130

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019a). Dynamic Leader Based Collective Intelligence for Maximum Power point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manag. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zeng, C., Wang, L., Guo, Y., Chen, G., Guo, Z., et al. (2021c). Parameter Identification of Proton Exchange Membrane Fuel Cell via Levenberg-Marquardt Backpropagation Algorithm. Int. J. Hydrogen Energ. 46, 22998–23012. doi:10.1016/j.ijhydene.2021.04.130

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019b). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Zhang, J., Liu, G., Yu, W., and Ouyang, M. (2008). Adaptive Control of the Airflow of a PEM Fuel Cell System. J. Power Sourc. 179, 649–659. doi:10.1016/j.jpowsour.2008.01.015

CrossRef Full Text | Google Scholar

Zhang, X., Li, S., He, T., Yang, B., Yu, T., Li, H., et al. (2019). Memetic Reinforcement Learning Based Maximum Power point Tracking Design for PV Systems under Partial Shading Condition. Energy 174, 1079–1090. doi:10.1016/j.energy.2019.03.053

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhao, D., Li, F., Ma, R., Zhao, G., and Huangfu, Y. (2020). An Unknown Input Nonlinear Observer Based Fractional Order PID Control of Fuel Cell Air Supply System. IEEE Trans. Ind. Applicat. 56, 5523–5532. doi:10.1109/TIA.2020.2999037

CrossRef Full Text | Google Scholar