Review and Perspectives of Machine Learning Methods for Wind Turbine Fault Diagnosis

Introduction

Wind power has gained remarkable attention in the past decade because wind energy is one of the rapidly clean energy sources and has received worldwide support for renewable energy development (MUA, 2017). In recent years, in order to achieve the goal of carbon peak and carbon neutralization, China has commercialized the use of renewable energy, expanded the use of renewable energy, and demonstrated its determination to reach the peak of carbon dioxide emission by 2030 and carbon neutralization by 2060. As the main force of global renewable energy development, China attaches great importance to new energy, especially wind power generation. According to the statistics of the Global Wind Energy Commission (GWEC), the newly installed capacity of the country has reached 65.1 GW 2) in 2019 (Elizondo et al., 2019). The large-scale development and utilization of wind energy have brought huge opportunities for the development of the market economy, and also raised important crucial challenges related to reliability, cost-effectiveness, and energy blade images of the security. On the one hand, wind turbines (WTs) are often located in remote areas, operated in harsh working environments for a long time, and have withstood randomly varying weather conditions, wind shear, temperature, wind speed, and load, thereby frequent WT failures. As shown in Figure 1, the highest proportion of fault rate of WT components is the electrical system (Hahn et al., 2007), followed by the control system and sensor. On the other hand, the high cost of operation and maintenance (OM) of WTs underscores the urgency of fault diagnosis. Evidently, fault diagnosis and the timely maintenance of WTs can reduce huge financial losses.

FIGURE 1

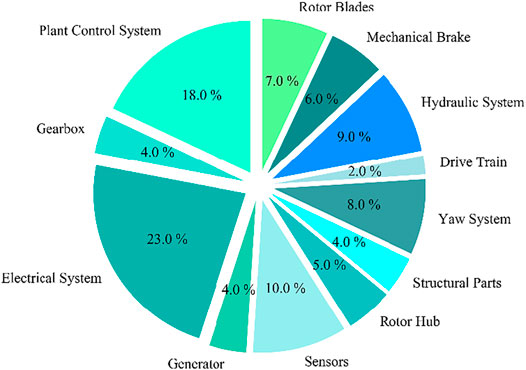
FIGURE 1. Fault rate of wind turbine components (Hahn et al., 2007).

Given the preceding reasons, fault warning and fault diagnosis of WTs should be performed. The fault diagnosis method based on machine learning (ML) is suggested to detect the operating conditions of the WT for it can minimize the downtime and reduce OM cost WTs, and extend the service life of these turbines. With the advent of the era of fault diagnosis technology, many local and international experts and scholars have proposed some efficient fault diagnosis methods for various components (Liu et al., 2015), such as power system (Qiao and Lu, 2015; Zappalá et al., 2019), mechanical (Wang et al., 2016a; Chen et al., 2016b; Garg and Dahiya, 2017; Salameh et al., 2018), and driving faults (Nasiri et al., 2015; Zeng et al., 2015), etc. Among these methods, generator (Hossain et al., 2015; Yang et al., 2017) and gearbox faults (Wang et al., 2016b; Igba et al., 2016; Teng et al., 2016; Wang et al., 2019) are mostly studied. Fault diagnosis methods are classified into fault diagnosis methods based on analytical models, knowledge-based methods, and data-driven fault diagnosis methods (Chen et al., 2016a).

The analytical model-based WT fault diagnosis methods need to analyze and model the system to achieve real-time diagnoses of the faults, which are often directly related to WT model parameters (Gao et al., 2015; Zhong et al., 2018). With a further understanding of the fault diagnosis mechanism of WT, modeling is implemented to increase the accuracy of fault diagnosis. However, in the process of analytical model-based WT fault diagnosis methods by uses system residuals to model the internal subsystem of the WTs for state estimation and online approximation; nevertheless, this process has difficulty in ensuring the accuracy of fault diagnosis (Liu et al., 2017; Cho et al., 2018). Consequently, inevitable errors and unknown interference terms will result, and the aforementioned process is insufficient to guarantee robustness.

Knowledge-based WT fault diagnosis methods rely on expert experience in wind power-related fields (da Silva et al., 2012; Yang et al., 2016). The accuracy of fault diagnosis results depends on the extensiveness of expert experience and knowledge the level of WT fault diagnosis experts, which lack self-learning and recognition abilities. Knowledge-based WT fault diagnosis methods cannot acquire new knowledge from the diagnosed engineering examples during the operation of WT. Hence, poor diagnosis accuracy may be resulted.

Without relying on prior experiences, data-driven WT fault diagnosis methods uses data mining technology to obtain hidden useful information to characterize the fault and normal states of the system, and eventually realize real-time fault diagnosis (Ding, 2012; Qin, 2012). The WT supervisory control and data acquisition (SCADA) system contains real-time online data and extensive offline data. The use and analysis of data mining is necessary to obtain detailed fault characteristics, thereby realizing real-time WT fault diagnosis. Data-driven WT fault diagnosis methods include the ML, multivariate statistical analysis, signal analysis, and information fusion methods (Yin et al., 2014).

As shown in Figure 2, the fault diagnosis methods of WT based on ML can be generally divided into supervised, unsupervised, and semi-supervised learning methods. Although some literature reviews on WT fault diagnosis (Liu et al., 2015) and condition monitoring (de Azevedo et al., 2016) have been published, there still lack of comprehensive review on the ML-based fault diagnosis method of ML. Therefore, the current study provides a systemic and pertinent state-of-the-art review on recent studies on ML methods and techniques that have been used for WT fault diagnosis. In particular, this research summarizes the research methods in WT fault diagnosis, presents the strengths and shortcomings of existing methods, and reveals the challenges and recommendations of future research direction in this domain.

FIGURE 2

FIGURE 2. ML methods for WT fault diagnosis.

Fault Diagnosis of Wind Turbine

Numerous countries have earlier previously conducted research on WT technology, and European countries and the US have made some progress in fault diagnosis and prediction (Habibi et al., 2019). For example, Siemens’ SCADA system is widely used in major wind power generation industries (Dao et al., 2018).

Compared with European and American countries, China’s wind power industry started late, but WT fault diagnosis research has made some progress in recent years. Since the progress and development of artificial intelligence and ML in recent years, the fault diagnosis methods of WT have been intensively studied. The WT structure is shown in Figure 3. The main components of WT include wind wheel, gearbox, generator, converter, yaw system, pitch system, hydraulic system control system, integration control system, and auxiliary system (Lin et al., 2016).

FIGURE 3

FIGURE 3. Main structure of WT.

The wind wheel is key to the energy conversion of WT, and operational stability directly affects the efficiency and safety of WT. As the operating time of WT increases, the failure rate of the wind wheel and other components also increases, which seriously affects the working performance of WT. In a non-stationary state, the frequency component of the WT failure at the generator output will expand over the bandwidth proportional to the speed, thereby making its diagnosis capabilities considerably complicated. Therefore, Dahiya (2018) proposed a fault diagnosis method of WT based on wavelet analysis, using electrical signals to diagnose rotor eccentric faults. The effectiveness of this method under varying speed and load conditions has been verified through experiments.

Gearboxes are one of the important WT, but the most expensive WT sub-assemblies. Gearboxes are often operating under extreme temperature and high speed of rotation, which will cause a high fault rate and irreversible damage to WT. At present, many studies and research have been conducted on the fault diagnosis of WT gearboxes (Salameh et al., 2018). Du et al. (2015) proposed a convex optimization-based WT generator gearbox fault diagnosis method. This method considers identifying multiple features from the superimposed signal of WT gearbox, and makes full use of the potential a priori information, that is, multiple faults with similar spectrum have different morphological waveforms, which can be sparse represented on the joint of redundant dictionaries. The proposed framework is verified by diagnosing multiple faults of gearbox in wind farm. (Zhang et al., 2017) used the Morlet wavelet-based continuous wavelet transform for actual wind turbine gear fault diagnosis. This diagnosis uses the signal analysis method, which has considerably refined time frequency characteristics and achieved satisfactory results.

A generator is the core equipment for generating electricity through WT, which converts kinetic energy into electrical energy. Generators will also experience a high failure rate owing to the harsh environment, large load fluctuation, and diverse operating parameters of this equipment. Numerous publications have specially reviewed the WT generator fault diagnosis, including those involved in avoiding incorrect internal pattern recognition caused by heavy noise, Chen et al. (2016b) extract inherent modulation information by decomposing the signal into mono-components on an orthogonal basis using empirical wavelet transform (EWT). Moreover, before EWT, they applied wavelet spatial adjacent coefficient denoising with data-driven threshold to improve signal-to-noise ratio (SNR), which is considered to be a powerful tool for WT generator fault diagnosis. Yang et al. (2017) considered the shortcomings of sparse representation results affected by dictionaries, and proposed a novel data-driven fault diagnosis method based on shift-invariant dictionary learning and sparse representation for WT generator, which can effectively identify the WT generator. The coefficients obtained can be considerably sparse based on the learned shift-invariant dictionary, and the impulse signal extracted nearly approximating to the real signal.

The converter is a critical component of the WT energy conversion, and the WT outputs current with stable frequency and amplitude to the grid through the converter. Converters have poor stability and are often impacted by high-temperature and high-pressure working circumstances, and the long-term operation will cause irreversible damage to the WT system. Toubakh et al. (Toubakh and Sayed-Mouchaweh, 2016) analyzed the converter fault caused by parameter drift, and proposed a fault diagnosis method of the WT converter based on a hybrid dynamic classifier, which can monitor the normal operation of converters in the discrete mode affected by parameter failure. The parameter drift under conditions is used for fault diagnosis in the early period of the WT converter. Liang et al. (2020) proposed a fault diagnosis method based on WT converters. A series of inherent mode functions are obtained through the overall empirical mode decomposition processing of the measured output voltage. Thereafter, the standard entropy is calculated according to the inherent model functions statistical characteristics, the extracted information is used to describe the diagnostic characteristics, and the fault diagnosis of the fan system is performed. The diagnostic accuracy is 99.57%, and its performance was impressive.

The yaw system is an important WT component and can drive the WT engine room to revolve around the tower centerline, thereby maintaining the verticality of the wind wheel scanning surface and wind direction vertical. Yaw system failures often occur owing to its harsh operating environment and load fluctuation, thereby affecting the power generation efficiency of WTs. To qualitatively evaluate the zero-offset error of the yaw system, Pei et al. (2018) proposed a data-driven method for WT yaw system fault diagnosis, which can detect the zero-point shifting fault by analyzing the power characteristics of different yaw angles. If the yaw angle measurement error is greater than a predetermined threshold, then the zero-point shift fault will be triggered, which can detect the fault in time and improve the WT performance. In the case of yaw system faults, Ouanas et al. (2018) proposed a fault diagnosis method of WT yaw system based on the signal analysis method. By filtering the inverter signal provided by the yaw drive, the discrete wavelet transform and empirical mode decomposition method were used to eliminate redundant information. Faults from the envelope of the Hilbert transform are detected, thereby verifying its effectiveness.

Pitch control system is the speed control device of WT and can adjust power change by changing the blade angle of attack. Given to the variable external wind conditions of WT and complicated internal system structure of the pitch system, abnormal output power, blade damages of the s, and even unit collapse can easily be caused, in which the failure rate is high. Many studies have proposed fault diagnosis methods for pitch systems. Habibi et al. (2017) proposed the fault diagnosis method of the WT pitch system by using a nonlinear model and presented the problem of maximizing energy extraction by designing the optimal desired state. Experiments have been performed to verify the practicability of the proposed method. Lan et al. (2018) conducted a study based on the adaptive step-by-step sliding window observer’s state estimation and fault indicator functions of a pitch system, which can effectively deal with the nonlinear fault distribution function and identify the pitch fault of WTs.

A hydraulic system is an important WT component and plays a essential role in the yaw, pitch, and transmission chain braking of WTs. Hydraulic system function in all-weather, open-air and high-altitude running conditions, which is prone to failures such as oil leakage and spool jamming, thereby making maintenance difficult. In the case of WT hydraulic system faults, Yang et al. (2011) proposed a fault detection method for WT hydraulic system based on the Petri net model. First, Petri net theory is used to establish a model for each discrete operating state of the WT hydraulic pitch system, and a fault Petri net model is built. Thereafter, a system reliability index is obtained based on the fault qualitative analysis and calculation of the Petri net. The Petri net model calculation is simple, which is ultilized to the WT hydraulic system fault diagnosis and has a broad application prospect.

Machine Learning Methods for Wind Turbine Fault Diagnosis

ML refers to a computer that learns from a limited amount of data without specialist intervention to train an inductive model and uses this model thereafter to guide future decisions (Clifton et al., 2013; Stetco et al., 2019). The ML method has been used for fault diagnosis in WT (Leahy et al., 2016), which consists of inputs, outputs, models, and objective functions. Given the WT data sample data$x=\left\{x_1,x_2,\dots x_n\right\}$ (x represents a data set containing n samples) and fault category y, n represent the total number of data sample. Thereafter, we use the training sample${\{x_i,y_i\}}_1^M$ (${\{x_i,y_i\}}_1^M\in \{x,y\}$) to train the model and obtain the approximate value $f\left(x\right)$ to fit the real value y. Moreover, $y^{\ast }$ represents the mapping relationship between x and y, and M is the total number of training samples.

$y^{\ast }=argmi{n}_f\left(E_{xy}L\left(y,f\left(x\right)\right)\right)=argmi{n}_f\left(E_x\left(E_y\left(L\left(y,f\left(x\right)\right)\right)|x\right)\right)(1)$

In Equation 1, L represents a loss function, and the average loss of the training set is called empirical risk. The goal of ML is to minimize empirical risk. Frequently employed loss functions include 0–1, square, absolute value, and log loss function.

The problem of overfitting is one of the key issues in the ML method. Therefore, empirical and structural risks should be minimized. The regular term $J\left(f\right)$ is introduced to measure the model complexity. The frequently employed regular terms are Lasso and Ridge regression. The final optimized objective function can be expressed as follows:

$Obj=min\frac{1}{M}{\displaystyle \sum _{i=1}^{M}L\left(y,f\left(x\right)\right)+\lambda J\left(f\right)}(2)$

ML methods are divided into supervised, unsupervised, and semi-supervised learning methods (Lei et al., 2020). The current study also classifies the ML-based WT fault diagnosis methods as the supervised, unsupervised, and semi-supervised learning methods, which are analyzed and discussed in the following sections.

Supervised Learning Methods for Wind Turbine Fault Diagnosis

Supervised learning is a process of adjusting classifier parameters using samples of a known class to achieve the desired performance. In supervised learning (Schwenker and Trentin, 2014; Zhou, 2018), the computer is received the example inputs and its required outputs, given input and output, and the target is to learn a general rules of mapping input to output. Supervised learning methods are widely used in the WT fault diagnosis field. As shown in Figure 4, supervised learning methods have different algorithms for specific problems. First, we take WT fault diagnosis (Jiménez et al., 2019) as the research object to obtain data from the SCADA of WTs; divide the training, validation, and the test sets and perform data preprocessing on the data set; and normalize the data after processing the missing values. Second, an ML algorithm is chosen to train the training set which is used for modeling. Thirdly, the test set is used to evaluate the model quality. Lastly, an accurate fault classification is obtained by continuously optimizing the fault diagnosis model of the WT.

FIGURE 4

FIGURE 4. Flowchart of WT fault diagnosis based on the supervised Learning method.

Artificial Neural Network

Artificial neural network (ANN) (Agatonovic-Kustrin et al., 2000; Xi et al., 2020) is one of the most frequently used supervised learning algorithms. ANN consists of numerous neurons and is divided into input layer, hidden layer, and output layer. ANN is widely used in the fault diagnosis field (Samanta et al., 2003; Saravanan and Ramachandran, 2010). By learning from known fault samples, the mapping relationship between fault characteristics and fault categories is established to detect whether a device is faulty. Figure 5 shows a three-layer simple WT fault diagnosis model based on ANN, $x_1,x_2,\dots ,x_n$ are the input characteristics of WT, n is the total sample of input characteristics, and m is the total fault types of WT.

FIGURE 5

FIGURE 5. ANN-based WT fault diagnosis model.

The frequently employed neural network methods include adaptive resonance theory (ART), self-organizing map (SOM) neural network and radial basis function (RBF) neural network.

Zhang et al. (Zhang and Wang, 2014). proposed an ANN-based fault diagnosis method for the WT main bearing based on the WT SCADA system data. The difference between the theoretical and the actual parameter values can identify the early stage of the main bearing faults of WT. To decrease the time of ANN for WT fault detection, Bielecki et al. (2014) proposed a hybrid method of ART and RBF neural networks for online detection of the operating status of WT, which can monitor the status of WT in time, identify the early fault conditions and have good real-time performance. However, the actual engineering in a wind farm cannot collect all information on the fault, and the ANN cannot make accurate fault diagnosis. Therefore, Zhao (Zhao et al., 2015) proposed to apply the SOM neural network to the fault diagnosis of WT and to train the network through the sample data of the normal WT state. This is judged whether the wind turbine malfunctions according to the position of the output neuron in the output layer. Accordingly, the SOM neural network method can effectively diagnose the WT fault with good robustness.

Although the fault diagnosis of ANN has high precision and good robustness, this method requires numerous parameters for modeling, and the training model takes a long time. China’s wind power industry started late, but WT fault diagnosis research has been developed in the recent years. However, WT fault data samples are considerably lacking, and the accuracy and completeness of the WT data samples directly affect the accuracy of fault diagnosis classification. This issue is currently the main drawback restricting the development of ANN in WT fault diagnosis.

Support Vector Machine

Support vector machine (SVM) is a kernel-based ML method used in regression problems and classification tasks introduced by Vapnik (2013). The main idea is to find two parallel hyperplanes to separate two sets of data in a multi-dimensional space and maximize the margin between the hyperplanes. SVM formulation ensures that the decision hyperplane is constructed with structural risk minimization to obtain a balance between empirical risk and complexity of model (Deka, 2014). SVM is mainly used in nonlinear problems, by building a classification hyperplane as a decision plane, in which the isolation boundry between negative and positive samples is maximized. As shown in Figure 6, any hyperplane can be represented by a normal vector W and a constant b (intercept) as follows:

$w^{T}x+b=1(3)$

$w^{T}x+b=0(4)$

$w^{T}x+b=-1(5)$

For point $\text{A}(x_1,y_1)$, any two hyperplanes have a geometric interval d.

FIGURE 6

FIGURE 6. Interval and support vector machine.

SVM is to find a hyperplane to make the data points separable, in which the minimum geometric distance is the largest. The SVM solution process can be regarded as the solution process of a convex quadratic problem, which has a global optimal solution. Thus, SVM is widely used in the fault diagnosis field.

To solve the local optimal phenomenon caused by the improper selection of sample parameters, Laouti et al. (2011) chose a radial basis function as the kernel parameter of SVM, which can immediately detect the WT blade pitch positionand generator failureand has good generalization performance. To further solve the problem of overfitting or underfitting caused by the improper selection of nuclear parameters, Tang et al. (2014) proposed a method of WT fault diagnosis based on the Shannon wavelet SVM (SWSVM) and manifold learning. In this method, mixed-domain features are extracted to construct a high-dimensional feature set, manifold learning is used to compress the high-dimensional feature set into low-dimensional eigenvectors, and low-dimensional eigenvectors are inputted into an SWSVM to recognize WT gearbox faults. Gao et al. (2018) proposed a novel fault diagnosis method of WT that combines mean decomposition, multi-scale entropy, least squares, and SVM. In this method, the WT raw vibration signal is divided into several groups for preprocessing. Thereafter, the mean decomposition method is applied to group the signals to obtain the product function. Moreover, the feature parameters are obtained using the multi-scale entropy method of processing the main product function to obtain the feature vector. The characteristic parameters were input into the least squares SVM, which was trained. This method can significantly enhance the fault classification ability of a single SVM and classify the fault type precisely. In the case of single kernel parameters and parameter optimization, Zhao et al. (2018) proposed a fault diagnosis method of WT based on random subspace identification and multi-kernel SVM. Compared with the traditional SVM, the multi-kernel SVM can successfully identify the bearing fault of the WT and has higher fault diagnosis accuracy. In the classification problem, there are not only two classification problems, but also multi classification problems. SVM can also show good classification ability in the face of two classification problems. (Liu K. et al., 2020) used multi-SVM machine to diagnose the fault of renewable energy power grid, which effectively improves the accuracy of fault diagnosis. (Xue et al., 2017). proposed a fault intelligent diagnosis method combining optimal composition of symptom parameters (SPOC) and multi-SVM to diagnose the motor fault, and realized the fault detection and identification of multiple motor faults. In recent years, with the wide application of SVM, experts began to optimize and improve SVM, put forward some machine learning algorithms derived from SVM, put them into the field of fault diagnosis, and achieved good results. (Zhang and Zhou, 2014; Tang et al., 2019).introduced margin mean and margin variance on the basis of SVM and proposed a large margin distributed machine (LDM), and this method has better classification performance than SVM. (Tang et al., 2020a) used LDM to detect the fault of WT’s pitch system and optimized it with state transition algorithm (STA), which significantly improved the accuracy of fault detection.

SVM uses inner product kernel function to turn the raw data into linear data through mapping the raw data to a high-dimensional space. However, modeling WT big data is difficult, and the selection of kernel parameters also affects the fault diagnosis accuracy. Moreover, guaranteeing the classification of multi-type WT fault problems is difficult.

Decision Tree

Decision tree (DT) is composed of multiple judgment nodes, and a classification or regression model is formed by the tree structure (Safavian and Landgrebe, 1991). The basic idea is simple, and Figure 7 shows a WT fault diagnosis model based on DT.

FIGURE 7

FIGURE 7. WT fault diagnosis method based on decision tree.

Rabah et al. (Benkercha and Moulahoum, 2018) proposed a fault diagnosis method for a grid-connected WT generator system based on the DT algorithm with high prediction performance and high accuracy. Abdallah et al. (2018) adopted the DT algorithm to perform fault diagnosis on WT, continuously sampled extensive data from thousands of WT at a high rate, and trained integrated DT classifier. Compared with other ML algorithms, DT is easy to implement but it has limitations in dealing with missing values. The WT fault diagnosis process, there are few samples of fault type and more samples of fault-free type. For DT that deals with data with inconsistent sample sizes in various categories, information gain is biased toward features with additional numerical values, which is easy to overfit and minimally used in WT fault diagnosis.

Ensemble Learning

The basic concept of ensemble learning (Polikar, 2012; Liu et al., 2019) is to adjust and train multiple base learners as ensemble members into a strong learner that should have greater performance on average than any other ensemble member. Thereafter, a model is estabilshed by optimizing the loss function to advance the performance of fault classification. The frequently employed ensemble learning methods include bagging, boosting.

Bootstrap aggregating, also called bagging (Breiman, 1996) applied in regression and statistical classification, is an ML ensemble that obtains a new data set by returning the samples, trains a better base learner based on each new data set, and eventually combines the base learners. The algorithm reduces variance and helps to prevent overfitting. Typical bagging algorithm including random forest (RF). A diagnosis method (Cabrera et al., 2015) was presented for detecting the faults of WT gearboxes, which is based on Random Forest. First, the condition parameters of the vibration signal are extracted by wavelet packet decomposition and used as the input feature of the classification problem. Second, a study approximates the parameter space to find the best mother wave set, and select the best feature through the internal ranking of the random forest classifier. Lastly, the RF algorithm is used to detect the fault of the WT gearbox. To further improve the fault detection rate, Li et al. (2016) proposed a method based on deep RF fusion (DRFF) to improve the fault detection performance of the WT gearboxes. Two deep Boltzmann machines are used to characterize the parameter values of the wavelet packet transform, and the output of the two deep Boltzmann machines is fused into an integrated DRFF model using an RF algorithm. The results indicate that DRFF may improve fault diagnosis capabilities for gearboxes compared with conventional RF.

Boosting (Freund and Schapire, 1996) adjusts the algorithm by giving considerable importance to the bad classification that results in significant improvements in performance of classification. The bagging algorithm focuses on reducing bias facilitates prevention of overfitting. Many algorithms are based on boosting methods, such as XGBoost and LightGBM. Zhang et al. (2018) proposed an efficient WT fault detection method based on the RF and XGBoost. RF is used to rank the features by importance, while XGBoost trains the ensemble classifier for each specific fault based on the top-ranking features. The proposed ensemble classifier can protect against overfitting and experiments verifies the robustness of this method. To enhance the fault diagnosis accuracy, Tang et al. (2020b) proposed the adaptive LightGBM method for the WT gearbox fault detection. The correlation of the WT data samples is analyzed using the maximum information coefficient to realize the feature selection of fault detection. Meanwhile, the LightGBM method after Bayesian hyperparameter optimization is used for the fault detection of WT gearbox. Experiments prove that this method has a low false alarm rate and missing detection rates.

Ensemble learning is widely used in fault diagnosis and early warning of WT with high accuracy. However, some algorithms have slow convergence speed, weak learners rely heavily on one another, and over-fitting problems occur. When using the ensemble methods, the number of iterations, number of base learners, and weights are the issues that should be considered.

Deep Learning

Deep learning was proposed by Hinton et al. (LeCun et al., 2015), and the basic idea is a ML process that includes a multi-level deep network structure through a certain training method based on sample data. Deep learning combines low level features to form a considerably abstract high-level representation to discover the distributed feature representations of data. Deep learning (Schmidhuber, 2015; Goodfellow et al., 2016) is widely used in image processing, data mining, fault diagnosis (Helbing and Ritter, 2018), and other fields. Different deep learning (Jiang et al., 2018) configurations have also been introduced such as deep belief nets (DBNs), deep auto-encoder (DAE) network, and convolutional neural networks (CNNs).

Toward the WT gearbox faults, Qin et al. (2018) proposed a novel fault diagnosis method that combines DBNs and improved logical Sigmoid unit for the WT gearbox. The integrated approach, which uses the optimized Morlet wavelet transform, kurtosis index, and soft-thresholding is used to extract impulse components from original signals to advance the accuracy of dignosis. Compared with the traditional Sigmoid method, the WT gearbox fault diagnosis method based on deep confidence network and improved logical Sigmoid unit has the higher comprehensive performance. To achieve anomaly diagnosis and fault analysis of WT components, Zhao et al. (2018) proposed a deep learning method based on DAE networks using the WT SCADA data, while the Boltzmann machine builds a deep automatic encoder network model. This method can realize the early warning of the faulty component and derive the physical location of the faulty WT component through the residual of the deep autoencoder network model. Since the diverse operating status of WT with a large amount of noise interference, which leads to a decrease in the accuracy of fault diagnosis of WT. To solve this problem, Chang et al. (2020) proposed a fault diagnosis method for WT based on a concurrent convolution neural network (CeCNN). The raw WT data do not require any prior knowledge, and the characteristics are learned adaptively and directly from input with high accuracy and powerful generalization ability. The convolutional layers of different branches select kernels of varying scales at the same level, thereby improving the accuracy of the WT fault diagnosis. Yi and Jiang (2020) proposed a DAE-based discriminative feature learning for WT blade icing fault detection.

Although deep learning has a strong learning ability and high fault diagnosis accuracy, it requires extensive data and computing power with high cost and high hardware requirements, which are current issues should be considered.

Unsupervised Learning Methods for Wind Turbine Fault Diagnosis

The basic idea of unsupervised learning is the process that a machine learns unlabeled data to reveal the hidden structure, explain the key features of data, and divides them into several categories. Representative technique is clustering. Many algorithms typically used in unsupervised learning are based on the clustering method. Unlike supervised learning methods that analyzes class-labeled instances, unsupervised learning (Figueiredo et al., 2002; Zhang T. and Zhou Z. H., 2018) does not need all information, but trains the information of unlabeled samples. The sample set is clustered according to the similarity between the samples to minimize the intraclass variance and maximize the interclass variance, thereby establishing the model. Unsupervised learning methods can classify and predict test data by extracting hidden concepts and relationships in the data set, which are widely used in fault diagnosis, data mining, and image processing among others. Many methods are typically employed in unsupervised learning, such as the K-means algorithm, fuzzy C-means (FCM), hierarchical clustering method, Gaussian mixture model, and other methods (Hastie et al., 2009).

K-Means

K-means clustering (Kanungo et al., 2002; Jain, 2010) is a simple unsupervised learning method which aims to divide n observations into K clusters, in which the observation belongs to the cluster with the nearest mean. First, we initialize cluster centers and determine K initial points in the data as the center of clustering; Second, we calculate the distance from each point to the center and assign it to the nearest cluster. Third, we recalculate the cluster center to minimize the internal sum. Lastly, the allocation and update operations are repeated until the centers of all clusters no longer change. If all points are allocated to the same cluster as before, then K-means clustering is completed. For example, given the data set of WTs, K-means algorithm was used for clustering and the five types of clustering result is shown in Figure 8.

FIGURE 8

FIGURE 8. K-means clustering.

To overcome the sensitivity of K-means to the choice of the initial cluster centers, Yiakopoulos et al. (2011) proposed a K-means clustering method for fault diagnosis of rolling bearings, and the initial centers are selected using features extracted from simulated signals. The fault detection experiments on three types of bearings show that this method can successfully classify faults. Khediri et al. (2012) proposed an unsupervised learning process based on kernel technology, which can separate different non-linear process modes, and effectively detect faults, and reduce the false alarm rate. Kusiak et al. (Kusiak and Verma, 2012) used three different operating curves (i.e., power rotor and blade pitch curves) to monitor the performance of wind farms, and proposed a multivariate outlier based on Mahalanobis distance and K-means clustering. This method, uses the skewness and kurtosis of bivariate data as metrics to evaluate the WT performance, which is simple to apply and has a rapid convergence speed.

K-means clustering is simple to implement and has a good effect on WT fault diagnosis. However, the choice of the initial cluster center K is difficult to grasp and even cause difficulty in convergence in the case of non-convex data sets. WT has many fault-free samples and few samples of faults, which will result in poor clustering effect when the amount of data is unbalanced.

Fuzzy C-Means

The FCM algorithm (Bezdek et al., 1984; Pal et al., 2005) is a clustering algorithm in which each data point can belong to more than one cluster. The basic idea is to maximize the similarity between objects divided into the same cluster while minimizing the similarity between viaroius clusters.

Given the WT gearboxes fault detection, Luo et al.(Luo and Huang, 2014) proposed a fault diagnosis method based on global local mean decomposition and FCM clustering. In this method, the known sample was clustered using the FCM clustering, and the test sample was classified and recognized, which has simple implementation and good diagnosis results. Although the WT fault diagnosis methods require supervision and training based on historical samples of known faults, collecting samples of known faults is time-consuming and expensive. Given the lack of complete characteristics of known samples in WT, Li et al. (2015) presented a method based on the kernel FCM (KFCM)clustering to the fault diagnosis of the WT gearbox. The KFCM clustering algorithm is used to classify the samples of known samples, and the classification center of each known fault is obtained. Similarity parameters are also calculated to diagnose whether the new data samples belong to the known faults. This method can accurately and effectively diagnose the known and unknown faults of WT.

Some issues should be considered when the FCM algorithm is used in the WT fault diagnosis. For example, a large fault-free sample size and extremely small fault sample size may lead to failure, thereby ensuring that the optimal solution of the fault diagnosis model is found.

Hierarchical Clustering

Hierarchical clustering (Johnson, 1967; Corpet, 1988) is a cluster analysis method in unsupervised learning, which builds a model by establishing a hierarchical structure of clusters. The hierarchical clustering method can be represented as a tree structure (i.e., “tree diagram”, which includes roots and leaves. In clustering tree species, the original data points of different categories are the lowest level of the tree, and the top level of the tree is the root node of a cluster. As shown in Figure 9, the hierarchical clustering method (Navarro et al., 1997) involves a process that starts from the leaves and successively merges clusters called agglomerative hierarchical clustering; or a process that begins from the root and recursively splits the clusters called divisive hierarchical clustering. The hierarchical clustering method uses Euclidean distance to calculate the distance between the data points of different categories.

FIGURE 9

FIGURE 9. Hierarchical clustering method.

Li Y. et al. (2018) proposed a fault diagnosis method based on adaptive multi-scale morphological filters and improved hierarchical arrangement entropy to identify varoius health situations of gearboxes, and used the hierarchical aggregation method to reduce noise fault features extracted from the signal. Liu and Ge (2018) presented a weighted random forest scheme based on hierarchical clustering selection for fault classification in complex industrial processes. The application of the hierarchical clustering method to offline model selection in RF can reduce the complexity of online fault classification.

In the fault diagnosis process of WT, the need to calculate the proximity matrix in the hierarchical clustering algorithm, is time-consuming, and unsuitable for use in the WT big data sets. Hierarchical clustering method is appropriate for the clustering of small data sets, and real-time issues should be considered when dealing with the WT big data.

Gaussian Mixture Model

The Gaussian mixture model (GMM) (Reynolds, 2009) assumes that all data points conform to the Gaussian distribution, and is generated from a mixed finite number of probability models with unknown parameters. GMM can be regarded as the process of fitting a linear combination of multiple Gaussian distribution functions to perform data distribution.

Heyns et al. (2012) proposed a Gaussian hybrid model to detect WT gearbox failures and calculate the negative log-likelihood of the gearbox bearing vibration signal segment, which represents the healthy gearbox. This method is suitable for nonlinear and non-stationary wind turbine gearbox vibration signals. Given the highly complex and unstable operating conditions of WT, Dong et al. (2013) proposed a multi-parameter WT health assessment framework that considers dynamic operating conditions. After the characteristic parameter selection and GMM based multi-regime modeling, the operation status of WT can be evaluated, which can effectively detect WT faults. In response to frequent WT faults, Luis et al. (Avendaño-Valencia et al., 2017) proposed a fault diagnosis method for WT based on a GMM random coefficient model. The vibration response signals of WT that change with time under the environment and operating conditions are extracted and the model coefficients are determined through the GMM random coefficient framework. The method offering significant performance improvements and most fault levels and types are represented to be correctly diagnosed.

GMM is effective in handling the big volume of WT data samples, but it has a large calculation amount and slow convergence. Selecting the number of sub-models in advance is difficult and is sensitive to abnormal points. When processing small data set samples in WT, the result cannot meet the requirements.

Semi-supervised Learning Methods for Wind Turbine Fault Diagnosis

Semi-supervised learning (Chapelle et al., 2009; Zhou et al., 2014) is a learning paradigm that detects some common features of labeled data samples and unlabeled data samples to help determine the model characteristics and to disseminate labels from labeled data to unlabeled ones, which is an ML method between supervised and unsupervised learning. In selecting data sets, combining unlabeled samples and labeled samples in the training process can improve training accuracy. There are four mainstream paradigms for semi-supervised learning (Zhu, 2005), are the semi-supervised SVM (S3VM), generative model-based, disagreement-based, and graph-based methods. Disagreement-based semi-supervised learning (Blum and Mitchell, 1998) started with the work on co-training (Zhou and Li, 2005) by Blum, which is less affected by the non-convexity of the loss function and the data size and is mainly used in the field of human-computer interaction. The graph-based method (Camps-Valls et al., 2007) was developed by the graph min-cut method (Blum and Chawla, 2001) proposed by Blum, but it is rarely seen in WT fault diagnosis. The method based on S3VM and generative model is also applied in WT fault diagnosis.

S3VM

S3VM (Bennett and Demiriz, 1998) involves the development of SVM in semi-supervised learning (Wang et al., 2017). The major idea of S3VM is to mark unlabeled samples to maximize the interval after the hyperplane is divided. The frequently used S3VM is a transductive SVM (TSVM). The basic idea of this method can be presented as five steps. The first step involves training an SVM classifier with labeled samples. The second step entails using SVM to predict the classification results of unlabeled data. The third step aims to find the opposite label in the predicted unlabeled data that may be wrong for the labeled sample to swap the label, and use the existing labeled sample and unlabeled sample to retrain SVM; The fourth step involves repeating the second and third steps until the best S3VM classifier is obtained. The fifth step entails using use the S3VM classifier to label the unlabeled samples and predict the classification results.

The S3VM methods are widely used in the field of WT fault diagnosis. Liu C. et al. (2020) proposed a fault diagnosis method for rolling bearing based on S3VM using only a few labeled samples to build a model with good classification effect. In order to reduce false alarm rates and improve the discriminative ability of incipient fault features, Mao et al. (2020) proposed an online method for early fault detection of bearings using a semi-supervised architecture. A safe semi-supervised SVM (S4VM) is introduced to identify the sequentially arrived data of the goal bearing as anomalous or normals and fault states and a stacked noise reduction automatic encoder is used to extract depth features from the normal state data and fault state data of the bearing. According to the S4VM generalization error upper bound to adaptively identify the occurrence of an incipient fault. Optimal margin distribution learning machine (ODM), which is also classified based on split hyperplane, has also appeared semi-supervised ODM(ssODM) in recent years, and has been applied to wind turbine fault detection with good performance (Zhang T. and Zhou Z.-H., 2018).

S3VM predicts the unlabeled samples, adds the prediction results to the labeled data set and improves the fault diagnosis rate. However, S3VM should determine a few known WT data samples as a guide. Accordingly, we cannot ensure such WT data samples with delicate information and it is uncertain to know how many WT data samples are needed to achieve an effective S3VM model.

Generative Models

The main idea of the semi-supervised generative model is that the probability that unlabeled samples belong to each category as a set of missing parameters. Thereafter, the expectation maximization (EM) algorithm is used to perform maximum likelihood estimate on the parameters of the generated model. Generative model methods (Zhu, 2005; Kingma et al., 2014) include mixed Gaussian distribution, mixture multinomial distribution, and hidden Markov model.

Ge et al.(Xin et al., 2018) proposed a semi-automatic fault detection method based on a probabilistic model in the form of a hybrid Gaussian with good robustness. Wang et al. (Wang et al., 2015) proposed a comprehensive method based on semi-supervised learning, using a small amount of labeled data and a large amount of unlabeled process data to construct a neighborhood weighted graph. By solving the optimization problem, the optimal regression function and the optimal prediction label matrix of unlabeled data are acquired. This method can obtain the promised results of fault detection and fault diagnosis in the monitoring process. To achieve automatic detections, Omid et al. (Geramifard et al., 2013) introduced a semi-parametric method based on the hidden Markov model for fault detection and diagnosis of synchronous motors. After training the hidden Markov model classifier (parameter stage), which is based on each probabilistic (non-parametric stage) hidden Markov model. Moreover, the probabilistic inference are used to compute two matrices to solve the efficiency problem in the fault classification process. Li X. et al. (2018) presented a fault detection method on a multivariate Bayesian control scheme and a hidden semi-Markov model to predict early bearing failures of gearboxes. The method of using the continuous-time hidden semi-Markov decision process to characterize the failure process of the gearbox bearing system, which can predict the early failure of the gearbox bearing and detect the remaining useful life at each sampling epoch.

The semi-supervised generative model method has good robustness, but the fault diagnosis model has low accuracy, long model training time, and many iterations. These issues must be considered in WT fault diagnosis.

Conclusion and Perspectives

Given the rapid development of early wind power generation, wind power equipment has entered a high failure period, and the fault diagnosis methods of WT have high requirements for their operation and maintenance stability. Accordingly, the development fault prediction, fault diagnosis, fault detection, and condition monitoring of WT have improved. Various studies have proposed various methods and strategies for the fault diagnosis and detection of various WT components (Faiz and Moosavi, 2016). Following studies and research on the most recent WT fault diagnosis methods, the current study gathers a review of WT fault diagnosis methods and techniques based onML. Given the many uncertainties in the WT operation, many issues should continue to be considered in the ML-based fault diagnosis of WT.

Improvement of ML algorithms effects. Many types of ML algorithms have advantages and disadvantages, in which among the research fields in the future include improving algorithm performance, optimizing algorithm parameters, combining algorithms, and studying new algorithms. Given that the algorithm has advantages and disadvantages, the need to adopt the advantages and bypass the disadvantages in the algorithm have become urgent issues to be addressed. Moreover, a single algorithm cannot detect all WT faults. Hence, the combined algorithm will become a hot research topic in the future. The advantages and disadvantages of existing algorithms indicated that future research involves proposing and improving new algorithms.

Comprehensive simulation of WT fault conditions. The wind power generation system is a typical complex system, given the uncertain severity and probability of faults. In the research on the WT fault mechanism, only a single fault is modeled, and the single component faults of WT are accompanied by multiple faults, which causes serious damage to WT. All WT units are interconnected and their variables are highly coupled. The occurrence of a fault in a particular component affects all remaining units. Therefore, additional compound fault models should be established to conduct a comprehensive analysis of the WT system.

Research on the feature selection method. WT have many characteristic parameters because the operation state of WT is time-varying Redundant and useless feature parameters will inevitably exist in WT feature extraction. Given the need to extract additional fault features, the research on optimized feature extraction algorithms will become popular in the future, thereby enabling us to better describe and detect the status of WT.

Multi-parameter information fusion. A single sensor or piece of single parameter information cannot acquire dedicated WT operating status information, which entails difficulty in accurately reflecting the fault or normal state of each WT component. Therefore, a multi-parameter information fusion method is adopted to obtain additional parameter information from multiple sensors and improve the efficiency of fault diagnosis.

Establishment of remote WT fault diagnosis system. The WT fault diagnosis system should be able to predict fault and provide the period plan maintenance to keep the WT minimum downtime and maintain long-distance condition monitoring. Long-term available historical data should be provided by the WT fault diagnosis system to set the correct alarm for preventive maintenance. In large wind farms, multiple wind power generation systems must be installed for fault diagnosis and early warning. The need to develop a low-cost and high-efficient remote WT fault diagnosis system should also be considered in the future.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 62173050 and 61403046), the Natural Science Foundation of Hunan Province, China (Grant No. 2019JJ40304), Changsha University of Science and Technology “The Double First Class University Plan” International Cooperation and Development Project in Scientific Research in 2018 (Grant No. 2018IC14), the Research Foundation of the Education Bureau of Hunan Province (Grant No.19K007), Hunan Provincial Department of Transportation 2018 Science and Technology Progress and Innovation Plan Project (Grant No. 201843), Energy Conservation and Emission Reduction Hunan University Student Innovation and Entrepreneurship Education Center, Innovative Team of Key Technologies of Energy Conservation, Emission Reduction and Intelligent Control for Power-Generating Equipment and System, CSUST, Hubei Superior and Distinctive Discipline Group of Mechatronics and Automobiles (XKQ2021003 and XKQ2021010), Major Fund Project of Technical Innovation in Hubei (Grant No. 2017AAA133), and Guangxi Key Laboratory of Trusted Software (No.201728), Graduate Scientific Research Innovation Project of Changsha University of Science and Technology (No. 2021-89).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdallah, I., Dertimanis, V., Mylonas, H., Tatsis, K., Chatzi, E., Dervili, N., et al. (2018). “Fault Diagnosis of Wind Turbine Structures Using Decision Tree Learning Algorithms with Big Data,” in 2018 European Safety and Reliability Conference (ESREL 2018), Trondheim, Norway, 3053–3061. doi:10.1201/9781351174664-382

CrossRef Full Text | Google Scholar

Agatonovic-Kustrin, S., Beresford, R., and analysis, b. (2000). Basic Concepts of Artificial Neural Network (ANN) Modeling and its Application in Pharmaceutical Research. J. Pharm. Biomed. Anal. 22 (5), 717–727. doi:10.1016/S0731-7085(99)00272-1

CrossRef Full Text | Google Scholar

Avendaño-Valencia, L. D., Fassois, S. D., and Processing, S. (2017). Damage/fault Diagnosis in an Operating Wind Turbine under Uncertainty via a Vibration Response Gaussian Mixture Random Coefficient Model Based Framework. Mech. Syst. Signal Process. 91, 326–353. doi:10.1016/j.ymssp.2016.11.028

CrossRef Full Text | Google Scholar

Benkercha, R., and Moulahoum, S. (2018). Fault Detection and Diagnosis Based on C4.5 Decision Tree Algorithm for Grid Connected PV System. Solar Energy 173, 610–634. doi:10.1016/j.solener.2018.07.089

CrossRef Full Text | Google Scholar

Bennett, K. P., and Demiriz, A. (1998). “Semi-supervised Support Vector Machines,” in Advances in Neural Information Processing Systems, 368–374.)

Google Scholar

Bezdek, J. C., Ehrlich, R., and Full, W. J. (1984). FCM: The Fuzzy C-Means Clustering Algorithm. Comput. Geosciences 10 (2-3), 191–203. doi:10.1016/0098-3004(84)90020-7

CrossRef Full Text | Google Scholar

Bielecki, A., Barszcz, T., Wójcik, M., and Bielecka, M. (2014). “Hybrid System of ART and RBF Neural Networks for Classification of Vibration Signals and Operational States of Wind Turbines,” in International Conference on Artificial Intelligence and Soft Computing (Springer), 3–11. doi:10.1007/978-3-319-07173-2_1

CrossRef Full Text | Google Scholar

Blum, A., and Chawla, S. (2001). “Learning from Labeled and Unlabeled Data Using Graph Mincuts,” in ICML '01: Proceedings of the Eighteenth International Conference on Machine Learning, 19–26.

Google Scholar

Blum, A., and Mitchell, T. (1998). “Combining Labeled and Unlabeled Data with Co-training,” in Proceedings of the eleventh annual conference on Computational learning theory, 92–100. doi:10.1145/279943.279962

CrossRef Full Text | Google Scholar

Breiman, L. (1996). Bagging Predictors. Mach Learn. 24 (2), 123–140. doi:10.1007/BF00058655

CrossRef Full Text | Google Scholar

Cabrera, D., Sancho, F., Sánchez, R.-V., Zurita, G., Cerrada, M., Li, C., et al. (2015). Fault Diagnosis of spur Gearbox Based on Random forest and Wavelet Packet Decomposition. Front. Mech. Eng. 10 (3), 277–286. doi:10.1007/s11465-015-0348-8

CrossRef Full Text | Google Scholar

Camps-Valls, G., Bandos Marsheva, T. V., and Zhou, D. (2007). Semi-supervised Graph-Based Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sensing 45 (10), 3044–3054. doi:10.1109/TGRS.2007.895416

CrossRef Full Text | Google Scholar

Chang, Y., Chen, J., Qu, C., and Pan, T. (2020). Intelligent Fault Diagnosis of Wind Turbines via a Deep Learning Network Using Parallel Convolution Layers with Multi-Scale Kernels. Renew. Energ. 153, 205–213. doi:10.1016/j.renene.2020.02.004

CrossRef Full Text | Google Scholar

Chapelle, O., Scholkopf, B., and Zien, Eds., A. (2009). Semi-Supervised Learning. IEEE Trans. Neural Netw. 20 (3), 542. doi:10.1109/TNN.2009.2015974

CrossRef Full Text | Google Scholar

Chen, J., Li, Z., Pan, J., Chen, G., Zi, Y., Yuan, J., et al. (2016a). Wavelet Transform Based on Inner Product in Fault Diagnosis of Rotating Machinery: A Review. Mech. Syst. Signal Process. 70-71, 1–35. doi:10.1016/j.ymssp.2015.08.023

CrossRef Full Text | Google Scholar

Chen, J., Pan, J., Li, Z., Zi, Y., and Chen, X. (2016b). Generator Bearing Fault Diagnosis for Wind Turbine via Empirical Wavelet Transform Using Measured Vibration Signals. Renew. Energ. 89, 80–92. doi:10.1016/j.renene.2015.12.010

CrossRef Full Text | Google Scholar

Cho, S., Gao, Z., and Moan, T. (2018). Model-based Fault Detection, Fault Isolation and Fault-Tolerant Control of a Blade Pitch System in Floating Wind Turbines. Renew. Energ. 120, 306–321. doi:10.1016/j.renene.2017.12.102

CrossRef Full Text | Google Scholar

Clifton, A., Kilcher, L., Lundquist, J. K., and Fleming, P. (2013). Using Machine Learning to Predict Wind Turbine Power Output. Environ. Res. Lett. 8 (2), 024009. doi:10.1088/1748-9326/8/2/024009

CrossRef Full Text | Google Scholar

Corpet, F. (1988). Multiple Sequence Alignment with Hierarchical Clustering. Nucleic Acids Res. 16 (22), 10881–10890. doi:10.1093/nar/16.22.10881

PubMed Abstract | CrossRef Full Text | Google Scholar

Dao, P. B., Staszewski, W. J., Barszcz, T., and Uhl, T. (2018). Condition Monitoring and Fault Detection in Wind Turbines Based on Cointegration Analysis of SCADA Data. Renew. Energ. 116, 107–122. doi:10.1016/j.renene.2017.06.089

CrossRef Full Text | Google Scholar

de Azevedo, H. D. M., Araújo, A. M., and Bouchonneau, N. (2016). A Review of Wind Turbine Bearing Condition Monitoring: State of the Art and Challenges. Renew. Sustainable Energ. Rev. 56, 368–379. doi:10.1016/j.rser.2015.11.032

CrossRef Full Text | Google Scholar

Ding, S. X. (2012). Data-driven Design of Model-Based Fault Diagnosis Systems. IFAC Proc. Volumes 45 (15), 840–847. doi:10.3182/20120710-4-SG-2026.00105

CrossRef Full Text | Google Scholar

Dong, Y., Fang, F., and Gu, Y. (2013). Dynamic Evaluation of Wind Turbine Health Condition Based on Gaussian Mixture Model and Evidential Reasoning. J. Renew. Sustainable Energ. 5 (3), 033117. doi:10.1063/1.4808018

CrossRef Full Text | Google Scholar

Du, Z., Chen, X., Zhang, H., and Yan, R. (2015). Sparse Feature Identification Based on union of Redundant Dictionary for Wind Turbine Gearbox Fault Diagnosis. IEEE Trans. Ind. Electron. 62 (10), 6594–6605. doi:10.1109/TIE.2015.2464297

CrossRef Full Text | Google Scholar

Elizondo, J. L., Rivera, M., and Wheeler, P. (2019). “Wind Energy Development and Technology in the World: A Brief Overview,” in 2019 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON) (IEEE), 1–5. doi:10.1109/CHILECON47746.2019.8987714

CrossRef Full Text | Google Scholar

Faiz, J., and Moosavi, S. M. M. (2016). Eccentricity Fault Detection - from Induction Machines to DFIG-A Review. Renew. Sustainable Energ. Rev. 55, 169–179. doi:10.1016/j.rser.2015.10.113

CrossRef Full Text | Google Scholar

Figueiredo, M. A. T., Jain, A. K., and intelligence, m. (2002). Unsupervised Learning of Finite Mixture Models. IEEE Trans. Pattern Anal. Mach. Intell. 24 (3), 381–396. doi:10.1109/34.990138

CrossRef Full Text | Google Scholar

Freund, Y., and Schapire, R. E. (1996). “Experiments with a New Boosting Algorithm,” in Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, 148–156.

Google Scholar

Gao, Q. W., Liu, W. Y., Tang, B. P., and Li, G. J. (2018). A Novel Wind Turbine Fault Diagnosis Method Based on Intergral Extension Load Mean Decomposition Multiscale Entropy and Least Squares Support Vector Machine. Renew. Energ. 116, 169–175. doi:10.1016/j.renene.2017.09.061

CrossRef Full Text | Google Scholar

Gao, Z., Cecati, C., and Ding, S. X. (2015). A Survey of Fault Diagnosis and Fault-Tolerant Techniques-Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 62 (6), 3757–3767. doi:10.1109/TIE.2015.2417501

CrossRef Full Text | Google Scholar

Garg, H., and Dahiya, R. (2017). Current Signature Analysis and its Application in the Condition Monitoring of Wind Turbine for Rotor Faults. Energy Syst. 8 (3), 495–510. doi:10.1007/s12667-016-0208-6

CrossRef Full Text | Google Scholar

Geramifard, O., Xu, J.-X., and Kumar Panda, S. (2013). Fault Detection and Diagnosis in Synchronous Motors Using Hidden Markov Model-Based Semi-nonparametric Approach. Eng. Appl. Artif. Intelligence 26 (8), 1919–1929. doi:10.1016/j.engappai.2013.06.005

CrossRef Full Text | Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT press.

Google Scholar

Habibi, H., Howard, I., and Simani, S. (2019). Reliability Improvement of Wind Turbine Power Generation Using Model-Based Fault Detection and Fault Tolerant Control: A Review. Renew. Energ. 135, 877–896. doi:10.1016/j.renene.2018.12.066

CrossRef Full Text | Google Scholar

Habibi, H., Rahimi Nohooji, H., and Howard, I. (2017). Power Maximization of Variable-Speed Variable-Pitch Wind Turbines Using Passive Adaptive Neural Fault Tolerant Control. Front. Mech. Eng. 12 (3), 377–388. doi:10.1007/s11465-017-0431-4

CrossRef Full Text | Google Scholar

Hahn, B., Durstewitz, M., and Rohrig, K. (2007). “Reliability of Wind Turbines,” in Wind Energy (Springer), 329–332. doi:10.1007/978-3-540-33866-6_62

CrossRef Full Text | Google Scholar

Hastie, T., Tibshirani, R., and Friedman, J. (2009). “Unsupervised Learning,” in The Elements of Statistical Learning (Springer), 485–585. doi:10.1007/978-0-387-84858-7_14

CrossRef Full Text | Google Scholar

Helbing, G., and Ritter, M. (2018). Deep Learning for Fault Detection in Wind Turbines. Renew. Sustainable Energ. Rev. 98, 189–198. doi:10.1016/j.rser.2018.09.012

CrossRef Full Text | Google Scholar

Heyns, T., Heyns, P. S., and De Villiers, J. P. (2012). Combining Synchronous Averaging with a Gaussian Mixture Model novelty Detection Scheme for Vibration-Based Condition Monitoring of a Gearbox. Mech. Syst. Signal Process. 32, 200–215. doi:10.1016/j.ymssp.2012.05.008

CrossRef Full Text | Google Scholar

Himani, R., and Dahiya, R. (2018). Condition Monitoring of Wind Turbine for Rotor Fault Detection under Non Stationary Conditions. Ain Shams Eng. J. 9 (4), 2441–2452. doi:10.1016/j.asej.2017.04.002

CrossRef Full Text | Google Scholar

Hongshan, Z., Gao, Y., Liu, H., Li, L., and Energy, C. (2019). Fault Diagnosis of Wind Turbine Bearing Based on Stochastic Subspace Identification and Multi-Kernel Support Vector Machine. J. Mod. Power Syst. Clean. Energ. 7 (2), 350–356. doi:10.1007/s40565-018-0402-8

CrossRef Full Text | Google Scholar

Hossain, M. M., Ali, M. H., and reviews, S. e. (2015). Future Research Directions for the Wind Turbine Generator System. Renew. Sustainable Energ. Rev. 49, 481–489. doi:10.1016/j.rser.2015.04.126

CrossRef Full Text | Google Scholar

Igba, J., Alemzadeh, K., Durugbo, C., and Eiriksson, E. T. (2016). Analysing RMS and Peak Values of Vibration Signals for Condition Monitoring of Wind Turbine Gearboxes. Renew. Energ. 91, 90–106. doi:10.1016/j.renene.2016.01.006

CrossRef Full Text | Google Scholar

Jain, A. K. (2010). Data Clustering: 50 Years beyond K-Means. Pattern recognition Lett. 31 (8), 651–666. doi:10.1016/j.patrec.2009.09.011

CrossRef Full Text | Google Scholar

Jiang, G., He, H., Yan, J., and Xie, P. (2019). Multiscale Convolutional Neural Networks for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Ind. Electron. 66 (4), 3196–3207. doi:10.1109/TIE.2018.2844805

CrossRef Full Text | Google Scholar

Jiménez, A. A., Muñoz, C. Q. G., Márquez, F. P. G. J. R. E., and Safety, S. (2019). Dirt and Mud Detection and Diagnosis on a Wind Turbine Blade Employing Guided Waves and Supervised Learning Classifiers. Reliability Engineering%System Saf. 184, 2–12. doi:10.1016/j.ress.2018.02.013

CrossRef Full Text | Google Scholar

Johnson, S. C. (1967). Hierarchical Clustering Schemes. Psychometrika 32 (3), 241–254. doi:10.1007/BF02289588

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanungo, T., Mount, D. M., Netanyahu, N. S., Piatko, C. D., Silverman, R., Wu, A. Y., et al. (2002). An Efficient K-Means Clustering Algorithm: Analysis and Implementation. IEEE Trans. Pattern Anal. Machine Intell. 24 (7), 881–892. doi:10.1109/TPAMI.2002.1017616

CrossRef Full Text | Google Scholar

Khediri, I. B., Weihs, C., and Limam, M. (2012). Kernel K-Means Clustering Based Local Support Vector Domain Description Fault Detection of Multimodal Processes. Expert Syst. Appl. 39 (2), 2166–2171. doi:10.1016/j.eswa.2011.07.045

CrossRef Full Text | Google Scholar

Kingma, D. P., Mohamed, S., Rezende, D. J., and Welling, M. (2014). “Semi-supervised Learning with Deep Generative Models,” in Advances in neural information processing systems, 3581–3589.

Google Scholar

Kusiak, A., and Verma, A. (2013). Monitoring Wind Farms with Performance Curves. IEEE Trans. Sustain. Energ. 4 (1), 192–199. doi:10.1109/TSTE.2012.2212470

CrossRef Full Text | Google Scholar

Lan, J., Patton, R. J., and Zhu, X. (2018). Fault-tolerant Wind Turbine Pitch Control Using Adaptive Sliding Mode Estimation. Renew. Energ. 116, 219–231. doi:10.1016/j.renene.2016.12.005

CrossRef Full Text | Google Scholar

Laouti, N., Sheibat-Othman, N., and Othman, S. (2011). Support Vector Machines for Fault Detection in Wind Turbines. IFAC Proc. Volumes 44 (1), 7067–7072. doi:10.3182/20110828-6-IT-1002.02560

CrossRef Full Text | Google Scholar

Leahy, K., Hu, R. L., Konstantakopoulos, I. C., Spanos, C. J., and Agogino, A. M. (2016). “Diagnosing Wind Turbine Faults Using Machine Learning Techniques Applied to Operational Data,” in 2016 IEEE International Conference on Prognostics and Health Management (ICPHM) (IEEE), 1–8. doi:10.1109/ICPHM.2016.7542860

CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. nature 521 (7553), 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, Y., Yang, B., Jiang, X., Jia, F., Li, N., and Nandi, A. K. (2020). Applications of Machine Learning to Machine Fault Diagnosis: A Review and Roadmap. Mech. Syst. Signal Process. 138, 106587. doi:10.1016/j.ymssp.2019.106587

CrossRef Full Text | Google Scholar

Li, C., Sanchez, R.-V., Zurita, G., Cerrada, M., Cabrera, D., Vásquez, R. E., et al. (2016). Gearbox Fault Diagnosis Based on Deep Random forest Fusion of Acoustic and Vibratory Signals. Mech. Syst. Signal Process. 76-77, 283–293. doi:10.1016/j.ymssp.2016.02.007

CrossRef Full Text | Google Scholar

Li, X., Makis, V., Zuo, H., Cai, J., and Engineering, I. (2018a). Optimal Bayesian Control Policy for Gear Shaft Fault Detection Using Hidden Semi-markov Model. Comput. Ind. Eng. 119, 21–35. doi:10.1016/j.cie.2018.03.026

CrossRef Full Text | Google Scholar

Li, Y., Li, G., Yang, Y., Liang, X., Xu, M., and Processing, S. (2018b). A Fault Diagnosis Scheme for Planetary Gearboxes Using Adaptive Multi-Scale Morphology Filter and Modified Hierarchical Permutation Entropy. Mech. Syst. Signal Process. 105, 319–337. doi:10.1016/j.ymssp.2017.12.008

CrossRef Full Text | Google Scholar

Liang, J., Zhang, K., Al-Durra, A., and Zhou, D. (2020). A Novel Fault Diagnostic Method in Power Converters for Wind Power Generation System. Appl. Energ. 266, 114851. doi:10.1016/j.apenergy.2020.114851

CrossRef Full Text | Google Scholar

Lin, Y., Tu, L., Liu, H., and Li, W. (2016). Fault Analysis of Wind Turbines in China. Renew. Sustainable Energ. Rev. 55, 482–490. doi:10.1016/j.rser.2015.10.149

CrossRef Full Text | Google Scholar

Liu, C., Gryllias, K., and Processing, S. (2020a). A Semi-supervised Support Vector Data Description-Based Fault Detection Method for Rolling Element Bearings Based on Cyclic Spectral Analysis. Mech. Syst. Signal Process. 140, 106682. doi:10.1016/j.ymssp.2020.106682

CrossRef Full Text | Google Scholar

Liu, H., Chen, C., Lv, X., Wu, X., and Liu, M. (2019). Deterministic Wind Energy Forecasting: A Review of Intelligent Predictors and Auxiliary Methods. Energ. Convers. Management 195, 328–345. doi:10.1016/j.enconman.2019.05.020

CrossRef Full Text | Google Scholar

Liu, K., Dong, W., Dong, H., Wei, J., and Xiao, S. (2020b). A Complex Fault Diagnostic Approach of Active Distribution Network Based on SBS-SFS Optimized Multi-SVM. Math. Probl. Eng. 2020, 1–12. doi:10.1155/2020/8423571

CrossRef Full Text | Google Scholar

Liu, W. Y., Tang, B. P., Han, J. G., Lu, X. N., Hu, N. N., He, Z. Z., et al. (2015). The Structure Healthy Condition Monitoring and Fault Diagnosis Methods in Wind Turbines: A Review. Renew. Sustainable Energ. Rev. 44, 466–472. doi:10.1016/j.rser.2014.12.005

CrossRef Full Text | Google Scholar

Liu, X., Gao, Z., and Chen, M. Z. Q. (2017). Takagi-Sugeno Fuzzy Model Based Fault Estimation and Signal Compensation with Application to Wind Turbines. IEEE Trans. Ind. Electron. 64 (7), 5678–5689. doi:10.1109/TIE.2017.2677327

CrossRef Full Text | Google Scholar

Liu, Y., and Ge, Z. (2018). Weighted Random Forests for Fault Classification in Industrial Processes with Hierarchical Clustering Model Selection. J. Process Control. 64, 62–70. doi:10.1016/j.jprocont.2018.02.005

CrossRef Full Text | Google Scholar

Luo, X., and Huang, X. (2014). Fault Diagnosis of Wind Turbine Based on Elmd and Fcm. Tomej 8 (1), 716–720. doi:10.2174/1874155X01408010716

CrossRef Full Text | Google Scholar

Mao, W., Tian, S., Fan, J., Liang, X., and Safian, A. (2020). Online Detection of Bearing Incipient Fault with Semi-supervised Architecture and Deep Feature Representation. J. Manufacturing Syst. 55, 179–198. doi:10.1016/j.jmsy.2020.03.005

CrossRef Full Text | Google Scholar

MUA. (2017). Global Wind Report. Brussels: Global Wind Energy Council.

Google Scholar

Nasiri, M., Milimonfared, J., Fathi, S. H., and Reviews, S. E. (2015). A Review of Low-Voltage Ride-Through Enhancement Methods for Permanent Magnet Synchronous Generator Based Wind Turbines. Renew. Sustainable Energ. Rev. 47, 399–415. doi:10.1016/j.rser.2015.03.079

CrossRef Full Text | Google Scholar

Navarro, J. F., Frenk, C. S., and White, S. D. M. (1997). A Universal Density Profile from Hierarchical Clustering. ApJ 490 (2), 493–508. doi:10.1086/304888

CrossRef Full Text | Google Scholar

Ouanas, A., Medoued, A., Mordjaoui, M., Lebaroud, A., and Sayad, D. (2018). Fault Diagnosis in Yaw Drive Induction Motor for Wind Turbine. Wind Eng. 42 (6), 576–595. doi:10.1177/0309524X18780379

CrossRef Full Text | Google Scholar

Pal, N. R., Pal, K., Keller, J. M., and Bezdek, J. C. (2005). A Possibilistic Fuzzy C-Means Clustering Algorithm. IEEE Trans. Fuzzy Syst. 13 (4), 517–530. doi:10.1109/TFUZZ.2004.840099

CrossRef Full Text | Google Scholar

Pei, Y., Qian, Z., Jing, B., Kang, D., and Zhang, L. (2018). Data-driven Method for Wind Turbine Yaw Angle Sensor Zero-point Shifting Fault Detection. Energies 11 (3), 553. doi:10.3390/en11030553

CrossRef Full Text | Google Scholar

Polikar, R. (2012). “Ensemble Learning,” in Ensemble Machine Learning (Springer), 1–34. doi:10.1007/978-1-4419-9326-7_1

CrossRef Full Text | Google Scholar

Qiao, W., and Lu, D. (2015). A Survey on Wind Turbine Condition Monitoring and Fault Diagnosis-Part I: Components and Subsystems. IEEE Trans. Ind. Electron. 62 (10), 6536–6545. doi:10.1109/TIE.2015.2422112

CrossRef Full Text | Google Scholar

Qin, S. J. (2012). Survey on Data-Driven Industrial Process Monitoring and Diagnosis. Annu. Rev. Control 36 (2), 220–234. doi:10.1016/j.arcontrol.2012.09.004

CrossRef Full Text | Google Scholar

Qin, Y., Wang, X., and Zou, J. (2019). The Optimized Deep Belief Networks with Improved Logistic Sigmoid Units and Their Application in Fault Diagnosis for Planetary Gearboxes of Wind Turbines. IEEE Trans. Ind. Electron. 66 (5), 3814–3824. doi:10.1109/TIE.2018.2856205

CrossRef Full Text | Google Scholar

Raghavendra. N, S., and Deka, P. C. (2014). Support Vector Machine Applications in the Field of Hydrology: a Review. Appl. soft Comput. 19, 372–386. doi:10.1016/j.asoc.2014.02.002

CrossRef Full Text | Google Scholar

Reynolds, D. (2009). Gaussian Mixture Models. Encyclopedia of biometrics 741, 659–663. doi:10.1007/978-0-387-73003-5_196

CrossRef Full Text | Google Scholar

Safavian, S. R., and Landgrebe, D. (1991). A Survey of Decision Tree Classifier Methodology. IEEE Trans. Syst. Man. Cybern. 21 (3), 660–674. doi:10.1109/21.97458

CrossRef Full Text | Google Scholar

Salameh, J. P., Cauet, S., Etien, E., Sakout, A., Rambault, L., and Processing, S. (2018). Gearbox Condition Monitoring in Wind Turbines: A Review. Mech. Syst. Signal Process. 111, 251–264. doi:10.1016/j.ymssp.2018.03.052

CrossRef Full Text | Google Scholar

Samanta, B., Al-Balushi, K. R., and processing, s. (2003). Artificial Neural Network Based Fault Diagnostics of Rolling Element Bearings Using Time-Domain Features. Mech. Syst. Signal Process. 17 (2), 317–328. doi:10.1006/mssp.2001.1462

CrossRef Full Text | Google Scholar

Saravanan, N., and Ramachandran, K. I. (2010). Incipient Gear Box Fault Diagnosis Using Discrete Wavelet Transform (DWT) for Feature Extraction and Classification Using Artificial Neural Network (ANN). Expert Syst. Appl. 37 (6), 4168–4181. doi:10.1016/j.eswa.2009.11.006

CrossRef Full Text | Google Scholar

Schmidhuber, J. (2015). Deep Learning in Neural Networks: An Overview. Neural networks 61, 85–117. doi:10.1016/j.neunet.2014.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwenker, F., and Trentin, E. (2014). Pattern Classification and Clustering: A Review of Partially Supervised Learning Approaches. Pattern Recognition Lett. 37, 4–14. doi:10.1016/j.patrec.2013.10.017

CrossRef Full Text | Google Scholar

Silva, J. C. d., Saxena, A., Balaban, E., and Goebel, K. (2012). A Knowledge-Based System Approach for Sensor Fault Modeling, Detection and Mitigation. Expert Syst. Appl. 39 (12), 10977–10989. doi:10.1016/j.eswa.2012.03.026

CrossRef Full Text | Google Scholar

Stetco, A., Dinmohammadi, F., Zhao, X., Robu, V., Flynn, D., Barnes, M., et al. (2019). Machine Learning Methods for Wind Turbine Condition Monitoring: A Review. Renew. Energ. 133, 620–635. doi:10.1016/j.renene.2018.10.047

CrossRef Full Text | Google Scholar

Tang, B., Song, T., Li, F., and Deng, L. (2014). Fault Diagnosis for a Wind Turbine Transmission System Based on Manifold Learning and Shannon Wavelet Support Vector Machine. Renew. Energ. 62, 1–9. doi:10.1016/j.renene.2013.06.025

CrossRef Full Text | Google Scholar

Tang, M., Ding, S. X., Yang, C., Cheng, F., Shardt, Y. A. W., Long, W., et al. (2019). Cost-sensitive Large Margin Distribution Machine for Fault Detection of Wind Turbines. Cluster Comput. 22, 7525–7537. doi:10.1007/s10586-018-1854-3

CrossRef Full Text | Google Scholar

Tang, M., Hu, J., Kuang, Z., Wu, H., Zhao, Q., and Peng, S. (2020a). Fault Detection of the Wind Turbine Variable Pitch System Based on Large Margin Distribution Machine Optimized by the State Transition Algorithm. Math. Probl. Eng. 2020, 1–9. doi:10.1155/2020/9718345

CrossRef Full Text | Google Scholar

Tang, M., Zhao, Q., Ding, S. X., Wu, H., Li, L., Long, W., et al. (2020b). An Improved LightGBM Algorithm for Online Fault Detection of Wind Turbine Gearboxes. Energies 13 (4), 807. doi:10.3390/en13040807

CrossRef Full Text | Google Scholar

Teng, W., Ding, X., Zhang, X., Liu, Y., and Ma, Z. (2016). Multi-fault Detection and Failure Analysis of Wind Turbine Gearbox Using Complex Wavelet Transform. Renew. Energ. 93, 591–598. doi:10.1016/j.renene.2016.03.025

CrossRef Full Text | Google Scholar

Toubakh, H., and Sayed-Mouchaweh, M. (2016). Hybrid Dynamic Classifier for Drift-like Fault Diagnosis in a Class of Hybrid Dynamic Systems: Application to Wind Turbine Converters. Neurocomputing 171, 1496–1516. doi:10.1016/j.neucom.2015.07.073

CrossRef Full Text | Google Scholar

Vapnik, V. (2013). The Nature of Statistical Learning Theory. Springer science & business media.

Google Scholar

Wang, J., Peng, Y., and Qiao, W. (2016a). Current-aided Order Tracking of Vibration Signals for Bearing Fault Diagnosis of Direct-Drive Wind Turbines. IEEE Trans. Ind. Electron. 63 (10), 6336–6346. doi:10.1109/TIE.2016.2571258

CrossRef Full Text | Google Scholar

Wang, L., Zhang, Z., Long, H., Xu, J., and Liu, R. (2017b). Wind Turbine Gearbox Failure Identification with Deep Neural Networks. IEEE Trans. Ind. Inf. 13 (3), 1360–1368. doi:10.1109/TII.2016.2607179

CrossRef Full Text | Google Scholar

Wang, T., Han, Q., Chu, F., and Feng, Z. (2019). Vibration Based Condition Monitoring and Fault Diagnosis of Wind Turbine Planetary Gearbox: A Review. Mech. Syst. Signal Process. 126, 662–685. doi:10.1016/j.ymssp.2019.02.051

CrossRef Full Text | Google Scholar

Wang, W., Xi, J., Chong, A., and Li, L. (2017). Driving Style Classification Using a Semisupervised Support Vector Machine. IEEE Trans. Human-mach. Syst. 47 (5), 650–660. doi:10.1109/THMS.2017.2736948

CrossRef Full Text | Google Scholar

Wang, X., Feng, H., and Fan, Y. (2015). Fault Detection and Classification for Complex Processes Using Semi-supervised Learning Algorithm. Chemometrics Intell. Lab. Syst. 149, 24–32. doi:10.1016/j.chemolab.2015.10.019

CrossRef Full Text | Google Scholar

Xi, L., Wu, J., Xu, Y., Sun, H., and Systems, L. (2021). Automatic Generation Control Based on Multiple Neural Networks with Actor-Critic Strategy. IEEE Trans. Neural Netw. Learn. Syst. 32 (6), 2483–2493. doi:10.1109/TNNLS.2020.3006080

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, G., Hamzaoui, N., and Antoni, J. (2018). Semi-automated Diagnosis of Bearing Faults Based on a Hidden Markov Model of the Vibration Signals. Measurement 127, 141–166. doi:10.1016/j.measurement.2018.05.040

CrossRef Full Text | Google Scholar

Xue, H., Wang, M., Li, Z., and Chen, P. (2017). Sequential Fault Detection for Sealed Deep Groove ball Bearings of In-Wheel Motor in Variable Operating Conditions. J. Vibroeng 19 (8), 5947–5959. doi:10.21595/jve.2017.18413

CrossRef Full Text | Google Scholar

Yang, B., Liu, R., and Chen, X. (2017). Fault Diagnosis for a Wind Turbine Generator Bearing via Sparse Representation and Shift-Invariant K-SVD. IEEE Trans. Ind. Inf. 13 (3), 1321–1331. doi:10.1109/TII.2017.2662215

CrossRef Full Text | Google Scholar

Yang, T., Pen, H., Wang, Z., and Chang, C. S. (2016). Feature Knowledge Based Fault Detection of Induction Motors through the Analysis of Stator Current Data. IEEE Trans. Instrum. Meas. 65 (3), 549–558. doi:10.1109/TIM.2015.2498978

CrossRef Full Text | Google Scholar

Yang, X., Li, J., Liu, W., and Guo, P. (2011). Petri Net Model and Reliability Evaluation for Wind Turbine Hydraulic Variable Pitch Systems. Energies 4 (6), 978–997. doi:10.3390/en4060978

CrossRef Full Text | Google Scholar

Yi, H., and Jiang, Q. (2020). Discriminative Feature Learning for Blade Icing Fault Detection of Wind Turbine. Meas. Sci. Technol. 31, 115102. doi:10.1088/1361-6501/ab9bb8

CrossRef Full Text | Google Scholar

Yiakopoulos, C. T., Gryllias, K. C., and Antoniadis, I. A. (2011). Rolling Element Bearing Fault Detection in Industrial Environments Based on a K-Means Clustering Approach. Expert Syst. Appl. 38 (3), 2888–2911. doi:10.1016/j.eswa.2010.08.083

CrossRef Full Text | Google Scholar

Yin, S., Wang, G., and Karimi, H. R. (2014). Data-driven Design of Robust Fault Detection System for Wind Turbines. Mechatronics 24 (4), 298–306. doi:10.1016/j.mechatronics.2013.11.009

CrossRef Full Text | Google Scholar

Zappalá, D., Sarma, N., Djurović, S., Crabtree, C. J., Mohammad, A., and Tavner, P. J. (2019). Electrical & Mechanical Diagnostic Indicators of Wind Turbine Induction Generator Rotor Faults. Renew. Energ. 131, 14–24. doi:10.1016/j.renene.2018.06.098

CrossRef Full Text | Google Scholar

Zeng, R., Xu, L., Yao, L., Finney, S. J., and Wang, Y. (2016). Hybrid HVDC for Integrating Wind Farms with Special Consideration on Commutation Failure. IEEE Trans. Power Deliv. 31 (2), 789–797. doi:10.1109/TPWRD.2015.2440354

CrossRef Full Text | Google Scholar

Zhang, D., Qian, L., Mao, B., Huang, C., Huang, B., and Si, Y. (2018). A Data-Driven Design for Fault Detection of Wind Turbines Using Random Forests and XGboost. IEEE Access 6, 21020–21031. doi:10.1109/ACCESS.2018.2818678

CrossRef Full Text | Google Scholar

Zhang, T., and Zhou, Z.-H. (2014). “Large Margin Distribution Machine,” in Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining 2014 (New York, New York, USA: Association for Computing Machinery), 313–322. doi:10.1145/2623330.2623710

CrossRef Full Text | Google Scholar

Zhang, T., and Zhou, Z.-H. (2018b). “Semi-Supervised Optimal Margin Distribution Machines,” in Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence: IJCAI 2018, 3104–3110. doi:10.24963/ijcai.2018/431

CrossRef Full Text | Google Scholar

Zhang, T., and Zhou, Z. H. (2018a). “Optimal Margin Distribution Clustering,” in Proceedings of the AAAI Conference on Artificial Intelligence.

Google Scholar

Zhang, Y., Lu, W., and Chu, F. (2017). Planet Gear Fault Localization for Wind Turbine Gearbox Using Acoustic Emission Signals. Renew. Energ. 109, 449–460. doi:10.1016/j.renene.2017.03.035

CrossRef Full Text | Google Scholar

Zhang, Z.-Y., and Wang, K.-S. (2014). Wind Turbine Fault Detection Based on SCADA Data Analysis Using ANN. Adv. Manuf. 2 (1), 70–78. doi:10.1007/s40436-014-0061-6

CrossRef Full Text | Google Scholar

Zhao, H., Liu, H., Hu, W., and Yan, X. (2018). Anomaly Detection and Fault Analysis of Wind Turbine Components Based on Deep Learning Network. Renew. Energ. 127, 825–834. doi:10.1016/j.renene.2018.05.024

CrossRef Full Text | Google Scholar

Zhao, L., Zuowei Pan, Z., Changsheng Shao, C., and Qianzhi Yang, Q. (2015). Application of SOM Neural Network in Fault Diagnosis of Wind Turbine. IET. doi:10.1049/cp.2015.0446

CrossRef Full Text | Google Scholar

Zhong, M., Xue, T., and Ding, S. X. (2018). A Survey on Model-Based Fault Diagnosis for Linear Discrete Time-Varying Systems. Neurocomputing 306, 51–60. doi:10.1016/j.neucom.2018.04.037

CrossRef Full Text | Google Scholar

Zhou, S., Chen, Q., and Wang, X. (2014). Fuzzy Deep Belief Networks for Semi-supervised Sentiment Classification. Neurocomputing 131, 312–322. doi:10.1016/j.neucom.2013.10.011

CrossRef Full Text | Google Scholar

Zhou, Z.-H. (2018). A Brief Introduction to Weakly Supervised Learning. Natl. Sci. Rev. 5 (1), 44–53. doi:10.1093/nsr/nwx106

CrossRef Full Text | Google Scholar

Zhou, Z. H., and Li, M. (2005). “Semi-Supervised Regression with Co-training,” in Proceedings of the 19th international joint conference on Artificial intelligence IJCAI, 908–913.

Google Scholar

Zhu, X. J. (2005). Semi-supervised Learning Literature Survey. University of Wisconsin-Madison Department of Computer Sciences.

Google Scholar

Zhuang Li, Z., Rui Jiang, R., Zhiyong Ma, Z., and Yibing Liu, Y. (2015). “Fault Diagnosis of Wind Turbine Gearbox Based on Kernel Fuzzy C-Means Clustering,” in International Conference on Renewable Power Generation, 1–4. doi:10.1049/cp.2015.0418

CrossRef Full Text | Google Scholar