- 1Department of Electrical Engineering, School of Mechatronics and Information Engineering, Putian University, Putian, China
- 2State Grid Sanming Electric Power Supply Company, Sanming, China
Power transformer is an essential component for the stable and reliable operation of electrical power grid. The traditional transformer fault diagnostic methods based on dissolved gas analysis are limited due to the low accuracy of fault identification. In this study, an effective transformer fault diagnosis system is proposed to improve identification accuracy. The proposed approach combines an improved genetic algorithm (IGA) with the XGBoost to form a hybrid diagnosis network. The combination of the improved genetic algorithm and the XGBoost (IGA-XGBoost) forms the basic unit of the proposed method, which decomposes and reconstructs the transformer fault recognition problem into several minor problems IGA-XGBoosts can solve. The results of simulation experiments show that the IGA performs excellently in the combined optimization of input feature selection and the XGBoost parameter, and the proposed method can accurately identify the transformer fault types with an average accuracy of 99.2%. Compared to IEC ratios, dual triangle, support vector machine and common vector approach the diagnostic accuracy of the proposed method is improved by 30.2, 47.2, 11.2, and 3.6%, respectively. The proposed method can be a potential solution to identify the transformer fault types.
1 Introduction
Power transformers are one of the most expensive, complex, and momentous equipment in electrical power systems. The faults of any power transformer online could cause considerable damage to the power system and lead to the interruption of the power supply. Therefore, the early detection of faults in transformers is vital to improving the reliability of the power system. Suffered the electrical and thermal stress during the operation, the transformer oil and organic insulating inside the transformer will be decomposed and generate different gases. Commonly, these dissolved gases include hydrogen (H2), methane (CH4), acetylene (C2H2), ethylene (C2H4), ethane (C2H6) and can provide abundant information about the internal states of the transformer. Based on the gas chromatography methods, the composition of the dissolved gases can be qualitatively and quantitatively measured and then used for the identification of the latent fault. There are three main kinds of chromatographic analysis method (Cheng and Yu, 2018) of dissolved gases namely the characteristic gas method (Fu et al., 2012), the gas production rate method (Nogami et al., 1995; Xi Chen et al., 2010; Zeng et al., 2011), and the three-ratio method (Jiang et al., 2014; Dhote and Helonde, 2012; Liu et al., 2020). The above methods generally utilize the concentration of a specific gaseous molecule or the ratios of several different molecules indicate the state of a power transformer (Shang et al., 2019). In addition, several improved methods have been proposed and applied for transformer fault diagnosis, including the Roger method (Ghoneim et al., 2016), the basic triangular diagram (Singh and Bandyopadhyay, 2010), the dual triangle method (Shang et al., 2019), etc. However, these methods have their inherent shortcomings. For example, most of these traditional diagnosis methods only make a limited contribution to a transformer’s fault diagnosis due to low diagnostic accuracy (Yadaiah and Ravi, 2011). Meanwhile, the three-ratio and improved three-ratio methods have disadvantages of incomplete coding and excessively absolute coding boundary (Cheng and Yu, 2018). Therefore, due to these defects of traditional methods, it is necessary to investigate new transformer fault diagnosis methods.
With the rapid development of computer science and artificial intelligence algorithms, many models are conducted by combining intelligence techniques with DGA methods to accurately detect fault types. The utilization of artificial neural network (ANN) (Colorado et al., 2011; Bhalla et al., 2012; Yi et al., 2016; Meng et al., 2010; Castro and Miranda, 2005; Miranda and Castro, 2005; Souahlia et al., 2012), expert system (Lin et al., 1993; Wang et al., 2000; Saha and Purkait, 2004; Mani and Jerome, 2014; Li et al., 2009), fuzzy theory (Huang et al., 1997; Mofizul Islam et al., 2000; Zhou et al., 1997; Fan et al., 2017; Naresh et al., 2008), grey system (Dong et al., 2003; Cheng et al., 2018), support vector machine (SVM) (Fei and Zhang, 2009; Fei et al., 2009; Liu et al., 2016; Niu Wu et al., 2010; Yin et al., 2011) and other theories have significantly improved the accuracy of fault identification. However, deficiencies occur together with these intelligent diagnostic approaches. Based on the ANN method, the intelligent fault diagnostic method is susceptible to be overfitting and may get a local optimum (Yuan et al., 2019). As for the expert system, the accuracy of this diagnostic method depends on the completeness of the expert knowledge, and this method cannot learn from new data samples automatically (Weigen Chen et al., 2009). In addition, fuzzy theory depends exceedingly on the experience of the researcher and is difficult to acquire an appropriate relationship between the input and output variables (Žarković and Stojković, 2017). SVM is originally a binary classification algorithm which makes it difficult to determine the parameters for multi-classification problem (Zhu et al., 2018). A single intelligent approach for transformer fault diagnosis has various shortcomings and can not reflect all the operation status of the transformer. Various intelligent algorithms can be combined to form a hybrid network for mutual complementation to solve complex problems, which has been applied in electricity. Researchers in (Xi et al., 2020) proposed a deep-reinforcement-learning-based three-network double-delay actor-critic (TDAC) control strategy for the automatic generation control (AGC) to deal with the strong random disturbance issues caused by renewable energy. Researchers in (Zhang et al., 2020) proposed a predictive control (MPC) based model combined with real-time optimal mileage based dispatch (OMD) for generating company responding to AGC dispatch signals in real-time. The above hybrid networks perform excellently in dealing with complex problems. As for the transformer fault diagnosis, a diagnostic method can be conducted with a hybrid network that combines different algorithms.
To achieve the objective of improving the accuracy of transformer fault diagnosis, a machine learning algorithm named XGBoost was employed as the classifier for the transformer fault identification in this paper, which is a scalable end-to-end tree boosting system (Chen and Guestrin, 2016). An improved genetic algorithm (IGA) is used for input feature selection and the XGBoost’s optimization. Then an intelligent diagnostic method based on the combination of the IGA and the XGBoost classifier (IGA-XGBoost) is built. The remainder of this paper is organized as follows. Section 2 presents the details of the proposed method, and section 3 shows the experimental results and performance analysis. Section 4 is the conclusion of this paper.
2 Proposed Methods
In this section, the proposed method for power transformer faults detection and recognition is explained in detail. Different methods based on the artificial intelligence algorithms and DGA methods have been proposed to classify transformer faults, and the most significant issue which impacts the accuracy of fault classification is the appropriate selection of input features and classifiers (Tightiz et al., 2020). Consideration has been given to these two aspects in the proposed method.
2.1 Candidate Input Features
Intelligent transformer faults diagnosis methods proposed by other researchers commonly combine DGA methods with artificial intelligence algorithms in the last decades. The gas ratios or gas concentrations used in DGA methods are adopted as the inputs of these intelligent fault diagnosis methods. Nonetheless, not all the gas ratios or gas concentrations have the same significance for fault identification. Using uninformative features as inputs leads to artificial noise and poor performance in transformer faults diagnosis. Hence, effective features should be selected as the input, and uninformative features must be removed. In this study, following the traditional DGA methods, the concentrations of the dissolved gases or the ratios of several different gases are collected as candidate feature set for the input feature selection, as shown in Table 1. In Table 1, TH = CH4 + C2H4 + C2H2 and TH1 = CH4 + C2H4 + C2H2 + C2H6.

TABLE 1. The candidate feature set for intelligent fault diagnosis methods. Gas concentrations (ppm) and ratio of gas concentrations in the table.
2.2 Genetic Algorithm
2.2.1 Tradtional Genetic Algorithm and Improved Genetic Algorithm
It is common practice to separate the process of input feature selection from the classifier optimization process, which neglects interaction between the feature selection and the classifier optimization may lead to unreliable results (Daelemans et al., 2003). Combined optimization of the feature selection and the classifier’ parameters can be achieved by genetic algorithm within a single approach. Since the traditional genetic algorithm (TGA) is prone to get trapped in the local optimal and fails to find the optimal global solution. In this paper, some improvements have been made to the TGA to enhance its global search capability, and an IGA is obtained. The IGA is utilized to combine the feature selection process with the classifier optimization process and assess which combination of input features and classifier’s parameters substantially impact the accuracy of fault diagnosis to gain the optimal input features and the classifier’s parameters. The difference between the TGA and the IGA is shown in Figure 1. Figure 1A shows the structure of the TGA, and Figure 1B shows the structure of the IGA. From 1A, it can be found that the main processes of the TGA include the population selection process and the population reproduction process. Two modifications make the IGA differ from the TGA: the high mutation rate of 0.3, and the other is the addition of elitist selection in the population selection process.
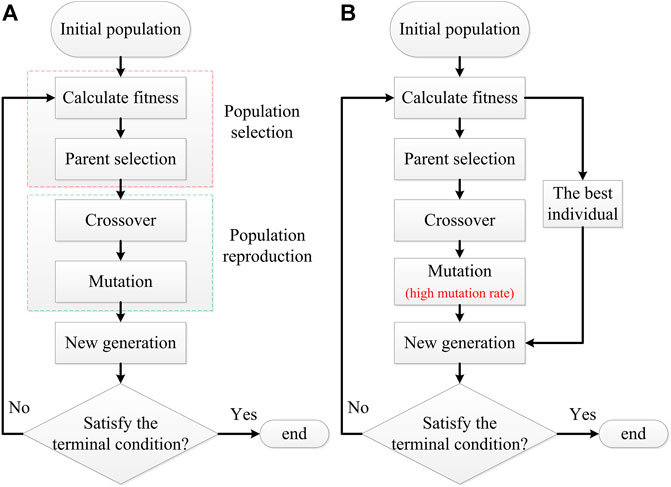
FIGURE 1. The structures of the TGA and the IGA, (A) is TGA’s structure, (B) is IGA’s structure. The IGA differs from GA with two modifications: the high mutation rate of 0.3, and the other is the addition of elitist selection in the population selection process.
In the population selection process of the TGA, the generation of candidate solutions after initialization is called the population. Each individual of the generated population has its chromosome coding to represent the parameters of the classifier and the input features extracted from DGA data, as shown in Figure 2. Each chromosome coding contains n bit strings, of which L1 to Ln-1 represent the classifier’s parameters, and the Ln bit string is used for the input feature selection. For feature selection, the bit with the value “1” in the Ln bit string represents the corresponding DGA feature is selected, and “0” means no selection. For the parameters setting of the classifier, the bit strings of parameters would be converted from the binary value to decimal value with a specific range by Eq. 1.
Here p represents chromosome coding of parameter, minp represents minimum value of the parameter, maxp represents maximum value of the parameter, d represents decimal value of bit string, and l represents length of bit string.

FIGURE 2. Structure of chromosome coding. Chromosome coding contains n bit strings, of which L1 to Ln-1 represent the classifier’s parameters, and the Ln bit string represents the DGA data used for the input feature.
The individuals of the population will then be selected for propagation by weighing their fitness values. The fitness values measure the population’s performance. The fitness function described in Eq. 2 uses the average accuracy of cross-validation for evaluation, and the higher the fitness value represents a better individual.
Here, k is the fold number of the cross-validation.
The probability of each individual of the population being selected is calculated in Eq. 3 by the roulette wheel selection method.
Here, n is the total number of individuals in each generation.
Then in the population reproduction process, crossover and mutation are employed to generate a new generation by the selected individuals of the population with a random mechanism. Crossover exchanges chromosome’s segments between two selected individuals stochastically, and the bit value in the chromosome will be converted from “0” to “1” or vice versa occasionally in the mutation process. New individuals are formed through crossover and mutation, which are different from the original. A new generation is created in this way. Population reproduction and selection processes can be repeated under the “survival of the fittest” to achieve an optimal result.
In the roulette wheel selection method, the greater the individual’s fitness is, the higher the possibility of such an individual would survive, but the optimal individual of each iteration still has a certain probability of being eliminated. Also, the process of crossover and mutation may lead to the disappearance of the optimal individual. Compared with TGA, the optimal individual of each iteration is added directly into the new generation in the IGA to avoid the disappearance of each iteration’s optimal individual as shown in Figure 1B, which is called elitist selection. Besides, the mutation rate is set at 0.3 instead of the conventional low value to make the IGA jump out of the local optimum. These two modifications can effectively improve the global search capability of the IGA and the accuracy of transformer fault identification, as will be discussed in the Simulation Result.
2.2.2 Performance Measures
The main objective of the IGA is to enhance search capability for the optimization problem and gain better solutions. To analyze the enhancement of search capability, the following performance measures are defined (Sugihara, 1997).
1) Average fitness value f(k): the average of the value obtained within k generations in n runs.
Here, fb(k) is the best fitness values obtained within k generations; n is the number of independent runs.
2) Likelihood of evolution leap Lel(k): the probability of average leaps within k generations among n independent runs. When a solution of one generation is better than the best solution obtained before the generation, the generation is said to be a leap.
Here, l is the average number of leaps within k generations; n is the number of independent runs.
3) Likelihood of optimality Lopt(k): the probability of obtaining optimal solutions within k generation in n independent runs.
Here, m is the number of runs which produced an optimal solution within k generations; n is the number of independent runs.
2.3 Transformer Fault Diagnosis System
The XGBoost is a scalable tree boosting system that has been successfully applied in world-class machine learning and data mining competition because it is robust enough to avoid overfitting (Zhang and Zhan, 2017). In addition, the XGBoost algorithm can take advantage of the original data directly without normalization. Thus, the XGBoost is utilized as the classifier of the transformer fault diagnosis system in this study. The DGA data is not fed directly into the classifier in the proposed method. Since 18 features are collected from DGA methods, as shown in Table 1, the application of complete input data is too time-consuming and could lower the accuracy of faults classification due to the artificial noise. Figure 3 shows the structure of the IGA-XGBoost. The IGA selects the input features fed to the XGBoost to decrease the input volume from 18 to a smaller number in the IGA-XGBoost. In addition, at the same time as input feature selection, the parameters of the XGBoost are decided by the IGA. The parameters of the XGBoost being decided by the IGA include eta, max_depth, min_child_weight, n_estimators, and n_gamma. The transformer fault diagnosis system described in Figure 4 is developed based on the IGA-XGBoost. Transformer states are classified into six categories, which contain normal (N), partial discharge (PD), high-energy discharge (D1), low-energy discharge (D2), low and middle-temperature overheat (T1&T2), and high-temperature overheating (T3). The fault recognition problem is decomposed and reconstructed into several more minor problems that can be solved one by one. Four IGA-XGBoost classifiers are used to detect and identify transformer faults. The IGA-XGBoost1 is trained to separate the normal samples from the fault samples. The selected fault samples by the IGA-XGBoost1 are fed to the trained IGA-XGBoost2 and classified as PD, D, and T. Then, the IGA-XGBoost3 and the IGA-XGBoost4 are used to identify the D1, D2, T1&2, and T3.
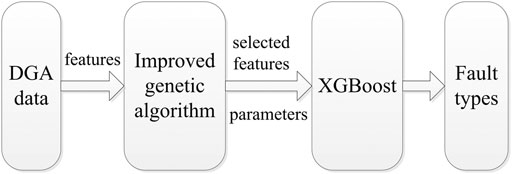
FIGURE 3. Structure of the IGA-XGBoost. The IGA is used for the combined optimization of the input features and the XGBoost parameters, and the trained XGBoost is used to identify the fault types.
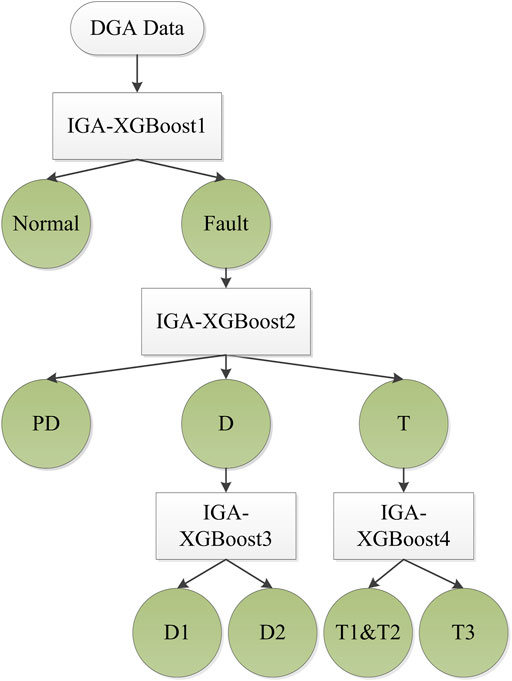
FIGURE 4. Structure of the transformer fault diagnosis system based on the IGA-XGBoost. Transformer states are classified into six categories, and four IGA-XGBoost classifiers are used to diagnose the fault type step by step in the transformer fault diagnosis system.
3 Simulation Result
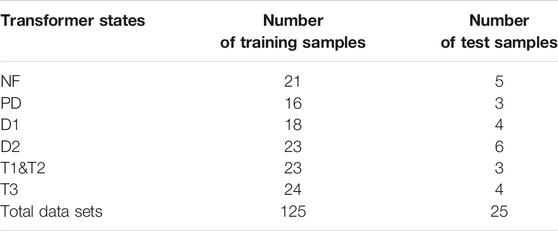
The DGA data set employed in this study is originated from Ref (Kirkbas et al., 2020). The data is divided into the training data set (125 samples) and the test data set (25 samples). These samples correspond to six states of the transformer. For each fault state, the number of samples used for the training and test process is shown in Table 2.
3.1 Performance of the Proposed Method
The proposed method is used for transformer fault diagnosis and compared with another transformer fault diagnosis system based on the TGA and the XGBoost, which has the same structure as the proposed method shown in Figure 4. The only difference between these two methods is that one uses the TGA while the other uses the IGA. To ensure the validity of the selected features and classifier parameters by IGA in the training process, the average accuracy of 8-fold cross-validation is taken as the fitness value. Therefore, the fitness curve is the average accuracy curve of cross-validation. The maximum generation number was 200. The initial population scale was set at 200, and the fitness of each iteration’s best individual was collected to form the best fitness curve shown in Figure 5. Figure 5 portrays the operation of the proposed method in five different independent implementations. Figure 6 compares the proposed method and the transformer fault diagnosis system based on the TGA and the XGBoost for the global best fitness value in the training process.
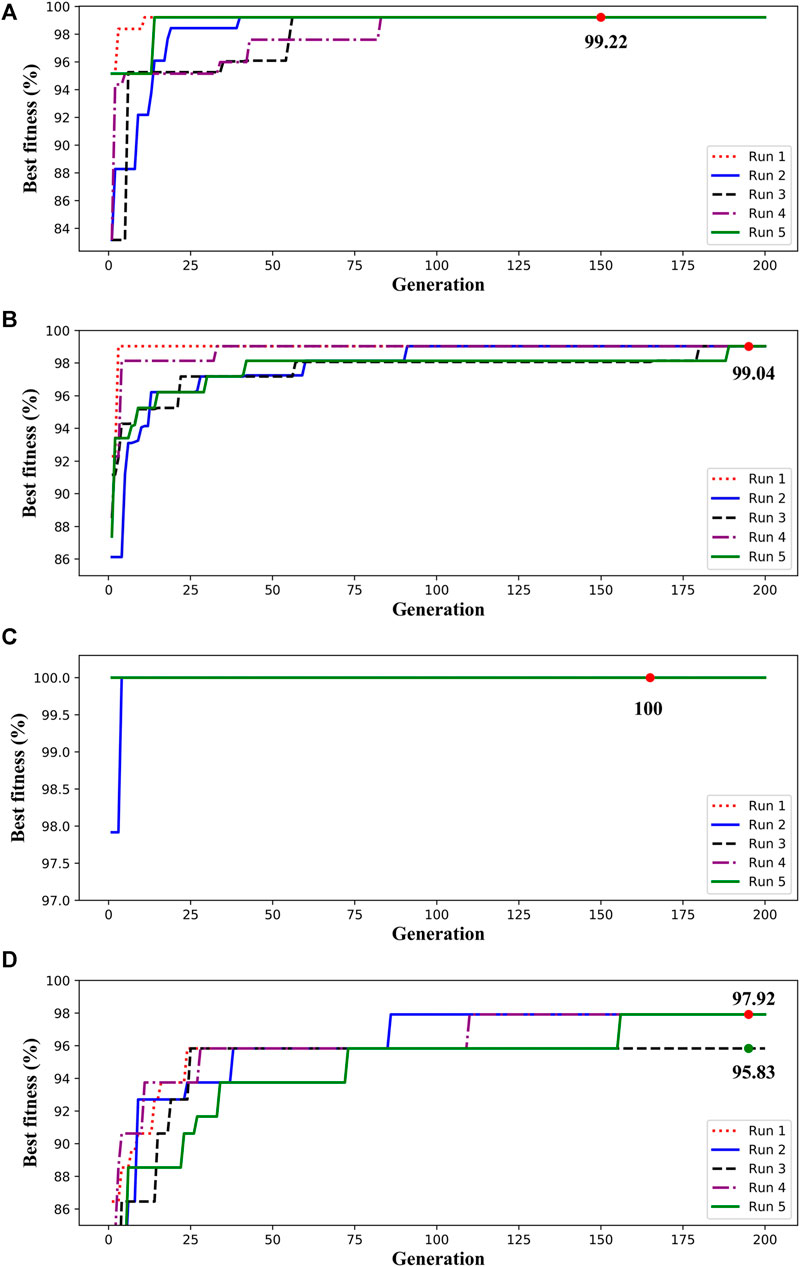
FIGURE 5. Performance of the transformer fault diagnosis system in training process, (A) is the best fitness curves of the IGA-XGBoost1 for N-F identification, (B) is the best fitness curves of the IGA-XGBoost2 for PD-D-T identification, (C) is the best fitness curves of the IGA-XGBoost3 for D1-D2 identification, (D) is the best fitness curves of the IGA-XGBoost4 for T1&2-T3 identification.
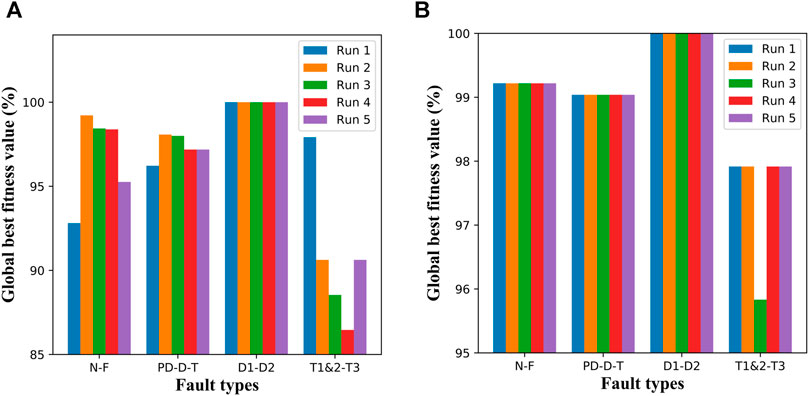
FIGURE 6. The comparison of the global best fitness value among methods, (A) is the global best fitness value of the TGA, (B) is the global best fitness value of the IGA. The higher the global fitness value represents a better solution.
It can be seen from Figure 5 that the proposed method can achieve the same fitness value for the normal or fault (N-F) identification in different independent experiments using the IGA-XGBoost1. The global best fitness value can reach 99.22%. When detecting PD, D, or T fault (PD-D-T), the IGA-XGBoost2 also can gain the same high global fitness value of 99.04%. Besides, the proposed method can even 100% distinguish D1 and D2 faults (D1-D2) using the IGA-XGBoost3. Although the global fitness value was not as high as that of other faults identification when detecting T1&2 or T3 fault (T1&2-T3), most of them reached 97.92%, with only one fitness value reaching 95.83%. Compared with the method based on the traditional GA and the XGBoost, as can be seen from Figure 6A, the global fitness value of the method based on the traditional GA and the XGBoost varies with independent implementations, and its global best fitness value is also significantly lower than that of the proposed method (see Figure 6B). For N-F identification, the global best fitness value of the method based on the TGA ranged from 92.8 to 98.4%. As for T1&2-T3 identification, the global best fitness value of the method based on the TGA ranged from 86.5 to 98.1%. It can be seen from the above results that the IGA can achieve better solutions.
Performance measures such as average fitness value, likelihood of evolution leap, and likelihood of optimality have been taken into consideration to measure the enhancement of the IGA in the optimization problem. Table 3 shows the average fitness value in the 100th and 200th generations for both the TGA and the IGA. Table 4 shows the likelihood of evolution leap in the 100th and 200th generations for both the TGA and the IGA. Table 5 shows the likelihood of optimality in the 100th and 200th generations for both TGA and the IGA. As can be seen from Table 3, compared with TGA, the average fitness values of IGA after 200 generations have increased 2.4, 1.7, 6.6% when detecting N-F, PD-D-T, and T1&2-T3, respectively. Besides, the average fitness values of IGA after 100 generations are higher than that of TGA after 200 generations, which proves that IGA has better search capability than the TGA. Table 4 shows the average number of evolution leaps of the IGA is higher than the TGA, which indicates that the IGA has a continuous change in solution from one generation to the next. Table 5 shows the probability of obtaining the optimal solution, the average likelihood of optimality of the IGA is 95%, compared to 30% of the TGA, which guarantees a feasible solution. The above results show that the IGA can get the optimal solution stably and reliably. For the test, Table 6 shows the recognition accuracy of different methods for the test samples. The results in Table 6 show that the proposed method has the best performance in transformer fault diagnosis with an average identification accuracy of 99.2%, compared to 94.4% of the method based on the TGA and XGBoost. Combined with the results of the test samples and the above results, it is shown that the proposed method can effectively and reliably identify transformer faults.
3.2 Comparison With Other Methods
In Table 7, the performance of the proposed method is also compared with other methods. The compared methods include DGA methods and intelligent transformer fault diagnosis methods, including IEC ratios, dual triangle, support vector machine, and common vector approach. The common vector approach has been recently introduced for the transformer fault diagnosis, and the support vector machine is a commonly used algorithm for transformer fault diagnosis. The result shows that the accuracy of DGA methods is relatively low, such as IEC ratios with an accuracy of 60% and the dual triangle method with an accuracy of 52%. In contrast to the DGA methods, intelligent transformer fault diagnosis methods based on intelligence algorithms and DGA methods have remarkable performance. The accuracy of the transformer fault identified by the proposed method is the highest, reaching 99.2%. Compared to 88% for support vector machines and 96% for CVA, the diagnostic accuracy of the proposed method was improved by 11.2 and 3.6%, respectively. The result proves that the proposed method can effectively improve the accuracy of transformer fault identification.
4 Conclusion
A novel and effective transformer fault diagnosis system based on the IGA-XGBoost is conducted to diagnose transformer fault types and verified in this paper. The modifications improve the global search capability of the IGA, and the IGA can get the optimal combined solution of input feature selection and the XGBoost classifier optimization reliably and stably. Based on the IGA, the IGA-XGBoost can accurately deal with different recognition problems, including N-F, PD-D-T, D1-D2, and T1&2-T3. Due to the excellent performance of the IGA-XGBoost, the average accuracy of the proposed transformer fault diagnosis system has been improved to 99.2%. Compared to IEC ratios, Dual triangle, SVM, and CVA, the simulation results demonstrate that the proposed method can be a reliable solution for transformer fault diagnosis.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: doi: 10.1016/j.epsr.2020.106346.
Author Contributions
The individual contributions of authors are as follows: data curation, MZ; methodology, ZL; supervision, XC; validation, YH; writing (original draft), ZW. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Fujian Province Young and Middle-aged Teacher Education and Research Project (Grant No. JAT190592), China.
Conflict of Interest
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bhalla, D., Bansal, R. K., and Gupta, H. O. (2012). Function Analysis Based Rule Extraction from Artificial Neural Networks for Transformer Incipient Fault Diagnosis. Int. J. Electr. Power Energ. Syst. 43, 1196–1203. doi:10.1016/j.ijepes.2012.06.042
Castro, A. R. G., and Miranda, V. (2005). Knowledge Discovery in Neural Networks with Application to Transformer Failure Diagnosis. IEEE Trans. Power Syst. 20, 717–724. doi:10.1109/TPWRS.2005.846074
Chen, T., and Guestrin, C. (2016). XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–794. doi:10.1145/2939672.2939785
Chen, Xi., Chen, W., and Gan, D. (2010).Properties and Gas Production Law of Surface Discharge in Transformer Oil-Paper Insulation. In 2010 Annual Report Conference on Electrical Insulation and Dielectic Phenomena. IEEE, 1–4. doi:10.1109/CEIDP.2010.5724049
Cheng, L., and Yu, T. (2018). Dissolved Gas Analysis Principle-Based Intelligent Approaches to Fault Diagnosis and Decision Making for Large Oil-Immersed Power Transformers: A Survey. Energies 11, 913. doi:10.3390/en11040913
Cheng, L., Yu, T., Wang, G., Yang, B., and Zhou, L. (2018). Hot Spot Temperature and Grey Target Theory-Based Dynamic Modelling for Reliability Assessment of Transformer Oil-Paper Insulation Systems: A Practical Case Study. Energies 11, 249. doi:10.3390/en11010249
Colorado, D., Hernández, J. A., Rivera, W., Martínez, H., and Juárez, D. (2011). Optimal Operation Conditions for a Single-Stage Heat Transformer by Means of an Artificial Neural Network Inverse. Appl. Energ. 88, 1281–1290. doi:10.1016/j.apenergy.2010.10.006
Daelemans, W., Hoste, V., De Meulder, F., and Naudts, B. (2003). Combined Optimization of Feature Selection and Algorithm Parameters in Machine Learning of Language. In European Conference on Machine Learning. Springer, 84–95. doi:10.1007/978-3-540-39857-8_10
Dhote, N., and Helonde, J. (2012). Diagnosis of Power Transformer Faults Based on Five Fuzzy Ratio Method. WSEAS Trans. Power Syst. 7, 12.
Dong, M., Yan, Z., and Taniguchi, Y. (2003).Fault Diagnosis of Power Transformer Based on Model-Diagnosis with Grey Relation. In Proceedings of the 7th International Conference on Properties and Applications of Dielectric Materials (Cat. No.03CH37417). IEEE, 1158–1161. doi:10.1109/ICPADM.2003.1218629
Fan, J., Wang, F., Sun, Q., Bin, F., Liang, F., and Xiao, X. (2017). Hybrid RVM-ANFIS Algorithm for Transformer Fault Diagnosis. IET Generation, Transm. Distribution 11, 3637–3643. doi:10.1049/iet-gtd.2017.0547
Fei, S.-w., Wang, M.-J., Miao, Y.-b., Tu, J., and Liu, C.-l. (2009). Particle Swarm Optimization-Based Support Vector Machine for Forecasting Dissolved Gases Content in Power Transformer Oil. Energ. Convers. Manag. 50, 1604–1609. doi:10.1016/j.enconman.2009.02.004
Fei, S.-w., and Zhang, X.-b. (2009). Fault Diagnosis of Power Transformer Based on Support Vector Machine with Genetic Algorithm. Expert Syst. Appl. 36, 11352–11357. doi:10.1016/j.eswa.2009.03.022
Fu Wan, W., Weigen Chen, W., Xiaojuan Peng, X., and Jing Shi, J. (2012).Study on the Gas Pressure Characteristics of Photoacoustic Spectroscopy Detection for Dissolved Gases in Transformer Oil. In 2012 International Conference on High Voltage Engineering and Application. IEEE, 286–289. doi:10.1109/ICHVE.2012.6357108
Ghoneim, S. S. M., Taha, I. B. M., and Elkalashy, N. I. (2016). Integrated ANN-Based Proactive Fault Diagnostic Scheme for Power Transformers Using Dissolved Gas Analysis. IEEE Trans. Dielect. Electr. Insul. 23, 1838–1845. doi:10.1109/TDEI.2016.005301
Jiang, X. Q., Gong, Y., Han, S., and Zhou, K. (2014). Application of the Improved Three-Ratio Method in Chromatographic Analysis of Locomotive Transformer Oil. Amr 1030-1032, 29–33. doi:10.4028/www.scientific.net/amr.1030-1032.29
Ke Meng, K., Zhao Yang Dong, Y., Dian Hui Wang, D. H., and Kit Po Wong, K. P. (2010). A Self-Adaptive RBF Neural Network Classifier for Transformer Fault Analysis. IEEE Trans. Power Syst. 25, 1350–1360. doi:10.1109/TPWRS.2010.2040491
Kirkbas, A., Demircali, A., Koroglu, S., and Kizilkaya, A. (2020). Fault Diagnosis of Oil-Immersed Power Transformers Using Common Vector Approach. Electric Power Syst. Res. 184, 106346. doi:10.1016/j.epsr.2020.106346
Li, J., Chen, X., and Wu, C. (2009).Application of Comprehensive Relational Grade Theory in Expert System of Transformer Fault Diagnosis. In 2009 International Workshop on Intelligent Systems and Applications. IEEE, 1–4. doi:10.1109/iwisa.2009.5072742
Lin, C. E., Ling, J.-M., and Huang, C.-L. (1993). An Expert System for Transformer Fault Diagnosis Using Dissolved Gas Analysis. IEEE Trans. Power Deliv. 8, 231–238. doi:10.1109/61.180341
Liu, Q., Huang, G., Mao, C., Shang, Y., and Wang, F. (2016).Recognition of Dissolved Gas in Transformer Oil by Ant colony Optimization Support Vector Machine. In 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE). IEEE, 1–4. doi:10.1109/ICHVE.2016.7800837
Liu, Z.-x., Song, B., Li, E.-w., Mao, Y., and Wang, G.-l. (2015). Study of "code Absence" in the IEC Three-Ratio Method of Dissolved Gas Analysis. IEEE Electr. Insul. Mag. 31, 6–12. doi:10.1109/MEI.2015.7303257
Mani, G., and Jerome, J. (2014). Intuitionistic Fuzzy Expert System Based Fault Diagnosis Using Dissolved Gas Analysis for Power Transformer. J. Electr. Eng. Tech. 9, 2058–2064. doi:10.5370/JEET.2014.9.6.2058
Miranda, V., and Castro, A. R. G. (2005). Improving the IEC Table for Transformer Failure Diagnosis with Knowledge Extraction from Neural Networks. IEEE Trans. Power Deliv. 20, 2509–2516. doi:10.1109/TPWRD.2005.855423
Mofizul Islam, S., Wu, T., and Ledwich, G. (2000). A Novel Fuzzy Logic Approach to Transformer Fault Diagnosis. IEEE Trans. Dielect. Electr. Insul. 7, 177–186. doi:10.1109/94.841806
Naresh, R., Sharma, V., and Vashisth, M. (2008). An Integrated Neural Fuzzy Approach for Fault Diagnosis of Transformers. IEEE Trans. Power Deliv. 23, 2017–2024. doi:10.1109/TPWRD.2008.2002652
Niu Wu, N., Xu Liangfa, L., and Hu Sanguo, S. (2010).Fault Diagnosis Method for Power Transformer Based on Ant colony -SVM Classifier. In 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE). IEEE, 629–631. doi:10.1109/ICCAE.2010.5451326
Nogami, T., Yokoi, Y., Ichiba, H., and Atsumi, Y. (1995). Gas Discrimination Method for Detecting Transformer Faults by Neural Network. Elect. Eng. Jpn. 115, 93–103. doi:10.1002/eej.4391150109
Saha, T. K., and Purkait, P. (2004). Investigation of an Expert System for the Condition Assessment of Transformer Insulation Based on Dielectric Response Measurements. IEEE Trans. Power Deliv. 19, 1127–1134. doi:10.1109/TPWRD.2004.829100
Shang, H., Xu, J., Zheng, Z., Qi, B., and Zhang, L. (2019). A Novel Fault Diagnosis Method for Power Transformer Based on Dissolved Gas Analysis Using Hypersphere Multiclass Support Vector Machine and Improved D-S Evidence Theory. Energies 12, 4017. doi:10.3390/en12204017
Singh, S., and Bandyopadhyay, M. (2010). Dissolved Gas Analysis Technique for Incipient Fault Diagnosis in Power Transformers: A Bibliographic Survey. IEEE Electr. Insul. Mag. 26, 41–46. doi:10.1109/MEI.2010.5599978
Souahlia, S., Bacha, K., and Chaari, A. (2012). MLP Neural Network-Based Decision for Power Transformers Fault Diagnosis Using an Improved Combination of rogers and Doernenburg Ratios DGA. Int. J. Electr. Power Energ. Syst. 43, 1346–1353. doi:10.1016/j.ijepes.2012.05.067
Sugihara, K. (1997).Measures for Performance Evaluation of Genetic Algorithms. In Proc. 3rd. joint Conference on Information Sciences. State College, Commonwealth of Pennsylvania: Citeseer, 172–175.
Tightiz, L., Nasab, M. A., Yang, H., and Addeh, A. (2020). An Intelligent System Based on Optimized Anfis and Association Rules for Power Transformer Fault Diagnosis. ISA Trans. 103, 63–74. doi:10.1016/j.isatra.2020.03.022
Wang, Z., Liu, Y., and Griffin, P. J. (2000). A Combined Ann and Expert System Tool for Transformer Fault Diagnosis. In 2000 IEEE Power Engineering Society Winter Meeting. Conf. Proc. 2, 1261–1269. (Cat. No. 00CH37077) (IEEE).
Weigen Chen, W., Chong Pan, C., Yuxin Yun, Y., and Yilu Liu, Y. (2009). Wavelet Networks in Power Transformers Diagnosis Using Dissolved Gas Analysis. IEEE Trans. Power Deliv. 24, 187–194. doi:10.1109/TPWRD.2008.2002974
Xi, L., Wu, J., Xu, Y., and Sun, H. (2020). Automatic Generation Control Based on Multiple Neural Networks with Actor-Critic Strategy. IEEE Trans. Neural Netw. Learn. Syst. PP, 2483–2493. doi:10.1109/TNNLS.2020.3006080
Xu, W., Zhou, Z., Chen, H., and Wang, D. (1997). Fault Diagnosis of Power Transformers: Application of Fuzzy Set Theory, Expert Systems and Artificial Neural Networks. IEE Proc. - Sci. Meas. Tech. 144, 39–44. doi:10.1049/ip-smt:19970856
Yadaiah, N., and Ravi, N. (2011). Internal Fault Detection Techniques for Power Transformers. Appl. Soft Comput. 11, 5259–5269. doi:10.1016/j.asoc.2011.05.034
Yann-Chang Huang, Y-C., Hong-Tzer Yang, H-T., and Ching-Lien Huang, C-L. (1997). Developing a New Transformer Fault Diagnosis System through Evolutionary Fuzzy Logic. IEEE Trans. Power Deliv. 12, 761–767. doi:10.1109/61.584363
Yi, J.-H., Wang, J., and Wang, G.-G. (2016). Improved Probabilistic Neural Networks with Self-Adaptive Strategies for Transformer Fault Diagnosis Problem. Adv. Mech. Eng. 8, 168781401562483. doi:10.1177/1687814015624832
Yin, J., Zhu, Y., and Yu, G. (2011).Power Transformer Fault Diagnosis Based on Support Vector Machine with Cross Validation and Genetic Algorithm. In 2011 International Conference on Advanced Power System Automation and Protection. IEEE, 309–313. doi:10.1109/APAP.2011.6180419
Yuan, F., Guo, J., Xiao, Z., Zeng, B., Zhu, W., and Huang, S. (2019). A Transformer Fault Diagnosis Model Based on Chemical Reaction Optimization and Twin Support Vector Machine. Energies 12, 960. doi:10.3390/en12050960
Žarković, M., and Stojković, Z. (2017). Analysis of Artificial Intelligence Expert Systems for Power Transformer Condition Monitoring and Diagnostics. Electric Power Syst. Res. 149, 125–136. doi:10.1016/j.epsr.2017.04.025
Zeng, W., Yang, Y., Gan, C., Li, H., and Liu, G. (2011).Study on Intelligent Development of Power Transformer On-Line Monitoring Based on the Data of DGA. In 2011 Asia-Pacific Power and Energy Engineering Conference. IEEE, 1–4. doi:10.1109/appeec.2011.5749107
Zhang, L., and Zhan, C. (2017).Machine Learning in Rock Facies Classification: An Application of XGBoost. In International Geophysical Conference, Qingdao, China, 17-20 April 2017. Tulsa: Society of Exploration Geophysicists and Chinese Petroleum Society, 1371–1374. doi:10.1190/IGC2017-351
Zhang, X., Xu, Z., Yu, T., Yang, B., and Wang, H. (2020). Optimal Mileage Based Agc Dispatch of a Genco. IEEE Trans. Power Syst. 35, 2516–2526. doi:10.1109/tpwrs.2020.2966509
Keywords: transformer fault diagnosis, genetic algorithm, XGBoost, dissolved gas analysis, performance measures
Citation: Wu Z, Zhou M, Lin Z, Chen X and Huang Y (2021) Improved Genetic Algorithm and XGBoost Classifier for Power Transformer Fault Diagnosis. Front. Energy Res. 9:745744. doi: 10.3389/fenrg.2021.745744
Received: 22 July 2021; Accepted: 21 September 2021;
Published: 08 October 2021.
Edited by:
Lei Xi, China Three Gorges University, ChinaReviewed by:
Narottam Das, Central Queensland University, AustraliaXiaoshun Zhang, Shantou University, China
Copyright © 2021 Wu, Zhou, Lin, Chen and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhanhong Wu, emhhbmhvbmcud3VAb3V0bG9vay5jb20=
 Zhanhong Wu
Zhanhong Wu Mingbiao Zhou2
Mingbiao Zhou2