Generalized Perturbation Theory Based Total Sensitivity and Uncertainty Analysis for High-Fidelity Neutronics Calculation

Neutronics calculation for nuclear reactor with high-fidelity technology can significantly reduce the uncertainties propagated from numerical approximation error and model error. However, the uncertainty of input parameters inevitably exists, especially for nuclear data. On the other hand, resonance self-shielding calculation is essential for multi-group assumption based high-fidelity neutronics calculation, which introduce the implicit effect for calculation responses. In order to fully consider the implicit effects in the process of uncertainty quantification, a generalized perturbation theory (GPT) based implicit sensitivity calculation method is proposed in this paper. Combining the explicit sensitivity coefficient, which can be quantified using classic perturbation theory, the total sensitivity coefficient of calculation responses is obtained. Then the total sensitivity and uncertainty module is established in self-developed neutron transport code with high-fidelity technology-HNET. To verify the accuracy of the sensitivity calculation methods proposed in this paper, a two-dimensional fuel pin problem is chosen to verify the sensitivity results, and the numerical results show good agreement with results calculated by a direct perturbation method. Finally, uncertainty analysis for two-dimensional fuel pin problem is performed and some general conclusions are obtained from the numerical results.

Introduction

With the rapid development of high-performance computing power, high-fidelity calculation method has gradually become an essential method to depict neutron physical phenomena, and the calculation results affects the design, construction, and even the economic and safety aspects of the nuclear reactor. Nevertheless, uncertainties inevitably exist in the process of high-fidelity neutron physics calculations. In general, there are three basic uncertainty sources, including modeling error, numerical solution error and input parameter uncertainties (R.N. Bratton, et al., 2014). The first two uncertainty sources can be effectively decreased by using well-established high-fidelity numerical method for neutronics calculation, but the uncertainty of the multi-group cross sections is still significant (M. Pusa, 2012; C. Wan et al., 2017), especially for advanced reactor, e.g., High Temperature Gas-cooled Reactor (D. She et al., 2021). Meanwhile, the traditional conservative assumptions and large safety margins do not meet research requirements and Best-Estimation Plus Uncertainty (BEPU), which is proposed by IAEA, has now become the mainstream scheme for safety analysis for nuclear power plant (IAEA, 2008). Therefore, the method used to propagate and quantify uncertainty needs to be taken into full consideration when BEPU is regarded as the evaluation criteria.

The basic uncertainty quantification method includes statistical sampling method and deterministic method. The deterministic method, also known as perturbation theory-based method, requires the sensitivity vectors of calculation responses with respect to nuclear cross sections, and finally the uncertainty can be quantified by using ‘‘Sandwich Formula”, which is more suitable for high-fidelity neutron physics calculation due to its high efficiency in analyzing neutron reaction cross sections for all nuclides of the system. Forward and adjoint calculation for neutron transport equation based on the multi-group approximation for nuclear cross section library need to be solved firstly in order to obtain the sensitivity coefficient vectors. However, the neutron reaction cross section has significant resonance self-shielding phenomenon in the intermediate energy segment for some nuclides, and this phenomenon has a non-negligible impact on the numerical solutions in light water reactor (LWR). Therefore, the resonance self-shielding calculation needs to be firstly performed to obtain the effective resonance cross-section. Based on the idea of uncertainty propagation method, the uncertainty of the multi-group cross sections will be firstly propagated to the effective resonance cross section through the resonance self-shielding calculation. In order to ensure the reasonable propagation of the uncertainty, the uncertainty of effective resonance cross section needs to be quantified reasonably. At the same time, for the purpose of accurately describing the influence of the multi-group microscopic nuclear cross sections on system responses, sensitivity analysis of effective resonance cross-section with respect to the multi-group cross section must be quantified, in other words, the implicit sensitivity must be taken into consideration.

The uncertainty analysis based on the sensitivity coefficient vectors were firstly applied to the fast reactor analysis, in which the implicit impact has negligible influence on the uncertainty results, and the explicit sensitivity analysis scheme is proposed and established in this research (C.R. Weisbin, et al., 1976). Based on this scheme, explicit sensitivity analysis for LWR with high-fidelity deterministic transport simulation can be performed (Q. Wu, et al., 2018; J. Ma, et al., 2020). However, many sensitivity and uncertainty research neglect the influence of performing implicit sensitivity, from the research of (E. Greenspan, et al., 1978) and (M. L. Williams, et al., 2001), it is concluded that the implicit part had a similar influence compared with the explicit part to the total sensitivity results and in some problems, the implicit part had a magnitude that was more that 40% of the explicit part. In this case, the research of total sensitivity and uncertainty analysis has been performed by Y. Liu, et al. (2015), B. Foad, and Takeda (2015), M. Dion and Marleau (2013) and C. M. Perfetti and Rearden (2013). The results also indicated that for LWR problems, the implicit part cause significant effect, and the total sensitivity and analysis scheme should be established for LWR to provide convincing sensitivity and uncertainty analysis results for the calculated responses with respect to the multi-group microscopic cross sections. However, the analysis scheme is still not adequate enough because the above research introduced some assumptions. In this paper, total sensitivity including implicit and explicit sensitivity is studied based on the generalized perturbation theory, in which subgroup calculation method is applied when performing resonance calculation. Using the verified sensitivity analysis results, the total uncertainty analysis scheme is finally established for LWR problem.

In the following sections, the theory background of total sensitivity coefficient calculation method, classical perturbation theory based explicit sensitivity analysis, generalized perturbation theory based implicit sensitivity analysis, uncertainty analysis with Sandwich Rule is firstly present. Then the implementation of total sensitivity and uncertainty analysis scheme used in this research is descripted in detail. For the purpose of verifying the accuracy of sensitivity results, the direct perturbation (DP) sensitivity analysis is performed for VERA two-dimensional fuel pin problem. Finally, the total SU analysis of the VERA single cell problem is performed and total SU results are obtained.

Theories

Method of Quantifying the Total Sensitivity Coefficient

The sensitivity coefficient for k_eff with respect to multi-group microscopic cross section ${\sigma }_{x,g}^i$ can be expressed as:

$S_{k_{eff},{\sigma }_{x,g}^i}=\frac{{\sigma }_{x,g}^i}{k_{eff}}\frac{d{k}_{eff}}{d{\sigma }_{x,g}^i}(1)$

x is reaction type identifier, i is nuclide identifier and g is energy group identifier. Considering that the effective resonance cross section of reaction y nuclide j in group h can be perturbated by${\sigma }_{x,g}^i$, using the chain rule and Eq. 1 can be then written as (B.T. Rearten and Jessee, 2016):

$\begin{array}{l}{S}_{k_{eff},{\sigma }_{x,g}^i}^{tot}=\frac{{\sigma }_{x,g}^i}{k_{eff}}\frac{d{k}_{eff}}{d{\sigma }_{x,g}^i}=\frac{{\sigma }_{x,g}^i}{k_{eff}}\frac{\partial k_{eff}}{\partial {\sigma }_{x,g}^i}+{\displaystyle \sum _j\frac{{\sigma }_{y,h}^j}{k_{eff}}\frac{\partial k_{eff}}{\partial {\sigma }_{y,h}^j}}\times \frac{{\sigma }_{x,g}^i}{{\sigma }_{y,h}^j}\frac{\partial {\sigma }_{y,h}^j}{\partial {\sigma }_{x,g}^i}\\ =S_{k_{eff},{\sigma }_{x,g}^i}^{\exp }+{\displaystyle \sum _j{S}_{k_{eff},{\sigma }_{y,h}^j}^{\exp }}{S}_{{\sigma }_{y,h}^j,{\sigma }_{x,g}^i}^{imp}\end{array}(2)$

It can be found that the total sensitivity coefficient for k_eff with respect to multi-group cross section${\sigma }_{x,g}^i$ consists of two parts: $S_{{\sigma }_{y,h}^j,{\sigma }_{x,g}^i}^{imp}$is the implicit sensitivity coefficient for effective resonance cross section ${\sigma }_{y,h}^j$with respect to multi-group cross section ${\sigma }_{x,g}^i$; $S_{k_{eff},{\sigma }_{x,g}^i}^{\exp }$ and $S_{k_{eff},{\sigma }_{y,h}^j}^{\exp }$ are both explicit sensitivity coefficients which represents the impact of cross sections on the responses directly through neutron transport equation. The methods for quantifying the implicit and explicit sensitivity are given below.

It needs to be emphasized that according to the division pattern for resonance nuclides and resonance energy group, total sensitivity analysis can be divided into three conditions:

1) For multi-group cross sections of non-resonance nuclides in resonance energy group, both implicit and explicit effect need to be taken into consideration;

2) For multi-group cross sections of resonance nuclides in resonance energy group, only the implicit effect needs to be considered;

3) For multi-group cross sections of both resonance and non-resonance nuclides in non-resonance energy group, only the explicit effect needs to be taken into consideration.

Method of Quantifying the Explicit Sensitivity

The classical perturbation theory can be used to quantify the sensitivity coefficients of k_eff to the effective resonance cross sections of different reaction type of different nuclides. In nuclear reactor physics system, the forward and adjoint neutron transport equations can be written as the operator forms,

$\left(A-\lambda B\right)\Psi =0(\mathrm{3a})$

$\left(A^{\text{*}}-{\lambda }^{\text{*}}{B}^{\text{*}}\right){\Psi }^{\text{*}}=0(\mathrm{3b})$

$A$ represents neutron leakage, absorption and scattering term, $B$represents the fission source term, $\Psi$is the forward neutron angular flux. $A^{\text{*}}$and$B^{\text{*}}$are the adjoint form of operators $A$ and$B$. ${\Psi }^{\text{*}}$represents the adjoint neutron angular flux. $\lambda$ and $\lambda \text{*}$are the eigenvalue of forward and adjoint neutron transport equations, respectively. According to the mathematical derivation, the explicit sensitivity coefficient of k_eff due to the perturbation of effective resonance cross sections $\sigma$can be eventually expressed as (J. Ma et al., 2020),

$S_{k_{eff},\sigma }=-\sigma \langle {\Psi }^{\ast }\left(\frac{\partial A}{\sigma }-\frac{1}{k_{eff}}\frac{\partial B}{\sigma }\right)\Psi \rangle /\langle {\Psi }^{\ast }\frac{1}{k_{eff}}B\Psi \rangle (4)$

Based on Eq. 4, the sensitivity coefficient of k_eff with respect to the effective resonance cross sections can be quantified, and only once forward transport calculation and adjoint calculation is required. Equation 4 indicates that the denominator is the function of forward flux, adjoint flux, eigenvalue and the fission source operator, whereas numerator would vary with targeted reaction type. The denominator and the derivation term in numerator could be obtained based on the discrete form of neutron transport equation according to our previous research (J. Ma et al., 2020), and the exact form of explicit sensitivity coefficients won’t be given in this paper.

Method of Quantifying the Implicit Sensitivity

As introduced in Method of Quantifying the Total Sensitivity Coefficient, the key issue in the study of implicit sensitivity is to study the effect of multi-group microscopic cross section on the effective resonance cross section. Generally, the effective resonance cross section in group g can be written as:

${\sigma }_{x,g}={\displaystyle {\int }_g{\sigma }_x\left(E\right)\varphi \left(E\right)dE}/{\displaystyle {\int }_g\varphi \left(E\right)dE}(5)$

$\varphi \left(E\right)$ is the neutron flux in group g; ${\sigma }_x\left(E\right)$ is fine-group cross section in group g。According to the definition of sensitivity coefficient, the relative sensitivity of ${\sigma }_{x,g}$ with respect to multi-group microscopic cross section ${\alpha }_g$is:

$\begin{array}{l}{S}_{{\sigma }_{x,g},{\alpha }_g}=\frac{d{\sigma }_{x,g}/{\sigma }_{x,g}}{d{\alpha }_g/{\alpha }_g}\\ ={\alpha }_g\{\frac{{\displaystyle {\int }_g\varphi (E)\frac{\partial {\sigma }_x(E)}{\partial {\alpha }_g}dE}}{{\displaystyle {\int }_g\varphi (E){\sigma }_x(E)dE}}+\frac{{\displaystyle {\int }_g{\sigma }_x(E)\frac{\partial \varphi (E)}{\partial {\alpha }_g}dE}}{{\displaystyle {\int }_g\varphi (E){\sigma }_x(E)dE}}-\frac{{\displaystyle {\int }_g\frac{\partial \varphi (E)}{\partial {\alpha }_g}dE}}{{\displaystyle {\int }_g\varphi (E)dE}}\}\\ =\underset{S^{dir}}{\underbrace{{\alpha }_g\frac{{\displaystyle {\int }_g\varphi (E)\frac{\partial {\sigma }_x(E)}{\partial {\alpha }_g}dE}}{{\displaystyle {\int }_g\varphi (E){\sigma }_x(E)dE}}}}+\underset{S^{indir}}{\underbrace{{\alpha }_g{\displaystyle {\int }_g(\frac{{\sigma }_x(E)}{{\displaystyle {\int }_g\varphi (E){\sigma }_x(E)dE}}-\frac{1}{{\displaystyle {\int }_g\varphi (E)dE}}})\frac{\partial \varphi (E)}{\partial {\alpha }_g}dE}}\end{array}(6)$

It can be found that Eq. 6 can be divided into two parts: the first part is the direct part, it represent the change of effective resonance cross section ${\sigma }_x\left(E\right)$ caused directly by the perturbation of multi group cross section ${\alpha }_g$; the second part is the indirect part, it represent multi group cross section ${\alpha }_g$firstly influence the neutron flux $\varphi \left(E\right)$, and further influence the effective resonance cross section ${\sigma }_x\left(E\right)$.

The neutron flux $\varphi \left(E\right)$ in Eq. 5 is the solution of neutron slowing-down equation. The operator form of slowing-down equation can be expressed as:

$B\varphi \left(E\right)=Q\left(E\right)(7)$

$B$is the disappearing term, $Q$ is the effective source term. Take the derivative on each term of Eq. 7 with multi group cross section $\alpha$:

$B\frac{\partial \varphi \left(\text{E}\right)}{\partial \alpha }=\frac{\partial Q\left(E\right)}{\partial \alpha }-\frac{\partial B}{\partial \alpha }\varphi \left(E\right)(8)$

Equation 8 describes the basic relationship between the perturbation of microscopic cross-section $\alpha$ and the weighting function $\varphi \left(E\right)$. Theoretically, if the variation of the operators Q and$B$are obtained, the derivative term $\partial \varphi \left(E\right)/\partial \alpha$ can be solved directly based on Eq. 8, and the relative sensitivity coefficients of effective resonance cross section ${\sigma }_{x,g}$with respect to microscopic cross section $\alpha$ can be calculated using Eq. 6. In fact, the derivative terms $\partial B/\partial \alpha$ and $\partial Q/\partial \alpha$can be calculated directly utilizing the direct perturbation method. However, the perturbation calculations need to be achieved for different nuclides, energy groups, and reaction types, which will introduce an unacceptable calculated amount and computational complexity in the study of implicit sensitivity analysis.

Fortunately, the indirect part of Eq. 6 can be determined for multiple perturbations by combining the generalized adjoint equation and the slowing equation instead of explicitly calculating the derivative term $\partial \varphi \left(E\right)/\partial \alpha$. Based on the generalized perturbation theory, introducing a generalized adjoint function ${\Gamma }_{x,g}^{\ast }\left(E\right)$ for reaction type x and energy group g, which represents the value of weighted function $\varphi \left(E\right)$ to the effective resonance section ${\sigma }_{x,g}$ rather than the neutron value. Then the generalized adjoint form of the slowing down equation can be written as:

$B^{\text{*}}{\mathrm{\Gamma }}_{x,g}^{\ast }\left(E\right)=\frac{{\sigma }_x\left(E\right)}{{\displaystyle {\int }_g\varphi \left(E\right){\sigma }_x\left(E\right)dE}}-\frac{1}{{\displaystyle {\int }_g\varphi \left(E\right)dE}}(9)$

$B^{\text{*}}$ is the adjoint form of operator $B$.

Multiply both sides of Eq. 8 by the generalized adjoint function ${\Gamma }_{x,g}^{\ast }\left(E\right)$, and integrating over group g:

${\displaystyle {\int }_g(B\frac{\partial \varphi (E)}{\partial \alpha }){\mathrm{\Gamma }}_{x,g}^{\ast }(E)dE=}{\displaystyle {\int }_g(\frac{\partial Q(E)}{\partial \alpha }-\frac{\partial B}{\partial \alpha }\varphi (E)){\mathrm{\Gamma }}_{x,g}^{\ast }(E)}dE(10)$

According to the characteristics of the adjoint operator, the left term of Eq. 10 can be written as:

${\displaystyle {\int }_g\left(B\frac{\partial \varphi (E)}{\partial \alpha }\right){\mathrm{\Gamma }}_{x,g}^{\ast }(E)dE=}{\displaystyle {\int }_g\left(\frac{\partial \varphi (E)}{\partial \alpha }\right)B^{\ast }}{\mathrm{\Gamma }}_{x,g}^{\ast }(E)dE(11)$

Substituting Eqs. 9–11 into Eq. 6, the relative sensitivity coefficient of effective resonance cross section with respect to a certain type microscopic cross section can be calculated by:

$S_{{\sigma }_{x,g},{\alpha }_g}=\underset{S^{dir}}{\underbrace{{\alpha }_g\frac{{\displaystyle {\int }_g\frac{\partial {\sigma }_x(E)}{\partial {\alpha }_g}\varphi (E)dE}}{{\displaystyle {\int }_g{\sigma }_x(E)\varphi (E)dE}}}}+\underset{S^{indir}}{\underbrace{{\alpha }_g{\displaystyle {\int }_g{\mathrm{\Gamma }}_{x,g}^{\ast }(E)(\frac{\partial Q(E)}{\partial {\alpha }_g}-\frac{\partial B}{\partial {\alpha }_g}\varphi (E))}dE}}(12)$

Subgroup method is using to perform resonance self-shielding calculation in HNET. Before performing the implicit sensitivity analysis, it is necessary to briefly introduce the subgroup resonance calculation method. Differ from the traditional resonance calculation method, which subdivides the energy group depending on the value of neutron energy, subgroups are defining according to the cross section itself which drastic changes. S o a few subgroups can contain the resonance energy interval. The neutron flux varies weakly due to the smooth value of cross section in one subgroup, which leads to a high efficiency resonance computation compared with the traditional resonance self-shielding calculation method, and subgroup method currently became one of the most widely used resonance calculation method.

According to the subgroup method, the cross section in the resonance energy group is divided into several intervals within one cross section range, and each interval is a so-called subgroup. Each subgroup corresponds to several discrete energy segments, the energy segment set is expressed as:

$\Delta E_{g,i}\in \left\{E|{\sigma }_{g,i}<\sigma \le {\sigma }_{g,i+1}\right\}(13)$

Subgroup cross section and subgroup probability, which are called subgroup parameters, are used to describes the properties of subgroup, and can be expressed as:

${\sigma }_{x,g,i}=\frac{{\displaystyle {\int }_{\Delta E_{g,i}}{\sigma }_x\left(E\right)\varphi \left(E\right)\text{d}E}}{{\displaystyle {\int }_{\Delta E_{g,i}}\varphi \left(E\right)\text{d}E}}(\mathrm{13a})$

$p_{g,i}=\frac{\Delta E_{g,i}}{\Delta E_g}(\mathrm{13b})$

After obtaining the subgroup parameters, the subgroup flux density can be obtained by solving the subgroup transport equation, then the subgroup flux is used as weight function to obtain the effective resonance self-shielding cross section. For energy group g, the transport equation of subgroup i is:

$\mathbf{\Omega }\cdot \nabla {\varphi }_{g,i}+{\Sigma }_{t,g,i}{\varphi }_{g,i}=Q_{g,i}(\mathrm{13a})$

$Q_{g,i}=p_{g,i}{\Sigma }_p(\mathrm{13b})$

$Q_{g,i}$is source term in subgroup i, ${\Sigma }_p$ is potential cross section, ${\Sigma }_{t,g,i}$ is the total cross section in subgroup i. The operator form of slowing-down equation in subgroup i can be expressed as:

$B_{g,i}{\varphi }_{g,i}=Q_{g.i}(14)$

The flux density of subgroup i can be obtained by solving Eq. 14, then the effective resonance self-shielding cross section can be calculated by:

${\sigma }_{x,g}={\displaystyle \sum _{i=1}^I{\sigma }_{x,g,i}{\varphi }_{g,i}}/{\displaystyle \sum _{i=1}^I{\varphi }_{g,i}}(15)$

Based on the generalized perturbation theory, the generalized adjoint subgroup transport equation needs to be established firstly in order to obtain the relative sensitivity coefficient of the effective resonance self-shielding cross section with respect to the multi-group cross section, the subgroup generalized adjoint transport equation can be written as:

$-\mathbf{\Omega }\nabla {\Gamma }_{g,i}^{\ast }+{\Sigma }_{t,g,i}{\mathrm{\Gamma }}_{g,i}^{\ast }=Q_{g,i}^{\ast }(16)$

The Operator Form Is

$B_{g,i}^{\ast }{\mathrm{\Gamma }}_{g,i}^{\ast }=Q_{g.i}^{\ast }(17)$

$B_g^{\ast }$ is subgroup adjoint transport term, ${\Gamma }_g^{\ast }$ is the generalized subgroup adjoint neutron flux, $Q_g^{\ast }$is the generalized adjoint source, which is defined by:

$Q_{g,i}^{\ast }=\frac{{\sigma }_{x,g,i}}{{\displaystyle {\sum }_{i=1}^N{\displaystyle {\int }_V{\displaystyle {\int }_{\Omega }{\varphi }_{g,i}{\sigma }_{x,g,i}dVd\Omega }}}}-\frac{1}{{\displaystyle {\sum }_{i=1}^N{\displaystyle {\int }_V{\displaystyle {\int }_{\Omega }{\varphi }_{g,i}dVd\Omega }}}}(18)$

Once obtaining the specific form of the generalized adjoint source term, it then can be used as the external source term of the generalized adjoint equation solver in HNET in order to obtain the generalized adjoint function ${\mathrm{\Gamma }}_{x,g}^{\ast }$.

Finally, considering the exact form of ${\sigma }_x\left(E\right)$ and ${\Gamma }_{x,g}^{\ast }$ when subgroup method is used to apply the subgroup method and combining Eq. 18, the relative sensitivity coefficient of the effective resonance self-shielding cross section with respect to the multi-group microscopic cross section can be calculated by:

$\begin{array}{l}{S}_{{\sigma }_{x,g}^j,{\alpha }_{y,g\prime }^k}={\alpha }_{y,g\prime }^k{\displaystyle \sum _{i=1}^I\left(\frac{{\displaystyle {\int }_{\Omega }\frac{\partial {\sigma }_{x,g,i}^j}{\partial {\alpha }_{y,g\prime }^k}{\varphi }_{g,i}d\Omega }}{{\displaystyle {\int }_{\Omega }{\sigma }_{x,g,i}^j{\varphi }_{g,i}d\Omega }}\right)}\\ +{\alpha }_{y,g\prime }^k{\displaystyle \sum _{i=1}^I{\displaystyle \sum _Z{V}_Z{\displaystyle {\int }_{\Omega }{\mathrm{\Gamma }}_{x,g,i}^{\ast }\left(\frac{\partial Q_{g,i}}{\partial {\alpha }_{y,g\prime }^k}-\frac{\partial L_{g,i}}{\partial {\alpha }_{y,g\prime }^k}{\varphi }_{g,i}\right)}}}d\Omega \end{array}(19)$

Method of Quantifying the Uncertainty

After obtaining the sensitivity vectors, the relative uncertainty can be then calculated using “Sandwich Formula”. In the following part, the derivation of Sandwich Formula will be introduced briefly.

The nuclear reactor physics system k_eff can be written as the function of a series of multi-group microscopic cross sections, which is shown in Eq. 20.

$k_{eff}=R({\sigma }_1,{\sigma }_2,\dots \dots {\sigma }_n)(20)$

$\sigma$represents the multi-group microscopic cross section for a nuclide reaction type, and$\overline{k}$, $\overline{\sigma }$represent the expected value. Using the first order linearity approximation, the Taylor expansion form of Eq. 20 can be rewritten as,

$k_{eff}={\overline{k}}_{eff}+\delta k_{eff}=R({\overline{\sigma }}_1,{\overline{\sigma }}_2,\cdots {\overline{\sigma }}_n)+{\displaystyle \sum _i^n\frac{\partial k_{eff}}{\partial {\sigma }_i}}\delta {\sigma }_i(21)$

Presumptively, the input parameters in reactor system satisfy the$p({\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n)$, which is a joint probability density function, the variance of k_eff can be calculated using the following form,

$\begin{array}{l}var\left(k_{eff}\right)={\displaystyle \int {\left({\displaystyle \sum _{i=1}^n\left(\frac{\partial k_{eff}}{\partial {\sigma }_i}\right)}\delta {\sigma }_i\right)}^2}p({\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n)d{\sigma }_{1}d{\sigma }_2\cdots d{\sigma }_n\\ \begin{array}{ccc}\begin{array}{cc}& \end{array}& & =\end{array}{\displaystyle \sum _{i=1}^n{\left(\frac{\partial k_{eff}}{\partial {\sigma }_i}\right)}^2}{D}_{{\sigma }_i}+2{\displaystyle \sum _{i\ne j=1}^n\frac{\partial k_{eff}}{\partial {\sigma }_i}\frac{\partial k_{eff}}{\partial {\sigma }_j}}{\Sigma }_{{\sigma }_i{\sigma }_j}\end{array}(22)$

k$\Sigma$ is the covariance of two parameters, $D$is the variance of a specific parameter. Then the relative variance of k_eff, i.e. the square of the k_eff relative uncertainty, due to multi-group microscopic cross sections can be written as

$\begin{array}{l}\frac{var\left(k_{eff}\right)}{k_{eff}^2}={\displaystyle \sum _{i=1}^n{\left(\frac{{\sigma }_i}{k_{eff}}\frac{\partial k_{eff}}{\partial {\sigma }_i}\right)}^2}\frac{D_{{\sigma }_i}}{{\sigma }_i^2}+2{\displaystyle \sum _{i\ne j=1}^n\left(\frac{{\sigma }_i}{k_{eff}}\frac{\partial k_{eff}}{\partial {\sigma }_i}\right)(\frac{{\sigma }_j}{k_{eff}}\frac{\partial k_{eff}}{\partial {\sigma }_j}})\frac{{\Sigma }_{{\sigma }_i{\sigma }_j}}{{\sigma }_i{\sigma }_j}\\ ={\displaystyle \sum _{i=1}^n{\left(S_{k_{eff},{\sigma }_i}\right)}^2}{D}_{{\sigma }_i}^{relative}+2{\displaystyle \sum _{i\ne j=1}^n{S}_{k_{eff},{\sigma }_i}{S}_{k_{eff},{\sigma }_j}}{\Sigma }_{{\sigma }_i{\sigma }_j}^{relative}\end{array}(23)$

Considering the definition of sensitivity coefficient, the matrix form of relative uncertainty of k_eff can be rewritten as,

$\frac{var\left(k_{eff}\right)}{k_{eff}^2}=S_{k_{eff},\sigma }{\Sigma }^{relative}{\left(S_{k_{eff},\sigma }\right)}^T(24)$

Equation 24 is the so-called “Sandwich Rule”. Once obtaining the sensitivity vectors for k_eff with respect to multi-group microscopic cross sections and the relative covariance matrix, Eq. 24 can be used to quantify the relative uncertainty of nuclear reactor physics system k_eff.

Implementation

Implementation Flow

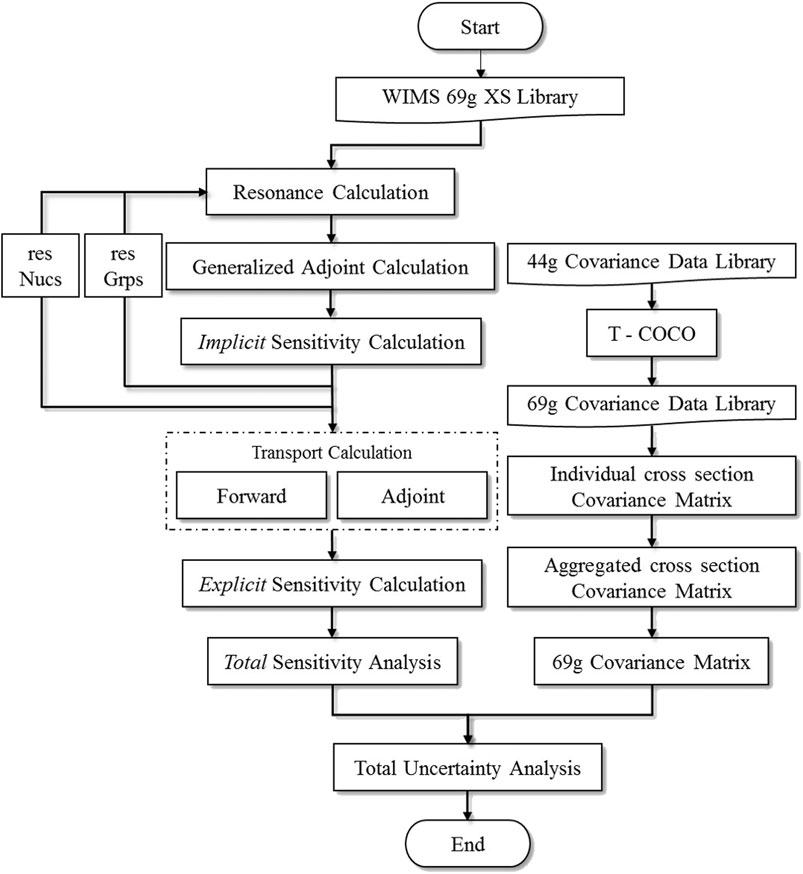
In this section, the total sensitivity and uncertainty analysis scheme with the calculation flow is established, and the details will be discussed. Figure 1 shows the implementation flow of the total sensitivity and uncertainty analysis. The fundamental evaluated nuclear data library is WIMS 69 g library, which is the basic input for the resonance and transport calculations. And the ZZ-SCALE6.0/COV-44G library, which contains the uncertainty and correlation information for multi-group cross sections, is the basic uncertainty source. High-fidelity Neutron Transport program (HNET), which is a self-developed deterministic 3D high-fidelity neutron transport code, is applied to solve the subgroup transport equations, forward neutron transport equations, adjoint neutron transport equations, and the generalized adjoint equation. The effective resonance multi-group cross sections are calculated by using subgroup resonance calculation method. Then a total sensitivity and uncertainty analysis module is developed for quantifying the sensitivity and uncertainty of k_eff propagated from the multi-group microscopic nuclear cross sections in HNET. The computational steps of generalized perturbation theory-based total sensitivity and uncertainty (SU) analysis can be summarized as follows:

1) The relative covariance matrix in 69 g energy group structure is generated from the well-developed 44 g energy group relative covariance library by using home-developed covariance matrix generation code T-COCOO.

2) The subgroup resonance calculation is performed to calculate the effective multi-group macro cross sections using 69 g nuclear data library, the subgroup parameters and subgroup neutron flux for establishing generalized adjoint equation can be generated at the same time.

3) Based on the subgroup parameters and subgroup neutron flux obtained in step 2, the generalized adjoint equation can be established, and it can be solved by directly using adjoint neutron transport solver after adding a generalized neutron source in the source term.

4) The k_eff implicit sensitivity coefficient can be calculated using the solution in step 3 for all resonance nuclides and resonance energy groups.

5) The forward flux, adjoint flux and the eigenvalue is obtained by solving the forward and adjoint equations, and the k_eff explicit sensitivity coefficients for all nuclide is calculated.

6) Total k_eff sensitivity coefficients are calculated using both implicit and explicit sensitivity coefficients obtained in step 4 and step 5.

7) Using the total sensitivity obtained in step6 and the relative covariance obtained in step 1, total k_eff uncertainty can be quantified using the Sandwich Rule.

FIGURE 1

FIGURE 1. Flowchart of the total sensitivity and uncertainty analysis.

Direct Perturbation Scheme

Sensitivity coefficient calculated using central difference direct perturbation method is considered relatively precise if the linear relation is strong and the perturbation is feasible. In this way, this method is always used to verify the sensitivity coefficient calculated by other methods. For sensitivity coefficient of k_eff with respect to certain multi-group microscopic cross section using central difference direct perturbation method, the k_eff of the system is computed for three times: firstly, with the unperturbed cross sections$\alpha$and obtains unperturbed $k_{eff}$ ; then with an adequate increased cross section${\alpha }^{+}$ and obtains $k_{eff}^{{\alpha }^{+}}$; with the same value decreased input cross section ${\alpha }^{-}$ and obtains $k_{eff}^{{\alpha }^{-}}$. Finally, DP method-based sensitivity coefficient of k_eff with respected to cross section $\alpha$ can be calculated by

$S_{k_{eff},\alpha }=\frac{\left(k_{eff}^{{\alpha }^{+}}-k_{eff}^{{\alpha }^{-}}\right)/k_{eff}}{\left({\alpha }^{+}-{\alpha }^{-}\right)/\alpha }(25)$

In this paper, DP method is used to verify the sensitivity coefficient calculated using proposed generalized perturbation theory. Three types of sensitivity coefficient, including implicit, explicit and total sensitivity coefficient are verified, and the calculation methods can be summarized as follows:

1) Total sensitivity coefficients: Complete calculation including resonance self-shielding calculation and neutron transport calculation need to be performed for three times, with unperturbed, positive perturbed and negative perturbed multi-group cross sections respectively.

2) Explicit sensitivity coefficients: Only the neutron transport calculation needs to be performed for three times, with unperturbed, positive perturbed and negative perturbed effective resonance self-shielding cross sections respectively.

3) Implicit sensitivity coefficients: Firstly, resonance self-shielding calculation needs to be performed for three times, with unperturbed, positive perturbed and negative perturbed multi-group cross sections respectively. Secondly, the neutron transport calculation needs to be performed for three times, with unperturbed, positive perturbed and negative perturbed effective resonance self-shielding cross sections respectively.

Calculation Model and Uncertainty Sources

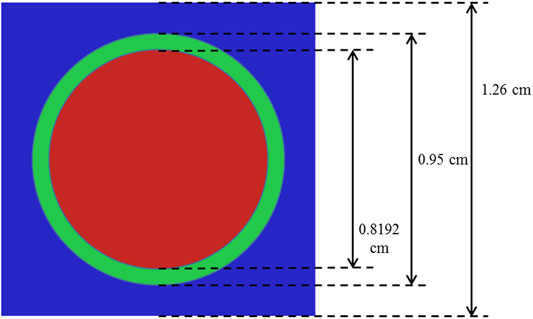
A two-dimensional fuel pin cell problem was chosen for the purpose of verifying the sensitivity coefficient calculated by using generalized perturbation theory proposed in this paper and perform total sensitivity and uncertainty analysis. More detail descriptions of this problem can be found in (A.T. Godfrey, 2013). The main calculation parameters of this problem is summarized in Table 1. The geometry information and computing mesh are illustrated in Figure 2. Meanwhile, the WIMS 69 energy group nuclear data library is used to perform subgroup resonance calculation, adjoint and transport calculations.

TABLE 1

TABLE 1. Calculation parameters of this problem.

FIGURE 2

FIGURE 2. Radial geometry for pin cell problem.

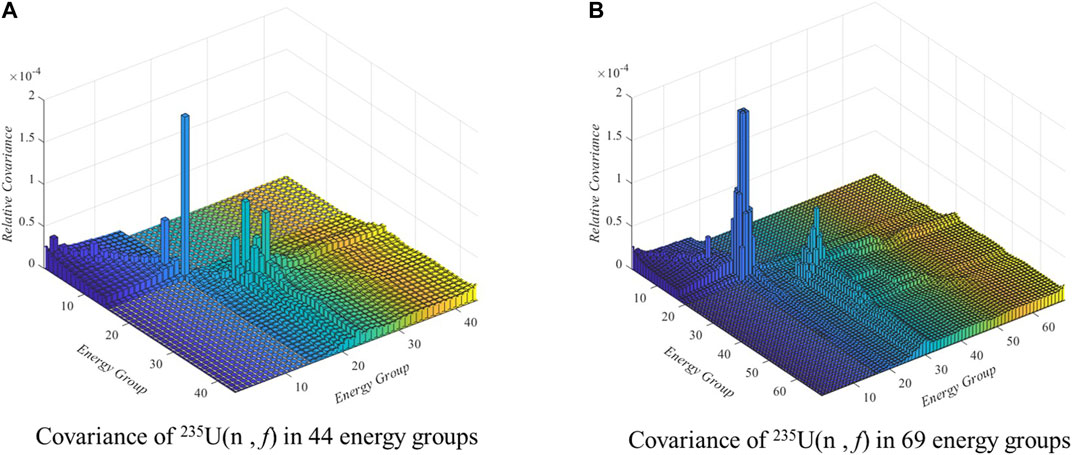
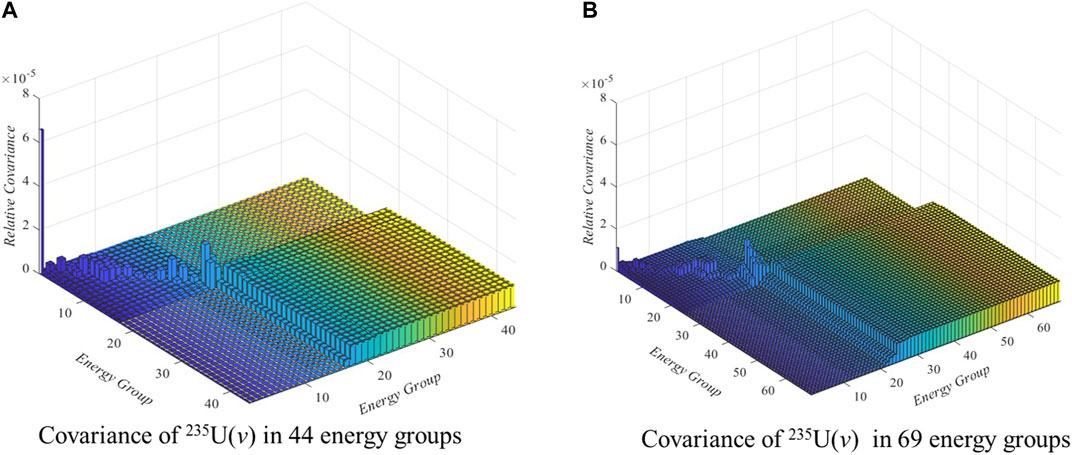
The sensitivity vectors are calculated using the WIMS 69-group structure nuclear data library, which is different from the 44 g group structure relative covariance library, so the problem-related 69 g relative covariance library needs to be firstly constructed from the well-evaluated 44 g group structure using a former proposed covariance matrix transforming method (D. Wang, et al., 2016). The comparison of relative covariance matrix of two typical nuclide neutron reaction cross section, including ²³⁵U 5) and ²³⁸U (n, γ) in 44 g group structure and 69 g group structure are shown in Figures 3, 4 respectively.

FIGURE 3

FIGURE 3. Comparison of relative covariance matrix for ²³⁵U (n, f).

FIGURE 4

FIGURE 4. Comparison of relative covariance matrix for ²³⁵U (v).

Numerical Results

Sensitivity Coefficient Verification

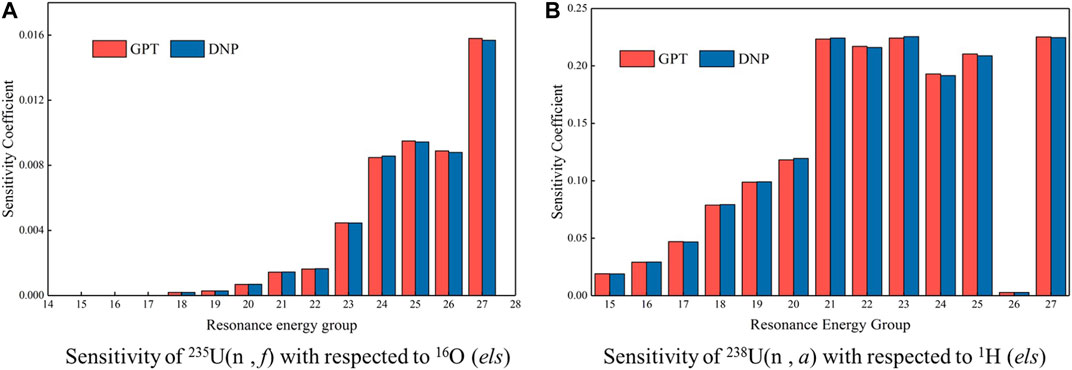
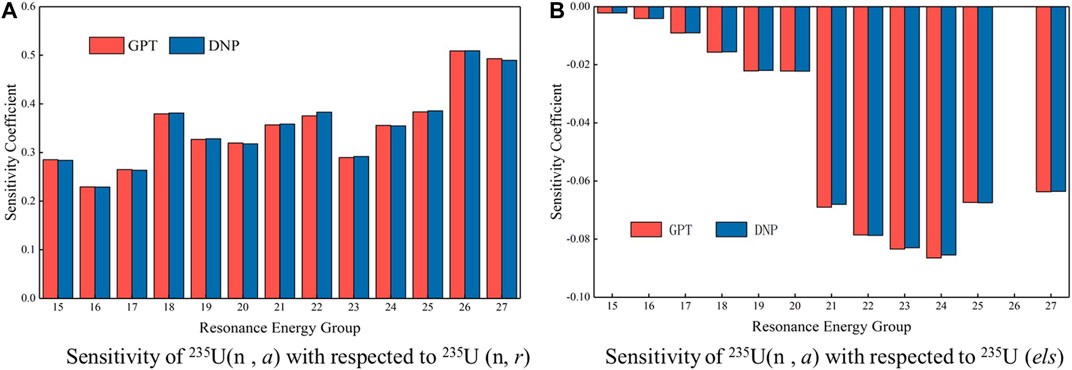
The 2D pin cell problem is firstly used to verify the implicit sensitivity coefficients calculated based on the proposed generalized perturbation theory method. According to the linear relationship test, 2% relative perturbation factor is in the region with strongest linear relationship, so a 2% relative perturbation of multigroup cross sections is used in the DP method for sensitivity verification. The comparisons of implicit sensitivity coefficients, which is divided into resonance nuclides and non-resonance nuclides, calculated by using the DP and GPT methods for some typical nuclides are illustrated in Figures 5, 6, respectively.

FIGURE 5

FIGURE 5. Comparisons of implicit sensitivity coefficients for non-resonance nuclides.

FIGURE 6

FIGURE 6. Comparisons of implicit sensitivity coefficients for resonance nuclides.

Figures 5, 6 suggest that the implicit sensitivity coefficients for both resonance and non-resonance nuclides calculated by GPT and DP methods agree well for selected reaction types in all resonance energy groups. Most relative error in these energy groups is less than 1%, but in group 22, the relative error of implicit sensitivity coefficients of absorption cross section of ²³⁵U with respect to radiative capture cross section of ²³⁵U is 1.89%, which is a little large, but it is still acceptable. These comparisons indicate that acceptable accuracy of implicit sensitivity analysis is achievable by using generalized perturbation theory proposed in this paper.

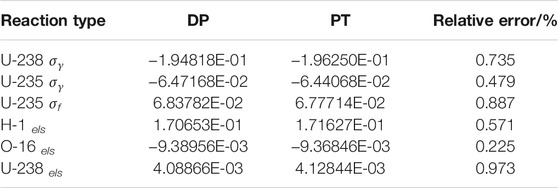
It is worth noted that the ability of calculation for explicit sensitivity coefficient is verified in our precious work (J. Ma et al., 2020) and verification will not be performed in this paper. For the verification of total sensitivity, the integral sensitivity coefficients (integrating with volume and energy) of selected cross sections of representative isotopes and reaction types in resonance energy groups are summarized in Table 2 for comparison. The comparison results also demonstrate that accurate total sensitivity coefficient can be obtained, and the total sensitivity and uncertainty can be then performed.

TABLE 2

TABLE 2. Comparison of total sensitivity coefficients.

Total Sensitivity Analysis

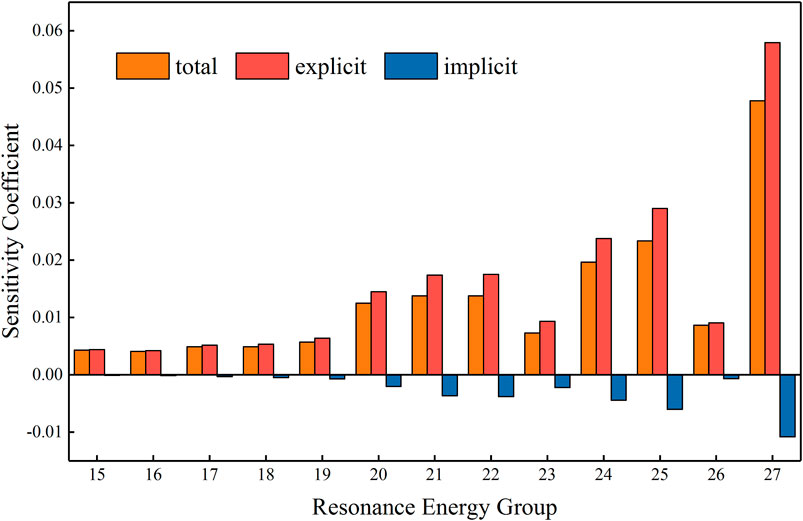
Before performing the total sensitivity analysis, it is worth investigate that the relative importance of implicit sensitivity compared with the explicit part. Figure 7 illustrates the implicit sensitivity, explicit sensitivity and total sensitivity of k_eff with respect to elastic scattering cross section of ¹H. According to Figure 7, in most energy group, the explicit sensitivity coefficients group are positive, while the implicit part are negative, thus the total sensitivity is less than explicit part in these energy groups. It suggests that if the implicit sensitivity is neglected, the sensitivity will be overestimated. It leads to a fact that the implicit sensitivity needs to be considered in detail when performing total SU analysis.

FIGURE 7

FIGURE 7. Comparisons of implicit/explicit sensitivity coefficients.

Three kinds of sensitivity coefficients, including total, explicit and implicit part of k_eff with respect to some representative reaction type cross section of both resonance and non-resonance nuclides are illustrated in Table 3. It also can be found in Table.3 that the implicit effect has a nonnegligible impact for the sensitivity analysis for LWR, especially for the sensitivity coefficient for resonance nuclides in resonance energy groups.

TABLE 3

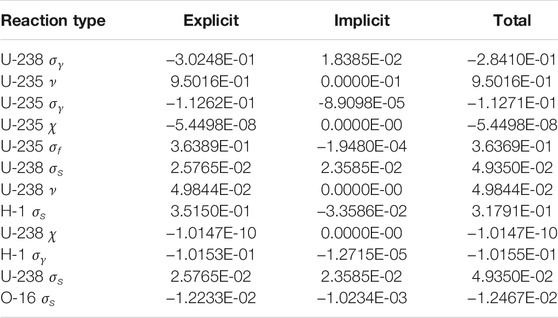
TABLE 3. Sensitivity coefficients of k_eff with respect to some. Representative reaction types of cross section.

Total Uncertainty Analysis

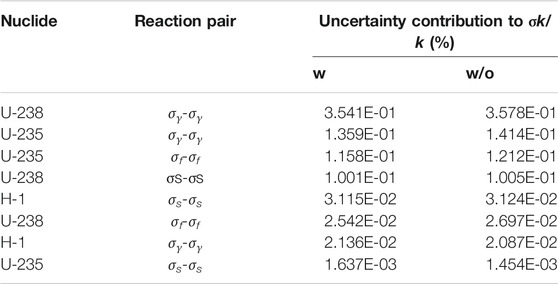
The uncertainty contribution of some important nuclide reaction cross section with and without considering the implicit part is presented in Table 4. It can be found in Table 4 that although the implicit part is essential in sensitivity analysis, it has nonsignificant influences on uncertainty results. The first reason is that compared with the explicit part, the absolute value of implicit part is relatively small; the second reason is that uncertainty is quantified by using Sandwich Formula, the nuclide reaction cross section may have significant influence on eigenvalue, yet it has small uncertainty itself. Although the total uncertainty results barely effected by implicit sensitivity, considering the implicit influence ensure the reasonable propagation for uncertainty of input parameters, the implicit sensitivity needs to be fully investigated when performing total sensitivity and uncertainty analysis.

TABLE 4

TABLE 4. Implicit effect on uncertainty contributions.

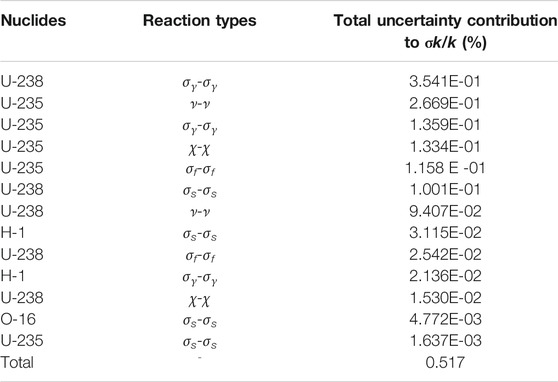
The total uncertainty contributions of some important reactions to k_eff, taken both implicit and explicit influence into consideration, are shown in Table 5. The most three significant contributors to the total uncertainty of k_eff are σ_γ of ²³⁸U, ν of ²³⁵U and σ_γ of ²³⁵U respectively. This conclusion is similar to the uncertainty contribution results without considering the implicit effect. The total uncertainty contribution due to these representative nuclides reaction types to k_eff is 0.517%, compared with the results of 0.522% when implicit part is ignored, it also suggests that the implicit effect has little influence on the uncertainty quantification results.

TABLE 5

TABLE 5. Total uncertainty contribution.

Conclusion

In recent years, sensitivity and uncertainty quantification on nuclear reactor core physics key parameters, especially the simulation results calculated by high-fidelity simulation method, has raised more and more concerns. For LWR problems, total sensitivity analysis needs to be divided into explicit part, which can be calculated using classical perturbation theory, and implicit part, which is not studied widely. However, the implicit part needs to be investigated particularly for SU analysis on LWR problems.

In this paper, a generalized perturbation theory-based method is proposed to quantify the implicit sensitivity coefficient. Combining with the explicit sensitivity coefficient, total sensitivity of reactor core k_eff is quantified, and then total uncertainty contribution for typical nuclides and reaction types is calculated using “Sandwich Formula”. For the purpose of verifying the accuracy of sensitivity coefficient quantified in this research, a two-dimensional fuel pin cell problem released in VERA core physics benchmark is firstly chosen to perform sensitivity quantification using both GPT method and DP method. The comparison results indicate that implicit sensitivity coefficient calculated in this paper by proposed GPT method has acceptable accuracy. Then the total sensitivity analysis is performed and the results suggest that implicit impact is nonnegligible when perform sensitivity analysis for LWR problems. Finally, total k_eff uncertainty of the two-dimensional fuel pin cell problem due to representative nuclides cross sections were quantified. According to the results, total uncertainty of k_eff propagated from multi-group cross sections is about 0.517%, and three most significant contributors are capture reaction of ²³⁸U, average number of neutrons emitted per fission event of ²³⁵U and capture reaction of ²³⁸U. The numerical results also suggest that the implicit part of sensitivity coefficient cannot be ignored, otherwise the reasonable uncertainty propagation cannot be ensured. While the implicit part has an unremarkable influence on the quantified total uncertainty of k_eff for the investigated problem.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CH is responsible for the research thought; JM is responsible for the formul derivation and code development; GL, LK, PL and FR help for the verification and a part of calculation.

Funding

This work was supported by the National Key R&D Program of China 2018YFE0180900 and the Chinese National Natural Science Foundation Project 12075067.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bratton, R. N., Avramova, M., and Ivanov, K. (2014). Oecd/nea Benchmark for Uncertainty Analysis in Modeling (Uam) for Lwrs - Summary and Discussion of Neutronics Cases (Phase I). Nucl. Eng. Technology 46 (3), 313–342. doi:10.5516/net.01.2014.710

CrossRef Full Text | Google Scholar

Dion, M., and Marleau, G. (2013). Resonance Self-Shielding Effects on Eigenvalue Sensitivity. Idaho, USA: M&C 2013.

Google Scholar

Foad, B., and Takeda, T. (2015). Sensitivity and Uncertainty Analysis for UO 2 and MOX Fueled PWR Cells. Ann. Nucl. Energ. 75 (JAN), 595–604. doi:10.1016/j.anucene.2014.08.068

CrossRef Full Text | Google Scholar

Godfrey, A. T. (2013). VERA Core Physics Benchmark Progression Problem Specifications, Revision 2. CASL-U-2012-0131-002. Nashville, TN: Oak Ridge National Laboratory.

Google Scholar

Greenspan, E., Karni, Y., and Gilai, D. (1978). High Order Effects in Cross Section Sensitivity Analysis. Beersheva (Israel): Negev Univ.

Google Scholar

IAEA (2008). Best Estimate Safety Analysis for Nuclear Power Plants: Uncertainty Evaluation. in Safety Reports Series 52, 1–211.

Google Scholar

Liu, Y., Cao, L., Wu, H., Zu, T., and Shen, W. (2015). Eigenvalue Implicit Sensitivity and Uncertainty Analysis with the Subgroup Resonance-Calculation Method. Ann. Nucl. Energ. 79, 18–26. doi:10.1016/j.anucene.2015.01.012

CrossRef Full Text | Google Scholar

Ma, J., Hao, C., Liu, L., and Zhou, Y. (2020). Perturbation Theory-Based Whole-Core Eigenvalue Sensitivity and Uncertainty (SU) Analysis via a 2D/1D Transport Code. Sci. Technology Nucl. Installations 2020 (2), 1–13. doi:10.1155/2020/94285802020

CrossRef Full Text | Google Scholar

Perfetti, C. M., and Rearden, B. T. (2013). “Continuous-energy Eigenvalue Sensitivity Coefficient Calculations in TSUNAMI-3D,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science & Engineering (M&C 2013), Sun Valley, Idaho, USA, May 5-9, 2013 (LaGrange Park, Illinois: American Nuclear Society).

Google Scholar

Pusa, M. (2012). Incorporating Sensitivity and Uncertainty Analysis to a Lattice Physics Code with Application to CASMO-4. Ann. Nucl. Energ. 40 (1), 153–162. doi:10.1016/j.anucene.2011.10.013

CrossRef Full Text | Google Scholar

Rearden, B. T., and Jessee, M. A. (2016). Oak Ridge National Laboratory, Oak Ridge, Tennessee. Available from Radiation Safety Information Computational Center as CCC-834. SCALE Code System, ORNL/TM-2005/39. Version 6.2.1.

Google Scholar

She, D., Xia, D., Guo, J., Wei, C-L., Zhang, J., Li, F., et al. (2021). Prediction calculations for the first criticality of the HTR-PM using the PANGU code. Nucl. Sci. Tech. 32, 90, 2021. doi:10.1007/s41365-021-00936-5

CrossRef Full Text | Google Scholar

Wan, C., Cao, L., Wu, H., and Shen, W. (2017). Total Sensitivity and Uncertainty Analysis for LWR Pin-Cells with Improved UNICORN Code. Ann. Nucl. Energ. 99, 301–310. doi:10.1016/j.anucene.2016.09.014

CrossRef Full Text | Google Scholar

Wang, D., Hao, C., Zhao, Q., and Wu, Z. (2016). Study of the Transform Method of Multi-Group Nuclear Cross Section Covariance Matrix. Nucl. Power Eng. 37 (No. 2). doi:10.13832/j.jnpe.2016.02.0001

CrossRef Full Text | Google Scholar

Weisbin, C. R., Marable, J. H., Lucius, J. L., Peelle, R. W., Mynatt, F. R., Oblow, E. M., et al. (1976). Application of Forss Sensitivity and Uncertainty Methodology to Fast Reactor Benchmark Analysis. Trans. Am. Nucl. Soc. 24. doi:10.2172/7337288

CrossRef Full Text | Google Scholar

Williams, M. L., Broadhead, B. L., and Parks, C. V. (2001). Eigenvalue Sensitivity Theory for Resonance-Shielded Cross Sections. Nucl. Sci. Eng. 138 (2), 177–191. doi:10.13182/nse00-56

CrossRef Full Text | Google Scholar

Wu, Q., Yu, J., Shi, G., Tang, X., Yu, Y., Li, Q., et al. (2018). Eigenvalue Sensitivity and Uncertainty Analysis Based on a 2-D/1-D Whole-Core Transport Code KYADJ. Ann. Nucl. Energ. 122, 185–192. doi:10.1016/j.anucene.2018.08.044

CrossRef Full Text | Google Scholar