Distributed Imitation-Orientated Deep Reinforcement Learning Method for Optimal PEMFC Output Voltage Control

In order to improve the stability of proton exchange membrane fuel cell (PEMFC) output voltage, a data-driven output voltage control strategy based on regulation of the duty cycle of the DC-DC converter is proposed in this paper. In detail, an imitation-oriented twin delay deep deterministic (IO-TD3) policy gradient algorithm which offers a more robust voltage control strategy is demonstrated. This proposed output voltage control method is a distributed deep reinforcement learning training framework, the design of which is guided by the pedagogic concept of imitation learning. The effectiveness of the proposed control strategy is experimentally demonstrated.

Introduction

The voltage of a proton exchange membrane fuel cell (PEMFC) is highly dependent on the temperature, pressure, humidity, and gas flow rate (Yang et al., 2018; Sun et al., 2019). In addition, the output voltage of PEMFC also fluctuates widely with varying load current (Yang et al., 2019a; Yang et al., 2021a). In order to improve the stability of the PEMFC output voltage, the PEMFC DC-DC converters should output a stable bus voltage in the event of fluctuating input voltage and output load so as to normalize the load (Yang et al., 2021b; Yang et al., 2021c).

There are a number of existing PEMFC output voltage control methods based on control of DC-DC converters, including the PID control algorithm (Swain and Jena, 2015), fractional order PID algorithm (Yang et al., 2019a; Yang et al., 2019b; Yang et al., 2020), sliding mode control algorithm (Bougrine et al., 2013; Jiao and Cui, 2013), model predictive control algorithm (Bemporad et al., 2002; Ferrari-Trecate et al., 2002), robust control method (Olalla et al., 2010), and optimal control algorithm (Jaen et al., 2006; Olalla et al., 2009; Montagner et al., 2011; Moreira et al., 2011) methods, and so on. Among them, the PID algorithms are traditional control algorithms whose advantages include simple structure and fast calculation speed. However, these are incompatible with non-linear PEMFC systems. The fractional order PID algorithm is an expanded algorithm based on the PID algorithm, which offers better robustness, but which cannot be adapted for non-linear PEMFC systems. Sliding mode control is an excellent candidate for variable structure systems such as DC-DC converters; however, it is not suitable for PEMFC systems in practice as it is affected by the “jitter” problem. The model prediction algorithm offers higher accuracy and strong robustness; however, the algorithm is heavily reliant on mathematical models, making the control results in reality very different from the theoretical ones. The goal of robust control is to establish feedback control laws accounting for system uncertainty in order to increase the robustness of closed-loop systems. However, the control performance of a controller employing robust control is compromised it as cannot operate at the optimal point.

Optimal control is one of the more advanced control algorithm designs. By expressing the performance of a system as an objective function of time, state, error, and other combinations, optimal control selects an appropriate control law which enables the objective function to include extreme values in order to obtain the optimal performance of the system. As described by Jaen et al. (2006), the average model of the converter is linearised, and the optimal LQR is obtained by solving the algebraic Riccati equation using the pole configuration, frequency domain metric or integral metric as the optimisation objective function; however, this LQR is not robust enough to cope with large disturbances in the system. Montagner et al. (2011) designed a discrete LQR and determined the existence of the Lyapunov function for the closed-loop system using the LMI method, thus ensuring the stability of the system. Olalla et al. (2009) organised the LQR optimisation problem in the form of an LMI, which was then solved using convex optimisation to obtain a robust linear quadratic regulator. In the study by Moreira et al. (2011), the application of a digital LQR with Kalman state observer for controlling a BUCK converter was tested in a series of simulations. However, the structure of the above optimal algorithm is complex and computationally intensive, leading to a reduction in its control real-time performance in practice (Li and Yu, 2021).

For these reasons, there remains the need for a simple structured model-free PMEFC optimal control algorithm for guiding DC-DC converters (Li et al., 2021).

The DDPG algorithm (Lillicrap et al., 2015) is a data-driven model-free optimal control algorithm, a kind of deep reinforcement learning, which is characterised by strong self-adaptive capability and decision-making ability, and which can arrive at decisions within a few milliseconds. It is used widely in power system control and robot coordination control, and for addressing UAV control problems (Zhang et al., 2016; Qi, 2018; Zhang et al., 2018; Zhang et al., 2019; Zhang and Yu, 2019; Zhang et al., 2020; Zhang et al., 2021; Zhang et al., 2021). However, the poor training efficiency of the DDPG algorithm explains the low robustness of controllers belonging to this class of algorithms, and their ineligibility for PEMFC systems.

In order to stabilise the output characteristics of the PEMFC and improve the stability of its output voltage, a data-driven output voltage control strategy for controlling the duty cycle of the DC-DC converter is proposed in this paper. To this end, an imitation-oriented twin delay deep deterministic policy gradient (IO-TD3) algorithm is proposed, the design of which reflects the idea of imitation learning. In this paper, we propose a distributed deep reinforcement learning training framework for improving the robustness of the PEMFC control policy. The effectiveness of the proposed control policy is experimentally demonstrated by comparing the proposed method with a number of existing algorithms.

This paper makes the following unique contributions to the research field:

1) A 75 kw ninth order output voltage PEMFC dynamic control model that takes into account the DC/DC converter is demonstrated.

2) A PEMFC output voltage control strategy based on an imitation-oriented twin delay deep deterministic policy gradient algorithm for the purpose of increasing robustness is proposed.

The remainder of this paper comprises the following sections: the PEMFC model is demonstrated in The PEMFC Model, and the proposed algorithm is described in Proposed Method; the experimental results are analysed and discussed in Experiment, and the findings in this paper are summarised in Conclusion.

The PEMFC Model

PEMFC Modelling and Characterization

A PEMFC is a device that converts chemical energy directly into electrical energy by means of an electrochemical reaction, the individual output voltage of which can be expressed as follows:

$V_{\text{cell }}=E-{\eta }_{\text{act }}-{\eta }_{\text{ohm }}-{\eta }_{\text{con }}(1)$

For a fuel cell stack consisting of N single cells connected in series, the output voltage V can be expressed as follows:

$V=N{V}_{\text{cell }}(2)$

Theoretically, the electric potential of the PEMFC varies with temperature and pressure, as expressed in the following equation:

$E=1.229-0.85\times {10}^{-3}\left(T-298.15\right)+4.3085\times {10}^{-5}T\left(\ln p_{{\text{H}}_2}+\ln p_{0_2}/2\right)(3)$

Thermodynamic Electric Potential

The thermodynamic electric potential of the single cell (i.e., the Nernst electric potential) can be obtained from the mechanism of the electrochemical reaction of the gas inside the PEMFC. This is represented by the following equation:

$E=\frac{\Delta G}{2F}+\frac{\Delta S}{2F}\left(T-T_{\text{ref}}\right)+\frac{RT}{2F}\left(\ln p_{{\text{H}}_2}+\frac{1}{2}\ln p_{0_2}\right)(4)$

Activation Overvoltage

The activation overvoltage of the PEMFC is expressed as follows:

${\eta }_{\text{act}}={\xi }_1+{\xi }_{2}T+{\xi }_{3}T\ln c\left({\text{O}}_2\right)+{\xi }_{4}T\ln I(5)$

Whereby $c\left({\text{O}}_2\right)$ is the concentration of dissolved oxygen at the cathode catalyst interface, which can be expressed by Henry’s law as follows:

$c\left({\text{O}}_2\right)=P_{{\text{O}}_2}/5.08\times {10}^6\exp \left(-498/T\right)(6)$

Ohmic Voltage Drop

The ohmic overvoltage is represented by the following equation:

${\eta }_{\text{ohm }}=I{R}_{\text{int }}=I\left(R_{\text{m}}+R_{\text{c}}\right)(7)$

Empirically, the internal resistance of the PEMFC is expressed as follows:

$R_{\text{int}}=0.01605-3.5\times {10}^{-5}T+8\times {10}^{-5}i(8)$

Dense Differential Polarization Overvoltage

The differential overvoltage can be expressed as follows:

${\eta }_{\text{con}}=-\beta \ln \left(J/J_{\max }\right)(9)$

Dynamic and Capacitive Characteristics of the Double Layer Charge

The dynamic characteristics of the double layer charge of the PEMFC are similar to those of the capacitor, and the equivalent circuit diagram is shown in Figure 1A:

FIGURE 1

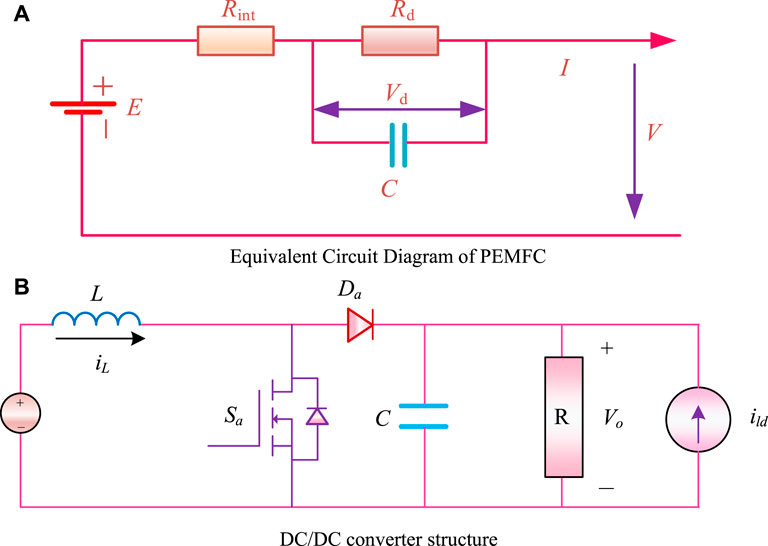
FIGURE 1. PEMFC equivalent circuit and DC-DC converter. (A)Equivalent Circuit Diagram of PEMFC. (B)DC/DC converter structure.

As detailed in the figure, the polarization voltage across R_d is V_d and the differential equation for the voltage change of a single cell is expressed as follows:

$\text{d}{V}_{\text{d}}/\text{d}t=I/C-V_{\text{d}}/R_{\text{d}}C(10)$

PEMFC Stack Voltage

The stack voltage is defined as the value of the voltage at the front end of the PEMFC as it passes through the DC/DC converter. It is assumed that hydrogen is supplied from a hydrogen tank, and is available in sufficient quantities at all times. The air, on the other hand, is controlled by a proportional valve, which allows the air to be controlled efficiently and in time to meet the PEMFC requirements.

Eq. 11 can be obtained from The Law of Conservation of Mass, and the Ideal Gas Law:

$\frac{V_o}{8.314T}\times \frac{d{P}_{H2}}{dt}=m_{h2}-K\left(P_{H2}-P_{EH2}\right)-\frac{0.5NI}{F}(11)$

DC-DC Boost Converter Model

The output voltage of the PEMFC is the tap voltage of the DC/DC converter. A boost converter is essentially a step-up power converter, i.e., the voltage is raised and then outputted. An DC/DC boost converter circuit is shown in Figure 1B:

Whereby the input and output voltage relationship are controlled output voltage by the switch duty cycle, as expressed in Equation:

$V_{\text{ou}}=\left(\frac{1}{1-u}\right)\times V_{\text{stack}}(12)$

The differential equation for V_out is as follows:

$\{\begin{array}{l}\frac{\text{d}{i}_L}{ \text{d}t}=\frac{1}{L}\cdot V_{\text{stack}}\hfill \\ \frac{\text{d}{V}_{\text{out}}}{\text{d}t}=\frac{1}{C}\cdot \left(-i_{\text{ost}}\right)\hfill \end{array}(13)$

Proposed Method

Framework of Control Policy

The control model includes a PEMFC stack, a DC/DC converter and its controller. The controller of the DC/DC converter is equated to an intelligent agent which is trained to adapt to the non-linear characteristics of the PEMFC so as to improve the overall output voltage control performance. When applied online, the intelligent agent outputs the optimal duty cycle according to the state of the DC-DC converter and the state of the output voltage. The control interval of the agent is 0.01 s.

Agent

1) Action space

The action space is set to u/100, as follows:

$\{\begin{array}{l}a=\left[u/100\right]\\ \text{0}\le u\le u_{\max }\end{array}(14)$

2) State space

The state space is expressed as follows:

$\left[e{\displaystyle {\int }_0^{t}edtU}\right](15)$

3) Reward function

The reward function is expressed as follows:

$\text{r}\left(t\right)=-\left[{\mu }_1{e}^2\left(t\right)+{\mu }_{2}u\left(t-1\right)\right]+\beta (16)$

$\alpha =\{\begin{array}{l}-0.3e^2\left(t\right)>0.09\\ 0e_{st}^2\left(t\right)\le 0.09\end{array}(17)$

DDPG

The Deterministic Policy Gradient (DDPG) policy determines an action via the policy function µ(s), which is shown in the following equation:

$a_i=\mu \left(s_t\mathrm{|}{\theta }^{\mu }\right)(18)$

This deep reinforcement learning algorithm uses a value network to fit the function Q(s) and the objective function $J\left({\theta }^{\mu }\right)$, the latter which is defined as follows:

$J\left({\theta }^{\mu }\right)=E_{\theta ,x}\left[r_1+\gamma r_2+{\gamma }^2{r}_3+\cdots \right](19)$

In this arrangement, the Q function can be expressed as the expected value of the reward for selecting an action under µ(s).

In each step, a specific policy is randomly selected for the agent to be executed, and the best policy is selected by maximizing the fusion objective function. The different policy will be executed in different steps, so that an experience replay pool can be obtained for each agent. Finally, the gradient of the fusion objective function ${\nabla }_{\theta i}J$ is solved for the policy parameters of each agent, as expressed in the following equation:

${\nabla }_{{\theta }_i}J\approx \frac{1}{S}{\displaystyle \sum _j{\nabla }_{{\theta }_j}}{\mu }_i\left(O_i^j\right){\nabla }_{a_j}{Q}_i^{\mathrm{ϵ}}\cdot {\left(x^j,a_1^j,\cdots ,a_i,\cdots ,a_N^j\right)|}_{ai=\mu i\left(O_i\right)}(20)$

Nevertheless, the DDPG algorithm suffers from low robustness. The main reasons for this are as follows:

1) The algorithm lacks effective bootstrapping techniques, and so it tends to fall into the local optimum solution, which undermines the robustness of the strategy.

2) Overestimation of the Q-value leads to overfitting of the algorithm’s policy, thus making it less robust.

Framework for Offline Training of IO-TD3

In order to address the low robustness of the DDPG algorithm, the IO-TD3 algorithm incorporates the following two innovations:

1) An imitation-oriented distributed training framework for deep reinforcement learning; and,

2) An Integrated anti-Q overestimation policy.

The large-scale deep reinforcement learning training framework for the IO-TD3 algorithm is illustrated.

The algorithm contains three roles, an explorer, an expert and a leader. A total of 36 parallel systems are included in the algorithm, each containing the same PEMFC system and different load disturbances, so as to enhance sample diversity.

Explorer

The Explorer contains only one actor network. The explorers in different parallel systems employ their own different exploration principles. The explorers described in this paper use the following exploration principles: greedy strategy, Gaussian noise, and OU noise.

The explorer in parallel system 1–6 uses an ε-greedy strategy with the following actions:

$a_{\epsilon }^l=\{\begin{array}{ll}{\pi }_{\varphi }^l\left(s\right)\hfill & \text{With}\epsilon \text{probability}\hfill \\ a_{\text{rand}}^l\hfill & \text{With}1-\epsilon \text{probability}\hfill \end{array}(21)$

The explorer in parallel system 7–12 uses an OU noise exploration strategy with the following actions:

$a_{OU}^j={\pi }_{\varphi }^j\left(s\right)+N_{OU}^j(22)$

The Gaussian noise exploration strategy used in parallel system 13–18 has the following actions:

$a_{\text{Gaussian}}^m={\pi }_{\varphi }^m\left(s\right)+N_{\text{Gaussian}}^m(23)$

Expert

On the basis of imitation learning, the proposed algorithm employs a large number of expert samples, which are used as learning samples, so that the algorithm can be effectively guided to learn correctly during the early stages of training. In this proposed method, the duty cycle of the DC/DC converter is controlled, whereby the parallel systems generate expert samples for the Leader (described below).

The expert itself uses a variety of controllers based on different principles, including PSO-PID and GA-PID algorithms. The objective function for parameter optimization is as follows:

$F\left(t\right)={\displaystyle {\int }_0^{\infty }t}{\left(e\left(t\right)\right)}^2\text{d}t(24)$

Leader

The leader (termed “Leader”) entails a complete agent structure which includes a two-actor network, two critic networks, and an experience pool. It learns samples from the explorer and the critic in order to obtain the optimal control strategy, and periodically sends the latest parameters to the actor network for all the explorers.

The critic in each leader employs an integrated mitigation Q over-estimation technique.

1) The critic in Leader uses the Clipped Double Q-learning technique to calculate the target value:

$y_t^1=r\left(s_t,a_t\right)+\gamma {\min }_{i=\mathrm{1,2}}{Q}_{{\theta }_i^{\prime }}\left(s_{t+1},{\pi }_{{\varphi }_1}\left(s_{t+1}\right)\right)(25)$

2) The critic network inside Leader uses a policy delay update policy. d updates to the actor network are performed after every d update to the critic.

3) The critic inside Leader uses a goal policy smoothing regularization strategy. The critic introduces a regularization method for reducing the variance of the goal values by bootstrapping the estimates of similar state action pairs.

$y_t=r\left(s_t,a_t\right)+{\text{E}}_{\epsilon }\left[Q_{{\theta }^{\prime }}\left(s_{t+1},{\pi }_{{\varphi }^{\prime }}\left(s_{t+1}\right)+\epsilon \right)\right](26)$

Smooth regularization is also achieved by adding a random noise to the target strategy and averaging over the mini-batch:

$y_t=r\left(s_t,a_t\right)+\gamma {\min }_{i=\mathrm{1,2}}{Q}_{{\theta }_t}\left[s_{t+1},{\pi }_{{\varphi }^{\prime }}\left(s_{t+1}\right)+\epsilon \right](27)$

$\epsilon \sim \mathrm{clip}\left[N\left(0,\sigma \right),-c,c\right](28)$

Experiment

In order to verify the superior effectiveness of the proposed method, the IO-TD3 algorithm control strategy was tested against the following methods in case: Ape-x-MADDPG control algorithm (40), MATD3 control algorithm (41), MADDPG coordinated control algorithm (37), BP neural network control algorithm, RBF neural network control algorithm, PSO optimized PID control algorithm (PSO-PID), GA optimized PID control algorithm (GA-PID), PID control algorithm (PID), Fuzzy-FOPID control algorithm (Fuzzy-FOPID), and the PSO-optimized FOPID control algorithm (PSO-FOPID). The first six (including the IO-TD3 algorithm) are referred to as advanced algorithms, and the last five are conventional algorithms.

At 1 s, the load current magnitude appears as a load disturbance which begins at 72.6 A and rises to 250.0 A. The results are shown in Figure 2A,B.

1) Comparison between proposed algorithm and advanced algorithms. As shown in Figure 2A, the IO-TD3 algorithm has a better response time, smoother output voltage profile and no overshoot. The proposed algorithm’s minimum output voltage value is smaller than that of the other advanced algorithms. Conversely, each of the output voltages of the other advanced algorithms is characterized by large overshoot, and these results are affected by varying degrees of overshoot and oscillation, which can lead to unstable output voltages. The IO-TD3 algorithm therefore has the best control performance.

2) Possible reasons for these promising patterns are as follows: firstly, other DRL algorithms tend to fall into local optima; they amount to sub-optimal control strategies as they are not effectively guided in pre-learning, resulting in large output voltage overshoot and output voltage fluctuations, which undermine PEMFC output performance.

FIGURE 2

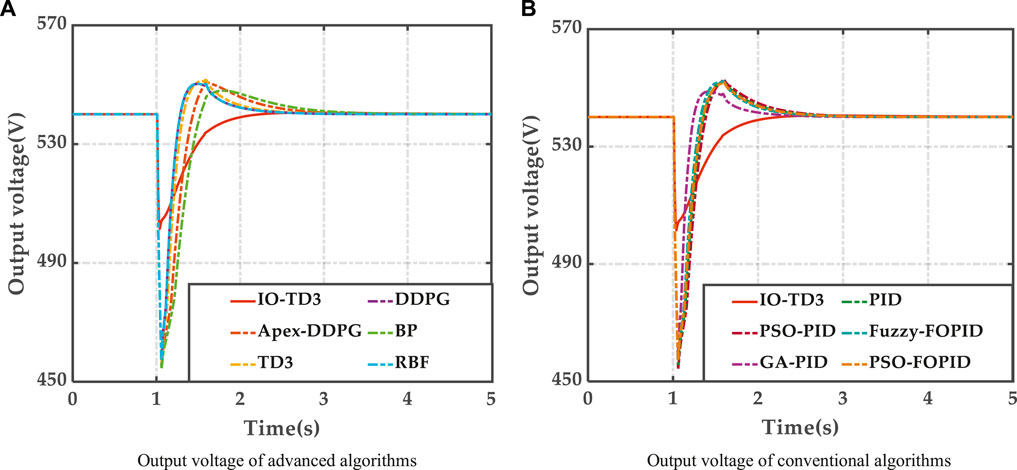
FIGURE 2. Results of Case 1. (A) Output voltage of advanced algorithms (B) Output voltage of conventional algorithms

The BP and RBF algorithms are too dependent on the trained samples, resulting in limited control performance. A neural network control algorithm which lacks self-exploration will have lower adaptive ability, leading to poorer control performance.

The PSO-PID and GA-PID algorithms within the conventional control algorithm group lack the adaptive capability for adjusting the PID parameters, and therefore struggle to adapt to the non-linearity of the PEMFC environment. The PSO-FOPID algorithm enables greater robustness in the environment, but is impaired by poor adaptive capability due to its fixed coefficients, which ultimately leads to severe output voltage overshoot and oscillation. The Fuzzy-FOPID algorithm, despite its better adaptive capability, is underpinned by overly simple rules, resulting in poor control accuracy and therefore a large overshoot despite the fast response of the algorithm.

In summary, the IO-TD3 controller is a more suitable candidate for practical output voltage control systems, with its short response times, and good dynamic and static performance indicators.

Conclusion

In this paper, an imitation-oriented deep reinforcement learning output voltage control strategy for controlling the duty cycle of a DC-DC converter has been proposed. The proposed method is an imitation-oriented twin delay deep deterministic (IO-TD3) policy gradient algorithm, the design of which is structured on the concept of imitation learning. It embodies a distributed deep reinforcement learning training framework designed to improve the robustness of the control policy. The effectiveness of the proposed control policy has been experimentally demonstrated. The simulation results show that the IO-TD3 algorithm has superior control performance compared to other deep reinforcement learning algorithms (e.g., Ape-x-MADDPG, MATD3, MADDPG). Compared to other control algorithms (BP, RBF, PSO-PID, GA-PID, PID, Fuzzy-FOPID, PSO-FOPID), the IO-TD3 algorithm is more adaptable, and, in relation to the output voltage of the PEMFC, has better response speed and stability, and can more effectively track and control the output voltage in a timely and effective manner.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JL: conceptualization, methodology, software, data curation, writing-original draft preparation, visualization, investigation, software, validation. YL: Writing-Reviewing and editing. TY: Supervision.

Funding

This work was jointly supported by National Natural Science Foundation of China (U2066212).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bemporad, A., Borrelli, F., and Morari, M. (2002). Model Predictive Control Based on Linear Programming - the Explicit Solution. Ieee Trans. Automat. Contr. 47, 1974–1985. doi:10.1109/tac.2002.805688

CrossRef Full Text | Google Scholar

Bougrine, M. D., Benalia, A., and Benbouzid, M. H. (2013). “Nonlinear Adaptive Sliding Mode Control of a Powertrain Supplying Fuel Cell Hybrid Vehicle,” in 3rd International Conference on Systems and Control (Algiers, Algeria: IEEE), 714–719.

CrossRef Full Text | Google Scholar

Ferrari-Trecate, G., Cuzzola, F. A., Mignone, D., and Morari, M. (2002). Analysis of Discrete-Time Piecewise Affine and Hybrid Systems. Automatica 38, 2139–2146. doi:10.1016/s0005-1098(02)00142-5

CrossRef Full Text | Google Scholar

Jaen, C., Pou, J., Pindado, R., Sala, V., and Zaragoza, J. (2006). “A Linear-Quadratic Regulator with Integral Action Applied to PWM DC-DC Converters,” in IECON 2006 - 32nd Annual Conference on IEEE Industrial Electronics (Paris, France: IEEE), 2280–2285.

CrossRef Full Text | Google Scholar

Jiao, J., Cui, X., and Cui, X. (2013). Robustness Analysis of Sliding Mode on DC/DC for Fuel Cell Vehicle. Jestr 6, 1–6. doi:10.25103/jestr.065.01

CrossRef Full Text | Google Scholar

Li, J., and Yu, T. (2021). A New Adaptive Controller Based on Distributed Deep Reinforcement Learning for PEMFC Air Supply System. Energ. Rep. 7, 1267–1279. doi:10.1016/j.egyr.2021.02.043

CrossRef Full Text | Google Scholar

Li, J., Yu, T., Zhang, X., Li, F., Lin, D., and Zhu, H. (2021). Efficient Experience Replay Based Deep Deterministic Policy Gradient for AGC Dispatch in Integrated Energy System. Appl. Energ. 285, 116386. doi:10.1016/j.apenergy.2020.116386

CrossRef Full Text | Google Scholar

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous Control with Deep Reinforcement Learning. arXiv preprint arXiv:1509.02971.

Google Scholar

Montagner, V. F., Maccari, L. A., Dupont, F. H., Pinheiro, H., and Oliveira, R. C. L. F. (2011). “A DLQR Applied to Boost Converters with Switched Loads: Design and Analysis,” in XI Brazilian Power Electronics Conference (Natal, Brazil: IEEE), 68–73.

CrossRef Full Text | Google Scholar

Moreira, C. O., Silva, F. A., Pinto, S. F., and Santos, M. B. (2011). “Digital LQR Control with Kalman Estimator for DC-DC Buck Converter,” in 2011 IEEE EUROCON - International Conference on Computer as a Tool (Lisbon, Portugal: IEEE), 1–4.

CrossRef Full Text | Google Scholar

Olalla, C., Leyva, R., El Aroudi, A., and Queinnec, I. (2009). Robust LQR Control for PWM Converters: An LMI Approach. Ieee Trans. Ind. Electron. 56, 2548–2558. doi:10.1109/tie.2009.2017556

CrossRef Full Text | Google Scholar

Olalla, C., Queinnec, I., Leyva, R., and Aroudi, A. E. (2010). “Robust Control Design of Bilinear DC-DC Converters with Guaranteed Region of Stability,” in 2010 IEEE International Symposium on Industrial Electronics (Bari, Italy: IEEE), 3005–3010.

CrossRef Full Text | Google Scholar

Qi, X. (2018). Rotor Resistance and Excitation Inductance Estimation of an Induction Motor Using Deep-Q-Learning Algorithm. Eng. Appl. Artif. Intelligence 72, 67–79. doi:10.1016/j.engappai.2018.03.018

CrossRef Full Text | Google Scholar

Sun, L., Jin, Y., Pan, L., Shen, J., and Lee, K. Y. (2019). Efficiency Analysis and Control of a Grid-Connected PEM Fuel Cell in Distributed Generation. Energ. Convers. Manage. 195, 587–596. doi:10.1016/j.enconman.2019.04.041

CrossRef Full Text | Google Scholar

Swain, P., and Jena, D. (2015). “PID Control Design for the Pressure Regulation of PEM Fuel Cell,” in 2015 International Conference on Recent Developments in Control, Automation and Power Engineering (RDCAPE) (Noida, India: IEEE), 286–291.

CrossRef Full Text | Google Scholar

Yang, B., Li, D., Zeng, C., Chen, Y., Guo, Z., Wang, J., et al. (2021a). Parameter Extraction of PEMFC via Bayesian Regularization Neural Network Based Meta-Heuristic Algorithms. Energy 228, 120592. doi:10.1016/j.energy.2021.120592

CrossRef Full Text | Google Scholar

Yang, B., Swe, T., Chen, Y., Zeng, C., Shu, H., Li, X., et al. (2021b). Energy Cooperation between Myanmar and China under One Belt One Road: Current State, Challenges and Perspectives. Energy 215, 119130. doi:10.1016/j.energy.2020.119130

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manage. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019a). Dynamic Leader Based Collective Intelligence for Maximum Power point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manage. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zeng, C., Wang, L., Guo, Y., Chen, G., Guo, Z., et al. (2021c). Parameter Identification of Proton Exchange Membrane Fuel Cell via Levenberg-Marquardt Backpropagation Algorithm. Int. J. Hydrogen Energ. 46, 22998–23012. doi:10.1016/j.ijhydene.2021.04.130

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019b). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Zhang, X., Li, S., He, T., Yang, B., Yu, T., Li, H., et al. (2019). Memetic Reinforcement Learning Based Maximum Power point Tracking Design for PV Systems under Partial Shading Condition. Energy 174, 1079–1090. doi:10.1016/j.energy.2019.03.053

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhang, X., Xu, H., Yu, T., Yang, B., and Xu, M. (2016). Robust Collaborative Consensus Algorithm for Decentralized Economic Dispatch with a Practical Communication Network. Electric Power Syst. Res. 140, 597–610. doi:10.1016/j.epsr.2016.05.014

CrossRef Full Text | Google Scholar

Zhang, X., and Yu, T. (2019). Fast Stackelberg Equilibrium Learning for Real-Time Coordinated Energy Control of a Multi-Area Integrated Energy System. Appl. Therm. Eng. 153, 225–241. doi:10.1016/j.applthermaleng.2019.02.053

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Xu, Z., and Fan, Z. (2018). A Cyber-Physical-Social System with Parallel Learning for Distributed Energy Management of a Microgrid. Energy 165, 205–221. doi:10.1016/j.energy.2018.09.069

CrossRef Full Text | Google Scholar

Zhang, Y., Mou, Z., Gao, F., Jiang, J., Ding, R., and Han, Z. (2020). UAV-enabled Secure Communications by Multi-Agent Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 69, 11599–11611. doi:10.1109/tvt.2020.3014788

CrossRef Full Text | Google Scholar