Robust Stability Control for Electric Vehicles Connected to DC Distribution Systems

DC power distribution systems will play an important role in the future urban power distribution system, while the charging and discharging requirements of electric vehicles have a great impact on the voltage stability of the DC power distribution systems. A robust control method based on H_∞ loop shaping method is proposed to suppress the effect of uncertain integration on voltage stability of DC distribution system. The results of frequency domain analysis and time domain simulation show that the proposed robust controller can effectively suppress the DC bus voltage oscillation caused by the uncertain integration of electric vehicle, and the robustness is strong.

Introduction

Electric vehicles have become an important part of the low-carbon economy and the world is also in the stage of transformation from fuel vehicles to new energy vehicles (Needell et al., 2016; Wang et al., 2019; Ding et al., 2020; Connor et al., 2021; Zhang et al., 2021). Large-scale electric vehicles will be connected to the distribution network in the future. At present, the distribution network in the world is mainly in the form of AC power supply, and it is necessary to realize the charging of electric vehicles through AC/DC conversion links (Amamra and Marco, 2019; Li et al., 2019; Dong et al., 2021). So many electric energy conversion links will bring problems such as increased loss and reduced power efficiency (Rasheed et al., 2019). DC distribution systems has the advantages of low power loss, high power quality, and easy integration of DC distributed generations and loads (Rashad et al., 2018; Zhao et al., 2018; Dastgeer et al., 2019; Lin et al., 2019), which is gradually becoming the new direction of urban distribution system development in the future. However, the random charging of electric vehicles will cause uncertainty disturbance to the DC distribution system, which will easily lead to system oscillation and even instability (Staats et al., 1998; Tian et al., 2016).

Therefore, how to improve the stability of DC distribution system under the uncertain integration of electric vehicles has become a hot research topic at present. Scholars have put forward corresponding stability control methods from various points which can be summarized as follows:

1) Charging power adjustment method (Tabari and Yazdani, 2014; Tabari and Yazdanil, 2016). This strategy can effectively improve the system stability without changing system parameters or hardware, but it will have an impact on the charging rate of electric vehicles.

2) Virtual inertia control method. The first-order inertia compensation function is introduced into the outer loop of power control, which can improve the system damping and enhance the system stability after the electric vehicle is connected.

3) Virtual DC motor control method (Radwan and Mohamed, 2012; Alipoor et al., 2015). Based on the conventional double closed-loop control, the virtual DC motor is introduced to enhance the damping of the system by simulating the inertia of DC generator.

4) Nonlinear control (Tan et al., 2016; Tabari and Yazdani, 2014). Using nonlinear compensation function, fuzzy control, and other methods to improve system damping, but the control algorithm is more complex.

Most of the above studies do not consider the influence of uncertainty caused by random charging of electric vehicles. Therefore, this paper studies the robust stability control of electric vehicles connected to DC distribution system. In the manuscript, a model of the DC/DC converter control system is established and a robust stability controller based on H_∞ loop shaping method is designed to improve the stability of DC bus voltage and suppress system oscillation under uncertainty.

The major contributions of this paper are summarized as follows:

1) The uncertain integration of electric vehicles and the parameter perturbation of the controller affect the voltage stability of the DC distribution system. Therefore, H_∞ loop shaping method is introduced for DC/DC converters to improve the robust stability of the system.

2) A robust controller is designed for a DC distribution system with two EVs integration, and a high-order transfer function is obtained. For practical engineering application, the Hankel singular value algorithm is used to reduce the order. And the frequency domain analyses verify the control effect before and after order reduction.

3) A simulation model is established with DIgSILENT software, in which six scenarios are simulated. The simulation results show that the DC distribution system has good robustness to uncertain disturbances with the designed controller.

The remainder of this paper is organized as follows. In Topology of DC Distribution System with Electric Vehicle, a model of the flexible DC distribution system with electric vehicle is established. H_∞Loop Shaping Method introduces the H_∞ loop forming method, and the robust controller is designed for DC/DC converter. Frequency domain analysis is performed to verify the effectiveness of the robust controller in Frequency Domain Analysis. In Simulation Verification and Analysis, the effectiveness of the designed robust controller is verified by simulation. Finally, conclusions are summarized in Conclusion.

Topology of DC Distribution System With Electric Vehicle

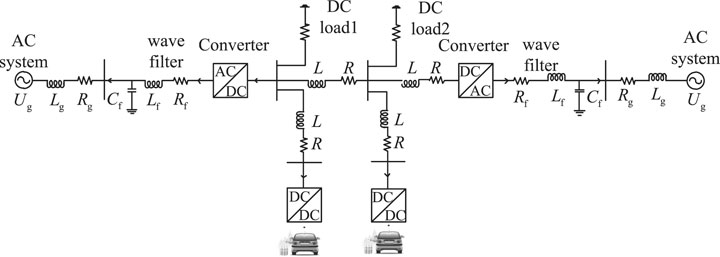
The typical topology of DC distribution system is shown in Figure 1. Its main equipment includes interconnected AC/DC lines, interconnected AC/DC converters, DC distributed generations and DC loads, and DC/DC choppers, etc. The dynamic interaction among various equipment makes the stability of the system complex.

FIGURE 1

FIGURE 1. Structure drawing of double-end DC distribution system with electric vehicle.

The AC/DC interconnected converter in Figure 1 is based on the conventional three-phase bidirectional full-control rectifier bridge (Yazdani and Iravani, 2010), and its control mode adopts P-U_dc droop control, and the DC/DC chopper is based on the conventional Buck-Boost circuit.

Control Strategy of Electric Vehicle

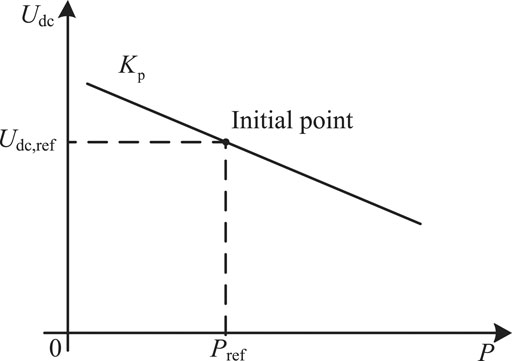
Conventional control strategies of electric vehicle chopper are mainly divided into constant power, constant current and constant voltage control (Peng et al., 2021). In Figure 1, droop control is adopted for both sides of interconnected AC/DC converters to maintain the DC voltage stability in the system, while constant power control is adopted for electric vehicle chopper to realize the power balance in the system. When the electric vehicle is connected to the system for charging without certainty, the power of the system at the beginning will mutate and deviate from P_ref. According to the P-U_dc droop control curve of AC/DC converter, as shown in Figure 2, when the power is abrupt, the reference value of the direct current voltage U_dc,ref in the system will also be abrupt, which will cause the fluctuation of the direct current voltage U_dc in the system.

FIGURE 2

FIGURE 2. P-U_dc droop control schematic diagram.

However, when a robust controller is attached to the DC/DC converter, the power imbalance in the system caused by the uncertain connection of loads will be greatly reduced, and the fluctuation of DC voltage in the system will be reduced. In Figure 2, K_p is the droop coefficient. The constant power control model of the chopper of electric vehicle is shown in the following Eqs (1) and (2).

$I_{\text{dcref}}=(P_{\mathrm{dcref}}-P_{\mathrm{dc}})G_{\mathrm{p}}\left(s\right)(1)$

$\alpha =(I_{\mathrm{dcref}}-I_{\mathrm{dc}})G_{\mathrm{i}}\left(s\right)(2)$

Where: $\alpha$ is the chopper switch control signal; $I_{\text{dc}}$ and $I_{\text{dcref}}$ respectively represent the DC current signal and its reference value of the current inner loop; $G_{\mathrm{i}}\left(s\right)=K_{\text{ip}}+K_{\mathrm{ii}}/s$ is the current inner loop proportional integral (PI) controller, where $K_{\text{ip}}$ and $K_{\text{ii}}$ respectively represent the proportional and integral coefficients of the current inner loop PI controller; $P_{\text{dc}}$ and $P_{\text{dcref}}$ represent the active power signal and its reference value of the power outer loop respectively; $G_{\text{p}}\left(s\right)=K_{\text{pp}}+K_{\mathrm{pi}}/s$ is the power outer loop proportional integral (PI) controller, where $K_{\text{pp}}$ and $K_{\text{pi}}$ represent the proportional and integral coefficients of the power outer loop PI controller respectively.

Chopper constant power control strategy is based on the accurate mathematical model of the system to design the controller. However, due to the change of the operating environment, the change of the operating scene and the aging and damage of the equipment components, there will be some errors in the system model, so that the controller can not effectively control the system with errors. The robust control method based on H_∞ loop shaping method is to design the controller for the system perturbed model, and the additional robust controller can ensure the voltage stability of the system under certain load disturbance and parameter perturbation.

Controlled Object Model

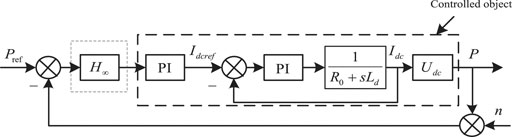
According to the actual control system, the control object of current inner loop is $1\text{/}(R_0+s{L}_{\text{d}})$, the control object of power outer loop is $U_{\text{dc}}$, the double closed-loop control block diagram of constant power control is shown in Figure 3, where $R_0$ and $L_{\text{d}}$ are the energy storage inductance and resistance of chopper, and n is the noise signal of voltage and current transformers during sampling. The left dotted line frame in the figure represents the robust stability controller designed, and the right dotted line box is the controlled object of the system.

FIGURE 3

FIGURE 3. Block diagram of constant power control of chopper.

Therefore, it can be seen from the black dotted box on the right side of Figure 3 that the controlled object $G\left(s\right)$ is:

$G\left(s\right)=\frac{U_{\mathrm{dc}}\left(K_{\mathrm{ip}}{K}_{\mathrm{pp}}{s}^2+\left(K_{\mathrm{ip}}{K}_{\mathrm{pi}}+K_{\mathrm{pp}}{K}_{\mathrm{ii}}\right)s+K_{\mathrm{ii}}{K}_{\mathrm{pi}}\right)}{L_{\mathrm{d}}{s}^3+\left(R_0+K_{ip}\right)s^2+K_{\mathrm{ii}}s}(3)$

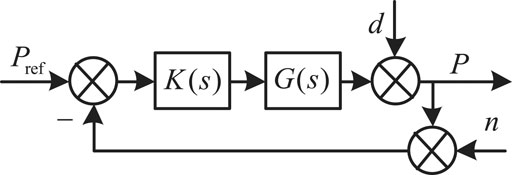
The constant power control block diagram shown in Figure 3 is transformed into the standard feedback structure diagram shown in Figure 4, Wherein, K(s) represents the robust controller H_∞, and d represents the output disturbance. According to Figure 4, the relationship between the system output power P and the noise signal n can be obtained:

$P=\frac{GK}{1+GK}\left({\mathit{P}}_{r\text{ef}}-n\right)+\frac{1}{1+GK}d(4)$

FIGURE 4

FIGURE 4. Standard feedback structure diagram.

As can be seen from Eq. 4, in order to reduce the influence of output disturbance d on system stability, $\sigma \left(\frac{1}{1+GK}\right)\ll 1$, that is $\sigma \left(GK\right)\gg 1$ needs to be satisfied. In order to reduce the influence of transformer noise on system stability, it is required to satisfy $\sigma \left(\frac{GK}{1+GK}\right)\ll 1$, that is, $\sigma \left(GK\right)\ll 1$. Therefore, in the design of robust controller, anti-interference and noise reduction of transformer should be considered in a compromise. Considering that the output disturbance d mainly occurs in the low frequency domain, while the noise n of the transformer is significant in the high frequency domain, so the design of robust controller is considered in low frequency band $\sigma \left(GK\right)\gg 1$ and high frequency band $\sigma \left(GK\right)\ll 1$. $\sigma (\cdot )$ stands for finding the singular value.

H_∞ Loop Shaping Method

Design Steps of H_∞ Loop Shaping Method

H_∞ loop shaping method combines the advantages of H_∞ technology and loop shaping method. When using this method to design robust controller, it can achieve the requirements of robust stability and robust performance at the same time. The design of robust controller is divided into the following three steps (Zhou et al., 1996):

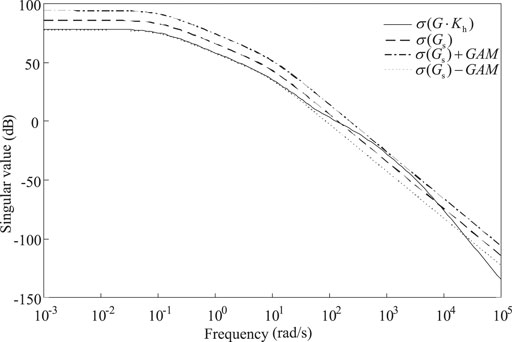
1) Loop shaping. The requirements of the system for low, medium and high frequency are as follows: ① the low-frequency open-loop singular value is large, so as to improve the anti-disturbance ability of the system; ② the intermediate frequency curve transition is gentle, and its slope should be between (−40)dB/sec and (−20)dB/sec, so as to broaden the bandwidth of the system; ③ the high-frequency open-loop singular value is small, so as to improve the ability of the system to deal with unmodeled dynamics. According to the above requirements, the open-loop singular value shape $G_{\text{s}}\left(s\right)$ of the expected system is determined as (Shen, 2016):

$G_s\left(s\right)=\frac{a}{b{s}^2+cs+d},b\ne 0(5)$

Among them, parameter a determines the low-frequency gain, b and c are used to adjust the cut-off frequency of the singular value curve, and d represents the steady-state error of the system.

 2) Robust stabilization.

The maximum robust stability margin is calculated:

${\epsilon }_{\max }={\left(\inf {\Vert \left[\begin{array}{l}I\\ K\end{array}\right]{\left(I+G_{s}K\right)}^{-1}{M}^{-1}\Vert }_{\infty }\right)}^{-1}=\sqrt{1-{\Vert \begin{array}{cc}N& M\end{array}\Vert }_H^2}<1(6)$

Where N(s) and M(s) are the normalized left coprime decomposition of the expected system $G_{\text{s}}\left(s\right)$, and ${\epsilon }_{\max }$ represents the maximum allowable uncertainty disturbance of the system. When ${\epsilon }_{\max }$ is 0.15–1, the system is considered to have good robust stability. If ${\epsilon }_{\max }\ll 1$, it is considered that the robustness of the system is not enough, and the loop shaping must be carried out again in 1) Loop shaping to obtain the desired shape of open-loop singular value.

 3) Select $\epsilon \le {\epsilon }_{\max }$ and get the robust controller K(s) from loopsyn command in MATLAB.

Robust Controller Design

The structure diagram of double terminal DC distribution system is established as shown in Figure 1, in which the parameters of DC distribution system and the parameters of each converter are shown in Tables 1, 2 respectively.

TABLE 1

TABLE 1. DC distribution system parameters.

TABLE 2

TABLE 2. Converter control parameters.

From Eq. 3, the open-loop transfer function of the controlled object is obtained as follows:

$G\left(s\right)=\frac{0.022s^2+19.8s+1760}{0.005s^3+0.21s^2+11s}(7)$

According to the requirements of loop forming in 1) Loop shaping, the expected open-loop singular value curve is selected as follows:

$G_s\left(s\right)=\frac{20000}{s^2+9.86s+1.01}(8)$

${\epsilon }_{\max }=0.3833$ can be obtained from Eq. 6, which meets the requirements of the system for robustness. The robust controller K(s) is obtained by loopsyn command, as shown in Eq. 9:

$\begin{array}{l}K\left(\text{s}\right)=\frac{4.441\times {10}^{-16}{\text{s}}^8+9.512\times {10}^{-12}{\text{s}}^7+4.338\times {10}^7{s}^6+1.822\times {10}^{11}{s}^5+}{s^8+9439s^7+2.744\times {10}^7{s}^6+2.447\times {10}^{10}{s}^5+7.098\times {10}^{12}{s}^4+}\to \\ \begin{array}{ccc}& & \frac{1.876\times {10}^{13}{s}^4+8.627\times {10}^{14}{s}^3+2.44\times {10}^{16}{\text{s}}^2+1.087\times {10}^{13}s+1.199\times {10}^{19}}{5.38\times {10}^{14}{s}^3+4.645\times {10}^{15}{s}^2+4.762\times {10}^{14}s+1.16\times {10}^{11}}\end{array}\end{array}(9)$

Because the order of the controller is 8, which is not conducive to practical engineering application, Hankel singular value algorithm is used to reduce the order, as shown in Eq. 10:

$K_h=\frac{\text{0}{\text{.}0033233\text{s}}^5+4.338\times {10}^7{s}^4+4.529\times {10}^9{s}^3+2.092\times {10}^{11}{s}^2+5.956\times {10}^{12}s+1.199\times {10}^9}{s^6+5343s^5+5.558\times {10}^6{s}^4+1.701\times {10}^9{s}^3+1.311\times {10}^{11}{s}^2+1.134\times {10}^{12}s+1.16\times {10}^{11}}(10)$

Comparing the frequency response curves of the robust controller before and after order reduction, as shown in Figure 5, it can be found that the control effect is basically the same before and after order reduction.

FIGURE 5

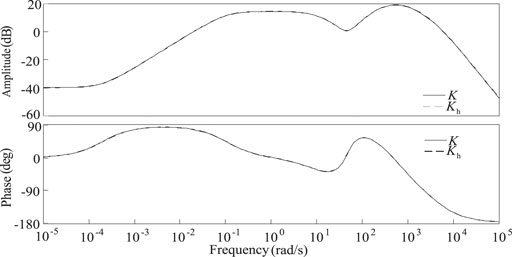
FIGURE 5. The frequency response curves of the robust controller before order reduction and after order reduction.

Frequency Domain Analysis

The curves of open-loop singular value and closed-loop singular value of the system before and after the additional robust controller for EVs are compared, as shown in Figures 6, 7 respectively. It can be found that the low-frequency gain of the open-loop singular value is larger and the high-frequency value decays rapidly by adding the robust controller, and the low-frequency amplitude of the closed-loop singular value is 0 and the peak is smaller after adding the robust controller, which is conducive to the signal tracking and disturbance suppression.

FIGURE 6

FIGURE 6. Open-loop singular value curve after adding robust controller.

FIGURE 7

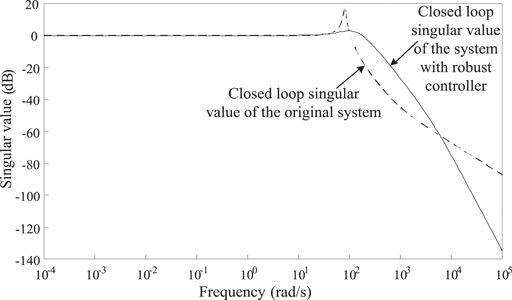
FIGURE 7. The closed-loop singular value curves of the system before and after the addition of the robust controller.

Simulation Verification and Analysis

In order to verify the effectiveness of the designed robust controller, the system shown in Figure 1 is built in DIgSILENT simulation software, in which two DC buses are used to simulate different integrated points of electric vehicles. Using the control variable method, only the analyzed parameters and load disturbance are variable. This paper analyzes the voltage fluctuation of DC distribution system before and after adding robust controller when one or two electric vehicles are connected with preset chopper parameters (Table 2) and the proportion and integral coefficient of chopper power outer loop and current inner loop change.

In this paper, the following six working conditions are simulated and analyzed.

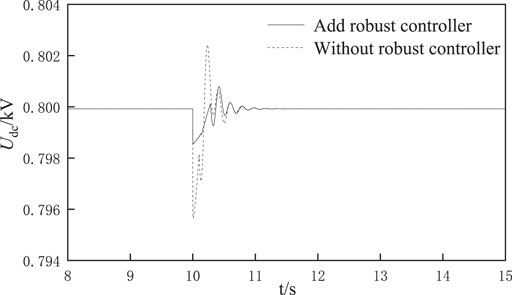
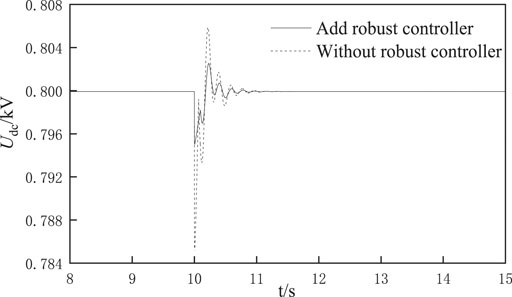
Condition 1:when an electric vehicle is connected (Chopper operates with parameters in Table 2). The left DC bus is connected to the electric vehicle at 10 s, and the simulation ends at 15 s. The fluctuation of DC voltage of left DC bus before and after adding robust controller is shown in Figure 8.It can be seen from Figure 8 that when an electric vehicle is connected to the system, the DC bus voltage oscillates, and the oscillation amplitude is large, which makes the stability problem of the system decrease; while the oscillation amplitude of the system with a robust controller is small, and the adjustment time is short, because the system with a robust controller is less sensitive to the integration of the electric vehicle, and can still maintain the operation of the system in a better station.

FIGURE 8

FIGURE 8. DC bus voltage waveform when an electric vehicle is connected to the system.

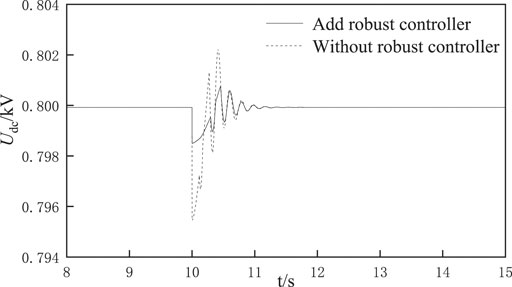
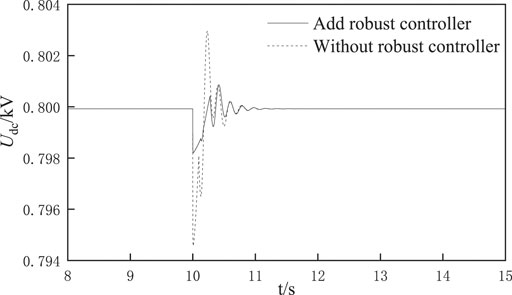
Condition 2:when two electric vehicles are connected at the same time (Chopper operates with parameters in Table 2). The two DC buses are connected to the electric vehicle at 10 s, and the simulation ends at 15 s. The fluctuation of DC voltage of left DC bus before and after adding robust controller is shown in Figure 9.It can be seen from Figure 9 that when two electric vehicles are connected to the system, the DC bus voltage impulse system is larger and the oscillation time is longer than when one electric vehicle is connected to the system; similarly, adding a robust controller based on uncertainty modeling can reduce the oscillation amplitude and the regulation time of the system.

FIGURE 9

FIGURE 9. DC bus voltage waveform when two electric vehicle is connected to the system.

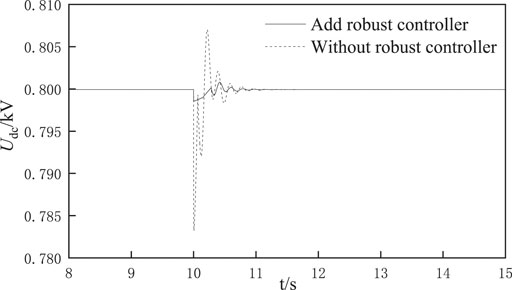
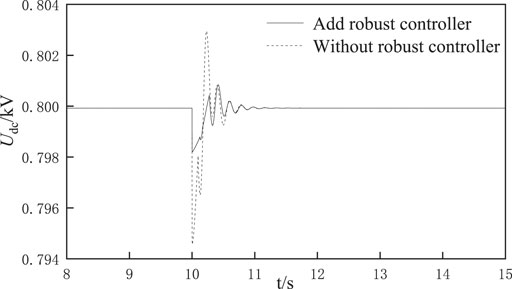
Condition 3:when an electric vehicle is connected, its chopper parameter $K_{\text{pp}}$ is perturbed. The left DC bus connected to the electric vehicle at 10 s, and the simulation ends at 15 s. The chopper parameter $K_{\text{pp}}$ becomes 0.4, and other parameters remain unchanged. The fluctuation of DC voltage of left DC bus before and after adding robust controller is shown in Figure 10.As can be seen from Figure 10, compared with the chopper operating with preset parameters (Table. 2), when the chopper parameter $K_{\text{pp}}$ is perturbed, the DC bus voltage oscillation amplitude is larger and the oscillation time is longer; when the robust controller is added, the sensitivity to the perturbation change of control parameters is lower, the oscillation amplitude change is smaller and the adjustment time is shorter.

FIGURE 10

FIGURE 10. DC bus voltage waveform when chopper $K_{\text{pp}}$ is perturbed.

Condition 4:$K_{\text{ip}}$ parameter perturbation of chopper when an electric vehicle is connected. Assuming the left DC bus is connected to the electric vehicle at 10 s and the simulation is finished at 15 s, the chopper parameter $K_{\text{ip}}$ becomes 0.4. The fluctuation of DC voltage of left DC bus before and after adding robust controller is shown in Figure 11.As can be seen from Figure 11, compared with the chopper operating with preset parameters (Table 2), the DC bus voltage oscillation amplitude is larger when the chopper parameter $K_{\text{ip}}$ is perturbed, while the sensitivity to the perturbation change of control parameters is lower when the robust controller is added, and the oscillation amplitude changes less, and the adjustment time is shorter.

FIGURE 11

FIGURE 11. DC bus voltage waveform when chopper $K_{\text{ip}}$ is perturbed.

Condition 5:when an electric vehicle is connected, its chopper parameter $K_{\text{pi}}$ is perturbed. The left DC bus is connected to the electric vehicle at 10 s, and the chopper parameter $K_{\text{pi}}$ is changed to 100 at 15 s. The fluctuation of DC voltage of left DC bus before and after adding robust controller is shown in Figure 12.As can be seen from Figure 12, compared with the chopper operating with preset parameters (Table 2), the DC bus voltage oscillation amplitude increases when the chopper parameter $K_{\text{pi}}$ of electric vehicle is perturbed, while the sensitivity of the added robust controller to the perturbation changes of control parameters is lower, the oscillation amplitude changes less, and the regulation time is shorter.

FIGURE 12

FIGURE 12. DC bus voltage waveform when chopper $K_{\text{pi}}$ is perturbed.

Condition 6:when an electric vehicle is connected, its chopper parameter $K_{\text{ii}}$ is perturbed. The left DC bus is connected to the electric vehicle at 10 s and the simulation is finished at 15 s, and the chopper parameter $K_{\text{ii}}$ becomes 13.75. The fluctuation of DC voltage of left DC bus before and after adding robust controller is shown in Figure 13.As can be seen from Figure 13, compared with the chopper operating with preset parameters (Table 2), when the chopper parameter $K_{\text{ii}}$ is perturbed, the DC bus voltage oscillation amplitude increases, and the minimum oscillation amplitude reaches 0.794 kV; while the robust controller is added, the sensitivity to the perturbation changes of control parameters is lower, the oscillation amplitude changes less, and the adjustment time is shorter.From the above simulation results, it can be seen that the robust controller based on H_∞ loop shaping method fully considers the influence of electric vehicle integration and chopper parameter perturbation on DC voltage stability, which can effectively improve the stability of the system and ensure the robustness.

FIGURE 13

FIGURE 13. DC bus voltage waveform when chopper $K_{\text{ii}}$ is perturbed.

Conclusion

In order to suppress the influence of uncertain integration of electric vehicles in DC distribution systems, a robust stability controller is designed based on loop shaping method in this paper, with the advantages of.

1) The robust controller can improve the voltage stability of the system effectively, without establishing the precise mathematical model of the system, and the sensitivity to load disturbance and parameter perturbation is weak.

2) When the order of robust controller is high and it is difficult to be used in engineering practice, Hankel singular value algorithm can be used to reduce the order, and the control effect before and after reduction is basically the same.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, WT, YW, SS, YC, PY, and SW; methodology, WT, YW, and SS; validation, WT, PY, YC, SW, and SS; formal analysis, WT, YW, and SW; writing-original draft preparation, WT, YW, and SW; writing-review and editing, WT, SS, and YW; All authors have read and agreed to the published version of the manuscript.

Funding

The Science and Technology Project of State Grid Shandong Electric Power Company, “Research on the Application of Flexible Direct Current Transmission Technology in Shandong Power Grid under the Framework of New Generation Power System” (grant number 52062618008J).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alipoor, J., Miura, Y., and Ise, T. (2015). Power System Stabilization Using Virtual Synchronous Generator with Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 3 (2), 451–458. June. doi:10.1109/JESTPE.2014.2362530

CrossRef Full Text | Google Scholar

Amamra, S.-A., and Marco, J. (2019). Vehicle-to-Grid Aggregator to Support Power Grid and Reduce Electric Vehicle Charging Cost. IEEE Access 7, 178528–178538. doi:10.1109/ACCESS.2019.2958664

CrossRef Full Text | Google Scholar

Connor, W. D., Wang, Y., Malikopoulos, A. A., Advani, S. G., and Prasad, A. K. (2021). Impact of Connectivity on Energy Consumption and Battery Life for Electric Vehicles. IEEE Trans. Intell. Veh. 6 (1), 14–23. March 2021. doi:10.1109/TIV.2020.3032642

CrossRef Full Text | Google Scholar

Dastgeer, F., Gelani, H. E., Anees, H. M., Paracha, Z. J., and Kalam, A. (2019). Analyses of Efficiency/energy-Savings of DC Power Distribution Systems/microgrids: Past, Present and Future. Int. J. Electr. Power Energ. Syst. 104, 89–100. doi:10.1016/j.ijepes.2018.06.05710.1016/j.ijepes.2018.06.057

CrossRef Full Text | Google Scholar

Ding, X., Wang, Z., Zhang, L., and Wang, C. (2020). Longitudinal Vehicle Speed Estimation for Four-Wheel-Independently-Actuated Electric Vehicles Based on Multi-Sensor Fusion. IEEE Trans. Veh. Technol. 69 (11), 12797–12806. Nov. 2020. doi:10.1109/TVT.2020.3026106

CrossRef Full Text | Google Scholar

Dong, L., Wang, C., Li, M., Sun, K., Chen, T., and Sun, Y. (2021). User Decision-Based Analysis of Urban Electric Vehicle Loads. CSEE J. Power Energ. Syst. 7 (1), 190–200. Jan. doi:10.17775/CSEEJPES.2020.00850

CrossRef Full Text | Google Scholar

Tan, L., Wu, B., Rivera, S., Ise, T., et al. (2016). Comprehensive DC Power Balance Management in High-Power Three-Level DC–DC Converter for Electric Vehicle Fast Charging. IEEE Trans. Power Electron. 31 (1), 89–100.

Google Scholar

Li, Y., Zhao, T., Liu, C., Zhao, Y., Wang, P., Gooi, H. B., et al. (2019). An Interactive Decision-Making Model Based on Energy and Reserve for Electric Vehicles and Power Grid Using Generalized Stackelberg Game. IEEE Trans. Ind. Applicat. 55 (4), 3301–3309. July-Aug. doi:10.1109/TIA.2018.2870834

CrossRef Full Text | Google Scholar

Lin, G., Li, Y., Liu, J., and Li, C. (2019). Resonance Analysis and Active Damping Strategy for Shipboard DC Zonal Distribution Network. Int. J. Electr. Power Energ. Syst. 105, 612–621. doi:10.1016/j.ijepes.2018.08.038

CrossRef Full Text | Google Scholar

Needell, Z. A., McNerney, J., Chang, M. T., and Trancik, J. E. (2016). Potential for Widespread Electrification of Personal Vehicle Travel in the united states. Nat. Energ. 1 (9), 16 112–116 118. Aug. doi:10.1038/nenergy.2016.112

CrossRef Full Text | Google Scholar

Peng, K., Wei, Z., Chen, J., and Li, H. (2021). Hierarchical Virtual Inertia Control of DC Distribution System for Plug-And-Play Electric Vehicle Integration. Int. J. Electr. Power Energ. Syst. 128, 106769. doi:10.1016/j.ijepes.2021.106769

CrossRef Full Text | Google Scholar

Radwan, A. A. A., and Mohamed, Y. A.-R. I. (2012). Assessment and Mitigation of Interaction Dynamics in Hybrid AC/DC Distribution Generation Systems. IEEE Trans. Smart Grid 3 (3), 1382–1393. doi:10.1109/TSG.2012.2201965

CrossRef Full Text | Google Scholar

Rashad, M., Ashraf, M., Bhatti, A. I., and Minhas, D. M. (2018). Mathematical Modeling and Stability Analysis of DC Microgrid Using SM Hysteresis Controller. Int. J. Electr. Power Energ. Syst. 95, 507–522. doi:10.1016/j.ijepes.2017.09.001

CrossRef Full Text | Google Scholar

Rasheed, A., Khan, S., Gelani, H. E., and Dastgeer, F. (2019). “AC vs. DC Home: An Efficiency Comparison,” in International Symposium on Recent Advances in Electrical Engineering. Islamabad, Pakistan: (RAEE), 1–6. doi:10.1109/RAEE.2019.8887064

CrossRef Full Text | Google Scholar

Shen, X. (2016). Robust Control Based on Hinf Loop-Shaping of Variable-Speed Variable-Pitch Wind turbine[D]. Harbin: Harbin University of Science and Technology. in chinese.

Staats, P. T., Grady, W. M., Arapostathis, A., and Thallam, R. S. (1998). A Statistical Analysis of the Effect of Electric Vehicle Battery Charging on Distribution System Harmonic Voltages. IEEE Trans. Power Deliv. 13 (2), 640–646. doi:10.1109/61.660951

CrossRef Full Text | Google Scholar

Tabari, M., and Yazdanil, A. (2016). A Mathematical Model for a Stability-Enhanced DC Distribution System for Power System Integration of Plug-In Electric vehicles[C]//IEEE Power and Energy Society General Meeting. Boston, USA: 5p. July 17-21. doi:10.1109/pesgm.2016.7741152

CrossRef Full Text

Tabari, M., and Yazdani, A. (2014). Stability of a Dc Distribution System for Power System Integration of Plug-In Hybrid Electric Vehicles. IEEE Trans. Smart Grid 5 (5), 2564–2573. doi:10.1109/TSG.2014.2331558

CrossRef Full Text | Google Scholar

Tian, L. C., Wu, B., Rivera, S., and Yaramasu, V. (2016). Comprehensive DC Power Balance Management in High-Power Three-Level DC-DC Converter for Electric Vehicle Fast Charging. IEEE Trans. Power Electron. 34, 89–100. doi:10.1109/TPEL.2015.2397453

CrossRef Full Text | Google Scholar

Wang, B., Dehghanian, P., Wang, S., and Mitolo, M. (2019). Electrical Safety Considerations in Large-Scale Electric Vehicle Charging Stations. IEEE Trans. Ind. Applicat. 55 (6), 6603–6612. Nov.-Dec. doi:10.1109/TIA.2019.2936474

CrossRef Full Text | Google Scholar

Yazdani, A., and Iravani, R. (2010). Voltage-sourced Converters in Power System: Modeling, Control, and Applications. WileyIEEE Press. Voltage-Sourced Converters in Power Systems. doi:10.1002/9780470551578

CrossRef Full Text

Zhang, J., Salman, M., Zanardelli, W., Ballal, S., and Cao, B. (2021). An Integrated Fault Isolation and Prognosis Method for Electric Drive Systems of Battery Electric Vehicles. IEEE Trans. Transp. Electrific. 7 (1), 317–328. March 2021. doi:10.1109/TTE.2020.3025107

CrossRef Full Text | Google Scholar

Zhao, X., Peng, K., Zhang, X., Liu, J., Zhao, Y., and Chen, J. (2018). Research on Influencing Factors and Improving Methods for DC Distribution System Stability. J. Eng. 2019 (16), 2147–2153. doi:10.1049/joe.2018.8557

CrossRef Full Text | Google Scholar

Zhou, K., Doyle, J. C., and Glover, K. (1996). Robust and Optimal Control. Engle wood Cliffs, NJ: Prentice-Hall.