Specific Heat Capacity of Confined Water in Extremely Narrow Graphene Nanochannels

Specific heat capacity of extremely confined water determines its performance in the heat transfer as the sizes of devices decrease to nanoscales. Here, we report the basic data of the specific heat capacity of water confined in narrow graphene nanochannels below 5 nm in height using molecular dynamics simulations. The results show that the specific heat capacity of confined water is size-dependent, and the commensurability effect of the specific heat capacity presents as the confinement decreases to 1.7 nm. The deviation of specific heat capacity of confined water with that of bulk water is attributed to the variation of configuration features, including density distribution and hydrogen bonds, and vibration features, including velocity auto-correlation function and vibrational density of states. This work unveils the confinement effects and their physical mechanisms of the specific heat capacity of nanoconfined water, and the data provided here have wide prospects for energy applications at nanoscales.

Introduction

Specific heat capacity is an important thermophysical property that measures the ability of energy storage of the substance, defined as the amount of heat required to increase the temperature by 1 K of a substrate per unit mass. Due to the high specific heat capacity, water is widely used as a medium in the heat transfer and cooling process of devices (Steeneveld et al., 2014; Izadi et al., 2020). As the sizes of many devices such as lab-on-chips, NEMS, and electronic chips are reduced to nanoscale, rapid heat dissipation becomes a challenge restricting the development of nanodevices (Lee et al., 2013). The thermophysical properties of nanoconfined water (Sun et al., 2020), especially specific heat capacity, determines whether it can still function at nanoscales.

The specific heat capacity of nanoconfined water and other liquids attracted a large amount of attention from researchers. Tombari et al. (2005a), Tombari et al. (2005b) investigated the specific heat capacity of water confined in glass nanopores in a mean diameter of 4 nm using calorimetry. They found that the isobaric specific heat capacity deviated from the bulk value and attributed it to the reduction in the density due to the nanoconfinement. The same method was used to study the specific heat capacity of benzene confined in MCM-41 mesopores (Nagoe et al., 2015). Except calorimetry, inelastic neutron scattering technique was also developed to estimate the specific heat capacity of liquids confined in nanopores (Gautam et al., 2018). Nevertheless, directly experimental measurements of specific heat capacity of nanoconfined water are still limited because of the challenge of precise control and measure of the small amount of water.

As an effective and powerful alternative tool, molecular dynamics (MD) simulation has presented excellent performance in the study of thermophysical properties of water at nanoscales, such as viscosity (Neek-Amal et al., 2016; Zhou et al., 2021), thermal conductivity (Zhao et al., 2020a; Zhao et al., 2020b), diffusion coefficient (Zhao et al., 2020c), and dielectric constant (Hamid et al., 2021). And it becomes a common sense that molecular behaviors of water under nanoconfinement deviate from bulk behaviors (Sofos et al., 2013; Sofos and Karakasidis, 2021) because of the large surface-to-volume ratio and the enhanced effects of surface properties including surface wettability and surface morphology (Shadloo-Jahromi et al., 2020; Shadloo-Jahromi et al., 2021). Thus, the thermophysical properties generally depend on the size of nanochannels or pores (Sofos et al., 2013; Zhao et al., 2020a; Zhao et al., 2020b; Zhao et al., 2020c; Hamid et al., 2021; Sofos and Karakasidis, 2021; Zhou et al., 2021). Studies on the specific heat capacity of water and other fluids using the MD method (Gautam et al., 2018; Alkhwaji et al., 2021) further demonstrated the potential of the MD method on the investigation of water at nanoscales. Recently, Lu et al. (Jin et al., 2021) using the MD method investigated the size-dependent specific heat capacity of water confined in the copper nanochannels higher than 5 nm, and they found that the specific heat capacity of water increased with the increase in channel size until a constant plateau. However, the previous studies on other thermophysical properties proved that more dramatic variations of thermophysical properties presented in the confined water contained in extremely narrow nanochannels with size below 5 nm (Neek-Amal et al., 2016; Zhao et al., 2020b; Sun et al., 2021a; Sun et al., 2021b) which is a data blank of specific heat capacity left by the previous works (Jin et al., 2021).

In this work, we investigate the specific heat capacity of water confined in extremely narrow graphene nanochannels with heights lower than 5 nm by using the MD method. The size-dependent effect and the commensurability effect of specific heat capacity are reported. The underlying mechanisms are unveiled from the configuration features, including density distribution and hydrogen bond, and vibration features, including velocity auto-correlation function (VACF) and vibrational density of states (VDOS). This work can not only provide data of the heat capacity of nanoconfined water but also enrich the mechanism of how nanoconfinement affects the thermophysical properties of water. The obtained results will finally benefit on a variety of energy applications.

Simulation Methods

Simulation Model and Dynamics Setting

The MD simulation system is shown in Figure 1. Water films are confined in two-dimensional nanochannels constructed by two separated graphene sheets in size of L_x × L_y = 39.335 Å × 38.327 Å and with separations of L_z ranging from 6.332 to 50.656 Å. The size of simulation boxes is the same as the graphene sheets in x- and y-directions but slightly larger than the separation between graphene sheets to eliminate the boundary effects in z-direction. Water molecules are simulated with the widely used three-point SPC/E model where the energy parameter ε_O-O is 0.0067 eV and the size parameter σ_O-O is 3.166 Å (Berendsen et al., 1987). Interactions between graphene and water molecules are modeled by 12-6 Lennard–Jones (LJ) potential with a cutoff radius of 10 Å and the electrostatic forces are calculated with PPPM algorithm with an accuracy of 10⁻⁴. The energy parameter between graphene and water molecules is selected as ε_C-O = 0.6 ε_O-O, according with the hydrophobicity of graphene, and the size parameter is simply chosen as σ_C-O = σ_O-O, similar to estimated value 3.263 Å in the literature (Bavi and Ghadak, 2021). The density of water is 1 g/cm³, and the corresponding number of water molecules varies with the height of the nanochannels (defined as H = L_z–σ = 1 to 15 σ, where σ is short for σ_O-O). Periodic boundary conditions are used in all directions. The graphene walls are frozen during the simulations. The time step is 1 fs. Before data collection, we carry out 1.1 ns simulation to achieve equilibrium under NVT ensemble controlled by a Nosé–Hoover thermostat. Then the temperature T and internal energy U of water are sampled with an interval of 100 fs during a 5-ns simulation.

FIGURE 1

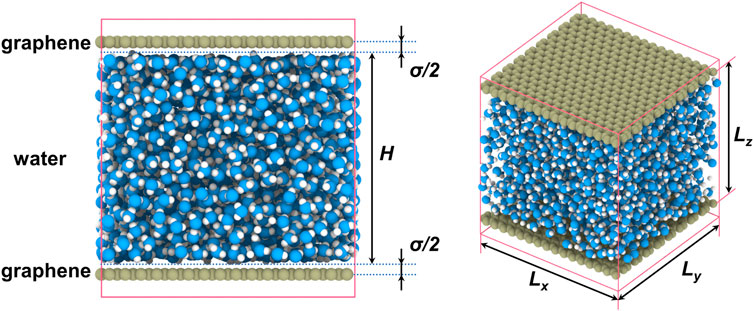
FIGURE 1. Schematic of simulation system. Color codes: oxygen atom in blue, hydrogen atom in white, and carbon atom in green.

Calculation of Specific Heat Capacity

It is necessary to mention that the specific heat capacity here specifically refers to the isochoric specific heat capacity (c_v = (∂u/∂T)_v, where u is the specific internal energy, defined as internal energy per unit mass, U/m) own to the constant volume of water. However, inasmuch as the difference between isochoric specific heat capacity and isobaric specific heat capacity at 300 K is small enough to be ignored in general, only 1.2% in bulk water (Haynes, 2014; Sekerka, 2015), hereafter, no distinction is made between isochoric specific heat capacity and isobaric specific heat capacity unless it significantly affects the conclusion.

There are three general different methods to calculate the specific heat capacity (Pathria and Beale, 2011; Alkhwaji et al., 2021; Jin et al., 2021). The first two methods are straightforward and assume that the specific heat capacity is independent of temperature in a small range (Alkhwaji et al., 2021; Jin et al., 2021). The first method is based on the following equation (Alkhwaji et al., 2021):

$c_{\mathrm{v}}=\frac{\langle U_2\rangle -\langle U_1\rangle }{\langle T_2\rangle -\langle T_1\rangle }\cdot \frac{1}{m},(1)$

where <···> represents the mean of the variable. T₁ = 295 K and T₂ = 305 K are simulated in this case, respectively. The second method fits the specific heat capacity with the following relationships (Jin et al., 2021):

$\begin{array}{l}U\left(t\right)=k_U\cdot t+U_0,\\ T\left(t\right)=k_T\cdot t+T_0,\\ c_{\mathrm{v}}=\frac{k_U}{k_T\text{·}m},\end{array}(2)$

where k_U and k_T are rates of variation of internal energy U and temperature T with time t, respectively. In this case, the equilibrium temperature is set as 295 K and then the temperature rises to 305 K at a rate of 2 K/ns. The fundament of the third method is statistical mechanics, based on the relationship between c_v and the mean square deviation of U, as follows (Pathria and Beale, 2011; Alkhwaji et al., 2021):

$c_{\mathrm{v}}=\frac{\langle U^2\rangle -{\langle U\rangle }^2}{k_B{T}^2\cdot m},(3)$

where k_B is the Boltzmann constant. In this case, the temperature is at 300 K. Besides, previous simulation studies (Jorgensen and Tirado-Rives, 2005; Vega et al., 2010) reported that the specific heat capacity calculated with classical simulation was slightly larger than the experimental result, 4.13 J/(g K) (Haynes, 2014). Vega et al. (2010) attributed the deviation to the missing of nuclear quantum effects in classical MD simulation. Thus, a quantum contribution -0.520 J/(g K) at 300 K should be added on the raw specific heat capacity (Alkhwaji et al., 2021).

We calculate the specific heat capacity of free bulk water first to test the simulation model and methods. Independence checks, including box size, number of water molecules, relaxation time, convergence accuracy of PPPM algorithm, sampling interval, and simulation time, have been carefully performed to ensure the validity of simulations. (see Section 1 of Supplementary Material). The corrected c_v of bulk water at 300 K calculated with three methods (reported as 4.026 ± 0.023 J/(g K), 4.037 ± 0.002 J/(g K) and 4.099 ± 0.038 J/(g K), respectively) is similar to each other, demonstrating the equivalent of three methods, and approaches the experimental value, demonstrating that the classical SPC/E water model can well describe the heat capacity of water with quantum correction. Inasmuch as the specific heat capacity with the third method is in most excellent agreement with the experimental value (see Figure 2A), has advantages in speed and robustness, and is independent of the constant hypothesis; the third method is chosen to calculate c_v of confined water next. So far, both the validity and reliability of the simulation model and calculation method are demonstrated.

FIGURE 2

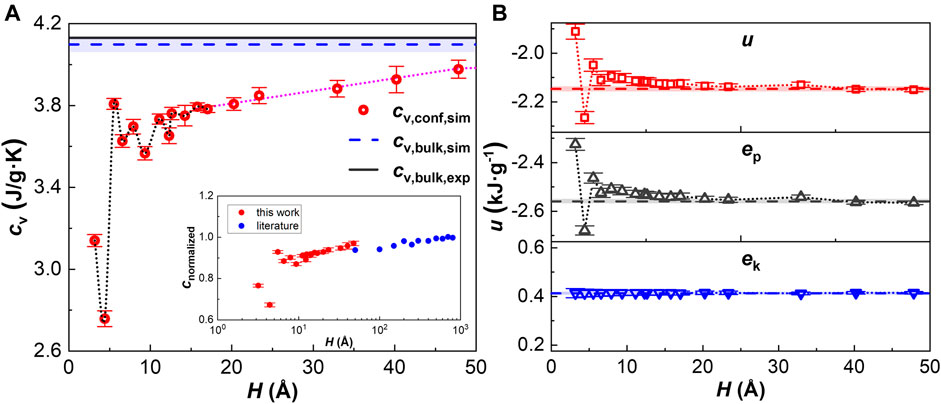
FIGURE 2. Specific heat capacity and specific internal energy at 300 K. (A) Specific heat capacity as a function of channel size. Dotted black line shows the fluctuations, dotted blue line represents linear fitting, and the turning point where they intersect corresponds to H = 5.5 σ. Inset: literature comparison (Jin et al., 2021). (B) Specific internal energy as a function of channel size. Dash lines represent the corresponding bulk value.

Results and Discussion

Specific Heat Capacity of Nanoconfined Water

The specific heat capacity c_v of nanoconfined water is shown in Figure 2. To intuitively show the deviation of c_v from the bulk value, the normalized specific heat capacity c_normalized, the ratio of c_v of water confined in graphene nanochannels to the bulk value, is plotted against the channel heights in the inset of Figure 2, and values of c_normalized of water confined in copper nanochannels (ratio to the fitted asymptotic value) ranging from 50 Å to 800 Å (Jin et al., 2021) are plotted in this inset as well for comparison. It is found that c_v of confined water is lower than that of the free bulk water, and the deviation generally increases as H reduces. In the channel higher than 5.5 σ, the variation of c_v is monotonic. But below this critical point, c_v oscillates with H simultaneously. This phenomenon occurs due to an underlying physical mechanism. Neek-Amal et al. (2016) found the similar oscillation of viscosity of confined water in extremely narrow graphene nanochannels and named it commensurability effects resulting from the layered structure due to the nanoconfinement. They demonstrated that the local minimum viscosity corresponds to the local maximum distance of water layers, and vice versa. The same correlation applies to heat capacity as well. As far as we know, the commensurability effects in c_v of nanoconfined water are reported here for the first time. For the specific internal energy, its variation, mainly determined by the potential energy, shows the opposite trend compared to c_v (see Figure 2B). The different variations of c_v and the specific internal energy demonstrate that c_v measures the sensitivity of internal energy to temperature but not the value of internal energy (Tombari et al., 2005b), although they do have a relationship, which will be discussed in VACF and VDOS.

To explain the deviation of c_v in nanoconfined water, we have to turn to the configurations and vibrations of nanoconfined water, which determine c_v. As these two aspects are not independent but closely related (Tombari et al., 2005a), the configurational characteristics, including density distribution and hydrogen bonds, will be discussed first, followed by the vibrational characteristics, including VACF and VDOS.

Density Distribution and Hydrogen Bond

Configurations of water confined in graphene nanochannels are different from those in bulk due to the confinement effects by the channel walls (Sun et al., 2020; Zhou et al., 2021; Zhao et al., 2020a; Zhao et al., 2020b; Zhao et al., 2020c). Specifically speaking, the repulsive force confines the water molecules in the nanochannel, while the potential well or adsorption interaction changes the structure of confined water (Zhao et al., 2020b). Compared with the homogeneous bulk water, confined water is inhomogeneous. Density distribution of water (Kalashami et al., 2018) confined in typical channels in size of H = 2 σ, 5.5 σ, 10.5 σ, 15 σ, representing those in height lower than the critical point, near the critical point, and higher than the critical point, respectively, clearly shows the difference of configuration of confined water from the bulk water (see Figure 3A, other cases are shown in Supplementary Figure S7). In wide nanochannels, density adjacent to the wall is significantly higher than the bulk value, forming three significant density peaks on each side, and the intensity of the corresponding density peaks is almost the same in different nanochannels, while the density in the middle region tends toward the bulk value and density distribution is flat. We define confined water with this kind of density distribution as 3P-B-3P. As the channel height goes down to H = 5.5 σ, the bulk region no longer exists, and the third (also the weakest) peaks overlap with each other; thus, only five peaks remain, but the intensity of density peaks enhances compared with that in the wide nanochannels. As the channel height continues to descend to H = 2 σ, only the peaks closest to the wall remain and the intensity of density peaks is extraordinarily increased. Besides, although the middle peak is weak, the number of density peak of hydrogen atoms is one more than that of oxygen atoms, indicating a dramatic variation of structure. We define confined water with these kinds of density distribution as xP-0-xP, where x ≤ 3. The differences in the structure and properties among 3P-B-3P confined water in different nanochannels mainly result from the fraction of the bulk volume, but the differences among xP-0-xP confined water are caused by complicated factors including the number of peaks and the commensurability effects (details in Supplementary Figure S7). So far, it can be reasonably inferred that the decrease in specific heat capacity of confined water and the appearance of critical point are definitely related to the structure variation indicated by the density distribution. To intuitively show the configurational variation of water in nanochannels, we further take snapshots for each case, representing water molecules by oxygen atoms (see Figure 3A). In contrast to bulk water, layered structure in confined water, corresponding to the peaks in density distribution, appears adjacent to the wall. The anisotropic crystal-like characteristic can result in a great influence on c_v of confined water (Levchenko et al., 2007; Shi et al., 2012).

FIGURE 3

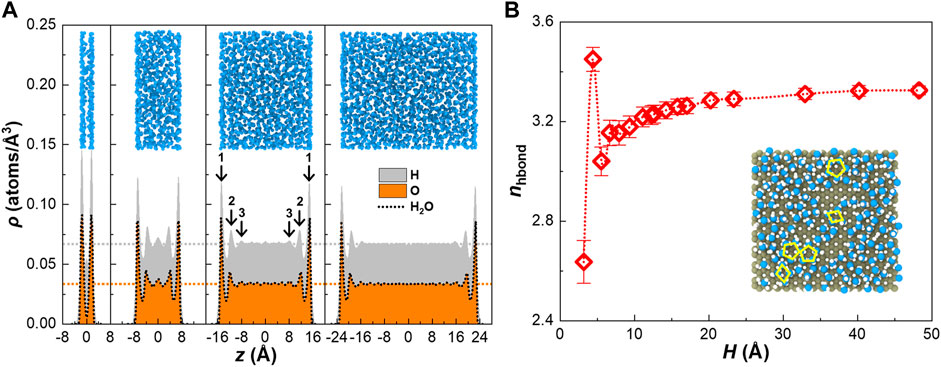
FIGURE 3. Density distribution and mean coordination number of hydrogen bond of water. (A) Density distribution of water perpendicular to the wall varies with channel height; the dotted horizontal lines refer to the bulk value; peaks corresponding to water layers are labeled with numbers; snapshots are configurations of water molecules represented by oxygen atoms, where water layers appear at two sides near the wall. (B) Mean coordination number of hydrogen bonds of water depends on the channel height; snapshot is the top view of the first water layer.

One of the potential effects, maybe the most critical one, of the structure variation on the specific heat capacity is the weakening of connection with hydrogen bonds among water molecules. Hydrogen bond essentially is a kind of strong electrical interaction, and an amount of special properties of water is mainly resulted from the hydrogen bonds, including the higher specific heat capacity than other common substances. To demonstrate this point, we calculate the specific heat capacity of virtual water without charges, reported as 1.305 ± 0.006 J/(g K), much lower than the real water but consistent with the theoretical value for ideal triatomic molecule, 1.15–1.62 J/(g K). The interactions among water molecules with hydrogen bonds can be quantified by the mean coordination number of hydrogen bonds per water molecule n_hbond. Generally, the ordered layer-structure of water adjacent to the graphene wall is not conducive to the formation of hydrogen bonds and can decrease the value of n_hbond. To form hydrogen bonds, two neighboring water molecules need to be in the appropriate orientation and distance, so there needs to be enough space to adjust the position of the water molecules. However, the space in the near-wall region is limited. On the one hand, water molecules lost half the space and opportunities to form hydrogen bonds because of the steric barrier of the wall; on the other hand, the high density of water due to the adsorption of the wall further reduces the available space. Therefore, water molecules cannot sufficiently connect with hydrogen bonds to other water molecules near the wall (Vila Verde et al., 2012) but tend to form rhombic and pentagonal rings (see the inset of Figure 3B). Previous experimental work demonstrated that the specific heat capacity of water at the surface is indeed lower than the bulk value (Levchenko et al., 2007; Shi et al., 2012). In narrow channels, the near-wall region takes most of the portion and the effect of graphene wall is significant. But in wide channels, the effect of near-wall region is relatively non-sensitive, and thus, the thermophysical properties including the specific heat capacity and n_hbond tend toward the bulk value. To demonstrate this point, we calculate the hydrogen bonds among water molecules confined in different nanochannels using a geometric definition, the same as that in the previous work (Sun et al., 2021b; Kumar et al., 2007). As expected, n_hbond exhibits an increasing trend against the channel height (see Figure 3B). With the channel size increasing, it gradually approaches to the bulk value, 3.31 (consistent with the value for SPC/E water model in the literature (Kumar et al., 2007)), namely, the variation of n_hbond is qualitatively consistent with the variation of specific heat capacity and inverse to that of specific internal energy. We further evaluate the correlation between n_hbond and specific heat capacity and the correlation between n_hbond and specific internal energy, respectively. Pearson’s product-moment correlation coefficient between n_hbond and specific heat capacity is reported as −0.94, while that between n_hbond and specific internal energy is reported as 0.88 after expelling the special point at H = 1.4 σ (discussed in Section 4 of Supplementary Material). Thus, we quantitatively demonstrate that hydrogen bond indeed has a huge influence on the specific heat capacity of water and the internal energy. Therefore, from the configurational aspect, we conclude that the graphene walls change the structure of water confined in the nanochannels and inhibit the formation of hydrogen bonds, and thus reduce the specific heat capacity of water. In addition, we discuss the effect of structure variation on the specific heat capacity from the perspective of radial distribution function (RDF) in Section 3 of Supplementary Material, which further supports the conclusion in this Section.

VACF and VDOS

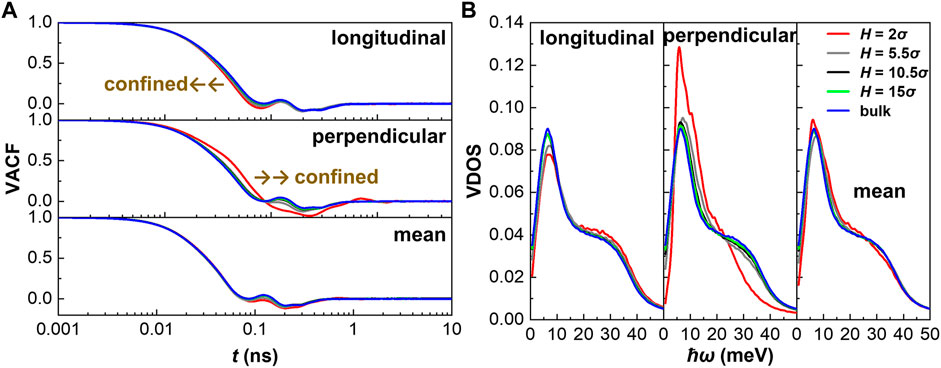
After the discussion of the “static” configurational features including density distribution and hydrogen bond, we next analyze the specific heat capacity from the “dynamic” vibration features of confined water including VACF and VDOS, which are more directly connected to the heat capacity. We first calculate the VACF of water molecules represented by oxygen atom (see Figure 4A), defined as follows:

$VACF\left(t\right)=\frac{\langle {\displaystyle {\sum }_i{v}_i(t+t_0)\cdot v_i\left(t_0\right)}\rangle }{\langle {\displaystyle {\sum }_i{v}_i\left(t_0\right)\cdot v_i\left(t_0\right)}\rangle },(4)$

where v_i is the velocity of atom indexed i, t₀ is the time origin, and t is the correlation time. VACF here shows that the motion modes are different in the longitudinal (x- and y-) direction and perpendicular (z-) direction. Thus, we compare VACF in different nanochannels in longitudinal and perpendicular directions, respectively. We find that VACF in the longitudinal direction converges fastest in the channel with H = 2 σ but slower in bulk, while it is contrary in the perpendicular direction. Anisotropic motion modes in different directions and in channels with different heights indicate the discrepancy of vibrational features from bulk.

FIGURE 4

FIGURE 4. VACF and VDOS of water molecules represented by oxygen atoms.

We then calculate VDOS of water, where the water molecule is represented by oxygen atom, in different channels (see Figure 4B), using the following relationship:

$VDOS\left(\omega \right)={\displaystyle \int VACF\left(t\right)\exp (-2\pi i\omega t)}dt,(5)$

where ω is the vibrational angular frequency of atoms. High frequency motion corresponds to higher energy state. Thus, the abscissa of Figure 4B is customarily expressed as ħω in unit of energy, where ħ is the reduced Planck constant.

VDOS represents the possibility distribution of vibration modes. In general, a sharp characteristic peak in VDOS corresponds to a harmonic vibration mode, while others correspond to the anharmonic vibration modes. Nevertheless, both of them have contributions to the specific heat capacity. As SPC/E is a rigid water model with fixed bond and angle, the single peak in the VDOS, corresponding to 5.93 meV, represents the translational motion of water molecules. It is found that VDOS of the peak is higher than the bulk value and decreases with channel size in the longitudinal direction but, on the contrary, in the perpendicular direction. The most significant distinction appears in the nanochannel with H = 2 σ, where the peak in the perpendicular direction is extraordinarily higher than that in the longitudinal direction and other cases, showing a solid-like vibration feature.

Nevertheless, no matter in the longitudinal or the perpendicular direction, the VDOS of low-energy modes decline and that of the high-energy modes increase in the confined water, consistent with the enhancement of the internal energy, or more accurately speaking, the potential energy. The special low energy mode corresponding to ω tending to zero is proportional to the diffusion coefficient. As predicted by the intercept of VDOS, the diffusion coefficient in longitudinal direction is higher than those in the perpendicular direction. That is to say, the diffusion coefficient is anisotropic. One can also infer that the diffusion coefficients of confined water are lower than the bulk value in all directions and decrease as the channel size decreases, which is consistent with results reported in the literature (Zhao et al., 2020c; Cui et al., 2021). It is demonstrated that the movement of water molecules confined in the nanochannel is restricted, basically due to the adsorption of the wall.

The contribution of vibration modes at different energy states to c_v, defined as c_v |_ω, can be roughly estimated using the following expression (Gautam et al., 2018):

$c_{\text{v}}{|}_{\omega }=VDOS\left(\omega \right)\cdot \frac{k_B}{m}{\left(\frac{\hslash \omega }{k_{B}T}\right)}^2\frac{e^{\hslash \omega /k_{B}T}}{{(e^{\hslash \omega /k_{B}T}-1)}^2}.(6)$

Thus, we know that the contribution of lower energy mode is greater if the VDOS are the same. Then it can therefore be simply inferred that c_v of nanoconfined water will decrease as the VDOS of low-energy modes decreases and that of high-energy modes increases. In summary, from the vibrational aspect, we conclude that the reduction of c_v of nanoconfined water results from the decline of low-energy vibration modes, induced by the extra fluid–solid interaction and the changed structure.

Conclusion

In this work, we perform MD simulations to investigate the specific heat capacity of water confined in extremely narrow graphene nanochannels from the aspects of configuration and vibration. It is found that the specific heat capacity of confined water is lower than the bulk value and decreases with the reduction in channel height. In particular, commensurability effect appears as the channel height reduces to 5.5 σ, about 1.7 nm. From density distribution, it is found that layer structure appears adjacent to the graphene walls and makes the structure of confined water different from the bulk water. When the channel height is lower than 5.5 σ, the layers begin to mix with each other, which results in the commensurability effect. Such structure is not suitable for the formation and maintenance of hydrogen bonds. As the proportion of layer structure accounted in the channels increases with the decrease of channel height, the coordination number of hydrogen bonds decreases. The reduction in the number of hydrogen bonds results in the decline of the specific heat capacity. Furthermore, the configuration variation leads to the variation of vibration modes. And the VDOS of low-energy vibration modes decrease, while those of the high energy vibration modes increase. As the lower energy vibration modes contribute more to the specific heat capacity than the higher energy vibration modes, the specific heat capacity of water decreases in nanochannel. This work demonstrates the inhibition of the extremely narrow graphene nanochannels on the specific heat capacity of water confined in them and unveils their underlying physical mechanisms. The results lay a foundation for the subsequent academic research and provide the basic data of the specific heat capacity of water confined in nanochannels for applications in energy engineering.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

RZ, XM, HL, and CS conceived and designed the simulations. RZ performed the simulations, analyzed the data, and wrote the first draft of the manuscript. CS and BB revised the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

The study was funded by the National Natural Science Foundation of China for the general project no. 51876169.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.736713/full#supplementary-material

References

Alkhwaji, A., Elbahloul, S., Abdullah, M. Z., and Bakar, K. F. B. A. (2021). Selected water thermal properties from molecular dynamics for engineering purposes. J. Mol. Liquids 324, 114703. doi:10.1016/j.molliq.2020.114703

CrossRef Full Text | Google Scholar

Bavi, O., and Ghadak, F. (2021). Possibility of making aerophobic surfaces by nanoprotrusions: an investigation of atomic-scale friction of the air-solid interfaces. Phys. Chem. Chem. Phys. 23, 4711–4717. doi:10.1039/d0cp06404a

PubMed Abstract | CrossRef Full Text | Google Scholar

Berendsen, H. J. C., Grigera, J. R., and Straatsma, T. P. (1987). The Missing Term in Effective Pair Potentials. J. Phys. Chem. 91, 6269–6271. doi:10.1021/j100308a038

CrossRef Full Text | Google Scholar

Cui, S. H., Fu, J. F., Guo, M. L., Zhao, Z. X., Sun, C. Z., and Wang, Y. J. (2021). Diffusion of High-Temperature and High-Pressure CH4 Gas in SiO2 Nanochannels. Front Energ. Res 9, 667640. doi:10.3389/fenrg.2021.667640

CrossRef Full Text | Google Scholar

Gautam, S., Kolesnikov, A. I., Rother, G., Dai, S., Qiao, Z.-A., and Cole, D. (2018). Effects of Confinement and Pressure on the Vibrational Behavior of Nano-Confined Propane. J. Phys. Chem. A. 122, 6736–6745. doi:10.1021/acs.jpca.8b05028

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamid, I., Jalali, H., Peeters, F. M., and Neek-Amal, M. (2021). Abnormal in-plane permittivity and ferroelectricity of confined water: From sub-nanometer channels to bulk. J. Chem. Phys. 154, 114503. doi:10.1063/5.0038359

CrossRef Full Text | Google Scholar

Haynes, W. M. (2014). CRC Handbook of chemistry and physics. Florida: CRC press.

Google Scholar

Izadi, A., Siavashi, M., Rasam, H., and Xiong, Q. (2020). MHD enhanced nanofluid mediated heat transfer in porous metal for CPU cooling. Appl. Therm. Eng. 168, 114843. doi:10.1016/j.applthermaleng.2019.114843

CrossRef Full Text | Google Scholar

Jin, L., Noraldeen, S. F. M., Zhou, L., and Du, X. (2021). Effects of solid/liquid interface on size-dependent specific heat capacity of nanoscale water films: Insight from molecular simulations. Fluid Phase Equilibria 537, 113001. doi:10.1016/j.fluid.2021.113001

CrossRef Full Text | Google Scholar

Jorgensen, W. L., and Tirado-Rives, J. (2005). Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. 102, 6665–6670. doi:10.1073/pnas.0408037102

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalashami, H. G., Neek-Amal, M., and Peeters, F. M. (2018). Slippage dynamics of confined water in graphene oxide capillaries. Phys. Rev. Mater. 2, 74004. doi:10.1103/physrevmaterials.2.074004

CrossRef Full Text | Google Scholar

Kumar, R., Schmidt, J. R., and Skinner, J. L. (2007). Hydrogen bonding definitions and dynamics in liquid water. J. Chem. Phys. 126, 204107. doi:10.1063/1.2742385

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, W., Kim, K., Jeong, W., Zotti, L. A., Pauly, F., Cuevas, J. C., et al. (2013). Heat dissipation in atomic-scale junctions. Nature 498, 209–212. doi:10.1038/nature12183

PubMed Abstract | CrossRef Full Text | Google Scholar

Levchenko, A. A., Kolesnikov, A. I., Ross, N. L., Boerio-Goates, J., Woodfield, B. F., Li, G., et al. (2007). Dynamics of Water Confined on a TiO2(Anatase) Surface†. J. Phys. Chem. A. 111, 12584–12588. doi:10.1021/jp076033j

CrossRef Full Text | Google Scholar

Nagoe, A., Oguni, M., and Fujimori, H. (2015). Low-temperature heat capacities of confined liquid benzene, implying the behavior of ordinary bulk liquids. J. Phys. Condens. Matter 27, 455103. doi:10.1088/0953-8984/27/45/455103

PubMed Abstract | CrossRef Full Text | Google Scholar

Neek-Amal, M., Peeters, F. M., Grigorieva, I. V., and Geim, A. K. (2016). Commensurability Effects in Viscosity of Nanoconfined Water. ACS Nano 10, 3685–3692. doi:10.1021/acsnano.6b00187

PubMed Abstract | CrossRef Full Text | Google Scholar

Pathria, R., and Beale, P. D. (2011). Statistical Mechanics. Florida: CRC press, 744.

Google Scholar

Sekerka, R. F. (2015). Thermal Physics: Thermodynamics and Statistical Mechanics for Scientists and Engineers. Netheralands: Elsevier.

Google Scholar

Shadloo-Jahromi, A., Kharati-Koopaee, M., and Bavi, O. (2020). Friction factor calculation in nanochannels comprising different wall hydrophobicities and superhydrophobic structures: Molecular dynamic simulations. Int. Commun. Heat Mass Transfer 117, 104763. doi:10.1016/j.icheatmasstransfer.2020.104763

CrossRef Full Text | Google Scholar

Shadloo-Jahromi, A., Kharati-Koopaee, M., and Bavi, O. (2021). Molecular dynamics simulation of fluid flow through nanochannels consisting of different superhydrophobic patterns. Int. Commun. Heat Mass Transfer 124. doi:10.1016/j.icheatmasstransfer.2021.105278

CrossRef Full Text | Google Scholar

Shi, Q., Boerio-Goates, J., Woodfield, K., Rytting, M., Pulsipher, K., Spencer, E. C., et al. (2012). Heat Capacity Studies of Surface Water Confined on Cassiterite (SnO2) Nanoparticles. J. Phys. Chem. C 116, 3910–3917. doi:10.1021/jp2088862

CrossRef Full Text | Google Scholar

Sofos, F., Karakasidis, T. E., and Liakopoulos, A. (2013). Fluid Flow at the Nanoscale: How Fluid Properties Deviate from the Bulk. Nanosci Nanotechnol Lett. 5, 457–460. doi:10.1166/nnl.2013.1555

CrossRef Full Text | Google Scholar

Sofos, F., and Karakasidis, T. E. (2021). Nanoscale slip length prediction with machine learning tools. Sci. Rep. 11, 12520. doi:10.1038/s41598-021-91885-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Steeneveld, G. J., Koopmans, S., Heusinkveld, B. G., and Theeuwes, N. E. (2014). Refreshing the role of open water surfaces on mitigating the maximum urban heat island effect. Landscape Urban Plann. 121, 92–96. doi:10.1016/j.landurbplan.2013.09.001

CrossRef Full Text | Google Scholar

Sun, C., Zhou, R., Zhao, Z., and Bai, B. (2021). Extending the Classical Continuum Theory to Describe Water Flow through Two-Dimensional Nanopores. Langmuir 37, 6158–6167. doi:10.1021/acs.langmuir.1c00298

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, C., Zhou, R., Zhao, Z., and Bai, B. (2020). Nanoconfined Fluids: What Can We Expect from Them? J. Phys. Chem. Lett. 11, 4678–4692. doi:10.1021/acs.jpclett.0c00591

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, C., Zhou, R., Zhao, Z., and Bai, B. (2021). Unveiling the hydroxyl-dependent viscosity of water in graphene oxide nanochannels via molecular dynamics simulations. Chem. Phys. Lett. 778, 138808. doi:10.1016/j.cplett.2021.138808

CrossRef Full Text | Google Scholar

Tombari, E., Salvetti, G., Ferrari, C., and Johari, G. P. (2005). Heat capacity of water in nanopores. J. Chem. Phys. 123, 214706. doi:10.1063/1.2131063

PubMed Abstract | CrossRef Full Text | Google Scholar

Tombari, E., Salvetti, G., Ferrari, C., and Johari, G. P. (2005). Thermodynamic functions of water and ice confined to 2nm radius pores. J. Chem. Phys. 122, 104712. doi:10.1063/1.1862244

PubMed Abstract | CrossRef Full Text | Google Scholar

Vega, C., Conde, M. M., McBride, C., Abascal, J. L. F., Noya, E. G., Ramirez, R., et al. (2010). Heat capacity of water: A signature of nuclear quantum effects. J. Chem. Phys. 132, 046101. doi:10.1063/1.3298879

PubMed Abstract | CrossRef Full Text | Google Scholar

Vila Verde, A., Bolhuis, P. G., and Campen, R. K. (2012). Statics and dynamics of free and hydrogen-bonded OH groups at the air/water interface. J. Phys. Chem. B 116, 9467–9481. doi:10.1021/jp304151e

CrossRef Full Text | Google Scholar

Zhao, Z. X., Sun, C. Z., and Zhou, R. F. (2020). Thermal conductivity of confined-water in graphene nanochannels. Int. J. Heat Mass. Tran 152, 119502. doi:10.1016/j.ijheatmasstransfer.2020.119502

CrossRef Full Text | Google Scholar

Zhao, Z. X., Zhou, R. F., and Sun, C. Z. (2020). Hierarchical thermal transport in nanoconfined water. J. Chem. Phys. 153, 234701. doi:10.1063/5.0030738

CrossRef Full Text | Google Scholar

Zhao, Z. X., Zhou, R. F., and Sun, C. Z. (2020). Molecular Dynamics Study of Water Diffusivity in Graphene Nanochannels. Int. J. Thermophys. 41. doi:10.1007/s10765-020-02660-5

CrossRef Full Text | Google Scholar

Zhou, R. F., Sun, C. Z., and Bai, B. F. (2021). Wall friction should be decoupled from fluid viscosity for the prediction of nanoscale flow. J. Chem. Phys. 154, 074709. doi:10.1063/5.0039228

CrossRef Full Text | Google Scholar