A Hierarchical Game Theory Based Demand Optimization Method for Grid-Interaction of Energy Flexible Buildings

Introduction

Backgrounds

With the continuous increase in power consumption and the high penetration of renewable energy generations, peak load and power imbalance have become two major challenges for an electrical grid; these challenges significantly affect the reliability, quality and energy efficiency of the grid (Arteconi et al., 2019). The peak load usually results from end-user energy behaviors (e.g., the power demands of buildings or industrial production during office hours/peak hours). Power imbalances generally result from a sudden loss of power supply or an increase in power demand. Redundant capacities of power plants and adequate operating reserves are essentially required by power generation sectors. Energy storage devices/systems (e.g., electric vehicles, batteries, and pumped-storage hydroelectricity) can also be employed as operating reserves. However, these methods are usually limited by either geographic conditions or high initial/operation costs and low storage capacities (Yan et al., 2020). In contrast, methods that use incentive benefits (i.e., implement the power demand response programs) to encourage end-users to manage their power usage behaviors are considered a more promising solution for peak load and power imbalance of grids.

Buildings are the largest electricity consumers worldwide and have great potential for power demand management in practice. In the United States, China, and Europe, the proportion of electricity used in construction in total electricity consumption reached 39.1, 20.6, and 29.4%, respectively (Electrical and Mechanical Services Department of Hong Kong, 2012; DoE, 2014). With the wide applications of building automation systems, IT technologies, smart meters and energy storage, buildings have demonstrated their great capabilities and willingness to participate in the demand management of grids through the bidirectional interaction between buildings and smart grids (Reynders et al., 2018). “Energy flexible buildings” (EFBs), which have the capacity to manage their energy demand and production according to local climate conditions, user needs, and grid requirements, have been proposed by the International Energy Agency (IEA) (Jensen et al., 2017). More specifically, Wang proposed the concept of ‘grid-friendly and grid-responsive’ buildings in a research report, where energy flexible buildings are required to work in synergy with (i.e., be responsive to) the grid or avoid additional stresses (i.e., be friendly) on the power grid balance (Wang, 2016). The energy flexibility of buildings can be greatly enhanced with the use of passive/active thermal storage. For instance, building thermal mass is an inherent passive storage of building structures and internal furniture for building load shifting and demand limiting by using precooling and room temperature set-point reset (Liang et al., 2020). Wang summarized three typical categories of active storage used in buildings to enhance energy flexibility: conventional storage (e.g., chilled water storage), small-scale storage (e.g., phase-change material), and innovative use of existing building facilities (e.g., fire water tanks) for load shifting, demand limitation and management. The increasing usage of power generation in buildings is a trend for sustainable building design and significantly affects the demand and flexibility characteristics of buildings (Zhong et al., 2016). Above all, buildings have the potential to be an excellent carrier for demand-side energy consumption management to solve grid imbalance.

Literature Review

How to explore the energy flexibility of buildings and to coordinate a variety of buildings with different energy flexibilities for effective interactions with smart grids are challenging. The key issue is how to accommodate the interests of all participants involved in the interactions between grids and buildings (Xu et al., 2020). In fact, driven by attractive electricity prices and various incentive policies, buildings may change their power demand flexibly and responsively. The altered aggregate power demand of buildings will affect electricity prices once a dynamic pricing mechanism is adopted in a smart grid. In contrast, the adjusted electricity prices will also induce buildings to change their energy behaviors to lower their operation cost. Further adjustments to electricity prices and building demands will continue until optimal operation is approached (Saad et al., 2012; Huang et al., 2019). A dynamic pricing method based on genetic algorithm is proposed by Huang et al.to improve two-way interaction and reduce power imbalance (Huang and Sun, 2019). They also proposed the collaborative demand response of nearly zero energy buildings to respond to the dynamic pricing of cluster-level performance improvement, which provides decision makers with computationally efficient demand response control for almost zero-energy buildings, thereby realizing full collaboration and helping To improve performance (Basar and Olsder, 1999).

At the same time, as an iterative and interactive power demand management strategy, mutual matching of supply-demand between EFBs and smart grid can be analyzed by game theory. Game theory is a mathematical theory and method for studying interactive phenomena whose nature is characterized by struggle or competition (Huang et al., 2017). Previous studies have investigated the feasibility of using game theory to solve the supply-demand interaction problem. Huang et al. reviewed the related research on cluster energy consumption planning when EFB buildings are connected to the grid. The authors pointed out the importance of consumer participation in the interaction of supply and demand and proposed an information interaction platform structure based on game theory, thereby aiming to improve the reliability of energy planning strategies for building clusters (Chen et al., 2019). Chen et al. used game theory as a tool to define the strategies of participants in the Israeli construction market; the authors combined these strategies with various incentives in the interaction of supply and demand and analyzed the strategy combination that optimally improved the market to help the expansion of the Israeli EFB market (Najafi-Ghalelou et al., 2018). Afshin et al. conducted game modeling on the internal energy interaction problem of a building complex, ensured the global optimal solution through mixed integer programming, and determined the individual strategies in equilibrium through general algebraic modeling system optimization software. The results of this case study showed that the internal energy interaction strategy of the building complex can improve the power exchange capacity and reduce the power cost (Lv and Ai, 2016). Lv et al. proposed a new dynamic energy management strategy that interacts with an active power distribution system based on multigrid-connected microgrids; the strategy was aimed at a higher-level benefit distribution network and multiple smart grid units participating in the interaction. A high-level interaction between smart grid units and benefit distribution networks is described by two-level programming, and the smart grid units are modeled by using an innovative interactive energy game matrix (Li and Wang, 2020). In a study by Li et al., an online multi-objective coordinated control strategy composed of two control optimization schemes was proposed for predictive scheduling and real-time optimal control of the energy system of zero-energy buildings. The strategy is based on a cooperative game model and is tested and evaluated by simulating energy storage system scheduling in a typical period in a zero-energy building. The control variables and target weights are finally optimized, and energy costs and grid fluctuations are minimized (Zhao, 2001). The abovementioned studies regard the smart grid and buildings as two participants simultaneously engaged in decision-making and thereby provide a guiding idea for analyzing supply-demand interaction from the perspective of game theory. The traditional game model regards the building and the power grid as equal participants in the buying and selling relationship; however, this view differs from reality, and consequently, the final Nash equilibrium is inaccurate.

The economic competition relationship between the power grid and buildings is usually defined as a hierarchical planning problem in which one party is dominant and the other party is subordinate. Specifically, the power grid precedes buildings in making decisions on electricity prices, and the buildings then respond to the electricity price plans formulated by the grid and determine the power purchase demand to maximize the buildings’ own benefits. Additionally, because the power grid needs to consider the response of buildings to electricity prices when making decisions (excessive prices will cause buildings to be more self-produced and self-sold), the energy demand of buildings can also counteract the power grid’s pricing plan. This game model of interaction between different levels of decision-making is called the Stackelberg model (Yang et al., 2013). In the production and operation of some commodities with poor price elasticity, the company that decides the strategy first in the Stackelberg model does not have the first-mover advantage, but the company that determines the output later has the latter-mover advantage. Therefore, traditional electricity sales models adopt monopoly or national production and operation methods. However, when renewable energy and energy storage systems are connected, the price demand elasticity of electricity usage in buildings increases. Under the Stackelberg model, the grid side can ensure its own first-mover advantage while incentivizing the buildings to reduce their consumption, and the revenue of electricity is also higher than that under the traditional Cournot model, so it is beneficial to use the Stackelberg model to solve the game equilibrium in the game analysis.

In a study by Peng et al., the Stackelberg model was used to optimize the time-of-use (TOU) pricing strategy of the grid. The model satisfied equilibrium user demand and reduced the potential cost of the utility by encouraging buildings to purchase electricity through low trough and low pricing and by encouraging the self-production of buildings through high peak pricing (Yang et al., 2014). On this basis, Jie et al. optimized the utility problem of building user comfort based on the new effect function for determining the optimal power consumption and grid pricing under real-time electricity prices (RTPs) (Srinivasan et al., 2017). Srinivasan et al. selected dynamic pricing strategies based on game theory for the Singapore electricity market and compared the economic benefits of three pricing strategies: half-hour pricing, time-of-use electricity pricing, and day-and-night electricity pricing (DN). The results show that RTP can reduce the peak load of the residential and commercial sectors by 10 and 5%, respectively; and increase profits by 15.5 and 18.7%, respectively (Tang et al., 2019). Tang et al. used the Stackelberg model to maximize the profits of buildings and power grids by considering the impact of uncertainties (Zhang et al., 2019).

However, the game model used in the literature cited above does not classify the types of buildings that the game applies to and ignores the impact of different building system conditions on the interaction of supply and demand.

Research Gaps and Main Contributions

In previous studies, when considering grid interactions or games between EFBs and smart grids, buildings were often considered to have the same energy “flexibility”. In fact, buildings with different energy systems and different control strategies have different energy flexibilities and energy consumption patterns, which affect the results of the supply-demand interaction of the game with the power grid. To obtain better demand response optimization results with more realistic performances, this paper constructs three typical flexible buildings with different energy systems and energy control strategies and proposes a hierarchical demand optimization method based on game theory to coordinate these buildings with different energy flexibilities for effective grid interaction with smart grids. The remainder of this paper is arranged as follows. In Principle of the Hierarchical Optimization Method, the principle of hierarchical optimization methods will be explained in detail, and the specific interactive game model and internal strategy selection algorithm will be established in Hierarchical Optimization Implementation Based on Game Theory. Finally, in Case Study, the rationality of the two-tier optimization scheme will be analyzed by using case analysis.

Principle of the Hierarchical Optimization Method

Structure of the Optimization Methods

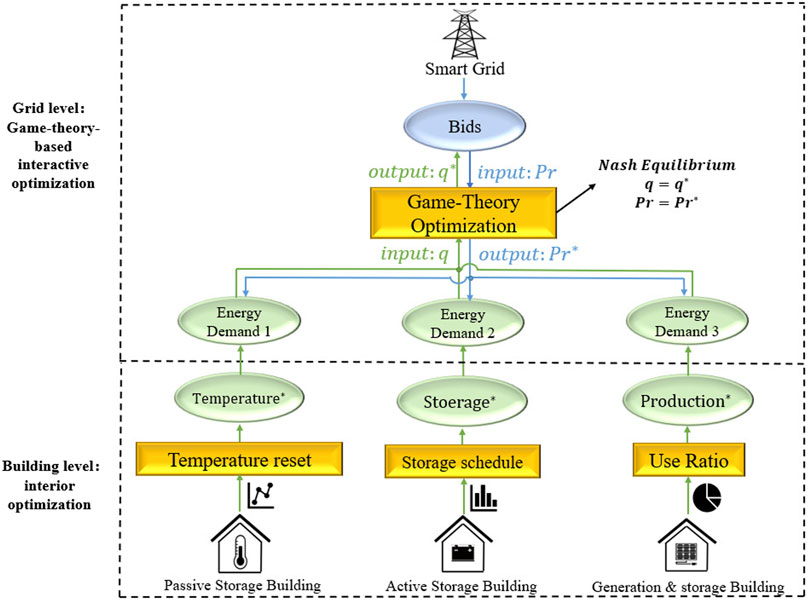
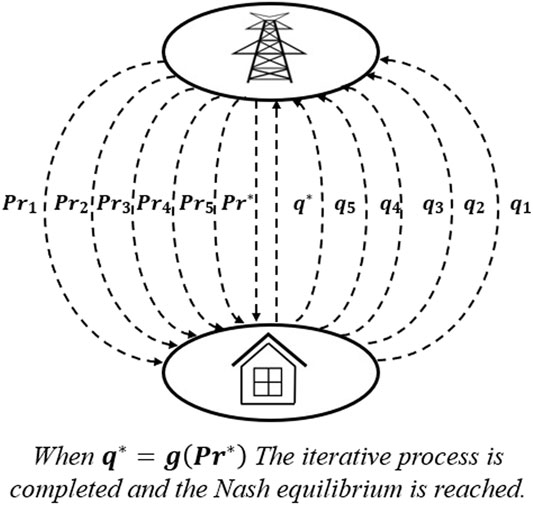
As shown in Figure 1, the proposed hierarchical game theory-based demand optimization method consists of two optimization strategies at the grid and building levels. At the grid level, a demand-price interaction model between buildings and the grid is established to use game theory to identify the Nash equilibrium solutions, which are used to determine the optimized energy demand of buildings and the associated electricity prices by accommodating the interests of all participants involved. At this level, buildings can adjust their energy consumption patterns in response to the real-time electricity price or other incentive policies to pursue the lowest possible electricity cost. However, the power grid will also provide the corresponding RTP according to the energy consumption of the building at different times to ensure maximum profit for the building. This kind of supply-demand interaction level analysis of building energy strategy is a typical non-cooperative game problem. Building energy demand and grid quotations are bargained at the game level; when the demand and the quotations reach the Nash equilibrium, the mutual benefits of both parties can be maximized.

FIGURE 1

FIGURE 1. The framework of the proposed hierarchical optimization strategy.

At the building level, three types of EFBs with different energy flexibilities are investigated to achieve their maximum interests by using appropriate control strategies during the interaction with the grid; the details of the building system conditions are shown in Table 1. Type-1 buildings are “passive storage buildings”, which can adjust their energy usage by changing the indoor air temperature of the air-conditioning system with a certain degree of thermal comfort sacrifice. Considering that the acceptable temperature change range is small (e.g., 2°C), the energy flexibility is limited. Type-2 buildings are “active storage buildings”, which can purchase excess electricity during periods of low electricity prices and use active energy storage systems to transfer the excess electricity to use during periods of high electricity prices. The energy flexibility is generally moderate, and buildings have a certain degree of initiative in the game, which requires the grid to set peak electricity prices with more consideration of the building’s acceptance. Type-3 buildings, which both generate and store energy, have relatively considerable energy flexibility by controlling both their own energy generation and consumption patterns. Such buildings can purchase low-priced or sell high-priced electricity as much as possible and therefore have a strong initiative in the game with the power grid. In summary, the building energy flexibility or the ability of a building to adjust energy consumption in response to electricity prices depends on the system conditions of the building. How to encourage buildings with different energy flexibilities to take part in the grid interaction game and maximize their own interests by using appropriate control strategies is the other key of the proposed optimization method.

TABLE 1

TABLE 1. Three types of typical energy flexible buildings.

Game-Based Interactive Optimization at Grid-Level

The optimization objective of the grid level is to achieve the Nash equilibrium of the EFB-grid game interaction. The three elements that make up game $G$ are its participants $\sigma$ (two or more), their strategies $S$, and the benefits gained by strategies $U$; game $G=\{\sigma ,S,U\}$. The interactive participants of the supply and demand strategy proposed in this paper are the EFB cluster and the smart grid. The strategy determined by the grid is the electricity price ($Pr$), and the strategy determined by the EFBs is its energy demand scheme ($q$). Grid pricing is based on the intensity of the demand of EFBs, and this demand is also affected by the acceptance of the current electricity price, which is $Pr=f\left(q\right),q=g\left(Pr\right).$ The grid first quotes the EFBs, and then the EFBs adjusts their own demand based on their acceptance of the current electricity price and feeds the electricity price back to grid. After receiving the electricity price, the grid adjusts the quotation strategy and sends the price to the EFBs. Both parties repeat this process until $P{r}^{\ast }=f\left(q^{\ast }\right),q^{\ast }=g\left( P{r}^{\ast }\right)$; that is, the supply and demand strategies given by the grid and EFBs meet the expectations of both parties. The game process enters a dynamic equilibrium process; this equilibrium state is called the Nash equilibrium, and the process is shown in Figure 2. Under the Nash equilibrium, the strategies of both participants of the game will no longer change because breaking the balance will not be more beneficial to either of them. Unlike the “maximum profit,” which exists in an ideal state, the profit of both parties at this time is the real profit after concession to guarantee the transaction. The definition of the Nash equilibrium is as follows:

FIGURE 2

FIGURE 2. Participant’s strategies converge when the game towards Nash equilibrium.

A strategy vector $s^{\ast }=\{s_i^{\ast },s_{-i}^{\ast }\}$ that is in the Nash equilibrium state needs to satisfy $U\left(s^{\text{∗}}\right)\ge U(s_i^{\text{∗}},s_{-i}^{\text{∗}})$.

In the above definition, $s_i^{\text{∗}}$ is the strategy of game player $i$, $s_{-i}^{\text{∗}}$ is the strategy of all other players, and $U$ is the profit that the strategy can promote.

To model the game objective on the building side, the mathematical description of the game objective is as follows:

$\{\begin{array}{c}\forall Q\in \varnothing ,Q\ne Q^{\ast },U_{building}\left(P{r}^{\ast },Q\right)\le ,U_{building}\left(Pr,Q^{\ast }\right)\\ Q^{\ast }=argma{x}_{\left(Q\right)}{U}_{building}\end{array}(1)$

where $\varnothing$ is the value range of the building strategy, $U_{building}$ is the building revenue, $Q$ is the decision value of the building demand, $Q^{\text{∗}}$ is the optimal decision value of building demand under Nash equilibrium, $Pr$ is the dynamic electricity price set by the grid, and $P{r}^{\text{∗}}$ is the maximum value under Nash equilibrium. Building energy demand under this balance is the most conducive to the common economic benefits of the building complex and the power grid and can be used as a reliable energy optimization result under the demand response strategy.

The mathematical description corresponding to the grid strategy is:

$\{\begin{array}{c}\forall Pr\in P,Pr\ne P{r}^{\ast },U_{grid}\left(Q^{\ast },Pr\right)\le ,U_{grid}\left(Q,P{r}^{\ast }\right)\\ P{r}^{\ast }=argma{x}_{\left(Pr\right)}{U}_{grid}\end{array}(2)$

where $P$ is the value range of the grid strategy and $U_{grid}$ is the grid revenue.

The premise of the existence of the Nash equilibrium is that the players of the game abide by the basic rules of the transaction, and any conflicting strategy that only considers unilateral interests will lead to the failure of the transaction. Therefore, it is necessary to define the value range of the game strategy set:

$\{\begin{array}{c}\varnothing =\left\{Q|Q\in R^N,Q_{min}\le Q\le Q_{max}\right\}\\ P=\left\{Pr|Pr\in R^N,Q_{min}\le Q\left(Pr\right)\le Q_{max}\right\}\end{array}(3)$

In Equation 3, $R^N$ is the complete set of strategies, $Q_{min}$,$Q_{max}$ is the value range of energy consumption under the rules, and $Q\left(Pr\right)$ is the building demand in response to electricity prices.

Internal Optimization at Building-Level

To determine the energy demand scheme that can minimize the overall cost of a building, the cost optimization objective function must be constructed first. The building cost is composed of three main parts: user dissatisfaction, mismatch cost (these two will not be directly reflected in the bill), and the electricity purchase cost of the transaction with the grid.

User Dissatisfaction

User dissatisfaction is an indicator that describes the degree of dissatisfaction of users in the building with the current thermal comfort conditions when the demand is limited to deviate from the normal level. It should be noted that even under the original energy demand, due to differences in the definition of thermal comfort by users, there will still be a small number of users who are dissatisfied with the current thermal environment, so there is a unique positive minimum for user dissatisfaction, and It has the property of monotonically increasing with the degree of deviation from the minimum point, so the quadratic function is used for description in this study. Assuming that there are $M$ buildings in a building cluster, a day is divided into $N$ periods, where the user dissatisfaction at time $k$ with building $i$ is defined in Eq. 4:

$S_i^k\left(q_{i,k}^d\right)=-{\alpha }_i\cdot q_{i,k}^b\cdot q_{i,k}^d+\frac{{\alpha }_i}{2}\cdot {\left(q_{i,k}^d\right)}^2(4)$

where $q_{i,k}^d$ is the optimized power demand of building $i$ at time $k$ after participating in the dynamic electricity price game, $q_{i,k}^b$ is the original power demand of building $i$ at time $k$, and ${\alpha }_i$ is the preset coefficient of building user’s acceptance of dissatisfaction with the building, changes with differences in building use and user attributes. Its main function is to transform user dissatisfaction into an economic cost of the same order of magnitude as the electricity purchase cost, and to characterize its importance in the total cost. There are a large number of relevant studies that provide guidance on the value of this parameter, this paper uses the value method in literature (Tang et al., 2019; Zhang et al., 2019).

Mismatch Cost

Mismatch costs refer to the hidden costs, such as energy storage loss and machine loss, incurred when the building demand is shifted or changed. It is determined by the difference between the optimized and original demand at the same time, the minimum value is 0 when the two are equal. It has the same monotonicity and concavity as the user dissatisfaction, so it can also be described by a quadratic function. The building mismatch cost at time $k$ of building $i$ is defined in Eq. 5:

$D_i^k={\rho }_i\cdot {\left(q_{i,k}^d-q_{i,k}^b\right)}^2(5)$

where ${\rho }_i$ is a preset parameter describing the transfer cost level of building $i$ demand. It converts the mismatch cost into an economic cost of the same order of magnitude as the power purchase cost, and characterize its importance in the total cost. The value method can be referred to literature (Tang et al., 2019; Zhang et al., 2019).

Power Purchase Cost

The electricity purchase cost, which is the most intuitive economic cost, refers to the electricity bill paid by the building. The power purchase cost of building $i$ at time $k$ is defined in Eq. 6.:

$B_i^k=P{r}^k\cdot q_{i,k}^d(6)$

where $P{r}^k$ is the dynamic electricity price at time $k$.

Hierarchical Optimization Implementation Based on Game Theory

Grid-Level: The Solution of Nash Equilibrium in the Stackelberg Model

During the interaction between the EFB and the grid, biding of the grid will affect the motivation of the EFB to purchase electricity, while the degree of the EFB’s dependence on electricity will also affect the grid’s biding strategy. The grid’s actions always precede those of EFBs; this accords with the application conditions of the Stackelberg model. The principle of backward induction is used to determine the optimal energy use plan of the buildings under the Nash equilibrium of the game and the optimal price of the power grid.

Demand Strategy of Energy Flexible Buildings

Determining the energy demand plan that minimizes the overall cost of the building is a cost function conditional extreme value problem with $q_{i,k}^b$ as the independent variable, and the Lagrange multiplier method is used to solve the problem. The Lagrange multiplier ${\lambda }_i$ is introduced, and the cost function is combined with the constraints to construct the Lagrange function.

$L={\displaystyle \sum _{k=1}^N\left\{{\rho }_i\cdot {\left(q_{i,k}^d-q_{i,k}^b\right)}^2-\left[{\alpha }_i\cdot q_{i,k}^b\cdot q_{i,k}^d+\frac{{\alpha }_i}{2}\cdot {\left(q_{i,k}^d\right)}^2\right]+{\beta }_i^k\cdot \mathit{P}{\mathit{r}}^k\right\}+{\lambda }_i\cdot \delta }(7)$

In Eq. 7, $\delta$ is the constraint condition. The cost function in Eq. 7 is a comprehensive cost that takes into account the explicit and hidden costs in the building operation period. Literature (Zhang et al., 2019) proves the rationality of the cost function.

By expanding the Lagrange function and finding the partial derivatives of the independent variables $q_{i,k}^b$ and ${\lambda }_i$, we obtain:

$\{\begin{array}{c}\left(2{\rho }_i+{\alpha }_i\right)q_{i,k}^d-\left(2{\rho }_i+{\alpha }_i\right)q_{i,k}^b+{\beta }_i^k\cdot P{r}^k+{\lambda }_i=0\\ \delta =0\end{array}(8)$

In fact, different types of EFBs have different constraints. For passive storage buildings, the energy consumption change caused by temperature resetting is the optimized amount of building energy consumption. According to the law of conservation of energy, the electricity demand before and after optimization meet the following constraints:

${\delta }_1:{\displaystyle {\sum }_{k=1}^N{q}_{i,k}^d}-{\displaystyle {\sum }_{k=1}^N{q}_{i,k}^b}+{\displaystyle {\sum }_{k=1}^N{q}_{i,k}^t} =0(9)$

In Eq. 9, $q_{i,k}^t$ is the building power consumption of building $i$ affected by the change of indoor temperature presetting at time $k$.

For active storage buildings, the excess load during the low electricity consumption period is stored in the energy storage system and transferred to the peak period to reduce the peak electricity consumption. This type of building does not have an independent capacity device, and the total electricity demand after participating in the dynamic electricity price game should be consistent with the benchmark demand, that is, meet the constraint conditions:

${\delta }_2:{\displaystyle \sum _{k=1}^N{q}_{i,k}^d}-{\displaystyle \sum _{k=1}^N{q}_{i,k}^b}=0(10)$

For generation and storage buildings, while the load transfer is completed through the energy storage system, photovoltaic and wind power generation systems can be used to assist the power supply to help the building improve its power purchase demand. Due to the building’s own production capacity, the actual demand after the building side participates in the dynamic electricity price game is less than the benchmark demand, and both types of demand satisfy the following numerical relationship:

${\delta }_3: {\displaystyle \sum _{k=1}^N{q}_{i,k}^d}-{\displaystyle \sum _{k=1}^N{q}_{i,k}^b}+{\displaystyle \sum _{k=1}^N{q}_{i,k}^r}=0(11)$

In Eq. 11, $q_{i,k}^r$ is the distributed energy production capacity at time $k$ of building $i$.

Due to the backward compatibility of building equipment, it is generally believed that buildings with stronger energy flexibility can also use the energy control strategy of buildings with weaker energy flexibility. If a building uses all three types of energy control strategies at the same time, its demand will meet the constraint conditions:${\delta }_4:{\displaystyle \sum _{k=1}^N{q}_{i,k}^d}-{\displaystyle \sum _{k=1}^N{q}_{i,k}^b}+{\displaystyle \sum _{k=1}^N{q}_{i,k}^r}+{\displaystyle \sum _{k=1}^N{q}_{i,k}^t}=0$. However, in fact, considering that the use of the energy control strategy of buildings with weaker energy flexibility has higher marginal costs, we assume that buildings will use the best match energy control strategy conform to their system conditions in this study.${\delta }_1$, ${\delta }_2$, and ${\delta }_3$ are put into Eq. 8, and the independent variable $q_{i,k}^d$ is solved to obtain:

The optimized power demand of passive storage buildings:

$q_{i,k}^d=q_{i,k}^b-\frac{{\beta }_i^k\cdot P{r}^k}{2{\rho }_i+{\alpha }_i}+\frac{{\displaystyle {\sum }_{k=1}^N{\beta }_i^k\cdot P{r}^k}}{N\cdot \left(2{\rho }_i+{\alpha }_i\right)}-\frac{{\displaystyle {\sum }_{k=1}^N{q}_{i,k}^t}}{N}(12)$

The optimized power demand of active storage buildings:

$q_{i,k}^d=q_{i,k}^b-\frac{{\beta }_i^k\cdot P{r}^k}{2{\rho }_i+{\alpha }_i}+\frac{{\displaystyle {\sum }_{k=1}^N{\beta }_i^k\cdot P{r}^k}}{N\cdot \left(2{\rho }_i+{\alpha }_i\right)}(13)$

The optimized power demand of generation & storage buildings:

$q_{i,k}^d=q_{i,k}^b-\frac{{\beta }_i^k\cdot P{r}^k}{2{\rho }_i+{\alpha }_i}+\frac{{\displaystyle {\sum }_{k=1}^N{\beta }_i^k\cdot P{r}^k}}{N\cdot \left(2{\rho }_i+{\alpha }_i\right)}-\frac{{\displaystyle {\sum }_{k=1}^N{q}_{i,k}^r}}{N}(14)$

Therefore, the energy demand plan that minimizes the overall cost of building $k$ at time $i$ has been determined. To prove that the scheme exists in the Nash equilibrium of the game, the second-order partial derivative of $q_{i,k}^d$ is calculated by Eq. 7, and the Hessian matrix is derived:

$\frac{{\partial }^{2}U}{\partial q_{i,k}^d\partial q_{j,k}^d}=\{\begin{array}{cc}\left(2{\rho }_i+{\alpha }_i\right)& i=j\\ o& i\ne j\end{array}(15)$

The preset parameters ${\rho }_i$ and ${\alpha }_i$ are all positive values, so the diagonal element is greater than zero, and the matrix is positive definite. The relationship between the Hessian matrix and the concave convexity of the function shows that the objective function has a unique minimum value and thus that the Nash equilibrium exists and is unique. The calculation result of formulas Eqs 12, 14– is the construction energy demand strategy corresponding to the Nash equilibrium in the game.

In Equations 12, 14, there are still parameters $q_{i,k}^t$ and $q_{i,k}^r$ that need to be determined. Among them, the key parameter “indoor temperature” for determining $q_{i,k}^t$ is the internal energy control strategy corresponding to passive storage buildings, which will be introduced in Indoor Temperature Resetting . $q_{i,k}^r$ can be calculated by the mathematical models of wind power generation and photovoltaic power generation (Kusakana and Vermaak, 2014; Guo et al., 2019). The energy production at each moment can be used immediately or transferred to subsequent moments through energy storage equipment. Through the internal energy control strategy analysis in Energy Generation and Active Storage, the most reasonable immediate use share can be determined as the internal energy control strategy of generation & storage buildings. Since energy storage involves only the transfer of energy within a day and does not affect total energy consumption. The corresponding energy storage can be directly determined by the difference (i.e., $q_{i,k}^d$-$q_{i,k}^d$) of the building demand before and after the grid interactive hierarchical optimization as the internal energy control strategy of the active storage buildings.

Biding Strategy of Grid

The income from grid sales after deducting comprehensive costs is defined as the grid’s revenue. The explicit cost is the direct cost consumed by the power grid, and the hidden cost is the various energy losses caused by the change in the amount of power generated by the power grid in response to user demand fluctuations. The grid’s revenue is defined as the following equation:

$P=P{r}^k\cdot q_{i,k}^d-f\left(q_{i,k}^d\right)-D_f(16)$

where $q_k^d$ is the total purchased power of the building group at time $k$, $f\left(q_{i,k}^d\right)$ is the direct economic cost of power generation by the grid, and $D_f$ is the hidden cost caused by demand fluctuations.

$q_k^d={\displaystyle \sum _{i\in \theta }{q}_{i,k}^d}(17)$

$f\left(q_k^d\right)=a{\left(q_k^d\right)}^2+b\left(q_k^d\right)+c(18)$

$D_f=\frac{1}{N}{\displaystyle \sum _{k=1}^N\sqrt{{\left(q_k^d-q_{k,ave}^d\right)}^2}}(19)$

In Equation 18, a, b, and c are the preset constants, and $q_{k,ave}^d$ is the average energy consumption of the building during the day.

Equations 12–14 show that $q_k^d$ in the power grid revenue function is affected by the electricity price:

$q_k^d={\sum }_{i\in \theta }{q}_{i,k}^d=f\left(P{r}^k\right)(20)$

Substituting $f\left(P{r}^k\right)$ into Eq. 16, we obtain:

$P=P{r}^k\cdot f\left(P{r}^k\right)- a{(f\left(P{r}^k\right))}^2-b\left(f\left(P{r}^k\right)\right)-c-\frac{1}{N}{\displaystyle \sum _{k=1}^N\left(f\left(P{r}^k\right)-g\left(P{r}^k\right)\right)}(21)$

Let $\frac{\partial P}{\partial P{r}^k}=0$; then, the corresponding dynamic electricity price $P{r}^k$ is the optimal pricing strategy under the game.

Building-Level: Energy Control Strategy Under Nash Equilibrium

Indoor Temperature Resetting

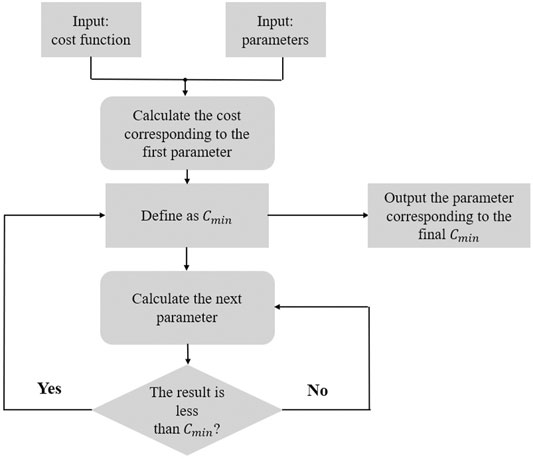
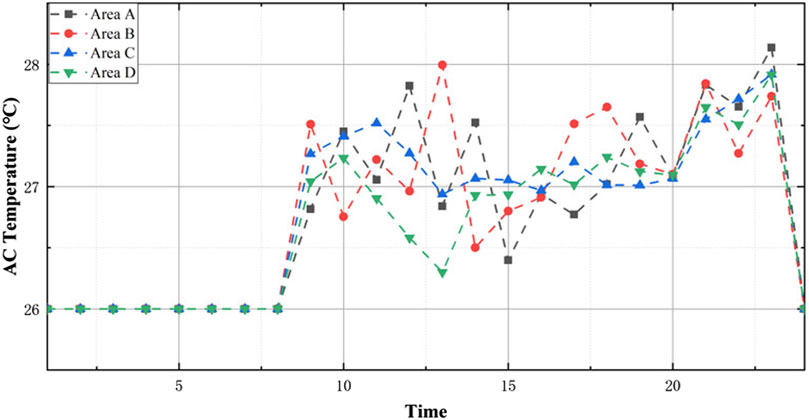
Changes in air-conditioning temperature can significantly affect building energy consumption. Previous studies have shown that an increase in indoor temperature by 1°C in the southeastern coastal area can bring approximately 3–6% energy savings (Lai et al., 2013). However, increasing the air-conditioning temperature may also lead to an increase in the hidden cost of the building; this cost is reflected mainly in the cost of user dissatisfaction caused by the reduction of thermal comfort in the building and the mismatched cost caused by fluctuations in energy consumption. To balance the benefits produced by the reduction of energy consumption and the losses caused by the increase in hidden costs, the building cost function is traversed in a 0–2°C increase in air-conditioning temperature. The air-conditioning temperature resetting value corresponding to the lowest total cost of the building is taken as the optimal internal energy control strategy of the building under these conditions. The running logic is shown in Figure 3.

1. Input the objective function and parameters.

2. Calculate the total building cost corresponding to the first set of parameters in the traversal domain (e.g., an indoor temperature of 26–28 °C) when the building demand and grid pricing are iterated to the Nash equilibrium, define the cost as $C_{min}$, and record the calculation parameters.

3. Calculate the cost of all parameters in the traversal domain in turn, and compare the size with $C_{min}$. If the size is less than $C_{min}$, define the cost corresponding to the parameter as the new $C_{min}$, and record the current calculation parameters.

4. When all parameters in the traversal domain are involved in the calculation, the final $C_{min}$ is output, and the corresponding indoor temperature is the optimal building internal energy control strategy.

FIGURE 3

FIGURE 3. Logic diagram of temperature resetting optimization.

Energy Generation and Active Storage

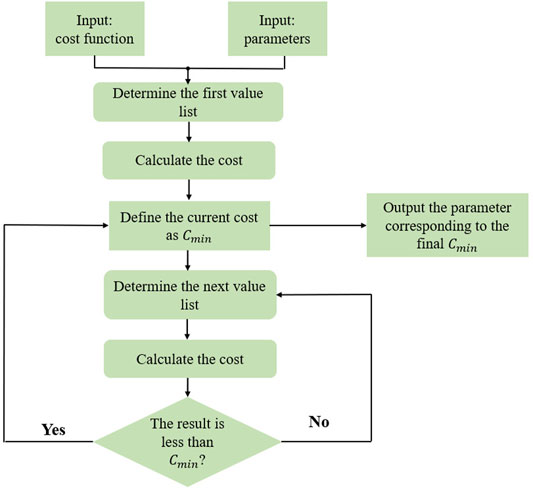
The internal control strategy used by generation & storage buildings is to determine the appropriate share of energy produced by the on-site energy generation systems for storage. During periods of low electricity prices, the energy produced by renewable energy in some buildings can be transferred to peak electricity consumption through energy storage systems. The energy produced during the peak period should be used to minimize the purchasing cost. Through the traversal calculation within a 0–100% energy usage rate per hour, the output capacity usage plan corresponding to the lowest construction cost is output as the optimal internal energy control strategy. When the traversal operation is used to determine the optimal share, because the energy storage at the previous moment can theoretically be used at any subsequent time, the traversal domain at every hour will be affected by the previous time except the first hour. The operating logic is shown in Figure 4.

1. Input the objective function and parameters.

2. Read the first parameter in the traversal domain (a generation usage share of 0–100%) at the first hour, and calculate the possible traversal domain at the second hour under this value; then, read the first parameter in the traversal domain at the second moment; then, calculate out the possible traversal domain at the third hour; and so on. Then, record the 24 parameters as a list.

3. Calculate the total construction cost of the parameters in this list when the construction demand and grid pricing are iterated to the Nash equilibrium; the total construction cost is defined as $C_{min}$.

4. Read all the parameters in the traversal domain at the first moment, repeat step 2, generate the corresponding value list, and calculate the total cost of the building.

5. Compare the calculation result with $C_{min}$; if the result is less than $C_{min}$, define the result as the new $C_{min}$.

6. When all the parameters in the traversal domain are involved in the calculation, the final $C_{min}$ is output, and the corresponding real-time use share of the building capacity is the optimal building internal energy control strategy.

FIGURE 4

FIGURE 4. Logic diagram of capacity utilization share control optimization program.

Case Study

Building and System Description

In this paper, some typical buildings of Hong Kong Polytechnic University are selected to provide and generate necessary building energy consumption and energy flexibility data. Buildings adopt central air-conditioning systems and providing energy storage capacity for the building complex by installed phase change material (PCM) storage tank in series with chiller, charging during the low power period is used for the joint power supply during the peak period. In the optimization calculation of passive storage buildings, the PCM air-conditioning system is replaced with an ordinary central air-conditioning system with similar system parameters. At this time, the campus buildings will rely on the energy passive storage of building’s thermal mass during the peak period of electricity consumption to regulate demand. In the period of low electricity consumption, considering the marginal cost of sacrificing user dissatisfaction, the demand will be maintained at the baseline level. The renewable power generation system is connected to the building complex to construct a simulated building complex equivalent to generation and storage buildings, and the system parameters refer to the Hong Kong Zero Carbon Building (ZCB) (Jian and Wang, 2010). A distributed energy system that uses building integrated photovoltaics (BIPV), CIGS thin film solar cells and small wind power generation equipment to provide production capacity for buildings, and cooperates with PCM air-conditioning to complete energy output and transfer. The campus buildings can be divided into four areas according to different functions and locations; these areas are equivalent to four large buildings. The division of each area is shown in Table 2. The data sources, such as building benchmark energy consumption requirements, local meteorological parameters, and time-of-use electricity prices, are based on field observations created on July 3, 2017.

TABLE 2

TABLE 2. Building zoning in Hong Kong Polytechnic University.

Demand Optimization Results and Strategy Analysis

Passive Storage Buildings

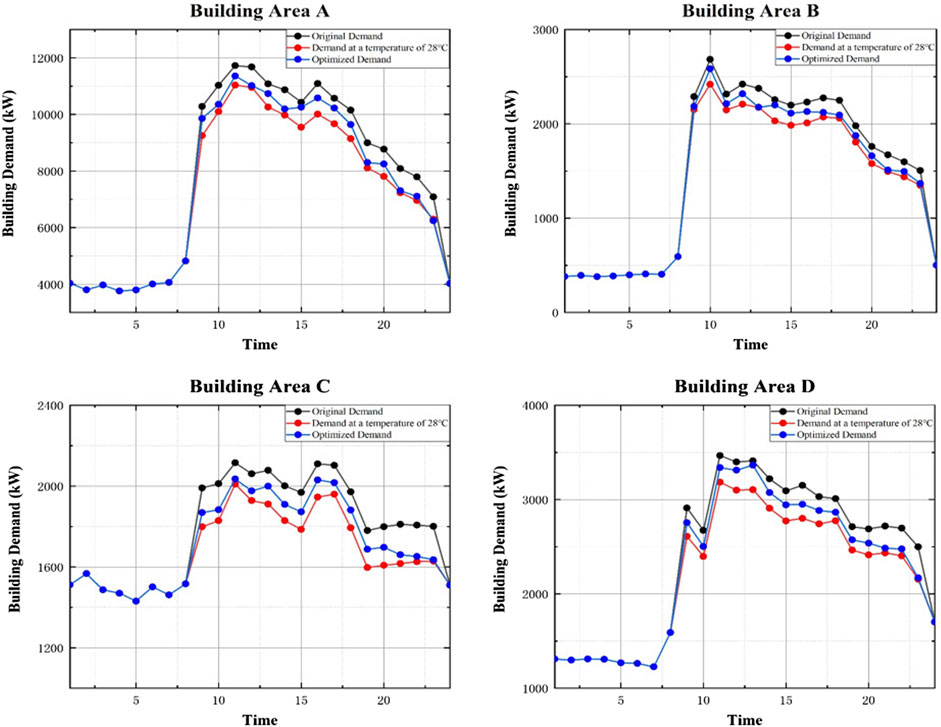
Figure 5 shows the energy interaction strategy of each building when the building’s renewable energy system and energy storage system are not connected. In the interactive optimization of the game built on the power grid, during the low electricity consumption period, the energy consumption demand is consistent with the benchmark energy demand, and the user passively accepts the electricity price set by the grid; during the peak period, the user will consider the economic stimulus of the high price. The preset temperature of indoor air conditioners can be adjusted to reduce electricity demand. The peak power consumption reduced in this way can reduce the cost of direct power consumption while also reducing the peak-to-valley power consumption difference of the building and alleviating grid imbalance.

FIGURE 5

FIGURE 5. Optimized demand profiles of four areas of passive storage buildings.

The gray, red and blue curves in Figure 5 represent the original building load (e.g., indoor temperature of 26°C), the building load when the indoor temperature is fixed at 28°C, and the optimized demand when the indoor temperature of different areas changes in different periods, respectively. Due to the impact of unsatisfactory and mismatched costs, the excessive increase in building air-conditioning temperature increases the hidden cost of the building. To balance the reduction in power purchase costs and the increase in hidden costs, the internal optimization method described in Indoor Temperature Resetting is used as the building internal strategy to determine the optimal indoor temperature, as shown in Figure 6, thus resulting in the optimized hourly energy demand for each area, as shown by the blue curve in Figure 5. The load affected by the temperature fluctuation of the air conditioner is calculated using Hongye load calculation software (Lüth et al., 2018). For the convenience of calculation, the relationship between load and temperature is assumed to be linear.

FIGURE 6

FIGURE 6. The optimal air-conditioning temperature strategy of passive storage buildings.

Active Storage Buildings

Figure 7 shows the energy requirements of buildings after the energy storage system is connected. During low electricity consumption periods, electricity charges are relatively low, and users purchase excessive electricity, thereby transferring low-cost electricity to the peak electricity consumption through the energy storage system, reducing high-cost electricity purchases and thereby meeting economic needs. As a result, the peak-to-valley difference in building power consumption is significantly reduced, and grid imbalance is alleviated.

FIGURE 7

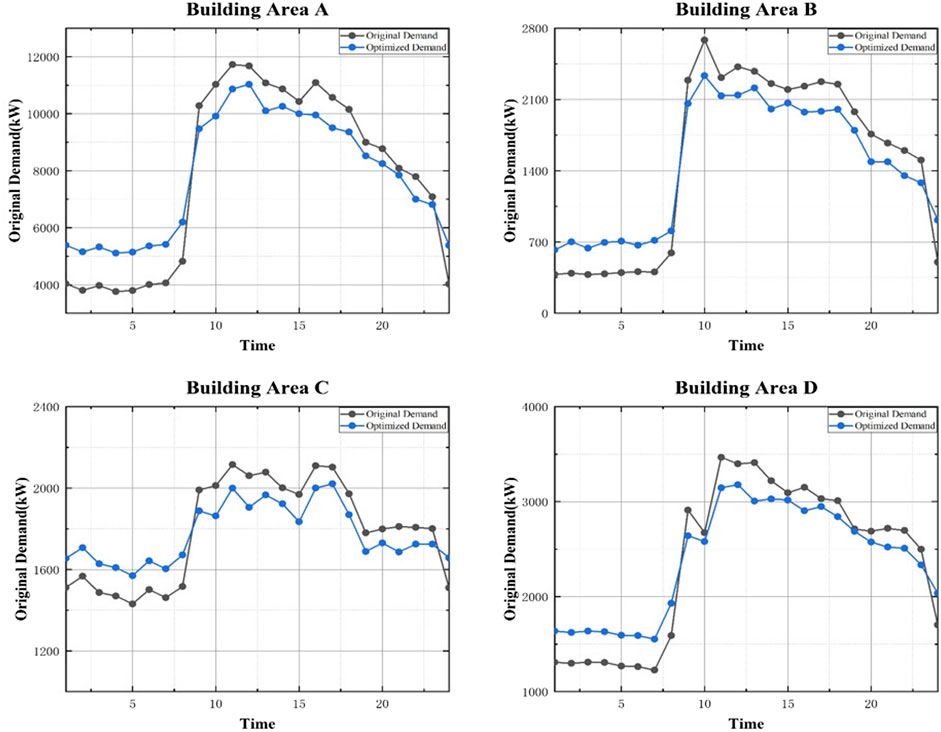
FIGURE 7. Optimized demand profiles of four campus accounts on the test day of active storage buildings.

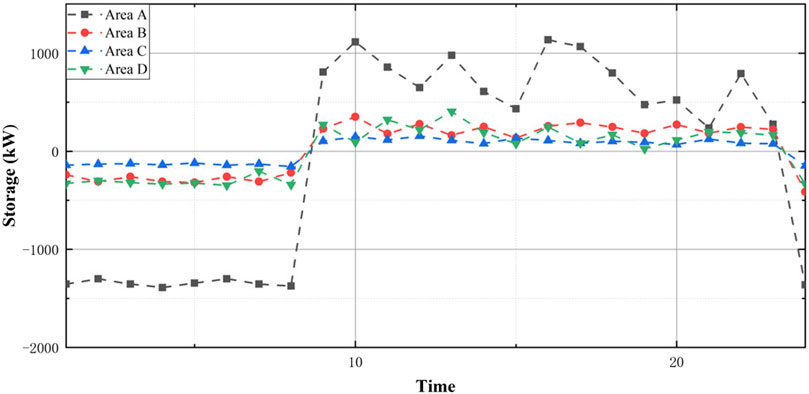
As described in Demand Strategy of Energy Flexible Buildings, because the energy storage system will not affect the total energy consumption of the building throughout the test day, the interaction strategy under this system condition can be determined before the internal strategy. Furthermore, there is no need to separately filter the internal strategy, and the energy storage at each time can be determined by the difference between the energy consumption before and after optimization. The result is shown in Figure 8.

FIGURE 8

FIGURE 8. The optimal storage strategy of active storage buildings.

Generation and Storage Buildings

Figure 9 shows the energy demand of buildings when the renewable capacity system and the energy storage system are connected as the building interaction strategy. While the energy storage system reduces the high-cost power purchase during peak periods through load shifting, the system can also reduce the excessive power purchases of users during the low period through the self-production and self-sale of renewable energy; on this basis, the renewable energy system can also reduce the power purchases by users during peak periods. This article is based on the relevant measurement data of Hong Kong’s ZCB renewable energy power generation. Using the output calculation model given in the literature (Kusakana and Vermaak, 2014; Guo et al., 2019) for data processing, the simulated distributed energy system is transplanted to the campus building of Hong Kong Polytechnic University for data analysis of generation & storage buildings.

FIGURE 9

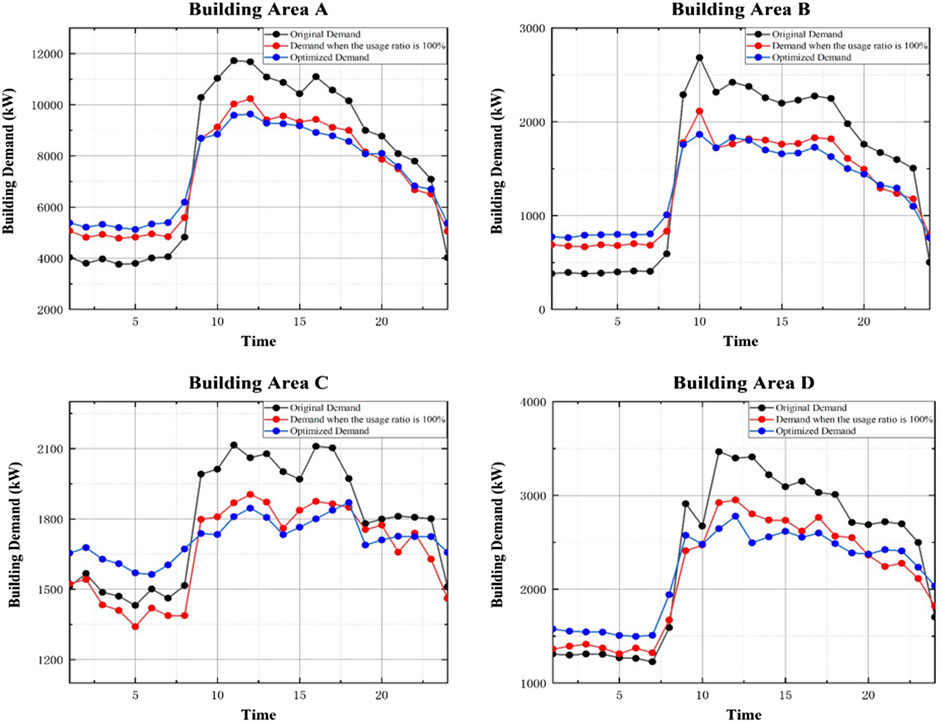
FIGURE 9. Optimized demand profiles of four campus accounts on the test day of generation and storage buildings.

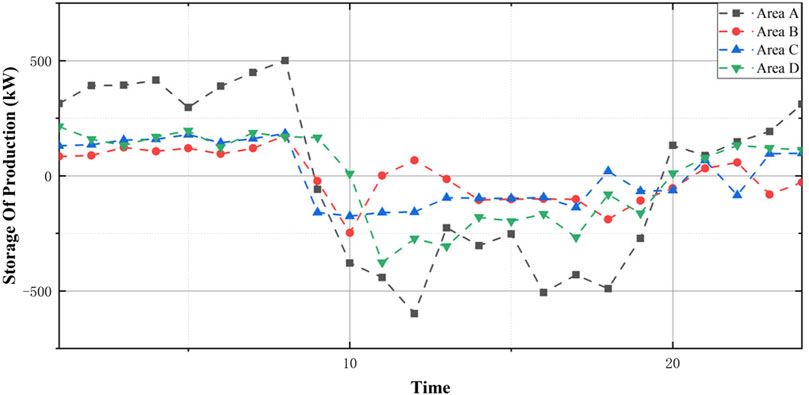
The red curve in Figure 9 is the building energy consumption curve when all renewable energy production capacity is fully used in real time. Compared with the blue curve representing the final optimization result, after using a reasonable internal energy control strategy optimization, the peak energy consumption of the building is significantly reduced, the fluctuation of energy consumption is reduced, and the hidden cost of the grid can be significantly controlled. The specific output storage value is shown in Figure 10 as the building’s internal strategy.

FIGURE 10

FIGURE 10. The optimal storage of production strategy of generation & storage buildings.

Economic Analysis

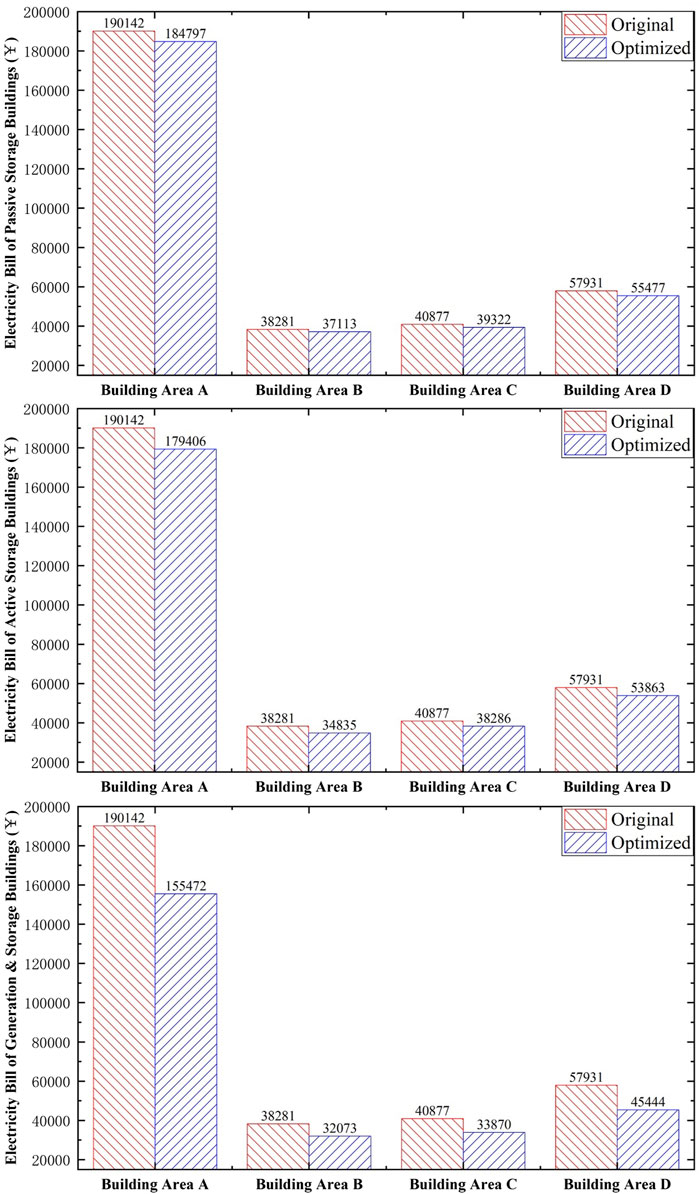
Figure 11 shows the electricity purchase cost of each building area under three different system conditions. For passive storage buildings, by sacrificing a certain degree of comfort, the peak energy consumption is reduced, and consequently, the electricity purchase cost is directly reduced by 3–4.4%. For active storage buildings, since the use of stored energy during peak periods reduces the demand for electricity, the cost of electricity purchases can be reduced, consider the increase in cost caused by excessive power purchase during the low electricity consumption period, the electricity bills of different area have been reduced by 5.5–8.8%. For generation & storage buildings, With the further improvement of building energy flexibility, peak electricity consumption has been greatly reduced, the total daily electricity purchase bill of the building decreased by 13.7–18%.

FIGURE 11

FIGURE 11. Total electricity bills of buildings with different systems.

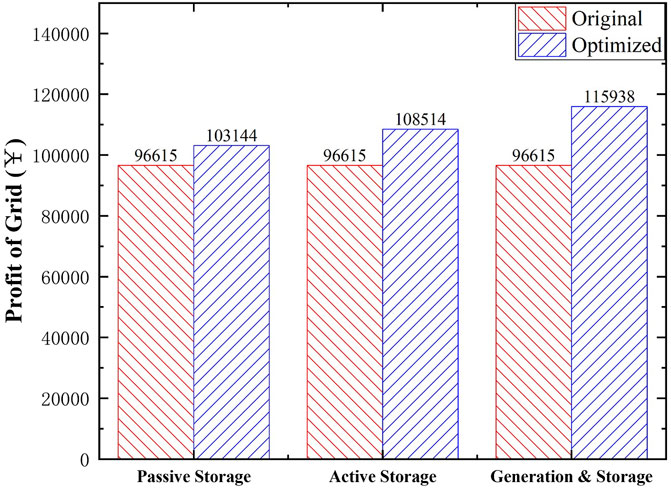
After adopting the hierarchical optimization method, although the direct sales revenue of smart grid will decrease because of the reduction of the building electricity purchase cost, the peak-to-valley difference is also significantly reduced due to building energy demand optimization, thereby effectively reducing the hidden costs caused by grid imbalance. As shown in Figure 12, the grid’s total income has increased by 8, 12.3, and 20%.

FIGURE 12

FIGURE 12. Comprehensive grid income when interacting with buildings with different systems.

Discussion

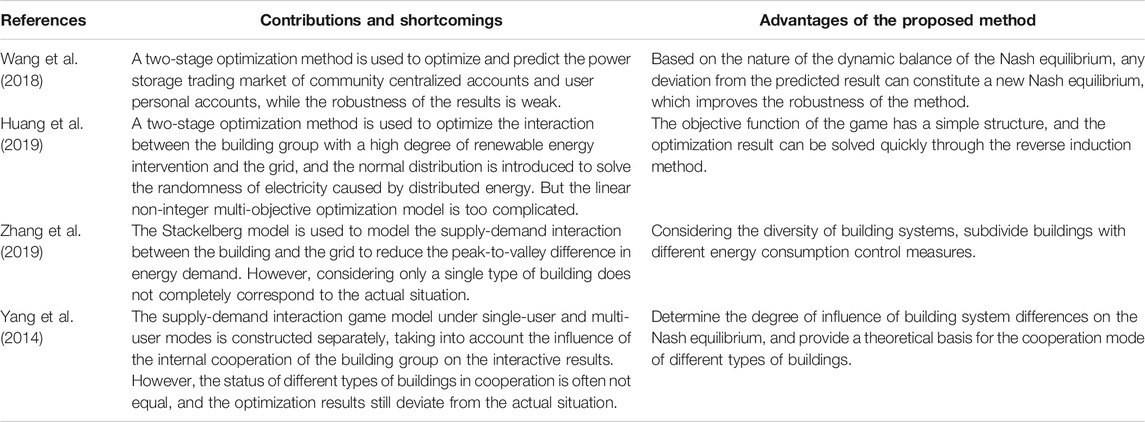
The effectiveness and advantages of the hierarchical optimization method proposed in this paper are discussed by comparing with several optimization methods that have been used in previous studies. References (Yang et al., 2014; Zhang et al., 2019) are selected for comparison of optimization methods based on game theory, and references (Wang et al., 2018; Huang et al., 2019) are introduced for comparison of two-stage optimization methods. The analysis details are shown in Table 3.

TABLE 3

TABLE 3. Methodological comparison.

Conclusion

A hierarchical demand optimization method based on game theory is proposed for achieving the optimal grid interaction between smart grids and energy flexible buildings. Considering the impact of the diversity of the EFB system on the outcome of the game, a case study of three types of buildings with different energy flexibilities is conducted. The following remarkable conclusions can be drawn.

1. Game theory can be used as an efficient mathematical tool to coordinate buildings with different energy flexibilities for effective interactions with smart grids. The Stackelberg model can be effectively used to identify the hierarchical game equilibrium in the economic competition between the power grid and buildings.

2. The effectiveness of the proposed method is quantitatively verified in a case study that consists of three typical energy flexible buildings in Hong Kong. Results show that the proposed hierarchical demand optimization method can consecutively reduce grid fluctuations by 30, 44, and 50% while increasing the comprehensive income of the grid by 8–20%; for the demand side (the EFB), peak demand is reduced by 6–22%, and electricity costs are reduced by 3–18%.

3. Building energy flexibility conditions have a significant impact on the decision-making and ultimate benefits in the game. During the demand side energy consumption optimization and result analysis, full consideration of the building system diversity can make the forecast results more accurate. Buildings with larger energy flexibility can have lower peak power demand, which will bring smaller fluctuations to the grid and occupy a more active position in the game with the grid. Compared with active storage and passive storage buildings, the electricity price of the generation & storage buildings with the strongest energy flexibility is reduced by 10–11.8% and 12.6–14% during the peak electricity consumption period, the whole-day electricity cost is reduced by 13 and 16% respectively.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization, CY; Data curation, JX; Investigation, YX; Methodology, CY; Writing-original draft, JX and YX; Writing-review and editing, JS and KS; Writing-review and data provision, XX.

Funding

The authors gratefully acknowledge the support of the National Key Research and Development Program of China (2018YFE0116300), the National Natural Science Foundation of China (No. 51708287), the Priority Academic Program Development of Jiangsu Higher Education Institutions, and a grant of the Qingdao Hisense Hitachi Air-conditioning Systems Co., Ltd., and Science and Technology Research and Development Project of CSCEC (No. CSCEC-2019-Z-3).

Conflict of Interest

JS and KS were employed by Qingdao Hisense Hitachi Air-conditioning Systems Co., Ltd. Contributed to the writing-review, editing of the paper, and provided funding for this research. XX is employed by the Second Construction Co., Ltd., China Construction Third Engineering Bureau. Contributed to the review of the paper, and provided data for this research.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arteconi, A., Mugnini, A., and Polonara, F. (2019). Energy Flexible Buildings: A Methodology for Rating the Flexibility Performance of Buildings with Electric Heating and Cooling Systems. Appl. Energ. 251, 113387. doi:10.1016/j.apenergy.2019.113387

CrossRef Full Text | Google Scholar

Basar, T., and Olsder, G. J. (1999). Dynamic Noncooperative Game Theory. London: Accademic Press. 30. doi:10.1016/0377-2217(95)90173-6

CrossRef Full Text

Chen, C., Pearlmutter, D., and Schwartz, M. (2019). Promoting green Building in Israel: A Game Theory-Based Analysis. Building Environ. 163, 106277. doi:10.1016/j.buildenv.2019.106227

CrossRef Full Text | Google Scholar

DoE (2014). Buildings Energy Databook. Washington, D.C.: Energy Efficiency & Renewable Energy Department.

Electrical and Mechanical Services Department of Hong Kong (2012). Hong Kong Energy End-Use Data. Available at: www.emsd.gov.hk/emsd/e_download/pee/HKEEUD 2012.pdf.

Google Scholar

Guo, S., Yang, H., Li, Y., Zhang, Y., and Long, E. (2019). Energy Saving Effect and Mechanism of Cooling Setting Temperature Increased by 1 °C for Residential Buildings in Different Cities. Energy and Buildings 202, 109335. doi:10.1016/j.enbuild.2019.109335

CrossRef Full Text | Google Scholar

Huang, P., and Sun, Y. (2019). A Collaborative Demand Control of Nearly Zero Energy Buildings in Response to Dynamic Pricing for Performance Improvements at Cluster Level. Energy 174, 911–921. doi:10.1016/j.energy.2019.02.192

CrossRef Full Text | Google Scholar

Huang, P., Xu, T., and Sun, Y. (2019). A Genetic Algorithm Based Dynamic Pricing for Improving Bi-directional Interactions with Reduced Power Imbalance. Energy and Buildings 199, 275–286. doi:10.1016/j.enbuild.2019.07.003

CrossRef Full Text | Google Scholar

Huang, Z., Yu, H., Peng, Z., and Feng, Y. (2017). Planning Community Energy System in the Industry 4.0 Era: Achievements, Challenges and a Potential Solution. Renew. Sustain. Energ. Rev. 78, 710–721. doi:10.1016/j.rser.2017.04.004

CrossRef Full Text | Google Scholar

Jensen, S. Ø., Marszal-Pomianowska, A., Lollini, R., Pasut, W., Knotzer, A., Engelmann, P., et al. (2017). IEA EBC Annex 67 Energy Flexible Buildings. Energy and Buildings 155, 25–34. doi:10.1016/j.enbuild.2017.08.044

CrossRef Full Text | Google Scholar

Jian, Y., and Wang, R. (2010). Comparative Study of Software thermal Model Affecting Load Calculation Results[J]. J. Beijing Univ. Technol. (12), 53–58.

Google Scholar

Kusakana, K., and Vermaak, H. J. (2014). Hybrid Diesel Generator/renewable Energy System Performance Modeling. Renew. Energ. 67, 97–102. doi:10.1016/j.renene.2013.11.025

CrossRef Full Text | Google Scholar

Lai, A., Leung, M. K., Yau, R., and Ng, E. (2013). Hong Kong First Zero Carbon Building: Design Principles, Features and Technologies. In: PLEA2013 - 29th Conference, Sustainable Architecture for a Renewable Future, Munich, Germany 10-12 September 2013.

Li, H., and Wang, S. (2020). Model-based Multi-Objective Predictive Scheduling and Real-Time Optimal Control of Energy Systems in Zero/low Energy Buildings Using a Game Theory Approach. Automation in Construction 113, 103139. doi:10.1016/j.autcon.2020.103139

CrossRef Full Text | Google Scholar

Liang, P., Zhang, S., Xu, L., and Li, Y. (2020). Thermal Performance Optimization and Evaluation of a Redial Finned Shell-And-Tube Latent Heat thermal Energy Storage Unit. Appl. Therm. Eng. 166, 114753. doi:10.1016/j.applthermaleng.2019.114753

CrossRef Full Text | Google Scholar

Lüth, A., Zepter, J. M., Crespo del Granado, P., and Egging, R. (2018). Local Electricity Market Designs for Peer-To-Peer Trading: The Role of Battery Flexibility. Appl. Energ. 229, 1233–1243. doi:10.1016/j.apenergy.2018.08.004

CrossRef Full Text | Google Scholar

Lv, T., and Ai, Q. (2016). Interactive Energy Management of Networked Microgrids-Based Active Distribution System Considering Large-Scale Integration of Renewable Energy Resources. Appl. Energ. 163, 408–422. doi:10.1016/j.apenergy.2015.10.179

CrossRef Full Text | Google Scholar

Najafi-Ghalelou, A., Zare, K., and Nojavan, S. (2018). Optimal Scheduling of Multi-Smart Buildings Energy Consumption Considering Power Exchange Capability. Sustain. Cities Soc. 41, 73–85. doi:10.1016/j.scs.2018.05.029

CrossRef Full Text | Google Scholar

Reynders, G., Amaral Lopes, R., Marszal-Pomianowska, A., Aelenei, D., Martins, J., and Saelens, D. (2018). Energy Flexible Buildings: An Evaluation of Definitions and Quantification Methodologies Applied to thermal Storage. Energy and Buildings 166, 372–390. doi:10.1016/j.enbuild.2018.02.040

CrossRef Full Text | Google Scholar

Saad, W., Han, Z., Poor, H., and Basar, T. (2012). Game-theoretic Methods for the Smart Grid: an Overview of Microgrid Systems, Demand-Side Management, and Smart Grid Communications. IEEE Signal. Process. Mag. 29, 86–105. doi:10.1109/msp.2012.2186410

CrossRef Full Text | Google Scholar

Srinivasan, D., Rajgarhia, S., Radhakrishnan, B. M., Sharma, A., and Khincha, H. P. (2017). Game-Theory Based Dynamic Pricing Strategies for Demand Side Management in Smart Grids. Energy 126, 132–143. doi:10.1016/j.energy.2016.11.142

CrossRef Full Text | Google Scholar

Tang, R., Wang, S., and Li, H. (2019). Game Theory Based Interactive Demand Side Management Responding to Dynamic Pricing in price-based Demand Response of Smart Grids. Appl. Energ. 250, 118–130. doi:10.1016/j.apenergy.2019.04.177

CrossRef Full Text | Google Scholar

Wang, D., Qiu, J., Reedman, L., Meng, K., and Lai, L. L. (2018). Two-stage Energy Management for Networked Microgrids with High Renewable Penetration. Appl. Energ. 226, 39–48. doi:10.1016/j.apenergy.2018.05.112

CrossRef Full Text | Google Scholar

Wang, S. (2016). Making Buildings Smarter, Grid-Friendly, and Responsive to Smart Grids. Sci. Technol. Bulid. Environ. 22 (6), 629e632. doi:10.1080/23744731.2016.1200888

CrossRef Full Text | Google Scholar

Xu, Y., Yan, C., Liu, H., Wang, J., Yang, Z., and Jiang, Y. (2020). Smart Energy Systems: A Critical Review on Design and Operation Optimization. Sustain. Cities Soc. 62, 102369. doi:10.1016/j.scs.2020.102369

CrossRef Full Text | Google Scholar

Yan, C., Wang, F., Pan, Y., Shan, K., and Kosonen, R. (2020). A Multi-Timescale Cold Storage System within Energy Flexible Buildings for Power Balance Management of Smart Grids. Renew. Energ. 161, 626–634. doi:10.1016/j.renene.2020.07.079

CrossRef Full Text | Google Scholar

Yang, J., Zhang, G., and Ma, K. (2014). Matching Supply with Demand: A Power Control and Real Time Pricing Approach. Int. J. Electr. Power Energ. Syst. 61, 111–117. doi:10.1016/j.ijepes.2014.03.014

CrossRef Full Text | Google Scholar

Yang, P., Tang, G., and Nehorai, A. (2013). A Game-Theoretic Approach for Optimal Time-Of-Use Electricity Pricing. EEE Trans. Power Syst. 28 (2), 884. doi:10.1109/tpwrs.2012.2207134

CrossRef Full Text | Google Scholar

Zhang, X., Gao, G., Zhang, Z., and Yang, L. (2019). Demand Response-Based Optimal Dispatching of Building Integrated Energy System. Power Demand Side Manage. 4, P28–P34.

Google Scholar

Zhao, X. (2001). Nature of Nonlinear Cournot Model and Stackelberg Model. CNKI:SUN:JSDN.0. 2001-03-001. J. Jishou Univ (Nat. Scie. Ed.).

Zhong, J., Ju, X., and Lu, Y. (2016). Distributed Renewable Energy Building Application Development Path and Policy Guidance. Bull Chin Acad Sci. 31, 2. doi:10.16418/j.issn.1000-3045.2016.02.008

CrossRef Full Text

Glossary

${\alpha }_i$ preset coefficient of the building i user’s acceptance of dissatisfaction.

a, b, c Preset constants that affect the cost of power generation

${\rho }_i$ preset parameter describing the transfer cost level of the building i demand

${\lambda }_i$ Lagrange multiplier

$q_{i,k}^b$ the original power demand of the building $i$ at time $k$

$S_i^k$ user dissatisfaction at time $k$ of the building i

$P{r}^k$ dynamic electricity price at time $k$.

∅ value range of building strategy

$Q$ decision value of building demand

$P$ value range of grid strategy

$U_{grid}$ grid revenue

$Q_{min}$, $Q_{max}$ value range of energy consumption under the rules

$q_{i,k}^t$ demand of the building $i$ affected by the change of the air-conditioning preset temperature at time $k$

$q_{i,k}^d$ the optimized power demand of the building $i$ at time $k$

$D_i^k$ building mismatch cost at time $k$ of the building $i$

$B_i^k$ power purchase cost of the building $i$ at time $k$

$U_{building}$ building revenue

$Q^{\text{∗}}$ optimal decision value of building demand under Nash equilibrium

$P{r}^{\text{∗}}$ optimal decision value under Nash equilibrium

$R^N$ complete set of strategies

$Q\left(Pr\right)$ building demand in response to electricity prices.

$q_{i,k}^r$ distributed energy production capacity at the time $k$ of the building $i$

EFB Energy Flexible Building

IEA International Energy Agency

DN Day and Night Price

TOU Time-of-use Price

RTP Real-time Prices.