Long-Term Global Solar Radiation Prediction in 25 Cities in Morocco Using the FFNN-BP Method

This article presents different combinations of input parameters based on an intelligent technique, using neural networks to predict daily global solar radiation (GSR) for twenty-five Moroccan cities. The collected measured data are available for 365 days and 25 stations around Morocco. Different input parameters are used, such as clearness index K_T, day number, the length of the day, minimal temperature T_min, maximal temperature T_max, average temperature T_average, difference temperature $\Delta T$, ratio temperature T-Ratio, average relative humidity RH, solar radiation at the top outside atmosphere TOA, average wind speed Ws, altitude, longitude, latitude, and solar declination. A different combination was employed to predict daily GSR for the considered locations in order to find the most adequate input parameter that can be used in the prediction procedure. Several statistical metrics are applied to evaluate the performance of the obtained results, such as coefficients of determination (R²), mean absolute percentage error (MAPE), root mean square error (RMSE), normalized root mean square error (NRMSE), mean bias error (MBE), test statistic (TS), linear regression coefficients (the slope “a” and the constant “b”), and standard deviation (σ). It is found that the usage of input parameters gives highly accurate results in the artificial neural network (FFNN-BP) model, obtaining the lowest value of the statistical metrics. The results showed the best input of 25 locations, 12 inputs for Er-Rachidia, Marrakech, Medilt, Taza, Oujda, Nador, Tetouan, Tanger, Al-Auin, Dakhla, Settat, and Safi, seven inputs for Fes, Ifrane, Beni-Mellal, and Meknes, six inputs for Agadir and Rabat, five inputs for Sidi Ifni, Essaouira, Casablanca and Kenitra, four inputs for Ouarzazate, Lareche, and Al-Hoceima. In terms of accuracy, R² of the selected best inputs parameters varies between 0.9860% and 0.9920%, the range value of MBE (%) being from −0.1076% to −0.5931%, the RMSE between 0.1990 and 0.4580%, the range value of the NRMSE between 0.0355 and 0.8938, and the lowest value MAPE between 0.0019 and 0.0060%. This technique could be used to predict other parameters for locations where measurement instrumentation is unavailable or costly to obtain.

Introduction

In the last decade, energy demand has been growing internationally, with the rise in population growth and economic development. Thus, it becomes essential for the fulfillment of economic prosperity (Khan et al., 2016). Lately, the installed capacity of renewable energy has undergone a significant increase, reducing dangerous residues or the emissions of fossil fuel (Sayigh, 2017). All communities call for energy resources that fulfill essential needs, such as wellness, heating, eating, room comfort, accessibility, and connectivity and function as conceptual processes (Owusu and Asumadu-Sarkodie, 2016). Renewable energy, such as solar energy, wind energy, thermal energy, and hydroelectric energy, is widely accepted as the key tool for global sustainable economic development. Likewise, there seem to be two fundamental reasons behind the focus on sustainable energy: one is deforestation and global climate change, and the other is the possibility that fossil fuels will inevitably dry up and there will be no more oil, gas, and coal. That could also be said about nuclear energy since nuclear fuel stocks are not limitless (Kumar and Kumar, 2017).

Solar photovoltaic technology is gaining importance when it comes to addressing the issue of energy development for a number of reasons: the potential to transform solar radiation directly into power, the low cost, and the decreased pollution (Yu et al., 2017). In addition, the growth of the renewable energy industry thus produces new employment opportunities and contributes to improvement in air quality. However, the installation of solar electricity, such as photovoltaic (PV), concentrated solar power (CSP), or hybrid PV thermal installations, involves high-quality, decade-long time series of solar radiation data (Polo et al., 2020; Belmahdi and Bouardi, 2020). The long-term variability of solar radiation plays a major role in predicting the risk of the potential electricity production of a solar power plant being surpassed or unachieved and impacts the financial incentives that the project is expected to achieve. In this context, the information and behavior of solar radiation are very important for many sectors, such as agriculture, architect, design, and technology (Owusu and Asumadu-Sarkodie, 2016; Kaba et al., 2018). Generally, solar radiation energy has two components: terrestrial global and extraterrestrial solar energy (Rahimikhoob, 2010). The terrestrial solar radiation has direct (H_b) and diffuse (H_d) components. The sum of Hb*cosθ and H_d represents the global solar radiation (H_g); θ is the zenith angle. The measurement of energy use among houses, the development of heating ventilation and air-conditioning systems, and the use of solar energy need appropriate H_g data (Zhao et al., 2019; Liu et al., 2018). In particular, both direct and diffuse components are required to receive solar radiation on a slanted surface (Muneer et al., 2007). The best method for collecting data regarding solar radiation is focused on observations employing adequate equipment, but the measurements are rather time-consuming, the costs are high and the weather stations installation and management are demanding. For example, since 2019, there have been 17 cities in China where H_g and H_d, respectively, have been calculated (Feng et al., 2018) and 20 cities in Morocco where the solar radiation and other parameters have been collected through the project “proper.ma” (Aarich et al., 2018). In particular, there are challenges regarding long-term background measurement data, such as station changes and incomplete observations. However, the estimation and prediction of global solar radiation play a very important role. Several models have been developed in the literature to estimate and predict global solar radiation, which means it is difficult to choose the most accepted and efficient model for a particular use. In research areas, various solar radiation models have been developed for several years and they are categorized into three major models: empirical or analytical models, machine learning models, which use computational intelligence techniques, and satellite remote sensing models, as reported in Yang et al. (2020). Among all the presented models, all researchers have agreed on the importance of the results given by the Artificial Neural Network (ANN) (Kashyap et al., 2015; Al-Dahidi et al., 2019). The ANN was reported as the most used artificial intelligence technique for the prediction in several fields (Kashyap et al., 2015; Jiang, 2009). Celik and Muneer have presented and interpreted the relationship between solar radiation and other climatic parameters of the location selected (Celik and Muneer, 2013).

Generally, the ANN is the most used technique for the forecast or estimation of several things. For example, in Turkey, Sözen et al. (2004) have used the simple ANN to predict the solar radiation intensity using various parameters, such as latitude, longitude, altitude, month’s number, average sunshine duration, and average temperature. The measurement data were collected from 17 different weather stations, where measurement data from 11 stations for training algorithm and other six measurement data are used for testing. In a different review, the same neural networks were used to predict the solar potential for 12 weather stations from Turkey. The performance of the results is validated by calculating the value MAPE = 6.78% and R² = 99.78% (Sözen et al., 2005). Sharifi et al. (2016) have implemented the feedforward neural network (FFNN) with four inputs in one hidden layer, one output layer, and Levenberg–Marquardt as a training algorithm. Using data from six stations, they have estimated the daily global radiation for two different countries, Iran (Tabriz and Urmia) and the United States (Grand Island, North Platte, Lincoln, and Scottsbluff). The used inputs are the daily mean clearness index (K_T), range temperature (ΔT), theoretical sunshine duration (N), and extraterrestrial radiation (R_a). The accuracy of the developed model was tested in terms of the average median absolute error (MAE = 7.4%), root mean square error (RMSE = 9.8%), and U95 = 27.35%. In Oman, Al-Alawi and Al-Hinai (1998) have used the FFNN with backpropagation training algorithm to predict global solar radiation. Eight input layers were implemented in ANN, namely, location, month, mean pressure, temperature, vapor pressure, relative humidity, wind speed, and sunshine duration. The accuracy of the results was tested by Mean Absolute Percentage Error percentage (MAPE) with 7.3%. In Morocco, Bounoua et al. (2021) have used the neural network method, 22 empirical models, and tree-based ensemble methods to estimate the daily GSR in five studies locations. In terms of accuracy, the proposed methods were evaluated using R², NRMSE, and NMAE. As a result, the random forest method outperforms the other techniques with the highest value of R² and lowest value of NRMSE and NMAE.

In China, Lam et al. (2008) have applied the multi-layer FNN (MLFFNN) to estimate the daily global solar radiation using measured sunshine duration for 40 cities covering nine major thermal climatic zones and sub-zones in China. Six input layers were used: latitude, longitude, altitude, day number, temperature, and sunshine ratio. The quality of the estimated results was verified by the calculation of the statistical performance. The MBE values vary between 16.9% underestimation to 18.6% overestimation, and RMSE values vary in the range from 9.1 to 20.5%. In another paper, in Zimbabwe, Chiteka and Enweremadu (2016) have implemented the FFANN to predict the global horizontal irradiation (GHI) using geographical and meteorological data for 20 locations. 12 locations were used in the ANN training algorithm and other data from eight locations were included in the simulation with seven inputs, namely, altitude, latitude, longitude, relative humidity, pressure, clearness index, and average ambient temperature, one hidden layer, and one input layer. The quality of the predicted results is carried out by calculating the performance indexes such as coefficient of determination R², RMSE, MAE, and MAPE with the following values 99.894%, 0.223 Kwh/m², 0.17 Kwh/m², and 2.56%, respectively.

In Italy, Alsina et al. (2016) have applied the FFNN to forecast the monthly average daily global solar radiation (MDGSR) for 45 different locations. Different input parameters were taken into account, such as meteorological and geographical coordinates. The measurement data from 17 destinations have been used for training, whereas other collected data have been for testing the ANN. The most appropriate input parameters are the automatic relevance determination (ARD) and Bayesian method. The appropriate architecture of the suggested ANNs contained seven input parameters, i.e., TOA, duration of day, number of rainy days, average temperature, latitude, and altitude. The quality and accuracy of the model were tested and validated by calculating the MPE, which varied from 1.67 to 4.25%, NRMSE 1.01–1.65%, and MPBE from -0.20 to 0.03%.

In Spain, Hontoria et al. (2005) have implemented MLP to predict the solar radiation map. This study collected the measurement data from seven different lections. The aim was to generate a time series of hourly solar radiation using specific characteristics, such as temperature and latitude. In other articles in Egypt, Elminir et al. (2007) have proposed two kinds of ANN to predict the hourly and daily diffuse solar radiation using the Multi-Layer Perceptron (MLP) with backpropagation training algorithm. A different type of parameters is selected for the input of the ANN, such as hour, day, month, year, hourly global radiation, and hourly extraterrestrial solar radiation, and the output was the hourly diffuse radiation. On the other hand, three different inputs were considered input layers of the neural network, namely, global solar radiation, extraterrestrial solar radiation, and sunshine ratio for predicting daily diffuse solar radiation. The results of the study using the ANN model were compared with those of the linear regression models and were used for the models on the hourly and daily scales. In both, the ANN results are more accurate in predicting diffuse solar radiation. In India, Alam et al. (2006) have implemented the feedforward backpropagation network (FFBPN) to predict the solar radiation, and the selected inputs were the latitude, longitude, attitude, months of years, rainfall ration, mean duration of sunshine per hour, and ratio of relative humidity. The performance of the predicted results was calculated using the RMSE = 1.65% and MBE = 2.79%. Mehleri et al. (2010a) have used the neural network radial basis function (NNRBF) to predict solar radiation on the inclined surface by applying the optimum angle for a specific site. The NNRBF used the tilted angle and orientation as input and fuzzy logic for the training algorithm. The accuracy of the results was validated by calculating the coefficient of determining R² = 99.99%. In another study, the same researchers have used the RBFNN to predict the solar radiation on inclined surfaces and total solar irradiance on a horizontal surface. The extraterrestrial radiation, solar zenith angle, and solar incidence angle on a tilted plane are considered input data for Athens, Greece. The performance of the results is validated by the R² = 96%. On the other hand, three different ANN models were developed in Ajaccio, France, by Notton et al. (2012) to predict the hourly solar radiation on an inclined surface for Mediterranean locations. Different parameters were chosen as inputs: the declination angle, hour, zenith angle, hourly extraterrestrial horizontal irradiation, and hourly global irradiation. The first and second models of ANN predicted the hourly global solar radiation for two angles 45° and 60° and the third model for angles 45° and 90°. The obtained results showed that R² in the three models is equal to 99.79%, 99.82%, and 99.70%, respectively. Moreover, Celik and Muneer (2013), in Iskenderun, Turkey, have adopted a model using the generalized regression neural networks (GRNN) to estimate the solar radiation on an inclined surface. Three parameters are used here as input data: global solar irradiation on a horizontal surface, declination, and hour angles. The accuracy of the results is validated by R² for evaluated values as 98.7% at 14.9 kwh/m².

In Algeria, a simplified hybrid model was developed by Gairaa et al. (2016) using the linear autoregressive moving average (ARMA) model combined with ANN to predict the daily global solar irradiation using measurement data from two locations. The input of the proposed model is the clearness index, while the output is the daily global solar radiation. The calculated performance error metrics were MPE = 18.1 and 2.7% for the first location and MAPE = 7.26 and 1.39% for the second locations. In another publication in the same country, Mellit et al. (2005) have combined the ANN with Markov transition matrix (MTM) to predict daily global solar radiation. The output data were the daily global solar radiation and the geographical coordinates, such as latitude, longitude, and altitude, were the input data of the neural network layer. The performance of the hybrid ANN-MTM model was calculated to verify the accuracy of the predicted results and was given as RMSE = 8%, R² varying in the range of [0.9 0.92] (Belmahdi et al., 2020a).

According to the cited references above, there are various applications of the ANNs to predict/estimate or forecast global solar radiation in different locations and angles. Here, we can cite the predicted solar radiation at the horizontal and tilted surface: different meteorological and geographical coordinates have been considered by multiple authors, e.g., latitude, longitude, altitude, wind speed, clearness index, air temperature, sunshine duration, top of atmosphere (TOA) radiation, and rainfall. Table 1 illustrates the most often used input parameters in ANNs categorized into geographic coordinates and climatologic parameters.

TABLE 1

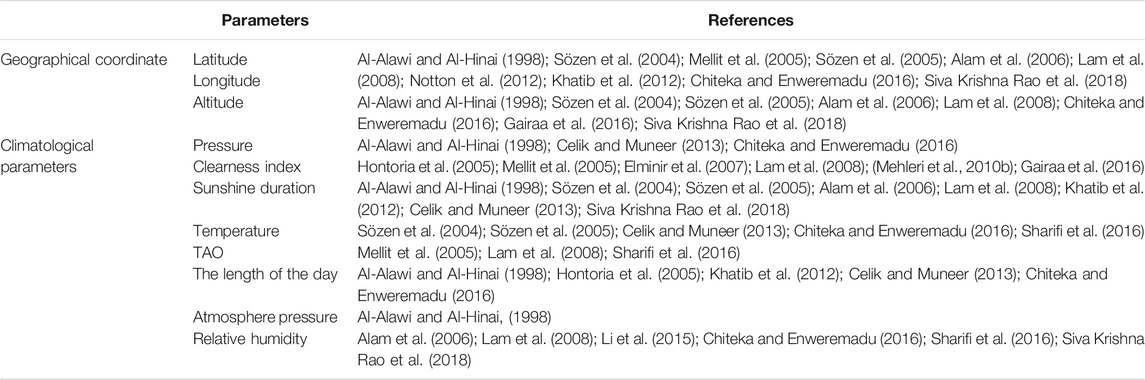
TABLE 1. Current parameters adopted in the literature to predict and estimate global solar radiation.

In this context, this research is specifically intended to suggest an intelligent paradigm for evaluating and identifying the appropriate input possibilities that can include the highest potential correlations and simplifications with this proposed study, relying on the fact that predictions of solar radiation can be enhanced with ANN models using different input parameters, e.g., location, weather information, and neighboring stations, and other input parameters. According to Yadav and Chandel (2014), the solar radiation predicted by ANNs is correct compared to that by empirical models. Moreover, the ANNs have different single layers, FFBP, or combined with other techniques, and the second is the most widely used in solar radiation. It has forward relations between inputs and outputs across various hidden layers. The main contribution of this study is to investigate and predict daily global solar radiation based on various combination inputs for 25 cities in Morocco. In fact, relying on the FFNN-BP methods, the suggested method would promote correlations among all feasible input configurations in order to select the best input parameters that can provide better results with the lowest values of statistical indicator performance, which present a good approximation with measured data.

Meteorological Climate in Morocco

Morocco has a wonderful opportunity to access sustainable energy options that will address two of the burning issues in the country: electricity availability and global warming challenges. Generally, Morocco has a powerful capacity in sustainable resources, primarily solar and wind, with the potential level of generation varying from 20,000 to 25,000 MW (Šimelytė et al., 2020; Belmahdi and El Bouardi, 2020). On a world wide scale, Morocco holds the sixth rank for solar and the seventh place for wind. The average daily value of solar radiation intensity in Morocco is close to 5.80 kWh/m²/day. Meanwhile, Morocco has many sustainable energy programs being implemented and one of the biggest solar energy programs in the world is expected to cost $7.8 billion. This innovative and practical national effort focuses on creating a potential of 2,000 MW by 2020. This generation capacity constitutes 38% of mounted energy by the end of 2008 and 14% of electrical power by 2020.

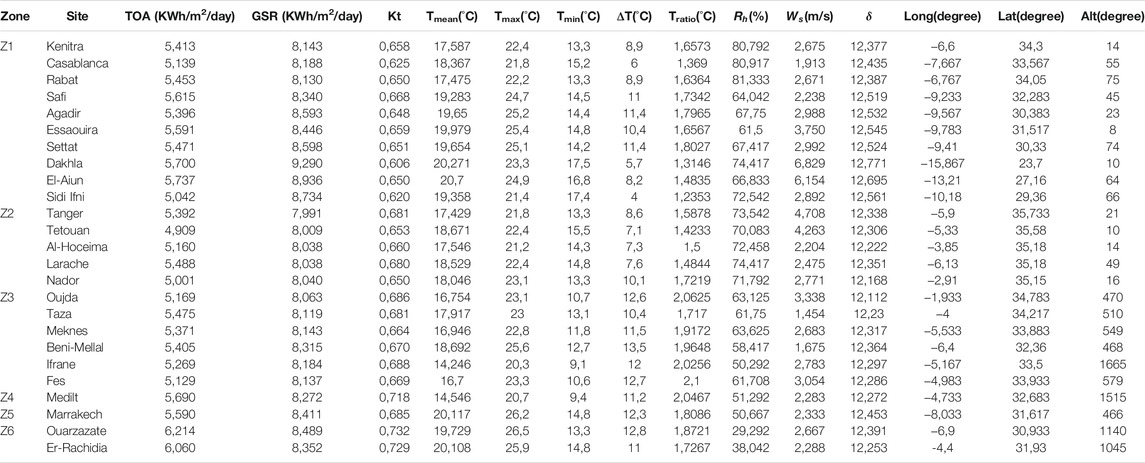
In this context, it is necessary to analyze and predict the solar radiation behavior for all considered locations in Morocco. The solar radiation depends on and is affected by various parameters, such as altitude and longitude. However, this research aims to present data for 25 various regions with different climatic conditions and geographical features prevalent in all parts of Morocco. The locations are divided to six zones characterized by the following parameters: the latitude varies from 23,7° to 35,733° and the longitude varies from −15,867° to −2,91°, whereas the altitude varies from 8 to 1665 m. Table 2 presents the average data of the 25 locations and geographical coordinates.

TABLE 2

TABLE 2. Average data of 25 locations and geographical coordinates.

Morocco's climate is both Mediterranean and Atlantic, varying from dry to hot season combined with a cool and rainy season. The influence of the sea modulates temperature differences, tempers seasons, and raises the humidity of the environment. Bouhal et al. (2018) and Allouhi et al. (2015) have presented Morocco in six different zones adopted according to the Moroccan Agency for Renewable Energies and Energy Efficiency for concentrated solar power use, as presented in Figure 1.

FIGURE 1

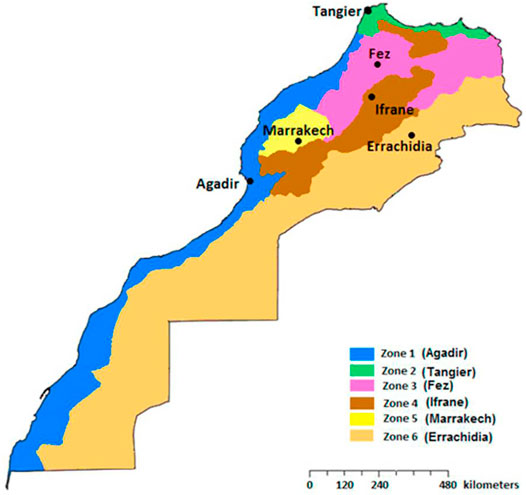
FIGURE 1. Climatic zoning of Morocco [adapted from National Agency for the Development of Renewable Energy and Energy Efficiency (ADEREE)].

Artificial Neural Networks

The application of the ANN has gained growing interest in recent years to address several real-world problems. It has been widely used to address several difficult issues where conventional issue approaches either struggled or proved to be ineffective or unsuccessful (Kamruzzaman et al., 2006). ANN is widely used in various fields, such as solar energy, wind (Tagliaferri et al., 2015), electricity (Khwaja et al., 2020), mechanics (Sterjovski et al., 2005), astrophysics (George and Huerta, 2018), partial differential equations (ShekariBeidokhti and Malek, 2009), polymers (Amirian et al., 2018; Kaplan, 2018) or in optimization, control, modeling, and solar radiation forecasting (Belmahdi et al., 2020b).

The neural network structure schematically mimics a human brain network, containing thousands of neurons that are specifically linked to each other. Throughout the biological context, the neuron receives a variety of inputs from other inputs and integrates them in some direction. Every other neuron is responsible for performing basic computation only. Meanwhile, the effects of the procedure are usually nonlinear, and the output is the final product. In either scenario, the configuration of an artificial neuron is easier than a biological neuron (Pacheco-Vega et al., 2001; Kamruzzaman et al., 2006). In addition, the complex architecture of the biological neural networks translates the area of the ANN. Feedforward ANNs (FF-ANNs) are formed through recurring ANNs and repeated ANNs, like feedback loops (Yalçın et al., 2020). The FNNs are those ANNs with only single-way interactions between their neurons (Bebis and Georgiopoulos, 1994).

The ANNs are considered in the research area as data-driven models (Chakraborty et al., 1992; Boland et al., 2001; Durna and Şahin, 2020) and consist of two layers considered as input and output: the first is to receive the data, while the second is the hidden layer displaying the simulated results (Yalcintas and Akkurt, 2005). The hidden layer also learns, memorizes, and creates relationships between output and input data (Moreno et al., 2011). Generally, the ANN training mechanism is related by changing the weights of every connection. The connection between the neural network layer may be investigated by weighting coefficients (w) and bias (B) for increasing processor and activation function, such that the network tries to generate the optimal performance close to the real performance, as illustrated in Figure 2 (Yilmaz and Özer, 2009).

FIGURE 2

FIGURE 2. Structure architecture of an MLP neural network.

Following the initial training phase, performance can be viewed as network integration and it is important to follow a backpropagation (BP) appropriate learning algorithm to minimize the errors during the simulation (Riahi-Madvar et al., 2011). The main objective of using the BP algorithm method is to reduce the size of a network error. The BP based on gradient descent can be calculated by the following equation (Al-Alawi and Al-Hinai, 1998):

$e=0.5{\displaystyle \sum _{k=1}^N{\left(O_k-t_k\right)}^2},(1)$

where N represents the number of processors, $O_k$ is the output result in the K-th processor, and $t_k$ denotes the target values.

In the BP algorithm, there are two steps of the training process: one to reproduce the input signal across the network and the other to follow the output by adjusting the weights in the network. Those are the error indicators that are back-spread to the hidden layer(s) throughout the network operation. The output layer error is being used as the basis for correcting the relation weights between both the origin and the hidden layers (Khare and Nagendra, 2007). The modification of both the relation weights between the input and the hidden layers and the corresponding recalculation of the output values will once more be a small sensitivity point since the iterative procedure is carried out before the error decreases. The BP training algorithm begins by copying and pasting the simulation data collection to the network, and the simulation data collection is made up of input and output vectors. Once certain vectors are dynamically introduced to the neural network, the following equations are implemented:

$Z_j={\displaystyle \sum _{ij}{W}_{ij}\left(X_i+b_j\right),i=\mathrm{1,2},\mathrm{....}n;j=\mathrm{1,2},\mathrm{....}h},(2)$

where Z_j represents the input to the j-th hidden layer neuron, X_i is the numerical value of the i-th input vector, W_ij is the weight of the i-th input layer neuron to the j-th hidden layer neuron, n and h represent the number of the input and hidden layer neurons, respectively, and b_j is the bias value for the j-th hidden layer neuron.

The function in the output of the hidden layer using the sigmoid function is determined as follows:

$h_j=f\left(Z_j\right)=\frac{1}{1+e^{-Z_j}},j=\mathrm{1,2},\mathrm{....}h,(3)$

with f representing the transfer function for the hidden layer.

In addition, the performance of the network will not be equivalent to the target performance during the training process. Consequently, the output error is measured as the difference between the output and the desired input of the network. If the output error does not reach the acceptable level, the network adjusts the interaction weights according to the output error significance; instead, the training data are re-entered to the network and the output of the network is determined (Battiti, 1992). The training process will proceed until the network reaches the optimal degree of tolerance. If the error value is below the tolerance range, the network should become a “qualified” network (Haykin, 1988). Then, BP algorithm is outlined in the following seven steps:

1) Initialize the network weights.

2) Analyze the first input vector from the training data and present it to the network.

3) Propagate the input vector across the network to get an output.

4) Determine the error by calculating the difference between the output and the input.

5) The error will be propagated back to the network.

6) Change the weights to eliminate the cumulative error.

7) Repeat steps (2) to (7) for the next input vector until those errors are satisfactorily minimal.

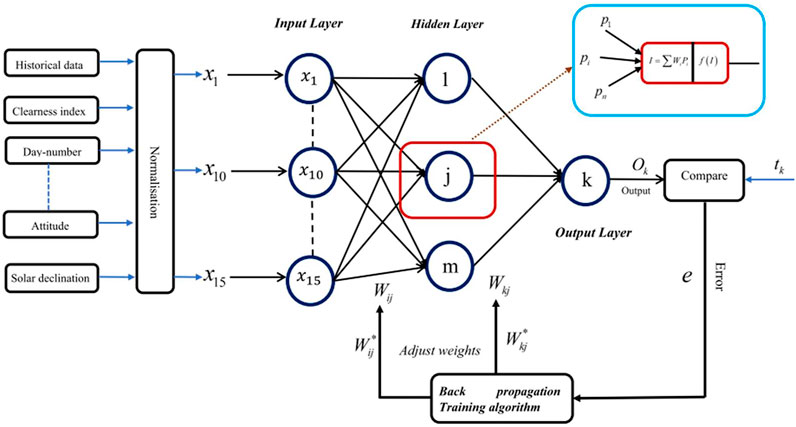
The BP algorithm includes two adaptive variables, a learning rate η and a moment term μ, which will improve the training method by eliminating the local minimum. η identifies the measure provided along the iterative gradient of descent learning method, and μ is used to encourage the gradient descent operation because it is trapped to a local minimum. Figure 3 depicts the FFNN with a backpropagation algorithm structure.

FIGURE 3

FIGURE 3. Structure of FFNN with backpropagation algorithm.

The definition “feedforward” implies that a neuron association occurs either from the neurons in the input layer to other neurons in the hidden layer or from the neurons in the hidden layer to the neurons in the output layer, and the neurons inside the layer are not interconnected.

Prediction Model Architecture

The described FFNN-BP model is implemented to predict the daily global solar radiation in 25 different Moroccan cities (El Mghouchi et al., 2016; El Mghouchi et al., 2019). The FFNN-BP model operates with the monitoring of the learning approach and the Levenberg–Marquardt training algorithm, as illustrated by Al-Alawi and Al-Hinai (1998). The training step is the most important and essential aspect of the neural network. The training algorithm is used to adopt and fix the ANNs by training and changing the weight to find the accurate output (Sözen et al., 2005). The used structure of the FFNN-BP model is shown in Figure 4.

FIGURE 4

FIGURE 4. Structure of used FFNN-BP model.

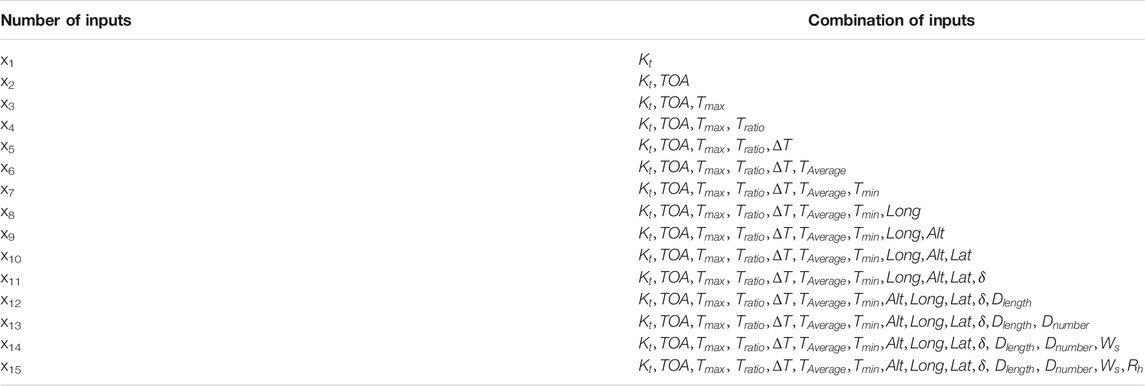
The data collected across different locations were separated into “training dataset” and “validation dataset” and were rendered taking into account weather conditions. The FFNN-BP model used 15 input data organized in the following vector as input parameters:

$X=\left[x_1{x}_2\cdots \cdots x_{15}\right].(4)$

Table 3 presents the vector X input variable of the network. While the ten neurons are used in one hidden layer, they are followed by one output layer. At the first step, we used the data collected from station 1 for 1 year for neural network training, which offered 365 pairs of input and outputs for training when the neural network started the training process. It is noticed that some error function was well-defined until the training process described in Eq. 1 approaches a minimum value. After this step, the predicted model was used for testing, where the data from a similar station are used.

TABLE 3

TABLE 3. Climatological and geographical parameters.

Some of the 15 input parameters used and computed are as follows: sun declination δ, the length of the day D_length, TOA, and $K_t$. They are calculated using the given formulas in the literature by the following equations (Belmahdi et al., 2020b; Rajendran and Smith, 2016):

$\delta =23.45\sin \left[0.986\left(N+284\right)\right],(5)$

$D_{length}=24\left[1-{\cos }^{-1}\left[\tan \left(\delta \right).\tan \left(\lambda \right)./\pi \right]\right],(6)$

$TOA={\int }^{day}{I}_0{E}_0\sin \left(h\right)dt,(7)$

$Kt=\frac{DGSR}{TOA},(8)$

where N represents the Julian day, λ is the longitude, I₀ is the solar constant, h is the solar elevation, and E₀ is the correction of the Earth–Sun distance.

In order to test the quality and the performance of the used FFNN-BP model, we propose to calculate and compare several errors metrics. These error metrics are widely used in the research area to test the validity and accuracy of the results, like in photovoltaics (Al-Dahidi et al., 2019; Louzazni et al., 2020). In this article, the error metrics are organized into two categories, as given by Gueymard (2014). The details about the error metrics are mentioned in the following equations:

1) Indicators of dispersion

Mean bias error (MBE)

$MBE=\frac{1}{K}{\displaystyle \sum _{i=1}^K\left(G_{forcast,i}-G_{\exp ,i}\right)}.(9)$

Root mean square error (RMSE)

$RMSE=\sqrt{\frac{1}{K}{\displaystyle \sum _{i=1}^K\left(G_{forcast,i}-G_{\exp ,i}\right)}}.(10)$

Normalized root mean square error (NRMSE)

$NRMSE=\sqrt{\frac{1}{K}{\displaystyle \sum _{i=1}^K\left(G_{forcast,i}-G_{\exp ,i}\right)}}/\frac{1}{K}{\displaystyle \sum _{i=1}^K{G}_{{\exp }_{,i}}}.(11)$

Mean absolute percentage error (MAPE)

$MAPE=\frac{100}{K}{\displaystyle \sum _{i=1}^K\left|\frac{G_{forcast,i}-G_{\exp ,i}}{G_{\exp ,i}}\right|}.(12)$

2. Indicators of overall performance

Coefficient of Determination R²

$R²=1-\frac{{\displaystyle \sum _{i=1}^K{\left(G_{forcast,i}-G_{\exp ,i}\right)}^2}}{{\displaystyle \sum _{i=1}^K{\left(G_{forcast,i}-{\overline{G}}_{\exp ,i}\right)}^2}}.(13)$

The linear regression coefficients are as follows:

$Y=aG+b,(14)$

$a=\frac{\overline{G_{forecast}{G}_{\exp }}-\overline{G_{\exp }}\overline{G_{forecast}}}{{\overline{G^2}}_{\exp }-{\overline{G}}_{\exp }^2},(15)$

$b={\overline{G}}_{forecast}-a{\overline{G}}_{\exp },(16)$

where K is the total number of observations, $G_{forecast}$ and $G_{\exp }$ are the forecasted and measured values of daily global solar radiation (daily GSR), respectively, ${\overline{G}}_{forecast}$ and ${\overline{G}}_{\exp }$ represent the average of forecasted and measured values of daily solar radiation.

It should be mentioned that the smaller values of MBE, RMSE, NRMSE, and MAPE show more accuracy than the predicted values and an ideal case is zero. All these statistical indicators or error metrics have the added advantage of indicating whether the estimated values are statistically significant or not at a particular confidence level. The error formulations of MBE and RMSE provide quantitative measures that have the same physical units as the dependent variable. The NRMSE and R² are dimensionless and the MAPE provides quantitative measures in percentage.

Result Analysis and Discussion

The feedforward backpropagation was used to predict daily global solar radiation using the neural network toolbox of MATLAB 2012 software. Particularly, other authors have pointed out a multi-step prediction model: collecting data, creating a network, configuring the network, modeling, initializing weight and biases, training the network, and validating and using the network. One of the most important issues in this article is how the model was selected to perform a series of solar radiation values transversely.

Firstly, the Quantile-Quantile (Q-Q) graph is used to evaluate the goodness of fit for the used FFNN-BP model and recognize the performance models of global solar radiation values. For daily GSR, the Q-Q graph, presented in Figure 5, shows the comparison of simulated daily global solar radiation generated by ANN model. Against the measured data, an overestimation and an underestimation of solar radiation for 25 locations appear. Although the graphs of all study places accurately simulated the global solar radiation, this result indicates that the FFNN-BP model is accurate to be employed in all study locations of Morocco.

FIGURE 5

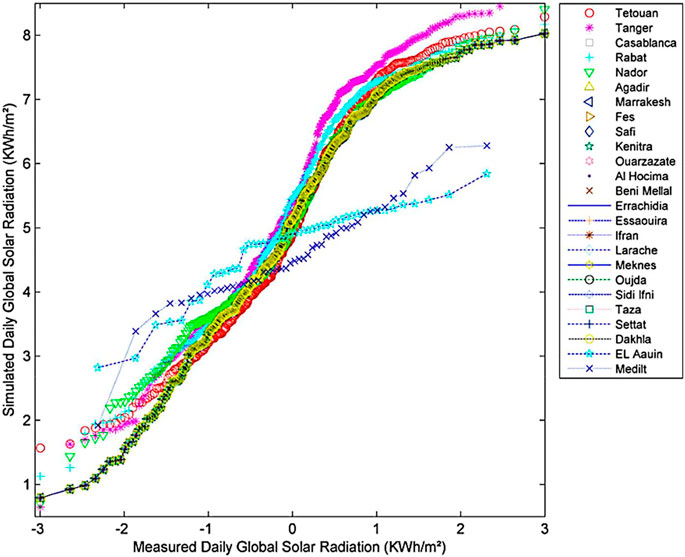
FIGURE 5. Q-Q plot of measured and simulated daily global solar radiation generated by FFNN-BP model for 25 Moroccan locations.

In the following prediction, all inputs parameters variables are applied to train and validate the FFNN-BP model. These input parameters data are divided into three categories, 80% for training, 10% for testing, and 10% for validation, to choose the most suitable input scenario of the models. It is noted that Rao et al. (Siva Krishna Rao et al., 2018) and Huang et al. (Huang and Shih, 2003) have explained the multiple steps phases of the ANN architecture. We adopt in this article the methodology used in (Huang and Shih, 2003), adopted as the first step (training). It is useful to start with a minimum number of neurons in the hidden layer of artificial Intelligent (AI). The number of these neurons will continually increase and retraining of the AI is continued, until the significant training of ANN is achieved and a suitable number is selected, as indicated in Table 4. After several trials, the ten neurons are considered a hidden layer (Yadav et al., 2014; Mba et al., 2016); the standard criteria for choosing among of ANN models are Mean Square Error (MSE). Moreover, various experimental parameters data used in the proposed models are presented in Table 4.

TABLE 4

TABLE 4. ANN models with different input combinations.

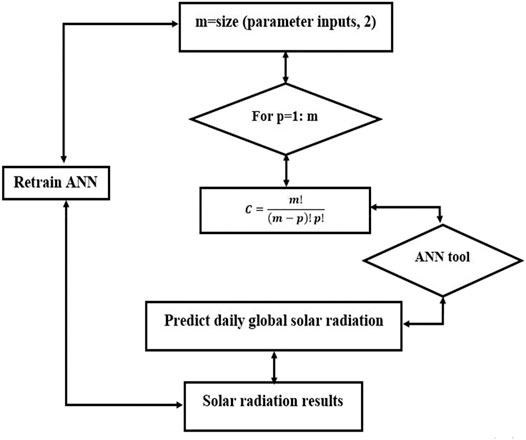
Binomial coefficient or combination can be estimated using the following mathematical expression:

$C={\displaystyle \sum }_{p=1}^m{C}_m^p={\displaystyle \sum }_{p=1}^m\frac{m!}{\left(m-p\right)!p!},(17)$

where C is the number of all combinations and m is the total number of inputs.

Hence, 32,767 combinations were found. All results should be compared for selecting the optimum inputs parameters that can predict the output parameters. After several trials, we found a total of 125 considered an adequate combination to predict the daily global solar radiation of all considered study locations in Morocco. In addition, the ANN process started with the selection of input combinations. For a good fitting, we train the network more before predicting the output results. In another study, Silva et al. (Siva Krishna Rao et al., 2018) have developed six ANNs using several input data with 32 possible combinations of inputs. The input parameters are as follows: theoretical sunshine hours (S₀), sunshine hours (S), extraterrestrial radiation (H_o), daily minimum and maximum of temperature, difference of daily maximum temperature, and difference of daily minimum temperature. The methodology adopted in this study is presented in Figure 6.

FIGURE 6

FIGURE 6. The proposed methodology adopted.

Furthermore, the selected input parameters are tested using the linear relationship with measured daily global solar radiation (Table A1). The expression of the linear relationship is given in the following equation:

$M_{DGSR}=b_0+b_1{K}_t+b_{2}TOA+b_3{T}_{\max }+\cdots \cdots b_{15}{R}_{rh}.(18)$

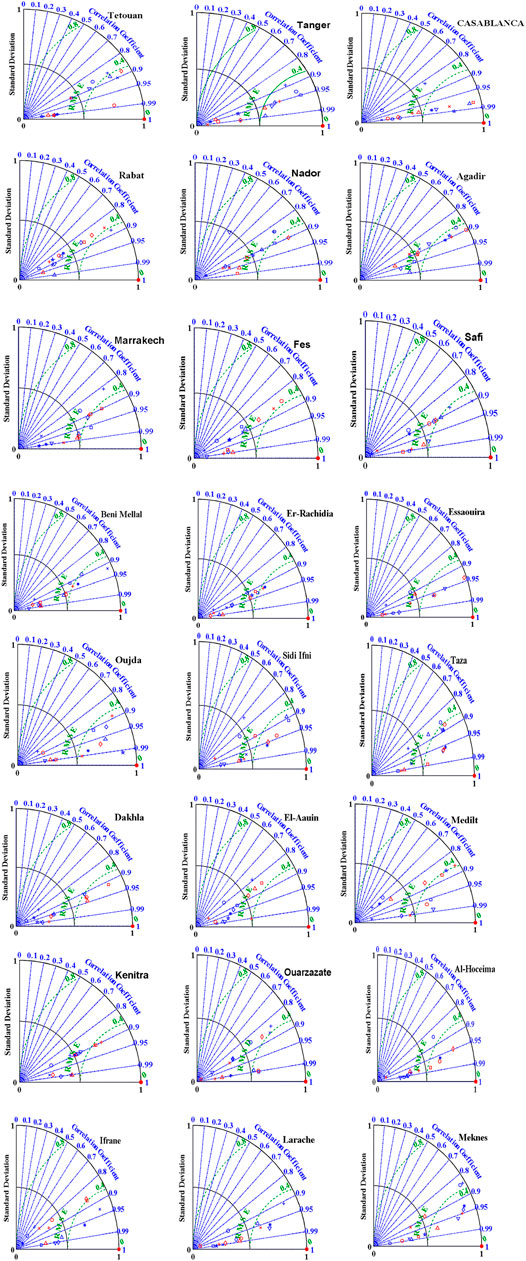
For a more specific analysis, the Taylor diagram is used as a comparative method between measured and predicted values. The following statistical error metrics, correlation coefficient (R²), root mean square error (RMSE), and standard deviation (σ), were combined in a polar diagram (two-dimensional). In order to compare the performance of the most suitable input-output parameters of all considered locations, all graphs based on the statistical error metrics are presented in Figure 7. The illustrated figures present the lowest value of RMSE and standard deviation (σ). The highest value of R² represents the accuracy relationship between measured and predicted values.

FIGURE 7

FIGURE 7. Taylor diagrams of twenty-five study locations in Morocco.

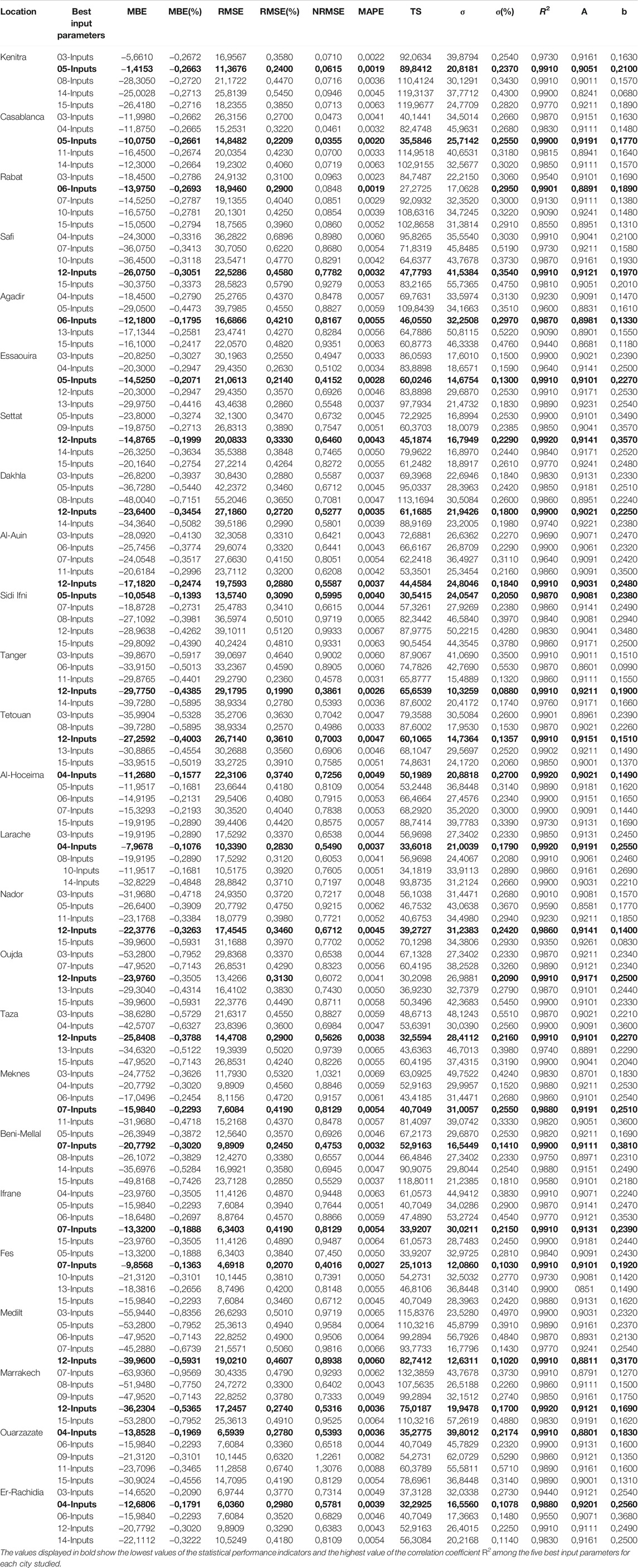
The FFNN-BP model performance is presented with the top five selected input parameters of all twenty-five cities and is shown in Table 5.

TABLE 5

TABLE 5. Best five inputs parameters of 25 location in Morocco.

The FFNN-BP models, based on different input parameters, have the capability of finding relationships between the variation of each input parameter and the variation of the output parameters. This variation is related to the daily GSR using the proposed method. All statistical metrics performance of the five best inputs parameters indicates that the ANN performs better. Based on R² results, all five best inputs of six zones have shown high prediction accuracy. Best performance in the first zone is obtained by the lowest value of MBE, RMSE, NRMSE, MAPE, TS, and$\sigma$, respectively. It is reported that the twelve input parameters are the most selected of the following cities: Safi, Settat, Dakhla, and Al-Auin; however, the inputs D_number,W_s, and R_h are based on MBE, RMSE, NMRSE, MAPE, TS and K_t, TOA, T_max, T_ratio, ΔT, T_average, T_min, Alt, Long, δ, and D_length, which have shown excellent estimation. Rabat and Agadir present six input parameters for Kenitra, Casablanca, Essaouira, and Sidi Ifni and five input parameters were selected as the most suitable. For the second zone, the selected input parameters are twelve for Tanger, Tetouan, and Nador, whereas four input parameters are considered as the best input parameters of Al-Hoceima and Laareche. For the third zone, twelve parameters were found for Oujda and Taza as the best input data. For the other locations, seven parameters are found as the best inputs. One site in the fourth and five zones shows that the twelve parameters are the best inputs. The other zones present two best inputs. For Ouarzazate, there are four parameters and for Er-Rachidia, there are twelve parameters. According to the results, it is suitable to obtain the founded input parameters as basic information for developing new solar radiation based on different meteorological data and parameters coordinates.

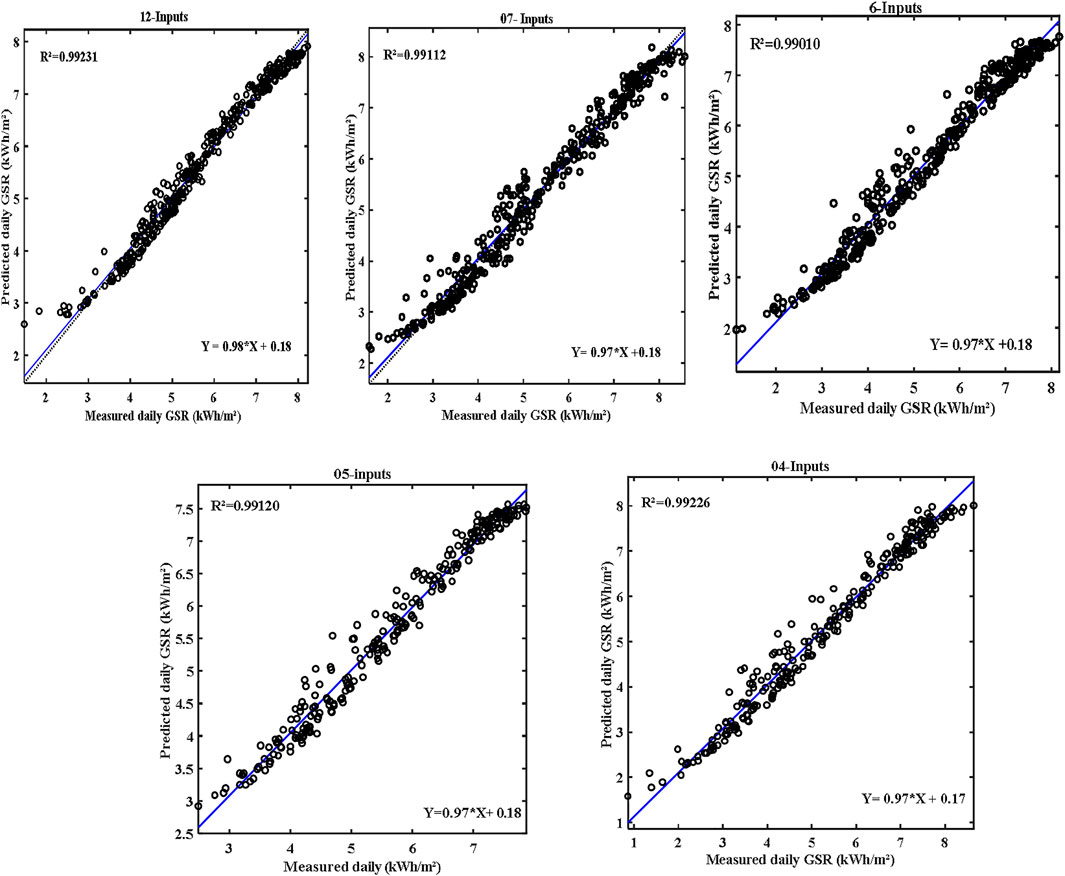
Figure 8 presents the scattered plot of daily GSR values predicted by the proposed model of the best-found parameters (twelve, four to seven inputs) with measured daily GSR values. The figures show that the lowest values of daily GSR below demonstrate that the perfect fit was very close to the observed values. The showed values indicate that the FFNN-BP model shows good interpretation and good practicality for daily GSR.

FIGURE 8

FIGURE 8. Scatter plot of daily GSR predicted values by the best six inputs vs. measured values.

Table 6 presents a brief comparison of multiple studies for different locations using several meteorological, astronomical, and geographical data as input parameters between the present study and others previously cited in the literature in order to predict the daily global solar radiation. The comparison metric is based on the coefficient of determination (R²). Therefore, most of the cited studies for the prediction of daily global solar radiation used different algorithms have generally presented close results to another one. According to the statistical metrics, it can be noted that the highest value of the coefficient of determination corresponds to the appropriate models. As we can see from Table 6, it clearly appears that the current study presents the appropriate model compared to other studies cited in the literature. The R² value of the proposed model is 99.20, which ensures that the proposed model performs better than other existing methods.

TABLE.6

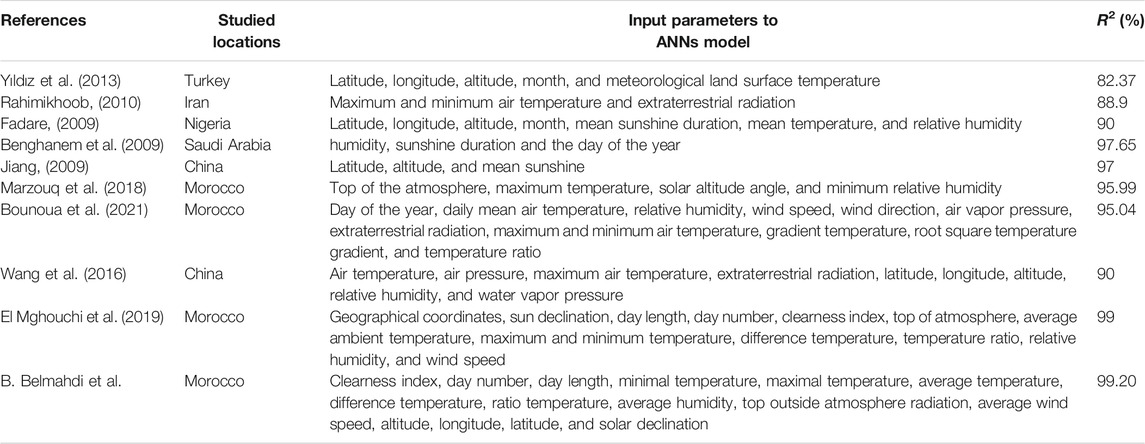
TABLE.6. Metrics comparison of current study with the existing literature studies in the prediction of daily global solar radiation.

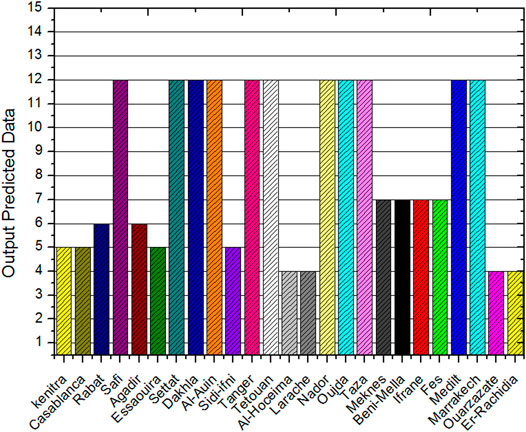
Figure 9 ranks the twenty-five studied locations in terms of predicted outputs. The best results of the selected input parameters for Ouarzazate, Al-Hoceima, and Lareche cities are K_t, TOA, T_max, and T_ratio. The best results of the selected input parameters for Kenitra, Casablanca, Essaouira, and Sidi Ifni are K_t, TOA, T_maxT_ratio, and ΔT. The K_t, TOA, T_maxT_ratio, ΔT, and T_average are the selected input parameters for Rabat and Agadir city. The best seven input parameters for the considered location (Meknes, Beni-Mellal, Ifrane, and Fes) are K_t, TOA, T_maxT_ratio, ΔT, T_average, and T_min. Er-Rachidia, Marrakech, Midelt, Taza, Oujda, Nador, Tetouan, Tanger, Al-Auin, Dakhla, and Settat City are the locations considered for twelve input parameters (K_t, TOA, T_maxT_ratio, ΔT, T_average, Alt, Long, Lat, δ, D_length, D_number, W_s, and R_h). The analysis indicator shows that the increase in input numbers improves the accuracy and adaptability of the ANN model.

FIGURE 9

FIGURE 9. Output predicted data and the best selected parameters for all Moroccan cities.

In order to compare the agreement between measured daily average global solar radiation and the predicted one for twenty-five Moroccan selected locations, the relative difference values are 4.84 and 6.75% for the ANN model and the mean, max, min value of the predicted and measured model are 5.493, 5.09, 5.19 and 5.796, 5.39, and 5.49, respectively, as presented in Figure 9, revealing the high accuracy of the ANN model in simulation. The selected model also seems well adapted to predict daily global solar radiation in other study locations successfully.

Conclusion

The article presents the FFNN-BP model and its application in predicting the daily global solar radiation. A feedforward backpropagation is employed using different metrological and geographical coordinates. The proposed neural network runs with ten neurons and the log-sigmoid transfer function of the hidden layer and the output layers are employed for the prediction model. Geographical and meteorological parameters, such as K_t, TOA, T_maxT_ratio, ΔT, T_average, T_min, Alt, Long, Lat, δ, D_length, D_number, W_s, and R_h , have been used as input variables and daily global solar radiation as outputs variables. Each step was increasing the number of inputs to determine the most accurate and suitable parameters. As the results have shown, all parameters are qualified to demonstrate their adaptability and efficiency for the study weather conditions. The best twelve, seven, six, five, and four input parameters with the proposed model in this study can also be preferred to predict daily GSR with high logical accuracy and faster performance analysis. This obtained result is an indication of a good matching between measured and predicted global solar radiation. Following the same procedures, this technique could be used to predict other outputs data of different locations where measurement instrumentation is unavailable or costly to obtain. The statistical error metrics calculated for each predicted value and the Taylor diagrams show the good ability of the proposed models in predicting daily solar radiation. This result can be useful for installing several solar energy capacities, such as photovoltaic farms or solar collectors.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author Contributions

BB collected the data, conceived the analysis procedure, and provided the analysis tools, the methodology, and the software. BB and ML designed the analysis procedure and supervised it. BB and ML was responsible for the original draft preparation. BB, ML, and AB contributed to the investigation. MA, DC, PC, and AB reviewed the manuscript. All authors read and approved the final manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix 1

TABLE A1

TABLE A1. Linear relationship for best input of 25 cities.

References

Aarich, N., Erraissi, N., Akhsassi, M., Bennouna, A., Asselman, A., Barhdadi, A., et al. (2018). Photovoltaic DC Yield Maps for All Morocco Validated with Ground Measurements. Energy Sustain. Dev. 47, 158–169. doi:10.1016/j.esd.2018.10.003

CrossRef Full Text | Google Scholar

Al-Dahidi, S., Ayadi, O., Adeeb, J., and Louzazni, M. (2019). Assessment of Artificial Neural Networks Learning Algorithms and Training Datasets for Solar Photovoltaic Power Production Prediction. Front. Energ. Res. 7, 130. doi:10.3389/fenrg.2019.00130

CrossRef Full Text | Google Scholar

Al-Alawi, S. M., and Al-Hinai, H. A. (1998). An ANN-Based Approach for Predicting Global Radiation in Locations with No Direct Measurement Instrumentation. Renew. Energ. 14 (1), 199–204. doi:10.1016/s0960-1481(98)00068-8

CrossRef Full Text | Google Scholar

Alam, S., Kaushik, S. C., and Garg, S. N. (2006). Computation of Beam Solar Radiation at normal Incidence Using Artificial Neural Network. Renew. Energ. 31 (10), 1483–1491. doi:10.1016/j.renene.2005.07.010

CrossRef Full Text | Google Scholar

Allouhi, A., Jamil, A., Kousksou, T., El Rhafiki, T., Mourad, Y., and Zeraouli, Y. (2015). Solar Domestic Heating Water Systems in Morocco: An Energy Analysis. Energy Convers. Manag. 92, 105–113. doi:10.1016/j.enconman.2014.12.055

CrossRef Full Text | Google Scholar

Alsina, E. F., Bortolini, M., Gamberi, M., and Regattieri, A. (2016). Artificial Neural Network Optimisation for Monthly Average Daily Global Solar Radiation Prediction. Energ. Convers. Manag. 120, 320–329. doi:10.1016/j.enconman.2016.04.101

CrossRef Full Text | Google Scholar

Amirian, E., Dejam, M., and Chen, Z. (2018). Performance Forecasting for Polymer Flooding in Heavy Oil Reservoirs. Fuel 216, 83–100. doi:10.1016/j.fuel.2017.11.110

CrossRef Full Text | Google Scholar

Battiti, R. (1992). First- and Second-Order Methods for Learning: Between Steepest Descent and Newton’s Method. Neural Comput. 4 (2), 141–166. doi:10.1162/neco.1992.4.2.141

CrossRef Full Text | Google Scholar

Bebis, G., and Georgiopoulos, M. (1994). Feed-forward Neural Networks. IEEE Potentials 13 (4), 27–31. doi:10.1109/45.329294

CrossRef Full Text | Google Scholar

Belmahdi, B., and Bouardi, A. E. (2020). Simulation and Optimization of Microgrid Distributed Generation: a Case Study of University Abdelmalek Essaâdi in Morocco. Proced. Manuf. 46, 746–753. doi:10.1016/j.promfg.2020.03.105

CrossRef Full Text | Google Scholar

Belmahdi, B., and El Bouardi, A. (2020). Solar Potential Assessment Using PVsyst Software in the Northern Zone of Morocco. Proced. Manuf. 46, 738–745. doi:10.1016/j.promfg.2020.03.104

CrossRef Full Text | Google Scholar

Belmahdi, B., Louzazni, M., and El Bouardi, A. (2020). One Month-Ahead Forecasting of Mean Daily Global Solar Radiation Using Time Series Models. Optik (Stuttg). 219, 165207. doi:10.1016/j.ijleo.2020.165207

CrossRef Full Text | Google Scholar

Belmahdi, B., Louzazni, M., and El Bouardi, A. (2020). A Hybrid ARIMA–ANN Method to Forecast Daily Global Solar Radiation in Three Different Cities in Morocco. Eur. Phys. J. Plus 135 (11), 925. doi:10.1140/epjp/s13360-020-00920-9

CrossRef Full Text | Google Scholar

Benghanem, M., Mellit, A., and Alamri, S. N. (2009). ANN-based Modelling and Estimation of Daily Global Solar Radiation Data: A Case Study. Energ. Convers. Manag. 50 (7), 1644–1655. doi:10.1016/j.enconman.2009.03.035

CrossRef Full Text | Google Scholar

Boland, J., Scott, L., and Luther, M. (2001). Modelling the Diffuse Fraction of Global Solar Radiation on a Horizontal Surface. Environmetrics 12 (2), 103–116. doi:10.1002/1099-095x(200103)12:2<103:aid-env447>3.0.co;2-2

CrossRef Full Text | Google Scholar

Bouhal, T., Agrouaz, Y., Kousksou, T., Allouhi, A., El Rhafiki, T., Jamil, A., et al. (2018). Technical Feasibility of a Sustainable Concentrated Solar Power in Morocco through an Energy Analysis. Renew. Sustain. Energ. Rev. 81 (1), 1087–1095. doi:10.1016/j.rser.2017.08.056

CrossRef Full Text | Google Scholar

Bounoua, Z., Ouazzani Chahidi, L., and Mechaqrane, A. (2021). Estimation of Daily Global Solar Radiation Using Empirical and Machine-Learning Methods: A Case Study of Five Moroccan Locations. Sustain. Mater. Technol. 28, e00261. doi:10.1016/j.susmat.2021.e00261

CrossRef Full Text | Google Scholar

Celik, A. N., and Muneer, T. (2013). Neural Network Based Method for Conversion of Solar Radiation Data. Energ. Convers. Manag. 67, 117–124. doi:10.1016/j.enconman.2012.11.010

CrossRef Full Text | Google Scholar

Chakraborty, K., Mehrotra, K., Mohan, C. K., and Ranka, S. (1992). Forecasting the Behavior of Multivariate Time Series Using Neural Networks. Neural Networks 5 (6), 961–970. doi:10.1016/s0893-6080(05)80092-9

CrossRef Full Text | Google Scholar

Chiteka, K., and Enweremadu, C. C. (2016). Prediction of Global Horizontal Solar Irradiance in Zimbabwe Using Artificial Neural Networks. J. Clean. Prod. 135, 701–711. doi:10.1016/j.jclepro.2016.06.128

CrossRef Full Text | Google Scholar

Durna, B., and Şahin, A. D. (2020). Mapping of Daylight Illumination Levels Using Global Solar Radiation Data in and Around Istanbul, Turkey. Weather 75 (1), 19–25. doi:10.1002/wea.3386

CrossRef Full Text | Google Scholar

El Mghouchi, Y., Ajzoul, T., and El Bouardi, A. (2016). Prediction of Daily Solar Radiation Intensity by Day of the Year in Twenty-Four Cities of Morocco. Renew. Sustain. Energ. Rev. 53, 823–831. doi:10.1016/j.rser.2015.09.059

CrossRef Full Text | Google Scholar

El Mghouchi, Y., Chham, E., Zemmouri, E. M., and El Bouardi, A. (2019). Assessment of Different Combinations of Meteorological Parameters for Predicting Daily Global Solar Radiation Using Artificial Neural Networks. Build. Environ. 149, 607–622. doi:10.1016/j.buildenv.2018.12.055

CrossRef Full Text | Google Scholar

Elminir, H. K., Azzam, Y. A., and Younes, F. I. (2007). Prediction of Hourly and Daily Diffuse Fraction Using Neural Network, as Compared to Linear Regression Models. Energy 32 (8), 1513–1523. doi:10.1016/j.energy.2006.10.010

CrossRef Full Text | Google Scholar

Fadare, D. A. (2009). Modelling of Solar Energy Potential in Nigeria Using an Artificial Neural Network Model. Appl. Energ. 86 (9), 1410–1422. doi:10.1016/j.apenergy.2008.12.005

CrossRef Full Text | Google Scholar

Feng, L., Lin, A., Wang, L., Qin, W., and Gong, W. (2018). Evaluation of sunshine-based Models for Predicting Diffuse Solar Radiation in China. Renew. Sustain. Energ. Rev. 94, 168–182. doi:10.1016/j.rser.2018.06.009

CrossRef Full Text | Google Scholar

Gairaa, K., Khellaf, A., Messlem, Y., and Chellali, F. (2016). Estimation of the Daily Global Solar Radiation Based on Box-Jenkins and ANN Models: A Combined Approach. Renew. Sustain. Energ. Rev. 57, 238–249. doi:10.1016/j.rser.2015.12.111

CrossRef Full Text | Google Scholar

George, D., and Huerta, E. A. (2018). Deep Neural Networks to Enable Real-Time Multimessenger Astrophysics. Phys. Rev. D 97 (4), 44039. doi:10.1103/physrevd.97.044039

CrossRef Full Text | Google Scholar

Gueymard, C. A. (2014). A Review of Validation Methodologies and Statistical Performance Indicators for Modeled Solar Radiation Data: Towards a Better Bankability of Solar Projects. Renew. Sustain. Energ. Rev. 39, 1024–1034. doi:10.1016/j.rser.2014.07.117

CrossRef Full Text | Google Scholar

Haykin, S. (1988). Neural Networks: A Comprehensive Foundation. 2nd Edition. Prentice-Hall.

Hontoria, L., Aguilera, J., and Zufiria, P. (2005). An Application of the Multilayer Perceptron: Solar Radiation Maps in Spain. Sol. Energ. 79 (5), 523–530. doi:10.1016/j.solener.2004.11.013

CrossRef Full Text | Google Scholar

Huang, S.-J., and Shih, K.-R. (2003). Short-term Load Forecasting via ARMA Model Identification Including Non-Gaussian Process Considerations. IEEE Trans. Power Syst. 18 (2), 673–679. doi:10.1109/tpwrs.2003.811010

CrossRef Full Text | Google Scholar

Jiang, Y. (2009). Computation of Monthly Mean Daily Global Solar Radiation in China Using Artificial Neural Networks and Comparison with Other Empirical Models. Energy 34 (9), 1276–1283. doi:10.1016/j.energy.2009.05.009

CrossRef Full Text | Google Scholar

Kaba, K., Sarıgül, M., Avcı, M., and Kandırmaz, H. M. (2018). Estimation of Daily Global Solar Radiation Using Deep Learning Model. Energy 162, 126–135. doi:10.1016/j.energy.2018.07.202

CrossRef Full Text | Google Scholar

Kamruzzaman, J., Begg, R., and Sarker, R. A. (2006). Artificial Neural Networks in Finance and Manufacturing. Idea Group Pub.

Kaplan, Y. A. (2018). A New Model for Predicting the Global Solar Radiation. Environ. Prog. Sustain. Energ. 37 (2), 870–880. doi:10.1002/ep.12721

CrossRef Full Text | Google Scholar

Kashyap, Y., Bansal, A., and Sao, A. K. (2015). Solar Radiation Forecasting with Multiple Parameters Neural Networks. Renew. Sustain. Energ. Rev. 49, 825–835. doi:10.1016/j.rser.2015.04.077

CrossRef Full Text | Google Scholar

Khan, S. A. R., Zaman, K., and Zhang, Y. (2016). The Relationship between Energy-Resource Depletion, Climate Change, Health Resources and the Environmental Kuznets Curve: Evidence from the Panel of Selected Developed Countries. Renew. Sustain. Energ. Rev. 62, 468–477. doi:10.1016/j.rser.2016.04.061

CrossRef Full Text | Google Scholar

Khare, M., and Nagendra, S. M. S. (2007). Artificial Neural Networks in Vehicular Pollution Modelling. Springer.

Khatib, T., Mohamed, A., Sopian, K., and Mahmoud, M. (2012). Solar Energy Prediction for Malaysia Using Artificial Neural Networks. Int. J. Photoenergy 2012, 419504. doi:10.1155/2012/419504

CrossRef Full Text | Google Scholar

Khwaja, A. S., Anpalagan, A., Naeem, M., and Venkatesh, B. (2020). Joint Bagged-Boosted Artificial Neural Networks: Using Ensemble Machine Learning to Improve Short-Term Electricity Load Forecasting. Electr. Power Syst. Res. 179, 106080. doi:10.1016/j.epsr.2019.106080

CrossRef Full Text | Google Scholar

Lam, J. C., Wan, K. K. W., and Yang, L. (2008). Solar Radiation Modelling Using ANNs for Different Climates in China. Energ. Convers. Manag. 49 (5), 1080–1090. doi:10.1016/j.enconman.2007.09.021

CrossRef Full Text | Google Scholar

Li, H., Cao, F., Bu, X., and Zhao, L. (2015). Models for Calculating Daily Global Solar Radiation from Air Temperature in Humid Regions-A Case Study. Environ. Prog. Sustain. Energ. 34 (2), 595–599. doi:10.1002/ep.12018

CrossRef Full Text | Google Scholar

Liu, Y., Yang, L., Zheng, W., Liu, T., Zhang, X., and Liu, J. (2018). A Novel Building Energy Efficiency Evaluation index: Establishment of Calculation Model and Application. Energ. Convers. Manag. 166, 522–533. doi:10.1016/j.enconman.2018.03.090

CrossRef Full Text | Google Scholar

Louzazni, M., Mosalam, H., and Khouya, A. (2020). A Non-linear Auto-Regressive Exogenous Method to Forecast the Photovoltaic Power Output. Sustain. Energ. Technol. Assessments 38, 100670. doi:10.1016/j.seta.2020.100670

CrossRef Full Text | Google Scholar

Marzouq, M., Bounoua, Z., Mechaqrane, A., Fadili, H. E., Lakhliai, Z., and Zenkouar, K. (2018). ANN-based Modelling and Prediction of Daily Global Solar Irradiation Using Commonly Measured Meteorological Parameters. IOP Conf. Ser. Earth Environ. Sci. 161 (1), 012017. doi:10.1088/1755-1315/161/1/012017

CrossRef Full Text | Google Scholar

Mba, L., Meukam, P., and Kemajou, A. (2016). Application of Artificial Neural Network for Predicting Hourly Indoor Air Temperature and Relative Humidity in Modern Building in Humid Region. Energy Build. 121, 32–42. doi:10.1016/j.enbuild.2016.03.046

CrossRef Full Text | Google Scholar

Mehleri, E. D., Zervas, P. L., Sarimveis, H., Palyvos, J. A., and Markatos, N. C. (2010). A New Neural Network Model for Evaluating the Performance of Various Hourly Slope Irradiation Models: Implementation for the Region of Athens. Renew. Energ. 35 (7), 1357–1362. doi:10.1016/j.renene.2009.11.005

CrossRef Full Text | Google Scholar

Mehleri, E. D., Zervas, P. L., Sarimveis, H., Palyvos, J. A., and Markatos, N. C. (2010). Determination of the Optimal Tilt Angle and Orientation for Solar Photovoltaic Arrays. Renew. Energ. 35 (11), 2468–2475. doi:10.1016/j.renene.2010.03.006

CrossRef Full Text | Google Scholar

Mellit, A., Benghanem, M., Arab, A. H., and Guessoum, A. (2005). A Simplified Model for Generating Sequences of Global Solar Radiation Data for Isolated Sites: Using Artificial Neural Network and a Library of Markov Transition Matrices Approach. Sol. Energ. 79 (5), 469–482. doi:10.1016/j.solener.2004.12.006

CrossRef Full Text | Google Scholar

Kumar, M., and Kumar, A. (2017). Performance Assessment and Degradation Analysis of Solar Photovoltaic Technologies: A Review. Renew. Sustain. Energ. Rev. 78, 554–587. doi:10.1016/j.rser.2017.04.083

CrossRef Full Text | Google Scholar

Moreno, A., Gilabert, M. A., and Martínez, B. (2011). Mapping Daily Global Solar Irradiation over Spain: A Comparative Study of Selected Approaches. Sol. Energ. 85 (9), 2072–2084. doi:10.1016/j.solener.2011.05.017

CrossRef Full Text | Google Scholar

Muneer, T., Younes, S., and Munawwar, S. (2007). Discourses on Solar Radiation Modeling. Renew. Sustain. Energ. Rev. 11 (4), 551–602. doi:10.1016/j.rser.2005.05.006

CrossRef Full Text | Google Scholar

Notton, G., Paoli, C., Vasileva, S., Nivet, M. L., Canaletti, J.-L., and Cristofari, C. (2012). Estimation of Hourly Global Solar Irradiation on Tilted Planes from Horizontal One Using Artificial Neural Networks. Energy 39 (1), 166–179. doi:10.1016/j.energy.2012.01.038

CrossRef Full Text | Google Scholar

Owusu, P. A., and Asumadu-Sarkodie, S. (2016). A Review of Renewable Energy Sources, Sustainability Issues and Climate Change Mitigation. Cogent Eng. 3 (1), 1167990. doi:10.1080/23311916.2016.1167990

CrossRef Full Text | Google Scholar

Pacheco-Vega, A., Sen, M., Yang, K. T., and McClain, R. L. (2001). Neural Network Analysis of Fin-Tube Refrigerating Heat Exchanger with Limited Experimental Data. Int. J. Heat Mass. Transf. 44 (4), 763–770. doi:10.1016/s0017-9310(00)00139-3

CrossRef Full Text | Google Scholar

Polo, J., Fernández-Peruchena, C., Salamalikis, V., Mazorra-Aguiar, L., Turpin, M., Martín-Pomares, L., et al. (2020). Benchmarking on Improvement and Site-Adaptation Techniques for Modeled Solar Radiation Datasets. Sol. Energ. 201, 469–479. doi:10.1016/j.solener.2020.03.040

CrossRef Full Text | Google Scholar

Rahimikhoob, A. (2010). Estimating Global Solar Radiation Using Artificial Neural Network and Air Temperature Data in a Semi-arid Environment. Renew. Energ. 35 (9), 2131–2135. doi:10.1016/j.renene.2010.01.029

CrossRef Full Text | Google Scholar

Rajendran, P., and Smith, H. (2016). Modelling of Solar Irradiance and Daylight Duration for Solar-Powered UAV Sizing. Energy Explor. Exploit. 34 (2), 235–243. doi:10.1177/0144598716629874

CrossRef Full Text | Google Scholar

Siva Krishna Rao, D. V., Premalatha, M., and Naveen, C. (2018). Analysis of Different Combinations of Meteorological Parameters in Predicting the Horizontal Global Solar Radiation with ANN Approach: A Case Study. Renew. Sustain. Energ. Rev. 91, 248–258. doi:10.1016/j.rser.2018.03.096

CrossRef Full Text | Google Scholar

Riahi-Madvar, H., Ayyoubzadeh, S. A., and Atani, M. G. (2011). Developing an Expert System for Predicting Alluvial Channel Geometry Using ANN. Expert Syst. Appl. 38 (1), 215–222. doi:10.1016/j.eswa.2010.06.047

CrossRef Full Text | Google Scholar

Sayigh, A. (2017). Photovoltaics for Sustainable Electricity and Buildings. Springer International Publishing.

Sharifi, S. S., Rezaverdinejad, V., and Nourani, V. (2016). Estimation of Daily Global Solar Radiation Using Wavelet Regression, ANN, GEP and Empirical Models: A Comparative Study of Selected Temperature-Based Approaches. J. Atmos. Solar Terrestrial Phys. 149, 131–145. doi:10.1016/j.jastp.2016.10.008

CrossRef Full Text | Google Scholar

Shekari Beidokhti, R., and Malek, A. (2009). Solving Initial-Boundary Value Problems for Systems of Partial Differential Equations Using Neural Networks and Optimization Techniques. J. Franklin Inst. 346 (9), 898–913. doi:10.1016/j.jfranklin.2009.05.003

CrossRef Full Text | Google Scholar

Šimelytė, A. (2020). “Chapter 13 - Promotion of Renewable Energy in Morocco,” in Energy Transformation Towards Sustainability. Editors M. Tvaronavičienė, and S. Ślusarczyk (Elsevier), 249–287.

Google Scholar

Sözen, A., Arcaklioǧlu, E., Özalp, M., and Kanit, E. G. (2004). Use of Artificial Neural Networks for Mapping of Solar Potential in Turkey. Appl. Energ. 77 (3), 273–286. doi:10.1016/s0306-2619(03)00137-5

CrossRef Full Text | Google Scholar

Sözen, A., Arcaklıoğlu, E., Özalp, M., and Çağlar, N. (2005). Forecasting Based on Neural Network Approach of Solar Potential in Turkey. Renew. Energ. 30 (7), 1075–1090. doi:10.1016/j.renene.2004.09.020

CrossRef Full Text | Google Scholar

Sterjovski, Z., Nolan, D., Carpenter, K. R., Dunne, D. P., and Norrish, J. (2005). Artificial Neural Networks for Modelling the Mechanical Properties of Steels in Various Applications. J. Mater. Process. Technol. 170 (3), 536–544. doi:10.1016/j.jmatprotec.2005.05.040

CrossRef Full Text | Google Scholar

Tagliaferri, F., Viola, I. M., and Flay, R. G. J. (2015). Wind Direction Forecasting with Artificial Neural Networks and Support Vector Machines. Ocean Eng. 97, 65–73. doi:10.1016/j.oceaneng.2014.12.026

CrossRef Full Text | Google Scholar

Wang, L., Kisi, O., Zounemat-Kermani, M., Salazar, G. A., Zhu, Z., and Gong, W. (2016). Solar Radiation Prediction Using Different Techniques: Model Evaluation and Comparison. Renew. Sustain. Energ. Rev. 61, 384–397. doi:10.1016/j.rser.2016.04.024

CrossRef Full Text | Google Scholar

Yadav, A. K., and Chandel, S. S. (2014). Solar Radiation Prediction Using Artificial Neural Network Techniques: A Review. Renew. Sustain. Energ. Rev. 33, 772–781. doi:10.1016/j.rser.2013.08.055

CrossRef Full Text | Google Scholar

Yadav, A. K., Malik, H., and Chandel, S. S. (2014). Selection of Most Relevant Input Parameters Using WEKA for Artificial Neural Network Based Solar Radiation Prediction Models. Renew. Sustain. Energ. Rev. 31, 509–519. doi:10.1016/j.rser.2013.12.008

CrossRef Full Text | Google Scholar

Yalcintas, M., and Akkurt, S. (2005). Artificial Neural Networks Applications in Building Energy Predictions and a Case Study for Tropical Climates. Int. J. Energ. Res. 29 (10), 891–901. doi:10.1002/er.1105

CrossRef Full Text | Google Scholar

Yalçın, M. E., Ayhan, T., and Yeniçeri, R. (2020). Reconfigurable Cellular Neural Networks and Their Applications, 17840.

Yang, L., Cao, Q., Yu, Y., and Liu, Y. (2020). Comparison of Daily Diffuse Radiation Models in Regions of China without Solar Radiation Measurement. Energy 191, 116571. doi:10.1016/j.energy.2019.116571

CrossRef Full Text | Google Scholar

Yilmaz, A. S., and Özer, Z. (2009). Pitch Angle Control in Wind Turbines above the Rated Wind Speed by Multi-Layer Perceptron and Radial Basis Function Neural Networks. Expert Syst. Appl. 36 (6), 9767–9775. doi:10.1016/j.eswa.2009.02.014

CrossRef Full Text | Google Scholar

Yu, L., Li, Y. P., Huang, G. H., and An, C. J. (2017). A Robust Flexible-Probabilistic Programming Method for Planning Municipal Energy System with Considering Peak-Electricity price and Electric Vehicle. Energ. Convers. Manag. 137, 97–112. doi:10.1016/j.enconman.2017.01.028

CrossRef Full Text | Google Scholar

Yıldız, B. Y., Şahin, M., Şenkal, O., Pestemalcı, V., and Emrahoğlu, N. (2013). A Comparison of Two Solar Radiation Models Using Artificial Neural Networks and Remote Sensing in turkey. Energy Sourc. A Recover. Util. Environ. Eff. 35 (3), 209–217. doi:10.1080/15567036.2011.650276

CrossRef Full Text | Google Scholar

Zhao, Q., Yao, W., Zhang, C., Wang, X., and Wang, Y. (2019). Study on the Influence of Fog and Haze on Solar Radiation Based on Scattering-Weakening Effect. Renew. Energ. 134, 178–185. doi:10.1016/j.renene.2018.11.027

CrossRef Full Text | Google Scholar