Study on Thermophysical Properties of a Lead–Bismuth-Based Graphene Nanofluid

Incorporating graphene nanoparticles with high thermal conductivity into a lead-based coolant can significantly increase its thermal conductivity and specific heat capacity, thereby increasing the core power density of lead–bismuth cooled reactors, reducing the amount of coolant required, and ultimately realizing a miniaturized and lightweight reactor design. The purpose of the design is of great significance to the engineering application of lead–bismuth stacks in remote areas and open seas. In this study, the thermophysical properties of metal-based graphene nanofluids are analyzed by comparing and analyzing prediction models established for the thermal conductivity, viscosity, and specific heat capacity. The strengthening mechanism of nanofluids is summarized, and a series of suitable calculation formulae for the thermophysical properties of lead–bismuth-based graphene nanofluids is proposed. The research results show that incorporating graphene nanoparticles into a lead–bismuth-based coolant can significantly improve its thermal conductivity and specific heat capacity. When the nanoparticle suspension is relatively stable, the thermal conductivity, specific heat capacity, and viscosity increase significantly with the concentration of graphene nanoparticles. When the concentration reaches 20%, the thermal conductivity and specific heat capacity of the nanofluid are enhanced by approximately 80 and 20%, respectively, whereas the viscosity is also increased by approximately 100%. Therefore, it is important to appropriately select the parameters for the addition of nanoparticles to maximize the effect of lead–bismuth-based graphene nanofluids on the heat transfer performance of the reactor core.

Introduction

High-performance lead–bismuth cooled reactor technology characterized by miniaturization and weight reduction is expected to change the mode of remote energy supply. The abundant energy supply provided by such reactors can fundamentally reduce or eliminate the need for logistics and other infrastructure related to energy equipment, bringing about an innovative development of nuclear power equipment. High-performance lead–bismuth cooled reactor technology has broad application prospects in military and civilian fields such as in nuclear-powered ships, nuclear-powered missiles, land-based mobile nuclear power supplies, underwater nuclear energy networks, nuclear-powered torpedoes, offshore drilling platforms, and deep-sea operation equipment capabilities. Minimizing the volume and weight of the reactor can help significantly improve the flexibility and maneuverability of nuclear power plants while ensuring sufficient power supply. For high-performance lead–bismuth cooled reactors, the amount of coolant in the primary loop is a major factor influencing the volume and weight of the reactor, and it is an important research parameter for reactor performance optimization (Li et al., 2020). To enhance the heat transfer ability of a lead–bismuth coolant, graphene nanoparticles can be added to further improve its thermal conductivity and heat exchange capabilities, thus realizing high-performance lead–bismuth-based graphene nanofluids. The properties of graphene nanoparticles are shown in Table 1 (Lei and Zhang, 2017). A lead–bismuth-based graphene nanofluid can increase the core power density of high-performance lead–bismuth cooled reactors and reduce the amount of coolant required in the primary cooling system of the reactor, ultimately achieving a miniaturized and lightweight design of the reactor.

TABLE 1

TABLE 1. The properties of graphene nanoparticles.

The basic concept of nanofluids was first conceived by Choi and Eastman (1995) By adding nanoscale solid particles into a base solution, the heat conductivity of the solution can be significantly improved. Qiao (2010) carried out experiments on the preparation and performance of graphene nanofluids and proposed a suitable prediction model. Yimin (2014) studied the heat conduction and heat exchange enhancement mechanisms of nanofluids and proposed a thermal conductivity model considering nanofluid aggregation structures. Shu (2019) studied the thermal properties and heat transfer of water-based graphene nanofluids. Shukla et al. (2016) proposed a new calculation model for the thermal conductivity coefficient of nanofluids with spherical and non-spherical shapes based on Brownian motion. Demirkır and Ertürk (2020) studied the rheological characteristic and thermal properties of water-based graphene nanofluids. The above results have shown that nanoparticles can help significantly improve the thermophysical properties of the base fluid.

However, conventional nanometer-sized particles dispersed in water or ethylene glycol as the base fluid easily form sediments and affect the stability of the suspension because of the significant difference in the specific densities between the base fluid and the particles, which limits the ability to enhance the heat transfer of the fluid. Ma and Liu (2007) proposed to use a liquid metal or a low-melting alloy as the heat transfer medium to cool computer chips and further analyzed their use as the base fluid with graphene nanoparticles, which were added to the liquid metal alloy to introduce the concept of an “ultimate coolant” with ultra-high thermal conductivity. Men (2010) studied a liquid metal-based nanofluid as a heat transfer medium using a single-phase fluid model, a discrete phase model, and a Eulerian–Eulerian (E–E) model to study its flow and heat transfer effect under forced convection-based natural convection. Zhou et al. (2020) used metal gallium as the base liquid and added alumina (Al₂O₃), diamond, and carbon nanotubes as nanoparticles to study the influence of the nanoparticles on the heat transfer performance of the base metal liquid. The results showed that when Re = 1,000 and φ = 6%, the Nusselt numbers of the nanofluids Ga–CNT, Ga–Diam, and Ga–Al₂O₃ could be enhanced by 17.3, 16.1, and 2.1%, respectively, compared with that of pure liquid metal Ga. A nanoparticle fluid with a high concentration of graphene nanoparticles is the best choice for heat transfer enhancement.

Current research on graphene nanofluids mainly involves conducting experiments and model predictions at normal temperatures. Few studies have been performed under high-temperature and high-heat-flux conditions, and the mechanism whereby nanoparticles improve the thermal conductivity and specific heat capacity of the fluid has not been thoroughly investigated. The proposed model of the mechanism cannot be widely applied to scenarios where different types of nanoparticles improve the thermophysical properties of the fluid. Therefore, this study uses high-temperature lead–bismuth liquid metal as the base liquid and compares it with sodium, gallium, and other liquid metals to study the effects of the concentration, temperature, particle size, and other factors on the thermal conductivity, viscosity, and specific heat capacity. A prediction model for the thermal conductivity, viscosity, and specific heat capacity of a graphene-based nanofluid is established, laying a theoretical foundation for the subsequent application of lead–bismuth-based graphene nanofluids as the cooling medium in lead–bismuth cooled reactors.

Factors Affecting the Stability of Lead–Bismuth-Based Graphene Nanofluids

A certain amount of nanoparticles was added to the base liquid to form nanofluids. Nanoparticles, due to their small-scale effect, irregular Brownian motion, and strong surface effect, form agglomerates with a number of weakly connected interfaces and then precipitate, ultimately affecting the stability of the nanofluid. Therefore, the basis for studying the thermophysical properties of nanofluids is to ensure their uniform and stable distribution in the base fluid without agglomeration. The resultant force experienced by the nanoparticles can be expressed as in Eq. 1 (Agarwal et al., 2013):

$F_F=F_{\text{b}}+F_{\text{f}}+F_u+F_A+F_R(1)$

where F_b is the Brownian force experienced by the nanoparticles, F_f is the buoyancy force; F_u is the interphase resistance; F_A is the van der Waals force; F_R is the electrostatic repulsion force.

The mass force on the nanoparticles can be temporarily ignored due to their nanometer size. Only the van der Waals force and the electrostatic repulsion force on the nanoparticles are considered. The force analysis shows that the stability of the nanofluid depends on the relative magnitude of the repulsive and suction forces. When the repulsion force is greater than the suction force, the Brownian motion causing nanoparticle collisions can be sufficiently prevented so as to avoid agglomeration and precipitation. Adjusting the balance between the suction and repulsion of the suspended nanoparticles by different means can keep the suspension in a stable state for a longer time. Based on the type of repulsive force, the repulsive force experienced by the dispersed nanoparticles can be divided into spatial repulsion and charge repulsion, as shown in Figure 1 (Balanta et al., 2011).

FIGURE 1

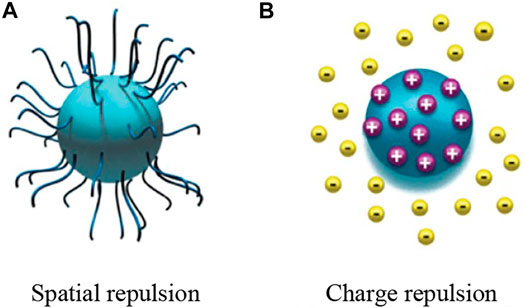
FIGURE 1. Types of repulsion forces acting on nanoparticles. (A) Spatial repulsion (B) Charge repulsion.

From a microscopic viewpoint, the influence of nanofluid stability mainly includes three aspects (Wu et al., 2020): 1) There are multiple dispersion systems in the nanofluids. Nanoparticles have a large specific surface area and high surface energy. They tend to agglomerate with each other, which reduces their surface energy. 2) The small-scale effect, irregular Brownian motion, and the resulting collisions between nanoparticles cause uneven forces and settlement. 3) Nanoparticles are prone to agglomeration under the action of electrostatic repulsion and spatial repulsion. Once agglomeration occurs, the surrounding nanoparticles in the suspension will also be adsorbed and agglomerated, thereby affecting the stability of the nanofluid. Based on the aforementioned micromechanism analysis and experimental research, the factors affecting the stability of nanofluids mainly include the particle density, particle shape, fluid viscosity, dispersant, and pH value. The above factors often affect the thermal conductivity, specific heat capacity, and other thermophysical properties.

Thermal Conductivity of Lead–Bismuth-Based Graphene Nanofluid

The thermal conductivity is an important thermophysical property of lead–bismuth-based graphene nanofluids. Numerous research results have shown that nanoparticle addition can help significantly improve the thermal conductivity of fluids. The mechanism whereby nanoparticles improve the thermal conductivity of the base fluid can be mainly divided into the following four aspects.

Thermal Conduction Mechanism of Nanofluid

Brownian Motion and Micro Convection Effect of Nanoparticles

According to the Brownian motion theory (Einstein, 1956), nanoparticles suspended in a liquid are affected by the surrounding liquid molecules, and the particles keep moving randomly. The smaller the particle size, the higher the movement speed and the more frequent the movement; hence, the frequency of energy exchange between the nanoparticles and the fluid is higher, thereby improving the thermal conductivity of the fluid.

Agglomeration and Percolation Structure of Nanoparticles

In the process of energy transfer in the nanofluids, the ideal state is when the nanoparticles can be uniformly distributed in the base fluid at a relatively high concentration without agglomeration (Wang et al., 2012). In fact, the nanoparticles collide with each other in the base fluid because of their irregular Brownian motion, easily leading to agglomeration and large-cluster formation. The speed of these agglomerates is lower than those of the individual particles. The greater vertical force will accelerate the precipitation of the particles. The agglomeration phenomenon will reduce the energy transfer rate inside the nanofluid and reduce the enhanced heat transfer performance.

Theoretical Studies on Liquid Layer Formed by Nanoparticles and Base Liquid

Based on experimental observations, researchers have found that an ordered liquid layer nanostructure is formed around the nanoparticles. This solid-like structure plays a leading role in the thermal conduction process from solid to liquid, which increases the effective thermal conductivity of the nanofluid. The thickness can be given as follows (Ma, 2008):

${\text{d}}_{\text{s}}=\frac{1}{\sqrt{3}}{\left(\frac{4M}{{\rho }_{\text{f}}{N}_A}\right)}^{\frac{1}{3}}(2)$

where M is the mass fraction of the liquid, ρ_f is the density of the liquid, and N_A is Avogadro’s constant (6.022×10²³/mol).

From the formula, find that the thickness of the nanostructure is only related to the base fluid. The other influencing factors need to be continuously improved, and whether the main heat conduction mechanism of the liquid layer is solid heat conduction or liquid heat conduction requires further research.

Ballistic Transport and Nonlocal Effect

A ballistic transport phenomenon occurs when the nanoparticle diameter is smaller than the free path of the phonon and when there is no scattering inside the molecule. At this time, the internal thermal conductivity of the nanoparticle is insufficient. The diffusion capacity at the liquid interface is dominant. However, some experimental results have shown that this local effect cannot explain the improved thermal conductivity of nanofluids (Nie et al., 2008).

Thermophoresis Theory

Thermophoresis is due to the existence of a temperature gradient. The molecules on the high-temperature side are impacted more strongly than those on the low-temperature side, leading to a directional movement of the molecules. However, experiments have shown that this phenomenon has largely no influence on the thermal conductivity of nanofluids and that it is several orders of magnitude lower than the effect produced by Brownian motion (Koo and Kleinstreuer, 2005).

Radiation Heat Transfer

From a molecular dynamics simulation, the energy transfer speed between two particles increases sharply when the distance between them is < 1 µm. Therefore, it can be considered that near-field radiation may have a greater effect on thermal conductivity. However, some researchers pointed out that near-field radiation does not significantly enhance the heat conduction of nanofluids, even when the intensity of near-field radiation is greater than that of blackbody radiation (Koo and Kleinstreuer, 2005; Ben-Abdallah, 2006).

Figure 2 shows the schematic of each theory (Zhao et al., 2013).

FIGURE 2

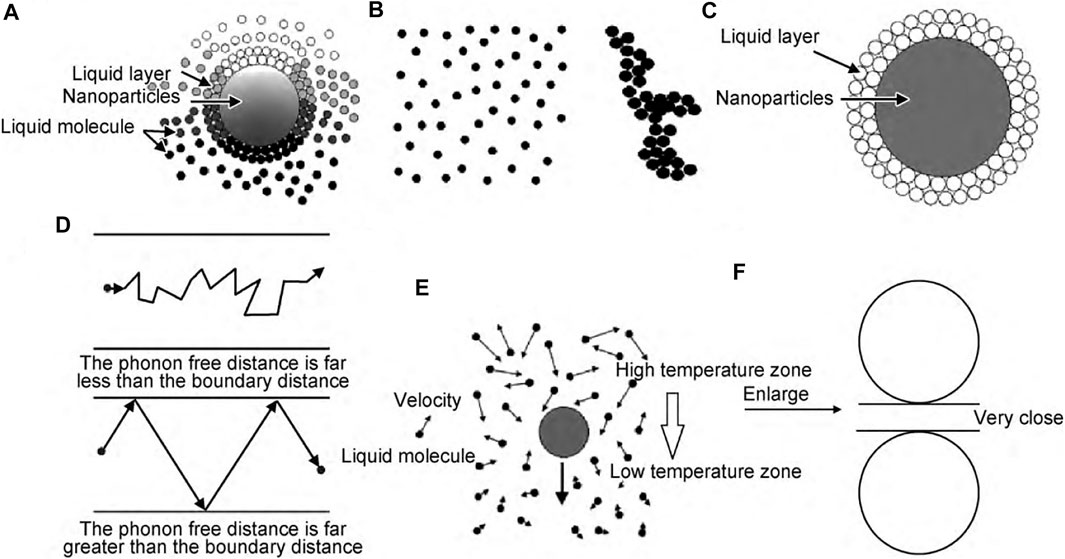
FIGURE 2. Nanofluid heat conduction mechanism. (A) Nanoparticle Brownian motion and microconvection, (B) Nanoparticle agglomeration and penetration, (C) Nanoparticle liquid layer, (D) Ballistic transport and nonlocal effects, (E) Thermophoresis theory, (F) Radiation heat transfer.

Thermal Conductivity Calculation Model

Based on the aforementioned heat conduction and heat transfer mechanism, domestic and foreign scholars have established a thermal conductivity calculation model for nanofluids.

In 1873, Maxwell (1904) studied the mechanism whereby small solid particles added to a liquid improve the thermal conductivity ability and provided a solid–liquid two-phase flow basic heat conduction model. Thereafter, scholars mainly improved and revised this theoretical model. Although the basic model does not accurately predict the thermal conductivity of solid–liquid fluids, the law of thermal conductivity has been verified by subsequent experiments.

$\frac{{\text{k}}_{\text{eff}}}{k_f}=\frac{k_p+2k_f-2\phi \left(k_f-k_p\right)}{k_p+2k_f+2\phi \left(k_f-k_p\right)}(3)$

where k_p is the thermal conductivity of the particles, k_f is the thermal conductivity of the liquid, and φ is the volume fraction of the particles.

Wu and Zhao (2013) analyzed the effects of the size and shape of nanoparticles on the thermal conductivity of nanofluids and proposed that the thermal conductivity of slender-particle nanofluids is much higher than those of spherical nanoparticles. Nanoparticles that are uniformly dispersed have a higher thermal conductivity.

Hamilton and Crosser (1962) proposed the H-C thermal conductivity model for the effect of the nanoparticle shape on the thermal conductivity of the suspension:

$\frac{{\text{k}}_{\text{eff}}}{k_f}=\frac{k_p+\left(\text{m}-1\right)k_f-\left(m-1\right)\phi \left(k_f-k_p\right)}{k_p+\left(m-1\right)k_f+\phi \left(k_f-k_p\right)}(4)$

$\psi =\frac{S_V}{S_P}(5)$

where m is the shape factor, m = 3/ψ, S_V is the surface area of the spherical particle with the same particle volume, and S_P is the surface area of the particle.

Leal (1973) proposed a model for the thermal conductivity of spherical particles with a solid–liquid two-phase flow. This model fully considers the influence of the Brownian force on the thermal conductivity of the suspension.

$\frac{{\text{k}}_{\text{e}ff}}{k_f}=1+\phi \left[\frac{1.176{\left(k_p-k_f\right)}^2}{{\left(k_p+2k_f\right)}^2}+5\left(0.6-0.028\frac{k_p-k_f}{k_p+2k_f}\right)\right]P{e}_f^{3/2}(6)$

here, $P{\text{e}}_f=r^2\gamma \rho c_{pf}/k_f$, where r is the particle radius, γ is the velocity gradient, ρ is the density, and c_pf is the specific heat capacity.

Yimin (2014) studied nanoparticle molecular dynamics and micromolecular heat transfer process, comprehensively considered the volume fraction, particle size, base fluid temperature, interface thermal resistance, and other factors of the nanoparticles, proposed a thermal conductivity calculation model for the nanofluid:

$\frac{{\text{k}}_{eff}}{{\text{k}}_{\text{f}}}=\frac{k_p+2k_f-2\phi \left(k_f-k_p\right)}{k_p+2k_f+\phi \left(k_f-k_p\right)}+\frac{18\phi HA{k}_{B}T}{{\pi }^2\rho d_p^6}\tau (7)$

where H is the total heat transfer coefficient; T is the fluid temperature; A is the heat transfer surface area; d_p is the particle size; k_B is the Boltzmann’s constant, and τ is the relaxation time constant.

Later, Yimin et al. (2002) proposed a thermal conductivity calculation model for the agglomeration of nanoparticles considering the characteristics of nanoparticle agglomeration in the base fluid. Notably, this model ignores the effect of the interface thermal resistance on the thermal conductivity:

$\frac{{\text{k}}_{eff}}{{\text{k}}_{\text{f}}}=\frac{k_p+2k_f-2\phi \left(k_f-k_p\right)}{k_p+2k_f+\phi \left(k_f-k_p\right)}+\frac{{\rho }_{\text{p}}\phi C_p}{2k_f}\sqrt{\frac{k_{B}T}{3\pi r_c\mu }}(8)$

where ρ_p is the particle density, C_p is the specific heat capacity of the particle, φ is the particle volume fraction, r_c is the particle radius, and μ is the dynamic viscosity of the fluid.

Chu et al. (2013) established a calculation model for the thermal conductivity of graphene nanofluids, as expressed in Eq. 9. This model fully considers the volume fraction, thickness, length, interface thermal resistance, and particle flatness of graphene nanoparticles. However, in different base fluid systems, the interface thermal resistance and flatness of the nanoparticles need to be measured experimentally, which makes this model more uncertain.

$\frac{{\text{k}}_{eff}}{{\text{k}}_{\text{f}}}=\frac{3+2{\eta }^2\phi /\left[k_f\left(\frac{2R_k}{L}+13.4\sqrt{t}\right)\right]}{3-\eta \phi }(9)$

where η is the flatness of the graphene nanoparticles, R_k is the interface thermal resistance, L is the length of the particle, and t is the thickness of the particles.

Shukla et al. (2016) provided a thermal conductivity model of the nanofluid considering Brownian motion, as expressed in Eq. 10. This model considers the interface thermal resistance of the particles and the microenergy transfer due to Brownian motion.

$\frac{{\text{k}}_{eff}}{{\text{k}}_{\text{f}}}=\left(1-\phi \right)+\phi {\left[\frac{k_p}{k_f}+{\left(\frac{\pi }{6\phi }\right)}^{1/3}\times \frac{\psi }{\pi N_u}\right]}^{-1}(10)$

where ψ is the sphericity of the nanoparticles, and its value for spherical particles is 1. k_p is the thermal conductivity of the particle, k_f is the thermal conductivity of the fluid, and φ is the volume fraction of the particles. $N_{\text{u}}=f(\mathrm{Re},\mathrm{Pr})$, where Re is the Reynolds number, and Pr is the Prandtl number; when the nanoparticles are relatively static with respect to the base fluid, Pr < 1 and Re << 1; at this time, the Nusselt number N_u can be 2.

The thermal conductivity calculation model of nanofluid is organized as shown in Table 2.

TABLE 2

TABLE 2. Thermal conductivity calculation models for nanofluids.

Fully considered the theoretical mechanism and theoretical calculation model for the thermal conductivity of nanofluids and analyzed the factors affecting the nanofluids. Taking spherical nanoparticles as an example, selected different thermal conductivity theoretical calculation models and carried out the calculation process, with the volume fraction of the nanoparticles set in the range of 0–20%. Figure 3 shows the calculation result.

FIGURE 3

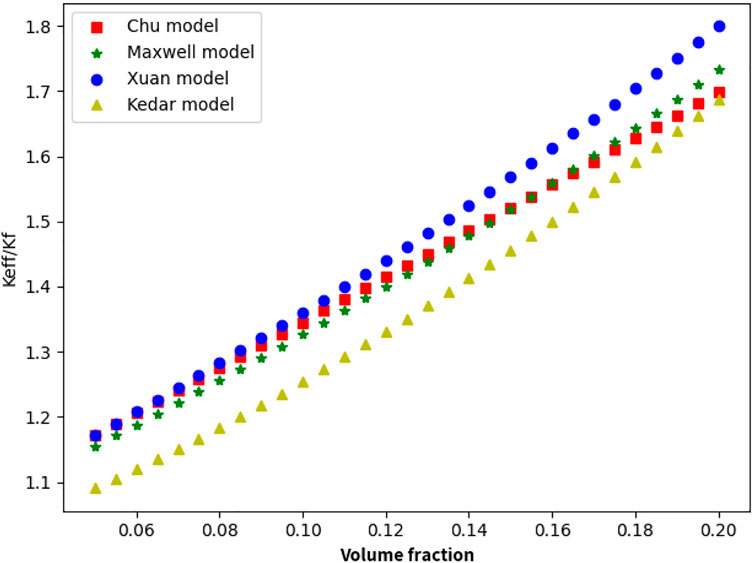
FIGURE 3. Variation in the thermal conductivity with nanoparticle concentration (T = 600 K, r = 20 nm).

The results show that the selected models can reflect the change law of the thermal conductivity of the nanofluids with respect to the nanoparticle concentration, with the prediction made by Xuan model’s tending to be higher. From the experimental result, recommending using the theoretical calculation model proposed by Xuan et al., which considers the occurrence of agglomeration. This model is based on Maxwell’s model. It fully considers the laws of molecular dynamics and thermodynamics and theoretically reflects accurately the thermal conductivity of lead–bismuth-based graphene nanofluids. The variations in the thermal conductivity with the concentration, temperature, and particle size of the graphene nanoparticles were studied separately, and experimental simulation calculations were carried out. The results were compared with lead–bismuth (LBE), sodium, and gallium as base fluids, as shown in Figures 4–6:

FIGURE 4

FIGURE 4. Thermal conductivity changes with nanoparticle concentration (T = 600 K, r = 20 nm).

FIGURE 5

FIGURE 5. Thermal conductivity change with temperature (φ = 0.2, r = 20 nm).

FIGURE 6

FIGURE 6. Thermal conductivity change with particle size (T = 600 K, φ = 0.2).

The results indicate that the specific thermal conductivity of the nanofluid improves with the increase in the concentration, and the thermal conductivity of the lead–bismuth-based liquid is greater than those of sodium and gallium. When the concentration reaches 20%, the thermal conductivity of the LBE base fluid increases by 80%. The thermal conductivity of the nanofluids improved with increasing temperature, whereas the change with temperature is relatively gentle. When considering the influence of temperature on the nanofluids, it can be considered as a factor. Under similar temperature conditions, the thermal conductivity of lead–bismuth-based nanofluids is greater than those of sodium and gallium. The thermal conductivity of nanofluids decreases with increasing particle size, and when the particle size is sufficiently small, the thermal conductivity decreases rapidly with increasing particle size. When the diameter of the subsequent nanoparticles (approximately 500 nm) increases or when they form agglomerates, the effect of the particle size on the thermal conductivity can be ignored. The thermal conductivity of the nanofluid is sensitive to changes in the concentration. To improve the thermal conductivity of the nanofluid, the volume fraction of the nanoparticle can be increased as much as possible under the premise of keeping the nanoparticle suspension stable.

Viscosity of Lead–Bismuth-Based Graphene Nanofluids

Rheological properties are vital to the heat transfer process of nanofluids. The rheological properties of nanofluids directly affect their heat transfer ability. Adding nanoparticles can help increase their viscosity. The volume concentration of the nanoparticles increases to a certain extent, and the fluid properties of the nanofluids will change from Newtonian to non-Newtonian. At this time, the fluid heat transfer is unfavorable (Aiguo et al., 2017).

The particle concentration, particle shape, particle size, base fluid density, and base fluid temperature affect the viscosity of nanofluids. The expression for the nanofluid viscosity is as follows:

${\mu }_{\text{eff}}=f\left({\mu }_f,\phi ,r,K,\xi ,T\right)(11)$

where μ_f is the viscosity of the fluid, φ is the volume fraction of the nanoparticles, r is the particle size, K is the particle shape coefficient, ξ is the electromotive force, which represents the electroviscous effect, and T is the temperature.

A nanofluid is essentially a special solid–liquid two-phase suspension system. Most scholars combined the classic suspension system viscosity ball theory model proposed by Einstein in 1906 (Einstein, 1905), combined with experiments to predict the law of viscosity change of nanofluids. The small-sphere model assumes that spherical particles are uniformly suspended in a diluted linear viscous fluid and that the suspended particles are rigid spheres with no charge on the surface or any interaction. The viscosity of the nanofluid can be expressed as:

$\frac{{\mu }_{\text{e}ff}}{{\mu }_f}=1+2.5\phi (12)$

where φ is the volume fraction of the nanoparticles.

Brinkman (1952) considered the interaction between particles on the basis of Einstein’s model, with the applicable range of the volume fraction extended to 4%. Brinkman’s model can be expressed as:

$\frac{{\mu }_{\text{e}ff}}{{\mu }_f}={\left(1-\phi \right)}^{-2.5}(13)$

Batchelor (1977) assumed that a nanofluid is a suspension of isotropic rigid spheres, considered the influence of Brownian motion, and proposed the following model:

$\frac{{\mu }_{eff}}{{\mu }_f}=1+2.5\phi +6.5{\phi }^2(14)$

Krieger and Dougherty (1959) proposed a semi-empirical formula assuming a spherical particle suspension at a high shear rate, which can be expressed as:

$\frac{{\mu }_{eff}}{{\mu }_f}={\left(1-\frac{\phi }{{\phi }_m}\right)}^{-2.5{\phi }_m}(15)$

where φ_m is the maximum volume fraction, which is approximately a constant of 0.605.

Thomas et al. (Su et al., 2013) proposed a viscosity calculation formula suitable for spherical particles with a high particle volume concentration.

$\frac{{\mu }_{eff}}{{\mu }_f}=1+2.5\phi +10.05{\phi }^2+0.00273e^{16.6\phi }(16)$

Based on the influences of the base fluid viscosity, particle concentration, and particle size on the viscosity of nanofluids, Corcione (2011) derived a formula for calculating the viscosity when the nanoparticle size is in the range of 25–200 nm.

$\frac{{\mu }_{eff}}{{\mu }_f}=\frac{1}{1-34.87{\left(d_p/d_f\right)}^{-0.3}{\phi }^{1.3}}(17)$

${\text{d}}_{\text{f}}=0.1{\left(\frac{6M}{N_A\pi {\rho }_{f0}}\right)}^{1/3}(18)$

where D_p is the nanoparticle diameter, M is the molar weight of the liquid, N_A is Avogadro’s constant, and ρ_f0 is the density of the base liquid at 303.15 K.

The viscosity calculation model of nanofluids is organized as shown in Table 3.

TABLE 3

TABLE 3. Viscosity calculation models for nanofluids.

Figure 7 shows the variation in the nanofluid viscosity with the concentration obtained using the above viscosity calculation model. As shown, the Massimo model is only suitable when the nanoparticle concentration is low. Other models reflect the effect of nanoparticle concentration on the viscosity of nanofluids, this is, the concentration of nanofluid increases with increase in the volume fraction of the nanoparticles. The improvement in viscosity is twofold when the concentration reaches 20%. To better predict the viscosity of higher-concentration lead–bismuth-based graphene nanofluids, the more accurate Thomas model can be selected.

FIGURE 7

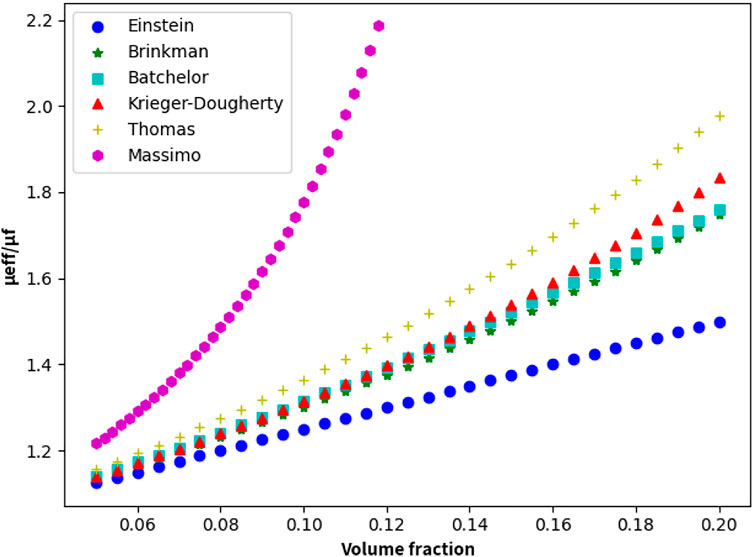
FIGURE 7. Different models used to predict the change in the nanofluid viscosity with particle concentration (T = 600 K).

For the relationship between the viscosity of the metal fluid and the temperature variation, the Vogel-Fulcher-Tammann (VFT) formula is commonly used (Xie et al., 1988). This formula can predict the nanofluid viscosity with temperature variation.

$\eta ={\eta }_0{e}^{\frac{A\times T_0}{T-T_0}}(19)$

where η₀, T₀, and A are specific parameters. Taking the logarithm on both sides of Eq. 19, finding that lnη has a linear relationship with 1/(T−T₀).

The viscosity of graphene nanofluid decreases with the increase in the temperature at low concentrations. Figure 8 shows its variation law, which is the same as the variation trend in the viscosity of the base fluid. With the increase in the concentration of graphene nanoparticles, the interaction force between the base fluid and the particles increases, thereby increasing the fluid viscosity.

FIGURE 8

FIGURE 8. Dynamic viscosity of nanofluids versus temperature (φ = 0.2).

Specific Heat Capacity of Lead–Bismuth-Based Graphene Nanofluid

The specific heat capacity is an important thermophysical property of reactor cooling fluids and represents the ability of a cooling medium to transfer and store heat. Pacheco et al. (Romero et al., 2002) reported that the specific heat capacity of conventional fluids must be higher than 2.25 J g⁻¹ K⁻¹ and should operate stably in the temperature range of 600–800°C in order to be competitive with fossil fuel-based energy in terms of pricing. For lead–bismuth cooled reactors, the specific heat capacity of the lead–bismuth base is relatively low, which is far from meeting this requirement. Improving the heat capacity of the lead–bismuth coolant can help reduce the amount of coolant required, decrease the volume of the body, and improve the heat storage capacity, heat transfer conductivity efficiency, and stability of the heat exchange system. Some researchers conducted extensive and in-depth studies on the heat capacity of nanofluids. A large number of experiments have proven that nanoparticles can effectively increase the specific heat capacity of the base fluid (Tiznobaik and Shin, 2013).

Specific Heat Capacity Enhancement Mechanism

Studies on the specific heat capacity enhancement mechanism of nanofluids have been mainly based on specific experimental characterization and calculation simulation prediction. Accordingly, researchers proposed three nanofluid specific heat capacity enhancement mechanisms (Ho and Pan, 2014):

1) Nanoparticles with higher specific heat capacity.

A higher specific heat capacity of the nanoparticles helps improve the specific heat capacity of the nanofluid. However, some researchers have pointed out that when SiO₂ nanoparticles are added to a base liquid of inorganic salts, such as nitrate, with a higher specific heat capacity, the specific heat capacity can also result in a higher strengthening effect than the base liquid. Therefore, the mechanism whereby the nanoparticles themselves improve the specific heat capacity remains to be discussed (Tian et al., 2020).

2) Specific surface energy of nanoparticles and thermal resistance of solid–liquid interface.

The specific surface area of nanoparticles is high because of their small-size effect; thus, the number of atoms on the surface accounts for the total number of atoms. More external atoms are active compared with the atoms close to the center because of the uneven force on the inside and outside, forming a higher vibration entropy. As a result, nanomaterials have a higher specific surface energy and specific heat capacity. The contact part between the nanoparticles and the base fluid has interface thermal resistance. The interface thermal resistance is higher because of its high specific surface area, which can bring additional heat storage. Thus, the specific heat capacity of the nanofluid is enhanced.

3) Formation of a semi-solid layer between the surface of the nanoparticle and the base fluid.

The surface of the nanoparticles adsorbs the molecules of the base fluid, and the liquid atoms form an aligned and ordered atomic arrangement, resulting in the formation of a semi-solid layer structure. The intermolecular bonding is tight because of the formation of a structure similar to the crystal structure, resulting in a potential barrier phenomenon in the semi-solid. Sufficient energy must be absorbed to break away from the constraints of the nanoparticles, which will increase the specific heat capacity of the nanofluids.

Calculation Model for Specific Heat Capacity

Currently, most studies have concentrated on medium and low-temperature nanofluids, with few studies on the specific heat capacity of high-temperature and high-heat-flux nanofluids. The established nanofluid specific heat capacity calculation models can be described as follows:

Pak and Cho (1998) proposed a nanofluid specific heat capacity model in 1998. This model is based on the mixing concept of an ideal gas mixture, called a simple mixing model. The formula is as follows:

$C_{peff}=\left(1-\phi \right)C_{pf}+\phi C_{pp}(20)$

where φ is the volume fraction of the nanoparticles, and C_peff, C_pf, and C_pp are the specific heat capacities of the nanofluids, base fluids, and nanoparticles, respectively.

Xuan and Roetzel (2000) considered the density factor and proposed a correction formula for the specific heat capacity of nanofluids as follows:

$C_{peff}=\frac{\left(1-\phi \right){\left(\rho C_p\right)}_f+\phi {\left(\rho C_p\right)}_p}{\left(1-\phi \right){\rho }_f+\phi {\rho }_p}(21)$

Based on the semi-solid layer model proposed by Shin and Banerjee (2014) and the heat transfer mechanism of the specific heat capacity, a semi-solid layer with a thickness of approximately 1 nm can be formed on the surface of the nanoparticles. Based on a high-temperature molten salt base, a new high-temperature nanofluid specific heat capacity calculation model has been proposed as follows:

$C_{peff}=\frac{{\phi }_p{\rho }_p{C}_{pp}+{\phi }_f{\rho }_f{C}_{pf}+{\phi }_s{\rho }_s{C}_{ps}}{{\phi }_p{\rho }_p+{\phi }_f{\rho }_f+{\phi }_s{\rho }_s}(22)$

The density of the semi-solid layer in this formula cannot be accurately measured using current observation and measurement data methods; therefore, the model needs to be improved and revised. Therefore, Shin et al. made the following assumptions: the thickness of the semi-solid layer structure was set to approximately 1 nm, and the density and specific heat capacity of the semi-solid were made equal to those of the nanoparticles. Based on the above assumptions, an improved specific heat capacity prediction model was proposed, as follows:

$C_{peff}=\frac{M_x{C}_{pp}+\frac{M\varphi }{m_p}{m}_{bs}{C}_{pbs}+\left(M-m\varphi -\frac{m\varphi }{m_p}{m}_{bs}\right)C_{pf}}{M}(23)$

${\text{m}}_{\text{p}}={\rho }_p{V}_p=\left({\rho }_p\pi D_p^3\right)/6(24)$

$m_{bs}={\rho }_{bs}{V}_{bs}={\rho }_{bs}\frac{4}{3}\pi \left[{\left(\frac{D_p}{2}+\delta +d\right)}^3-{\left(\frac{D_p}{2}+d\right)}^3\right](25)$

where C_peff, C_pp, C_pbs, and C_pf are the specific heat capacities of the nanofluid, nanoparticles, semi-solid layer, and base fluid, respectively; M, m_p, and m_bs are the total mass of the nanofluid, the mass of the nanoparticles, and the mass of the semi-solid layer structure, respectively; φ is the mass fraction of the nanoparticles; δ is the thickness of the semi-solid layer, and d is the gap width.

Fakoor Pakdaman et al. (2012) obtained the calculation model of the specific heat capacity in the temperature range of 313–343 K based on the correlation formula of the least-squares method and combined with the experimental data.

Alade et al. (2020) applied the genetic algorithm/support vector regression (GA/SVR) model to accurately evaluate nanoparticles in the volume fraction range of 3.7–9.3%.

The calculation model of specific heat capacity of nanofluid is organized as shown in Table 4.

TABLE 4

TABLE 4. Specific heat capacity calculation models for nanofluids.

The above model is used to analyze and study the addition of lead–bismuth-based graphene, as shown in Figure 9.

FIGURE 9

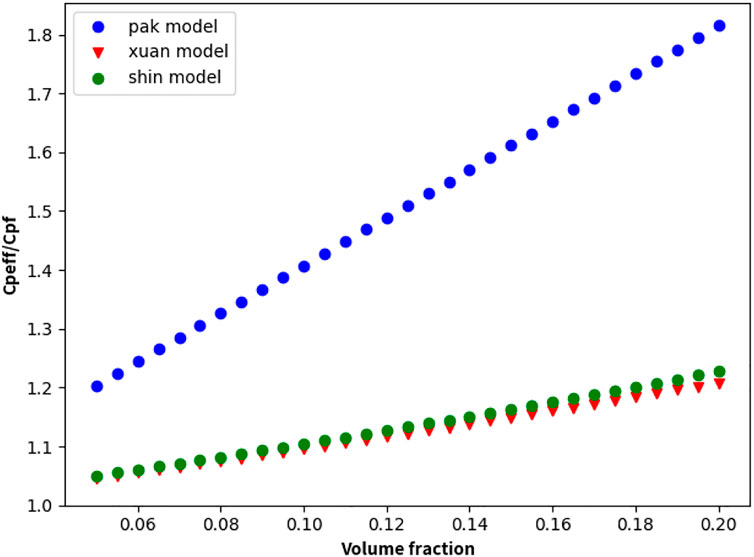
FIGURE 9. Variation in the specific heat capacity of lead–bismuth-based graphene nanofluid with nanoparticle concentration.

Studies have shown that nanoparticles can help effectively increase the specific heat capacity of the lead–bismuth base. However, in the case of Xuan’s and Shin’s models, finding that the improvement in the specific heat capacity of graphene is limited, approximately 20%. Based on existing experimental research on the specific heat capacity of nanofluids, Shin’s model more accurately reflects the change law of the specific heat capacity with the concentration.

Currently, although there are many theories, experiments, and models on the specific heat capacity of nanofluids, they are limited to model prediction and theoretical analysis of specific experimental data. It is difficult to accurately measure microstructures such as of semi-solid layers and liquid separation surfaces. Accurate theoretical mechanism and calculation models are lacking. In particular, there are few research results on high-temperature nanofluids, such as metal bases, and further investigation is required.

Conclusion

This study combined related research progress in existing nanofluids and thermal properties of lead–bismuth-based graphene nanofluids for analysis, research, and calculation. The following conclusions can be drawn from the study results:

1) On the premise of ensuring the stability of the nanofluid, the thermal conductivity of the nanofluid increases with increasing nanoparticle concentration. The thermal conductivity of the fluid can be increased by 80% when the concentration reaches 20%. The thermal conductivity of the nanofluids improves with increasing temperature, though the increase degree is limited. As the particle size of the nanoparticles increases, or with the occurrence of agglomeration, the particle size of the agglomerates formed by nanoparticles becomes larger, and the thermal conductivity of the nanofluid decreases. The particle size increases to a certain extent, and the impact on the thermal conductivity can be ignored.

2) Nanoparticle concentration and fluid temperature are both important parameters influencing the viscosity of the nanofluids. The viscosity of the nanofluids increases with the increase in the concentration and decrease in temperature. However, the other parameters affecting the nanofluids can only be determined experimentally, and the theoretical model for the viscosity of nanofluids needs to be further studied.

3) The current strengthening mechanism of the specific heat capacity of liquids by nanoparticles is not perfect. The measurement technology used for the specific heat capacity of nanofluids at high temperatures needs to be improved. The existing calculation model is limited to specific experimental characterization, and the prediction model cannot accurately reflect the general law of specific heat capacity of nanofluids. In recent years, some scholars have tried to calculate and study the specific heat capacity of nanofluids through molecular dynamics simulations, which is a new research direction for the strengthening mechanism of nanofluids.

In short, nanofluid technology has broad practical prospects for enhancing the thermophysical properties of metals such as lead and bismuth. The addition of graphene to a lead–bismuth stack coolant can effectively improve all aspects of its thermal and physical properties, reduce the amount of coolant required, increase the thermal power density, and reduce the volume and weight of the lead–bismuth stack, making it possible to implement lead–bismuth stacks in remote areas and ocean environments, thus providing a solid theoretical foundation.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

TY: Data curation, Writing—Original draft preparation. PZ: Supervision. QL: Conceptualization, Methodology. YZ: Visualization, Investigation. TY: Writing—Reviewing and Editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agarwal, D. K., Vaidyanathan, A., and Kumar, S. S. (2013). Synthesis and Characterization of Kerosene–Alumina Nanofluids[J]. Appl. Therm. Eng. 60 (1-2), 275–284. doi:10.1016/j.applthermaleng.2013.06.049

CrossRef Full Text | Google Scholar

Alade, I. O., Rahman, M. A. A., and Saleh, T. A. (2020). An Approach to Predict the Isobaric Specific Heat Capacity of Nitrides/ethylene Glycol-Based Nanofluids Using Support Vector Regression. J. Energ. Storage 29, 101313. doi:10.1016/j.est.2020.101313

CrossRef Full Text | Google Scholar

Balanta, A., Godard, C., and Claver, C. (2011). Pd Nanoparticles for C-C Coupling Reactions. Chem. Soc. Rev. 40 (10), 4973–4985. doi:10.1039/c1cs15195a

PubMed Abstract | CrossRef Full Text | Google Scholar

Batchelor, G. K. (1977). The Effect of Brownian Motion on the Bulk Stress in a Suspension of Spherical Particles. J. Fluid Mech. 83 (1), 97–117. doi:10.1017/s0022112077001062

CrossRef Full Text | Google Scholar

Ben-Abdallah, P. (2006). Heat Transfer through Near-Field Interactions in Nanofluids. Appl. Phys. Lett. 89 (11), 113117. doi:10.1063/1.2349857

CrossRef Full Text | Google Scholar

Brinkman, H. C. (1952). The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 20 (4), 571. doi:10.1063/1.1700493

CrossRef Full Text | Google Scholar

Choi, S. U. S., and Eastman, J. A. (1995). Enhancing thermal Conductivity of Fluids with nanoparticles[R]. IL (United States): Argonne National Lab.

Chu, K., Li, W.-S., and Tang, F.-l. (2013). Flatness-dependent thermal Conductivity of Graphene-Based Composites. Phys. Lett. A 377 (12), 910–914. doi:10.1016/j.physleta.2013.02.009

CrossRef Full Text | Google Scholar

Corcione, M. (2011). Empirical Correlating Equations for Predicting the Effective thermal Conductivity and Dynamic Viscosity of Nanofluids. Energ. Convers. Manag. 52 (1), 789–793. doi:10.1016/j.enconman.2010.06.072

CrossRef Full Text | Google Scholar

Demirkır, Ç., and Ertürk, H. (2020). Rheological and thermal Characterization of Graphene-Water Nanofluids: Hysteresis Phenomenon[J]. Int. J. Heat Mass Transfer 149, 119113. doi:10.1016/j.ijheatmasstransfer.2019.119113

Google Scholar

Einstein, A. (1905). Eine neue bestimmung der moleküldimensionen[D]. Zürich: ETH Zurich.

Einstein, A. (1956). Investigations on the Theory of the Brownian Movement[M]. Chelmsford, Massachusetts, USA: Courier Corporation.

Fakoor Pakdaman, M., Akhavan-Behabadi, M. A., and Razi, P. (2012). An Experimental Investigation on Thermo-Physical Properties and Overall Performance of MWCNT/heat Transfer Oil Nanofluid Flow inside Vertical Helically Coiled Tubes. Exp. Therm. Fluid Sci. 40, 103–111. doi:10.1016/j.expthermflusci.2012.02.005

CrossRef Full Text | Google Scholar

Hamilton, R. L., and Crosser, O. K. (1962). Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fund. 1 (3), 187–191. doi:10.1021/i160003a005

CrossRef Full Text | Google Scholar

Ho, M. X., and Pan, C. (2014). Optimal Concentration of Alumina Nanoparticles in Molten Hitec Salt to Maximize its Specific Heat Capacity. Int. J. Heat Mass Transfer 70, 174–184. doi:10.1016/j.ijheatmasstransfer.2013.10.078

CrossRef Full Text | Google Scholar

Koo, J., and Kleinstreuer, C. (2005). Impact Analysis of Nanoparticle Motion Mechanisms on the thermal Conductivity of Nanofluids. Int. Commun. Heat mass transfer 32 (9), 1111–1118. doi:10.1016/j.icheatmasstransfer.2005.05.014

CrossRef Full Text | Google Scholar

Krieger, I. M., and Dougherty, T. J. (1959). A Mechanism for Non-newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheology 3 (1), 137–152. doi:10.1122/1.548848

CrossRef Full Text | Google Scholar

Leal, L. G. (1973). On the Effective Conductivity of a Dilute Suspension of Spherical Drops in the Limit of Low Particle Peclet Number. Chem. Eng. Commun. 1 (1), 21–31. doi:10.1080/00986447308960412

CrossRef Full Text | Google Scholar

Lei, H., and Zhang, L. (2017). Research on the Physical Properties and Application of Graphene[J]. J. Shangrao Normal Univ. 37 (06), 37–40.

CrossRef Full Text | Google Scholar

Li, Z., Guo, H., Chang, Z., et al. (2020). Development and Military Application of Foreign lead-bismuth Reactors[J]. Foreign Nucl. News 2020 (07), 29–31.

Google Scholar

Ma, K. (2008). Research on the Heat Dissipation Method of Liquid Metal chips[D]. Beijing: Graduate University of Chinese Academy of Sciences (Technical Institute of Physics and Chemistry).

Ma, K.-Q., and Liu, J. (2007). Nano Liquid-Metal Fluid as Ultimate Coolant. Phys. Lett. A 361 (3), 252–256. doi:10.1016/j.physleta.2006.09.041

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1904). A Treatise on Electricity and Magnetism. 2nd ed[M]. Cambridge, U.K: Oxford University Press.

Men, Y. (2010). Research on the Flow and Heat Transfer Characteristics of Liquid Metal and nanofluids[D]. Harbin: Harbin Institute of Technology.

Nie, C., Marlow, W. H., and Hassan, Y. A. (2008). Discussion of Proposed Mechanisms of thermal Conductivity Enhancement in Nanofluids[J]. Int. J. Heat Mass transfer 51 (5-6), 1342–1348. doi:10.1016/j.ijheatmasstransfer.2007.11.034

CrossRef Full Text | Google Scholar

Pak, B. C., and Cho, Y. I. (1998). Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles. Exp. Heat Transfer 11 (2), 151–170. doi:10.1080/08916159808946559

CrossRef Full Text | Google Scholar

Qiao, F. (2010). Preparation and Properties of Ag and Graphene nanofluids[D]. Qingdao: Qingdao University of Science and Technology.

Romero, M., Buck, R., and Pacheco, J. E. (2002). An Update on Solar Central Receiver Systems, Projects, and Technologies. J. Sol. Energ. Eng. 124 (2), 98–108. doi:10.1115/1.1467921

CrossRef Full Text | Google Scholar

Shin, D., and Banerjee, D. (2014). Specific Heat of Nanofluids Synthesized by Dispersing Alumina Nanoparticles in Alkali Salt Eutectic. Int. J. Heat Mass Transfer 74, 210–214. doi:10.1016/j.ijheatmasstransfer.2014.02.066

CrossRef Full Text | Google Scholar

Shu, Yu. (2019). Thermophysical Properties and Flow and Heat Transfer Characteristics of Water-Based Graphene nanofluids[D]. Mianyang: Southwest University of Science and Technology.

Shukla, K. N., Koller, T. M., Rausch, M. H., and Fröba, A. P. (2016). Effective thermal Conductivity of Nanofluids - A New Model Taking into Consideration Brownian Motion. Int. J. Heat Mass Transfer 99, 532–540. doi:10.1016/j.ijheatmasstransfer.2016.03.129

CrossRef Full Text | Google Scholar

Si, A., Wang, H., Gao, Y., et al. (2017). Experimental Study on Viscosity of Water-Based Graphene Nanofluid[J]. Henan Sci. Technol. 2017 (05), 134–136.

Google Scholar

Su, Z., Zhou, T., Liu, M., and Zou, W. (2013). Study on the Thermophysical Properties of Liquid lead-bismuth Alloy[J]. Nucl. Technol. 36 (09), 37–41.

Google Scholar

Tian, H., Zhou, J., and Guo, C. (2020). Progress of Specific Heat Enhancement of Molten Salt thermal Energy Storage Materials[J]. Chem. Industry Eng. Prog. 39 (2), 584–595. doi:10.16085/j.issn.1000-6613.2019-0798

Google Scholar

Tiznobaik, H., and Shin, D. (2013). Enhanced Specific Heat Capacity of High-Temperature Molten Salt-Based Nanofluids. Int. J. Heat Mass Transfer 57 (2), 542–548. doi:10.1016/j.ijheatmasstransfer.2012.10.062

CrossRef Full Text | Google Scholar

Wang, J. J., Zheng, R. T., Gao, J. W., and Chen, G. (2012). Heat Conduction Mechanisms in Nanofluids and Suspensions. Nano Today 7 (2), 124–136. doi:10.1016/j.nantod.2012.02.007

CrossRef Full Text | Google Scholar

Wu, J. M., and Zhao, J. (2013). A Review of Nanofluid Heat Transfer and Critical Heat Flux Enhancement-Research gap to Engineering Application. Prog. Nucl. Energ. 66, 13–24. doi:10.1016/j.pnucene.2013.03.009

CrossRef Full Text | Google Scholar

Wu, T., Liu, J., Chen, B., Du, L., and Yang, W. (2020). Research Progress on Nanofluid Fuel Stability and Metal Particle Modification Methods[. J].Propulsion Technol. 41 (03), 481–492. doi:10.13675/j.cnki.tjjs.190313

Google Scholar

Xie, C., Tian, Y., and Bao, Y. (1988). Viscosity of Liquid alloy Al-4.5 Cu[D]. Journal of Northwestern Polytechnical University 2, 219–227.

Xuan, Y., and Roetzel, W. (2000). Conceptions for Heat Transfer Correlation of Nanofluids. Int. J. Heat Mass transfer 43 (19), 3701–3707. doi:10.1016/s0017-9310(99)00369-5

CrossRef Full Text | Google Scholar

Yimin, X., Hu, W., and Li, Q. (2002). Simulation of the Aggregation Structure and thermal Conductivity of Nanofluids[J]. J. Eng. Thermophys. 2002 (02), 206–208.

Google Scholar

Yimin, X. (2014). Index. Sci. China:Technical Sci. 44 (03), 269–279. doi:10.1215/9780822377016-017

CrossRef Full Text | Google Scholar

Yimin, X. (2014). Nanofluid Energy Transfer Theory and Application[J]. Sci. China: Technol. Sci. 44 (03), 269–279. doi:10.1360/092013-1236

Google Scholar

Zhao, G., Cao, L., Song, L., and Lu, T. (2013). Research and Analysis on the Heat Conduction Mechanism of Nanofluids[J]. J. Shenyang Univ. Aeronautics Astronautics 30 (04), 7–11.

Google Scholar

Zhou, X., Jiang, Y., Wang, Y., Jiang, Y., and Huang, H. (2020). Comprehensive Heat Transfer Performance Analysis of Liquid Metal Based Nanofluid Laminar Flow in Circular Tube. Int. J. Mech. Sci. 175, 105530. doi:10.1016/j.ijmecsci.2020.105530

CrossRef Full Text | Google Scholar