An Equivalent Rotor Speed Compensation Control of PMSG-Based Wind Turbines for Frequency Support in Islanded Microgrids

Frequency regulation is a critical issue in the islanded microgrids, especially the integration of high penetration of the wind power generator. In order to provide inertial and primary frequency support to the wind power system, this article proposes an equivalent rotor speed compensation control scheme of PMSG for frequency support in the islanded microgrids. A new variable combining pitch angle and rotor speed is defined as the equivalent rotor speed. The equivalent rotor speed versus de-loaded power curve is designed to preserve a part of active power among the whole wind speed area. And the inertia control scheme is optimized by adding a virtual compensation variable to the equivalent rotor speed to obtain the reference of the machine-side converter control loop. Adopting the proposed scheme, the PMSG-based wind turbine can achieve a similar frequency regulation performance to synchronous generators. Simulation results demonstrate the feasibility and effectiveness of the proposed control scheme.

Introduction

With the rapid development of renewable energy in recent years, distributed power generation technologies such as photovoltaics (PV), wind power, and biogas have attracted more and more attention from the international community due to their cleanliness, low energy consumption, and flexible control (Li et al., 2016). At the same time, microgrids that can effectively integrate distributed energy sources have gradually become an important part of modern power grids.

Wind power is mostly connected to the grid through power electronic converters, which lack the kinetic energy (KE) of the rotor and cannot provide inertia to the grid. Wind power usually operates in the maximum power point tracking (MPPT) mode, and its output is random and volatile, which makes it unable to participate in the frequency and voltage regulation of the grid (Adam et al., 2015). Therefore, high penetration of wind powers brings about the frequency stability issue due to the reduction of the overall inertia and primary frequency capability (Zhao et al., 2019; Zhu et al., 2021a). An approach for alleviating the above problems is that wind power participates in the frequency response of the grid.

The existing approaches for variable speed wind turbines (VSWTs) can be divided into inertial control and de-loaded control. In inertial control, the VSWTs operate in MPPT mode, and the rotational kinetic energy (KE) is released to deliver temporary power for improving inertial response. Mostly, inertial control is to change the active power in proportion to the rate of change of frequency or frequency deviation or both of them (Sun et al., 2019; Zeng et al., 2019). For compromise of the frequency regulation performance and rotor speed safe operation, some adaptive gains methods were proposed (Zhang et al., 2012; Zhao et al., 2015; Wu et al., 2019; Zhao et al., 2020). In (Zhao et al., 2015), the control gains of frequency regulation schemes (FRS) under different wind speeds are adjusted based on the wind speed. In (Wu et al., 2019), the gains of additional frequency deviation loops are adaptively tuned depended on the rotor speed measurement. In (Zhao et al., 2020), time-varying gains determined based on desired frequency-response time are designed to raise frequency nadir and to eliminate frequency second drop. In (Zhang et al., 2012), an adaptive droop gain is designed, which is a function of real-time rotor speed and wind power penetration level.

For the de-loaded control, a part of the active power of VSWTs can be reserved through the pitch angle control, the overspeed control, or the combination of both (Chang-Chien et al., 2011; Margaris et al., 2012; Zertek et al., 2012; Wu et al., 2018; Luo et al., 2019; Tang et al., 2019).

Based on the de-loaded control, the droop control is adopted to akin to the synchronous generators, which can provide minutes-term primary frequency support. In (Gao et al., 2019), a comprehensive frequency regulation scheme that combines the stepwise inertial control and variable-droop control is proposed. A coordinated control scheme that flexibly switches between additional power control, tracking curve control, and pitch angle adjustment control at different start-up stages is proposed, which can effectively improve insufficient frequency support. A variable-droop control scheme that considers optional rotor KE is proposed in (Liu et al., 2019). However, the rotor KE estimation required the wind speed information and parameters of the wind turbine. Some adaptive gains methods are proposed in (Lee et al., 2016; Wu et al., 2019; Zhao et al., 2020), which introduce the additional frequency increase of inertia control into the power control loop by adjusting the parameters of the additional signal.

Due to the rotor speed limit, the overspeed de-loaded control is only adapted for low wind areas. Therefore, in (Zhang et al., 2012), three wind speed areas are defined: low wind speed area where de-loaded operation is merely by the rotor speed control; medium wind speed area where de-loaded operation is conducted by the combining pitch angle control and the rotor speed control; and high wind speed area where the modified pitch angle control is conducted alone. However, it required accurate wind speed information to determine the wind speed area, and the calculation of de-loaded power reference needs both parameters of wind turbine and wind speed. In (Chang-Chien et al., 2014), since the power output is controlled only by pitch adjustment, they continually activate the pitch regulation over the whole wind speed region. Thus, the frequent pitch activation inevitably increases pitch servo fatigue and blade stress. In (Tang et al., 2019), the strategy can make full use of the inertial response of wind turbine generators (WTGs) at all pitch positions to sustain the dispatched active power and the blade loads of wind turbines are alleviated.

Compared with doubly fed induction generator-based wind turbine generation (DFIG-WTG), permanent magnet synchronous generator-based wind turbine generation (PMSG-WTG) can provide a much stronger inertial response thanks to their full power converter, and it accommodates a wider range of rotor speed (Wu et al., 2016). In most literature, FRS are designed based on the power tracking control for DFIG-WTG. The additional power from the supplementary control loop is added to the maximum power reference or de-loaded power reference to provide frequency support.

However, for PMSG-WTG, rotor speed tracking is an alternative attractive control method that rotor speed is directly manipulated to captured wind energy. Only a few studies are focused on the FRS based on rotor speed control. An algorithm to extract the maximum KE without stalling wind turbine (WT) is proposed in (Kayikci and Milanovic, 2009), in which the electric torque is increased stepwise by increasing the rotor speed of the WT to provide virtual inertia. However, the mechanical torque was assumed constant in this study. In (LI et al., 2017), an additional reference torque is added on the torque reference of the generator-side converter to respond to the change of system frequency. In (Zhu et al., 2021b), the comprehensive coordinated control strategy containing a variable coefficient integrated inertial control and virtual capacitor control is proposed.

The purpose of this study is to investigate a new FRS for PMSG-WTG based rotor speed control during the whole wind speed area. A combined variable of rotor speed and de-loaded compensation pitch angle is defined and named “equivalent rotor speed”, which helps to realize the de-loaded control during the whole wind speed area. The inertial and primary frequency response is generated through adding a virtual rotor speed deviation, which results in the rotor speed or pitch angle adjustment being coupled with grid frequency deviation to increase or decrease active power output.

The remainder of this article is organized as follows: in Section The Traditional Frequency Regulation Scheme for PMSG-WTG, the conventional rotor speed control structure of PMSG-WTG is introduced; in Section The Proposed Frequency Regulation Scheme, the basic principle of the proposed scheme is introduced in detail, including the equivalent rotor speed versus de-loaded power curve and the calculation scheme of the virtual compensation variable to change the reference rotor speed; and in Section Case Study, a simulation model of an islanded microgrid is built, and the proposed scheme is compared with the method in (LI et al., 2017). The effectiveness of the proposed control scheme participating in the system frequency response under various wind speed and load changes is verified. Finally, a brief conclusion is drawn in Section Conclusion.

The Traditional Frequency Regulation Scheme for PMSG-WTG

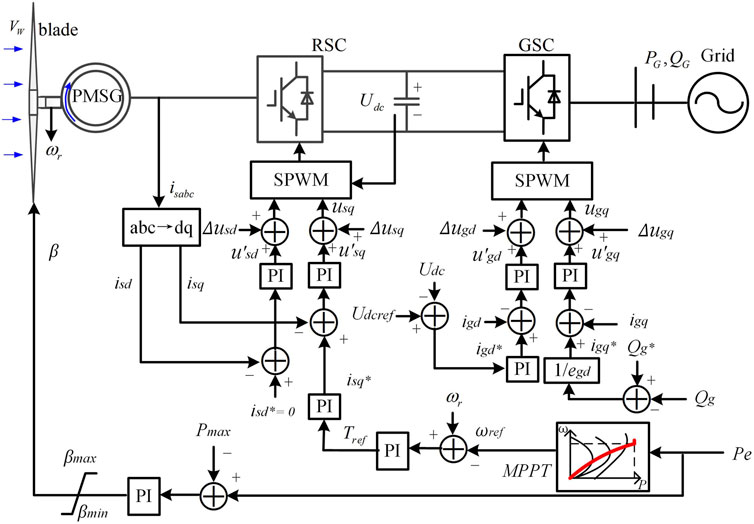
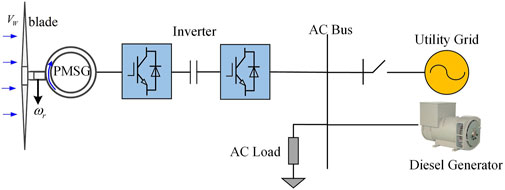
The diagram of PMSG-WTG based rotor speed control strategy modeling (Hu et al., 2017) is shown in Figure 1, which is mainly composed of wind turbines, PMSG and power electronic converters. The aerodynamic rotor of the WT is directly coupled to the PMSG without any gearbox. The PMSG is connected to the grid through the machine-side converter (MSC) and the grid-side converter (GSC) to control the generator’s speed and power.

FIGURE 1

FIGURE 1. Block diagram of a model of the PMSG based wind turbine Generators.

The captured mechanical power from the wind, P_m, is defined by (Sun et al., 2019)

$P_{\text{m}}=\frac{1}{2}\rho \pi R^2{v}_w^3{C}_{\text{p}}\left(\lambda ,\beta \right),(1)$

where ρ is air density, R is radius, v_w is wind speed, λ is tip speed ratio, λ = ω_rR/v_w, ω_r is rotor speed, β is pitch angle, and C_p(λ,β) is the power coefficient.

As in (Ekanayake and Jenkins, 2004), C_p(λ,β) can be expressed as

$C_{\text{p}}\left(\lambda ,\beta \right)=(0.44-0.0167\beta )sin\left[\frac{\pi (\lambda -3)}{5-0.3\beta }\right]-0.00184(\lambda -3)\beta .(2)$

A maximum mechanical power rotor speed characteristic curve is pre-defined, and the rotor speed reference is inquired according to the electromagnetic power measurement (Sun et al., 2019). When the wind speed increases, the rotor speed of the WT accelerates due to the increase in the captured power P_m. In order to achieve the balance of the system, the electromagnetic power P_e controlled by the rotor speed controller increases. The increased P_e flows into the DC link capacitor. Then, the GSC injects the active power delivered by the MSC into the power grid to maintain a constant DC link voltage. When the wind speed continues to increase and the electromagnetic power reaches the rated power, the pitch angle control starts to act to ensure that the wind turbine runs at constant power.

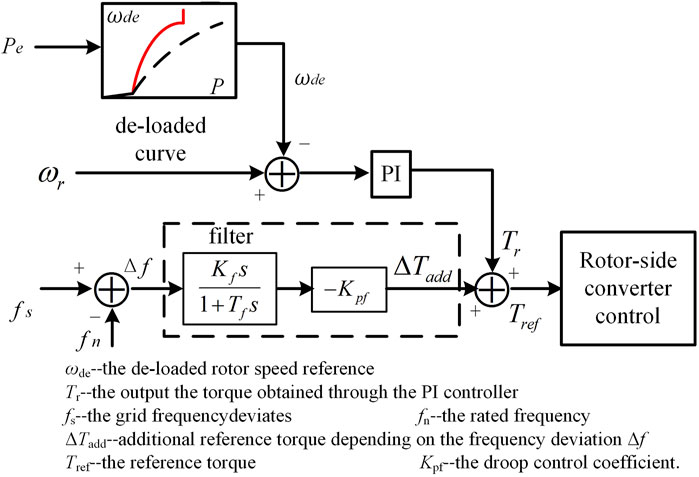
However, this type of wind turbine runs in the maximum power tracking mode and cannot respond to the frequency variation of the system. In (LI et al., 2017), a typical frequency regulation scheme that the torque is adjusted according to frequency deviation is proposed, as shown in Figure 2.

FIGURE 2

FIGURE 2. Traditional frequency regulation control scheme.

The maximum power tracking control mode is instead of a de-loaded power tracking mode. The de-loaded rotor speed reference, ω_de, is provided for the speed controller, and the output of the torque T_r is obtained through the PI controller. When the grid frequency f_s deviates from the rated frequency f_n, an additional reference torque ΔT_add depending on the frequency deviation Δf is added on T_r. Then, the reference torque T_ref is obtained and transmitted to the inner control loop. The captured active power is adjusted by the inner loop response and the rotor speed tracks ω_de. Due to the rapid regulation effects of the GSC control system, the GSC and then the active power from MSC are immediately injected into the grid to maintain a constant DC link voltage.

The additional reference torque ΔT_add is determined according to the frequency deviation Δf and the droop control coefficient K_pf, which can be expressed as

$\Delta T_{\text{add}}=-K_{\text{pf}}\Delta f.(3)$

However, the additional ΔT_add has a conflict with the speed controller. T_r from the speed controller is used to regulate the rotor speed tracking the reference value. ΔT_add is dependent on the frequency deviation. This conflict influences both speed regulation and frequency support. At the same time, this scheme does not consider the coordination of the torque control and the pitch angle control. In the medium and high wind speed area, pitch angle control is necessary to regulate the active power due to the rotor speed limit. Further, K_pf is a fixed value, which cannot be changed adaptively under different wind speed conditions. When the wind speed is in the low area, the additional reference torque ΔT_add is too large, which causes the rotor speed to drop too fast. When the wind speed is in the high area, the additional reference torque ΔT_add for the frequency regulation will be insufficient.

The Proposed Frequency Regulation Scheme

The Block Diagram of the Proposed Frequency Regulation Scheme

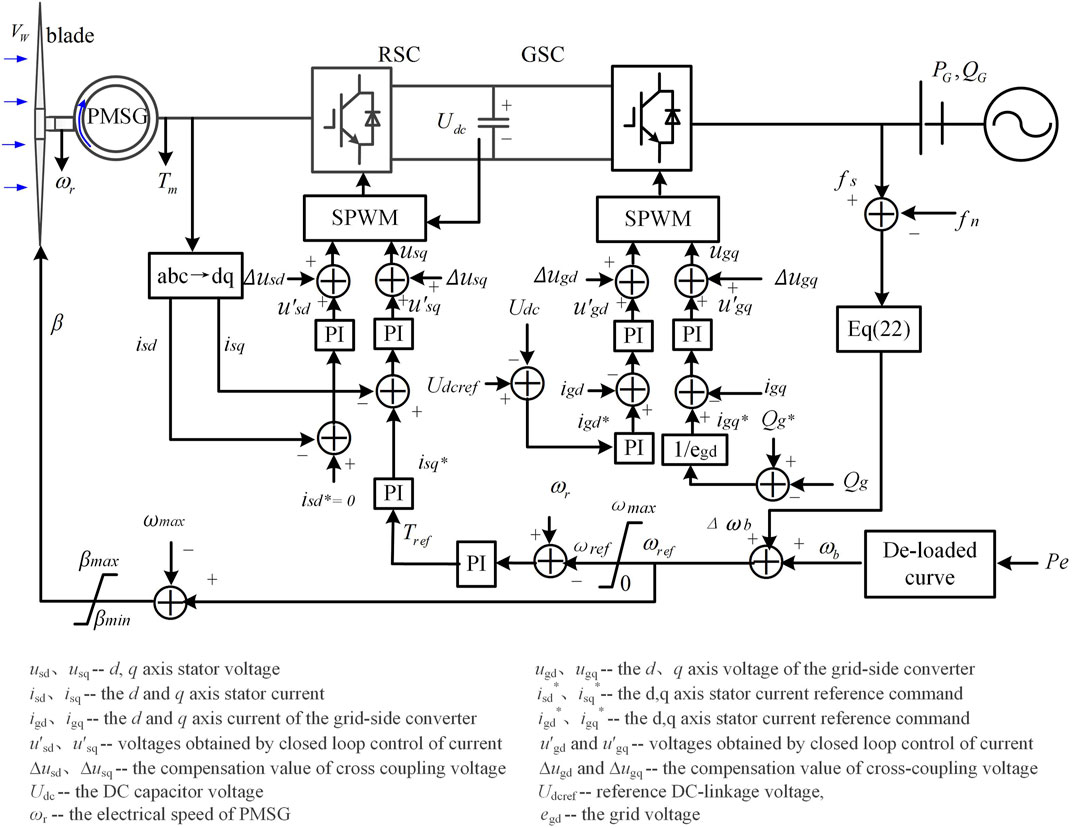
The block diagram of the scheme proposed in this article is shown in Figure 3.

FIGURE 3

FIGURE 3. The proposed frequency regulation scheme.

To realize the de-loaded control for PMSG during the whole wind speed range, this article defines a new variable, named equivalent rotor speed "ω_b" here, which combines the rotor speed and the de-loaded pitch angle.

${\omega }_{\mathbf{b}}={\omega }_{\mathbf{de}}+{\beta }_{\mathbf{de}}.(4)$

ω_de is de-loaded rotor speed in the low wind speed area and β_de is the de-loaded pitch angle in the medium and high wind speed area.

Further, the equivalent rotor speed versus de-loaded power curve is obtained through the wind turbine modeling data fitting. Depending on this curve, the corresponding ω_b can be queried according to the electromagnetic power P_e. The detail is given in subsection The Equivalent Rotor Speed-Active Power Curve below.

To directly couple grid frequency with rotor speed, a compensation variable Δω_b is obtained based on the frequency deviation. By adding the Δω_b on ω_b, the reference rotor speed ω_ref is obtained

${\omega }_{\mathbf{ref}}={\omega }_{\mathbf{b}}+\Delta {\omega }_{\mathbf{b}}.(5)$

Since the equivalent rotor speed ω_b contains the sum of the per-unit value of the rotor speed and pitch angle, these two values should be separated to obtain rotor speed reference or pitch angle reference for the controller. Fortunately, pitch angle act only when the rotor speed reaches ω_max (1. p.u in this article). Hence, a limiter is added behind the equivalent rotor speed ω_ref. When ω_ref is less than ω_max, ω_ref is directly used as the reference value of the rotor speed control loop. When ω_ref is larger than ω_max, the rotor speed reference is ω_max, and the pitch angle reference β_ref can be obtained by subtracting ω_max from ω_ref. Hence, the pitch angle can help the de-loaded control and response to frequency variation when ω_ref exceeds ω_max. How to obtain Δω_b is explained in subsection The Calculation Method of the Virtual Compensation Rotor Speed below.

The Equivalent Rotor Speed-Active Power Curve

As in (Zhang et al., 2012), the de-loaded rotor speed and de-loaded pitch angle can be calculated by the following expressions:

$\{\begin{array}{c}{C}_{\mathbf{p,de}}\left({\lambda }_{\mathbf{de}},0\right)=\left(1-d\%\right)C_{\mathbf{p,max}}\left({\lambda }_{\mathbf{opt}},0\right)v_1<v<v_2\\ C_{\mathbf{p,de}}\left({\lambda }_{\mathbf{ref}},{\beta }_{\mathbf{de}}\right)=\left(1-d\%\right)C_{\mathbf{p,max}}\left({\lambda }_{\mathbf{opt}},0\right)v_2<v<v_3\\ C_{\mathbf{p,de}}\left({\lambda }_{\mathbf{ref}},{\beta }_{de}\right)=\left(1-d\%\right)C_{\mathbf{p,rated}}\left({\lambda }_{\mathbf{ref}},{\beta }_0\right)v_3<v.\end{array}(6)$

where v₁ is the cut-in wind speed, v₂ is the demarcation point of the wind speed between the low and medium wind speed area, v₃ is the demarcation point of the wind speed between the medium and high wind speed area, λ_opt is the optimal tip speed ratio, and C_p,max is the maximum wind energy capture coefficient. λ_de is the tip speed ratio when de-loaded ratio is d%, λ_ref is the reference tip speed ratio in overspeed control and, C_p,rated is the wind energy capture coefficient when operating at rated power, β₀ is the pitch angle reference when the wind turbines operate at the rated power, β_de is the de-loaded pitch angle in the de-loaded control mode, and d% is the de-loaded ratio of the wind turbine. The de-loaded ration d% is given 10% in this article.

In the low wind speed, λ_opt and C_p,max can be obtained through Eq. 2. Hence, λ_de can be calculated by Eq. 6, and then we can calculate ω_de by λ_de= ω_deR/v.

In the medium wind area, λ_ref= ω_maxR/v, λ_opt and C_p,max have been obtained through Eq. 2. The pitch angle (β_de) can be calculated through Eq. 6.

In the high wind area, we can calculate C_p,rated by Eq. 1. Then, because λ_ref has been known, β₀ can be obtained by Eq. 2. Hence, β_de can be obtained by Eq. 6.

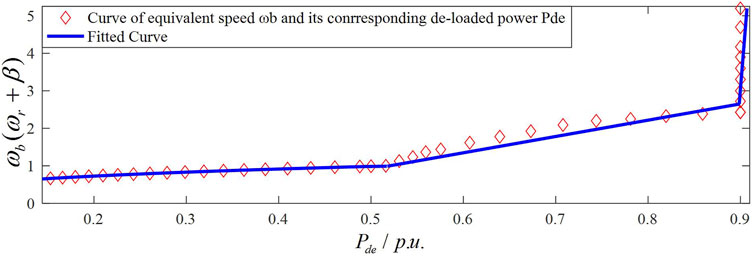
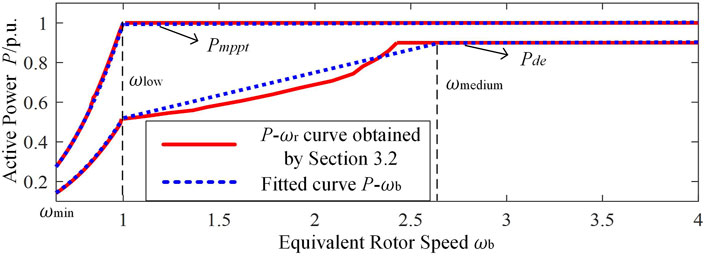
Therefore, based on Eq. 4 and Eq. 6, the offline fitting data of the de-loaded power P_de and ω_b under different wind speed areas can be obtained. The data and the fitting ω_b-P_de curve is shown in Figure 4.

FIGURE 4

FIGURE 4. The equivalent rotor speed ω_b active power P_de curve.

FIGURE 5

FIGURE 5. The active power equivalent rotor speed ω_b curve in the whole wind speed area.

Corresponding to wind speed area, the ω_b-P_de curve can be divided into three segments. The first segment is the low wind speed area, where P_de is less than 0.53 p.u. The pitch angle control is disabled; that is, β is 0. According to Eq. 4, ω_b is equal to ω_de. The second segment is the medium wind speed area, where the power is greater than 0.53 p.u. The third one is the high wind speed area, where P_de is greater than or equal to 0.9 p.u. In the second and the third segments, pitch angle control is enabled.

Considering the accuracy and complexity, the following piecewise function is employed to fit the ω_b-P_de curve:

${\omega }_b=\{\begin{array}{l}{k}_1\sqrt[3]{P_{\mathrm{de}}}\begin{array}{cc}& P_{\mathrm{de}}\end{array}\le 0.53\mathrm{p}\mathrm{.u}\mathrm{.}\\ \frac{P_{\mathrm{de}}-b_3}{k_3}\begin{array}{cc}& 0.53\mathrm{p}\mathrm{.u}\mathrm{.}<P_{\mathrm{de}}\le 0.9\mathrm{p}\mathrm{.u}.\end{array}\\ \frac{P_{\mathrm{de}}-b_4}{k_4}\begin{array}{cc}& P_{\mathrm{de}}\ge 0.9\mathrm{p}\mathrm{.u}\mathrm{.}\end{array}\end{array}(7)$

By using the curve fitting tool to perform linear regression on the offline data, the value of each fitting parameter in Eq. 7 can be obtained, which are as follows: k₁ = 0.5218; k₃ = 0.2393; b₃ = 0.29; k₄ = 0.003; and b₄ = 0.89.

The Calculation Method of the Virtual Compensation Rotor Speed

The virtual compensation rotor speed Δω_b is introduced to generate both inertial and primary frequency responses. In Section The Equivalent Rotor Speed-Active Power Curve, Eq. 7 has been obtained, which describes the relationship between the de-loaded power P_de and the equivalent rotor speed ω_b. According to the inverse function of Eq. 7, we can obtain the P-ω_b curve as in

$P_{\mathrm{de}}=\{\begin{array}{l}{k}_1{\omega }_b^3\begin{array}{cc}& {\omega }_{\min }<{\omega }_{\mathrm{b}}\end{array}\le {\omega }_{\mathrm{b}\mathit{low}}\\ k_3{\omega }_{\mathrm{b}}+b_3\begin{array}{cc}& {\omega }_{\mathrm{b}low}<\omega \le {\omega }_{\mathrm{b}medium}\end{array}\\ k_4{\omega }_{\mathrm{b}}+b_4\begin{array}{cc}& \omega \ge {\omega }_{\mathrm{b}medium}.\end{array}\end{array}(8)$

where ω_min is the cut-in rotor speed of the WT and ω_blow is the demarcation equivalent rotor speed between the low wind speed area and the medium wind speed area. The value of ω_blow is equal to the rated rotor speed ω_max, which is 1 p.u. ω_bmedium is the demarcation equivalent rotor speed between the medium wind speed area and the high wind speed area, and its value is 2.6 p.u. When ω_b exceeds ω_bmedium, the active power should be kept constant.

The maximum power curve can be approximately is give in

$P_{\mathbf{mppt}}=\{\begin{array}{l}{k}_2{\omega }_b^3{\omega }_{\min }<{\omega }_{\mathrm{b}}\le {\omega }_{\mathrm{b}low}\\ \frac{k_4{\omega }_{\mathrm{b}}+b_4}{k_4}+0.1{\omega }_{\mathrm{b}}\ge {\omega }_{\mathrm{b}low}\end{array}.(9)$

where k₂ is the maximum power coefficient, k₂ = 0.98.

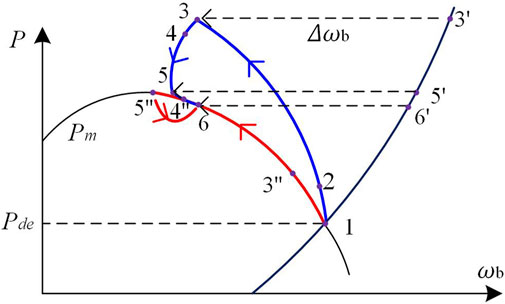
The P_de-ω_b curve and P_mppt-ω_b curve in the low wind speed area are given in Figure 6. Assume that PMSG-WTG initially operates at the de-loaded stable point 1′.

FIGURE 6

FIGURE 6. The active power equivalent rotor speed ω_b curve in the low wind speed area.

Generally, the output active power of PMSG is regulated based on the frequency deviation Δf, and its expression is

$\Delta P_e= -\frac{\Delta P_{max}}{(f_b-f_a)}\Delta f,(10)$

where ΔP_max is the maximum frequency regulation power, f_a and f_b correspond to the system frequency regulation interval, and ΔP_max is the limit frequency regulation power.

To prevent the rotor speed lower than the optimal rotor speed during the frequency regulation process, the value of ΔP_max is the difference between the maximum power P_mppt and the de-loaded power with maximum power rotor speed ω_b2, that is,

$\Delta P_{\mathbf{max}}=P_{\mathbf{2}}-P_{\mathbf{3}}=k_{\mathbf{2}}{\omega }_{b2}^3-k_{\mathbf{1}}{\omega }_{b2}^3,(11)$

where P₂ is the maximum power at operating point ‘2′ and P₃ is the de-loaded power with maximum power rotor speed at point ‘3'.

Assuming a frequency dips event occurs, the electromagnetic power P_e should increases, which is equivalent to an increase of the rotor speed Δω_b′

$P_1\prime =P_1+\Delta P_{\mathbf{e}}=k_1{({\omega }_{\mathrm{b1}}+\Delta {\omega }_{\mathbf{b}}\prime )}^3= k_1({\omega }_{b1}^3+3{\omega }_{b1}^2\Delta {\omega }_{\mathbf{b}}\prime +3{\omega }_{b1}\Delta {\omega }_{\mathbf{b}}{\prime }^{2+}\Delta {\omega }_{\mathbf{b}}{\prime }^3)(12)$

Since the rotor speed regulation range is not large, 1>ω_b1>>Δω_b′. Hence, the higher-order terms with Δω_b′ can be ignored, and then Eq. 12 can be simplified

$P_1\prime =P_1+\Delta P_{\text{e}}\approx k_1\Delta \left({\omega }_{b1}^3+3{\omega }_{b1}^2\Delta {\omega }_{\text{b}}\prime \right).(13)$

Combining Eq. 13 and Eq. 9,

$\Delta P_{\text{e}}=3{\omega }_{b1}^2\Delta {\omega }_{\text{b}}\prime =-\frac{\Delta P_{\mathbf{max}}}{\Delta f_{\mathbf{max}}}\Delta f(14)$

The initial de-loaded power P₁ and the maximum power P₂ can be expressed as

$P_1=(1-d\%)P_2.(15)$

Then, considering Eq. 8, Eq. 9, and Eq. 15,

$(1-d\%)k_2{\omega }_{b2}^3=k_1{\omega }_{b1}^3.(16)$

From Eq. 16, the following expression can be derived as

${\omega }_{b2}=\sqrt[3]{\frac{k_1{\omega }_{b1}^3}{k_2(1-d\%)}}.(17)$

Substitute Eq. 17 into Eq. 11, the following expression can be derived:

$\Delta P_{\mathbf{max}}=\frac{k_2{k}_1{\omega }_{b1}^3}{k_2(1-d\%)}-\frac{k_1^2{\omega }_{b1}^3}{k_2(1-d\%)}.(18)$

Further, substitute Eq. 18 into Eq. 10, the following expression is obtained:

$\Delta {\omega }_{\text{b}}\prime =-\frac{k_1(k_2-k_1){\omega }_{b1}}{3k_2(1-d\%)\Delta f_{\max }}\Delta f.(19)$

Observing Figure 6, Δω_b′ is the difference between the equivalent rotor speed of the point ‘1′ and the equivalent rotor speed of the point ‘1'' after the frequency regulation.

In fact, ω_b1 is difficult to measure in engineering application. Therefore, ω_b1 is replaced with ω_b, and Eq. 19 can be written as

$\Delta {\omega }_{\text{b}}=-\frac{k_1(k_2-k_1){\omega }_{\text{b}}}{3k_2(1-d\%)\Delta f_{\max }}\Delta f.(20)$

ω_b is always larger than or equal to ω_b1. Hence, by replacing ω_b1 with ω_b, Δω_b is larger and results in releasing more active power.

In the medium wind speed area, since the adjustment range of ω_b increases, Δω_b' can no longer be ignored. When the frequency dips event occurs, the electromagnetic power can be expressed as

$P_4\prime =P_4+\Delta P_{\text{e}}=k_3\left({\omega }_{\mathbf{b4}}+\Delta {\omega }_{\mathbf{b}}\prime \right)+b_3.(21)$

In the high wind speed area, ΔP_max is a constant value, 0.1 p.u.

Using the same analysis approach in the low wind speed area, the relationship between Δω_b and Δf in the medium and high wind speed can be derived. The expression of Δω_b-Δf can be obtained as

$\Delta {\omega }_{\text{b}}=\{\begin{array}{c}-\frac{k_1(k_2-k_1){\omega }_{\text{b}}}{3k_2(1-d\%)(f_{\text{b}}-f_{\text{a}})}\Delta f{\omega }_{\text{b}}\le {\omega }_{\mathrm{b}\mathit{low}}\\ -\frac{k_3\left(k_2-k_1\right){\omega }_{\text{b}}+b_3\left(k_2-k_1\right)}{(1-d\%)k_2{k}_3\left(f_{\text{b}}-f_{\text{a}}\right)} \Delta f{\omega }_{\mathrm{b}\mathit{low}}<{\omega }_{\text{b}}\le {\omega }_{\mathrm{b}medium}\\ -\frac{0.1}{k_4\left(f_{\text{b}}-f_{\text{a}}\right)}\Delta f{\omega }_{\text{b}}>{\omega }_{\mathrm{b}medium}\end{array}.(22)$

Dynamic Process of Frequency Regulation of the Proposed Control Scheme

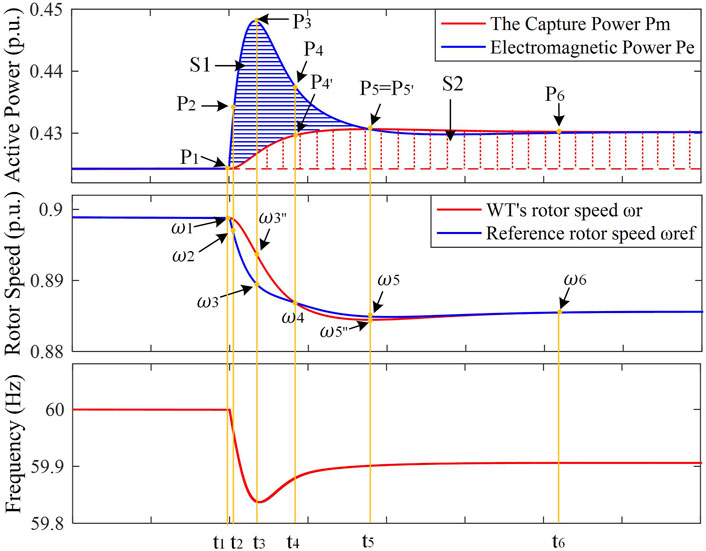
The dynamic response of PMSG participating in frequency regulation when the frequency drops is illustrated in Figure 7. The trajectory of active power and rotor speed is shown in Figure 8.

FIGURE 7

FIGURE 7. The dynamic response process of PMSG participating in frequency regulation.

FIGURE 8

FIGURE 8. The trajectory of active power P_e and the equivalent rotor speed ω_b.

In Figure 7, the area of S₁ between the mechanical power and the captured power by the wind turbine represents the rotational KE released by the wind turbine. It is mainly used to provide the inertial response and affects the rate of frequency change and frequency nadir. The area of S₂ represents the increase in the captured energy by the wind turbine, which is mainly used to provide primary frequency regulation and affect the steady frequency of the system.

The frequency regulation dynamic process is divided into six periods, and the dynamic process in each period is analyzed, respectively.

t < t₁: within this time range, P_e is equal to the captured power P_m, the rotor speed remains a constant value, and the PMSG-WTG operates in de-loaded mode.

t₁<t < t₂: at t = t₁, the load suddenly increases and the frequency drops. According to Eq. 22, Δω_b decreases. Since the rotor speed of the PMSG decoupled with the grid frequency, the rotor speed ω_r remains unchanged at the moment. According to Eq. 7, ω_ref decreases and the deviation Δω_e between ω_r and ω_ref increases. Therefore, through PI control, the electromagnetic torque reference T_ref increases. That is, P_e of the PMSG increases. According to the rotor mechanical equation, the rotor speed ω_r decreases. Due to ω_r decreasing, the capture wind power P_m increases, and its torque T_m also increases.

t₂<t < t₃: as P_e increases, depending on the P_de-ω_b curve, ω_b increases. During this period, because Δf is increasing and the change range of ω_b is small, Δω_b plays a dominant role at this time, so that ω_ref decreases and its reduction value is larger than the reduction value of ω_r. Δω_e increases. Therefore, T_ref increases after the PI controller, resulting in the increase of P_e. ω_r continues to decrease because of the increase of P_e. When t = t₃, Δω_e reaches the maximum value and P_e reaches the maximum value. Based on the ω_b-P_de curve, ω_b also reaches its maximum value.

t₃<t < t₄: during this period, as the frequency starts to recovery, Δω_b starts to decrease, and the change of ω_ref is smaller than the one of ω_r, which causes the Δω_e to decrease. P_e also begins to decrease, but it is still larger than P_m. ω_b also begins to decrease with the decrease of P_e. According to Eq. 7, ω_ref will decrease. According to the rotor mechanical equation, ω_r decreases. t₄<t < t₅: since P_e is still larger than P_m, according to the rotor mechanical equation, ω_r and ω_ref continue to decrease, and the deviation Δω_e continues to decrease, resulting in the decrease of T_ref and P_e. As ω_r decreases, P_m increases. When t = t₅, P_m is equal to P_e for the first time.

t > t₅: since the decrease of ω_r is slightly slower than ω_ref, P_m is slightly larger than P_e. Therefore, ω_r increases. When t = t₆, P_m is equal to P_e and ω_r is equal to ω_ref. At this time, the PMSG-WTG reaches a new steady-state operating point.

Case Study

An islanded microgrid simulation model of wind power-diesel generators is built. The diagram of the islanded microgrid is shown in Figure 9. The rated power of the diesel unit is 70 kW. The nominal RMS voltage and frequency are 5 kV and 50 Hz, respectively.

FIGURE 9

FIGURE 9. The structure diagram of the independent microgrid model.

Various scenarios of wind speed and load changes are set to verify the effectiveness of the proposed frequency regulation scheme. The following three schemes are used to compare with the proposed control scheme.

1) The proposed frequency regulation scheme.

2) The conventional frequency regulation scheme.

3) The variable coefficient control scheme in (Zhu et al., 2021b).

4) The de-loaded control scheme (PMSG does not participate in frequency regulation).

Low Wind Speed Area

Case 1: the wind speed is set as 9 m/s; the load suddenly increases by 15 kW at 50 s.The simulation result is shown in Figure 10.As can be seen in Figure 10, when the PMSG adopts the traditional scheme, the rotor speed does not exceed the lower limiter. When the PMSG adopts the proposed scheme, the frequency nadir (FN) is 59.84 Hz, which is 0.02 Hz larger than the one of the PMSG-WTG adopting the traditional scheme, and 0.01 Hz larger than the one of the variable coefficient control scheme. The steady frequency is 59.91 Hz, which is 0.01 larger than the other two control scheme. Compared with the traditional frequency regulation scheme and the variable coefficient control scheme, the proposed scheme shows a better performance. The reason is that the active power for the frequency support increases with the increase of the wind speed, which validates that the proposed control scheme has a potential wind speed adaptability.

FIGURE 10

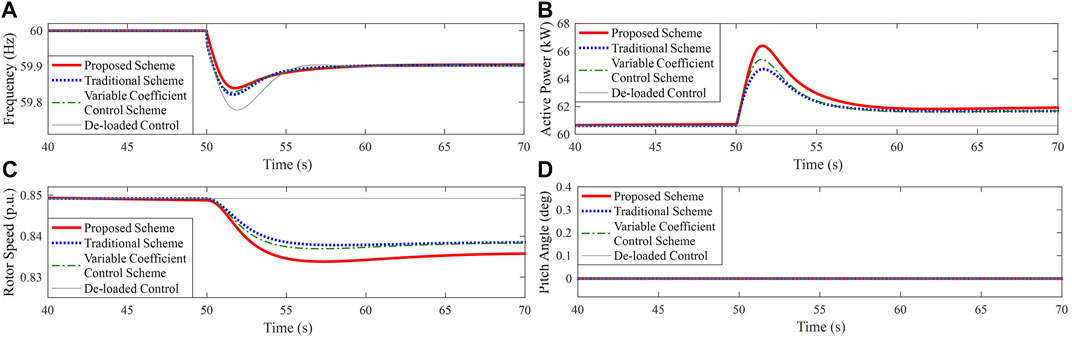
FIGURE 10. Results for Case 1. (A) System frequency; (B) Active power of PMSG; (C) Rotor speed of PMSG; (D) Pitch angle.

Case 2: the wind speed is set as 9 m/s; the load suddenly decreases by 15 kW at 50 s.The simulation result is shown in Figure 11.Observing the simulation results, when PMSG adopts the proposed frequency regulation scheme, the system frequency peak and deviation are smaller than those of PMSG-WTG adopting the other two control schemes, which validates that the proposed scheme has a better frequency regulation performance.

FIGURE 11

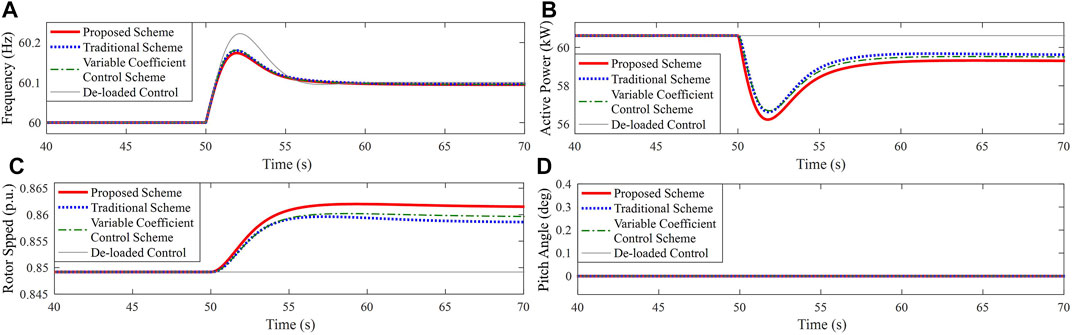
FIGURE 11. Results for Case 2. (A) System frequency; (B) Active power of PMSG; (C) Rotor speed of PMSG; (D) Pitch angle.

Medium Wind Speed Area

Case 3: the wind speed is set as 11 m/s; the load suddenly increases by 15 kW at 50 s.The simulation result is shown in Figure 12.As shown in Figure 12A, when the PMSG adopts the proposed scheme, the FN is 59.88 Hz, which is 0.11 Hz higher than when the PMSG does not participate in frequency regulation and 0.1 Hz and 0.09 Hz higher than those of the traditional scheme and the variable coefficient control scheme, respectively. The steady frequency is 59.92 Hz, which is 0.03 Hz larger than when the PMSG does not participate in frequency regulation, 0.019 Hz larger than that adopting the traditional scheme, and 0.019 Hz larger than the variable coefficient control scheme.As shown in Figure 12B, the proposed scheme’s additional power is greater than that of the other frequency regulation schemes. The reduced rotor speed is used to provide inertia support. The peak power when the PMSG-WTG adopts the traditional scheme is 107.5 kW, the variable coefficient control scheme is 107.7 kW, and that of PMSG-WTG adopting the proposed scheme is 116.1 kW.During the process of frequency regulation, the PMSG-WTG operates in the safe rotor speed range, as shown in Figure 12C. Due to the potential self-adaption, the rotor speed of the proposed scheme converges to a lower value of 0.9739 p.u. and more KE is released during this period.As shown in Figure 12D, the pitch angle control is activated to provide de-loaded and frequency support control. Before the load changes, the PMSG-WTG operates in the de-loaded mode, and the pitch angle is approximately 0.094 deg. After the load changes, the pitch angle is decreased to release extra power for frequency support. In fact, the pitch angle control and rotor speed control are difficult to coordinate for the other two control schemes in the medium wind speed area. When the PMSG adopts the proposed scheme, pitch angle drops deeper than that of adopting other schemes. Therefore, the proposed scheme can better co-utilize pitch angle and rotor speed control to provide frequency support.

FIGURE 12

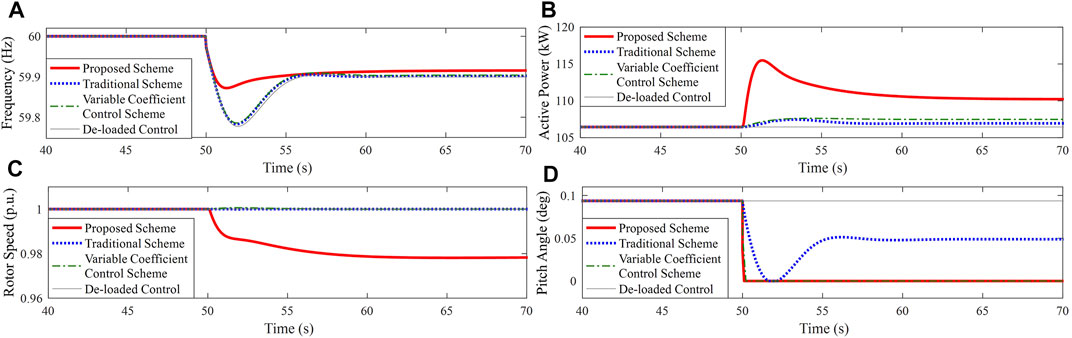
FIGURE 12. Results for Case 3. (A) System frequency; (B) Active power of PMSG; (C) Rotor speed of PMSG; (D) Pitch angle.

Case 4: the wind speed is set as 11 m/s; the load suddenly decreases by 15 kW at 50 s.The simulation result is shown in Figure 13. When the load decreases, if the PMSG-WTG is expected to regulate the frequency, the rotor speed should increase. However, the rotor speed has reached the maximum value during de loaded control in Figure 13C. Thus, the frequency deviation can be only suppressed by increasing the pitch angle, as shown in Figure 13D. When the PMSG adopts the proposed scheme, more active power can be released due to its potential self-adaption, as shown in Figure 13B. In Figure 13A, the peak frequency of the proposed scheme is 60.195 Hz, which is 0.01 Hz lower than the one of the variable coefficient control scheme, 0.03 Hz lower than that of the traditional scheme, and 0.04 Hz lower than that of the PMSG-WTG which does not participate in frequency regulation. The steady frequency is 60.08 Hz of the proposed scheme and variable coefficient control scheme, which is 0.02 Hz lower than that of the PMSG adopting the traditional scheme and 0.03 Hz lower than that of the PMSG which does not participate in frequency regulation.

FIGURE 13

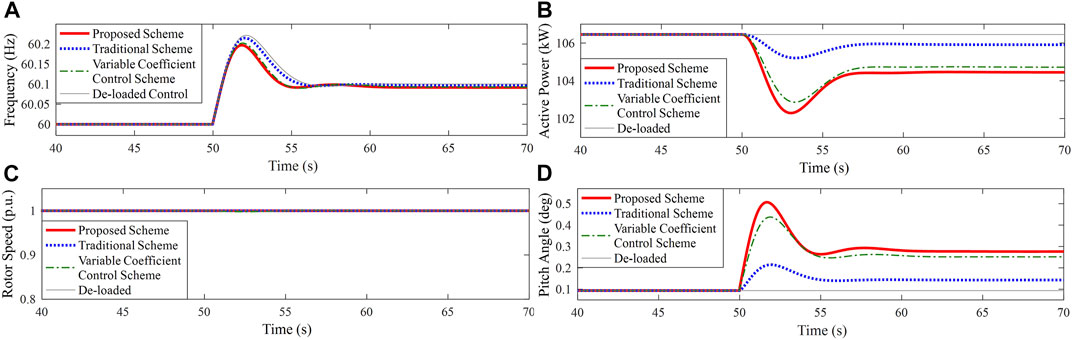
FIGURE 13. Results for Case 4. (A) System frequency; (B) Active power of PMSG; (C) Rotor speed of PMSG; (D) Pitch angle.

High Wind Speed Area

Case 5: the wind speed is set as 14 m/s; the load suddenly increases by 15 kW at 50 s.The simulation result is shown in Figure 14.In a high wind speed area, the frequency is regulated by the pitch angle control. Figure 14C shows that the rotor speed keeps 1 p.u. for all the control schemes. When the PMSG adopts the proposed scheme, there is a deeper pitch angle drop than that of the other two control scheme, as seen in Figure 14D.As shown in Figure 14A, when the PMSG adopts the proposed scheme, the FN is 59.86 Hz, More active power can be released due to potential self adaption of the proposed scheme in Figure 14B. Which is 0.07 Hz higher than that of the traditional scheme and 0.05 Hz higher than that of the variable coefficient control scheme. The steady frequency of the proposed scheme is 59.92 Hz, while the steady frequency of the traditional scheme and the traditional scheme is 59.9 and 59.91 Hz, respectively. Because of the adaptability of the proposed scheme, there is a deeper reduction of the pitch angle than that of other schemes.

FIGURE 14

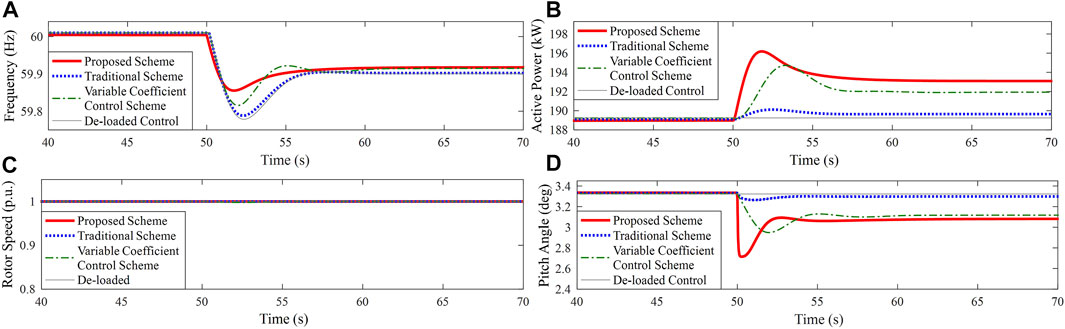
FIGURE 14. Results for Case 5. (A) System frequency; (B) Active power of PMSG; (C) Rotor speed of PMSG; (D) Pitch angle.

Radom Wind Speed

Case 6: the actual measured wind speed (medium wind speed area) in Northeast China is introduced into the simulation model as seen in Figure 15A.Due to the change of wind speed, the output active power increases or decreases, resulting in the grid-side frequency fluctuation, as shown in Figure 15A and Figure 15B. Because of the wind turbines’ participation in frequency regulation, all the traditional scheme, the variable coefficient control scheme, and the proposed scheme improve the frequency response. Compared with the other two control schemes, the proposed scheme has a potential adaptation, and additional power for frequency support adaptively changes with wind speed variation. As illustrated in Figure 15D and Figure 15E, when the PMSG adopts the proposed scheme, the rotor speed and pitch angle reduce more than other schemes, especially when wind speed is in a large section. Hence, the PMSG releases more active power. The proposed scheme provides better active power support so that the frequency fluctuation is small.The results of these cases clearly show that the proposed scheme can provide better frequency support than the other schemes for the whole wind speed range, regardless of low, medium, high, or random wind speeds. It has the potential to provide adaptive frequency support for different wind speeds.

FIGURE 15

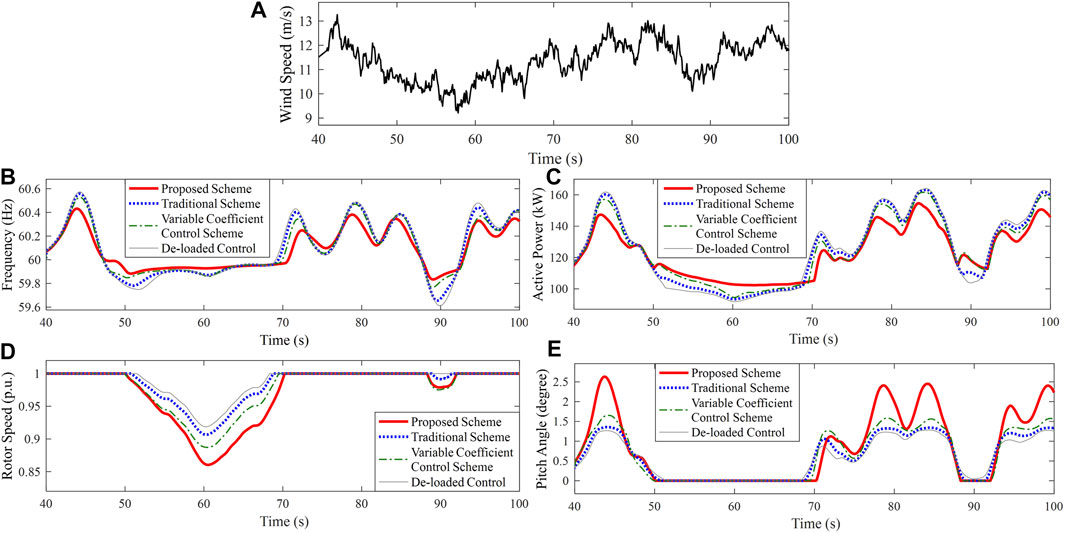
FIGURE 15. Results for Case 6. (A) Random wind speed; (B) System frequency; (C) Active power of PMSG; (D) Rotor speed of PMSG; (E) Pitch angle.

Conclusion

This article proposes an equivalent rotor speed compensation control scheme of PMSG-WTG for frequency support in islanded microgrids. A new equivalent rotor speed variable of combined pitch angle and rotor speed is defined, which can find the rotor speed reference or compensation pitch angle reference according to the active power measurement. As a result, the wind turbine can simply regulate the rotor speed and pitch angle for de-loaded control during the whole wind speed area.

A virtual compensation rotor speed is provided to render PMSG-WTG rotor speed directly coupling grid frequency to generate both the inertial and primary frequency response. The virtual compensation rotor speed adaptively adjusts depending on the frequency deviation to maintain the proper torque comprising of the frequency regulation performance and wind turbine safe operation. Further, the pitch angle and torque are coordinated and regulated to provide frequency support in the medium and high wind speed area.

The simulation results under various conditions show that the proposed scheme has a potential self-adaption and provides adaptive frequency support for the whole wind area.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

CZ and YL contributed to the conception and design of the study. CZ, YL, and YZ wrote the first draft of the manuscript. HL wrote sections of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Conflict of Interest

Author YZ was employed by State Grid Shandong Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adam, Milczarek., Mariusz, Malinowski., and Josep, M. Guerrero. (2015). Reactive Power Management in Islandedmicrogrid-Proportional Power Sharing in Hierarchical Droop Control. IEEE Transa-ctions on Smart Grid. 6 (4), 1631–1637. doi:10.1109/TSG.2015.2396639

CrossRef Full Text | Google Scholar

Chang-Chien, L.-R., Lin, W.-T., and Yin, Y.-C. (2011). Enhancing Frequency Response Control by DFIGs in the High Wind Penetrated Power Systems. IEEE Trans. Power Syst. 26 (2), 710–718. doi:10.1109/tpwrs.2010.2052402

CrossRef Full Text | Google Scholar

Chang-Chien, L.-R., Sun, C.-C., and Yeh, Y.-J. (2014). Modeling of Wind Farm Participation in AGC. IEEE Trans. Power Syst. 29 (3), 1204–1211. doi:10.1109/tpwrs.2013.2291397

CrossRef Full Text | Google Scholar

Ekanayake, J., and Jenkins, N. (2004). Comparison of the Response of Doubly Fed and Fixed-Speed Induction Generator Wind Turbines to Changes in Network Frequency. IEEE Trans. Energ. Convers. 19 (4), 800–802. doi:10.1109/tec.2004.827712

CrossRef Full Text | Google Scholar

Gao, D. W., Wu, Z., Yan, W., Zhang, H., Yan, S., and Wang, X. (2019). Comprehensive Frequency Regulation Scheme for Permanent Magnet Synchronous Generator‐based Wind Turbine Generation System. IET Renew. Power Generation. 13 (2), 234–244. doi:10.1049/iet-rpg.2018.5247

CrossRef Full Text | Google Scholar

Hu, J., Wang, S., Tang, W., and Xiong, X. (2017). Full‐Capacity Wind Turbine with Inertial Support by Adjusting Phase‐Locked Loop Response. IET Renew. Power Generation 11 (1), 44–53. doi:10.1049/iet-rpg.2016.0155

CrossRef Full Text | Google Scholar

Kayikci, M., and Milanovic, J. V. (2009). Dynamic Contribution of DFIG-Based Wind Plants to System Frequency Disturbances. IEEE Trans. Power Syst. 24 (2), 859–867. doi:10.1109/tpwrs.2009.2016062

CrossRef Full Text | Google Scholar

Lee, J., Jang, G., Muljadi, E., Blaabjerg, F., Chen, Z., and Cheol Kang, Y. (2016). Stable Short-Term Frequency Support Using Adaptive Gains for a DFIG-Based Wind Power Plant. IEEE Trans. Energ. Convers. 31 (3), 1068–1079. doi:10.1109/TEC.2016.2532366

CrossRef Full Text | Google Scholar

Li, Shichun., Huang, Yuehua., and Wang, Lingyun., (2017). Modeling of Primary Frequency Modulation Auxiliary Control System for Doubly-Fed Wind Turbines Based on Speed Controln. Proc. CSEE 37 (24), 7077–7086.

Google Scholar

Li, Xialin., Guo, Li., Wang, Chengshan., and Li, Yunwei. (2016). Overview of Research on Key Technologies of DC Microgrid. Proc. CSEE 36 (1), 2–17.

Google Scholar

Liu, T., Pan, W., Quan, R., and Liu, M. (2019). A Variable Droop Frequency Control Strategy for Wind Farms that Considers Optimal Rotor Kinetic Energy. IEEE Access 7, 68636–68645. doi:10.1109/access.2019.2914496

CrossRef Full Text | Google Scholar

Luo, H., Hu, Z., Zhang, H., and Chen, H. (2019). Coordinated Active Power Control Strategy for Deloaded Wind Turbines to Improve Regulation Performance in AGC. IEEE Trans. Power Syst. 34 (1), 98–108. doi:10.1109/tpwrs.2018.2867232

CrossRef Full Text | Google Scholar

Margaris, I. D., Papathanassiou, S. A., Hatziargyriou, N. D., Hansen, A. D., and Sorensen, P. (2012). Frequency Control in Autonomous Power Systems with High Wind Power Penetration. IEEE Trans. Sustain. Energ. 3 (2), 189–199. doi:10.1109/tste.2011.2174660

CrossRef Full Text | Google Scholar

Sun, C., Ali, S. Q., Joos, G., and Bouffard, F. (2019). “Improved VSG Control for Type-IV Wind Turbine Generator Considering Operation Limitations,” in 2019 IEEE Energy Conversion Congress and Exposition (ECCE), 29 Sept.-3 Oct. 2019 (Baltimore, MD, USA: IEEE), 2085–2091. doi:10.1109/ecce.2019.8912663

CrossRef Full Text | Google Scholar

Tang, X., Yin, M., Shen, C., Xu, Y., Dong, Z. Y., and Zou, Y. (2019). Active Power Control of Wind Turbine Generators via Coordinated Rotor Speed and Pitch Angle Regulation. IEEE Trans. Sustain. Energ. 10 (2), 822–832. doi:10.1109/tste.2018.2848923

CrossRef Full Text | Google Scholar

Wu, Y.-K., Yang, W.-H., Hu, Y.-L., and Dzung, P. Q. (2019). Frequency Regulation at a Wind Farm Using Time-Varying Inertia and Droop Controls. IEEE Trans. Ind. Applicat. 55 (1), 213–224. doi:10.1109/tia.2018.2868644

CrossRef Full Text | Google Scholar

Wu, Z., Gao, W., Gao, T., Yan, W., Zhang, H., Yan, S., et al. (2018). State-of-the-art Review on Frequency Response of Wind Power Plants in Power Systems. J. Mod. Power Syst. Clean. Energ. 6 (1), 1–16. doi:10.1007/s40565-017-0315-y

CrossRef Full Text | Google Scholar

Wu, Z., Gao, W., Wang, X., Kang, M., Hwang, M., Kang, Y. C., et al. (2016). Improved Inertial Control for Permanent Magnet Synchronous Generator Wind Turbine Generators. IET Renew. Power Generation 10 (9), 1366–1373. doi:10.1049/iet-rpg.2016.0125

CrossRef Full Text | Google Scholar

Zeng, X., Liu, T., Wang, S., Dong, Y., and Chen, Z. (2019). Comprehensive Coordinated Control Strategy of PMSG-Based Wind Turbine for Providing Frequency Regulation Services. IEEE Access 7, 63944–63953. doi:10.1109/access.2019.2915308

CrossRef Full Text | Google Scholar

Zertek, A., Verbic, G., and Pantos, M. (2012). A Novel Strategy for Variable-Speed Wind Turbines' Participation in Primary Frequency Control. IEEE Trans. Sustain. Energ. 3 (4), 791–799. doi:10.1109/tste.2012.2199773

CrossRef Full Text | Google Scholar

Zhang, Z.-S., Sun, Y.-Z., Lin, J., and Li, G.-J. (2012). Coordinated Frequency Regulation by Doubly Fed Induction Generator-Based Wind Power Plants. IET Renew. Power Gener. 6 (1), 38–47. doi:10.1049/iet-rpg.2010.0208

CrossRef Full Text | Google Scholar

Zhao, Jingjing., Li, Min., and He, Xinqin. (2019). Coordinated Control Scheme of Wind Power and Energy Storage in Frequency Regulation Based on Torque Limit Control. Trans. China Electrotechnical Soc. 34 (23), 4982–4990.

Google Scholar

Zhao, J., Lv, X., and Fu, Y. (2015). “Wind-solar Diesel Microgrid Frequency Adjustment Technology Based on Variable Coefficient-Based Virtual Inertia and Overspeed Control Coordination of Doubly-Fed Wind Turbines”,. J. Electrotechnical Eng. 30 (5), 59–68. (In Chinese).

Google Scholar

Zhao, X., Xue, Y., and Zhang, X.-P. (2020). Fast Frequency Support from Wind Turbine Systems by Arresting Frequency Nadir Close to Settling Frequency. IEEE Open J. Power Energ. 7, 191–202. doi:10.1109/oajpe.2020.2996949

CrossRef Full Text | Google Scholar

Zhu, Xiaorong., Zheng, Li., and Meng, Fanqi. (2021). Stability Analysis of DC Microgrid Based on Different Grid Structures. Trans. China Electrotechnical Soc. 36 (1), 166–178.

Google Scholar

Zhu, Y., Liu, S., and Wang, W. (2021). Comprehensive Coordinated Control Strategy of PMSG‐based Wind Turbine for System Inertia Support. IET Renew. Power Generation 15, 1915–1926. doi:10.1049/rpg2.12115

CrossRef Full Text | Google Scholar