Integrated Energy System Planning Based on Life Cycle and Emergy Theory

Integrated energy system (IES) is of great significance in the construction of the modern energy system. Reasonable planning is one of the important means to improve the economy of the IES and promote the consumption of renewable energy. However, the complex coupling characteristics between energy sources make it difficult to quantify the production efficiency of multi-energy heterogeneous resources uniformly in the economic benefit model during the planning cycle. Quantifying the production efficiency of the IES for planning is currently an urgent problem to be solved. This study proposes a planning method for the IES based on the life cycle and emergy theory. First, emergy theory is applied to quantify the production efficiency of the IES. A complete economic benefit model is established based on life cycle theory. Second, a bi-level planning model of the IES is established. The upper-level model aims at minimizing the whole life cycle cost of the IES to plan the capacity and location of the coupling equipment. The lower-level model aims at maximizing the emergy yield ratio of the IES to provide the operating data for the upper level. Finally, comparing experimental evaluations with traditional planning schemes considering annual average cost and energy quality coefficient, the method in this study reduces planning costs by 23.16% and increases the consumption rate of renewable energy by 4.26%. It can be seen that the planning method proposed in this study improves the planning economy and the level of renewable energy consumption of the IES.

Introduction

Integrated energy system (IES) is an effective way to centralized supply of multi-energy and improves the absorptive capacity of renewable energy. A large number of renewable energy access lead to increase in the uncertainty of energy supply and affect energy utilization (Li et al., 2021). A reasonable IES planning scheme is an effective way to realize energy cascade utilization and ensure system economy. However, there is a complex coupling relationship among energy production, transmission, and utilization in the IES (Dou et al., 2020). In the system long time scale, the planning, construction, production, and other economic activities increased the difficulty for reasonable quantitative system energy conversion efficiency and the system construction of the comprehensive assessment of the economic benefit. Multi-energy centralized planning faces huge challenges (Heleno and Ren, 2020). The emergy theory can unify the measurement methods of various energy forms in the IES (Wei et al., 2020). It is also conducive to realizing the unified quantification of heterogeneous energy. The life cycle (LC) theory can coordinate the economic benefits of each stage in the whole LC of the IES (Harris et al., 2020). This is beneficial in obtaining the full LC assessment of economic benefits in the planning process based on the LC theory. Therefore, in the process of IES planning, facing the challenges of incomplete description of the economic behavior process in the LC of the system and difficulties in the unified quantification of multiple types of resources, it is urgent to carry out IES planning research based on LC and emergy theory. It is conducive to the rational allocation of resources and the improvement of energy utilization efficiency.

The IES couples each energy subsystem through the energy hub (EH). The site selection of EHs has significant influence on the system’s economic efficiency and energy utilization efficiency. Therefore, at present, research studies on IES planning are mostly based on different coupling modes of different energies. The selection of EHs is based on economic benefits, energy utilization efficiency, and other factors. According to different coupling modes, some research studies established planning models of electric–gas coupling model (Xie et al., 2020) and electric–heat–gas coupling model (Zhang et al., 2015) based on the operation of typical scenarios. The advantages and disadvantages of planning schemes of different coupling modes have been compared and analyzed. In terms of planning objectives, based on the medium and long-term load forecasting (Gan et al., 2017; Jiang et al., 2017), operation cost (Salimi et al., 2015; Pazouki and Haghifam, 2016; Gao et al., 2018; Wang et al., 2019a), investment cost (Bai et al., 2019), carbon trading cost (Wang et al., 2018a), environmental pollution cost (Zhang and Gao, 2016), and energy conversion efficiency (Gao et al., 2017; Wang et al., 2019b; Zeng et al., 2019) have been set as the goals to establish the EH planning model of the IES. A multi-objective EH planning model (Garmabdari et al., 2020) and a multi-layer EH planning model (Zhang et al., 2017) based on typical operation scenarios and combined with a general performance flow model of the system have also been proposed. The objective of the current research on IES planning is mainly to determine the economic benefits of the system according to the market value of the equipment and energy in the system (Wang et al., 2018b) and to establish equipment selection and capacity allocation model of the EH. In this process, the energy quality coefficients based on the exergy theory are applied to uniformly quantify the energy values of different energy forms usually based on different energy coupling methods (Chen et al., 2018). The energy conversion efficiency is described by the quantified energy value (Tian et al., 2019). However, existing research studies rarely quantify the social resources involved in the LC of the system by considering the economic benefits of the whole LC of system planning, construction, operation, and scrapping, so that the composition of energy conversion efficiency is not comprehensive.

In this study, on the IES containing renewable energy, LC theory is introduced to quantify the economic benefits of the whole LC. The economic benefits of EH construction and scrapping stages are taken into account to improve the description of the whole life cycle cost (LCC) of the system. The emergy theory is used to take the input of social resources into account and refine energy conversion efficiency of the system. The main contributions of the study are as follows:

1) The energy conversion efficiency in the IES planning process is accurately quantified based on emergy theory. It is conducive to improving the energy efficiency of the system.

2) The LCC of the system planning, construction, operation, and scrapping in the process of siting and sizing the EH of the IES is calculated based on LC theory. It is conducive to improving the economic benefits of the whole LC of the system.

3) The IES planning method based on LC and emergy theory is proposed. It is conducive to ensuring the economic benefits of the system in the whole LC while improving energy efficiency.

The structure of this article is as follows. In the second section, the subsystem models and main energy equipment models of the IES are established. In the third section, emergy analysis of the IES is carried out to obtain the energy value model of the system output energy. In the fourth section, a bi-level IES planning model based on LC and emergy theory is established. In the fifth section, the effectiveness of different planning objectives on the planning result is analyzed using experimental evaluations. And the rationality and validity of the proposed method was also verified. The main achievements of this study are summarized in the sixth section.

Integrated Energy System Model

Energy Hub Model

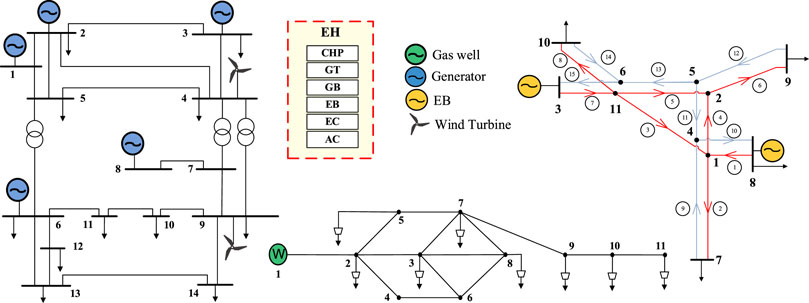
A typical IES structure is shown in Figure 1. EH is an important hub of the IES in the process of energy conversion, transmission, and supply. An EH mainly includes combined heat and power (CHP), gas turbine (GT), electric boiler (EB), gas-fired boiler (GB), electric chiller (EC), and absorption chiller (AC).

FIGURE 1

FIGURE 1. IES structure based on EHs.

The essence of an EH is to describe the function between the input and output pluripotent in the IES. Without considering the energy conversion process under the premise of transient conditions, we can use the EH model (Yao et al., 2018) to describe the ideal steady state of the EH:

$\left[\begin{array}{c}{L}_1\\ L_2\\ ⋮\\ L_n\end{array}\right]=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1m}\\ c_{21}& c_{22}& \cdots & c_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ c_{n1}& c_{n2}& \cdots & c_{nm}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ ⋮\\ P_m\end{array}\right],(1)$

where L_i (i = 1, 2, … , n) is the output of the ith energy form of the EH, P_j (j = 1, 2, … , m) is the input of the ith energy form of the EH, and c_ij is the conversion efficiency of i to j.

Energy Network Model

Energy network models mainly include the models of electrical power system (EPS), natural gas system (NGS), and district heat system (DHS). EPS mainly includes the constraints of three-phase power flow, power balance, generator output, node voltage, line power, and generator climbing (Correa-Posada and Sanchez-Martin, 2015; Eeea and Esa, 2019). NGS mainly includes the constraints of pipe flow, natural gas well, flow balance, compressor, pipe storage, and node pressure (Gao et al., 2017; Wei et al., 2017). DHS mainly considers the constraints of node flow balance, node power access feature fusion, load, and heat transfer characteristics (Dong et al., 2018).

Emergy Analysis of the Integrated Energy System

Emergy refers to the production of a product or service directly or indirectly by the consumption of the total available energy (Odum, 2012). It aims to convert different forms of energy into a unified value. The unit is solar emjoule, which is used to interpret a variety of social and natural value theory quantitative relations of energy and materials in the system. Through energy and material and economic flows, the IES links natural resources and human production activities closely together. It can be considered as a complete energy ecosystem. In this study, integrated analysis of the process of energy production, transportation, and supply of the IES is performed. Based on the general steps of emergy analysis (Zhang et al., 2016), the emergy analysis of the IES can be done and valued, as shown in Figure 2.

FIGURE 2

FIGURE 2. IES emergy analytical structure.

In this study, considering the power of the IES comes from thermal power, wind power generation, and power generation equipment in the EH, all power is sold to the system load demand. Certain energy loss occurs in the process of power transmission and supply, and Figure 2 shows the economic flow between the system and user (a dotted line). Based on the way to value associated with the power of energy flow and computational algorithms, IES the can value Y₁ of the output power can be expressed as follows:

$Y_1=(R_1+F_1+F_2+F_3+F_4+N_1+N_2+N_3+N_5)\frac{E_{Y_1}}{E_{p,EH}^{in}+E_{Y_1}},(2)$

where R₁ is the emergy of the loss of wind. F₁ is the thermal power unit generated electricity. F₂ is the emergy of the power consumption of natural gas. F₃ is the operation and maintenance costs of emergy consumption of the system. F₄ is the human resources value system consumption. N₁ is the asset’s wreck value of power generation equipment. N₂ is the asset’s wreck value of wind power equipment. N₃ is the asset’s worth of the EH. N₅ is the asset’s wreck value of power distribution facilities. $E_{Y_1}$ is the electric power consumed by the user. $E_{p,EH}^{in}$ is the electricity consumed by the EH coupling equipment.

In the IES, the user’s consumption of natural gas is mainly from gas wells, and the energy of the system output of natural gas Y₂ can be expressed as follows:

$Y_2=(F_2+N_3+N_6)\frac{E_{Y_2}}{E_{g,EH}^{in}+E_{Y_2}},(3)$

where $E_{Y_2}$ is the amount of gas consumed within the IES, $E_{g,EH}^{in}$ is the flow of gas consumption in the EH coupling device, and N₆ is the asset’s wreck value of gas distribution device.

In the IES, heating and cooling needs hot/cold water from natural gas waste heat utilization, electric boiler, and electric machine. In this study, the unified value calculation for hot and cold water is carried out, and the system output of hot and cold water can be expressed as follows:

$\begin{array}{l}{Y}_3+Y_4\\ =(R_1+F_1+F_2+F_3+F_4+N_1+N_2+N_3+N_5)\frac{E_{p,EH}^{in}}{E_{p,EH}^{in}+E_{Y_1}}\\ +(F_2+N_3+N_6)\frac{E_{g,EH}^{in}}{E_{g,EH}^{in}+E_{Y_2}}+N_7+N_4+R_2+R_3+F_3+F_4,\end{array}(4)$

where R₃ is the emergy of the oxygen the IES has used, R₄ is the emergy of the water the IES has used, N₄ is the asset’s worth of the EC and EB, and N₇ is the asset’s wreck value of heating and cooling distribution device.

The energy output is the ratio of the system output value and economic input values. The economy input values are derived from the human society economy. The primary energy is derived from a variety of means of production and labour services. The higher the emergy yield ratio, the higher the production efficiency of the system. The emergy yield ratio E_YR is as follows:

$E_{YR}=Y/F.(5)$

Bi-Level Programming Model for IES Based on the Theory of LC and Emergy

Objective Function

This study considers IES system energy conversion efficiency and economical aspects and optimizes the IES configuration research. The optimization goal includes minimization of the LCC and maximization of the emergy yield ratio.

1) The objective function 1: minimization of the LCC.

Based on the LC theory, equipment purchase cost, replacement cost, material handling cost, annual maintenance cost, annual operation cost, residual value, and waste treatment equipment costs of the IES are considered synthetically. The LCC of the IES is calculated using the following equation:

$\begin{array}{l}\min C_{LC}\\ ={\displaystyle \sum _{n=1}^N{C}_n{P}_n+{\displaystyle \sum _{n=1}^N{\displaystyle \sum _{j=1}^{R_n}\frac{C_n{P}_n}{{(1+i)}^{j{t}_n}}}}}(1-r)+{\displaystyle \sum _{n=1}^{L_p}\frac{M}{{(1+i)}^n}(1-t_r)+{\displaystyle \sum _{n=1}^{L_p}\frac{B}{{(1+i)}^n}(1-t_r)}}+\frac{S}{{(1+i)}^{L_p}}{t}_r-{\displaystyle \sum _{n=1}^{L_p}\frac{D}{{(1+i)}^n}{t}_r,}\end{array}(6)$

where N is the number of devices used in the IES. C_n is the initial investment cost of equipment n. P_n is the installed capacity of equipment n. R_n is the number of energy supplements of equipment n. i is the interest rate. t_r is the tax rate. L_p is the life of the design project. M is the system maintenance costs. B is the use of the energy cost in a year. S is the processing cost of abandoned equipment. D is the depreciation expense of equipment for a year.

The number of times rebuilding the equipment (R_n), the cost of equipment maintenance in a year (M), the use of the energy cost in a year (B), and the depreciation cost for a year (D) are as follows:

$R_n=\text{floor}\left(\frac{L_p}{L_n}\right)-1\text{,}(7)$

$M=r_M{\displaystyle \sum _{\text{n}=1}^N{C}_n{P}_n},(8)$

$B={\displaystyle \sum _{d=1}^{365}{\displaystyle \sum _{t=1}^{24}{E}_{grid}^d\left(t\right){\pi }_e\left(t\right)+F_{tot}^d\left(t\right){\pi }_{gas}}},(9)$

$D=r_D{\displaystyle \sum _{n=1}^N{C}_n{P}_n},(10)$

where floor(x) is a function that is used to calculate the biggest integer no greater than x. r_M is the equipment maintenance rate. $E_{grid}^d\left(t\right)$ is the thermal power unit capacity on day d in time t. ${\pi }_e\left(t\right)$ is the price of coal in time t. $F_{tot}^d\left(t\right)$ is the amount of gas use. ${\pi }_{gas}$ is the price of gas. r_D is the allowance for depreciation of equipment. L_n is the service life of equipment n.

2) The objective function 2: maximization of the emergy yield ratio.

According to the definition of the emergy yield ratio in Section 3, it is expressed as follows:

$\max E_{YR}=Y/F.(11)$

Constraints

The constraints mainly include equipment capacity, equipment operation, and energy balance. In this study, the unit to be selected for the EH includes the CHP, GT, EB, GB, EC, and AC. Considering the physical significance of optimized variables and the actual situation, equipment capacity needs to be maintained within a certain range, namely:

$Q_{i,\text{m}in}\le Q_i^r\le Q_{i,\max },(12)$

where i = 1, 2, 3, 4, 5, and 6 represent the CHP, GT, EB, GB, EC, and AC. Q_i,min is the lowest installed capacity of the ith equipment. $Q_i^r$ is the installed capacity of the ith equipment. Q_i,max is the highest installed capacity of the ith equipment.

The operation constraints of equipment are mainly rated power constraints of equipment. The operation constraints of the EH are as follows:

$P_{i,\min }\le P_i^r\le P_{i,\max },(13)$

where P_i,min is the lowest operating power of the ith equipment, $P_i^r$ is the actual operating power of the ith equipment, and P_i,max is the rated power of the ith equipment.

Model Transformation

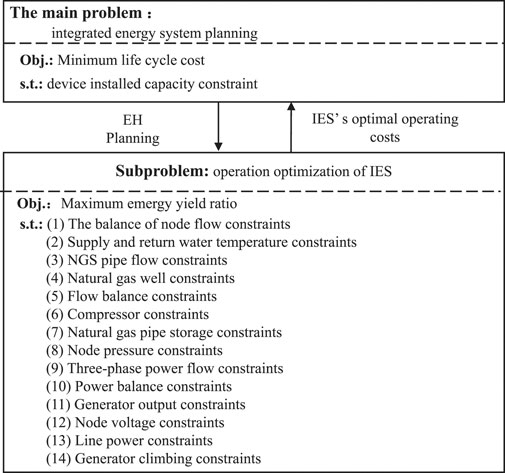
It can be seen that the EH planning model in IES considering the whole LCC and emergy yield ratio is a very complex mixed integer nonlinear programming model. According to the multi-level optimization theory, based on the idea of decomposition coordination, the model is decomposed into the bi-level programming model, as shown in Figure 3.

FIGURE 3

FIGURE 3. EH bi-level programming model framework.

In Figure 3, the first layer model is EH planning, which is the main problem in IES and is used to determine the installation type, location, and capacity of coupling equipment in the EH. The objective function is the system LCC minimization. The constraints include the installed capacity constraints and the discrete capacity constraints of the selected node. The second layer model is used to simulate the optimal operation mode of the IES in each scenario under the given EH site selection scheme. The objective function is to maximize the output rate of the system. Constraints include heat supply network node flow balance, change in the return water temperature and flow of natural gas pipeline network, air source, gas flow rate balance, air compressor, gas network management, gas network node pressure, trends in power system, power balance, generator output, node voltage, line power, and generating set climbing capacity. It is a typical optimal flow problem. This is a typical bi-level programming model; KKT conditions can be used to transform the lower targets into upper constraints and then into a mixed integer nonlinear programming model. The Lagrange multiplier method is used to solve the problem.

The parameter transfer relationship of the two-layer programming model is as follows: the first-layer planning model transfers the EH planning scheme (EH type, location, and capacity) to the operational sub-problem of the second layer, the second layer optimizes the running simulation for each scenario of the IES on this basis and returns the calculation result (the output of each unit in each scenario) to the first layer, and then the first layer plans to calculate the final objective function value (the system LCC).

Model Solving Process

The model solving process of this study is shown in Figure 4, which first generates a random run scenario, and then the selection of the EH site and optimization of the IES operation strategy including the EH are carried out considering the LCC of the system and the emergy output rate.

FIGURE 4

FIGURE 4. Solving process.

Experimental Evaluations

Experiment Settings

The simulation and optimization analysis are based on MATLAB and GAMS platform in the win10 operating system, i7CPU, 2.20 GHz processor environment. The IES structure with renewable energy as an example is shown in Figure 5. The IES mainly consists of a modified IEEE 14-node EPS, an 11-node NGS (Abeysekera et al., 2016), and a DHS based on literature modification (Zhu et al., 2018). Heterogeneous energy flows through the EH to achieve coupling and complete energy type conversion. The equipment to be selected in the EH includes CHP, GT, EB, GB, EC, and AC. Based on the equipment parameter data in Wang et al. (2017), the specific parameter data in Table 1 are formed after modification and supplementation. In the NGS, the minimum pressure is 22.5 mbar. The upper flow limit of the pipeline 12–14 is 150 m³/h. The candidate nodes are 4, 11, and 9 of the EPS, 1 and 7 of the NGS, and 8 and 11 of the DHS.

FIGURE 5

FIGURE 5. IES test case.

TABLE 1

TABLE 1. EH equipment parameter.

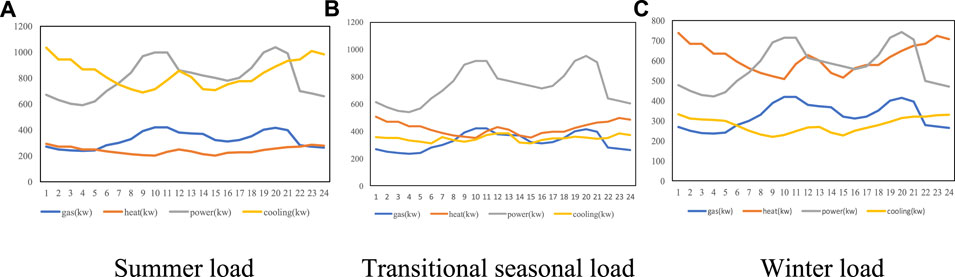
After generating the scenario by Latin cube sampling according to the historical load data and minimizing it by the k-means clustering method, the load is divided into three categories: heating season, transition season, and cooling season. Figure 6 shows the three types of IES load situations under different scenarios.

FIGURE 6

FIGURE 6. Daily load of a typical scenario.

Then, based on the models in the typical load scenarios, a complex bi-level programming model is transformed into a general mixed-integer nonlinear model using STEP 2 in Figure 4. Finally, based on the model transformation results, STEP 3 in Figure 4 is used to obtain the site selection of EHs, taking into account the 30-year service LC of the system.

For comparative analysis, the following four different programming target modes are set in the calculation example:

S1: the upper target is the lowest full LCC, and the lower target is the maximum energy yield.

S2: the upper target is the lowest LCC, and the lower target is the maximum energy conversion efficiency of the system based on energy and quality coefficient.

S3: the upper target is the lowest annual operating and construction cost of the system, and the lower target is the maximum output rate.

S4: the upper target is the lowest annual operating and construction cost of the system, and the lower target is the maximum energy conversion efficiency of the system based on energy and quality coefficient.

Analysis of Results

1) Analysis of planning results of S1

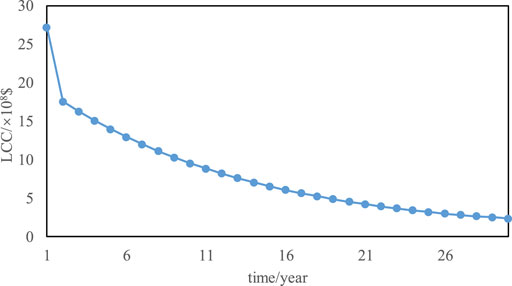
The planning results of S1 are shown in Table 2. Due to large fluctuation of the electrical load, it needs to be balanced in time. Coupled with the power flow constraint, the node load far from the thermal power unit on the EPS still needs to be supplied by other equipment in time. Due to the uncertainty of renewable energy output, the load demand cannot be satisfied in time. The four nodes are connected with a typhoon power unit. When the output of renewable energy exceeds the load demand, the coupling equipment in the EH is used to absorb surplus power. When the output of renewable energy cannot meet the load demand, the electric energy supplied by other energy networks is obtained through the EH. Due to the characteristics of high energy conversion efficiency and relatively low construction cost of electricity-cold coupling equipment and electricity-heat coupling equipment, it is more inclined to choose the coupling equipment that uses electric energy for energy conversion and supply when meeting the system load demand. As the coupling equipment to be selected in the EH is mainly used for energy conversion and supply of natural gas, the EH is connected to node 1 of the NGS. Despite the influence of seasonal factors, heat load demand is relatively stable; at the same time, since the DHS itself has certain energy storage ability, it can make full use of the tube. Hence, the EH is connected to the DHS to increase the ability of energy conversion. Therefore, large-capacity AC and GB are selected to connect to the 8 nodes of NGS in order to give priority to the use of excess heat energy in NGS and DHS for energy supply. The annual investment of the whole LC is shown in Figure 7.

2) Analysis of planning results of S2

TABLE 2

TABLE 2. EH planning results under S1.

FIGURE 7

FIGURE 7. Annual capital input in the whole LC of the IES.

The planning results of S2 are shown in Table 3. S2 aims at the lower level with the maximum energy conversion efficiency of the system based on energy and mass coefficient. Because the energy conversion efficiency based on energy and quality coefficient does not consider the economic factors of the system, the system does not consider the economic benefits during operation, which leads to the increase in the operation cost. However, the intermediate output rate of S1 is the energy conversion efficiency of the system that considers economic input and human resource input and can coordinate energy conversion efficiency and economic benefits. Since the four nodes in the EPS are connected to wind turbines with large capacity but small load, the EH of S2 is still connected to the four nodes in the EPS. Node 8 in the DHS is an important cold/hot load point. In order to ensure energy conversion efficiency and load demand, it is still connected to node 8 in the DHS. Therefore, in Table 3, the EH planning result of S2 is the same as that of S1 and the access location is the same as that of S1. Some equipment chooses models with large energy conversion efficiency, but the LCC increases.

3) Analysis of planning results of S3

TABLE 3

TABLE 3. EH planning results under S2.

The planning results of S3 are shown in Table 4. S3 takes the lowest annual operating and construction cost of the system as the upper target and the lower target with the maximum output rate, respectively. The lower level target of S3 is still the system emergy output rate, and some economic factors have been taken into account, leading to the same access location of the EH as S1. On the premise of meeting the load demand, in order to pursue a lower construction and operation cost, the construction cost of coupling equipment that uses electric energy for energy conversion and supply is relatively high and the equipment with relatively small capacity and low price is selected. Since the upper model does not consider the cost of the system in the construction and scrapping stages, the lower model puts forward certain requirements on most economic behaviors of the system through emergy utilization, thus ensuring the economic benefits of the system operation. Therefore, in Table 4, compared with the results of S1, the planning results in objective model 3 have the same access location as that of S1. However, as the economic behaviors considered in the upper goal are less than those in the lower model, the economic benefits of the part are better than S1 and the emergy output rate is lower than S1.

4) Analysis of planning results of S4

TABLE 4

TABLE 4. EH planning results under S3.

The planning results of S4 are shown in Table 5. The upper target of S4 is the lowest annual operating and construction cost of the system, and the lower target is the maximum energy conversion efficiency of the system based on energy and quality coefficient. Electric energy has the highest grade of energy, so the coupling conversion efficiency is relatively high when using electric energy for energy conversion. Since S4 considers the maximum energy conversion efficiency of the system, it will choose a larger capacity electrical coupling device. Therefore, EH is connected to the 6 nodes of the EPS with the thermal power unit. Node 11 is the connection hub of multiple water supply pipelines; since the pipeline diameter is large, transmission speed is fast, and it can effectively improve the heating efficiency, the EH is connected to node 11 of the NGS. This mode is the most traditional planning model, and the objective function lacks the planning of the economic behavior of the whole LC of the system, resulting in the neglect of part of the cost in the planning process of the EH. Therefore, in Table 5, the planning result of S4 is higher than that of S3, and the whole LCC is higher than that of S3. Meanwhile, the economic benefit of S3 is worse than that of S1, indicating that the economic benefit of S4’s planning result is better than that of S1.

5) EH configuration schemes in different target modes consume renewable energy

TABLE 5

TABLE 5. EH planning results under S4.

The consumption of renewable energy under the configuration results of S1, S2, S3, and S4 in different scenarios is compared and analyzed, as shown in Table 6.

TABLE 6

TABLE 6. Comparison of planning results of different scenarios.

For EH planning based on emergy theory, the input of economic resources of the system is considered in the lower operating model. The system will have better economic benefits after two-layer economic benefit planning, and the wind abandoning cost has a great impact on the planning result, which improves the consumption of wind power and other renewable energy. As the social significance of environmental protection increases year by year, the unit price of environmental governance costs increases year by year, which leads to the increasing influence of the absorption rate of renewable energy on the annual cost of the system year by year and promotes the scheduling quantity of renewable energy in the planning process. Therefore, in Table 6, the S1 target mode has the highest absorption rate of wind power, S2 is similar to S3, and S4 is the smallest. Since the LCC not only includes the system operating cost, the LCC with the construction operating cost as the planning goal under the same lower planning goal is higher than the LCC considering the economic behavior in the system LC.

Conclusion

In this study, the whole LC theory and emergy theory are introduced, and the bi-level programming model of the IES is established to optimize the selection of the equipment in EHs. Among them, the upper-level model takes the cost of system planning, construction, operation, and scrapping into consideration, aiming at the minimum cost of the whole LC to provide the siting and sizing scheme for the lower level model. Considering the input of social resources, the lower level model of operation takes the maximum output rate of the system emergy into account to provide the optimal operation cost for the upper level of model. Finally, after transforming the complex bi-level model into a mixed-integer nonlinear model by KKT conditions, the Lagrange multiplier method is adopted to solve the model. The effectiveness of the IES programming method proposed in this paper is verified by experimental evaluations. The following conclusions are mainly drawn from the results of our experiment:

1) The introduction of the planning model of emergy theory can effectively unify and quantify heterogeneous energy sources in the IES, including social resources, which is conducive to coordinating the economic benefits of system investment and energy utilization. Compared with planning with energy quality coefficients, planning costs can be reduced by 11.43%.

2) The planning model with the introduction of LC theory can effectively integrate the costs of all stages of system planning, construction, operation and scrapping. The system cost description is improved. Compared with planning by considering the average annual cost, the planning cost can be reduced by 21.40%.

3) For the IES containing renewable energy, compared with the traditional planning scheme, the planning scheme of LC theory and emergy theory is beneficial to improve the absorption rate of wind power and other renewable energy, reduce the total cost of the system, and improve the utilization rate of resources. Compared with planning in consideration of the average annual cost and energy quality coefficient, the planning cost has been reduced by 23.16% and the renewable energy consumption rate has increased by 4.26%.

4) In the future research, the planning method of the energy network will be further studied on the basis of the article and the integrity of the theory and the method of IES planning will be improved.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

JW: conceptualization, methodology, and writing. WD: data curation, software, validation, reviewing, and editing. DY: data curation, software, reviewing, and editing.

Funding

This study received funding from the Science and Technology Project of State Grid Corporation of China “Research on key technologies of planning and design of county energy Internet for energy transition” (5400-202119156A-0-0-00). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication. All authors declare no other competing interests.

Conflict of Interest

JW, WD, and DY were employed by the company NARI Group Corporation.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The content of this manuscript has been presented in part at the 8th Renewable Power Generation Conference (RPG 2019), Shao Y., Dou X., Wang J., et al. “Integrated energy system planning with distributed generation based on emergy theory”, 8th Renewable Power Generation Conference (RPG 2019), 2019. The article has obtained the copyright to be reused for publication.

References

Abeysekera, M., Wu, J., Jenkins, N., and Rees, M. (2016). Steady State analysis of gas networks with distributed injection of alternative gas. Appl. Energ. 164, 991–1002. doi:10.1016/j.apenergy.2015.05.099

CrossRef Full Text | Google Scholar

Bai, H., Yin, S., and Li, H. (2019). Optional planning of multi-energy Stations considering Carbon-trading cost. J. Electron. Power Sci. Tech. 34 (1), 11–19.

Google Scholar

Chen, B., Liao, Q., Liu, D., and Wang, W. (2018). Comprehensive Evaluation Indices and Methods for Regional Integrated Energy System. Automation Electric Power Syst. 42 (4), 174–182.

Google Scholar

Correa-Posada, C. M., and Sanchez-Martin, P. (2015). Integrated power and natural gas model for energy adequacy in Short-term operation. IEEE Trans. Power Syst. 30 (6), 3347–3355. doi:10.1109/tpwrs.2014.2372013

CrossRef Full Text | Google Scholar

Dong, S., Wang, C., and Xu, S. (2018). Day-ahead optimal Scheduling of electricity-gas-heat integrated energy System considering dynamic characteristics of network. Automation Electric Power Syst. 42 (13), 12–19.

Google Scholar

Dou, X., Wang, J., Wang, Z., Li, L., Bai, L., Ren, S., et al. (2020). A dispatching method for integrated energy System based on dynamic time-interval of model predictive control. J. Mod. Power Syst. Clean Energ. 8 (5), 841–852. doi:10.35833/mpce.2019.000234

CrossRef Full Text | Google Scholar

Eeea, B., and Esa, C. (2019). Modified JAYA algorithm for optimal power flow incorporating renewable energy Sources considering the cost, emission, power loss and voltage profile improvement. Energy 178, 598–609.

Google Scholar

Gan, L., Chen, Y., Liu, Y., and Xiong, W. (2017). Coordinative optimization of multiple energy flows for microgrid with renewable energy resources and case Study. Electric Power Automation Equipment 37 (6), 275–281.

Google Scholar

Gao, M., Wang, K., and He, L. (2018). Probabilistic Model Checking and Scheduling Implementation of an Energy Router System in Energy Internet for Green Cities. IEEE Trans. Ind. Inf. 14 (4), 1501–1510. doi:10.1109/tii.2018.2791537

CrossRef Full Text | Google Scholar

Gao, M., Wang, K., and He, L. (2017). Probabilistic Model Checking for Green Energy Router System in Energy Internet. Proc. Int. Conf. 2017 IEEE Global Communications Conference. Singapore. doi:10.1109/glocom.2017.8254465

CrossRef Full Text | Google Scholar

Garmabdari, R., Moghimi, M., and Yang, F. (2020). Multi-objective optimisation and planning of grid-connected cogeneration Systems in presence of grid power fluctuations and energy Storage dynamics. Energy, 212.

CrossRef Full Text | Google Scholar

Harris, A., Soban, D., Smyth, B. M., and Best, R. (2020). A probabilistic fleet analysis for energy consumption, life cycle cost and greenhouse gas emissions modelling of bus technologies. Appl. Energ., 261.

CrossRef Full Text | Google Scholar

Heleno, M., and Ren, Z. (2020). Multi-energy microgrid planning considering heat flow dynamics. IEEE Trans. Energ. Convers. (99), 1. 1. doi:10.1109/tec.2020.3041572

CrossRef Full Text | Google Scholar

Jiang, H., Wang, K., Wang, Y., and Gao, M. (2017). Energy Big Data: A Survey. IEEE Access 4, 3844–3861.

Google Scholar

Li, X., Wang, W., and Wang, H. (2021). A novel bi-level robust game model to optimize a regionally integrated energy System with large-Scale centralized renewable-energy Sources in Western China. Energy (10), 120513.

CrossRef Full Text | Google Scholar

Odum, H., T. (2012). Handbook of emergy evaluation. . https://cep.ees.ufl.edu/emergy/publications/folios.shtml (accessed May 14, 2019).

Pazouki, S., and Haghifam, M.-R. (2016). Optimal planning and Scheduling of energy hub in presence of wind, Storage and demand response under uncertainty. Int. J. Electr. Power Energ. Syst. 80 (9), 219–239. doi:10.1016/j.ijepes.2016.01.044

CrossRef Full Text | Google Scholar

Salimi, M., Ghasemi, H., Adelpour, M., and Vaez‐ZAdeh, S. (2015). Optimal planning of energy hubs in interconnected energy Systems: a case Study for natural gas and electricity. IET Generation, Transm. Distribution 9 (8), 695–707. doi:10.1049/iet-gtd.2014.0607

CrossRef Full Text | Google Scholar

Tian, L., Cheng, L., and Guo, J. (2019). Multi-energy System Valuation Method Based on Emergy Analysis. Power Syst. Tech. 43 (8), 2925–2934. doi:10.13335/j.1000-3673.pst.2018.2310

CrossRef Full Text | Google Scholar

Wang, G., Yang, Y., Wang, S., Zhang, H., and Wang, Y. (2019). Efficiency analysis and experimental validation of the ocean thermal energy conversion with phase change material for underwater vehicle. Appl. Energ. 248 (AUG.15), 475–488. doi:10.1016/j.apenergy.2019.04.146

CrossRef Full Text | Google Scholar

Wang, W., Wang, D., and Jia, H. (2017). Steady State analysis of electricity-gas regional integrated energy System with consideration of NGS network Status. Proc. CSEE 37 (5), 1293–1304.

Google Scholar

Wang, Y., Wang, Y., Huang, Y., Li, F., Zeng, M., Li, J., et al. (2019). Planning and operation method of the regional integrated energy System considering economy and environment. Energy 171 (MAR.15), 731–750. doi:10.1016/j.energy.2019.01.036

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, N., Zhuo, Z., Kang, C., and Kirschen, D. (2018). Mixed-integer linear programming-based optimal configuration planning for energy hub: Starting from Scratch. Appl. Energ. 210 (jan.15), 1141–1150. doi:10.1016/j.apenergy.2017.08.114

CrossRef Full Text | Google Scholar

Wang, Z., Tang, Y., and Qiao, B. (2018). Research on Integrated Natural Gas and Electric Power System Optimal Power Flow and its Environmental Synergy. Proc. CSEE 38, 111–120.

Google Scholar

Wei, J., Zhang, Y., Wang, J., Cao, X., and Khan, M. A. (2020). Multi-period planning of multi-energy microgrid with multi-type uncertainties using chance constrained information gap decision method. Appl. Energ., 260.

CrossRef Full Text | Google Scholar

Wei, Z., Zhang, S., and Sun, G. (2017). Power-to-gas considered peak load Shifting research for integrated electricity and natural-gas energy Systems. Proc. CSEE 37 (16), 4601–4609.

Google Scholar

Xie, S., Hu, Z., Wang, J., and Chen, Y. (2020). The optimal planning of Smart multi-energy Systems incorporating transportation, natural gas and active distribution networks. Appl. Energ. 269, 115006. doi:10.1016/j.apenergy.2020.115006

CrossRef Full Text | Google Scholar

Yao, S., Gu, W., and Zhang, X. (2018). Effect of heating network characteristics on ultra-short-term Scheduling of integrated energy System. Automation Electric Power Syst. 42 (14), 89–96.

Google Scholar

Zeng, H., Liu, T., and He, C. (2019). Multi-objective Optimization for Integrated Natural-gas and Electricity Energy System Considering Power-to-gas. Electr. Meas. Instrumentation 56 (8), 99–107.

Google Scholar

Zhang, L., and Gao, J. (2016). Exploring the effects of international tourism on China's economic growth, energy consumption and environmental pollution: Evidence from a regional panel analysis. Renew. Sust. Energ. Rev. 53, 225–234. doi:10.1016/j.rser.2015.08.040

CrossRef Full Text | Google Scholar

Zhang, S., Yuan, J., and Cheng, H. (2016). Optimal Distributed Generation Planning in Active Distrbution Network Considering Demand Side Management and Nerwork Reconfiguration. Proceeding of the CSEE 36, 1–9.

Google Scholar

Zhang, X., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2017). Optimal expansion planning of energy hub with multiple energy infrastructures. IEEE Trans. Smart Grid 6 (5), 2302–2311.

Google Scholar

Zhang, X., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2015). Optimal expansion planning of Energy hub with multiple energy infrastructures. IEEE Trans. Smart Grid 6 (5), 2302–2311. doi:10.1109/tsg.2015.2390640

CrossRef Full Text | Google Scholar

Zhu, J., Ye, Q., and Zou, J. (2018). Short-term operation Service mechanism of ancillary Service in the UK electricity market and its enlightenment. Automation Electric Power Syst. 42 (17), 1–8.

Google Scholar