A New Two-Stage Approach with Boosting and Model Averaging for Interval-Valued Crude Oil Prices Forecasting in Uncertainty Environments

In view of the intrinsic complexity of the oil market, crude oil prices are influenced by numerous factors that make forecasting very difficult. Recognizing this challenge, numerous approaches have been introduced, but little work has been done concerning the interval-valued prices. To capture the underlying characteristics of crude oil price movements, this paper proposes a two-stage forecasting procedure to forecast interval-valued time series, which generalizes point-valued forecasts to incorporate uncertainty and variability. The empirical results show that our proposed approach significantly outperforms all the benchmark models in terms of both forecasting accuracy and robustness analysis. These results can provide references for decision-makers to understand the trends of crude oil prices and improve the efficiency of economic activities.

1 Introduction

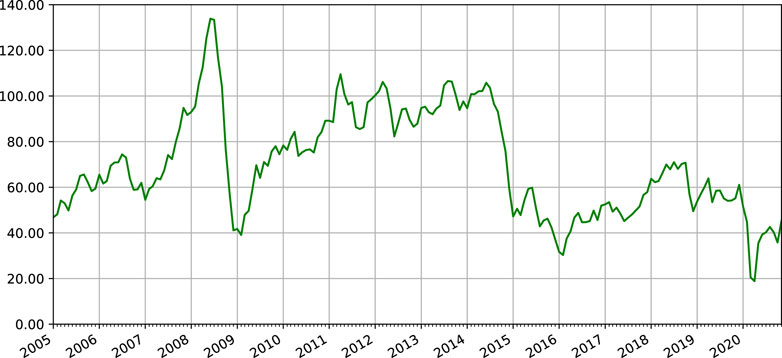
As one of the most important commodities, crude oil plays a vital role in various fields. In the past decades, crude oil prices have been extremely volatile (see Figure 1). The oil-related industries are highly sensitive to oil price changes (Ebrahim et al., 2014; Taghizadeh-Hesary et al., 2016). Accurate prediction of crude oil prices and the market volatility is valuable for market participants to make risk management plans and investment decisions (Zaabouti et al., 2016; Zhang et al., 2020). The crude oil prices are volatile, and are dependent on many factors such as market trends, sentiments and stock markets. The aforementioned factors make the crude oil prices unstable and makes its prediction complicated and challenging. Thus, we aim to develop a reliable model for crude oil price forecasting.

FIGURE 1

FIGURE 1. Crude oil West Texas Intermediate (WTI), January 2005–December 2020.

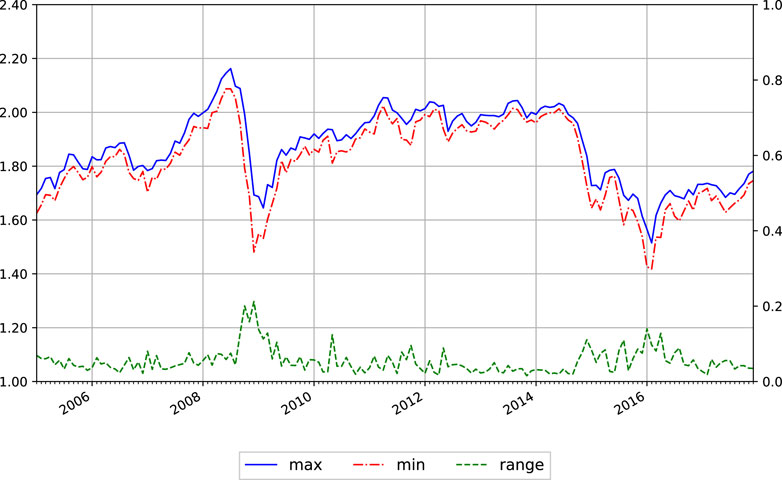
In recent literatures, most of the existing methods focus on the point-valued crude oil closing prices (Abramson and Finizza, 1995; Zhang et al., 2008; Kilian, 2009; Zhang et al., 2009; Shin et al., 2013; Zhao et al., 2017; Binder et al., 2018; Álvarez-Díaz, 2019). However, the use of closing prices has the disadvantage that it does not take into account the oil price variation information within a given period time, e.g., the midpoint and range of crude oil prices in October 2008 are about $\$76.61$/bbl and $\$36.31$/bbl respectively. While the midpoint and range of crude oil prices in November 2009 are around $\$77.99$/bbl and $\$5.42$/bbl respectively.

Such forecasts with point-valued crude oil price data have not been particularly successful when compared with the interval-valued time series forecasts (see Sun et al., 2019). What is more, recent studies also provide empirical evidence suggesting that ITS models have achieved great success on improving the forecast accuracy in a wide range of fields such as stock price forecasting (Maia and de Carvalho, 2011; Xiong et al., 2017) and forecasting in energy markets, such as electric power demand (García-Ascanio and Maté, 2010; Hu et al., 2015), and crude oil prices (Yang et al., 2016). By accessing more information (e.g., highs, lows, midpoints, and range), an interval-based method is expected to be superior to the point-based method (Sun et al., 2018). Here, highs and lows are points of inflection for prices. The price range is the difference between two boundaries, which gives the interval length. It can be regarded as a measure of volatility to reflect the price fluctuation. For example, instead of traditional point-based method, Yang et al. (2012) introduce interval dummy variables in the autoregressive conditional interval models. Sun et al. (2019) apply a threshold autoregressive interval-valued model. Qiao et al. (2019) develop an interval-valued factor pricing model. Conclusions from prior studies suggest that interval-valued time series (ITS) models may produce more accurate forecasts.

Therefore, the desirable characteristics of the interval modeling make them ideal candidates for the prediction of crude oil prices. In addition, it is well known that a large set of factors are responsible for changes in the crude oil price, including overall economic conditions, demand and supply, monetary policy, as well as speculative trading (Hamilton, 2008; Yoshino and Taghizadeh-Hesary, 2014). Thus, the number of potential predictors can be very large. In such cases, interval-valued variable selection is considered necessary and becomes the critical step in achieving promising forecasting performances in data-rich environments. On the other hand, in practice, when only some of the variables are selected to include as the predictors in a model, model misspecification is unavoidable, which can worsen the model forecast performance of the model. Therefore, model averaging is considered to take a weighted average of possible combinations of selected interval-valued predictors.

For these reasons, this paper proposes a new two-stage procedure for interval valued crude oil price forecasting based on boosting and model averaging. First, we extend the $L_2$ boosting method by Buhlmann (2006) to achieve variable selection for the interval model. Several penalized methods have been proposed to achieve variable selection. Examples include the class of Bridge estimators (Frank and Friedman, 1993), where the Lasso-type estimators are included a special case (Knight and Fu, 2000), or the smoothly clipped absolute deviation (SCAD) estimator (Fan and Li, 2001). Instead of these regularized (penalized) methods, Donald et al. (2009) apply information criteria for moment selection, Ng and Bai (2009) develop boosting for variable selection, where variable selection and shrinkage are performed simultaneously to increase prediction accuracy. The proposed vector boosting algorithm can achieve significant dimension reduction when a long list of interval-valued variables is available.

Next, we extend the LsoMA method developed by Liao et al. (2019) to average predictions from interval models with interval-valued exogenous variables to reduce model uncertainty. The idea of model averaging (MA) is first introduced to combine predictions from many forecasting models by Bates and Granger (1969) and has received great interest in econometrics and statistics. Model averaging is an extension of model selection which can substantially reduce the selection bias induced by selecting only one candidate model. Hoeting et al. (1999) provide a comprehensive summary of previous research on Bayesian model averaging (BMA) where models are weighted by the posterior model probabilities. Unlike BMA, frequentist model averaging (FMA) usually select the optimal weighting with the smallest information criteria scores (Buckland et al., 1997; Hjort and Claeskens, 2003; Hjort and Claeskens, 2006; Zhang and Liang, 2011; Zhang et al., 2012; Xu et al., 2014), Mallows model averaging (MMA) by Hansen (2007), jackknife model averaging (JMA) by Hansen and Racine (2012). Liao and Tsay (2016) extend MMA to the situation of the VAR models.

Univariate and bivariate methods are broadly the two main approaches in the interval modeling literature. In the univariate method, models are presented separately for a pair of attributes of interval variables (e.g., midpoint and range). The two attributes are estimated separately (De Carvalho et al., 2004; Maia et al., 2008), thus only information of one attribute is used in estimating model parameters at a time. Unlike the univariate method, the bivariate method estimates the two attributes simultaneously (e.g., Cheung et al., 2009; He et al., 2010; Lima Neto and De Carvalho, 2010; Arroyo et al., 2011; González-Rivera and Lin, 2013), which is more desirable in ITS forecasting. Therefore, in this paper, in order to consider possible interdependence between midpoint and range, the LsoMA methods are constructed following the bivariate modeling approach to efficiently use the contained information.

This paper proposes a two-stage vector boosting model averaging (2SVBMA) forecasting framework: Stage 1 uses vector $L_2$ Boosting to select interval-valued variables; Stage 2 uses the leave-subject-out cross-validation model averaging method with exogenous interval-valued variables to average interval-valued predictions. Our procedure combines the merits of these two techniques and can be easily adapted to any new situation. We compare our 2SVBMA method with other competing methods including model selection methods by Akaike information criterion (AIC), Bayesian information criterion (BIC), Hannan-Quinn (HQ), and model averaging methods by smoothed AIC, smoothed BIC (Buckland et al., 1997), smoothed HQ, and MMA in interval model. The empirical results indicate that the 2SVBMA method has better forecasting performance than the commonly used model selection and averaging methods.

Our proposed 2SVBMA forecasting procedure has a few appealing features. First, this approach extends the forecasting success of point-valued data models of crude oil price to interval-valued data models, which is capable of assessing and forecasting the changes in both the trend and volatility of crude oil prices simultaneously due to the informational gain from interval-valued data. Second, our vector boosting method provides a parsimony and feasible solution to the interval-valued variable selection problem for interval models. Third, the extended interval-valued LsoMA model with interval-valued exogenous variables demonstrates the gains in forecast accuracy through forecast combination. By doing so, our approach improves crude oil price forecasting performances significantly.

The remainder of this paper is organized as follows. Section 2 first proposes 2SVBMA methodology, starts with extended $L_2$ boosting to interval-valued variable selection and develops the LsoMA with interval-valued model with interval-valued exogenous variables. Section 3 provides the empirical implementations. Section 4 discusses the empirical results. Section 5 concludes.

2 Methodology

2.1 Model Framework

Let $(\mathrm{\Omega },\mathcal{F},P)$ be a probability space, where Ω is the set of elementary events, $\mathcal{F}$ is the $\sigma$-field of events, and $P:\mathcal{F}\to [\mathrm{0,1}]$ is the $\sigma$-additive probability measure. An interval random variable is defined as a measurable mapping $X:\mathcal{F}\to [x_L,x_U]\in \mathbb{R}$, such that for all $x\in [x_L,x_U]$ there is a set $A_X(x)\in \mathcal{F}$, where $A_X(x)=\{w\in \mathrm{\Omega }|X(w)=x\}$ with $x\in [x_L,x_U]$ (Arroyo et al., 2011; González-Rivera and Lin, 2013). A stochastic ITS ${\{y_t=[y_{L,t},y_{U,t}]\}}_{t=1}^T$ can be represented by its midpoint and range, i.e., $y_t=<y_{c,t},y_{r,t}>$, where $y_{c,t}=\frac{1}{2}(y_{L,t}+y_{U,t})$ and $y_{r,t}=y_{U,t}-y_{L,t}$. Assume that {y_t} is stationary and follows a vector autoregressive models with interval-valued exogenous variables:

$\begin{array}{ccc}\hfill {\mathbf{y}}_t& =\hfill & \sum _{i=1}^p{\mathit{\alpha }}_i{\mathbf{y}}_{t-i}+\sum _{j=1}^q{\mathit{\beta }}_j{\mathbf{x}}_{t-j}+{\mathit{\epsilon }}_t\hfill \\ \hfill & \equiv \hfill & {\mathbf{\Pi }}^{\prime }{\mathbf{z}}_t+{\mathit{\epsilon }}_t,t=1,\dots ,T,\hfill \end{array}(1)$

where ${\mathbf{y}}_t\triangleq {(y_{c,t},y_{r,t})}^{\prime }$, ${\mathbf{x}}_{t-j}\triangleq {(x_{c,t-j},x_{r,t-j})}^{\prime }$, and ${\mathit{\epsilon }}_t={({\epsilon }_{c,t},{\epsilon }_{r,t})}^{\prime }$ is an interval-valued sequence with mean zero and covariance matrix $\mathbb{E}{\mathit{\epsilon }}_t{\mathit{\epsilon }}_t^{\prime }\equiv \mathrm{\Sigma }$ , and ${\mathit{\alpha }}_i$ and ${\mathit{\beta }}_j$ are the coefficient matrix that satisfies ${\sum }_{i=1}^p\Vert {\mathit{\alpha }}_i\Vert <\infty$ and ${\sum }_{j=1}^q\Vert {\mathit{\beta }}_j\Vert <\infty$, ${\mathbf{z}}_t={({\mathbf{y}}_{t-1}^{\prime },\dots ,{\mathbf{y}}_{t-p}^{\prime },{\mathbf{x}}_{t-1}^{\prime },\dots ,{\mathbf{x}}_{t-q}^{\prime })}^{\prime }$ is a $2(p+q)\times 1$ vector, $\mathbf{\Pi }={({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_p,{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_q)}^{\prime }$ is a $2(p+q)\times 2$ vector, and the assumed initial data are ${\{{\mathbf{y}}_t\}}_{t=-p+1}^0$. This data generating process guarantees the natural order of the intervals, i.e., the lower bound is smaller than or equal to the upper bound.

In matrix form, (1) is represented by

${\mathbf{Y}}_c=\mathbf{Z}{\mathbf{\Pi }}_c+{\mathit{\epsilon }}_c,(2)$

and

${\mathbf{Y}}_r=\mathbf{Z}{\mathbf{\Pi }}_r+{\mathit{\epsilon }}_r,(3)$

where ${\mathbf{Y}}_c={(y_{c,1},\dots ,y_{c,T})}^{\prime }$, ${\mathbf{Y}}_r={(y_{r,1},\dots ,y_{r,T})}^{\prime }$, $\mathbf{Z}={({\mathbf{z}}_1,\dots ,{\mathbf{z}}_T)}^{\prime }$, $\mathbf{\Pi }\equiv ({\mathbf{\Pi }}_c,{\mathbf{\Pi }}_r)$, ${\mathit{\epsilon }}_c={({\epsilon }_{c,1},\dots ,{\epsilon }_{c,T})}^{\prime }$, and ${\mathit{\epsilon }}_r={({\epsilon }_{r,1},\dots ,{\epsilon }_{r,T})}^{\prime }$.

The least squares estimators of ${\mathbf{\Pi }}_c$ and ${\mathbf{\Pi }}_r$ are given by

${\widehat{\mathbf{\Pi }}}_c={({\mathbf{Z}}^{\prime }\mathbf{Z})}^{-1}{\mathbf{Z}}^{\prime }{\mathbf{Y}}_c,(4)$

and

${\widehat{\mathbf{\Pi }}}_r={({\mathbf{Z}}^{\prime }\mathbf{Z})}^{-1}{\mathbf{Z}}^{\prime }{\mathbf{Y}}_r.(5)$

2.2 First Stage: Vector Boosting

We first extend $L_2$Boosting regularization method to interval model to select a subset of interval-valued variables. ${\mathbf{Z}}_k$ is the $k^{th}$ row in $\mathbf{Z}$. They are the potential interval-valued variables that will be selected by vector boosting. ${\mathbf{Z}}_{k,t}$ is the $t^{th}$ element in ${\mathbf{Z}}_k$ and Π_k is the corresponding $k^{th}$ interval-valued coefficient of $\mathbf{\Pi }$, where $k=1,\dots ,p+q$. Let $m$ denote the $m^{th}$ iteration in the vector boosting procedure, and $\bar{M}$ denote the maximum number of iteration. At each step $m$, the interval-valued variable ${\widehat{\widehat{\mathbf{\Pi }}}}_{km}$ that is most relevant to the “current interval-valued residual” is selected. Denote ${\mathbf{F}}_{m,t}$ as the strong learner and ${\mathbf{f}}_{m,t}$ as the weak learner for $k=1,\dots ,p+q$. Let ${\widehat{\mathit{\epsilon }}}_m={\left({\widehat{\mathit{\epsilon }}}_{m,1},\dots ,{\widehat{\mathit{\epsilon }}}_{m,T}\right)}^{\prime }$, ${\mathbf{f}}_m={\left({\mathbf{f}}_{m,1},\dots ,{\mathbf{f}}_{m,T}\right)}^{\prime }$ and ${\mathbf{F}}_m={\left({\mathbf{F}}_{m,1},\dots ,{\mathbf{F}}_{m,T}\right)}^{\prime }$.

Vector $L_2$ Boosting performs an interval-valued variable selection for $\mathbf{Y}$ using the following procedure:

1. When $m=0$, the initial weak learner for ${\mathbf{y}}_t$ is

${\mathbf{F}}_{0,t}={\mathbf{f}}_{0,t}=\frac{1}{T}\sum _{t=1}^T{\mathbf{y}}_t.(6)$

2. For each step. $m=1,\dots ,\bar{M}$

1) Compute the “current interval-valued residual,” ${\widehat{\mathit{\epsilon }}}_{m,t}={\mathbf{y}}_t-{\mathbf{F}}_{m-1,t}$.

2) Regress the current interval-valued residual ${\widehat{\mathit{\epsilon }}}_{m,t}={({\widehat{\mathit{\epsilon }}}_{c,m,t},{\widehat{\mathit{\epsilon }}}_{r,m,t})}^{\prime }$ on each ${\mathbf{Z}}_{k,t}$. The estimator ${\widehat{\mathbf{\Pi }}}_k$ is obtained as

$\begin{array}{ll}\hfill {\widehat{\mathbf{\Pi }}}_{c,k}& ={\min }_{{\mathbf{\Pi }}_{c,k}}\sum _{t=1}^T{\left({\widehat{\mathit{\epsilon }}}_{c,m,t}-{\mathbf{Z}}_{k,t}{\mathbf{\Pi }}_{c,k}\right)}^2,\hfill \end{array}(7)$

$\begin{array}{ll}\hfill {\widehat{\mathbf{\Pi }}}_{r,k}& ={\min }_{{\mathbf{\Pi }}_{r,k}}\sum _{t=1}^T{\left({\widehat{\mathit{\epsilon }}}_{r,m,t}-{\mathbf{Z}}_{k,t}{\mathbf{\Pi }}_{r,k}\right)}^2.\hfill \end{array}(8)$

The interval-valued variables that has the minimum sum of squared residuals is picked up, such that

$k_m=\arg {\min }_{k\in \{1,\dots ,p+q\}}\sum _{t=1}^T{\left({\widehat{\mathit{\epsilon }}}_{m,t}-{\mathbf{Z}}_{k,t}{\widehat{\mathbf{\Pi }}}_k\right)}^2.(9)$

3) The weak learner is

${\mathbf{f}}_{m,t}={\mathbf{Z}}_{k_m,t}{\widehat{\mathbf{\Pi }}}_{k_m},(10)$

where ${\mathbf{Z}}_{k_m,t}$ is the interval-valued variable that is selected.

4) The strong learner ${\mathbf{F}}_{m,t}$ is updated as

${\mathbf{F}}_{m,t}={\mathbf{F}}_{m-1,t}+c_m{\mathbf{f}}_{m,t},(11)$

with $c_m>0$, where $c_m$ is a learning rate, which can be seen as a small step size when updating ${\mathbf{F}}_{m,t}$.

To avoid overfitting, a version of AIC is used to choose the optimal number of iteration $\widehat{M}$. Define ${\mathbf{P}}_m={\mathbf{Z}}_{k_m}{({\mathbf{Z}}_{k_m}^{\prime }{\mathbf{Z}}_{k_m})}^{-1}{\mathbf{Z}}_{k_m}^{\prime }$ to be an $T\times T$ matrix. From Equation (10),

$\begin{array}{ll}\hfill {\mathbf{Z}}_{k_m}{\widehat{\mathbf{\Pi }}}_{k_m}& ={\mathbf{P}}_m{\widehat{\mathit{\epsilon }}}_m\hfill \\ \hfill {\mathbf{f}}_m& ={\mathbf{P}}_m\left(\mathbf{Y}-{\mathbf{F}}_{m-1}\right).\hfill \end{array}(12)$

The strong learner at each step $m$ is

$\begin{array}{ll}\hfill {\mathbf{F}}_m& ={\mathbf{F}}_{m-1}+c_m{\mathbf{P}}_m\left(\mathbf{Y}-{\mathbf{F}}_{m-1}\right)\hfill \\ \hfill & =\left[{\mathbf{I}}_{T\times T}-\prod _{a=0}^m\left({\mathbf{I}}_{T\times T}-c_{k_a}{\mathbf{P}}_{k_a}\right)\right]\mathbf{Y}=:{\mathbf{B}}_m\mathbf{Y}.\hfill \end{array}$

AIC is given as

$AIC(m)=\text{log}({\widehat{\sigma }}_m^2)+\frac{1+\text{trace}({\mathbf{B}}_m)/T}{1-(\text{trace}({\mathbf{B}}_m)+2)/T}.(13)$

where $\text{log}({\widehat{\sigma }}_m^2)=\frac{1}{T}{\sum }_{t=1}^T{\left({\widehat{\mathit{\epsilon }}}_m-c_m{\mathbf{f}}_{m,t}\right)}^2$. Then $\widehat{M}=\arg {\min }_{m=1,\dots ,\bar{M}}AIC(m)$.

2.3 Second Stage: LsoMA

After selecting these important exogenous interval-valued variables, LsoMA technique is extended to interval candidate models with interval-valued exogenous variables, which is adopted to reduce model uncertainty and increase forecast accuracy.

Consider $S$ candidate models used to approximate the DGP in Eq. (1) with $S$ to be infinite if the sample size is going to infinity. The $s$th ($1\le s\le S$) candidate model is given by

$\begin{array}{ccc}\hfill {\mathbf{y}}_t& =\hfill & \sum _{i=1}^{i_s}{\mathit{\alpha }}_i{\mathbf{y}}_{t-i}+\sum _{j=1}^{j_s}{\mathit{\beta }}_j{\mathbf{x}}_{t,j}+{\mathit{\epsilon }}_t,\hfill \\ \hfill & \equiv \hfill & {\mathbf{z}}_t^{{(s)}^{\prime }}{\mathbf{\Pi }}^{(s)}+{\mathit{\epsilon }}_t,t=S+1,\dots ,T,\hfill \end{array}$

where ${\mathbf{z}}_t^{(s)}={({\mathbf{y}}_{t-1}^{\prime },\dots ,{\mathbf{y}}_{t-i_s}^{\prime },{\mathbf{x}}_{t,1}^{\prime },\dots ,{\mathbf{x}}_{t,j_s}^{\prime })}^{\prime }$, ${\mathbf{\Pi }}^{(s)}={({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_{i_s},{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_{j_s})}^{\prime }$, and $1\le i_s,j_s\le S$. Then in matrix form, we have

$\mathbf{Y}={\mathbf{Z}}^{(s)}{\mathbf{\Pi }}^{(s)}+\mathit{\epsilon },$

where $\mathbf{Y}={({\mathbf{y}}_{S+1},\dots ,{\mathbf{y}}_T)}^{\prime }$, ${\mathbf{Z}}^{(s)}={({\mathbf{z}}_{S+1}^{(s)},\dots ,{\mathbf{z}}_T^{(s)})}^{\prime }$, and $\mathit{\epsilon }={({\mathit{\epsilon }}_{S+1},\dots ,{\mathit{\epsilon }}_T)}^{\prime }$. For each candidate model, we use multivariate least squares (LS) method to estimate parameters and thus the LS estimator of ${\mathbf{\Pi }}^{(s)}$ is ${\widehat{\mathbf{\Pi }}}^{(s)}={({\mathbf{Z}}^{{(s)}^{\prime }}{\mathbf{Z}}^{(s)})}^{-1}{\mathbf{Z}}^{{(s)}^{\prime }}\mathbf{Y}$, and the corresponding estimator of conditional mean $\mathit{\mu }$ is ${\widehat{\mathit{\mu }}}^{(s)}={\mathbf{Z}}^{(s)}{\widehat{\mathbf{\Pi }}}^{(s)}$ in $s$th candidate model.

Let the weight vector $\mathbf{w}={(w_1,\dots ,w_S)}^{\prime }\in \mathcal{W}=\{w\in {[\mathrm{0,1}]}^S:{\sum }_{s=1}^S{w}_s=1\}$. Then the model averaging estimator of conditional mean $\mathit{\mu }$ is $\widehat{\mathit{\mu }}(\mathbf{w})={\sum }_{s=1}^S{w}_s{\widehat{\mathit{\mu }}}^{(s)}$. To obtain the optimal weights, it is common to minimize the following squared loss function:

$L(\mathbf{w})=\Vert \mathit{\mu }-\mathit{\mu }(\mathbf{w}){\Vert }^2.(14)$

However, this loss is infeasible because of the unknown conditional mean $\mathit{\mu }$. We follow the spirit of Liao et al. (2019) to use the following feasible leave-subject-out cross-validation criterion of choosing weights

$LsoMA(\mathbf{w})=\text{trace}\{(\mathbf{Y}-\widetilde{\stackrel{̃}{\mathit{\mu }}}(\mathbf{w})){\mathbf{\Sigma }}^{-1}{(\mathbf{Y}-\widetilde{\stackrel{̃}{\mathit{\mu }}}(\mathbf{w}))}^{\prime }\},(15)$

where ${\widetilde{\stackrel{̃}{\mathit{\mu }}}}^{(s)}={({\widetilde{\stackrel{̃}{\mathit{\mu }}}}_{S+1}^{{(s)}^{\prime }},\dots ,{\widetilde{\stackrel{̃}{\mathit{\mu }}}}_T^{{(s)}^{\prime }})}^{\prime }$, ${\widetilde{\stackrel{̃}{\mathit{\mu }}}}_{S+t}^{(s)}={\mathit{\psi }}_t^{(s)}{\widetilde{\stackrel{̃}{\mathit{\mu }}}}_{[t]}^{(s)}$, ${\mathit{\psi }}_t^{(s)}$ is the selected matrix to select observations at time point $S+t$, ${\widetilde{\stackrel{̃}{\mathit{\mu }}}}_{[t]}^{(s)}$ is the leave-subject-out cross-validation estimator after deleting some observations around $S+t$, and $\widetilde{\stackrel{̃}{\mathit{\mu }}}(\mathbf{w})={\sum }_{s=1}^S{w}_s{\widetilde{\stackrel{̃}{\mathit{\mu }}}}^{(s)}$; see more discussions in Liao et al. (2019). Minimizing this criterion, we have

$\widehat{\mathbf{w}}={\mathit{arg}\mathit{min}}_{\mathbf{w}\in \mathcal{W}}LsoMA(\mathbf{w}),(16)$

and thus the model averaging estimator is $\widehat{\mathit{\mu }}(\widehat{\mathbf{w}})$. As Liao et al. (2019) proved, the weight obtained by minimizing the feasible cross-validation criterion $LsoMA(\mathbf{w})$ is asymptotically optimal in the sense of achieving the lowest possible quadratic errors, i.e.,

$\frac{L(\widehat{\mathbf{w}})}{{\inf }_{\mathbf{w}\in H_T}L(\mathbf{w})}=1+o_p(1).$

This shows that the squared error loss obtained from the selected weight vector $\widehat{\mathbf{w}}$ is asymptotically equivalent to the infeasible optimal averaging estimator.

3 Empirical Implementations

This section applies the proposed 2SVBMA procedure to forecast the real price of crude oil. Data and preliminary analysis are introduced in Section 3.1. Then the selected interval-valued factors are introduced in Section 3.2. Section 3.3 introduces the candidate models. Section 3.4 provides competing methods.

3.1 Data and Preliminary Analysis

Following Wang et al. (2017), Chai et al. (2018) and Yu et al. (2019), the daily point-valued WTI crude oil prices are used to construct the interval-valued monthly prices. $y_{U,t}$ and $y_{L,t}$ denote the daily maximum and minimum prices within $t$th month. $y_{c,t}=(y_{U,t}+y_{L,t})/2$ and $y_{r,t}=y_{U,t}-y_{L,t}$ are the midpoint and range from an interval-valued price observation $y_t=⟨y_{c,t},y_{r,t}⟩$. The data period used in the research is from January 2005 to December 2017. Data on crude oil prices are collected from the US Energy Information Administration (EIA). Figure 2 presents the interval-valued crude oil prices: the range ($y_{r,t}$, right y-Axis), the maximum ($y_{U,t}$, left y-Axis), and minimum (y_L,t, left y-Axis) prices within 1 month, where we can see that the boundaries and ranges are interlinked, e.g., a strong increase in volatility ($y_{r,t}$) is accompanied by a significant decrease in crude oil prices during the second half of 2008.

FIGURE 2

FIGURE 2. Interval valued crude oil prices from EIA, January 2005–December 2017.

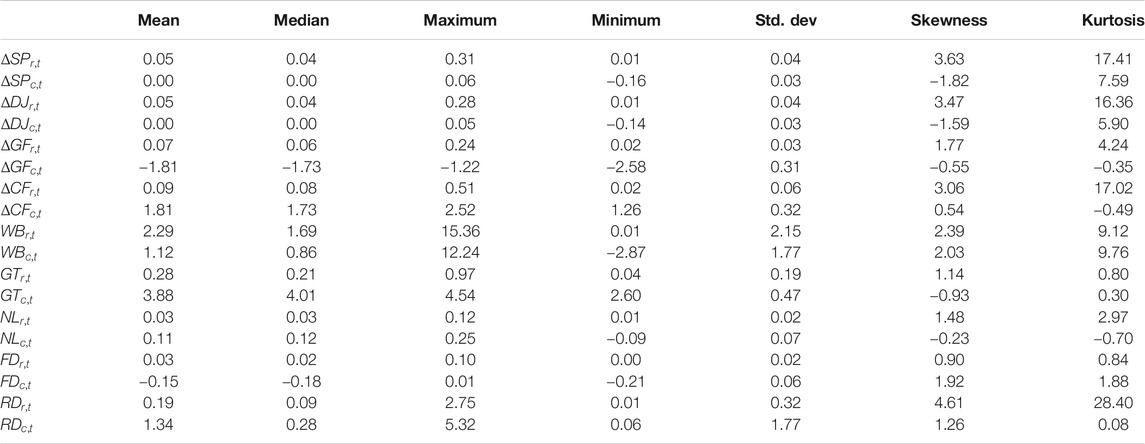
Table 1 presents the summary of statistical characteristics. First, it is shown that the spread of ranges is slightly smaller than the volatility in the boundaries ($D{y}_{U,t}=y_{U,t}-y_{avg,t-1}$ and $D{y}_{L,t}=y_{L,t}-y_{avg,t-1}$), where $y_{avg,t}$ is the monthly prices from EIA. In addition, the skewness and leptokurtic kurtosis are different among $y_{r,t}$, $D{y}_{L,t}$ and $D{y}_{U,t}$. Compared with Dy_L,t and $D{y}_{U,t}$, $y_{r,t}$ is with greater skewness and higher leptokurtic. We can see from Table 1 that the interval-valued data can capture more information than the point-valued data.

TABLE 1

TABLE 1. Basic statistical analysis on monthly interval-valued crude oil prices.

3.2 Interval-Valued Control Variables in the First Stage

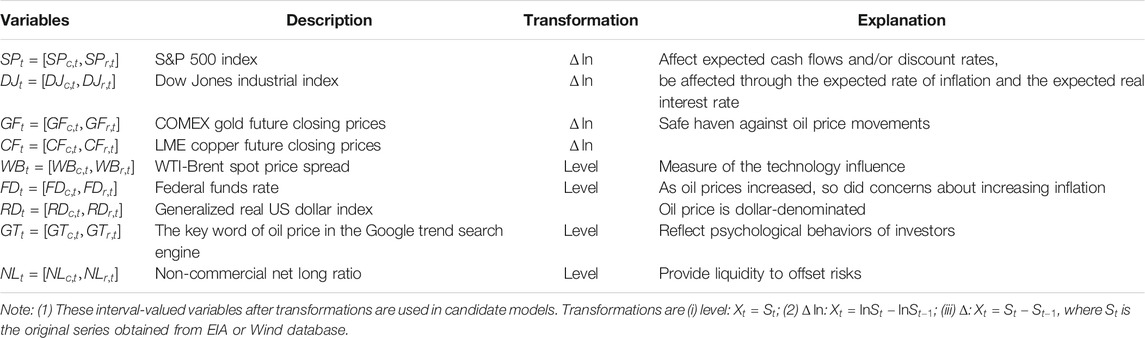
The potential choices of monthly interval-valued explanatory variables from various aspects are considered in this section, including the stock market, commodity market, technology factor, search query data, speculation, monetary market and currency market (Pan et al., 2014; Wang et al., 2016; Wang et al., 2017; Chai et al., 2018; Yu et al., 2019); see Table 2 for more discussions. First, the Augmented Dickey-Fuller tests suggest that the null hypothesis for the original control variables is hardly rejected at the 5% significance level, except for non-commercial net long ratio ($N{L}_t$) and the Federal funds rate ($F{D}_t$). For stationarity, we use the Hukuhara’s difference of interval-valued exogenous variables. The Hukuhara’s difference between a pair of intervals is essentially equal to the regular difference between points in intervals. As Yang et al. (2016) mentioned, the concept of interval with Hukuara’s difference is useful and suitable for econometric analysis of interval data. Take S&P 500 index ($S{P}_t$) as an example. It is defined as $\mathrm{\Delta }S{P}_t=S{P}_t-S{P}_{t-1}=[\tilde{\mathrm{\Delta }}S{P}_{c,t},\tilde{\mathrm{\Delta }}S{P}_{r,t}]$, where $\mathrm{\Delta }$ is the Hukuhara’s difference between intervals, and $\tilde{\mathrm{\Delta }}$ is the regular difference between intervals. This implies that the midpoints and centers of these interval-valued exogenous variables are stationary after Hukuhara’s difference. Similarly, we have $\mathrm{\Delta }D{J}_t$, $\mathrm{\Delta }G{F}_t$, $\mathrm{\Delta }C{F}_t$ and $\mathrm{\Delta }R{D}_t$; see specific definitions in Table 2.

TABLE 2

TABLE 2. Monthly interval-valued exogenous variables.

Second, Table 3 provides a summary of statistical characteristics. It is shown that no matter whether the time series is transferred by Hukuhara’s difference, the midpoints and ranges for interval-valued control variables appear to have different skewness and leptokurtic kurtosis properties. This suggests that using one attribute of ITS contains partial information only. Thus, it is highly desirable to utilize the information contained in interval-valued data.

TABLE 3

TABLE 3. Basic statistical analysis on monthly interval-valued explanatory variables.

Third, we use the extended $L_2$ Boosting regularization method to select interval-valued control variables. Specifically, we set the lag length $L=12$ for every control variable and thus the number of the potential explanatory interval-valued variables equals $12\times 9=108$. For vector boosting, we start with the learning rate $c=0.01$, iteration = 100 times. These parameters are adjusted during training. After using various training sets, $\mathrm{\Delta }S{P}_{t+h-1}$, $\mathrm{\Delta }G{F}_{t+h-1}$, $\mathrm{\Delta }G{F}_{t+h-2}$, $\mathrm{\Delta }G{F}_{t+h-3}$, $W{B}_{t+h-1}$, and $G{T}_{t+h-4}$ are selected with duplicates removed and used to do h-step-ahead out-of-sample forecasts of interval-valued crude oil prices.

Furthermore, these selected interval-valued control variables have important economic interpretation for crude oil prices as follows:

$\mathrm{\Delta }S{P}_{t+h-1}$: It provides information of fundamentals and volatility contained in S&P 500. The movement of S&P 500 Index may closely mirror that of the crude oil prices (e.g., Kilian, 2009; Miller and Ratti, 2009; Balcilar et al., 2015; Ding et al., 2016). As discussed in Kilian (2009) and Miller and Ratti (2009), the oil price shocks influence stock prices by affecting expected cash flows and discount rates, since crude oil is an important input in production and its price can influence the costs for the manufacturing and transport sectors.

$\mathrm{\Delta }G{F}_{t+h-j}$ (j = 1,2,3): It is the logarithmic difference between Comex gold future prices at $t+h-j$ and $t+h-j-1$, which provides information in Comex gold future market (e.g., Baur and Lucey, 2010; Reboredo, 2013; Souček, 2013; Kang et al., 2017). Gold serves as store of value especially during periods of economic uncertainties. Oil prices can affect levels of inflation (Zhao et al., 2016). Gold investment can be used as a hedge against inflation and currency depreciation. It can also be viewed as a safe haven against the stock market turbulence for investors.

$W{B}_{t+h-1}$: It is WTI-Brent spot price spread, which is the price difference between crude oil and the byproducts refined from it. The crack spread gives the profit margin that a refinery can expect. Thus, a tight spread can be seen as a indicator that refiners may slow production to tighten supply.

$G{T}_{t+h-4}$: It is the search query data collected from Internet, which has been widely applied as indicator when analyzing the crude oil prices and has been demonstrated to be effective in improving forecasts performance (Fantazzini and Fomichev, 2014; Li et al., 2015a; Wu et al., 2021; Yang et al., 2021). The keyword “oil price” is searched in the Google Trend search engine. Search query data is expected to reflect the psychological aspects of investors when they making strategic investment decisions in the crude oil market (Li et al., 2015b).

3.3 Model Averaging in the Second Stage

3.3.1 Candidate Models

We consider 6 lagged dependent variables ${\mathbf{y}}_{t-1},\dots ,{\mathbf{y}}_{t-6}$ and 6 exogenous variables selected from vector boosting. As we use monthly interval-valued crude oil prices, the maximum lag is set to 6, including the past half year information. Exogenous variables are sorted by relevance to ${\mathbf{y}}_t$ during the estimation period. Then, 12 nested interval predictive candidate models are considered as:

Model 1. ${\mathbf{y}}_{t+h}={\mathit{\alpha }}_1{\mathbf{y}}_{t+h-1}+{\mathit{\epsilon }}_{t+h}$.

Model 2. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^2{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\epsilon }}_{t+h}$.

Model 3. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^3{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\epsilon }}_{t+h}$.

Model 4. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^4{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\epsilon }}_{t+h}$.

Model 5. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^5{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\epsilon }}_{t+h}$.

Model 6. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\epsilon }}_{t+h}$.

Next, 6 exogenous variables are added to Model 6 to construct Models 7–12, sorted by relevance to $\mathbf{Y}$:

Model 7. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\beta }}_1\mathrm{\Delta }S{P}_{t+h-1}+{\mathit{\epsilon }}_{t+h}$.

Model 8. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\beta }}_1\mathrm{\Delta }S{P}_{t+h-1}+{\mathit{\beta }}_2\mathrm{\Delta }G{F}_{t+h-1}+{\mathit{\epsilon }}_{t+h}$.

Model 9. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\beta }}_1\mathrm{\Delta }S{P}_{t+h-1}+{\mathit{\beta }}_2\mathrm{\Delta }G{F}_{t+h-1}+{\mathit{\beta }}_3\mathrm{\Delta }G{F}_{t+h-2}+{\mathit{\epsilon }}_{t+h}$.

Model 10. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\beta }}_1\mathrm{\Delta }S{P}_{t+h-1}+{\mathit{\beta }}_2\mathrm{\Delta }G{F}_{t+h-1}+{\mathit{\beta }}_3\mathrm{\Delta }G{F}_{t+h-2}+{\mathit{\beta }}_4\mathrm{\Delta }G{F}_{t+h-3}+{\mathit{\epsilon }}_{t+h}$.

Model 11. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\beta }}_1\mathrm{\Delta }S{P}_{t+h-1}+{\mathit{\beta }}_2\mathrm{\Delta }G{F}_{t+h-1}+{\mathit{\beta }}_3\mathrm{\Delta }G{F}_{t+h-2}+{\mathit{\beta }}_4\mathrm{\Delta }G{F}_{t+h-3}+{\mathit{\beta }}_{5}W{B}_{t+h-1}+{\mathit{\epsilon }}_{t+h}$.

Model 12. ${\mathbf{y}}_{t+h}={\sum }_{i=1}^6{\mathit{\alpha }}_i{\mathbf{y}}_{t+h-i}+{\mathit{\beta }}_1\mathrm{\Delta }S{P}_{t+h-1}+{\mathit{\beta }}_2\mathrm{\Delta }G{F}_{t+h-1}+{\mathit{\beta }}_3\mathrm{\Delta }G{F}_{t+h-2}+{\mathit{\beta }}_4\mathrm{\Delta }G{F}_{t+h-3}+{\mathit{\beta }}_{5}W{B}_{t+h-1}+{\mathit{\beta }}_{6}G{T}_{t+h-4}+{\mathit{\epsilon }}_{t+h}$.

These candidate models are used for LsoMA in the second stage. We do $h$-step-ahead prediction with $h\in \{\mathrm{1,4,8,12}\}$.

3.4 Competing Methods

In this paper, we compare 2SVBMA forecasts with various competing methods, including AIC, BIC, HQ, Mallows model averaging (MMA; Liao et al., 2019), smoothed AIC (SAIC), smoothed BIC (SBIC) and smoothed Hannan-Quinn (SHQ) based on the same set of candidate models (model 1 - model 12).

The AIC criterion for the $s$th candidate model $(1\le s\le 15)$ is $AI{C}^{\left(s\right)}=\ln |{\widehat{\mathbf{\Sigma }}}^{\left(s\right)}|+2s{2}^2/T$, where $\widehat{s}$ minimizes $AI{C}^{\left(s\right)}$ and ${\widehat{\mathbf{\Sigma }}}^{(s)}={(T-S)}^{-1}{(\mathbf{Y}-{\widetilde{\stackrel{̃}{\mathit{\mu }}}}^{(s)})}^{\prime }(\mathbf{Y}-{\widetilde{\stackrel{̃}{\mathit{\mu }}}}^{(s)})$ as the residual covariance matrix from the $s$th candidate model. Similarly, BIC and HQ are model selection methods, minimizing the corresponding criteria $BI{C}^{\left(s\right)}=\ln |{\widehat{\mathbf{\Sigma }}}^{\left(s\right)}|+\left(\ln T\right)s{2}^2/T$, $H{Q}^{\left(s\right)}=\ln |{\widehat{\mathbf{\Sigma }}}^{\left(s\right)}|+2\left(\ln \ln T\right)s{2}^2/T$, respectively. These three selected candidate models ares used as benchmark models.

Four model averaging (or forecast combination) methods are considered here. MMA proposed by Liao and Tsay (2016) is an extension of Mallows criterion to vector regression models. Specifically, the multivariate Mallow criterion for model averaging takes the following form:

$C_T\left(\mathbf{w}\right)=\left(T-S\right)\text{trace}\left(\tilde{\mathbf{\Sigma }}{\left(S\right)}^{-1}\widehat{\mathbf{\Sigma }}\left(\mathbf{w}\right)\right)+2\cdot 2^2{\mathbf{s}}^{\prime }\mathbf{w}$

where $\tilde{\mathbf{\Sigma }}\left(S\right)=\frac{1}{T-S-2S}{\sum }_{t=S+1}^T{\widehat{\epsilon }}_t\left(S\right){\widehat{\epsilon }}_t{\left(S\right)}^{\prime }$, $\widehat{\mathbf{\Sigma }}\left(\mathbf{w}\right)=\frac{1}{T-S}{\sum }_{t=S+1}^T{\widehat{\epsilon }}_t\left(\mathbf{w}\right){\widehat{\epsilon }}_t{\left(\mathbf{w}\right)}^{\prime }$, and ${\mathbf{s}}^{\prime }\mathbf{w}={\sum }_{s=1}^{S}w\left(s\right)s$. The Mallows weight vector is defined by:

$\widehat{\epsilon }=\arg \underset{w\in W}{\min }{C}_T\left(\mathbf{w}\right).$

SAIC, SBIC and SHQ are simple model averaging methods with the weights

$w_{AIC,s}=\exp \left(-AI{C}^{\left(s\right)}/2\right)/\sum _{s=1}^S\left(-AI{C}^{\left(s\right)}/2\right),$

and

$w_{BIC,s}=\exp \left(-BI{C}^{\left(s\right)}/2\right)/\sum _{s=1}^S\left(-BI{C}^{\left(s\right)}/2\right),$

and

$w_{HQ,s}=\exp \left(-H{Q}^{\left(s\right)}/2\right)/\sum _{s=1}^S\left(-H{Q}^{\left(s\right)}/2\right),$

respectively.

4 Empirical Results

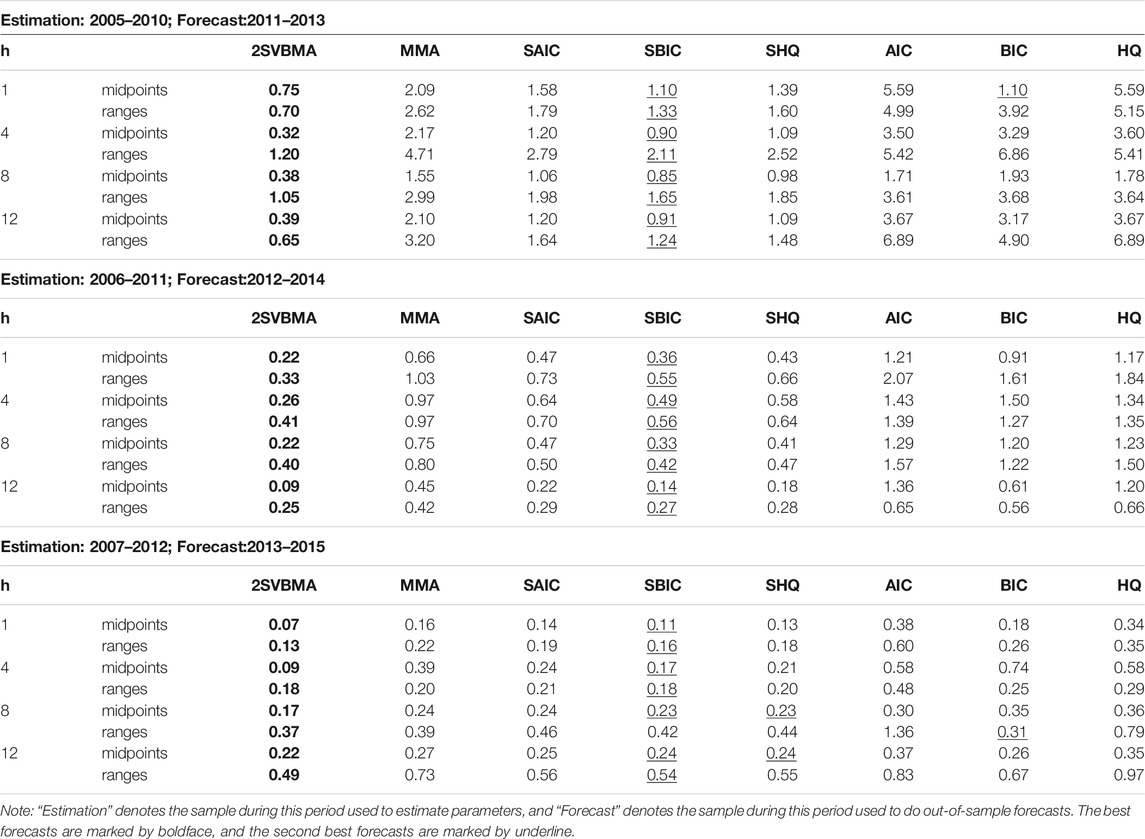
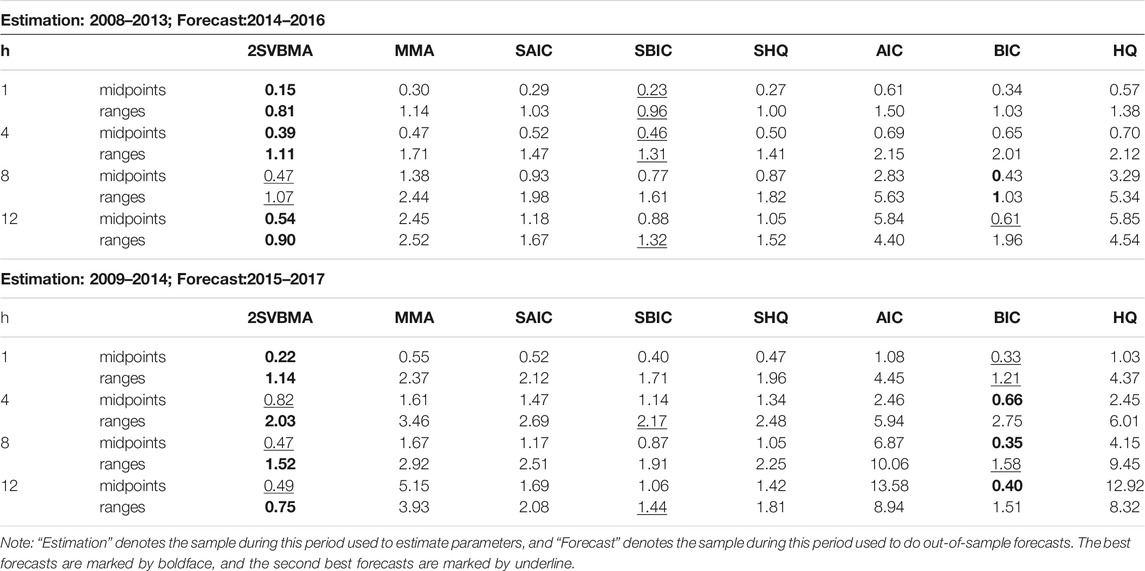
This section compares the forecasting performance of the proposed 2SVBMA approach with various competing methods presented in previous studies by using interval-valued crude oil prices. The whole sample from 2005 January to 2017 December are divided into two parts: one is used for parameter estimation, and the other is used for out-of-sample forecasting. Various subsamples for estimation and forecast are used to test prediction accuracy; see Tables 4, 5.

TABLE 4

TABLE 4. MSPE ($10^{-2}$) of the recursive prediction for interval-valued crude oil prices (I).

TABLE 5

TABLE 5. MSPE ($10^{-2}$) of the recursive prediction for interval-valued crude oil prices (II).

Tables 4, 5 report the MSPEs of $h$-step-ahead (1,4,8,12) forecasts for the interval-valued crude oil prices using various estimation and forecast samples. First, it is worth noticing that for the horizons of 1, 4, 8 and 12 months, the 2SVBMA method outperforms other competing methods in most cases; out of the 48 cases considered, with respect to RMSFE of midpoints and ranges, it yields the best outcomes 42 times and the second best outcomes 6 times. Intuitively, the proposed 2SVBMA method selects the important factors at the first stage and then give the optimal weights averaging across the 12 nested regression forecasts. Second, 2SVBMA based on LsoMA outperforms various model averaging and model selection methods, including MMA. One possible explanation is that leave-subject-out cross-validation is more suitable for vector autoregressive situations with heteroscedastic and auto-correlated errors. Additionally, as shown in Liao et al. (2019), the approximate unbiasedness of LsoMA and its asymptotic optimality in terms of obtaining the lowest quadratic errors are established. This is why LsoMA outperforms other model averaging methods (i.e., SAIC, SBIC, and SHQ) in the second stage.

Second, the SBIC estimators always produce the second-best forecasts after the 2SVBMA estimator among all model averaging methods, while SAIC achieves higher forecast criteria than other model averaging methods. Similarly, BIC always yields best forecasts among all model selection methods, while the AIC estimator achieves higher MSFE in most cases. This happens because AIC prefers selecting the relatively complicated model, which is inappropriate for out-of-sample forecasting even though it has good in-sample fitting. A simple model may be better for out-of-sample forecasting.

Furthermore, it is shown that at the second stage, model averaging forecasts outperform model selection forecasts in almost 90% of all cases. The significant advantages of model averaging support the argument of Rapach et al. (2010) that “model uncertainty and instability seriously impair the forecasting ability of individual predictive regression models.”

Overall, the proposed approach using interval-valued data is capable of assessing and forecasting the changes in both level and volatility. We can see from the results that forecasting with model averaging is generally better than obtaining the predictions from just one model (model selection). Since we may choose a very different model when there are small changes in the original data set, which may lead to a big change in the final conclusions, resulting in non-effective decision-making due to the unstable forecasting process. The proposed method is able to help obtain more stable decision-making when a long list of interval-valued predictors is available in a wide range of fields, for example, the daily trading strategy in the finance field.

5 Conclusion

We propose a novel 2SVBMA forecasting procedure to capture the relevant information available in the interval format and the underlying characteristics of crude oil price movements. Vector $L_2$Boosting in the first stage and LsoMA in the second stage are extended to interval models with interval-valued exogenous variables. Empirical results show that our proposed approach outperforms other competing model averaging and model selection methods in terms of MSFE of midpoints and ranges.

There are some limitations and potential extensions of our study. First, more advanced optimization algorithms for interval-valued variable selection can be proposed in future work. Second, the candidate models with different structures in model averaging methods can further be developed to enhance forecasting. It would also be interesting to develop interval-based machine learning methods to improve forecast accuracy. Furthermore, the proposed methodology in this paper can be extended to the vector autoregressive (VAR) model, which can cover more applications in economics and finance.

In general, 2SVBMA provides a methodological framework for interval-valued data forecasting when there are a large number of potential predictors. For example, this methodology can be used to quantify the impact of COVID-19 pandemic on oil and gas industry. 2SVBMA can also provide implications for the post-COVID recovery management. The accurate prediction of crude oil prices will assist policy makers in understanding issues affecting different oil industry segments, and help governments be better prepared for the recovery.

6 Compliance With Ethical Standards

The authors thank a number of the participants at Symposium on Interval Data Modelling: Theory and Applications (SIDM 2019) in Beijing for their valuable comments and suggestions. This work was partially supported by National Natural Science Foundation of China (Nos. 71973116, 71988101, 72073126, 72091212), and the disciplinary funding of Central University of Finance and Economics. The authors declare no competing interests. This article does not contain any studies with human participants performed by any of the authors.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All three authors contributed equally to this work and the order of authorship has nothing other than alphabetical significance.

Funding

This work was partially supported by National Natural Science Foundation of China (Nos. 71973116, 71988101, 72073126, 72091212), the funding of Forecasting and Monitoring of COVID-19 in countries along "Belt and Road" and Related Economic Impacts (ANSO-SBA-2020-12), and the disciplinary funding of Central University of Finance and Economics.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abramson, B., and Finizza, A. (1995). Probabilistic Forecasts from Probabilistic Models: a Case Study in the Oil Market. Int. J. Forecast. 11, 63–72. doi:10.1016/0169-2070(94)02004-9

CrossRef Full Text | Google Scholar

Álvarez-Díaz, M. (2019). Is it Possible to Accurately Forecast the Evolution of Brent Crude Oil Prices? an Answer Based on Parametric and Nonparametric Forecasting Methods. Empirical Econ. 59, 1285–1305. doi:10.1007/s00181-019-01665-w

CrossRef Full Text | Google Scholar

Arroyo, J., González-Rivera, G., and Maté, C. (2011). “Forecasting with Interval and Histogram Data: Some Financial Applications,” in Handbook of Empirical Economics and Finance. Editors A. Ullah, and D. E. A. Giles (New York: Chapman & Hall), 247–279.

Google Scholar

Balcilar, M., Gupta, R., and Miller, S. M. (2015). Regime Switching Model of Us Crude Oil and Stock Market Prices: 1859 to 2013. Energ. Econ. 49, 317–327. doi:10.1016/j.eneco.2015.01.026

CrossRef Full Text | Google Scholar

Bates, J. M., and Granger, C. W. J. (1969). The Combination of Forecasts. Or 20, 451–468. doi:10.2307/3008764

CrossRef Full Text | Google Scholar

Baur, D. G., and Lucey, B. M. (2010). Is Gold a Hedge or a Safe haven? an Analysis of Stocks, Bonds and Gold. Financial Rev. 45, 217–229. doi:10.1111/j.1540-6288.2010.00244.x

CrossRef Full Text | Google Scholar

Binder, K. E., Pourahmadi, M., and Mjelde, J. W. (2018). The Role of Temporal Dependence in Factor Selection and Forecasting Oil Prices. Empirical Econ. 58, 1–39. doi:10.1007/s00181-018-1574-9

CrossRef Full Text | Google Scholar

Buckland, S. T., Burnham, K. P., and Augustin, N. H. (1997). Model Selection: An Integral Part of Inference. Biometrics 53, 603–618. doi:10.2307/2533961

CrossRef Full Text | Google Scholar

Buhlmann, P. (2006). Boosting for High-Dimensional Linear Models. Ann. Stat. 34, 559–583. doi:10.1214/009053606000000092

CrossRef Full Text | Google Scholar

Chai, J., Xing, L.-M., Zhou, X.-Y., Zhang, Z. G., and Li, J.-X. (2018). Forecasting the Wti Crude Oil price by a Hybrid-Refined Method. Energ. Econ. 71, 114–127. doi:10.1016/j.eneco.2018.02.004

CrossRef Full Text | Google Scholar

Cheung, Y.-L., Cheung, Y.-W., and Wan, A. T. K. (2009). A High-Low Model of Daily Stock price Ranges. J. Forecast. 28, 103–119. doi:10.1002/for.1087

CrossRef Full Text | Google Scholar

De Carvalho, F. A. T., Lima Neto, E. A., and Tenorio, C. P. (2004). “A New Method to Fit a Linear Regression Model for Interval-Valued Data,” in Lecture Notes in Computer Science, K12004 Advances in Artificial Intelligence (Berlin: Springer-Verlag).

CrossRef Full Text | Google Scholar

Ding, H., Kim, H.-G., and Park, S. Y. (2016). Crude Oil and Stock Markets: Causal Relationships in Tails? Energ. Econ. 59, 58–69. doi:10.1016/j.eneco.2016.07.013

CrossRef Full Text | Google Scholar

Donald, S. G., Imbens, G. W., and Newey, W. K. (2009). Choosing Instrumental Variables in Conditional Moment Restriction Models. J. Econom. 152, 28–36. doi:10.1016/j.jeconom.2008.10.013

CrossRef Full Text | Google Scholar

Ebrahim, Z., Inderwildi, O. R., and King, D. A. (2014). Macroeconomic Impacts of Oil price Volatility: Mitigation and Resilience. Front. Energ. 8, 9–24. doi:10.1007/s11708-014-0303-0

CrossRef Full Text | Google Scholar

Fan, J., and Li, R. (2001). Variable Selection via Nonconcave Penalized Likelihood and its oracle Properties. J. Am. Stat. Assoc. 96, 1348–1360. doi:10.1198/016214501753382273

CrossRef Full Text | Google Scholar

Fantazzini, D., and Fomichev, N. (2014). Forecasting the Real price of Oil Using Online Search Data. Ijcee 4, 4–31. doi:10.1504/ijcee.2014.060284

CrossRef Full Text | Google Scholar

Frank, L. E., and Friedman, J. H. (1993). A Statistical View of Some Chemometrics Regression Tools. Technometrics 35, 109–135. doi:10.1080/00401706.1993.10485033

CrossRef Full Text | Google Scholar

García-Ascanio, C., and Maté, C. (2010). Electric Power Demand Forecasting Using Interval Time Series: A Comparison between Var and Imlp. Energy Policy 38, 715–725. doi:10.1016/j.enpol.2009.10.007

CrossRef Full Text | Google Scholar

González-Rivera, G., and Lin, W. (2013). Constrained Regression for Interval-Valued Data. J. Business Econ. Stat. 31, 473–490. doi:10.1080/07350015.2013.818004

CrossRef Full Text | Google Scholar

Hamilton, J. D. (2008). “Understanding Crude Oil Prices,”. (no. w14492).

CrossRef Full Text | Google Scholar

Hansen, B. E. (2007). Least Squares Model Averaging. Econometrica 75, 1175–1189. doi:10.1111/j.1468-0262.2007.00785.x

CrossRef Full Text | Google Scholar

Hansen, B. E., and Racine, J. S. (2012). Jackknife Model Averaging. J. Econom. 167, 38–46. doi:10.1016/j.jeconom.2011.06.019

CrossRef Full Text | Google Scholar

He, A. W. W., Kwok, J. T. K., and Wan, A. T. K. (2010). An Empirical Model of Daily Highs and Lows of West texas Intermediate Crude Oil Prices. Energ. Econ. 32, 1499–1506. doi:10.1016/j.eneco.2010.07.012

CrossRef Full Text | Google Scholar

Hjort, N. L., and Claeskens, G. (2006). Focused Information Criteria and Model Averaging for the Cox hazard Regression Model. J. Am. Stat. Assoc. 101, 1449–1464. doi:10.1198/016214506000000069

CrossRef Full Text | Google Scholar

Hjort, N. L., and Claeskens, G. (2003). Frequentist Model Average Estimators. J. Am. Stat. Assoc. 98, 879–899. doi:10.1198/016214503000000828

CrossRef Full Text | Google Scholar

Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T. (1999). Bayesian Model Averaging: a Tutorial. Stat. Sci. 14, 382–417. doi:10.1214/ss/1009212519

CrossRef Full Text | Google Scholar

Hu, Z., Bao, Y., Chiong, R., and Xiong, T. (2015). Mid-term Interval Load Forecasting Using Multi-Output Support Vector Regression with a Memetic Algorithm for Feature Selection. Energy 84, 419–431. doi:10.1016/j.energy.2015.03.054

CrossRef Full Text | Google Scholar

Kang, S. H., McIver, R., and Yoon, S.-M. (2017). Dynamic Spillover Effects Among Crude Oil, Precious Metal, and Agricultural Commodity Futures Markets. Energ. Econ. 62, 19–32. doi:10.1016/j.eneco.2016.12.011

CrossRef Full Text | Google Scholar

Kilian, L. (2009). Not all Oil price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market. Am. Econ. Rev. 99, 1053–1069. doi:10.1257/aer.99.3.1053

CrossRef Full Text | Google Scholar

Knight, K., and Fu, W. (2000). Asymptotics for Lasso-type Estimators. Ann. Stat. 28, 1356–1378. doi:10.1214/aos/1015957397

CrossRef Full Text | Google Scholar

Li, D., Linton, O., and Lu, Z. (2015a). A Flexible Semiparametric Forecasting Model for Time Series. J. Econom. 187, 345–357. doi:10.1016/j.jeconom.2015.02.025

CrossRef Full Text | Google Scholar

Li, X., Ma, J., Wang, S., and Zhang, X. (2015b). How Does Google Search Affect Trader Positions and Crude Oil Prices? Econ. Model. 49, 162–171. doi:10.1016/j.econmod.2015.04.005

CrossRef Full Text | Google Scholar

Liao, J.-C., and Tsay, W.-J. (2016). Multivariate Least Squares Forecasting Averaging by Vector Autoregressive Models. Available at SSRN 2827416.

Google Scholar

Liao, J., Zong, X., Zhang, X., and Zou, G. (2019). Model Averaging Based on Leave-Subject-Out Cross-Validation for Vector Autoregressions. J. Econom. 209, 35–60. doi:10.1016/j.jeconom.2018.10.007

CrossRef Full Text | Google Scholar

Lima Neto, E. d. A., and De Carvalho, F. d. A. T. (2010). Constrained Linear Regression Models for Symbolic Interval-Valued Variables. Comput. Stat. Data Anal. 54, 333–347. doi:10.1016/j.csda.2009.08.010

CrossRef Full Text | Google Scholar

Maia, A. L. S., and de Carvalho, F. d. A. T. (2011). Holt's Exponential Smoothing and Neural Network Models for Forecasting Interval-Valued Time Series. Int. J. Forecast. 27, 740–759. doi:10.1016/j.ijforecast.2010.02.012

CrossRef Full Text | Google Scholar

Maia, A. L. S., De Carvalho, F. d. A. T., and Ludermir, T. B. (2008). Forecasting Models for Interval-Valued Time Series. Neurocomputing 71, 3344–3352. doi:10.1016/j.neucom.2008.02.022

CrossRef Full Text | Google Scholar

Miller, J. I., and Ratti, R. A. (2009). Crude Oil and Stock Markets: Stability, Instability, and Bubbles. Energ. Econ. 31, 559–568. doi:10.1016/j.eneco.2009.01.009

CrossRef Full Text | Google Scholar

Ng, S., and Bai, J. (2009). Selecting Instrumental Variables in a Data Rich Environment. J. Time Ser. Econom. 1, 4. doi:10.2202/1941-1928.1014

CrossRef Full Text | Google Scholar

Pan, Z., Wang, Y., and Yang, L. (2014). Hedging Crude Oil Using Refined Product: A Regime Switching Asymmetric Dcc Approach. Energ. Econ. 46, 472–484. doi:10.1016/j.eneco.2014.05.014

CrossRef Full Text | Google Scholar

Qiao, K., Sun, Y., and Wang, S. (2019). Market Inefficiencies Associated with Pricing Oil Stocks during Shocks. Energ. Econ. 81, 661–671. doi:10.1016/j.eneco.2019.04.016

CrossRef Full Text | Google Scholar

Rapach, D. E., Strauss, J. K., and Zhou, G. (2010). Out-of-sample Equity Premium Prediction: Combination Forecasts and Links to the Real Economy. Rev. Financ. Stud. 23, 821–862. doi:10.1093/rfs/hhp063

CrossRef Full Text | Google Scholar

Reboredo, J. C. (2013). Is Gold a Hedge or Safe haven against Oil price Movements? Resour. Pol. 38, 130–137. doi:10.1016/j.resourpol.2013.02.003

CrossRef Full Text | Google Scholar

Shin, H., Hou, T., Park, K., Park, C.-K., and Choi, S. (2013). Prediction of Movement Direction in Crude Oil Prices Based on Semi-supervised Learning. Decis. Support Syst. 55, 348–358. doi:10.1016/j.dss.2012.11.009

CrossRef Full Text | Google Scholar

Souček, M. (2013). Crude Oil, Equity and Gold Futures Open Interest Co-movements. Energ. Econ. 40, 306–315. doi:10.1016/j.eneco.2013.07.010

CrossRef Full Text | Google Scholar

Sun, Y., Han, A., Hong, Y., and Wang, S. (2018). Threshold Autoregressive Models for Interval-Valued Time Series Data. J. Econom. 206, 414–446. doi:10.1016/j.jeconom.2018.06.009

CrossRef Full Text | Google Scholar

Sun, Y., Zhang, X., Hong, Y., and Wang, S. (2019). Asymmetric Pass-Through of Oil Prices to Gasoline Prices with Interval Time Series Modelling. Energ. Econ. 78, 165–173. doi:10.1016/j.eneco.2018.10.027

CrossRef Full Text | Google Scholar

Taghizadeh-Hesary, F., Rasoulinezhad, E., and Kobayashi, Y. (2016). Oil price Fluctuations and Oil Consuming Sectors: An Empirical Analysis of Japan. Econom. Pol. Ener. Environ. (2), 33–51. doi:10.3280/EFE2016-002003

Wang, X., Zhang, Z., and Li, S. (2016). Set-valued and Interval-Valued Stationary Time Series. J. Multivariate Anal. 145, 208–223. doi:10.1016/j.jmva.2015.12.010

CrossRef Full Text | Google Scholar

Wang, Y., Liu, L., and Wu, C. (2017). Forecasting the Real Prices of Crude Oil Using Forecast Combinations over Time-Varying Parameter Models. Energ. Econ. 66, 337–348. doi:10.1016/j.eneco.2017.07.007

CrossRef Full Text | Google Scholar

Wu, B., Wang, L., Lv, S.-X., and Zeng, Y.-R. (2021). Effective Crude Oil price Forecasting Using New Text-Based and Big-Data-Driven Model. Measurement 168, 108468. doi:10.1016/j.measurement.2020.108468

CrossRef Full Text | Google Scholar

Xiong, T., Li, C., and Bao, Y. (2017). Interval-valued Time Series Forecasting Using a Novel Hybrid Holti and Msvr Model. Econ. Model. 60, 11–23. doi:10.1016/j.econmod.2016.08.019

CrossRef Full Text | Google Scholar

Xu, G., Wang, S., and Huang, J. Z. (2014). Focused Information Criterion and Model Averaging Based on Weighted Composite Quantile Regression. Scand. J. Statist 41, 365–381. doi:10.1111/sjos.12034

CrossRef Full Text | Google Scholar

Yang, W., Han, A., Cai, K., and Wang, S. (2012). Acix Model with Interval Dummy Variables and its Application in Forecasting Interval-Valued Crude Oil Prices. Proced. Comp. Sci. 9, 1273–1282. doi:10.1016/j.procs.2012.04.139

CrossRef Full Text | Google Scholar

Yang, W., Han, A., Hong, Y., and Wang, S. (2016). Analysis of Crisis Impact on Crude Oil Prices: a New Approach with Interval Time Series Modelling. Quantitative Finance 16, 1917–1928. doi:10.1080/14697688.2016.1211795

CrossRef Full Text | Google Scholar

Yang, Y., Guo, J. e., Sun, S., and Li, Y. (2021). Forecasting Crude Oil price with a New Hybrid Approach and Multi-Source Data. Eng. Appl. Artif. Intelligence 101, 104217. doi:10.1016/j.engappai.2021.104217

CrossRef Full Text | Google Scholar

Yoshino, N., and Hesary, F. T. (2014). Monetary Policy and Oil price Fluctuations Following the Subprime Mortgage Crisis. Ijmef 7, 157–174. doi:10.1504/ijmef.2014.066482

CrossRef Full Text | Google Scholar

Yu, L., Zhao, Y., Tang, L., and Yang, Z. (2019). Online Big Data-Driven Oil Consumption Forecasting with Google Trends. Int. J. Forecast. 35, 213–223. doi:10.1016/j.ijforecast.2017.11.005

CrossRef Full Text | Google Scholar

Zaabouti, K., Ben Mohamed, E., and Bouri, A. (2016). Does Oil price Affect the Value of Firms? Evidence from Tunisian Listed Firms. Front. Energ. 10, 1–13. doi:10.1007/s11708-016-0396-8

CrossRef Full Text | Google Scholar

Zhang, X., Lai, K. K., and Wang, S.-Y. (2008). A New Approach for Crude Oil price Analysis Based on Empirical Mode Decomposition. Energ. Econ. 30, 905–918. doi:10.1016/j.eneco.2007.02.012

CrossRef Full Text | Google Scholar

Zhang, X., and Liang, H. (2011). Focused Information Criterion and Model Averaging for Generalized Additive Partial Linear Models. Ann. Stat. 39, 174–200. doi:10.1214/10-aos832

CrossRef Full Text | Google Scholar

Zhang, X., Wan, A. T. K., and Zhou, S. Z. (2012). Focused Information Criteria, Model Selection, and Model Averaging in a Tobit Model with a Nonzero Threshold. J. Business Econ. Stat. 30, 132–142. doi:10.1198/jbes.2011.10075

CrossRef Full Text | Google Scholar

Zhang, X., Yu, L., Wang, S., and Lai, K. K. (2009). Estimating the Impact of Extreme Events on Crude Oil price: An Emd-Based Event Analysis Method. Energ. Econ. 31, 768–778. doi:10.1016/j.eneco.2009.04.003

CrossRef Full Text | Google Scholar

Zhang, Y., Li, J., Liu, H., Zhao, G., Tian, Y., and Xie, K. (2020). Environmental, Social, and Economic Assessment of Energy Utilization of Crop Residue in china. Front. Energ. 15, 308–319. doi:10.1007/s11708-020-0696-x

CrossRef Full Text | Google Scholar

Zhao, L., Zhang, X., Wang, S., and Xu, S. (2016). The Effects of Oil price Shocks on Output and Inflation in china. Energ. Econ. 53, 101–110. doi:10.1016/j.eneco.2014.11.017

CrossRef Full Text | Google Scholar

Zhao, Y., Li, J., and Yu, L. (2017). A Deep Learning Ensemble Approach for Crude Oil price Forecasting. Energ. Econ. 66, 9–16. doi:10.1016/j.eneco.2017.05.023

CrossRef Full Text | Google Scholar