Distribution Optimal Power Flow With Energy Sharing Via a Peer-To-Peer Transactive Market

The technology advancement and cost decline of renewable and sustainable energy increase the penetration of distributed energy resources (DERs) in distribution systems. Transactive energy helps balance the local generation and demand. Peer-to-peer (P2P) energy trading is a promising business model for transactive energy. Such a market scheme can increase the revenue of DER owners and reduce the waste of renewable energy. This article proposes an equilibrium model of a P2P transactive energy market. Every participant seeks the maximum personal interest, with the options of importing or providing energy from/to any other peer across different buses of the distribution network. The market equilibrium condition is obtained by combining the Karush–Kuhn–Tucker conditions of all problems of individual participants together. The energy transaction price is endogenously determined from the market equilibrium condition, which is cast as a mixed-integer linear program and solved by a commercial solver. The transactive energy flow is further embedded in the optimal power flow problem to ensure operating constraints of the distribution network. We propose a remedy to recover a near optimal solution when the second-order cone relaxation is inexact. Finally, a case study demonstrates that the proposed P2P market benefits all participants.

Introduction

With the development of modern society and economy, the energy consumption is continuously increasing. However, due to the depletion of nonrenewable energy and the greenhouse gas emission from burning fossil-fuel energy, it is imperative to develop renewable and sustainable energy (Liu et al., 2020). The technology advancement and cost decline contribute to the high penetration of distributed energy resources (DERs), such as solar photovoltaics, wind turbine, and energy storage devices, in the power system (Hou et al., 2021). In such circumstances, there could be multiple generation sources that are volatile and owned by profit-driven entities. The Feed-in Tariff (FiT) scheme has been implemented as an effective tool to encourage DERs investment and owners’ participation in energy trading (Pyrgou et al., 2016). In the FiT scheme, DER owners can sell their excessive energy to main grid at a designed price. But the FiT scheme has been criticized for lacking competition (Butler and Neuhoff, 2008) and offering participants limited benefits (Tushar et al., 2015).

The transactive energy system is proposed to manage the energy generation and consumption and facilitate energy trading in the power system. The transactive energy scheme helps balance the local renewable energy generation and demand in the timeframe of real-time within a distribution network (Abrishambaf et al., 2019).

With the advancement of Information and Communication Technology (ICT), peer-to-peer (P2P) energy trading has been designed and expected to be a promising business model for the transactive energy scheme in future power systems (Abdella and Shuaib, 2018). P2P trading is composed of energy buyers and sellers, power system operators, and P2P service servers. A peer in the P2P market can sell surplus energy to local peers and can choose to act as an energy buyer or seller based on personal preferences and needs (Giotitsas et al., 2015). All peers can exchange energy with each other directly, without the involvement of utility companies. The implement of P2P energy trading enables all peers to engage in energy trading, thus creating a competitive energy market. Both the energy buyer and the seller can benefit from P2P transaction because they can utilize excessive renewable energy and reach a mutually satisfactory price and quantity (Mengelkamp et al., 2018). The P2P transactive market can also balance local energy supply and demand, thus reducing energy transmission losses. Furthermore, it can improve the power system reliability and reduce infrastructure investment (Shrestha et al., 2019).

Recently, P2P energy trading has attracted great attention as never before and an increasing number of researches have been conducted to facilitate the P2P trading mechanism. The state-of-the-art of P2P energy trading is presented as follows.

There are many articles summarizing the design and architecture of the P2P energy trading market. Tushar et al. (2020a) provided a detailed overview in the P2P energy trading field and discussed the solution techniques implemented in the P2P market. The key elements in the P2P market can be divided into virtual layer and physical layer. The virtual layer has the transaction data flow and the market mechanism while the physical layer consists of the power grid and communication infrastructure to guarantee that the physical energy transaction is carried out successfully. Zhang et al. (2018) proposed a four-layer system architecture in the P2P market, providing evaluation criteria to identify related technologies, facilities, and designs. The proposed architecture has three dimensions. The first dimension consists of business layer, control layer, ICT layer, and physical power grid layer, which form the basic framework in the P2P market. The second and third dimensions are classified according to the size of participants and energy trading process, respectively. Sousa et al. (2019) categorized the community-based P2P structure into full market, community-based market, and hybrid market according to the degree of connection and communication. In the full market, the peers can directly trade with each other without centralized coordination. By contrast, the community-based market requires a community manager to arrange the energy transactions within the community or between communities. The hybrid market is the combination of the above two market structures. Long et al. (2018a) categorized the P2P energy trading based on the existence of an intermedia. Without an intermedia, prosumers can directly control their DERs and a P2P market coordinator is needed to collect participants’ information and provide price signal. With an intermedia, a third party can manage prosumers’ energy and act as a market coordinator. In summary, the previously proposed P2P market architecture can be mainly classified as three types based on the degree of decentralization: decentralized market, centralized market, and hybrid market, as shown in Figure 1.

FIGURE 1

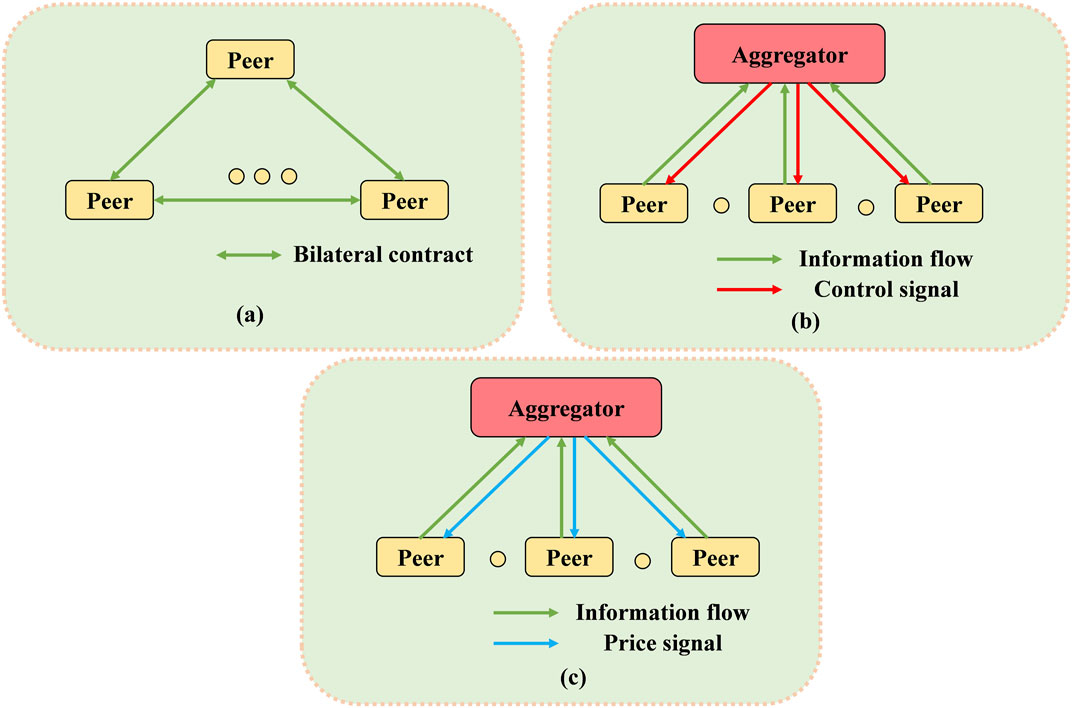
FIGURE 1. Three types of P2P market architecture: (A) decentralized market; (B) centralized market; (C) hybrid market.

1) Decentralized market: In a decentralized P2P energy market, peers can negotiate and trade with each other directly without the intermediary. The market participants can decide their transaction amount and price to maximize their personal interest and satisfy own preferences. Sorin et al. (2018) proposed a decentralized P2P market design based on multi-bilateral economic dispatch (MBED). The authors described a relaxed consensus + innovation (RCI) approach to solve the MBED. Such a market can cater to consumers’ product differentiation preference and maximize society surplus. Morstyn et al. (2019) established a bilateral contract network for scalable P2P energy trading for real-time and forward market. The utility-maximizing preferences of agents satisfy full substitutability, which guarantees a stable result in the distributed price-adjustment process. Guerrero et al. (2019) designed a decentralized P2P scheme with a self-interested agent. The pricing mechanism builds on continuous double auction (CDA). This scheme is also the first decentralized P2P architecture considering distribution network constraints. Alvaro-Hermana et al. (2016) presented a P2P energy trading application scene in electric vehicles (EV) with the objective of minimizing EV users’ energy expense. The implementation of P2P trading benefits users involved in the market and decreases charging impact on grid. Tushar et al. (2020b) proposed a P2P trading design based on coalition formation game. In such a prosumer-centric market, a prosumer can decide to join the P2P market or not by evaluating the P2P market’s attractiveness. Prosumers can also choose whom to cooperate or not to achieve more benefit.

2) Centralized market: In a centralized market, an aggregator communicates with peers and manages the operation of DERs. The aggregator collects information from participants and makes proper control decisions of devices to reach a common target, for example, maximizing financial benefit or achieving an environmentally friendly goal. Kang et al. (2017) implemented localized P2P energy trading among plug-in hybrid electric vehicles (PHEVs). Local aggregators communicate with PHEVs, acquire their charging and discharging demand, and allocate energy with a goal of maximizing social welfare. Alam et al. (2017) proposed a P2P energy trading model with a Pareto optimality method. The proposed model requires the centralized manager to solve a multiobjective optimization problem, including microgrid energy cost minimization and individual cost optimization, and finally obtain Pareto optimality results, eliminating unfair cost distribution. Long et al. (2018b) developed a two-stage aggregated control method in P2P energy sharing where an energy sharing aggregator controls DERs to reduce total energy cost. An adjusted supply and demand ratio pricing mechanism is proposed to benefit all participants. Nguyen et al. (2018) proposed a centralized P2P trading mechanism in a local community with rooftop PV and battery. The objective of the aggregator is to minimize the total energy cost and the problem is formulated as a mixed integer linear programming (MILP). Long et al. (2017) introduced a centralized P2P energy trading to maximize the local energy balance. A linear programming is implemented to solve the market.

3) Hybrid market: Hybrid market is the combination of decentralized and centralized markets, in which a peer can decide to switch from the conventional energy market to the P2P energy market with the price signal from the aggregator. On one hand, the hybrid market requires an aggregator to manage and supervise transaction activities compared with the decentralized market. On the other hand, peers can control their devices, achieve self-interest, and protect personal privacy in comparison with the centralized market. Long et al. (2018a) presented three representative P2P market designs with different pricing mechanisms. They are, respectively, bill sharing, mid-market rate, and auction-based pricing strategy. Qi et al. (2019) constructed a P2P transaction model, with the aim of maximizing prosumers’ benefit. The proposed model considers the impact of distribution network constraint on P2P transaction. Zhang et al. (2016) devised a bidding platform “Elecbay” based on the noncooperative game theory, in which all peers make their decision independently. The agents with flexibility of demand in the platform can mathematically lead to Nash equilibrium. Morstyn and McCulloch (2019) proposed a P2P market based on multiclass energy management, in which a distributed price-directed optimization mechanism is constructed to respect prosumer preferences and minimize external cost.

Game theory approaches, optimization methods, and auction-based approaches are widely used in designing P2P energy trading. Game theory is used in a competitive circumstance in which a player’s decision and action will affect other players’ outcomes and vice versa. Game theory approaches are grouped into two parts: noncooperative and cooperative game theory (Tushar et al., 2018). The author summarized several P2P energy management domains adopting game theory approached, including electric vehicle, DERs, energy storage, and energy service. Optimization methods are widely used in the P2P scheme. In Nguyen et al. (2018), an agent with rooftop PV and battery participates in P2P energy trading and proposes a centralized P2P trading mechanism in a local community with rooftop PV and battery and a mixed integer linear programming is proposed to minimize the total energy cost. Morstyn and McCulloch (2019) used the distributed convex optimization method alternating direction method of multipliers (ADMM) to solve the multiclass energy management problem. Auction-based approaches can be applied to markets with multiple energy buyers and sellers. Continuous double auction is used to match energy sellers and buyers and bidding strategies is proposed to facilitate agent’s bid and ask (Guerrero et al., 2019). An iterative double auction algorithm is proposed based on consortium blockchain to disclose hidden information about electric vehicles (Kang et al., 2017).

However, there are still some research gaps in the existing research works. Many studies did not concentrate on individual P2P market participant’s interest, and such a market mechanism might damage personal interest. Many pricing designs in the P2P energy sharing market did not reflect the true value of transactive energy resources in different supply–demand scenarios and could not guarantee every participant’s benefit from the market. P2P transaction should be conducted via physical distribution network, whereas the operating constraints are rarely taken into consideration.

In this article, we study transactive energy in a P2P market with participants at different buses of a distribution network. The main contributions are twofold.

1) We propose an equilibrium model of a P2P transactive market. Every participant is rational and pursues profit maximum, with the options of importing or providing energy from/to any other peer across different buses of the distribution network. The market equilibrium condition is obtained by combining the Karush–Kuhn–Tucker (KKT) conditions of all problems of individual participants together. Specifically, the price is endogenously determined from the market equilibrium condition, rather than bid by the providers, which is different from existing works and better reflects the value of resources in accordance with the supply–demand relation. The market equilibrium condition is further cast as a mixed-integer linear program and solved by a commercial solver.

2) We formulate the distribution optimal power flow (OPF) problem considering the transactive energy flow at the market equilibrium. To solve the nonlinear OPF problem, the second-order cone relaxation is performed. If the convex relaxation is inexact, a feasible recovery procedure is suggested to recover a near-optimal solution. The procedure entails solving second-order cone programs and is thus efficient. Such a framework offers a new paradigm to study power system operation with P2P transactive energy.

The remainder of this article is organized as follows. The P2P transaction scheme, the mathematical model of the P2P market, and the market equilibrium condition are presented in P2P Transactive Scheme and the Market Equilibrium. The distribution OPF problem considering the transactive energy flow of the P2P market and the solution technique are given in Optimal Power Flow With Transactive Energy. Case studies are reported in Case Study. Finally, Conclusion concludes the article.

P2P Transactive Scheme and the Market Equilibrium

In this section, a P2P transactive energy scheme is proposed. The problems of energy sellers and buyers are then presented. At last, the market equilibrium condition is given and cast as an MILP.

Problem Description

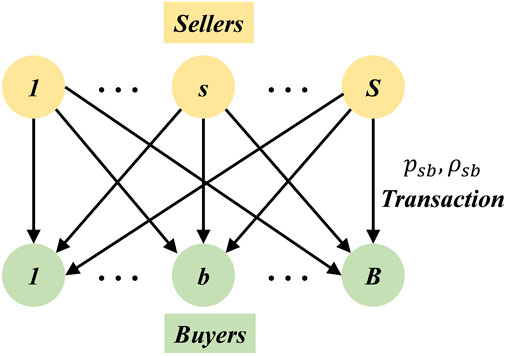
The transaction structure of the P2P energy-sharing market proposed in this article is shown in Figure 2. In this article, a peer who has excessive energy and shares energy with other people is identified as a typical energy seller $s$. Similarly, a peer with deficit energy is recorded as a typical energy buyer $b$. In a time period, there are total $S$ energy sellers and $B$ energy buyers joining in the P2P market. The solid arrow connecting seller $s$ and buyer $b$ in Figure 2 represents P2P transaction between them. The variables $p_{sb}$ and ${\rho }_{sb}$ present the transaction energy amount and transaction price, respectively. In such a market, the following assumptions are made without loss of generality:

1) The infrastructure has been installed to operate P2P sharing scheme.

2) Associated stakeholders in the P2P market are rational and maximize their own interest. A contract with $p_{sb}$ and ${\rho }_{sb}$ is reached to ensure the transaction. The transaction is expected to be carried out hourly.

3) Energy sellers can choose to sell their surplus energy to the main grid in the FiT scheme or trade in the P2P market. Similarly, buyers can also purchase energy from the grid or the P2P market, with the hope to minimize their costs. A seller or buyer can sell or buy energy at a higher or lower price in the P2P market compared with traditional power utility. Otherwise, people will have no incentive to participate in P2P sharing.

4) The P2P market is operated by an aggregator. It collects supply and demand information from participants and clears the market. Then, it sends transaction results to the distribution grid.

5) All players are self-interested and they will not form an alliance. Besides, we assume all players tell their true supply and demand information to the aggregator.

FIGURE 2

FIGURE 2. The structure of P2P energy sharing market.

Mathematic Formulation

The models of sellers, buyers, and total P2P market are presented in the following subsections.

Seller’s Problem

A rational energy seller $s$ seeks contract amount $p_{sb}$ with energy buyer $b$ to reach maximum profit. The optimal problem of seller $s$ is

$\begin{array}{c}max: {\displaystyle \sum }_{\mathit{b}\in \mathit{B}}{\mathit{\rho }}_{\mathit{sb}}{\mathit{p}}_{\mathit{sb}}+{\mathit{\lambda }}^{\mathit{sell}}\left({\mathit{P}}_{\mathit{s}}-{\displaystyle \sum }_{\mathit{b}\in \mathit{B}}{\mathit{p}}_{\mathit{sb}}\right)-{\mathit{\lambda }}^{\mathit{cost}}{\displaystyle \sum }_{\mathit{b}\in \mathit{B}}{\mathit{p}}_{\mathit{sb}}\end{array}(1)$

$s.t. :\underset{\mathit{b}\in \mathit{B}}{\Sigma }{\mathit{p}}_{\mathit{sb}}\le P_s\mathit{:}{\mathit{\upsilon }}_{\mathit{s}}(2)$

$p_{sb}\ge 0:{\mathit{\omega }}_{\mathit{sb}},\forall b\in B(3)$

where $p_{sb}$ and ${\rho }_{sb}$ are decision variables. $p_{sb}$ is the transaction amount between seller $s$ and buyer $b$ and ${\rho }_{sb}$ is the transaction price associated with $p_{sb}$. However, the price ${\rho }_{sb}$ is out of control of seller $s$ and buyer$b$ but is decided by solving the market equilibrium problem. $P_s$ is the excessive energy for sale of seller $s$, which comes from rooftop PV system, PV power station, wind turbine, or energy stored in batteries. ${\lambda }^{sell}$ is FiT and ${\lambda }^{cost}$ is the transaction cost, such as grid tariff for using the grid facilities. The objective function (Eq. 1) is seller’s profit maximization problem. The first term represents the total revenue of trading with $B$ energy buyers in the P2P market. The second term is the total revenue of selling energy to the main grid. Sellers can sell their energy to the main grid if they still have surplus energy after P2P market transaction. The third term is the transaction cost in the P2P market.

Constraint (Eq. 2) limits that the total P2P trading amounts should not be more than seller’s initial surplus energy. Constraint (Eq. 3) imposes non-negativity condition on the P2P trading amount. ${\upsilon }_s$ and ${\omega }_{sb}$ after the colon are dual variables of the constraints.

Buyer’s Problem

A rational energy buyer $b$ seeks contract amount $p_{sb}$ with energy seller $s$ to reach minimum energy cost. The optimal problem of buyer $b$ is

$\begin{array}{c}min: {\displaystyle \sum }_{\mathit{s}\in \mathit{S}}{\mathit{\rho }}_{\mathit{sb}}{\mathit{p}}_{\mathit{sb}}+{\mathit{\lambda }}_{\mathit{b}}^{\mathit{buy}}\left({\mathit{D}}_{\mathit{b}}-{\displaystyle \sum }_{\mathit{s}\in \mathit{S}}{\mathit{p}}_{\mathit{sb}}\right)\end{array}(4)$

$\begin{array}{c}s.t.:\left({\mathit{D}}_{\mathit{b}}-{\displaystyle \sum }_{\mathit{s}\in \mathit{S}}{\mathit{p}}_{\mathit{sb}}\right)\ge 0:{\mathit{\gamma }}_{\mathit{b}}\end{array}(5)$

$\begin{array}{c}{\mathit{p}}_{\mathit{sb}}\ge 0:{\varpi }_{\mathit{sb}},\forall s\in S\end{array}(6)$

where $p_{sb}$ and ${\rho }_{sb}$ are also decision variables and have been defined in Seller’s Problem. $D_b$ is the total energy demand of energy buyer $b$. ${\lambda }^{buy}$ is the price when the buyer purchases energy from the main grid. In this article, we assume the main grid charges energy buyers in a time-and-level-of-use(TLOU) structure, which will be presented in following content. The objective function (Eq. 4) is buyer’s cost minimization problem. The first term denotes the total cost of trading with $S$ energy sellers in the P2P market. The second term is the total cost of buying energy from the main grid. Buyers can buy energy from the main grid to satisfy their remaining demand after P2P trading.

Constraint (Eq. 5) shows that the total P2P trading amounts should not exceed buyer’s demand. ${\gamma }_b$ and ${\varpi }_{sb}$ after the colon are dual variables of the constraints.

Time-And-Level-Of-Use Price

Energy buyers purchase energy from the main grid at the TLOU price, which consists of two dimensions: time of day and level of consumption (Gomez-Herrera and Anjos, 2019). The structure of TLOU is as follows:

$\begin{array}{c}{\mathit{\lambda }}_{\mathit{t}}^{\mathit{buy}}={\mathit{\lambda }}_{0\mathit{t}}^{\mathit{buy}}+{\mathit{k}}_{\mathit{t}}{\mathit{D}}_{\mathit{t}},\mathit{ }{\mathit{k}}_{\mathit{t}}\ge 0,{\mathit{D}}_{\mathit{t}}\ge 0\end{array}(7)$

where ${\lambda }_t^{buy}$ is the TLOU price and ${\lambda }_{0t}^{buy}$ is the benchmark price in period $t$ , respectively. $k_t{D}_t$ is a level-wise part in which $D_t$ is the total energy demand satisfied by grid and $k_t$ is a non-negative slope coefficient. Compared with time-of-use (TOU), such a price scheme can preclude rebound demand peaks when ${\lambda }_{0t}^{buy}$ changes because more consumption is accompanied by higher price. Besides, TLOU can also reduce demand fluctuation and benefit power system operation. In this article, the use of TLOU can also make sure the problem is convex.

Equilibrium Model

In summary, all the participants in the P2P market consider their own interest optimal problem at the same time. Sellers or buyers increase or lower the transaction price ${\rho }_{sb}$ and they can reach mutually satisfactory price finally. In such a circumstance, the P2P market can be described as an equilibrium model:

$\begin{array}{c}\{\begin{array}{c}selle\mathit{r}\mathrm{’}s problem \left(1\right) ,s\in S\\ bu\mathit{y}\mathrm{’}s problem \left(4\right),b\in B\end{array}\end{array}(8)$

where all participants’ interests are taken into consideration and solved simultaneously.

Problem Reformulation

In equilibrium problem (Eq. 8), it is crucial that sellers and buyers have consistent decision variables $p_{sb}$ and ${\rho }_{sb}$. However, the product term ${\rho }_{sb}{p}_{sb}$ makes problem (Eqs. 1, 4) nonconvex and intractable in the traditional fixed-point method. Reformulating the primal optimal problem to its KKT conditions is a probable way to solve the problem.

It is worth mentioning that the transaction price ${\rho }_{sb}$ is beyond the control of both seller $s$ and buyer $b$ and will be endogenously determined at the market equilibrium point. We regard ${\rho }_{sb}$ as a constant while acquiring KKT conditions of sellers and buyers.

The KKT condition of seller $s$ is:

$\begin{array}{c}-{\mathit{\rho }}_{\mathit{sb}}+{\mathit{\lambda }}^{\mathit{sell}}+{\mathit{\lambda }}^{\mathit{cost}}+{\mathit{\upsilon }}_{\mathit{s}}-{\mathit{\omega }}_{\mathit{sb}}=0,\forall b\in B\\ 0\le \left({\mathit{P}}_{\mathit{s}}-{\displaystyle \sum }_{\mathit{b}\in \mathit{B}}{\mathit{p}}_{\mathit{sb}}\right)\perp {\mathit{\upsilon }}_{\mathit{s}}\ge 0 \\ 0\le {\mathit{p}}_{\mathit{sb}}\perp {\mathit{\omega }}_{\mathit{sb}}\ge 0,\forall b\in B\end{array}(9)$

The expression $0\le a\perp b\ge 0$ means $a$ and $b$ are non-negative and at least one of them is 0. In vector notation, the $a\perp b$means $a^{T}b=0$.

The KKT condition of each buyer $b$ at the TLOU price scheme is

$\begin{array}{c}{\mathit{\rho }}_{\mathit{sb}}-\left[2{\mathit{k}}_{\mathit{t}}\left({\mathit{D}}_{\mathit{b}}-{\displaystyle \sum }_{\mathit{s}\in \mathit{S}}{\mathit{p}}_{\mathit{sb}}\right)+{\mathit{\lambda }}_0^{\mathit{buy}}\right]+{\mathit{\gamma }}_{\mathit{b}}-{\varpi }_{\mathit{sb}}=0,\forall s\in S\\ 0\le \left({\mathit{D}}_{\mathit{b}}-{\displaystyle \sum }_{\mathit{s}\in \mathit{S}}{\mathit{p}}_{\mathit{sb}}\right)\perp {\mathit{\gamma }}_{\mathit{b}}\ge 0\\ 0\le {\mathit{p}}_{\mathit{sb}}\perp {\varpi }_{\mathit{sb}}\ge 0,\forall s\in S\end{array}(10)$

Since the sellers and buyers have consistent values of ${\rho }_{sb}$ and $p_{sb}$, the KKT condition (Eqs. 9, 10) can be put together, which forms a dual equilibrium problem (Eq. 11).

$\begin{array}{c}\{\begin{array}{c}KKT condition\left(9\right),s\in S\\ KKT condition\left(10\right),b\in B\end{array}\end{array}(11)$

Problem (Eq. 11) is composed of a set of linear and nonlinear constraints. The decision variable $p_{sb}$ can be obtained by solving the equilibrium problem (Eq. 11) and the market clearing price ${\rho }_{sb}$ is determined automatically in (Eq. 9) or (Eq. 10), where both the equations are same. In our model, ${\rho }_{sb}$ is no less than the ${\lambda }^{sell}$ plus ${\lambda }^{cost}$, otherwise sellers will quit the P2P market. The reason is that sellers can choose to trade with higher bidder.

However, the equilibrium problem (Eq. 11) is a nonlinear problem and intrinsically hard because of the existence of nonlinear complementary slackness constraints.

Big-M Method

To deal with the complementary slackness constraints in the equilibrium problem (Eq. 11), we introduce a big-M method proposed in Fortuny-Amat and Mccarl (1981). Take complementary slackness constraint in KKT conditions (Eq. 9) as an example:

$0\le ({\mathit{P}}_{\mathit{s}}-{\displaystyle \sum }_{\mathit{b}\in \mathit{B}}{\mathit{p}}_{\mathit{sb}})\perp {\mathit{\upsilon }}_{\mathit{s}}\ge 0(12)$

If the primal constraint is not binding, its dual variable ${\upsilon }_s$ is zero; similarly, if dual variable ${\upsilon }_s$ is positive, the primal constraint is binding. To depict the character, we can introduce an auxiliary binary vector $z$ and a constant parameter $M$ and transform the nonlinear constraints into linear constraints. The dimension of $z$ is compatible with $S$. The new constraints yield:

$0\le (P_s-{\displaystyle \sum _{b\in B}{p}_{sb}})\le M\left(1-z_s\right)(13)$

$0\le {\upsilon }_s\le M{z}_s(14)$

where $M$ is a manually selected parameter. The value of $M$ deserves discussion. In one respect, it should be large enough to cover the maximum points of (Eqs. 13, 14); in other respect, a smaller value contributes to the convergence and saves computation time.

However, the above constraints lack an optimization problem. We create an MILP to implement constraints (Eqs. 13, 14):

$\mathit{min}:{\mathit{z}}_{\mathit{s}}({\mathit{P}}_{\mathit{s}}-{\displaystyle \sum _{b\in B}{\mathit{p}}_{\mathit{sb}}})+\left(1-{\mathit{z}}_{\mathit{s}}\right){\upsilon }_{\mathit{s}}(15)$

$\mathrm{s}\mathrm{.t}\mathrm{.}\left(\mathrm{13}\right),\left(14\right)(16)$

The objective function (Eq. 15) should be zero if the question is feasible. Otherwise, if the optimal value is positive, the complementary slackness constraint is violated. In the objective function, the product term $z_s{\upsilon }_s$ is composed of a binary variable and a dual variable. It can be linearized by an additional variable $h_{s2}$ , subject to:

$0\le h_{s2}\le M{z}_s;0\le {\upsilon }_s-h_{s2}\le M\left(1-z_s\right)(17)$

Similarly, the reformulation can be applied to the first term $z_s(P_s-{\displaystyle \sum }_{b\in B}{p}_{sb})$.

$\begin{array}{l}0\le h_{s1}\le M\left(1-z_s\right)\\ 0\le (P_s-{\displaystyle \sum _{b\in B}{p}_{sb}})-h_{s1}\le M{z}_s\end{array}(18)$

Finally, the objective function (Eq. 15) can be written as an MILP:

$\begin{array}{l}\mathit{min:}{\mathit{h}}_{\mathit{s1}}+{\upsilon }_s-h_2\\ s.t.\left(16\right),\left(17\right),\left(18\right)\end{array}(19)$

Feasible solution can be obtained by solving above MILP through the commercial optimization problem solver, such as MOSEK.

Optimal Power Flow With Transactive Energy

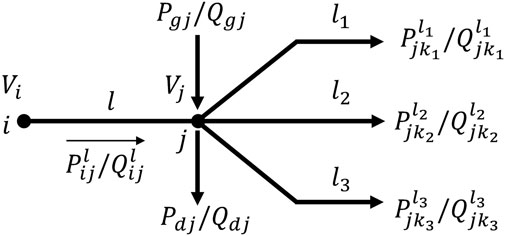
In this section, we implement P2P energy sharing in the optimal power flow problem of a microgrid-based distribution network. A distribution system operator (DSO) controls the distribution network with an operation goal to minimize the total energy cost. Many distribution networks are radial network with tree topology. The typical connection of a radial network is shown in Figure 3. Without loss of generality, a peer in the P2P market is a bus in distribution network, whose role is, e.g., a traditional energy consumer, a prosumers with DERs, or a local solar power station, etc. Branch flow model (BFM) is used in radial distribution power grid (Baran and Wu, 1989b) (Baran and Wu, 1989a). The radial network can be described by a graph $G=\left[N,L\right]$, where $N$ and $L$ are the bus set and distribution line set, respectively.

FIGURE 3

FIGURE 3. A typical connection of radial network.

Branch Flow Model

The mathematical formulation of BFM is described as follows, with an objective function to minimize total energy generation cost. $x$is the feasible set of BFM solutions.

$\mathit{min:F}\left(\mathit{x}\right)={\displaystyle \sum _{i\in N}{a}_i{P}_{gi}^2+b_i{P}_{gi}+c_i}(20)$

$s.t.:P_{ij}^l-r_{ij}^l{I}_{ij}^l+P_{gj}-P_{dj}={\displaystyle \sum _{k\in c\left(j\right)}{P}_{jk}^l,\forall j\in N,l\in L}(21)$

$\begin{array}{c}{\mathit{Q}}_{\mathit{ij}}^{\mathit{l}}-{\mathit{x}}_{\mathit{ij}}^{\mathit{l}}{\mathit{I}}_{\mathit{ij}}^{\mathit{l}}+{\mathit{Q}}_{\mathit{gj}}-{\mathit{Q}}_{\mathit{dj}}={\displaystyle \sum }_{\mathit{k}\in \mathit{c}\left(\mathit{j}\right)}{\mathit{Q}}_{\mathit{jk}}^{\mathit{l}},\forall \mathit{j}\in \mathit{N},l\in L\end{array}(22)$

$\begin{array}{c}{\mathit{V}}_{\mathit{j}}={\mathit{V}}_{\mathit{i}}-2\left({\mathit{P}}_{\mathit{ij}}^{\mathit{l}}{\mathit{r}}_{\mathit{ij}}^{\mathit{l}}+{\mathit{Q}}_{\mathit{ij}}^{\mathit{l}}{\mathit{x}}_{\mathit{ij}}^{\mathit{l}}\right)+{\left({\mathit{z}}_{\mathit{ij}}^{\mathit{l}}\right)}^2{\mathit{I}}_{\mathit{ij}}^{\mathit{l}},\forall l\in L\end{array}(23)$

$\begin{array}{c}{\mathit{V}}_{\mathit{i}}{\mathit{I}}_{\mathit{ij}}^{\mathit{l}}={\left({\mathit{P}}_{\mathit{ij}}^{\mathit{l}}\right)}^2+{\left({\mathit{Q}}_{\mathit{ij}}^{\mathit{l}}\right)}^2,\forall l\in L\end{array}(24)$

$\begin{array}{c}{\mathit{P}}_{\mathit{gi}}^{\mathit{n}}\le {\mathit{P}}_{\mathit{gi}}\le {\mathit{P}}_{\mathit{gi}}^{\mathit{m}},\forall i\in N\end{array}(25)$

$\begin{array}{c}{\mathit{Q}}_{\mathit{gi}}^{\mathit{n}}\le {\mathit{Q}}_{\mathit{gi}}\le {\mathit{Q}}_{\mathit{gi}}^{\mathit{m}},\forall i\in N\end{array}(26)$

$\begin{array}{c}{\mathit{V}}_{\mathit{i}}^{\mathit{n}}\le {\mathit{V}}_{\mathit{i}}\le {\mathit{V}}_{\mathit{i}}^{\mathit{m}},\forall i\in N\end{array}(27)$

$\begin{array}{c}\sqrt{{\left({\mathit{P}}_{\mathit{ij}}^{\mathit{l}}\right)}^2+{\left({\mathit{Q}}_{\mathit{ij}}^{\mathit{l}}\right)}^2}\le {\mathit{S}}_{\mathit{l}},\forall l\in L\end{array}(28)$

where constraints (Eqs. 21, 22) are bus active/reactive power balance condition. Constraint (Eq. 23) is the forward voltage drop in branch $l$. The apparent power injection at the head bus of branch $l$ is described in (Eq. 24). In proposed BFM, the initial bus is $i$ and branch $l$ is defined as the line between bus $i$and $j$. For constant parameters, $r_{ij}^l$/$x_{ij}^l$ is the resistance/reactance of branch $l$. $z_{ij}^l=\sqrt{{\left(r_{ij}^l\right)}^2+{\left(x_{ij}^l\right)}^2}$is the impedance value. $P_{dj}/Q_{dj}$ are fixed active/reactive power demand at bus $j$. For variables, $V_i$/$V_j$ and $I_{ij}^l$ are square voltage and current magnitude. $P_{ij}^l$/$Q_{ij}^l$ presents the active/reactive power flow in branch $l$. $P_{gj}/Q_{gj}$ denotes active/reactive power generation at bus $j$. The right-hand part of (Eq. 21) and (Eq. 22) are power flow started with bus $j$.

Constraints (Eqs. 25–28) are the physical network operating constraints, which represent the active and reactive generation capacities, nodal voltage constraint, and power flow limits in each line.

In the above constraints (Eq. 24) is a quadratic equation, which makes the BFM nonlinear and nonconvex. To solve the nonconvex problem Farivar and Low (2013) proposed a second-order cone program (SOCP) method to make convex relaxation, which replaces the equality constraint (Eq. 24) with the following inequality constraint in a canonical form:

$\begin{array}{c}\Vert \begin{array}{c}2{\mathit{P}}_{\mathit{ij}}^{\mathit{l}}\\ 2{\mathit{Q}}_{\mathit{ij}}^{\mathit{l}}\\ {\mathit{I}}_{\mathit{ij}}^{\mathit{l}}-{\mathit{V}}_{\mathit{i}}\end{array}\Vert \le {\mathit{I}}_{\mathit{ij}}^{\mathit{l}}+{\mathit{V}}_{\mathit{i}}\end{array}(29)$

Such a SOCP convex relaxation is exact for BFM under some mild conditions, such as the objective function is convex and cost is strictly increasing in line losses. However, the relaxation may be inexact if the objective function violates the above mild conditions, thus resulting in infeasible solution.

Denote the BFM constraints with SOCP concisely as Cons-BFM.

Feasibility Recovery

To make sure the convex relaxation is exact Wei et al. (2017) proposed a method based on the convex-concave program to evaluate the initial SOCP result and run the feasibility recovery procedure if SOCP is inexact. Guo et al. (2020) made some improvement based on the method, gaining better convergence performance. Detailed method introduction is as follows:

Denote Following Convex Quadratic Functions

$\begin{array}{c} {\mathit{f}}_{\mathit{l}}\left(\mathit{x}\right)={\mathit{V}}_{\mathit{i}}{\mathit{I}}_{\mathit{ij}}^{\mathit{l}},\forall l\in L\\ {\mathit{g}}_{\mathit{l}}\left(\mathit{x}\right)={\left({\mathit{P}}_{\mathit{ij}}^{\mathit{l}}\right)}^2+{\left({\mathit{Q}}_{\mathit{ij}}^{\mathit{l}}\right)}^2,\forall l\in L\end{array}(30)$

Define a gap function to show the gap in (Eq. 24) caused by the SOCP relaxation at $x^{\ast }$:

$Gap\left({\mathit{x}}^{\mathit{*}}\right)={\Sigma }_l\left[f_l\left({\mathit{x}}^{\mathit{*}}\right)-{\mathit{g}}_{\mathit{l}}\left({\mathit{x}}^{\mathit{*}}\right)\right](31)$

where $x^{\ast }$ is the solution from BFM with SOCP convex relaxation. If the gap does not exceed predetermined tolerance value $\epsilon$, the relaxation is exact. Otherwise, operate the following feasibility recovery procedure to obtain exact optimal solution:

Algorithm 1: Feasibility Recovery Procedure

1. Set an initial penalty coefficient ${\mathit{\rho }}^1>0$, a penalty growth rate $\mathit{\tau }>1$, and a penalty upper bound ${\mathit{\rho }}^{\mathit{M}}$. Let the initial iteration index $\mathit{k}=1$, and the initial point ${\mathit{x}}^1={\mathit{x}}^{\mathit{*}}.$

2. Form linear approximation of ${\mathit{g}}_{\mathit{l}}\left(\mathit{x}\right)$ at ${\mathit{x}}^{\mathit{k}}:$

 $\overline{{\mathit{g}}_{\mathit{l}}}\left(\mathit{x},{\mathit{x}}^{\mathit{k}}\right)={\mathit{g}}_{\mathit{l}}\left({\mathit{x}}^{\mathit{k}}\right)+\nabla {\mathit{g}}_{\mathit{l}}{\left({\mathit{x}}^{\mathit{k}}\right)}^{\mathit{T}}\left(\mathit{x}-{\mathit{x}}^{\mathit{k}}\right)$

And solve the following approximation of ${\mathit{g}}_{\mathit{l}}\left(\mathit{x}\right)$ at ${\mathit{x}}^{\mathit{k}}$

 $\min \mathit{ }\mathit{F}\left(\mathit{x}\right)+{\mathit{\rho }}^{\mathit{k}}{\displaystyle \sum }_{\mathit{l}}{\mathit{s}}_{\mathit{l}}$

 $\mathit{s}.\mathit{t}.\mathit{ }\mathit{Cons}-\mathit{BFM};{\mathit{s}}_{\mathit{l}}\ge 0,\mathit{ }\forall \mathit{l}\in \mathit{L};$

 ${\mathit{f}}_{\mathit{l}}\left({\mathit{V}}_{\mathit{i}}^{\mathit{k}},{\mathit{I}}_{\mathit{ij}}^{\mathit{l}}\right)-\mathit{ }\overline{{\mathit{g}}_{\mathit{l}}}\left(\mathit{x},{\mathit{x}}^{\mathit{k}}\right)\le {\mathit{s}}_{\mathit{l}},\mathit{ }\forall \mathit{l}\in \mathit{L}$

where ${\mathit{s}}_{\mathit{l}}$ is an auxiliary variable and the optimal solution is (${\mathit{x}}^{\mathit{k}+1},{\mathit{s}}^{\mathit{k}+1})$

3. If the relxation gap $\mathit{Gap}\left({\mathit{x}}^{\mathit{k}+1}\right)\le \mathit{\epsilon }$, terminate and report the optimal solution; otherwise, update ${\mathit{\rho }}^{\mathit{k}+1}=\min \left(\mathit{\tau }{\mathit{\rho }}^{\mathit{k}},{\mathit{\rho }}^{\mathit{M}}\right),\mathit{k}\leftarrow \mathit{k}+1$, and go to step 2

A Two-Stage Method

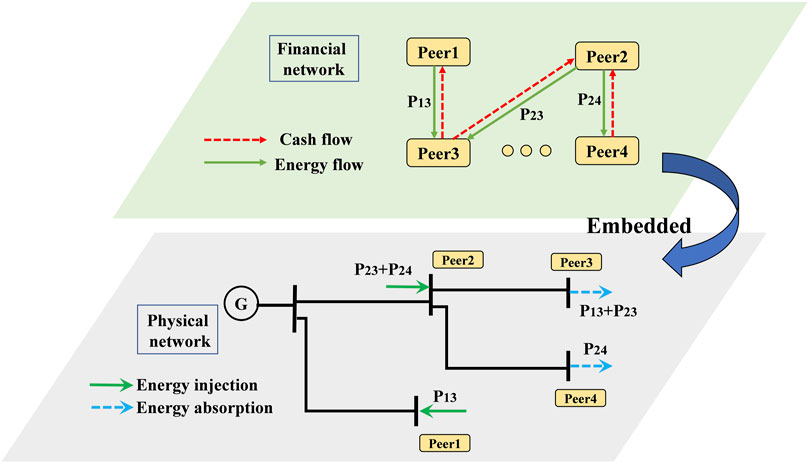
P2P market transactions should be implemented in physical power system network. First, the aggregator in the P2P market collects the transaction information and solves the P2P equilibrium problem. Second, the aggregator submits P2P transaction results to DSO. The DSO solves an optimal power flow problem in BFM to minimize total energy cost under network operating constraints.

Figure 4 shows how P2P transaction is embedded in the physical distribution network. After reaching an agreement in the P2P financial network, the supply buses inject energy into physical network and receive cash payment while the demand buses absorb energy from the physical network and pay for this transactive energy.

FIGURE 4

FIGURE 4. P2P transaction embedded in physical network.

Case Study

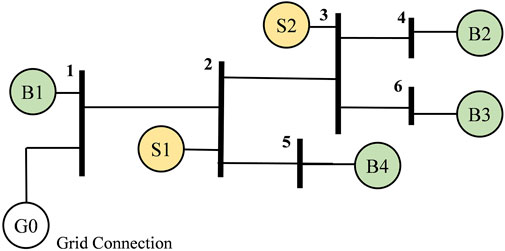
To testify the proposed P2P model in this article, we implement our model in a 6-bus radial distribution network system. The system structure is presented in Figure 5 and G0 connects transmission line. B1-B4 represent the energy buyers participating in the P2P market and S1-S2 are sellers who own PV plants and sell surplus energy. The parameter setting is in the next subsection. All experiments are carried out on a 64-bit laptop with Intel Core i7-7500U CPU with 2.7 GHz and 8 GB RAM. The equilibrium problem and OPF problem are coded in MATLAB with YALMIP interface. Commercial solver MOSEK 9.2.29 is used to solve SOCP.

FIGURE 5

FIGURE 5. 6-Bus radial network system.

Benchmark Parameter Setting

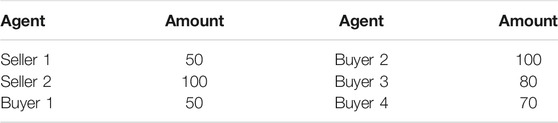
In our P2P market model, the transaction is expected to be solved hourly. In one time period, the seller’s supply and buyer’s demand are shown in Table 1. We assume that the sellers sell their surplus to energy main grid at ${\lambda }^{sell}=0.4\text{ \$}/kWh$. The grid tariff for using the network system is ${\lambda }^{cost}=0.01\text{ \$}/kWh$. Buyers can buy energy through P2P transactions or they can purchase electricity from grid at TLOU price. $TLOUprice=0.5+0.001P^{\text{*}}$, where $P^{\text{*}}$ represents the electricity quantity from grid. In the above assumption, the sellers are forbidden to buy from grid and sell to the P2P market simultaneously and the TLOU price is higher than the FiT value; otherwise, an arbitrage opportunity arises.

TABLE 1

TABLE 1. Production and consumption amount/kWh.

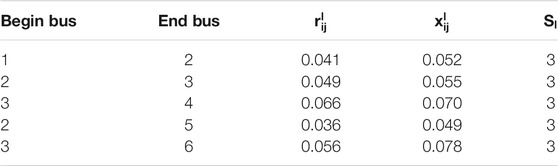
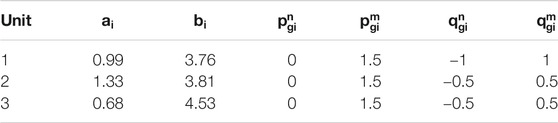
There are three generators located in buses 2, 3, and 4 respectively. The detailed line data and generator parameters are listed in Tables 2, 3. The reference value is 1 MVA and all the parameters and results are given in p.u. The voltage magnitude limits are $V_i^n=0.9$, $V_i^m=1.05$. The initial power demands at buses are $p_i^d=0.5$, $q_i^d=0.1$.

TABLE 2

TABLE 2. Line data (in p.u.).

TABLE 3

TABLE 3. Generator parameters (in p.u.).

Numerical Result

In the first stage, after solving the equilibrium problem, we can obtain the following P2P market model solution.

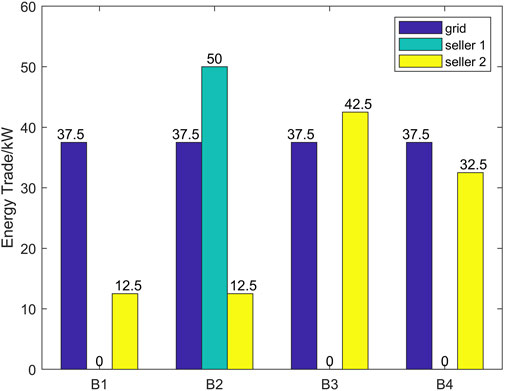
Figure 6 depicts where buyers purchase their energy. Without P2P transaction, they can only satisfy their demands through the main grid. With the P2P market, consumers can allocate their demand between main grid and P2P market to reduce their costs. In our test case, all buyers purchase same quantity from grid and all P2P transaction prices are 0.575$/kWh, which is also the main grid marginal price. As a result, it is no difference for the buyer to choose whom to trade in the P2P market. The result is reasonable because if a buyer offers a higher price, all sellers will trade with him and other buyers will also improve their prices successively; if a buyer offers a lower price, he will loss all sellers and a rational participant will avoid the option. In this condition, the equilibrium price gradually converges to the highest main grid marginal price.

FIGURE 6

FIGURE 6. Buyers’ energy resources.

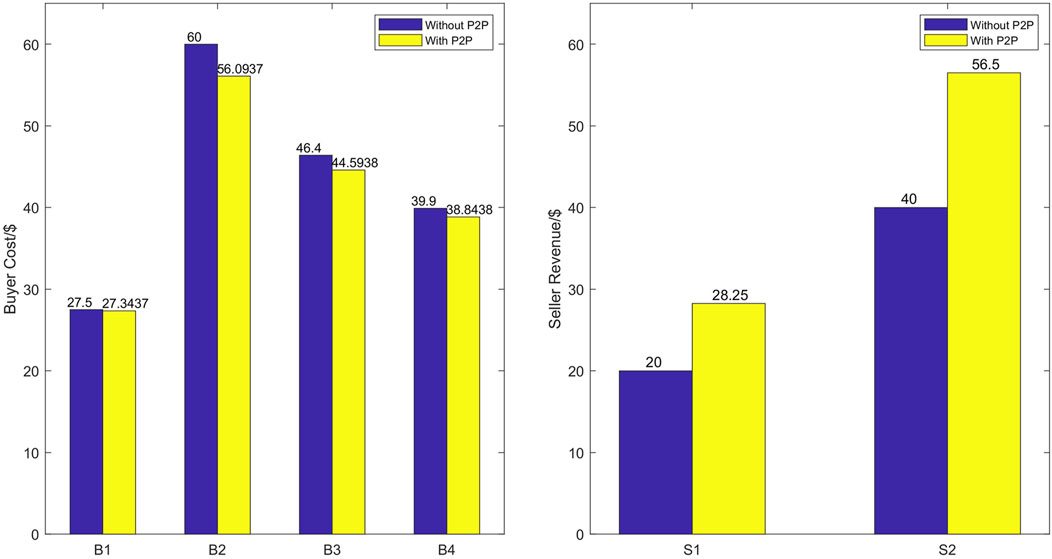
Figure 7 shows the buyers’ costs and sellers’ revenues comparison between the two scenarios, without and with the P2P market. The left one shows that all buyers benefit from the P2P market and have less cost, in which B2 has the most significant reduction in total energy cost because he has the largest amount consumption in the P2P market. Sellers also earn more profit through P2P sharing.

FIGURE 7

FIGURE 7. Costs and revenues comparison between two scenarios.

Finally, Table 4 summarizes the total cost and revenue of P2P market participants during the trading period. Owing to the introduction of P2P market, the sellers and buyers can discover transaction price in P2P trading. The price is not less than the FiT value and not more than TLOU. Therefore, buyers’ cost decreases and sellers’ revenue increases, with an improvement of $ 31.675 in market benefit. The local welfare gets improvement compared with market without the P2P market.

TABLE 4

TABLE 4. Comparison of total cost and Revenue/$.

Discussion of Parameter M

In Big-M Method, we claim the value of parameter M is manually specified. It should be neither too big nor too small. In a benchmark case study, the numerical value of M is 150. To find out the performance of the optimization impacted by the value of M, we change the numerical value of M from 10 to 1,000 and record their feasibility and calculation time of equilibrium problem. The results are provided in Table 5.

TABLE 5

TABLE 5. Comparison of different value of M.

In Table 5, fail means the equilibrium problem is infeasible in solver MOSEK. In our benchmark test, the value of M should not be less than 100, which is also the maximum value of seller’s supply and buyer’s demand. When M is equal to or larger than maximum supply or demand value, the results of market benefit are identical. In terms of calculation time, we can find time increases with M’s value improvement. In view of the above finding, we can obtain some instructions about the selection of M. On one hand, it should not be less than the maximum value of seller’s supply and buyer’s demand. On the other hand, it should not be too large to save calculation time.

Sensitivity Analysis

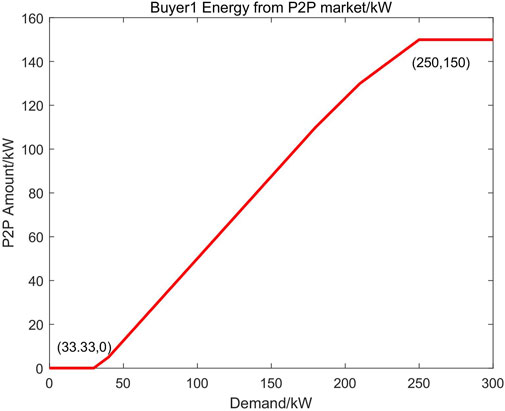
We keep other participants’ supply and demand and change buyer 1’s demand. The buyer 1′ energy bought from P2P market also changes accompanied with demand increase, as shown in Figure 8. And the important turning points $\left(33.33,0\right),\left(\mathrm{250,150}\right)$ are declared in Figure 8. If the demand is less than $33.33kW$, compared with other energy buyers, buyer 1 faces relatively lower TLOU price in the grid market and he has no incentive to offer a much higher price in the P2P market, so he will not buy any energy from the P2P market. If the demand is higher than $33.33kW$ and less than $250kW$, buyer 1 will be charged at a higher TLOU price by grid, so he will buy energy from the P2P market and compete with participants, thus leading to an equilibrium problem. If the demand is higher than $250kW$, buyer 1 faces a much higher TLOU price, so he will buy as much energy in the P2P market as possible. In such a scenario, buyer 1 has market power and consumes all P2P energy.

FIGURE 8

FIGURE 8. Buyer 1’s energy from the P2P market.

Performance of Feasibility Recovery Procedure

In this subsection, we evaluate the performance of FRP. In the first stage, the aggregator solves the equilibrium problem in the P2P market and submits P2P transaction information to DSO. In the second stage, the DSO solves BFM with SOCP relaxation. When the initial SOCP relaxation is inexact and the relaxation gap exceeds predetermined tolerance value $\epsilon ={10}^{-6}$, the initial solution is infeasible and will be passed to FRP. In FRP, we set ${\rho }^1={10}^{-4}$, $\tau =2$, $\epsilon ={10}^{-6}$, and ${\rho }^M=10$. The initial point is the infeasible solution from BFM with SOCP relaxation.

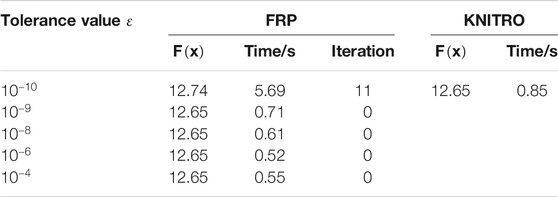
To evaluate the performance of the solution from FRP, we compare it with a solution from NLP solver KNITRO, which can handle the nonconvex optimization problem. The results are shown in Table 6. $F\left(x\right)$is the total electricity generation costs in BFM.

TABLE 6

TABLE 6. Comparison of FRP and KNITRO.

In FRP, we change the value of $\epsilon$ and investigate the algorithm performance. When $\epsilon ={10}^{-10}$, the SOCP is inexact and the initial result is passed to FRP, which needs 11 iterations to converge. The average time is 0.5–0.6 s per iteration in FRP. However, $\epsilon ={10}^{-10}$ is a fairly strict criterion on SOCP relaxation. If we increase the value of $\epsilon$, the SOCP relaxation is exact and will not use FRP. The final result is 12.65. In KNITRO, the average processing time is 0.85 s and the result is 12.65.

In conclusion, we can observe that in a 6-bus distribution network, SOCP relaxation is exact when the tolerance value $\epsilon$ is not extremely strict, and the solutions of FRP and KNITRO are the same. When we further reduce tolerance value, the SOCP relaxation is inexact and the FRP needs 11 iterations to converge. The result is slightly different from 12.65 because such strict tolerance is not applicable in real world and may affect the final solution. In general, the value range of $\epsilon$is ${10}^{-6}\sim {10}^{-4}$. We provided more detailed discussions about FRP in our previous work (Wei et al., 2017).

Additional Case Study

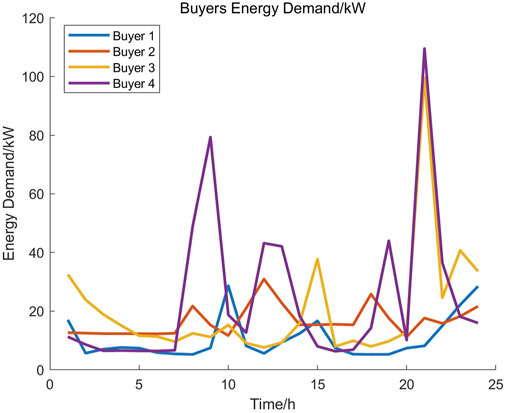
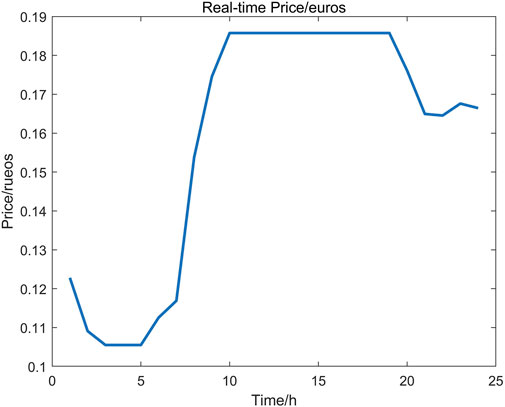
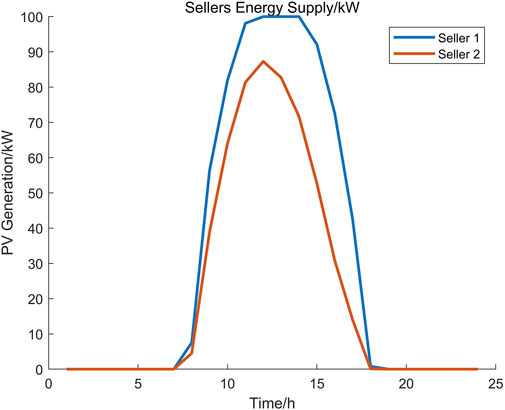
To further validate our proposed P2P model, we provide a realistic case study simulated over one day with 1 h time-step. We collect four realistic energy buyers’ demand and real-time electricity price from 200 Irish residents over the year of 2009, as shown in Figures 9, 10. Energy sellers’ renewable energy generation curve is shown in Figure 11, which comes from the solar PV simulation data in Ireland. All data set has been processed and scaled to benchmark parameter setting, which can be found in our Supplementary Material. The constant coefficient $k_t=0.001$ in time-and-level of use price. And the FiT is proportionate to real-time price, such as 0.7. Transaction cost ${\lambda }^{cost}=0.005$.

FIGURE 9

FIGURE 9. Buyers’ energy demand in 24 h

FIGURE 10

FIGURE 10. Real-time electricity price in 24 h

FIGURE 11

FIGURE 11. Sellers’ energy supply in 24 h

Table 7 summarizes every P2P market participant’s cost and revenue comparison during one day. Both energy sellers and buyers can benefit from the introduction of the P2P market. The additional case study using realistic data further validates our proposed P2P model, which can benefit all participants.

TABLE 7

TABLE 7. Comparison of participant’s cost and revenue/euros.

Conclusion

In this article, we have proposed a novel P2P market framework to model the equilibrium of P2P transactive energy. The transaction price is determined endogenous by solving the KKT conditions of all peers’ optimization problem. The equilibrium condition can be transformed to an MILP which can be processed by commercial solvers. The transaction energy flow information is further submitted to the distribution system operator and used to solve optimal power flow, so that network operation constraints can be guaranteed. The case study demonstrates that our proposed P2P market benefits all participants. The society also benefits from the P2P market.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BZ: conceptualization, writing-original draft preparation, software. YF: funding acquisition, validation. WW: conceptualization, methodology, writing-review and editing. YX: validation. SH: project administration. SM: supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Scientific and Technological Project of State Grid Qinghai Electric Power Company, China (SGQH0000DKJS2000127).

Conflict of Interest

Author YF and YX are employed by State Grid Qinghai Electric Power Company, China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.701149/full#supplementary-material

References

Abdella, J., and Khaled, S. (2018). “Peer to Peer Distributed Energy Trading in Smart Grids: A Survey.”. Energies. 11 (6), 1560. doi:10.3390/en11061560

CrossRef Full Text | Google Scholar

Abrishambaf, O., Lezama, F., Faria, P., and Vale, Z. (2019). “Towards Transactive Energy Systems: An Analysis on Current Trends.”Energ. Strategy Rev.26., 100418. doi:10.1016/j.esr.2019.100418

CrossRef Full Text | Google Scholar

Alam, M. R., St-Hilaire, M., and Kunz, T. (2017). “An Optimal P2P Energy Trading Model for Smart Homes in the Smart Grid.”Energy Efficiency. 10 (6),1475–1493. doi:10.1007/s12053-017-9532-5

CrossRef Full Text | Google Scholar

Alvaro-Hermana, R., Fraile-Ardanuy, J., Zufiria, P. J., Knapen, L., and Janssens, D. (2016). Peer to Peer Energy Trading with Electric Vehicles. IEEE Intell. Transport. Syst. Mag.8 (3), 33–44. doi:10.1109/MITS.2016.2573178

CrossRef Full Text | Google Scholar

Baran, M., and Wu, F. F. (1989a). Optimal Sizing of Capacitors Placed on a Radial Distribution System. IEEE Trans. Power Deliv.4 (1), 735–743. doi:10.1109/61.19266

CrossRef Full Text | Google Scholar

Baran, M. E., and Wu, F. F. (1989b). Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing. IEEE Trans. Power Deliv.4 (2), 1401–1407. doi:10.1109/61.25627

CrossRef Full Text | Google Scholar

Butler, L., and Neuhoff, K. (2008). Comparison of Feed-In Tariff, Quota and Auction Mechanisms to Support Wind Power Development. Renew.Energ.33 (8), 1854–1867. doi:10.1016/j.renene.2007.10.008

CrossRef Full Text | Google Scholar

Farivar, M., and Low, S. H. (2013). Branch Flow Model: Relaxations and Convexification-Part. IEEE Trans. Power Syst. 28, 2554–2564. doi:10.1109/TPWRS.2013.2255317

CrossRef Full Text | Google Scholar

Fortuny-Amat, J., and McCarl, B. (1981). A Representation and Economic Interpretation of a Two-Level Programming Problem. J.Oper. Res. Soc.32 (9), 783–792. doi:10.2307/2581394

CrossRef Full Text | Google Scholar

Giotitsas, C., Pazaitis, A., and Kostakis, V. (2015). “A Peer-To-Peer Approach to Energy Production.”Technology Soc.42, 28–38. doi:10.1016/j.techsoc.2015.02.002

CrossRef Full Text | Google Scholar

Gomez-Herrera, J. A., and Anjos, M. F. (2019). “Optimization-Based Estimation of Power Capacity Profiles for Activity-Based Residential Loads.”Int. J.Electr. Power Energ. Syst.104 (2018), 664–672. doi:10.1016/j.ijepes.2018.07.023

CrossRef Full Text | Google Scholar

Guerrero, J., Chapman, A. C., Verbic, G., and Gregor, V. (2019). Decentralized P2P Energy Trading under Network Constraints in a Low-Voltage Network. IEEE Trans. Smart Grid. 10, 5163–5173. doi:10.1109/tsg.2018.2878445

CrossRef Full Text | Google Scholar

Guo, Z., Wei, W., Chen, L., Wang, Z., and Mei, S. (2020). “Operation of Distribution Network Considering Compressed Air Energy Storage Unit and its Reactive Power Support Capability.”IEEE Trans. Smart Grid.11 (4), 2954–2965. doi:10.1109/TSG.2020.2966742

CrossRef Full Text | Google Scholar

Hou, K., Tang, P., Liu, Z., Jia, H., and Zhu, L. (2021). “Reliability Assessment of Power Systems with High Renewable Energy Penetration Using Shadow Price and Impact Increment Methods.”Front. Energ. Res.9 (March), 1–11. doi:10.3389/fenrg.2021.635071

CrossRef Full Text | Google Scholar

Kang, J., Yu, R., Huang, X., Maharjan, S., Zhang, Y., and Hossain, E. (2017). “Enabling Localized Peer-To-Peer Electricity Trading Among Plug-In Hybrid Electric Vehicles Using Consortium Blockchains. IEEE Trans. Ind. Inf.13 (6), 3154–3164. doi:10.1109/TII.2017.2709784

CrossRef Full Text | Google Scholar

Liu, B., Chen, J., Wang, H., and Wang, Q. (2020). “Renewable Energy and Material Supply Risks: A Predictive Analysis Based on an LSTM Model.”Front. Energ. Res.8 (September), 1–12. doi:10.3389/fenrg.2020.00163

CrossRef Full Text | Google Scholar

Long, C., Wu, J., Zhang, C., Cheng, M., and Al-Wakeel, A. (2017). “Feasibility of Peer-To-Peer Energy Trading in Low Voltage Electrical Distribution Networks.”Energ. Proced.105, 2227–2232. doi:10.1016/j.egypro.2017.03.632

CrossRef Full Text | Google Scholar

Long, C., Wu, J., Zhang, C., Thomas, L., Cheng, M., and Jenkins, N. (2018a). “Peer-to-Peer Energy Trading in a Community Microgrid.” IEEE Power and Energy Society General Meeting. 2018 (July): 1–5. doi:10.1109/PESGM.2017.8274546

CrossRef Full Text | Google Scholar

Long, C., Wu, J., Zhou, Y., and Jenkins, N. (2018b). “Peer-to-Peer Energy Sharing through a Two-Stage Aggregated Battery Control in a Community Microgrid.”Appl.Energ.226 (April), 261–276. doi:10.1016/j.apenergy.2018.05.097

CrossRef Full Text | Google Scholar

Mengelkamp, E., Gärttner, J., Rock, K., Kessler, S., Orsini, L., and Weinhardt, C. (2018). “Designing Microgrid Energy Markets.”Appl.Energ.210, 870–880. doi:10.1016/j.apenergy.2017.06.054

CrossRef Full Text | Google Scholar

Morstyn, T., and McCulloch, M. D. (2019). “Multiclass Energy Management for Peer-To-Peer Energy Trading Driven by Prosumer Preferences.”IEEE Trans. Power Syst.34 (5), 4005–4014. doi:10.1109/TPWRS.2018.2834472

CrossRef Full Text | Google Scholar

Morstyn, T., Teytelboym, A., Mcculloch, M. D., and McCulloch, (2019). “Bilateral Contract Networks for Peer-To-Peer Energy Trading.”IEEE Trans. Smart Grid. 10 (2), 2026–2035. doi:10.1109/TSG.2017.2786668

CrossRef Full Text | Google Scholar

Nguyen, S., Peng, W., Sokolowski, P., Alahakoon, D., and Yu, X. (2018). “Optimizing Rooftop Photovoltaic Distributed Generation with Battery Storage for Peer-To-Peer Energy Trading.”Appl.Energ.228, 2567–2580. doi:10.1016/j.apenergy.2018.07.042

CrossRef Full Text | Google Scholar

Pyrgou, A., Kylili, A., and Fokaides, P. A. (2016). “The Future of the Feed-In Tariff (FiT) Scheme in Europe: The Case of Photovoltaics.”Energy Policy.95, 94–102. doi:10.1016/j.enpol.2016.04.048

CrossRef Full Text | Google Scholar

Qi, M., Yang, H., Wang, D., Luo, Y., Zhang, S., and Liao, S. (2019). “Prosumers Peer-To-Peer Transaction Decision Considering Network Constraints.”2019 3rd IEEE Conference on Energy Internet and Energy System Integration. Ubiquitous Energy Network Connecting Everything. EI2 2019, no. 71931003, 643–647. doi:10.1109/EI247390.2019.9061909

CrossRef Full Text | Google Scholar

Shrestha, A., Bishwokarma, R., Chapagain, A., Banjara, S., Aryal, S., Mali, B., et al. (2019). “Peer-to-Peer Energy Trading in Micro/Mini-Grids for Local Energy Communities: A Review and Case Study of Nepal.”IEEE Access.7, 131911–131928. doi:10.1109/ACCESS.2019.2940751

CrossRef Full Text | Google Scholar

Sorin, E., Bobo, L., and Pierre, P. (2018). Consensus-Based Approach to Peer-To-Peer Electricity Markets with Product Differentiation. IEEE Trans.Power Syst. 34 (2), 994–1004. doi:10.1109/TPWRS.2018.2872880

Google Scholar

Sousa, T., Soares, T., Pinson, P., Moret, F., Baroche, T., and Sorin, E. (2019). “Peer-to-Peer and Community-Based Markets: A Comprehensive Review.”Renew.Sustainable Energ. Rev.104. (January), 367–378. doi:10.1016/j.rser.2019.01.036

CrossRef Full Text | Google Scholar

Tushar, W., Chai, B., Yuen, C., Smith, D. B., Wood, K. L., Yang, Z., et al. (2015). “Three-Party Energy Management with Distributed Energy Resources in Smart Grid.”IEEE Trans. Ind. Electron.62.(4), 2487–2498. doi:10.1109/TIE.2014.2341556

CrossRef Full Text | Google Scholar

Tushar, W., Yuen, C., Mohsenian-rad, H., Saha, T., Vincent Poor, H., and Wood, K. L. (2018). “Transforming Energy Networks via Peer-To-Peer Energy Trading: The Potential of Game-Theoretic Approaches.” IEEE Signal Processing Magazine.35, (July), 90–111. doi:10.1109/msp.2018.2818327

CrossRef Full Text | Google Scholar

Tushar, W., Saha, T. K., Yuen, C., Azim, M. I., Morstyn, T., Poor, H. V., et al. (2020a). “A Coalition Formation Game Framework for Peer-To-Peer Energy Trading.” Appl.Energ.261. (December 2019), 114436. doi:10.1016/j.apenergy.2019.114436

CrossRef Full Text | Google Scholar

Tushar, W., Saha, T. K., Yuen, C., Smith, D., and Poor, H. V. (2020b). “Peer-to-Peer Trading in Electricity Networks: An Overview.”IEEE Trans. Smart Grid. 11 (4), 3185–3200. doi:10.1109/TSG.2020.2969657

CrossRef Full Text | Google Scholar

Wei, W., Wang, J., Li, N., and Mei, S. (2017). Optimal Power Flow of Radial Networks and its Variations: A Sequential Convex Optimization Approach. IEEE Trans. Smart Grid. 8 (6), 2974–2987. doi:10.1109/TSG.2017.2684183

CrossRef Full Text | Google Scholar

Zhang, C., Wu, J., Cheng, M., Zhou, Y., and Long, C. (2016). “A Bidding System for Peer-To-Peer Energy Trading in a Grid-Connected Microgrid.” Energ. Proced.103. (April), 147–152. doi:10.1016/j.egypro.2016.11.264

CrossRef Full Text | Google Scholar

Zhang, C., Wu, J., Zhou, Y., Cheng, M., and Long, C. (2018). “Peer-to-Peer Energy Trading in a Microgrid.” Appl.Energ.220 (December 2017), 1–12. doi:10.1016/j.apenergy.2018.03.010

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

BFM Branch flow model

DERs Distributed energy resources

DSO Distribution system operator

FiT Feed-in Tariff

FRP Feasibility recovery procedure

ICT Information and Communication Technology

KKT Karush–Kuhn–Tucker conditions

MILP Mixed-integer linear program

OPF Optimal power flow

P2P Peer-to-Peer

SOCP Second-order cone program

TLOU Time-and-level-of-use

Indices and sets

$B$ Set of energy buyers

$S$ Set of energy sellers

$b$ The index of energy buyer

$s$ The index of energy seller

$N$ Set of buses in radial distribution network

$L$ Set of lines in radial distribution network

$c\left(j\right)$ Child buses of bus $j$

$i,j,k$ The index of bus

$l$ The index of line

Parameters

$t$ Index of time periods

${\lambda }^{sell}$ Feed-in Tariff

${\lambda }^{cost}$ P2P transaction cost

${\lambda }_b^{buy}$ The TLOU price of energy buy$b$

${\lambda }_0^{buy}$ Initial electricity price in TLOU

$k_t$ Constant coefficient in TLOU

$P_s$ The excessive energy for sell of seller $s$

$D_b$ The energy demand of buyer $b$

$M$ Constant parameter in big-M method

$a_i$, $b_i$, $c_i$ Coefficients of the production cost function.

$P_{dj}$, $Q_{dj}$ Fixed active and reactive power demand

$r_{ij}^l$, $x_{ij}^l$, $z_{ij}^l$ Resistance, reactance and impedance of line $l$

$P_{gi}^n$, $P_{gi}^m$ Active generation limits at bus $i$

$Q_{gi}^n$, $Q_{gi}^m$ Reactive generation limits at bus $i$

$V_i^n$, $V_i^m$ Square voltage magnitudes limits at bus $i$

$S_l$ Apparent power flow capacity of line $l$

Variables

$p_{sb}$ P2P transaction amount between seller $s$ and buyer $b$

${\rho }_{sb}$ P2P transaction price between seller $s$ and buyer $b$

$P_{gi}$, $Q_{gi}$ Active and reactive power generation at bus $i$

$P_{ij}^l/P_{jk}^l$,$Q_{ij}^l/Q_{jk}^l$ Active and reactive power flow in line $l$

$I_{ij}^l$ Square current magnitude in line $l$

$V_i$ Square voltage magnitude at bus $i$

$x$ The feasible set of BFM solution