Automatic Generation Control for Distributed Multi-Region Interconnected Power System with Function Approximation

Solving the energy crisis and environmental pollution requires large-scale access to distributed energy and the popularization of electric vehicles. However, distributed energy sources and loads are characterized by randomness, intermittence and difficulty in accurate prediction, which bring great challenges to the security, stability and economic operation of power system. Therefore, this paper explores an integrated energy system model that contains a large amount of new energy and combined cooling heating and power (CCHP) from the perspective of automatic generation control (AGC). Then, a gradient Q(σ,λ) [GQ (σ,λ)] algorithm for distributed multi-region interconnected power system is proposed to solve it. The proposed algorithm integrates unified mixed sampling parameter and linear function approximation on the basis of the Q(λ) algorithm with characteristics of interactive collaboration and self-learning. The GQ (σ,λ) algorithm avoids the disadvantages of large action spaces required by traditional reinforcement learning, so as to obtain multi-region optimal cooperative control. Under such control, the energy autonomy of each region can be achieved, and the strong stochastic disturbance caused by the large-scale access of distributed energy to grid can be resolved. In this paper, the improved IEEE two-area load frequency control (LFC) model and the integrated energy system model incorporating a large amount of new energy and CCHP are used for simulation analysis. Results show that compared with other algorithms, the proposed algorithm has optimal cooperative control performance, fast convergence speed and good robustness, which can solve the strong stochastic disturbance caused by the large-scale grid connection of distributed energy.

Introduction

To cope with the fossil energy crisis and environmental pollution, many countries around the world are vigorously developing distributed energy, which can promote the transformation of low-carbon and intelligent power system (Xu et al., 2020; Kumar et al., 2020; An et al., 2020; Suh et al., 2017). However, the distributed energy and loads, such as wind power, photovoltaic and electric vehicles, are intermittent and stochastic (Solanki et al., 2017; Xi et al., 2015; Zhang et al., 2021; Mukherjee and Gupta, 2016; Wang, 2020). The rapid growth of their installed capacity poses a huge challenge to power system. The traditional centralized automatic generation control (AGC) cannot easily meet the development requirements and operating conditions for smart grid (Jaleeli et al., 1992). Therefore, solving the strong stochastic disturbance caused by large-scale grid connections of distributed energy from the perspective of AGC, has become an urgent challenge in the field of power system.

Nowadays, the AGC control methods can be divided into two categories: conventional analytic and machine learning. The proportional-integral-derivative (PID) control, optimal control and robust control are representations of conventional analytical control methods (Yan et al., 2013). Based on a fuzzy logic approach, the fractional-order PID controller uses a genetic algorithm to change the controller parameters accurately and improve the dynamic response of AGC for two-region interconnected power system significantly (Ismayil et al., 2015). An optimal PI/PID method based on the social learning adaptive bacterial foraging algorithm was proposed in (Xie et al., 2016) to improve the convergence speed and merit-seeking accuracy of the algorithm. To obtain the dynamic control performance, the study adopted a PI-structured optimal controller based on a full state feedback strategy in the application of optimal control methods to AGC (Yamashita and Taniguchi, 2016). To overcome system perturbations, the study introduced robust control into complex power systems with large-scale access to renewable energy (Sharma et al., 2017). Thus, the dynamic performance and control stability of AGC can be improved. As another aspect of AGC control methods, reinforcement learning algorithms are representative of machine learning methods. The Q-learning algorithm based on the Markov decision process relies on a closed-loop feedback structure formed by the value function and control action under the control performance standard (CPS). This algorithm can improve the robustness and adaptability of the whole AGC system significantly (Yu et al., 2011). Based on multi-step backward Q (λ) learning, the optimal power allocation algorithm for AGC commands introduces a multi-step foresight capability to solve the delayed return problem caused by large time lag links in thermal power units (Yu et al., 2011). Based on the average payoff model, the full-process R (λ) learning controller can be directly introduced to the practical power grid to learn to imitate the output of other controllers online (Yu and Yuan, 2010). Hence, without building an accurate simulation model for offline prelearning, the controller can also improve the learning efficiency and applicability in practical power system (Xi et al., 2020; Zhang et al., 2020).

However, with the increasing access to a high proportion of new energy resources, grid patterns shift, thereby resulting in increased stochastic disturbances (Hou et al., 2021; Fu et al., 2021; Dehnavi and Ginn, 2019). The aforementioned methods cannot meet the optimal frequency control requirements of smart grid. Hence, scholars have proposed a series of distributed intelligent AGC methods. The forecasting model control, hierarchical recursive, adaptive control, reinforcement learning, and deep learning have been introduced into the distributed AGC controller. In particular, the wolf pack hunting (WPH) strategy based on the multi-agent systems-stochastic consensus game framework, which considers the integrated objectives of frequency deviation and short-term economic dispatch, can achieve the optimal power dispatch of AGC so as to solve coordinated control and power autonomy problems effectively (Xi et al., 2016). In order to promote the intelligence of AGC systems through the combination of reinforcement learning and artificial emotion, an artificial emotion reinforcement learning controller for AGC can generate different control strategies according to the environment of power system (Yin et al., 2017). As for realizing the optimal coordinated control of power systems, the DPDPN algorithm combines the decision mechanism of reinforcement learning with the prediction mechanism of a deep neural network to allocate power order among the various generators (Xi et al., 2020). Meanwhile, the distributed energy and loads, such as wind power, photovoltaic, biomass power and electric vehicles, continue to increase at a massive scale (Wang et al., 2015). This trend causes strong stochastic disturbances in the power grid and leads to a dramatic increase in the difficulty of a frequency control for the power grid. Therefore, a new AGC method must be investigated to address the problem of strong stochastic perturbations.

For the situation of low-dimensional state-action pairs, the reinforcement learning method uses a table to record value functions, with each state or state-action pair allocated storage space to record function values (Zhang et al., 2018; Sun and Yang, 2019; Xi et al., 2021). However, the increased access to distributed energy and the expansion of the installed capacity of generators cause the state-action pair storage space to expand geometrically. This drawback limits the dynamic optimization speed of reinforcement learning algorithms. Thus, the optimal control efficiency of AGC is reduced greatly. To solve the problem of storage space for state-action pairs, this study proposes a gradient Q(σ,λ) [GQ (σ,λ)] algorithm for distributed multi-region cooperative control. Linear function approximation with mixed sampling parameter is adopted to combine the full sampling algorithm with the pure expectation algorithm judiciously. Through the GQ (σ,λ) algorithm, the power allocation commands of each region for distributed AGC can be obtained. Thus, the stochastic disturbances caused by large-scale new energy access to the grid can be solved. The improved IEEE two-area load frequency control (LFC) model and integrated energy system model incorporating a large amount of new energy and combined cooling heating and power (CCHP) are simulated, and the results verify the effectiveness of the GQ (σ,λ) algorithm. Compared with other reinforcement learning algorithms, GQ (σ,λ) has better learning ability, better cooperative control performance, faster convergence and better robustness.

GQ(σ,λ) Algorithm

Q(λ) Algorithm

As one of the classical reinforcement learning algorithms, Q-learning is based on the discrete-time Markov decision process, which is a value function iteration rooted in online learning and dynamic optimization technology (Watkins and Dayan, 1992). Based on Q-learning, the Q (λ) algorithm integrates eligibility trace with the characteristics of multi-step backtracking update to improve the convergence speed. The Q (λ) algorithm uses eligibility trace to obtain two types of heuristic information, namely, frequency and gradual reliability of controller behavior (Barto and Sutton, 1998). This information can accurately and effectively reflect the influence of previous multi-step state-action pairs on subsequent decisions. Eligibility trace is mainly used to solve the problem of time reliability allocation in delayed reinforcement learning. It is a temporary record of previous state tracks and action information. For any state-action pair, eligibility trace is attenuated with timeliness (Xi et al., 2018). The iterative updating formula of eligibility trace is as follows:

$e_{k+1}\left(s,a\right)=\{\begin{array}{c}\gamma \lambda e_k\left(s,a\right)+1,\left(s,a\right)=\left(s_k,a_k\right)\\ \gamma \lambda e_k\left(s,a\right),\text{ otherwise }\end{array}(1)$

where e_k (s,a) is the eligibility trace of the kth iteration under state s and action a, γ is the discount factor, and λ is the attenuation factor of eligibility trace.

According to the reward value obtained by the agent through the current exploration, the error of the Q value function and its evaluation are calculated as follows:

${\rho }_k=R_k+\gamma Q_k\left(s_{k+1},a_g\right)-Q_k\left(s_k,a_k\right)(2)$

${\delta }_k=R_k+\gamma Q_k\left(s_{k+1},a_g\right)-Q_k\left(s_k,a_g\right)(3)$

where R_k is the reward function of the kth iteration, a_g is the action of the greedy policy, ρ_k is the Q value function error of the agent at the kth iteration, and δ_k is the evaluation of the function error.

The iterative update process of the Q(λ) algorithm is as follows:

$Q_{k+1}\left(s,a\right)=Q_k\left(s,a\right)+\alpha {\delta }_k{e}_k\left(s,a\right)(4)$

$Q_{k+1}\left(s_k,a_k\right)=Q_{k+1}\left(s_k,a_k\right)+\alpha {\rho }_k(5)$

where α is the value function learning factor. When the value of α is large, it can accelerate the iterative updating and learning speed of the Q value function. While the value of α is small, the stability of the control system is improved.

Q(σ,λ) Algorithm

On the basis of the Q (λ) algorithm, this study proposes the Q (σ,λ) algorithm, which combines on-policy learning and off-policy learning. The mixed sampling parameter σ is introduced to unify the Sarsa algorithm (full sampling) and Expected-sarsa algorithm (pure expectation) (Long et al., 2018). As one of the classic algorithms in on-policy learning, the Sarsa algorithm uses a greedy policy to update the target strategy synchronously while evaluating the Q value function through the current target action strategy (Rummery and Niranjan, 1994). The Expected-sarsa algorithm, as an off-policy learning algorithm, uses the function expectation value of the next state-action pair to evaluate the Q value function (Seijen et al., 2009). Although the Expected-sarsa algorithm is computationally more complex than Sarsa, it eliminates the variance caused by the random selection of the next action. Given the same exploration path, Expected-sarsa performs significantly better than Sarsa.

Therefore, the mixed sampling parameter σ is introduced to integrate the Expected-sarsa algorithm and Sarsa algorithm and unify the advantages and disadvantages of on-policy and off-policy learning. The range of the mixed sampling parameter is (0,1). Although 0 < σ < 1, the control performance of the algorithm is better than that at σ = 0 or 1. The iterative update of the Q (σ,λ) algorithm is obtained by linear weighting between the update of the full sampling Sarsa algorithm (σ = 1) and the update of the pure expectation Expected-sarsa algorithm (σ = 0).

${\delta }_k^{\sigma }=R_k+\gamma \left[\sigma Q_k\left(s_{k+1},a_{k+1}\right)+\left(1-\sigma \right){\displaystyle \sum _{a\in A}\pi \left(s_{k+1},a\right)Q_k\left(s_{k+1},a\right)}\right]-Q_k\left(s_k,a_k\right)(6)$

$Q_k\left(s_k,a_k\right)=Q_k\left(s_k,a_k\right)+\alpha {\delta }_k^{\sigma }{e}_k\left(s,a\right)(7)$

where π (s_k+1,a) is the value function of the decision-making strategy under state s_k+1 and action a and δ_k^σ is the evaluation of the function error at the kth iteration.

The eligibility trace is also updated iteratively as follows:

$e_{k+1}\left(s,a\right)=\{\begin{array}{c}\gamma \lambda e_k\left(s,a\right)\left[\sigma +\left(1-\sigma \right)\pi \left(a_k|s_k\right)\right]+1,Q_k\left(s_k,a_k\right)=\underset{a\in A}{\max }{Q}_k\left(s_k,a\right)\\ \gamma \lambda e_k\left(s,a\right)\left[\sigma +\left(1-\sigma \right)\pi \left(a_k|s_k\right)\right],\mathrm{otherwise}\end{array}(8)$

GQ(σ,λ) Algorithm

In this paper, the linear function approximation and mixed sampling parameter are combined to solve the problem of insufficient storage space in traditional reinforcement learning algorithms. The sampling problem is also solved using random approximation under double time scales (Yang et al., 2019). Moreover, the GQ (σ,λ) algorithm, which combines mixed sampling with function approximation, is proposed. The algorithm is oriented to a multi-agent system, which reduces the time needed for an intelligent algorithm to explore the path of multi-agent state-action pairs. Meanwhile, the optimal decision-making strategy can be obtained quickly. This strategy can solve the optimal cooperative control problem and promote the stochastic complex dynamic characteristics of multi-agent system (Sun et al., 2016).

The agent calculates the value function error of the decision-making strategy through the reward value R obtained from the current exploration, which is expressed as shown:

${\delta }_k^{\sigma }=R_k+\gamma \left[\sigma Q\left(s_{k+1},a_{k+1}\right)\pi \left(s_{k+1},a_{k+1}\right)+\left(1-\sigma \right)V_k^{\pi }\left(s_{k+1}\right)\right]-Q\left(s_k,a_k\right)\pi \left(s_k,a_k\right)(9)$

where V_k^π (s_k+1) is the function expectation value of the decision-making strategy under state s_k+1.

The decision-making strategy of the GQ (σ,λ) algorithm is updated iteratively as follows:

${\pi }_{k+1}\left(s_k,a_k\right)={\pi }_k\left(s_k,a_k\right)+\alpha \frac{1}{2}{\nabla }_{\pi \left(s_k,a_k\right)}(10)$

where ∇_{π (sk,ak)} is the gradient of the decision-making strategy under state s_k and action a_k, that is, the optimal function approximation value of the decision-making strategy at (s_k,a_k), which can be calculated as follows:

${\nabla }_{\pi \left(s_k,a_k\right)}=2\left[{\delta }_k^{\sigma }{e}_k\left(s,a\right)-\gamma {\upsilon }_k\left(s_k,a_k\right){\omega }_k\left(s_k,a_k\right)\right](11)$

where e_k (s, a) is the eligibility trace of the kth iteration under state s and action a, it can be calculated by Eq. 8. υ_k (s_k,a_k) and ω_k (s_k,a_k) are the Q value function error and evaluation of the kth iteration under state s_k and action a_k, respectively. The iterative updates of υ_k (s_k,a_k) and ω_k (s_k,a_k) are as follows:

${\upsilon }_{k+1}\left(s_k,a_k\right)=\sigma \left(1-\lambda \right)Q\left(s_k,a_k\right)e_k\left(s,a\right)+\left(1-\sigma \right)\left[V_k^{\pi }\left(s_k\right)-\lambda Q\left(s_k,a_k\right)\right]e_k\left(s,a\right)(12)$

${\omega }_{k+1}\left(s_k,a_k\right)={\omega }_k\left(s_k,a_k\right)+\beta \left[{\delta }_k^{\sigma }{e}_k\left(s,a\right)-Q\left(s_k,a_k\right){\omega }_k\left(s_k,a_k\right)\right](13)$

where β is the learning factor of the Q value function.

After several trial-error iterations, the decision-making strategy π (s,a) converges to a relatively fixed optimal action strategy, which speeds up the convergence of reinforcement learning, so as to obtain the optimal cooperative control strategy.

Design of AGC Controller

Control Framework of AGC System Based on GQ (σ,λ)

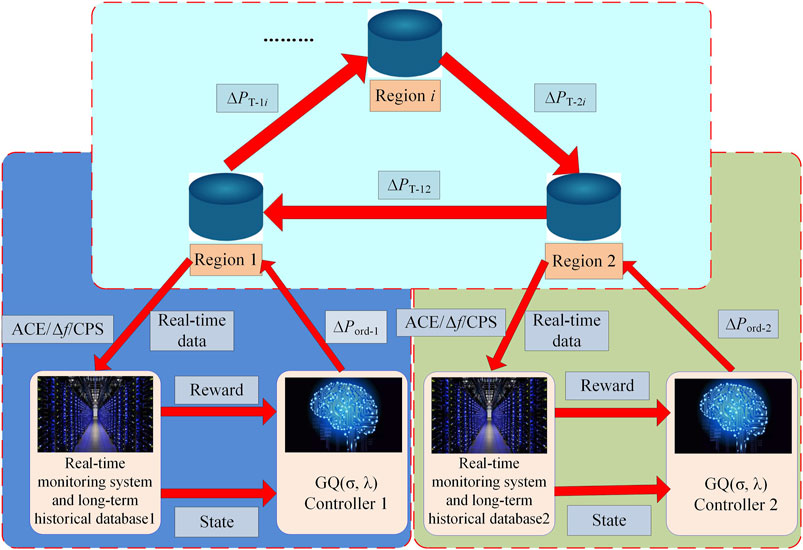
The control framework of AGC system based on GQ (σ,λ) is shown in Figure 1. The input of the GQ (σ,λ) controller of the ith regional power grid is the state under the current environment and the calculated reward value from the “real-time monitoring system and long-term historical database”. The GQ (σ,λ) controller can realize online learning and give control signals. The control action is the general AGC regulation command ∆P_ord-i of dispatching the terminal of ith regional power grid.

FIGURE 1

FIGURE 1. Control framework of AGC system based on GQ (σ,λ).

Construction of Reward Function

Considering the problem of environmental pollution, this paper takes the linear weighting of ACE and carbon emission (CE) as the comprehensive, objective function. The CE value of the regional power grid is equal to the product of the unit output power and unit CE intensity coefficient. The reward function of each regional power grid is constructed as follows:

$R=-\eta {\left[\mathrm{A}\mathrm{C}\mathrm{E}\left(t\right)\right]}^2-\left(1-\eta \right)\left({\displaystyle \sum _{k=1}^m{B}_k\left[\Delta P_k\left(t\right)\right]}\right)/1000,\Delta P_k^{\min }\le \Delta P_k\left(t\right)\le \Delta P_k^{\max }(14)$

where ACE (t) is the instantaneous value of ACE, ΔP_k (t) is the actual output power of the kth unit, and η and 1-η are the weights of ACE and CE, respectively. The η value of each area is the same, and thus, the η value is set to 0.5.

Parameter Setting

In the design of the AGC controller, five system parameters, namely, α, β, γ, λ and σ, are set. After numerous trial-error iterations, the best control performance can be obtained when the parameters shown in Table 1 are set.

1) The learning factor of the decision-making strategy α (0 < α < 1), measure the influence of action selection strategy on iterative updating of decision-making strategy. The larger α can accelerate the convergence speed of the decision-making strategy, while the smaller α can ensure that the system can fully search other actions in the space.

2) The learning factor of the value function β (0 < β < 1), weigh the stability of GQ (σ,λ) algorithm. Larger β can accelerate the iterative updating speed of the value function, and when β is smaller, the stability of the system will be greatly improved. The parameter setting of learning factor is to have fast learning speed as much as possible under the condition of ensuring stability.

3) The discount factor of the value function γ (0 < γ < 1), weigh the importance of current and future reward. The closer the value is to 1, the more emphasis is placed on long-term rewards; otherwise, more emphasis is on immediate rewards. Considering that the agent pursues long-term returns, the value close to one should be adopted.

4) The attenuation factor of the eligibility trace λ (0 < λ < 1), reflect the degree of influence on convergence rate and non Markov effect. The larger λ is, the slower the eligibility trace of the previous historical state-action pair will decay, and the more reputation will be allocated. The smaller λ is, the less reputation will be allocated.

5) The mixed sampling parameter σ (0 ≤ σ ≤ 1), unify on-policy and off-policy learning. With different values, the linear weighting between full sampling algorithm and pure expectation algorithm will be different. The smaller σ is, the more full sampling is preferred in the process of strategy optimization, that is, the iterative update is carried out through the value function.

TABLE 1

TABLE 1. Parameters setting.

GQ(σ,λ) Procedure

The execution procedure of the AGC system based on the GQ (σ,λ) algorithm is shown in Figure 2. Before the controller runs online, extensive prelearning is needed to achieve the optimal action set and thereby obtain the optimal coordination control of online system operations.

FIGURE 2

FIGURE 2. Execution procedure of the GQ (σ,λ) algorithm.

Example Analysis

Improved IEEE Two-Area LFC Power System

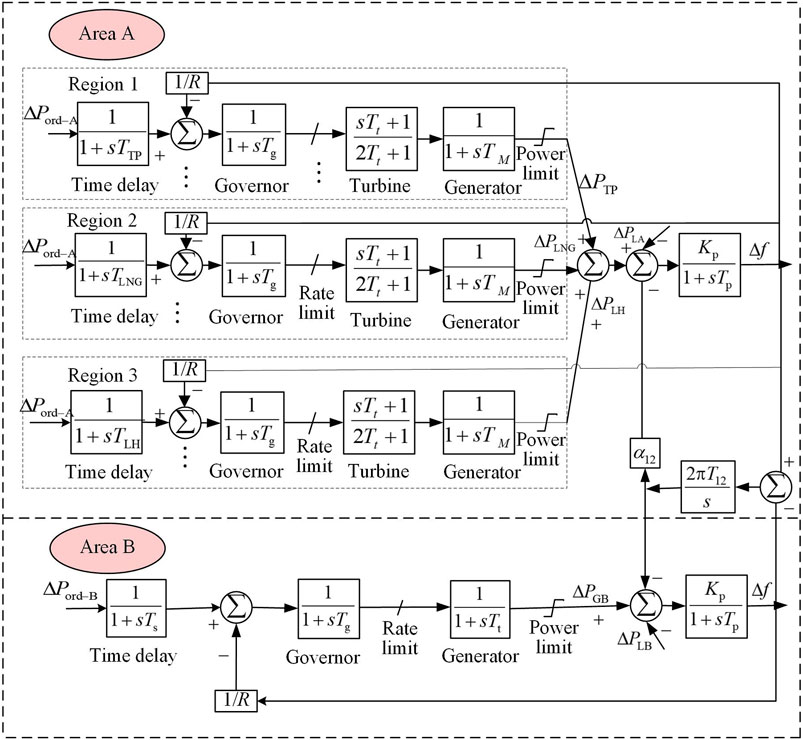
Based on the IEEE standard two-area LFC model (Ray et al., 1999), the improved model replaces one equivalent unit in area A with three area power grids to analyze the control performance of the GQ (σ,λ)algorithm. The frame structure is shown in Figure 3, and the system parameters are selected from the model parameters in reference (Xi et al., 2020). Area A has 20 generating units, including thermal power (TP), liquefied natural gas (LNG) and large hydropower (LH). The specific parameters of the units are taken from reference (Zhang and Yu, 2015).

FIGURE 3

FIGURE 3. Improved model of IEEE two-area LFC power system.

Before online operations, numerous offline trials and errors are needed to explore the CPS state and to obtain the optimal action strategy, optimize the Q function, and then introduce it into the integrated energy system model for online optimization operation.

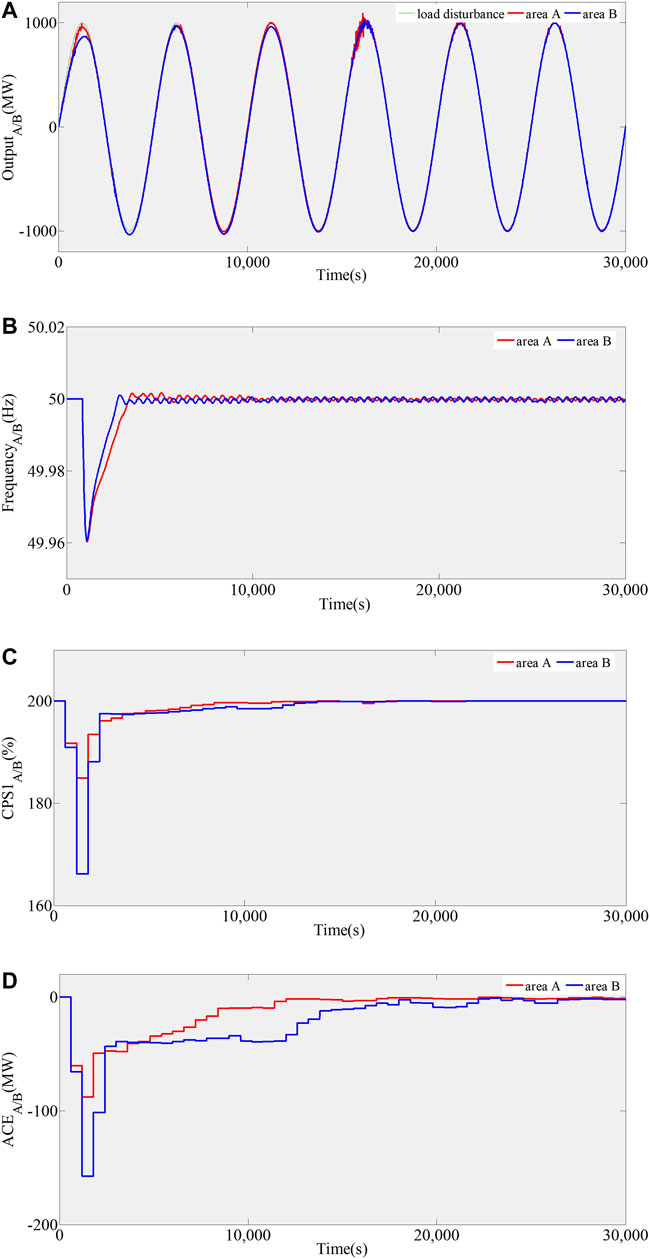
A continuous sinusoidal load disturbance with a period of 5,000 s and an amplitude of 1,000 MW is introduced into the two-area LFC model. Figure 4 shows the prelearning process of the two areas generated by the continuous sinusoidal load disturbance. As shown in Figures 4A,B, the GQ (σ,λ) algorithm can track the load disturbance quickly in two areas, and the frequency deviation is far less than the standard value and is relatively stable. The control performance of AGC is evaluated by the average value of CPS1 (CPS1_AVE-10-min) and ACE (ACE_AVE-10-min) every 10 min. As shown in Figures 4C,D, the index value of CPS1 in area A is kept in the qualified range of 180–200%, and the value of ACE is kept in the range of -100-0 MW until a stable value is reached. Meanwhile, the index value of CPS1 in area B is kept in the qualified range of 165–200%, and the value of ACE is kept in the range of −160-0 MW until a stable value is reached.

FIGURE 4

FIGURE 4. Pre-learning of the GQ (σ,λ) algorithm in area A and B, 4 (A), 4 (B), 4 (C), 4 (D).

Integrated Energy System

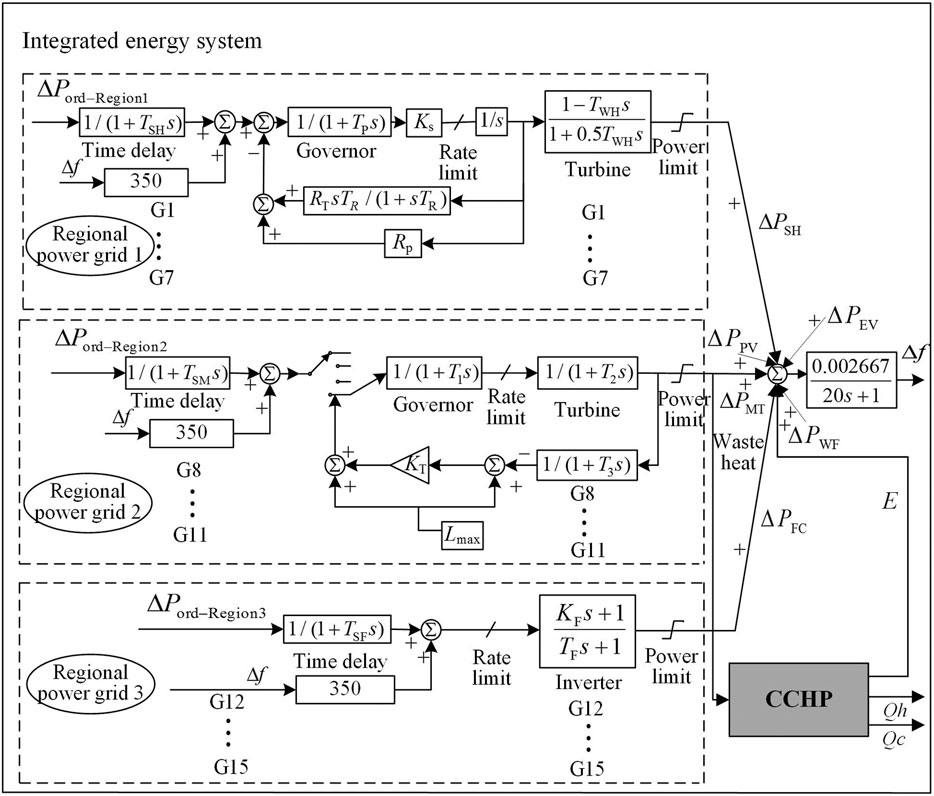
This paper establishes a small-scale integrated energy system model incorporating a large amount of new energy and CCHP, including photovoltaic (PV), wind farm (WF), electric vehicle (EV), small hydropower (SH), micro gas turbine (MT), fuel cell (FC) units. Given the randomness and uncontrollability of PV, WF, and EV, the output models of the three new energy are simplified. That is, they are treated as a random disturbance of the AGC system, and do not participate in system frequency regulation. The model structure of the built integrated energy system is shown in Figure 5, and the system parameters are selected from the reference (Xi et al., 2020). The total regulated power is 2,350 kW, and each adjustable unit (SH, MT, and FC) is regarded as a different agent. The relevant parameters of each unit in the integrated energy system model are taken from reference (Saha et al., 2008).

FIGURE 5

FIGURE 5. The model of integrated energy system.

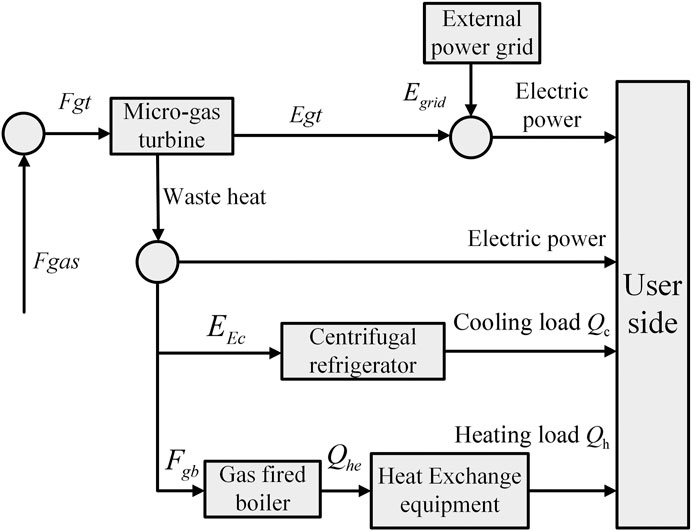
The introduced CCHP system is shown in Figure 6. This system can realize the complementary and collaborative optimal operation of multiple energy sources (Fang et al., 2012). It uses the waste heat of MT to produce electric energy and meet heating and cooling requirements. The structure of the CCHP system is mainly composed of MT, centrifugal refrigerator device and heat exchange equipment, which is a multi generation energy system integrating heating, cooling and power generation. The purpose is to reduce the emissions of carbides and harmful gases and thereby greatly improve energy efficiency.

FIGURE 6

FIGURE 6. The structure of CCHP system.

Periodic Impulse Load Disturbance

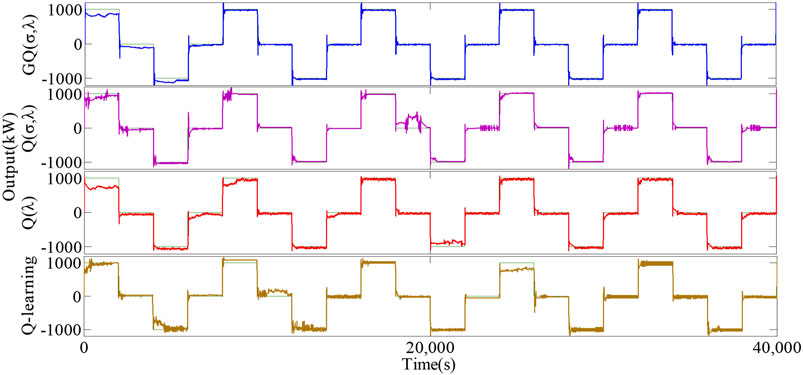
After adequate prelearning, a periodic impulse load disturbance is introduced into the integrated energy system model to simulate the random load disturbance (i.e., regular sudden increase and decrease) in the random environment of power system, so as to analyze the performance of the proposed algorithm. The period of periodic impulse disturbance is 8,000 s, and the amplitude is 1,000 kW.

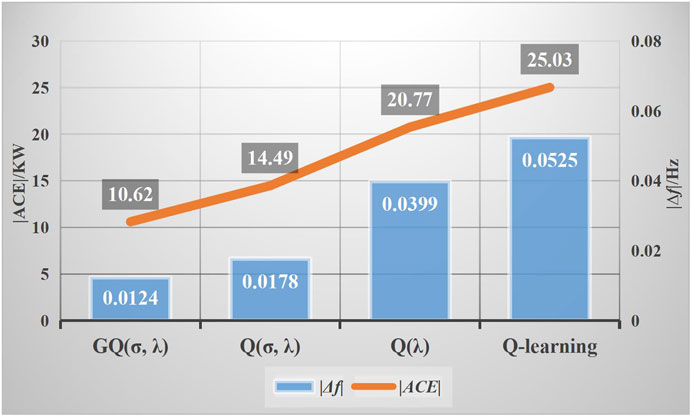
Under the given impulse load disturbance, the long-term control performance of the GQ (σ,λ) algorithm is evaluated by statistical experimental results within 24 h. At the same time, Q (σ,λ), Q(λ), and Q-learning are introduced to test the control performance of the four control algorithms. Figures 7, 8 respectively show the output power curve and control performance of different algorithms under periodic pulse load disturbance. Figure 7 shows that under the four control algorithms, the actual output of the unit can effectively track the load disturbance. Meanwhile, the GQ (σ,λ) algorithm has a relatively fast convergence speed, and the output power curve is relatively smooth and can thus suitably fit the load disturbance curve. As shown in Figure 8, GQ (σ,λ), relative to other control algorithms, can reduce |ACE| by 26.71–57.57% and |Δf| by 30.34–76.38%. The result further proves that GQ (σ,λ) has optimal control performance, fast dynamic optimization speed, and strong robustness under load disturbance.

FIGURE 7

FIGURE 7. Controller outputs of different algorithms under impulsive disturbance.

FIGURE 8

FIGURE 8. Control performance of different algorithms under impulsive disturbance.

AGC Control Performance Under Random White Noise Disturbance

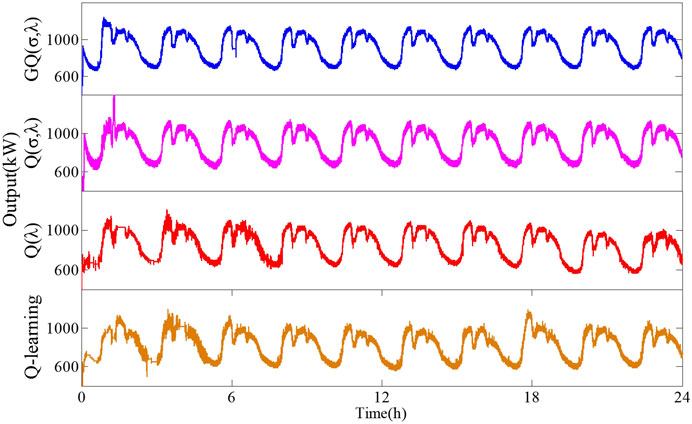
The random white noise load disturbance is applied to the integrated energy system model to simulate the complex condition in which the power system load changes randomly at every moment in the large-scale grid-connected environment of unknown new energy. The results are expected to verify the application effect of the GQ (σ,λ) algorithm in the strong random grid environment. Similarly, the long-term performance of GQ (σ,λ), Q (σ,λ), Q(λ), and Q-learning algorithms are tested by random white noise disturbance within 24 h.

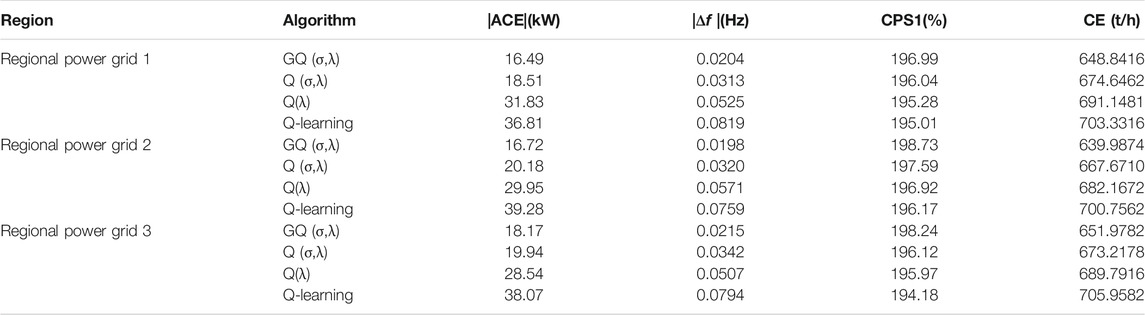
The controller outputs of the different algorithms under random white noise are shown in Figure 9. The GQ (σ,λ) algorithm can follow the load disturbance faster and more accurately than the other three algorithms. The statistical results of the simulation experiments are shown in Table 2. Relative to the other algorithms, GQ (σ,λ) can reduce |ACE| by 17.15–57.43%, and |∆f| by 38.13–73.91%, CPS1 by 1.14–2.56%, and CE by 4.15–8.67% in regional power grid 2. Moreover, the data analysis reveals that GQ (σ,λ) has the better adaptive ability, better coordinated and optimized control performance, and less carbon emission than the other algorithms.

FIGURE 9

FIGURE 9. Controller outputs of different algorithms under random white noise disturbance.

TABLE 2

TABLE 2. The data statistics under random white noise disturbance.

Conclusion

A control framework of an integrated energy system incorporating a large amount of distributed energy and CCHP is built in this paper. A novel GQ (σ,λ) algorithm for a distributed multi-region interconnected power system is also proposed to find the equilibrium solution so as to obtain the optimal cooperative control and solve the problem of strong random disturbances caused by the large-scale grid connection of distributed energy.

The proposed algorithm, which is based on the Q (λ) algorithm and features interactive collaboration and self-learning, adopts linear function approximation and mixed sampling parameter to organically unify full sampling and pure expectation. The GQ (σ,λ) algorithm can reduce the storage space of state-action pairs required by the control algorithm, so as to obtain the distributed multi-region optimal cooperative control quickly.

The improved IEEE two-area LFC model and integrated energy system model with CCHP are used for example analysis. The results show that compared with other algorithms, GQ (σ,λ) has better cooperative control performance and less carbon emission. Moreover, it can solve the random disturbance problem caused by the large-scale access of distributed energy in integrated energy system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YL: literature review, writing, language editing and proofreading. LZ: mathematical analysis, writing, and simulation. LX: framework formation, and writing. QS: analysis and revised the manuscript. JZ: analysis with constructive discussions.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51707102).

Conflict of Interest

LZ was employed by the company Zigong Power Supply Company, State Grid Sichuan Electric Power Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

An, Y., Zhao, Z. H. H., Wang, S. K., et al. (2020). Coordinative Optimization of Hydro-Photovoltaic-Wind-Battery Complementary Power Stations. CSEE J. Power Energ. Syst. 6 (2), 410–418. doi:10.17775/CSEEJPES.2019.00330

Google Scholar

Barto, A. G., and Sutton, R. S. (1998). Reinforcement Learning: An Introduction. IEEE Trans. Neural Networks 9 (5), 1054.

CrossRef Full Text | Google Scholar

Dehnavi, G., and Ginn, H. L. (2019). Distributed Load Sharing Among Converters in an Autonomous Microgrid Including PV and Wind Power Units. IEEE Trans. Smart Grid 10 (4), 4289–4298. doi:10.1109/tsg.2018.2856480

CrossRef Full Text | Google Scholar

Fang, F., Wang, Q. H., and Shi, Y. (2012). A Novel Optimal Operational Strategy for the CCHP System Based on Two Operating Modes. IEEE Trans. Power Syst. 27 (2), 1032–1041. doi:10.1109/tpwrs.2011.2175490

CrossRef Full Text | Google Scholar

Fu, W., Zhang, K., Wang, K., Wen, B., Fang, P., and Zou, F. (2021). A Hybrid Approach for Multi-step Wind Speed Forecasting Based on Two-Layer Decomposition, Improved Hybrid DE-HHO Optimization and KELM. Renew. Energ. 164, 211–229. doi:10.1016/j.renene.2020.09.078

CrossRef Full Text | Google Scholar

Hou, K., Tang, P., Liu, Z., et al. (2021). Reliability Assessment of Power Systems with High Renewable Energy Penetration Using Shadow price and Impact Increment Methods. Front. Energ. Res. 9Article ID 635071. doi:10.3389/fenrg.2021.635071

CrossRef Full Text | Google Scholar

Ismayil, C., Kumar, R. S., and Sindhu, T. K. (2015). Optimal Fractional Order PID Controller for Automatic Generation Control of Two-Area Power Systems. Int. Trans. Electr. Energ. Syst. 25, 3329–3348. doi:10.1002/etep.2038

CrossRef Full Text | Google Scholar

Jaleeli, N., VanSlyck, L. S., Ewart, D. N., Fink, L. H., and Hoffmann, A. G. (1992). Understanding Automatic Generation Control. IEEE Trans. Power Syst. 7 (3), 1106–1122. doi:10.1109/59.207324

CrossRef Full Text | Google Scholar

Kumar, S., Saket, R. K., Dheer, D. K., Holm‐Nielsen, J. B., and Sanjeevikumar, P. (2020). “Reliability Enhancement of Electrical Power System Including Impacts of Renewable Energy Sources: a Comprehensive Review. IET Generation, Transm. Distribution 14 10, 1799–1815. doi:10.1049/iet-gtd.2019.1402

CrossRef Full Text | Google Scholar

Long, Y., Shi, M., Qian, Z., Meng, W., and Pan, G. (2018). “A Unified Approach for Multi-step Temporal-Difference Learning with Eligibility Traces in Reinforcement Learning,” in Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI-18), Stockholm, Sweden.

Google Scholar

Mukherjee, J. C., and Gupta, A. (2016). Distributed Charge Scheduling of Plug-In Electric Vehicles Using Inter-aggregator Collaboration. IEEE Trans. Smart Grid 8 (1), 331–341. doi:10.1109/TSG.2016.2515849

Google Scholar

Ray, G., Prasad, A. N., and Prasad, G. D. (1999). A New Approach to the Design of Robust Load-Frequency Controller for Large Scale Power Systems. Electric Power Syst. Res. 51 (1), 13–22. doi:10.1016/s0378-7796(98)00125-4

CrossRef Full Text | Google Scholar

Rummery, G. A., and Niranjan, M. (1994). On-line Q-Learning Using Connectionist Systems. Technical Report.

Saha, A. K., Chowdhury, S., and Chowdhury, S. P. (2008). “Modelling and Simulation of Microturbine in Islanded and Grid-Connected Mode as Distributed Energy Resource,” in Power & Energy Society General Meeting-conversion & Delivery of Electrical Energy in the Century, Pittsburgh, USA. doi:10.1109/pes.2008.4596532

CrossRef Full Text | Google Scholar

Seijen, H. V., Hasselt, H. V., Whiteson, S., and Wiering, M. (2009). “A Theoretical and Empirical Analysis of Expected Sarsa,” in 2009 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning, Nashville, USA.

Google Scholar

Sharma, G., Ibraheem, , , and Bansal, R. C. (2017). DFIG Based AGC of Power System Using Robust Methodology. Energ. Proced. 105, 590–595. doi:10.1016/j.egypro.2017.03.360

CrossRef Full Text | Google Scholar

Solanki, B. V., Raghurajan, A., Bhattacharya, K., and Canizares, C. A. (2017). Including Smart Loads for Optimal Demand Response in Integrated Energy Management Systems for Isolated Microgrids. IEEE Trans. Smart Grid 8 (4), 1739–1748. doi:10.1109/tsg.2015.2506152

CrossRef Full Text | Google Scholar

Suh, J., Yoon, D.-H., Cho, Y.-S., and Jang, G. (2017). Flexible Frequency Operation Strategy of Power System with High Renewable Penetration. IEEE Trans. Sustain. Energ. 8 (1), 192–199. doi:10.1109/tste.2016.2590939

CrossRef Full Text | Google Scholar

Sun, Q. Y., and Yang, L. X. (2019). From independence to Interconnection-A Review of AI Technology Applied in Energy Systems. CSEE J. Power Energ. Syst. 5 (1), 21–34. doi:10.17775/CSEEJPES.2018.00830

Google Scholar

Sun, L., Yao, F., and Chai, S. (2016). “Leader-following Consensus for High-Order Multi-Agent Systems with Measurement Noises,” in 2016 8th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China (IHMSC). doi:10.1109/ihmsc.2016.175

CrossRef Full Text | Google Scholar

Wang, T., O'Neill, D., and Kamath, H. (2015). Dynamic Control and Optimization of Distributed Energy Resources in a Microgrid. IEEE Trans. Smart Grid 6 (6), 2884–2894. doi:10.1109/tsg.2015.2430286

CrossRef Full Text | Google Scholar

Wang, S. C. (2020). Current Status of PV in China and its Future Forecast. CSEE J. Power Energ. Syst. 6 (1), 72–82. doi:10.17775/CSEEJPES.2019.03170

Google Scholar

Watkins, C. J. C. H., and Dayan, P. (1992). Q-learning. Machine Learn. 8 (3), 279–292. doi:10.1023/a:1022676722315

CrossRef Full Text | Google Scholar

Xi, L., Yu, T., Yang, B., and Zhang, X. (2015). A Novel Multi-Agent Decentralized Win or Learn Fast Policy hill-climbing with Eligibility Trace Algorithm for Smart Generation Control of Interconnected Complex Power Grids. Energ. Convers. Manag. 103 (10), 82–93. doi:10.1016/j.enconman.2015.06.030

CrossRef Full Text | Google Scholar

Xi, L., Yu, T., Yang, B., Zhang, X., and Qiu, X. (2016). A Wolf Pack Hunting Strategy Based Virtual Tribes Control for Automatic Generation Control of Smart Grid. Appl. Energ. 178, 198–211. doi:10.1016/j.apenergy.2016.06.041

CrossRef Full Text | Google Scholar

Xi, L., Chen, J., Huang, Y., Xu, Y., Liu, L., Zhou, Y., et al. (2018). Smart Generation Control Based on Multi-Agent Reinforcement Learning with the Idea of the Time Tunnel. Energy 153, 977–987. doi:10.1016/j.energy.2018.04.042

CrossRef Full Text | Google Scholar

Xi, L., Wu, J., Xu, Y., and Sun, H. (2020). Automatic Generation Control Based on Multiple Neural Networks with Actor-Critic Strategy. IEEE Trans. Neural Netw. Learn. Syst., 1–11. in press. doi:10.1109/TNNLS.2020.3006080

PubMed Abstract | CrossRef Full Text | Google Scholar

Xi, L., Yu, L., Xu, Y., Wang, S., and Chen, X. (2020). A Novel Multi-Agent DDQN-AD Method-Based Distributed Strategy for Automatic Generation Control of Integrated Energy Systems. IEEE Trans. Sustain. Energ. 11 (4), 2417–2426. doi:10.1109/tste.2019.2958361

CrossRef Full Text | Google Scholar

Xi, L., Zhang, L., Liu, J., Li, Y., Chen, X., Yang, L., et al. (2020). A Virtual Generation Ecosystem Control Strategy for Automatic Generation Control of Interconnected Microgrids. IEEE Access 8, 94165–94175. doi:10.1109/access.2020.2995614

CrossRef Full Text | Google Scholar

Xi, L., Zhou, L., Liu, L., et al. (2020). A Deep Reinforcement Learning Algorithm for the Power Order Optimization Allocation of AGC in Interconnected Power Grids. CSEE J. Power Energ. Syst. 6 (3), 712–723. doi:10.17775/CSEEJPES.2019.01840

Google Scholar

Xi, L., Zhou, L., Xu, Y., and Chen, X. (2021). A Multi-step Unified Reinforcement Learning Method for Automatic Generation Control in Multi-Area Interconnected Power Grid. IEEE Trans. Sustain. Energ. 12 (2), 1406–1415. doi:10.1109/tste.2020.3047137

CrossRef Full Text | Google Scholar

Xie, P., Li, Y. H., Liu, X. J., et al. (2016). Optimal PI/PID Controller Design of AGC Based on Social Learning Adaptive Bacteria Foraging Algorithm for Interconnected Power Grids. Proc. CSEE 36 (20), 5440–5448. doi:10.13334/j.0258-8013.pcsee.152424

Google Scholar

Xu, D., Zhou, B., Wu, Q., Chung, C. Y., Li, C., Huang, S., et al. (2020). Integrated Modelling and Enhanced Utilization of Power-To-Ammonia for High Renewable Penetrated Multi-Energy Systems. IEEE Trans. Power Syst. 35 (6), 4769–4780. doi:10.1109/tpwrs.2020.2989533

CrossRef Full Text | Google Scholar

Yamashita, K., and Taniguchi, T. (2016). Optimal Observer Design for Load-Frequency Control. Int. J. Electr. Power Energ. Syst. 8 (2), 93–100. doi:10.1016/0142-0615(86)90003-7

Google Scholar

Yan, W., Zhao, R., and Zhao, X. (2013). Review on Control Strategies in Automatic Generation Control. Power Syst. Prot. Control. 41 (8), 149–155.

Google Scholar

Yang, L., Zhang, Y., Zheng, Q., et al. (2019). Gradient Q(σ,λ): A Unified Algorithm with Function Approximation for Reinforcement Learning. arXiv, 02877.

Yin, L., Yu, T., Zhou, L., Huang, L., Zhang, X., and Zheng, B. (2017). Transm. Distribution 11 (9), 2305–2313. doi:10.1049/iet-gtd.2016.1734

CrossRef Full Text

Yu, T., and Yuan, Y. (2010). Optimal Control of Interconnected Power Grid CPS Based on R(λ) Learning of the Whole Process of Average Compensation Model. Automation Electric Power Syst. 34, 27–33.

Google Scholar

Yu, T., Wang, Y., Zhen, W., et al. (2011). Multi-step Backtrack Q-Learning Based Dynamic Optimal Algorithm for Auto Generation Control Order Dispatch. Control. Theor. Appl. 28 (1), 58–64.

Google Scholar

Yu, T., Zhou, B., Chan, K. W., and Lu, E. (2011). Stochastic Optimal CPS Relaxed Control Methodology for Interconnected Power Systems Using Q-Learning Method. J. Energ. Eng. 137 (3), 116–129. doi:10.1061/(asce)ey.1943-7897.0000017

CrossRef Full Text | Google Scholar

Zhang, X., and Yu, T. (2015). Virtual Generation Tribe Based Collaborative Consensus Algorithm for Dynamic Generation Dispatch of AGC in Interconnected Power Grids. Proc. CSEE 35 (15), 3750–3759. doi:10.13334/j.0258-8013.pcsee.2015.15.002

Google Scholar

Zhang, D., Han, X. Q., Han, X., and Deng, C. (2018). Review on the Research and Practice of Deep Learning and Reinforcement Learning in Smart Grids. Csee Jpes 4 (3), 362–370. doi:10.17775/cseejpes.2018.00520

CrossRef Full Text | Google Scholar

Zhang, X., Xu, Z., Yu, T., Yang, B., and Wang, H. (2020). Optimal Mileage Based AGC Dispatch of a GenCo. IEEE Trans. Power Syst. 35 (4), 2516–2526. doi:10.1109/tpwrs.2020.2966509

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar