A locational Marginal Price-Based Partition Optimal Economic Dispatch Model of Multi-Energy Systems

The large-scale penetration of renewable energy and deeply integrated multiple energy forms pose a major challenge for the accounting and allocation process of additional adjustment cost in multi-energy system and electricity market. The variable wind power and the operating status of multi-energy systems faced by the electricity market have driven researchers towards the decision of electricity spot market with complicated pricing mechanism. This paper presents a locational marginal price-based partition optimal economic dispatch model of multi-energy system with a high proportion of renewable energy. First, a model of the additional adjustment cost of multi-energy adjustable units to improve the power grid adjustment capacity is studied based on the power balance model of multi-energy conversion and storage. In the second, to improve the effectiveness of the ESM mechanism, an optimal economic dispatch model is established, with the goal of minimizing the additional adjustment cost of multi-energy adjustable units. Moreover, according to the characteristics of the model and the mechanism of locational marginal price-based economic dispatch, a solution method based on lagrangian relaxation is proposed. The incentive compatible locational marginal price is obtained. Finally, a simulation model of multi-energy systems based on IEEE 39-nodes power system and 7-nodes natural gas system is established. And the model is based on operating data of an actual grid with high proportion of renewable energy in Northeast China. The results of the examples show that the proposed method can effectively improve the efficiency and flexibility of multi-energy system. Another advantage of the proposed method is that the capabilities of the complementary multi-energy coordination can be promoted.

Introduction

The real-time transaction mechanism of multi-agent decision effort in multi-energy system (MES) facilitates the clean and efficient development of power grids, and has become a hot issue in the field of power system research (Jiang and Ai, 2017; Peng and Tao, 2018). In MES environment, a reasonable pricing mechanism (PM) can be used to implement market-oriented construction and optimization of the supply and demand balance of power commodities. Such mechanism can also be used for increasing the grid-connected capacity of renewable energy and other issues (PrudhvirajKiran and Pindoriya, 2020; Fang and Cui, 2020). At present, the traditional way of pricing mechanism mainly used in electricity spot market (ESM) is zonal marginal price (ZMP) and locational marginal price (LMP) (Jovanovic et al., 2017; Gong et al., 2018; Fang et al., 2020b). A key challenge in designing efficient ESM is the flexible price signals and reduce overall market operating costs in a complex power network. Therefore, the LMP is the pricing method adopted by most electricity spot markets in most countries or regions, which can provide the transmission line capacity constraints and the ability to inhibit branch blocking.

With the continuous expansion of the multi-energy system and electricity spot market, constructing a sophisticated LMP has become a key research topic in the future energy system. In order to study the effect mechanism of power network topology changes on LMP, (Choi and Xie. 2017) studied a LMP model based on grid topology state evaluation. And a simple analytical congestion price equation is proposed, which can improve the LMP model rationality and calculation quality. Morstyn et al. (2020) proposed a distributed energy bilateral trading strategy based on peer-to-peer (P2P) energy trading and probabilistic locational marginal pricing, which can effectively improve the grid-connected capacity of renewable energy and system flexibility. In order to increase the solution accuracy and efficiency of the LMP, (Hajiabadi and Samadi. 2019) proposed a nodal marginal price solution strategy based on unit-based LMP_S index; the test results show that the strategy can improve the incremental profit of unit. Faqiry et al. (2020) proposed a day-ahead electricity market (EM) clearing model based on distributed LMP, and a transactive day-ahead EM model under different renewable energy confidence intervals was constructed to solve the problem of line congestion and renewable energy uncertainty; the results show that the proposed method can reduce the impact of random events such as peak load and renewable energy fluctuations on the grid. Vaskovskaya et al. (2018) proposed a LMP model based on price-bonding factor that effectively decompose the LMP model and improve the rationality of PM for transmission capacity and voltage. Aiming at investigating spatiotemporal correlations among various uncertainty sources, (Fang et al. (2020a) established a distributionally-robust chance constrained multi-interval optimal power flow model, that can establish LMP with uncertainty. Similarly, (Fang et al., 2019) proposed an EM clearing model that takes into account economy and reliability for the uncertainty of wind power and load; the simulation results show that the proposed method can fully reflect the changes in system cost caused by wind power and load uncertainty, and improve the effectiveness of the PM. Zheng et al. (2020) proposed a LMP forecasting model considering congestion and network loss for short-term LMP forecasting with high accuracy and robustness. Considering the problems of energy balance, network loss, and voltage stability in the EM, (Hanif et al., 2019) proposed a new distribution locational marginal price model, which can effectively improve the optimal allocation of flexible resources in the electricity market. The above studies have made in-depth studies on various aspects of the ESM, such as clearing methods, price mechanisms, and flexible distribution.

In recent years, the scale of renewable energy has continued to expand. Hence, the increasing multi-energy conversion and storage have been connected to the grid, resulting in the complexity of the pricing mechanism of multi-energy coordination (Teng et al., 2019a; Teng et al., 2019b; Zhang et al., 2021). Multi-energy system has advanced energy conversion technology and information transmission technology (Gao et al., 2020; Teng et al., 2019c; Yang et al., 2020). Additionally, during the operation of the traditional ESM, only the adjustment cost of conventional generation in the power system is considered, and the coordination effect of multiple energy is ignored. The lack of rationality of the cost-sharing method restricts the development of the multi-energy coordinated ESM. Therefore, multi-energy coordinated ESM clearing model with a growing importance in the ESM for PM is the best method, which can enhance the flexibility and rationality of price signals in ESM.

Based on the above analysis, multi-energy adjustable units with obvious differences of adjustment characteristics in time scale and capacity scale should be constructed. LMP model calculation efficiency should be improved. With that as motivation, a locational marginal price-based partition optimal economic dispatch model of multi-energy system is proposed in the article, which including multi-energy adjustable units, the process of lagrangian relaxation and locational price. Based on the obtained results, the contributions of this paper are as following, briefly.

(1) The characteristics of multi-energy conversion and storage are studied. Based on this, the mechanism of the additional adjustment cost of the multi-energy adjustable units considering the balance of supply and demand is studied. An additional adjustment cost allocation mechanism is established in multi-energy coordinated electricity spot market environment. It provides a theoretical basis for calculating the adjustment additional cost of electricity spot market in grid with multi-energy coordinated.

(2) An optimal economic dispatch model of multi-energy system based on the additional adjustment costs is proposed. The objective function is to minimize the operating costs and adjustment costs of multi-energy adjustable units. The constraints include the power network constraints, gas network constraints, and multi-energy adjustable equipment constraints. This model plays an important role for pricing mechanism of multi-energy systems coordinated dispatch.

(3) Lagrangian relaxation is applied as optimized algorithm to solve the problem of dispatch. Based on the results it is possible to accomplish a safe, efficient and flexible multi-energy system. Another advantage of the proposed method is that decrease the run time of the proposed problem.

This paper is structured as following. Multi-Energy System and Additional Adjustment Cost illustrates a systems model with multi-energy conversion and storage and additional adjustment cost. Partition Optimal Economic Dispatch Model of Multi-Energy System proposes a partition optimal economic dispatch model of multi-energy system. Solving Algorithm presents a solution method based on lagrangian relaxation. Case Study verifies the performance of the proposed model in simulation. Conclusion presents the conclusion.

Multi-Energy System and Additional Adjustment Cost

The Structure of Multi-Energy System

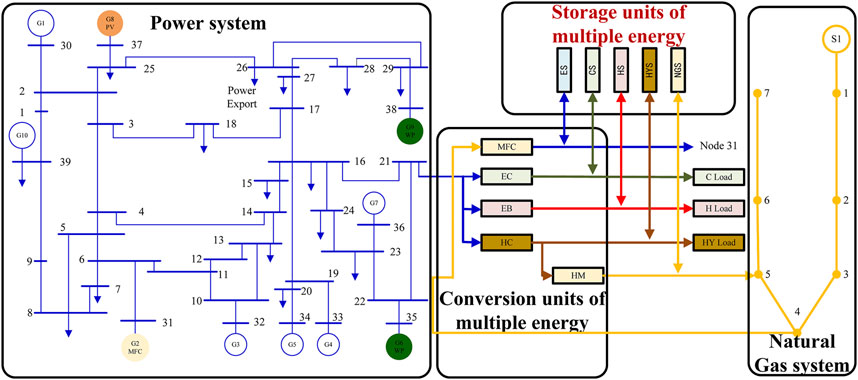
The structure of multi-energy system is shown in Figure 1, including wind power, photovoltaic, natural gas sources, multi-energy adjustable units (MEAUs) and multi-energy loads. Among them, MEAUs include conventional generation, multi-energy conversion units (such as electric boiler, electric cooling, power to hydrogen, hydrogen methanation and methane fuel cell) and multi-energy storage units (such as electricity storage, cold storage, heat storage, hydrogen storage and natural gas storage). Electric and natural gas energy from renewable energy and natural gas sources are converted and stored before being delivered to user terminals. The multi-energy system has the characteristics of high efficiency, cleanliness and flexibility, compared with the traditional independent energy supply system.

FIGURE 1

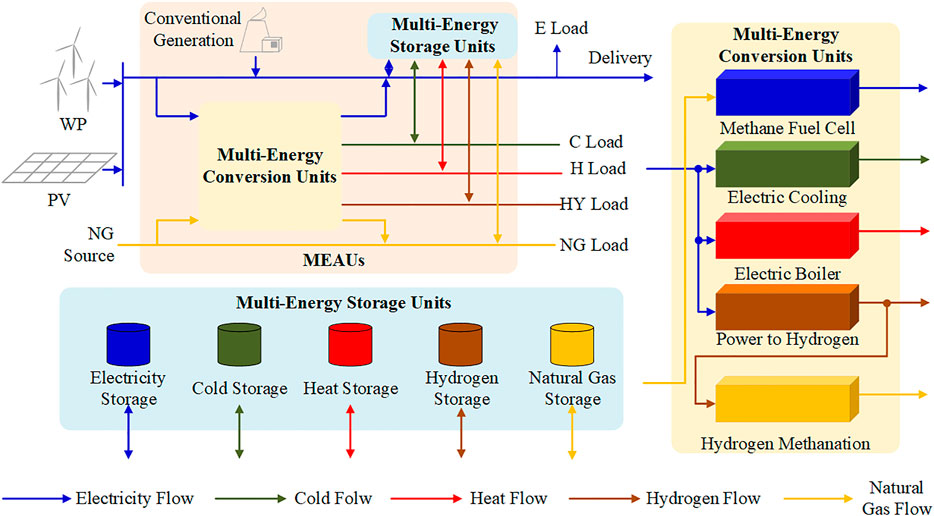
FIGURE 1. The structure of a grid with high proportion of renewable energy and multi-energy conversion and storage.

The Model of Multi-Energy Conversion Units

The model of multi-energy conversion units is:

$P_{sw,t}^{out}={\psi }_{sw,t}{\eta }_{sw}{P}_{sw,t}^{in}(1)$

$P_{sw,t}^{out}={\left[P_{sw,e,t}^{out},P_{sw,h,t}^{out},P_{sw,c,t}^{out},P_{sw,hy,t}^{out},P_{sw,ng,t}^{out}\right]}^T(2)$

${\psi }_{sw,t}=diag\left(1,{\alpha }_{1,t},{\alpha }_{2,t},{\alpha }_{3,t}\left(1-{\beta }_t\right),{\alpha }_{3,t}{\beta }_t\right)(3)$

${\eta }_{sw}=\left[\begin{array}{cc}0& {\eta }_{MFC}\\ {\eta }_{EB}& 0\\ {\eta }_{EC}& 0\\ {\eta }_{HC}& 0\\ {\eta }_{HC}{\eta }_{HM}& 0\end{array}\right](4)$

$P_{sw,t}^{in}={\left[P_{sw,e,t}^{in},P_{sw,ng,t}^{in}\right]}^T(5)$

where $\hspace{0.17em}{P}_{sw,t}^{out}$ is output power vector of multi-energy conversion units. ${\psi }_{sw,t}$ is partition coefficient vector. $P_{sw,t}^{in}$ is input power vector. $\hspace{0.17em}{\eta }_{sw}$ is energy conversion efficiency vector. Specifically, $P_{sw,e,t}^{out}$, $P_{sw,h,t}^{out}$, $P_{sw,c,t}^{out}$, $P_{sw,hy,t}^{out}$, and $P_{sw,ng,t}^{out}$ are output power of electricity, heat, cold, hydrogen and natural gas respectively. $\hspace{0.17em}{P}_{sw,e,t}^{in}$ and $P_{sw,ng,t}^{in}$ are input power of electricity and natural gas respectively.$\hspace{0.17em}{\eta }_{EB}$, ${\eta }_{EC}$, ${\eta }_{HC}$, ${\eta }_{HM}$, and ${\eta }_{MFC}$ are conversion efficiency of electric boiler, electric cooling, power to hydrogen, hydrogen methanation and methane fuel cell respectively.${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and $\beta$are partition coefficient of electric boiler, electric cooling, power to hydrogen and hydrogen methanation respectively.

The Model of Multi-Energy Storage Units

The model of multi-energy storage units is:

$S_t=S_{t-1}+{\eta }^{cha}{E}^{-1}{P}_t^{ch}\Delta t-{\eta }^{dis-1}{E}^{-1}{P}_t^{dis}\Delta t(6)$

$S_t={\left[S_{ES,t},S_{HS,t},S_{CS,t},S_{HYS,t},S_{NGS,t}\right]}^T(7)$

${\eta }^{cha}=diag\left({\eta }_{ES}^{cha},{\eta }_{HS}^{cha},{\eta }_{CS}^{cha},{\eta }_{HYS}^{cha},{\eta }_{NGS}^{cha}\right)(8)$

${\eta }^{cha}=diag\left({\eta }_{ES}^{dis},{\eta }_{HS}^{dis},{\eta }_{CS}^{dis},{\eta }_{HYS}^{dis},{\eta }_{NGS}^{dis}\right)(9)$

$E=diag\left(E_{ES},E_{HS},E_{CS},E_{HYS},E_{NGS}\right)(10)$

$P_t^{ch}={\left[P_{ES,t}^{ch},P_{HS,t}^{ch},P_{CS,t}^{ch},P_{HYS,t}^{ch},P_{NGS,t}^{ch}\right]}^T(11)$

$P_t^{dis}={\left[P_{ES,t}^{dis},P_{HS,t}^{dis},P_{CS,t}^{dis},P_{HYS,t}^{dis},P_{NGS,t}^{dis}\right]}^T(12)$

where $S_t$ is state of multi-energy vector. ${\eta }^{cha}$ and ${\eta }^{dis}$ are multi-energy charging and discharging efficiency vector. $E$ is multi-energy capacity vector. $P_t^{ch}$ and $P_t^{dis}$ are multi-energy charging and discharging power vector. Specifically, $S_{ES,t}$, $S_{HS,t}$, $S_{CS,t}$, $S_{HYS,t}$ and $S_{NGS,t}$ are state of electricity storage, heat storage, cold storage, hydrogen storage and natural gas storage respectively.${\eta }_{ES}^{cha}$, ${\eta }_{HS}^{cha}$, ${\eta }_{CS}^{cha}$, ${\eta }_{HYS}^{cha}$ and ${\eta }_{NGS}^{cha}$ are energy charging efficiency of electricity storage, heat storage, cold storage, hydrogen storage and natural gas storage respectively.${\eta }_{ES}^{dis}$, ${\eta }_{HS}^{dis}$, ${\eta }_{CS}^{dis}$, ${\eta }_{HYS}^{dis}$ and ${\eta }_{NGS}^{dis}$ are energy discharging efficiency of electricity storage, heat storage, cold storage, hydrogen storage and natural gas storage respectively.$E_{ES}$, $E_{HS}$, $E_{CS}$, $E_{HYS}$ and $E_{NGS}$ are energy capacity of electricity storage, heat storage, cold storage, hydrogen storage and natural gas storage respectively.$P_{ES,t}^{ch}$, $P_{HS,t}^{ch}$, $P_{CS,t}^{ch}$, $P_{HYS,t}^{ch}$ and $P_{NGS,t}^{ch}$ are energy charging power of electricity storage, heat storage, cold storage, hydrogen storage and natural gas storage respectively.$P_{ES,t}^{dis}$, $P_{HS,t}^{dis}$, $P_{CS,t}^{dis}$, $P_{HYS,t}^{dis}$ and $P_{NGS,t}^{dis}$ are energy discharging power of electricity storage, heat storage, cold storage, hydrogen storage and natural gas storage respectively.

The Model of Additional Adjustment Cost

The coordinated operation of multi-energy coordinated grid with a high proportion of renewable energy needs to meet multi-energy power balance. On the one hand, it satisfies the regional multi-energy load demand and the power transmission demand; on the other hand, the multi-energy coordinated adjustment of the reserve capacity change caused by the uncertainty of renewable energy is to ensure the stable operation of the regional power grid. Therefore, the additional adjustment cost refers to the adjustment cost of MEAUs under the uncertainty of wind power and photovoltaic in multi-energy coordinated ESM. Specifically, the uncertainty of wind power and photovoltaic will lead to system adjustment requirements.

Based on the uncertainty fluctuation coefficient of wind power, the increase and decrease power of wind power are:

$P_{wp,t}^{uR}=\text{max}\left\{0,P_{wp,t}-P_{wp,t-1}\right\}{\alpha }_{wp,t}(13)$

$P_{wp,t}^{dR}=\text{max}\left\{0,P_{wp,t-1}-P_{wp,t}\right\}{\alpha }_{wp,t}(14)$

where $P_{wp,t}^{uR}$ and $P_{wp,t}^{dR}$ are increase and decrease power of wind power respectively. $P_{wp,t}$ is actual value of wind power output power. ${\alpha }_{wp,t}$ is uncertainty fluctuation coefficient of wind power, which can be calculated by statistical methods. In particular, the error rate under a certain confidence interval can be used as the value of the wind power uncertainty fluctuation coefficient, which is calculated by calculating the error rate between the actual value of wind power output and the predicted value at a certain moment.

The increase and decrease power of PV are:

$P_{pv,t}^{uR}=\text{max}\left\{0,P_{pv,t}-P_{pv,t-1}\right\}{\alpha }_{pv,t}(15)$

$P_{pv,t}^{dR}=\text{max}\left\{0,P_{pv,t-1}-P_{pv,t}\right\}{\alpha }_{pv,t}(16)$

where $P_{pv,t}^{uR}$ and $P_{pv,t}^{dR}$ are increase and decrease power of photovoltaic respectively. $P_{pv,t}$ is actual value of photovoltaic output power. ${\alpha }_{pv,t}$ is uncertainty fluctuation coefficient of photovoltaic.

The dispatch costs of MEAUs include operating cost and additional adjustment cost.

The dispatch costs of conventional generation are:

$\begin{array}{c}{C}_{cpu,i,t}=c_{cpu,i}^{op}{P}_{cpu,i,t}{U}_{cpu,i,t}^{op}\Delta t+c_{cpu,i}^{on}{U}_{cpu,i,t}^{on}\\ +c_{cpu,i}^{uR}{P}_{cpu,i,t}^{uR}+c_{cpu,i}^{dR}{P}_{cpu,i,t}^{dR}\end{array}(17)$

where $C_{cpu,i,t}$ is dispatch cost of conventional generation $i$at time$t$.$c_{cpu,i}^{op}$, $c_{cpu,i}^{on}$, $c_{cpu,i}^{uR}$ and $c_{cpu,i}^{dR}$ are cost coefficients of operating, start-up, upgrade reserve and downgrade reserve respectively. $P_{cpu,i,t}$ is output power of conventional generation. $U_{cpu,i,t}^{op}$ and $U_{cpu,i,t}^{on}$ are state value of operating and start-up respectively with 0-1. $P_{cpu,i,t}^{uR}$ and $P_{cpu,i,t}^{dR}$ are upgrade reserve power and downgrade reserve power respectively. $\Delta t$ is time interval.

The dispatch costs of multi-energy conversion units are:

$C_{sw,t}=c_{sw}{P}_{sw,t}^{out}\Delta t+c_{sw}^{uR}{P}_{sw,t}^{uR}+c_{sw}^{dR}{P}_{sw,t}^{dR}(18)$

$c_{sw}=\left[c_{MFC},c_{EB},c_{EC},c_{HC},c_{HM}\right](19)$

$c_{sw}^{uR}=\left[c_{MFC}^{uR},c_{EB}^{uR},c_{EC}^{uR},c_{HC}^{uR},c_{HM}^{uR}\right](20)$

$c_{sw}^{dR}=\left[c_{MFC}^{dR},c_{EB}^{dR},c_{EC}^{dR},c_{HC}^{dR},c_{HM}^{dR}\right](21)$

where $C_{sw,t}$ is dispatch cost of multi-energy conversion unit.$c_{sw}$, $c_{sw}^{uR}$ and $c_{sw}^{dR}$ are cost coefficients of operating, upgrade reserve and downgrade reserve respectively. $P_{sw,t}^{uR}$ and $P_{sw,t}^{dR}$ are upgrade reserve power vector and downgrade reserve power vector respectively.

The dispatch costs of multi-energy storage units are:

$C_{s,t}=c_s\left(P_t^{ch}+P_t^{dis}\right)\Delta t+c_s^{uR}{P}_t^{dis\_uR}+c_s^{dR}{P}_t^{ch\_dR}(22)$

$c_s=\left[c_{ES},c_{HS},c_{CS},c_{HYS},c_{NGS}\right](23)$

$c_s^{uR}=\left[c_{ES}^{uR},c_{HS}^{uR},c_{CS}^{uR},c_{HYS}^{uR},c_{NGS}^{uR}\right](24)$

$c_s^{dR}=\left[c_{ES}^{dR},c_{HS}^{dR},c_{CS}^{dR},c_{HYS}^{dR},c_{NGS}^{dR}\right](25)$

where $C_{s,t}$ is dispatch cost of multi-energy storage unit.$c_s$, $c_s^{uR}$ and $c_s^{dR}$ are cost coefficients of operating, upgrade reserve and downgrade reserve respectively. $P_t^{dis\_uR}$ and $P_t^{ch\_dR}$ are upgrade reserve power vector and downgrade reserve power vector respectively.

Partition Optimal Economic Dispatch Model of Multi-Energy System

The essence of the partition optimal economic dispatch model is to build a day-ahead dispatch model with an efficient solution for the multi-energy systems. The model can determine the output and reserve of MEAUs, and can also provide the required price signal for the electricity spot market.

Objective Function

The objective function is as follow:

$\begin{array}{c}min{C}_{MC}\left({\psi }_{sw},P_{sw}^{in},P^{ch},P^{dis},P_{cpu},U_{cpu}^{op},U_{cpu}^{on},\left\{P^{uR}\right\},\left\{P^{dR}\right\}\right)\\ ={\displaystyle \sum _{t\in T}\left({\displaystyle {\sum }_{i\in I}{C}_{cpu,i,t}+C_{sw,t}+C_{s,t}+c_{wp,t}^{cur}{P}_{wp,t}^{cur}+c_{pv,t}^{cur}{P}_{pv,t}^{cur}}+{\displaystyle {\sum }_{m\in M}{c}_{load,m,t}^{cut}{P}_{load,m,t}^{cut}}\right)}\end{array}(26)$

where $C_{MC}$ is dispatch cost function. It is a function of output power, partition coefficient, upgrade reserve power, downgrade reserve power and equipment condition of MEAUs as decision variables. $C_{cpu,i,t}$ is dispatch cost of conventional generation. $C_{sw,t}$ is dispatch cost of multi-energy conversion unit. $C_{s,t}$ is dispatch cost of multi-energy storage unit. $c_{wp,t}^{cur}$ and $c_{pv,t}^{cur}$ are penalty cost coefficient of wind curtailment and photovoltaic curtailment respectively. $P_{wp,t}^{cur}$ and $P_{pv,t}^{cur}$ are power of wind curtailment and photovoltaic curtailment respectively. $c_{load,m,t}^{cut}$ is penalty cost coefficient of load shedding. $P_{load,m,t}^{cut}$ is power of load shedding.

Constraints

Power Balance Constraints

Power balance constraints refer to the multi-energy power balance, including electricity, heat, cold, hydrogen, and natural gas.

$\begin{array}{c}{P}_{wp,t}+P_{pv,t}+{\displaystyle {\sum }_{i\in I}{P}_{cpu,i,t}+P_{sw,e,t}^{out}+\left(P_{ES,t}^{dis}-P_{ES,t}^{ch}\right)}\\ ={\displaystyle {\sum }_{j\in J}{P}_{load,e,j,t}+P_{load,e,t}^{Tran}+P_{grid,e,t}}\end{array}(27)$

$P_{sw,h,t}^{out}+\left(P_{HS,t}^{dis}-P_{HS,t}^{ch}\right)=P_{load,h,t}(28)$

$P_{sw,c,t}^{out}+\left(P_{CS,t}^{dis}-P_{CS,t}^{ch}\right)=P_{load,c,t}(29)$

$P_{sw,hy,t}^{out}+\left(P_{HYS,t}^{dis}-P_{HYS,t}^{ch}\right)=P_{load,hy,t}(30)$

$P_{NGS,t}+P_{sw,ng,t}^{out}+\left(P_{NGS,t}^{dis}-P_{NGS,t}^{ch}\right)=P_{load,ng,t}(31)$

where, $P_{load,e,t}^{Tran}$ is electric power delivery. $P_{load,e,j,t}$ is electricity power in node$j$.$P_{load,h,t}$, $P_{load,c,t}$, $P_{load,hy,t}$ and $P_{load,ng,t}$ are heat load, cold load, hydrogen load and natural gas load respectively. $P_{grid,e,t}$ is network loss. $P_{NGS,t}$ is natural gas power of source.

Transmission Capacity Constraints

Transmission capacity constraints refer to the transmission capacity constraints in power and natural gas networks. Since active power is the main commodity traded in the ESM, the power network transmission capacity is calculated using the power transmission distribution factor. According to the laws of fluid mechanics, the calculation of natural gas network transmission capacity should be based on pipeline flow and pressure equations.

$\begin{array}{l}{h}_{l,t}=H_{l-wp}^{wp}{P}_{wp,t}+H_{l-pv}^{pv}{P}_{pv,t}+{\displaystyle {\sum }_{i\in I}{H}_{l-i}^{cpu}{P}_{cpu,i,t}+H_{l-sw}^{sw}{P}_{sw,e,t}^{out}+H_{l-ES}^{ES}\hspace{0.17em}\left(P_{ES,t}^{dis}-P_{ES,t}^{ch}\right)}\\ \hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}-{\displaystyle {\sum }_{j\in J}{H}_{l-load,e}^{load}{P}_{load,e,j,t}-H_{l-load,e}^{Tran}{P}_{load,e,t}^{Tran}}\end{array}(32)$

$h_l^{\text{min}}\le h_{l,t}\le h_l^{\text{max}}(33)$

where $h_l$ is flow of branch $l$ in power networks. $H$ is power transfer distribution factor of wind power, photovoltaic, conventional generation, multi-energy conversion units, multi-energy storage units and electricity load respectively. $h_l^{\text{max}}$ and $h_l^{\text{min}}$ is upper and lower limits of transmission capacity respectively.

$Q_{pq,t}=\omega \sqrt{\frac{\left|p_{p,t}-p_{q,t}\right|D_{pq}^5}{f_{pq}{L}_{pq}\rho }}(34)$

$Q_{pq,t}=\frac{P_{NGS,p,t}+P_{NGS,q,t}}{2HH{V}_{GAS}}(35)$

$Q_{pq}^{\text{min}}\le Q_{pq,t}\le Q_{pq}^{\text{max}}d(36)$

$p^{\text{min}}\le p_{p,t}\le p^{\text{max}}(37)$

$p^{\text{min}}\le p_{q,t}\le p^{\text{max}}(38)$

where $Q_{pq}$ is flow rate of pipeline $pq$ in natural gas networks. $\omega$ is natural gas constant. $p_{p,t}$ and $p_{q,t}$ are pressure of node $p$ and node $q$ respectively. $D_{pq}$ is diameter of pipeline. $f_{pq}$ is coefficient of friction of pipeline. $L_{pq}$ is length of pipeline. $\rho$ is proportion of natural gas. $P_{NGS,p,t}$ is natural gas power of node$q$. $HH{V}_{GAS}$ is high heating value of natural gas. $Q_{pq}^{\text{max}}$ and $Q_{pq}^{\text{min}}$ are upper and lower limits of flow rate of pipeline respectively. $p^{\text{max}}$ and $p^{\text{min}}$ are upper and lower limits of pressure of node respectively.

Reserve constraints

The reserve constraints refer to the upgrade reserve and downgrade reserve under certain adjustment requirements causing by the uncertainty of renewable energy.

${\displaystyle {\sum }_{i\in I}\left(P_{cpu,i,t}^{uR}\right)+P_{sw,e,t}^{uR}+P_{ES,t}^{dis\_uR}\ge P_{wp,t}^{uR}+P_{pv,t}^{uR}}(39)$

${\displaystyle {\sum }_{i\in I}\left(P_{cpu,i,t}^{dR}\right)+P_{sw,e,t}^{dR}+P_{ES,t}^{dis\_dR}\ge P_{wp,t}^{dR}+P_{pv,t}^{dR}}(40)$

Conventional generation constraints

Conventional generation constraints include upper and lower limits of output, ramping and start-up.

$P_{cpu}^{\text{min}}{U}_{cpu,i,t}^{op}\le P_{cpu,i,t}\le P_{cpu}^{\text{max}}{U}_{cpu,i,t}^{op}(41)$

$P_{cpu,i,t}^{uR}\le P_{cpu}^{uR\_\text{max}}{U}_{cpu,i,t}^{on}(42)$

$P_{cpu,i,t}^{dR}\le P_{cpu}^{dR\_\text{max}}{U}_{cpu,i,t}^{on}(43)$

$\left(U_{cpu,i,t}^{on}-U_{cpu,i,t-1}^{on}\right)\left(T_{i,t}^{on}-T_i^{on}\right)\ge 0(44)$

$\left(U_{cpu,i,t-1}^{on}-U_{cpu,i,t}^{on}\right)\left(T_{i,t}^{off}-T_i^{off}\right)\ge 0(45)$

where $P_{cpu}^{\text{max}}$ and $P_{cpu}^{\text{min}}$ are upper and lower limits of output of conventional generation respectively. $P_{cpu}^{uR\_\text{max}}$ and $P_{cpu}^{dR\_\text{max}}$ are maximum value of upgrade reserve power and downgrade reserve power respectively. $T_{i,t}^{on}$ and $T_i^{on}$ are limits of run time and minimum downtime respectively. $T_{i,t}^{off}$ and $T_i^{off}$ are limits of downtime and minimum startup time respectively.

Multi-Energy Conversion Unit Constraints

Multi-energy conversion unit constraints refer to the power upper and lower limits of electric boiler, electric cooling, power to hydrogen, hydrogen methanation and methane fuel cell.

$P_{sw}^{\text{min}}\le P_{sw,t}^{out}+P_{sw,t}^{uR}+P_{sw,t}^{dR}\le P_{sw}^{\text{max}}(46)$

$P_{sw,t}^{\text{max}}={\left[P_{MFC}^{\text{max}},P_{EB}^{\text{max}},P_{EC}^{\text{m}ax},P_{HC}^{\text{m}ax},P_{HM}^{\text{max}}\right]}^T(47)$

$P_{sw,t}^{\text{min}}={\left[P_{MFC}^{\text{min}},P_{EB}^{\text{min}},P_{EC}^{\text{min}},P_{HC}^{\text{min}},P_{HM}^{\text{min}}\right]}^T(48)$

where $P_{MFC}^{\text{max}}$ and $P_{MFC}^{\text{min}}$ are power upper and lower limits of methane fuel cell respectively. $P_{EB}^{\text{max}}$ and $P_{EB}^{\text{min}}$ are power upper and lower limits of electric boiler respectively. $P_{EC}^{\text{m}ax}$ and $P_{EC}^{\text{min}}$ are power upper and lower limits of electric cooling respectively. $P_{HC}^{\text{m}ax}$ and $P_{HC}^{\text{min}}$ are power upper and lower limits of power to hydrogen respectively. $P_{MFC}^{\text{max}}$ and $P_{MFC}^{\text{min}}$ are power upper and lower limits of hydrogen methanation respectively.

Multi-Energy Storage Unit Constraints

Multi-energy storage unit constraints refer to the power and capacity limits of electricity storage, cold storage, heat storage, hydrogen storage and natural gas storage.

$S^{\text{min}}\le S_t\le S^{\max }(49)$

$P^{ch\_\text{min}}\le P_t^{ch}+P_t^{ch\_dR}\le P^{ch\_\text{max}}(50)$

$P^{dis\_\text{min}}\le P_t^{dis}+P_t^{dis\_uR}\le P^{dis\_\text{max}}(51)$

where $S^{\max }$ and $S^{\min }$ are capacity vector upper and lower limits of multi-energy storage unit respectively. $P^{ch\_\text{max}}$ and $P^{ch\_\text{min}}$ are energy charging vector upper and lower limits respectively. $P^{dis\_\max }$ and $P^{dis\_\min }$ are energy discharging vector upper and lower limits respectively.

Solving Algorithm

Lagrangian relaxation algorithm solution method is proposed, taking into account the characteristics of optimal economic dispatch model of multi-energy system. The approach carries out the optimization of the dispatch model by using multiple iterations to reduce the dual gap between the objective function and the original function. At the same time, the incentive-compatible LMP is calculated. The principle is to calculate the partial derivative of the optimal objective cost function to different nodes, and use the lagrangian multiplier in the solution process to calculate the price.

Lagrangian relaxation problem rewritten by the original objective function is:

$LR:\hspace{0.5em}L=\text{min}{Z}_{LR}(52)$

The relaxation problem can be decomposed into 4 subproblems:

$\text{min}{Z}_{LR}=\text{min}{Z}_{ZR}^1+\text{min}{Z}_{ZR}^2+\text{min}{Z}_{ZR}^3+\text{min}{Z}_{ZR}^4(53)$

where

$\begin{array}{l}{Z}_{ZR}^1=\\ {\displaystyle \sum _{t\in T}\left({\displaystyle \sum _{i\in I}\begin{array}{c}{c}_{cpu,i}^{op}{P}_{cpu,i,t}{U}_{cpu,i,t}^{op}+c_{cpu,i}^{on}{U}_{cpu,i,t}^{on}\\ +c_{cpu,i}^{uR}{P}_{cpu,i,t}^{uR}+c_{cpu,i}^{dR}{P}_{cpu,i,t}^{dR}\end{array}}\right)}\\ -{\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in I}{\lambda }_t{P}_{cpu,i,t}}}-{\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in I}{\mu }_{1,t}{H}_{l-i}^{cpu}{P}_{cpu,i,t}}}\\ -{\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in I}{\gamma }_{1,t}{P}_{cpu,i,t}^{uR}}}-{\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in I}{\gamma }_{2,t}{P}_{cpu,i,t}^{dR}}}\\ +{\displaystyle \sum _{t\in T}{\nu }_{1,t}\left(P_{cpu,i,t}-P_{cpu}^{\text{max}}{U}_{cpu,i,t}^{op}\right)}\\ +{\displaystyle \sum _{t\in T}{\nu }_{2,t}\left(P_{cpu}^{\text{min}}{U}_{cpu,i,t}^{op}-P_{cpu,i,t}\right)}\\ +{\displaystyle \sum _{t\in T}{\nu }_{3,t}\left(P_{cpu,i,t}^{uR}-P_{cpu}^{uR\_\text{max}}{U}_{cpu,i,t}^{on}\right)}\\ +{\displaystyle \sum _{t\in T}{\nu }_{4,t}\left(P_{cpu,i,t}^{dR}-P_{cpu}^{dR\_\text{max}}{U}_{cpu,i,t}^{on}\right)}\end{array}$

$\begin{array}{c}{Z}_{ZR}^2=\\ {\displaystyle \sum _{t\in T}\left(c_{sw}{P}_{sw,t}^{out}\Delta t+c_{sw}^{uR}{P}_{sw,t}^{uR}+c_{sw}^{dR}{P}_{sw,t}^{dR}\right)}\\ -{\displaystyle \sum _{t\in T}{\lambda }_t{P}_{sw,e,t}^{out}}-{\displaystyle \sum _{t\in T}{\mu }_{1,t}{H}_{l-sw}^{sw}{P}_{sw,e,t}^{out}}\\ -{\displaystyle \sum _{t\in T}{\gamma }_{1,t}{P}_{sw,e,t}^{uR}}-{\displaystyle \sum _{t\in T}{\gamma }_{2,t}{P}_{sw,e,t}^{dR}}\\ +{\displaystyle \sum _{t\in T}{\pi }_{1,t}\left\{\left(P_{sw,e,t}^{out}+P_{sw,e,t}^{uR}+P_{sw,e,t}^{dR}\right)-P_{sw,e}^{\text{max}}\right\}}\\ +{\displaystyle \sum _{t\in T}{\pi }_{2,t}\left\{P_{sw,e}^{\text{min}}-\left(P_{sw,e,t}^{out}+P_{sw,e,t}^{uR}+P_{sw,e,t}^{dR}\right)\right\}}\end{array}$

$\begin{array}{c}{Z}_{ZR}^3=\\ {\displaystyle \sum _{t\in T}\left(c_s\left(P_t^{ch}+P_t^{dis}\right)\Delta t+c_s^{uR}{P}_t^{dis\_uR}+c_s^{dR}{P}_t^{ch\_dR}\right)}\\ -{\displaystyle \sum _{t\in T}{\lambda }_t\left(P_{ES,t}^{dis}-P_{ES,t}^{ch}\right)}-{\displaystyle \sum _{t\in T}{\mu }_{1,t}{H}_{l-ES}^{ES}\left(P_{ES,t}^{dis}-P_{ES,t}^{ch}\right)}\\ -{\displaystyle \sum _{t\in T}{\gamma }_{1,t}{P}_{ES,t}^{dis\_uR}}-{\displaystyle \sum _{t\in T}{\gamma }_{2,t}{P}_{ES,t}^{dis\_dR}}\\ +{\displaystyle \sum _{t\in T}{\varpi }_{1,t}\left\{\left(P_{ES,t}^{ch}+P_{ES,t}^{ch\_dR}\right)-P_{ES}^{ch\_\text{max}}\right\}}\\ +{\displaystyle \sum _{t\in T}{\varpi }_{2,t}\left\{P_{ES}^{ch\_\text{min}}-\left(P_{ES,t}^{ch}+P_{ES,t}^{ch\_dR}\right)\right\}}\\ +{\displaystyle \sum _{t\in T}{\sigma }_{1,t}\left\{\left(P_{ES,t}^{dis}+P_{ES,t}^{dis\_dR}\right)-P_{ES}^{dis\_\text{max}}\right\}}\\ +{\displaystyle \sum _{t\in T}{\sigma }_{2,t}\left\{P_{ES}^{dis\_\text{min}}-\left(P_{ES,t}^{dis}+P_{ES,t}^{dis\_dR}\right)\right\}}\end{array}$

$\begin{array}{c}{Z}_{ZR}^4=\\ {\displaystyle \sum _{t\in T}\left(c_{wp,t}^{cur}{P}_{wp,t}^{cur}+c_{pv,t}^{cur}{P}_{pv,t}^{cur}+{\displaystyle \sum }_{m\in M}{c}_{load,m,t}^{cut}{P}_{load,m,t}^{cut}\right)}\\ +{\displaystyle \sum _{t\in T}{\lambda }_t\left\{{\displaystyle \sum _{j\in J}{P}_{load,e,j,t}+P_{load,e,t}^{Tran}+P_{grid,e,t}-\left(P_{wp,t}+P_{pv,t}\right)}\right\}}\\ +{\displaystyle \sum _{t\in T}{\mu }_{1,t}\left\{h_{l,t}-\left[\begin{array}{l}{H}_{l-wp}^{wp}{P}_{wp,t}+H_{l-pv}^{pv}{P}_{pv,t}\\ -{\displaystyle \sum _{j\in J}{H}_{l-load,e}^{load}{P}_{load,e,j,t}-H_{l-load,e}^{Tran}{P}_{load,e,t}^{Tran}}\end{array}\right]\right\}}\\ +{\displaystyle \sum _{t\in T}{\mu }_{2,t}\left(h_{l,t}-h_l^{\text{max}}\right)}+{\displaystyle \sum _{t\in T}{\mu }_{3,t}\left(h_l^{\text{min}}-h_{l,t}\right)}+{\displaystyle \sum _{t\in T}{\gamma }_{1,t}\left\{P_{wp,t}^{uR}+P_{pv,t}^{uR}\right\}}\\ +{\displaystyle \sum _{t\in T}{\gamma }_{2,t}\left\{P_{wp,t}^{dR}+P_{pv,t}^{dR}\right\}}\end{array}$

where $\left\{\lambda \right\},\left\{\mu \right\},\left\{\gamma \right\},\left\{\nu \right\},\left\{\pi \right\},\left\{\varpi \right\},\left\{\sigma \right\}$ are lagrangian multiplier of Eqs. 26, 27, 32, 33, 39–43, 46, 50, 51 respectively. The constraints are Eqs. 28–31, 34–38, 44–51. $Z_{ZR}^1$ is sub-problem of dynamic programming include $P_{cpu},U_{cpu}^{op},U_{cpu}^{on}$ and $\left\{\lambda \right\},\left\{\mu \right\},\left\{\gamma \right\},\left\{\nu \right\}$. $Z_{ZR}^2$ is sub-problem of dynamic programming include ${\psi }_{sw},P_{sw}^{in}$ and $\left\{\lambda \right\},\left\{\mu \right\},\left\{\gamma \right\},\left\{\pi \right\}$. $Z_{ZR}^3$ is sub-problem of dynamic programming include $P^{ch},P^{dis}$ and $\left\{\lambda \right\},\left\{\mu \right\},\left\{\gamma \right\},\left\{\varpi \right\},\left\{\sigma \right\}$. $Z_{ZR}^4$ is sub-problem of linear programming, which can be solved by CPLEX.

The lagrangian dual problem is:

$LD:\text{max}L=\text{max}\left(\text{min}{Z}_{LR}\right)(54)$

the surrogate subgradient method is adopted to update the lagrange multiplier for solving the dual problem. The solving process is shown in Figure 2.

FIGURE 2

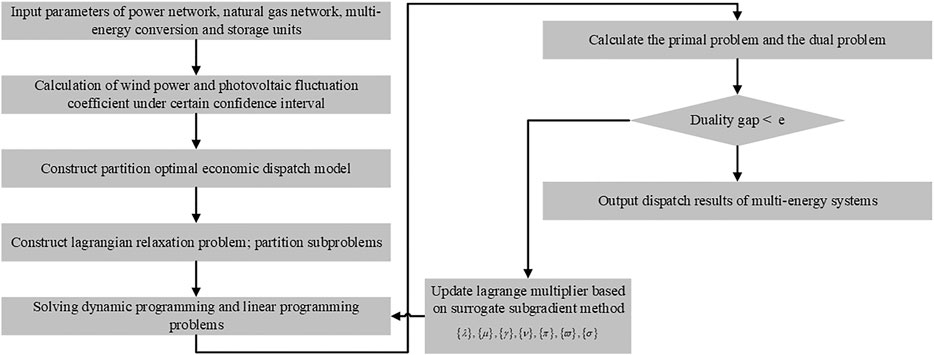
FIGURE 2. The solving process of the locational marginal price-based partition optimal economic dispatch model of multi-energy system.

In the process of solving the model, according to the definition of LMP, the node $j$ price is

$LM{P}_{ME,j}=\frac{\partial L^{\ast }}{\partial P_{load,e,j}}(55)$

where $LM{P}_{ME,j}$ is node $j$ price. $L^{\ast }$ is the optimal solution of optimization problem.

The process of solving algorithm is summarised in Algorithm 1.

Case Study

Experiment Setup

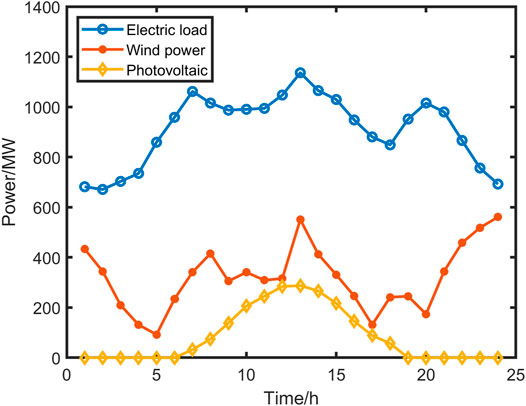
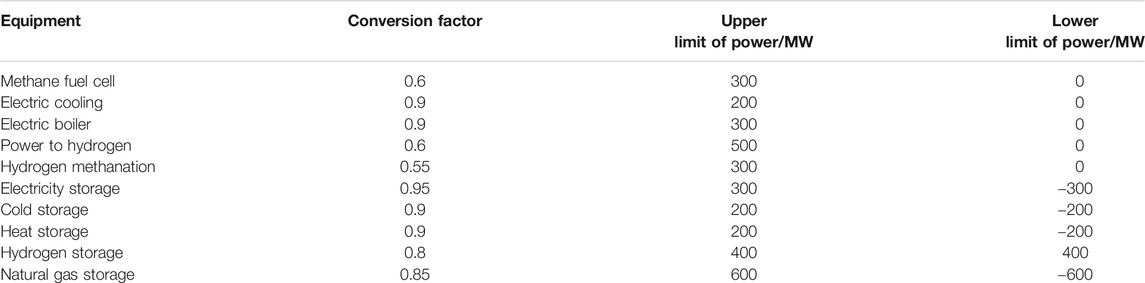
In this section of paper, a simulation system coupling IEEE 39-nodes power system and 7-nodes natural gas system is established, which is shown in Figure 3. Operating data adopt an actual power grid in Northeast China. In the power network, node 38 is wind power with a capacity of 300 MW; node 35 is wind power with a capacity of 300 MW; node 37 is photovoltaic with a capacity of 300 MW; and node 31 is methane fuel cell with a capacity of 200 MW. Wind power and photovoltaic provide 42% of the total generation capacity of the test system. Typical power curves of wind power, photovoltaic and electrical loads are shown in Figure 4. The parameters of the multi-energy conversion and storage unit are shown in Table 1. The dispatching cycle is 24 h. The time interval is 1 h. The model is verified with the PC, and the host is 6148 CPU, 2.40 GHz and 128 GB RAM memory.

FIGURE 3

FIGURE 3. The diagram of simulation system.

FIGURE 4

FIGURE 4. Typical power curves of wind power, photovoltaic and electrical loads.

TABLE 1

TABLE 1. The Parameters of The Multi-Energy Conversion and Storage Units.

Two scenarios are given in this section: 1) only considering the regulation capability of conventional generations; 2) considering the regulation capability of multi-energy systems.

Simulation results

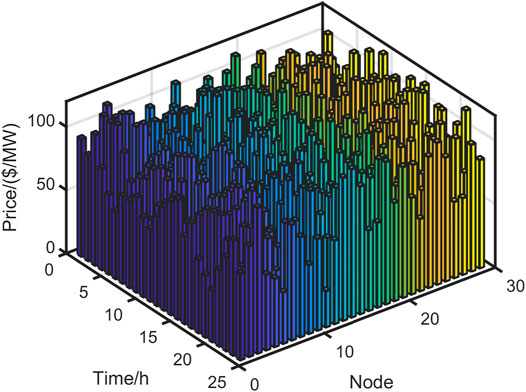
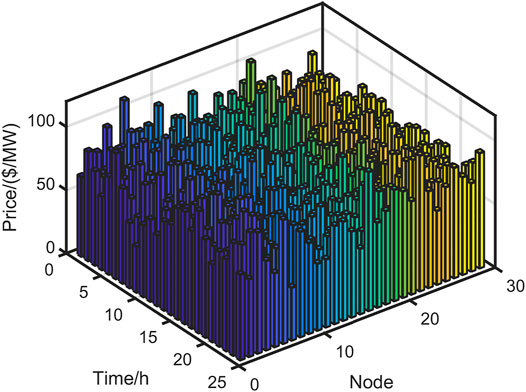
The results for the prices are showed in Figure 5 and Figure 6 respectively. Computation time are 27.38 s and 31.56 s respectively. In scenario 1, since only considered the conventional generation, the system frequently adjusts prices to provide the reserve adjustment demand. In other word, the adjustment ability to deal with uncertainty is insufficient. It can be seen from the Figure 5 that there is a large differentiation between peak electricity prices and valley electricity prices. The electricity prices fluctuate greatly, which easily leads to line congestion in power system. In particular, the maximum price of node 26 is 115.38 $/MW, and the minimum price is 38.46 $/MW over the whole dispatching cycle. The price differentiation can easily cause a decline in power transmission capacity, and the system will appear abandon curtailment of renewable energy. In contrast, the fluctuation of electricity prices is relatively small in scenario 2. Due to the system has multi-energy coordination capabilities, it can effectively deal with the uncertainty of renewable energy. Moreover, the overall price can better reflect the actual supply and demand relationship in ESM. In particular, the maximum price of node 26 is 85.23 $/MW, and the minimum price is 56.92 $/MW over the whole dispatching cycle. The transmission capacity of external power is more stable. The results of price show that the coordination ability of multi-energy system is much higher than a single conventional generation. Furthermore, the reasonable additional adjustment cost sharing mechanism makes the adjustment willingness of multi-energy adjustable units stronger. The overall system cost also lower than only considering the adjustment process of conventional generation.

FIGURE 5

FIGURE 5. The distribution of LMP in scenario 1.

FIGURE 6

FIGURE 6. The distribution of LMP in scenario 2.

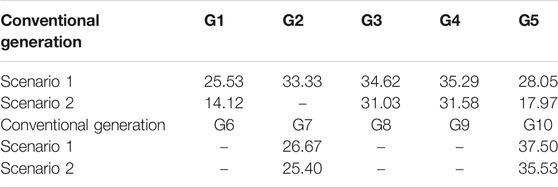
Table 2 is the results of cost of conventional generations to test whether the low cost occurs in the process of optimal dispatch. For each conventional generation, the scheduling cost of scenario 2 is lower than that of scenario 1. In particular, scheduling costs of G1 and G5 with peak shaving capabilities, have obvious differences in two scenarios. It shows that the balance adjustment of supply and demand caused by the uncertainty of renewable energy is mainly undertaken by conventional generation with peak shaving capabilities, and they have to be paid higher costs. However, in scenario 2, the multi-energy adjustable units provide the system with adjustment capabilities. The system can strive to with the minimum cost for the multi-energy balance.

TABLE 2

TABLE 2. The Cost Comparison of Conventional Generations (*10⁶$).

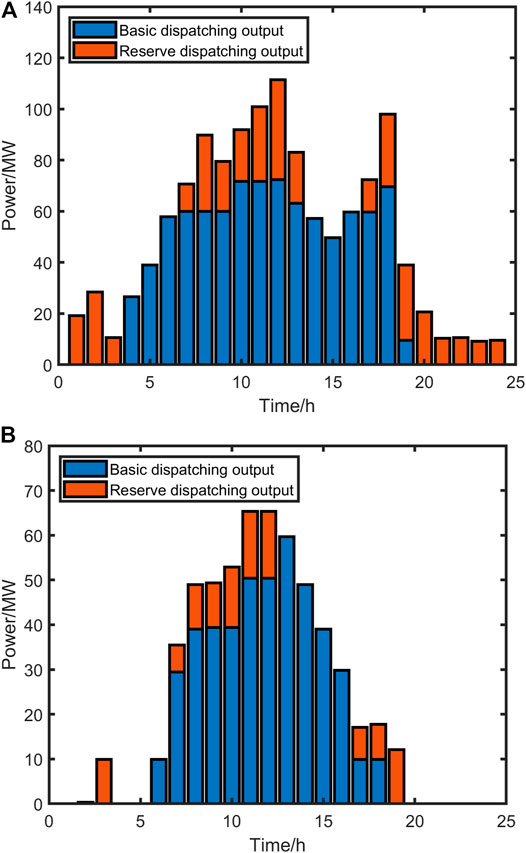
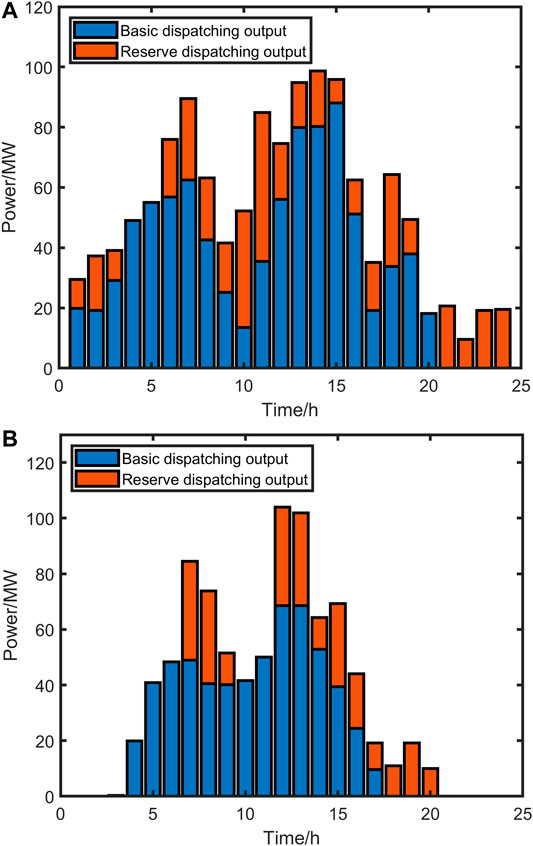
Figure 7 is the power of basic dispatch and reserve of G1 in two scenarios. And Figure 8 is the power of basic dispatching and reserve of G5 in two scenarios. In general, the basic dispatching and reserve of the conventional generation in scenario 2 are less than the results in scenario 1. And the reserve changes caused by wind power and photovoltaic will be undertaken by the multi-energy adjustable units during the peak load period in scenario 2. It shows that scenario 2 has more diversified adjustment means, and the multi-energy adjustable units can operate intelligently according to the price signal, which is the main reason for the decrease in system operating costs. The conventional generation still needs to make standby adjustments to the uncertainty of renewable energy during the valley load period in scenario 1, but it is not necessary in scenario 2. The adjustment power can be 0 during the valley load period in scenario 2. The main reason for the above situation is that a reasonable price signal is calculated in scenario 2, which can direct the multi-energy storage unit to peak shaving, and there is a willingness to leave a certain margin for adjustment.

FIGURE 7

FIGURE 7. The power of basic dispatching and reserve of G1. (A) Scenario 1. (B) Scenario 2.

FIGURE 8

FIGURE 8. The power of basic dispatching and reserve of G5. (A) Scenario 1. (B) Scenario 2.

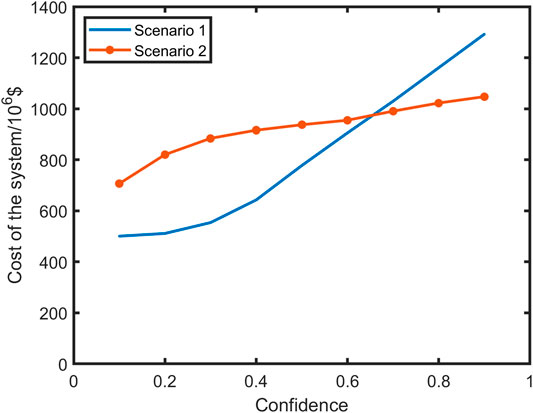
Figure 9 is the comparison of total cost changes under different confidence levels of fluctuation coefficient of renewable energy in two scenarios. It can be seen that the overall operating cost of scenario 2 with multi-energy adjustable units is higher than scenario 1 when the confidence level of the fluctuation coefficient of renewable energy is in (0.1, 0.6). Since the improvement of the confidence level, the demand for adjustment of renewable energy fluctuations will increase. Scenario 1 has a single adjustment method and cannot reflect the actual supply and demand relationship. Therefore, the rising trend of the cost curve is obvious. On the contrary, the overall system cost has also increased in scenario 2. The rate of increase gradually decreases due to the stronger adjustment ability of the multi-energy adjustable units. The operating cost of scenario 2 is less than the cost of scenario 1 under a certain confidence interval, which indicates that the uncertainty of renewable energy has enormous influence on the operating cost of the system.

FIGURE 9

FIGURE 9. The comparison of total cost changes under different confidence levels in two scenarios.

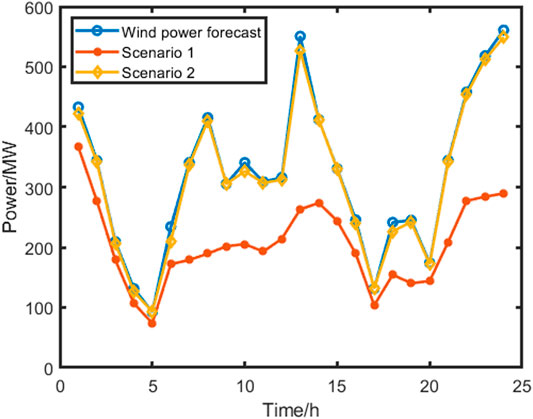
Figure 10 is the comparison of wind power in two scenarios. It presents the actual output of wind power in the system under two scenarios. Scenario 1 does not get the support of multi-energy systems. Therefore, the proportion of wind power is relatively small, and wind curtailment often occurs. On the contrary, the proportion of wind power generation is significantly increased due to the consideration of multi-energy regulation capabilities in scenario 2. The partition optimal economic dispatch model of multi-energy system can bring more adjustment means to the system operation. The potential of wind power will be obtained. Moreover, total operating cost of the system can be reduced.

FIGURE 10

FIGURE 10. The comparison of wind power in two scenarios.

Conclusion

In this paper, a locational marginal price-based partition optimal economic dispatch model of multi-energy system with a high proportion of renewable energy is proposed. And a solution method based on lagrangian relaxation is established for clearing and dynamic price. The results demonstrate that the proposed optimal economic dispatch model can improve the rationality of the pricing mechanism, the regulation ability of the multi-energy coordination, and the flexibility of multi-energy system.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HJ was responsible for the specific work of this paper. YT and TZ guided the work of this article. ZW and BD carried out some of the calculation work.

Funding

The authors acknowledge the funding of the National Key Research and Development Plan (2017YFB0902100).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Choi, D.-H., and Xie, L. (2017). Impact of Power System Network Topology Errors on Real-Time Locational Marginal price. J. Mod. Power Syst. Clean. Energ. 5, 797–809. doi:10.1007/s40565-017-0280-5

CrossRef Full Text | Google Scholar

Fang, X., and Cui, M. (2020). Analytical Model of Day-Ahead and Real-Time price Correlation in Strategic Wind Power Offering. J. Mod. Power Syst. Clean Energ. 8, 1024–1027. doi:10.35833/MPCE.2019.000598

CrossRef Full Text | Google Scholar

Fang, X., Hodge, B.-M., Du, E. S., Kang, C. Q., and Li, F. (2019). Introducing Uncertainty Components in Locational Marginal Prices for Pricing Wind Power and Load Uncertainties. IEEE Trans. Power Syst. 34, 2013–2024. doi:10.1109/TPWRS.2018.2881131

CrossRef Full Text | Google Scholar

Fang, X., Sedzro, K. S., Yuan, H. Y., Ye, H. X., and Hodge, B.-M. (2020a). Deliverable Flexible Ramping Products Considering Spatiotemporal Correlation of Wind Generation and Demand Uncertainties. IEEE Trans. Power Syst. 35, 2561–2574. doi:10.1109/TPWRS.2019.2958531

CrossRef Full Text | Google Scholar

Fang, X. X., Yang, Z. F., Yu, J., Zhou, P., Zhao, W. J., and Lai, X. W. (2020b). Theoretical Analysis and Extension of Locational Marginal price. Proc. CSEE 40, 379–390. doi:10.13334/j.0258-8013.pcsee.190023

Google Scholar

Faqiry, M., Edmonds, L., Wu, H., and Pahwa, A. (2020). Distribution Locational Marginal price-based Transactive Day-Ahead Market with Variable Renewable Generation. Appl. Energ. 259, 114103. doi:10.1016/j.apenergy.2019.114103

CrossRef Full Text | Google Scholar

Gao, H. H., Qin, X., Barroso, R. J. D., Hussain, W., Xu, Y., and Yin, Y. (2020). Collaborative Learning-Based Industrial Iot Api Recommendation for Software-Defined Devices: the Implicit Knowledge Discovery Perspective. IEEE Trans. Emerg. Top. Comput. Intell. 99, 1–11. doi:10.1109/TETCI.2020.3023155

CrossRef Full Text | Google Scholar

Gong, G. J., Wang, H. J., Zhang, T., Chen, Z. M., Wei, P. F., Su, C., et al. (2018). Research on Electricity Market about Spot Trading Based on Blockchain. Proc. CSEE 38, 6955–6966+7129. doi:10.13334/j.0258-8013.pcsee.172645

Google Scholar

Hajiabadi, M. E., and Samadi, M. (2019). Locational Marginal price Share: a New Structural Market Power index. J. Mod. Power Syst. Clean. Energ. 7, 1709–1720. doi:10.1007/s40565-019-0532-7

CrossRef Full Text | Google Scholar

Hanif, S., Zhang, K., Hackl, C. M., Barati, M., Gooi, H. B., and Hamacher, T. (2019). Decomposition and Equilibrium Achieving Distribution Locational Marginal Prices Using Trust-Region Method. IEEE Trans. Smart Grid 10, 3269–3281. doi:10.1109/TSG.2018.2822766

CrossRef Full Text | Google Scholar

Jiang, Z., and Ai, Q. (2017). Agent-based Simulation for Symmetric Electricity Market Considering price-based Demand Response. J. Mod. Power Syst. Clean. Energ. 5, 810–819. doi:10.1007/s40565-017-0270-7

CrossRef Full Text | Google Scholar

Jovanovic, N., Garcia-Gonzalez, J., Barquin, J., and Cerisola, S. (2017). Electricity Market Short-Term Risk Management via Risk-Adjusted Probability Measures. IET Generation Transm. Distribution 11, 2599–2607. doi:10.1049/iet-gtd.2016.1731

CrossRef Full Text | Google Scholar

Morstyn, T., Teytelboym, A., Hepburn, C., and McCulloch, M. D. (2020). Integrating P2P Energy Trading with Probabilistic Distribution Locational Marginal Pricing. IEEE Trans. Smart Grid 11, 3095–3106. doi:10.1109/TSG.2019.2963238

CrossRef Full Text | Google Scholar

Peng, X., and Tao, X. (2018). Cooperative Game of Electricity Retailers in China's Spot Electricity Market. Energy 145, 152–170. doi:10.1016/j.energy.2017.12.122

CrossRef Full Text | Google Scholar

PrudhvirajKiran, D. P. B. S., and Pindoriya, N. M. (2020). Stochastic Energy Management of Microgrid with Nodal Pricing. J. Mod. Power Syst. Clean Energ. 8, 102–110. doi:10.35833/MPCE.2018.000519

CrossRef Full Text | Google Scholar

Teng, Y., Sun, P., Luo, H. H., and Chen, Z. (2019a). Autonomous Optimization Operation Model for Multi-Source Microgrid Considering Electrothermal Hybrid Energy Storage. Proc. CSEE 39, 5316–5324+5578. doi:10.13334/j.0258-8013.pcsee.181922

Google Scholar

Teng, Y., Wang, Z. D., Jin, H. Y., Zhou, G. P., and Chen, Z. (2019b). A Model and Coordinated Optimization for the Multi-Energy Storage System of Electricity Heat Hydrogen to Regulation Enhancement of Power Grid. Proc. CSEE 39, 7209–7217+7494. doi:10.13334/j.0258-8013.pcsee.182564

Google Scholar

Teng, Y., Wang, Z., Li, D. Y., Ma, Q., Hui, Q., and Li, S. B. (2019c). Multi-energy Storage System Model Based on Electricity Heat and Hydrogen Coordinated Optimization for Power Grid Flexibility. CSEE J. Power Energ. Syst. 5, 266–274. doi:10.17775/CSEEJPES.2019.00190

CrossRef Full Text | Google Scholar

Vaskovskaya, T., Thakurta, P. G., and Bialek, J. (2018). Contribution of Transmission and Voltage Constraints to the Formation of Locational Marginal Prices. Int. J. Electr. Power Energ. Syst. 101, 491–499. doi:10.1016/j.ijepes.2018.04.004

CrossRef Full Text | Google Scholar

Yang, X. X., Zhou, S. J., and Cao, M. (2020). An Approach to Alleviate the Sparsity Problem of Hybrid Collaborative Filtering Based Recommendations: the Product-Attribute Perspective from User Reviews. Mobile Netw. Appl. 25, 376–390. doi:10.1007/s11036-019-01246-2

CrossRef Full Text | Google Scholar

Zhang, N., Sun, Q. Y., Wang, J. W., Yang, L. X., Sun, Q., Wang, J., et al. (2021). Distributed Adaptive Dual Control via Consensus Algorithm in the Energy Internet. IEEE Trans. Ind. Inf. 17, 4848–4860. doi:10.1109/TII.2020.3031437

CrossRef Full Text | Google Scholar

Zheng, K., Wang, Y., Liu, K., and Chen, Q. (2020). Locational Marginal price Forecasting: a Componential and Ensemble Approach. IEEE Trans. Smart Grid 11, 4555–4564. doi:10.1109/TSG.2020.2985070

CrossRef Full Text | Google Scholar