Impedance Modeling and Analysis of Medium-Frequency Oscillation Caused by VSC-HVDC Connected to Local Weak Grid and DFIG-Based Wind Farms

In the northwest of China, a strategy to transmit the wind-thermal–bundled power from the local grid and doubly fed induction generator (DFIG)–based wind farms through a voltage source converter–based HVDC (VSC-HVDC) can be widely applied. However, since the local grid is usually weak, a new type of electrical oscillation in the medium-frequency region may occur in the sending-end converter (SEC) of VSC-HVDC with PQ-control. The mechanism of this oscillation caused by the interaction between the DFIG, local grid, and SEC is not entirely understood. In this study, the sequence impedance model of the sending-end converter (SEC) of VSC-HVDC with the PQ-control outer loop and PLL is derived with the explicit analytic expression, and then, the oscillation mechanism is explored based on the intuitive analysis of the system impedance frequency characteristics. Compared with the subsynchronous oscillation (SSO) caused by the DFIG or power inverter, the theoretical analysis shows that this medium-frequency oscillation (MFO) mainly originates from the SEC due to its negative damping effect between about 100 and 200 Hz. In addition, the impact of the system controller parameters and operating conditions of the DFIG, local grid, and SEC on the oscillation characteristics is analyzed in detail. Finally, the correctness of the theoretical analysis is validated by time-domain simulation.

1 Introduction

In Northwest China, large-scale wind power is generally bundled with local thermal power and then transmitted to the load centers in the eastern coast, as the wind power is fluctuant and intermittent while the thermal power is controllable (Sun et al., 2017; Gao et al., 2018). Recently, the VSC-HVDC technology is developing rapidly due to its advantage in the wind power integration (Flourentzou et al., 2009; Yang et al., 2018; Chen et al., 2020; Sun et al., 2020; Xiong et al., 2021). Therefore, the strategy to transmit the large-scale wind power through VSC-HVDC in the local grid will be widely applied. However, the proposed transmission mode may face potential stability issues induced by the power electrical converters, especially given that the local grid in Northwest China is usually weak. Several oscillation incidents related to VSC-HVDC have occurred worldwide. In 2013, an SSO around 20 Hz occurred in the Nanao VSC-HVDC project in China and led to the outage of the integrated DFIG-based wind farms (Lyu et al., 2018). In addition, a 250–350 Hz current oscillation was observed in the North Sea VSC-HVDC project in Germany from the converter to the grid (Christoph et al., 2015; Zhou et al., 2019). Similarly, for the proposed system, the interaction between the DFIG-based wind farms, local grid, and VSC-HVDC may cause a new type of electrical oscillation issue, which is worthy of further study.

Currently, the impedance method is suitable for the stability issue caused by the grid-connected units due to its simple mathematical expression and stability criterion (Cespedes and Sun, 2014). There have been a lot of studies concentrating on the stability issue of the DFIG-based wind farms and VSC-HVDC based on the impedance method. For instance, the effect of the control parameters on the stability of the grid-connected converter is investigated in Wang et al. (2017), Wen et al. (2017), Xu et al. (2019), and Wang et al. (2020). However, in the above references, only the inner loop and PLL are considered in the modeling, while the influence of the outer loop is ignored. Thus, the accuracy of the stability analysis is doubtful. Recent references (Khazaei et al., 2018; Liu and Xie, 2019; Zhou et al., 2020) take the outer loop into account as well. However, the impedance model with the outer loop is normally given in matrix format instead of the explicit analytic expression, which is not clear and intuitive when it comes to illustrating the impedance characteristics. In addition, all of the above references only consider the outer loop of a power inverter instead of a converter. In Liu et al. (2021), Liu and Xie (2017), Miao (2012), Vieto and Sun (2018), Koralewicz et al. (2020), Yan et al. (2019), Yang et al. (2020), SSO existing in the DFIG-based wind farms interfaced with the series-compensated line or AC grid is investigated, and the impact of the various factors on SSO is analyzed. However, the influence of the integrated DFIG on the oscillation over the supersynchronous frequency region is not considered. Besides, few references consider the stability of the proposed system which transmits wind power in combination with thermal power through the SEC.

In particular, the interaction between the DFIG and VSC-HVDC is deeply analyzed in author’s previous work (Sun et al., 2019). However, the system stability will be affected in a different way when the wind-thermal–bundled power is transmitted from the local grid and DFIG-based wind farms to the SEC with PQ-control instead of the amplitude–frequency control. Since the local grid is integrated and the control strategy of the SEC is changed, the interaction mechanism will be more complicated in the proposed transmission mode. The similar system of a VSC-HVDC connected to the DFIG-based wind farm or the thermal power plant has been preliminarily analyzed in Chen et al. (2018), Liu et al. (2018), and Zou et al. (2018). However, they mainly focus on SSO or high-frequency oscillation issues, while MFO is not considered. In addition, the control strategy of the SEC in the proposed transmission mode is different from that in the above studies since the output power of the wind-thermal–bundled system should be controlled by the SEC (Yogarathinam et al., 2017) and then transmitted to the power grid. Thus, the outer loop of the SEC cannot be ignored since it reflects the effect of the control strategy. In short, the stability of the proposed transmission mode is not yet systematically comprehended. Therefore, this work aims to explore the interaction between the DFIG, local grid, and SEC with PQ-control in the medium-frequency region.

The main contributions of this study are summarized as:

• The potential MFO risk of the SEC with PQ-control in the medium-frequency region is analyzed when it transmits the wind-thermal–bundled power from the local grid and DFIG-based wind farms.

• To analyze the interaction mechanism in the proposed transmission mode, the sequence impedance model of the SEC with the PQ-control outer loop and PLL is derived with the explicit analytic expression, which is clear and intuitive when it comes to illustrating the impedance characteristics.

• The coupling between the inner loop, outer loop, and PLL of the SEC is analyzed according to the derived impedance models, and their influence on the system stability can be intuitively found based on the analytic impedance expression and the corresponding impedance frequency characteristics. Compared with the power inverter, the mechanism and characteristics of MFO caused by the SEC are different.

• The impact of the local grid strength and the integration of DFIG-based wind farms on the system stability is analyzed as well. Compared with SSO caused by the DFIG, the controller parameters and operating conditions of the DFIG have a different influence on this MFO which mainly originates from the SEC.

The rest of this article is organized as follows. The structure and oscillation phenomenon of the system is investigated in Section 2. Section 3 derives and validates the sequence impedance models of the SEC, the DFIG, and the local grid. In Section 4, the mechanism explanation of the oscillation is revealed based on the derived models, and the impact of various factors on the oscillation is analyzed. Section 5 validates the correctness of the theoretical analysis by time-domain simulation. Finally, conclusions are drawn in Section 6.

2 Structure and Oscillation Phenomenon of the System

The configuration of the investigated system is briefly introduced in this section. Then, time-domain simulation and spectrum analysis are conducted to analyze the potential electrical oscillation in the system.

2.1 System Configuration

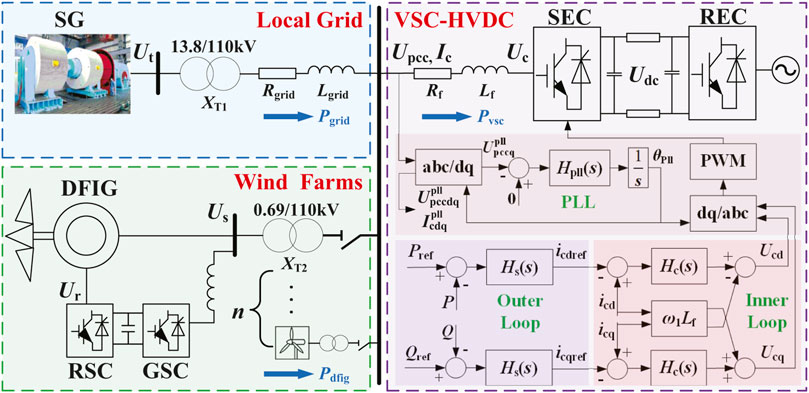
The investigated system shown in Figure 1 contains three parts: the local grid with a thermal power unit, the DFIG-based wind farms, and the VSC-HVDC system. Both the thermal power and wind power are stepped up to 110 kV and then transmitted to the main grid via VSC-HVDC. In order to keep the transmission power stable, the constant power control is used in the SEC, while the receiving-end converter (REC) regulates the DC voltage. Since the wind power is fluctuant while the thermal power is controllable, the local thermal power keeps the total output power constant by means of its self-regulation (Xiao et al., 2016; Yogarathinam et al., 2017; Shah et al., 2018). Besides, the thermal power unit also maintains the stable AC voltage and frequency on the point of common coupling (PCC).

FIGURE 1

FIGURE 1. VSC-HVDC connected to the local grid and DFIG-based wind farms.

Initially, the wind farms contain 200 DFIG wind turbines (WTs), which run in the maximum power point tracking mode (GE 1.5 MW). The capacity of the VSC-HVDC is 500 MW. Normally, it requires the thermal power unit to stabilize the fluctuation of full wind power with at least 40% rated loads. Therefore, the capacity of the local thermal power unit is set to 500 MW. To simplify the modeling, the equivalent aggregated model of the DFIG is adopted (Kunjumuhammed et al., 2017; Peng et al. 2020), since the impact of DFIG integration on the system is of concern instead of the internal action among the turbines.

2.2 Oscillation Phenomenon

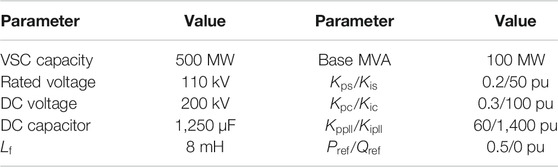
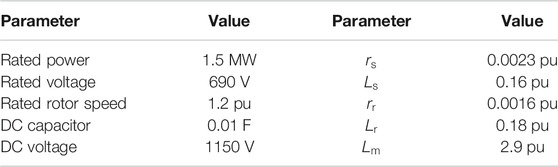
A detailed simulation model of the system shown in Figure 1 is established with a switching device model of the VSC-HVDC in MATLAB/Simulink, associated with the SimPowerSystems Blockset. To investigate the potential oscillation risk existing in the system, two scenarios are analyzed. The system parameters are listed in Tables 1–3.

TABLE 1

TABLE 1. Parameters of VSC-HVDC.

TABLE 2

TABLE 2. Parameters of the DFIG.

TABLE 3

TABLE 3. Parameters of synchronous machine and AC line.

2.2.1 Scenario 1: The Effect of the Outer Loop of the SEC

Initially, the wind farms are not integrated. The short circuit ratio (SCR) of the local grid is set to 6.8, and the output active power of VSC-HVDC is set to 0.5 pu. At t = 6 s, the SCR decreases to 5.1. To analyze the effect of the PQ-control outer loop of the SEC, the simulation models both with and without the outer loop are adopted. Figure 2A shows the active power response on the PCC. Since the local grid strength decreases, it can be found that the oscillation emerges with the outer loop considered, while the system is still stable with the outer loop ignored. Thus, the outer loop of the SEC influences the system stability.

FIGURE 2

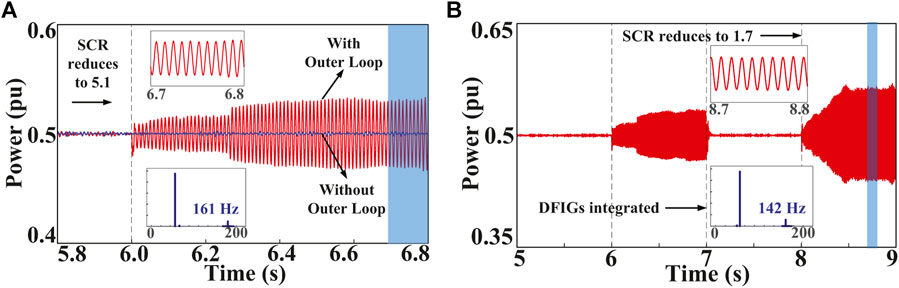
FIGURE 2. Oscillation phenomenon. (A) The effect of the outer loop of the SEC. (B) The effect of the integration of the DFIG.

2.2.2 Scenario 2: The Effect of the Integration of the DFIG

The condition is the same as in scenario 1, and the outer loop of SEC is considered. At t = 7 s, the wind farms are integrated under the wind speed at 10 m/s. At t = 8 s, the SCR further decreases to 1.7. According to Figure 2B, the electrical oscillation can be suppressed due to the integration of the DFIG. However, the electrical oscillation emerges again when the local grid becomes even more weak. Discrete Fourier transform (DFT) is applied for the spectrum analysis of the current on the PCC. The current contains an oscillation component at 161 Hz in the abc frame before the integration and reduces to 142 Hz after the integration.

Therefore, the oscillatory behavior of the system can be influenced by the parameters’ variation of the SEC, the DFIG, and the local grid. The frequency region of the electrical oscillation is about 100–200 Hz, which belongs to MFO.

3 System Modeling and Stability Criterion

In this section, the sequence impedance model of the sending-end converter (SEC) with the power loop and PLL is derived in detail with the explicit analytic expression and validated. Then, the impedance models of the DFIG and the local AC grid are built as well.

3.1 Impedance Model of the SEC With PQ-Control

3.1.1 Model With PLL and Current Loop

The control method of the SEC and REC is discussed in Section 2.1, and the control structure of the SEC is depicted in Figure 1. Since the impact of the REC on the stability is small due to the isolation provided by the DC link, only the impedance model of the SEC needs to be built in detail. The control of the SEC is based on the dq reference frame, in which the d-axis is orientated to the PCC voltage $U_{\text{pcc}}$ and the q-axis leading the d-axis by ${90}^{\circ }$.

The voltage equation of the SEC in the dq frame is expressed as

$\{\begin{array}{c}{U}_{\text{pccd}}=U_{\text{cd}}-s{L}_{\text{f}}{i}_{\text{cd}}+{\omega }_1{L}_{\text{f}}{i}_{\text{cq}}\\ U_{\text{pccq}}=U_{\text{cq}}-s{L}_{\text{f}}{i}_{\text{cq}}-{\omega }_1{L}_{\text{f}}{i}_{\text{cd}}\end{array},(1)$

where $U_{\text{c}}$ represent the output voltage and current of the SEC, the subscripts “d” and “q” denote the d-axis and q-axis components, s is the differential operator, ${\omega }_1$ is the base frequency, and $L_{\text{f}}$ is the filter inductance of the converter. Note that the influence of the filter capacitance is ignored since it only dominates in the middle–high frequency region.

The small-signal model of the current controller of the SEC can be described as

$\{\begin{array}{c}\text{Δ}{U}_{\text{cdref}}=H_{\text{c}}\left(s\right)\left(\text{Δ}{i}_{\text{cdref}}-\text{Δ}{i}_{\text{cd}}\right)+\text{Δ}{U}_{\text{pccd}}-{\omega }_1{L}_{\text{f}}\text{Δ}{i}_{\text{cq}}\\ \text{Δ}{U}_{\text{cqref}}=H_{\text{c}}\left(s\right)\left(\text{Δ}{i}_{\text{cqref}}-\text{Δ}{i}_{\text{cq}}\right)+\text{Δ}{U}_{\text{pccq}}+{\omega }_1{L}_{\text{f}}\text{Δ}{i}_{\text{cd}}\end{array},(2)$

where the subscript “ref” denotes the reference, and $K_{\text{pc}}$ and $K_{\text{ic}}$ are the proportional and integral gains of the current controller $H_{\text{c}}\left(s\right)$ of the SEC. According to the control loop, $U_{\text{cd}}=U_{\text{cdref}}$ and $U_{\text{cq}}=U_{\text{cqref}}$ when the DC dynamics is not considered since it is normally stable.

Then, the influence of the PLL dynamics is taken into account. PLL is used for phase tracking of $U_{\text{pcc}}$. However, when the system is disturbed by a small-signal perturbation, the phase θ of $U_{\text{pcc}}$ cannot be synchronized accurately and an angle deviation $\text{Δ}\theta$ is introduced due to the PLL dynamics. Thus, the PLL output angle ${\theta }_{\text{pll}}$ can be expressed as ${\theta }_{\text{pll}}=\theta +\text{Δ}\theta$. Therefore, the system has two dq frames during the transient process of PLL: one is the system dq frame defined by θ, while the other is the controller dq frame defined by ${\theta }_{\text{pll}}$. Note that the variables in the controller dq frame are denoted with the superscript “pll.” The small-signal disturbance relationship of the converter voltage and current between the two frames have been derived in detail in Wang et al. (2017), Wen et al. (2017), and Sun et al. (2019)

$\{\begin{array}{l}{\text{ΔU}}_{\text{cdq}}^{\text{pll}}{=\text{ΔU}}_{\text{cdq}}{+\text{G}}_{\text{pll}}^{\text{u}}\left(\text{s}\right){\text{ΔU}}_{\text{pccdq}}\\ {\text{ΔI}}_{\text{cdq}}^{\text{pll}}{=\text{ΔI}}_{\text{cdq}}{+\text{G}}_{\text{pll}}^{\text{i}}\left(\text{s}\right){\text{ΔU}}_{\text{pccdq}}\end{array}.(3)$

For simplicity, the voltage and current are expressed in matrix form: $U_{\text{cdq}}={\left[U_{\text{cd}}{U}_{\text{cq}}\right]}^{\text{T}}$, ${\text{I}}_{\text{cdq}}={\left[i_{\text{cd}}{i}_{\text{cq}}\right]}^{\text{T}}$. The transfer function matrices ${\text{G}}_{\text{pll}}^{\text{u}}\left(s\right)$ and ${\text{G}}_{\text{pll}}^{\text{i}}\left(s\right)$ in Eq. 3 are defined as

${\text{G}}_{\text{pll}}^{\text{u}}\left(s\right)=\left[\begin{array}{cc}0& U_{\text{cq}}{T}_{\text{pll}}\left(s\right)\\ 0& -U_{\text{cd}}{T}_{\text{pll}}\left(s\right)\end{array}\right],G_{pll}^i\left(s\right)=\left[\begin{array}{cc}0& i_{\text{cq}}{T}_{\text{pll}}\left(s\right)\\ 0& -i_{\text{cd}}{T}_{\text{pll}}\left(s\right)\end{array}\right],(4)$

where $T_{\text{pll}}\left(s\right)=H_{\text{pll}}\left(s\right)/\left(s+U_{\text{pccd}}{H}_{\text{pll}}\left(s\right)\right)$ and $K_{\text{ppll}}$ and $K_{\text{ipll}}$ are the proportional and integral gains of the PLL controller $H_{\text{pll}}\left(s\right)$ of the SEC.

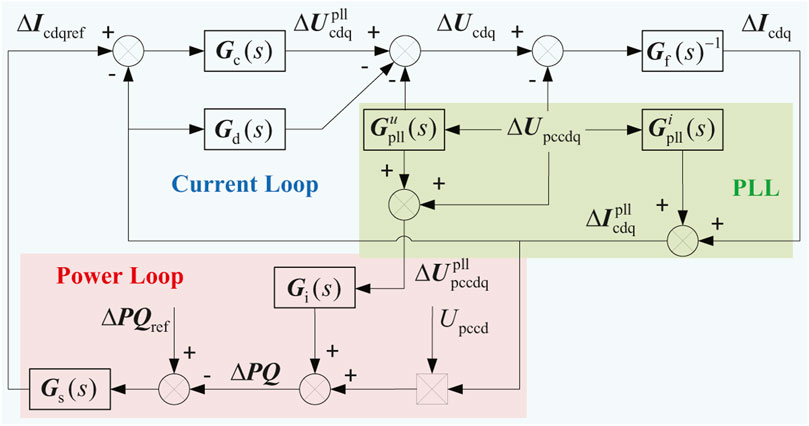
According to Figures 1–3, the small-signal circuit model of the SEC with the current loop and PLL is obtained and shown in the blue and green blocks of Figure 3. ${\text{G}}_{\text{c}}\left(s\right)$ is the transfer function matrix of the current controller, ${\text{G}}_{\text{d}}\left(s\right)$ is the transfer function of the decoupling gain of the current controller, and ${\text{G}}_{\text{f}}\left(s\right)$ represents the impedance of the filter

${\text{G}}_{\text{c}}\left(s\right)=\left[\begin{array}{cc}{H}_{\text{c}}\left(s\right)& 0\\ 0& H_{\text{c}}\left(s\right)\end{array}\right],{\text{G}}_{\text{d}}\left(s\right)=\left[\begin{array}{cc}0& {\omega }_1{L}_{\text{f}}\\ -{\omega }_1{L}_{\text{f}}& 0\end{array}\right],{\text{G}}_{\text{f}}\left(s\right)=\left[\begin{array}{cc}s{L}_{\text{f}}& -{\omega }_1{L}_{\text{f}}\\ {\omega }_1{L}_{\text{f}}& s{L}_{\text{f}}\end{array}\right].(5)$

FIGURE 3

FIGURE 3. Small-signal circuit model of the sending-end station of VSC-HVDC.

According to Figure 3, the small-signal propagation path of the converter current in the current loop can be described as

${\text{ΔI}}_{\text{cdq}}=\left[{\text{ΔI}}_{\text{cdqref}}{\text{G}}_{\text{c}}\left(s\right)-\left({\text{ΔI}}_{\text{cdq}}+{\text{G}}_{\text{pll}}^{\text{i}}\left(s\right){\text{ΔU}}_{\text{pccdq}}\right)\cdot \left({\text{G}}_{\text{c}}\left(s\right)+{\text{G}}_{\text{d}}\left(s\right)\right)-{\text{G}}_{\text{pll}}^{\text{u}}\left(s\right){\text{ΔU}}_{\text{pccdq}}-{\text{ΔU}}_{\text{pccdq}}\right]{\text{G}}_{\text{f}}{\left(s\right)}^{-1}.(6)$

3.1.2 Model With Power Loop

Then, the influence of the outer loop with PQ-control is taken into account. The small-signal model of the power controller of the SEC can be described as

$\{\begin{array}{c}\text{Δ}{i}_{\text{cdref}}=H_{\text{s}}\left(s\right)\left(\text{Δ}{P}_{\text{ref}}-\text{Δ}P\right)\\ \text{Δ}{i}_{\text{cqref}}=H_{\text{s}}\left(s\right)\left(\text{Δ}{Q}_{\text{ref}}-\text{Δ}Q\right)\end{array},(7)$

where $K_{\text{ps}}$ and $K_{\text{is}}$ are the proportional and integral gains of the power controller $H_{\text{s}}\left(s\right)$ of the SEC and $\text{Δ}{P}_{\text{ref}}$ and $\text{Δ}{Q}_{\text{ref}}$ are equal to zero in small-signal analysis since they are constant.

The small-signal analysis is applied to the measured power, which is defined as $P=U_{\text{pccd}}{i}_{\text{cd}}+U_{\text{pccq}}{i}_{\text{cq}}$, $Q=U_{\text{pccd}}{i}_{\text{cq}}-U_{\text{pccq}}{i}_{\text{cd}}$. Notice that the steady-state q-axis terminal voltage $U_{\text{pccq}}=0$. Then, the small-signal reference current of the converter can be obtained as follows

$\{\begin{array}{c}\text{Δ}P=U_{\text{pccd}}\text{Δ}{i}_{\text{cd}}+\text{Δ}{U}_{\text{pccd}}{i}_{\text{cd}}+\text{Δ}{U}_{\text{pccq}}{i}_{\text{cq}}\\ \text{Δ}Q=U_{\text{pccd}}\text{Δ}{i}_{\text{cq}}+\text{Δ}{U}_{\text{pccd}}{i}_{\text{cq}}-\text{Δ}{U}_{\text{pccq}}{i}_{\text{cd}}\end{array},(8)$

$\{\begin{array}{c}\text{Δ}{i}_{\text{cdref}}=-H_{\text{s}}\left(s\right)\left(U_{\text{pccd}}\text{Δ}{i}_{\text{cd}}+\text{Δ}{U}_{\text{pccd}}{i}_{\text{cd}}+\text{Δ}{U}_{\text{pccq}}{i}_{\text{cq}}\right)\\ \text{Δ}{i}_{\text{cdref}}=-H_{\text{s}}\left(s\right)\left(U_{\text{pccd}}\text{Δ}{i}_{\text{cq}}+\text{Δ}{U}_{\text{pccd}}{i}_{\text{cq}}-\text{Δ}{U}_{\text{pccq}}{i}_{\text{cd}}\right)\end{array}.(9)$

In addition, the small-signal propagation path of the power loop is depicted in the red block of Figure 3, where the power is expressed in matrix form: $\Delta \text{PQ}={\left[\Delta P\Delta Q\right]}^{\text{T}}$. In combination with Eqs. 8,9, the reference current can be derived as

${\text{ΔI}}_{\text{cdqref}}=-{\text{G}}_{\text{s}}\left(s\right)\left[U_{\text{pccd}}\left(\Delta {\text{I}}_{\text{cdq}}+{\text{G}}_{\text{pll}}^{\text{i}}\left(s\right)\Delta U_{\text{pccdq}}\right)+{\text{G}}_{\text{i}}\left(s\right)\left(\Delta U_{\text{pccdq}}+{\text{G}}_{\text{pll}}^{\text{u}}\left(s\right)\Delta U_{\text{pccdq}}\right)\right],(10)$

where ${\text{G}}_{\text{s}}\left(s\right)$ is the transfer function matrix of the power controller and ${\text{G}}_{\text{i}}\left(s\right)$ is the transfer function of the current

${\text{G}}_{\text{s}}\left(s\right)=\left[\begin{array}{cc}{H}_{\text{s}}\left(s\right)& 0\\ 0& H_{\text{s}}\left(s\right)\end{array}\right],{\text{G}}_{\text{i}}\left(s\right)=\left[\begin{array}{cc}{i}_{\text{cd}}& i_{\text{cq}}\\ i_{\text{cq}}& -i_{\text{cd}}\end{array}\right].(11)$

Then, the dq impedance of the SEC seen from the terminal is derived by combining Eq. 6

${\text{Z}}_{\text{vsc}}\left(s\right)=-\left[\left(1+U_{\text{pccd}}{\text{G}}_{\text{s}}\left(s\right)\right)\left({\text{G}}_{\text{c}}\left(s\right)+{\text{G}}_{\text{d}}\left(s\right)+{\text{G}}_{\text{f}}\left(s\right)\right)\right]\cdot {\left[1+{\text{G}}_{\text{s}}\left(s\right){\text{G}}_{\text{c}}\left(s\right){\text{G}}_{\text{i}}\left(s\right)+\left(1+{\text{G}}_{\text{s}}\left(s\right){\text{G}}_{\text{c}}\left(s\right){\text{G}}_{\text{i}}\left(s\right)\right){\text{G}}_{\text{pll}}^{\text{u}}\left(s\right)+\left(\left(1+U_{\text{pccd}}{\text{G}}_{\text{s}}\left(s\right)\right){\text{G}}_{\text{c}}\left(s\right)+{\text{G}}_{\text{d}}\left(s\right)\right){\text{G}}_{\text{pll}}^{\text{i}}\left(s\right)\right]}^{-1}.(12)$

However, the expression of the dq impedance model of the SEC is hard to understand since it has four components and each one does not contain an explicit physical meaning. Instead, to analyze intuitively and conveniently, the dq impedance model of the SEC can be transformed into the sequence impedance model by combining Eq. 12 and the following equation (Shah and Parsa, 2017)

${\text{Z}}_{\text{pn}}\left(s\right)={\left[\begin{array}{cc}1& 1\\ -j& j\end{array}\right]}^{-1}{\text{Z}}_{\text{dq}}\left(s\right)\left[\begin{array}{cc}1& j\\ 1& -j\end{array}\right],(13)$

where ${\text{Z}}_{\text{pn}}\left(s\right)$ and ${\text{Z}}_{\text{dq}}\left(s\right)$ represent the 2 × 2 impedance matrixes in the sequence-domain and dq-domain. The 2 × 2 sequence impedance of the SEC can be obtained by substituting ${\text{Z}}_{\text{vsc}}\left(s\right)$ in Eq. 12 with ${\text{Z}}_{\text{dq}}\left(s\right)$. The off-diagonal elements of ${\text{Z}}_{\text{pn}}$ represent the coupling between the positive and the negative components, and their influence on the stability is well analyzed in Zhang et al. (2019), which found that the model without off-diagonal elements is very close to the detailed model over the supersynchronous frequency range, whereas some overpessimistic conclusions are exhibited at the low-frequency range. Liu et al. (2021) also pointed out that the frequency coupling effect caused by the off-diagonal elements mainly influences the analysis of SSO. Therefore, the off-diagonal elements are not considered in this study since the investigated MFO region is much higher than the SSO range. In addition, since the system stability under the balanced condition is considered in this study, the positive sequence impedance model of the SEC is derived as

$Z_{\text{vsc}}\left(s\right)=-\frac{\left(1+U_{\text{pccd}}{H}_{\text{s}}\left(s-j{\omega }_1\right)\right)H_{\text{c}}\left(s-j{\omega }_1\right)+s{L}_{\text{f}}}{1-\frac{1}{2}\left[\left(H_{\text{c}}\left(s-j{\omega }_1\right)-j{\omega }_1{L}_{\text{f}}\right)I_{\text{c}}+U_{\text{pccd}}\right]T_{\text{pll}}\left(s-j{\omega }_1\right)}.(14)$

According to Eq. 14, the sequence impedance of the SEC has an explicit analytic expression, which is intuitive and convenient for further analysis. The denominator of Eq. 14 mainly reflects the impact of the PLL dynamics. $I_{\text{c}}$ is a negative value as a converter. Obviously, the current loop is directly coupled with the power loop in the numerator and directly coupled with PLL in the denominator. The power loop and PLL are decoupled in the denominator in the condition that $U_{\text{pccq}}=0$, and thus, the measured power is the same in both the controller dq frame and the system dq frame.

3.2 Impedance Model of the DFIG

The control structure of the DFIG is depicted in Figure 1. The RSC regulates the power flowing between the stator and the grid, while the grid-side converter (GSC) regulates the DC voltage. Some simplifications are taken into account. For instance, the influence of the GSC and the excitation branch can be ignored since their magnitudes are sufficiently large in the investigated frequency region. Then, the positive sequence impedance model of the DFIG can be expressed as (Miao, 2012; Vieto and Sun, 2018; Sun et al., 2019; Liu et al., 2021)

$Z_{\text{dfig}}\left(s\right)=\frac{\left(r_{\text{r}}+H_{\text{r}}\left(s-j{\omega }_1\right)-j{K}_{\text{dr}}\right)/S_{\text{lip}}\left(s\right)+s{L}_{\text{r}}+r_{\text{s}}+s{L}_{\text{s}}}{1-\frac{1}{2}\left(i_{\text{rd}}{H}_{\text{r}}\left(s-j{\omega }_1\right)/S_{\text{lip}}\left(s\right)+U_{\text{rd}}\right)T_{\text{pll}-\text{rsc}}\left(s-j{\omega }_1\right)},(15)$

where $K_{\text{pr}}$ and $K_{\text{ir}}$ are the proportional and integral gains of the RSC current controller $H_{\text{r}}\left(s\right)$. Besides, $T_{\text{pll}-\text{rsc}}\left(s\right)=H_{\text{pll}-\text{rsc}}\left(s\right)/\left(s+U_{\text{rd}}{H}_{\text{pll}-\text{rsc}}\left(s\right)\right)$ and $K_{\text{ppll}-\text{rsc}}$ is the proportional gain of the PLL controller $H_{\text{pll}-\text{rsc}}\left(s\right)$ of the RSC. The slip of the rotor is expressed as $S_{\text{lip}}\left(s\right)=\left(s-j{\omega }_{\text{r}}\right)/s$ and ${\omega }_{\text{r}}$ is the rotor angular frequency. The rotor slip is a variable and can be expressed as a transfer function with the frequency. Besides, definitions of other parameters in the equation are explained in the above references.

3.3 Impedance Model of the Local Grid

The impedance of the local grid includes the internal impedance of the synchronous generator (SG) and the line impedance. The line impedance is expressed as $Z_{\text{line}}\left(s\right)=R_{\text{line}}+j{X}_{\text{line}}$. The impedance model of the SG has been well derived in Huang et al. (2021), which is expressed as

$\{\begin{array}{c}{Z}_{\text{d}}\left(s\right)={\omega }_{\text{sg}}\left[\left({X^{\prime }}_d-{X^{″}}_d\right)\left({T^{\prime }}_{d}s+a_{\text{d}}\right)G\left(s\right)+{X^{″}}_d\right]\\ Z_{\text{q}}\left(s\right)={\omega }_{\text{sg}}\left[\left({X^{\prime }}_q-{X^{″}}_{\text{q}}\right)\left({T^{\prime }}_{q}s+a_{\text{q}}\right)G\left(s\right)+{X^{″}}_{\text{q}}\right]\end{array},(16)$

where $G\left(s\right)=1/\left[{T^{\prime }}_{\text{d}}{T^{″}}_{\text{d}}{s}^2+\left({T^{\prime }}_{\text{d}}+{T^{″}}_{\text{d}}\right)s+1\right]$, a_d (X_d − X″d)/(X′_d − X″_d), and $a_{\text{q}}=\left(X_{\text{q}}-{X^{″}}_{\text{q}}\right)/\left({X^{\prime }}_{\text{q}}-{X^{″}}_{\text{q}}\right)$. ${\omega }_{\text{sg}}$ is the rotor speed and ${T^{\prime }}_{\text{d}}$, ${T^{″}}_{\text{d}}$ and ${T^{\prime }}_{\text{q}}$, ${T^{″}}_{\text{q}}$ are the transient and subtransient time constants in the dq frame. $X_{\text{d}}$, ${X^{\prime }}_{\text{d}}$, ${X^{″}}_{\text{d}}$ and $X_{\text{q}}$, ${X^{\prime }}_{\text{q}}$, ${X^{″}}_{\text{q}}$ are the stator, transient, and subtransient reactances in the dq frame. The positive sequence impedance of the SG is derived as $Z_{\text{sg}}\left(s\right)=j\left(Z_{\text{d}}\left(s\right)+Z_{\text{q}}\left(s\right)\right)/2$. Therefore, $Z_{\text{grid}}\left(s\right)=Z_{\text{line}}\left(s\right)+Z_{\text{sg}}\left(s\right)$. However, according to the spectrum analysis in Section 2, the investigated MFO region of the system significantly exceeds the low-frequency oscillation, which refers to the dynamics of the generator sets (Baltas et al., 2021). Therefore, the influence of the generator on this new type of electrical oscillation can be ignored. In addition, $Z_{\text{sg}}\left(s\right)$ is relatively small compared with $Z_{\text{line}}\left(s\right)$ in the investigated MFO frequency region, especially when the local grid is weak (Wang et al., 2019). Therefore, only the impedance of the transmission line is considered in this study for the sake of simplified analysis. That is, $Z_{\text{grid}}\left(s\right)=Z_{\text{line}}$. This assumption is proved in the next part.

3.4 Validation and Stability Criterion

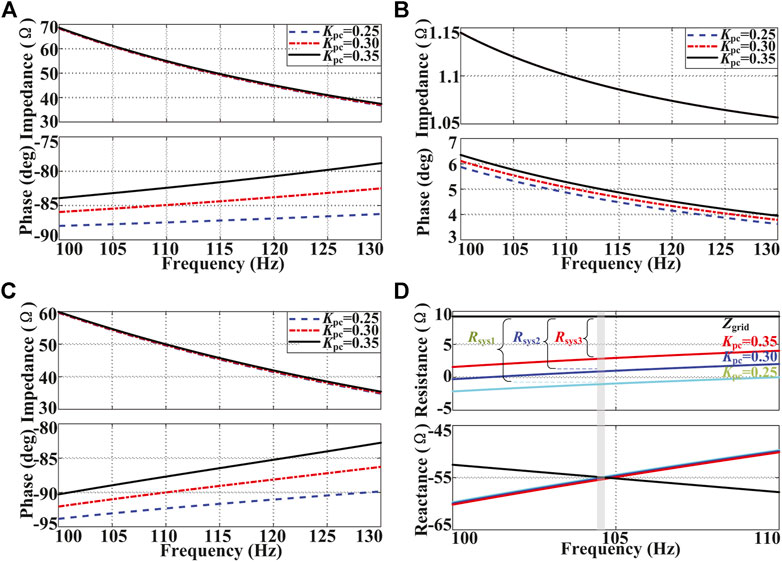
The verification and comparison of the impedance models are performed in Figure 4. The positive sequence impedance of the SEC is measured from 0 to 200 Hz with 40 points using the method of injecting current. A perturbation current (about 2% of rated current) at the measured frequency points is applied, and the related voltage is measured. The harmonic voltage and current in different frequency points are analyzed using the DFT tool. Thereby, the impedance is calculated by dividing the voltage by current at each frequency point. The operating condition for the measurement is given in Tables 1–3. As shown in Figures 4A,B, the impedance models of the SEC with or without PQ-control have been validated. It can be found that the PQ-control will influence the magnitude of $Z_{\text{vsc}}\left(s\right)$ and the frequency of the abrupt change in the phase angle. As shown in Figure 4C, compared with the impedance model of the power inverter derived in Zhou et al. (2020), the risk region of the SEC is shifted from the supersynchronous frequency region to the MFO region. As shown in Figure 4D, the impedance of the SG can be ignored in the MFO region due to its magnitude being relatively small compared with $Z_{\text{line}}\left(s\right)$ with SCR = 5.1 in the MFO region.

FIGURE 4

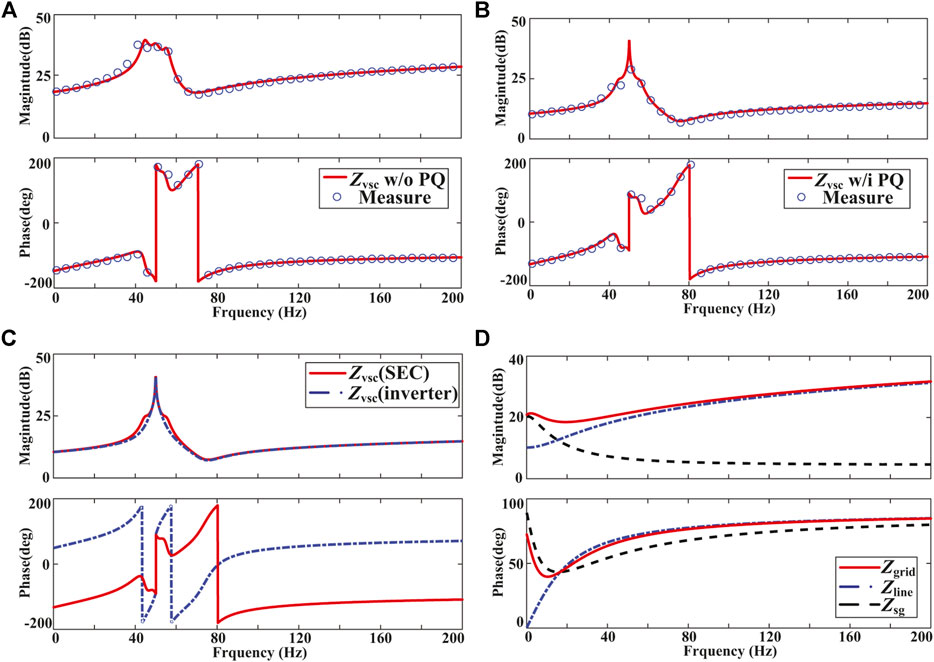
FIGURE 4. Validation and comparison of the impedance models; (A) validation of $Z_{\text{vsc}}\left(s\right)$ without PQ-control; (B) validation of $Z_{\text{vsc}}\left(s\right)$ with PQ-control; (C) comparison of $Z_{\text{vsc}}\left(s\right)$ for the SEC and the inverter; and (D) comparison of $Z_{\text{sg}}\left(s\right)$, $Z_{\text{line}}\left(s\right)$ and $Z_{\text{grid}}\left(s\right)$.

Thereby, to investigate the interaction mechanism, the equivalent circuit model of the whole system is established by aggregating the impedance model of each part on the PCC, as shown in Figure 5A. In small-signal impedance analysis, the local grid is normally modeled as the Thevenin equivalent circuit, while the SEC and the wind farm are modeled as the Norton equivalent circuit. According to the impedance network model proposed in Liu et al. (2018), the system impedance can be aggregated by the parallel connection of wind farm impedance and AC grid impedance and then connected in series with SEC impedance. As shown in Figure 5B, the resistance and reactance of the whole system can be represented by the sum of each part.

FIGURE 5

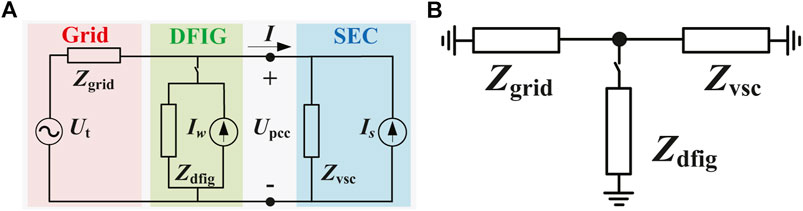
FIGURE 5. (A) Equivalent circuit model of the whole system. (B) Equivalent impedance network model of the whole system.

The stability criterion based on the second-order RLC series resonance circuit has been widely applied in recent works (Miao, 2012; Liu and Xie, 2017) to assess the system stability. By combining with this criterion and the derived impedance models, the oscillation mechanism and characteristics can be analyzed based on the impedance-frequency curves, which are more intuitive and convenient compared with the Nyquist plots

$\{\begin{array}{c}{R}_{\text{sys}}=\text{Re}\left(Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)+Z_{\text{vsc}}\left(s\right)\right)>0\\ X_{\text{sys}}=\text{Im}\left(Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)+Z_{\text{vsc}}\left(s\right)\right)=0\end{array},(17)$

where $R_{\text{sys}}$ and $X_{\text{sys}}$ are the system resistance and reactance.

4 Mechanism and Characteristics Analysis

According to the equivalent impedance model of the system built in Section 3, the impact of local grid strength and SEC parameters on the system stability are analyzed in this section. Then, the effect of the integration of the DFIG-based wind farms on the oscillation is analyzed as well.

4.1 Local Grid Strength

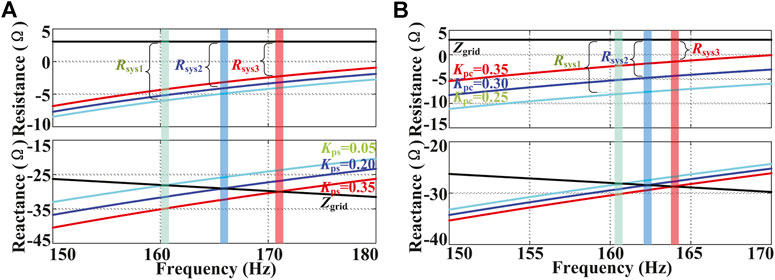
To analyze the impact of local grid strength on the electrical oscillation, the variation of the SCR from 5.1 to 1.7 is analyzed under the same operating condition as Scenario 1 in Section 2.2 without the SEC outer loop and the integrated DFIG. The impedance-frequency curves of the grid and the SEC are depicted in Figure 6A. It can be found that both the resistance and reactance of the SEC follow a parabolic trend increase with the negative value. Note that in Figure 6A and the following figures, the grid reactance is represented by its opposite number $-X_{\text{grid}}$ to better find out the frequency intersection point, while the grid resistance is still $R_{\text{grid}}$. According to Eq. 17, when the system equivalent reactance $X_{\text{sys}}=0$$\left(X_{\text{vsc}}=-X_{\text{grid}}\right)$, the system will be stable when the system equivalent resistance $R_{\text{sys}}=R_{\text{vsc}}+R_{\text{grid}}>0$. When reducing the SCR of the local grid, the grid resistance follows a small increase, while the grid reactance follows a significant increase and thus the intersection point for $X_{\text{vsc}}=-X_{\text{grid}}$ is shifted to the left, which means the resonant frequency of the system is reduced. Then, the system equivalent resistance $\left(R_{\text{sys}}=R_{\text{vsc}}+R_{\text{grid}}\right)$ changes from positive to negative at the corresponding resonant frequency. In Figure 6A, the system equivalent resistance decreases from $R_{\text{sys}1}$ to $R_{\text{sys}3}$. Therefore, the system stability is weakened with the reduction of the SCR. The fast uptrend of $R_{\text{vsc}}$ and $X_{\text{vsc}}$ in the investigated MFO region plays a key role in the oscillation, while the reduction of the SCR has an incentive effect.

FIGURE 6

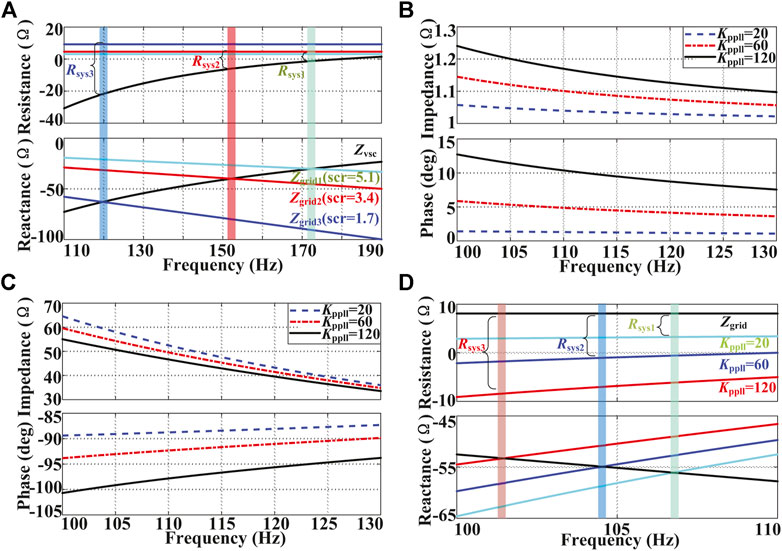
FIGURE 6. Impact of SCR on the impedance-frequency curves. (A)$Z_{\text{vsc}}\left(s\right)$ and $Z_{\text{grid}}\left(s\right)$ and impact of $K_{\text{ppll}}$ on the impedance-frequency curves. (B)$Z_{\text{pll}}\left(s\right)$; (C)$Z_{\text{vsc}}\left(s\right)$; and (D)$Z_{\text{vsc}}\left(s\right)$ and $Z_{\text{grid}}\left(s\right)$.

4.2 Controller Parameters of the SEC

4.2.1 PLL Parameters of the SEC

According to Eq. 14, since the power loop is directly coupled with the current loop instead of PLL in the numerator, the term $\left(1+H_{\text{s}}\left(s-j{\omega }_1\right)\right)$ can be regarded as a disturbance term to the current loop and thus can be ignored in the analysis of the PLL parameters. Besides, the decoupling term can also be ignored for its small influence. Then, the impedance model of the SEC can be simplified as

$Z_{\text{vsc}}\left(s\right)=-\frac{H_{\text{c}}\left(s-j{\omega }_1\right)+s{L}_{\text{f}}}{1-\frac{1}{2}\left(I_{\text{c}}{H}_{\text{c}}\left(s-j{\omega }_1\right)+U_{\text{pccd}}\right)T_{\text{pll}}\left(s-j{\omega }_1\right)}.(18)$

The numerator of Eq. 18 represents the impedance of the SEC without considering the influence of PLL. According to Eq. 19, it can be found that the resistance of the SEC will be positive without the influence of PLL since $K_{\text{pc}}>0$. The phase angle of $Z_{\text{vsc},\text{nopll}}\left(s\right)$ will be less than $-{90}^{\circ }$ because of the existence of the resistance term $K_{\text{pc}}$

$Z_{\text{vsc},\text{nopll}}\left(s\right)=K_{\text{pc}}-j\left(\frac{K_{\text{ic}}}{\omega -{\omega }_1}-\omega L_{\text{f}}\right).(19)$

Then, the denominator of Eq. 18 which represents the influence of PLL is analyzed. Since $K_{\text{ppll}}\gg K_{\text{ipll}}/\left(\omega -{\omega }_1\right)$ in the investigated MFO region, the integral gain of PLL can be ignored. Besides, $U_{\text{pccd}}=1$ is considered in the further analysis. Thus, the denominator of Eq. 18 can be simplified as

$Z_{\text{pll}}\left(s\right)=\frac{1}{2}\frac{K_{\text{ppll}}^2\left(1-I_{\text{c}}{K}_{\text{pc}}\right)+K_{\text{ppll}}{I}_{\text{c}}{K}_{\text{ic}}+2{\left(\omega -{\omega }_1\right)}^2}{K_{\text{ppll}}^2+{\left(\omega -{\omega }_1\right)}^2}+j\frac{1}{2}\frac{K_{\text{ppll}}^2{I}_{\text{c}}{K}_{\text{ic}}+K_{\text{ppll}}\left(1+I_{\text{c}}{K}_{\text{pc}}\right){\left(\omega -{\omega }_1\right)}^2}{\left(\omega -{\omega }_1\right)\left[K_{\text{ppll}}^2+{\left(\omega -{\omega }_1\right)}^2\right]},(20)$

$\angle Z_{\text{pll}}\left(s\right)=arctan\frac{K_{\text{ppll}}^2{I}_{\text{c}}{K}_{\text{ic}}+K_{\text{ppll}}\left(1+I_{\text{c}}{K}_{\text{pc}}\right){\left(\omega -{\omega }_1\right)}^2}{\left(\omega -{\omega }_1\right)\left[K_{\text{ppll}}^2\left(1-I_{\text{c}}{K}_{\text{pc}}\right)+K_{\text{ppll}}{I}_{\text{c}}{K}_{\text{ic}}+2{\left(\omega -{\omega }_1\right)}^2\right]}.(21)$

According to Eq. 20, both Re$\left(Z_{\text{pll}}\left(s\right)\right)$ and Im$\left(Z_{\text{pll}}\left(s\right)\right)$ follow a parabolic trend increase with the increase of $K_{\text{ppll}}$. Therefore, the magnitude of $Z_{\text{pll}}\left(s\right)$ has a positive correlation with $K_{\text{ppll}}$. According to Eq. 21, since the coefficients of $K_{\text{ppll}}^2$ and $K_{\text{ppll}}$ in the numerator are larger than the denominator, $\angle Z_{\text{pll}}\left(s\right)$ also has a positive correlation with $K_{\text{ppll}}$. By contrast, $\angle Z_{\text{pll}}^{-1}\left(s\right)$ has a decreasing trend and may cause the phase angle of $Z_{\text{vsc}}\left(s\right)$ to be over $-{90}^{\circ }$ in the investigated MFO region. Therefore, it can be found that the negative damping effect of the SEC is mainly caused by the influence of PLL.

The increase of $K_{\text{ppll}}$ from 20 to 120 pu is analyzed under the same operating condition as in Section 4.1, with SCR = 1.7. The corresponding influence on the impedance-frequency curves of $Z_{\text{pll}}\left(s\right)$ and $Z_{\text{vsc}}\left(s\right)$ is illustrated in Figures 6B,C. Obviously, the variational tendency of the curves aligns with the above analysis. In addition, both the resistance and reactance-frequency curves of the SEC and the local grid are depicted in Figure 6D. With the increase of $K_{\text{ppll}}$, the resistance of the SEC changes from positive to negative, while the negative value of the reactance of the SEC becomes smaller. Thus, the system resonant frequency is reduced, and the system resistance at the corresponding resonant frequency decreases from $R_{\text{sys}1}$ to $R_{\text{sys}3}$, which is changed from positive to negative. That means the larger the $K_{\text{ppll}}$, the more significant the negative effects of PLL on the system stability.

4.2.2 Current Loop Parameters of the SEC

According to Eq. 18, $Z_{\text{vsc}}\left(s\right)$ can be expressed as the quotient of $Z_{\text{vsc},\text{nopll}}\left(s\right)$ and $Z_{\text{pll}}\left(s\right)$, and the influence of the SEC current loop is represented in both of them. First, the influence of $K_{\text{pc}}$ is analyzed. According to (19), with $K_{\text{pc}}$ increases nearby the critical points of the oscillation, Re$\left(Z_{\text{vsc},\text{nopll}}\left(s\right)\right)$ is increased and thus the strength of the system damping while Im$\left(Z_{\text{vsc},\text{nopll}}\left(s\right)\right)$ remains unchanged. According to Eq. 20 and Eq. 21, Re$\left(Z_{\text{pll}}\left(s\right)\right)$ decreases linearly while Im$\left(Z_{\text{pll}}\left(s\right)\right)$ increases linearly with the increase of $K_{\text{pc}}$, which means $\angle Z_{\text{pll}}\left(s\right)$ becomes more positive while $\angle Z_{\text{pll}}^{-1}\left(s\right)$ becomes more negative. Thus, the influence of $K_{\text{pc}}$ on $Z_{\text{vsc},\text{nopll}}\left(s\right)$ and $Z_{\text{pll}}\left(s\right)$ is opposite. However, the influence of $K_{\text{pc}}$ on $Z_{\text{pll}}\left(s\right)$ is represented in the term $\left(I_{\text{c}}{K}_{\text{pc}}+1\right)$ and thus the variation of $K_{\text{pc}}$ has small influence on this term. Therefore, the influence of $K_{\text{pc}}$ is mainly reflected in $Z_{\text{vsc},\text{nopll}}\left(s\right)$ instead of $Z_{\text{pll}}\left(s\right)$.

The increase of $K_{\text{pc}}$ from 0.25 to 0.35 pu is analyzed under the same operating condition as in Section 4.1, with SCR = 1.7 and $K_{\text{ppll}}$ = 60 pu. The corresponding influence on the impedance-frequency curves of $Z_{\text{vsc},\text{nopll}}\left(s\right)$, $Z_{\text{pll}}\left(s\right)$ and $Z_{\text{vsc}}\left(s\right)$ is illustrated in Figures 7A–C. In addition, both the resistance- and reactance-frequency curves of the SEC and the local grid are depicted in Figure 7D. According to Figure 7C, with $K_{\text{pc}}$ increases nearby the critical points of the oscillation, $\angle Z_{\text{vsc}}\left(s\right)$ changes from more than $-{90}^{\circ }$ to less than $-{90}^{\circ }$, which means that the resistance of the SEC changes from negative to positive. Correspondingly, the reactance of the SEC changes very little since the sine function is around the peak zone. Thus, the system resistance at the corresponding resonant frequency becomes positive. In Figure 7D, the system equivalent resistance increases from $R_{\text{sys}1}$ to $R_{\text{sys}3}$ due to the increase of SEC resistance with $K_{\text{pc}}$, which also validates the above analysis. Hence, the system stability has a positive correlation with $K_{\text{pc}}$.

FIGURE 7

FIGURE 7. Impact of $K_{\text{pc}}$ on the impedance-frequency curves. (A)$Z_{\text{vsc},\text{nopll}}\left(s\right)$; (B)$Z_{\text{pll}}\left(s\right)$; (C)$Z_{\text{vsc}}\left(s\right)$; and (D)$Z_{\text{vsc}}\left(s\right)$ and $Z_{\text{grid}}\left(s\right)$.

In addition, the influence of $K_{\text{ic}}$ is analyzed. According to Eq. 19, with $K_{\text{ic}}$ increases, Im$\left(Z_{\text{vsc},\text{nopll}}\left(s\right)\right)$ is decreased while Re$\left(Z_{\text{vsc},\text{nopll}}\left(s\right)\right)$ remains unchanged. By comparison with that, the influence of $K_{\text{ic}}$ on $Z_{\text{pll}}\left(s\right)$ can also be ignored and thus $Z_{\text{pll}}^{-1}\left(s\right)$ is regarded as constant. Note that Re$\left(Z_{\text{vsc},\text{nopll}}\left(s\right)\right)$ remains unchanged during the variation of $K_{\text{ic}}$; thus, the resistance of the SEC is only determined by $Z_{\text{pll}}^{-1}\left(s\right)$ which can be expressed as $Z_{\text{pll}}^{-1}\left(s\right)=R_{\text{pll}}-j{X}_{\text{pll}}$, where $R_{\text{pll}}$, $X_{\text{pll}}>0$. Therefore, $Z_{\text{vsc}}\left(s\right)$ can be expressed as

$Z_{\text{vsc}}\left(s\right)=\left[H_{\text{c}}\left(s-j{\omega }_1\right)+s{L}_{\text{f}}\right]\left(R_{\text{pll}}-j{X}_{\text{pll}}\right)=R_{\text{pll}}{K}_{\text{pc}}-X_{\text{pll}}\left(\frac{K_{\text{ic}}}{\omega -{\omega }_1}-\omega L_{\text{f}}\right)-j\left[X_{\text{pll}}{K}_{\text{pc}}+R_{\text{pll}}\left(\frac{K_{\text{ic}}}{\omega -{\omega }_1}-\omega L_{\text{f}}\right)\right].(22)$

According to Eq. 22, the increase of $K_{\text{ic}}$ leads to the decrease of both the resistance and reactance of the SEC and thus causes the higher system resonant frequency. Then, the system resistance at the corresponding resonant frequency is reduced. Thus, the system stability has a negative correlation with $K_{\text{ic}}$.

4.2.3 Power Loop Parameters of the SEC

The term $\left(1+H_{\text{s}}\left(s-j{\omega }_1\right)\right)$ is reconsidered when focusing on the effect of the power loop of the SEC. As discussed before, only the influence of the power loop on $Z_{\text{vsc},\text{nopll}}\left(s\right)$ needs to be analyzed since it has no effect on $Z_{\text{pll}}\left(s\right)$

$Z_{\text{vsc},\text{nopll}}\left(s\right)=H_{\text{c}}\left(s-j{\omega }_1\right)\left(1+H_{\text{s}}\left(s-j{\omega }_1\right)\right)+s{L}_{\text{f}}=K_{\text{pc}}\left(1+K_{\text{ps}}\right)-\frac{K_{\text{ic}}{K}_{\text{is}}}{{\left(\omega -{\omega }_1\right)}^2}-j\left(\frac{K_{\text{ic}}\left(1+K_{\text{ps}}\right)+K_{\text{is}}{K}_{\text{pc}}}{\omega -{\omega }_1}-\omega L_{\text{f}}\right).(23)$

Obviously, the influence of the outer loop and inner loop on the impedance of the SEC is coupled directly. Considering ${\left(\omega -{\omega }_1\right)}^2{K}_{\text{pc}}{K}_{\text{ps}}>K_{\text{ic}}{K}_{\text{is}}$ at the investigated MFO region, it can be found that the resistance of the SEC is improved slightly due to the consideration of the power loop at the same frequency. However, the reactance of the SEC becomes more negative and thus the resonant frequency point is shifted to the right, and the system resistance is reduced at the new resonant frequency. Then, further analysis of the interaction between the current loop and the power loop is provided. According to Eq. 23, when $K_{\text{pc}}$ or $K_{\text{ps}}$ increases, the resistance of the SEC becomes more positive while the reactance becomes more negative, and thus, the system stability is improved. $K_{\text{ps}}$ increasing from 0.05 to 0.35 pu is analyzed under the same operating condition as in Section 4.1, with the SEC outer loop and SCR = 5.1. The corresponding influence on the resistance- and reactance-frequency curves of the SEC and the local grid is illustrated in Figure 8A. The system equivalent resistance increases from $R_{\text{sys}1}$ to $R_{\text{sys}3}$ due to the increase of SEC resistance with $K_{\text{ps}}$. The variational tendency of the curves aligns with the above analysis.

FIGURE 8

FIGURE 8. Impact of different factors on $Z_{\text{vsc}}\left(s\right)$ and $Z_{\text{grid}}\left(s\right)$. (A)$K_{\text{ps}}$. (B)$K_{\text{pc}}$.

In addition, when $K_{\text{ic}}$ or $K_{\text{is}}$ increases, both the resistance and reactance of the SEC become more negative. Note that the reduction of the reactance is in favor of the system stability, while the reduction of the resistance has an opposite effect. Since $\left(\omega -{\omega }_1\right)>\left(1+K_{\text{ps}}\right)K_{\text{is}}$, the variation of the resistance is larger than that of the reactance with $K_{\text{is}}$ increases, which means that the system resistance at the corresponding resonant frequency becomes negative and thus weakens the system stability. Likewise, the influence of $K_{\text{ic}}$ is similar to that of $K_{\text{is}}$. Besides, the coefficient of $K_{\text{pc}}$ and $K_{\text{ic}}$ in Eq. 23 is $\left(1+K_{\text{ps}}\right)$, while the coefficient of $K_{\text{ps}}$ and $K_{\text{is}}$ is $K_{\text{pc}}$. Thus, the influence of the power loop is lower than that of the current loop because $\left(1+K_{\text{ps}}\right)>K_{\text{pc}}$. This analysis is verified by comparing Figures 8A,B, which show that the influence of $K_{\text{pc}}$ ranges from 0.2 to 0.3 pu, with $K_{\text{ps}}$ = 0.2 pu.

4.3 Operating Condition and Controller Parameters of the DFIG

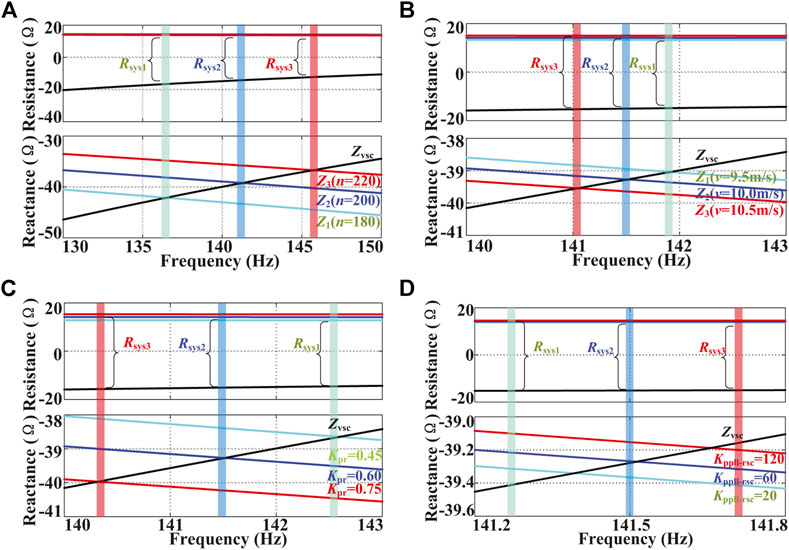
4.3.1 Number of Grid-Connected DFIG-WTs

The integration of the DFIG-based wind farms is not considered in the above subsections when focusing on the influence of the control parameters of the SEC. In this part, the effect of the number of grid-connected DFIG-WTs on the system stability is analyzed. According to Eq. 15, since the PLL dynamics of the DFIG mainly reflects the nearby fundamental frequency (Vieto and Sun, 2018; Sun et al., 2019), it can be neglected during the analysis in the investigated MFO region. Besides, $K_{\text{pr}}$ is dominant in the RSC current control loop, while $K_{\text{ir}}$ is less important and can be ignored in the following analysis. Thus, the equivalent resistance and reactance of the multiple DFIG-WTs can be simplified as (Sun et al., 2019)

$\begin{array}{cc}{R}_{\text{dfig}}=\frac{r_{\text{r}}+K_{\text{pr}}}{n{S}_{\text{lip}}}+\frac{r_{\text{s}}}{n},& X_{\text{dfig}}=\frac{\omega \left(L_{\text{r}}+L_{\text{s}}\right)}{n}\end{array},(24)$

where n represents the number of DFIG-WTs. According to Eq. 24, the DFIG represents as a resistance-inductance since the rotor slip $S_{\text{lip}}=\left(s-j{\omega }_{\text{r}}\right)/s$ is positive in the investigated MFO region. It is contrary to the SSO mechanism that the DFIG represents as an inductance in series with a negative resistance in the SSO frequency region. Compared with SSO caused by the DFIG, the frequency of the electrical oscillation studied in this article is about 100–200 Hz, which is a kind of MFO. The negative damping of the system is induced by the SEC instead of the DFIG, which means that the mechanism of this electrical oscillation is totally different from that of SSO caused by the DFIG (Sun et al., 2019).

According to Figure 5, the integration of the DFIG is equivalent to inserting an impedance on the PCC, which is in parallel with the local grid. The parallel impedance is still resistive and inductive in the investigated MFO region, which can be expressed as

$Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)\approx \frac{-X_{\text{grid}}{X}_{\text{dfig}}+j{X}_{\text{grid}}{R}_{\text{dfig}}}{R_{\text{dfig}}+j\left(X_{\text{grid}}+X_{\text{dfig}}\right)}=\frac{X_{\text{grid}}\left[X_{\text{grid}}{R}_{\text{dfig}}+j\left(R_{\text{dfig}}^2+X_{\text{grid}}{R}_{\text{dfig}}+X_{\text{dfig}}^2\right)\right]}{R_{\text{dfig}}^2-{\left(X_{\text{grid}}+X_{\text{dfig}}\right)}^2},(25)$

where $R_{\text{grid}}$ is neglected due to its small value. According to Eq. 25, since $X_{\text{dfig}}\gg R_{\text{dfig}}$ in the investigated MFO region, the reduction of Re$\left(Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)\right)$ is much larger than Im$\left(Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)\right)$ with the increase of n. Thus, the resonant frequency point of the system shifts to the right, and the corresponding system resistance changes from negative to positive. The influence of n increasing from 180 to 220 is analyzed in Figure 9A under the same operating condition as Scenario 2 in Section 2.2, with SCR = 1.7. The system equivalent resistance increases from $R_{\text{sys}1}$ to $R_{\text{sys}3}$ due to the increase of SEC resistance with frequency. It can be concluded that the larger the n nearby the critical points of the oscillation, the more positive the effect of DFIG-WTs on the system stability. In addition, since $R_{\text{dfig}}$ and $X_{\text{dfig}}$ are the inverse proportional function of n, the influence of n on the system is significant when n is not large.

FIGURE 9

FIGURE 9. Impact of different factors on $Z_{\text{vsc}}\left(s\right)$ and $Z_{\text{grid}}\left(s\right)$. (A)n; (B) wind speeds; (C)$K_{\text{pr}}$; and (D)$K_{\text{ppll}-\text{rsc}}$.

4.3.2 Wind Speed

According to Eq. 24, the resistance of the DFIG can be expressed as $\left(r_{\text{r}}+K_{\text{pr}}\right)/n{S}_{\text{lip}}+r_{\text{s}}/n$. Contrary to the SSO mechanism of the DFIG, the rotor slip $S_{\text{lip}}=\left(s-j{\omega }_{\text{r}}\right)/s$ is positive in the investigated MFO region. With the increase of the wind speed, the rotor speed ${\omega }_{\text{r}}$ is increased while the rotor slip decreases. Thus, the rotor resistance $\left(r_{\text{r}}+K_{\text{pr}}\right)/n{S}_{\text{lip}}$ is larger when the wind speed is high, which means that the DFIG will provide more positive damping for the whole system. The influence of wind speeds in the range of 9.5–10.5 m/s on the system impedance is analyzed in Figure 9B. The system equivalent resistance changes from $R_{\text{sys}1}$ to $R_{\text{sys}3}$, which is increased slightly due to the increase of Re$\left(Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)\right)$ with wind speed. Therefore, the increase of the wind speed leads to better system stability.

4.3.3 Current Loop Parameters of the RSC

With the increase of $K_{\text{pr}}$, the rotor resistance $\left(r_{\text{r}}+K_{\text{pr}}\right)/n{S}_{\text{lip}}$ is increased directly since the rotor slip is positive in the investigated MFO region, which means that the DFIG will provide more positive damping for the whole system when $K_{\text{pr}}$ is relatively large. The influence of $K_{\text{pr}}$ in the range of 0.45–0.75 pu on the system impedance is analyzed in Figure 9C. The system equivalent resistance changes from $R_{\text{sys}1}$ to $R_{\text{sys}3}$, which is increased slightly due to the increase of Re$\left(Z_{\text{dfig}}\left(s\right)\left|\right|Z_{\text{grid}}\left(s\right)\right)$ with $K_{\text{pr}}$. Therefore, the influence of $K_{\text{pr}}$ is similar to that of the wind speed, which is helpful for the system stability.

4.3.4 PLL Parameters of the DFIG

In this part, the influence of PLL parameters of the DFIG is reconsidered based on the impedance model in Eq. 15. The influence of $K_{\text{ppll}-\text{rsc}}$ increasing from 20 to 120 pu on the system impedance is illustrated in Figure 9D. Note that when the bandwidth of PLL increases with $K_{\text{ppll}-\text{rsc}}$, the equivalent resistance of the system increases slightly from $R_{\text{sys}1}$ to $R_{\text{sys}3}$, while the reactance almost remains unchanged in the investigated MFO region. By combining Figures 9A–D, the change of the system impedance caused by the PLL parameters of the DFIG is much smaller than other factors. Thus, it is not an efficient method to improve the system stability by adjusting $K_{\text{ppll}-\text{rsc}}$ of the DFIG.

5 Simulation Verification

The impact of the controller parameters and the operating condition of the system on the oscillation are investigated in Section 4. The time-domain simulations are conducted to validate the correctness of the theoretical analysis.

5.1 Local Grid Strength

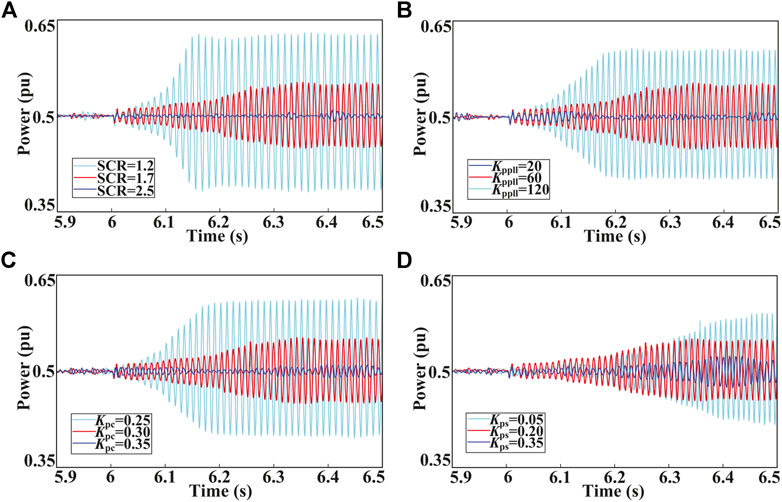
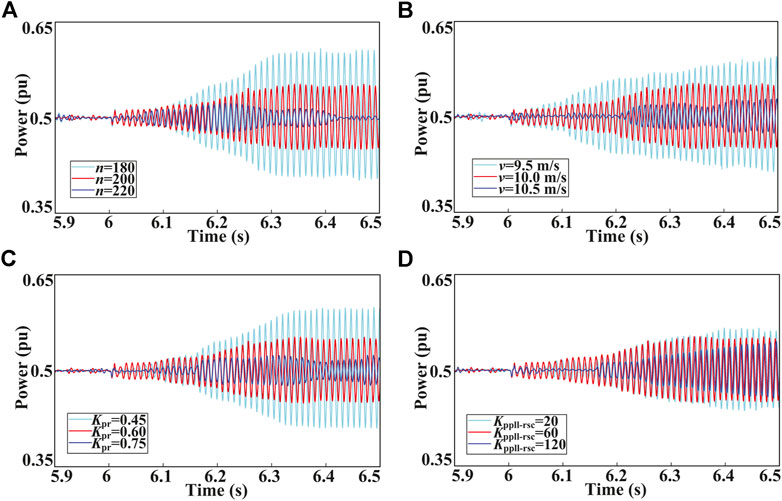
The impact of the local grid strength is analyzed under the following operating condition: the number of grid-connected DFIG-WTs is 200, the wind speed is 10 m/s, SCR of the local grid is 3.4, and other system parameters are the same as in Section 2.2. Figure 10A shows the output active power responses on the PCC for a sudden change of the SCR from 1.2 to 2.5 at t = 6 s. Obviously, the oscillation state changes from convergent to divergent with the decrease of the SCR. Therefore, the system stability has a positive correlation with the local grid strength. The simulation results align with the analysis in Section 4.1.

FIGURE 10

FIGURE 10. Output power varies with (A) SCR, (B)$K_{\text{ppll}}$, (C)$K_{\text{pc}}$, and (D)$K_{\text{ps}}$.

5.2 Control Parameters of the SEC

The impact of the PLL, current loop, and power loop of the SEC on the oscillation characteristics is analyzed under the same operating condition as in Section 4.1, with a sudden change of the SCR from 3.4 to 1.7 at t = 6 s. As shown in Figure 10B, the output active power responses on the PCC with $K_{\text{ppll}}$ in the range of 20–120 pu are measured. With $K_{\text{ppll}}$ increases, the oscillation state changes from convergent to invariable, which means that the oscillation is intensified when $K_{\text{ppll}}$ is large. As can be seen in Figure 10C, the oscillation state changes from divergent to convergent when $K_{\text{pc}}$ increases from 0.2 to 0.3 pu, which means that the system stability has a positive correlation with $K_{\text{pc}}$. Figure 10D illustrates the simulation results when $K_{\text{ps}}$ changes from 0.05 to 0.35 pu. When $K_{\text{ps}}$ increases, the divergence speed of the oscillation becomes slower, which means that the system stability has a positive correlation with $K_{\text{ps}}$. By comparing the waveforms in Figure 10C, it can be found that $K_{\text{ps}}$ has less impact on the oscillation than $K_{\text{pc}}$. The above conclusions agree with the analysis in Section 4.2.

5.3 Operating Condition and Controller Parameters of the DFIG

The impact of n, wind speed, RSC current loop, and PLL of the DFIG on the oscillation characteristics is analyzed under the same operating condition as in Section 5.2, with other control parameters of the SEC kept unchanged. Figure 11A shows that the output active power responds to the number of grid-connected DFIG-WTs, which ranges from 180 to 220. Obviously, the oscillation is gradually suppressed while the n increases. As shown in Figure 11B, the simulation results with the wind speed changes from 9.5 to 10.5 m/s are depicted. It can be observed that the system stability has a positive correlation with the wind speed. The output active power responses on the PCC with $K_{\text{pr}}$ from 0.45 to 0.75 pu are depicted in Figure 11C. As can be seen, the oscillation state changes from divergent to convergent when $K_{\text{pr}}$ increases. Figure 11D illustrates the simulation results when $K_{\text{ppll}-\text{rsc}}$ changes from 20 to 120 pu. When $K_{\text{ppll}-\text{rsc}}$ increases, the divergence speed of the oscillation becomes slightly slower. It can be found that $K_{\text{ppll}-\text{rsc}}$ has little influence on the oscillation compared with other parameters. In conclusion, the above simulation results align with the analysis in Section 4.3.

FIGURE 11

FIGURE 11. Output power varies with (A) number of DFIG-WTs, (B) wind speed, (C)$K_{\text{pr}}$, and (D)$K_{\text{ppll}-\text{rsc}}$.

6 Conclusion

A SEC with PQ-control faces the potential risk of a new type of electrical oscillation in the medium-frequency region when it transmits the wind-thermal–bundled power from the local grid and DFIG-based wind farms. In this study, the sequence impedance model of the SEC with the explicit analytic expression is derived to help understand the mechanism and characteristics of MFO. This oscillation mainly originates from the SEC, while the local AC grid strength and the integration of DFIG-based wind farms also have an influence on it. With regard to the SEC controllers, the system stability is weakened with the increased proportional gain of the PLL controller. In addition, system stability has a positive correlation with the proportional gains of both the current loop and the power loop. However, the influence of the power loop is not as large as that of the current loop. Regarding the influence of the local grid strength, the oscillation risk increases when the local grid is weak. Contrary to the SSO mechanism of the DFIG, the risk of this oscillation decreases when relatively more DFIG-WTs are integrated at a high wind speed. Besides, system stability has a positive correlation with the proportional gains of the RSC current loop, while the influence of PLL of the RSC is slight. In conclusion, these factors can influence the system resistance at the resonant frequency, and the oscillation may appear due to the negative damping under the undesired operating conditions and controller parameters of the DFIG, local grid, and SEC. All the theoretical analyses are verified by time-domain simulation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

KS and WY contributed to the conception and design of the study. CY and JW organized case studies. KS wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work was supported by the National Key R&D Program of China (2019YFB1505400).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.693903/full#supplementary-material

References

Baltas, G. N., Lai, N. B., Tarraso, A., Marin, L., Blaabjerg, F., and Rodriguez, P. (2021). Ai-based Damping of electromechanical oscillations by using grid-connected converter. Front. Energ. Res. 9, 598436. doi:10.3389/fenrg.2021.598436

CrossRef Full Text | Google Scholar

Cespedes, M., and Jian Sun, J. (2014). Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 29, 1254–1261. doi:10.1109/TPEL.2013.2262473

CrossRef Full Text | Google Scholar

Chen, C., Du, W., Du, W., Wang, H., and Littler, T. (2018). Sub-synchronous oscillations in power systems caused by grid-connected wind farms - a survey of mechanism studies. Csee Jpes 4, 495–503. doi:10.17775/CSEEJPES.2018.00560

CrossRef Full Text | Google Scholar

Chen, J., Li, L., Dong, F., Wang, X., Sheng, H., Sun, C., et al. (2020). An improved coordination method of multi-terminal mmc-hvdc system suitable for wind farm clusters integration. Int. J. Electr. Power Energ. Syst. 117, 105652. doi:10.1016/j.ijepes.2019.105652

CrossRef Full Text | Google Scholar

Christoph, B., Christian, R., Andreas, M., and Jochen, J. (2015). “Borwin1-first experiences with harmonic interactions in converter Dominated grids,” in Proc. 2015 Int. ETG Congress, Bonn, Germany, November 17–18, 2015, 592–602.

Google Scholar

Flourentzou, N., Agelidis, V. G., and Demetriades, G. D. (2009). Vsc-based hvdc power transmission systems: an overview. IEEE Trans. Power Electron. 24, 592–602. doi:10.1109/TPEL.2008.2008441

CrossRef Full Text | Google Scholar

Gao, B., Hu, Y., Song, R., Li, R., Zhang, X., Yang, L., et al. (2018). Impact of DFIG‐based wind farm integration on sub‐synchronous torsional interaction between HVDC and thermal generators. IET Generation, Transm. Distribution 12, 3913–3923. doi:10.1049/iet-gtd.2018.0328

CrossRef Full Text | Google Scholar

Huang, L., Xin, H., Yuan, H., Wang, G., and Ju, P. (2021). Damping effect of virtual synchronous machines provided by a Dynamical virtual impedance. IEEE Trans. Energ. Convers. 36, 570–573. doi:10.1109/TEC.2020.3040605

CrossRef Full Text | Google Scholar

Khazaei, J., Beza, M., and Bongiorno, M. (2018). Impedance analysis of modular multi-level converters connected to weak ac grids. IEEE Trans. Power Syst. 33, 4015–4025. doi:10.1109/TPWRS.2017.2779403

CrossRef Full Text | Google Scholar

Koralewicz, P., Shah, S., Gevorgian, V., Wallen, R., Jha, K., Mashtare, D., et al. (2020). Impedance analysis and phil Demonstration of reactive power oscillations in a wind power plant using a 4-mw wind turbine. Front. Energ. Res. 8, 156. doi:10.3389/fenrg.2020.00156

CrossRef Full Text | Google Scholar

Kunjumuhammed, L. P., Pal, B. C., Oates, C., and Dyke, K. J. (2017). The adequacy of the present practice in Dynamic aggregated modeling of wind farm systems. IEEE Trans. Sustain. Energ. 8, 23–32. doi:10.1109/TSTE.2016.2563162

CrossRef Full Text | Google Scholar

Liu, B., Li, Z., Wang, H., Dong, X., Su, W., Li, G., et al. (2021). Impedance modeling of Dfig wind farms with various rotor speeds and frequency coupling. IEEE Trans. Circuits Syst. 68, 406–410. doi:10.1109/TCSII.2020.2997927

CrossRef Full Text | Google Scholar

Liu, H., and Xie, X. (2019). Comparative studies on the impedance models of vsc-based renewable generators for ssi stability analysis. IEEE Trans. Energ. Convers. 34, 1442–1453. doi:10.1109/TEC.2019.2913778

CrossRef Full Text | Google Scholar

Liu, H., Xie, X., and Liu, W. (2018). An Oscillatory Stability Criterion Based on the Unified $dq$ -Frame Impedance Network Model for Power Systems With High-Penetration Renewables. IEEE Trans. Power Syst. 33, 3472–3485. doi:10.1109/TPWRS.2018.2794067

CrossRef Full Text | Google Scholar

Liu, H., Xie, X., Zhang, C., Li, Y., Liu, H., and Hu, Y. (2017). Quantitative ssr analysis of series-compensated Dfig-based wind farms using aggregated rlc circuit model. IEEE Trans. Power Syst. 32, 474–483. doi:10.1109/TPWRS.2016.2558840

CrossRef Full Text | Google Scholar

Lyu, J., Cai, X., Amin, M., and Molinas, M. (2018). Sub‐synchronous oscillation mechanism and its suppression in MMC‐based HVDC connected wind farms. IET Generation, Transm. Distribution 12, 1021–1029. doi:10.1049/iet-gtd.2017.1066

CrossRef Full Text | Google Scholar

Miao, Z. (2012). Impedance-model-based ssr analysis for type 3 wind generator and series-compensated network. IEEE Trans. Energ. Convers. 27, 984–991. doi:10.1109/TEC.2012.2211019

CrossRef Full Text | Google Scholar

Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2020). Two-stage variable proportion coefficient based frequency support of grid-connected Dfig-wts. IEEE Trans. Power Syst. 35, 962–974. doi:10.1109/TPWRS.2019.2943520

CrossRef Full Text | Google Scholar

Shah, R., Sánchez, J. C., Preece, R., and Barnes, M. (2018). Stability and control of mixed AC-DC systems with VSC‐HVDC: a review. IET Generation, Transm. Distribution 12, 2207–2219. doi:10.1049/iet-gtd.2017.1140

CrossRef Full Text | Google Scholar

Shah, S., and Parsa, L. (2017). Impedance modeling of three-phase voltage source converters in Dq, sequence, and phasor Domains. IEEE Trans. Energ. Convers. 32, 1139–1150. doi:10.1109/TEC.2017.2698202

CrossRef Full Text | Google Scholar

Sun, B., Yu, Y., and Qin, C. (2017). Should china focus on the Distributed Development of wind and solar photovoltaic power generation? a comparative study. Appl. Energ. 185, 421–439. doi:10.1016/j.apenergy.2016.11.004

CrossRef Full Text | Google Scholar

Sun, K., Xiao, H., You, S., Li, H., Pan, J., Li, K.-J., et al. (2020). Frequency secure control strategy for power grid with large-scale wind farms through hvdc links. Int. J. Electr. Power Energ. Syst. 117, 105706. doi:10.1016/j.ijepes.2019.105706

CrossRef Full Text | Google Scholar

Sun, K., Yao, W., Fang, J., Ai, X., Wen, J., and Cheng, S. (2020). Impedance modeling and stability analysis of grid-connected Dfig-based wind farm with a vsc-hvdc. IEEE J. Emerg. Sel. Top. Power Electron. 8, 1375–1390. doi:10.1109/JESTPE.2019.2901747

CrossRef Full Text | Google Scholar

Vieto, I., and Sun, J. (2018). Sequence impedance modeling and analysis of type-iii wind turbines. IEEE Trans. Energ. Convers. 33, 537–545. doi:10.1109/TEC.2017.2763585

CrossRef Full Text | Google Scholar

Wang, L., Peng, J., You, Y., and Ma, H. (2019). Iterative approach to impedance model for small‐signal stability analysis. IET Renew. Power Generation 13, 78–85. doi:10.1049/iet-rpg.2018.5265

CrossRef Full Text | Google Scholar

Wang, Q., Yao, W., Fang, J., Ai, X., Wen, J., Yang, X., et al. (2020). Dynamic modeling and small signal stability analysis of Distributed photovoltaic grid-connected system with large scale of panel level Dc optimizers. Appl. Energ. 259, 114132. doi:10.1016/j.apenergy.2019.114132

CrossRef Full Text | Google Scholar

Wang, X., Harnefors, L., and Blaabjerg, F. (2018). Unified impedance model of grid-connected voltage-source converters. IEEE Trans. Power Electron. 33, 1775–1787. doi:10.1109/TPEL.2017.2684906

CrossRef Full Text | Google Scholar

Wen, B., Boroyevich, D., Burgos, R., Mattavelli, P., and Shen, Z. (2017). Inverse nyquist stability criterion for grid-tied inverters. IEEE Trans. Power Electron. 32, 1548–1556. doi:10.1109/TPEL.2016.2545871

CrossRef Full Text | Google Scholar

Xiao, H., Du, W., Song, Y., Wang, Q., Ding, J., Chen, D., et al. (2016). Wind-thermal-bundled power transmission by ac/dc system and coordinated control - a review. 12th IET International Conference on AC and DC Power Transmission (ACDC 2016), Beijing, China, January, 2016. doi:10.1049/cp.2016.0470

CrossRef Full Text | Google Scholar

Xiong, Y., Yao, W., Wen, J., Lin, S., Ai, X., Fang, J., et al. (2020). Two-level combined control scheme of vsc-mtdc integrated offshore wind farms for onshore system frequency support. IEEE Trans. Power Syst. 36, 1. doi:10.1109/TPWRS.2020.2998579

CrossRef Full Text | Google Scholar

Xu, J., Qian, Q., Zhang, B., and Xie, S. (2019). Harmonics and stability analysis of single-phase grid-connected inverters in Distributed power generation systems considering phase-locked loop impact. IEEE Trans. Sustain. Energ. 10, 1470–1480. doi:10.1109/TSTE.2019.2893679

CrossRef Full Text | Google Scholar

Yan, C., Yao, W., Wen, J., Fang, J., Ai, X., and Wen, J. (2020). Modelling and comparison analysis of grid‐connected DFIG‐based wind farm in weak grid. IET Renew. Power Generation 14, 2406–2415. doi:10.1049/iet-rpg.2019.1382

CrossRef Full Text | Google Scholar

Yan, C., Yao, W., Wen, J., Fang, J., Ai, X., and Wen, J. (2020). Optimal Design of probabilistic robust Damping controllers to suppress multiband oscillations of power systems integrated with wind farm. Renew. Energ. 158, 75–90. doi:10.1016/j.renene.2020.05.008

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Yu, T., Shu, H. C., Zhang, C.-K., Yao, W., et al. (2018). Passive control Design for multi-terminal vsc-hvdc systems via energy shaping. Int. J. Electr. Power Energ. Syst. 98, 496–508. doi:10.1016/j.ijepes.2017.12.028

CrossRef Full Text | Google Scholar

Yogarathinam, A., Kaur, J., and Chaudhuri, N. R. (2017). Impact of inertia and effective short circuit ratio on control of frequency in weak grids interfacing lcc-hvdc and Dfig-based wind farms. IEEE Trans. Power Deliv. 32, 2040–2051. doi:10.1109/TPWRD.2016.2607205

CrossRef Full Text | Google Scholar

Zhang, C., Cai, X., Molinas, M., and Rygg, A. (2019). Frequency‐domain modelling and stability analysis of a DFIG‐based wind energy conversion system under non‐compensated AC grids: impedance modelling effects and consequences on stability. IET Power Electro. 12, 907–914. doi:10.1049/iet-pel.2018.5527

CrossRef Full Text | Google Scholar

Zhou, Q., Ding, Y., Mai, K., Bian, X., and Zhou, B. (2019). Mitigation of subsynchronous oscillation in a vsc-hvdc connected offshore wind farm integrated to grid. Int. J. Electr. Power Energ. Syst. 109, 29–37. doi:10.1016/j.ijepes.2019.01.031

CrossRef Full Text | Google Scholar

Zhou, W., Wang, Y., Torres-Olguin, R. E., and Chen, Z. (2020). Effect of reactive power characteristic of offshore wind power plant on low-frequency stability. IEEE Trans. Energ. Convers. 35, 837–853. doi:10.1109/TEC.2020.2965017

CrossRef Full Text | Google Scholar

Zou, C., Rao, H., Xu, S., Li, Y., Li, W., Chen, J., et al. (2018). Analysis of resonance between a vsc-hvdc converter and the ac grid. IEEE Trans. Power Electron. 33, 10157–10168. doi:10.1109/TPEL.2018.2809705

CrossRef Full Text | Google Scholar