Potential of Photovoltaic Panels on Building Envelopes for Decentralized District Energy Systems

The expected increase of the penetration of distributed renewable energy technologies into the electricity grid is expected to lead to major challenges. As a main stakeholder, authorities often lack the appropriate tools to frame and encourage the transition and monitor the impact of energy transition policies. This paper aims at combining relatively detailed modeling of the PV generation potential on the building’s envelope while retaining the energy system optimization approach. The problem is addressed as a multiobjective, mixed-integer linear programming problem. Compared to the existing literature in the field, the proposed approach combines advanced modeling of the energy generation potential from PV panels with detailed representation of the district energy systems, thus allowing an accurate representation of the interaction between the energy generation from PV and the rest of the system. The proposed approach was applied to a typical residential district in Switzerland. The results of the application of the proposed method show that the district can achieve carbon neutrality based on PV energy alone, but this requires covering all the available district’s rooftops and part of the district’s facades. Whereas facades are generally disregarded due to their lower generation potential, the results also allow concluding that facade PV can be economically convenient for a wide range of electricity prices, including those currently used by the Swiss grid operators. Achieving self-sufficiency at district scale is challenging: it can be achieved by covering approximately 42–100% of the available surface when the round-trip efficiency decreases from 100 to 50%. The results underline the importance of storage for achieving self-sufficiency: even with 100%, round-trip efficiency for the storage, very large capacities are required. However, energy demand reduction through renovation would allow reaching self-sufficiency with half of the PV and storage capacity required.

1 Introduction

Political authorities and other stakeholders in the energy value chain have the responsibility to implement energy transition pathways by increasing decentralized renewable energy generation. As a main stakeholder, authorities often lack the appropriate tools to frame and encourage the transition and monitor the impact of energy transition policies. Network operators as well need appropriate frameworks and guidelines to implement the transition with a business perspective.

The electrification of the buildings stock has the potential to lower local pollutant emissions and increase the energy system efficiency, especially when coupled with local renewable energy sources (Henchoz et al., 2015; Suciu et al., 2016). In terms of small, decentralized renewable energy generation systems, roofs constitute the most obvious solution for the integration of PV generation in buildings (Lucon, 2014). However, while the recent decrease in PV systems’ investment costs made rooftop PV a proven, cost-convenient choice in many parts of the world [even in absence of subsidies (Lang et al., 2015)], today more than 90% of the solar potential on the top of roofs is still unexploited.

In urban environments, however, the limited available space for including locally generated renewable energy compared to the energy demand represents an additional challenge towards complete decarbonization of the energy system. As a result of this challenge, together with the low cost of PV modules, research in recent years also investigated the role of facades in an urban context.

Initial feasibility studies focused on a general estimation of the potential from PV facades, introducing the concept of vertically oriented surfaces (Chwieduk, 2009). These early studies, however, did not consider photovoltaic (PV) panels or shadow modeling, thus generally overestimating the PV generation potential. However, even when these aspects are taken into account, existing literature shows that the inclusion of PV panels from different oriented roofs and facades can be beneficial for matching electricity demand profiles. As a relevant example, Freitas et al. (2018) showed the economic feasibility of facades for the case of two building blocks in Portugal and demonstrated that including facades has the effect of reducing the required storage size.

To expand the scope from single buildings to whole districts, 3D simulation software using ray tracing technique like LiDAR in combination with geographic information systems (GIS) tools was developed (Redweik et al., 2013; Catita et al., 2014; Walter and Kämpf, 2015) and commonly used to estimate solar potential on all surfaces in a district (Kämpf et al., 2010; Verso et al., 2015; Desthieux et al., 2018). The use of these tools also allowed the inclusion of surrounding buildings in the model, a necessary condition to include the effect of shading on the potential of PV generation from facades. In addition, the sky view factor is a commonly used indicator for determining the amount of diffuse irradiation on the surface (Brito et al., 2017; Chatzipoulka et al., 2018), whose use becomes even more relevant in the case of PV systems on facades.

The solar potential on facades is in general lower than that on roofs (Rehman et al., 2018). However, a previous research suggested that facade PV can be crucial to achieving high levels of decarbonization and self-sufficiency in urban environments. Redweik et al. (2013) showed that the combined PV potential on roofs and facades exceeds the nonbaseload demand for a district located in Portugal and could furthermore contribute up to 75% of the total electricity demand. Also, Aguacil et al. (2019) suggested taking PV installation on facades into account, especially for high-rise buildings. Li and Liu (2018) and Díez-Mediavilla et al. (2019) even suggested that facades can be competitive with roof installations.

The potential for facades also strongly depends on the location: at lower latitudes [such as in the case of Portugal Redweik et al. (2013)], rooftop solar is economically superior to facades, as in the latter case, the payback increased from 10 to 20 years. At higher altitudes, however, the situation can be different: Horn et al. (2018), based on the results of a case-study application in Germany, suggested that the solar potential on facades can exceed that on roofs during the winter months, as a result of the sun being low in the sky. Clearly, the orientation of the surface also has a role in the performance of the system. As a relevant example, Pantić et al. (2016) determined a 12-year carbon and a 10-year payback time of PV panels mounted on south-oriented facades in Serbia.

A comparative analysis of the state of the art of research about the role of facades in urban energy systems is represented in Table 1. The analysis shows one of the main gaps in the existing literature: most available studies only consider facade PV systems on their own and do not explore the importance of their interaction with the rest of the building energy system (BES). These studies are usually conducted from the perspective of urban planners and architects and are aimed at assessing the solar potential on the complete envelope to find the best concept and designs of buildings.

TABLE 1

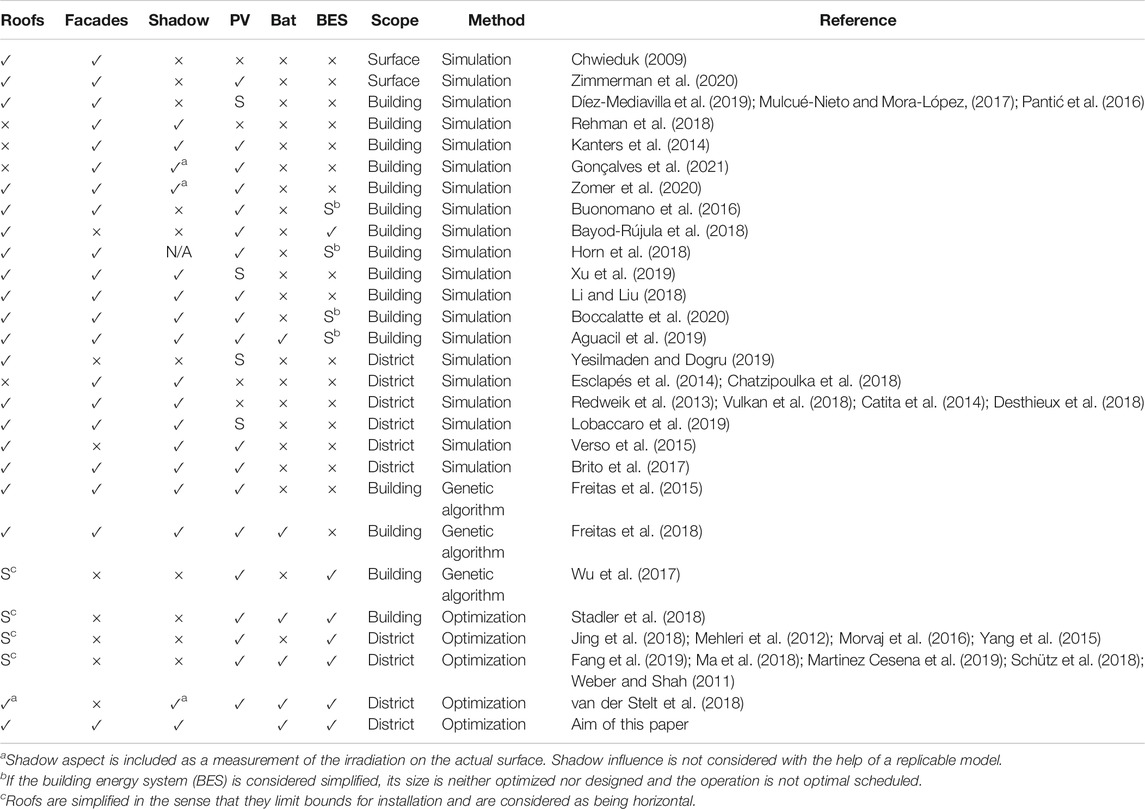
TABLE 1. Literature overview. ✓ = yes, aspect included, × = no, not included, S = simplified, N/A = not answered, PV = photovoltaic panels, BAT = battery, and BES = building energy system.

On the other hand, papers focusing on the design of the energy system of buildings which include irradiation models are generally focused on two aspects. On the one hand, irradiation models are required to assess the solar contribution to the heating and cooling demand (Girardin, 2012b). On the other hand, irradiation models are also used for modeling the contribution of solar panels (both thermal and PV) to BES (Wu et al., 2017; Stadler et al., 2018). However, in most cases, these studies rely on the use of global irradiation to model the incoming solar radiation. This corresponds to assuming horizontal panels (Duffie and Beckman, 2013), a simplification that was shown to generate a relevant error (overestimation or underestimation, depending on the case) in the calculation of how much energy is generated by solar systems (Middelhauve et al., 2021). Therefore, based on the aforementioned literature review and to the best of our knowledge, we believe that there is a gap in the academic literature related to the intersection of energy system design in buildings and the solar potential on facades.

This work accordingly aims to investigate the following research contributions and questions:

• Close the gap between architects assessing solar potential on building surfaces and engineers designing solar-based energy systems.

• Integrate different PV panel orientation possibilities together with a shadow model from the surroundings in the optimization approach of energy systems.

• Investigate the choice on the economic and environmental rationale for installing PV panels on facades and, if so, on which ones.

• Discuss the question of the role of PV systems and particularly of facade PV in urban districts, focusing on the amount of PV that

• is needed to be self-sufficient;

• can be installed while being economically beneficial.

• Estimate the amount of electricity generated from the district that, from the perspective of the electricity grid, needs to be distributed or stored and the related costs.

Whereas it would be impossible to achieve a general conclusion based on one single study, this work aims at suggesting a potential methodological approach to address this gap in the scientific literature and presents the application to a specific case study in order to showcase the potential of the proposed approach.

2 Materials and Methods

This work seeks to integrate PV modules on both roofs and facades in the optimal design and scheduling of energy conversion and storage technologies. Furthermore, the aim is to investigate the response of a fully integrated multienergy system on the district level to the inclusion of high shares of solar energy. In the proposed approach, buildings interact with each other in two ways: 1) by contributing to the overall electricity balance of the district, both consuming and generating electricity, and 2) by shading neighboring surfaces and roofs, thus influencing the actual potential for local solar generation.

To be able to take both the optimal integration at the building level and the behavior of the whole district into account, a mixed-integer linear programming (MILP) framework is formulated, where unit sizes and installation decisions in each building are used as the main optimization variables. The approach is based on the general formulation of the BES, which can be then applied to different building types in a district. The model derives from the BES framework described by Stadler (2019), to which the reader is referred for further details. In this paper, special attention is dedicated to the further development of the oriented irradiation modeling proposed in earlier work from the authors Middelhauve et al. (2021), which is modified to include the modeling of shading effects between different buildings in the districts similar to the work by Schüler (2018).

To clearly differentiate decision variables from input parameters, a bold typeset is used to represent all decision variables. Additional parameter values can be found in the Supplementary Material. As all sets are predefined, normal and capital typeset is used. The main problem sets are the set of buildings B and their allocated facades F and the set of available conversion and storage units U; the different days of the year are represented by periods in the set P, to which hourly timesteps are allocated and contained in set T. The sets A and Y are used to express the orientation of the PV panels with azimuth and tilt angles, respectively.

The BES modeling framework includes multiple unit technologies that can contribute to satisfying the different energy demands (Figure 1). Both the space heating (SH) and domestic hot water (DHW) demands can be fulfilled by a gas boiler, converting natural gas into thermal energy, or by heat pumps (HPs) and electrical heaters, both converting electricity to thermal energy. PV panels are also considered as energy conversion units, converting incoming solar irradiation to electricity. The system also includes storage technologies: thermal and electrical storage. For thermal storage, two different tanks are considered: one for SH and one for DHW. Electricity energy storage is considered in the form of lithium-ion batteries.

FIGURE 1

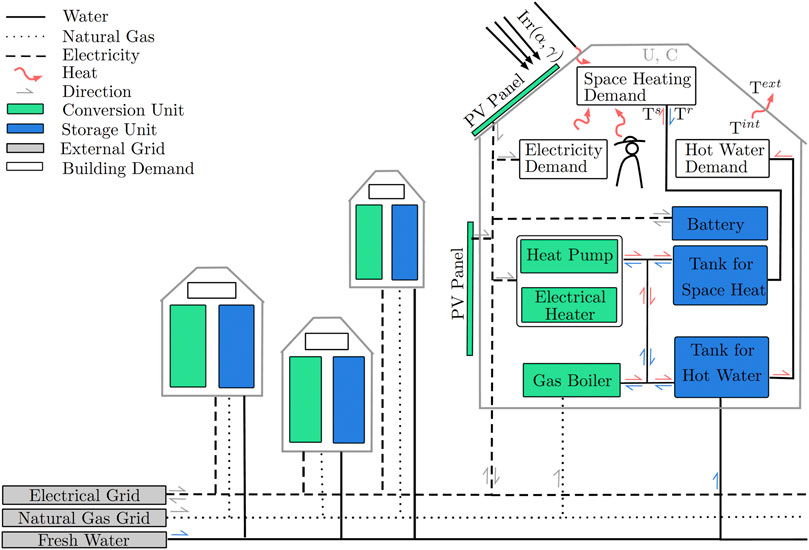
FIGURE 1. Overview of the district energy system. U, C: building heat transfer and capacity factor, Irr: irradiation, and T: temperatures.

In the proposed models, buildings are differentiated not only based on their construction characteristics (surface, volume, roof type, etc.) but also by their usage, such as residential or industrial, and their renovation state. In addition to having an effect on the total yearly demand, these aspects also influence the hourly energy demand profiles, which in turn have a relevant effect on the overall energy balance of the district.

2.1 Problem Objectives

The MILP problem is defined with the minimization of the BES costs as the main problem objective. This involves the combination of two separate contributions: operating and capital expenses. As these two objectives are generally competing (solutions with high capital expenses (CAPEX) have low operational expenses (OPEX), and vice versa), the problem must be approached using a multiobjective optimization (MOO) approach. The MOO problem is implemented using the ϵ-constraint method, thus considering the OPEX as the main problem objective and solving different optimization problems where the CAPEX is constrained at incrementally increasing values. The same principle is then repeated after inverting the roles of the two objectives. The annual OPEX consist of the expenses and gains related to the interaction with the national electricity and natural gas grids.

${\mathit{C}}_b^{op}=\sum _{p\in \text{P}}\sum _{t\in \text{T}}\left(c^{el,+}\cdot {\dot{E}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{g}\mathit{r},+}-c^{el,-}\cdot {\dot{E}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{g}\mathit{r},-}+c^{ng,+}\cdot {\dot{H}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{g}\mathit{r},+}\right)\cdot d_t\cdot d_p\forall b\in \text{B}(1)$

In Eq. 1, c^el,+, c^el,−, and c^ng,+ represent the electricity purchase and selling price and the natural gas purchase price; ${\dot{H}}_{b,p,t}^{gr,+}$ represents the energy flow of natural gas purchased from the grid for building b at time step t and typical day p; similarly, ${\dot{E}}_{b,p,t}^{gr,+}$ and ${\dot{E}}_{b,p,t}^{gr,-}$ represent the electricity flows from and to the grid. Annual values are integrated over each typical period p and accounted with their frequency d.

The annual CAPEX include the investment and replacement costs of the unit technologies with different expected lifetimes.

$\begin{array}{ll}\hfill {\mathit{C}}_b^{cap}& =\frac{i(1+i)}{{(1+i)}^n-1}\left({\mathit{C}}_b^{inv}+{\mathit{C}}_b^{rep}\right)\hfill \end{array}(\mathrm{2a})$

$\begin{array}{ll}\hfill {\mathit{C}}_b^{inv}& =\sum _{u\in \mathit{U}}{b}_{b,u}\cdot \left(i_{b,u}^{c1}\cdot {\mathit{y}}_{\mathit{b},\mathit{u}}+i_{b,u}^{c2}\cdot {\mathit{f}}_{\mathit{b},\mathit{u}}\right)\hfill \end{array}(\mathrm{2b})$

$\begin{array}{ll}\hfill {\mathit{C}}_b^{rep}& =\sum _{u\in \mathit{U}}\sum _{r\in \mathit{R}}\frac{1}{{\left(1+i\right)}^{r\cdot l_u}}\cdot \left(i_{b,u}^{c1}\cdot {\mathit{y}}_{\mathit{b},\mathit{u}}+i_{b,u}^{c2}\cdot {\mathit{f}}_{\mathit{b},\mathit{u}}\right)\forall b\in \text{B}\hfill \end{array}(\mathrm{2c})$

In Eq. 2a, expenses are annualized over the project time horizon n using the project interest rate i (Turton, 2012, Ch. 10). The parameters i^c1 and i^c2 represent the linear version of the unit cost function with bare module b^u (Stadler, 2019). If the project horizon exceeds the lifetime of a unit (l^u), the unit must be replaced and purchased again (Eq. 2c). For units with a lifetime greater than or equal to the project time horizon, the total number of replacements (R) is zero (Stadler, 2019).

2.2 Key Performance Indicators

In addition to the problem objectives, key performance indicators (KPIs) are defined to provide additional information regarding the performance of the system. For readability, the following equations are expressed with annual values. The self-consumption (SC) and the self-sufficiency (SS) are KPIs used to evaluate the performance of the system in terms of its interaction with the grid.

$\begin{array}{ll}\hfill \mathit{S}\mathit{C}& =\frac{\left({\sum }_{b\in \text{B}}{\mathit{E}}_{\mathit{b}}^{\mathit{p}\mathit{v},+}\right)-{\mathit{E}}^{\mathit{T}\mathit{R},-}}{\left({\sum }_{b\in \text{B}}{\mathit{E}}_{\mathit{b}}^{\mathit{p}\mathit{v},+}\right)}\hfill \end{array}(\mathrm{3a})$

$\begin{array}{ll}\hfill \mathit{S}\mathit{S}& =\frac{\left({\sum }_{b\in \text{B}}{\mathit{E}}_{\mathit{b}}^{\mathit{p}\mathit{v},+}\right)-{\mathit{E}}^{\mathit{T}\mathit{R},-}}{\left({\sum }_{b\in \text{B}}{\mathit{E}}_{\mathit{b}}^{\mathit{p}\mathit{v},+}\right)-{\mathit{E}}^{\mathit{T}\mathit{R},-}+{\mathit{E}}^{\mathit{T}\mathit{R},+}}\hfill \end{array}(\mathrm{3b})$

In Eq. 3a, SC represents the share of the generated electricity from all PV panels E^pv,+ consumed within the district (Luthander et al., 2015). In Eq. 3b, SS represents the ratio of the onsite generated electricity consumption to the total electricity demand (Luthander et al., 2015).

The benefit for selling the generated electricity to the grid and for avoiding electricity import is measured by annual revenues (AR) (Hartner et al., 2017). In this study, electricity can only be generated by PV panels; hence, their associated revenues are the only ones considered in the following Eq. 4:

$\mathit{A}\mathit{R}=(c^{el,+}\cdot \mathit{S}\mathit{C}+c^{el,-}\cdot (1-\mathit{S}\mathit{C}))\cdot \left(\sum _{b\in \text{B}}{\mathit{E}}_{\mathit{b}}^{\mathit{p}\mathit{v},+}\right)(4)$

Additional KPIs are used to evaluate how the system performs in terms of greenhouse gas (GHG) emissions, here included based on their CO₂ equivalence (Lucon, 2014).

${\mathit{G}}^{lca}={\mathit{G}}^{bes}+{\mathit{G}}^{op}(5)$

As shown in Eq. 5, the total global warming potential (GWP) G^lca is divided into the share coming from the operation G^op and the construction of the BES G^bes (Middelhauve et al., 2020).

${\mathit{G}}^{op}=\sum _{p\in \text{P}}\sum _{t\in \text{T}}\left(g_{p,t}^{el}\cdot {\mathit{E}}_{p,t}^{TR,+}-g_{p,t}^{el}\cdot {\mathit{E}}_{p,t}^{TR,-}+g^{ng}\cdot \sum _{b\in \text{B}}{\dot{\mathit{H}}}_{b,p,t}^{gr,+}\right)\cdot d_p\cdot d_t(6)$

Equation. 6 shows how the GWP from the system’s operations is calculated, where the period and time-dependent emission parameters g_p,t are accounted for the GWP per kWh consumed electricity E (Kantor and Santecchia, 2019) or natural gas H. The parameter d_t accounts for the duration of each timestep within a period and d_p for the frequency of each period within 1 year.

The database Ecoinvent (Wernet et al., 2016) documents the environmental impact of energy processes and materials and provides life cycle assessments of the different technologies. To assess the GWP of different unit technologies, the indicator “GWP 100a” of the method “IPCC 2013” documented in the online version 3.6 of Ecoinvent is adopted. This indicator considers GHG emissions based on the GWP published by the Intergovernmental Panel on Climate Change (IPCC) for a time horizon of 100 years. The GWP of different unit technologies G^bes is expressed in Eq. 7.

${\mathit{G}}^{bes}=\sum _{b\in \text{B}}\sum _{u\in \text{U}}\frac{1}{l_u}\cdot \left(i_u^{g1}\cdot {\mathit{y}}_{\mathit{b},\mathit{u}}+i_u^{g2}\cdot {\mathit{f}}_{\mathit{b},\mathit{u}}\right)(7)$

In addition to the total GWP of the system, the carbon payback time (CPT) is used as an additional KPI of the system.

$\mathit{C}\mathit{P}\mathit{T}=\frac{{\mathit{G}}^{\mathit{b}\mathit{e}\mathit{s},\mathit{p}\mathit{v}}}{{\sum }_{b\in \text{B}}{\sum }_{p\in \text{P}}{\sum }_{t\in \text{T}}(g_{p,t}^{el}\cdot {\mathit{E}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{p}\mathit{v},+})\cdot d_t\cdot d_p}(8)$

In Eq. 8, the CPT is calculated based on the indirect emissions of all PV panels G^bes,pv installed in the district and on the avoided emission while operating them (Kourkoumpas et al., 2018).

2.3 Energy Demand

As this study aims at estimating the extent to which decentralized renewable energy generation can be integrated into BES, three types of energy demands are considered in the model: SH, DHW, and electricity.

2.3.1 SH Demand

The general form of the SH demand can be expressed by the first-order dynamic model of buildings (Stadler, 2019).

${\dot{\mathit{Q}}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{S}\mathit{H}}={\dot{Q}}_{b,p,t}^{gain}-U_b\cdot A_b^{era}\cdot ({\mathit{T}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{i}\mathit{n}\mathit{t}}-T_{p,t}^{ext})-C_b\cdot A_b^{era}\cdot ({\mathit{T}}_{\mathit{b},\mathit{p},\mathit{t}+\mathit{1}}^{\mathit{i}\mathit{n}\mathit{t}}-{\mathit{T}}_{\mathit{b},\mathit{p},\mathit{t}}^{\mathit{i}\mathit{n}\mathit{t}})\forall b\in \text{B}\forall p\in \text{P}\forall t\in \text{T}(9)$

In Eq. 9, Q^gain represents internal heat gains from appliance, people, and solar irradiation and A^era represents the energy reference area (ERA), which has to be heated. The heat transfer coefficient U consists of the heat transfer by conduction and air renewal, whereas the thermal heat capacity C describes the response time of the internal temperature (Girardin, 2012a). The internal building temperature T^int is considered as a variable to be optimized. This allows the building heat capacity to work as an additional, free thermal storage for the BES, thus making it possible to use available surplus electricity from PV modules. Clearly, comfort should also be taken into account: this is done through the introduction of a penalty cost in the optimization problem objective of 0.2 CHF/K per hour when the indoor temperature exceeds predefined bounds.

The heat gain is made of two contributions: internal gains resulting from the usage of the building (${\dot{Q}}^{int}$) and solar irradiation $({\dot{Q}}_{b,p,t}^{irr})$.

${\dot{Q}}_{b,p,t}^{int}=A_b^{net}\cdot \sum _{r\in Rooms}{f}_{b,r}\cdot f_{r,p}^u\cdot ({\mathrm{\Phi }}_{r,p,t}^P+{\mathrm{\Phi }}_{r,p,t}^{A+L})\forall b\in \text{B}\forall p\in \text{P}\forall t\in \text{T}(10)$

The internal gains (Eq. 10) mainly represent the immediate consequence of people occupancy (superscript P) and of the usage of electric appliances and lights (superscript A + L). Demand profiles for different building and room usage are taken from the Swiss standard norm SIA (2015a). The total gains for each building result from the sum of the gains of each room of the building. A usage factor f^u is used to account for monthly/weekly variations related to the specific usage of each building and room type (SIA, 2015a). f_b,r represents the fraction of the total building’s surface allocated to each room r. The internal gains are normalized to the internal net surface of the building A^net, calculated as the heated surface without the base surface of inner and outer walls.

The Swiss norm SIA (2015a) also gives details about solar gains, based on a detailed knowledge of each building’s geometry.

${\dot{Q}}_{b,p,t}^{irr}=\sum _{f\in \text{F}}\frac{A^g}{A_{f,b}}\cdot f^s\cdot g\cdot ir{r}_{f,p,t}({\alpha }_f,{\gamma }_f)\forall b\in \text{B}\forall p\in \text{P}\forall t\in \text{T}(11)$

Perez (2014) details typical ratios of glass to facades surface A^g/A_f for each building type (Eq. 11). The g-values measure the amount of solar irradiation which is transferred to heat. It is assumed that shading devices are used for irradiation greater than 200 W/m² (Perez, 2014). f^s is a constant factor = 0.9 accounting for dirt and nonperpendicular irradiation on the windows (SIA, 2015a). The solar irradiation on the facades irr_f depends on the facade’s azimuth orientation α_f and the tilt angle γ.

All thermal loads are included in the heat cascade to satisfy the second law of thermodynamics. As the thermal load of SH ${\dot{Q}}^{SH}$ is variable, variable return and supply temperatures would lead to nonlinearity. This is dealt with by discretizing supply and return temperature levels. A detailed description of the approach proposed to deal with this nonlinearity of the BES model is presented in the Supplementary Material.

2.3.2 DHW Demand

Typical DHW demand is stated in standardized national norms (SIA, 2015a; SIA, 2015b). Similar to the internal heat gains, the DHW profile is specific to each room type and usage.

$Q_b^{dhw}=A_b^{net}\cdot \sum _{r\in Rooms}{f}_{b,r}\cdot f_{r,p}^u\cdot V_r^{dhw,ref}\cdot \frac{n^{ref}}{A_r^{net}}\cdot c_p^{dhw}\cdot {\rho }^{dhw}(T^{dhw}-T^{cw})\forall b\in \text{B}(12)$

In Eq. 12, the factor $n^{ref}/A_r^{net}$ expresses the number of reference units per net surface of the specific room. The cold water temperature is assumed to be constant at T^cw = 10^◦C, whereas the hot water temperature has to be delivered at T^dhw = 60^◦C to meet sanitary standards. The thermodynamic properties ${(\rho \cdot c_p)}^{dhw}$ are the density and the specific heat capacity of water. The daily profiles are derived from the occupancy profiles in combination with the activity profiles of the rooms SIA (2015a).

2.3.3 Electricity Demand

Two different methods are used to estimate the electricity demand, based on the availability of measurements from the existing buildings. When measurements are available, the electricity demand is modeled using the available measured data, after removing the heating demand Holweger et al. (2019). When measured data are not available, the electricity demand is calculated based on the profiles provided by the Swiss standard norm SIA (2015a).

${\dot{E}}_{b,p,t}^B=A_b^{net}\cdot \sum _{r\in Rooms}{f}_{b,r}\cdot f_{r,p}^u\cdot {\dot{E}}_{r,p,t}^{A+L}\forall b\in \text{B}\forall p\in \text{P}\forall t\in \text{T}(13)$

The electricity demand of the appliances and light of the different rooms are combined in the E^A+L term (Eq. 13). $A_b^{net}$, f_b,r, and $f_{r,p}^u$ factors are the same used to calculate the DHW demand.

2.4 Energy System

The energy system of the building includes all the different unit technologies that are used to fulfill the building’s energy demand. Energy can be exchanged with the electricity grid in both directions, whereas hot water and natural gas can only be supplied by the grid to the building. To account for the possibility that electricity can be both generated and consumed in the district itself, the load is balanced at the level of the district’s transformer. To ensure that no energy is accumulated between different periods, cyclic constraints are imposed both on the indoor building temperature and on the thermal and electrical energy storage systems. Cyclic constraints reset the state to its initial status at the end of each period. As a common practice in MILP of energy systems, the decision to purchase a unit is represented by a binary variable, whereas the unit size is represented by a continuous variable.

In this study, the validity range for PV installations has to be extended in comparison to previous studies (Middelhauve et al., 2021), in order to allow full installations on the building’s envelope. Simply extending the interval would drastically overestimate the cost for extensive PV installations, whereas linearizing the cost function in the vicinity of higher PV sizes would penalize small rooftop installations. Therefore, the cost function was piecewise linearized. For more insights about the modeling of the energy system, the reader might consult the Supplementary Material and refer to Stadler (2019) for the full description of the energy systems modeled in this study.

2.5 Solar Irradiation

The hourly irradiation is modeled using the anisotropic irradiation model which was first proposed by Perez et al. (1986) and later improved for all sky conditions (Perez et al., 1993). The skydome discretization (Robinson and Stone, 2004) is applied using the Ladybug plug-in of the Grasshopper suite (Roudsari and Adrian Smith Gordon Gill Architecture, 2013) to include the oriented irradiation into MILP formulation. For more information about modeling-oriented irradiation in MILP problems, the reader should refer to Middelhauve et al. (2021) and Schüler (2018). In the remaining part of this section, the focus is on the inclusion of facades, the main element of novelty in this work. Compared to roofs, the direct solar irradiation on facades highly depends on shading from neighboring buildings, making it necessary to include detailed shadow modeling. The shadow modeling employed in this study only includes the shadow from surrounding buildings, not from other obstacles (such as trees). Figure 2 visualizes an exemplary geometric relation between two buildings.

FIGURE 2

FIGURE 2. Exemplary visualization of the geometry for facade 1, with distance d¹² to building two and the sky limiting angle β.

The positions of buildings and facades are given in x, y, and z coordinates, where y points to the north and x to the east. The coordinate z is the elevation. The assumption is that the shortest distance is between the center point of the facades and the center point of the building (Figure 2).

$\begin{array}{ll}\hfill x_{f,b}& =|x_b-x_f|\hfill \end{array}(\mathrm{14a})$

$\begin{array}{ll}\hfill y_{f,b}& =|y_b-y_f|\hfill \end{array}(\mathrm{14b})$

$\begin{array}{ll}\hfill d_{f,b}& =\sqrt{{(y_{f,b})}^2+{(x_{f,b})}^2}\forall f\in \text{F},b\in \text{B}\hfill \end{array}(\mathrm{14c})$

Equations 14 show how the distance between buildings b and facades f in x and y coordinates is calculated. The sky limiting angle β represents the lowest elevation angle from which irradiation reaches the facades (Figure 2).

$\tan ({\beta }_{f,b})=\frac{h_b+z_b-z_f}{d_{f,b}}\forall f\in \text{F},b\in \mathbf{B}(15)$

In Eq. 15, the reference point for the sky limiting angle is the bottom of each facade (z_f). Based on this assumption, the building height’s effect on the electricity yield is only based on its role in the calculation of the total available surface (higher buildings have a larger facade surface available). A building’s height only influences the shading of other buildings’ solar generation potential, but not of its own. This is considered a conservative assumption in order not to overestimate the energy generated by PV panels installed on facades. The facades of high-rise buildings can be divided into several parts, applying the proposed approach.

The sky direction is expressed by the azimuth angle α, which is 0° for the north direction and 180° for the south orientation. Figure 3 shows the different azimuth angles of the facades, surrounded buildings, and skydome patches.

FIGURE 3

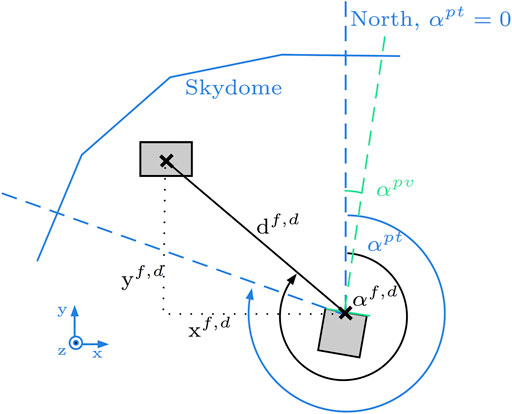
FIGURE 3. Outline sketch of different azimuth angles. The azimuth orientation of the facades is identical to possible PV modules α_pv. α_f,b: azimuth direction of surrounding buildings and α_pt: azimuth direction of each patch of the skydome.

Equation 16 shows how the azimuth position of building b is calculated. Knowing the signs of both catheti makes it possible to assess the correct quadrant for azimuth angle α_f,b ∈ [0^◦, 360^◦].

${\alpha }_{f,b}=\arctan \left(\frac{x_b-x_f}{y_b-y_f}\right)\forall f\in \text{F},b\in \text{B}(16)$

As a building is receiving irradiation from all patches of the skydome (pt ∈S), the sky limiting angle β is to be calculated for all sky directions.

$\tan ({\beta }_{f,b,\alpha })=\frac{h_b+z_b-z_f}{d_{f,b}}\cdot \cos (\mathrm{\Delta }\alpha )=\tan ({\beta }_{f,b})\cdot \cos ({\alpha }_{f,b}-{\alpha }_{pt})\forall f\in \mathbf{F},b\in \mathbf{B},\forall pt\in \mathbf{S}(17)$

In Eq. 17, the sky limiting angle β is the greatest in the azimuth direction α_f,b of the building causing the shadow. Finally, the highest sky limiting angle β_f,α in each azimuth direction α_pt of the skydome is selected among all surrounding buildings for each facade f (Eq. 18).

${\beta }_{f,\alpha }=\max \{{\beta }_{f,b,\alpha }:b\in \text{B}\}\forall f\in \text{F},{\alpha }_{pt}|pt\in \text{S}(18)$

The sky limiting angle in each azimuth direction is then used to determine the shaded irradiation. Thereby, the method is similar to the calculation of intermodular shading of PV modules on flat roofs (Middelhauve et al., 2021).

$s_{f,pt}=\left\{\begin{array}{cc}0\hfill & {ϵ}_{pt}\le {\beta }_{f,\alpha }\hfill \\ \frac{{ϵ}_{pt}+6-{\beta }_{f,\alpha }}{12}\hfill & {\beta }_{f,\alpha }-6<{ϵ}^{pt}<{\beta }_{f,\alpha }+6\hfill \\ 1\hfill & {ϵ}_{pt}\ge {\beta }_{f,\alpha }+6\hfill \end{array}\right.\forall f\in \text{F},({\alpha }_{pt},{ϵ}_{pt})|pt\in \text{S}(19)$

The skydome is piecewise linearized over the evaluation angle of one patch, which varies 12^◦, with ϵ_pt marking the central point (Eq. 19) of each patch. The resulting shading factor of one patch s_pt ∈ [0; 1] is equal to zero for completely shaded patches and one for completely unshaded patches.

$\begin{array}{ll}\hfill ir{r}_{f,pv}({\alpha }_{pv},{\gamma }_{pv})=& (-1)\cdot \sum _{pt\in \text{S}}{s}_{f,pt}\cdot ir{r}_{pt}({\alpha }_{pv},{\gamma }_{pv})\hfill \\ \hfill & \forall {\alpha }_{pv}\in \text{A},\forall {\gamma }_{pv}\in \text{Y}\hfill \end{array}(20)$

Equation 20 finally shows how the irradiation on facades is calculated when taking into account shading from neighboring buildings. As possible PV panels can only have the same orientation of the facades they are installed on, the azimuth and tilt orientation of the facades are equivalent to the orientation of the PV panel. In contrast to the azimuth angle, the tilt angle of the facades is always the same γ_pv = 90^◦. The irradiation of each oriented patch of the skydome irr_pt is transferred to the perpendicular irradiation, which is received on the PV panels. This is achieved using the principle of a two-stage rotation in a three-dimensional space, which is treated in detail in Middelhauve et al. (2021).

2.6 Data-Driven Approach

The data layers of Table 2 are used to represent multiple configurations of decentralized energy demand and generation. Except for the grid topology and measurement (Holweger et al., 2019), the approach uses Open Government Data (OGD) including the climatic conditions, building database (Federal Statistical Office, 2019) with roof and facade geometries (Federal Office of Topography swisstopo, 2019; Swiss Federal Office of Energy - Geoinformation - Sonnendach.ch, 2018), energy demand standards (SIA, 2016; 2015a), and statistical values (Girardin, 2012b).

TABLE 2

TABLE 2. List of the necessary data layers.

2.7 Case Study

The method is demonstrated on a typical, central European, periurban, residential area comprising 31 buildings, mostly single and multifamily houses (Figure 4A). The buildings considered are all connected to the same measured transformer (TR3716); the other buildings of the district are used solely for their shadowing effect. Figure 4B shows that whereas the largest share of the PV generation potential lies in the building roofs, facades also have significant potential. As expected, the south-oriented facades have the largest potential, followed by the east- and west-oriented facades. It is interesting to notice that the specific solar potential of the most promising south-oriented facades is higher than that of the least promising roofs. A large amount of annual input profiles requires clustering of the solar irradiation and the external temperature. The K-medoids clustering, commonly applied to combined heat and power systems (Domínguez-Muñoz et al., 2011), allows identifying 10 typical days and two extreme periods. While detailed information is available in the supplementary material, Table 3 provides an overview of the main building-related parameters.

FIGURE 4

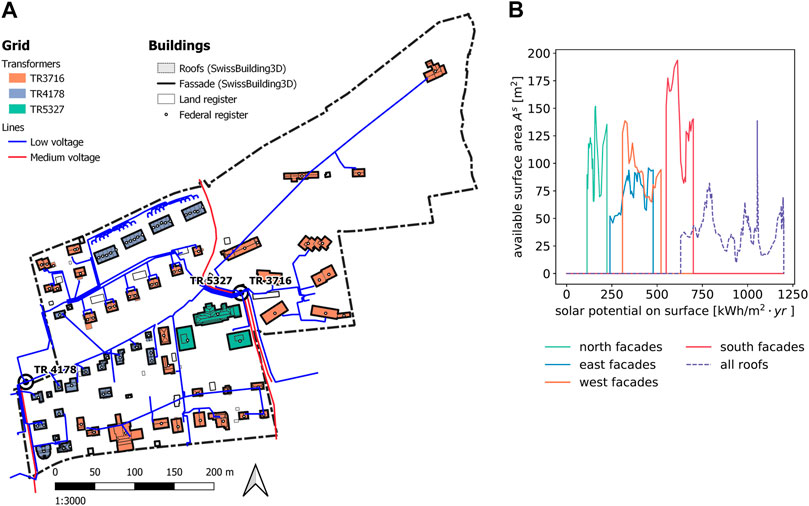
FIGURE 4. Details of the case-study area. (A) Map of the area, a typical central European periurban residential area. (B) Solar PV potential on roof and facade as a function of the orientation.

TABLE 3

TABLE 3. Input data for 31 buildings. All buildings are connected to the same low-voltage grid.

3 Results

3.1 What Is the Potential of Energy Generation From PV in the District?

The results of the optimization confirm what is observed about the per-surface generation potential. The conclusions resulting from the analysis of the potential from installing PV on facades are different depending on what side of the coin one looks at. The general trend, as expected from what is shown in Figures 4B, is that rooftop PV has a much better performance compared to facade-installed PV, which is clearly shown by the fact that panels are first installed on roofs (Figure 5A). The comparison of Figures 5A,B shows clearly the reason: in cost intensive solutions, the cost for facades dominates the total PV-related investment, while it still provides less than half of the total energy generated. However, looking at the same figures from another perspective, facades have the potential to increase the total energy generation from PV by approximately 97%. While they might not represent the most cost-efficient solution, they certainly can play an important role in improving the SS of the district.

FIGURE 5

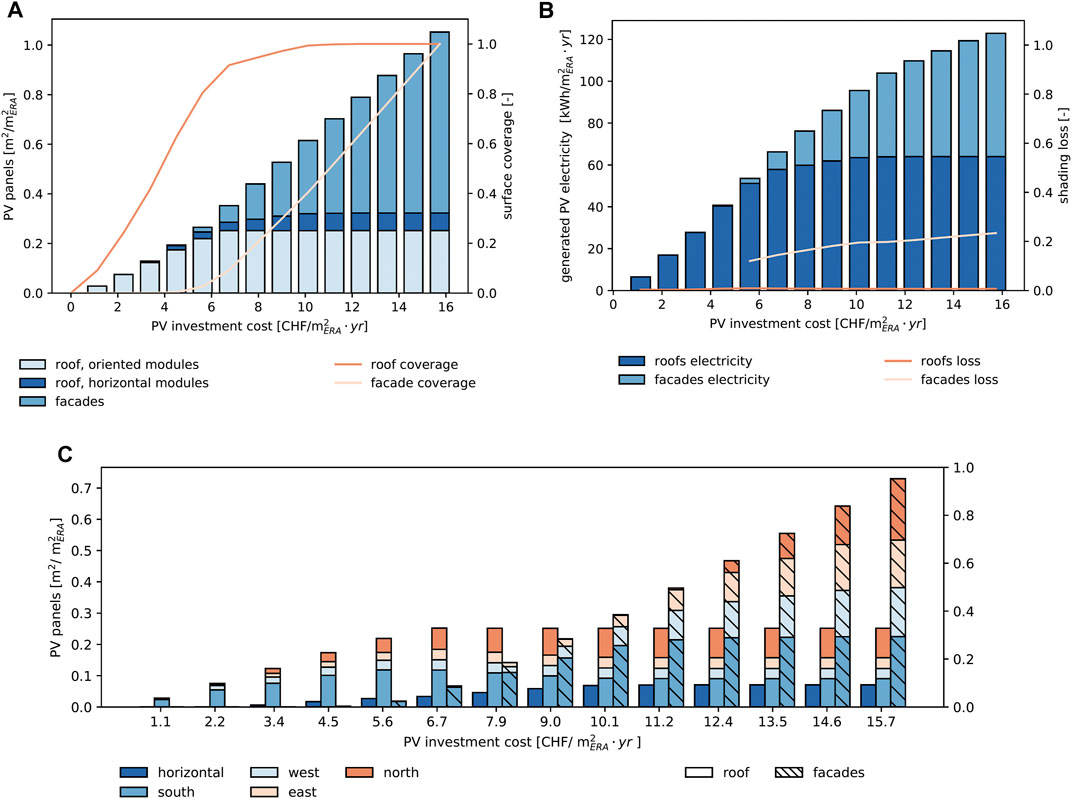
FIGURE 5. Economically best PV installation for 31 residential buildings, normalized to total energy reference area (ERA) in the district. (A) Area of installed modules sorted by orientation type, PV modules with tilt = 0^◦ are horizontal, tilt angles = 90^◦ are facades, and oriented modules summarize all other tilt angles. (B) Annual generated electricity and shading losses depending on surface type. (C) Area of installed PV sorted by sky direction. Aggregated azimuth angles: 316°- 45° North, 46°-135° East, 136°-225° South, 226°-315° West.

Looking more in detail at the surfaces where PV panels are installed (Figure 5C), it can be noticed that some of the vertical surfaces are used even when roofs are not fully exploited yet. This is a consequence of two factors: first, the fact that (as shown in Figure 4B) some facades have a higher specific PV generation potential than some roofs, as in the case of the south-oriented facades compared to tilted, north-oriented roofs; second, the fact that the CAPEX constraint is not enforced at the district level, but at building level. This implies that when at the district level there might still be 10% of roofs available, this might not be true at the building level, where the optimizer is then “forced” to start using facades instead.

3.2 Do We Need to Install PV on Facades? Step 1: Carbon Neutrality

The results of the optimization for a list of Pareto optimal solutions are shown in Figure 6. More specifically, Figure 6A shows that the district can become approximately carbon neutral already for a relatively low overall investment cost (approx. 12 CHF/m²yr). This result is achieved also thanks to a significant contribution of energy generated from the PV panels installed on facades, which contribute to approximately 40% of the total PV surface installed or 60% of the available facade area, corresponding to PV deployment on all well-oriented facades.

FIGURE 6

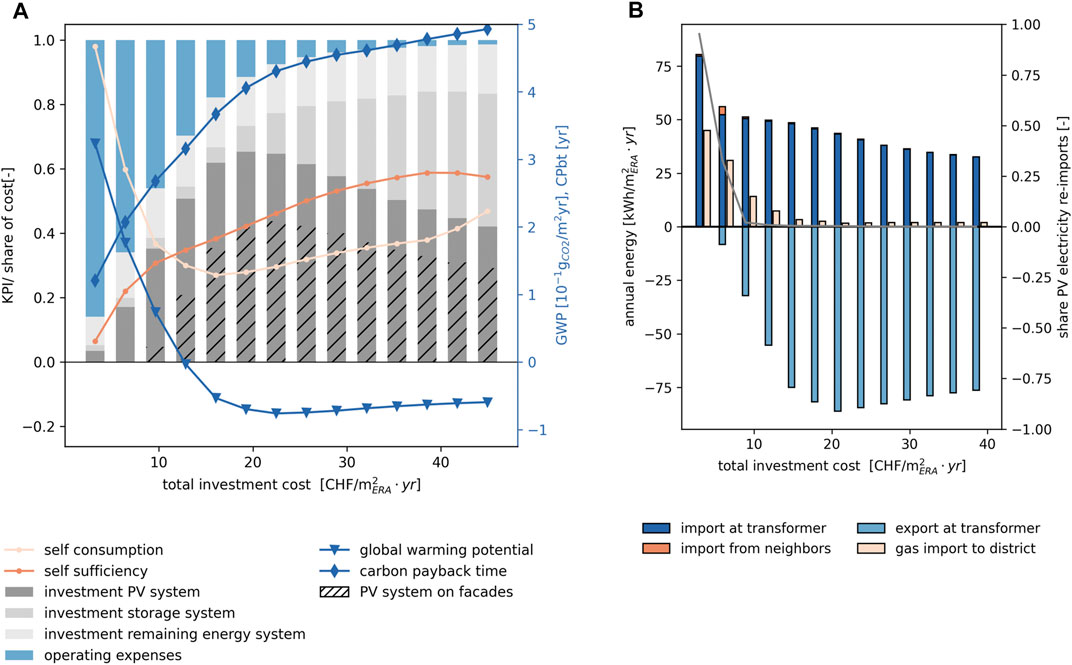
FIGURE 6. Results of the MOO of 31 buildings in one low-voltage grid, normalized to total ERA in the district. (A) performance indicators and cost distribution of identified energy systems; (B) electricity exchange and gas imports for the district.

Further increasing the allowed CAPEX only leads to a limited improvement in terms of the total GWP of the solution, which saturates at a total innvestment cost of approximately 20 CHF/m²yr (Figure 6A). Beyond this limit, the overall GWP of the solution actually worsens: the increase in PV surface installed is compensated by the lower specific generation of PV panels installed on facades and on the increasing battery capacity, which has little contribution to the overall energy balance but increases costs and GWP potential. As current tariffs (electricity cost = 20ct/kWh and feed-in price = 8 ct/kWh) favor self-consuming locally generated energy over selling it to the grid, solutions with increased CAPEX bound tend to shift towards the increase of battery capacity to reduce energy exchanges with the grid. This is shown clearly in Figure 6B: moving towards high-CAPEX solutions, the imports at the district transformer decrease, together with exports: the energy locally generated increases only marginally, while the focus is shifted towards using it locally to maximize revenues.

3.3 How Much PV Solar Energy Can Be Generated Locally and Cost-Efficiently?

The results presented in Figure 6 represent Pareto optimal solutions for the two competing objectives of minimizing OPEX and CAPEX. However, the choice of the individual prosumer will be influenced by the profitability of the investment, which is a result of the combined effects of CAPEX and OPEX. Policymakers and grid operators might be interested in knowing how different energy prices can influence the profitability of a PV investment and hence the amount of PV installed and of resulting energy generated. From the prosumer perspective, this translates into the question “how much PV panels can I install if I aim for the investment to pay back by the end of the PV panels’ lifetime?” From the policymaker perspective, the question instead is “how should tariffs be set in order to achieve the desired decentralized energy generation from PV panels?” The extent to which facade solutions are cost-efficient depends on the installed surface, as shown in Figure 7. Point A represents the surface of installed PV panels for which lifetime revenues and investment are equal. This shows that, with current tariffs, large surfaces of facades could be covered with PV panels, while still achieving a positive economic performance. This is strongly influenced by the choice of tariffs by the system operator.

FIGURE 7

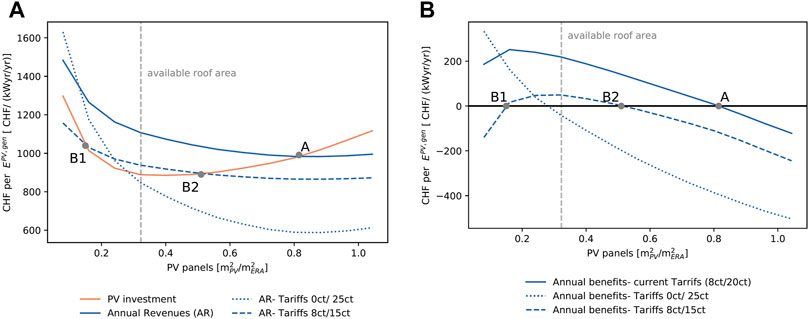
FIGURE 7. (A) PV investment per generated PV electricity E^PV,gen and implicit revenues for different feed-in/demand prices. Economic point: investment in PV and connected revenues are balanced. Point A: current tariffs (8 ct feed-in; 20 ct demand price). Points B1 and B2: exemplary tariffs with two break-even points. (B) Annual benefits, which are the annual revenues (AR) subtracted by the PV investment.

At current tariffs (0.20/0.08 CHF/kWh), large facade surfaces can be covered with PV panels in conditions where lifetime revenues are larger than the investment cost. Lowering the purchase price (e.g., 0.15/0.08 CHF/kWh) tends to worsen the economic performance in the whole surface range, as it affects the portion of the generated solar energy that is self-consumed. In this case, according to the optimization’s results, there is a limited window where PV is convenient: for installed surfaces below Point B1, the fixed component of the investment is predominant. For installed surfaces higher than B2 the combination of two factors makes these solutions economically unfavorable: first, new PV panels are installed on surfaces that generate less energy per unit of surface installed. Second, every new panel will mostly contribute to the AR with energy that is sold to the grid (and not self-consumed), which is paid less to the prosumer. Finally, the effect of decreasing feed-in tariffs to 0 CHF/kWh is shown by the dotted line. In this case, facades should be discarded: only self-consumed energy matters, so the most economically convenient choice is to install only a few panels and only on roofs.

Evidently, the location of the economic break-even point depends on a combination of the two tariffs. This can be seen more clearly in Figure 8, where Figure 8A shows the position of Point B1 (the lowest installed surface that makes the installation of PV panels economically favorable). Moving towards the upper white area would substantially mean eliminating the entry barrier to new producers, especially smaller ones. This can be achieved by a combination of feed-in and purchase tariffs. It is however more interesting to look at the position of Point B2 (highest economically favorable surface) in Figure 8B. This figure shows the importance of increasing feed-in prices if the objective is to maximize generation. For instance, even at today’s demand price, increasing the purchase price from 0.08 CHF/kWh to 0.10 CHF/kWh would theoretically make all roof and facade surface economically convenient. The results also show the extent of the variation. The average annual electricity generation from installed PV can range between 100 and 280 kWyr/yr, showing that appropriately choosing electricity tariffs can lead to an increase of almost 200% of the yearly energy generated by PV panels in the district. In the same figure, the dashed line represents the tipping point between the end of the roof surface available and the start of using facade surfaces. As it can be seen, even with today’s energy prices, facades (at least the ones with the highest solar irradiation) can be used for PV generation profitably. Understandably, increasing demand and feed-in prices plays in favor of increased profitability of facade surfaces. As mentioned above, at (0.20/0.10 CHF/kWh) tariffs, also the north-oriented facades become potentially valid for PV panel installation from an economic perspective.

FIGURE 8

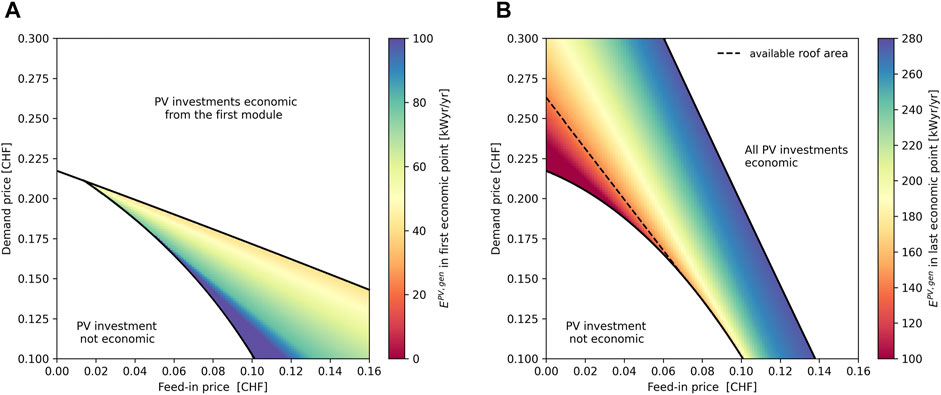
FIGURE 8. Variation of the PV yearly generation to achieve break-even as a function of feed-in and demand prices. (A) First break-even point (B1); (B) last break-even point (B2 or A) in Figure 7.

3.4 How Much PV Is Needed to Achieve Self-Sufficiency?

In previous results, it was shown that the district can achieve carbon neutrality relatively easily and with current tariffs, most facades are economically feasible. But how much PV is actually needed to cover the electricity demand at all times? In fact, not all generated energy is used locally. As shown in Figure 6A, the SC is below 60% for all scenarios, while a significant part of the generated energy is sold to the grid and purchased back in a second moment, thus using the grid as electricity storage. Including reimports in the definition of SS and assuming that the grid-as-storage works with 100% round-trip efficiency lead to the minimum required area of PV per ERA = 0.44 (Point S) to achieve self-sufficiency. Depending on the efficiency that is assumed for the grid-as-storage, the amount of surface covered by panels increases.

If the storage is assumed to be lithium-ion batteries (which would be the most likely case for district-level storage, connected to the same low-voltage grid as the district), it is possible to assume a relatively high round-trip efficiency for the grid-as-storage. In Figure 9A, the line for η = 0.85 can be used as a reference, showing that, in this case, the PV surface needs to be increased only marginally. Another relevant point in Figure 9 is represented by the “last economic point,” which is the largest amount of PV panels that can be installed with the expectation of recovering the investment within the panels’ lifetime with current tariffs. The efficiency of the grid-as-storage that allows SS at this point is approximately 0.59. Incidentally, this is quite similar to the round-trip efficiency of pumped hydro storage (PHS), today the most common way of doing grid-level storage in Switzerland. Further insights about storage systems for electricity are available at (Barnhart, 2018; Blanco and Faaij, 2018). Finally, the case of η = 0.40 is shown, a relatively optimistic example of the round-trip efficiency of power-to-gas storage systems. In this case, the results show that the available surface is simply not sufficient, and even covering all roofs and facades with PV panels would not allow achieving SS of the district. The actual minimum efficiency that needs to be achieved by the selected combination of storage technologies to achieve SS (that is, the efficiency that allows achieving SS when all surfaces in the district buildings are covered with PV panels) is η = 0.50. Power-to-gas-to-power storage systems should aim at achieving at least this round-trip efficiency if they should be used for grid storage purposes.

FIGURE 9

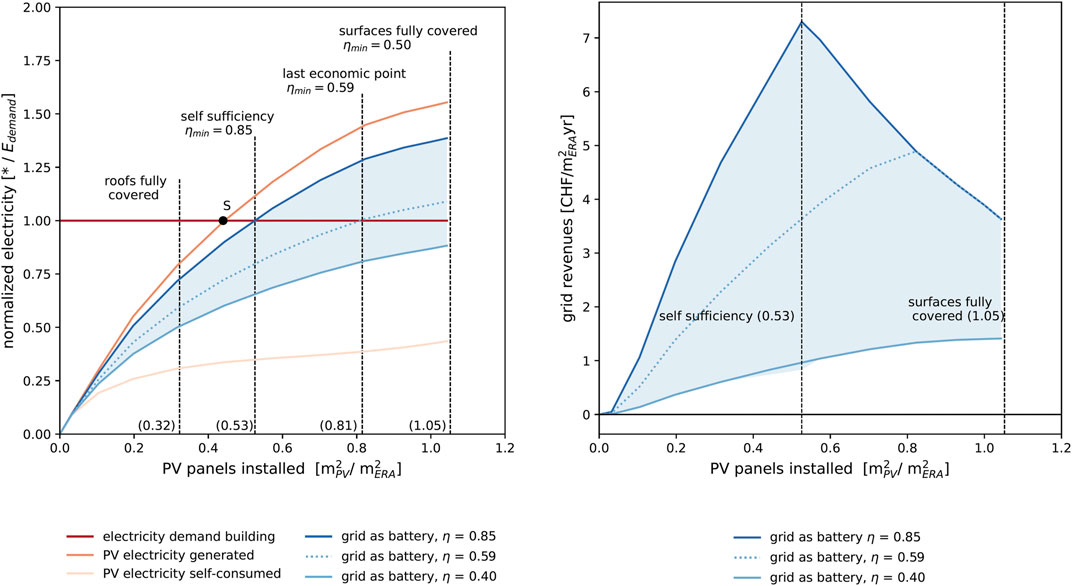
FIGURE 9. (A) The need for PV panels of 31 buildings balanced at the transformer to reach self-sufficiency (SS) with reimport for different round-trip efficiencies η. Point S: full SS with ideal storage (η = 100%) in place. (B) Revenues as a function of installed PV capacity and grid efficiency from the perspective of the grid. The grid operator buys electricity at a feed-in tariff of 0.08 CHF/kWh and resells for electricity price 0.20 CHF/kWh.

Figure 9B shows the perspective of the grid operator when looking at the importance of the efficiency of the grid-as-storage. Grid revenues are obtained due to the difference between feed-in and purchase electricity prices but also depend on the amount of energy that is lost in the irreversibilities of the storage charge/discharge process. The results show that the grid can, with the reference tariff assumed in this study, have positive income even with low storage efficiency. However, the grid also has a clear interest in working with high round-trip efficiency. The highest grid revenues are achieved at the point of complete SS. When the PV capacity is exceeding the need, the district does not need to purchase extra electricity but keeps selling surplus electricity; hence, the grid revenues only decrease.

3.5 How Much Energy Storage Is Needed to Achieve Self-Sufficiency?

The results shown in the previous sections highlighted the fact that the district requires a relevant amount of storage in order to become self-sufficient, in addition to the thermal and electrical storage installed in individual buildings. The actual amount of district storage required is shown in Figure 10B, relative to the total amount of energy locally generated by PV panels. The results show that the storage capacity required in the case of ideal storage (100% round-trip efficiency) to achieve SS is prohibitive: more than 35 kWh/m².

FIGURE 10

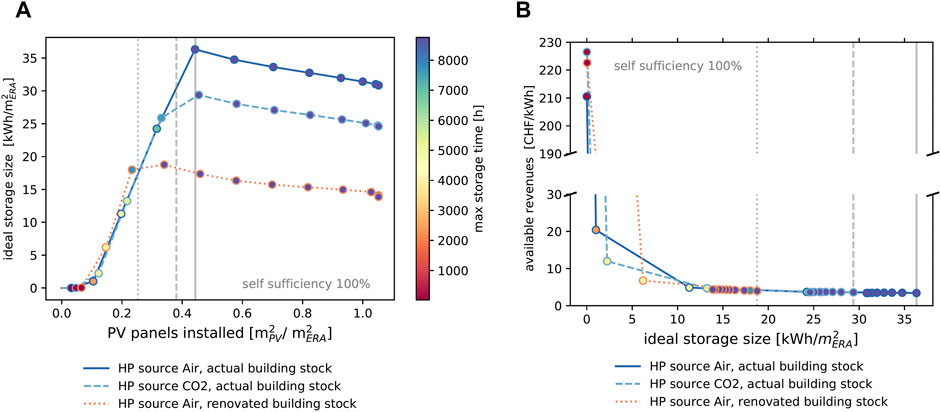
FIGURE 10. Key identifiers of a required storage system with round-trip efficiency η = 100% (equivalent to Point S in Figure 9A) to store surplus PV electricity for different efficiency strategies. (A) Required storage size and time; (B) directly available price from buying at a feed-in tariff of 0.08 CHF/kWh and selling at for electricity price 0.20 CHF/kWh.

There are different ways to decrease the need for storage. One way is to increase the energy conversion efficiency [e.g., a district heating network using CO₂ HPs (Suciu et al., 2016)]; another possibility is to decrease the demand by retrofitting the buildings (Streicher et al., 2020). The results of this analysis are shown in Figure 10A. Three main scenarios are addressed:

• Reference case (air-source HP, actual building stock) referring to the results shown in the previous part of the paper.

• Improved HP case, where high-efficiency HPs using a CO₂ network as a cold source. The annual coefficient of performance (COP) for the HPs in the district increases from 3.25–3.9 to 4.1–4.5 by switching from ambient air to CO₂. The value depends on different operation strategies in Pareto optimal solutions.

• Renovated building stock case, with standard HPs but with isolated buildings (achieved with assumed heat transfer factor U = 0.8 W/(m²K) and design return/supply temperatures $T_0^{r/s}=$ 41.5/33.9°C (Girardin, 2012b)).

The results show, as expected, that increasing the efficiency of the building stock, a very expensive measure (Streicher et al., 2020), is the most efficient solution to decrease the amount of district-level storage required to achieve SS. This result provides additional ground to the general trend of policies. For all three scenarios, the maximum storage time, which is the longest time of a positive state of charge, is in the long-time storage domain, meaning that seasonal storage is required.

Regardless of the type of retrofitting solution, can we afford this much storage in the system? Grid operators recur to a variety of means to store energy (from existing PHS to simply balancing the grid with centralized power generation). However, the capacity of the medium voltage grid is limited to host a high level of PV penetration in the low-voltage grid (Gupta et al., 2021). It can be worth answering this question by looking at how much money would be directly available in the district by using the revenues generated by the different demand/feed-in electricity prices. The results of this analysis are shown in Figure 10B. Only the scenario with very limited PV panels installed generates notable revenues. In this case, the storage can have multiple annual cycles and generate more revenues.

The reason behind the sharp increase in required storage size when the PV surface installed increases can be seen in Figure 11. At the low range, storage is only used for daily balancing purposes, thus requiring a very limited amount of storage size. In Figure 11, the first line appears basically flat, as the required daily storage is low. At higher PV surfaces installed, achieving SS requires seasonal storage. All solutions where the ratio between PV installed surface and the heated surface is above approximately 20% show demand for seasonal storage. The state of charge of the storage peaks at the end of the summer and then gradually decreases during the winter.

FIGURE 11

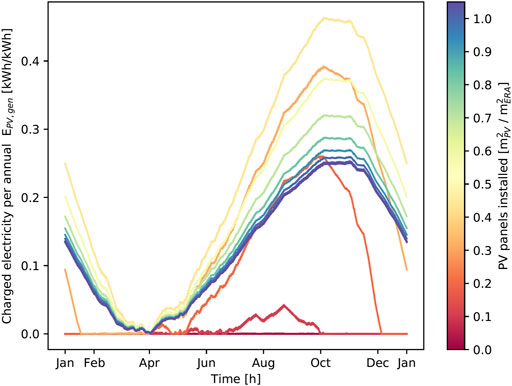
FIGURE 11. State of charge of a storage system aiming at self-sufficiency (SS) for different levels of PV penetration.

4 Conclusion

This paper aimed at investigating the potential of the residential district to increase their sustainability, even achieving climate neutrality and SS, by using a combination of PV power generation and different energy conversion units.

The problem was addressed as a multiobjective, MILP problem, with the OPEX and CAPEX of the system as competing objectives and the installed sizes and operating load of the different energy conversion units (including PV panels and batteries) as optimization variables. Compared to the existing literature in the field, the proposed approach combines advanced modeling of the energy generation potential from PV panels with a detailed representation of the district energy systems, down to the system of each individual building, thus allowing an accurate representation of the interaction between the energy generation from PV and the rest of the system. The proposed approach was applied to a typical, central European, residential district located in Switzerland, in the proximity of the metropolitan area of Geneva. The results of the application of the proposed method to the case study allowed drawing the following conclusions, which are further summarized in Table 4.

TABLE 4

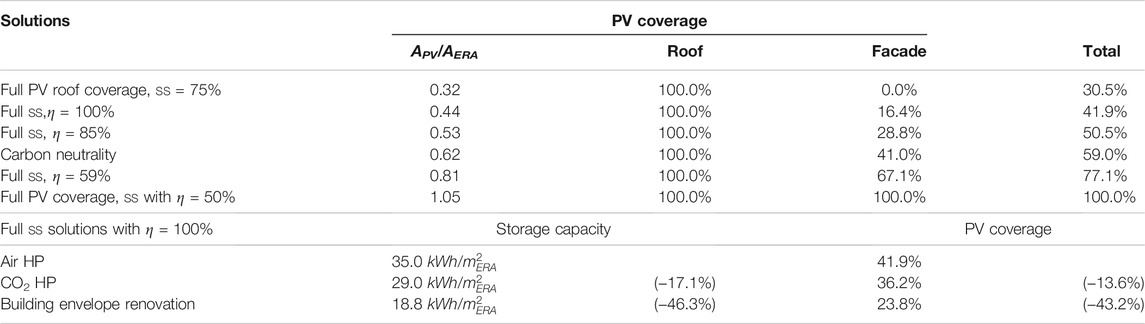
TABLE 4. Overview of identified solutions for a future decentralized district. Self-sufficiency (SS), round-trip efficiency η of the electric storage system.

Facade PV specific energy potential facades have a high theoretical potential, based on their surface compared to roofs: the total facade surface in the district sums to about twice as much that of rooftops. However, the worse angle with respect to solar irradiation and the shading among buildings have the effect of significantly worsening their electricity generation potential. Overall, however, the installation of PV panels on facades has the potential of increasing the total energy generated by approximately 97%.

PV placement order: the results of the MOO show that, as excepted, PV panels are prioritized on roofs (first horizontal, then south-west-east-north) and only then on facades (south, west/east, and north). This is clearly due to the higher specific energy generation potential of roofs compared to facades. The moment of the day when solar power is generated counts only to a smaller extent.

Solar-driven district carbon neutrality facades can play an important role in the energy systems of districts. The results of the MOO show that it is relatively cost-efficient to achieve carbon neutrality, but this is only possible if PV panels are also installed on facades, based on the current energy conversion units and building stock. Further additions of PV panels and batteries allow reducing operating costs but have little effect on further reducing the total GWP potential of the energy system.

The economic convenience of facade PV facades is costly and less cost-efficient compared to rooftop solar. However, the results of the analysis of the influence of electricity prices (both for purchasing electricity from the grid and feed-in) showed that there are many combinations of tariffs that make many (if not all) facades economically convenient over their lifetime. These results thus highlighted the influence that electricity prices have on the maximum PV surface that can be covered while still being economically viable. Current tariffs would allow up to 80% of the total available surface to be covered.

Achieving district self-sufficiency even if climate neutrality can be achieved relatively easily, the same cannot be said for SS. This is because solar energy is not available at the times when it is needed, thus requiring feeding part of the energy to the grid and purchasing it back at a different time. Depending on the assumption for the round-trip efficiency of the grid considered as a storage unit, it is more or less challenging to achieve SS for the district. This objective can be achieved by covering from approx. 40 to 100% of the available surface when the round-trip efficiency decreases from 100 to 50%.

The results underlined the importance and the fact that even when assuming a 100% round-trip efficiency for the storage, very large storage capacities are required. The results also showed that the grid revenues generated by the difference between retail and feed-in prices are not sufficient to pay for the storage that is required to make the district self-sufficient, suggesting that public funding would be crucial for supporting these developments. This is true already at relatively low installed PV capacity (A_PV/A_ERA = 0.2), when storage starts to be required for seasonal instead of daily storage, thus increasing dramatically the required capacity and storage time.

The role of building renovation of the solutions tested in this study, building renovation, with its important effect of energy demand reduction, was identified as the most promising in synergy with PV generation. This is because building renovation allows reducing both the required installed PV and storage capacity to achieve SS by half.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

LM—Main author, conception, and design of the work. Data collection, analysis, and interpretation, Developer of applied methods generating/plotting results. Drafting the article. LG—Expert on the part of building energy systems and development of data-driven approach of the building stock. FB—Author, drafting the article. Critical revision of the article. FM—Supervising professor, conception and design of the work, critical revision of the article.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This project is carried out within the frame of the Swiss Centre for Competence in Energy Research on the Future Swiss Electrical Infrastructure (SCCER-FURIES/JA-RED) with the financial support of the Swiss Innovation Agency (Innosuisse-SCCER program). The authors would like to thank Romande Energy, especially Arnoud Bifrare, for his support on the case study, as well as the Commune de Rolle for easing the access to geodata in the early phase of the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.689781/full#supplementary-material

References

Administration cantonale vaudoise (2019). Géodonnées Etat de Vaud , Registre cantonal des bâtiments (RCB). Lausanne: Office de l’information sur le territoire (OIT).

Google Scholar

Aguacil, S., Lufkin, S., and Rey, E. (2019). Active Surfaces Selection Method for Building-Integrated Photovoltaics (BIPV) in Renovation Projects Based on Self-Consumption and Self-Sufficiency. Energy and Buildings. 193, 15–28. doi:10.1016/j.enbuild.2019.03.035

CrossRef Full Text | Google Scholar

Barnhart, C. J. (2018). Energy and Carbon Intensities of Stored Solar Photovoltaic Energy. A Compr. Guide Solar Energ. Syst., 351–360. doi:10.1016/B978-0-12-811479-7.00017-8

CrossRef Full Text | Google Scholar

Bayod-Rújula, A. A., Yuan, Y., Martínez-Gracia, A., Wang, J., Uche, J., and Chen, H. (2018). Modelling and Simulation of a Building Energy Hub. Proceedings. 2, 1431. doi:10.3390/proceedings2231431

CrossRef Full Text | Google Scholar

Blanco, H., and Faaij, A. (2018). A Review at the Role of Storage in Energy Systems With a Focus on Power to Gas and Long-Term Storage. Renew. Sustainable Energ. Rev. 81, 1049–1086. doi:10.1016/j.rser.2017.07.062

CrossRef Full Text | Google Scholar

Boccalatte, A., Fossa, M., and Ménézo, C. (2020). Best Arrangement of BIPV Surfaces for Future NZEB Districts While Considering Urban Heat Island Effects and the Reduction of Reflected Radiation from Solar Façades. Renew. Energ. 160, 686–697. doi:10.1016/j.renene.2020.07.057

CrossRef Full Text | Google Scholar

Brito, M. C., Freitas, S., Guimarães, S., Catita, C., and Redweik, P. (2017). The Importance of Facades for the Solar PV Potential of a Mediterranean City Using LiDAR Data. Renew. Energ. 111, 85–94. doi:10.1016/j.renene.2017.03.085

CrossRef Full Text | Google Scholar

Buonomano, A., Calise, F., Palombo, A., and Vicidomini, M. (2016). BIPVT Systems for Residential Applications: An Energy and Economic Analysis for European Climates. Appl. Energ. 184, 1411–1431. doi:10.1016/j.apenergy.2016.02.145

CrossRef Full Text | Google Scholar

Catita, C., Redweik, P., Pereira, J., and Brito, M. C. (2014). Extending Solar Potential Analysis in Buildings to Vertical Facades. Comput. Geosciences 66, 1–12. doi:10.1016/j.cageo.2014.01.002

CrossRef Full Text | Google Scholar

Chatzipoulka, C., Compagnon, R., Kaempf, J., and Nikolopoulou, M. (2018). Sky View Factor as Predictor of Solar Availability on Building Façades. Solar Energy 170, 1026–1038. doi:10.1016/j.solener.2018.06.028

CrossRef Full Text | Google Scholar

Chwieduk, D. A. (2009). Recommendation on Modelling of Solar Energy Incident on a Building Envelope. Renew. Energ. 34, 736–741. doi:10.1016/j.renene.2008.04.005

CrossRef Full Text | Google Scholar

Desthieux, G., Carneiro, C., Camponovo, R., Ineichen, P., Morello, E., Boulmier, A., et al. (2018). Solar Energy Potential Assessment on Rooftops and Facades in Large Built Environments Based on Lidar Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 4, 14. doi:10.3389/fbuil.2018.00014

CrossRef Full Text | Google Scholar

Díez-Mediavilla, M., Rodríguez-Amigo, M. C., Dieste-Velasco, M. I., García-Calderón, T., and Alonso-Tristán, C. (2019). The PV Potential of Vertical Façades: A Classic Approach Using Experimental Data from Burgos, Spain. Solar Energy. 177, 192–199. doi:10.1016/j.solener.2018.11.021

CrossRef Full Text | Google Scholar

[Dataset] DOE (2020). Weather Data | EnergyPlus, U.S. Department of Energy’s (DOE) Building Technologies Office (BTO) and National Renewable Energy Laboratory (NREL). Available at: Https://energyplus.net/weather.

Google Scholar

Domínguez-Muñoz, F., Cejudo-López, J. M., Carrillo-Andrés, A., and Gallardo-Salazar, M. (2011). Selection of Typical Demand Days for CHP Optimization. Energy and Buildings. 43, 3036–3043. doi:10.1016/j.enbuild.2011.07.024

CrossRef Full Text | Google Scholar

Duffie, J. A., and Beckman, W. A. (2013). Solar Engineering of thermal Processes/John A. Duffie, William A. 4th ed edn. Beckman (Hoboken): John Wiley.

Google Scholar

Esclapés, J., Ferreiro, I., Piera, J., and Teller, J. (2014). A Method to Evaluate the Adaptability of Photovoltaic Energy on Urban Façades. Solar Energy. 105, 414–427. doi:10.1016/j.solener.2014.03.012

CrossRef Full Text | Google Scholar

Fang, X., He, X., and Huang, J. (2019). A Strategy to Optimize the Multi-Energy System in Microgrid Based on Neurodynamic Algorithm. Appl. Soft Comput. 75, 588–595. doi:10.1016/j.asoc.2018.06.053

CrossRef Full Text | Google Scholar

[Dataset] Federal Office of Meteorology and Climatology MeteoSwiss (2019). Solar Potential of All Roofs and Facades in Switzerland

Google Scholar

[Dataset] Federal Office of Topography swisstopo (2019). swissBUILDINGS3D 2.0 - 3D Building Models of Switzerland

Google Scholar

[Dataset] Federal Statistical Office (2019). Federal Register of Buildings and Dwellings (RBD)

Google Scholar

Freitas, S., Catita, C., Redweik, P., and Brito, M. C. (2015). Modelling Solar Potential in the Urban Environment: State-Of-The-Art Review. Renew. Sustainable Energ. Rev. 41, 915–931. doi:10.1016/j.rser.2014.08.060

CrossRef Full Text | Google Scholar

Freitas, S., Reinhart, C., and Brito, M. C. (2018). Minimizing Storage Needs for Large Scale Photovoltaics in the Urban Environment. Solar Energy 159, 375–389. doi:10.1016/j.solener.2017.11.011

CrossRef Full Text | Google Scholar

Girardin, A. (2012a). Thermal Storage Aiming at Increasing the Share of Used Heat Rejected From a Cooling Process

Google Scholar

Girardin, L. (2012b). A GIS-Based Methodology for the Evaluation of Integrated Energy Systems in Urban Area. Ph.D. Thesis. Lausanne: EPFL. doi:10.5075/epfl-thesis-5287

CrossRef Full Text | Google Scholar

Gonçalves, J. E., van Hooff, T., and Saelens, D. (2021). Simulating Building Integrated Photovoltaic Facades: Comparison to Experimental Data and Evaluation of Modelling Complexity. Appl. Energ. 281, 116032. doi:10.1016/j.apenergy.2020.116032

CrossRef Full Text | Google Scholar

Gupta, R., Sossan, F., and Paolone, M. (2021). Countrywide PV Hosting Capacity and Energy Storage Requirements for Distribution Networks: The Case of Switzerland. Appl. Energ. 281, 116010. doi:10.1016/j.apenergy.2020.116010

CrossRef Full Text | Google Scholar

Hartner, M., Mayr, D., Kollmann, A., and Haas, R. (2017). Optimal Sizing of Residential PV-Systems From a Household and Social Cost Perspective. Solar Energy. 141, 49–58. doi:10.1016/j.solener.2016.11.022

CrossRef Full Text | Google Scholar

Henchoz, S., Weber, C., Maréchal, F., and Favrat, D. (2015). Performance and Profitability Perspectives of a CO2 Based District Energy Network in Geneva's City Centre. Energy. 85, 221–235. doi:10.1016/j.energy.2015.03.079

CrossRef Full Text | Google Scholar

Holweger, J., Dorokhova, M., Bloch, L., Ballif, C., and Wyrsch, N. (2019). Unsupervised Algorithm for Disaggregating Low-Sampling-Rate Electricity Consumption of Households. Sustainable Energ. Grids Networks. 19, 100244. doi:10.1016/j.segan.2019.100244

CrossRef Full Text | Google Scholar

Horn, S., Bagda, E., Brandau, K., and Weller, B. (2018). Einfluss der Bauwerkintegrierten Photovoltaik in Fassaden bei der energetischen Bilanzierung von Gebäuden (Teil 1). Bauphysik. 40, 68–73. doi:10.1002/bapi.201810007

CrossRef Full Text | Google Scholar

Jing, R., Wang, M., Liang, H., Wang, X., Li, N., Shah, N., et al. (2018). Multi-Objective Optimization of a Neighborhood-Level Urban Energy Network: Considering Game-Theory Inspired Multi-Benefit Allocation Constraints. Appl. Energ. 231, 534–548. doi:10.1016/j.apenergy.2018.09.151

CrossRef Full Text | Google Scholar

Kämpf, J. H., Montavon, M., Bunyesc, J., Bolliger, R., and Robinson, D. (2010). Optimisation of Buildings' Solar Irradiation Availability. Solar Energy. 84, 596–603. doi:10.1016/j.solener.2009.07.013

CrossRef Full Text | Google Scholar

Kanters, J., Wall, M., and Dubois, M.-C. (2014). Development of a Façade Assessment and Design Tool for Solar Energy (FASSADES). Buildings. 4, 43–59. doi:10.3390/buildings4010043

CrossRef Full Text | Google Scholar

Kantor, I., and Santecchia, A. (2019). D5.7 – Report on LC Assessment Tools Based on the Results of MORE and EPOS. Coordinated Prod. Better Resource Efficiency.

Google Scholar

Klauser, D. (2016). Solarpotentialanalyse für Sonnendach.ch Schlussbericht. Bern: Tech. rep., Bundesamt für Energie BFE.

Google Scholar

Kourkoumpas, D.-S., Benekos, G., Nikolopoulos, N., Karellas, S., Grammelis, P., and Kakaras, E. (2018). A Review of Key Environmental and Energy Performance Indicators for the Case of Renewable Energy Systems When Integrated With Storage Solutions. Appl. Energ. 231, 380–398. doi:10.1016/j.apenergy.2018.09.043

CrossRef Full Text | Google Scholar

Lang, T., Gloerfeld, E., and Girod, B. (2015). Don׳t Just Follow the Sun - A Global Assessment of Economic Performance for Residential Building Photovoltaics. Renew. Sustainable Energ. Rev. 42, 932–951. doi:10.1016/j.rser.2014.10.077

CrossRef Full Text | Google Scholar

Li, Y., and Liu, C. (2018). Techno-Economic Analysis for Constructing Solar Photovoltaic Projects on Building Envelopes. Building Environ. 127, 37–46. doi:10.1016/j.buildenv.2017.10.014

CrossRef Full Text | Google Scholar

Lobaccaro, G., Lisowska, M. M., Saretta, E., Bonomo, P., and Frontini, F. (2019). A Methodological Analysis Approach to Assess Solar Energy Potential at the Neighborhood Scale. Energies. 12, 3554. doi:10.3390/en12183554

CrossRef Full Text | Google Scholar

Lucon, O. (2014). Buildings. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. United Kingdom and New York: Cambridge University Press.

Google Scholar

Luthander, R., Widén, J., Nilsson, D., and Palm, J. (2015). Photovoltaic Self-Consumption in Buildings: A Review. Appl. Energ. 142, 80–94. doi:10.1016/j.apenergy.2014.12.028

CrossRef Full Text | Google Scholar

Ma, T., Wu, J., Hao, L., Lee, W.-J., Yan, H., and Li, D. (2018). The Optimal Structure Planning and Energy Management Strategies of Smart Multi Energy Systems. Energy. 160, 122–141. doi:10.1016/j.energy.2018.06.198

CrossRef Full Text | Google Scholar

Martinez Cesena, E. A., Mancarella, P., et al. (2019). Energy Systems Integration in Smart Districts: Robust Optimisation of Multi-Energy Flows in Integrated Electricity, Heat and Gas Networks. IEEE Trans. Smart Grid. 10, 1122–1131. doi:10.1109/TSG.2018.2828146

CrossRef Full Text | Google Scholar

Mehleri, E. D., Sarimveis, H., Markatos, N. C., and Papageorgiou, L. G. (2012). A Mathematical Programming Approach for Optimal Design of Distributed Energy Systems at the Neighbourhood Level. Energy. 44, 96–104. doi:10.1016/j.energy.2012.02.009

CrossRef Full Text | Google Scholar

Middelhauve, L., Baldi, F., Stadler, P., and Maréchal, F. (2021). Grid-Aware Layout of Photovoltaic Panels in Sustainable Building Energy Systems. Front. Energ. Res. 8, 573290. doi:10.3389/fenrg.2020.573290

CrossRef Full Text | Google Scholar

Middelhauve, L., Santecchia, A., Girardin, L., and Marechal, F. (2020). “Key Performance Indicators for Decision Making in Building Energy Systems,” in Proceedings of ECOS 2020, Osaka, Japan.

Google Scholar

Morvaj, B., Evins, R., and Carmeliet, J. (2016). Optimization Framework for Distributed Energy Systems With Integrated Electrical Grid Constraints. Appl. Energ. 171, 296–313. doi:10.1016/j.apenergy.2016.03.090

CrossRef Full Text | Google Scholar

Mulcué-Nieto, L. F., and Mora-López, L. (2017). A Novel Methodology for the Pre-Classification of Façades Usable for the Decision of Installation of Integrated PV in Buildings: The Case for Equatorial Countries. Energy. 141, 2264–2276. doi:10.1016/j.energy.2017.11.150

CrossRef Full Text | Google Scholar

[Dataset] OpenStreetMap contributors (2017). Planet Dump Retrieved from. Available at: https://planet.osm.org Published: https://www.openstreetmap.org.

Google Scholar

Pantic, L., Pavlovic, T., Milosavljevic, D., Mirjanic, D., Radonjic, I., and Radovic, M. (2016). Electrical Energy Generation with Differently Oriented Photovoltaic Modules as Façade Elements. Therm. Sci. 20, 1377–1386. doi:10.2298/TSCI150123157P

CrossRef Full Text | Google Scholar

Perez, D. (2014). A Framework to Model and Simulate the Disaggregated Energy Flows Supplying Buildings in Urban Areas. Lausanne, EPFL: Ph.D. thesis. Publisher.

Google Scholar

Perez, R., Seals, R., and Michalsky, J. (1993). All-weather Model for Sky Luminance Distribution-Preliminary Configuration and Validation. Solar Energy. 50, 235–245. doi:10.1016/0038-092X(93)90017-I

CrossRef Full Text | Google Scholar

Perez, R., Stewart, R., Arbogast, C., Seals, R., and Scott, J. (1986). An Anisotropic Hourly Diffuse Radiation Model for Sloping Surfaces: Description, Performance Validation, Site Dependency Evaluation. Solar Energy. 36, 481–497. doi:10.1016/0038-092x(86)90013-7

CrossRef Full Text | Google Scholar

Redweik, P., Catita, C., and Brito, M. (2013). Solar Energy Potential on Roofs and Facades in an Urban Landscape. Solar Energy. 97, 332–341. doi:10.1016/j.solener.2013.08.036

CrossRef Full Text | Google Scholar

Rehman, N., Anderson, T., and Nates, R. (2018). Diffuse Solar Potential of Facades in an Urban Context under Different Sky Conditions. Asia Pacific Solar Research Conference, Sydney, December 4-6, 2018.

Google Scholar

[Dataset] Remund, J., Kunz, S., Meteotest, , and of Energy, M. S. F. O. (2003). METEONORM - Global Meteorological Database for Engineers, Planners and Education

Google Scholar

Robinson, D., and Stone, A. (2004). Irradiation Modelling Made Simple: the Cumulative Sky Approach and its Applications

Google Scholar

Romande Energie, S. A. (2018). Distribution Networks Database. Published: www.romande-energie.ch.

Google Scholar

Roudsari, M. S., and Adrian Smith Gordon Gill Architecture, A. (2013). “Ladybug: A Parametric Environmental Plugin for Grasshopper to Help Designers Create an Environmentally-Conscious Design,” in Proceedings of BS2013, (Chambéry France).

Google Scholar

Schüler, N. C. (2018). Computational Methods for Multi-Criteria Decision Support in Urban Planning. Ph.D. Thesis. Lausanne: EPFL. doi:10.5075/epfl-thesis-8877

CrossRef Full Text | Google Scholar

Schütz, T., Hu, X., Fuchs, M., and Müller, D. (2018). Optimal Design of Decentralized Energy Conversion Systems for Smart Microgrids Using Decomposition Methods. Energy. 156, 250–263. doi:10.1016/j.energy.2018.05.050

CrossRef Full Text | Google Scholar

SIA (2015a). 2024:2025 Raumnutzungsdaten für die Energie- und Gebäudetechnik. Zürich: Schweizerischer Ingenieur und Architektenverein.

Google Scholar

SIA (2015b). SIA 385/2:2015 Anlagen für Trinkwarmwasser in Gebäuden - Warmwasserbedarf, Gesamtanforderungen und Auslegung. Zürich: Schweizerischer Ingenieur und Architektenverein.

Google Scholar

SIA (2016). SIA 380/1:2016 Heizwärmebedarf. Schweizerischer Ingenieur und Architektenverein. Zürich: Schweizerischer Ingenieur und Architektenverein.

Google Scholar

Stadler, P., Girardin, L., Ashouri, A., and Maréchal, F. (2018). Contribution of Model Predictive Control in the Integration of Renewable Energy Sources Within the Built Environment. Front. Energ. Res. 6, 22. doi:10.3389/fenrg.2018.00022

CrossRef Full Text | Google Scholar

Stadler, P. M. (2019). Model-based Sizing of Building Energy Systems with Renewable Sources. Lausanne: EPFL. doi:10.5075/epfl-thesis-9560

CrossRef Full Text | Google Scholar

Streicher, K. N., Mennel, S., Chambers, J., Parra, D., and Patel, M. K. (2020). Cost-effectiveness of Large-Scale Deep Energy Retrofit Packages for Residential Buildings Under Different Economic Assessment Approaches. Energy and Buildings. 215, 109870. doi:10.1016/j.enbuild.2020.109870

CrossRef Full Text | Google Scholar

Suciu, R., Stadler, P., Ashouri, A., and Maréchal, F. (2016). Towards Energy-Autonomous Cities Using CO2 Networks and Power to Gas Storage. Proc. ECOS. 2016.

Google Scholar

[Dataset] Swiss Federal Office of Energy - Geoinformation - Sonnendach.ch (2018). 3D Data of Roof Area by the Swiss Federal Office of Topography Swisstopo

Google Scholar

Turton, R. (2012). Analysis, Synthesis, and Design of Chemical Processes. 4th ed edn. Upper Saddle River, NJ: Prentice-Hall.

Google Scholar

van der Stelt, S., AlSkaif, T., and van Sark, W. (2018). Techno-Economic Analysis of Household and Community Energy Storage for Residential Prosumers With Smart Appliances. Appl. Energ. 209, 266–276. doi:10.1016/j.apenergy.2017.10.096

CrossRef Full Text | Google Scholar

Verso, A., Martin, A., Amador, J., and Dominguez, J. (2015). GIS-Based Method to Evaluate the Photovoltaic Potential in the Urban Environments: The particular Case of Miraflores de la Sierra. Solar Energy. 117, 236–245. doi:10.1016/j.solener.2015.04.018

CrossRef Full Text | Google Scholar

Vulkan, A., Kloog, I., Dorman, M., and Erell, E. (2018). Modeling the Potential for PV Installation in Residential Buildings in Dense Urban Areas. Energy and Buildings. 169, 97–109. doi:10.1016/j.enbuild.2018.03.052

CrossRef Full Text | Google Scholar

Walter, E., and Kämpf, J. H. (2015). “A Verification of CitySim Results Using the BESTEST and Monitored Consumption Values,” in Proceedings of the 2nd Building Simulation Applications conference.

Google Scholar

Weber, C., and Shah, N. (2011). Optimisation Based Design of a District Energy System for an Eco-Town in the United Kingdom. Energy. 36, 1292–1308. doi:10.1016/j.energy.2010.11.014

CrossRef Full Text | Google Scholar

Wernet, G., Bauer, C., Steubing, B., Reinhard, J., Moreno-Ruiz, E., and Weidema, B. (2016). The Ecoinvent Database Version 3 (Part I): Overview and Methodology. Int. J. Life Cycle Assess. 21, 1218–1230. doi:10.1007/s11367-016-1087-8

CrossRef Full Text | Google Scholar

Wu, R., Mavromatidis, G., Orehounig, K., and Carmeliet, J. (2017). Multiobjective Optimisation of Energy Systems and Building Envelope Retrofit in a Residential Community. Appl. Energ. 190, 634–649. doi:10.1016/j.apenergy.2016.12.161

CrossRef Full Text | Google Scholar

Xu, S., Huang, Z., Wang, J., Mendis, T., and Huang, J. (2019). Evaluation of Photovoltaic Potential by Urban Block Typology: A Case Study of Wuhan, China. Renew. Energ. Focus. 29, 141–147. doi:10.1016/j.ref.2019.03.002

CrossRef Full Text | Google Scholar

Yang, Y., Zhang, S., and Xiao, Y. (2015). Optimal Design of Distributed Energy Resource Systems Coupled With Energy Distribution Networks. Energy. 85, 433–448. doi:10.1016/j.energy.2015.03.101

CrossRef Full Text | Google Scholar

Yesilmaden, H., and Dogru, A. (2019). Finding the Best Locations for Photovoltaic Panel Installation in Urbanized Areas. Fresenius Environ. Bull. 28, 619–625.

Google Scholar

Zimmerman, R., Panda, A., and Bulović, V. (2020). Techno-Economic Assessment and Deployment Strategies for Vertically-Mounted Photovoltaic Panels. Appl. Energ. 276, 115149. doi:10.1016/j.apenergy.2020.115149

CrossRef Full Text | Google Scholar

Zomer, C., Custódio, I., Goulart, S., Mantelli, S., Martins, G., Campos, R., et al. (2020). Energy Balance and Performance Assessment of PV Systems Installed at a Positive-Energy Building (PEB) Solar Energy Research centre. Solar Energy. 212, 258–274. doi:10.1016/j.solener.2020.10.080

CrossRef Full Text | Google Scholar

Glossary

AR annual revenues

BES building energy system

CAPEX capital expenses

COP coefficient of performance

CPT carbon payback time

DHW domestic hot water

ERA energy reference area

GHG greenhouse gas

GIS geographic information systems

GWP global warming potential

HP heat pump

IPCC Intergovernmental Panel on Climate Change

KPI key performance indicator

MILP mixed-integer linear programming

MOO multiobjective optimization

OPEX operational expenses

PHS pumped hydro storage

PV photovoltaic

SC self-consumption

SH space heating

SS self-sufficiency

Nomenclature

Parameter

α azimuth angle (°)

β design limiting angle (°)

∈ elevation angle (°)

η efficiency [-]

γ tilt angle (°)

Φ specific heat gain (kW/m²)

ρ density (kg/m³)

A area (m²)

b bare module

C heat capacity coefficient (kW/m²K)

c energy tariff (CHF/kWh)

c_p specific heat capacity [kJ/(kg K)]

d distance (m)

d_p frequency of periods per year (d/yr)

d_t frequency of timesteps per period (h/d)

F bound unit size (⋄)

f^s solar factor

f^u usage factor

f_b,r spatial fraction of room in building

g g - value

g global warming potential streams (kg_{CO2, eq}/kWh)

h height (m)

i interest rate

i^c1 fixed investment cost (CHF)

i^c2 continuous investment cost (CHF/⋄)

i^g1 fixed impact factor (kg_{CO2, eq})

i^g2 continuous impact factor (kg_{CO2, eq}/⋄)

irr irradiation density (kWh/m²)

l lifetime (yr)

n number/quantity project horizon (yr)

n number/quantity project horizon (yr)

Q thermal energy (kWh)

s shading factor supply

T temperature (K)

U heat transfer coefficient (kW/m²K)

V volume (m³)

x, y, z coordinates

Variables

C cost (CHF)

E electricity (kW(h))

f sizing variable (⋄)

G global warming potential (kg_{CO2, eq})

H natural gas or freshwater (kW(h))

Q thermal energy (kWh)

R residual heat (kWh)

T temperature (K) temperature (K)

y decision variable, binary

Sets

A azimuth (α)

B building (b)

I interval (i)

K temperature interval (c)

P period (p)

R replacement (r)

S skydome patch (pt)

T timestep (t)

U utility (u)

Y tilt (γ)

Superscripts

+ supply

− demand

A appliance

B building

bes building energy system

cap capital

cw cold water

dhw domestic hot water

el electricity

era energy reference area

ext external

g glass

gain heat gain

gr grid

int internal

inv investment

irr irradiation density (kWh/m²) irradiation

L light

lca life cycle assessment

max maximum

min minimum

net netto

ng natural gas

op operation

P people

pv photovoltaic panel

r return

ref reference

rep replacement

s supply

SH space heating

TR transformer