Numerical Study of the Impingement of Water Film on a Small Attached Bulging Plate on a Vertical Plane

In the passive containment cooling system of AP1000, the condensed water is expected to flow down on the inner surface of the steel wall of the containment, and recover to the in-containment refueling water storage tank (IRWST), therefore, to maintain the long-term coolability of the passive residual heat removal system. However, there are attached bulging plates on the inner surface for various engineering needs, such as supporting, and the impingement of condensed water film on these bulging plates can reduce the amount of the recovered water. In this article, a 3-D Eulerian wall film model in FLUENT was used to study a series of flow behaviors when a water film impinged on the bulging plate on a plane surface. The loss ratio of falling film impinging on attached plates of different sizes under different flow rates were calculated and in good agreement with the experiment results. Four stages of the film behavior during the impingement were identified and analyzed; in addition, the influences of the bulging height of attached plate and flow rate were studied. And a correlation between the loss ratio of impinging water film, the bulging height of the attached plate, and the Weber number was obtained.

Introduction

In the design of AP1000, the Passive Residual Heat Removal (PRHR) system and Passive Containment Cooling system (PCCS), as shown in Figure 1, will play an important role in the long-term cooling process under severe accident scenarios. In this process, water vapor released from the primary loop or produced from the In-containment Refueling Water Storage Tank (IRWST) forms condensate on the inner wall of the containment and eventually returns to IRWST through the designated collecting water channels, which ensures the water utilization of IRWST and thus maintains the long-term coolability of PRHR. However, there are attached bulging plates on the inner surface for various engineering needs, such as supporting, the impingement of condensed water on these bulging plates can reduce the recovery. Therefore, predicting the loss of condensate recovery under impingement condition is important for PRHR long-term coolability (Cummins et al., 2003).

FIGURE 1

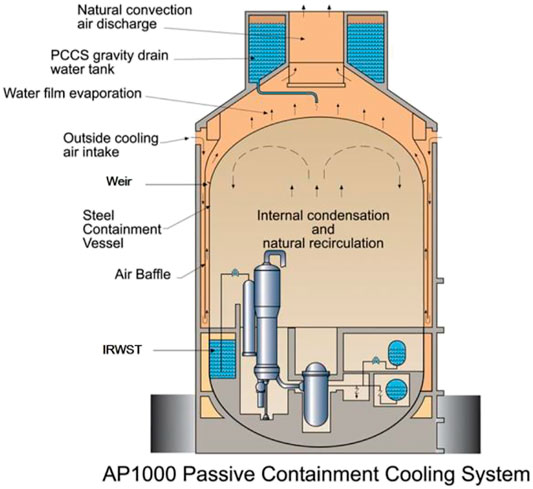
FIGURE 1. AP1000 passive containment cooling system. (Image courtesy of Westinghouse Electric Corporation).

The flow behavior of falling liquid film on the outer surface of the containment vessel has been closely studied: Ambrosini et al. (2002), Wei et al. (2012), and Guzanov et al. (2018) studied the water film falling down a flat plate experimentally; Ye and Yan (2006) reviewed studies of the stability and breakdown of falling film; Wang et al. (2016) studied evaporation of falling film; and Tian and Li (2006) and Yang (2018) studied falling film on a wall numerically.

However, there were only few studies on the flow behavior of falling film impingement on the attached plate on the inner surface of the containment vessel (Wang et al., 2013) (Tang et al., 2017); one of the reasons for this is no validated simulation method to effectively estimate the loss. The Eulerian Wall Film (EWF) model in the software FLUENT has the advantages of high computational efficiency and good simulation of liquid wall film flow (Ye and Yan, 2006) (Yang, 2018), and when a EWF model is used to simulate the full size model, computational expense is relatively small comparing to other models, such as volume of fluid model (VOF). Therefore, in this study, the EWF model was used to simulate impingement of water film on a small attached bulging plate on a vertical plane surface, and the results were validated with experiment results, thereafter an empirical correlation was developed between the loss ratio of impinging water film, the bulging height of the attached plate, and the Weber number.

Numerical Model

Numerical Model and Boundary Conditions

The numerical model was developed based on tests carried out on Water Film Test (WAFT) facility. The schematic of WAFT facility is shown in Figure 2. A steel plate was carefully manufactured to maintain a good planarity, and then painted with nonorganic zinc paint (Carbozinc 11 HSN). The water-delivery system consists of a supply tank, a flow meter and valves, a distribution box and drain. When performing the WAFT, water was evenly distributed to the upper part of the plate through the water film distribution box, and then spread on the plate as a flowing film. Then the film impinged on the attached burging plate at the lower part, while part of the water film splashed away from the plate, the rest part was collected through the recovery trough and weighed to evaluate the loss ratio.

FIGURE 2

FIGURE 2. Schematic of WAFT experiment facility.

The experimental plates and their welding methods are shown in Figure 3. The plate is 5 m long and 1.2 m wide, the end of the plate is provided with a recovery trough with an open width of 0.1 m, and an attached plate is disposed 3 m downstream the water distribution box. The measuring errors of the flow meter and the weighting sensor were less than 1%.

FIGURE 3

FIGURE 3. Schematic of test plate and attached plate.

Different attached bulging plates with various bulging height and length were tested, and attached plates were fixed on the plate surface with corner welding. The height of the welding foot is h, and the height of the attached plate is H, and the ratio of welding foot height is defined as follows:

$\delta =h/H(1)$

During the experiment, the influence of various factors on liquid film splashing were tested by changing the flow rate, the flow temperature, the size of the attachment plate, and the ratio of the welding foot height separately.

In the numerical study, the test plate surface and the three-dimensional space above it with a height varying from 0.1 m (for 10 mm attached plate) to 0.15 m (for 40 mm attached plate) were selected carefully to eliminate its effect on the loss ratio. In the simulation, each part in the experiment was modeled and calculated in exact proportion to the experiment. The side view of the model is shown in Figure 4.

FIGURE 4

FIGURE 4. Side view of the 3-D model.

Model specification and experimental parameters are shown in Table 1. The boundary condition of surface above the test plate was set as the pressure outlet. In the calculation domain, liquid film flowed in from the upper inlet and spread on the wall surface. After the liquid film was fully developed downstream from the inlets, it impinged on the attached plate at the lower part of the test plate. The liquid lost from splashing is ejected away from the upper pressure outlet, and rest of the liquid collected in the recovery trough with an open width of 0.1 m. The specification of boundary conditions is shown in Table 2.

TABLE 1

TABLE 1. The geometric dimensions of the 3-D model.

TABLE 2

TABLE 2. Boundary conditions.

The following three assumptions were made in the modeling:

1) The fluctuation of liquid film was not considered due to limitation of EWF model.

2) Mass energy exchange between liquid film and air is not considered; in other words, the evaporation loss of liquid film during impingement and flow process was not considered.

3) The filter was not considered in the modeling, and the filter was on the opening of the recovery trough which in the experiment has negligible effect on the loss ratio.

Governing Equations

Since only the flow and splashing behaviors of falling film on the large plate was studied in this article, the heat transfer and energy equations were not considered. Assuming that the fluid is incompressible, its steady-state continuity equation is written as follows:

$\frac{\partial }{\partial x_i}\left(\rho u_i\right)=S_{\max }(2)$

Here, $\rho$ is the fluid density, $u_i$ is the fluid velocity in the i direction, and $S_{\max }$ is the source term.

The momentum equation can be described as:

$\frac{\partial }{\partial x_j}\left(p{u}_i{u}_j\right)=-\frac{\partial }{\partial x_i}+\frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial u_i}-\frac{2}{3}{\partial }_{ij}\frac{\partial u_i}{\partial x_j}\right)\right]+\frac{\partial }{\partial x_j}\left(-\rho u_i^{\prime }{u}_j^{\prime }\right)+{\text{S}}_{mom-i}(3)$

In Eq. 3, p is the pressure, $\mathit{\mu }$ is the dynamic viscosity, $\mathit{\mu }$ is the Kronecker function, ${\text{S}}_{mon-i}$ is the source term, and $\rho u_i^{\prime }{u}_j^{\prime }$ is Reynolds stress based on Boussinesq Assumption.

As the impinging loss is not sensitive to the turbulent model, realizable k-$\text{ε}$ turbulence model is chosen based on the experiment result to describe the turbulent flow of the liquid film, and the simulated k and $\text{ε}$ transport equation of turbulence model is given separately as:

$\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{u_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_i}\right]+G_k+G_b-\rho \epsilon =S_k(4)$

In Eq. 4, $k$ is the turbulent kinetic energy, $G_k$ is the turbulent kinetic energy generated by the mainstream velocity gradient, $G_b$ is the turbulent kinetic energy generated by buoyancy lift, ${\sigma }_k$ is the Prandtl number of k equation and the value is 1.0, and $\epsilon$ is the turbulence dissipation rate.

$\frac{\partial }{\partial x_i}\left(\rho \epsilon u_i\right)=\frac{\partial }{\partial x_1}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_E}\right)\frac{\partial \epsilon }{\partial x_i}\right]+\rho C_1{S}_{\epsilon }-\rho C_2\frac{{\epsilon }^2}{K+\sqrt{v\epsilon }}+C_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{G}_b+S_{\epsilon }(5)$

In Eq. 5, $\mu$ is the volume-weighted viscosity coefficient and ${\mu }_t$ is the turbulent viscosity coefficient.

$c_1=\max \left[0.43,\frac{\eta }{\eta +5}\right],\eta =S\frac{k}{\epsilon },C_2=1.9{\sigma }_{\epsilon }=1.9C_{1\epsilon }=1.44{\mu }_t=\rho C_{\mu }\frac{k}{{\epsilon }^2}$

Here, $C_{\mu }$ is a coefficient sensitive to average flow and turbulence variation, it is not a constant in the model used in the article, and its specific calculation method can be referred from the study by Shih et.al (1995) (Shih et al., 1995).

The EWF model can be used to predict the production and flow of thin liquid film on the wall surface; in addition, the model can also be used to simulate the phenomenon of liquid droplet splashing, stripping, and film separation. In its assumption, thickness of the film is small compared to the radius of curvature of the surface so that the properties do not vary across the thickness of the film and that films formed are thin enough so that the liquid flow in the film can be considered parallel to the wall, with an assumed quadratic shape (ANSYS, Inc., 2013).

Conservation of mass for a two-dimensional film in a three-dimensional domain is given as follows:

$\frac{\partial h}{\partial t}+{\nabla }_s\cdot \left[h{\overrightarrow{V}}_l\right]=\frac{m_s}{{\rho }_l}(6)$

In Eq. 6, ${\overrightarrow{V}}_l$ is the mean film velocity and $m_s$ is the mass source per unit wall area due to droplet collection, film separation, film stripping, and phase change.

Conservation of film momentum is given as follows:

$\frac{\partial h{\overrightarrow{V}}_l}{\partial t}+{\nabla }_s\cdot \left(h{\overrightarrow{V}}_l{\overrightarrow{V}}_l\right)=-\frac{h{\nabla }_s{P}_L}{{\rho }_l}+\left({\overrightarrow{g}}_{\tau }\right)h+\frac{3}{2{\rho }_l}{\overrightarrow{\tau }}_{fs}-\frac{3v_l}{h}{\overrightarrow{V}}_l+\frac{q}{{\rho }_l}(7)$

$\text{w}\text{h}\text{e}\text{r}\text{e}{P}_L=P_{Gas}+P_h+P_{\sigma },P_h=-\rho h\left(\overrightarrow{n}\cdot \overrightarrow{g}\right)P_{\sigma }=\sigma {\nabla }_s\left({\nabla }_{s}h\right)$

In Eq. 7, the terms on the left-hand side represent transient and convection effects, respectively. On the right-hand side, the first term includes the effects of gas-flow pressure, the gravity component normal to the wall surface and surface tension; the last three terms represent the effect of gravity in the direction parallel to the film, the viscous shear force at the gas-film interface, and the viscous force in the film, respectively.

During the simulation, the EWF model was enabled both in the boundary setting of the plane surface and the attachment plate, and at the same time, the discrete phase model (DPM) option, which is to track the splashing droplets, at the attachment plate and welding is set to reflect, while the option of the plane surface is set to trap, to ensure that the liquid film flows on the plate before impinging on the attachment plate.

Grid Independence

Structured grid division was adopted to divide the calculation area. Due to the application of the standard near-wall model, the y + value of the first layer grid close to the experimental board remained at about 20, while the y + value of the first layer grid near other walls remained above 20. In this article, different grid models are chosen to verify the grid independence by evaluating the water film mass loss in 10 min. The grid independence verification results are shown in Figure 5. To integrate the computational efficiency and accuracy, the model of 480,000 grids was selected in this study.

FIGURE 5

FIGURE 5. Film losses with different mesh numbers.

Results and Discussion

Comparison Between Simulation and Experiment Results of Film Loss

To verify the capability of the current numerical model to predict the film loss, simulation results were compared with the corresponding experimental results under different test conditions. As shown in Figure 6, the loss after film impinging on the attached plate at a small flow rate was very small, and the calculated value was in agreement with the experimental value. In the case of medium flow (500 m³/h) and large flow (1,000 m³/h), the liquid film loss ratio increased significantly, and the error between the calculated value and the experimental value also increased and reached 8%.

FIGURE 6

FIGURE 6. Comparison of simulation results and test results of film loss.

Analysis of Impinge Behavior of Falling Film

As shown in Figure 7, the whole process of falling film impinging on the attached plate can be divided into four stages: stage of film impinging attached plate, the first stage of film reaggregation, stage of film separation, and the second film reaggregation.

FIGURE 7

FIGURE 7. Schematic of film impinging on the attached plate.

The results of film thickness and velocity are shown in Figure 8. The velocity range of film flow in the first three figures is 0–1 m/s; the velocity range in the last one is 0–2 m/s, all the velocity direction is along the plate.

FIGURE 8

FIGURE 8. Analysis of falling film thickness and velocity field.

At the first stage, when water film impinged on the attached plate, it would change the flow direction and flow along the welding line. At the second stage, the film begins to flow in three main directions. According to the assumption of no slip condition, the viscous sublayer still flows close to the wall because it remains relatively stationary with the wall, and the liquid in the turbulent core area was affected by the surface tension and internal force of the liquid. Most of the liquid flows in the direction of the welding line for a certain distance and then continues to flow back to the surface of the attached plate, while a small part of the liquid droplets overcome the influence of surface tension and then escape.

At the first stage of film reaggregation, when the length of the attached plate is short and the height of the welding seam is high enough, the liquid film may not be able to complete the first reaggregation on the attached plate after impacting on the attached plate and directly flow into the return tank in the form of jet flow. It can be seen from the distribution of the liquid film thickness on the attached plate is less than that before the attached plate.

At the stage of film impinge, the escaped droplets after impinging on the attached plate is the main source of film loss, for example, film recovery loss.

At the stage of film separation, it can be seen that the boundary layer of liquid film presents an obvious separation phenomenon in the process of wall surface separation, according to O'rourke's liquid film separation criterion (O’Rourke and Amsden, 1996):

$c_s\frac{{\rho }_l{\left[\left({\overline{u}}_l-v_w\right)t_1\right]}^2\sin \theta }{1+\cos \theta }>P_{gas}(8)$

where $c_s$ is a constant affected by the shape of pressure distribution along the wall, ${\overline{u}}_l$ is the mean velocity across the separation edge, $v_w$ is the wall velocity, and $t_1$ is the unit vector whose direction is tangent of ${\overline{u}}_l-v_w$. As shown in Eq. 8, the main influence factor is the mean relative film velocity ${\overline{u}}_l-v_w$ when film separates on the edge, which is consistent with what the velocity field shows.

At the second stage of film reaggregation, because of the difference of film velocity, the time required for the liquid after exiting the edge to return to the main board for reaggregation is different, which results in the uneven film thickness distribution on the plate below the attached plate. In addition, it can be found that the film thickness on the plate below the attached plate is larger than that on the attached plate, because some of the droplets participating in the second aggregation directly flow over the attached plate and back to the plate after impinging on the attached plate.

Study of Influence of Film Flow Rate on Film Loss

As shown in Figure 9, the film loss ratio defined in Eq. 9 was small with small flow rate, and with increasing the film flow, the film loss ratio slightly decreased after increasing when impinging on the no.2 and no.3 attached plate. The dimensions of the attached plate are listed in Table 3.

${\eta }_{loss}=\left(1-\frac{{\dot{m}}_{trough}}{{\dot{m}}_{inlet}}\right)\frac{b}{a}(9)$

where ${\dot{m}}_{trough}$ is the mass increasing rate in the recovery trough, ${\dot{m}}_{inlet}$ is the inlet flow rate, and a and b are the length and width of the attached plate.

FIGURE 9

FIGURE 9. Influence of film flow rate on the film loss ratio.

TABLE 3

TABLE 3. Sizes of different attached plates.

According to O ′Rourke et al. (O’Rourke and Amsden, 1996) and Wu p K (Wu et al., 1995) et al., the process of film separation and droplet stripping from the film is mainly affected by the Weber number, which is also the main reason that affects film loss ratio after impinging on the attached plate. Therefore, the relationship between film loss ratio, the attached plate height, and the Weber number is studied. Then the splashing space number He is defined as follows:

$He=\frac{H}{L}(10)$

where $L$ is the open width of the recovery trough and H is the attached plate height. By comparing the relationship between liquid film loss ratio and the Weber number and the He number, the relationship is obtained based on simulation results, which includes more than 18 loss ratios for attached plates of different sizes as shown in Table 3, and under three flow rates100, 500, and 1,000 m³/h.

${\eta }_{loss}=0.25H{e}^{0.72}1n\left(We\right)+1.33H{e}^{0.78}$

$\left(0.02\le \text{We}\le 0.76,\cdot 0.1\le \text{He}\le 0.4\right)(11)$

And the predicted film loss ratios were compared with the test results of large flow rates (500 m³/h and 1,000 m³/h, for the lower flow rate which is 100 m³/h film is not distributed evenly in the tests), and they were in good agreement within 10% relative error as shown in Figure 10.

FIGURE 10

FIGURE 10. The comparison between experiment loss ratios and predicted ones.

Conclusion

In this study, the flow behavior of the falling film impacting on an attached burging plate on a plane surface was analyzed numerically. The numerical scheme of the falling film impinging behavior of the falling film was established using the code FLUENT. The film recovery loss was in good agreement with the experiment results. It was found that the behavior of the falling film impingement can be divided into four stages: stage of film impinging attached plate, the first stage of film reaggregation, stage of film separation, and the second film reaggregation. By studying these four stages, conclusions are as follows.

When the liquid film impinging on the attached plate at a small flow rate, the general loss rate is small, while at medium and large flow rates, the impinging process has a large film loss ratio, and the film loss ratio is affected by the size of the attached plate. The correlation between the loss ratio and the Weber number, and the nondimensional height of the attached plate was formed as ${\eta }_{loss}=0.25H{e}^{0.72}1n\left(We\right)+1.33H{e}^{0.78}$.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

PH contributed to the conception and design of the study. ZH organized the database and performed the analysis. ZH wrote the first draft of the manuscript. PH wrote sections of the manuscript and contributed to manuscript revision, read, and approved the submitted version.

Funding

The research is supported by State Key Science and Technology project (2017ZX06002003-002-003).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ambrosini, W., Forgione, N., and Oriolo, F. (2002). Statistical Characteristics of a Water Film Falling Down a Flat Plate at Different Inclinations and Temperatures. Int. J. Multiphase Flow 28 (9), 1521–1540. doi:10.1016/s0301-9322(02)00039-3

CrossRef Full Text | Google Scholar

ANSYS Fluent Theory Guide, ANSYS, Inc., 275 Technology Drive Canonsburg, PA 15317, November 2013.

Google Scholar

Cummins, W. E., Corletti, M. M., and Schulz, T. L. (2003). Westinghouse AP1000 Advanced Passive Plant. Cordoba, Spain: Proceedings of ICAPP ’03.

Guzanov, V. V., Bobylev, A. V., Heinz, O. M., Kharlamov, S. M., Kvon, A. Z., and Markovich, D. M. (2018). Characterization of 3-D Wave Flow Regimes on Falling Liquid Films. Int. J. Multiphase Flow 99, 474–484. doi:10.1016/j.ijmultiphaseflow.2017.11.013

CrossRef Full Text | Google Scholar

O’Rourke, P. J., and Amsden, A. A. (1996). A Particle Numerical Model for Wall Film Dynamics in Port-Injected EnginesSAE International, Technical Paper 961961 1. doi:10.4271/961961

Google Scholar

Shih, T.-H., Liou, W. W., Shabbir, A., Yang, Z., and Zhu, J. (1995). A New K-ϵ Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 24 (3), 227–238. doi:10.1016/0045-7930(94)00032-t

CrossRef Full Text | Google Scholar

Tang, C., Qin, M., Zhang, X., Zhang, P., Li, J., and Huang, Z. (2017). Dynamics of Droplet Impact on Solid Surface with Different Roughness. Int. J. Multiphase Flow 96, 56–69. doi:10.1016/j.ijmultiphaseflow.2017.07.002

CrossRef Full Text | Google Scholar

Tian, R., and Li, Z. Q. (2006). Numerical Study of Water Film Wave Flowing on Wall”. Nucl. Power Eng. 27 (5), 29–32. doi:10.3969/j.issn.0258-0926.2006.05.006

Google Scholar

Wang, T., Faria, D., Stevens, L. J., Tan, J. S. C., Davidson, J. F., and Wilson, D. I. (2013). Flow Patterns and Draining Films Created by Horizontal and Inclined Coherent Water Jets Impinging on Vertical Walls. Chem. Eng. Sci. 102 (1), 585–601. doi:10.1016/j.ces.2013.08.054

CrossRef Full Text | Google Scholar

Wang, X., Chang, H., Corradini, M., Cong, T., and Wang, J. (2016). Prediction of Falling Film Evaporation on the AP1000 Passive Containment Cooling System Using ANSYS FLUENT Code. Ann. Nucl. Energ. 95, 168–175. doi:10.1016/j.anucene.2016.05.014

CrossRef Full Text | Google Scholar

Wei, S., Song, J., and Hu, P. (2012). Statistical Characteristics of Water Film Falling Down Large Flat Plate. At. Energ. Sci. Techn. 46 (6), 674–678. doi:10.7538/yzk.2012.46.06.0674

Google Scholar

Wu, P.-K., Miranda, R. F., and Faeth, G. M. (1995). Effects of Initial Flow Conditions on Primary Breakup of Nonturbulent and Turbulent Round Liquid Jets. Atomiz Spr 5 (2), 175–196. doi:10.1615/atomizspr.v5.i2.40

CrossRef Full Text | Google Scholar

Yang, X. (2018). Numerical Analysis of Water Film Flow Characteristics on the Large Flat Plate”. Proc. Nuthos- 12, 655-662.

Google Scholar

Ye, X., and Yan, W. (2006). Review on Flow Stability and Breakdown of Thin Liquid Films. J. North China Electricity Power Univ. 33 (6), 63–67. doi:10.3969/j.issn.1007-2691.2006.06.015

Google Scholar