Design Optimization and Dynamic Simulation of Steam Cycle Power Plants: A Review

After more than one century from its first use for electric power production, steam cycles are still the object of continuous research and development efforts worldwide. Indeed, owing to its favorable thermodynamic properties, steam cycles are not only used in coal-fired power plants but in a large variety of applications such as combined cycles, concentrated solar power plants and polygeneration plants. On the other hand, to cope with the efficiency and flexibility requirements set by today’s energy markets, the design and the operation of steam cycles must be carefully optimized. A key rule is played by the simulation and optimization codes developed in the last 30 years. This paper provides an introduction to the main types of simulation and optimization problems (design, off-design operation and dynamic), an overview of the mathematical background (possible solution approaches, numerical methods and available software), and a review of the main scientific contributions.

Introduction

Steam cycles have been used for electric power generation from coal since the early 1900’s. These first coal-fired power units featured outputs in the range 1–10 MW and the steam generator already included an economizer, an evaporator, and a superheater (Harvey et al., 2020). According to the same reference, the first steam cycle had an efficiency of only 1.6% while those built about 10 years later reached an efficiency of about 15% thanks also to the adoption of regenerative feedwater preheaters. Steam reheating was first adopted in 1920’s and once-through supercritical boilers in the 1950’s. Unit sizes reached the standard of 300 MW already in the 1930’s. After more than one century, the global installed capacity of coal-fired steam cycles is above 1500 GW (IEA, 2019) and manufacturers supply full turnkey Advanced Ultra Super Critical (A-USC) units with sizes up to 1.1 GW (General Electric, 2020). Although someone can consider steam cycles as an obsolete technology, it is important to mention that steam cycles are still an object of research and development efforts to improve their efficiency, operational flexibility, and range of applicability (i.e., tailoring their design for novel concepts of power plants). Indeed, today the use of steam cycles is not limited to coal-fired power plants but they are employed as heat recovery systems in many other types of power plants, with either fossil or renewable energy sources. Examples of conventional steam cycle-based power plants include coal-fired power plants (Speight, 2013), gas-steam turbine combined-cycles (Kehlhofer et al., 2009), and nuclear power plants (Rinzic, 2017) (either boiling water reactor or pressurized water reactor); examples of novel plant concepts include concentrated solar power plants (Peinado Gonzalo et al., 2019), integrated solar combined-cycles (Dersch et al., 2004), waste to energy plants (Bogale and Viganò, 2014), integrated gasification combined-cycles (Martelli et al., 2011), electricity/hydrogen/synfuels polygeneration plants (Larson et al., 2009), power plants with CO₂ capture and storage (Spinelli et al., 2015) and all the cycles that are specifically designed for industrial processes (typically for combined heat and power applications or for heat recovery). An overview of the state-of-the-art in steam turbine and steam cycle technology can be found in the recent publication (Gulen, 2020).

A key rule in the research and development activities is being played by simulation and optimization codes, which are used to predict the effects of the design/control improvements on the performance of the overall power plant. The results of such models are applied to guide the development activities while limiting very costly experimental campaigns. Computer-aided plant simulation approaches have been developed first by the chemical engineering community since the late 70’s. One of the first successful examples is the ASPEN project (Advanced System for Process Engineering) funded by the United States Department of Energy in 1977 to researchers of MIT (Prof. Larry Evans) to develop a code for the simulation of complex chemical processes for the conversion of coals and synthetic fuels, as well as electrolyte and multi-phase systems (Mertens et al., 2014). The ASPEN project led to the foundation of the well-known Aspen Tech company. As far as steam cycles are concerned, to the best of our knowledge, the first simulation codes were PRESTO (Choo and Staiger, 1982), a computer code developed by NASA, and PEPSE (Cooke, 1983), developed in the early 70’s for nuclear and conventional steam cycles. Only later, in the late 80’s, other power plant simulation codes were developed, mainly spurred by the need of optimizing the design and part-load operation of combined cycles. Elmasri (formerly a professor at MIT) developed GT PRO (Elmasri, 1988); a computer program for the design simulation of combined cycle power plants (over the years, GT PRO was expanded and today it is commercialized by Thermoflow). Erbes and Cohn (Erbes et al., 1989) developed GATE for the simulation of gas turbines and combined cycles (then the code was expanded and commercialized with the name “GATE cycle”). Prof. Lozza (Politecnico di Milano) (Lozza, 1988; Lozza, 1990) developed a computer program for the thermodynamic optimization of heat recovery steam cycles including accurate correlations for the assessment of the steam turbine efficiency (the code was merged with those developed by other researchers of Politecnico di Milano for simulating gas turbines originating the GS “Gas Steam” simulation code (Consonni, 1983; Chiesa and Macchi, 2004)). Another widely used steam cycle simulation code is IPSEpro, first published in 1991 as IPSE by Perz (1990).

As far as cycle design codes are concerned, it is important to note that the design step of a steam cycle is a critical task since decisions taken at this stage affect not only efficiency and costs but also the operational issues (control strategy to be implemented, minimum stable load, efficiency at part-load, maximum ramp-up rate, start-up time, etc.). For conventional power plants, the optimal design criteria are well-known industrial standards. These design criteria, refined over tens of years of industrial experience, essentially target the minimum levelized cost of electricity at full load, corresponding to the optimal trade-off between efficiency and costs (material cost, manufacturing cost, installation cost, operating and maintenance costs) (Kehlhofer et al., 2009; Gülen, 2019). However, it is not always possible to extend such design criteria to novel concepts (e.g., concentrated solar power plants, integrated solar combined cycles, hydrogen/synfuels/electricity polygeneraiton plants) because of the different thermodynamics (Martelli et al., 2012) (i.e., efficiency is not maximized following the same criteria developed for combined cycles or conventional fired steam cycles), specific design constraints (e.g., metal dusting on some heat exchangers processing syngas (Spinelli et al., 2015)) and more tight operational constraints (e.g., solidification temperature of the molten salts in CSP plants (Trabucchi et al., 2017; Elsido et al., 2018)). For these plants, computer-aided optimization approaches are essential to assess the performance and costs of the possible steam cycle configurations.

Off-design simulation codes are essential tools for both the design phase of the power plant and the operation of existing cycles. During the design phase of a power plant, off-design simulation codes are used to assess the performance of the cycle when operating at part-loads and/or site conditions (e.g, cooling water temperature, ambient temperature, fuel type) different from those considered in the design phase. These steady-state simulators can be used also to determine the optimal part-load control strategy of the steam cycle (i.e., throttling, sliding-pressure boiler, partial-admission turbine) and check possible part-load operating issues (e.g., steam overheating in heat recovery steam generators, steaming in economizers, molten salt solidification in CSPs). It is important to notice that the part-load assessment is today very important for steam cycle power plants which are asked to provide reserve capacity and balancing services (e.g., spinning reserve, frequency control, secondary reserve) to the electricity market. For these units it essential to keep high efficiency also at low loads and reduce the minimum load as much as possible.

Another challenge posed by today’s electricity market is the dynamic flexibility of dispatchable units (i.e., quick start-up/shut-down, and fast ramping up/down). In this regard, steam cycles are penalized compared to gas turbines by the larger thermal capacity of the system (boiler metal and fluid inventory) and the use of thicker components (turbine, drums, headers), in which temperature gradients cause severe thermo-mechanical stresses. However, novel technological solutions (see, e.g., the warm-keeping and pre-warming system for steam turbines (Pehle et al., 2020) and optimized start-up sequences are being developed to alleviate this penalty. In this regard, a key rule is being played by dynamic simulation codes, which are used in academia and industry as virtual test benches prior to the much more expensive field-tests. These dynamic simulators are capable of handling the configuration complexity of steam cycles (featuring multiple pressure levels and/or a cascade of feedwater preheaters, multiple turbine sections, and multiple pumps), the implementation of the control structures, and dynamic boundary conditions.

Review papers that systematically analyze scientific publications on certain topics are very valuable. However, a limited number of review papers on the topic under investigation have been published. Relevant review papers found in the literature include Maffezzoni (Maffezzoni, 1992) (in 1992, issues on the modeling and simulation of power plants), Liu et al. (2012) (in 2012, a state-of-the-art review on modeling and simulation of the thermal power plant), Alobaid et al. (2017) (in 2017, a state-of-the-art review on the dynamic simulation of thermal power plants), Subramanian et al. (2018) (in 2018, a state-of-the-art review on modeling and simulation of energy systems) and Avagianos et al. (2020) (in 2020, a state-of-the-art review on modeling and simulation of solid-fuel thermal power plants for flexible and off-design operation). Although the topics discussed range from steady-state to dynamic simulation models, these reviews were mostly specific to one modeling technique (e.g., steady-state or dynamic) or a narrow field of application (e.g., coal power or concentrated solar power). This first-of-its-kind review paper provides researchers, and practitioners with detailed information on both steady-state and dynamic process simulation and optmizaiton models, applied to various types of thermal power plants.

An overview of the main scientific contributions and related software targeting the simulation and optimization of steam cycles will be shown. For the sake of clarity, the review is arranged in three parts. The first one (Mathematical Background) focuses on the approaches proposed for the design optimization of conventional steam cycle power plants. Design Calculation and Optimization of Conventional Steam Cycle Power Plants reviews the main contributions and software for the design and design optimization of non-conventional steam cycles. Finally, Design Calculation and Optimization of Non-Conventional Steam Cycles provides an exhaustive overview of the literature and related codes for the dynamic simulation.

Mathematical Background

Steady-State Simulation and Optimization

The steady-state model of a steam cycle power plant, similarly to chemical processes, consists of a set of equations describing the thermo-chemical phenomena occurring in each piece of equipment. These equations are the thermodynamic property models of each stream (equation of state and flash calculation routines computing the density, enthalpy, entropy, and vapor fraction of each stream), the constitutive equations of each equipment unit (energy, mass, and atomic balance equations, performance correlations) and the flowsheet topology equations (linking the output of a unit with the input of the downstream unit). The pressures, temperatures, mass flow rates, composition, vapor fraction, enthalpy, entropy, the density of each stream of the power plant as well as the power input/output of each equipment unit are unknown variables $x_k$ to be found. If the specifications set by the user on the input parameters (e.g., fuel composition and flow rate, performance parameters of the equipment units, evaporation, reheating and condensation pressures, superheating and reheating temperatures) are properly defined, the system of the above-mentioned equations has equal number m of variables $x_i$ and equations $f_j(\mathit{x}$) = 0. We can write this system of equations using the more convenient vectorial form:

$\mathit{f}(\mathit{x)=}\mathbf{0}(1)$

Such system (Eq. 1) is nonlinear, since some equations (e.g., equation of states, energy balance, performance correlations for the units) are nonlinear, sparse, since only a few variables appear in each equation, and it may involve hundreds of variables and equations if the power plant features many streams and units.

Power plant and process simulation software are based on either the equation-oriented or the sequential modular approach to solve the nonlinear system of equations. The equation-oriented approach consists of solving the system of the equation as a whole using specifically developed numerical algorithms, like the well-known Newton Raphson algorithm or the Powell dogleg algorithm (Biegler et al., 1997). On the one hand, these algorithms very fast convergence rates (e.g., quadratic for the Newton-Raphson algorithm), but, on the other hand, they require a guessed starting solution (to be assumed by the software user) not too far from the system solution and continuously differentiable equations $\mathit{f}(\mathit{x)}$ with non-singular Jacobian. From a practical point of view, the user has to guess a reasonably good starting value for all the proprieties (pressures, temperatures, mass flow rates, compositions, etc) of each stream and all the variables of the equipment units. This task may be very time-consuming and, depending on the user knowledge of the power plant, prone to inaccuracy. Providing an inaccurate starting guess likely hinders the convergence of the iterative algorithm with a very limited possibility of debugging. Numerical issues occur also if the Jacobian of the function $\mathit{f}(\mathit{x)}$ is singular or nearly singular in some regions. Advanced techniques can be adopted to mitigate these convergence issues, like integrating the Newton algorithm with the Armijo line search to make it more robust to bad starting points, and adopting the Powell dogleg method or continuation methods to mitigate the effect of Jacobian singularity (Biegler et al., 1997). Recent software alleviates the user’s effort in initializing the solution by adopting ad hoc routines (e.g., doing some iterations with the sequential modular approach). Examples of the commercial process and power plant simulation software based on the equation-oriented approach are gPROMS (2021) and Ebsilon Professiona (2021); Aspen Tech (2021) can employ both modes (sequential-modular or equation oriented).

The sequential-modular approach is based on the idea of solving the flowsheet units (pump, boiler, turbine, etc) in sequence, essentially following the flow of available pieces of information. Starting from the unit with known input streams and specifications (e.g., the pump), its output flow properties are computed by solving the constitutive equations of the unit (energy, mass, and atomic balance, performance correlations). Then, the downstream unit (e.g., the boiler) can be computed since the conditions of its input flow are known. If a required input stream is not known, since it is the outlet of a downstream unit, it is guessed to allow the calculation of the unit. Such guessed stream is called “tear stream” and this guessed value must be iteratively updated till convergence. Sequential-modular software performs four key steps:

1) Flowsheet partitioning and loop identification: closed loops (recycles) of material and information streams between units are identified automatically using a simple routine.

2) Convergence order definition: the calculation order of the equipment units is determined either manually or automatically with a routine (typically starting from the input flows with known specifications and following the flowsheet topology).

3) Tear stream identification: the closed loops (recycles) must be “opened” by tearing at least one stream of the loop (i.e., guessing the value for the properties of at least one stream of the loop). Such tear streams ${\mathit{x}}_T$ are selected either manually or automatically by the software using ad hoc algorithms.

4) Tear stream convergence: the tear streams properties ${\mathit{x}}_T$ are first guessed by the user, then they need to be updated by the software to reach simulation convergence. The process simulation with opened loops (tear stream) can be seen as a transfer function $\mathit{g}$ which, given the value assumed in the previous iteration ${\mathit{x}}_T^k$ computes a new value ${\mathit{x}}_T^{k+1}$, as shown in Eq. 2:

${\mathit{x}}_T^{k+1}=\mathit{g}\left({\mathit{x}}_T^k\right)(2)$

Figure 1 shows an example of a steam cycle where the tear stream is the feedwater pump inlet flow. Simulation convergence occurs when it is assumed a value ${\mathit{x}}_T^{\ast }$ such that the calculation of the flowsheet returns the same (within a certain tolerance) value: $\mathit{g}\left({\mathit{x}}_T^{\ast }\right)={\mathit{x}}_T^{\ast }$. In mathematics such a class of problems is called “fixed point problems”. The most basic iterative algorithm to solve such problems is called “direct substitution” and it consists of using the output of the current iteration as guessed value for the next one: ${\mathit{x}}_T^{k+1}$ = ${\mathit{x}}_T^k$. Such simple and intuitive approach has a good convergence rate only if the maximum eigenvalue ${\lambda }_{max}$ of the Jacobian matrix is close to zero. In the other cases, its convergence rate is very slow (if $\left|{\lambda }_{max}\right|$is approaching to 1) or it is scattered away from the solution (if $\left|{\lambda }_{max}\right|$>1). For this reason, current sequential-modular software integrate also relaxation and acceleration methods like the dominant eigenvalue method (Crowe and Nishio, 1975) and the wegstein method (Wegstein, 1958):

FIGURE 1

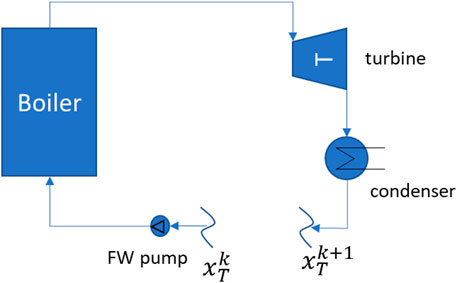
FIGURE 1. Example of a steam cycle simulated with the sequential-modular mode using the condenser outlet flow as tear stream.

Compared to equation-oriented software, the convergence issues of sequential modular ones increases rapidly with the number of recycle loops of the flowsheet because more tear variables need to be assumed and converged. Nested loops (i.e., loops sharing one or more streams) cause particular convergence issues because of the mutual influence. For these reasons, sequential-modular software must be carefully used when modeling steam cycle power plants that feature at least one (basic steam cycle) or multiple (e.g., heat recovery steam cycles with multiple pressure levels, coal-fired steam cycles with multiple regenerators) closed loops. If using general-purpose process simulation software (e.g., Aspen Tech, 2021), the tear streams and the convergence order should be carefully selected and initialized. Software specifically developed for simulating steam cycle power plants (e.g., Thermoflex/GT PRO/Steam Pro (Thermoflow, 2021)) feature ad hoc criteria to define the convergence order and the tear variables to minimize convergence issues. On the other hand, the main advantages of sequential modular software are the better robustness to solution initialization accuracy, the need of initializing only the tear variables, the easier debugging in case of convergence failure, and the possibility of integrating external equipment unit models (e.g., turbine meanline design code).

Adopting the same notation used so far for simulation problems, steady-state optimization problems arising in the design phase or operation phase in off-design or part-load conditions can be formulated as follows:

$\mathbf{min}\hspace{0.17em}c\left(\mathit{x},\mathit{z}\right)(3)$

$s.t.\hspace{1em}\mathit{f}\left(\mathit{x},\mathit{z}\right)=\mathbf{0}(4)$

$\mathit{g}\left(\mathit{x},\mathit{z}\right)\le \mathbf{0}(5)$

$\mathit{x}\in {\mathit{R}}^m,\hspace{1em}\mathit{z}\in {\mathit{R}}^{nc}\times {\left\{0,1\right\}}^{nb}(6)$

The variable $\mathit{z}$ denote the independent design or operational variables while the variables $\mathit{x}$ denote the dependent variables, corresponding to the simulation variables of Eq. 1 (i.e., pressures, temperatures, mass flow rates, composition, etc. of each stream and the power input/output of each equipment unit). Equation 3 indicates the objective function to be minimized (e.g., cost of electricity, heat rate, etc), Eq. 4 denotes the simulation model equations (same as Eq. 1) which are equality constraints of the optimization problem, Eq. 5 denote the possible inequality constraints (e.g., bounds on the variables, cap on the project budget, etc., desired net power output, etc.). We use m to denote the number of dependent variables, nc the number of continous/real independent variables and nb the number of independent binary variables. Notice that for a fixed value of $\mathit{z}$, the problem reduces to a simulation problem (finding $\mathit{x}$ such that $\mathit{ f}\left(\mathit{x},\mathit{z}\right)=\mathbf{0}$).

Since in general the objective function and some of the constraints are nonlinear and nonconvex, the optimization problem is nonlinear and nonconvex. If all variables are continuous (real), the problem is called NonLinear Program (NLP). If some of the optimization variables are binary or discrete, the optimization problem is a Mixed Integer NonLinear Program (MINLP).

The optimization problem can be tackled by adopting two main approaches:

- The equation-oriented approach: the large-scale NLP or MINLP defined by Eqs. 3–6 is solved using an optimization algorithm that finds (at the same time) the optimal values of independent variables $\mathit{z}$ and simulation variables $\mathit{x}$. On the one hand, this approach has the advantage of the computational effectiveness of today’s nonlinear solvers (e.g., BARON for MINLP (Tawarmalani and Sahinidis, 2005), SNOPT (Gill et al., 2005), and IPOPT (Biegler, 2010). On the other hand, it shares the same disadvantages of the equation-oriented mode for simulation (need of proving a good starting guess for all variables, convergence issues in case of poor starting guesses/ill-conditioned problems/Jacobian singularity, the limited possibility of debugging).

- The black-box approach: the optimization algorithm is kept at a higher hierarchical level than the simulation equations Eq. 4. At each iteration k, the optimization algorithm samples values of the independent decision variables ${\mathit{z}}_{\mathit{k}}$ and executes a simulation software to compute the value of the related dependent variables ${\mathit{x}}_{\mathit{k}}$, objective function $c({\mathit{x}}_{\mathit{k}},{\mathit{z}}_{\mathit{k}})$ and inequality constraints $\mathit{g}({\mathit{x}}_{\mathit{k}},{\mathit{z}}_{\mathit{k}})$. The power plant model equations are hidden in the simulation software and cannot be accessed by the optimization algorithm (hence the name “black-box optimization”). The simulation software needs to be linked to the optimization algorithm in such a way it receives the values of ${\mathit{z}}_{\mathit{k}}$, it is automatically executed and then it returns the values of objective function and constraints. Since most of today’s commercial plant simulation software have this capability, the black-box approach has become very popular. Indeed, the main advantage of this approach compared to the equation-oriented one is the possibility of using commercial power plant simulation software without the need to recoding all the model equations (very time-consuming activity). On the other hand, computational efficiency is the main disadvantage of the black-box approach: 1) the output of the plant simulation software is typically non-smooth and affected by numerical noise making it necessary to adopt derivative-free optimization algorithms (Martelli and Amaldi, 2014) (e.g., pattern search, simplex/complex, scatter search, evolutionary algorithms) which have slower convergence rates (or no convergence guarantees in case of meta-heuristic algorithms) compared to gradient-based algorithms (Conn et al., 2009), 2) each plant simulation is time-consuming and several hundreds of plant simulations are required to reach convergence of the optimization algorithm (Martelli and Amaldi, 2014). Since the number of required simulations grows exponentially with the number of independent optimization variables, the black-box approach is recommended only for problems with a limited number of optimization variables (<10–20 for non-smooth black-box problems, up to 100 for smooth problems).

Fort the above-listed reasons, the black-box approach is widely adopted for both power plant and chemical process optimization but is limited to problems with few independent design/operational variables. The equation-oriented approach is typically adopted in academia for large-scale problems involving a large number of binary/discrete optimization variables as the steam cycles described in the section Design Optimization of Steam Cycles With Multiple Heat Sources. A considerable amount of time is required to write all the optimization problem including all the power plant model equations $\mathit{f}\left(\mathit{x},\mathit{z}\right)=0$ in a suitable mathematical programming software (e.g., GAMS, 2021; AMPL, 2021; Pyomo, 2021).

Dynamic Simulation

The dynamic simulation problem of a power plant can be formulated as in Eq. 7:

$\mathit{f}(\mathit{x},\dot{\mathit{x}},\mathit{u})=\mathit{0}(7)$

Where $\mathit{x}$ denotes the time-dependent state variables (pressures, temperatures, mass flow rates, etc of each stream and unit of the plant), $\dot{\mathit{x}}$ denotes the derivative over time, and $\mathit{u}$ the time-dependent control variables (position of valves, inlet fuel flow rate, etc.). The equations $\mathit{f}$ are the same as the steady-state model with the exception that the energy and the mass balances of the units include the unsteady-flow terms (variation over time of mass and internal energy stored in the equipment unit). Since some of these equations are algebraic (e.g., the equation of state, the enthalpy-temperature-pressure functions, etc.) and some are differential (including time derivatives), the system of equations is called DAE (Differential Algebraic Equation). It is a very challenging class of problems that need either reformulation as a system of ODEs (Ordinary Differential Equations) or the use of ad hoc integration algorithms (see, e.g., the IDA package (IDA, 2021)).

Many approaches can be found in the literature to model the thermal-hydraulics of steam cycle power plants such as the mixture flow model and two-fluid models. The one-dimensional mixture flow model, also known as the homogeneous or three-equation flow model, assumes thermodynamic equilibrium between phases (water and steam). The mixture flow model is represented by three partial differential equations for mass, momentum, and energy that describe the dynamic behavior of the characteristic variables. For single-phase flow components (e.g., superheater, turbine section, and economizer), the three characteristic fluid variables are the local pressure, the total mass flux, and the fluid temperature or the fluid enthalpy for subcooled water or superheated steam. In the case of two-phase flow components (e.g., evaporator and condenser), the three variables are complemented by the void fraction. Due to its simplicity and applicability to a wide range of single and two-phase flow components, the mixture flow model is often used when the response of the total mixture and not of each constituent phase is required. Therefore, this flow model can be found in most dynamic simulation programs such as ASPEN Plus DYNAMICS, MODELICA, and MATLAB SIMULINK.

The two-fluid models, also known as the heterogeneous flow model, formulate separate conservation equations of mass, momentum, and energy for the gas and liquid phase. This formulation presents considerable difficulty because of mathematical complexity and the uncertainty in modeling the interaction between phases at the interphase boundary. Such relations cannot be derived from fundamental physical laws and in most cases are based on empirical assumptions. Solving the resulting differential equations requires higher computational effort and entails parameters that may cause numerical instability, especially due to improper selection of interfacial terms. Due to the increased number of differential equations and closure relations, the two-phase fluid models, in contrast to the mixture flow model, are related to higher computational costs and are suitable for thermodynamic non-equilibrium applications. Accordingly, the complex and time-consuming two-fluid models are only implemented in few simulation programs such as APROS (APROS, 2021) and RELAP.

To solve the one-dimensional partial differential equations, the finite difference solution method or the finite volume solution method is used. The partial differential equations are discretized concerning space and time and the non-linear terms are linearized. In the space discretization (integration over the corresponding element length), several discretization schemes such as the first-order upwind scheme, the second-order central differencing scheme, and the quadratic upwind interpolation are available. For time discretization, the implicit method is usually applied. The physical properties such as pressure, velocity, and enthalpy in the model can finally be calculated using the discretized conservation equations, the parameters for inlet and outlet flows, and the thermodynamic properties.

In optimal control problems, $\mathit{u}$ are time-dependent decision variables which need to be optimized to minimize a cost function $c$:

$\mathit{min }c(\mathit{x},\dot{\mathit{x}},\mathit{u)}(8)$

$\text{s}.\text{t}.\mathit{ f}(\mathit{x},\dot{\mathit{x}},\mathit{u)=}\mathbf{0}(9)$

$\mathit{g}(\mathit{x},\dot{\mathit{x}},\mathit{u})\le \mathbf{0}(10)$

In other words, the optimal control problem aims at finding the optimal trajectory of the control variables $\mathit{u}$. The main solution approaches adopted in the energy and process industry are called single-shooting, multiple-shooting, and collocation. A brief explanation is given below, while the interested reader can find further details, for example, in (Cellier and Kofman, 2006; Kunkel and Mehrmann, 2006; Biegler, 2007; Alobaid, 2018a).

Design Calculation and Optimization of Conventional Steam Cycle Power Plants

This section focuses on steam cycles which are widely adopted in the electric power industry, namely highly regenerative steam cycles for coal-fired power plants, and heat recovery steam cycles (also called “bottoming cycles”) for combined cycles. The scheme of a coal-fired steam cycle power plant is shown in Figure 2, while the scheme of a combined-cycle is illustrated in Figure 3.

FIGURE 2

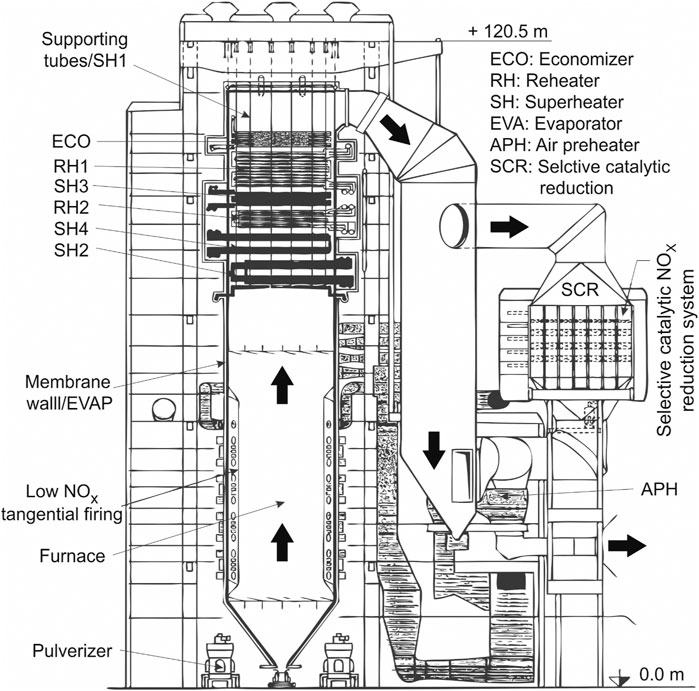
FIGURE 2. Schematic diagram of a hard-coal fired power plant (source Starkloff et al., 2015).

FIGURE 3

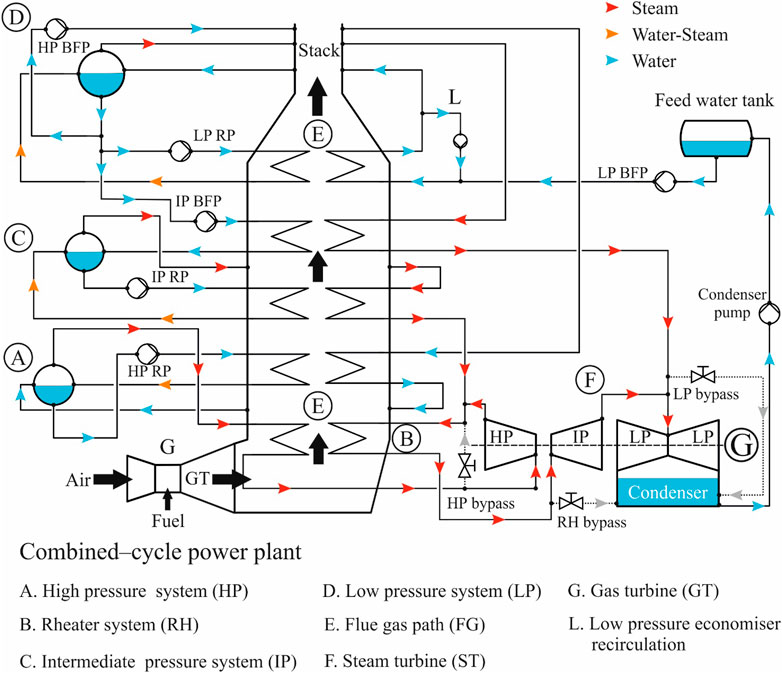
FIGURE 3. Schematic diagram of a modern CCPP including 1 + 1 arrangement of gas turbine and steam turbine units in combination with a triple-pressure, reheat, vertical heat recovery steam generator (source Alobaid et al., 2008).

Coal-Fired Power Plants

Despite limiting growth in the future use of coal, coal-fired power plants play a significant role in the global electricity supply. In 2018, the total share of worldwide electricity generation by coal-fired power plants accounted for 35% according to the International Energy Agency (IEA) (IEA, 2019). The specific contribution in the public electricity generation of each country depends on several factors such as the prices of coal and other fossil fuel (gas or oil), local resources, political economy and environmental regulation, and access to the world market. The list of coal categories is long and varies from (meta-) anthracite over bituminous and sub-bituminous coal to lignite. For power and heat generation, two types of coals are generally used, namely lignite (brown coal) and bituminous (hard coal). For the pre-drying process, a huge amount of the recirculated hot flue gas at a temperature of about 1,000°C is used. However, it is favorable to dry the brown coal using a low temperature medium or using one of the external pre-drying techniques (Walter and Epple, 2017).

The main component of a coal-fired power plant is the steam generator, where pulverized coal entrained with the primary airflow is combusted (see Figure 2). The energy stored in the chemical bonds of the coal is released in form of the thermal energy that is transferred to the working fluid (generally water) to generate steam for the Rankine cycle. State-of-the-art coal-fired power plants have single reheat and several low-pressure and high-pressure feedwater preheaters, reaching a net thermal process efficiency of about 46%. Some power plants are equipped with a second reheater stage. After leaving the steam generator, the flue gas may pass through different devices (air preheater, flue gas cleaning systems such as the selective catalytic reduction system, the electrostatic precipitator, and the desulphurization unit). Although all coal-fired power plants follow the same working principle, each plant is uniquely engineered, resulting in various operation modes and dynamic behavior. The specific design is influenced by different factors, including coal composition and handling (effect on e.g., mills, burners, furnaces, and heat exchangers), local emission regulation (effect on e.g., flue gas cleaning devices), water/steam cycle (sup-critical, supercritical or ultra-supercritical steam parameters), plant configuration (natural, forced circulation or once-through), reheater temperature control (e.g., attemperators, tilting burners, flue gas dampers). The plant size may range from a small industrial system to a large plant with up to 1,300 MW_el supercritical boiler (e.g., Rockport Generating Station in the United States).

With thermodynamic considerations, it is possible to prove that the efficiency of fired steam cycle power plants is favored by adopting regeneration (a cascade of regenerators fed by steam turbine extractions at optimized pressures), steam superheating at maximum temperature allowed by the boiler and turbine materials, one or more reheating at optimized pressure and maximum possible temperature, highest possible steam generation pressures allowed by boiler and turbine, and the lowest possible condenser pressures allowed by the cold heat sink (lake, river, sea, air), vacuum pump and sealing systems of the condenser. The interested reader can find further details about steam cycles in ref. (Spliethoff, 2010).

Combined-Cycle Power Plant

According to the International Energy Agency (IEA) in 2019 (IEA, 2019), gas-fired power generation accounted for approximately 24% of the total share of worldwide electricity generation, dominated by combined-cycle power plants. The first attempt to combine a gas turbine and a steam cycle was achieved by using the hot exhaust gas of the gas turbine to preheat the feed water of an existing large-scale steam power plant (instead of steam extractions). An alternative approach was to use the hot exhaust gas of the gas turbine to supply hot combustion air to the furnace of the steam generator. The modern layout of the combined-cycle power plant (CCPP) is the result of evolutionary development in the second half of the last century, driven by the increasing performance of the gas turbine. Korneuburg (A) power station, commissioned in 1960 in Austria, represents the first combined-cycle power plant according to the modern definition of the CCPP. The general idea is that the waste heat of a gas turbine is absorbed by a heat recovery steam generator (HRSG) installed downstream in the flue gas path of the gas turbine. The HRSG produces superheated steam, generating additional power in the steam turbine. The process efficiency of the Korneuburg (A) combined-cycle power plant did not exceed 32.5%. At that time, the GT operating temperature was very low (620°C) and the GT outlet temperature was 310°C so that a supplementary firing was required to support the steam cycle. Considerable developments were then carried out including high-temperature-resistant materials, low-NO_x combustors, and innovative cooling methods, which significantly improve the gas turbine performance. Furthermore, the single-pressure HRSG was replaced over time with dual-pressure and triple-pressure HRSGs to reduce the temperature mismatch between the flue gas path and the water/steam side. Nowadays, a 1 + 1 arrangement of gas turbine and steam turbine in combination with a triple-pressure reheat HRSG is state of the art (see Figure 3). Due to the high temperature at the gas turbine outlet (in the order of 650°C), the supplementary firing is omitted. Accordingly, the nominal process efficiency of a modern combined-cycle power plant can reach 60%. Large-scale CCPPs with efficiency levels greater than 60% (up to 62.2%) are now running in Irsching, Germany (Ratliff et al., 2007; Scholz et al., 2012) and Bouchain, France (Vandervort et al., 2016; Vandervort et al., 2017) with a net electrical power of about 605 MW_el per unit.

Differently from coal-fired steam cycles, owing to the presence of a pinch point between economizer oulet and evaporator inlet, the efficiency of heat recovery cycles adopted in combined cycles is increased by adopting no regenerators (as they would decrease the turbine power without useful effect on steam generated in the HRSG) and multiple levels of evaporation at optimized pressures. Further details on the thermodynamic fundamentals, possible arrangements, design criteria, and operational issues of these cycles can be found in (Kehlhofer et al., 2009; Speight, 2013).

Usual Design Procedure and Software

The usual practice for the design of steam cycles of conventional power plants (e.g., coal-fired power plants, combined cycles) consists of the following sequential procedure:

1) The structure of the cycle is defined (i.e., number of evaporation pressure levels, number of regenerators for feedwater preheating, number of reheating stages, etc.) according to the engineer’s experience and previous industrial projects. As a general criterion, increasing the plant size, more expensive and efficient designs are used to minimize the levelized cost of electricity. This results from the economy of scale on the capital cost, which allows increasing equipment number and sizes with limited penalization in the specific capital cost of the plant. For example, specific commercially available software like Steam Pro (Thermoflow, 2021), have predefined steam cycle arrangements that can be selected.

2) The thermodynamic steady-state simulation of the cycle at design conditions (full-load, nominal ambient/site conditions) is performed using an ad hoc software (either internally developed by the company/university, like GS (Consonni, 1983), or commercially available like Thermoflex/GT PRO/Steam Pro (Thermoflow, 2021), Aspen Tech (2021), Cycle Tempo (2021), Gate Cycle (2021) and Ebsilon Professional (2021) and setting the key design variables (steam pressures, steam temperatures, pinch temperature differences in the heat exchangers, etc.) according to the recommended industrial standards (Kehlhofer et al., 2009; Martelli et al., 2011b; Woodruff et al., 2017).

3) Possibly the key cycle variables are optimized by means of sensitivity analysis or linking the simulation code with a black-box optimization algorithm (e.g., genetic algorithm (Valdés et al., 2003), particle swarm optimizer (Eberhart and Kennedy, 1995), Smolyak grids, and polynomial approximations (Kieslich et al., 2018)).

4) A preliminary engineering design of the cycle equipment units (boiler, feedwater preheaters, condenser, steam turbine) is performed according to recommended industrial design criteria, commercially available software (e.g., PEACE (Thermoflow, 2021)), or ad hoc optimization approaches. For conceptual and preliminary studies, this design step is typically sufficient.

5) For front-end engineering studies, equipment units (e.g., boilers, turbine sections, heat exchangers, valves) need to be designed in detail in collaboration with the manufacturer, and their performance is assessed using ad hoc rating codes. For example, for boilers, rating software like FRNC-5PC (FRNC-5PC, 2021) is commonly adopted. Cycle and power plant simulation performed in step 4) need to be updated according to the rated performance of the equipment units.

6) Direct and indirect capital costs involved in the project are assessed. Depending on the level of accuracy desired for the project (conceptual study, front-end engineering, etc.), literature cost correlations (see e.g., (Turton et al., 2008; Carcasci et al., 2015; Elsido et al., 2019)), dedicated commercial software packages (e.g., PEACE (Thermoflow, 2021), Aspen economics (Aspen Tech, 2021)), or quotations from manufacturers are used.

7) Steady-state simulations at part-load and off-design conditions (e.g., different condensation temperatures due to variations in the cooling medium temperature) of the equipment units and whole cycle are performed to assess plant performance during extreme and most frequent operating conditions. General-purpose process simulation software like Aspen Plus, ad hoc commercially available software like Steam Master (Thermoflow, 2021) and Thermoflex (Thermoflow, 2021), or user-defined codes can be used.

8) Possibly, dynamic simulations are performed for the most critical phases (start-up, shut-down, ramp-up, and ramp-down) to check the achievable dynamic performance and design the control system. Results of the dynamic simulations during start-up and ramps may be used to assess thermo-mechanical stresses on the most critical equipment units.

Achieving a good steam cycle design may require several iterations among the different steps described above. Being an iterative procedure, there is no guarantee of finding the optimal design (i.e., the design achieving the maximum net present value across the whole lifetime of the power plant). Indeed, the ideal steam cycle design tool should be able to tackle all the steps at once, optimizing simultaneously cycle thermodynamic design, equipment design, costing, and part-load/off-design/dynamic operation. However, such an optimization problem would be extremely challenging owing to a large number of variables (mixed binary, discrete, and continuous) and nonlinear nonconvex constraints. For this reason, works available in the literature tackled only one or two of the above-mentioned design steps.

Design Optimization Approaches

As far as design optimization is concerned, the approaches can be classified into two major categories: black-box approaches and equation-oriented approaches (Biegler et al., 1997). The former approach consists of keeping the optimization algorithm separated from the cycle model: the optimization algorithm optimizes the independent design variables and calls the cycle simulation model as a black-box function to determine cycle performance. This allows using ad hoc commercially available or proprietary simulation software for cycle design, simulation, and costing while coding the optimization algorithm in other languages (Python, Matlab®, etc.). Due to the numerical noise and non-smoothness of the cycle simulator output (Martelli and Amaldi, 2014), derivative-free optimization algorithms are typically adopted. The equation-oriented approach consists of including dependent and independent design/simulation variables in the optimization problem, which features the cycle modeling/design equations as constraints of the optimization problem. Thus, simulation and optimization models have integrated into a large-scale (typically nonlinear) optimization problem. On one hand, gradient-based optimization algorithms with guaranteed quadratic/superlinear convergence rates can be adopted; on the other hand, depending on the type of solver, the number of variables, and problem nonlinearity, achieving convergence to the global optimum may be difficult (local minima, infeasible solutions, etc.).

Table 1 shows some relevant recent contributions focusing on the design optimization of conventional coal-fired steam cycle power plants. The table reports the objective of the study, the optimization variables, and the methodology adopted. Most of the studies optimize the key cycle variables: superheating steam pressure/temperature (subject to bounds set by the selected tube/headers materials), reheating pressure/temperature, pressures of the steam extractions for the feedwater preheaters, and condenser pressure. It can be noticed that only a few studies tackle the optimization of the cycle structure (number of feedwater preheaters, the arrangement of the steam turbine bleeds, and number of reheaters) because models and solutions algorithms are more sophisticated (owing to the discrete decisions).

TABLE 1

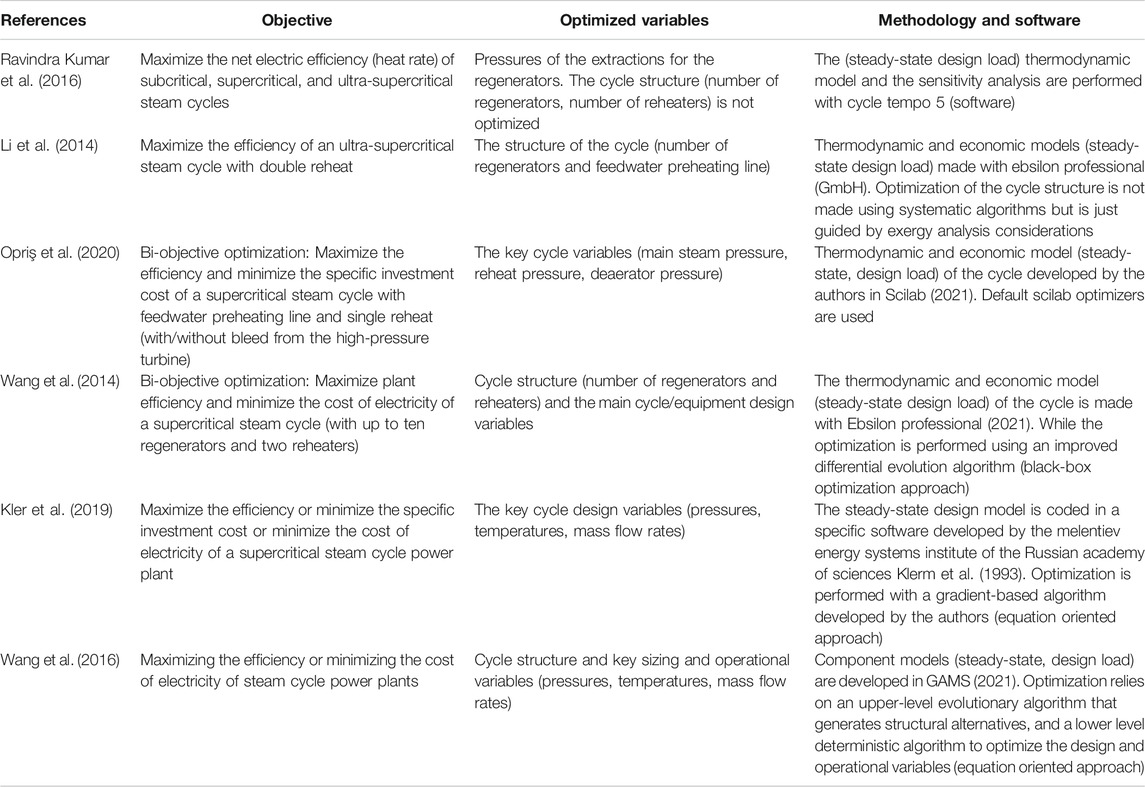
TABLE 1. List of recent contributions on the design optimization of conventional coal-fired steam cycle power plants.

Table 2 reports some of the most recent contributions on the optimization of heat recovery steam cycles for combined-cycle power plants. As explained in (Kehlhofer et al., 2009), the key cycle design variables are the number of evaporation levels, the steam evaporation pressures, the superheat temperatures, and the reheat pressure (if adopted). Additional key variables are those influencing the design of the HRSG and the heat transfer areas of the tube banks (economizers, evaporators, and superheaters/reheaters). For example, the pinch point temperature difference (minimum temperature difference between hot flue gases and boiling steam) influences both the heat transfer area of the evaporator and the raised mass flow rate of steam (Kehlhofer et al., 2009; Martelli et al., 2011)and it is used as an independent optimization variable in several works, e.g., (Carapellucci and Giordano, 2013; Martelli et al., 2011; Nadir and Ghenaiet, 2015).

TABLE 2

TABLE 2. List of recent contributions on the optimization of heat recovery steam cycles for combined-cycle power plants.

Design Calculation and Optimization of Non-Conventional Steam Cycles

Nowadays, steam cycles are used in a wide range of power plants such as waste to energy plants (WTE), biomass-fired plants, concentrated solar power plants (CSP), Integrated Gasification Combined Cycles (IGCCs), Integrated reforming combined cycles (IRCCs), Integrated Solar combined cycles (ISCC), Integrated waste-to-energy combined cycles, poly-generation plants (Elsido et al., 2019) for the coproduction of electricity, synfuels and heat, combined heat and power plants and tailored steam cycles providing steam and heat to process industries (often referred to “steam networks” or “steam utility systems”). As an example, the scheme of an ISCC power plant is represented in Figure 4.

FIGURE 4

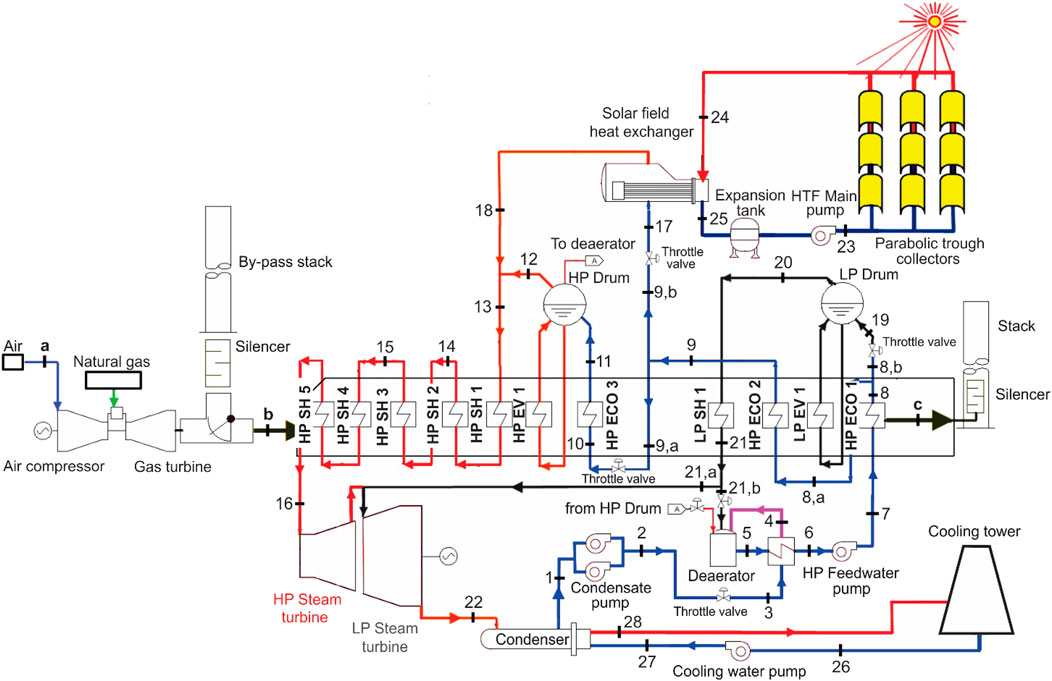
FIGURE 4. Schematic diagram of an ISCC power plant (source (Rashad et al., 2021; Temraz et al., 2020b)).

It is important to distinguish between steam cycles featuring a single major heat source (e.g., waste to energy plants, CSPs, fired CHP steam cycles serving the district heating network) and steam cycles recovering heat from multiple heat sources (IGCCs, IRCCs, polygeneration plants, steam networks for the process industry). For the first class of steam cycles, it is possible to extend the thermodynamic considerations derived for conventional steam cycles while for the second class it is necessary to deal with the overall plant heat integration.

Concentrated Solar Power Plants

A concentrated solar power (CSP) plant consists of a solar field, an energy storage system (optional), and a power block (see Figure 5). Different CSP technologies are mainly distinguished by concentrator and receiver systems such as parabolic trough and linear Fresnel reflectors as well as parabolic dish and solar tower reflectors. While parabolic trough and linear Fresnel reflectors concentrate direct sunlight on a line (line focus), the parabolic dish and solar tower technologies concentrate light on a point (point focus). Almost half of the capital expenditure for a CSP plant is related to the solar field that determines the amount of electrical output. Current developments aim at increasing the electrical conversion efficiency by using higher process temperatures, which in turn results in a decrease in the levelized cost of electricity (LCOE). Depending on the type and layout of the CSP, various cycles can be used in the power block (e.g., Rankine cycle, organic Rankine cycle, Stirling engines, Brayton cycle, or combined-cycle). CSPs are generally not dispatchable, supplying fluctuating electricity depending on the weather conditions. The possible integration of thermal energy storage (TES) in the CSP plant makes it highly dispatchable, providing a main competitive advantage of CSP against photovoltaics or concentrated photovoltaics (CPV). Consisting of a two-tank thermal energy storage system (hot and cold salt tanks), round-trip efficiencies above 97% were reported (Kuravi et al., 2013).

FIGURE 5

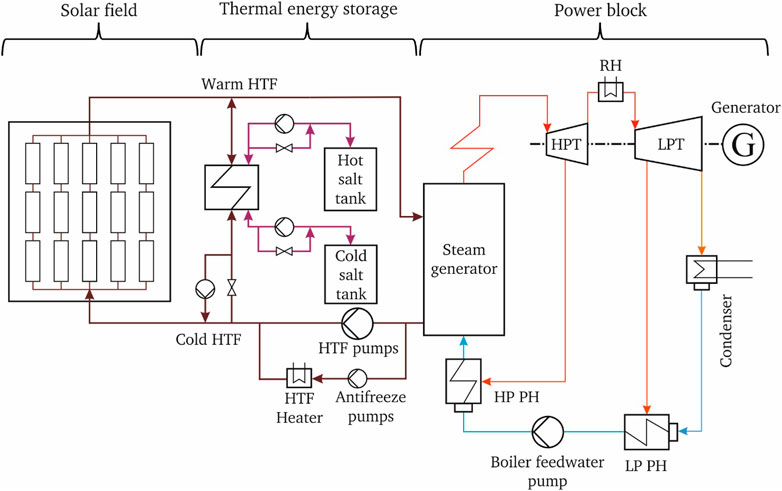
FIGURE 5. Schematic flow diagram of a modern concentrated solar power (source (Al-Maliki et al., 2016; Alobaid et al., 2017)).

Waste to Energy Power Plants

Non-conventional fuels, also known as alternative fuels or advanced fuels contribute to the substitution of fossil fuels. Most of these non-conventional fuels are derived from renewable energy sources such as biomass and some others are low-rank solid fuels including refuse-derived fuel, solid recovered fuel, municipal waste, and sewage sludge (a residual by-product of industrial and municipal wastewater treatment). For the thermal conversion of these fuels, both fluidized bed systems and waste incinerators use steam cycles to convert the combustion heat into electricity in an efficient way (see Figure 6).

FIGURE 6

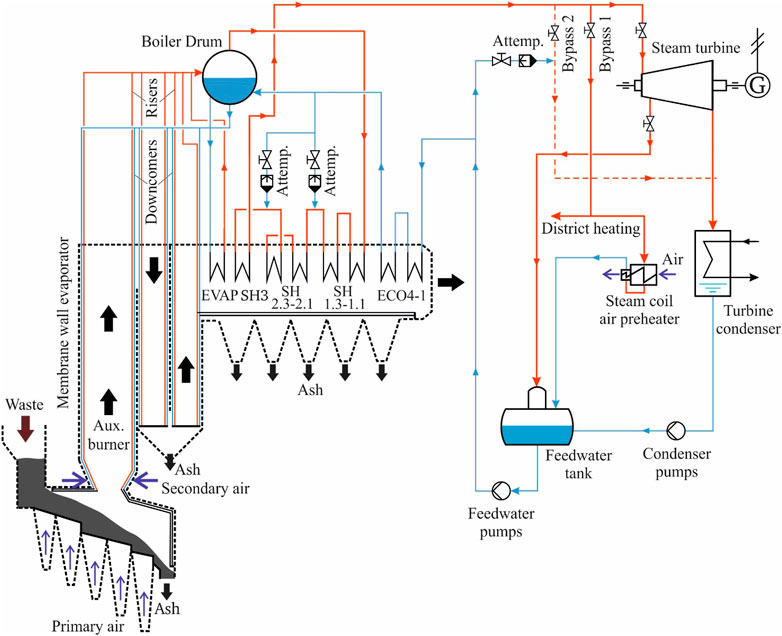
FIGURE 6. Schematic flow diagram of a modern waste incinerator power plant (source Alobaid et al., 2018a).

The fluidized bed combustors are a demonstrated technology for power and heat generation from non-conventional fuels, offering several advantages such as the continuous operation with the possibility of solid transport in and out of the bed, the high heat and mass transfer rates between gas and solids, the low NO_x emission in addition to simple SO_x capture. For example, Sumitomo Foster Wheeler will commission the world’s largest biomass-only fluidized bed furnace with a power output of about 300 MW_el in 2020, in Teesside, United Kingdom (Wheeler, 2016). Incineration is a proven technology for the large-scale disposal of solid waste. The heat released during combustion (lower heating value: approximately 10 MJ/kg) is used to generate steam for the Rankine cycle. The state-of-the-art waste incinerator burns 6 kg/s of waste (500 tons per day) and can reach an electrical gross efficiency of 30%. The design of WTE boilers is mainly influenced by the corrosive nature of the flue gases containing chlorine and sulfur (De Greef et al., 2013)). This translates into tight limitations on the maximum working temperatures of the tube banks (the superheating temperature is typically limited to 400–425°C (Bogale and Viganò, 2014)) and the need to replace the superheater tube quite often.

Design Optimization of Concentrated Solar Power and Waste to Energy Power Plants

For CSP and WTE plants, it is possible to extend the thermodynamic considerations made for coal-fired steam cycles. Their efficiency benefits from regenerators, high superheat temperatures, and high evaporation pressures. Thus, a limited number of interesting cycle configurations is possible and design optimization is mainly focusing on the cycle variables (pressures, temperatures) and arrangement of the steam tube banks within the steam generator. Table 3 reports the main contributions to the design optimization of CSP and WTE plants available in public literature.

TABLE 3

TABLE 3. List of recent contributions on the design optimization of CSP and WTE plants.

Design Optimization of Steam Cycles With Multiple Heat Sources

Once the cycle scheme (number of pressure levels, number of regenerators, with/without reheating, etc) and the heat exchanger network (HXs within the steam generator and outside) arrangement are fixed, calculating the design performance of unconventional steam cycles can also be performed using commercially available modular process simulation software, like Thermoflow (2021), CycleTempo (2021) and Aspen Tech (2021). The key challenge, which requires the use of advanced optimization approaches, is to find the optimal cycle scheme and HEN arrangement. Indeed, optimizing the cycle configuration and the HEN arrangement involves binary decisions (installing or not installing HXs, drums, pressure levels, turbine sections, etc). This combinatorial problem becomes even more challenging when dealing with steam cycles recovering heat from multiple heat sources (i.e., hot streams) because of the following two factors:

1) The thermodynamic analysis of the cycle efficiency is not easy since the heat source features a non-standard composite curve. Therefore, it is not obvious to assess the effects of the cycle options (reheating, regeneration, adopting multiple evaporation levels), and thermodynamic variables (pressures/temperatures) on efficiency.

2) Several possible arrangements/order/interconnections of the steam tube banks (i.e., the heat exchanger network, HEN) are possible and the optimal solution is not obvious. Moreover, building and simulating all the possible arrangements using conventional simulation codes might be extremely time-consuming.

Several approaches to tackle the heat integration of steam cycles into complex plants featuring multiple hot and cold streams have been proposed in the last decades mainly by the process engineering community. These approaches can be classified into three main categories:

1. Energy targeting methods: these methods aim at the definition of minimum utility requirements (i.e., maximum heat recovery) as well as the optimal selection and design of Rankine/steam cycles while avoiding computing the detailed structure of the HEN, which would significantly increase the complexity of the optimization problem. Examples of well-known energy targeting methods are Pinch Analysis (Kemp, 1982; Linnhoff and Hindmarsh, 1983), the LP transshipment model (Papoulias and Grossmann, 1983) and its extensions (Maréchal and Kalitventzeff, 1998) and (Maréchal and Kalitventzeff, 1999), and pinch location techniques (Duran and Grossmann, 1986). As shown in (Papoulias and Grossmann, 1983a), such a problem can be formulated as a Linear Program which can be easily solved. Also Pinch-analysis-based and exergy analysis based approaches have been proposed to optimize the efficiency of Rankine/steam cycles without dealing with the optimization of the HEN: for instance (Yu et al., 2015) defined a methodology predicting the Pinch position between the heat source and the working fluid to calculate the heat recovered and determine the optimum working fluid and operating conditions; (Maréchal and Kalitventzeff, 1998, 1999) proposed an energy targeting methodology to optimize the structure and flow rate of steam cycles and steam networks; (Martelli et al., 2011) developed an energy targeting optimization tool to maximize the efficiency of heat recovery steam cycles integrated with multiple heat sources. Floudas and Grossmann, (1986) extended the LP transshipment problem by (Papoulias and Grossmann, 1983) to the multi-period version, to consider different expected operating modes of the plant.

2. Cycle optimization techniques: optimization approaches and models aimed to optimize the detailed design of complex steam cycles and steam networks that provide heat and/or electric power to complex process plants and/or sell electricity to the electric grid. The main focus of the design of utility systems is the structure and operating variables of the cycle. Usually, the HEN is fixed in a previous step, reducing the degree of freedom of the problem in terms of possible integration options between both utility and process streams, i.e., the HEN structure within the process and boiler/steam generator is not optimized. The thermodynamic optimization of steam cycle variables was first investigated in the 1980s. One of the pioneering works in the systematic design of steam cycles is the one by Nishio et al. (1980), who integrated linear programming with a set of thermodynamic rules to determine the best plant structure and the steam cycle parameters. Nord et al. (2014) proposed a method for optimization of compact heat recovery steam cycles, Nadir and Ghenaiet (2015) and Valdés and Rapún (2011) on heat recovery steam generators, Wang et al. (2017) on regenerative steam cycles. Martelli et al. (2011) proposed a mathematical programming model, a linear approximation, and a two-stage algorithm to optimize the design of HRSCs and their integration with external hot and cold streams or steam users. The model has been applied to highly integrated plants: biomass to Fischer−Tropsch liquids plants, IGCCs with and without carbon capture and storage (CCS), integrated reforming combined cycles (Martelli et al., 2012), and coal-to-synthetic natural gas facilities (Martelli et al., 2013). Zhang et al. (2014) proposed an approach for the optimal design of HRSGs of polygeneration plants with and without external heat stream integration, to maximize the net power output of the HRSG. The superstructure of the HRSG has a fixed number of tube banks (i.e., sections of economizers, superheaters) and one evaporator for each pressure level. Manassaldi et al. (2016) extended the HRSG superstructure to include a wider variety of possible HRSG configurations and compared two optimization problems: i) the maximization of the total net power for a given total heat transfer area, and ii) the minimization of the total heat transfer area for a given total net power. Also, multi-period optimization approaches have been proposed for steam cycles and steam networks to find designs able to work in the expected operating modes/loads with high efficiency. Iyer and Grossmann (1998) tackled multiperiod optimization of utility systems and formulated the integrated design-operation problem as a large-scale MILP. Aviso et al. (2017) proposed a multi-period approach based on process-graph models for the synthesis of integrated energy systems and poly-generation systems, formulated as a MILP problem. Elsido et al. (2017) tackled the multi-period synthesis problem of CHP power plants with a two-stage problem decomposition: at the upper level a heuristic algorithm optimizes the design variables, and at the lower level the operation of the CHP units is optimized by solving a linearized MILP model. Shang and Kokossis (2005) developed a multi-period optimization model for the design and operation of flexible utility systems, such as back-pressure turbines, condensing turbines, boiler networks, considering the varying efficiencies for part load operation. More recently Jimenez et al. (2019), extended the transshipment methodology to synthetize site-wide heat recovery, distribution, and cogeneration systems with optimum operating conditions of the steam network system, accounting for interactions between utility system and processes.

3. Integrated optimization of HEN and steam cycle: due to the combinatorial nature of the HEN synthesis problem, only a few researchers have tackled the combined optimization of steam cycles/networks and HEN. These approaches aim at optimizing the synthesis of utility systems and HENs while considering all the possible integration options between process and utility systems. The first works are the sequential synthesis approaches proposed in (Duran and Grossmann, 1986; Maréchal and Kalitventzeff, 1998; Maré chal and Kalitventzeff, 1999; Papoulias and Grossmann, 1983; Papoulias and Grossmann, 1983c): In the first step a targeting method is used to determine the optimal cycle configuration and steam flow rates (without dealing with the combinatorial problem associated with the design of the HEN) and, in a second step, the HEN is optimized (for fixed steam and utility mass flow rates). More recently Mian et al. (2016), proposed an improved multiperiod version of the sequential synthesis methodology employing a derivative-free algorithm to improve the HEN solution by optimizing the penalty levels of the HX matches (Gundersen et al., 1996), the heat recovery approach temperatures, and the utility sizes. Luo et al. (2016) proposed a superstructure and a MINLP model for the integration of utility system and HEN, in which the integration between utility system and HEN is limited to steam condensate and boiler feedwater.

Huang et al. (2020) proposed a simplified simultaneous approach employing a fixed steam cycle/organic Rankine cycle structure and a pre-defined partition of the HEN superstructure into three subsections. The underlying assumption is that the steam flow is raised only in the boiler (i.e., no steam raised using hot process streams) and steam of the steam cycle can be used only as of the hot-end utility (i.e., condensers can provide heat only to the hot-end side of the cold process streams). Similarly, the ORC is confined to the low-temperature side of the HEN superstructure and it can be used only as a cold utility. The methodology has been applied to two industrial energy system case studies taken from literature, to demonstrate the capability of the method to find improved solutions compared to schemes without steam cycle/ORC integration.

Ma et al. (2018) addressed the multi-period design of an “interplant HEN” (i.e., connecting different plants) with a centralized utility system, where steam is employed as the heat transfer medium. The steam network connecting different plants includes only evaporating and condensing steam headers, without optimizing the arrangement of the heat exchangers inside the steam generators and without considering steam turbines. The authors proposed a multi-objective optimization problem, considering both cost and environmental impact.

To the best of our knowledge, the first and most complete approach for the simultaneous optimization of HEN and utility systems (including complex Rankine cycles) has been proposed in (Elsido et al., 2019; Elsido et al., 2020b; Martelli et al., 2017). The peculiarity of the model is to allow utility/Rankine cycle streams to be part of the well-known SYNHEAT HEN superstructure (Yee and Grossmann, 1990) with the same freedom in terms of matching options as process streams (see Figure 7). As a result, the MINLP is particularly challenging due to its nonconvexity and a large number of variables and constraints. The authors have proposed two ad-hoc algorithms, a structure-based problem decomposition (Martelli et al., 2017) and a bilevel decomposition approach using advanced linearization techniques (Elsido et al., 2019). The methodology has been applied to several real-world problems with up to 35 streams, such as the design and HEN of a NGCC, ORCs for different applications, IGCC, and integrated lignite and biomass-to-jet fuel production plant via gasification and Fischer-Tropsch synthesis, to demonstrate a considerable improvement in solution quality and CPU time over state-of-the-art.

FIGURE 7

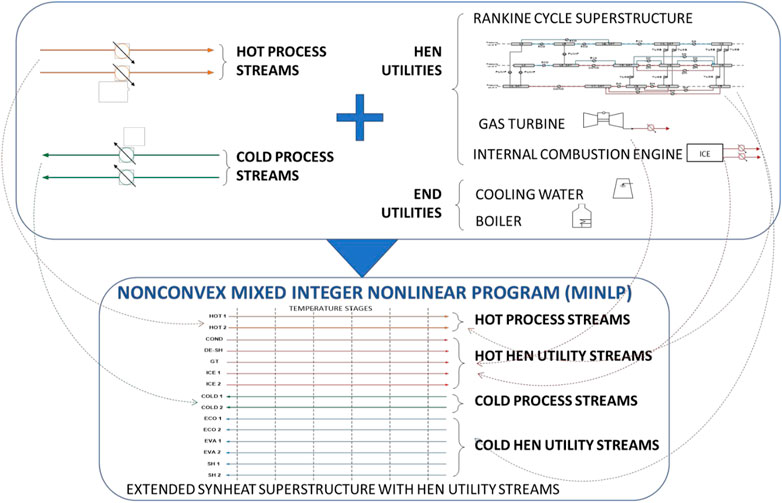
FIGURE 7. Integrated superstructure of Rankine (steam) cycle, utility systems (boilers, cooling water, gas turbines, etc), and heat exchanger network proposed by Elsido et al. (2019). for the design optimization of non-conventional steam cycles and steam networks (source Elsido et al., 2019).

Recently Elsido et al. (2020a) and Elsido et al. (2020b), extended the simultaneous synthesis methodology for the simultaneous multiperiod optimization of Steam/Rankine cycles and HENs capable of considering the off-design operating conditions expected across the lifetime, optimizing the operation of units (loads and on/off operation of boilers, gas turbines, etc) and including the integration with thermal energy storage systems. The methodology has been applied to real-world complex problems, namely a flexible Organic Rankine Cycle, an Integrated Gasification Combined-Cycle able to operate in two different modes, and a flexible Integrated Solar Combined-Cycle power plant. Despite the large number of hot/cold streams and technical design/operational constraints, the methodology provided very good solutions featuring cost-effective designs.

Dynamic Simulation

For the simulation of practical engineering applications, different process-modeling concepts can be applied, namely black-box process modeling, grey-box process modeling, and white-box process modeling (Cameron and Hangos, 2001). In black-box modeling, also known as data-driven models, the process parameters are determined using various regression technologies and artificial intelligence by combining the training data (experimental data) and network structure. By contrast, the process parameters in the white-box model are derived from mass, energy, and momentum conservation equations. Although the white-box process models show better accuracy compared to the black-box process, the white-box model shows unreliability in many cases because of the lack of relevant fundamental process details. The grey-box models are based on the physical structure that is improved by operating data (i.e., a combination of both black-box and white-box process models). Most of the process parameters are obtained through solving the conservation equations, while for unclear parameters or functions in the process, the black-box process modeling approach with operating data and optimization algorithms is applied. In this study, the white-box dynamic process modeling, applied to steam cycles available in the literature up to 2020 will be reviewed.

Process simulation models are crucial for increasing the efficiency and flexibility of thermal power plants. Usually, the design and optimization of a process start with steady-state process modeling, where the system operates continuously at its design base-load. The steady-state process models do not require control structures and mathematically are based on mass, momentum, species, and energy balances without the consideration of the time derivations. In the case of zero-dimensional modeling, the local discretization is also not considered. The modeling of the components such as heat exchanger, pump, condenser, turbine, etc., results in an algebraic system of equations with inputs and output parameters of components (pressure, enthalpy, mass flow, and concentration). In the case of one-dimensional modeling, the components are discretized between the inlet and the outlet along with the flow in a certain number of cells (numerical grid). At each discrete location, an algebraic system of equations is obtained. Using the steady-state process simulation models, analyses of the thermodynamic properties of the water-steam side and flue gas path, as well as mass and energy flows, can be evaluated for a series of operating points. For the process analysis during transient conditions, the dynamic process simulation models must be used, in which the time derivations in the conservation equations are taken into consideration. Dynamic process simulation models are a cost-efficient tool for assessing the control strategies, capabilities, and limitations of the system. Furthermore, they support unit commissioning and regular operation by estimating component lifetime and directing maintenance (Alobaid et al., 2017). Also, the effect of possible failures in control structures and electrical network on the system can be analyzed. The dynamic process simulation models are preferred for the proposal stage of a steam cycle project, e.g., to check whether the load changes according to specific customer requirements are feasible without unacceptable lifetime consumption in thick-walled components. However, these white-box dynamic process simulation models require detailed information on the process and its control structures. The inherent complexity of the governing differential conservation equations and the numerical solution methods leads to highly complex models with long development periods.

For the dynamic process modeling of the steam cycles, different process components such as heat exchanger, pump, drum, etc. are required. Also, automation and electrical systems are necessary to control and calculate the electrical power consumption of the process components during transients. The first process simulation software of a steam cycle plant dated back to the 1960s. The water/steam cycle was constructed using different components connected through lines. This embodiment (selecting from the library and connecting component by component) has mainly been maintained in most simulation software since. Nowadays, dynamic process simulation software combines graphical user interface with detailed sub-models for flow, thermodynamic, chemical reactions, mass and heat transfer, automation, and electrical systems, offering rapid assessments of the steam cycle process such as:

• efficiency and flexibility improvement

• process modifications and retrofitting

• analysis of control loops and optimization of controller parameter

• operating behavior at baseloads, off-design, start-up, and shutdown procedures

• security and safety analyses

• Investigation of malfunctions, e.g., steam turbine trip, failure of boiler feed pumps or condensate pumps, blackout, and other

• new design

Several commercial software for the dynamic process simulation of steam cycle processes are available, e.g., APROS, ASPEN PLUS DYNAMICS, FLOWNEX, DYMOLA, JModelica.org, SimulationX, and Power Plant Simulator and Designer (PPSD). Most of the software provides specialized component libraries for the time-dependent simulation, including the combined-cycle power plant, the coal-fired power plant, and the concentrated solar power plant. In other software, missing components have to be modeled by the user such as MATLAB SIMULINK or MODELICA that offer a generic programming tool. Major power plant providers such as ABB, EDF, and Siemens have simulation environment codes, aiming at improving power plant efficiency, flexibility, and emissions reduction. Recently published studies are dedicated to shifting the field of dynamic simulation away from commercial codes toward more openly accessible models and software tools (e.g., OpenModelica).

In the following sections, the dynamic process simulation models applied to fossil-based and renewable-based steam cycles will be shown.

Fossil-Based Steam Cycle

Dynamics of Combined-Cycle Power Plants

Recent combined-cycle power plants feature not only high efficiency but also a flexible unit dispatch. Fast response capability represents a competitive advantage for the operator in a changing market environment due to the increasing shares of renewable feed-in. The availability of wind turbines and photovoltaic solar panels is limited and difficult to predict. They normally provide fluctuating feed-in into the grid so that energy reserves, e.g., conventional thermal power plants or energy storage systems are required to achieve a balance between current electricity supply and demand. Three factors are essential to assess the practical flexibility of a thermal power plant: shut-down/start-up time, maximum load gradient (positive and negative), and minimum load. Only 20 min is necessary to start-up a simple-cycle gas turbine, independent of its initial temperature (Ruchti et al., 2011; Alobaid et al., 2012). However, the load transients of the CCPP are restricted by the thermal stresses in the thick-walled components of the bottoming steam cycle (e.g., ST rotor, ST casing, high-pressure drum, and outlet manifolds of HP superheater and final reheater). Approximately 50 min after an overnight shutdown (hot start-up) is required to complete the start-up procedure of a modern CCPP. For warm and cold start-ups, the CCPP can reach its nominal load in less than 90 and 150 min after the gas turbine ignition (Alobaid et al., 2012). The load gradient (positive and negative) of the CCPP can sustain challenging load gradients up to ±60%/min, as e.g., stipulated by the Great Britain Grid Code for primary frequency response. The minimum load is mainly determined by the gas turbine, where stable combustion, as well as CO and NO_x levels in compliance with emission regulations (country-specific regulation), should be conserved. The minimum load limit defines the lower boundary for negative load changes and is highly relevant to flexible operation when frequent cycling is anticipated. A lower minimum load limit significantly decreases the number of shutdowns and start-ups, representing an economically viable option for the operator in the electricity market. Typical gas turbines can decrease their load to 40–50%, with a possible further reduction to 20% if a sequential-combustion design is used (i.e., each GT burner can be shutdown entirely).

This section gives an overview of the published studies on dynamic simulation applied to combined-cycle power plants. Since the gas turbine is an inherently flexible component, the bulk of the studies in the literature are dedicated to the heat recovery steam generator due to its considerable inertia and delayed system response. Relevant published studies on the development and application of the dynamic process simulation models during load change, shutdown, and start-up procedures as well as during the malfunction cases are shown in Table 4. Special attention was paid to those studies that include measurement validation to achieve a fundamental competitive comparison between the model results and the operational data. The citation is selected among other references to give the reader an orientation to the application areas. The cyclic operation (load change) of CCPPs offers high profits in the short term, providing frequency-response, replacement, and spinning reserve services. In the medium and long time, this cyclic operation can lead to a lifetime reduction of the CCPPs due to thermo-mechanical fatigue, creep, and corrosion. In the literature, there are many studies on the response of the HRSG with (single-pressure, dual-pressure, and triple-pressure with and without reheater section) to GT load changes (among others: Shin et al. (2002), Pletl (2005), Alobaid et al. (2015a); see Table 4). For example Benato et al. (2016b), investigated the cyclic operation of a 380 MW combined-cycle power plant that consists of a gas turbine and a triple-pressure heat recovery steam generator with reheat. Different transient conditions are tested and the developed model was used to improve the plant flexibility. Alobaid et al. (2015a) and Ata et al. (2020) investigated the capability of different process simulation software to predict the behavior of a combined-cycle power plant during part loads and off-design operation using the process simulation software tools APROS, ASPEN PLUS DYNAMICS, and Power Plant Simulator and Designer (PPSD). Operational data from Prai Power Station, located in Malaysia is used for the validation of the developed model (see Figure 8). The comparison between three dynamic simulations using three different process software for the same power plant give more confidence in dynamic simulation for the design and optimization of CCPPs.

TABLE 4

TABLE 4. Overview of dynamic simulation studies applied to combined-cycle power plants.

FIGURE 8

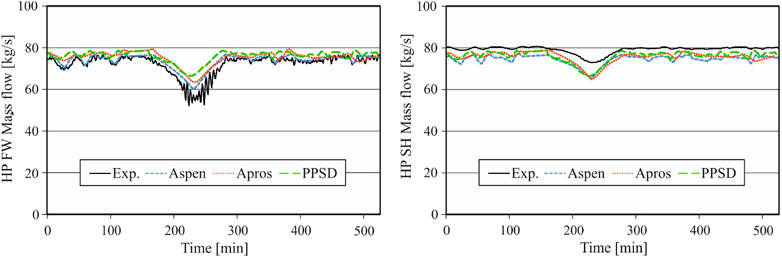
FIGURE 8. Operational data and simulated results of the high-pressure feed water and steam mass flow rates using three different software during a load change scenario (source Ata et al., 2020).

The rapid start-up capability represents a key benchmark for CCPPs compared to other conventional power plant technologies (e.g., coal-firing power plant and nuclear power plant). Generally, it is distinguished between three different types of start-up procedures, namely hot start-up after overnight shutdown, warm start-up after weekend shutdown, and cold start-up after a shutdown of several days. These definitions are too broad for practical purposes and therefore the metal temperatures of the thick-walled components such as ST rotor, ST casing, and HP drum are generally used to determine the type of start-up procedure. In the literature, the start-up simulation of the CCPPs receives considerable attention (see Table 4). Kim et al. (2000) studied the effect of CCPP cold start-up with a flue gas bypass on thermal stress in the drum of a single-pressure HRSG. The results show that the operation of the flue gas bypass can be scheduled to mitigate thermal stress peaks at the inner drum surface. Despite model simplifications, this work was one of the first studies that consider the thermal stress in combined-cycle operation. Alobaid et al. (2008) developed a dynamic process simulation model of a commercial-scale triple-pressure HRSG with reheat, based on the six-equation flow model of the thermo-hydraulic process simulation software APROS. The gas turbine was simplified as a time-dependent boundary condition of exhaust gas mass flow and temperature. A warm start-up procedure was simulated and the numerical results are in close agreement with measurement data. In another work of the same group Mertens et al. (2016), investigated the shutdown procedure followed by a hot start-up of a commercial-scale triple-pressure HRSG with reheat using APROS. The simulated results were compared with the operation data, showing generally good agreement (see Figure 9). However, the model underestimated the thermal inertia of the real plant, which in turn results in deviation, especially the sudden pressure drop after shutdown. Recently, the same group published several studies regarding hot, warm, and start-up procedures of the CCPP using different software such as ASPEN PLUS DYNAMICS and Power Plant Simulator and Designer (Alobaid et al., 2015b; Alobaid, 2018b; Sabia et al., 2019; Ata et al., 2020). Meinke (2013) developed a dynamic process simulation model of a triple-pressure HRSG with reheat based on the homogeneous flow model of the software DYMOLA/MODELICA. The model was validated with measurement data of a hot start-up procedure to 54% load, showing a fair agreement. Hack et al. (2012) presented a methodology for the dynamic simulation of HRSG during cold and warm start-up. The calculated thermal stresses combined with pressure stresses were applied to evaluate the material fatigue caused by start-up and shutdown cycles. Discontinuities such as weld connections and surface irregularities are considered by a factor that reduces the fatigue strength. The results show that there was a significant potential for reducing the start-up time, while keeping acceptable component life of the thick-walled components. Mertens et al. (2015) compared the dynamic behavior of two triple-pressure HRSG models (drum-type and once-through) for cold, warm, and hot start-up procedures using the software APROS. The study concludes that the once-through HRSG is favorable for combined-cycle plants with enhanced flexibility requirements, at the cost of slightly increased heat exchanger surface of the HP circuit (approximately 9% in the given case). Nannarone and Klein (2019) developed a flexible dynamic process simulation model using the Simulink™ environment. The model contains more than 100 process components including heat exchangers, valves, and turbines in addition to the control structures. The model was validated against operational data of three different start-up types (cold, warm, and hot start-ups). According to the authors, the simulation can identify the bottlenecks in the start-up procedure of the existing CCPP and devise several optimization actions. Accordingly, a reduction in the start-up times of 32.5 and 31.8% for cold and warm has been achieved. In another study presented by Albanesi et al. (2006), the cold start-up procedure was optimized for different stress constraints of the ST rotor by manipulation of the GT load and the valve position for ST admission. The required start-up time was reduced by 20 and 48% for a conservative stress constraint and a standard stress constraint, respectively. For optimization purposes Casella and Pretolani (2006), developed a simplified model of a triple-pressure HRSG using DYMOLA/MODELICA. The results show that the thermal stress peak is at the beginning of the ST loading phase and that both peak stress and start-up time can be considerably decreased with regard to the reference procedure.

FIGURE 9

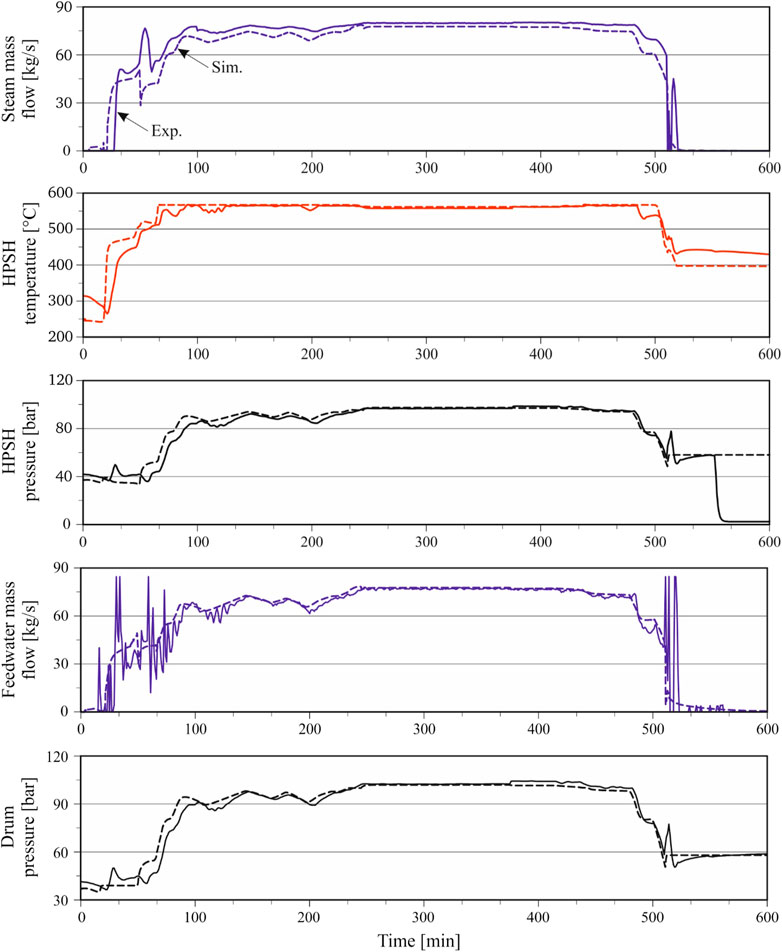
FIGURE 9. Operational data and simulated results of the high-pressure circuit during the hot start-up and shutdown procedure (source Mertens et al., 2016).

Dynamics of Coal-Fired Power Plant

Even though the technology of coal-fired power is well known, there is still potential for further improvement regarding load gradients, minimal load limit, and start-up procedure, which can be explored using dynamic simulation. At the early stage of development, the dynamic process simulation models of coal-fired power plants are used to reach higher efficiency and to reduce emissions at off-design operation points as well as to investigate the system behavior during malfunction cases (e.g., steam turbine trip, blackout, failure in feed water preheaters or pumps). Given challenges for the electricity market with the continuing expansion of intermittent renewables, the operational flexibility including load changes, start-up procedures and minimal load limit is recent of interest to utilities’ operators. This section summarizes the existing body of literature on dynamic process simulation applied to coal-fired power plants (see Table 5).

TABLE 5

TABLE 5. Overview of dynamic simulation studies applied to coal-fired power plants.

In 1982 Armor et al. (1982), presended one of the most detailed dynamic process simulation models of a coal-fired power plant (Mystic Unit 7 power plant with an electrical output of 550 MW) using a tool, so-called modular modeling system. Although the developed model of the thermal power plant was similar to the real plant, the fuel in the steam generator due to simplification reasons was replaced with oil. Representing the entire thermal power plant with this model was unconventional at that time. A promising match between the model and the operational data has been shown. Lu (1999) developed a dynamic process simulation model of Castle Peak B power plant in Hong Kong with an electrical output of 677 MW using MATLAB/SIMULINK. The model quality is evaluated against the response to step changes (a change in the main pressure step and a sudden position change of the main steam valve). Oko and Wang (2014) presented a dynamic process simulation model of an entire coal-fired power plant (500 MW_el) at the Didcot power station. The model was validated with measurements at steady-state operational points for 70, 80, 94.4, and 100% load. With the validated model, transient simulations have then been performed. Starkloff et al. (2015) developed a sub-critical, once-through steam generator of Heilbronn Power Station located in Germany with a thermal power input of 1860 MW and an electrical output of 760 MW. The number of model boundary conditions is minimized (only the coal composition, the inlet temperatures, and the mass flow rates of the cooling water into the condensers). The developed model and its implemented controls are evaluated during a load change scenario from 100 to 22.7% (see Figure 10: Operational data and simulated results of the high-pressure and reheater circuits during load change scenario (source Starkloff et al., 2015)). The numerical results were compared towards the operational data, showing very good agreement.

FIGURE 10

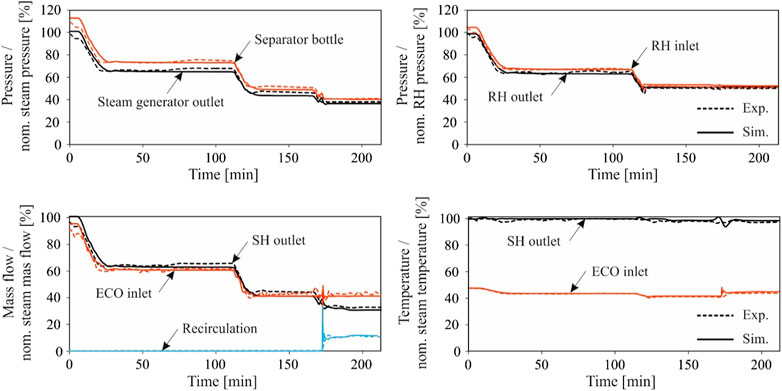
FIGURE 10. Operational data and simulated results of the high-pressure and reheater circuits during load change scenario (source Starkloff et al., 2015).

In coal-fired power plants, the start-up procedure represents the most crucial operation process since the thick-walled components expose high pressure and temperature gradients. The start-up curves of coal-fired power plants are often set based on operational experience and conservative assumptions. Here, the dynamic simulation models are of high relevance for the optimization of the start-up progress without exceeding the threshold values. Kruger et al. (2001) and Krüger et al. (2004) extended the drum-based boiler model of Astroem (Åström and Bell, 2000), giving a very good overview of the start-up procedure as well as the initial conditions. The standard classic start-up curves were simulated, followed by a stress-optimized start-up curve. Meinke et al. (2011) presented a detailed model of 508 MW_el hard coal-fired plants located in Rostock, Germany. All required process components and their related control structures were modeled using the simulation platform MODELICA and the non-commercial library ThermoPower. For the model validation, the authors compared the model predictions with the operational data during a start-up procedure from 0 to 9% after 37 h shutdown period. The results match very well with the operational data of the start-up procedure (240 min).

Taler et al. (2015) developed a dynamic simulation model of a large-scale lignite power plant with a sub-critical natural circulation boiler. The model was applied to optimize the start-up curves, taking into account the thermal stresses of the thick-walled components. Hübel et al. (2017) introduced a comprehensive dynamic simulation model of a coal-fired power plant using ThermalPower Library by Modelon. According to the authors, the model was able to reproduce a representative hot start scenario with acceptable deviations toward the measurement data. After model validation with the reference start-up, faster start-ups, less fuel consumption, and less emission were identified, maintaining the thermal and mechanical stress, caused by higher ramp rates, within reasonably range.

All in all, many dynamic process simulation studies on coal-fired power plants can be found in the literature, but the lack of available data for validation of the developed models represents here a major challenge. In the last decade, the attention of authors is shifted toward the integration of thermal energy storage as well as carbon capture and storage, especially oxyfuel combustion. Here, the dynamic process simulation models are mostly applied to evaluate the switch over from air to oxygen combustion and load changes. Although no large-scale oxyfuel-fired plants exist (measured data is not available), several works can be found in the literature, summarized in Table 5.

Dynamics of Renewable-Based Steam Cycles

Over the past years, renewable electricity generation has steadily increased. In 2018, the total share of worldwide electricity generation based on renewable energy sources (mainly wind power, solar, and hydropower) was 28% and this will expand to reach approximately 49% in 2050 according to the International Energy Agency (IEA). In the following section, the dynamic process simulation model applied for renewable-based power plants with steam cycles will be reviewed (see Table 6).

TABLE 6

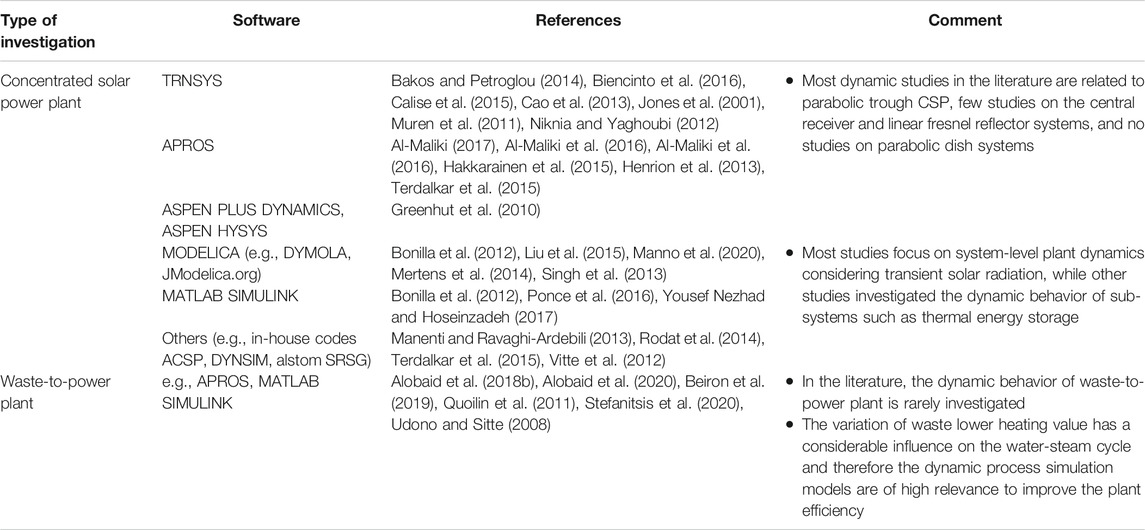
TABLE 6. Overview of dynamic simulation studies applied to concentrated solar power plants, geothermal power plants, and waste-to-power plants.

Dynamics of Concentrated Solar Power Plants

Since the CSP plant is dynamic, considerable numbers of dynamic studies that investigate the performance under different solar irradiance conditions can be found in the literature. Furthermore, start-up procedures, capacity, and dynamics of thermal storage systems during charge and discharge cycles, as well as the annual electrical power output, have been simulated and evaluated. For the dynamic process simulation of the CSPs, the well-known commercial software that used for other steam cycle applications is generally applied such as DYMOLA, TRNSYS, and APROS. The parabolic trough CSP plant is widely deployed and therefore is commonly used to validate the dynamic process simulation models. Other studies analyzed the dynamic behavior of the central receiver and linear Fresnel reflector systems. However, no studies in the field of dynamic simulation for parabolic dish systems have been published in the literature according to the authors’ best knowledge yet. García et al. (2011) presented one of the fundamental studies on the dynamic modeling of the parabolic trough CSP plant that is based on the 50 MW_el solar thermal power plant Andasol II in Granada, Spain. The model was generated using Wolfram’s MATHEMATICA 7 software. Al-Maliki et al. (2016) and Al-Maliki W. et el. (2016) used the design and measurement data from García et al. (2011) to develop a very detailed model of Andasol II, including the solar field, the thermal storage system, and the power block using the simulation software APROS. The comparison between measurement and simulation shows good agreement. According to the authors, the discrepancies raised in the modeling related to unknown operator behavior. Liu et al. (2015) evaluated the dynamic behavior of a thermal storage system integrated into a 1 MW_el central receiver direct steam generation plant. The model of the thermal storage system that consists of an oil-operated cold and hot tank, as well as a steam accumulator, is built in DYMOLA by means of the MODELICA library “ThermoSysPro”. Further published works on the application of dynamic process models to concentrated solar power plants can be found among others in Table 6.

Dynamics of Waste-To-Energy Power Plants

Although the solid waste is known for its varying composition (variation of lower heating value, which in turn has considerable influence on the water/steam cycle and accordingly on the plant operation), a limited number of dynamic simulation studies on fluidized bed systems fired by non-conventional fuels and incineration plants can be found in the literature (see Table 6). Despite the dynamic nature of the operation, the solid waste incinerator is almost not considered in the dynamic studies apart from a few exceptions such as the work of Alobaid et al. (2018b), who developed a dynamic simulation model of a waste incinerator using APROS. The model was used to investigate the influence of waste heating value variations on the plant efficiency as well as to evaluate the plant behavior at part loads and during the start-up procedures.

Conclusion

Although someone can consider steam cycles as an obsolete technology, the analysis of the literature has shown that steam cycles are still the object of research and development efforts to improve their efficiency, operational flexibility, and range of applicability (i.e., tailoring their design for novel concepts of power plants such as concentrated solar power plants, integrated solar combined-cycle, waste to energy plants, electricity/hydrogen/synfuels polygeneration plants). A key rule in the research and development activities is being played by simulation and optimization codes, which are used to predict the effects of the design/control improvements on the performance of the overall power plant.

Design Calculation and Optimization

As far as conventional steam cycles are concerned (i.e., coal-fired power plants, heat recovery steam cycles for combined cycles), the design calculation of conventional steam cycles can be performed with commercially available software, and the optimization of the independent cycle design variables can be performed either via sensitivity analysis or by linking the design calculation code with an external optimization algorithm (black-box optimization approach). Some works tackle the optimization of the cycle variables using the equation-oriented approach, although this requires the use of mathematical programming languages and the definition of the cycle modeling equations as constraints of the optimization problem. The optimization of the cycle configuration (also called structural optimization or synthesis) involves binary/discrete decisions and it can be handled with the black-box approach using specific algorithms able to handle function discontinuities and/or a limited number of binary variables (e.g., evolutionary algorithms). The same simulation and black-box optimization approaches can be applied to non-conventional cycles featuring a single heat source and a limited number of possible structural configurations, like concentrated solar power plants and waste-to-energy plants.

Significantly, more challenging is the design optimization of non-conventional steam cycles recovering heat from multiple heat sources (e.g., integrated gasification combined cycles, integrated solar combined cycles, polygeneration plants) because the combinatorial nature of heat exchanger network arrangement leads to a large number of possible structural configurations (to be combined with the possible cycle structural configurations). For this kind of plants, the energy targeting and the superstructure-based synthesis approaches developed by the process engineering community should be adopted. The most recent and complete superstructure-based approaches can account for the expected operating modes, off-design operation, and integration with thermal storage.

Dynamic Process Simulation

The dynamic simulation becomes an integral part of the design and operation of steam cycles. It is preferred for the proposal stage of a thermal power plant project, e.g., to check whether the load changes according to specific customer requirements are feasible without unacceptable lifetime consumption in thick-walled components. The dynamic simulation is also a cost-efficient approach to support unit commissioning and regular operation by estimating component lifetime and directing maintenance. The basic task for dynamic simulation models is to calculate the response of power plants and their control circuits to a change in load demand (e.g., load change and start-up). Furthermore, these models can reliably predict the power plant response to malfunctions (e.g., gas turbine load rejection, steam turbine trip, and blackout) and to modifications in design and control structures (e.g., once-through super-critical heat recovery steam generator and oxyfuel pulverized coal-fired power plant). In the literature, the dynamic process simulation models applied frequently to fossil-based and renewable-based steam cycles, showing that:

• At different part loads and off-design operations, the dynamic simulation models can follow the measurement with a maximum relative error of about 5–10%. Several parameters showed, however, a relative error of less than 5%.

• During start-up and shutdown procedures, the dynamic simulation models can reproduce the qualitative behavior of the real power plant but larger discrepancies between simulations and measurements were observed. These were attributed to incomplete information on real operation and control circuits.

• Several commercial software for the dynamic process simulation of steam cycle processes are available (e.g., APROS, ASPEN PLUS DYNAMICS). However, there are key challenges in modeling power plant dynamics such as the required information on the process and its control (e.g., detailed geometry data and specifications of the process components as well as the control circuits and the controller parameters including gain, integration time, and derivation time). Recently published studies are dedicated to shifting the field of dynamic simulation away from commercial software toward more openly accessible models and software tools (e.g., OpenModelica).

Possible Research Extensions

While the steady-state optimization of steam cycle power plants has been well studied in literature and several optimization approaches are available, none of the reviewed works performs the combined optimization of cycle design, off-design operation, and plant dynamics (start-up/shut-down, ramping). This open challenge should be the object of future research efforts since it is of high relevance for today’s electricity markets. Indeed, dispatchable power plants must be designed with increased flexibility requirements. However, since the dynamic flexibility of steam cycles is also limited by thermo-mechanical stresses acting on thick-wall components (e.g., steam turbine shaft and case, boiler tube headers, drums, etc), this calls for the development of a multidisciplinary design optimization approach combining steady-state design models, dynamic plant models as well as detailed mechanical models of the most critical equipment units. This further increases the complexity of the simulation/optimization problem calling for the development of ad hoc numerical approaches and computer codes.

Another research gap is concerns the dyanamic study of integrated gasification combined cycles. Indeed, while the dynamic of the combined-cycle power, coal-fired power, and concentrated solar power is well studied in the literature, the dynamic of integrated gasification combined cycles and the interaction with the syngas treatment unit is not well understood and have to be the subject of further study. Furthermore, little attention has been paid to the dynamic study of municipal waste incinerators.

Author Contributions

EM and CE wrote the sections on steam cycle optimization approaches while FA the sections on dynamic simulations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Michael Erbes (Enginomix), John Gulen (Bechtel Fellow), Paolo Chiesa, and Giovanni Lozza (Politecnico di Milano) for sharing their knowledge on steam cycle simulation codes.

References

Ahmed, A. S. E. D., Elhosseini, M. A., and Arafat Ali, H. (2018). Modelling and Practical Studying of Heat Recovery Steam Generator (HRSG) Drum Dynamics and Approach point Effect on Control Valves. Ain Shams Eng. J. 9 (4), 3187–3196. doi:10.1016/j.asej.2018.06.004

CrossRef Full Text | Google Scholar

Al-Maliki, W. A. K., Alobaid, F., Kez, V., and Epple, B. (2016). Modelling and Dynamic Simulation of a Parabolic Trough Power Plant. J. Process Control. 39, 123–138. doi:10.1016/j.jprocont.2016.01.002

CrossRef Full Text | Google Scholar

Al-Maliki, W. A. K., Alobaid, F., Starkloff, R., Kez, V., and Epple, B. (2016). Investigation on the Dynamic Behaviour of a Parabolic Trough Power Plant during Strongly Cloudy Days. Appl. Therm. Eng. 99, 114–132. doi:10.1016/j.applthermaleng.2015.11.104

CrossRef Full Text | Google Scholar

Al-Maliki, W. A. K. (2017). Modelling, Optimization and Dynamic Simulation of a Parabolic Trough Power Plant. Technische Universität Darmstadt.

Albanesi, C., Bossi, M., Magni, L., Paderno, J., Pretolani, F., Kuehl, P., and Diehl, M. (2006). “Optimization of the Start-Up Procedure of a Combined Cycle Power Plant,” in Paper presented at the Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, December 13–15, 2006. doi:10.1109/cdc.2006.376749

CrossRef Full Text | Google Scholar

Alobaid, F., Al-Maliki, W. A. K., Lanz, T., Haaf, M., Brachthäuser, A., Epple, B., et al. (2018a). Dynamic Simulation of a Municipal Solid Waste Incinerator. Energy 149, 230–249. doi:10.1016/j.energy.2018.01.170

CrossRef Full Text | Google Scholar

Alobaid, F., Al-Maliki, W. A. K., Lanz, T., Haaf, M., Brachthäuser, A., Epple, B., et al. (2018b). Dynamic Simulation of a Municipal Solid Waste Incinerator. Energy 149, 230–249. doi:10.1016/j.energy.2018.01.170

CrossRef Full Text | Google Scholar

Alobaid, F., Karner, K., Belz, J., Epple, B., and Kim, H.-G. (2014). Numerical and Experimental Study of a Heat Recovery Steam Generator during Start-Up Procedure. Energy 64, 1057–1070. doi:10.1016/j.energy.2013.11.007

CrossRef Full Text | Google Scholar

Alobaid, F., Mertens, N., Starkloff, R., Lanz, T., Heinze, C., and Epple, B. (2017). Progress in Dynamic Simulation of thermal Power Plants. Prog. Energ. Combustion Sci. 59, 79–162. doi:10.1016/j.pecs.2016.11.001

CrossRef Full Text | Google Scholar

Alobaid, F. (2018a). Numerical Simulation for Next Generation Thermal Power Plants. Springer. doi:10.1007/978-3-319-76234-0

CrossRef Full Text

Alobaid, F., Peters, J., Amro, R., and Epple, B. (2020). Dynamic Process Simulation for Polish lignite Combustion in a 1 MWth Circulating Fluidized Bed during Load Changes. Appl. Energ. 278, 115662. doi:10.1016/j.apenergy.2020.115662

CrossRef Full Text | Google Scholar

Alobaid, F., Pfeiffer, S., Epple, B., Seon, C. Y., and Kim, H. G. (2012). Fast Start-Up Analyses for Benson Heat Recovery Steam Generator. Energy 46 (1), 295–309. doi:10.1016/j.energy.2012.08.020

CrossRef Full Text | Google Scholar

Alobaid, F., Postler, R., Ströhle, J., Epple, B., and Kim, H.-G. (2008). Modeling and Investigation Start-Up Procedures of a Combined Cycle Power Plant. Appl. Energ. 85 (12), 1173–1189. doi:10.1016/j.apenergy.2008.03.003

CrossRef Full Text | Google Scholar

Alobaid, F., Starkloff, R., Pfeiffer, S., Karner, K., Epple, B., and Kim, H.-G. (2015a). A Comparative Study of Different Dynamic Process Simulation Codes for Combined Cycle Power Plants - Part A: Part Loads and Off-Design Operation. Fuel 153, 692–706. doi:10.1016/j.fuel.2015.02.010

CrossRef Full Text | Google Scholar

Alobaid, F., Starkloff, R., Pfeiffer, S., Karner, K., Epple, B., and Kim, H. G. (2015b). A Comparative Study of Different Dynamic Process Simulation Codes for Combined Cycle Power Plants - Part B: Start-Up Procedure. Fuel 153, 707–716. doi:10.1016/j.fuel.2015.02.011

CrossRef Full Text | Google Scholar

Alobaid, F. (2018b). Start-up Improvement of a Supplementary-Fired Large Combined-Cycle Power Plant. J. Process Control. 64, 71–88. doi:10.1016/j.jprocont.2018.02.007

CrossRef Full Text | Google Scholar

Alobaid, F., Ströhle, J., Epple, B., and Kim, H.-G. (2009). Dynamic Simulation of a Supercritical Once-Through Heat Recovery Steam Generator during Load Changes and Start-Up Procedures. Appl. Energ. 86 (7-8), 1274–1282. doi:10.1016/j.apenergy.2008.09.013

CrossRef Full Text | Google Scholar

AMPL (2021). AMPL Software Webpage. Available at: https://ampl.com/ (Accessed May 5, 2021).

Angerer, M., Kahlert, S., and Spliethoff, H. (2017). Transient Simulation and Fatigue Evaluation of Fast Gas Turbine Startups and Shutdowns in a Combined Cycle Plant with an Innovative thermal Buffer Storage. Energy 130, 246–257. doi:10.1016/j.energy.2017.04.104

CrossRef Full Text | Google Scholar

APROS (2021). Apros Product Website. Available at: https://www.apros.fi/applications/engineering-support/ (Accessed May 5, 2021).

Armor, A., W. Shor, S., DiDomenico, P., Bennett, W., and Smith, L. (1982). Dynamic Performance of Fossil-Fueled Power Plants. IEEE Trans. Power Apparatus Syst. PAS-101 (10), 4136–4146. doi:10.1109/tpas.1982.317092

CrossRef Full Text | Google Scholar

Aspen Tech (2021). Aspen Plus Process Simulation Software, Webpage. Available at: https://www.aspentech.com/en/products/engineering/aspen-plus (Accessed May 5, 2021).

Åström, K. J., and Bell, R. D. (2000). Drum-boiler Dynamics. Automatica 36 (3), 363–378. doi:10.1016/s0005-1098(99)00171-5

CrossRef Full Text | Google Scholar

Avagianos, I., Rakopoulos, D., Karellas, S., and Kakaras, E. (2020). Review of Process Modeling of Solid-Fuel Thermal Power Plants for Flexible and Off-Design Operation. Energies 13 (24), 6587. doi:10.3390/en13246587

CrossRef Full Text | Google Scholar

Aviso, K. B., Lee, J.-Y., Dulatre, J. C., Madria, V. R., Okusa, J., and Tan, R. R. (2017). A P-Graph Model for Multi-Period Optimization of Sustainable Energy Systems. J. Clean. Prod. 161, 1338–1351. doi:10.1016/j.jclepro.2017.06.044

CrossRef Full Text | Google Scholar

Babaelahi, M., Mofidipour, E., and Rafat, E. (2020). Combined Energy-Exergy-Control (CEEC) Analysis and Multi-Objective Optimization of Parabolic Trough Solar Collector Powered Steam Power Plant. Energy 201, 117641. doi:10.1016/j.energy.2020.117641

CrossRef Full Text | Google Scholar

Bachelier, C., and Stieglitz, R. (2017). Design and Optimisation of Linear Fresnel Power Plants Based on the Direct Molten Salt Concept. Solar Energy 152, 171–192. doi:10.1016/j.solener.2017.01.060

CrossRef Full Text | Google Scholar

Bakos, G. C., and Petroglou, D. A. (2014). Simulation Study of a Large Scale Line-Focus Trough Collector Solar Power Plant in Greece. Renew. Energ. 71, 1–7. doi:10.1016/j.renene.2014.03.053

CrossRef Full Text | Google Scholar

Bany Ata, A., Alobaid, F., Heinze, C., Almoslh, A., Sanfeliu, A., and Epple, B. (2020). Comparison and Validation of Three Process Simulation Programs during Warm Start-Up Procedure of a Combined Cycle Power Plant. Energ. Convers. Management 207, 112547. doi:10.1016/j.enconman.2020.112547

CrossRef Full Text | Google Scholar

Barigozzi, G., Perdichizzi, A., and Ravelli, S. (2011). Wet and Dry Cooling Systems Optimization Applied to a Modern Waste-To-Energy Cogeneration Heat and Power Plant. Appl. Energ. 88 (4), 1366–1376. doi:10.1016/j.apenergy.2010.09.023

CrossRef Full Text | Google Scholar

Beiron, J., Montañés, R. M., Normann, F., and Johnsson, F. (2019). Dynamic Modeling for Assessment of Steam Cycle Operation in Waste-Fired Combined Heat and Power Plants. Energ. Convers. Management 198, 111926. doi:10.1016/j.enconman.2019.111926

CrossRef Full Text | Google Scholar

Bejan, A., Tsatsaronis, G., and Moran, M. (1996). Thermal Design and Optimization. New York: John Wiley & Sons. doi:10.1615/ichmt.1996.transientconvheattransf.220

CrossRef Full Text

Benato, A., Bracco, S., Stoppato, A., and Mirandola, A. (2016a). Dynamic Simulation of Combined Cycle Power Plant Cycling in the Electricity Market. Energ. Convers. Management 107, 76–85. doi:10.1016/j.enconman.2015.07.050

CrossRef Full Text | Google Scholar

Benato, A., Bracco, S., Stoppato, A., and Mirandola, A. (2016b). LTE: A Procedure to Predict Power Plants Dynamic Behaviour and Components Lifetime Reduction during Transient Operation. Appl. Energ. 162, 880–891. doi:10.1016/j.apenergy.2015.10.162

CrossRef Full Text | Google Scholar

Benato, A., Stoppato, A., and Bracco, S. (2014). Combined Cycle Power Plants: A Comparison between Two Different Dynamic Models to Evaluate Transient Behaviour and Residual Life. Energ. Convers. Management 87, 1269–1280. doi:10.1016/j.enconman.2014.06.017

CrossRef Full Text | Google Scholar

Benato, A., Stoppato, A., and Mirandola, A. (2015). Dynamic Behaviour Analysis of a Three Pressure Level Heat Recovery Steam Generator during Transient Operation. Energy 90, 1595–1605. doi:10.1016/j.energy.2015.06.117

CrossRef Full Text | Google Scholar

Bhambare, K., Mitra, S. K., and Gaitonde, U. (2007). Modeling of a Coal-Fired Natural Circulation Boiler. OSTI.

Biegler, L. T. (2007). An Overview of Simultaneous Strategies for Dynamic Optimization. Chem. Eng. Process. Process Intensification 46 (11), 1043–1053. doi:10.1016/j.cep.2006.06.021

CrossRef Full Text | Google Scholar

Biegler, L. T., Grossmann, I. E., and Westerberg, A. W. (1997). Systematic Methods for Chemical Process Design. Prentice-Hall.

Biegler, L. T. (2010). Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes. SIAM. doi:10.1137/1.9780898719383

CrossRef Full Text

Biencinto, M., González, L., and Valenzuela, L. (2016). A Quasi-Dynamic Simulation Model for Direct Steam Generation in Parabolic Troughs Using TRNSYS. Appl. Energ. 161, 133–142. doi:10.1016/j.apenergy.2015.10.001

CrossRef Full Text | Google Scholar

Bogale, W., and Viganò, F. (2014). A Preliminary Comparative Performance Evaluation of Highly Efficient Waste-To-Energy Plants. Energ. Proced. 45, 1315–1324. doi:10.1016/j.egypro.2014.01.137

CrossRef Full Text | Google Scholar

Bongartz, D., Najman, J., and Mitsos, A. (2020). Deterministic Global Optimization of Steam Cycles Using the IAPWS-IF97 Model. Optimization Eng. 3 (21), 1095–1131. doi:10.1007/s11081-020-09502-1

CrossRef Full Text | Google Scholar

Bongartz, D., Najman, J., Sass, S., and Mitsos, A. (2018). MAiNGO–McCormick-Based Algorithm For Mixedinteger Nonlinear Global Optimization: Process Systems Engineering (AVT.SVT). RWTH Aachen University.

Bonilla, J., Yebra, L. J., Dormido, S., and Zarza, E. (2012). Parabolic-trough Solar thermal Power Plant Simulation Scheme, Multi-Objective Genetic Algorithm Calibration and Validation. Solar Energy 86 (1), 531–540. doi:10.1016/j.solener.2011.10.025

CrossRef Full Text | Google Scholar

Bracco, S. (2012). “Dynamic Simulation of Combined Cycles Operating in Transient Conditions: an Innovative Approach to Determine the Steam Drums Life Consumption,” in The 25th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, June 26–29, 2012, Perugia, Italy.

Google Scholar

Bui, M., Gunawan, I., Verheyen, V., Feron, P., Meuleman, E., and Adeloju, S. (2014). Dynamic Modelling and Optimisation of Flexible Operation in post-combustion CO2 Capture Plants-A Review. Comput. Chem. Eng. 61, 245–265. doi:10.1016/j.compchemeng.2013.11.015

CrossRef Full Text | Google Scholar

Calise, F., d’Accadia, M. D., Vicidomini, M., and Scarpellino, M. (2015). Design and Simulation of a Prototype of a Small-Scale Solar CHP System Based on Evacuated Flat-Plate Solar Collectors and Organic Rankine Cycle. Energ. Convers. Management 90, 347–363. doi:10.1016/j.enconman.2014.11.014

CrossRef Full Text | Google Scholar

Cameron, I. T., and Hangos, K. (2001). Process Modelling and Model Analysis. Elsevier.

Can Gülen, S., and Kim, K. (2014). Gas Turbine Combined Cycle Dynamic Simulation: a Physics Based Simple Approach. J. Eng. gas turbines Power 136 (1), 1–15. doi:10.1115/1.4025318

CrossRef Full Text | Google Scholar

Cao, F., Li, H., Zhao, L., Bao, T., and Guo, L. (2013). Design and Simulation of the Solar Chimney Power Plants with TRNSYS. Solar Energy 98, 23–33. doi:10.1016/j.solener.2013.05.022

CrossRef Full Text | Google Scholar

Carapellucci, R., and Giordano, L. (2013). A Comparison between Exergetic and Economic Criteria for Optimizing the Heat Recovery Steam Generators of Gas-Steam Power Plants. Energy 58, 458–472. doi:10.1016/j.energy.2013.05.003

CrossRef Full Text | Google Scholar

Carcasci, C., Pacifici, B., Winchler, L., Cosi, L., and Ferraro, R. (2015). Thermoeconomic Analysis of a One-Pressure Level Heat Recovery Steam Generator Considering Real Steam Turbine Cost. Energ. Proced. 82, 591–598. doi:10.1016/j.egypro.2015.11.877

CrossRef Full Text | Google Scholar

Casella, F., and Colonna, P. (2012). Dynamic Modeling of IGCC Power Plants. Appl. Therm. Eng. 35, 91–111. doi:10.1016/j.applthermaleng.2011.10.011

CrossRef Full Text | Google Scholar

Casella, F., Farina, M., Righetti, F., Faille, D., Tica, A., Gueguen, H., et al. (2011). An Optimization Procedure of the Start-Up of Combined Cycle Power Plants. IFAC Proc. Volumes 44 (1), 7043–7048. doi:10.3182/20110828-6-it-1002.00604

CrossRef Full Text | Google Scholar

Casella, F., and Pretolani, F. (2006). Fast Start-Up of a Combined-Cycle Power Plant: A Simulation Study with Modelica in Paper presented at the Modelica Conference, Vienna, September 4–5, 2006.

Cellier, F. E., and Kofman, E. (2006). Continuous System Simulation. Springer Science & Business Media.

Cha, H., Song, Y. S., Kim, K. J., Kim, J. R., and Kim, S. M. (2011). “Dynamic Simulation of a HRSG System for a Given Start-Up/Shut Down Curve,” in Paper presented at the ASME 2011 International Mechanical Engineering Congress and Exposition, Denver, CO, USA, November 11–17, 2011.

Google Scholar

Chacartegui, R., Sánchez, D., Muñoz, A., and Sánchez, T. (2011). Real Time Simulation of Medium Size Gas Turbines. Energ. Convers. Management 52 (1), 713–724. doi:10.1016/j.enconman.2010.07.050

CrossRef Full Text | Google Scholar

Chen, C., Han, L., and Bollas, G. M. (2016). Dynamic Simulation of Fixed‐bed Chemical‐looping Combustion Reactors Integrated in Combined Cycle Power Plants. Energ. Technology 4 (10), 1209–1220. doi:10.1002/ente.201600079

CrossRef Full Text | Google Scholar

Chen, C., Zhou, Z., and Bollas, G. M. (2017). Dynamic Modeling, Simulation and Optimization of a Subcritical Steam Power Plant. Part I: Plant Model and Regulatory Control. Energ. Convers. Management 145, 324–334. doi:10.1016/j.enconman.2017.04.078

CrossRef Full Text | Google Scholar

Chiesa, P., and Macchi, E. (2004). A Thermodynamic Analysis of Different Options to Break 60% Electric Efficiency in Combined Cycle Power Plants. J. Eng. Gas Turbines Power 126 (4), 770–785.

Google Scholar

Choo, Y. K., and Staiger, P. J. (1982). New Features And Applications Of PRESTO: A Computer Code For the Performance Of Regenerative, Superheated Steam Turbine Cycles: National Aeronautics and Space Administration. Scientific and Technical.

Conn, A. R., Scheinberg, K., and Vicente, L. N. (2009). Introduction to Derivative-free Optimization. SIAM.

Consonni, S. (1983). Performance Prediction of Gas/Steam Cycles for Power Generation. Princeton university MAE Dept, Ph.D Thesis n. 1983-T.

Conte, E., and Pedretti, C. (2011). “Thermo-Economic Optimization of the CCPP Design with Supplementary Firing Considering Off-Design Performance and Operating Profile,” in Turbine Technical Conference and Exposition, Vancouver, BC, Canada, June 6–10, 2011 (ASME 2011 Turbo Expo), 621–631. doi:10.1115/GT2011-45550

Google Scholar

Cooke, D. H. (1983). “Modeling of Off-Design Multistage Turbine Pressures by Stodola’s Ellipse,” in Paper presented at the Energy Incorporated PEPSE User’s Group Meeting, Richmond, VA.

Google Scholar

Crowe, C. M., and Nishio, M. (1975). Convergence Promotion in the Simulation of Chemical Processes-The General Dominant Eigenvalue Method. Aiche J. 21 (3), 528–533. doi:10.1002/aic.690210314

CrossRef Full Text | Google Scholar

Cycle Tempo (2021). Software Cycle Tempo Webpage. Available at: http://www.asimptote.nl/software/cycle-tempo/ (Accessed May 5, 2021).

De Greef, J., Villani, K., Goethals, J., Van Belle, H., Van Caneghem, J., and Vandecasteele, C. (2013). Optimising Energy Recovery and Use of Chemicals, Resources and Materials in Modern Waste-To-Energy Plants. Waste Management 33 (11), 2416–2424. doi:10.1016/j.wasman.2013.05.026

PubMed Abstract | CrossRef Full Text | Google Scholar

de Klerk, G., Rousseau, P., and Jestin, L. (2020). A Dynamic Modeling Methodology to Estimate the Magnitude of Unwanted Liquid Flows in High Temperature Boiler Components. J. Therm. Sci. Eng. Appl. 12 (5), 1–30. doi:10.1115/1.4046517

CrossRef Full Text | Google Scholar

Deng, K., Yang, C., Chen, H., Zhou, N., and Huang, S. (2017). Start-Up and Dynamic Processes Simulation of Supercritical Once-Through Boiler. Appl. Therm. Eng. 115, 937–946. doi:10.1016/j.applthermaleng.2017.01.016

CrossRef Full Text | Google Scholar

Dersch, J., Geyer, M., Herrmann, U., Jones, S. A., Kelly, B., Kistner, R., et al. (2004). Trough Integration into Power Plants – a Study on the Performance of Integrated Solar Combined Cycle Systems. Energy 29, 947–959. doi:10.1016/s0360-5442(03)00199-3

CrossRef Full Text | Google Scholar

Duran, M. A., and Grossmann, I. E. (1986). Simultaneous Optimization and Heat Integration of Chemical Processes. AIChE J. 32 (1), 123–138. doi:10.1002/aic.690320114

CrossRef Full Text | Google Scholar

Durán, M. D., Valdés, M., Rovira, A., and Rincón, E. (2013). A Methodology for the Geometric Design of Heat Recovery Steam Generators Applying Genetic Algorithms. Appl. Therm. Eng. 52 (1), 77–83. doi:10.1016/j.applthermaleng.2012.10.041

CrossRef Full Text | Google Scholar

Dutta, R., Nord, L. O., and Bolland, O. (2017). Prospects of Using Equilibrium-Based Column Models in Dynamic Process Simulation of post-combustion CO2 Capture for Coal-Fired Power Plant. Fuel 202, 85–97. doi:10.1016/j.fuel.2017.04.030

CrossRef Full Text | Google Scholar

Eberhart, R., and Kennedy, J. (1995). “A New Optimizer Using Particle Swarm Theory. MHS 95,” in Proceedings of the sixth international symposium on micro machine and human science, 39–43.

Google Scholar

Ebsilon Professional (2021). EBSILON Professional Software Webpage. Available at: www.ebsilon.com (Accessed May 5, 2021).

El Hefni, B., Bouskela, D., and Lebreton, G. (2011). “Dynamic Modelling of a Combined Cycle Power Plant with ThermoSysPro,” in Proceedings of the 8th International Modelica Conference, Dresden; Germany, March 20th-22nd (Technical Univeristy).

Google Scholar

Elmasri, M. A. (1988). GTPRO: A Flexible, Interactive Computer Program for the Design and Optimization of Gas Turbine Power Systems. Paper presented at the Turbo Expo: Power for Land, Sea, and Air.

Elsido, C., Bischi, A., Silva, P., and Martelli, E. (2017). Two-stage MINLP Algorithm for the Optimal Synthesis and Design of Networks of CHP Units. Energy, 403–426. doi:10.1016/j.energy.2017.01.014

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Grossmann, I. E. (2019). A Bilevel Decomposition Method for the Simultaneous Heat Integration and Synthesis of Steam/Organic Rankine Cycles. Comput. Chem. Eng. 128, 228–145. doi:10.1016/j.compchemeng.2019.05.041

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Grossmann, I. E. (2018). A Bilevel Decomposition Method for the Simultaneous Synthesis of Utility Systems, Rankine Cycles and Heat Exchanger Networks. Computer Aided Chem. Eng. 43, 373–378. doi:10.1016/b978-0-444-64235-6.50068-1

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Grossmann, I. E. (2020a). Multiperiod Optimization of Heat Exchanger Networks with Integrated Thermodynamic Cycles and Thermal Storages. Comput. Chem. Eng. 149, 107293. doi:10.1016/j.compchemeng.2021.107293

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Grossmann, I. E. (2020b). Simultaneous Multiperiod Optimization of Rankine Cycles and Heat Exchanger Networks. Computer Aided Chem. Eng. 48, 1495–1500. doi:10.1016/b978-0-12-823377-1.50250-0

CrossRef Full Text | Google Scholar

Elsido, C., Martelli, E., and Kreutz, T. (2019). Heat Integration and Heat Recovery Steam Cycle Optimization for a Low-Carbon lignite/biomass-to-jet Fuel Demonstration Project. Appl. Energ. 239, 1322–1342. doi:10.1016/j.apenergy.2019.01.221

CrossRef Full Text | Google Scholar

Erbes, M., Gay, R., and Cohn, A. (1989). Gate: A Simulation Code for Analysis of Gas-Turbine Power plantsTurbo Expo: Power for Land, Sea, and Air. Paper presented at the.

Floudas, C. A., and Grossmann, I. E. (1986). Synthesis of Flexible Heat Exchanger Networks for Multiperiod Operation. Comput. Chem. Eng. 10, 153–168. doi:10.1016/0098-1354(86)85027-x

CrossRef Full Text | Google Scholar

Frnc-, 5P. C. (2021). FRNC-5PC Software Webpage. Available at: http://www.pfrengineering.com/products/frnc-5pc/ (Accessed May 5, 2021).

Gams, (2021). General Algebraic Modeling System (GAMS) Webpage. Available at: https://www.gams.com/ (Accessed May 5, 2021).

García, I. L., Álvarez, J. L., and Blanco, D. (2011). Performance Model for Parabolic Trough Solar thermal Power Plants with thermal Storage: Comparison to Operating Plant Data. Solar Energy 85 (10), 2443–2460. doi:10.1016/j.solener.2011.07.002

CrossRef Full Text | Google Scholar

GateCycle (2021). Gate Cycle Webpage. Available at: http://www.wyattllc.com/GateCycle/GateCycle.html (Accessed April 20, 2021).

General Electric (2021). General Electric Webpage: "Can GE Deliver the Highest Efficiency for My Coal Power Plant?. Available at: https://www.ge.com/power/steam/steam-power-plants/advanced-ultra-supercritical-usc-ausc (Accessed May 5, 2021).

Google Scholar

Gill, P. E., Murray, W., and Saunders, M. A. (2005). SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. SIAM Rev. 47 (1), 99–131. doi:10.1137/s0036144504446096

CrossRef Full Text | Google Scholar

Giostri, A., Binotti, M., Astolfi, M., Silva, P., Macchi, E., and Manzolini, G. (2012). Comparison of Different Solar Plants Based on Parabolic through Technology. Solar Energy 86 (5), 1208–1221. doi:10.1016/j.solener.2012.01.014

CrossRef Full Text | Google Scholar

gPROMS (2021). The gPROMS Platform. Available at: https://www.psenterprise.com/products/gproms/platform.

Google Scholar

Greenhut, A. D., Tester, J. W., DiPippo, R., Field, R., Love, C., Nichols, K., et al. (2010). Solar–geothermal Hybrid Cycle Analysis for Low Enthalpy Solar and Geothermal Resources. Proc. World Geothermal Congr. 25–29.

CrossRef Full Text | Google Scholar

Grossmann, I. E., Viswanathan, J., Vecchietti, A., Ramesh, R., and Erwin, K. (2021). GAMS Solvers. DICOPT. Available at: http://www.gams.com/ (Accessed May 5, 2021).

Google Scholar

Gülen, S. C. (2019). Gas Turbines for Electric Power Generation. Cambridge University Press. 9781108241625.

Gulen, S. (2020). Steam Turbine-Quo Vadis?. Front. Energ. Res. 8, 1–20.

Google Scholar

Gundersen, T., Duvold, S., and Hashemi-Ahmady, A. (1996). An Extended Vertical MILP Model for Heat Exchanger Network Synthesis. Comput. Chem. Eng. 20 (21), S97. doi:10.1016/0098-1354(96)00027-0

CrossRef Full Text | Google Scholar

Gwebu, E. Z., and Rousseau, P. G. (2018). “Development and Validation of a Process Model for a Superheater Heat Exchanger in a Coal-Fired Power Plant Boiler,” in Paper presented at the International Heat Transfer Conference Digital Library, Beijing, China, August 11–15, 2018.

Google Scholar

Hack, H., Fan, Z., Seltzer, A., and Alvarez, J. (2012). Advanced Methods of HRSG Design for Life Cycle Optimization under Fast Startups. POWERGEN Int., 11–13.

Google Scholar

Hakkarainen, E., Tähtinen, M., and Mikkonen, H. (2015). “Dynamic Model Development of Linear Fresnel Solar Field,” in Paper presented at the ASME 2015 9th International Conference on Energy Sustainability collocated with the ASME 2015 Power Conference, the ASME 2015 13th International Conference on Fuel Cell Science, Engineering and Technology, and the ASME 2015 Nuclear Forum, San Diego, CA, USA, June 28–July 2, 2015.

Google Scholar

Han, X.-g., Qu, W.-h., Dong, Y., and Nie, H.-g. (2010). Dynamic Simulation Model of Gas Turbine Based on Simulink [J]. Aeroengine (3), 1–9.

Google Scholar

Harun, N., Nittaya, T., Douglas, P. L., Croiset, E., and Ricardez-Sandoval, L. A. (2012). Dynamic Simulation of MEA Absorption Process for CO2 Capture from Power Plants. Int. J. Greenhouse Gas Control. 10, 295–309. doi:10.1016/j.ijggc.2012.06.017

CrossRef Full Text | Google Scholar

Harvey, A., Larson, A., and Patel, S. (2020). History of Power: The Evolution of the Electric Generation Industry. Available at: https://www.powermag.com/history-of-power-the-evolution-of-the-electric-generation-industry/ (Accessed April 20, 2021).

Google Scholar

Hasan, N., Rai, J. N., and Arora, B. B. (2014). Optimization of CCGT Power Plant and Performance Analysis Using MATLAB/Simulink with Actual Operational Data. SpringerPlus 3 (1), 275. doi:10.1186/2193-1801-3-275

PubMed Abstract | CrossRef Full Text | Google Scholar

Henrion, T., Ponweiser, K., Band, D., and Telgen, T. (2013). Dynamic Simulation of a Solar Power Plant Steam Generation System. Simulation Model. Pract. Theor. 33, 2–17. doi:10.1016/j.simpat.2011.12.009

CrossRef Full Text | Google Scholar

Hentschel, J., Zindler, H., and Spliethoff, H. (2017). Modelling and Transient Simulation of a Supercritical Coal-Fired Power Plant: Dynamic Response to Extended Secondary Control Power Output. Energy 137, 927–940. doi:10.1016/j.energy.2017.02.165

CrossRef Full Text | Google Scholar

Huang, X., Lu, P., Luo, X., Chen, J., Yang, Z., Liang, Y., et al. (2020). Synthesis and Simultaneous MINLP Optimization of Heat Exchanger Network, Steam Rankine Cycle, and Organic Rankine Cycle. Energy 195, 116922. doi:10.1016/j.energy.2020.116922

CrossRef Full Text | Google Scholar

Hübel, M., Meinke, S., Andrén, M. T., Wedding, C., Nocke, J., Gierow, C., et al. (2017). Modelling and Simulation of a Coal-Fired Power Plant for Start-Up Optimisation. Appl. Energ. 208, 319–331. doi:10.1016/j.apenergy.2017.10.033

CrossRef Full Text | Google Scholar

IDA (2021). IDA Package Website. Available at: https://computing.llnl.gov/projects/sundials/ida (Accessed May 5, 2021).

IEA (2019). World Energy Outlook 2019. Available at: https://www.iea.org/reports/world-energy-outlook-2019.

Iyer, R. R., and Grossmann, I. E. (1998). Synthesis and Operational Planning of Utility Systems for Multiperiod Operation. Comput. Chem. Eng. 22, 979–993. doi:10.1016/s0098-1354(97)00270-6

CrossRef Full Text | Google Scholar

Jimenez, J., Azapagic, A., and Smith, R. (2019). Novel Methodology for Cogeneration Targeting with Optimum Steam Level Placement. Computer Aided Chem. Eng. 46, 1741–1746. doi:10.1016/b978-0-12-818634-3.50291-5

CrossRef Full Text | Google Scholar

Jin, B., Zhao, H., and Zheng, C. (2014a). Dynamic Modeling and Control for Pulverized-Coal-Fired Oxy-Combustion Boiler Island. Int. J. Greenhouse Gas Control. 30, 97–117. doi:10.1016/j.ijggc.2014.09.002

CrossRef Full Text | Google Scholar

Jin, B., Zhao, H., and Zheng, C. (2014b). Dynamic Simulation for Mode Switching Strategy in a Conceptual 600 MWe Oxy-Combustion Pulverized-Coal-Fired Boiler. Fuel 137, 135–144. doi:10.1016/j.fuel.2014.07.104

CrossRef Full Text | Google Scholar

Jones, S. A., Pitz-Paal, R., Schwarzboezl, P., Blair, N., and Cable, R. (2001). “TRNSYS Modeling of the SEGS VI Parabolic Trough Solar Electric Generating System,” in Proceedings of Solar Forum 2001: Solar Energy: The Power to Choose, Washington, DC, April 21–25, 2001.

Google Scholar

Kehlhofer, R., Hannemann, F., Stirnimann, F., and Rukes, B. (2009). Combined-Cycle Gas-Steam Turbine Power Plants. 3rd edition. PennWell. 978-1-59370-18-0.

Kemp, I. C. (1982). Pinch Analylis and Process Integration. A User Guide on Process Integration for the Efficient Use of Energy. Elsevier.

Kieslich, C. A., Boukouvala, F., and Floudas, C. A. (2018). Optimization of Black-Box Problems Using Smolyak Grids and Polynomial Approximations. J. Glob. Optimization 71, 845–869. doi:10.1007/s10898-018-0643-0

CrossRef Full Text | Google Scholar

Kim, T., Lee, D., and Ro, S. (2000). Analysis of thermal Stress Evolution in the Steam Drum during Start-Up of a Heat Recovery Steam Generator. Appl. Therm. Eng. 20 (11), 977–992. doi:10.1016/s1359-4311(99)00081-2

CrossRef Full Text | Google Scholar

Kler, A., Dekanova, N., and Schegoleva, P. (1993). Methods for Optimizing Complex Heat and Power Plants. Novosibirsk.

Kler, A. M., Zharkov, P. V., and Epishkin, N. O. (2019). Parametric Optimization of Supercritical Power Plants Using Gradient Methods. Energy 189, 116230. doi:10.1016/j.energy.2019.116230

CrossRef Full Text | Google Scholar

Krüger, K., Franke, R., and Rode, M. (2004). Optimization of Boiler Start-Up Using a Nonlinear Boiler Model and Hard Constraints. Energy 29 (12-15), 2239–2251. doi:10.1016/j.energy.2004.03.022

CrossRef Full Text | Google Scholar

Kruger, K., Rode, M., and Franke, R. (2001). “Optimal Control for Fast Boiler Start-Up Based on a Nonlinear Model and Considering the thermal Stress on Thick-Walled Components,” in Proceedings of the 2001 IEEE International Conference on Control Applications (CCA'01) (Cat. No. 01CH37204), Mexico City, Mexico, September 5–7, 2001.

Google Scholar

Kuczynski, K., Fitzgerald, F., Adams, D., Glover, F., White, V., Chalmers, H., et al. (2011). Dynamic Modelling of Oxyfuel Power Plant. Energ. Proced. 4, 2541–2547. doi:10.1016/j.egypro.2011.02.151

CrossRef Full Text | Google Scholar

Kumar, P. R., Raju, V. R., and Kumar, N. R. (2016). Simulation and Parametric Optimisation of thermal Power Plant Cycles. Perspect. Sci. 8, 304–306. doi:10.1016/j.pisc.2016.04.060

CrossRef Full Text | Google Scholar

Kunkel, P., and Mehrmann, V. (2006). Differential-algebraic Equations: Analysis and Numerical Solution, 2. European Mathematical Society.

Kuravi, S., Trahan, J., Goswami, D. Y., Rahman, M. M., and Stefanakos, E. K. (2013). Thermal Energy Storage Technologies and Systems for Concentrating Solar Power Plants. Prog. Energ. Combustion Sci. 39 (4), 285–319. doi:10.1016/j.pecs.2013.02.001

CrossRef Full Text | Google Scholar

Kuronen, J., Hotti, M., and Tuuri, S. (2018). Modelling and Dynamic Simulation of Cyclically Operated Pulverized Coal-Fired Power Plant in Proceedings of The 9th EUROSIM Congress on Modelling and Simulation, EUROSIM 2016, The 57th SIMS Conference on Simulation and Modelling SIMS 2016, Oulu, Finland, September 12–16, 2016.

Lappalainen, J., Blom, H., and Juslin, K. (2012). Dynamic Process Simulation as an Engineering Tool: A Case of Coal Plant Evaporator Analysis. VGB Powertech 92 (1-2), 62–68.

Google Scholar

Lappalainen, J., Tourunen, A., Mikkonen, H., Hänninen, M., and Kovács, J. (2014). Modelling and Dynamic Simulation of a Supercritical, Oxy Combustion Circulating Fluidized Bed Power Plant Concept—Firing Mode Switching Case. Int. J. Greenhouse Gas Control. 28, 11–24. doi:10.1016/j.ijggc.2014.06.015

CrossRef Full Text | Google Scholar

Larson, E. D., Fiorese, G., Liu, G., Williams, R. H., Kreutz, T. G., and Consonni, S. (2009). Co-production of Synfuels and Electricity from Coal + Biomass with Zero Net Carbon Emissions: an Illinois Case Study. Energy Procedia., 4371–4378. doi:10.1016/j.egypro.2009.02.251

CrossRef Full Text | Google Scholar

Laubscher, R., and Rousseau, P. (2020). Coupled Simulation and Validation of a Utility-Scale Pulverized Coal-Fired Boiler Radiant Final-Stage Superheater. Therm. Sci. Eng. Prog. 18, 100512. doi:10.1016/j.tsep.2020.100512

CrossRef Full Text | Google Scholar

Lawal, A., Wang, M., Stephenson, P., Koumpouras, G., and Yeung, H. (2010). Dynamic Modelling and Analysis of post-combustion CO2 Chemical Absorption Process for Coal-Fired Power Plants. Fuel 89 (10), 2791–2801. doi:10.1016/j.fuel.2010.05.030

CrossRef Full Text | Google Scholar

Lawal, A., Wang, M., Stephenson, P., and Obi, O. (2012). Demonstrating Full-Scale post-combustion CO2 Capture for Coal-Fired Power Plants through Dynamic Modelling and Simulation. Fuel 101, 115–128. doi:10.1016/j.fuel.2010.10.056

CrossRef Full Text | Google Scholar

Lee, H. H., Lee, J. C., Joo, Y. H., Oh, M., and Lee, C. H. (2014). Dynamic Modeling of Shell Entrained Flow Gasifier in an Integrated Gasification Combined Cycle Process. Appl. Energy 131, 425–440.

Le Grange, W., Lee, H.-H., Lee, J.-C., Joo, Y.-J., Oh, M., and Lee, C.-H. (2018). Dynamic Modeling of Shell Entrained Flow Gasifier in an Integrated Gasification Combined Cycle Process. Appl. Energ. 131, 425–440. doi:10.1016/j.apenergy.2014.06.044

CrossRef Full Text | Google Scholar

Li, B., Chen, T., and Yang, D. (2005). DBSSP––A Computer Program for Simulation of Controlled Circulation Boiler and Natural Circulation Boiler Start up Behavior. Energ. Convers. Management 46 (4), 533–549. doi:10.1016/j.enconman.2004.04.010

CrossRef Full Text | Google Scholar

Li, Y., Zhou, L., Xu, G., Fang, Y., Zhao, S., and Yang, Y. (2014). Thermodynamic Analysis and Optimization of a Double Reheat System in an Ultra-supercritical Power Plant. Energy 74, 202–214. doi:10.1016/j.energy.2014.05.057

CrossRef Full Text | Google Scholar

Linnhoff, B., and Hindmarsh, E. (1983). The Pinch Design Method for Heat Exchanger Networks. Chem. Eng. Sci. 38, 745–763. doi:10.1016/0009-2509(83)80185-7

CrossRef Full Text | Google Scholar

Liu, C., Wang, H., Ding, J., and Zhen, C. (2012). An Overview of Modelling and Simulation of thermal Power Plant. Int. J. Adv. Mechatronic Syst. 4 (2), 76–85. doi:10.1504/ijamechs.2012.048398

CrossRef Full Text | Google Scholar

Liu, J.-Z., Yan, S., Zeng, D.-L., Hu, Y., and Lv, Y. (2015). A Dynamic Model Used for Controller Design of a Coal Fired Once-Through Boiler-Turbine Unit. Energy 93, 2069–2078. doi:10.1016/j.energy.2015.10.077

CrossRef Full Text | Google Scholar

Liu, S., Faille, D., Fouquet, M., El-Hefni, B., Wang, Y., Zhang, J., et al. (2015). Dynamic Simulation of a 1MWe CSP tower Plant with Two-Level thermal Storage Implemented with Control System. Energ. Proced. 69, 1335–1343. doi:10.1016/j.egypro.2015.03.139

CrossRef Full Text | Google Scholar

Lopez-Negrete, R., D’Amato, F. J., Biegler, L. T., and Kumar, A. (2013). Fast Nonlinear Model Predictive Control: Formulation and Industrial Process Applications. Comput. Chem. Eng. 51, 55–64. doi:10.1016/j.compchemeng.2012.06.011

CrossRef Full Text | Google Scholar

Lozza, G. (1990). “Bottoming Steam Cycles for Combined Gas Steam Power Plants: a Theoretical Estimation of Steam Turbine Performance and Cycle Analysis,” in Proc. 1990 ASME Cogen-Turbo (New Orleans: Louisiana).

Google Scholar

Lozza, G. (1988). Thermodynamic Opitmization of Heat Recovery Steam CyclesProceedings of the II National congress “Gruppi Combinati: Prospettive Tecniche. Florence: economiche”.

Lu, S. (1999). Dynamic Modelling and Simulation of Power Plant Systems. Proc. Inst. Mech. Eng. A: J. Power Energ. 213 (1), 7–22. doi:10.1243/0957650991537392

CrossRef Full Text | Google Scholar

Luo, W., Wang, Q., Huang, X., Liu, Z., and Zheng, C. (2015). Dynamic Simulation and Transient Analysis of a 3 MWth Oxy-Fuel Combustion System. Int. J. Greenhouse Gas Control. 35, 138–149. doi:10.1016/j.ijggc.2015.02.003

CrossRef Full Text | Google Scholar

Luo, W., Wang, Q., Liu, Z., and Zheng, C. (2014). Dynamic Simulation of the Transition Process in a 3 MWth Oxy-Fuel Test Facility. Energ. Proced. 63, 6281–6288. doi:10.1016/j.egypro.2014.11.659

CrossRef Full Text | Google Scholar

Luo, X., Huang, X., El-Halwagi, M. M., Ponce-Ortega, J. M., and Chen, Y. (2016). Simultaneous Synthesis of Utility System and Heat Exchanger Network Incorporating Steam Condensate and Boiler Feed Water. Energy 113, 875–893. doi:10.1016/j.energy.2016.07.109

CrossRef Full Text | Google Scholar

Ma, J., Chang, C., Wang, Y., and Feng, X. (2018). Multi-objective Optimization of Multi-Period Interplant Heat Integration Using Steam System. Energy, 950–960. doi:10.1016/j.energy.2018.06.217

CrossRef Full Text | Google Scholar

Maffezzoni, C. (1992). Issues in Modelling and Simulation of Power Plants. IFAC Proc. Volumes 25 (1), 15–23. doi:10.1016/s1474-6670(17)50423-1

CrossRef Full Text | Google Scholar

Manassaldi, J. I., Arias, A. M., Scenna, N. J., Mussati, M. C., and Mussati, S. F. (2016). A Discrete and Continuous Mathematical Model for the Optimal Synthesis and Design of Dual Pressure Heat Recovery Steam Generators Coupled to Two Steam Turbines. Energy 103, 807–823. doi:10.1016/j.energy.2016.02.129

CrossRef Full Text | Google Scholar

Manassaldi, J. I., Mussati, S. F., and Scenna, N. J. (2011). Optimal Synthesis and Design of Heat Recovery Steam Generation (HRSG) via Mathematical Programming. Energy 36 (1), 475–485. doi:10.1016/j.energy.2010.10.017

CrossRef Full Text | Google Scholar

Manenti, F., and Ravaghi-Ardebili, Z. (2013). Dynamic Simulation of Concentrating Solar Power Plant and Two-Tanks Direct thermal Energy Storage. Energy 55, 89–97. doi:10.1016/j.energy.2013.02.001

CrossRef Full Text | Google Scholar

Manno, A., Amaldi, E., Casella, F., and Martelli, E. (2020). A Local Search Method for Costly Black-Box Problems and its Application to CSP Plant Start-Up Optimization Refinement. Optimization Eng., 1–36.

Google Scholar

Maréchal, F., and Kalitventzeff, B. (1998). Process Integration: Selection of the Optimal Utility System. Comput. Chem. Eng., S149–S156. doi:10.1016/s0098-1354(98)00049-0

CrossRef Full Text | Google Scholar

Maréchal, F., and Kalitventzeff, B. (1999). Targeting the Optimal Integration of Steam Networks: Mathematical Tools and Methodology. Comput. Chem. Eng., S133–S136. doi:10.1016/s0098-1354(99)80034-9

CrossRef Full Text | Google Scholar

Martelli, E., Amaldi, E., and Consonni, S. (2011). Numerical Optimization of Heat Recovery Steam Cycles: Mathematical Model, Two-Stage Algorithm and Applications. Comput. Chem. Eng., 2799–2823. doi:10.1016/j.compchemeng.2011.04.015

CrossRef Full Text | Google Scholar

Martelli, E., and Amaldi, E. (2014). PGS-COM: A Hybrid Method for Constrained Non-smooth Black-Box Optimization Problems. Brief Review, Novel Algorithm and Comparative Evaluation. Comput. Chem. Eng., 108–139. doi:10.1016/j.compchemeng.2013.12.014

CrossRef Full Text | Google Scholar

Martelli, E., Elsido, C., Mian, A., and Marechal, F. (2017). MINLP Model and Two-Stage Algorithm for the Simultaneous Synthesis of Heat Exchanger Networks, Utility Systems and Heat Recovery Cycles. Comput. Chem. Eng., 106, 663–689. doi:10.1016/j.compchemeng.2017.01.043

CrossRef Full Text | Google Scholar

Martelli, E., Kreutz, T., Carbo, M., Consonni, S., and Jansen, D. (2011). Shell Coal IGCCS with Carbon Capture: Conventional Gas Quench vs. Innovative Configurations. Appl. Energ., 3978–3989. doi:10.1016/j.apenergy.2011.04.046

CrossRef Full Text | Google Scholar

Martelli, E., Kreutz, T. G., Gatti, M., Chiesa, P., and Consonni, S. (2013). Numerical Optimization of Steam Cycles and Steam Generators Designs for Coal to FT Plants. Chem. Eng. Res. Des. 1467–1482. doi:10.1016/j.cherd.2013.02.026

CrossRef Full Text | Google Scholar

Martelli, E., Nord, L. O., and Bolland, O. (2012). Design Criteria and Optimization of Heat Recovery Steam Cycles for Integrated Reforming Combined Cycles with CO2 Capture. Appl. Energ. 255–268. doi:10.1016/j.apenergy.2011.10.043

CrossRef Full Text | Google Scholar

Marx-Schubach, T., and Schmitz, G. J. I. j. o. g. g. c. (2019). Modeling and Simulation of the Start-Up Process of Coal Fired Power Plants with post-combustion CO2 Capture. Int. J. Greenhouse Gas Control. 87, 44–57. doi:10.1016/j.ijggc.2019.05.003

CrossRef Full Text | Google Scholar

Matlab (2021). MATLAB Software Webpage. Available at: https://it.mathworks.com/products/matlab.html (Accessed May 5, 2021).

Mattos, H. A. d. S., Bringhenti, C., Cavalca, D. F., Silva, O. F. R., Campos, G. B. d., and Tomita, J. T. (2016). Combined Cycle Performance Evaluation and Dynamic Response Simulation. J. Aerospace Technology Management 8 (4), 491–497. doi:10.5028/jatm.v8i4.599

CrossRef Full Text | Google Scholar

Mehrgoo, M., and Amidpour, M. (2017). Constructal Design and Optimization of a Dual Pressure Heat Recovery Steam Generator. Energy 124, 87–99. doi:10.1016/j.energy.2017.02.046

CrossRef Full Text | Google Scholar

Meinke, S., Gottelt, F., Müller, M., and Hassel, E. (2011). “Modeling of Coal-Fired Power Units with Thermopower Focussing on Start-Up Process,” in Paper presented at the Proceedings of the 8th International Modelica Conference, Dresden; Germany, March 20th-22nd, 2011 (Technical Univeristy).

Google Scholar

Meinke, S. (2013). Modellierung thermischer Kraftwerke vor dem Hintergrund steigender Dynamikanforderungen aufgrund zunehmender Windenergie-und Photovoltaikeinspeisung: Forschungszentrum für Verbrennungsmotoren und Thermodynamik Rostock GmbH.

Mertens, N., Alobaid, F., Frigge, L., and Epple, B. (2014). Dynamic Simulation of Integrated Rock-Bed Thermocline Storage for Concentrated Solar Power. Solar Energy 110, 830–842. doi:10.1016/j.solener.2014.10.021

CrossRef Full Text | Google Scholar

Mertens, N., Alobaid, F., Lanz, T., Epple, B., and Kim, H.-G. (2016). Dynamic Simulation of a Triple-Pressure Combined-Cycle Plant: Hot Start-Up and Shutdown. Fuel 167, 135–148. doi:10.1016/j.fuel.2015.11.055

CrossRef Full Text | Google Scholar

Mertens, N., Alobaid, F., Starkloff, R., Epple, B., and Kim, H.-G. (2015). Comparative Investigation of Drum-type and Once-Through Heat Recovery Steam Generator during Start-Up. Appl. Energ. 144, 250–260. doi:10.1016/j.apenergy.2015.01.065

CrossRef Full Text | Google Scholar

Mertens, N. J., Alobaid, F., Epple, B., and Kim, H.-G. (2016). “Combined-cycle Start-Up Procedures: Dynamic Simulation and Measurement,” in ASME 2016 Power Conference collocated with the ASME 2016 10th International Conference on Energy Sustainability and the ASME 2016 14th International Conference on Fuel Cell Science, Engineering and Technology, Charlotte, NC, USA, June 26–30, 2016.

Google Scholar

Mian, A., Martelli, E., and Maréchal, F. (2016). Framework for the Multiperiod Sequential Synthesis of Heat Exchanger Networks with Selection, Design, and Scheduling of Multiple Utilities. Ind. Eng. Chem. Res., 168–186. doi:10.1021/acs.iecr.5b02104

CrossRef Full Text | Google Scholar

Mikkonen, H., Lappalainen, J., Pikkarainen, T., and Kuivalainen, R. (2017). Modelling and Dynamic Simulation of the 2nd Generation Oxy Fired Power Plant–Oxidant Fan Failure Case. Energ. Proced. 114, 561–572. doi:10.1016/j.egypro.2017.03.1198

CrossRef Full Text | Google Scholar

Montañés, R. M., Skaugen, G., Hagen, B., and Rohde, D. (2021). Compact Steam Bottoming Cycles: Minimum Weight Design Optimization and Transient Response of Once-Through Steam Generators. Front. Energy. Res. 9, 261.

Muren, R., Arias, D., Chapman, D., Erickson, L., and Gavilan, A. (2011). “Coupled Transient System Analysis: a New Method of Passive thermal Energy Storage Modeling for High Temperature Concentrated Solar Power Systems,” in Paper presented at the ASME 2011 5th International Conference on Energy Sustainability, Washington, DC, USA, August 7–10, 2011.

Google Scholar

Nadir, M., Ghenaiet, A., and Carcasci, C. (2016). Thermo-economic Optimization of Heat Recovery Steam Generator for a Range of Gas Turbine Exhaust Temperatures. Appl. Therm. Eng. 106, 811–826. doi:10.1016/j.applthermaleng.2016.06.035

CrossRef Full Text | Google Scholar

Nadir, M., and Ghenaiet, A. (2015). Thermodynamic Optimization of Several (Heat Recovery Steam Generator) HRSG Configurations for a Range of Exhaust Gas Temperatures. Energy 86, 685–695. doi:10.1016/j.energy.2015.04.023

CrossRef Full Text | Google Scholar

Nannarone, A., and Klein, S. A. (2019). Start-Up Optimization of a CCGT Power Station Using Model-Based Gas Turbine Control. J. Eng. Gas Turbines Power 141 (4). doi:10.1115/1.4041273

CrossRef Full Text | Google Scholar

Neuman, P., Pokorny, M., Varcop, L., Weiglhofer, W., and Javed, A. (2002). Engineering and Operator Training Simulator of Coal-Fired Steam Boiler. Proc. 10th Int. Conf. MATLAB 44, 8259–8264. doi:10.3182/20110828-6-IT-1002.00403

CrossRef Full Text | Google Scholar

Nevriva, P., Ozana, S., and Pies, M. (2011). Simulation of Power Plant Superheater Using Advanced Simulink Capabilities. Int. J. Circuits, Syst. Signal Process. 5 (1), 86–93.

Google Scholar

Ngoma, D. (2001). Untersuchungen zur Strömungsstabilität verschiedener Abhitzedampferzeugersysteme im Vergleich: Shaker.

Niknia, I., and Yaghoubi, M. (2012). Transient Simulation for Developing a Combined Solar thermal Power Plant. Appl. Therm. Eng. 37, 196–207. doi:10.1016/j.applthermaleng.2011.11.016

CrossRef Full Text | Google Scholar

Nishio, M., Itoh, J., Shiroko, K., and Umeda, T. (1980). A Thermodynamic Approach to Steam-Power System Design. Ind. Eng. Chem. Process Des. Development 19 (2), 306–312. doi:10.1021/i260074a019

CrossRef Full Text | Google Scholar

Nittaya, T., Douglas, P. L., Croiset, E., and Ricardez-Sandoval, L. A. (2014). Dynamic Modelling and Control of MEA Absorption Processes for CO2 Capture from Power Plants. Fuel 116, 672–691. doi:10.1016/j.fuel.2013.08.031

CrossRef Full Text | Google Scholar

Nord, L. O., Martelli, E., and Bolland, O. (2014). Weight and Power Optimization of Steam Bottoming Cycle for Offshore Oil and Gas Installations. Energy 76, 891–898. doi:10.1016/j.energy.2014.08.090

CrossRef Full Text | Google Scholar

Oko, E., and Wang, M. (2014). Dynamic Modelling, Validation and Analysis of Coal-Fired Subcritical Power Plant. Fuel 135, 292–300. doi:10.1016/j.fuel.2014.06.055

CrossRef Full Text | Google Scholar

Opriş, I., Cenuşă, V.-E., Norişor, M., Darie, G., Alexe, F.-N., and Costinas, S. (2020). Parametric Optimization of the Thermodynamic Cycle Design for Supercritical Steam Power Plants. Energ. Convers. Management 208, 112587.

Google Scholar

Papoulias, S. A., and Grossmann, I. E. (1983a). A Structural Optimization Approach in Process Synthesis-I. Comput. Chem. Eng. 7, 695–706. doi:10.1016/0098-1354(83)85022-4

CrossRef Full Text | Google Scholar

Papoulias, S. A., and Grossmann, I. E. (1983). A Structural Optimization Approach in Process Synthesis-II. Comput. Chem. Eng. 7, 707–721. doi:10.1016/0098-1354(83)85023-6

CrossRef Full Text | Google Scholar

Papoulias, S. A., and Grossmann, I. E. (1983c). A Structural Optimization Approach in Process Synthesis-III. Comput. Chem. Eng. 7, 723–734. doi:10.1016/0098-1354(83)85024-8

CrossRef Full Text | Google Scholar

Pehle, L., Łuczyński, P., Jeon, T., Wirsum, M., Mohr, W. F., and Helbig, K. (2020). “Comparison of Steam Turbine Pre-warming and Warm-Keeping Strategies Using Hot Air for Fast Turbine Start-Up,” in ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual. Online, September 21–25, 2020.

Google Scholar

Peinado Gonzalo, A., Pliego Marugán, A., and García Márquez, F. P. (2019). A Review of the Application Performances of Concentrated Solar Power Systems. Appl. Energ. 255, 113893. doi:10.1016/j.apenergy.2019.113893

CrossRef Full Text | Google Scholar

Perz, E. (1990). “A Computer Method for thermal Power Cycle Calculation,” in ASME 1990 International Gas Turbine and Aeroengine Congress and Exposition.

Google Scholar

Pletl, C. (2005). Experimente und numerische Simulation zum dynamischen Verhalten eines Abhitzedampferzeugers mit Zwangdurchlauf. VDI-Verlag.

Ponce, C. V., Sáez, D., Bordons, C., and Núñez, A. (2016). Dynamic Simulator and Model Predictive Control of an Integrated Solar Combined Cycle Plant. Energy 109, 974–986. doi:10.1016/j.energy.2016.04.129

CrossRef Full Text | Google Scholar

Postler, R., Epple, B., Kluger, F., Mönkert, P., and Heinz, G. (2011). “Dynamic Process Simulation Model of an Oxyfuel 250 MWel Demonstration Power Plant,” in Paper presented at the 2nd oxyfuel combustion conference, Queensland, Australia, September 12–16, 2011.

Google Scholar

Pyomo (2021). Pyomo Package Webpage. Available at: http://www.pyomo.org/about (Accessed May 5, 2021).

Quoilin, S., Aumann, R., Grill, A., Schuster, A., Lemort, V., and Spliethoff, H. (2011). Dynamic Modeling and Optimal Control Strategy of Waste Heat Recovery Organic Rankine Cycles. Appl. Energ. 88 (6), 2183–2190. doi:10.1016/j.apenergy.2011.01.015

CrossRef Full Text | Google Scholar

Rakopoulos, D., Avagianos, I., Almpanidis, D., Nikolopoulos, N., and Grammelis, P. (2017). Dynamic Modeling of a Utility Once-Through Pulverized-Fuel Steam Generator. J. Energ. Eng. 143 (4), 04016070. doi:10.1061/(asce)ey.1943-7897.0000426

CrossRef Full Text | Google Scholar

Rashad, A., Elweteedy, A., Temraz, A., and Gomaa, A. (2021). Investigating an Integrated Solar Combined Cycle Power Plant. Glob. J. Eng. Sci. 7, 1–14. doi:10.33552/GJES.2021.07.000652

CrossRef Full Text | Google Scholar

Ratliff, P., Garbett, P., and Fischer, W. (2007). The New Siemens Gas Turbine Sgt5-8000h for More Customer Benefit. VGB Powertech. 87 (9), 128–132. doi:10.1097/01.won.0000264822.57743.16

CrossRef Full Text | Google Scholar

Richter, M., Möllenbruck, F., Starinsk, A., Oeljeklaus, G., and Görner, K. (2015). “Flexibilization of Coal-Fired Power Plants by Dynamic Simulation,” in Proceedings of the 11th International Modelica Conference, Versailles, France, September 21-23, 2015.

Google Scholar

Richter, M., Oeljeklaus, G., and Görner, K. (2019). Improving the Load Flexibility of Coal-Fired Power Plants by the Integration of a thermal Energy Storage. Appl. Energ. 236, 607–621. doi:10.1016/j.apenergy.2018.11.099

CrossRef Full Text | Google Scholar

Rinzic, J. (2017). Steam Generators for Nuclear Power Plants. Woodhead Publishing.

Rodat, S., Souza, J. V. D., Thebault, S., Vuillerme, V., and Dupassieux, N. (2014). Dynamic Simulations of Fresnel Solar Power Plants. Energ. Proced. 49, 1501–1510. doi:10.1016/j.egypro.2014.03.159

CrossRef Full Text | Google Scholar

Rossi, I., Sorce, A., and Traverso, A. (2017). Gas Turbine Combined Cycle Start-Up and Stress Evaluation: A Simplified Dynamic Approach. Appl. Energ. 190, 880–890. doi:10.1016/j.apenergy.2016.12.141

CrossRef Full Text | Google Scholar

Roth, K., Scherer, V., and Behnke, K. (2005). Enhancing the Dynamic Performance of Electricity Production in Steam Power Plants by the Integration of Transient Waste Heat Sources into the Feed-Water Pre-heating System. Int. J. Energ. Technology Pol. 3 (1–2), 50–65. doi:10.1504/ijetp.2005.006739

CrossRef Full Text | Google Scholar

Rovira, A., Sánchez, C., Muñoz, M., Valdés, M., and Durán, M. D. (2011). Thermoeconomic Optimisation of Heat Recovery Steam Generators of Combined Cycle Gas Turbine Power Plants Considering Off-Design Operation. Energ. Convers. Management 52 (4), 1840–1849. doi:10.1016/j.enconman.2010.11.016

CrossRef Full Text | Google Scholar

Rovira, A., Valdés, M., and Durán, M. D. (2010). A Model to Predict the Behaviour at Part Load Operation of Once-Through Heat Recovery Steam Generators Working with Water at Supercritical Pressure. Appl. Therm. Eng. 30 (13), 1652–1658. doi:10.1016/j.applthermaleng.2010.03.023

CrossRef Full Text | Google Scholar

Ruchti, C., Olia, H., Franitza, K., Ehrsam, A., and Bauver, W. (2011). “Combined Cycle Power Plants as Ideal Solution to Balance Grid Fluctuations—Fast Start-Up Capabilities,” in Proc. of 43th Colloquium of Power Plant Technology, TU Dresden, September 18–19, 2011.

Google Scholar

Runvik, H. (2014). Modelling and Start-Up Optimization of a Coal-Fired Power Plant. MSc Thesis. Sweden: Lund University.

Sabia, G., Heinze, C., Alobaid, F., Martelli, E., and Epple, B. (2019). ASPEN Dynamics Simulation for Combined Cycle Power Plant - Validation with Hot Start-Up Measurement. Energy 187, 115897. doi:10.1016/j.energy.2019.115897

CrossRef Full Text | Google Scholar

Scholz, C., Zimmermann, H., and an der Ruhr, M. (2012). First Long-Term Experience with the Operational Flexibility of the SGT5-8000H.

Schuhbauer, C., Angerer, M., Spliethoff, H., Kluger, F., and Tschaffon, H. (2014). Coupled Simulation of a Tangentially Hard Coal Fired 700°C Boiler. Fuel 122, 149–163. doi:10.1016/j.fuel.2014.01.032

CrossRef Full Text | Google Scholar

Schuhbauer, C. (2013). Dynamic and Coupled Simulation of the 700° C Coal-Fired Power Plant. Dr. Hut.

Sciacovelli, A., Li, Y., Chen, H., Wu, Y., Wang, J., Garvey, S., et al. (2017). Dynamic Simulation of Adiabatic Compressed Air Energy Storage (A-CAES) Plant with Integrated thermal Storage - Link between Components Performance and Plant Performance. Appl. Energ. 185, 16–28. doi:10.1016/j.apenergy.2016.10.058

CrossRef Full Text | Google Scholar

Scilab (2021). Scilab Software Webpage. Available at: https://www.scilab.org/(Accessed May 5, 2021).

Shang, Z., and Kokossis, A. (2005). A Systematic Approach to the Synthesis and Design of Flexible Site Utility Systems. Chem. Eng. Sci. 60, 4431–4451. doi:10.1016/j.ces.2005.03.015

CrossRef Full Text | Google Scholar

Shin, J., Jeon, Y., Maeng, D., Kim, J., and Ro, S. (2002). Analysis of the Dynamic Characteristics of a Combined-Cycle Power Plant. Energy 27 (12), 1085–1098. doi:10.1016/s0360-5442(02)00087-7

CrossRef Full Text | Google Scholar

Sindareh-Esfahani, P., Habibi-Siyahposh, E., Saffar-Avval, M., Ghaffari, A., and Bakhtiari-Nejad, F. (2014). Cold Start-Up Condition Model for Heat Recovery Steam Generators. Appl. Therm. Eng. 65 (1-2), 502–512. doi:10.1016/j.applthermaleng.2014.01.016

CrossRef Full Text | Google Scholar

Singh, R., Miller, S. A., Rowlands, A. S., and Jacobs, P. A. (2013). Dynamic Characteristics of a Direct-Heated Supercritical Carbon-Dioxide Brayton Cycle in a Solar thermal Power Plant. Energy 50, 194–204. doi:10.1016/j.energy.2012.11.029

CrossRef Full Text | Google Scholar

Speight, J. G. (2013). Coal-Fired Power Generation Handbook. 1st edition. Salem, Massachussets: Wiley-Scrivener.

Spelling, J., Favrat, D., Martin, A., and Augsburger, G. (2012). Thermoeconomic Optimization of a Combined-Cycle Solar tower Power Plant. Energy 41 (1), 113–120. doi:10.1016/j.energy.2011.03.073

CrossRef Full Text | Google Scholar

Spinelli, M., Campanari, S., Romano, M. C., Consonni, S., Kreutz, T. G., Ghezel-Ayagh, H., et al. (2015). “Molten Carbonate Fuel Cells as Means for Post-Combustion CO2 Capture: Retrofitting Coal-Fired Steam Plants and Natural Gas-Fired Combined Cycles,” in ASME 2015 13th International Conference on Fuel Cell Science. V49001T49405A49400: Engineering and Technology, San Diego, CA, USA, June 28–July 2, 2015.

Google Scholar

Spliethoff, H. (2010). Power Generation from Solid Fuels. Springer Science & Business Media.

Starkloff, R., Alobaid, F., Karner, K., Epple, B., Schmitz, M., and Boehm, F. (2015). Development and Validation of a Dynamic Simulation Model for a Large Coal-Fired Power Plant. Appl. Therm. Eng. 91, 496–506. doi:10.1016/j.applthermaleng.2015.08.015

CrossRef Full Text | Google Scholar

Starkloff, R., Postler, R., Al-Maliki, W. A. K., Alobaid, F., and Epple, B. (2016). Investigation into Gas Dynamics in an Oxyfuel Coal Fired Boiler during Master Fuel Trip and Blackout. J. Process Control. 41, 67–75. doi:10.1016/j.jprocont.2016.03.003

CrossRef Full Text | Google Scholar

Stefanitsis, D., Nesiadis, A., Koutita, K., Nikolopoulos, A., Nikolopoulos, N., Peters, J., et al. (2020). Simulation of a CFB Boiler Integrated with a thermal Energy Storage System during Transient Operation. Front. Energ. Res. 8, 1–14. doi:10.3389/fenrg.2020.00169

CrossRef Full Text | Google Scholar

Subramanian, A., Gundersen, T., and Adams, T. (2018). Modeling and Simulation of Energy Systems: A Review. Processes 6 (12), 238. doi:10.3390/pr6120238

CrossRef Full Text | Google Scholar

Sun, B., Liu, Y., Chen, X., Zhou, Q., and Su, M. (2011). Dynamic Modeling and Simulation of Shell Gasifier in IGCC. Fuel Process. Technol. 92 (8), 1418–1425. doi:10.1016/j.fuproc.2011.02.017

CrossRef Full Text | Google Scholar

Sunil, P. U., Barve, J., and Nataraj, P. S. V. (2018). A Robust Heat Recovery Steam Generator Drum Level Control for Wide Range Operation Flexibility Considering Renewable Energy Integration. Energy 163, 873–893. doi:10.1016/j.energy.2018.08.167

CrossRef Full Text | Google Scholar

Taler, J., Węglowski, B., Taler, D., Sobota, T., Dzierwa, P., Trojan, M., et al. (2015). Determination of Start-Up Curves for a Boiler with Natural Circulation Based on the Analysis of Stress Distribution in Critical Pressure Components. Energy 92, 153–159. doi:10.1016/j.energy.2015.03.086

CrossRef Full Text | Google Scholar

Tawarmalani, M., and Sahinidis, N. V. (2005). A Polyhedral branch-and-cut Approach to Global Optimization. Math. programming 103 (2), 225–249. doi:10.1007/s10107-005-0581-8

CrossRef Full Text | Google Scholar

Temraz, A., Alobaid, F., Lanz, T., Elweteedy, A., and Epple, B. (2020a). Operational Flexibility of Two-phase Flow Test Rig for Investigating the Dynamic Instabilities in Tube Boiling Systems. Front. Energ. Res. 8, 1–12. doi:10.3389/fenrg.2020.517740

CrossRef Full Text | Google Scholar

Temraz, A., Rashad, A., Elweteedy, A., Alobaid, F., and Epple, B. (2020b). Energy and Exergy Analyses of an Existing Solar-Assisted Combined Cycle Power Plant. Appl. Sci. 10 (14), 4980. doi:10.3390/app10144980

CrossRef Full Text | Google Scholar

Terdalkar, R., Doupis, D., Clark, M., Joshi, A., and Wang, C. (2015). Transient Simulation of High Temperature High Pressure Solar tower Receiver. Energ. Proced. 69, 1451–1460. doi:10.1016/j.egypro.2015.03.093

CrossRef Full Text | Google Scholar

Thermoflow (2021). Thermoflow Products Webpage. Available at: http://www.thermoflow.com/products_overview.html (Accessed May 5, 2021).

Tică, A., Gueguen, H., Dumur, D., Faille, D., and Davelaar, F. (2012). “Hierarchical Nonlinear Model Predictive Control for Combined Cycle Start-Up Optimization,” in IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, December 10–13, 2012.

Google Scholar

Trabucchi, S., Casella, F., Maioli, T., Elsido, C., Franzini, D., and Ramond, M. (2017). Preliminary Analysis of the PreFlexMS Molten Salt Once-Through Steam Generator Dynamics and Control Strategy. AIP Conf. Proc. 1850, 030048. doi:10.1063/1.4984391

CrossRef Full Text | Google Scholar

Turton, R., Bailie, R. C., Whiting, W. B., and Shaeiwitz, J. A. (2008). Analysis, Synthesis, and Design of Chemical Processes. Third Edition. Pearson College Div.

Udono, K., and Sitte, R. (2008). Modeling Seawater Desalination Powered by Waste Incineration Using a Dynamic Systems Approach. Desalination 229 (1-3), 302–317. doi:10.1016/j.desal.2007.10.017

CrossRef Full Text | Google Scholar

Valdés, M., Durán, M. D., and Rovira, A. (2003). Thermoeconomic Optimization of Combined Cycle Gas Turbine Power Plants Using Genetic Algorithms. Appl. Therm. Eng. 23 (17), 2169–2182. doi:10.1016/s1359-4311(03)00203-5

CrossRef Full Text | Google Scholar

Valdés, M., and Rapún, J. L. (2011). Optimization of Heat Recovery Steam Generators for Combined Cycle Gas Turbine Power Plants. Appl. Therm. Eng. 21 (11), 1149–1159.

Google Scholar

Vandervort, C., Leach, D., and Scholz, M. (2016). “Advancements in H Class Gas Turbines for Combined Cycle Power Plants for High Efficiency, Enhanced Operational Capability and Broad Fuel Flexibility,” in 8th International Gas Turbine Congress, Brussels, Belgium, October 12–13, 2016.

Google Scholar

Vandervort, C., Wetzel, T., and Leach, D. (2017). Engineering and Validating A World Record Gas Turbine. Mech. Eng. 139 (12), 48–50. doi:10.1115/1.2017-dec-13

CrossRef Full Text | Google Scholar

Vitte, P., Manenti, F., Pierucci, S., Joulia, X., and Buzzi-Ferraris, G. (2012). Dynamic Simulation of Concentrating Solar Plants. CHEMICAL ENGINEERING 29.

Google Scholar

Walter, H., and Epple, B. (2017). Numerical Simulation of Power Plants and Firing Systems. Springer.

Walter, H., and Hofmann, R. (2011). How Can the Heat Transfer Correlations for Finned-Tubes Influence the Numerical Simulation of the Dynamic Behavior of a Heat Recovery Steam Generator? Appl. Therm. Eng. 31 (4), 405–417. doi:10.1016/j.applthermaleng.2010.08.015

CrossRef Full Text | Google Scholar

Wang, C., Liu, M., Li, B., Liu, Y., and Yan, J. (2017). Thermodynamic Analysis on the Transient Cycling of Coal-Fired Power Plants: Simulation Study of a 660 MW Supercritical Unit. Energy 122, 505–527. doi:10.1016/j.energy.2017.01.123

CrossRef Full Text | Google Scholar

Wang, J., Wojcik, J. D., and Zue, Y. (2012). Study of Supercritical Coal Fired Power Plant Dynamic Responses and Control for Grid Code ComplianceMathematical Modelling and Simulation of Power Plants and CO2 Capture WORKSHOP.

Wang, L., Lampe, M., Voll, P., Yang, Y., and Bardow, A. (2016). Multi-objective Superstructure-free Synthesis and Optimization of thermal Power Plants. Energy 116 (1), 1104–1116. doi:10.1016/j.energy.2016.10.007

CrossRef Full Text | Google Scholar

Wang, L., Yang, Y., Dong, C., Morosuk, T., and Tsatsaronis, G. (2014). Systematic Optimization of the Design of Steam Cycles Using MINLP and Differential Evolution. J. Energ. Resour. Technol. 136 (133), 031601. doi:10.1115/1.4026268

CrossRef Full Text | Google Scholar

Wang, M., Liu, G., and Hui, C. W. (2017). Novel Shortcut Optimization Model for Regenerative Steam Power Plant. Energy 138, 529–541. doi:10.1016/j.energy.2017.07.088

CrossRef Full Text | Google Scholar

Wegstein, J. H. (1958). Accelerating Convergence of Iterative Processes. Commun. ACM 1 (6), 9–13. doi:10.1145/368861.368871

CrossRef Full Text | Google Scholar

Wenjing, D., Jinbo, L., and Baoqiang, Y. (2020). Dynamic Characteristics Analysis of a Once-Through Heat Recovery Steam Generator. Appl. Therm. Eng., 115155.

Google Scholar

Wheeler, A. (2016). Amec Foster Wheeler Wins UK Biomass Fired CFB Boiler Contract. Pump Industry Analyst 2016 (9), 3. doi:10.1016/S1359-6128(16)30261-0

CrossRef Full Text | Google Scholar

Woodruff, E. B., Lammers, H. B., and Lammers, T. F. (2017). Steam Plant Operation. Tenth Edition. McGraw-Hill Education.

Yee, T., and Grossmann, I. (1990). Simultaneous Optimization Models for Heat Integration—II. Heat Exchanger Network Synthesis. Comput. Chem. Eng. 14 (10), 1165–1184. doi:10.1016/0098-1354(90)85010-8

CrossRef Full Text | Google Scholar

Yousef Nezhad, M. E., and Hoseinzadeh, S. (2017). Mathematical Modelling and Simulation of a Solar Water Heater for an Aviculture Unit Using MATLAB/SIMULINK. J. Renew. Sustainable Energ. 9 (6), 063702. doi:10.1063/1.5010828

CrossRef Full Text | Google Scholar

Yu, H., Feng, X., and Wang, Y. (2015). A New Pinch Based Method for Simultaneous Selection of Working Fluid and Operating Conditions in an ORC (Organic Rankine Cycle) Recovering Waste Heat. Energy 90, 36–46. doi:10.1016/j.energy.2015.02.059

CrossRef Full Text | Google Scholar

Zehtner, W., Spliethoff, H., and Woyke, W. (2008). Analysis and optimisation of operation of modern hard coal-fired power plants through simulationBetriebsanalyse und-optimierung moderner Steinkohlekraftwerke durch Simulation.

Zhang, J., Liu, P., Zhou, Z., Ma, L., Li, Z., and Ni, W. (2014). A Mixed-Integer Nonlinear Programming Approach to the Optimal Design of Heat Network in a Polygeneration Energy System. Appl. Energ., 146–154. doi:10.1016/j.apenergy.2013.09.057

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, C., Liu, M., Chong, D., and Yan, J. (2018). Improving Operational Flexibility by Regulating Extraction Steam of High-Pressure Heaters on a 660 MW Supercritical Coal-Fired Power Plant: A Dynamic Simulation. Appl. Energ. 212, 1295–1309. doi:10.1016/j.apenergy.2018.01.017

CrossRef Full Text | Google Scholar