A Powerful Bio-Inspired Optimization Algorithm Based PV Cells Diode Models Parameter Estimation

Accurate and reliable photovoltaic (PV) cell parameter identification is critical to simulation analysis, maximum output power harvest, and optimal control of PV systems. However, inherent high-nonlinear and multi-modal characteristics usually result in thorny obstacles to hinder conventional optimization methods to obtain a fast and satisfactory performance. In this study, a novel bio-inspired grouped beetle antennae search (GBAS) algorithm is devised to effectively identify unknown parameters of three different PV models, i.e., single diode model (SDM), double diode model (DDM), and triple diode model (TDM). Compared against beetle antennae search (BAS) algorithm, optimization efficiency of GBAS algorithm is markedly enhanced based on a cooperative searching group that consists of multiple individuals rather than a single beetle. Besides, a dynamic balance mechanism between local exploitation and global exploration is designed to increase the probability for a higher quality optimum. Comprehensive case studies demonstrate that GBAS algorithm can outperform other advanced meta-heuristic algorithms in both optimization precision and stability for estimating PV cell parameters, e.g., standard deviation (SD) of root mean square error (RMSE) obtained by GBAS algorithm is 64.34% smaller than the best value obtained by other algorithms in SDM, 61.86% smaller than that in DDM.

Introduction

In the past few decades, excessive utilization of natural resources causes rapid fossil fuels depletion (Sun et al., 2020) and serious environmental degradation (Song et al., 2018), which inevitably accelerates ecological destruction and global energy crisis (Yang et al., 2018b). Hence, energy revolution and transformation have become essential and imperative for social and economic development (Peng et al., 2020), which is also in line with global sustainable development strategy (Song et al., 2020). Obviously, exploitation and utilization of new energy resources and renewable energy (Yang et al., 2018a), such as solar (Zhang et al., 2019) and wind (Li et al., 2019), are extremely critical which has aroused widespread attentions worldwide (Zhang et al., 2020). Particularly, solar energy is deemed as one of the most effective alternatives (Yang et al., 2016; He et al., 2017).

Photovoltaic (PV) system is widely used for solar energy applications which own elegant merits, e.g., inexhaustible in supply, wide distribution, and pollution-free. Particularly, measured current-voltage (I-V) data based precise PV modeling is extremely critical to dynamic behavior analysis of PV system. Thus far, various PV models have been devised, among which two types of equivalent circuit models are most widely applied (Chin et al., 2015), i.e., single diode model (SDM) (Humada et al., 2016) and double diode model (DDM) (Abbassi et al., 2018). Meanwhile, other more complicated models, e.g., triple diode model (TDM) (Khanna et al., 2015) is barely investigated in recent reported literatures due to their huge computation burden resulted from a larger number of unknown parameters. However, more complicated physical behavior of PV systems is more likely to be more efficiently studied based on these models. Hence, three types of PV models, i.e., SDM, DDM, and TDM are all investigated in this study for a comprehensive evaluation of PV cell parameter identification.

Note that a reliable PV cell modeling mainly relies on an accurate identification of relevant model electrical parameters. In general, PV cell parameter identification is essential for performance analysis, optimal design (Youssef et al., 2017), real-time control, and maximum power point tracking (MPPT) of PV systems (Chaibi et al., 2019; Yang et al., 2019b). Nevertheless, the following two shortcomings make parameter identification difficult to achieve stable and satisfactory results in practical applications: (i) the parameters provided by manufacturer are unavailable and only tested under standard test condition (STC), while the practical operation condition is far from STC which might change the output characteristics of PV cells and (ii) these parameters are time-varying due to degradation and faults of PV cells (Gomes et al., 2017).

Until now, numerous methods have been developed to solve such high-nonlinear and multi-modal obstacle, which are categorized into three groups, i.e., analytical methods (Chan and Phang, 1987; Saleem and Karmalkar, 2009), deterministic techniques, and meta-heuristic algorithms. In general, analytical methods are based on some key points on I-V curves provided by manufacturer and a series of mathematical equations, which are characterized by simplicity and fast computation but relatively low accuracy (Wolf and Benda, 2013; Batzelis and Papathanassiou, 2016). Meanwhile, deterministic approaches and meta-heuristic algorithms can handle PV parameter estimation with some reference points of given I-V curves. However, deterministic techniques, such as least squares (Newton-based method) (Li et al., 2017) and iterative curve fitting (Villalva et al., 2009) are extremely strict with model characteristics. Moreover, they are highly sensitive to initial operation conditions, while inherent high-nonlinearity and multi-modality of PV systems always leads to premature convergence. Nevertheless, meta-heuristic algorithms can effectively avoid the shortcomings of the above two methods since they normally possess advantages of easy implementation (Zhang et al., 2021), high efficiency (Mahdavi et al., 2015), insensitivity to initial condition and gradient information (Roeva and Fidanova, 2018), etc. Hence, they are deemed as the most promising and efficient tools for PV cell parameter extraction.

Thus far, they have been widely adopted in PV cell parameter identification in recent years (Yang et al., 2020). For instance, genetic algorithm (GA) (Jervase et al., 2001), differential evolution (DE) (Ishaque and Salam, 2011), particle swarm optimization (PSO) (Ye et al., 2009), artificial bee colony (ABC) (Oliva et al., 2014; Yang et al., 2019a), bird mating optimizer (BMO) (Askarzadeh and Rezazadeh, 2013), whale optimization algorithm (WOA) (Elazab et al., 2018; Dasu et al., 2019), backtracking search algorithm (BSA) (Yu et al., 2018), month flame optimizer (MFO) (Allam et al., 2016), gray wolf optimization (GWO) (Yang et al., 2017; Nayak et al., 2019), biogeography-based optimization (BBO) (Niu et al., 2014), flower pollination algorithm (FPA) (Alam et al., 2015; Shang et al., 2018), harmony search (HS) (Askarzadeh and Rezazadeh, 2012), multiswarm spiral leader particle swarm optimization (MSLPSO) algorithm (Nunes et al., 2020), slime mold algorithm (SMA) (Mostafa et al., 2020) and so forth (Muangkote et al., 2019), along with their numerous hybrid/variants.

Inspiringly, beetle antennae search (BAS) algorithm is a recently developed biology-based meta-heuristic algorithm (Jiang and Li, 2018), which basically replicates the searching mechanism of long-horn beetles. Besides, the basic functioning mechanism of beetle’s antennae and its random walking behavior are all considered in optimization principles of BAS. Note that such strategy owns the superiorities of simple structure and easy implementation, while its convergence and local minimum avoidance have been verified via two typical test functions. However, the effectiveness and accuracy of original BAS algorithm are still worthy to be further improved.

Hence, a powerful grouped BAS (GBAS) algorithm (Hao et al., 2020) is employed in this paper for PV cell parameter identification, whose contributions/novelties can be summarized as follows:

• GBAS algorithm can improve the optimization efficiency with a cooperative group of multiple beetles instead of a single beetle, while it also can acquire a high-quality optimum by a dynamic balance between local exploitation and global exploration;

• Practical performance of GBAS is comprehensively validated by SDM, DDM, and TDM, respectively;

• Comprehensive case studies verify that GBAS algorithm outperforms other meta-heuristic algorithms in both solution optimization accuracy and stability.

The rest of this paper is organized as follows: The problem formulation of PV cell models and applied objective function are illustrated in section “PV Cell Modeling and Problem Formulation.” The main optimization principle of the proposed GBAS algorithm is elaborated in section “Grouped Beetle Antennae Search (GBAS) Algorithm.” Case studies results and detailed statistical analysis on various PV cell models are shown and analyzed in section “Case Studies.” Lastly, conclusions are given in section “Conclusion.”

PV Cell Modeling and Problem Formulation

The first step to study the characteristics of PV cells, or to develop a more accurate prediction and optimization of PV systems operation, is to establish an appropriate PV cell model. Then, PV cell parameters can be reliably extracted to more accurately depict the output I-V and power-voltage (P-V) characteristics for better analysis of PV cells. The most widely applied equivalent circuit models are SDM, DDM, and TDM.

Mathematical Modeling

In general, the main these structures of the three models are quite similar, thus a comprehensive summary is provided in Table 1 for more detailed demonstration.

TABLE 1

Table 1. Summary on three photovoltaic (PV) cell models.

As demonstrated in Table 1, I_L and V_L represent PV cell output current and output voltage, respectively; I_sh means shunt resistor current R_sh; while thermal voltage V_T is defined as

$$V_{\text{T}}=\frac{KT}{\text{q}}(1)$$

where T represents cell temperature; K = 1.38 × 10⁻²³J/K denotes Boltzmann constant; and q = 1.6×10⁻¹⁹C means electron charge, respectively.

Other variables can be referred in Nomenclature.

Objective Function

The main purpose of parameter identification is to find a group of proper parameters that can effectively minimize errors between experimental and simulated data, which can be quantitatively evaluated through objective functions. Here, RMSE is chosen as the objective function, as follows

$$\mathrm{RMSE}(x)=\sqrt{\frac{1}{N}\sum _{k=1}^N{(f(V_{\text{L}},{\text{I}}_{\text{L}},x))}^2}(2)$$

where x represents solution vector which contains the parameters need to be identified and N denotes number of experimental data, respectively.

For a more explicit and comprehensive illustration, the error functions f(V_L,I_L,x) for different PV models are summarized in Table 1.

Based on Table 2, for the sake of minimizing the error between experimental data and simulated data, RMSE(x) needs to be minimized by optimizing solution vector x. Note that objective function value is inversely proportional to the solution quality.

TABLE 2

Table 2. Error functions of three different models.

Grouped Beetle Antennae Search (GBAS) Algorithm

This section presents the main inspiration, and the optimization principle of the proposed GBAS algorithm.

Optimization Mechanism

GBAS algorithm is mainly inspired by the special and efficient food searching mechanism of long-horn beetles that depends on their antennae to sense an odor from food sources. Compared with only one single searching agent based BAS algorithm, GBAS utilizes a searching group that consists many individuals to enlarge the searching extent and ensure more potential high quality solutions can be detected. The whole searching can be divided into two stages, i.e., searching and detecting, while the weights during the two process are adaptively adjusted to avoid local optimums. Thus, a proper trade-off between local exploitation and global exploration can be achieved, upon which the optimization efficiency and accuracy can be greatly achieved, while more details of this algorithm can be referred to literature (Hao et al., 2020) for interested readers.

Design of GBAS for PV Cell Parameter Identification

The detailed optimization structure of GBAS algorithm for PV cell parameter identification is illustrated in this section.

Optimization Variables

As shown in Table 2, optimization variables are different in various equivalent circuit models for PV cell. To achieve an efficient parameter identification of PV cell, optimization variables are limited within their lower and upper bounds, as follows:

$$x_j^{\text{min}}\le x_j\le x_j^{\text{max}},j=1,2,\mathrm{\dots },J(3)$$

where x_j denotes the jth optimization variable; $x_j^{\text{min}}$ and $x_j^{\text{max}}$ represents the lower and upper bounds of the jth optimization variable; while J is the number of optimization variables, respectively.

If a beetle violates constraint (3), its position will be reset randomly within their lower and upper bounds by

$$x_j=x_j^{\text{min}}+r_2\left(x_j^{\text{max}}-x_j^{\text{min}}\right)(4)$$

where r₂ means a random value ranging from 0 to 1.

Parameter Setting

Seven parameters of GBAS algorithm, including C, ω_max, ω_min, d_max, δ_max, t_max, and n, should be carefully set for parameter identification of PV cell. Note that maximum iteration number t_max and population size n are two most important parameters. Generally speaking, a larger t_max or n will increase the probability to acquire optimal solutions with higher quality, but also result in longer computation time. To ensure GBAS can locate a high-quality optimum in a high convergence rate, they are determined via trial-and-error, as tabulated in Table 3.

TABLE 3

Table 3. Parameters of grouped beetle antennae search (GBAS) for parameter identification of photovoltaic (PV) cell.

Application Process

The application process of GBAS algorithm for parameter identification of PV cell is illustrated in Figure 1. Historical data of output voltage and current determined from different PV cells will be regarded as the inputs of GBAS, which is converted into objective function by Eq. (2). Then, according to a specific equivalent circuit model, GBAS can execute optimization procedure based on Table 3. Finally, GBAS output the identified parameters of PV cell.

FIGURE 1

Figure 1. Application process of grouped beetle antennae search (GBAS) for parameter identification of photovoltaic (PV) cell.

Case Studies

In this section, three different kinds of PV models, i.e., SDM, DDM, and TDM are adopted for parameter identification based on GBAS algorithm. For this purpose, a total of 26 pairs of benchmark experimental I-V dataset are utilized for a fair simulation and comparison (Kamali et al., 2016), which are extracted from a 57 mm diameter R.T.C. France solar cell under conditions of G = 1,000 W/m² and T = 33°C (T = 33°C is the cell temperature), as shown in Table 4. This dataset is widely applied to validate algorithms for PV cell parameters identification in prior studies (El-Naggar et al., 2012; Gong and Cai, 2013; Oliva et al., 2017; Yu et al., 2017; Chen et al., 2018). Due to the benchmark I-V dataset used for case studies are only determined under conditions of G = 1,000 W/m² and T = 33°C, thus there is only one single fitted I-V curve.

TABLE 4

Table 4. Benchmark experimental I-V dataset.

GBAS algorithm is in comparison with other seven meta-heuristic algorithms, e.g., PSO (Oliva et al., 2014), ABC (Yang et al., 2019a), WOA (Elazab et al., 2018), BSA (Dasu et al., 2019), MFO (Yu et al., 2018), GWO (Yang et al., 2017), and BAS algorithm. Particularly, their maximum iteration number is designed to be the same, i.e., 50,000, while all approaches are executed in 30 independent runs to acquire statistical results. Besides, population size of each algorithm is designed to be 30, 50, and 70 for SDM, DDM, and TDM, respectively. Note that parameters bounds of different PV cell models is illustrated in Table 5.

TABLE 5

Table 5. Parameters bounds of different photovoltaic (PV) cell models.

In particular, the best simulation results of eight methods are highlighted in bold. All case studies are undertaken by MATLAB 2019a through a personal computer with IntelR CoreTMi7 CPU at 2.0 GHz and 32 GB of RAM.

Results Discussion on SDM

The statistical results acquired by each algorithm for SDM, such as minimum, median, mean, maximum, and standard deviation (SD) of RMSE are demonstrated in Table 4. Note that RMSE can explicitly quantify solution accuracy, while SD of RMSE indicates algorithm reliability. Symbols “+,” “−,” and “=” mean the experimental performance of GBAS algorithm is better than, worse than, or similar to that of its competitors, respectively.

Table 6 explicitly illustrates that simulation results of GBAS algorithm outperform other algorithms in terms of minimum, median, mean, maximum and SD of RMSE, upon which GBAS algorithm is verified to achieve the highest optimization accuracy. Particularly, median and SD values of RMSE obtained by GBAS algorithm are 97.00 and 99.42% lower than that of BAS algorithm, which verifies cooperative group can astonishingly improve searching efficiency and convergence stability of GBAS algorithm. Besides, the proper balance between local exploitation and global exploration can avoid low-quality optimum stagnation.

TABLE 6

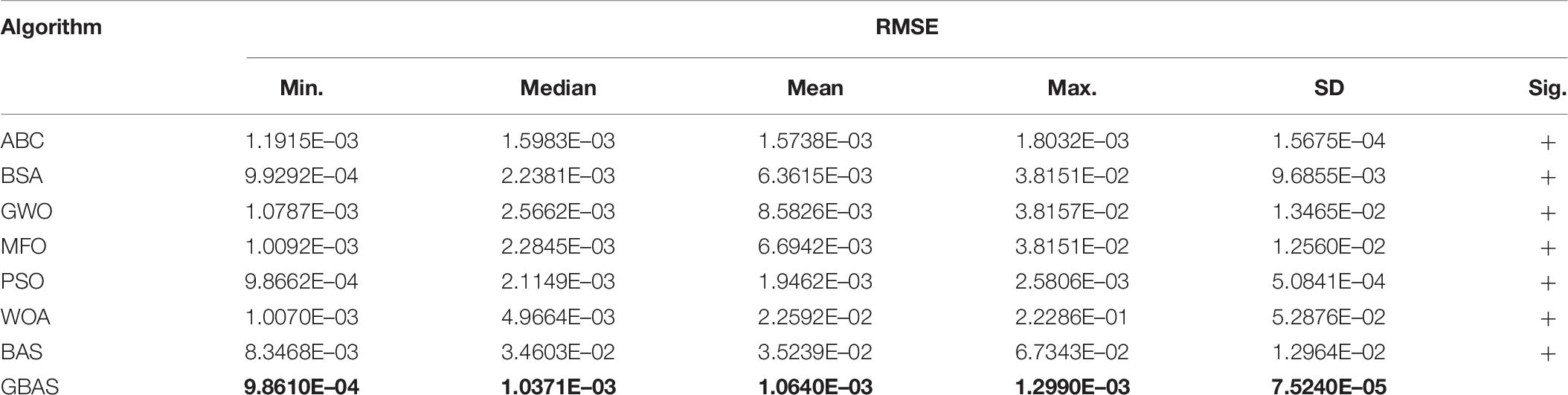
Table 6. Statistical results of root mean square error (RMSE) obtained by various algorithms for single diode model (SDM).

Moreover, optimal parameters identification results obtained by various algorithms, along with their RMSE are presented in Table 7, among which GBAS algorithm can acquire minimum RMSE, followed by PSO, BSA, WOA, MFO, GWO, ABC, and BAS algorithm.

TABLE 7

Table 7. Model parameters identified by various algorithms for single diode model (SDM).

The identification results are shown in Figure 2. The output I-V and P-V curves based on optimal parameters identified by GBAS algorithm are depicted in Figures 2A,B. Obviously, the model curves acquired by GBAS algorithm are highly consistent with actual data, which also reveals its superior performance for PV cell parameter identification.

FIGURE 2

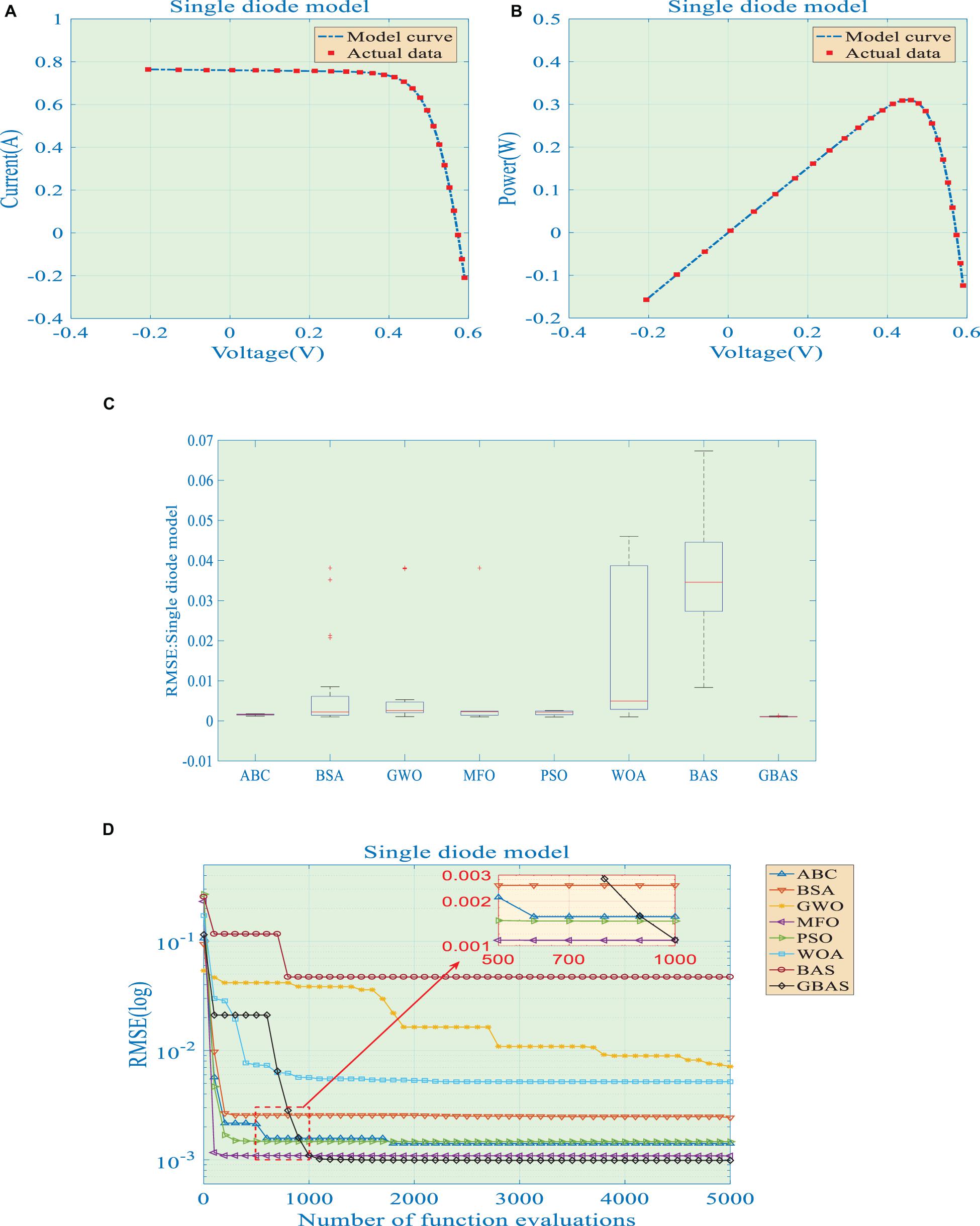
Figure 2. Identification results obtained by grouped beetle antennae search (GBAS) algorithm for SDM: (A) I-V curve; (B) P-V curve; (C) boxplot of RMSE; (D) convergence graph.

Figure 2C presents boxplot of various algorithms for SDM, which demonstrates distribution of simulation results based on various algorithms in 30 runs. One can readily observe that RMSE obtained by GBAS algorithm can distribute within the smallest range with minimal lower and upper bounds among all algorithms. This verifies that GBAS algorithm can simultaneously improve convergence stability and enhance searching ability. Besides, Figure 2D provides convergence graphs of various eight algorithms, among which BSA algorithm is difficult to acquire a high-quality optimal solution based on a single individual based global search. In contrast, GBAS algorithm can gradually find a better solution as it can properly balance local exploitation and global exploration via cooperative group.

Results Discussion on DDM

Statistical results of each algorithm for DDM are tabulated in Table 8, which illustrates that GBAS algorithm can obtain the optimal performance in median, mean, maximum and SD of RMSE. Although MFO can achieve minimum RMSE, minimum RMSE value obtained by MFO is only 0.15% lower than that of GBAS algorithm. Particularly, mean RMSE and SD obtained by GBAS algorithm are 44.13 and 84.51% lower than those obtained by MFO, respectively. Therefore, GBAS algorithm realizes the most desirable performance when both accuracy and reliability are taken into consideration for DDM.

TABLE 8

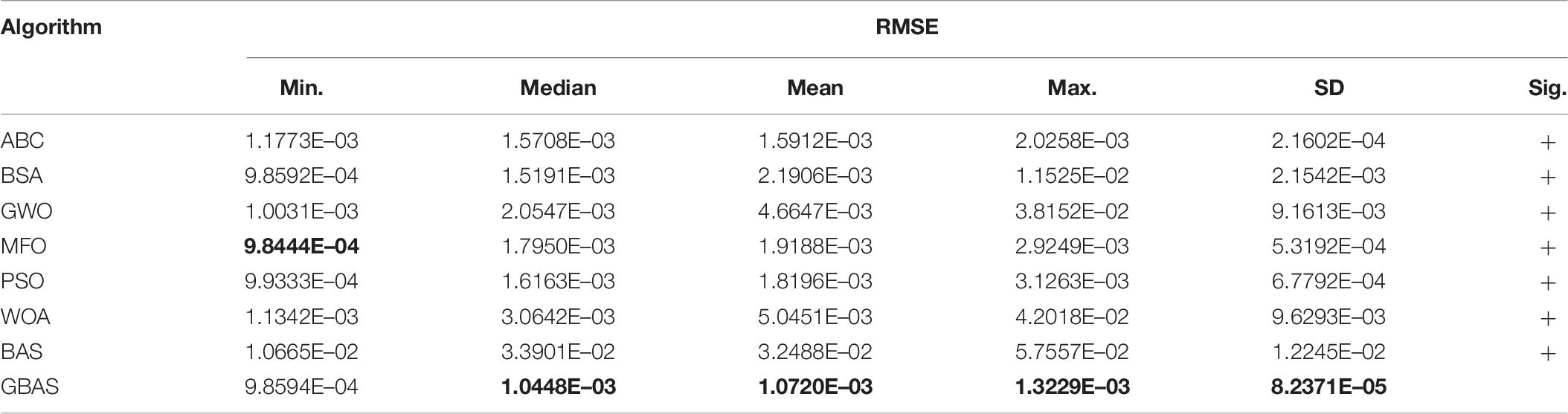
Table 8. Statistical results of root mean square error (RMSE) obtained by various algorithms for double diode model (DDM).

Table 9 illustrates the best model parameters and RMSE obtained by various strategies for DDM. Among which MFO obtains the best RMSE, followed by BSA, GBAS, PSO, GWO, WOA, ABC, and BAS algorithm.

TABLE 9

Table 9. Model parameters identified by various algorithms for double diode model (DDM).

The identification results are shown in Figure 3. Figures 3A,B demonstrate the output I-V and P-V curves acquired by GBAS algorithm and actual data, upon which it can be seen that model curve obtained by GBAS algorithm highly matches actual data. Boxplot of different algorithms is depicted in Figure 3C, upon which one can easily find that RMSE obtained by GBAS algorithm has the smallest distribution range and upper/lower bounds compared with others, which indicates that GBAS algorithm has accurate searching ability in PV parameter identification and stable global searching ability.

FIGURE 3

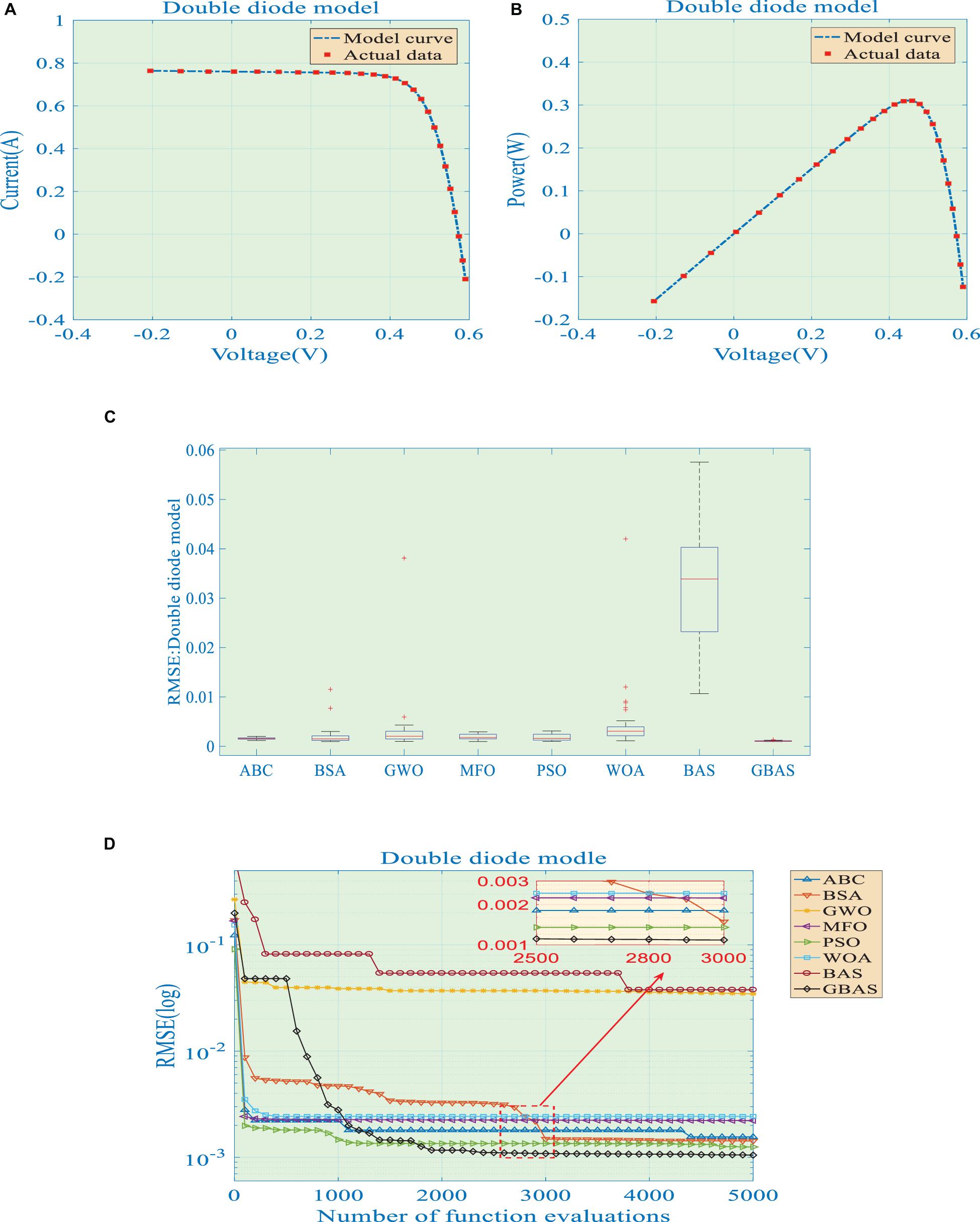
Figure 3. Identification results obtained by grouped beetle antennae search (GBAS) algorithm for double diode model (DDM): (A) I-V curve; (B) P-V curve; (C) boxplot of RMSE; (D) convergence graph.

In particular, Figure 3D provides convergence graphs of all algorithms. The results show that PSO can rapidly obtain an elegant solution in initial stage, but it is easy to produce premature convergence and difficult to find global optimum. In contrast, GBAS algorithm owns a high convergence rate and can avoid local optimum stagnation.

Results Discussion on TDM

For TDM, statistical results of each algorithm are tabulated in Table 10, upon which GBAS algorithm still performs quite satisfactory, which can obtain the best results in median, mean, maximum and SD of RMSE. Although BSA algorithm obtains the minimum RMSE, it performs worse than GBAS in other performance indices. For example, RMSE median and SD obtained by GBAS algorithm are 31.86 and 37.98% lower than those of ABC (second best), respectively. In addition, GBAS algorithm also performs well in the accuracy of PV cell parameter identification. Minimum RMSE obtained by GBAS algorithm is only 0.4% larger than that of BSA algorithm. Hence, GBAS algorithm owns the most satisfactory performance for TDM.

TABLE 10

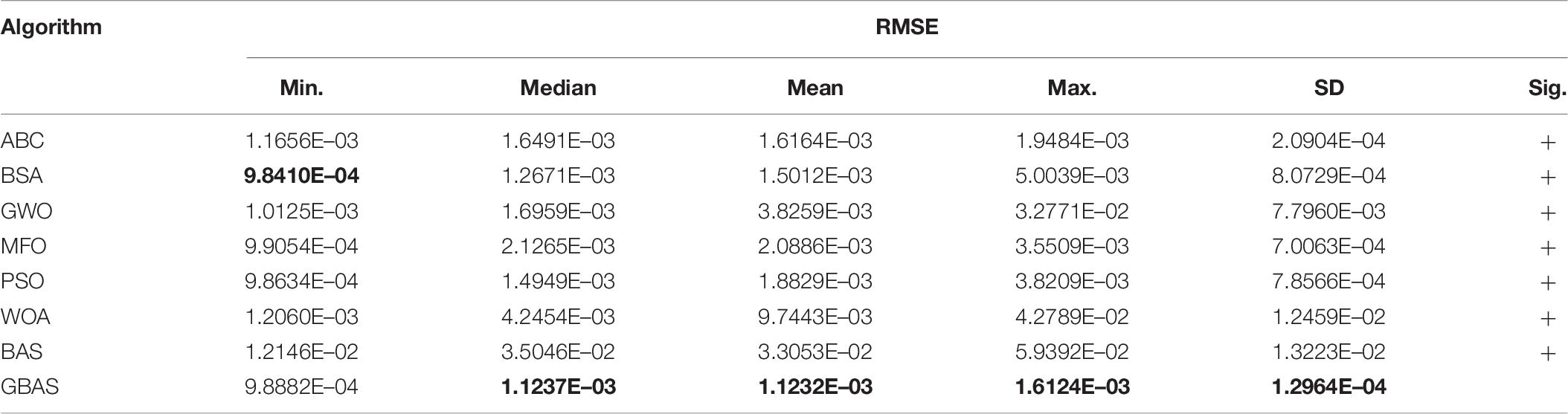
Table 10. Statistical results of root mean square error (RMSE) obtained by various algorithms for triple diode model (TDM).

The best parameters identification results based on various algorithms for TDM is demonstrated in Table 11. Apparently, BSA algorithm achieves the best RMSE, followed by PSO, GBAS algorithm, MFO, GWO, ABC, and BAS.

TABLE 11

Table 11. Model parameters identified by various algorithms for triple diode model (TDM).

The identification results are shown in Figure 4. Figures 4A,B demonstrate the output I-V and P-V curves acquired by GBAS algorithm and actual data, which can efficiently verify the precision of identified PV cell parameters. Figure 4C shows boxplot of different algorithms while. One can observe that GBAS algorithm is highly competitive in solution precision and stability compared with others.

FIGURE 4

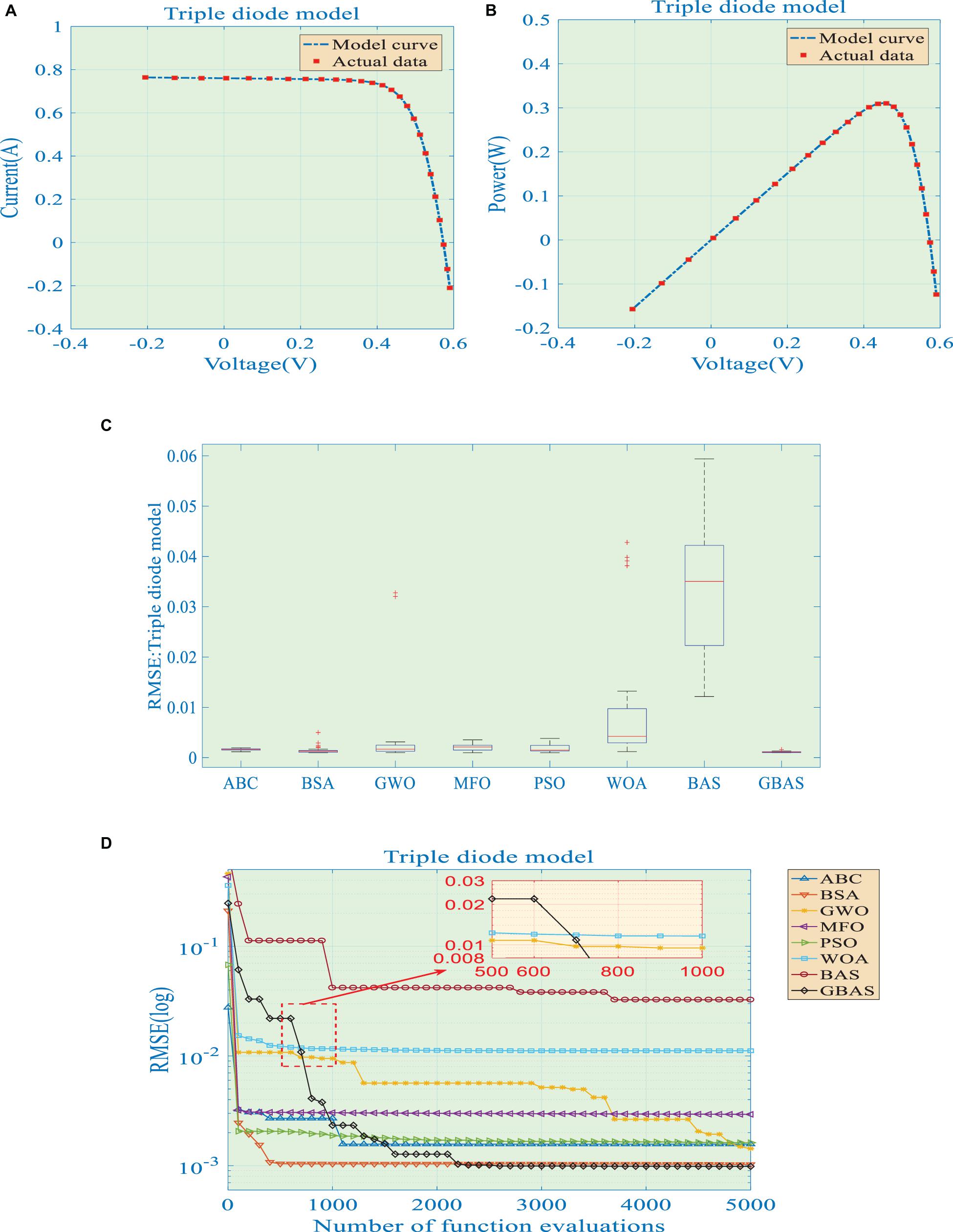
Figure 4. Identification results obtained by grouped beetle antennae search (GBAS) algorithm for triple diode model (TDM): (A) I-V curve; (B) P-V curve; (C) boxplot of RMSE; (D) convergence graph.

At last, Figure 4D provides convergence graphs of all algorithms, which shows that GBAS algorithm can realize a proper trade-off between local exploitation and global exploration to find the best solution. In contrast, others are easily to fall into a local optimum.

Statistical Results and Analysis

Note that SD of RMSE indicates parameter identification reliability, upon which GBAS algorithm can achieve more desirable performance than other competitors for SDM, DDM, and TDM. Moreover, SD of RMSE obtained by GBAS algorithm is much smaller than others for all models, which can effectively verify the outstanding reliability of GBAS algorithm. For example, SD of RMSE obtained by GBAS algorithm is 64.34% smaller than the best value obtained by other algorithms in SDM, 61.86% smaller than that in DDM.

In addition, the distribution of results acquired by various methods over 30 independent runs for SDM, DDM, and TDM are clearly shown in Figures 2–4, respectively. In each model, RMSE obtained by GBAS algorithm has the minimum upper and lower limits and the smallest range. Moreover, solution distribution also illustrates the superior performance of GBAS algorithm. Besides, Figure 5 provides radar charts of various algorithms, while the best ranking is assigned with 8 points and then decreased by 1 point in turn. Note that the marking and ranking basis of different algorithms is based on a comprehensive and overall comparison of their performance in PV cell parameter identification, i.e., optimization accuracy, optimization efficiency, convergence stability, and convergence speed. Based on the radar graphs, it can be explicitly and comprehensively illustrated that GBAS algorithm is much better than other algorithms.

FIGURE 5

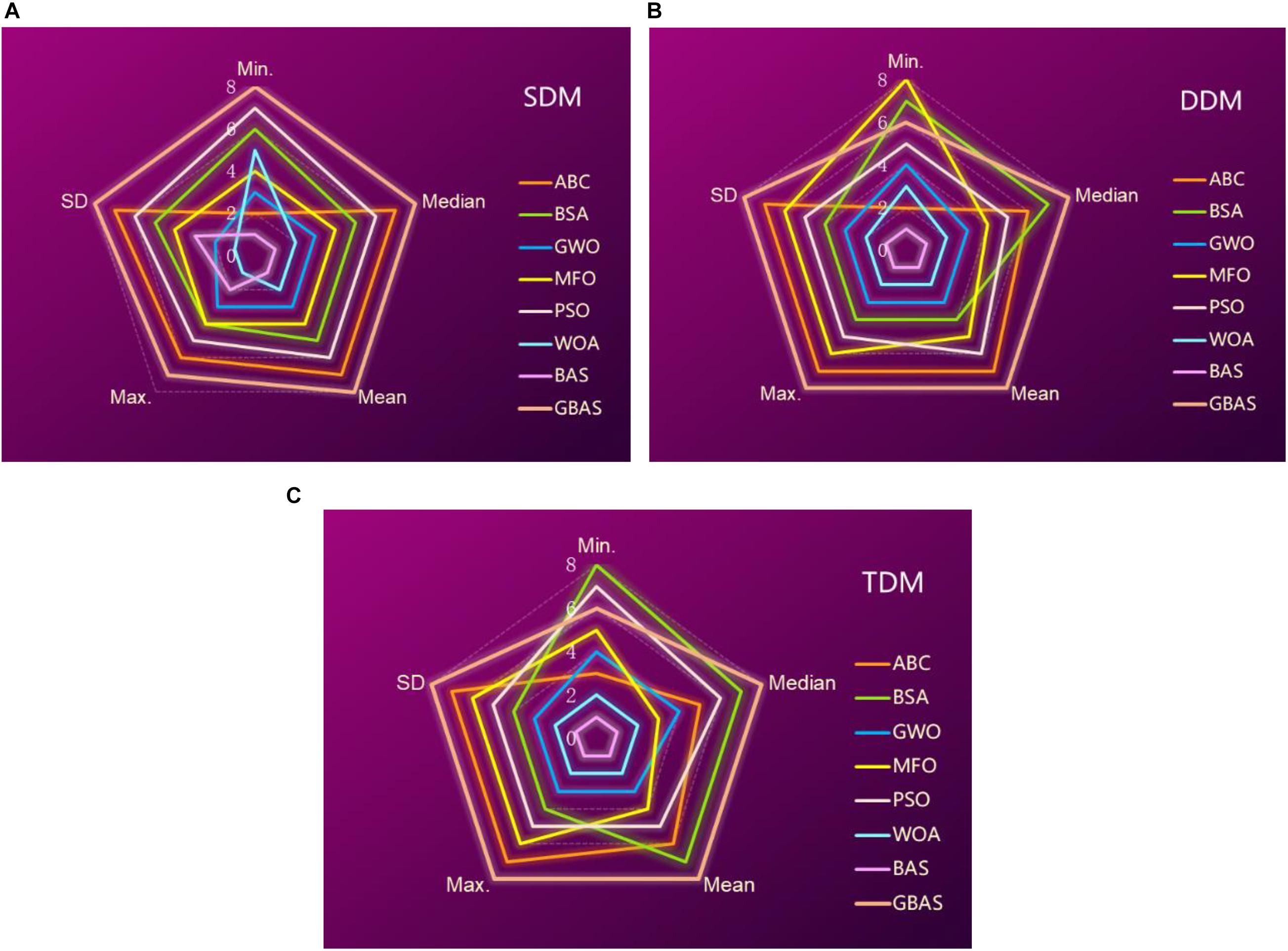
Figure 5. Radar graphs of various algorithms: (A) single diode model (SDM), (B) double diode model (DDM), and (C) triple diode model (TDM).

Conclusion

A powerful bio-inspired GBAS algorithm is adopted in this paper for accurate and efficient parameter estimation of different PV cell diode models, which contains the following three contributions/novelties:

• Compared with BAS algorithm, GBAS algorithm can effectively enhance global optimum searching efficiency via a cooperative group of multiple beetles instead of a single beetle. Besides, it also can acquire a high-quality optimum via a dynamic and proper balance between local exploitation and global exploration;

• GBAS algorithm is utilized in parameter identification of SDM, DDM, and TDM, upon which its effectiveness and feasibility have been validated. The SD of RMSE obtained by GBAS for SDM is 52.00, 99.22, 99.44, 99.40, 85.20, 99.86, and 99.42% lower to that of ABC, BSA, GWO, MFO, PSO, WOA, and BAS, respectively. Besides, under the DDM, the SD of RMSE of GBAS is 61.87, 96.18, 99.10, 84.51, 87.85, 99.14, and 99.33% lower to that of ABC, BSA, GWO, MFO, PSO, WOA, and BAS, respectively;

• Case studies demonstrate that GBAS algorithm can effectively enhance optimization accuracy and stability compared with other meta-heuristic algorithms.

Future researches on the proposed algorithm can mainly focus on optimization accuracy and convergence speed enhancement due to these two indices of the proposed GBAS algorithm still can be further improved. Based on this, GBAS can be verified for on-line parameter estimation to validate its practical response speed and optimization ability, which is quite useful and necessary in practical engineering applications.

It is noteworthy that the PV cell parameters provided by manufacturers or experiments are usually tested under STC, while the practical operation conditions can barely maintain at STC. Hence, for the sake of verifying the practical performance of the proposed GBAS, the experiments require to be carried out under various operation conditions. Besides, GBAS can also be combined with corresponding reliable control strategies to achieve reliable PV cell fault diagnosis, which can considerably enhance operation stability and reliability of PV systems.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

LS: conceptualization, writing – review and editing, and validation. JW: writing – original draft, formal analysis, data curation, and visualization. LT: methodology, software, and supervision. All authors contributed to the article and approved the submitted version.

Conflict of Interest

LS was employed by company Guangzhou Shuimuqinghua Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abbassi, R., Abbassi, A., Jemli, M., and Chebbi, S. (2018). Identification of unknown parameters of solar cell models: a comprehensive overview of available approaches. Renew. Sustain. Energy Rev. 90, 453–474. doi: 10.1016/j.rser.2018.03.011

CrossRef Full Text | Google Scholar

Alam, D. F., Yousri, D. A., and Eteiba, M. B. (2015). Flower pollination algorithm based solar PV parameter estimation. Energy Convers. Manag. 101, 410–422. doi: 10.1016/j.enconman.2015.05.074

CrossRef Full Text | Google Scholar

Allam, D., Yousri, D. A., and Eteiba, M. B. (2016). Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame optimization algorithm. Energy Convers. Manag. 123, 535–548. doi: 10.1016/j.enconman.2016.06.052

CrossRef Full Text | Google Scholar

Askarzadeh, A., and Rezazadeh, A. (2012). Parameter identification for solar cell models using harmony search-based algorithms. Solar Energy 86, 3241–3249. doi: 10.1016/j.solener.2012.08.018

CrossRef Full Text | Google Scholar

Askarzadeh, A., and Rezazadeh, A. (2013). Extraction of maximum power point in solar cells using bird mating optimizer-based parameters identification approach. Solar Energy 90, 123–133. doi: 10.1016/j.solener.2013.01.010

CrossRef Full Text | Google Scholar

Barukčić, M., Ćorluka, V., and Mikloševic, K. (2015). The irradiance and temperature dependent mathematical model for estimation of photovoltaic panel performances. Energy Convers. Manag. 101, 229–238. doi: 10.1016/j.enconman.2015.05.027

CrossRef Full Text | Google Scholar

Batzelis, E. I., and Papathanassiou, S. A. (2016). A method for the analytical extraction of the single-diode PV model parameters. IEEE Trans. Sustain. Energy 7, 504–512. doi: 10.1109/tste.2015.2503435

CrossRef Full Text | Google Scholar

Chaibi, Y., Allouhi, A., Salhi, M., and El-jouni, A. (2019). Annual performance analysis of different maximum power point tracking techniques used in photovoltaic systems. Prot. Control Mod. Power Syst. 4, 171–180.

Google Scholar

Chan, D. S. H., and Phang, J. C. H. (1987). Analytical methods for the extraction of solar-cell single- and double-diode model parameters from I-V characteristics. IEEE Trans. Electr. Dev. 34, 286–293. doi: 10.1109/t-ed.1987.22920

CrossRef Full Text | Google Scholar

Chen, X., Xu, B., Mei, C. L., Ding, Y. H., and Li, K. J. (2018). Teaching-learning-based artificial bee colony for solar photovoltaic parameter estimation. Appl. Energy 212, 1578–1588. doi: 10.1016/j.apenergy.2017.12.115

CrossRef Full Text | Google Scholar

Chen, X., and Yu, K. J. (2019). Hybridizing cuckoo search algorithm with biogeography-based optimization for estimating photovoltaic model parameters. Solar Energy 180, 192–206. doi: 10.1016/j.solener.2019.01.025

CrossRef Full Text | Google Scholar

Chin, V. J., Salam, Z., and Ishaque, K. (2015). Cell modelling and model parameters estimation techniques for photovoltaic simulator application: a review. Appl. Energy 154, 500–519. doi: 10.1016/j.apenergy.2015.05.035

CrossRef Full Text | Google Scholar

Dasu, B., Sivakumar, M., and Srinivasarao, R. (2019). Interconnected multi-machine power system stabilizer design using whale optimization algorithm. Prot. Control Mod. Power Syst. 4, 13–23.

Google Scholar

Easwarakhanthan, T., Bottin, J., Bouhouch, I., and Boutrit, C. (1986). Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Solar Energy 4, 1–12. doi: 10.1080/01425918608909835

CrossRef Full Text | Google Scholar

Elazab, O. S., Hasanien, H. M., Elgendy, M. A., and Abdeen, A. M. (2018). Parameters estimation of single- and multiple-diode photovoltaic model using whale optimisation algorithm. IET Renew. Power Gener. 12, 1755–1761. doi: 10.1049/iet-rpg.2018.5317

CrossRef Full Text | Google Scholar

El-Naggar, K. M., AlRashidi, M. R., AlHajri, M. F., and Al-Othman, A. K. (2012). Simulated annealing algorithm for photovoltaic parameters identification. Solar Energy 86, 266–274. doi: 10.1016/j.solener.2011.09.032

CrossRef Full Text | Google Scholar

Gomes, R. C. M., Vitorino, M. A., Correa, M. B. R., Fernandes, D. A., and Wang, R. X. (2017). Shuffled complex evolution on photovoltaic parameter extraction: a comparative analysis. IEEE Trans. Sustain. Energy 8, 805–815. doi: 10.1109/tste.2016.2620941

CrossRef Full Text | Google Scholar

Gong, W. Y., and Cai, Z. H. (2013). Parameter extraction of solar cell models using repaired adaptive differential evolution. Solar Energy 94, 209–220. doi: 10.1016/j.solener.2013.05.007

CrossRef Full Text | Google Scholar

Hao, J. F., Huang, J. H., Zhang, A. L., Ai, H. J., Zhang, Q., and Yang, B. (2020). Correction: optimal coordinated control of hybrid AC/VSC-HVDC system integrated with DFIG via cooperative beetle antennae search algorithm. PLoS One 15:e0244757. doi: 10.1371/journal.pone.0242316

PubMed Abstract | CrossRef Full Text | Google Scholar

He, X., Ai, Q., Qiu, R. C. M., Huang, W. T., Piao, L. J., and Liu, H. C. (2017). A big data architecture design for smart grids based on random matrix theory. IEEE Trans. Smart Grid 8, 674–686.

Google Scholar

Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar cell parameters extraction based on single and double-diode models: a review. Renew. Sustain. Energy Rev. 56, 494–509. doi: 10.1016/j.rser.2015.11.051

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2011). An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Solar Energy 85, 2349–2359. doi: 10.1016/j.solener.2011.06.025

CrossRef Full Text | Google Scholar

Ishaque, K., Salam, Z., Taheri, H., and Shamsudin, A. (2011). A critical evaluation of EA computational methods for photovoltaic cell parameter extraction based on two diode model. Solar Energy 85, 1768–1779. doi: 10.1016/j.solener.2011.04.015

CrossRef Full Text | Google Scholar

Jervase, J. A., Bourdoucen, H., and Al-lawati, A. M. (2001). Solar cell parameter extraction using genetic algorithms. Meas. Sci. Technol. 12, 1922–1925. doi: 10.1088/0957-0233/12/11/322

CrossRef Full Text | Google Scholar

Jiang, X. Y., and Li, S. B. A. S. (2018). Beetle antennae search algorithm for optimization problems. Int. J. Robot. Control 1, 1–5. doi: 10.5430/ijrc.v1n1p1

CrossRef Full Text | Google Scholar

Kamali, S. K., Rahim, N. A., Mokhlis, H., and Tyagi, V. V. (2016). Photovoltaic electricity generator dynamic modeling methods for smart grid applications: a review. Renew. Sustain. Energy Rev. 57, 131–172. doi: 10.1016/j.rser.2015.12.137

CrossRef Full Text | Google Scholar

Khanna, V., Das, B. K., Bisht, D., Vandana, P., and Singh, P. K. (2015). A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 78, 105–113. doi: 10.1016/j.renene.2014.12.072

CrossRef Full Text | Google Scholar

Li, G. D., Li, G. Y., and Zhou, M. (2019). Model and application of renewable energy accommodation capacity calculation considering utilization level of interprovincial tie-line. Prot. Control Mod. Power Syst. 4, 1–12.

Google Scholar

Li, W., Paul, M. C., Rolley, M., Sweet, T., Gao, M., Siviter, J., et al. (2017). A scaling law for monocrystalline PV/T modules with CCPC and comparison with triple junction PV cells. Appl. Energy 202, 755–771. doi: 10.1016/j.apenergy.2017.05.182

CrossRef Full Text | Google Scholar

Mahdavi, S., Shiri, M. E., and Rahnamayan, S. (2015). Metaheuristics in large-scale global continues optimization: a survey. Inf. Sci. 295, 407–428. doi: 10.1016/j.ins.2014.10.042

CrossRef Full Text | Google Scholar

Mostafa, M., Rezk, H., Aly, M., and Ahmed, E. M. (2020). A new strategy based on slime mould algorithm to extract the optimal model parameters of solar PV panel. Sustain. Energy Technol. Assess. 42:100849. doi: 10.1016/j.seta.2020.100849

CrossRef Full Text | Google Scholar

Muangkote, N., Sunat, K., Chiewchanwattana, S., and Kaiwinit, S. (2019). An advanced onlooker-ranking-based adaptive differential evolution to extract the parameters of solar cell models. Renew. Energy 134, 1129–1147. doi: 10.1016/j.renene.2018.09.017

CrossRef Full Text | Google Scholar

Nayak, B., Mohapatra, A., and Mohanty, K. B. (2019). Parameter estimation of single diode PV module based on GWO algorithm. Renew. Energy Focus 30, 1–12. doi: 10.1016/j.ref.2019.04.003

CrossRef Full Text | Google Scholar

Niu, Q., Zhang, L., and Li, K. (2014). A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells. Energy Convers. Manag. 86, 1173–1185. doi: 10.1016/j.enconman.2014.06.026

CrossRef Full Text | Google Scholar

Nunes, H. G. G., Silva, P. N. C., Pombo, J. A. N., Mariano, S. J. P. S., and Calado, M. R. A. (2020). Multiswarm spiral leader particle swarm optimisation algorithm for PV parameter identification. Energy Convers. Manag. 225:113388. doi: 10.1016/j.enconman.2020.113388

CrossRef Full Text | Google Scholar

Oliva, D., Cuevas, E., and Pajares, G. (2014). Parameter identification of solar cells using artificial bee colony optimization. Eenergy 72, 93–102. doi: 10.1016/j.energy.2014.05.011

CrossRef Full Text | Google Scholar

Oliva, D., Elaziz, M. A., and Hassanien, A. (2017). Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 200, 141–154. doi: 10.1016/j.apenergy.2017.05.029

CrossRef Full Text | Google Scholar

Peng, X. T., Yao, W., Yan, C., Wen, J. Y., and Cheng, S. J. (2020). Two-stage variable proportion coefficient based frequency support of grid-connected DFIG-WTs. IEEE Trans. Power Syst. 35, 962–974. doi: 10.1109/tpwrs.2019.2943520

CrossRef Full Text | Google Scholar

Ram, J. P., Manghani, H., Pillai, D. S., Babu, T. S., Miyatake, M., and Rajasekara, N. (2018). Analysis on solar PV emulators: a review. Renew. Sustain. Energy Rev. 81, 149–160. doi: 10.1016/j.rser.2017.07.039

CrossRef Full Text | Google Scholar

Roeva, O., and Fidanova, S. (2018). Comparison of different metaheuristic algorithms based on intercriteria analysis. J. Comput. Appl. Math. 340, 615–628. doi: 10.1016/j.cam.2017.07.028

CrossRef Full Text | Google Scholar

Saleem, H., and Karmalkar, S. (2009). An analytical method to extract the physical parameters of a solar cell from four points on the illuminated J-V curve. IEEE Electron Dev. Lett. 30, 349–352. doi: 10.1109/led.2009.2013882

CrossRef Full Text | Google Scholar

Shang, L. Q., Zhu, W. W., Li, P. W., and Guo, H. C. (2018). Maximum power point tracking of PV system under partial shading conditions through flower pollination algorithm. Prot. Control Mod. Power Syst. 3, 400–406.

Google Scholar

Song, D. R., Fan, X. Y., Yang, J., Liu, A. F., Chen, S. F., and Joo, Y. H. (2018). Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method. Appl. Energy 224, 267–279. doi: 10.1016/j.apenergy.2018.04.114

CrossRef Full Text | Google Scholar

Song, D. R., Zheng, S. Y., Yang, S., Yang, J., Dong, M., Su, M., et al. (2020). Annual energy production estimation for variable-speed wind turbines at high-altitude sites. J. Mod. Power Syst. Clean Energy doi: 10.35833/MPCE.2019.000240

CrossRef Full Text | Google Scholar

Sun, K., Yao, W., Fang, J. K., Ai, X. M., Wen, J. Y., and Cheng, S. J. (2020). Impedance modeling and stability analysis of grid-connected DFIG-based wind farm with a VSC-HVDC. IEEE J. Emerg. Sel. Top. Power Electron. 8, 1375–1390. doi: 10.1109/jestpe.2019.2901747

CrossRef Full Text | Google Scholar

Villalva, M. G., Gazoli, J. R., and Filho, E. R. (2009). Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electr. 24, 1198–1208. doi: 10.1109/tpel.2009.2013862

CrossRef Full Text | Google Scholar

Wolf, P., and Benda, V. (2013). Identification of PV solar cells and modules parameters by combining statistical and analytical methods. Solar Energy 93, 151–157. doi: 10.1016/j.solener.2013.03.018

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear maximum power point tracking control and model analysis of DFIG based wind turbine. Int. J. Electr. Power Energy Syst. 74, 429–436. doi: 10.1016/j.ijepes.2015.07.036

CrossRef Full Text | Google Scholar

Yang, B., Wang, J. B., Zhang, X. S., Yu, T., Yao, W., Shu, H. C., et al. (2020). Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 208:112595. doi: 10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H. C., Dong, J., and Jiang, L. (2018a). Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 210, 711–723. doi: 10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H. C., Zhang, Y. M., Chen, J., Sang, Y. Y., et al. (2018b). Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 119, 577–589. doi: 10.1016/j.renene.2017.12.047

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X. S., Li, H. F., Shu, H. C., Sang, Y. Y., et al. (2019a). Dynamic leader based collective intelligence for maximum power point tracking of PV systems affected by partial shading condition. Energy Convers. Manag. 179, 286–303. doi: 10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zhang, X. S., Yu, T., Shu, H. C., and Fang, Z. H. (2017). Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Energy Convers. Manag. 133, 427–443. doi: 10.1016/j.enconman.2016.10.062

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L. E., Yu, T., Li, H. F., Zhang, X. S., Shu, H. C., et al. (2019b). Novel bio-inspired memetic salp swarm algorithm and application to MPPT for PV systems considering partial shading condition. J. Clean. Prod. 215, 1203–1222. doi: 10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Ye, M. Y., Wang, X. D., and Xu, Y. S. (2009). Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 105, 094502–094502-8.

Google Scholar

Youssef, A., El-Telbany, M., and Zekry, A. (2017). The role of artificial intelligence in photo-voltaic systems design and control: a review. Renew. Sustain. Energy Rev. 78, 72–79. doi: 10.1016/j.rser.2017.04.046

CrossRef Full Text | Google Scholar

Yu, K. J., Liang, J. J., Qu, B. Y., Chen, X., and Wang, H. S. (2017). Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 150, 742–753. doi: 10.1016/j.enconman.2017.08.063

CrossRef Full Text | Google Scholar

Yu, K. J., Liang, J. J., Qu, B. Y., Cheng, Z. P., and Wang, H. S. (2018). Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. Energy 226, 408–422. doi: 10.1016/j.apenergy.2018.06.010

CrossRef Full Text | Google Scholar

Zagrouba, M., Sellami, A., Bouaïcha, M., and Ksouri, M. (2010). Identification of PV solar cells and modules parameters using the genetic algorithms: application to maximum power extraction. Solar Energy 84, 860–866. doi: 10.1016/j.solener.2010.02.012

CrossRef Full Text | Google Scholar

Zhang, H. X., Lu, Z. X., Hu, W., Wang, Y. T., Dong, L., and Zhang, J. T. (2019). Coordinated optimal operation of hydro-wind-solar integrated systems. Appl. Energy 242, 883–896. doi: 10.1016/j.apenergy.2019.03.064

CrossRef Full Text | Google Scholar

Zhang, X. S., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive distributed auction-based algorithm for optimal mileage based AGC dispatch with high participation of renewable energy. Int. J. Elect. Power Energy Syst. 124:106371. doi: 10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhang, X. S., Xu, Z., Yu, T., Yang, B., and Wang, H. (2020). Optimal mileage based AGC dispatch of a GenCo. IEEE Trans. Power Syst. 35, 2516–2526. doi: 10.1109/tpwrs.2020.2966509

CrossRef Full Text | Google Scholar

Nomenclature