- 1CNOOC Energy Technology & Services Limited, CNOOC EnerTech. Drilling and Production Co., Tianjin, China
- 2Zhanjiang Branch of CNOOC Ltd., Zhanjiang, China
- 3School of Urban Planning and Municipal Engineering, Xi'an Polytechnic University, Xi'an, China
- 4State Key Laboratory of Multiphase Flow in Power Engineering, Xi'an Jiaotong University, Xi'an, China
Fundamental understandings of nanoconfined methane (CH4) are crucial to improving the exploitation of tight gas. In this study, diffusivity, one of the key transport properties of high-temperature and high-pressure methane gas, is examined under confinement in the silica nanochannels by using molecular dynamics simulations by employing Einstein diffusion equation. It was found that the diffusivity of nanoconfined methane is obviously anisotropic, namely, the perpendicular diffusion coefficient is lower than that in the longitudinal direction. The anisotropic diffusivity of nanoconfined methane is attributed to the restricted effect of potential interactions from the atoms of walls, which is verified by analyzing the diffusivity of methane molecules in the potential wells with Lagrangian dynamics. The diffusion coefficients of nanoconfined methane decrease with the increase of atomic potentials in the wall, which can be explained by the density distributions of methane in the nanochannels. Furthermore, we reveal the dependence of the diffusivity of nanoconfined methane on the channel height and confining effect of the wall on the diffusivity of methane molecules. The obtained results can provide a molecular insight into the transport properties of methane confined in nanospace and a theoretical guidance for the efficient extraction of tight gas.
Introduction
Natural gas is a high-quality, efficient, green, and clean energy, which occupies an important position in the world's energy consumption. At present, however, the proportion of natural gas in the energy structure of many countries, such as China, is much lower than the world's average level. Therefore, the development and utilization of natural gas is a major policy to build a safe, efficient, clean, and low-carbon energy system for those countries. In recent years, along with the additional exploratory development of natural gas, a large number of tight gas reservoirs (Zou et al., 2009) have been discovered all around the world. It can be predicted that the exploitation of these unconventional gas reservoirs will continue to increase in the future. As a result, its extraction technology needs to be urgently improved. The existing data have indicated that there are a large number of pores in nanoscale in tight gas and shale gas reservoirs (Chalmers and Bustin, 2008; Curtis et al., 2012; Wang et al., 2014), meaning that the natural gas is confined in these nanoscale pores of the rocks. The transport properties of nanoconfined fluid (Sun et al., 2020) could present utterly different characteristics, compared with the bulk fluid because the specific surface area of the wall in the nanospace increases sharply, compared with the macrospace, and no longer have a neglected effect on the transport properties (Zhao et al., 2020a,b,c). Hence, it is necessary to study the transport characteristics of nanoconfined natural gas to improve the exploitation of unconventional gas reservoirs.
Diffusion is one of the important transport properties of fluids and also reflects the performance of mass transfer. Diffusion of nanoconfined fluids is closely related to applications, such as membrane separation (Cohen-Tanugi and Grossman, 2012; Wang et al., 2017), biomedicine (Ziemys et al., 2009; Dorfman et al., 2014), oil and gas extraction (Liu et al., 2018, 2020; Zhang et al., 2020), electrochemistry (Martí et al., 2006), and so on (Sokhan et al., 2004; Kim et al., 2013; Zaragoza et al., 2019), and has been widely studied in the past few years. Liu et al. (2004) studied the diffusion behavior and density distribution of argon in nanotube and found that the pore width directly affected the diffusion behavior and density distribution of argon. In the following year, they (Liu et al., 2005) analyzed the diffusion behavior of water in carbon nanotubes and concluded that the radial diffusion coefficient of confined water was lower than that in axial direction. Sofos et al. (2009) found the heterogeneity of the fluid diffusion coefficient by studying the diffusion properties of liquid argon in the Krypton nanochannels, that is, the diffusion coefficient near the wall was lower than that in the central region of the channels. Moulod and Hwang (2016) studied the self-diffusivity of water in graphene nanochannels, using the molecular dynamics (MD) method, and found that the diffusion coefficient of water in nanochannels at a certain height decreased linearly with the increase of the interatomic potential between graphene walls and water molecules. Pan et al. (2020) investigated the nanoconfined water dynamics in multilayer graphene nanopores and found that the water diffusion coefficient was close to the bulk value when the multilayer graphene nanopore diameter was larger than the critical nanopore diameter. Some studies on the diffusivity of nanoconfined methane (CH4) have been conducted as well. For example, Jiang et al. (2017) studied the transport properties, including diffusion coefficient and structural properties of dense methane flowing in a rough silicon nanochannel by using non-equilibrium multiscale MD simulation and found that the diffusion coefficients decreased with the increase of the strength of hydrophilic interaction in the near walls where the diffusion coefficients were lower than these in the central part of the nanochannel. They (Jiang et al., 2020) also analyzed the relationship between nanochannel width and mass transfer characteristics for dense methane nanofluidics, and concluded that the diffusion coefficients increased with the increase of nanochannel width and approached 80% of bulk value when the nanochannel width was 20 times the diameter of methane molecules. Overall, the existing studies on the diffusion behavior of nanoconfined liquid have found special phenomena such as anisotropy and size-dependence, but the corresponding mechanics has not been fully revealed. In addition, most of the studies only focused on the nanoconfined methane with normal temperature and pressure conditions, and there are very few reports on the diffusivity of high-temperature and high-pressure CH4 confined in the nanochannels.
Some studies on the diffusivity of nanoconfined methane, a major component of natural gas, have been conducted up to now (Sharma et al., 2015; Sui et al., 2015). However, most of the studies only focused on normal temperature and pressure conditions, and there are few reports on the diffusivity of high-temperature and high-pressure CH4 confined in the nanochannels. As we all know, natural gas is naturally deposited in the rock deep underground such that the untapped natural gas is in the state of high temperature and high pressure. The high temperature of deep reservoirs is attributed to the huge geothermal energy and chemical heat release, while the high pressure is formed because the tight gas exists in the rock underground. By definition, the temperature and the pressure of the deep gas reservoirs are exceeding 140°C and 40 MPa (di Primio and Neumann, 2008; Fang et al., 2015), respectively. Therefore, the studies on the diffusivity of high-temperature and high-pressure CH4 confined in the nanochannels would play a significant role in the improvement of the extraction technology of natural gas. In this paper, the focus is to study the diffusivity of high-temperature and high-pressure CH4 confined in silicon dioxide (SiO2) nanochannels by using the MD simulations and expound the corresponding physical mechanics from the molecular scale. It is expected that the results can provide theoretical guidance for the extraction of tight gas.
Simulation Methods
The MD simulations are performed in a sandwich system, where CH4 molecules are confined between two parallel SiO2 sheets added with the hydroxyl (–OH) groups, as shown in Figure 1A, to study the diffusivity of nanoconfined CH4. For the simulation model, the longitudinal direction, which is parallel to the silica sheets, refers to x- and y-directions, while the perpendicular direction, which is normal to the silica sheets, refers to z-direction. The length (Lx) and width (Ly) of the simulation system are fixed, which are 5.31 and 4.93 nm, respectively, while the spacing distance of the two SiO2 sheets is flexible and varied from 1.5 to 27.2 nm. The density of -OH groups is 9.52 nm−2, being consistent with the real conditions (Skelton et al., 2011; Liu et al., 2012; Sun et al., 2016). In order to truly reflect the high-temperature and high-pressure condition of CH4 confined in rock strata, the pressure and the temperature of CH4 in all simulations are 40 MPa and 413.15 K (140°C). For this condition, the state of methane is gas, and the corresponding density is 169.17 kg m−3 (Thermophysical Properties of Fluid Systems, 2009) (the number density is 0.102 nm−3). It is important to be noted that the anisotropic pressure of fluid in the nanopore has been found (Eslami and Müller-Plathe, 2011; Eslami and Mehdipour, 2012). Nevertheless, in this work, the reported pressure is the average pressure.
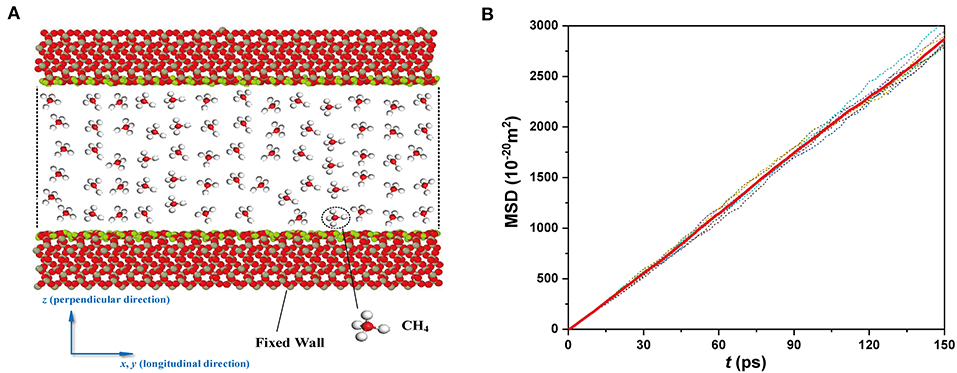
Figure 1. (A) Simulation system of CH4 confined in a nanochannel. The wall has the size of Lx = 5.31 nm and Ly = 4.93 nm. (B) The convergence curve of the MSD.
In the MD simulations, the atomic interactions are modeled by the 12-6 Lennard-Jones (LJ) potential model, coupling with long-range Coulomb interaction, as follows:
where εij and σij are the energy parameter and scale parameter in the LJ potential model, uij and rij, as well as qi and qj, are the interaction energy, distance, and the electrical charge between particles i and j. The CLAYFF force field is chosen to describe the silica nanochannel (Cygan et al., 2004; Zhou et al., 2021). The cut-off distance of LJ interactions 10 Å is used, and the long-range electrostatic interactions are computed by the particle–particle particle–mesh (PPPM) method. LJ potential energy parameters and atomic charge values of SiO2, –OH, and CH4 molecules are shown in Table 1. The interatomic potential energy parameters are calculated by Berthelot–Lorentz mixing rule.
The Einstein diffusion equation is employed to calculate the diffusion coefficient. According to the Einstein diffusion equation, diffusion coefficient is proportional to the mean square displacement (MSD), as follows:
where D is the diffusion coefficient, r is the position vector, t is the time, and d is the dimensionality of the system.
The MD simulations are performed on the platform of LAMMPS (Plimpton, 1995) with the NVT ensemble. A Nosè–Hoover thermostat is used to maintain the temperature. Periodic boundary conditions are applied in the longitudinal direction (x- and y-directions). The SiO2 sheets are fixed, but the -OH groups are flexible during the simulations. In the MD simulations, the time step is set to be 1 fs, and the first 500,000 steps (0.5 ns) are performed to relax and equilibrate the system. Then another 200,000 steps are used to calculate the diffusion coefficient with a sample time of 20 fs. We further calculate the MSD with the sample time of 5 and 10 fs in nanochannel with H = 4.74 nm. The consistent results with smaller sample times demonstrate the validity of the integration step of 20 fs chosen in this work. The CH4 molecules are initialized from a random distribution. The final MSD (see the solid line in Figure 1B) is obtained based on the average of five independent runs (see the dot line in Figure 1B). The diffusion coefficient is obtained by the final MSD, using the Einstein diffusion equation.
Results and Discussions
Anisotropic Diffusivity
Firstly, we investigated the directional correlation characteristics of the diffusivity of CH4 confined in the SiO2 nanochannels. Figure 2 displays the variations of MSD with time in all three directions in a channel height of 4.74 nm. It can be clearly seen that the slopes of MSD in x- and y-directions are almost the same but obviously higher than that in z-direction. Therefore, it is concluded that, according to the Einstein diffusion equation, the diffusion coefficient of confined CH4 in longitudinal directions is larger than the diffusion coefficient in the perpendicular direction. In other words, the diffusivity of nanoconfined CH4 is anisotropic. We should recognize that the unique diffusive behavior of nanoconfined fluids compared with the bulk fluids is all attributed to the additional effects of the wall on the fluid molecules. There are two different effects of walls on the diffusion of nanoconfined fluids: one is the wall interactions; the other is the confining effect of the wall. All of these two effects could inhibit the mobility of CH4 molecules in the perpendicular direction. Thus, we will discuss these two effects on the diffusion of high-temperature and high-pressure CH4 confined in the SiO2 nanochannels in detail in the following section.
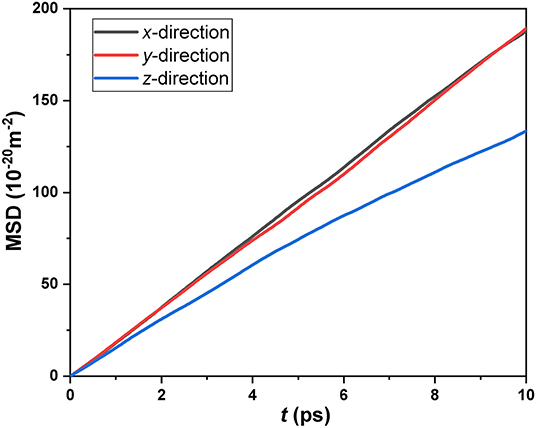
Figure 2. Mean square displacements of confined CH4 in the x-, y-, and z-directions for the channel height H = 4.74 nm.
Effect of Wall Interaction
Restrictions on Methane Diffusion
In the nanochannels, a large number of fluid molecules are within the action range of atomic interaction of the wall, which would have a non-negligible influence on the thermal motion of fluid molecules. The main interactions between the atoms in the walls and CH4 molecules are van der Waals force (detailed analysis—see Section Effect of Atomic Potentials in the Wall), which is the function of the distance between the atoms. Therefore, the movement of fluid molecules in the longitudinal directions is barely affected by the wall interaction because of the symmetric structure of the wall in the xy-plane, and the fluid molecules can move freely. However, the total interactions exerted on the fluid molecules by the walls are not balanced, except in the center of channels, while is the function of coordinate in z-direction, resulting in the inhomogeneous distributions of CH4 molecules, especially in the near-wall region due to the strong adsorption wall interactions. We call the two near-wall regions accumulating a vast of CH4 molecules as potential wells, as shown in Figure 3. The trap of CH4 molecules in the potential wall not only leads to the higher density but also the lower diffusion coefficient than the bulk fluid, meaning that the effect of wall interaction plays an important role in the anisotropic diffusivity of nanoconfined CH4.
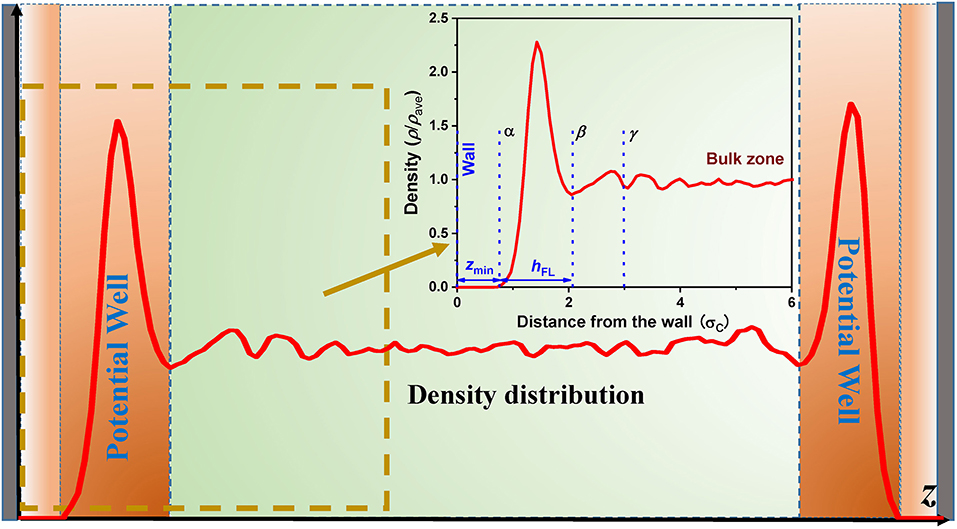
Figure 3. Schematic illustration of the density profiles in the nanochannel. The inserted figure is the enlarged view of the density profile near the wall, where the bulk density is 169.17 kg m−3.
A detailed density profile of CH4 molecules near the SiO2 walls is shown by an inserted figure in Figure 3. It can be seen that there are two regions with density peaks and one region without a fluid molecule close to the wall. The density peaks are in the potential well (Wang and Hadjiconstantinou, 2018) and the top adsorbed layer (Trinh et al., 2014), respectively. As mentioned above, the accumulation of CH4 molecules in the potential well is due to the adsorption of wall interaction, while the accumulation of CH4 molecules in the top adsorbed layer is attributed to the adsorption interaction of CH4 molecules accumulating in the potential well. Because the adsorption of wall interaction is much stronger than that produced by the CH4 molecules accumulating in the potential well, so the peak of the density profile in the potential well is much higher than that in the top absorbed layer. Thus, the fluid molecules in the potential well have the most pronounced effect on the diffusivity of nanoconfined fluids, so that we should focus on the diffusivity of CH4 molecules in the potential well. Furthermore, the minimum separation between the wall and the fluid (zmin), and potential well (hFL) for the nanoconfined LJ fluid can be well-approximated by the following functions, respectively (Wang and Hadjiconstantinou, 2017):
where ρave is the average dimensionless density of the fluid. It needs to be noted that CH4 is a non-polar molecule, which has a similar property as the LJ fluid. Therefore, zmin and hFL for the nanoconfined CH4 still can be well-approximated by Equations. (4) and (5), respectively.
The wall interaction causes a large number of CH4 molecules to accumulate in the potential well. As a result, the movement space of CH4 molecules in the potential well is squeezed in the perpendicular direction, which ultimately leads to the reduction of diffusivity of nanoconfined fluid. In order to prove that wall interaction has a restricted effect on the diffusion of fluid molecules, the Lagrangian dynamics method is employed to dynamically track the movement of CH4 molecules originally trapped in the potential well region at a certain time. Although the Eulerian fashion is generally more used to study the overall diffusion of the fluid molecules in a system, Lagrangian dynamics has obvious advantages for examining the diffusion of specific fluid molecules. For Lagrangian dynamics, we initially needed to determine the CH4 molecules located in the potential well at a certain time, and then continuously observe the trajectory of these molecules and analyze their diffusive behaviors. Figure 4 shows the time-varying MSD for different groups of fluid molecules confined in a SiO2 nanochannel, with a height of 13.9 nm, i.e., the CH4 molecules in the potential well and bulk CH4, respectively. It can be found that the perpendicular (z-direction) diffusion coefficient of fluid molecules in the potential well region is only 0.31 D (D is the diffusion coefficient of bulk CH4, and, according to Einstein diffusion equation, one-dimensional diffusion coefficient is 1/2 of the slope of MSD) for the time t < < tjump (tjump characterizes the time for the turnover of the fluid molecules in the potential well; Wang and Hadjiconstantinou, 2018). Then, the diffusion coefficient of fluid molecules increases from 0.31 to 0.715 D, with time t goes far beyond tjump. This is because more and more fluid molecules originally in the potential well escape from this restricted region to the region where they can move freely. This result can directly demonstrate that the movement of CH4 molecules is inhibited in the potential well due to the wall interaction.
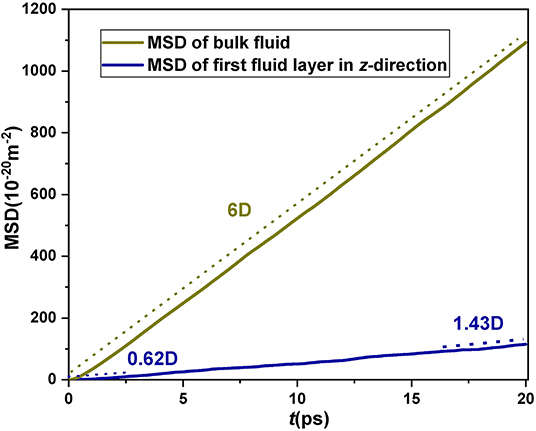
Figure 4. Mean square displacement vs. time for the CH4 molecules in the potential well (dark blue line) by Lagrangian dynamics in the nanochannel with height H = 13.74 nm.
Effect of Atomic Potentials in the Wall
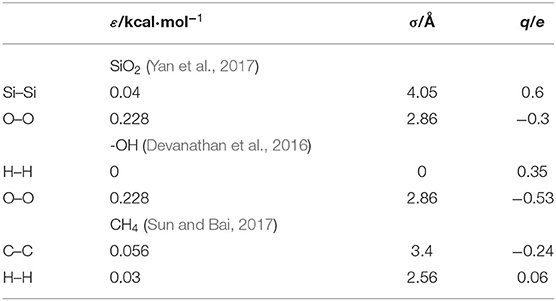
According to the above analysis, we find that the diffusive behavior of nanoconfined methane molecules is greatly affected by the wall interaction. It is very necessary to study the effect of atomic potentials in the wall to further reveal the effects of wall interaction on the diffusion of nanoconfined methane. It is obvious that there are two different forms of wall interaction acting on the methane molecules, i.e., one is van der Waals force, which can be modeled by the Lennard-Jones potential model, and the other is electrostatic force, which can be modeled by the Coulomb potential model. Because the methane molecule is a non-polar molecule, the electrostatic interaction of the wall on the methane molecules can be neglected. This fact also can be verified by the investigation of the local polarization density (LPD) of confined methane in the nanochannel. Figure 5 shows the LPD of methane confined in the silica nanochannel with a height of 4.74 nm. It can be seen that the peak of LPD for the nanoconfined methane is 0.01 C/m2, which is only 1/8 times of the peak of LPD for the nanoconfined water calculated by Jalali et al. (2020). This result indicates that the polarity of the methane molecule is so weak that its electrostatic force can be negligible. Therefore, we should focus on the van der Waals force of wall interaction acting on the methane molecules.
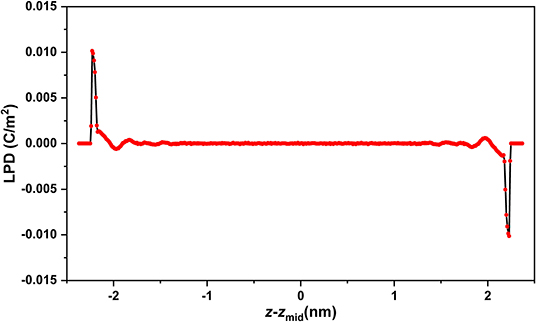
In order to analyze the effect of van der Waals force from the atoms in the wall on the methane molecules, we modified the potential interaction of the atoms in silica nanochannel by defining a relative energy parameter εr = ε/εos, where εos is the original energy parameter of atoms in the wall listed in Table 1, ε is the modified energy parameter of atoms in the wall. It needs to be noted that the interactions between atoms in the wall and methane molecules are changed with a ratio of . We calculated the variations of MSD with time for methane molecules in different nanochannels with varying εr from 0.1 to 10, as shown in Figure 6. It can be seen that the slopes of MSD in both longitudinal and perpendicular directions decrease with the increase of εr, meaning that the diffusion coefficients of nanoconfined methane decrease with the increase of wall interaction. These results are reasonable and consistent with the conclusion of Moulod and Hwang (2016), who investigated the water self-diffusivity confined in graphene nanogaps and found that the water self-diffusivity nearly linearly decreased with increasing the fluid-wall interatomic potentials. These results also can be explained from the perspective of density distribution. Figure 7 shows the density distribution of methane molecules along the z-direction for εr = 0.1, 1, and 10. It is found that the density peak becomes higher with the increase of εr, meaning that more and more methane molecules accumulate in the potential wells. The space for the movement of fluid molecules would be squeezed, owing to the accumulation of large numbers of molecules. Hence, the diffusive behavior of nanoconfined methane could be more strongly inhibited by the stronger wall interaction, and, finally, the diffusion coefficients of nanoconfined methane would decrease with increasing the atomic potentials in the wall.
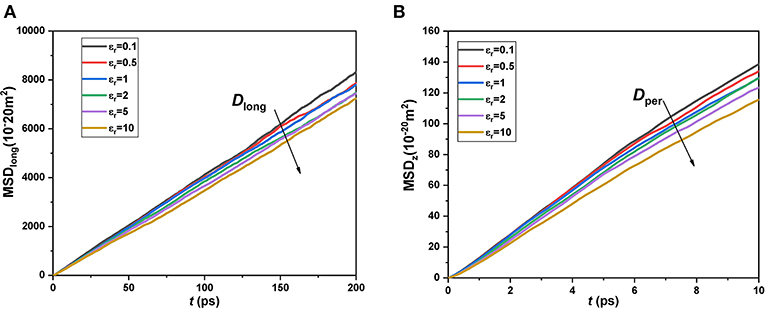
Figure 6. Mean square displacements of confined CH4 in channels with εr = 0.1–10. (A) Longitudinal; (B) Perpendicular.
Confining Effect of the Wall
The diffusive behavior of fluid molecules confined in a nanochannel is not only affected by the wall interaction but also inhibited by the space limitation of the wall. Figure 8 shows the MSD vs. time of CH4 molecules confined in a channel with a height of 10.1 nm (the red line in the figure). The dotted line in the figure is the extension line of the curve less than the time scale tL, as a guide to the eye. It can be seen from the figure that the height of the curve (red line) starts to be lower than the extension line, and this difference gradually increases as the time t exceeds tL. In other words, the slope of the curve is decreasing. This is because the fluid molecules, except the fluid molecules in the potential well, can diffuse freely as time t < tL. But the fluid molecules cannot diffuse indefinitely due to the limitation of space in the perpendicular direction. As time t > tL, more and more fluid molecules reach their maximum diffusion distance in the perpendicular direction, leading to a slower growth of MSD. Although the diffusion of fluid molecules in the longitudinal direction is not limited and MSD in these directions (x and y-directions) can always maintain a linear growth, the growth of total MSD in all three directions will gradually slow down under the influence of the diffusion in the perpendicular direction. In this case, tL is the cut-off point for the transition from three-dimensional diffusion (diffusion in three directions) to two-dimensional diffusion (diffusion in the perpendicular direction is restricted due to the limitation of the space, only can diffuse in the longitudinal direction) and is a positive correlation with the channel height. It needs to be noted that the effect of the wall on fluid molecules confined in a nanochannel is varied. For example, the nanoconfined fluid would present a sluggish dynamics under the effect of the wall (Eslami and Heydari, 2013; Eslami and Müller-Plathe, 2013). This effect is particularly evident in large-scale nanochannels.
Dependence on Channel Height
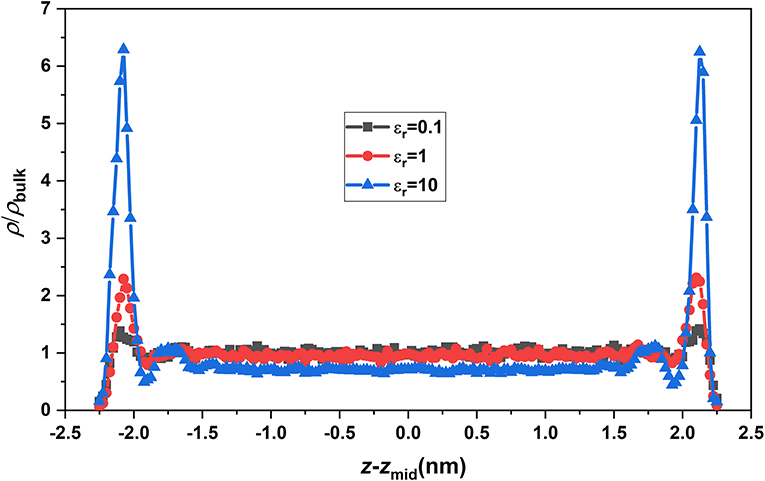
According to the above analysis, the special diffusive behavior of nanoconfined CH4, compared with the bulk CH4, is due to the effect of wall interaction and the confining effect of the wall. It is reasonable to infer that the diffusion coefficient of nanoconfined CH4 has significant dependence on the channel height because these effects of the wall on the nanoconfined fluid are sensitive to the channel height. We analyzed the longitudinal and perpendicular diffusion coefficients (Dlong and Dper) as well as the relative difference between them (|Dlong-Dper|/Dper), as shown in Figure 9, where the longitudinal and perpendicular diffusion coefficients are obtained as Dlong = |Dx+Dy|/2 and Dper = Dz, respectively. It is found that Dper obviously increases with the increase of channel width and gradually approaches Dlong. In other words, the anisotropy of the diffusion coefficient of nanoconfined methane is weakened as the channel height increases. This result is consistent with Jiang, Ouyang, Wang, Liu and Wang (2017) finding, who investigated the relationship between the channel width (the distance between the walls) and mass transfer characteristics for dense methane in the rough nanochannel and found that the values of the diffusion coefficient increase with the increase of the width of nanochannel. In order to further analyze the physical mechanism of the above phenomenon, we calculated the distribution of potential of mean force (PMF) in the different nanochannels, as shown in Figure 7. The PMF is correlated with the density profile and is estimated by the following equation (Shen et al., 2015; Jiménez-Ángeles et al., 2020):
where kB, T, ρz, and ρ0 are Boltzmann constant, temperature, local density, and bulk density. The PMF in Figure 10 can clearly show the interaction between wall and gas molecules. It can be seen in Figure 10 that potential well still exists near the wall in different channels. As we all know, the potential well is the low-lying area of PMF in the nanochannel. Once the fluid molecules are sucked into the potential well, only the fluid molecules with enough kinetic energy can escape from the area. Therefore, a large number of CH4 molecules are gathered in the potential well, which leads to a significant difference in the diffusive behavior of CH4 molecules in this region from the bulk region. This is the fundamental reason for the anisotropic diffusivity of CH4 confined in the nanochannels. It also can be found from Figure 10 that the proportion of potential well in the nanochannel decreases with the increase of channel height. Finally, the diffusive behavior of CH4 molecules in more regions will be consistent with that in the bulk region, so that the diffusion coefficient of CH4 confined in the nanochannel tends to be isotropic.
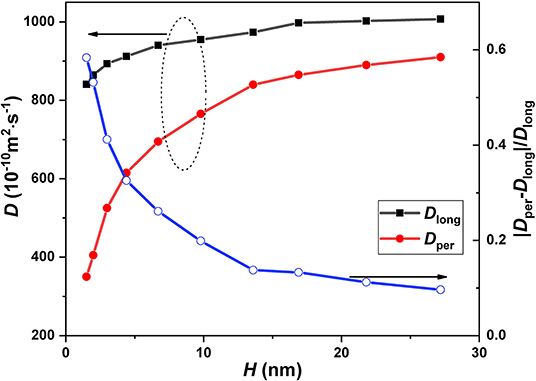
Figure 9. The diffusion coefficient (in the perpendicular and longitudinal directions) as the function of channel height. The blue line is the relative difference between the perpendicular diffusion coefficient and the longitudinal diffusion coefficient.
Conclusions
In this work, we adopt MD simulations with the Einstein diffusion formula to study the diffusivity of high-temperature and high-pressure methane confined in silica nanochannels and reveal its underlying physical mechanisms. The results show that the diffusion coefficients in the z-direction are obviously lower than those in the x and y-directions, indicating that the diffusion coefficients of nanoconfined methane molecules are anisotropic. The Lagrangian dynamics is used to trace the diffusive behavior of methane molecules in the potential well region at a certain time, and the result shows that the diffusion coefficient of these methane molecules is significantly lower than that in the bulk region at first. With the increase of methane molecules escaping from the potential well, the diffusion coefficient of those methane molecules original in the potential well begins to gradually increase. This result confirms that the potential well-formed by the effect of wall interaction significantly inhibits the diffusion of methane molecules in the perpendicular direction. Furthermore, it is found that the diffusion coefficients of nanoconfined methane decrease with the increase of the strength of wall interaction. That is because more and more methane molecules will accumulate in the potential wells with the increase of the strength of wall interaction, which causes the movement space of fluid molecules to be further squeezed and finally results in the decrease of diffusion coefficients. In addition, we also show that the wall has a confining effect on the diffusion of methane molecules. Meanwhile, the diffusion coefficient of nanoconfined methane molecules is dependent on channel height. With the increase of the channel height, the diffusion coefficient in the perpendicular direction increases, and the diffusion coefficient of nanoconfined methane tends to be isotropic, because the proportion of potential well in the channel decreases with the increase of the channel height. The obtained results are not only academic interest for the mass transport of nanoconfined fluids but also engineering interest for the extraction of unconventional gas reservoirs. It has a clear implication that the efficient extraction of tight gas can be realized by weakening the wall interactions and accordingly enhancing the diffusive mobility of methane. We hope that this study will benefit the enhancement of gas recovery efficiency and the reduction of energy consumed for the commercial tight gas extraction.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
SC performed the simulations, analyzed the data, and wrote the first draft of manuscript. JF, MG, and YW analyzed the data and discussed the simulation results. ZZ and CS conceived and designed the simulations and revised the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the Soft Science Research Program of Guangdong Province (Grant No. 2018B030323028), the National Natural Science Foundation of China for general project (Grant No. 51876169), and the Scientific Research Foundation of Xi'an Polytechnic University (Grant No. BS201931).
Conflict of Interest
CS, MG, and YW were employed by the company CNOOC Energy Technology & Services Limited, CNOOC EnerTech. Drilling and Production Co., and JF was employed by the company Zhanjiang Branch of CNOOC Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Chalmers, G. R. L., and Bustin, R. M. (2008). Lower Cretaceous gas shales in northeastern British Columbia, Part I: geological controls on methane sorption capacity. Bull. Can. Petroleum Geol. 56, 1–21. doi: 10.2113/gscpgbull.56.1.1
Cohen-Tanugi, D., and Grossman, J. C. (2012). Water desalination across nanoporous graphene. Nano Lett. 12, 3602–3608. doi: 10.1021/nl3012853
Curtis, M. E., Sondergeld, C. H., Ambrose, R. J., and Rai, C. S. (2012). Microstructural investigation of gas shales in two and three dimensions using nanometer-scale resolution imaging. Am. Assoc. Pet. Geol. Bull. 96, 665–677. doi: 10.1306/08151110188
Cygan, R. T., Liang, J.-J., and Kalinichev, A. G. (2004). Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 108, 1255–1266. doi: 10.1021/jp0363287
Devanathan, R., Chase-Woods, D., Shin, Y., and Gotthold, D. W. (2016). Molecular dynamics simulations reveal that water diffusion between graphene oxide layers is slow. Sci. Rep. 6:29484. doi: 10.1038/srep29484
di Primio, R., and Neumann, V. (2008). HPHT reservoir evolution: a case study from Jade and Judy fields, Central Graben, UK North Sea. Int. J. Earth Sci. 97, 1101–1114. doi: 10.1007/s00531-007-0206-y
Dorfman, K. D., Gupta, D., Jain, A., Muralidhar, A., and Tree, D. R. (2014). Hydrodynamics of DNA confined in nanoslits and nanochannels. Eur. Phys. J. Spec. Topics 223, 3179–3200. doi: 10.1140/epjst/e2014-02326-4
Eslami, H., and Heydari, N. (2013). Hydrogen bonding in water nanoconfined between graphene surfaces: a molecular dynamics simulation study. J. Nanoparticle Res. 16:2154. doi: 10.1007/s11051-013-2154-8
Eslami, H., and Mehdipour, N. (2012). Local chemical potential and pressure tensor in inhomogeneous nanoconfined fluids. J. Chem. Phys. 137:144702. doi: 10.1063/1.4757016
Eslami, H., and Müller-Plathe, F. (2011). Molecular dynamics simulation of water influence on local structure of nanoconfined polyamide-6,6. J. Phys. Chem. B 115, 9720–9731. doi: 10.1021/jp204423z
Eslami, H., and Müller-Plathe, F. (2013). How thick is the interphase in an ultrathin polymer film? Coarse-grained molecular dynamics simulations of polyamide-6,6 on graphene. J. Phys. Chem. C 117, 5249–5257. doi: 10.1021/jp400142h
Fang, J., Guo, P., Xiao, X., Du, J., Dong, C., Xiong, Y., et al. (2015). Gas-water relative permeability measurement of high temperature and high pressure tight gas reservoirs. Petroleum Explor. Dev. 42, 92–96. doi: 10.1016/S1876-3804(15)60010-6
Jalali, H., Ghorbanfekr, H., Hamid, I., Neek-Amal, M., Rashidi, R., and Peeters, F. M. (2020). Out-of-plane permittivity of confined water. Phys. Rev. E 102:022803. doi: 10.1103/PhysRevE.102.022803
Jiang, C., Ouyang, J., Wang, L., Liu, Q., and Wang, X. (2017). Transport properties and structure of dense methane fluid in the rough nano-channels using non-equilibrium multiscale molecular dynamics simulation. Int. J. Heat Mass Transf. 110, 80–93. doi: 10.1016/j.ijheatmasstransfer.2017.03.023
Jiang, C., Wang, X., Liu, Q., Wang, X., and Ke, C. (2020). Investigation of the relationship between nanochannel width and mass transfer characteristics for dense methane nanofluidics. Int. Commun. Heat Mass Transfer 118:104879. doi: 10.1016/j.icheatmasstransfer.2020.104879
Jiménez-Ángeles, F., Harmon, K. J., Nguyen, T. D., Fenter, P., and Olvera de la Cruz, M. (2020). Nonreciprocal interactions induced by water in confinement. Phys. Rev. Res. 2:043244. doi: 10.1103/PhysRevResearch.2.043244
Kim, J.-S., Choi, J. S., Lee, M. J., Park, B. H., Bukhvalov, D., Son, Y.-W., et al. (2013). Between scylla and charybdis: hydrophobic graphene-guided water diffusion on hydrophilic substrates. Sci. Rep. 3:2309. doi: 10.1038/srep02309
Liu, B., Li, X., Qi, C., Mai, T., Zhan, K., Zhao, L., et al. (2018). Pressure-driven supercritical CO2 transport through a silica nanochannel. RSC Adv. 8, 1461–1468. doi: 10.1039/C7RA11746A
Liu, Q., Yuan, S., Yan, H., and Zhao, X. (2012). Mechanism of oil detachment from a silica surface in aqueous surfactant solutions: molecular dynamics simulations. J. Phys. Chem. B 116, 2867–2875. doi: 10.1021/jp2118482
Liu, T., Gautam, S., Cole, D. R., Patankar, S., Tomasko, D., Zhou, W., et al. (2020). Structure and dynamics of ethane confined in silica nanopores in the presence of CO2. J. Chem. Phys. 152:084707. doi: 10.1063/1.5134451
Liu, Y., Wang, Q., Wu, T., and Zhang, L. (2005). Fluid structure and transport properties of water inside carbon nanotubes. J. Chem. Phys. 123:234701. doi: 10.1063/1.2131070
Liu, Y.-C., Wang, Q., and Lu, L.-H. (2004). Density inhomogeneity and diffusion behavior of fluids in micropores by molecular-dynamics simulation. J. Chem. Phys. 120, 10728–10735. doi: 10.1063/1.1730059
Martí, J., Nagy, G., Guàrdia, E., and Gordillo, M. C. (2006). Molecular dynamics simulation of liquid water confined inside graphite channels: dielectric and dynamical properties. J. Phys. Chem. B 110, 23987–23994. doi: 10.1021/jp0647277
Moulod, M., and Hwang, G. (2016). Water self-diffusivity confined in graphene nanogap using molecular dynamics simulations. J. Appl. Phys. 120:194302. doi: 10.1063/1.4967797
Pan, J., Xiao, S., Zhang, Z., Wei, N., He, J., and Zhao, J. (2020). Nanoconfined water dynamics in multilayer graphene nanopores. J. Phys. Chem. C 124, 17819–17828. doi: 10.1021/acs.jpcc.0c04897
Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi: 10.1006/jcph.1995.1039
Sharma, A., Namsani, S., and Singh, J. K. (2015). Molecular simulation of shale gas adsorption and diffusion in inorganic nanopores. Mol. Simul. 41, 414–422. doi: 10.1080/08927022.2014.968850
Shen, Z.-L., He, G.-H., Zhang, N., and Hao, C. (2015). Molecular dynamics simulation of reverse-osmotic salt rejection and water transport through double-walled carbon nanotube. Acta Phys. Chim. Sin. 31, 1025–1034. doi: 10.3866/PKU.WHXB201504141
Skelton, A. A., Fenter, P., Kubicki, J. D., Wesolowski, D. J., and Cummings, P. T. (2011). Stimulations of the quartz(1011)/water interface: a comparison of classical force fields, ab initio molecular dynamics, and x-ray reflectivity experiments. J. Phys. Chem. C 115, 2076–2088. doi: 10.1021/jp109446d
Sofos, F., Karakasidis, T., and Liakopoulos, A. (2009). Transport properties of liquid argon in krypton nanochannels: anisotropy and non-homogeneity introduced by the solid walls. Int. J. Heat Mass Transf. 52, 735–743. doi: 10.1016/j.ijheatmasstransfer.2008.07.022
Sokhan, V. P., Nicholson, D., and Quirke, N. (2004). Transport properties of nitrogen in single walled carbon nanotubes. J. Chem. Phys. 120, 3855–3863. doi: 10.1063/1.1643726
Sui, H., Yao, J., and Zhang, L. (2015). Molecular simulation of shale gas adsorption and diffusion in clay nanopores. Computation 3, 687–700. doi: 10.3390/computation3040687
Sun, C., and Bai, B. (2017). Gas diffusion on graphene surfaces. Phys. Chem. Chem. Phys. 19, 3894–3902. doi: 10.1039/C6CP06267A
Sun, C., Zhou, R., Zhao, Z., and Bai, B. (2020). Nanoconfined fluids: what can we expect from them? J. Phys. Chem. Lett. 11, 4678–4692. doi: 10.1021/acs.jpclett.0c00591
Sun, H., Sun, W., Zhao, H., Sun, Y., Zhang, D., Qi, X., and Li, Y. (2016). Adsorption properties of CH4 and CO2 in quartz nanopores studied by molecular simulation. RSC Adv. 6, 32770–32778. doi: 10.1039/C6RA05083B
Thermophysical Properties of Fluid Systems. Chemistry Web Book SDR 69. National Institution of Standards and Technology (NIST). Gaithersburg, MD. (2009).
Trinh, T. T., Bedeaux, D., Simon, J. M., and Kjelstrup, S. (2014). Thermodynamic characterization of two layers of CO2 on a graphite surface. Chem. Phys. Lett. 612, 214–218. doi: 10.1016/j.cplett.2014.08.026
Wang, G. J., and Hadjiconstantinou, N. G. (2017). Molecular mechanics and structure of the fluid-solid interface in simple fluids. Phys. Rev. Fluids 2:094201. doi: 10.1103/PhysRevFluids.2.094201
Wang, G. J., and Hadjiconstantinou, N. G. (2018). Layered fluid structure and anomalous diffusion under nanoconfinement. Langmuir 34, 6976–6982. doi: 10.1021/acs.langmuir.8b01540
Wang, Y., He, Z., Gupta, K. M., Shi, Q., and Lu, R. (2017). Molecular dynamics study on water desalination through functionalized nanoporous graphene. Carbon 116, 120–127. doi: 10.1016/j.carbon.2017.01.099
Wang, Y., Zhu, Y., Chen, S., and Li, W. (2014). Characteristics of the nanoscale pore structure in Northwestern Hunan Shale gas reservoirs using field emission scanning electron microscopy, high-pressure mercury intrusion, gas adsorption. Energy Fuels 28, 945–955. doi: 10.1021/ef402159e
Yan, Y., Dong, Z., Zhang, Y., Wang, P., Fang, T., and Zhang, J. (2017). CO2 activating hydrocarbon transport across nanopore throat: insights from molecular dynamics simulation. Phys. Chem. Chem. Phys. 19, 30439–30444. doi: 10.1039/C7CP05759H
Zaragoza, A., Gonzalez, M. A., Joly, L., López-Montero, I., Canales, M. A., Benavides, A. L., et al. (2019). Molecular dynamics study of nanoconfined TIP4P/2005 water: how confinement and temperature affect diffusion and viscosity. Phys. Chem. Chem. Phys. 21, 13653–13667. doi: 10.1039/C9CP02485A
Zhang, L., Liu, C., Liu, Y., Li, Q., Cheng, Q., and Cai, S. (2020). Transport property of methane and ethane in K-illite nanopores of shale: insights from molecular dynamic simulations. Energy Fuels 34, 1710–1719. doi: 10.1021/acs.energyfuels.9b04255
Zhao, Z., Sun, C., and Zhou, R. (2020b). Thermal conductivity of confined-water in graphene nanochannels. Int. J. Heat Mass Transf. 152:119502. doi: 10.1016/j.ijheatmasstransfer.2020.119502
Zhao, Z., Zhou, R., and Sun, C. (2020a). Molecular dynamics study of water diffusivity in graphene nanochannels. Int. J. Thermophys. 41. doi: 10.1007/s10765-020-02660-5
Zhao, Z., Zhou, R., and Sun, C. (2020c). Hierarchical thermal transport in nanoconfined water. J. Chem. Phys. 153:234701. doi: 10.1063/5.0030738
Zhou, R., Sun, C., and Bai, B. (2021). Wall friction should be decoupled from fluid viscosity for the prediction of nanoscale flow. J. Chem. Phys. 154:074709. doi: 10.1063/5.0039228
Ziemys, A., Ferrari, M., and Cavasotto, C. J. J. (2009). Nanotechnology, molecular modeling of glucose diffusivity in silica nanochannels. J. Nanosci. Nanotechnol. 9, 6349–6359. doi: 10.1166/jnn.2009.1822
Keywords: diffusivity, SiO2 nanochannels, nanoconfined fluid, tight gas, molecular dynamics
Citation: Cui S, Fu J, Guo M, Zhao Z, Sun C and Wang Y (2021) Diffusion of High-Temperature and High-Pressure CH4 Gas in SiO2 Nanochannels. Front. Energy Res. 9:667640. doi: 10.3389/fenrg.2021.667640
Received: 14 February 2021; Accepted: 09 April 2021;
Published: 07 May 2021.
Edited by:
Enhua Wang, Beijing Institute of Technology, ChinaReviewed by:
Hossein Eslami, Technische Universität Darmstadt, GermanyArturas Ziemys, Houston Methodist Research Institute, United States
Copyright © 2021 Cui, Fu, Guo, Zhao, Sun and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhixiang Zhao, enguemhhb0B4cHUuZWR1LmNu; Chengzhen Sun, c3VuLWN6QHhqdHUuZWR1LmNu
 Shuheng Cui1
Shuheng Cui1 Zhixiang Zhao
Zhixiang Zhao Chengzhen Sun
Chengzhen Sun