Characterization of Thin MAPb(I1–xBrx)3 Alloy Halide Perovskite Films Prepared by Sequential Physical Vapor Deposition

Lead iodide (PbI₂)-rich methylammonium lead bromide-iodide (MAPb(I_1–xBr_x)₃) thin-films were prepared by sequential physical vapor deposition of methylammonium lead tri-bromide (MAPbBr₃) on methylammonium lead tri-iodide (MAPbI₃) bottom layer. The structural, optical, morphological, and electrical properties of the thin-films were studied as the thickness of methylammonium bromide (MABr) was increased from 300 to 500 nm. X-ray diffractograms confirmed transformation of tetragonal MAPbI₃(x is 0.0) to the cubic-like structure of MAPbBr₃ (x is 1.0) as MAPb(I_1–xBr_x)₃ (x = 0.89–0.95) and PbI₂ were formed. The bromine mole ratio x decreased as MABr thickness increased. UV-Vis absorption spectra showed that the bandgap of the thin alloy film decreased from 2.21 to 2.14 eV as x decreased. Scanning electron micrographs depicted densely packed grains that entirely covered the substrate and contained very few pinholes. The average grain size increased from 150 to 320 nm as x decreased. Electrical properties showed high charge carrier mobility that increased linearly with MABr thickness. FTO/MAPb(I_1–xBr_x)₃/Au devices using fluorine-doped tin oxide (FTO) as substrate and gold (Au) as contacts were fabricated and current-voltage characteristics were determined. Space-charge-limited current theory was applied to charge carrier mobility and trap density of MAPb(I_1–xBr_x)₃ thin-films. The charge carrier mobility increased as x decreased. The power conversion efficiency (PCE) of FTO/MAPbBr₃/Au, FTO/MAPb(I_0.11Br_0.89)₃/Au and FTO/MAPbI₃/Au solar cells were 0.56, 0.62, and 1.15%. Devices including titanium dioxide compact layer (c-TiO2) and titanium dioxide mesoporous (m-TiO₂) layer as electron transport layers were also fabricated for the application of Mott-Shottky (M-S) theory. Analyses of dark current-voltage and capacitance-voltage curves of FTO/c-TiO₂/m-TiO₂/MAPb(I_0.11Br_0.89)₃ solar cells revealed a sizeable built-in voltage (V_bi) of 1.6 V and an accumulation of charge at interfaces for voltages greater than 0.2 V, respectively. Similar analyses for FTO/TiO₂/MAPbI₃/Au showed a small V_bi of 0.7 V and no charge carrier at interfaces. The work paves a way for reproducible growth of MAPb(I_1–xBr_x)₃ for solar cells and sheds more light on the degree of ion migration in mixed halide and pure halide perovskites.

Introduction

Recently, hybrid perovskite solar cells are gaining much attention in the photovoltaic community because of the excellent blend of stability, efficiency, and bandgap tunability. Pure 3D halide perovskites (HaP) have a general formula ABX₃, where A is a monovalent cation, B is a divalent cation and X is a halide anion. On the other hand, mixed hybrid perovskites (MHaP) include the hybridization of cations and halides. Cation-hybridization of HaP helps in stabilizing the performance of the solar cells. On the other hand, halide-hybridization changes the bandgap of the HaP. These MHaP result in stable and highly efficient hole-transport-layer free (HTLF) solar cells. Wu et al. (2019) showed that mixed hybrid perovskite HTLF solar cell based on triple cations and double anion hybrids maintained 80% of its 17.58% record power conversion efficiency (PCE) for more than 1,000 h under continuous illumination. Conversely, stable HTLF single-junction solar cells based on methylammonium lead tri-bromide (MAPbBr₃) sensitizers had a lower efficiency. Liang et al. (2018) showed that HTLF-MAPbBr₃ solar cells using graphite electrodes produced a high open-circuit voltage (V_oc) of 1.57 V but with only 8.70% PCE. The low efficiency of MAPbBr₃-solar cells is due to the poor absorption of MAPbBr₃ in the visible region of the electromagnetic spectrum.

Several efforts have been made to improve the PCE of MAPbBr₃-based solar cells by improving light absorption. Solar cells with iodide-bromide lead perovskites have shown better efficiencies than bromide-only solar cells. Ng et al. (2018) improved the efficiency of cesium lead tri-bromide (CsPbBr₃) by adding a small amount of iodide. Aharon et al. (2014) reported that halide hybrid perovskite thin films produced a more stable and efficient HTLF solar cell when compared with its non-hybrid halide perovskites counterpart, owing to their excellent blend of light absorption and hole-conduction properties. The sensitization of MAPbBr₃ with an organic dye, after crystallization, also improved the performance in MAPbBr₃ solar cells. McFarlane et al. (2019) showed that MAPbBr₃ films sensitized with red and blue organic dyes after crystallization produced more efficient devices than MAPbBr₃-only films.

Hybrid perovskites consisting of iodide-bromide (I-Br) have been prepared via different routes in the past. Misra et al. (2016) grew methylammonium iodide-bromide (MAPb(I_1–xBr_x)₃) thin-film alloys, where x is the mole fraction of Br in the solid solution with maximum value equals 0.4. The used a sequential deposition of methylammonium iodide (MAI) and a mixture of MAI + methylammonium bromide (MABr) solutions on a solution-prepared lead (II) iodide (PbI₂) thin-film. They showed that the MAPb(I_1–xBr_x)₃ (x is 0.4) and MAPbI₃ (x is 0.0) degraded under concentrated sunlight while MAPbBr₃ (x is 1) did not degrade. Zhang et al. (2016) grew MAPb(I_1–xBr_x)₃ single crystals by the inverse temperature crystallization method, using separately optimized precursor solutions of MAPbBr₃ and methylammonium lead tri-iodide (MAPbI₃). They were able to tune absorption in the entire visible spectrum by varying x from 0.0 to 1.0. Kulkarni et al. (2014) tuned the bandgap of MAPb(I_1–xBr_x)₃ over a wide spectral range by varying x from 0.0 to 1.0 using a sequential solution deposition method and discovered a blue shift in absorption onset upon the increase in bromine content. Gil-escrig et al. (2015) synthesized MAPb(I_1–xBr_x)₃ (x ranging from 0.0 to 0.6) by stacking MAPbBr₃ on MAPbI₃, which were prepared sequentially using vapor assisted and co-evaporation techniques, respectively. They saw a redshift in emission wavelength as the thickness of MAPbBr₃ increased and a PCE of 12.9%. Jang et al. (2015) formed I-Br nanocrystals by halide exchange reaction of MAPbBr₃ crystals with MAI in an isopropyl alcohol solution. They were able to prove that I-rich MAPb(I_1–xBr_x)₃ had a tetragonal phase, and showed higher PCE and charge carrier lifetimes. Pistor and Burwig (2018) synthesized MAPb(I_1–xBr_x)₃ by vacuum-based two source co-evaporation method and demonstrated a total and reversible halide exchange in MAPbI₃ and MAPbBr₃ upon exposure to the opposite MAX (X is I or Br) at a substrate temperature of 120°C. However, the preparation of MAPb(I_1–xBr_x)₃ by co-evaporation is not reproducible since it involves rate monitoring which fluctuates. Contrary to the results of Zhang et al. who illustrated complete solubility with x ranging from 0.0 to1.0, Lehmann et al. (2019) showed that there exists a miscibility gap for x in the range 0.29 to 0.92 for a solution synthesized powders of MAPb(I_1–xBr_x)₃ and strong phase separation for values of x ranging from 0.29 to 0.62. Most of these past methods are either solution-based or co-evaporation approaches. The problem with the solution approaches is that of toxicity of the commonly used solvents (Kim et al., 2018; Swartwout et al., 2019). Also, the co-evaporation methods are not reproducible since it involves monitoring the rate of deposition which is unsteady (Chen et al., 2014a; Borchert et al., 2019). We developed a greener and reproducible sequential physical vapor deposition (SPVD) technique for growing halide perovskite thin-films and have reported the crystal growth of MAPbI₃ (Fru et al., 2020a) and MAPbBr₃ thin-films (Fru et al., 2020b), using the same method. However, the preparation of thin MAPb(I_1–xBr_x)₃ films by SVPD is yet to be reported.

We report the formation of MAPb(I_1–xBr_x)₃ alloy by the stacking of MAPbBr₃ top layer on MAPbI₃ bottom layer, which is separately grown by SPVD. The aim is to improve absorption and reduce the bandgap of MAPbBr₃ absorber by using the MAPbI₃ bottom layer as an organic-inorganic sensitizer. The structural, optical, morphological, and electrical properties of the thin halide hybrid MAPb(I_1–xBr_x)₃ thin-films are studied as the MABr thickness is varied from 300 to 500 nm. The space-charge-limited current (SCLC) theory was applied to determine the trap density and carrier mobility of MAPb(I_1–xBr_x)₃ using FTO/MAPb(I_1–xBr_x)₃/Au structures, where FTO is fluorine-doped tin oxide (FTO). Analysis of the dark current-voltage and capacitance-voltage characteristics of FTO/c-TiO₂/m-TiO₂/MAPb(I_0.11Br_0.89)₃/Au and FTO/c-TiO₂/m-TiO₂/MAPbI₃/Au was performed to shed light on ion migration in MAPb(I_0.11Br_0.89)₃ and MAPbI₃. This study paves the way for the reproducible growth MAPb(I_1–xBr_x)₃ thin-films for charge-transport-layer free solar cells.

Experimental

Synthesis of Thin MAPb(I_1–xBr_x)₃ Alloy Film by SPVD

Figures 1A,B illustrate the process of growing MAPb(I_1–xBr_x)₃ thin alloy film using the SPVD technique. 15 × 20 mm glass substrates were trimmed and cleaned sequentially in acetone, isopropanol, and deionized water using an ultrasonic bath. The substrates were dried by blowing with a pressurized stream of pure nitrogen gas. PbI₂ (99.9%) and MAI (98%) powders were obtained from Sigma Aldrich and used as received. Before the deposition, the chamber was cleaned using a solution of extran diluted with deionized water (volume ratio 1:4) and high-pressure cleaner, to remove the effects of residual contaminants. PbI₂ and MAI powders were placed in two separate cylindrical boron nitride boats B₁ and B₂ and inserted into individual heating coils inside an evaporation jar. The coils are connected to a power supply via switches S1 and S2 as shown in Figures 1A,B. The evaporation chamber was evacuated to a pressure of 2.0 × 10^–5 mbar. An in-built quartz crystal monitor, placed at the same level as the substrate inside the evaporation chamber, was used to monitor the thickness of thin-films during the deposition process. The crystal monitor was calibrated for PbI₂ thickness measurement by setting the density to 6.16 g cm^–3 and Z-factor to 1.10, and MAI film thickness was monitored by setting the density to 1.20 g cm^–3 and Z-factor to 2.70. 100 nm thick PbI₂ thin-film was first deposited followed by the deposition of 500 nm thick MAI to form MAPbI₃. The heat generated from the heating crucibles raised the temperature of the substrates to 140°C during the deposition of PbI₂, and to 95°C during the deposit of MAI. Post-annealing of the sample was done in an oven with the temperature maintained at 100°C for 10 min. After the post-annealing process, the prepared MAPbI₃ was loaded in the evaporation chamber, with boats B1 and B2 now containing PbBr₂ and MABr, respectively, as shown in Figure 1B. PbBr₂ thickness was measured by setting the density to 6.66 g cm^–3 and Z-factor to 1.20 and MABr film thickness was monitored by selecting the density to 1.30 g cm^–3 and Z-factor to 2.80. The thickness of PbBr₂ was kept constant at 100 nm while that of MABr was varied from 300 to 500 nm, in steps of 100. Also, the heat generated from heating the crucibles raised the temperature of the substrates to 140°C during the deposition of PbBr₂ and 95°C during the deposit of MABr.

FIGURE 1

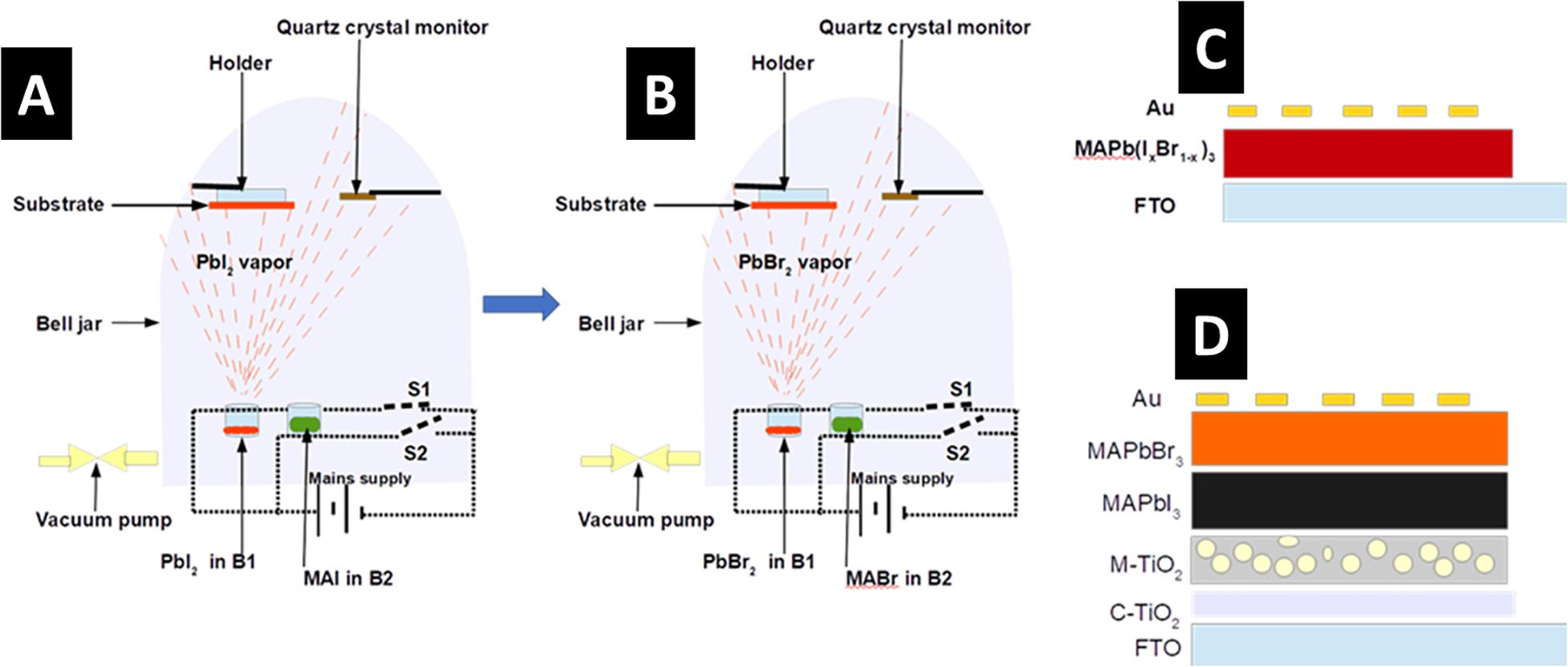
Figure 1. Schematic diagrams showing the synthesis process of thin MAPb(I_1–xBr_x)₃ alloy film and the structure of FTO/c-TiO₂/m-TiO₂/MAPb(I_1–xBr_x)₃/Au. (A) Synthesis of MAPbI₃ by SPVD, (B) synthesis of MAPbBr₃ by SPVD, (C) the FTO/MAPb(I_1–xBr_x)₃/Au solar cell architecture, (D) mesoporous FTO/c-TiO₂/m-TiO₂/MAPb(I_1–xBr_x)₃/Au solar cell architecture.

Device Fabrication

Figure 1C represents the schematic of FTO/MAPb(I_1–xBr_x)₃/Au devices fabricated solely for the determination of charge carrier mobility and trap density using the space-charge-limited current theory. The MAPb(I_1–xBr_x)₃ was grown on FTO as described above and gold (Au) contacts were later deposited on the MHaP through a 0.6 mm diameter shadow mask. Figure 1D shows the schematic diagrams of FTO/c-TiO₂/m-TiO₂/MAPb(I_1–xBr_x)₃/Au devices for dark capacitance-voltage analyses. The precursor solution for deposition titanium dioxide compact (c-TiO₂) layer was prepared by mixing 0.55 ml of titanium diisopropoxide bis(acetylacetonate) and 5 ml of 1-butanol to give 0.3 M TiO_x solution. The c-TiO₂ layer was deposited by spin-coating the 0.3 M TiO_x solution on FTO at 3,000 rpm for 30 s. The film was dried in an oven at 125°C for 5 min. The experiment is repeated once before annealing in a furnace at 500°C for 30 min to produce a compact-TiO₂ layer. TiO₂ paste was prepared by dissolving 1.2 g of TiO₂ nanoparticles in 10 ml of ethanol, 4 ml of terpineol, and 10% ethyl cellulose (0.6 g ethyl cellulose in 10 ml of ethanol). The mixture was stirred overnight at room temperature. The paste was spin-coated at 3,000 rpm for 30 s and dried at 125°C for 5 min before sintering at 500°C for 30 min to form the mesoporous-TiO₂ (m-TiO₂) layer. The MAPb(I_1–xBr_x)₃ thin alloy film was grown on the as described above. Finally, Au contacts were deposited through a 0.6 mm diameter shadow mask.

Thin-Film Characterization

XRD patterns of the thin-films were measured by a Bruker D2-Phaser X-ray diffractometer using Cu Kα radiation with a wavelength of 1.5405 Å. The angle between the incident and diffracted rays, 2θ was varied from 10 to 50° in steps of 0.05. The measured patterns were used to determine the structures, crystallinity, microstrain, and dislocation densities of the thin-films. The morphological properties were revealed by a Field Emission Scanning Electron Microscope (FE-SEM Zeiss Crossbeam 540), with an accelerating voltage of 2.0 kV. Grain size analysis was performed from the FE-SEM images following the American Standard for Testing Materials (ASTM) using the Image J Software. The optical absorption spectra of the films were recorded using the CARY 100 BIO UV-Vis spectrometer with a wavelength of incident light ranging from 400 to 800 nm.

Device Characterization

A 4192A LF Impedance Analyser with measurement frequency ranging from 5 Hz to 13 MHz, was used for the dark current density-voltage (J-V) and capacitance-voltage (C-V) measurements. The C-V measurements were conducted at a constant frequency of 1 MHz so that the defects within the device should not respond to electric field variations (Dharmadasa et al., 2019). The measured values were then used for Mott-Schottky (M-S) analysis to determine the presence of charge accumulation during device operation. Current density-voltage (J-V) characteristics and device performance parameters of the solar cells under illumination were determined using the automatic current-voltage measurement system (Osilla). The light measurements were performed under a solar simulator (Oriel LCS-100^TM Small Area So11A Series, Newport) with simulated solar output conditions of 100 mW/cm² and AM1.5 G reference spectral filtering.

Results and Discussion

Structural Properties

Figure 2A shows the X-ray diffractograms of MAPbI₃ on glass, MAPbBr₃ on glass, and MAPbBr₃ on MAPbI₃ bottom layer. The diffractogram of MAPbI₃ shows sharp planes corresponding to the pure tetragonal crystal structure and I4/mcm space group, according to the literature (Jeon et al., 2014; Saidaminov et al., 2015; Shi et al., 2015). The diffraction patterns of MAPbBr₃ matches the cubic crystal structure which has Pm3̄m space group (Peng et al., 2016; Wang et al., 2017; Tisdale et al., 2018). The thin MAPb(I_1–xBr_x)₃ film diffractograms (Figures 2A,B) show the presence of all the prominent peaks of cubic MAPbBr₃ and the (001) peak corresponding to PbI_2, but do not contain the principal (110) peak characterizing tetragonal MAPbI₃. This points to the fact that the tetragonal phase of MAPbI₃ is transformed to the cubic phase of MAPbBr₃ as MAPb(I_1–xBr_x)₃ is formed, consistent with previous reports (Noh et al., 2013; Gil-escrig et al., 2015; Pistor and Burwig, 2018). The value of bromine mole ratio x was determined using an empirical relationship between the bandgaps of the MAPb(I_1–xBr_x)₃ alloy and those of its MAPbI₃ and MAPbBr₃ components, given in Equation 1,

$\begin{array}{c}{E}_g[MAPb{(I_{1-x}B{r}_x)}_3]=\hfill \\ E_g[MAPb{I}_3]+\{E_g[MAPbB{r}_3]-E_g[MAPb{I}_3]-b\}x+b{x}^2\hfill \end{array}(1)$

FIGURE 2

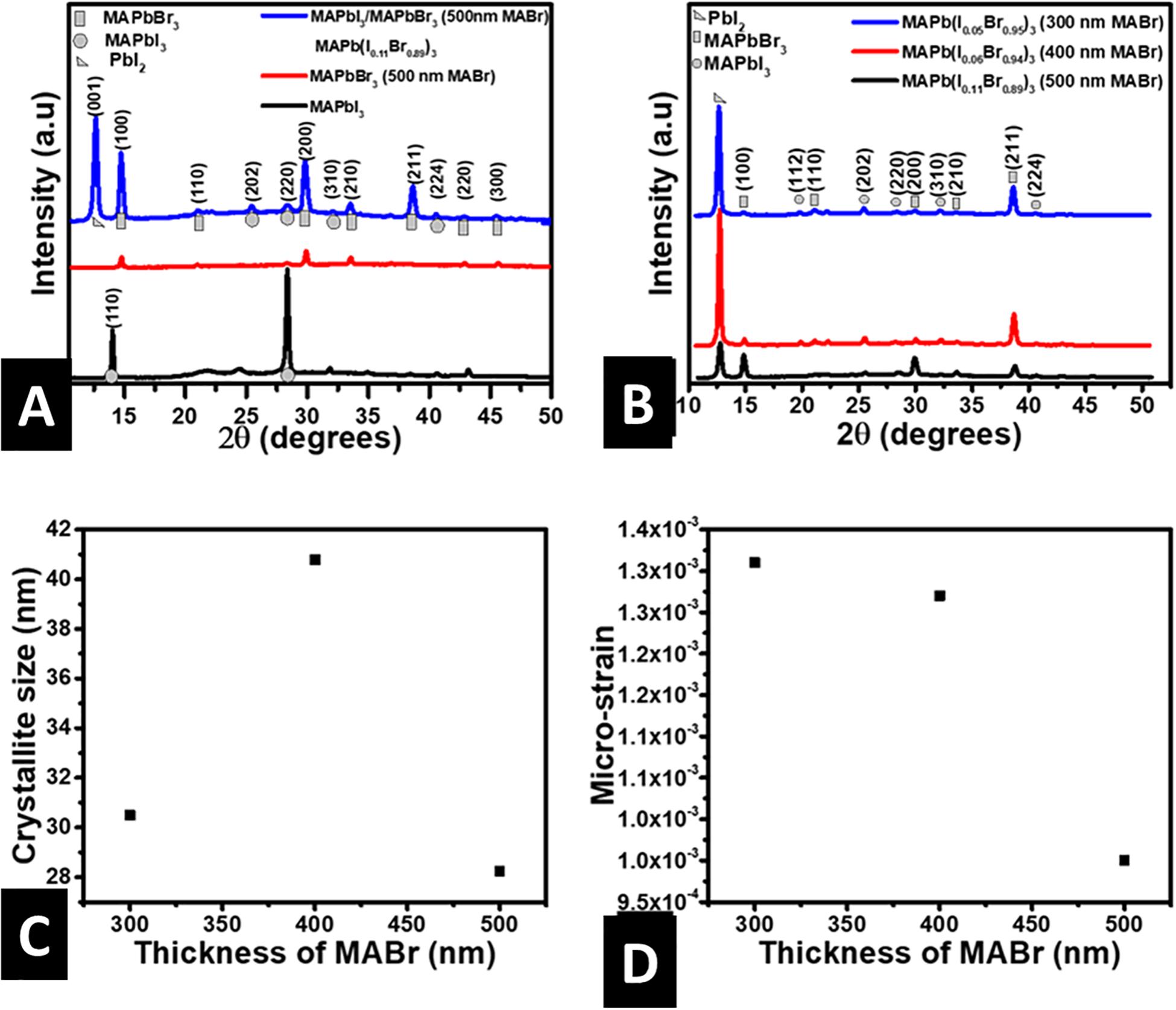
Figure 2. (A) XRD patterns of MAPbI₃, MAPbBr₃ (500 nm of MABr) and MAPbI₃/MAPbBr₃, (B) XRD patterns of MAPb(I_1–xBr_x)₃ for various thicknesses of MABr, (C) crystallite size against MABr thickness for MAPb(I_1–xBr_x)₃ thin-films, (D) microstrain against MABr thickness for MAPb(I_1–xBr_x)₃ thin-films.

where b is the bowing parameter that accounts for the curvature of the bandgap energies as a function of composition. Noh et al. (2013) obtained b as 0.33 for Br-I mixing of the MAPbI₃ and MAPbBr₃ components. Similarly, Zhang et al. (2016) obtained b as 0.21 for Br-I mixing upon tuning the bandgap of MAPb(I_1–xBr_x)₃ single crystal. The small values of b for MAPb(I_1–xBr_x)₃ are an indication that MAPbI₃ and MAPbBr₃ are fully miscible in solid solutions. By substituting the bandgaps (from the UV-Vis absorption analysis) and b as 0.33 into Equation 1, we obtained x to be 0.95 for 300 nm and 0.94 for 400 nm MABr which corresponds to structural formulae of MAPb(I₀.₀₅Br_0.95)₃ and MAPb(I₀.₀₆Br_0.94)₃, respectively. Similarly, x is 0.89 when the thickness of MABr equals 500 nm giving the structural formula as MAPb(I₀.₁₁Br₀.₈₉)₃. The values of x for pure MAPbI₃ and pure MAPbBr₃ are 0.0 and 1.0, respectively. Previous studies have shown that MAPb(I_1–xBr_x)₃ with such high amounts of x exists in the cubic phase (Noh et al., 2013; Zhang et al., 2016). Pistor and Burwig (2018) gave an elaborate explanation for the formation of MAPb(I_1–xBr_x)₃ by exposing MAPbI₃ to MABr vapor and MAPbBr₃ to MAI vapor. They proved that it was due to reversible halide exchange at high substrate temperatures and added that it is much easier to replace I with Br than to replaces Br with I. This is because of the smaller radius of Br and small formation enthalpies of MAPbBr₃. Furthermore, they showed that Br replaces I when MAPbI₃ is exposed to MABr vapor while I replace Br when MAPbBr₃ is exposed to MAI vapor. Thus, the high Br content we obtained shows a good correlation with the explanations of Pistor and Burwig. The presence of PbI₂ peak in the diffractograms of MAPb(I_1–xBr_x)₃ shown in Figures 2A,B, is consistent with previous results in the literature (Gil-escrig et al., 2015; Misra et al., 2016). The (001) peak characterizing PbI₂ is not seen in the diffractogram of MAPbI_3. However, it appears in the diffractogram of MAPb(I_1–xBr_x)₃. The shows that PbI₂ is formed with the MAPb(I_1–xBr_x)_3. The formation of PbI₂ alongside MAPb(I_1–xBr_x)₃ may include, amongst other processes, the decomposition of MAPbI₃ as a result of prolonged in-situ annealing and high substrate temperatures within the evaporation chamber as the MAPbBr₃ layer was being prepared. We have shown previously that post-annealing of MAPbI₃ thin-films at 100°C for 40 min leads to the appearance of a sharp PbI₂ peak, which decreases in intensity upon increasing the time to 60 min because the MAPbI₃ is formed again (Fru et al., 2020a). Similarly, annealing MAPbI₃ at temperatures beyond 120°C lead to the decomposition of MAPbI₃ to PbI₂ (Pistor and Burwig, 2018). The intensity of the PbI₂ peak reduces while that of the (100) peak increases as the thickness of MABr is increased from 400 to 500 nm. This may be due to the transformation of the available PbI₂ to MAPb(I_1–xBr_x)₃ as the MABr thickness increased. It could be because of the high temperature (140°C) of the substrate as PbBr₂ was being deposited on MAPbI₃ bottom layer. The exact mechanism of the transformation is not fully understood.

The Williamson-Hall (W-H) plot was used to determine the crystallite size and microstrain from the X-ray line broadening. The W-H plots (Supplementary Figure 1) are based on the Williamson-Hall relation given by Equation 2 (Williamson and Hall, 1953),

$\mathrm{\beta }\cos \mathrm{\theta }=\frac{K\mathrm{\lambda }}{D}+4\mathrm{\epsilon }\sin \mathrm{\theta }(2)$

where D is the crystallite, β is the full width at half maximum, λ is the wavelength, θ is the Bragg’s diffraction angle, ε is the microstrain and K is the Scherrer’s constant. The Scherrer’s constant is determined by the crystallite shape and is considered as 0.94 for spherical crystallites with cubic symmetry. Figures 2C,D shows how the average crystallite size and microstrain vary as the thickness of MABr is increased from 300 to 500 nm. The crystallite size is observed to range from 28 to 42 nm, in close agreement with the literature (Jang et al., 2015). Besides, the crystallite size first increases to 41 nm when the MABr thickness is 400 nm before decreasing to 28 nm as the thickness is increased to 500 nm. This correlates with the change in intensity of the PbI₂ peak shown in Figure 2B. Thus, the irregular variation in crystallite size could be due to the change in concentration of PbI₂ present in the thin-film. Figure 2D presents the microstrain of the MAPb(I_1–xBr_x)₃ as the MABr is increased from 300 to 500 nm. The microstrain decreases as the thickness MABr rises from 300 to 500 nm. Increasing the thickness of MABr from 300 to 500 nm causes the Br/I mole ratio to change from 24.0 to 7.0. The film containing 500 nm thick MABr with the smallest Br to I ratio has the least microstrain. Thus, the microstrain of MAPb(I_1–xBr_x)₃ decreases as the Br to I ratio decreases.

Optical Properties

Figures 3A,B show the absorbance of MAPbI₃, MAPbBr₃ and MAPb(I_1–xBr_x)₃, where x = 0.95, 0.94, and 0.89. As previously discussed, pure MAPbI₃ and MAPbBr₃ have values of x corresponding to 0.0 and 1.0, respectively. The respective absorption onsets of MAPbI₃, MAPbBr₃, and MAPb(I_0.11Br_0.89)₃ are seen at 785, 552, and 580 nm (Figure 3A), corresponding to bandgaps of 1.58, 2.25, and 2.14 eV, respectively. The bandgap of the MAPb(I_0.11Br_0.89)₃ is closer in value to that of MAPbBr₃. This is consistent with MAPb(I_0.11Br_0.89)₃ taking up the cubic crystal structure of MAPbBr₃ as revealed by XRD results above. Incorporating a small amount of I does not change MAPbBr₃ crystal structure (Lehmann et al., 2019). This is because Br-rich compositions have stronger intermolecular forces. Thus re-orientation of the cations is suppressed. Furthermore, pure MAPbI₃ absorbs more than MAPb(I_1–xBr_x)₃ and MAPbBr₃, and MAPb(I_1–xBr_x)₃ more than pure MAPbBr_3. This could be due to the presence of I in MAPbI₃ and MAPb(I_1–xBr_x)₃ thin-films. The greater the mole ratio of I in the structure, the higher its absorbance. Also, an increase in the I mole ratio causes a redshift in the absorption edge, indicative of a decrease in the optical bandgap. This decrease perhaps is because I has a greater ionic radius than Br which causes an expansion of the lattice (Dong et al., 2020). Figure 3B shows that the absorption intensity and onset of MAPb(I_1–xBr_x)₃ depend greatly on the value of x. As x decreases, the onset of absorption increases. A plot of the bandgap against x reveals a highly linear relationship with a positive slope, consistent with previous reports (Gil-escrig et al., 2015). The linear relationship shows that the bandgap of MAPb(I_1–xBr_x)₃ could be tuned for x ranging from 0.89 to 1.0 by increasing the thickness of MABr. This is quite a small range when compared to alloying using other methods but useful to form MAPb(I_1–xBr_x)₃ alloys with small I content which shows improved absorption than MAPbBr₃. Another prominent feature in the absorption spectrum of MAPb(I_1–xBr_x)₃ shown in Figure 3B is the sharp absorption onset, which according to Stranks et al. (2019), is an indication of low levels of energetic disorder. The onsets of absorption were used to calculate the bandgap and the results plotted against the x (Figure 3C). The bandgap is observed to increase linearly with x as expected for HaP with high Br content. The lattice constants of the cubic MAPb(I_1–xBr_x)₃ structures were computed using the same procedure reported in the literature (Fru et al., 2020b), and the results plotted against x as shown in Figure 3D. We observed that the lattice constant is inversely related to x, in agreement with the observation of Kulkarni et al. (2014) who used a solution sequential deposition method. Similarly, the bandgap is inversely related to the lattice constant, as shown in Supplementary Figure 2. Perhaps, the decrease in bandgap with increase MABr thickness is due to increase in the lattice constant. This is because an increase in the lattice constant causes the interatomic distance to increase. Therefore, the binding force between the valence electrons and nucleus is reduced. Thus, the energy required to convert a bound electron to a free or conduction electron reduces.

FIGURE 3

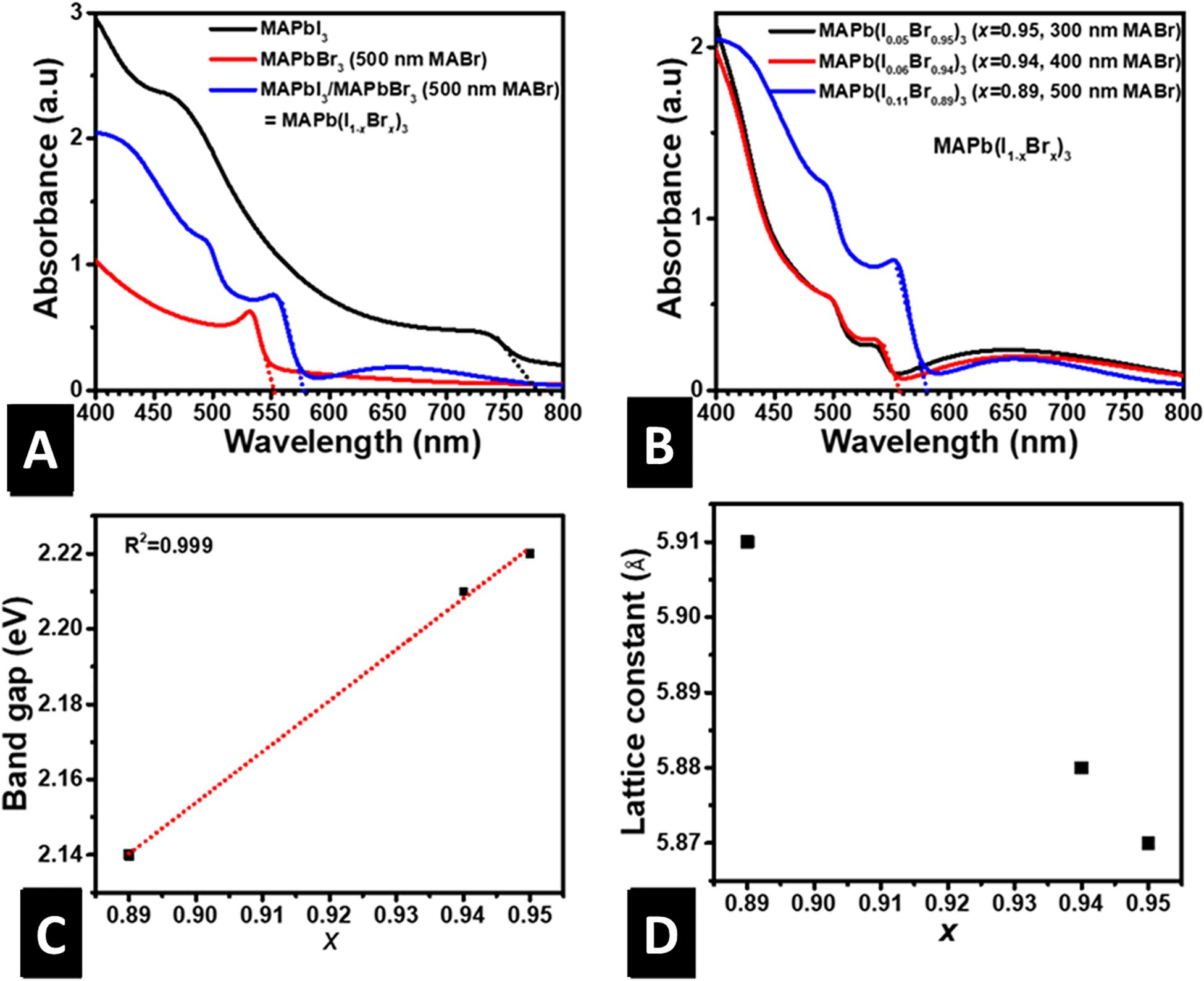
Figure 3. (A) Absorbance vs. wavelength of MAPbI₃, MAPbBr₃ and MAPb(I_0.11Br_0.89)₃, (B) Absorbance vs. wavelength of Pb(I_0.05Br_0.95)₃, MAPb(I_0.06Br_0.94)₃ and MAPb(I_0.11Br_0.89)₃, (C) Bandgap ofMAPb(I_1–xBr_x)₃ vs. bromine mole ratio x, (D) Lattice constant of MAPb(I_1–xBr_x)₃ vs. bromine mole ratio x.

Morphological Properties

Figure 4 shows the SEM micrographs and variation of average grain size with the thickness of MABr for MAPb(I_1–xBr_x)₃, where x = 0.95, 0.94, and 0.89. We observed that all the films showed full surface coverage of the substrate. The grains are densely packed, randomly oriented, and with few pinholes. The morphology evolves from a mixture of cuboidal grains and gel-like structures, at 300 nm MABr thickness, to one with only faceted bimodal distributed grains, when the thickness is 500 nm, which is characteristic of the cubic MAPbBr₃ structure (Fru et al., 2020b) shown in Supplementary Figure 3. This correlates well with the increase in the intensity of the (100) distinct peak for cubic MAPbBr₃ as the thickness of MABr is increased from 300 to 500 nm. The gel-like structures seen when the MABr thickness is 300 nm (MAPb(I_0.05Br_0.95)₃ can be linked to the rod-like structures that were seen on faceted grains solution deposited (MAPb(I_0.05Br_0.95)₃ by Kulkarni et al. (2014), and which were associated with high Br content. The average grain size is seen to increase from 150 to 320 nm as the thickness of MABr increases from 300 to 500 nm. The 500 nm MABr thick thin-film, with the most intense (100) characteristic peak corresponding to MAPbBr₃ (Figure 2B), has the highest average grain size. This points to the fact that an increase in average grain size could be due to a rise in the number and size of the MAPbBr₃ grains in the thin alloy films.

FIGURE 4

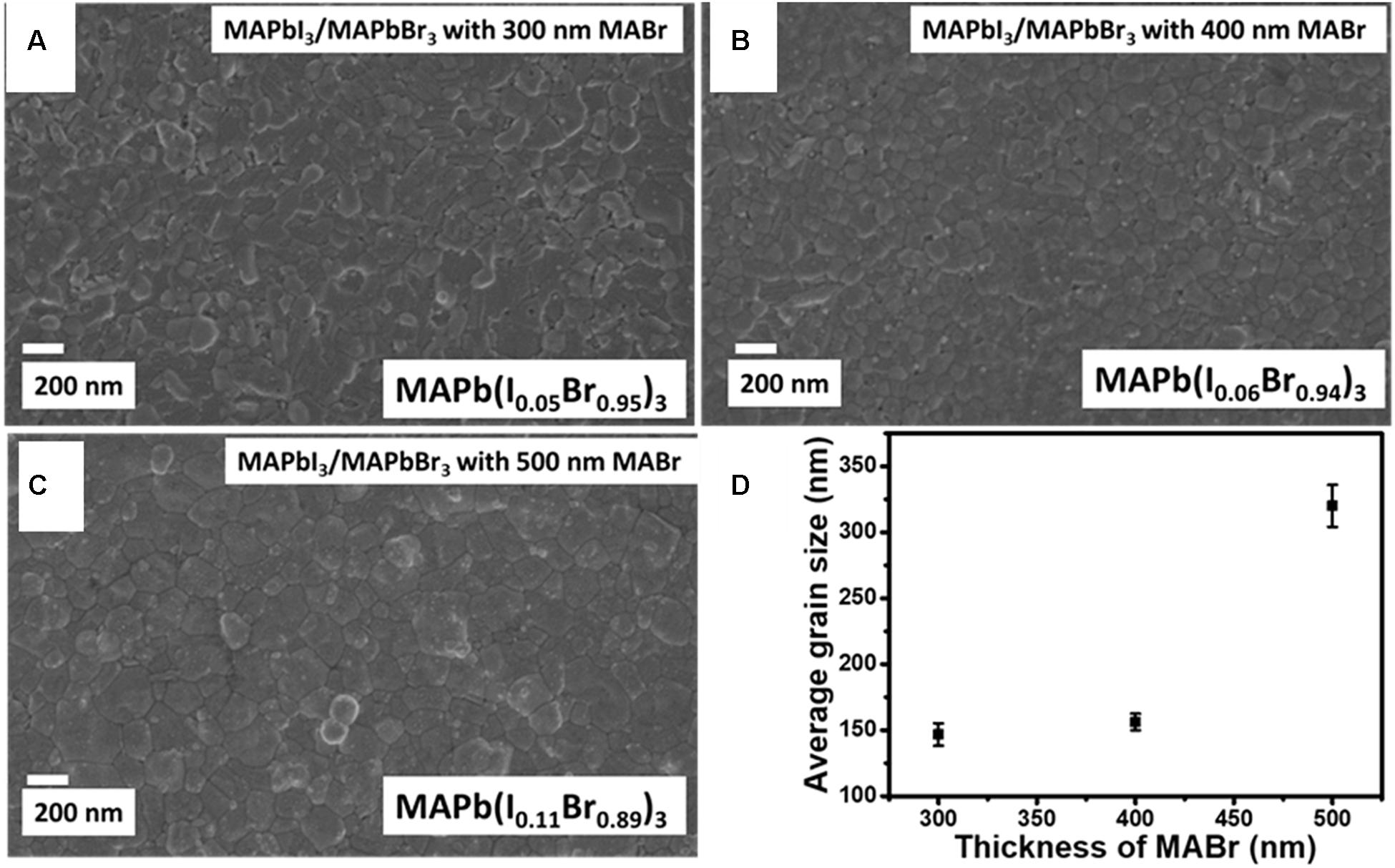
Figure 4. FE-SEM micrographs and average grain size of MAPb(I_1–xBr_x)₃ thin films for various MABr thicknesses, (A) MAPb(I_0.05Br_0.95)₃ having 300 nm of MABr, (B) MAPb(I_0.06Br_0.94)₃ having 400 nm of MABr, (C) MAPb(I_0.11Br_0.89)₃ having 500 nm of MABr, (D) the average grain size of MAPb(I_1–xBr_x)₃ thin films for various MABr thicknesses.

Electrical Properties

Figures 5A,B represents the semi-log and double-log plots of the dark current-voltage (I-V) characteristics of FTO/MAPb(I_1–xBr_x)₃/Au devices, respectively, where x is 0.95, 0.94, and 0.89. The semi-log I-V plot is meant to verify whether the contacts are ohmic, representing an infinite source of charge carriers. This confirms the possibility of using the space-charge-limited current (SCLC) measurement to calculate charge carrier mobility and trap density. The plots are nearly symmetrical, a sign that the contacts of the devices offer a very small barrier to charge injection, and SCLC measurement could be applied. The double-log plot shows two distinct regions for all values of x with slopes equals to 1.0 at low voltages and greater than 2.0 at high voltages, as shown in Figure 5B. This points to the fact that the charge transport mechanism in MAPb(I_1–xBr_x)₃ of the FTO/MAPb(I_1–xBr_x)₃/Au devices is ohmic conduction at low voltages, as is commonly reported in the literature (Röhr et al., 2017, 2018), and space charge limited at high voltages. Two factors are responsible for slopes greater than 2.0; the presence of traps and the existence of a built-in voltage (Röhr et al., 2018). Since the semi-log plot of the forward and reverse current-voltage characteristics are symmetric, then a slope greater than 2.0 is only due to the presence of charge traps. The trap density was calculated using Equation 3 as explained in our earlier report (Fru et al., 2020b).

$V_{TFL}=q{N}_t\frac{d^2}{2{\mathrm{\epsilon }}_o{\mathrm{\epsilon }}_r}(3)$

FIGURE 5

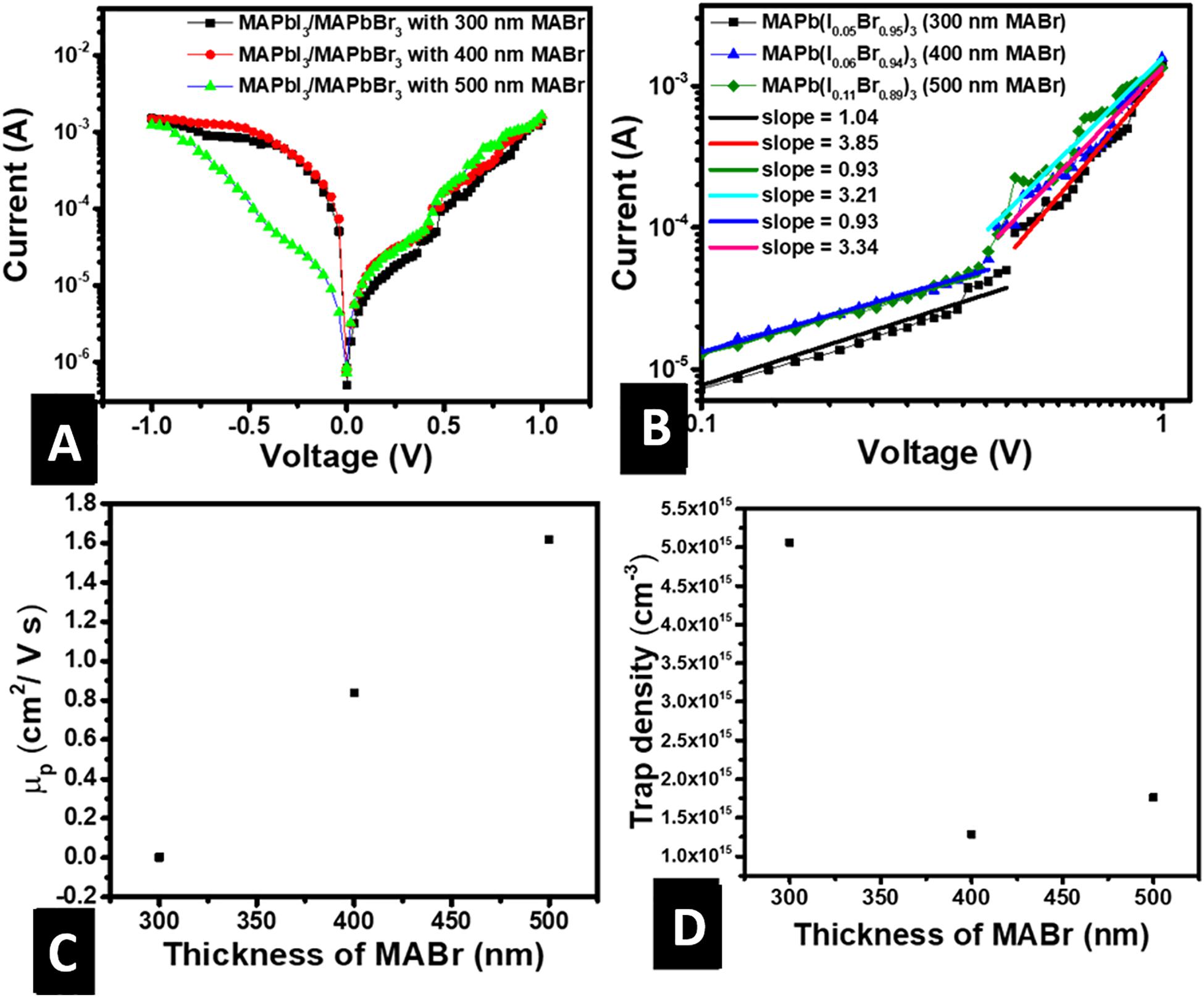
Figure 5. Dark current-voltage characteristics for FTO/MAPb(I_1–xBr_x)₃/Au from which the mobility and trap density are extracted using SCLC method. (A) Semi-log current-voltage characteristic showing ohmic contact, (B) double-log current-voltage characteristic for the calculation of trap density and mobility, (C) mobility of charge carriers in MAPb(I_1–xBr_x)₃ vs. thickness of MABr, (D) trap density in MAPb(I_1–xBr_x)₃ vs. thickness of MABr.

where N_t is trap density, d is film thickness, q is the electronic charge, V_TFL is the voltage at the point of transition from the ohmic to the space-charge-limited region, ε₀ is the vacuum permittivity, and ε_r the dielectric constant. The dielectric constant for halide perovskites at 295K is typically 25 (Le Corre et al., 2020). The N_t decreased non-uniformly as the thickness of MABr was increased, as shown in Figure 5D. This could be due to the increase in grain size as explained above.

The charge carrier mobility was estimated by SCLC interpretation of the dark I-V characteristics. SCLC mobility measurements for an ideal single-carrier device that contains a trap-free and un-doped semiconductor with no injection barriers are achieved using the Mott-Gunney law (Röhr et al., 2017, 2018). However, as previously explained, there is evidence of the presence of traps. Thus, the charge carrier mobility calculation was performed using the modified Mott-Gunney model shown in Equation 4 (Moiz et al., 2005),

$J=\frac{9}{8}{\mathrm{\epsilon }}_o{\mathrm{\epsilon }}_r\mathrm{\theta }{\mathrm{\mu }}_p\frac{V^2}{d^3}(4)$

where J is the current density, V is a voltage at the trap-filled limit (TFL); onset of space charge limited region, and θ is the trap factor and is calculated as explained in the literature (Moiz et al., 2005; Fru et al., 2020b). Figure 5C shows that the carrier mobility increases linearly with an increase in the thickness of MABr. This is consistent with the decrease in trap density and an increase in grain size, leading to less charge carrier scattering in the MAPb(I_1–xBr_x)₃ active layer as MABr thickness is increased. The calculated charge carrier mobility values are within the range for inorganic semiconductors (10^–4 − 10³ cm² V^–1 s^–1) (Yu et al., 2015). However, they are two orders of magnitude lower than values of single crystals calculated using the SCLC method (Saidaminov et al., 2015; Herz, 2017; Chen et al., 2018). This is expected since polycrystalline films have grain boundaries that tend to decrease the charge carrier mobility.

Figures 6A,B illustrates the plot of capacitance per unit area (C) against bias voltage (V) and Mott-Schottky (M-S) plots for FTO/c-TiO₂/m-TiO₂/MAPb(I_0.11Br_0.89)₃/Au solar cells, respectively. M-S analysis is a well-established experimental technique to determine the charge carrier density (N_d) and built-in voltage (V_bi) from C-V measurements. It is mostly applied in conventional semiconductor devices with p-n and semiconductor/metal junctions that have a fixed depletion layer and space charge region. The junction capacitance per unit area (C_dl) is given by Equation 5,

$\frac{1}{C_{dl}^2}=\frac{2{\mathrm{\epsilon }}_o{\mathrm{\epsilon }}_r}{q{N}_d}(V_{bi}-V)(5)$

FIGURE 6

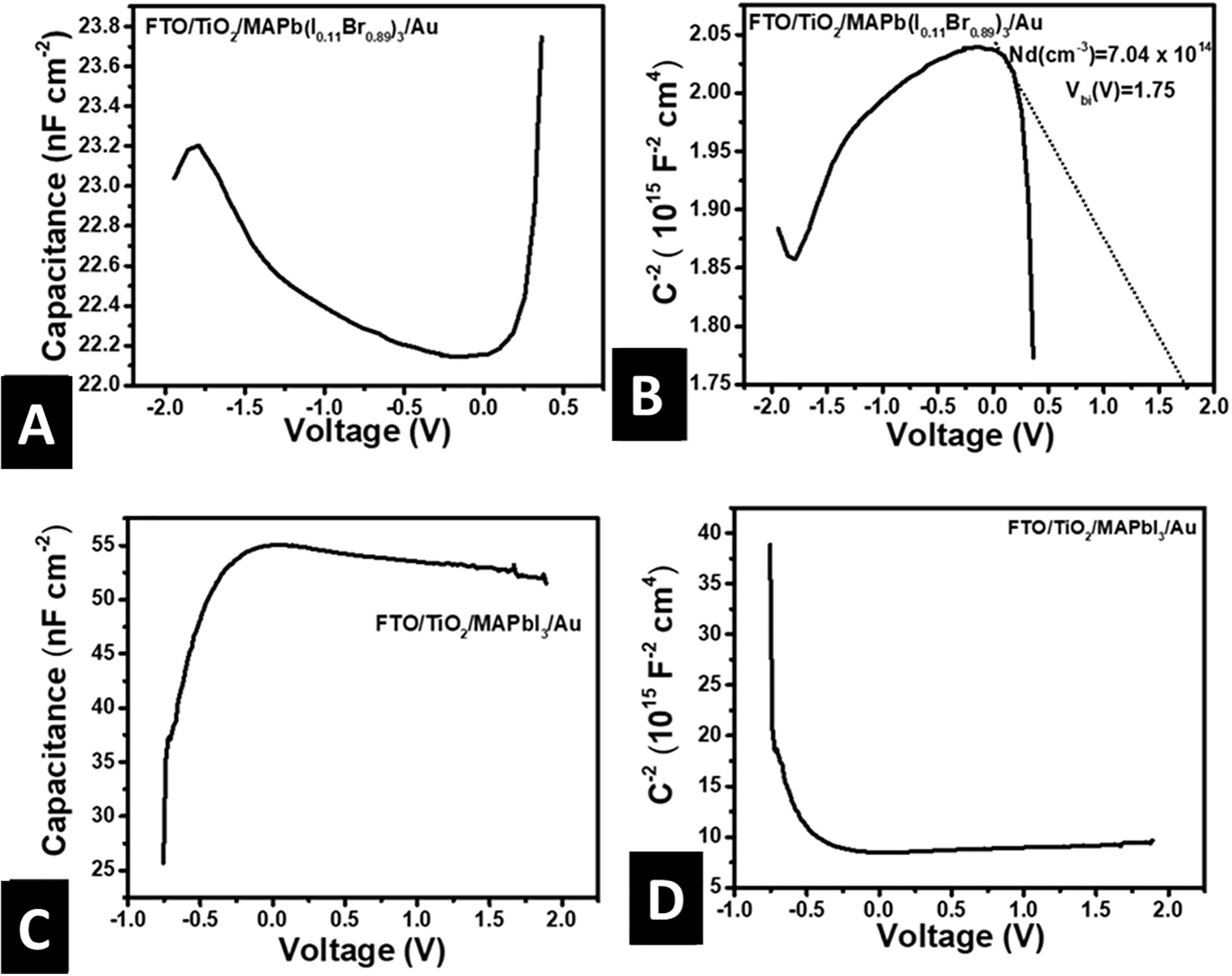
Figure 6. Dark current-voltage, capacitance-voltage and Mott-Schottky plots for FTO/c-TiO₂/m-TiO₂/MAPb(I_1–xBr_x)₃/Au solar cell. (A) Linear plot current density vs. voltage at forward and reverse bias showing barrier the potential, (B) semi-log plot of current vs. voltage, (C) linear plot of capacitance per unit area vs. voltage, (D) Mott-Schottky plot of inverse square capacitances per unit area vs. voltage.

where is the vacuum permittivity, ε_r is the dielectric constant of the donor, q is the electronic charge, V is the applied voltage. M-S plot is a graph of C_dl^–2 vs. V from which N_d is obtained from the gradient of the linear part and V_bi from an extrapolation of the linear part to the voltage axis (Figure 6B). The linear region with a negative slope exists on the plot under certain conditions which includes no electrons/holes in the space charge region and a homogenous distribution of the space charges (Shockley, 1948; Fischer et al., 2018). Our results show four distinct regions including an exponential increase in capacitance for voltages ranging from −0.5 to −2.0 V, a constant capacitance from −0.5 to 0.0 V, a linear dependence region from 0.0 to 0.2V, and an exponential increase in capacitance voltages greater than 0.2 V. Bera et al. (2017) obtained a similar deviation from the conventional straight line for other semiconductors. They attributed an exponential increase in capacitance with an increasing negative bias to the accumulation of electrons at the junctions, constant capacitance to a depletion region, and exponential capacitance at a forward bias to the accumulation of holes. Other reasons for constant capacitance may include depletion region exceeds the thickness of perovskite absorber (perovskite are entirely depleted), presence of injection barriers (Yadav et al., 2017), and accumulation of space charges at the interfaces (Hegedus and Shafarman, 2004; Almora et al., 2016; Fischer et al., 2018; Lee and Lee, 2019). Charge accumulation maybe due to a low level of doping, the intrinsic nature of the perovskites, and the presence of mobile ions (Fischer et al., 2018). The exponential capacitance, also known as the diffusion capacitance (Hegedus and Shafarman, 2004), has previously been attributed to the charged ions accumulation occurring at the TiO₂/perovskites and perovskites/Au interfaces in the literature (Almora et al., 2016; Fischer et al., 2018). The presence of capacitances other than the depletion capacitance shows N_d and V_bi cannot be determined from M-S plot. However, it reveals information on charge accumulation at interfaces that are due to ion migration. Thus, we could tell which of the optimum thin-films had a significant level of ion migration. This is useful in perovskite solar cells since a significant level of ion migration will cause hysteresis. There is a difference between V_bi (1.75 eV) from M-S plot and that from the knee of dark current density-voltage (J-V) characteristic (Supplementary Figure 4A). The dark J-V characteristic confirms that the device is highly rectifying with a large V_bi of 1.6 eV. However, the FTO/MAPb(I_1–xBr_x)₃/Au devices (Figure 5A) are only slightly rectifying. This means the rectification is a result of the introduction of TiO₂ and possibly at the TiO₂/MAPb(I_1–xBr_x)₃ junction. Thus, V_bi is the difference between Fermi levels of TiO₂ and MAPb(I_1–xBr_x)₃. The rectification could also be between the TiO₂ and gold electrodes if MAPb(I_1–xBr_x)₃ is intrinsic. The large V_bi at the p-n junction is fundamental for effective charge separation in solar cells leading to less recombination within the depletion layer (Lee and Lee, 2019; Rau and Kirchartz, 2019).

Figures 6C,D shows the C-V and M-S plots for FTO/TiO₂/MAPbI₃/Au solar cells, respectively. The capacitance increases sharply for the first decrease in negative bias, then stays nearly constant as negatives bias decreases to 0.0 and for an increase in the forward bias voltage from 0.0 to 2.0 V. Our C-V curves and Mott-Schottky plots were consistent with those obtained at lower frequencies by Liu and Zhang (2014) and Almora et al. (2016). The constant capacitance for the long-range of biasing voltage may be a sign that the depletion width exceeds the thickness of the perovskites absorber as earlier mentioned with no accumulation of charges at the interfaces. Supplementary Figures 4C,D stands for the J-V and semi-log I-V plots for FTO/TiO₂/MAPbI₃/Au solar cells. The knee in Supplementary Figure 4C shows that the device is rectifying with V_bi of 0.7 V. In our earlier work, we showed that FTO/MAPbI₃/Au device was near ohmic. Thus, the rectification may also be due to the difference between the work functions of the TiO₂ and the Au electrode.

Figure 7 shows the current density-voltage characteristic for FTO/MAPbBr₃/Au, FTO/MAPb(I_0.11Br_0.89)₃/Au, and FTO/MAPbI₃/Au solar cells under illumination. The power conversion efficiency (PCE), fill factor (FF), short circuit current density (J_sc), open-circuit voltage (V_oc), short resistance (R_sh), and series resistance (R_s) of the devices are presented in Table 1. The PCE of FTO/MAPbBr₃/Au, FTO/MAPb(I_0.11Br_0.89)₃/Au and FTO/MAPbI₃/Au solar cells were 0.56, 0.62, and 1.15%. These low PCE values could be due to the absence of charge transport layers and are comparable to those of other charge transport layer-free solar cells in the literature (Chen et al., 2014b; Peng et al., 2016; Duan et al., 2018). However, PCE values show that the halide perovskites are functional. The solar cell performance improves as x decreases. This could be due to the improvement in absorbance, decrease in bandgap and rise in charge carrier mobility as the bromine mole ratio decreased. Besides, the solar cell with x as 1.0 has the highest FF. This is consistent with the high R_sh value and could be because the MAPbBr₃ thin-film is very compact and does not have pinholes. The small V_oc values could be due to the absence of charge transport layers.

FIGURE 7

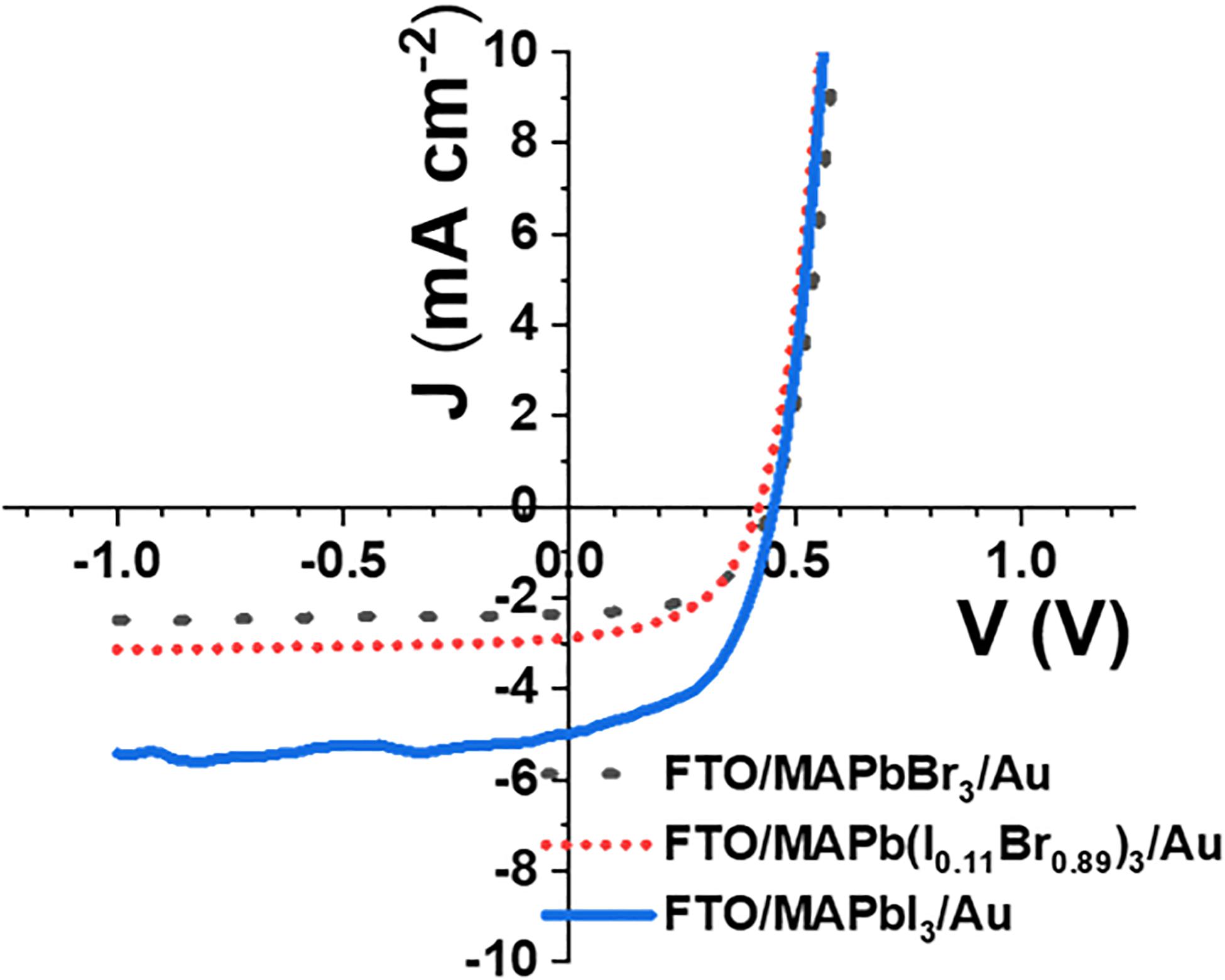
Figure 7. Current density—voltage characteristic for FTO/MAPbI₃/Au, FTO/MAPbBr₃/Au and FTO/MAPb(I_0.11Br_0.89)₃/Au solar cells under illumination.

TABLE 1

Table 1. The power conversion efficiency (PCE), fill factor (FF), short circuit current density (J_sc), open circuit voltage (V_oc), short resistance (R_sh) and series resistance (R_s) of FTO/MAPbBr₃/Au, FTO/MAPb(I_0.11Br_0.89)₃ and FTO/MAPbI₃/Au solar cells under illumination.

Conclusion

PbI₂-rich MAPb(I_1–xBr_x)₃ thin-films (x is 0.89, 0.94, and 0.95) were grown by stacking different MAPbBr₃ thin-films on MAPbI₃ bottom layer that were both prepared by SPVD. The bromine mole ratio x was varied by increasing the thickness of MABr from 300 to 500 nm. The value of x decreased as MABr thickness increased. Optical, electrical, morphological, and structural properties were found to depend on x. The optical and structural properties of the MAPb(I_1–xBr_x)₃ were compared with those of pure MAPbI₃ (x is 0.0) and MAPbBr₃ (x is 1.0). X-ray diffractograms revealed the transformation of tetragonal MAPbI₃ to the cubic phase of MAPbBr₃ as MAPb(I_1–xBr_x)₃ and PbI₂ were formed. The intensity of the PbI₂ phase formed with MAPb(I_1–xBr_x)₃ thin-film decreased as the thickness of MABr increased from 400 to 500 nm. The exact origin of the PbI₂ phase is not fully understood. However, it could be a result of the transformation of MAPbI₃ to PbI₂ due to prolonged annealing of the MAPbI₃ under-layer during the synthesis of the MAPbBr₃ top layer. This transformation was possibly caused by the high temperature (140°C) of the substrate as the PbBr₂ was being deposited. The microstrain of MAPb(I_1–xBr_x)₃ decreased as the thickness of MABr increased. This was attributed to the decrease in Br to I ratio. UV-Vis absorption spectra showed a decrease in bandgap of the thin MAPb(I_1–xBr_x)₃ film alloy from 2.21 to 2.14 eV as the thickness of MABr was increased from 300 to 500 nm. The bandgap was directly proportional to x and inversely related to the lattice constant, consistent with results obtained using other solution deposition techniques. The growth of MAPbBr₃ (100 nm PbBr₂ and 500 nm MABr) with bandgap 2.25 eV on MAPbI₃ (100 nm PbI₂ and 500 MAI) with bandgap 1.56 eV gave MAPb(I_0.11Br_0.89)₃ with bandgap of 2.14 eV. The Br mole ratio x in thin MAPb(I_1–xBr_x)₃ films was inversely proportional to its absorbance. FE-SEM micrographs depicted densely packed grains which on covered the substrate and containing few pinholes. The morphology of MAPb(I_1–xBr_x)₃ evolved from a mixture of cuboidal grains and gel-like structures at 300 nm MABr thickness to one with only faceted bimodal distributed grains at the thickness of 500 nm. This faceted cuboidal grain is a typical characteristic of the cubic MAPbBr₃. The average grain size increased from 150 to 320 nm as the thickness of MABr rose from 300 to 500 nm. The increase in average grain size was probably due to a rise in the number and size of MAPbBr₃ grains in the alloy. SCLC analysis of the dark J-V characteristics of FTO/TiO₂/MAPb(I_1–xBr_x)₃/Au devices showed relatively high charge carrier mobility values that increased linearly with MABr thickness. The SCLC analysis also revealed that the trap density decreased as x decreased. The PCE of FTO/MAPbBr₃/Au, FTO/MAPb(I_0.11Br_0.89)₃/Au and FTO/MAPbI₃/Au solar cells were 0.56%, 0.62% and 1.15%. This indicated that the PCE of the perovskite solar cells increased as x decreased. Study of the dark current density-voltage and capacitance-voltage curves of FTO/c-TiO₂/m-TiO₂/MAPb(I_0.11Br_0.89)₃/Au solar cells revealed a large V_bi of 1.6 V and an accumulation of charges at interfaces for voltages greater than 0.2 V. A similar analysis for FTO/TiO₂/MAPbI₃/Au device showed a small V_bi of 0.7 V and no charge at interfaces. The high V_bi of the FTO/c-TiO₂/m-TiO₂/MAPb(I_0.11Br_0.89)₃/Au solar cells was possibly caused by the electric field resulting from an accumulation of charged ions at the m-TiO₂/MAPb(I_0.11Br_0.89)₃ interface. This confirms that ion migration is very significant in mixed halide perovskites and insignificant in pure halide perovskites.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

JF: conceptualization, methodology, investigation, writing-original draft, and writing-review and editing. NN: supervision and writing-review and editing. MD: supervision and writing-review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the University of Pretoria, the National Research Foundation/the World Academy of Sciences (NRF-TWAS), and Grant Cost Centre N0115/115463 of the SARChI.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We wish to thank the University of Pretoria, National Research Foundation—The World Academy of Science (NRF-TWAS), and the Externally Funded UP Post-Doctoral Fellowship Programme: Grant Cost Centre N0115/115463 of the SARChI financial support.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.667323/full#supplementary-material

References

Aharon, S., Cohen, B., Bat, E., and Etgar, L. (2014). Hybrid lead halide iodide and lead halide bromide in efficient hole conductor free perovskite solar cell. J. Phys. Chem. C 118, 17160–17165. doi: 10.1021/jp5023407

CrossRef Full Text | Google Scholar

Almora, O., Aranda, C., Mas-marzá, E., and Garcia-belmonte, G. (2016). On mott-schottky analysis interpretation of capacitance measurements in organometal perovskite solar cells. Appl. Phys. Lett. 109:173903. doi: 10.1063/1.496612

CrossRef Full Text | Google Scholar

Bera, B., Chakraborty, A., Kar, T., Leuaa, P., and Neergat, M. (2017). Density of States, carrier concentration, and tlat band potential derived from electrochemical impedance measurements of N-doped carbon and their influence on electrocatalysis of oxygen reduction reaction. J. Phys. Chem. C 121, 20850–20856. doi: 10.1021/acs.jpcc.7b06735

CrossRef Full Text | Google Scholar

Borchert, J., Levchuk, I., Snoek, L. C., Rothmann, M. U., Snaith, H. J., Brabec, C. J., et al. (2019). Impurity tracking enables enhanced control and reproducibility of hybrid perovskite vapor deposition. ACS Appl. Mater. Interfaces. 11, 28851–28857. doi: 10.1021/acsami.9b07619

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C., Kang, H., Hsiao, S., Yang, P., Chiang, K., and Lin, H. (2014a). Efficient and uniform planar-type perovskite solar cells by simple sequential vacuum deposition. Adv. Mater. 26, 6647–6652. doi: 10.1002/adma.201402461

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L. C., Lee, K. L., and Lin, S. E. (2018). Observation of hybrid MAPBBr3 perovskite bulk crystals grown by repeated crystallizations. Crystals 8:260. doi: 10.3390/cryst8070260

CrossRef Full Text | Google Scholar

Chen, Z., Wang, J. J., Ren, Y., Yu, C., and Shum, K. (2014b). Schottky solar cells based on CsSnI3 thin-films. Appl. Phys. Lett. 101:093901. doi: 10.1063/1.4748888

CrossRef Full Text | Google Scholar

Dharmadasa, I. M., Rahaq, Y., Ojo, A. A., and Alanazi, T. I. (2019). Perovskite solar cells: a deep analysis using current–voltage and capacitance–voltage techniques. J. Mater. Sci. Mater. Electron. 30, 1227–1235. doi: 10.1007/s10854-018-0390-5

CrossRef Full Text | Google Scholar

Dong, C. R., Wang, Y., Zhang, K., and Zeng, H. (2020). Halide perovskite materials as light harvesters for solar energy conversion. Energy Chem. 2:100026. doi: 10.1016/j.enchem.2020.100026

CrossRef Full Text | Google Scholar

Duan, J., Zhao, Y., He, B., and Tang, Q. (2018). Simplified perovskite solar cell with 4.1% efficiency employing inorganic CsPbBr3 as light absorber. Small 14:1704443. doi: 10.1002/smll.201704443

PubMed Abstract | CrossRef Full Text | Google Scholar

Fischer, M., Tvingstedt, K., Baumann, A., and Dyakonov, V. (2018). Doping profile in planar hybrid perovskite solar cells identifying mobile ions. ACS Appl. Energy Mater. 1, 5129–5134. doi: 10.1021/acsaem.8b01119

CrossRef Full Text | Google Scholar

Fru, J. N., Nombona, N., and Diale, M. (2020a). Characterization of sequential physical vapor deposited methylammonium lead tri-iodide perovskite thin films. Vacuum 182:109727. doi: 10.1016/j.vacuum.2020.109727

CrossRef Full Text | Google Scholar

Fru, J. N., Nombona, N., and Diale, M. (2020b). Synthesis and characterisation of methylammonium lead tri-bromide perovskites thin films by sequential physical vapor deposition. Phys. B Phys. Condens. Matter 578:411884. doi: 10.1016/j.physb.2019.411884

CrossRef Full Text | Google Scholar

Gil-escrig, L., Sempere, A. M., Sessolo, M., and Bolink, H. J. (2015). Mixed iodide-bromide methylammonium lead poerovskite based diodes for light-emission and photovoltaics mixed iuodide-bromide methylammonium lead perovskite based diodes for light-emission and Photovoltaics. J. Phys. Chem. Lett. 6, 3743–3748. doi: 10.1021/acs.jpclett.5b01716

PubMed Abstract | CrossRef Full Text | Google Scholar

Hegedus, S. S., and Shafarman, W. N. (2004). Thin-film solar cells: device measurements and analysis. Adv. Mater. 176, 155–176. doi: 10.1002/pip.518

CrossRef Full Text | Google Scholar

Herz, L. M. (2017). Charge-carrier mobilities in metal halide perovskites: fundamental mechanisms and limits. ACS Energy Lett. 2, 1539–1548. doi: 10.1021/acsenergylett.7b00276

CrossRef Full Text | Google Scholar

Jang, D. M., Park, K., Kim, D. H., Park, J., Shojaei, F., Kang, H. S., et al. (2015). Reversible halide exchange reaction of organometal trihalide perovskite colloidal nanocrystals for full-range band gap tuning. Nano. Lett. 15:5191. doi: 10.1021/acs.nanolett.5b01430

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeon, N. J., Noh, J. H., Kim, Y. C., Yang, W. S., Ryu, S., and Seok, I. (2014). Solvent engineering for high-performance inorganic-organic hybrid perovskite solar cells. Nat. Mater. 13, 897–903. doi: 10.1038/NMAT4014

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, D. H., Whaitaker, J. B., Li, Z., van Hest, M. F. A. M., and Zhu, K. (2018). Outlook and challenges of perovskite solar cells toward terawatt-scale photovoltaic module technology. Joule 2, 1437–1451. doi: 10.1016/j.joule.2018.05.011

CrossRef Full Text | Google Scholar

Kulkarni, S. A., Baikie, T., Boix, P. P., Yantara, N., Mathews, N., and Mhaisalkar, S. (2014). Band-gap tuning of lead halide perovskites using a sequential deposition process. J. Mater. Chem. A 2, 9221–9225. doi: 10.1039/c4ta00435c

CrossRef Full Text | Google Scholar

Le Corre, V. M., Duijnstee, E. A., El, Tambouli O, Ball, J. M., Snaith, H. J., Lim, J., et al. (2020). Revealing charge carrier mobility and defect densities in metal halide perovskites via space-charge-limited current measurements. ACS Energy Lett. 6, 1087–1094. doi: 10.1021/acsenergylett.0c02599

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H., and Lee, C. (2019). Influence of electrical traps on the current density degradation of inverted perovskite solar cells. Mater 12:1644. doi: 10.3390/ma12101644

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, F., Franz, A., Daniel, M. T., Levcenco, S., Unold, T., Taubert, A., et al. (2019). The phase diagram of a mixed halide (Br. I) hybrid perovskite obtained by synchrotron X-ray. RSC Adv. 9, 11151–11159. doi: 10.1039/c8ra09398a

CrossRef Full Text | Google Scholar

Liang, Y., Wang, Y., Mu, C., Wang, S., Wang, X., Xu, D., et al. (2018). Achieving high open-circuit voltages up to 1.57 V in hole-transport-material-free MAPbBr3 solar cells with carbon electrodes. Adv. Energy Mater. 8, 1–6. doi: 10.1002/aenm.201701159

CrossRef Full Text | Google Scholar

Liu, W., and Zhang, Y. (2014). Electrical characterization of TiO₂/CH₃NH₃PhI₃ heterojunction solar cells. J. Mater. Chem. A. 2, 10244–10249.

Google Scholar

McFarlane, T. D., De Castro, C. S., Holliman, P. J., and Davies, M. L. (2019). Improving the light harvesting and colour range of methylammonium lead tri-bromide (MAPbBr3) perovskite solar cells through co-sensitisation with organic dyes. Chem. Commun. 55, 35–38. doi: 10.1039/c8cc07298a

PubMed Abstract | CrossRef Full Text | Google Scholar

Misra, R. K., Ciammaruchi, L., Aharon, S., Mogilyansky, D., and Etgar, L. (2016). Effect of halide composition on the photochemical stability of perovskite photovoltaic materials. Chem. Sus. Chem. 9, 2572–2577. doi: 10.1002/cssc.201600679

PubMed Abstract | CrossRef Full Text | Google Scholar

Moiz, S. A., Ahmed, M. M., and Karimov, K. S. (2005). Estimation of electrical parameters of OD organic semiconductor diode from measured I-V characteristics. Etri J. 27, 319–325. doi: 10.4218/etrij.05.0104.0100

CrossRef Full Text | Google Scholar

Ng, C. H., Ripolles, T. S., Hamada, K., Teo, S. H., Lim, H. N., Bisquert, J., et al. (2018). Tunable open circuit voltage by engineering inorganic cesium lead bromide/iodide perovskite solar cells. Sci. Rep. 8, 1–9. doi: 10.1038/s41598-018-20228-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Noh, J. H., Im, S. H., Heo, J. H., Mandal, T. N., and Seok, S. l (2013). Chemical management for colorful, efficient, and stable inorganic-organic hybrid nanostructured solar cells. J. Phys. Conf. Ser. 647:012069.

Google Scholar

Peng, W., Wang, L., Murali, B., Ho, K., Bera, A., Cho, N., et al. (2016). Solution-grown monocrystalline hybrid perovskite films for hole-transporter-free solar cells. Adv. Mater. 28, 3383–3390. doi: 10.1002/adma.201506292

PubMed Abstract | CrossRef Full Text | Google Scholar

Pistor, P., and Burwig, T. (2018). Thermal stability and miscibility of co-evaporated. J. Mater. Chem. A. 6, 11496–11506. doi: 10.1039/c8ta02775g

CrossRef Full Text | Google Scholar

Rau, U., and Kirchartz, T. (2019). Charge carrier collection and contact selectivity in solar cells Adv. Mater. Interfaces. 6:1900252. doi: 10.1002/admi.201900252

CrossRef Full Text | Google Scholar

Röhr, J. A., Kirchartz, T., and Nelson, J. (2017). On the correct interpretation of the low voltage regime in intrinsic single-carrier devices. J. Phys. Condens. Matter 29:205901. doi: 10.1088/1361-648X/aa66cc

PubMed Abstract | CrossRef Full Text | Google Scholar

Röhr, J. A., Shi, X., Haque, S. A., Kirchartz, T., and Nelson, J. (2018). Charge transport in spiro-OMeTAD investigated through space-charge-limited current measurements. Phys. Rev. Appl. 9:44017. doi: 10.1103/PhysRevApplied.9.044017

CrossRef Full Text | Google Scholar

Saidaminov, M. I., Abdelhady, A. L., Murali, B., Alarousu, E., Burlakov, V. M., Peng, W., et al. (2015). High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat. Commun. 6, 1–6. doi: 10.1038/ncomms8586

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, D., Adinolfi, V., Comin, R., Yuan, M., Alarousu, E., Buin, A., et al. (2015). Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science 80, 519–522. doi: 10.1126/science.aaa2725

PubMed Abstract | CrossRef Full Text | Google Scholar

Shockley, W. (1948). The theory of p-n junctions in semiconductors and p-n junction transistors. Bell. Syst. Tech. J. 28, 435–489. doi: 10.1002/j.1538-7305.1949.tb03645.x

CrossRef Full Text | Google Scholar

Stranks, S. D., Hoye, R. L. Z., Di, D., Friend, R. H., and Deschler, F. (2019). The physics of light emission in halide perovskite devices. Adv. Mater. 31:1803336. doi: 10.1002/adma.201803336

PubMed Abstract | CrossRef Full Text | Google Scholar

Swartwout, R., Hoerantner, M. T., and Bulovi, V. (2019). Scalable deposition methods for large-area production of perovskite thin films. Energy Environ. Mater. 2, 119–145. doi: 10.1002/eem2.12043

CrossRef Full Text | Google Scholar

Tisdale, J. T., Smith, T., Salasin, J. R., Ahmadi, M., Johnson, N., Ievlev, A. V., et al. (2018). Precursor purity effects on solution-based growth of MAPbBr3 single crystals towards efficient radiation sensing. Cryst. Eng. Comm. 20, 7818–7825. doi: 10.1039/c8ce01498a

CrossRef Full Text | Google Scholar

Wang, K. H., Li, L. C., Shellaiah, M., and Sun, K. W. (2017). Structural and photophysical properties of methylammonium lead tribromide (MAPbBr3) single crystals. Sci. Rep. 7, 1–14. doi: 10.1038/s41598-017-13571-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Williamson, G. K., and Hall, W. H. (1953). X-ray line broadening from filed aluminium and wolframL’elargissement des raies de rayons x obtenues des limailles d’aluminium et de tungsteneDie verbreiterung der roentgeninterferenzlinien von aluminium- und wolframspaenen. Acta Metall. 1, 22–31. doi: 10.1016/0001-6160(53)90006-6

CrossRef Full Text | Google Scholar

Wu, X., Xie, L. Q., Lin, K., Lu, J., Wang, K., Feng, W., et al. (2019). Efficient and stable carbon-based perovskite solar cells enabled by inorganic interface of CuSCN and carbon nanotubes Xin. Adv. Funct. Mater. 30:1908613. doi: 10.1039/C9TA02014D

CrossRef Full Text | Google Scholar

Yadav, P., Prochowicz, D., Saliba, M., Boix, P. P., Zakeeruddin, S. M., and Grätzel, M. (2017). Interfacial kinetics of efficient perovskite solar cells. Crystals 7:252. doi: 10.3390/cryst7080252

CrossRef Full Text | Google Scholar

Yu, G. F., Yu, M., Pan, W., Han, W. P., Yan, X., Zhang, J. C., et al. (2015). Electrical transport properties of an isolated CdS microrope composed of twisted nanowires. Nanoscale Res. Lett. 10, 1–7. doi: 10.1186/s11671-015-0734-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Y., and Li, Y. (2016). Perovskite CH3NH3Pb(BrxI1-x)3 single-crystals with controlled composition for fine-tuned bandgap towards optimized optoelectronic applications. J. Mater. Chem. C. 4, 9172–9178. doi: 10.1039/C6TC03592B

CrossRef Full Text | Google Scholar