Atomic Scale Structure of (Ag,Cu)2ZnSnSe4 and Cu2Zn(Sn,Ge)Se4 Kesterite Thin Films

Kesterite based materials are being researched and developed as affordable, efficient, and mechanically flexible absorber materials for thin film photovoltaics. Both (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ based devices have shown great potential in overcoming some of the remaining challenges for further increasing the conversion efficiency of kesterite based solar cells. This study therefore investigates the long range crystallographic structure and the local atomic scale structure of technologically relevant thin films by means of grazing incidence X-ray diffraction and low temperature X-ray absorption spectroscopy. As expected, the unit cell dimensions change about an order of magnitude more than the element specific average bond lengths. In case of Cu₂Zn(Sn,Ge)Se₄, the thin film absorbers show a very similar behavior as Cu₂Zn(Sn,Ge)Se₄ powder samples previously studied. Small amounts of residual S in the thin films were taken into account in the analysis and the results imply a preferential formation of Sn-S bonds instead of Ge-S bonds. In (Ag,Cu)₂ZnSnSe₄, the dependence of the Ag-Se and Cu-Se bond lengths on Ag/(Ag+Cu) might indicate an energetic advantage in the formation of certain local configurations.

1. Introduction

The quaternary compounds Cu₂ZnSnSe₄ and Cu₂ZnSnS₄ as well as some of their derivatives are well researched semiconductors (Giraldo et al., 2019). They can be used in multiple fields such as water splitting, charge transfer layers, thermoelectrics, and most prominently as absorbers in thin film solar cells (Nazligul et al., 2020). Their most mentioned advantages are the earth abundant, non-toxic and low cost elements, that the material is made of. Additionally, the direct band gap in the order of 1.0–1.5 eV enables the use in thin film technology as the absorption coefficient is high compared to traditional Si devices. The most prominent symptom of complications is that the conversion efficiency has not improved above the 12.6% record from 2013 (Wang et al., 2013; Son et al., 2019; Wong et al., 2019), while the theoretical limit is around 30% (Shockley and Queisser, 1961). In search of the cause, many studies have pointed out the low open-circuit voltage (V_oc) as a main culprit (Giraldo et al., 2019; Nazligul et al., 2020). This V_oc deficit and the low conversion efficiency may be directly connected to intrinsic properties of the bulk material. Off-stoichiometry, for example, can have benefits such as intrinsic doping and most of the current high efficiency devices are Cu poor and Zn rich (Giraldo et al., 2019). However, off-stoichiometry can also be connected to certain types of detrimental defects (Schorr et al., 2019). Parallels with Cu(In,Ga)(S,Se)₂ solar cell research have inspired a wide use of alloying in the kesterite research. Several elements have been used and tested in order to completely avoid, or at least reduce problems and defects connected to a specific element in the original Cu₂ZnSnSe₄ and Cu₂ZnSnS₄ compounds (Giraldo et al., 2019; Nazligul et al., 2020).

One of these intrinsic problems is the so called Cu-Zn disorder (Cu_Zn + Zn_Cu), which is one of several charge neutral defect complexes that may create recombination centers and therefore hinder device performance (Chen et al., 2010; Bourdais et al., 2016). To reduce the amount of these defects, the substitution of Cu by Ag has been controversially discussed in literature and tested in devices (Giraldo et al., 2019). Theoretical analysis of the defect formation energies yielded the proposal of a composition-graded (Cu_xAg_1−x)₂ZnSnSe₄ absorber to overcome the V_oc deficit (Yuan et al., 2015). Additional calculations and photoluminescence measurements seem to support that claim (Chagarov et al., 2016), nevertheless other studies found high densities of the respective antisite defects for Ag and Zn in Ag₂ZnSnSe₄ crystals (Cherns et al., 2018). Some solid solutions have adopted features of the stannite structure, thereby hindering a disorder (Gurieva et al., 2020). Thin film samples with different Ag/(Ag+Cu) ratios have shown improvements in performance and reduced defect concentrations in comparison to pure Cu₂ZnSnSe₄ or Cu₂ZnSnS₄ synthesized the same way (Li et al., 2015; Hages et al., 2016).

The Sn in the compounds also has intrinsic properties, that can be detrimental in a solar cell application. It is a potentially multivalent element, that has been connected to the formation of performance reducing deep defects (Biswas et al., 2010; Chen et al., 2013; Yee et al., 2015). Theoretical calculations proposed Ge as a potential candidate to replace Sn and overcome these issues (Shu et al., 2013). Experimentally, a substitution of Sn with Ge has shown multiple improvements, ranging from doping level concentrations of Ge helping the growth process (Giraldo et al., 2015, 2016) to actual alloying in different amounts (Collord and Hillhouse, 2016; Kim et al., 2016). The most prominent prove of concept in this line might be a close to record device with 12.3% conversion efficiency and a Ge/(Ge+Sn) ratio of 0.22 (Kim et al., 2016), exceeding pure Cu₂ZnSnSe₄ with a record conversion efficiency around 11.6% (Wong et al., 2019). Additionally a reduction of the V_oc deficit by replacing Sn with Ge has been shown (Choubrac et al., 2020).

Most alloying approaches do show multiple benefits, but also impose new challenges. One of the usual benefits is the possibility of band gap tuning by adjusting the elemental concentration, not just as a whole but also spatially resolved (Yuan et al., 2015; Collord and Hillhouse, 2016). As the end materials of the alloy series usually have different conduction band minima (CBM) and valence band maxima (VBM) and therefore also different band gap energies, a tuning of the band gap for optimal absorption or for band alignment on heterojunctions is possible (Giraldo et al., 2019; Nazligul et al., 2020). Both CBM and VBM mainly result from the interplay of orbitals from two elements in the structure. The VBM is formed by a hybridized state from Cu 3d or Ag 4d orbitals with anion p orbitals (Yuan et al., 2015). The CBM is the antibonding state of the hybridization between Sn or Ge s orbitals and the anions s orbitals (Shu et al., 2013). The distance between the elements directly influences the interaction of the orbitals and therefore the CBM or VBM. Hence, the band structure, which is key to device performance, is in turn connected to the very local structure, namely the bond length between specific elements. The influence of structural parameters smaller than the unit cell dimensions has been proven to be important in Cu(In,Ga)(S,Se)₂ (Wei et al., 1998; Vidal et al., 2010) as well as in kesterite type compounds (Botti et al., 2011). For Cu₂Zn(Sn,Ge)Se₄ powder samples a significant part of the band gap bowing parameter could be attributed to the structural changes due to alloying (Ritter et al., 2020). The elements sharing a lattice site in the (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ alloys are very different in size (Shannon, 1976), which must impose changes in both the long range structure and the atomic scale structure of the material. Therefore, a detailed knowledge of the local structure down to the bond length between specific elements, is key in understanding the effects of alloying on kesterite type thin films.

This work uses Extended X-ray Absorption Fine Structure Spectroscopy (EXAFS) to determine the element specific average bond lengths for all cations in technologically relevant (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ thin films. This method has been successfully applied to both kesterite (Zalewski et al., 2010; Ritter et al., 2020) and chalcopyrite (Eckner et al., 2013; Schnohr, 2015) materials to probe for subtle differences in atomic scale structure as a function of elemental concentrations. Additionally, X-ray diffraction was employed to measure the lattice parameters of the samples and thus to evaluate the change of the long range crystallographic structure with changing alloy composition.

2. Experimental

High efficiency kesterite thin films have been prepared by many different types of synthesis (Ratz et al., 2019; Todorov et al., 2020). Amongst the solution based approaches, methods employing nanoparticle-inks can decouple the primary kesterite formation from the thin film formation, are expected to scale up rather well and enable a compositional tuning (Todorov et al., 2020).

Ag- and Ge-alloyed CZTSe thin films used in this study were fabricated from nanoparticle-based techniques, as described in detail elsewhere (Hages et al., 2013, 2016). Briefly, (Ag,Cu)₂ZnSnS₄ and Cu₂Zn(Sn,Ge)S₄ nanoparticles were first synthesized using solution-based hot-injection synthesis. Nanoparticle films were subsequently deposited on molybdenum-coated soda lime glass substrates and heat treated in an evaporated selenium gas atmosphere at c. 500°C for 20 min (selenization) to form relatively large-grain (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ thin-films. A minor concentration of sulfur remains in the crystal lattice following selenization. This process yields solar cells with conversion efficiencies of nearly 10% (Hages et al., 2013). Samples were characterized using X-ray diffraction (XRD) and energy-dispersive X-ray spectroscopy (EDX). All samples analyzed in this study are nearly single phase (< 10% secondary phases), polycrystalline thin films. The low amount of secondary phases is an essential prerequisite for the EXAFS measurements in this study. Scanning electron microscopy showed these large grain films to have thicknesses around 0.5 μm. Representative images are shown in Supplementary Figure 1.

The structural properties of the (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ thin films were further investigated by grazing incidence X-ray diffraction (GIXRD) measurements. A PANAlytical X'Pert Pro MPD diffractometer, using Cu K_α radiation and a multilayer mirror to produce a parallel beam, were used to collect the GIXRD data. Detector scans with an incident angle of 1° were performed, in order to collect information from the bulk of the absorber. Resulting GIXRD patterns can be found in Supplementary Figure 2. To obtain the lattice parameters the LeBail refinement was performed, using the kesterite type structure (space group $I\bar{4}$) as the starting model for refinement. (Ag,Cu)₂ZnSnSe₄ or Cu₂Zn(Sn,Ge)Se₄ and the Mo phase were included in the refinement for each of the patterns.

To investigate element specific local structural parameters, low temperature EXAFS measurements were carried out at the P65 beamline of PETRA III at DESY in Hamburg, Germany (Welter et al., 2019). Fluorescence mode spectra were taken at the Cu, Zn, Ge, Ag, and Sn K-edge (8, 979, 9, 659, 11, 103, 25, 514, and 29, 200 eV, respectively). All samples were cooled down to 18 ±1 K by means of a liquid helium flow-through cryostat. This ensured the optimal signal to noise ratio and the precision needed to resolve subtle changes in the structural parameters. For each sample and each absorption edge a number of single spectra taken with the same experimental settings were merged. The comparison of these single spectra confirmed the good reproducibility of the measurements and the remaining variation is included in the final uncertainties. Background removal and normalization were performed with the DEMETER software package (Ravel and Newville, 2005). The Fourier transformation window in k-space was mainly determined by data quality and started at 3 Å⁻¹ for all spectra measured. The upper limit was set to 13 Å⁻¹ for spectra measured at the Zn, Ge, and Sn edge and to 11 Å⁻¹ for spectra measured at the Ag edge. For all Cu edge measurements the upper limit was given by the Zn edge starting beyond 12 Å⁻¹. The tapering parameter of the Hanning window function was 2 Å⁻¹ in all cases. Phase shifts and scattering amplitudes were calculated with FEFF9 (Rehr et al., 2010). The LARCH scripting library was used for fitting the mean value d (average bond length) and the variation σ² (bond length variation) of the nearest neighbor distance distribution in R-space. Final fits were executed with multiple k-weights of k², k³, and k⁴. Tests with higher (≥ 3) cumulants identified them to be negligible. They were thus set to zero. The fitting window was [1.5, 2.7 Å] at the Cu edge, [1.6, 2.7 Å] at the Zn edge, [1.5, 2.6 Å] at the Ge edge, [1.7, 2.8 Å] at the Ag edge, and [1.5, 2.6 Å] at the Sn edge with a tapering parameter of 0.8 Å. Both the amplitude reduction factor and the energy threshold were fixed to the average value determined from all spectra measured at one given absorption edge. All the above mentioned parameters were systematically varied to evaluate their influence on the final fitting results and to contribute to a valid estimation of the overall uncertainties.

3. Atomic Scale Structures

The EXAFS measurements allow the determination of an element specific average bond length. The average is both an average over effects like thermal vibrations (thermal disorder) as well as an average over all occurrences of a given element present in the probed sample volume (static or configurational disorder). The beam spot size is about 0.5 mm by 1.0 mm and the beam excites the entire thin film depth. For these reasons it is valid to assume, that every measurement contains information from the element under consideration in all configurations present in the material. Hence, to understand the element specific bond lengths obtained from the EXAFS measurements, the local motifs or building blocks have to be analyzed as they show the possible environments a cation can be found in. All local configurations around an anion in the ideal kesterite structure are displayed in Figure 1 together with the complete kesterite unit cell. Clearly, the kesterite structure is made up of tetrahedra containing a Se anion in the center and four cations around it. In standard Cu₂ZnSnSe₄, the tetrahedron can be found in the lower left front corner of the unit cell. It contains two Cu, one Zn, and one Sn cation. All other tetrahedra in the unit cell are just rotated versions of this first one. EXAFS is not sensitive to such a rotation. Hence for Cu₂ZnSnSe₄ only one kind of tetrahedron has to be considered. In case of Cu₂Zn(Sn,Ge)Se₄, the Sn is replaced by Ge in some tetrahedra as depicted in Figure 1E. So the (Sn,Ge) alloys are made up of two different kinds of tetrahedra, one with Sn and one with Ge. For (Ag,Cu)₂ZnSnSe₄, the situation is more complex, as there are two Cu atoms that can be replaced by Ag in the standard tetrahedron as depicted in Figures 1A–C. This results in four tetrahedra in total making up the ideal structure of (Ag,Cu)₂ZnSnSe₄. Note that, again, EXAFS cannot distinguish the configurations (Figures 1B,C) as they are equivalent in terms of cation species and atomic distances. For the (Sn,Ge) alloys, this means that the measured Sn-Se and Ge-Se bond lengths stem from only one tetrahedron each, while the measured Cu-Se and Zn-Se bond lengths represent an average over both tetrahedra. This average is weighted with the concentration of Ge or Sn in the given sample. For the (Ag,Cu) alloys, there are four possible tetrahedra, each of which is formed by one Sn, one Zn, and two of (Ag,Cu). Thus, the measured Zn-Se and Sn-Se bond lengths are an average over all four possible tetrahedra. The measured Cu-Se and Ag-Se bond lengths represent an average over three of the tetrahedra, only excluding the one configuration for which just the other element is present. There is no information, at this time, if any of the possible local configurations has a higher formation probability than the others. Consequently, the weighting factors with which the individual element specific bond lengths contribute to the measured average value are not precisely known.

FIGURE 1

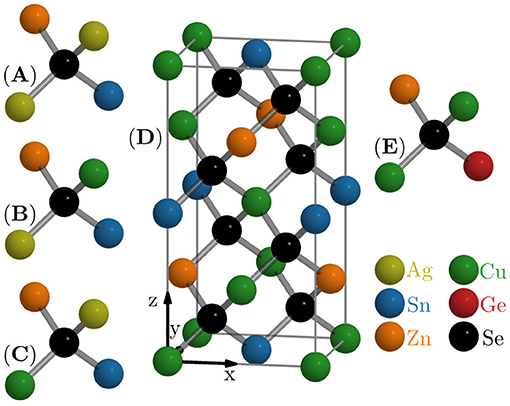
Figure 1. Unit cell of the kesterite-type Cu₂ZnSnSe₄ (D) and local tetrahedra for (Ag,Cu)₂ZnSnSe₄ (A–C) and Cu₂ZnGeSe₄ (E).

Additionally, any secondary phases or certain defects in the material, that alter the position or surrounding of an element, will also contribute to the element specific average bond length. In the case of Cu-Zn or Ag-Zn disorder, a swap of Cu or Ag with Zn within one tetrahedron is just equivalent to a rotation of one of the possible tetrahedra (see Figure 1). If instead just one (Cu,Ag) or Zn is replaced by the other, that would create a new kind of tetrahedron. This is true also for other types of defects that change the elemental composition of a tetrahedron, like the intrinsic V_Cu+${\text{Zn}}_{\mathrm{\text{Cu}}}^{2+}$ defect complex (Schorr et al., 2019). All these new or additional tetrahedra or even completely different local environments in secondary phases contribute to the average structural parameters obtained by EXAFS. Consequently, all deviations from the ideal structure depicted in Figure 1 will be contained in the EXAFS results and have to be accounted for in the discussion, if possible.

4. Element Specific Bond Lengths

Element specific average cation-Se bond lengths obtained from the low temperature EXAFS measurements of (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ thin film samples are plotted in Figure 2 as full symbols. Additionally, the results from a previous EXAFS study on Cu₂Zn(Sn,Ge)Se₄ powder samples are plotted as open symbols (Ritter et al., 2020). For most of the elements, the overall uncertainties are in the order of the symbol size in Figure 2 and are therefore not plotted. The estimated overall uncertainties comprise the influence of all analysis parameters as well as the fitting uncertainty and they are lower than 0.0025 Å whenever they are not depicted explicitly. A major difference between the two sample sets is residual sulfur in the thin film samples (S/(Se+S) < 10 %) (Hages et al., 2013), which is not present in the powder samples (Ritter et al., 2020). To account for this effect, a modified structural model was tested for all thin film samples. It included a mixed coordination shell with an individual bond length for each cation-Se and cation-S bond. The S/(S+Se) ratio was treated as additional fit parameter. The average bond lengths depicted in Figure 2 represent each cations average bond length to the Se neighbors and do not contain any cation-S contribution. The S/(S+Se) ratio determined by the fit varied around a few percent for Cu, Zn, and Ag. For the Ge edge, an acceptable fit with the modified model was not possible. Hence, the shown results for Ge-Se are derived with a structural model only containing Se. The Sn edge results, on the other hand, did show a S/(S+Se) ratio that was about 1.5–2 times higher than those obtained from the Cu, Zn, and Ag edge. This might be an indication of a preferential bonding between Sn and S or Ge and Se. Similar effects have been reported for other mixed cation-mixed anion compounds (Islam and Bunker, 1991; Kisiel et al., 1996; Lu et al., 1997). In the cited literature, the gain in binding energy when pairing the two larger species and the two smaller species was higher than the associated distortion energy resulting from the strain induced by the size differences. In case of (Sn,Ge) and (S,Se), however, the sum of the binding energies is nearly the same for either Ge-Se + Sn-S or Ge-S + Sn-Se (Dean, 1998) and hence the strain induced distortion energy becomes the decisive factor. This strain is evidently smaller when pairing the smaller anion (S) with the larger cation (Sn) and vice versa, thus favoring the formation of Sn-S bonds and suppressing the formation of Ge-S bonds. In all cases, not including S in the model shifted the average cation-Se bond length determined in the fit down within the order of magnitude of the overall uncertainty. This is due to all cation-S bonds being smaller than the corresponding cation-Se bonds. If these smaller bonds are included in the average cation-Se bond length, the fit result is lower because the determined average bond lengths then in fact corresponds to the average cation-anion bond lengths. This clearly demonstrates the need to account for the residual S in the structural model of the fit.

FIGURE 2

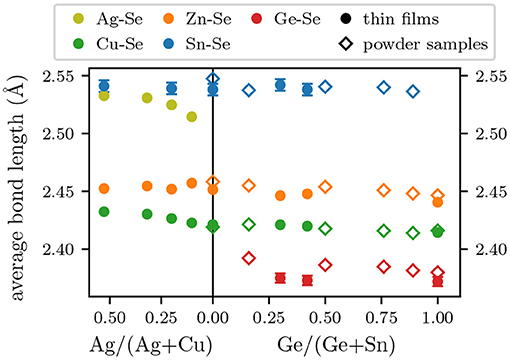
Figure 2. Element specific average bond lengths between cations and Se for all thin film samples (solid symbols) and powder sample values from Ritter et al. (2020) (open symbols) as a function of Ag/(Ag+Cu) (left) or Ge/(Sn+Ge) (right). In most cases, the error bars are about the size of the symbols or smaller and are therefore not plotted.

The average cation-Se bond lengths of the Cu₂Zn(Sn,Ge)Se₄ thin films are qualitatively very similar to the previously published results on Cu₂Zn(Sn,Ge)Se₄ powders shown in Figure 2 as open symbols (Ritter et al., 2020). The fact, that most thin film results are slightly lower than their corresponding powder values, may stem both from experimental differences like fluorescence vs. transmission EXAFS measurements or from physical differences between the samples like their composition. As mentioned before, most kesterite based devices are Cu poor and Zn rich. The thin film samples under investigation in this study all had a (Ag+Cu)/(Zn+Sn+Ge) ratio between 0.83 and 0.89 and a Zn/(Sn+Ge) ratio of 1.05–1.1. The powder samples had a Cu/(Zn+Sn+Ge) ratio of 1.0–1.09 and a Zn/(Sn+Ge) ratio of 1.0–1.2. Differences in the resulting defects could thus influence the element specific average bond lengths. Additionally, the selenization of nanocrystal inks leaves a so called fine-grain layer (about 0.2–0.5 μm thick) in between the large grain absorber layer and the Mo back contact (Hages et al., 2013). This layer mostly contains Se and C but also very low amounts of the original nanocrystals. They contribute to the average as discussed in 3 but ideally should not affect the average cation-Se bond lengths, as these nanocrystals are sulfides and therefore contribute to the average cation-S bond length.

Overall, the change of the element specific average bond lengths with composition is marginal compared to the difference between the different cations, especially so for those cations sharing a lattice site, namely Cu and Ag as well as Ge and Sn. This behavior is well-known for III-V and II-VI ternary alloys (Schnohr, 2015) and chalcopyrite Cu(In,Ga)Se₂ and Cu(In,Ga)S₂ (Schnohr et al., 2012; Eckner et al., 2013) and it is also visible for the Cu₂Zn(Sn,Ge)Se₄ kesterite powder samples (Ritter et al., 2020).

As mentioned above, the size difference of (Ag,Cu) and (Sn,Ge) is expected to affect both the atomic scale structure and the long range structure of the material. The lattice constants a and c determined from GIXRD measurements are depicted in Figure 3. Uncertainties are smaller than the symbol size and therefore are not plotted. The gray lines represent linear fits of the data. For (Ag,Cu)₂ZnSnSe₄ the shown lattice parameters are slightly lower than the ones reported by Gurieva et al. (2020), which is most likely due to the residual S, but they show the same dependence on Ag/(Ag+Cu). The lattice parameters change nearly linearly with composition which is in accordance with Vegard's law and therefore corresponds to the expected behavior. By increasing Ag/(Ag+Cu) the lattice constants increase whereas by increasing Ge/(Ge+Sn) they decrease. This is mainly due to the incorporation of a new element that is larger in case of Ag and smaller in case of Ge than its predecessor at the same lattice site. The changes from Cu₂ZnSnSe₄ to AgCuZnSnSe₄ are 2.5% in a but only 0.2% in c. From Cu₂ZnSnSe₄ to Cu₂ZnGeSe₄ they are 1.5% in a and 2.5% in c. This is vastly more than the changes in element specific average bond lengths, which are <0.6%. All these findings fit the following model of alloying, which was first proposed by Balzarotti et al. (1985). In this model, the cation sublattice is assumed to be relatively unchanged while the anion sublattice adjusts to the different sizes of the cations. Therefore, the alloyed (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ compounds are made up of the tetrahedral building blocks shown in Figure 1 and these building blocks scale in size with the lattice constants displayed in Figure 3. The anion position within each building block adjusts according to the nature of the surrounding cations, such that the average cation-anion bond lengths depicted in Figure 2, which are the average over the individual bond lengths of all building blocks weighted by the frequency of their occurrence (Ritter et al., 2020), do not change much with composition. The driving force behind this behavior is the distortion energy, which is significantly larger for bond stretching than for bond bending (Schnohr, 2015).

FIGURE 3

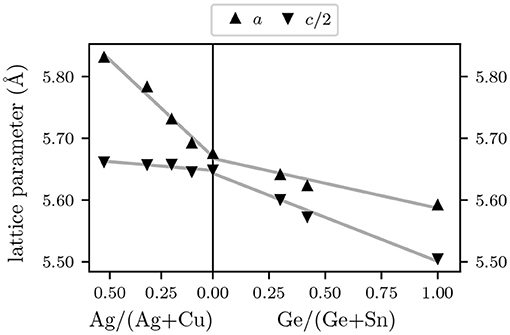
Figure 3. Lattice parameters a and c/2 as a function of Ag/(Ag+Cu) (left) or Ge/(Sn+Ge) (right) with linear fits as gray lines.

Figure 4 shows the same bond lengths as Figure 2 but on a zoomed-in scale for each element. This allows for a better evaluation of changes within the overall uncertainties. On the Cu₂Zn(Sn,Ge)Se₄ side, the Ge-Se, Cu-Se, and Zn-Se bond lengths show a small decrease with increasing Ge/(Ge+Sn). This trend fits the decreasing lattice constants (Figure 3) although the magnitude of the change is much smaller for the bond lengths than for the lattice constants as discussed above. The Sn-Se bond length does not show a clear trend within the uncertainty, which is partly due to the fact that no film with a Ge/(Ge+Sn) over 0.5 and only three samples in total could be analyzed.

FIGURE 4

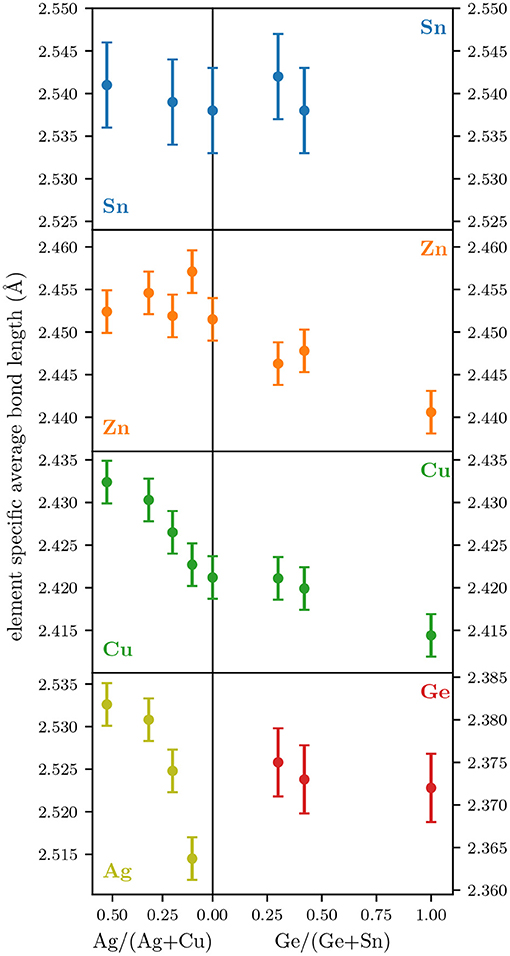
Figure 4. Element specific average bond lengths of all thin films for each cation species as a function of Ag/(Ag+Cu) (left) or Ge/(Sn+Ge) (right). Note the different scales on the left and right y-axis in the bottom most panel.

On the (Ag,Cu)₂ZnSnSe₄ side, the Zn-Se and Sn-Se bond lengths do not show any clear trend, especially in comparison to their uncertainty. In contrast, the Cu-Se and Ag-Se bond lengths both show a significant increase up to Ag/(Ag+Cu) = 0.3, above which the slope of the increase flattens. An increasing bond length is in accordance with the increase in lattice constants (Figure 3), but the non-linear dependence on composition cannot be explained by the lattice parameters, which change nearly linearly. In Cu(In,Ga)S₂ and Cu(In,Ga)Se₂ a non-linear slope of the bond lengths of the alloyed elements has been shown to be explicable by a non-random distribution of the alloyed elements on their lattice site (Eckner et al., 2013). The same might be true for this case. It is possible, that the formation of two mixed tetrahedra (Figures 1B,C) is energetically more or less favorable than the formation of one with only Ag (Figure 1A) and one with only Cu (Figure 1D) in it, thus changing the probability of occurrence for the mixed or non-mixed tetrahedra. From the significant difference in bond lengths for Ag-Se and Cu-Se visible in Figure 2 one can expect a difference in Ag-Se and Cu-Se bond lengths for the mixed tetrahedra compared to the ones with only Ag or only Cu, respectively. As discussed in 3, EXAFS measurements averages over all possible configurations Cu and Ag can potentially be found in and do not discern rotations of those. Therefore a change in probability of occurrence of these tetrahedra, would affect the EXAFS average results without creating a detectable long range order of the two elements, as the rotation and distribution of these tetrahedra throughout the sample, could still be random. So far no indication of a long range order of Ag and Cu in (Ag,Cu)₂ZnSnSe₄ has been reported. Nevertheless, if the distribution of Ag and Cu on the two positions in the tetrahedron was completely independent from each other, the frequency of occurrence for all configurations shown in Figure 1 could be calculated with binomial distributions and the resulting average bond length should show a more linear trend with composition (Schnohr, 2012; Schnohr et al., 2012). Another possible explanation for the non-linear slope of the average Cu-Se and Ag-Se bond lengths might be the different off-stoichiometry of the samples. The sample with Ag/(Ag+Cu) = 0.53 has both the highest (Cu+Ag)/(Zn+Sn) ratio and the highest Zn/Sn ratio of all investigated (Ag,Cu)₂ZnSnSe₄ thin films. As stated in 3 any type of defect, that changes the elemental composition of the tetrahedra, creates new local environments to consider. If any of these new configurations is energetically more favorable than others, it will shift the average bond lengths toward those of that particular configuration. To clarify this effect, EXAFS investigations of stoichiometric samples over the full Ag/(Ag+Cu) range would be of great interest. Investigating single phase stoichiometric material would reduce the amount of local configurations that need to be considered in evaluating any features of the element specific average cation-anion bond lengths. Studying the full compositional range would further allow to evaluate the slope of all element specific average bond lengths beyond Ag/(Ag+Cu) = 0.53, which might shed light on a potential non-random distribution of the Cu and Ag atoms on their respective lattice sites.

5. Conclusion

The element specific average bond lengths of technologically relevant (Ag,Cu)₂ZnSnSe₄ and Cu₂Zn(Sn,Ge)Se₄ thin films have been measured by low temperature EXAFS and compared to lattice parameters obtained from GIXRD. The change of the element specific average bond lengths is far smaller than the change of the lattice constants, as has been seen for many semiconductor alloys. At the same time, the bond lengths of the cations sharing the same lattice sites, namely Cu and Ag in (Ag,Cu)₂ZnSnSe₄ and Sn and Ge in Cu₂Zn(Sn,Ge)Se₄, are very different from each other. The results for Cu₂Zn(Sn,Ge)Se₄ are in good agreement with a previous study on Cu₂Zn(Sn,Ge)Se₄ powder samples. Furthermore, the inclusion of residual sulfur in the analysis indicates a preferential formation of Sn-S bonds instead of Ge-S bonds. The non-linearity with composition of the Ag-Se and Cu-Se average bond lengths in (Ag,Cu)₂ZnSnSe₄ might hint at an energetic advantage in the formation of certain local configurations.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

KR and CS perceived, designed, and organized this study. CH and RA were responsible for the synthesis and characterization of the thin film samples. GG and SS performed and evaluated the GIXRD measurements. KR, SE, CP, MR, EW, and CS conducted the EXAFS measurements and analysis. All authors contributed to the manuscript preparation and approved the final version.

Funding

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—SCHN 1283/2-1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Part of this research were carried out at the P65 beamline of PETRA III and we thank Dr. Ruidy Nemausat for his valuable help during the beamtime.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.656006/full#supplementary-material

References

Balzarotti, A., Motta, N., Kisiel, A., Zimnal-Starnawska, M., Czyżyk, M. T., and Podgórny, M. (1985). Model of the local structure of random ternary alloys: experiment versus theory. Phys. Rev. B 31, 7526–7539. doi: 10.1103/PhysRevB.31.7526

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, K., Lany, S., and Zunger, A. (2010). The electronic consequences of multivalent elements in inorganic solar absorbers: multivalency of Sn in Cu₂ZnSnS₄. Appl. Phys. Lett. 96:201902. doi: 10.1063/1.3427433

CrossRef Full Text | Google Scholar

Botti, S., Kammerlander, D., and Marques, M. A. L. (2011). Band structures of Cu₂ZnSnS₄ and Cu₂ZnSnSe₄ from many-body methods. Appl. Phys. Lett. 98:241915. doi: 10.1063/1.3600060

CrossRef Full Text | Google Scholar

Bourdais, S., Choné, C., Delatouche, B., Jacob, A., Larramona, G., Moisan, C., et al. (2016). Is the Cu/Zn disorder the main culprit for the voltage deficit in kesterite solar cells? Adv. Energy Mater. 6:1502276. doi: 10.1002/aenm.201502276

CrossRef Full Text | Google Scholar

Chagarov, E., Sardashti, K., Kummel, A. C., Lee, Y. S., Haight, R., and Gershon, T. S. (2016). Ag₂ZnSn(S,Se)₄: a highly promising absorber for thin film photovoltaics. J. Chem. Phys. 144:104704. doi: 10.1063/1.4943270

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., Walsh, A., Gong, X.-G., and Wei, S.-H. (2013). Classification of lattice defects in the kesterite Cu₂ZnSnS₄ and Cu₂ZnSnSe₄ earth-abundant solar cell absorbers. Adv. Mater. 25, 1522–1539. doi: 10.1002/adma.201203146

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., Yang, J.-H., Gong, X. G., Walsh, A., and Wei, S.-H. (2010). Intrinsic point defects and complexes in the quaternary kesterite semiconductor Cu₂ZnSnS₄. Phys. Rev. B 81:245204. doi: 10.1103/PhysRevB.81.245204

CrossRef Full Text | Google Scholar

Cherns, D., Griffiths, I. J., Jones, L., Bishop, D. M., Lloyd, M. A., and McCandless, B. E. (2018). Direct observation of high densities of antisite defects in Ag₂ZnSnSe₄. ACS Appl. Energy Mater. 1, 6260–6267. doi: 10.1021/acsaem.8b01274

CrossRef Full Text | Google Scholar

Choubrac, L., Bär, M., Kozina, X., Félix, R., Wilks, R. G., Brammertz, G., et al. (2020). Sn substitution by Ge: strategies to overcome the open-circuit voltage deficit of kesterite solar cells. ACS Applied Energy Mater. 3, 5830–5839. doi: 10.1021/acsaem.0c00763

CrossRef Full Text | Google Scholar

Collord, A. D., and Hillhouse, H. W. (2016). Germanium alloyed kesterite solar cells with low voltage deficits. Chem. Mater. 28, 2067–2073. doi: 10.1021/acs.chemmater.5b04806

CrossRef Full Text | Google Scholar

Dean, J. A. (1998). Lange's Handbook of Chmeistry. New York, NY; St. Louis, MI; San Francisco, CA; Auckland; Bogotá; Caracus; Lisbon; London; Madrid; Mexico; Milan; Montreal, QC; New Delhi; Paris; San Juan; São Paulo; Singapore; Sydney, NSW; Tokyo; Toronto, ON: McGraw-Hill, Inc.

Eckner, S., Kämmer, H., Steinbach, T., Gnauck, M., Johannes, A., Stephan, C., et al. (2013). Atomic-scale structure, cation distribution, and bandgap bowing in Cu(In,Ga)S₂ and Cu(In,Ga)Se₂. Appl. Phys. Lett. 103:081905. doi: 10.1063/1.4819225

CrossRef Full Text | Google Scholar

Giraldo, S., Jehl, Z., Placidi, M., Izquierdo-Roca, V., Pérez-Rodríguez, A., and Saucedo, E. (2019). Progress and perspectives of thin film kesterite photovoltaic technology: a critical review. Adv. Mater. 31:1806692. doi: 10.1002/adma.201806692

PubMed Abstract | CrossRef Full Text | Google Scholar

Giraldo, S., Neuschitzer, M., Placidi, M., Pistor, P., Perez-Rodriguez, A., and Saucedo, E. (2016). Cu₂ZnSnSe₄-based solar cells with efficiency exceeding 10% by adding a superficial Ge nanolayer: the interaction between Ge and Na. IEEE J. Photovolt. 6, 754–759. doi: 10.1109/JPHOTOV.2016.2535236

CrossRef Full Text | Google Scholar

Giraldo, S., Neuschitzer, M., Thersleff, T., López-Marino, S., Sánchez, Y., Xie, H., et al. (2015). Large efficiency improvement in Cu₂ZnSnSe₄ solar cells by introducing a superficial Ge nanolayer. Adv. Energy Mater. 5:1501070. doi: 10.1002/aenm.201501070

CrossRef Full Text | Google Scholar

Gurieva, G., Márquez, J. A., Franz, A., Hages, C. J., Levcenko, S., Unold, T., et al. (2020). Effect of Ag incorporation on structure and optoelectronic properties of (Ag₁−xCu_x)₂ZnSnSe₄ solid solutions. Phys. Rev. Mater. 4:054602. doi: 10.1103/PhysRevMaterials.4.054602

CrossRef Full Text | Google Scholar

Hages, C. J., Koeper, M. J., and Agrawal, R. (2016). Optoelectronic and material properties of nanocrystal-based CZTSe absorbers with ag-alloying. Sol. Energy Mater. Sol. Cells 145, 342–348. doi: 10.1016/j.solmat.2015.10.039

CrossRef Full Text | Google Scholar

Hages, C. J., Levcenco, S., Miskin, C. K., Alsmeier, J. H., Abou-Ras, D., Wilks, R. G., et al. (2013). Improved performance of ge-alloyed CZTGeSSe thin-film solar cells through control of elemental losses. Prog. Photovolt. Res. Appl. 23, 376–384. doi: 10.1002/pip.2442

CrossRef Full Text | Google Scholar

Islam, S. M., and Bunker, B. A. (1991). Studies of atomic correlations in quaternary semiconductor alloys using the extended x-ray absorption fine structure technique. Phys. Lett. A 156, 247–252. doi: 10.1016/0375-9601(91)90149-3

CrossRef Full Text | Google Scholar

Kim, S., Kim, K. M., Tampo, H., Shibata, H., and Niki, S. (2016). Improvement of voltage deficit of Ge-incorporated kesterite solar cell with 12.3% conversion efficiency. Appl. Phys Express 9:102301. doi: 10.7567/APEX.9.102301

CrossRef Full Text | Google Scholar

Kisiel, A., Łazewski, J., Zimnal-Starnawska, M., Burattini, E., and Mycielski, A. (1996). Manganese distribution in CdMnTeSe crystals. EXAFS data analysis. Acta Phys. Pol. A 90:1032. doi: 10.12693/APhysPolA.90.1032

CrossRef Full Text | Google Scholar

Li, W., Liu, X., Cui, H., Huang, S., and Hao, X. (2015). The role of Ag in (Ag,Cu)₂ZnSnS₄ thin film for solar cell application. J. Alloys Compd. 625, 277–283. doi: 10.1016/j.jallcom.2014.11.136

CrossRef Full Text | Google Scholar

Lu, Q., Bunker, B. A., Luo, H., Kropf, A. J., Kemner, K. M., and Furdyna, J. K. (1997). X-ray study of atomic correlations in zn₀.5cd₀.5se₀.5te₀.5 epitaxial thin films. Phys. Rev. B 55, 9910–9914. doi: 10.1103/PhysRevB.55.9910

CrossRef Full Text | Google Scholar

Nazligul, A. S., Wang, M., and Choy, K. L. (2020). Recent development in earth-abundant kesterite materials and their applications. Sustainability 12:5138. doi: 10.3390/su12125138

CrossRef Full Text | Google Scholar

Ratz, T., Brammertz, G., Caballero, R., Leon, M., Canulescu, S., Schou, J., et al. (2019). Physical routes for the synthesis of kesterite. J. Phys. 1:042003. doi: 10.1088/2515-7655/ab281c

CrossRef Full Text | Google Scholar

Ravel, B., and Newville, M. (2005). ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotr. Radiat. 12, 537–541. doi: 10.1107/S0909049505012719

PubMed Abstract | CrossRef Full Text | Google Scholar

Rehr, J. J., Kas, J. J., Vila, F. D., Prange, M. P., and Jorissen, K. (2010). Parameter-free calculations of X-ray spectra with FEFF9. Phys. Chem. Chem. Phys. 12:5503. doi: 10.1039/b926434e

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritter, K., Eckner, S., Preiß, C., Gurieva, G., Bischoff, T., Welter, E., et al. (2020). Atomic scale structure and its impact on the band gap energy for Cu₂Zn(Sn,Ge)Se₄ kesterite alloys. J. Phys. 2:035004. doi: 10.1088/2515-7655/ab9d8b

CrossRef Full Text | Google Scholar

Schnohr, C. S. (2012). Structural and electronic contributions to the bandgap bowing of (In,Ga)P alloys. J. Phys. 24:325802. doi: 10.1088/0953-8984/24/32/325802

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnohr, C. S. (2015). Compound semiconductor alloys: from atomic-scale structure to bandgap bowing. Appl. Phys. Rev. 2:031304. doi: 10.1063/1.4930002

CrossRef Full Text | Google Scholar

Schnohr, C. S., Käd'mmer, H., Stephan, C., Schorr, S., Steinbach, T., and Rensberg, J. (2012). Atomic-scale structure and band-gap bowing in Cu(In,Ga)Se₂. Phys. Rev. B 85:245204. doi: 10.1103/PhysRevB.85.245204

CrossRef Full Text | Google Scholar

Schorr, S., Gurieva, G., Guc, M., Dimitrievska, M., Pérez-Rodríguez, A., Izquierdo-Roca, V., et al. (2019). Point defects, compositional fluctuations, and secondary phases in non-stoichiometric kesterites. J. Phys. 2:012002. doi: 10.1088/2515-7655/ab4a25

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 32, 751–767. doi: 10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Shockley, W., and Queisser, H. J. (1961). Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519. doi: 10.1063/1.1736034

CrossRef Full Text | Google Scholar

Shu, Q., Yang, J.-H., Chen, S., Huang, B., Xiang, H., Gong, X.-G., et al. (2013). Cu₂Zn(Sn,Ge)Se₄ and Cu₂Zn(Sn,Si)Se₄ alloys as photovoltaic materials: structural and electronic properties. Phys. Rev. B 87:115208. doi: 10.1103/physrevb.87.115208

CrossRef Full Text | Google Scholar

Son, D.-H., Kim, S.-H., Kim, S.-Y., Kim, Y.-I., Sim, J.-H., Park, S.-N., et al. (2019). Effect of solid-H2S gas reactions on CZTSSe thin film growth and photovoltaic properties of a 12.62% efficiency device. J. Mater. Chem. A 7, 25279–25289. doi: 10.1039/C9TA08310C

CrossRef Full Text | Google Scholar

Todorov, T., Hillhouse, H. W., Aazou, S., Sekkat, Z., Vigil-Galan, O., Deshmukh, S. D., et al. (2020). Solution-based synthesis of kesterite thin film semiconductors. J. Phys. 2:012003. doi: 10.1088/2515-7655/ab3a81

CrossRef Full Text | Google Scholar

Vidal, J., Botti, S., Olsson, P., Guillemoles, J.-F., and Reining, L. (2010). Strong interplay between structure and electronic properties in CuIn(S,Se)₂: a first-principles study. Phys. Rev. Lett. 104:056401. doi: 10.1103/PhysRevLett.104.056401

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Winkler, M. T., Gunawan, O., Gokmen, T., Todorov, T. K., Zhu, Y., et al. (2013). Device characteristics of CZTSSe thin-film solar cells with 12.6% efficiency. Adv. Energy Mater. 4:1301465. doi: 10.1002/aenm.201301465

CrossRef Full Text | Google Scholar

Wei, S.-H., Zunger, A., Choi, I.-H., and Yu, P. Y. (1998). Trends in band-gap pressure coefficients in chalcopyrite semiconductors. Phys. Rev. B 58, R1710–R1713. doi: 10.1103/PhysRevB.58.R1710

CrossRef Full Text | Google Scholar

Welter, E., Chernikov, R., Herrmann, M., and Nemausat, R. (2019). A beamline for bulk sample x-ray absorption spectroscopy at the high brilliance storage ring PETRA III. AIP Conf. Proc. 2054:040002. doi: 10.1063/1.5084603

CrossRef Full Text | Google Scholar

Wong, L. H., Zakutayev, A., Major, J. D., Hao, X., Walsh, A., Todorov, T. K., et al. (2019). Emerging inorganic solar cell efficiency tables (version 1). J. Phys. 1:032001. doi: 10.1088/2515-7655/ab2338

CrossRef Full Text | Google Scholar

Yee, Y. S., Magyari-Köpe, B., Nishi, Y., Bent, S. F., and Clemens, B. M. (2015). Deep recombination centers in Cu₂ZnSnSe₄ revealed by screened-exchange hybrid density functional theory. Phys. Rev. B 92:195201. doi: 10.1103/PhysRevB.92.195201

CrossRef Full Text | Google Scholar

Yuan, Z.-K., Chen, S., Xiang, H., Gong, X.-G., Walsh, A., Park, J.-S., et al. (2015). Engineering solar cell absorbers by exploring the band alignment and defect disparity: the case of Cu- and Ag-based kesterite compounds. Adv. Funct. Mater. 25, 6733–6743. doi: 10.1002/adfm.201502272

CrossRef Full Text | Google Scholar

Zalewski, W., Bacewicz, R., Antonowicz, J., Pietnoczka, A., Evstigneeva, T., and Schorr, S. (2010). XAFS study of kesterite, kuramite and stannite type alloys. J. Alloys Compd. 492, 35–38. doi: 10.1016/j.jallcom.2009.11.158

CrossRef Full Text | Google Scholar