Electrode and Electrolyte Materials From Atomistic Simulations: Properties of LixFEPO4 Electrode and Zircon-Based Ionic Conductors

Li_xFePO₄ orthophosphates and fluorite- and pyrochlore-type zirconate materials are widely considered as functional compounds in energy storage devices, either as electrode or solid state electrolyte. These ceramic materials show enhanced cation exchange and anion conductivity properties that makes them attractive for various energy applications. In this contribution we discuss thermodynamic properties of Li_xFePO₄ and yttria-stabilized zirconia compounds, including formation enthalpies, stability, and solubility limits. We found that at ambient conditions Li_xFePO₄ has a large miscibility gap, which is consistent with existing experimental evidence. We show that cubic zirconia becomes stabilized with Y content of ~8%, which is in line with experimental observations. The computed activation energy of 0.92eV and ionic conductivity for oxygen diffusion in yttria-stabilized zirconia are also in line with the measured data, which shows that atomistic modeling can be applied for accurate prediction of key materials properties. We discuss these results with the existing simulation-based data on these materials produced by our group over the last decade. Last, but not least, we discuss similarities of the considered compounds in considering them as materials for energy storage and radiation damage resistant matrices for immobilization of radionuclides.

1. Introduction

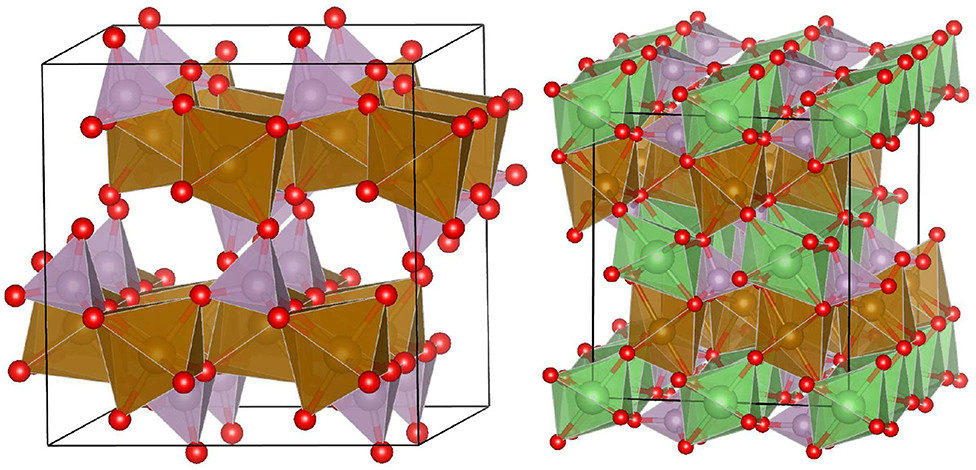
MPO₄ orthophosphates, with M cations being transition metals, rare-earth elements or actinides, are ceramic materials of interest in various research fields, including geochronology (Williams et al., 2007), geothermometry (Andrehs and Heinrich, 1998; Mogilevsky, 2007), energy storage (Iyer et al., 2006; Yamada et al., 2006; Dunn et al., 2015; Dong et al., 2017; Cerdas et al., 2018; Li et al., 2018; Phan et al., 2019), and nuclear waste management (Ewing and Wang, 2002; Neumeier et al., 2017a; Schlenz et al., 2018), to name but a few. Most of the potential applications come from high durability (e.g., radiation damage resistance) of these materials (Neumeier et al., 2017a; Phan et al., 2019). There exist large varieties of phosphate-based ceramics of different crystalline structures (e.g., cheralite, apatites, olivine, kosnarite, see Iyer et al., 2006; Neumeier et al., 2017a; Phan et al., 2019). The orthophosphates of interest for energy storage, FePO₄ and LiFePO₄, have olivine-type structure of orthorombic space group symmetry of Pnma in which Fe exists in an octahedral environment (Iyer et al., 2006; Maxisch and Ceder, 2006, see Figure 1 for visualization of the structures). It consists of eight-fold coordinated Fe³⁺ cations, which become reduced to Fe²⁺ upon incorporation of Li. Besides, there exist less stable FePO₄ monoclinic, orthorombic, and trigonal phases with Fe in tetrahedraly coordinated crystallographic positions (Iyer et al., 2006; Yamada et al., 2006; Dong et al., 2017). LiFePO₄ materials are one of the best known candidates for energy storage electrodes (Dunn et al., 2015; Cerdas et al., 2018). These exhibit high theoretical energy density of 170mAh/g and voltage of 3.5V (Phan et al., 2019). Because of this, these materials are considered for large scale energy storage devices, including batteries for hybrid and electric automobiles (Prosini et al., 2002; Dunn et al., 2015; Cerdas et al., 2018). Intercalation of Li ions into FePO₄ results in formation of a solid solution between Li cations and vacant sites (Phan et al., 2019). Depending on the sizes of mixing species, a solid solution compounds could form a thermodynamically stable solid solution or a compound with a mixture of two phases, each rich in one of the cations (Kowalski and Li, 2016; Ji et al., 2019a). The second case indicates formation of a temperature dependent miscibility gap. The two endmember phases may be of the same type, like in the case of Li_xFePO₄, or different phases, like in the monazite-xenotime system (Mogilevsky, 2007; Ji et al., 2019a). The formation of miscibility gap is correlated with the maximum solubility (Ji et al., 2019a). Such a temperature-dependent maximum solubility offers opportunity to use such a system as geothermometer (Andrehs and Heinrich, 1998; Mogilevsky, 2007). It is known from experiment that Li_xFePO₄ solid solution posses a wide miscibility gap at ambient temperature (Yamada et al., 2006; Meethong et al., 2007; Li et al., 2018; Phan et al., 2019). In particular, studies of Yamada et al. (2006) indicate relatively low Li solubility limits in Li_xFePO₄ system at x = 0.05 and 0.89. The thermodynamics of such a system, however, although has been modeled by CALPHAD method (Phan et al., 2019), has not been modeled in details using ab initio atomistic modeling methods and the results of various studies differ substantially (Phan et al., 2019).

FIGURE 1

Figure 1. Structures of FePO₄ (left) and LiFePO₄ (right).

Zirconium-based ceramics have been shown to posses interesting ion-conduction characteristics (Diazguillen et al., 2008; Mandal et al., 2008; Xia et al., 2010; Anithakumari et al., 2016; Li and Kowalski, 2018), with yttria stabilized zirconia being one of the fastest ionic conductors (Kilo et al., 2003; Krishnamurthy et al., 2005b). It is thus used as solid electrolyte in various energy storage devices (Zakaria et al., 2020). The fast oxygen conduction properties are associated with formation and distribution of vacant sites (in fluorite and pyrochlore, Bukaemskiy et al., 2021) and interesting short- and long-range ordering phenomena (Wuensch, 2000; Yamamura, 2003; Anithakumari et al., 2016; Drey et al., 2020; Kowalski, 2020; Bukaemskiy et al., 2021). For instance, certain pyrochlore compounds exhibit high ionic conductivity (e.g., Eu₂Zr₂O₇, Yamamura, 2003) and form a stable, cation-disordered solid phase (defect fluorite, Li et al., 2015). Such phases show interesting short- and long-range ordering (Shamblin et al., 2016; Drey et al., 2020; Kowalski, 2020; Bukaemskiy et al., 2021), with distribution of vacancies determining the amplitude of pre-exponential factor and efficiency of ionic conduction (Bukaemskiy et al., 2021). For instance, Bukaemskiy et al. (2021) demonstrated that the maximum of ionic conductivity in YO_1.5 − ZrO₂ system occurs at x = 0.146 due to vacancy avoidance phenomenon and related vacancy jump probability. This correlates well with the existing ionic conductivity data (Bukaemskiy et al., 2021). Cubic phase of zirconia (ZrO₂) becomes stabilized upon doping with tri-valent elements, e.g., Y (Li et al., 1994; Kilo et al., 2003; Krishnamurthy et al., 2005b) at about 8% content of dopant. The formed solid solution shows very high ionic conductivity that increases significantly with dopant amount (Ioffe et al., 1978; Bukaemskiy et al., 2021). These compounds are thus considered as solid electrolyte for energy storage devices (Zakaria et al., 2020).

In the last two decades, atomistic modeling became a widely used research technique in various research fields, including energy materials (Chroneos et al., 2013; Jahn and Kowalski, 2014; Wu et al., 2019). We used it intensively over the past decade for computation of, for instance, various physical and chemical properties of orthophosphate- and zircon-based ceramics (e.g., Kowalski et al., 2015; Ji et al., 2019a). This is because steady advancements in high performance computing and computational software, especially in ab initio methods-based codes, allows nowadays for computation of complex systems containing hundreds of atoms from first principles (Jahn and Kowalski, 2014). Regarding ceramic compounds considered here, computational studies have been used to deliver information on: the structural (Rustad, 2012; Feng et al., 2013; Blanca-Romero et al., 2014; Beridze et al., 2016; Huittinen et al., 2017), the electronic structure (Tang and Holzwarth, 2003; Blanca-Romero et al., 2014; Kowalski et al., 2017a; Lee et al., 2017), the elastic (Wang et al., 2005; Feng et al., 2013; Ali et al., 2016; Kowalski and Li, 2016; Ji et al., 2017a; Kowalski et al., 2017b), the thermodynamic (Mogilevsky, 2007; Feng et al., 2013; Li et al., 2014; Kowalski et al., 2015, 2016; Ji et al., 2017b; Neumeier et al., 2017b; Eremin et al., 2019), the thermochemical (Rustad, 2012; Beridze et al., 2016; Kowalski, 2020), the electrochemical (Krishnamurthy et al., 2005b; Lee et al., 2017), and the radiation damage resistance (Kowalski et al., 2016; Li et al., 2016; Ji et al., 2017c; Jolley et al., 2017) parameters as well as materials at high-pressure (López-Solano et al., 2010; Stavrou et al., 2012; Ali et al., 2016; Shein and Shalaeva, 2016; Gomis et al., 2017). The relevant research activity increases steadily worldwide, with most of the papers published just recently. One important aspect is the correct calculations of compounds with d- and f- elements that contain strongly correlated electrons [e.g., Fe, Ni, lanthanides (Ln), actinides (An)]. In a series of papers we have shown that standard DFT approach often fails for such cases and these compounds must be carefully computed, including proper accounting for the correlation effects (Beridze and Kowalski, 2014; Blanca-Romero et al., 2014; Kowalski et al., 2015; Li and Kowalski, 2018). These simulations must be performed with methods beyond the standard DFT+U approach and include derivation of the Hubbard U parameter and careful choice of projectors for estimation of occupancy of d− and f− levels within the DFT+U scheme (Maxisch and Ceder, 2006; Kvashnina et al., 2018; Kick et al., 2019). In particular, we apply the linear response method (Cococcioni and de Gironcoli, 2005) with Wannier orbitals as representation of d or f states (Kvashnina et al., 2018) and here we will demonstrate impact of these procedures on the estimation of formation enthalpies and solubility limits of Li_xFePO₄ compound.

In this contribution we provide an overview of the recent atomistic modeling activities on the orthophosphates and zirconates, focusing on the information that have been delivered by atomistic modeling activities at Forschungszentrum Jülich and that allowed on many occasions for better characterization of these materials, including long-term thermodynamic stability, thermochemical parameters, and thermal conductivity. Besides such overview, we present results of computation of thermochemical and thermodynamic parameters of Li_xFePO₄ solid solution, with focus on the formation of miscibility gap in this system, as well as simulation of yttria-stabilized zirconia with focus on prediction the phase stability and ionic conductivity in this class of materials. We especially highlight a cross-linking, interdisciplinary character of our research, from which the general science community could highly benefit.

2. Computational Approach

In all ab initio¹ calculations discussed here we used a density functional theory (DFT)-based quantum chemistry approach and calculations were performed with Quantum-ESPRESSO simulation package (Giannozzi et al., 2009). We applied the PBEsol exchange-correlation functional (Perdew et al., 2008), the ultrasoft pseudopotentials to represent the core electrons of the atoms (Vanderbilt, 1990) and the plane-wave energy cutoff of 50 Ryd. The PBEsol functional is specifically selected because it correctly reproduces slowly varying electron density limit and results in good structural parameters of solids (Perdew et al., 2008). This is important for consideration of, for instance, thermodynamics of solid solutions (Li et al., 2014; Kowalski and Li, 2016; Ji et al., 2019a). Following our broad experience on computation of lanthanide orthophosphates and zirconates (e.g., Blanca-Romero et al., 2014; Li et al., 2015; Beridze et al., 2016) we applied the self-consistent DFT+U approach. The DFT+U calculations were performed with the Hubbard U parameter values computed from first principles using the linear response method of Cococcioni and de Gironcoli (2005). In order to apply realistic projectors for occupations of d orbitals of Fe we used Poor Man Wannier scheme implemented in Quantum-ESPRESSO. This computational setup was extensively tested by us in several studies and, among others, proved to give very good results for orthophosphates and zirconates (Blanca-Romero et al., 2014; Beridze et al., 2016; Finkeldei et al., 2017). The activation barriers were computed using Nudged Elastic Band (NEB) method implemented in Quantum-ESPRESSO, with 10 images and climbing image procedure to compute the transition state. The exponential pre-factors were computed with the aid of transition state theory (Moynihan et al., 1982) and probability of vacancy migration derived by Bukaemskiy et al. (2021), so that the ionic conductivity, σ, is estimated using the modified here formula of Moynihan et al. (1982):

$\begin{array}{l}\sigma =[15.354x(1-2x){\left(\frac{1-3x}{1-2x}\right)}^2]n{(Ze)}^2/(6k_{b}T){\nu }_0{d}^2\\ exp(-E_a/(k_{b}T{N}_a)),& (1)\end{array}$

where Ze is the charge of the carrier, k_b is the Boltzmann constant, N_a is Avogadro number, d is the distance of the jump, E_a is the activation barrier, T is the temperature and ν₀ is the attempt frequency. The first part in the square bracket reflects the vacancy migration probability contribution to the pre-exponential factor derived by Bukaemskiy et al. (2021). The attempt frequency ν₀ was estimated from the computation of phonon spectra of the initial (IS) and transition states (TS), as

$\begin{array}{ll}{\nu }_0=\frac{{\displaystyle {\prod }_i^{3N-3}}{\nu }_{i,IS}}{{\displaystyle {\prod }_i^{3N-4}}{\nu }_{i,TS}}.& (2)\end{array}$

The computation of Li_xFePO₄ phases were performed with 2x2x1 supercells (96 atoms for FePO₄ and 112 atoms for LiFePO₄ phases) using the 2x2x2 k-point grid. The oxides were computed as: Fe₂O₃ (Pnmm symmetry, with supercell containing 30 atoms and 4x6x2 k-point grid), hexagonal P₂O₅ as is in Blanca-Romero et al. (2014) and Y₂O₃ as cubic oxide. The magnetic arrangements in iron phases were computed using the models of Whittingham et al. (2005) and Lee et al. (2017).

The Hubbard U parameters computed with the linear response method are listed in Table 1. As in our previous studies (Beridze and Kowalski, 2014; Beridze et al., 2016; Kvashnina et al., 2018; Sun et al., 2020) we see strong dependence on the Fe redox state, with the U parameter for Fe(III) being ~0.5 eV larger than for Fe(II). This is well-consistent with previous studies of FePO₄ and LiFePO₄ phases by Maxisch and Ceder (2006), who obtained 4.9 and 3.7eV for both phases (taken as effective value, U_eff = U−J), respectively.

TABLE 1

Table 1. The computed Hubbard U parameters for Fe in Fe₂O₃, FePO₄ and LiFePO₄ compounds.

3. Results and Discussion

3.1. Structural Data

The first test of a computational method is its ability to reproduce the measured lattice parameters of the computed crystalline solid. The lattice parameters of considered materials were measured by different studies and are well-known. These are collected in Table 2 and compared to the computed data.

TABLE 2

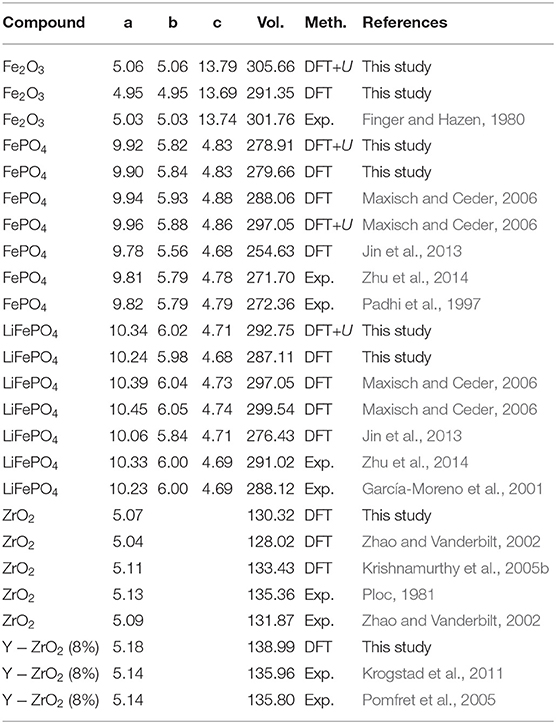
Table 2. The computed and measured lattice parameters of Fe₂O₃, FePO₄, LiFePO₄ and cubic zirconia compounds.

Our previous studies showed that the structural parameters of lanthanide-orthophosphates are very sensitive to the applied computational method, especially to the exchange-correlation functional (Blanca-Romero et al., 2014). A correct treatment of strongly correlated 4f electrons also plays an important role in those cases. Here, with our computational setup we got much better fit to the measured data than Maxisch and Ceder (2006), who applied the PBE exchange-correlation functional that tends to overestimate lattice parameters and volumes, which is also evident in the data collected in Table 2. Blanca-Romero et al. (2014) performed extensive tests of the capability of different DFT-based approaches to reproduce the measured lattice parameters and bond-distances of monazite-type lanthanide-orthophosphates. In that paper, we found that the standard DFT method with explicitly computed 4f electrons overestimates the lattice parameters and bond-lengths by up to 3%, which is consistent with previous studies (Wang et al., 2005; Rustad, 2012). A very good match to the experimental values of structural parameters was achieved applying the parameter free DFT+U method, with the PBEsol exchange-correlation functional (Perdew et al., 2008) and the Hubbard U parameters derived ab initio. An improved description of structures by the PBEsol exchange-correlation functional is an important property of that functional. It recovers the known solution for slowly varying electron densities and with that it improves the description of structural parameters over widely used GGA functionals such as PBE (see discussion by Perdew et al., 2008). It is evident also for zirconate-based materials. In our past studies of Nd_2−xZr_2+xO_7+x/2 compound, with the PBEsol exchange-correlation functional we got perfect match to the lattice parameter in case of the pyrochlore phase (Finkeldei et al., 2017).

In the most recent contribution we computed the MUO₄ compounds with M = Ni, Fe, Co, Cd, and found that only by using the correct projectors for estimation of occupation of d orbitals, e.g., Wannier functions, we could reproduce experimentally seen structural distortions (Murphy et al., 2021). The problem arises from the fact that with the standard DFT+U approach, when using atomic orbitals as projectors, the total occupancy of the d or f states of interest is much higher than the actual one (Kick et al., 2019; Murphy et al., 2021). As illustrated in Table 3, in our case it gives ~1.3 excess electrons for Fe(III) and ~0.5 for Fe(II). This is cured when using Wannier orbitals as projectors. Unfortunately, the forces and cell optimizations with this scheme are not yet implemented in Quantum-ESPRESSO or any equivalent codes, so we could not perform geometry optimization with such a more realistic approach.

TABLE 3

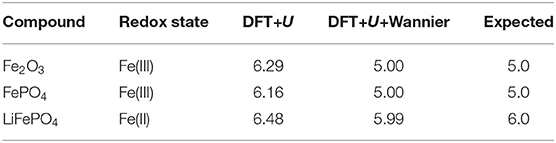
Table 3. The computed projected total number of d electrons per Fe atom in Fe₂O₃, FePO₄ and LiFePO₄ compounds using the DFT+U approach with atomic orbitals and Wannier functions as projectors.

3.2. Formation Enthalpies

The formation enthalpies from oxides for series of lanthanide orthophosphates have been measured by Ushakov et al. (2001) and of FePO₄ and LiFePO₄ by Iyer et al. (2006). Rustad (2012) noticed that there is a systematic offset between the computed and measured values for LnPO₄ of ~40 kJ/mol, with the computed enthalpies being less exothermic. Blanca-Romero et al. (2014) have shown that this offset is present also in the DFT+U calculations and is to a large extent Ln-cation independent, which rules out the 4f electrons correlations as a contributing factor. They attributed this to the overestimation of P-O bond lengths, and thus volumes, of the LnPO₄ and P₂O₅ compounds. Beridze et al. (2016) have found an identical offset for xenotime phase. When a constant shift of ~30 kJ/mol is applied to the computed formation enthalpies, the measured values are nicely reproduced. The computed formation enthalpies for FePO₄ and LiFePO₄ compounds are reported in Table 4. It is evident that DFT heavily underestimates the values (taking absolute values) by 40–100 kJ/mol. This is significantly improved with the DFT+U approach with an error of 20 kJ/mol. Best result, however, is obtained with the DFT+U method when Wanner functions are used as projectors of Fe d states occupations. In this scheme, the computed formation enthalpies are within 10 kJ/mol. Accurate prediction of formation enthalpies are crucial for correct estimate of thermodynamic parameters of solid solution, including solubilities (section 3.4).

TABLE 4

Table 4. The computed here with different methods and measured (Iyer et al., 2006) formation enthalpies from oxides of FePO₄ and LiFePO₄ compounds.

The most stable phase of ZrO₂ is monoclinic. However, upon doping with tri-valent elements it undergoes phase transition to cubic phase, with possible triclinic phase as an intermediate. The experimental evidence shows transition to that phase at ~8% of YO_1.5 (Lee et al., 2003; Götsch et al., 2016; Ahamer et al., 2017). In Figure 2, we show the results of computation of formation enthalpies for the three phases of ZrO₂ (monoclinic, tetragonal, and cubic). The results are plotted together with the experimental data of Lee et al. (2003). The computed values show clearly that at ~ 8% content of Y the enthalpy of cubic phase becomes the lowest and that phase most stable, which is well consistent with the aforementioned experimental data. Moreover, the computed formation enthalpy as a function of Y content is well consistent with the measured values. Also the computed enthalpy difference between monoclinic and cubic phases of ~14 kJ/mol is well consistent with the previous measurements and estimates (ranging from 6 to 22 kJ/mol, with the best measured value of 10 kJ/mol, Lee et al., 2003).

FIGURE 2

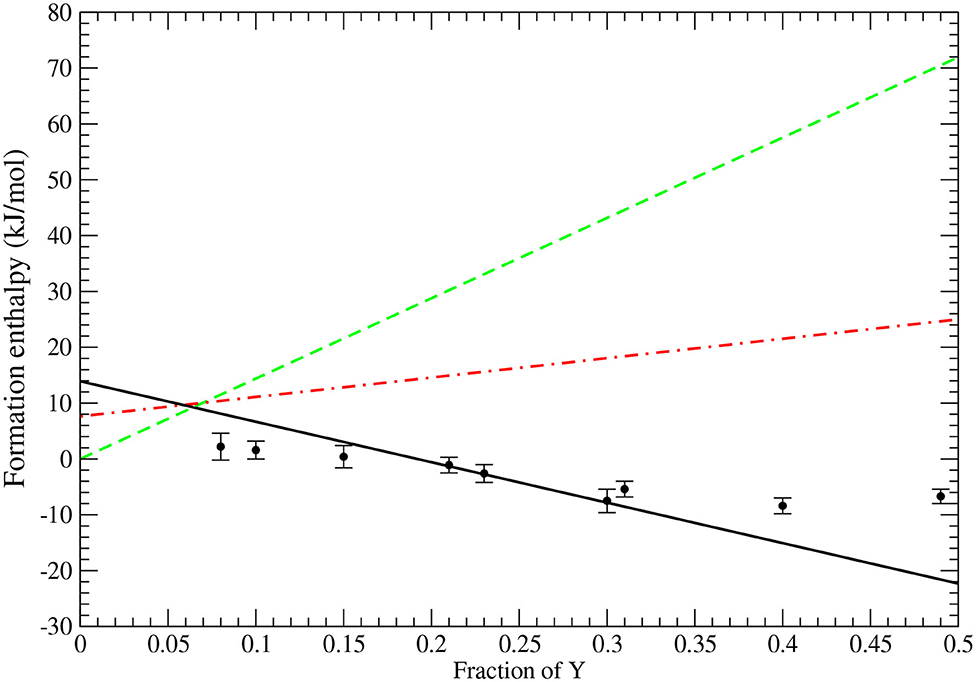
Figure 2. The computed formation enthalpies of YO_1.5 − ZrO₂ system. The lines represent results for monoclinic (dashed green), trigonal (dot-dashed red), and cubic (solid black) phases. The data comes from Lee et al. (2003).

3.3. Elastic, Thermodynamic, and Thermal Conductivity Parameters

Besides formation enthalpies, our previous studies show good ability of atomistic modeling to predict the elastic, thermodynamic, and thermal parameters of considered systems. Li et al. (2014), Kowalski and Li (2016), and Kowalski et al. (2017b) computed the elastic parameters of series of lanthanide orthophosphates and obtained good agreements with the available experimental data. With these computed data they provided good estimates of parameters that are key for modeling of solid solutions within these compounds. Maxisch and Ceder (2006) computed elastic parameters of FePO₄ and LiFePO₄ compounds, which we will use for estimates of thermodynamic parameters of solid solutions in Li_xFePO4 system (section 3.4). In the follow-up studies of lanthanide phosphate we computed heat capacities for series of these compounds and explained the quasirandom-like behavior of heat capacity along lanthanide series by the lanthanide cation-dependent contribution from thermal excitation of 4f electrons (Schottky effect, Kowalski et al., 2015, 2017b; Ji et al., 2017a). Ji et al. (2019b) computed thermal conductivity for series of lanthanide phosphates and were able to derive accurate information on phonon mean free path in these systems. These studies demonstrate that with appropriate computational setup, accurate information on various physical parameters can be delivered by atomistic simulations and materials effectively screened for desired physical characteristics. This has been used by us to deliver crucial information on orthophosphate-based ceramics for immobilization of actinides (Huittinen et al., 2017, 2018; Ji et al., 2019a).

Besides computing orthophosphate-type ceramics, we derived various parameters for fluorite- and pyrochlore-type compounds. Among those, with atomistic modeling we computed defect formation energies (Li et al., 2015; Li and Kowalski, 2018), barriers for oxygen diffusion (Li and Kowalski, 2018; Bukaemskiy et al., 2021), structural parameters (Finkeldei et al., 2017, 2020; Bukaemskiy et al., 2021), formation enthalpies (Finkeldei et al., 2017; Kowalski, 2020), and properties of doped systems (Finkeldei et al., 2017, 2020). Interestingly, we found that ability of a material to effectively conduct oxygen is also responsible for enhanced radiation damage resistance of selective pyrochlore compounds and stability of defect pyrochlore (defect fluorite) phase (Li et al., 2015; Li and Kowalski, 2018). In addition, Li and Kowalski (2018) have shown that the formation of split vacancy state for pyrochlore lanthanide-zirconates with lanthanide cations after Eu is responsible for the maximum ionic conductivity of Eu₂Zr₂O₇ pyrochlore (Yamamura, 2003).

3.4. Solid Solutions and Solubility

Formation and thermodynamic stability of solid solutions is a topic of studies in various research fields, including battery research (Meethong et al., 2007; Li et al., 2018; Phan et al., 2019). In the past we published a series of studies on lanthanide phosphate ceramic-type solid solutions in the context of geothermometry and nuclear waste management (Li et al., 2014; Kowalski and Li, 2016; Hirsch et al., 2017; Kowalski et al., 2017b; Neumeier et al., 2017b; Ji et al., 2019a). This is because the information gained allows for the assessment of long term stability of ceramic nuclear waste forms against phase separation. It was shown experimentally (Popa et al., 2007; Li et al., 2018; Phan et al., 2019) and by ab initio simulations (Li et al., 2014; Kowalski and Li, 2016) that single phase orthophosphate-based solid solutions are highly regular. The excess enthalpy of mixing, H^E, of a A_1−xB_xPO₄ mixed cation compound could be described by a simple equation (Popa et al., 2007):

$\begin{array}{ll}{H}^E=Wx(1-x),& (3)\end{array}$

where W is a Margules interaction parameters (Prieto, 2009). A solid solution is stable against formation of a miscibility gap if W < 2RT, where R is the gas constant. It has been demonstrated experimentally (Yamada et al., 2006; Li et al., 2018; Phan et al., 2019) that Li_xFePO₄ solid solution has a wide miscibility gap, for x between 0.05 and 0.89 at room temperature. However, there is a problem with derivation of consistent model for thermodynamic parameters of mixing for this system, including mixing enthalpy or Margules interaction parameters (Phan et al., 2019). It is thus of great interest to characterize W parameter for Li_xFePO₄ system using the computational methods that were proven by us for lanthanide phosphates (Kowalski and Li, 2016; Ji et al., 2019a).

The first systematic ab initio calculations of W parameters for monazite-type, orthophosphate solid solutions were performed by Li et al. (2014). In follow-up studies (Kowalski and Li, 2016), we explained the quadratic dependence of W parameter on the difference in molar volumes of endmembers (ΔV) by a strain energy-based model, in which

$\begin{array}{ll}W=\frac{E}{6V}{(\Delta V)}^2,& (4)\end{array}$

where E is the Young's modulus and V is the volume. These studies show that ΔV is an important parameter that determines the value of W parameter. Considering the elastic properties of both endmember phases, this equation can be also written as (Kowalski and Li, 2016):

$\begin{array}{ll}W=\frac{2G_A{B}_B}{(3B_B+4G_A)V}{(\Delta V)}^2,& (5)\end{array}$

where G_A is the shear modulus of the doped phase and B_B is the bulk modulus of the dopant phase. The Young's, shear and bulk moduli of FePO₄ and LiFePO₄ phases as computed by Maxisch and Ceder (2006) are given in Table 5. The values of Margules interaction parameter computed with the Equations (4) and (5) are also reported. These values are too low and would result in thermodynamically stable solid solution at all Li content (such forms at room temperature for W < 5 kJ/mol, Li et al., 2014), which is inconsistent with experimental data of Yamada et al. (2006).

TABLE 5

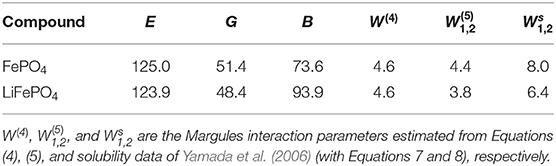
Table 5. The computed by Maxisch and Ceder (2006) with the DFT+U method Young's (E), shear (G) and bulk moduli (B) for FePO₄ and LiFePO₄ compounds. The values are given in GPa.

For lanthanide orthophosphates, Neumeier et al. (2017b) compared the derived ab initio W parameters with the calorimetric measurements of La_1−xLn_xPO₄ (Ln = Eu, Gd) solid solutions. The measured values are smaller than the computed ones. The reason for this discrepancy is the difference in the value of measured and computed ΔV. When Neumeier et al. (2017b) used the measured ΔV values and rescaled the ab initio computed values according to Equation (4) as:

$\begin{array}{ll}W={\left(\frac{\Delta V_{exp}}{\Delta V_{comp.}}\right)}^2{W}_{computed},& (6)\end{array}$

they obtained a good match to the measured values. However, in our estimate we used the experimental volumes (Table 2) and any such a correction would require significant error in one of the reported volumes. In order to obtain the Margules interaction parameters that are consistent with the measured solubilities (Yamada et al., 2006, see below), instead of the reported ΔV = 20 ų between the two endmember phases it should be ΔV = 26 ų. Our computed volumes, however, give even smaller difference of ΔV = 14 ų (Table 2).

The experimental maximum solubilities of Yamada et al. (2006) show slightly asymmetric solid solution with maximum solubility of Li in FePO₄ of x₁ = 0.05 and content/depletion of Li in LiFePO₄ of x₂ = 0.89. Such an offset between both solubilities is consistent with the prediction of Equation (5). With these measured solubilities, the Margules interaction parameters can be derived. The maximum solubilities x₁ and x₂ at the two ends of slightly asymmetric solid solution or the relevant Margules interaction parameters W₁ and W₂ can be derived by solving self-consistently two equations (Mogilevsky, 2007; Ji et al., 2019a):

$\begin{array}{lll}{W}_1{(1-x_1)}^2& +RTln(x_1/(1-x_2))=W_2{x}_2^2,& (7)\end{array}$

$\begin{array}{lll}{W}_2{(1-x_2)}^2& +RTln(x_2/(1-x_1))=W_1{x}_1^2.& (8)\end{array}$

These equations realize chemical equilibrium between Li (equilibrium concentration of x₁ in FePO₄) and Li-vacancy (equilibrium concentration of x₂ in LiFePO₄) in FePO₄ (first equation) and Li_xFePO₄ (second equation) phases, respectively, and are derived by equality of the respected chemical potentials (Mogilevsky, 2007). The self-consistent solution of Equations (7) and (8) can be easily done in a numerical way. The resulted Margules interaction parameters for Li_xFePO₄ solid solution obtained taking the measured solubilities as an input (Yamada et al., 2006) and assuming room temperature are given in Table 5. The derived W₁ = 8.0 kJ/mol and W₂ = 6.4 kJ/mol would result in an excess mixing enthalpy, H^E of 1.7 kJ/mol at x = 0.6 [computed as $H^E=(W_1(1-x)+W_{2}x)x(1-x)$, Li et al., 2014], which is in perfect agreement with the experimental measurements (~2.5±1.0 kJ/mol, Stevens et al., 2006; Phan et al., 2019). Interestingly, the same values can be derived from Equation (5) and elastic moduli reported in Table 5, assuming ΔV = 26 ų. We note that such an offset is plausible because we consider a solid solution between Li cation and a vacant site, while the considered models were designed strictly for mixing of two cation species. We also attempted direct computation of Margules interaction parameter by ab initio methods. We obtained values between 13 and 28 kJ/mol, depending on the computational approach. However, we notice that such a small value of energy (enthalpy) is very sensitive to the computational setup, and can not be derived here precisely because of the inability of computing forces with the Wannier projectors scheme (see section 3.2). Other studies also result in large spread of predicted values (Figure 2 in Phan et al., 2019) and indicate sensitivity of this parameter to other effects, including the electronic entropy of Fe in different redox state in the Li_xFePO₄ solid solution (Zhou et al., 2006).

In Figure 3, we plot the free energy of mixing at room temperature, using the Margules interaction parameters extracted form the maximum solubilities measurements of Yamada et al. (2006). With the horizontal line we indicate the widths of wide miscibility and spinodal gaps. This information is important for understanding of charging relationships in the Li_xFePO₄ system (Phan et al., 2019).

FIGURE 3

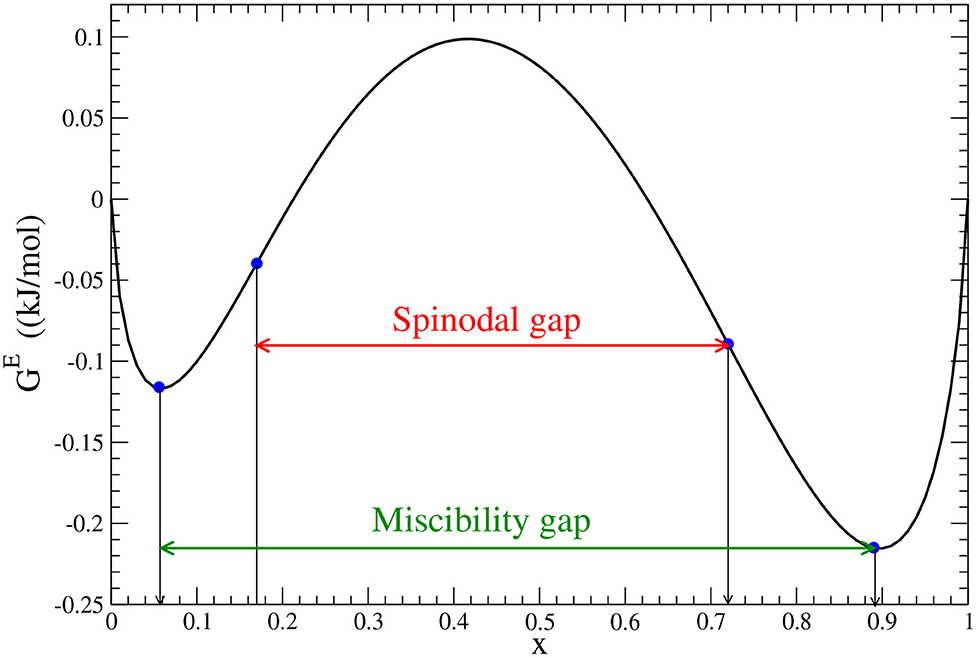
Figure 3. The mixing free energy for Li_xFePO₄ solid solution computed at room temperature, T, as $G^E=\left[W_1(1-x)+W_{2}x\right]x(1-x)+RT\left[xlnx+(1-x)\text{ln}(1-x)\right]$ (Li et al., 2014), assuming configurational entropy of ideal mixing and neglecting other entropy contributions. R is the gas constant. W₁ and W₂ Margules interaction parameters are these from last column of Table 5. The miscibility and spinodal gaps are indicated by minima and inflection points marked with blue circles.

3.5. Ionic Conductivity

Because of high ionic conductivity, yttria-stabilized zirconia (see Figure 4 for the structure) is commonly used as solid state electrolyte. Its ionic conduction properties have been investigated in many studies, including experimental (Strickler and Carlson, 1964, 1965; Ioffe et al., 1978; Li et al., 1994; Lee et al., 2001, 2003; Kilo et al., 2003; Zhang et al., 2007) as well as theoretical and atomistic modeling approaches (Kilo et al., 2003; Krishnamurthy et al., 2005b; Sizov et al., 2014; Bukaemskiy et al., 2021). The conductivity is usually described using Arrhenius-type equation (Ioffe et al., 1978; Ahamer et al., 2017) and the ionic conductivity can be written in the following simple form:

$\begin{array}{ll}\sigma T={\sigma }_{0}exp\left(\frac{-E_a}{k_{b}T}\right)& (9)\end{array}$

where σ₀ is the pre-exponential factor and E_a is the activation energy. In Table 6, we report the available experimental and computed data on E_a together with the results of our simulations. We note that molecular dynamics simulations could be also used for simulation of ionic diffusion, but for systems with activation barriers close to ~1 eV such a method requires long simulation times (e.g., 10 ns as applied by Sizov et al., 2014). Such simulation times are beyond the capability of ab initio molecular dynamics methods (capable of simulations at ps time scales) and could be performed only with less accurate description of interatomic interactions by simple interatomic potentials, like in studies of Sizov et al. (2014).

TABLE 6

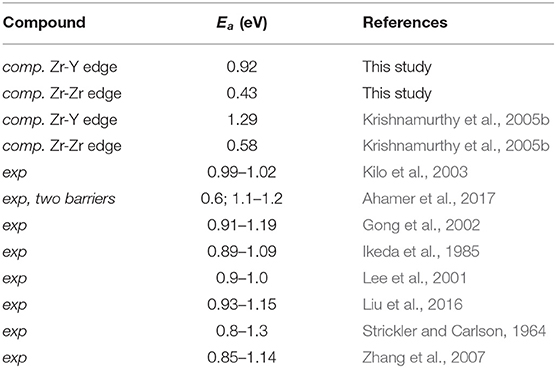
Table 6. The computed here and previously published data on E_a for ionic conductivity in Y-stabilized zirconia.

The computed activation energy of 0.92 eV is well-consistent with the measured values as well as with some previous theoretical predictions. Here, following the studies of Ahamer et al. (2017) and Guan et al. (2020) we assume diffusion along Y-Zr edge as a diffusion rate determining step. Interestingly, the activation barrier for transition along Zr-Zr edge is twice smaller as the one for transition along Y-Zr edge, which is in line with previous findings (Krishnamurthy et al., 2005b). The diffusion paths along these two edges are depicted in Figure 4. In the performed simulations with Eu as dopant, the activation barrier is comparable (0.97eV). This is consistent with previous studies showing similar effects of other tri-valent cations on stabilization of cubic zirconia and its ionic conductivity (Krishnamurthy et al., 2005a). With the derived activation barrier we also computed the attempt frequency, ν₀, using the transition state theory (Equation 2). We obtained value of 2.37 · 10¹²s⁻¹. With the computed activation energy and the attempt frequency, using Equation (1) we derived temperature and Y-content dependent ionic conductivity. The results are plotted in Figure 5 against the experimental data. Our model matches the measured values reasonably well, including temperature and Y content dependence. This is in great part due to inclusion of vacancy migration probability as estimated by Bukaemskiy et al. (2021) (see Equation 1). This shows that atomistic modeling and appropriate theoretical consideration can deliver accurate prediction for ionic conductivity in solid state electrolyte candidate materials. Nevertheless, as discussed by Ahamer et al. (2017) and Guan et al. (2020), the oxygen diffusion in yttria-stabilized zirconia is a complex process, which details, however, could be revealed by combination of computed and measured data.

FIGURE 4

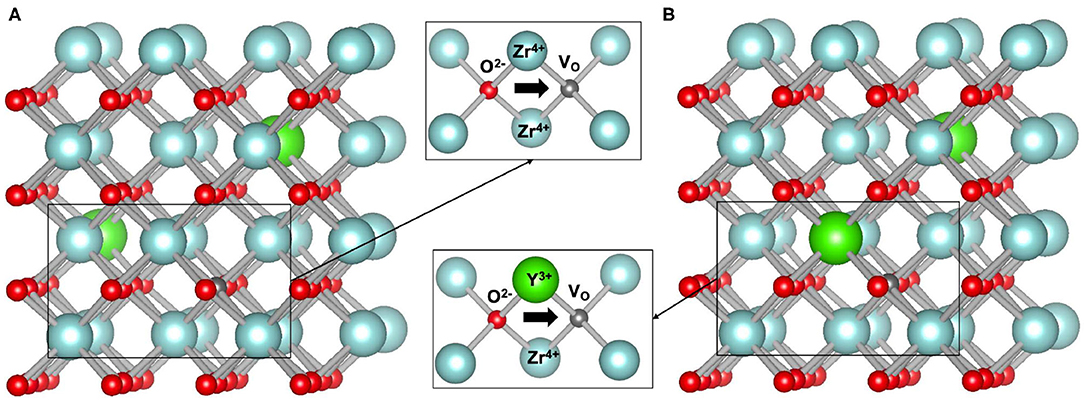
Figure 4. The structure of yttria-stabilized zirconia (YO_1.5 − ZrO₂ system) with indication of the oxygen diffusion mechanism along possible Zr-Zr (A) and Y-Zr (B) edges.

FIGURE 5

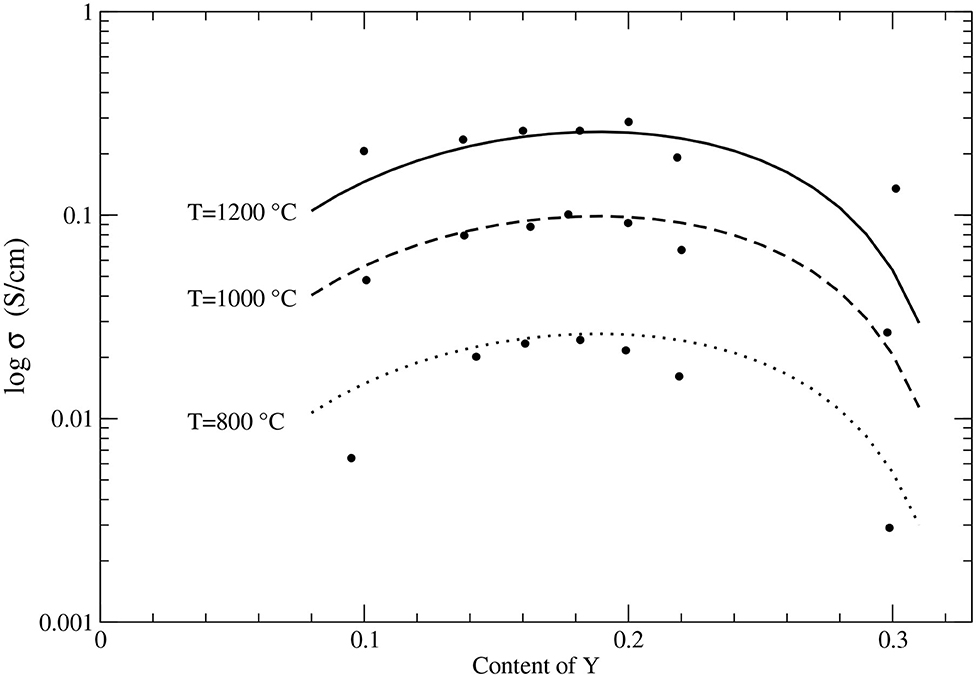
Figure 5. The computed (lines) ionic conductivity in YO_1.5 − ZrO₂ system. The data (black filled circles) come from Strickler and Carlson (1964) and Liu et al. (2016).

4. Conclusions

In this contribution we presented an overview of our decade-long atomistic modeling contribution to the research on orthophosphates and zirconates type ceramics. We discussed the atomistic modeling derivation of structural, thermodynamic, and diffusion properties that are of importance for application of these materials as compounds in energy storage devices. In particular, we discussed the importance of the application of parameter free DFT+U approach and selection of realistic projector functions for counting the occupations of strongly correlated d and f orbitals for the Hubbard model-based DFT+U scheme. Only with this approach we were able to correctly reproduce the measured formation enthalpies of FePO₄ and LiFePO₄ phases. The consideration of the thermodynamic properties of Li_xFePO₄ solid solutions indicates a system with a wide miscibility gap, which values and slight asymmetry are qualitatively consistent with the existing experimental data. Based on the measured solubility data we derived set of Margules interaction parameters that describe this solid solution. The resulting excess free energy of mixing shows wide miscibility and spinodal gaps at room temperature. We also discussed our studies of zirconium-based ceramics. In particular, we derived the stability diagram of yttrium-doped zirconia, showing that it stabilizes in cubic phase at Y content of ~8%, well in line with the experimental measurements. The computed formation enthalpies along YO_1.5 − ZrO₂ solid solution are also well consistent with the measured data. With the computation of transition state and application of vacancy distribution model we were able to derive activation energies and temperature-dependent ionic conductivities for oxygen diffusion in this material, that are well-consistent with the measured data. This shows the power of carefully set up atomistic modeling for computation of various properties of ceramic materials as compounds for energy storage devices.

We discussed various successfully studies of application of atomistic modeling to prediction of a set of physical and chemical properties of orthophosphates and zirconates. In most cases, the best results have been obtained by a joint computational and experimental approach, or at least by extensive testing and comparison to the available experimental data. Application of a reliable, state-of-the-art ab initio approach is also a crucial factor contributing to this success. With the steady increase in the availability of computational power we expect that atomistic modeling research will be applied to tackle even more complex problems, such as kinetically driven dissolution or corrosion processes, and for effective screening of materials for energy applications.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

PK, ZH, and OC contributed equally to computing the data. PK performed collective analysis of the data and editing of the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge the computing time granted by the JARA Vergabegremium and provided on the JARA Partition part of the supercomputers JURECA at Forschungszentrum Jülich and CLAIX at RWTH Aachen University.

Footnotes

1. ^In this contribution we call DFT methods an ab initio approach as the exchange-correlation functionals utilized in our studies were designed based on pure-theoretical considerations.

References

Ahamer, C., Opitz, A. K., Rupp, G. M., and Fleig, J. (2017). Revisiting the temperature dependent ionic conductivity of yttria stabilized zirconia (YSZ). J. Electrochem. Soc. 164, F790–F803. doi: 10.1149/2.0641707jes

CrossRef Full Text | Google Scholar

Ali, K., Arya, A., Ghosh, P. S., and Dey, G. K. (2016). A first principle study of the pressure dependent elastic properties of monazite LaPO₄. AIP Conf. Proc. 1728:020090. doi: 10.1063/1.4946141

CrossRef Full Text | Google Scholar

Andrehs, G., and Heinrich, W. (1998). Experimental determination of REE distributions between monazite and xenotime: potential for temperature-calibrated geochronology. Chem. Geol. 149, 83–96. doi: 10.1016/S0009-2541(98)00039-4

CrossRef Full Text | Google Scholar

Anithakumari, P., Grover, V., Nandi, C., Bhattacharyya, K., and Tyagi, A. K. (2016). Utilizing non-stoichiometry in Nd₂Zr₂O₇ pyrochlore: exploring superior ionic conductors. RSC Adv. 6, 97566–97579. doi: 10.1039/C6RA08722A

CrossRef Full Text | Google Scholar

Beridze, G., Birnie, A., Koniski, S., Ji, Y., and Kowalski, P. M. (2016). DFT+U as a reliable method for efficient ab initio calculations of nuclear materials. Prog. Nucl. Energ. 92, 142–146. doi: 10.1016/j.pnucene.2016.07.012

CrossRef Full Text | Google Scholar

Beridze, G., and Kowalski, P. M. (2014). Benchmarking the DFT+U method for thermochemical calculations of uranium molecular compounds and solids. J. Phys. Chem. A 118, 11797–11810. doi: 10.1021/jp5101126

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanca-Romero, A., Kowalski, P. M., Beridze, G., Schlenz, H., and Bosbach, D. (2014). Performance of DFT+U method for prediction of structural and thermodynamic parameters of monazite-type ceramics. J. Comput. Chem. 35, 1339–1346. doi: 10.1002/jcc.23618

PubMed Abstract | CrossRef Full Text | Google Scholar

Bukaemskiy, A. A., Vinograd, V. L., and Kowalski, P. M. (2021). Ion distribution models for defect fluorite ZrO₂-AO₁.5 (A=Ln, Y) solid solutions: I. Relationship between lattice parameter and composition. Acta Mater. 202, 99–111. doi: 10.1016/j.actamat.2020.10.045

CrossRef Full Text | Google Scholar

Cerdas, F., Titscher, P., Bognar, N., Schmuch, R., Winter, M., Kwade, A., et al. (2018). Exploring the effect of increased energy density on the environmental impacts of traction aatteries: a comparison of energy optimized lithium-ion and lithium-sulfur batteries for mobility applications. Energies 11:150. doi: 10.3390/en11010150

CrossRef Full Text | Google Scholar

Chroneos, A., Rushton, M., Jiang, C., and Tsoukalas, L. (2013). Nuclear wasteform materials: atomistic simulation case studies. J. Nucl. Mater. 441, 29–39. doi: 10.1016/j.jnucmat.2013.05.012

CrossRef Full Text | Google Scholar

Cococcioni, M., and de Gironcoli, S. (2005). Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 71:035105. doi: 10.1103/PhysRevB.71.035105

CrossRef Full Text | Google Scholar

Diazguillen, J., Diazguillen, M., Padmasree, K., Fuentes, A., Santamaria, J., and Leon, C. (2008). High ionic conductivity in the pyrochlore-type Gd₂ − yLa_yZr₂O₇ solid solution (0 ≤ y ≤ 1). Solid State Ion. 179, 2160–2164. doi: 10.1016/j.ssi.2008.07.015

CrossRef Full Text | Google Scholar

Dong, H., Guo, H., He, Y., Gao, J., Han, W., Lu, X., et al. (2017). Structural stability and Li-ion transport property of LiFePO₄ under high-pressure. Solid State Ion. 301, 133–137. doi: 10.1016/j.ssi.2017.01.026

CrossRef Full Text | Google Scholar

Drey, D. L., O'Quinn, E. C., Subramani, T., Lilova, K., Baldinozzi, G., Gussev, I. M., et al. (2020). Disorder in Ho₂Ti_2-xZr_xO₇: pyrochlore to defect fluorite solid solution series. RSC Adv. 10, 34632–34650. doi: 10.1039/D0RA07118H

CrossRef Full Text | Google Scholar

Dunn, J. B., Gaines, L., Kelly, J. C., James, C., and Gallagher, K. G. (2015). The significance of li-ion batteries in electric vehicle life-cycle energy and emissions and recycling's role in its reduction. Energy Environ. Sci. 8, 158–168. doi: 10.1039/C4EE03029J

CrossRef Full Text | Google Scholar

Eremin, N. N., Marchenko, E. I., Petrov, V. G., Mitrofanov, A. A., and Ulanova, A. S. (2019). Solid solutions of monazites and xenotimes of lanthanides and plutonium: atomistic model of crystal structures, point defects and mixing properties. Comput. Mater. Sci. 157, 43–50. doi: 10.1016/j.commatsci.2018.10.025

CrossRef Full Text | Google Scholar

Ewing, R., and Wang, L. (2002). Phosphates as nuclear waste forms. Rev. Mineral. Geochem. 48, 673–699. doi: 10.2138/rmg.2002.48.18

CrossRef Full Text | Google Scholar

Feng, J., Xiao, B., Zhou, R., and Pan, W. (2013). Anisotropy in elasticity and thermal conductivity of monazite-type REPO₄ (RE=La, Ce, Nd, Sm, Eu and Gd) from first-principles calculations. Acta Mater. 61, 7364–7383. doi: 10.1016/j.actamat.2013.08.043

CrossRef Full Text | Google Scholar

Finger, L. W., and Hazen, R. M. (1980). Crystal structure and isothermal compression of Fe₂O₃, Cr₂O₃, and V₂O₃ to 50 kbars. J. Appl. Phys. 51, 5362–5367. doi: 10.1063/1.327451

CrossRef Full Text | Google Scholar

Finkeldei, S., Kegler, P., Kowalski, P., Schreinemachers, C., Brandt, F., Bukaemskiy, A., et al. (2017). Composition dependent order-disorder transition in Nd_xZr₁ − xO₂ − 0.5x pyrochlores: a combined structural, calorimetric and ab initio modeling study. Acta Mater. 125, 166–176. doi: 10.1016/j.actamat.2016.11.059

CrossRef Full Text | Google Scholar

Finkeldei, S., Stennett, M. C., Kowalski, P. M., Ji, Y., de Visser-Týnová, E., Hyatt, N. C., et al. (2020). Insights into the fabrication and structure of plutonium pyrochlores. J. Mater. Chem. A 8, 2387–2403. doi: 10.1039/C9TA05795A

CrossRef Full Text | Google Scholar

García-Moreno, O., Alvarez-Vega, M., García-Jaca, J., Gallardo-Amores, J. M., Sanjuán, M. L., and Amador, U. Influence of the structure on the electrochemical performance of lithium transition metal phosphates as cathodic materials in rechargeable lithium batteries: A new high-pressure form of LiMPO4 (M = Fe Ni). Chem. Mater. (2001) 13, 1570–1576. doi: 10.1021/cm000596p

CrossRef Full Text | Google Scholar

Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. 21:395502. doi: 10.1088/0953-8984/21/39/395502

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomis, O., Lavina, B., Rodríguez-Hernández, P., Muñoz, A., Errandonea, R., Errandonea, D., et al. (2017). High-pressure structural, elastic, and thermodynamic properties of zircon-type HoPO₄ and TmPO₄. J. Phys. 29:095401. doi: 10.1088/1361-648X/aa516a

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, J., Li, Y., Tang, Z., Xie, Y., and Zhang, Z. (2002). Temperature-dependence of the lattice conductivity of mixed calcia/Yttria-stabilized zirconia. Mater. Chem. Phys. 76, 212–216. doi: 10.1016/S0254-0584(01)00522-3

CrossRef Full Text | Google Scholar

Götsch, T., Wallisch, W., Stöger-Pollach, M., Klötzer, B., and Penner, S. (2016). From zirconia to Yttria: sampling the YSZ phase diagram using sputter-deposited thin films. AIP Adv. 6:025119. doi: 10.1063/1.4942818

CrossRef Full Text | Google Scholar

Guan, S.-H., Zhang, K.-X., Shang, C., and Liu, Z.-P. (2020). Stability and anion diffusion kinetics of Yttria-stabilized zirconia resolved from machine learning global potential energy surface exploration. J. Chem. Phys. 152:094703. doi: 10.1063/1.5142591

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirsch, A., Kegler, P., Alencar, I., Ruiz-Fuertes, J., Shelyug, A., Peters, L., et al. (2017). Structural, vibrational, and thermochemical properties of the monazite-type solid solution La₁ − xPr_xO₄. J. Solid State Chem. 245, 82–88. doi: 10.1016/j.jssc.2016.09.032

CrossRef Full Text | Google Scholar

Huittinen, N., Arinicheva, Y., Kowalski, P., Vinograd, V., Neumeier, S., and Bosbach, D. (2017). Probing structural homogeneity of La₁ − xGd_xPO₄ monazite-type solid solutions by combined spectroscopic and computational studies. J. Nucl. Mater. 486, 148–157. doi: 10.1016/j.jnucmat.2017.01.024

CrossRef Full Text | Google Scholar

Huittinen, N., Scheinost, A. C., Ji, Y., Kowalski, P. M., Arinicheva, Y., Wilden, A., et al. (2018). A spectroscopic and computational study of Cm³+ Incorporation in lanthanide phosphate rhabdophane (LnPO₄ · 0.67H₂O) and monazite (LnPO₄). Inorg. Chem. 57, 6252–6265. doi: 10.1021/acs.inorgchem.8b00095

PubMed Abstract | CrossRef Full Text | Google Scholar

Ikeda, S., Sakurai, O., Uematsu, K., Mizutani, N., and Kato, M. (1985). Electrical-conductivity of yttria-stabilized zirconia single-crystals. J. Mater. Sci. 20, 4593–4600. doi: 10.1007/BF00559349

CrossRef Full Text | Google Scholar

Ioffe, A., Rutman, D., and Karpachov, S. (1978). On the nature of the conductivity maximum in zirconia-based solid electrolytes. Electrochim. Acta 23, 141–142. doi: 10.1016/0013-4686(78)80110-8

CrossRef Full Text | Google Scholar

Iyer, R. G., Delacourt, C., Masquelier, C., Tarascon, J.-M., and Navrotsky, A. (2006). Energetics of LiFePO₄ and polymorphs of its delithiated form, FePO₄. Electrochem. Solid-State Lett. 9, A46–A48. doi: 10.1149/1.2140496

CrossRef Full Text | Google Scholar

Jahn, S., and Kowalski, P. M. (2014). Theoretical approaches to structure and spectroscopy of earth materials. Rev. Mineral. Geochem. 78:691. doi: 10.2138/rmg.2014.78.17

CrossRef Full Text | Google Scholar

Ji, Y., Beridze, G., Bosbach, D., and Kowalski, P. M. (2017a). Heat capacities of xenotime-type ceramics: an accurate ab initio prediction. J. Nucl. Mater. 494, 172–181. doi: 10.1016/j.jnucmat.2017.07.026

CrossRef Full Text | Google Scholar

Ji, Y., Beridze, G., Li, Y., and Kowalski, P. M. (2017b). Large scale simulation of nuclear waste materials. Energy Proc. 127, 416–424. doi: 10.1016/j.egypro.2017.08.108

CrossRef Full Text | Google Scholar

Ji, Y., Kowalski, P. M., Kegler, P., Huittinen, N., Marks, N. A., Vinograd, V. L., et al. (2019a). Rare-earth orthophosphates from atomistic simulations. Front. Chem. 7:197. doi: 10.3389/fchem.2019.00197

CrossRef Full Text | Google Scholar

Ji, Y., Kowalski, P. M., Neumeier, S., Deissmann, G., Kulriya, P. K., and Gale, J. D. (2017c). Atomistic modeling and experimental studies of radiation damage in monazite-type LaPO₄ ceramics. Nucl. Instrum. Methods Phys. Res. Sect. B 393, 54–58. doi: 10.1016/j.nimb.2016.09.031

CrossRef Full Text | Google Scholar

Ji, Y., Marks, N. A., Bosbach, D., and Kowalski, P. M. (2019b). Elastic and thermal parameters of lanthanide-orthophosphate (LnPO₄) ceramics from atomistic simulations. J. Eur. Ceram. 39, 4264–4274. doi: 10.1016/j.jeurceramsoc.2019.05.038

CrossRef Full Text | Google Scholar

Jin, B., Qin Zhang, R., and Jiang, Q. (2013). Electronic and atomic structures of LiMPO₄ (M= Fe, Fe₁/4Mn₁/4Co₁/4Ni₁/4): a DFT study. Adv. Electrochem. 1, 22–26. doi: 10.1166/adel.2013.1005

CrossRef Full Text | Google Scholar

Jolley, K., Asuvathraman, R., and Smith, R. (2017). Inter-atomic potentials for radiation damage studies in CePO₄ monazite. Nucl. Instrum. Methods Phys. Res. B 393, 93–96. doi: 10.1016/j.nimb.2016.10.016

CrossRef Full Text | Google Scholar

Kick, M., Reuter, K., and Oberhofer, H. (2019). Intricacies of DFT+U, not only in a numeric atom centered orbital framework. J. Chem. Theory Comput. 15, 1705–1718. doi: 10.1021/acs.jctc.8b01211

PubMed Abstract | CrossRef Full Text | Google Scholar

Kilo, M., Argirusis, C., Borchardt, G., and Jackson, R. A. (2003). Oxygen diffusion in yttria stabilised zirconia-experimental results and molecular dynamics calculations. Phys. Chem. Chem. Phys. 5, 2219–2224. doi: 10.1039/B300151M

CrossRef Full Text | Google Scholar

Kowalski, P. M. (2020). Formation enthalpy of Ln₂B₂O₇-type (B=Ti,Sn,Hf,Zr) compounds. Scr. Mater. 189, 7–10. doi: 10.1016/j.scriptamat.2020.07.048

CrossRef Full Text | Google Scholar

Kowalski, P. M., Beridze, G., Ji, Y., and Li, Y. (2017a). Towards reliable modeling of challenging f electrons bearing materials: experience from modeling of nuclear materials. MRS Adv. 2, 491–497. doi: 10.1557/adv.2017.46

CrossRef Full Text | Google Scholar

Kowalski, P. M., Beridze, G., Li, Y., Ji, Y., Friedrich, C., Sasioglu, E., et al. (2016). Feasible and reliable ab initio approach to computation of materials relevant for nuclear waste management. Ceram. Trans. 258, 205–217. doi: 10.1002/9781119236016.ch21

CrossRef Full Text | Google Scholar

Kowalski, P. M., Beridze, G., Vinograd, V. L., and Bosbach, D. (2015). Heat capacities of lanthanide and actinide monazite-type ceramics. J. Nucl. Mater. 464, 147–154. doi: 10.1016/j.jnucmat.2015.04.032

CrossRef Full Text | Google Scholar

Kowalski, P. M., Ji, Y., Li, Y., Arinicheva, Y., Beridze, G., Neumeier, S., et al. (2017b). Simulation of ceramic materials relevant for nuclear waste management: case of La₁ − xEu_xPO₄ solid solution. Nucl. Instrum. Methods Phys. Res. Sect. B 393, 68–72. doi: 10.1016/j.nimb.2016.09.029

CrossRef Full Text | Google Scholar

Kowalski, P. M., and Li, Y. (2016). Relationship between the thermodynamic excess properties of mixing and the elastic moduli in the monazite-type ceramics. J. Eur. Ceram. Soc. 36, 2093–2096. doi: 10.1016/j.jeurceramsoc.2016.01.051

CrossRef Full Text | Google Scholar

Krishnamurthy, R., Srolovitz, D. J., Kudin, K. N., and Car, R. (2005a). Effects of lanthanide dopants on oxygen diffusion in Yttria-stabilized zirconia. J. Am. Ceram. 88, 2143–2151. doi: 10.1111/j.1551-2916.2005.00353.x

CrossRef Full Text | Google Scholar

Krishnamurthy, R., Yoon, Y.-G., Srolovitz, D. J., and Car, R. (2005b). Oxygen diffusion in yttria-stabilized zirconia: a new simulation model. J. Am. Ceram. 87, 1821–1830. doi: 10.1111/j.1151-2916.2004.tb06325.x

CrossRef Full Text | Google Scholar

Krogstad, J. A., Lepple, M., Gao, Y., Lipkin, D. M., and Levi, C. G. (2011). Effect of yttria content on the zirconia unit cell parameters. J. Am. Ceram. 94, 4548–4555. doi: 10.1111/j.1551-2916.2011.04862.x

CrossRef Full Text | Google Scholar

Kvashnina, K. O., Kowalski, P. M., Butorin, S. M., Leinders, G., Pakarinen, J., Bès, R., et al. (2018). Trends in the valence band electronic structures of mixed uranium oxides. Chem. Commun. 54, 9757–9760. doi: 10.1039/C8CC05464A

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J.-H., Yoon, S., Kim, B.-K., Kim, J., Lee, H.-W., and Song, H.-S. (2001). Electrical conductivity and defect structure of yttria-doped ceria-stabilized zirconia. Solid State Ion. 144, 175–184. doi: 10.1016/S0167-2738(01)00903-1

CrossRef Full Text | Google Scholar

Lee, K., Youn, Y., and Han, S. (2017). Identification of ground-state spin ordering in antiferromagnetic transition metal oxides using the Ising model and a genetic algorithm. Sci. Technol. Adv. Mater 18, 246–252. doi: 10.1080/14686996.2017.1300046

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. A., Navrotsky, A., and Molodetsky, I. (2003). Enthalpy of formation of cubic yttria-stabilized zirconia. J. Mater. Res. 18, 908–918. doi: 10.1557/JMR.2003.0125

CrossRef Full Text | Google Scholar

Li, P., Chen, I.-W., and Penner-Hahn, J. E. (1994). Effect of dopants on zirconia stabilization - an x-ray absorption study: I, trivalent dopants. J. Am. Ceram. 77, 118–128. doi: 10.1111/j.1151-2916.1994.tb06964.x

CrossRef Full Text | Google Scholar

Li, Y., and Kowalski, P. M. (2018). Energetics of defects formation and oxygen migration in pyrochlore compounds from first principles calculations. J. Nucl. Mater. 505, 255–261. doi: 10.1016/j.jnucmat.2017.11.005

CrossRef Full Text | Google Scholar

Li, Y., Kowalski, P. M., Beridze, G., Birnie, A. R., Finkeldei, S., and Bosbach, D. (2015). Defect formation energies in A₂B₂O₇ pyrochlores. Scr. Mater. 107, 18–21. doi: 10.1016/j.scriptamat.2015.05.010

CrossRef Full Text | Google Scholar

Li, Y., Kowalski, P. M., Beridze, G., Blanca-Romero, A., Ji, Y., Vinograd, V. L., et al. (2016). Atomistic simulations of ceramic materials relevant for nuclear waste management: cases of monazite and pyrochlore. Ceram. Trans. 255:165. doi: 10.1002/9781119234531.ch15

CrossRef Full Text | Google Scholar

Li, Y., Kowalski, P. M., Blanca-Romero, A., Vinograd, V., and Bosbach, D. (2014). Ab initio calculation of excess properties of solid solutions. J. Solid State Chem. 220, 137–141. doi: 10.1016/j.jssc.2014.08.005

CrossRef Full Text | Google Scholar

Li, Z., Yang, J., Li, C., Wang, S., Zhang, L., Zhu, K., et al. (2018). Orientation-dependent lithium miscibility gap in LiFePO₄. Chem. Mater. 30, 874–878. doi: 10.1021/acs.chemmater.7b04463

CrossRef Full Text | Google Scholar

Liu, T., Zhang, X., Wang, X., Yu, J., and Li, L. (2016). A review of zirconia-based solid electrolytes. Ionics 22, 2249–2262. doi: 10.1007/s11581-016-1880-1

CrossRef Full Text | Google Scholar

López-Solano, J., Rodríguez-Hernández, P., Munoz, A., Gomis, O., Santamaría-Perez, D., Errandonea, D., et al. (2010). Theoretical and experimental study of the structural stability of TbPO₄ at high pressures. Phys. Rev. B 81:144126. doi: 10.1103/PhysRevB.81.144126

CrossRef Full Text | Google Scholar

Mandal, B., Deshpande, S., and Tyagi, A. (2008). Ionic conductivity enhancement in Gd₂Zr₂O₇ pyrochlore by Nd doping. J. Mater. Res. 23, 911–916. doi: 10.1557/jmr.2008.0112

CrossRef Full Text | Google Scholar

Maxisch, T., and Ceder, G. (2006). Elastic properties of olivine Li_xFePO₄ from first principles. Phys. Rev. B 73:174112. doi: 10.1103/PhysRevB.73.174112

CrossRef Full Text | Google Scholar

Meethong, N., Huang, H.-Y. S., Carter, W. C., and Chiang, Y.-M. (2007). Size-dependent lithium miscibility gap in nanoscale Li₁ − xFePO₄. Electrochem. Solid-State Lett. 10:A134. doi: 10.1149/1.2710960

CrossRef Full Text | Google Scholar

Mogilevsky, P. (2007). On the miscibility gap in monazite-xenotime systems. Phys. Chem. Miner. 34, 201–214. doi: 10.1007/s00269-006-0139-1

CrossRef Full Text | Google Scholar

Moynihan, C. T., Gavin, D. L., and Syed, R. (1982). Pre-exponential term in the arrhenius equation for electrical conductivity of glass. J. Phys. Colloq. 43, C9-395–C9-398. doi: 10.1051/jphyscol:1982975

CrossRef Full Text | Google Scholar

Murphy, G. L., Zhang, Z., Tesch, R., Kowalski, P. M., Avdeev, M., Kuo, E. Y., et al. (2021). Tilting and distortion in rutile-related mixed metal ternary uranium oxides: a structural, spectroscopic, and theoretical investigation. Inorgan. Chem. 60, 2246–2260. doi: 10.1021/acs.inorgchem.0c03077

PubMed Abstract | CrossRef Full Text | Google Scholar

Neumeier, S., Arinicheva, Y., Ji, Y., Heuser, J. M., Kowalski, P. M., Kegler, P., et al. (2017a). New insights into phosphate based materials for the immobilisation of actinides. Radiochim. Acta 105, 961–984. doi: 10.1515/ract-2017-2819

CrossRef Full Text | Google Scholar

Neumeier, S., Kegler, P., Arinicheva, Y., Shelyug, A., Kowalski, P. M., Schreinemachers, C., et al. (2017b). Thermochemistry of La₁ − xLn_xPO₄ monazites (Ln=Gd, Eu). J. Chem. Thermodyn. 105, 396–403. doi: 10.1016/j.jct.2016.11.003

CrossRef Full Text | Google Scholar

Padhi, A. K., Nanjundaswamy, K. S., and Goodenough, J. B. (1997). Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 144:1188. Available online at: https://iopscience.iop.org/article/10.1149/1.1837571

Google Scholar

Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100:136406. doi: 10.1103/PhysRevLett.100.136406

PubMed Abstract | CrossRef Full Text | Google Scholar

Phan, A. T., Gheribi, A. E., and Chartrand, P. (2019). Modelling of phase equilibria of LiFePO4−FePO₄ olivine join for cathode material. Can. J. Chem. 97, 2224–2233. doi: 10.1002/cjce.23416

CrossRef Full Text | Google Scholar

Ploc, R. A. (1981). The lattice parameter of cubic ZrO₂ formed on zirconium. J. Nucl. Mater. 99, 124–128. doi: 10.1016/0022-3115(81)90146-X

CrossRef Full Text | Google Scholar

Pomfret, M. B., Stoltz, C., Varughese, B., and Walker, R. A. (2005). Structural and compositional characterization of yttria-stabilized zirconia: evidence of surface-stabilized, low-valence metal species. Anal. Chem. 77, 1791–1795. doi: 10.1021/ac048600u

PubMed Abstract | CrossRef Full Text | Google Scholar

Popa, K., Konings, R. J. M., and Geisler, T. (2007). High-temperature calorimetry of (La₁ − xLn_x)PO₄ solid solutions. J. Chem. Thermodyn. 39, 236–239. doi: 10.1016/j.jct.2006.07.010

CrossRef Full Text | Google Scholar

Prieto, M. (2009). Thermodynamics of solid solution-aqueous solution systems. Rev. Mineral. Geochem. 70, 47–85. doi: 10.2138/rmg.2009.70.2

CrossRef Full Text | Google Scholar

Prosini, P. P., Lisi, M., Zane, D., and Pasquali, M. (2002). Determination of the chemical diffusion coefficient of lithium in LiFePO₄. Solid State Ion. 148, 45–51. doi: 10.1016/S0167-2738(02)00134-0

CrossRef Full Text | Google Scholar

Rustad, J. R. (2012). Density functional calculations of the enthalpies of formation of rare-earth orthophosphates. Am. Mineral. 97:791. doi: 10.2138/am.2012.3948

CrossRef Full Text | Google Scholar

Schlenz, H., Peters, L., Roth, G., Hirsch, A., and Neumeier, S. (2018). 9. Phosphates as Safe Containers for Radionuclides. Technical report, Nukleare Entsorgung und Reaktorsicherheit.

Google Scholar

Shamblin, J., Feygenson, M., Neuefeind, J., Tracy, C., Zhang, F., Finkeldei, S., et al. (2016). Probing disorder in isometric pyrochlore and related complex oxides. Nat. Mater. 15, 507–511. doi: 10.1038/nmat4581

PubMed Abstract | CrossRef Full Text | Google Scholar

Shein, I. R., and Shalaeva, E. V. (2016). Pressure-induced zircon to monazite phase transition in Y₁ − xLa_xPO₄: first-principles calculations. J. Struct. Chem. 57, 1513–1518. doi: 10.1134/S0022476616080047

CrossRef Full Text | Google Scholar

Sizov, V. V., Lampinen, M. J., and Laaksonen, A. (2014). Molecular dynamics simulation of oxygen diffusion in cubic yttria-stabilized zirconia: effects of temperature and composition. Solid State Ionics 266, 29–35. doi: 10.1016/j.ssi.2014.08.003

CrossRef Full Text | Google Scholar

Stavrou, E., Tatsi, A., Raptis, C., Efthimiopoulos, I., Syassen, K., Mu noz, A., et al. (2012). Effects of pressure on the structure and lattice dynamics of TmPO₄: experiments and calculations. Phys. Rev. B 85:024117. doi: 10.1103/PhysRevB.85.024117

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevens, R., Dodd, J. L., Kresch, M. G., Yazami, R., Fultz, B., Ellis, B., et al. (2006). Phonons and thermodynamics of unmixed and disordered Li0.6FePO4. J. Phys. Chem. B 110, 22732–22735. doi: 10.1021/jp063831l

PubMed Abstract | CrossRef Full Text | Google Scholar

Strickler, D. W., and Carlson, W. G. (1964). Ionic conductivity of cubic solid solutions in the system CaO|Y₂O₃|ZrO₂. J. Am. Ceram. 47, 122–127. doi: 10.1111/j.1151-2916.1964.tb14368.x

CrossRef Full Text | Google Scholar

Strickler, D. W., and Carlson, W. G. (1965). Electrical conductivity in the ZrO₂-rich region of several M₂O₃ − ZrO₂ Systems. J. Am. Ceram. 48, 286–289. doi: 10.1111/j.1151-2916.1965.tb14742.x

CrossRef Full Text | Google Scholar

Sun, M., Stackhouse, J., and Kowalski, P. (2020). The +2 oxidation state of cr incorporated into the crystal lattice of UO₂. Commun. Mater. 1:13. doi: 10.1038/s43246-020-0014-5

CrossRef Full Text | Google Scholar

Tang, P., and Holzwarth, N. (2003). Electronic structure of FePO₄, LiFePO₄, and related materials. Phys. Rev. B 68:165107. doi: 10.1103/PhysRevB.68.165107

CrossRef Full Text | Google Scholar

Ushakov, S., Helean, K., and Navrotsky, A. (2001). Thermochemistry of rare-earth orthophosphates. J. Mater. Res. 16:2623. doi: 10.1557/JMR.2001.0361

CrossRef Full Text | Google Scholar

Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41:7892. doi: 10.1103/PhysRevB.41.7892

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Zhou, Y., and Lin, Z. (2005). First-principles elastic stiffness of LaPO₄ monazite. Appl. Phys. Lett. 87:051902. doi: 10.1063/1.2005392

CrossRef Full Text | Google Scholar

Whittingham, M. S., Song, Y., Lutta, S., Zavalij, P. Y., and Chernova, N. A. (2005). Some transition metal (oxy) phosphates and vanadium oxides for lithium batteries. J. Mater. Chem. 15, 3362–3379. doi: 10.1039/b501961c

CrossRef Full Text | Google Scholar

Williams, M. L., Jercinovic, M. J., and Hetherington, C. J. (2007). Microprobe monazite geochronology: understanding geologic processes by integrating composition and chronology. Annu. Rev. Earth Planet. Sci. 35, 137–175. doi: 10.1146/annurev.earth.35.031306.140228

CrossRef Full Text | Google Scholar

Wu, X., Kang, F., Duan, W., and Li, J. (2019). Density functional theory calculations: a powerful tool to simulate and design high-performance energy storage and conversion materials. Proc. Nat. Sci. Mater. 29, 247–255. doi: 10.1016/j.pnsc.2019.04.003

CrossRef Full Text | Google Scholar

Wuensch, B. (2000). Connection between oxygen-ion conductivity of pyrochlore fuel-cell materials and structural change with composition and temperature. Solid State Ion 129, 111–133. doi: 10.1016/S0167-2738(99)00320-3

CrossRef Full Text | Google Scholar

Xia, X.-L., Ouyang, J.-H., and Liu, Z.-G. (2010). Electrical properties of gadolinium-europium zirconate eramics. J. Am. Ceram. 93, 1074–1080. doi: 10.1111/j.1551-2916.2009.03505.x

CrossRef Full Text | Google Scholar

Yamada, A., Koizumi, H., Nishimura, S.-I., Sonoyama, N., Kanno, R., Yonemura, M., et al. (2006). Room-temperature miscibility gap in Li_xFePO₄. Nat. Mater. 5, 357–360. doi: 10.1038/nmat1634

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamamura, H. (2003). Electrical conductivity anomaly around fluorite-pyrochlore phase boundary. Solid State Ion. 158, 359–365. doi: 10.1016/S0167-2738(02)00874-3

CrossRef Full Text | Google Scholar

Zakaria, Z., Abu Hassan, S. H., Shaari, N., Yahaya, A. Z., and Boon Kar, Y. (2020). A review on recent status and challenges of yttria stabilized zirconia modification to lowering the temperature of solid oxide fuel cells operation. Int. J. Energy Res. 44, 631–650. doi: 10.1002/er.4944

CrossRef Full Text | Google Scholar

Zhang, C., Li, C.-J., Zhang, G., Ning, X.-J., Li, C.-X., Liao, H., et al. (2007). Ionic conductivity and its temperature dependence of atmospheric plasma-sprayed yttria stabilized zirconia electrolyte. Mater. Sci. Eng. B 137, 24–30. doi: 10.1016/j.mseb.2006.10.005

CrossRef Full Text | Google Scholar

Zhao, X., and Vanderbilt, D. (2002). Phonons and lattice dielectric properties of zirconia. Phys. Rev. B 65:075105. doi: 10.1103/PhysRevB.65.075105

CrossRef Full Text | Google Scholar

Zhou, F., Maxisch, T., and Ceder, G. (2006). Configurational electronic entropy and the phase diagram of mixed-valence oxides: the case of Li_xFePO₄. Phys. Rev. Lett. 97:155704. doi: 10.1103/PhysRevLett.97.155704

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y.-M., Ruan, Z.-W., Tang, S.-Z., and Thangadurai, V. (2014). Research status in preparation of FePO₄: a review. Ionics 20, 1501–1510. doi: 10.1007/s11581-014-1241-x

CrossRef Full Text | Google Scholar