Carbon Emission and Endogenous Growth Between Two Economic Systems

In recent years, many scholars have shown an increasing interest in the problem of pollution (carbon emission) in the endogenous growth but less concern about the interactions of polluting activities between two economy systems. This study explains the effects of carbon emission on the optimal balanced growth path by establishing an endogenous growth model involving exhaustible resources, human capital, physical capital, and labor time under one economy and a similar system involving two economic systems. The second system is used to analyze the interactions of polluting activities across the two economic systems that it covers. The results show that the negative externality (carbon emission) caused by one economy will bring remarkable adverse impacts on the optimal resource extraction and growth rates of other economies. If the people in one economy pay greater attention to the environmental problem (carbon emission), its own resource input will be lowered to reduce carbon emissions, but carbon emissions of another economy will be increased simultaneously to accelerate the economic growth. That is why carbon emission is one of the most challenging issues in global governance. Therefore, the global environmental pollution control needs the help of the cross-regional governance mechanism.

Introduction

The environment is the material basis and constraint to human survival. Man-made environmental problems came up with population growth and development. In recent times, one of the most challenging global environmental problems is the global climate change caused by greenhouse gases (primarily, carbon compounds). Carbon emission issues have attracted worldwide attention. How to allocate global environmental responsibility among countries is the focus of debate. According to the BP statistical review of world energy of 2018, the global carbon dioxide emissions rose by 2.2% to 33,444 million tons in 2017, which was higher than the 1.2% rise experienced in 2016 and is the fastest pace since 2013.

Economic growth raised the level of carbon emissions, which loop back into the economy through their adverse effects. Meadows et al. (1972) put forward the “Growth Limit Theory” in their research report to the club of Rome. They believed that economic growth would be constrained by natural resources and could not be sustained. In order to protect environmental resources, we must artificially reduce the speed of economic growth. The international community hopes to make economic growth both fair and sustainable by establishing an effective system to coordinate benefit distribution and cost sharing. However, in order to maximize their own interests, it is difficult for countries to reach an effective consensus on environmental responsibility. Stiglitz (1974) was the first literature to introduce the non-renewable resource into the field of a neoclassical growth model. A number of authors, thereafter, began to introduce flow pollution problems caused by non-renewable resources into the endogenous growth model. During recent years, there has been some focus on the interactions between economic growth and carbon emissions. Scholars pointed out that the growth rate of an unregulated market economy is sub-optimally high because the negative effects of pollution are not taken into account (Gradus and Smulders, 1993; Bovenberg and Smulders, 1995; Schou, 2000). The focus of some studies is on finding the optimal extraction and growth rates when considering the pollution problem (Michel and Rotillon, 1995; Withagen, 1995; Byrne, 1997; Reis, 2001; Dietz and Stern, 2015; Kollenbach, 2015; Aznar-Márquez and Ruiz-Tamarit, 2016). Other scholars focus far more on the policy effects in an endogenous growth model of pollution (Bovenberg and Smulders, 1996; Jones and Manuelli, 2001; Greiner, 2005; Chu and Lai, 2014; Afonso and Afonso, 2015; Lorente and Álvarez-Herranz, 2016; Bianco, 2017; Marsiglio, 2017). Although there are many scholars who have explored economic growth and carbon emissions, none of them considers the possibility of the interaction of polluting activities between the two economic systems, which is especially important when facing the problems of global pollution.

This study combines ideas from the areas of endogenous growth, environmental economics, and economic theory of non-renewable resources to examine how the conventional results from growth models with carbon emissions may be affected by the inclusion of the non-renewable resources. An endogenous growth model between the two economic systems is then built to analyze the interaction of polluting activities, with interesting and important conclusions. This study argues that, in the face of the increasingly severe contradiction between the global environmental deterioration and the demand for economic development, a global environmental regulation policy must be established to realize the clean technology progress of the global value chain under the condition of the heterogeneity of environmental regulation. In order to practice the development concept of “the unity of human destiny” and walk out of the extensive economic development mode of “pollution before governance,” we can realize the green sustainable development of the global economy.

The rest of this study is organized as follows: The basic model and primary results of one economy are outlined in section The Basic Model and Primary Results of One Economy. In section The Extended Model Between Two Economies, the extended model between the two economies is addressed. The conclusions and remarks are drawn in section Conclusions, while Appendices A–C are at the end of this article.

The Basic Model and Primary Results of One Economy

Basic Settings

The final output Y is a function of four inputs: physical capital K, stock of technology A, rate of resources use R, and labor time devoted to the final output production l₁. All of the variables considered in the model are functions of the time t. To enhance the readability of the study, the subscript (t) has been suppressed in the ensuing discussion. The C-D production function is:

$\begin{array}{ll}Y=K^{{\alpha }_1}{(A{l}_1)}^{{\alpha }_2}{R}^{{\alpha }_3},& (1)\end{array}$

where α_i (i = 1, 2, 3) is the elasticity coefficient and ${\displaystyle \sum _{i=1}^3}{\alpha }_i=1$. The investment in the physical capital is:

$\begin{array}{ll}\stackrel{•}{K}=Y-C& (2)\end{array}$

where K(0) = K₀, K(t) ≥ 0. Equation (2) is a constraint which considers the change of the physical capital over time. For the sake of simplicity, depreciation in K is not considered here. Aggregate consumption is denoted by C = xY, with 0 < x ≤ 1. Aggregate saving is $s=zY=\stackrel{.}{K}$, where 0 < z ≤ 1 and z = 1 − x. Human capital accumulation depends linearly on time spent on R&D activities (Romer, 1990):

$\begin{array}{ll}\stackrel{•}{A}=\xi (1-l_1)A,& (3)\end{array}$

where A(0) = A₀, A(t) ≥ 0. Equation (3) is the core of the neoclassical endogenous growth model which expresses that labor time may not only to be devoted to the final output but also in the R&D activity. The total number of skilled workers N is normalized to 1. l₂ = 1−l₁ is the R&D input of the human capital, wherein l_i > 0 for i = 1, 2. ξ > 0 is a productive parameter of the R&D activity. Technological change is costly and does not occur by chance; it depends rather on the effort devoted to it and is an outcome of one sector of our economy (Kamien and Schwartz, 1978; Romer, 1990; Scholz and Ziemes, 1999). The carbon stock Q moves during time according to

$\begin{array}{ll}\stackrel{•}{Q}=\frac{\partial Q}{\partial t}=-\tau Q+\psi R,& (4)\end{array}$

where 0 < τ ≤ 1 is a constant that expresses the capacity of the environment to assimilate carbon. 0 < ψ < 1 is the carbon emissions factor of using the non-renewable resource R (Di Vita, 2006). The social welfare, at any point in time, is a function of the flow of consumption C and the intensity of carbon Q (Smith, 1972; Aronsson and Löfgren, 1999; Di Vita, 2007). The instantaneous standard constant elasticity utility function can be indicated by

$\begin{array}{ll}U(Q,C)=\frac{{C_{}}^{1-{\theta }_{}}-1}{1-{\theta }_{}}-\frac{Q^{1+{\omega }_{}}-1}{1+{\omega }_{}}.& (5)\end{array}$

The inclusion of Q in our utility function indicates that we will pay a price to reduce the amount of accumulated carbon. Equation (5) has continuous first and second partial derivatives, with U_C > 0, U_CC < 0, U_Q < 0, U_QQ < 0, and U_CQ = 0. Second-order conditions ensure the concavity of the utility function. θ, ω > 0 are two more parameters representing the elasticity of the marginal utility with respect to the consumption and carbon concentration.

The social welfare associated with any particular time path for C and Q comes from summing the discounted flow, assuming that the social discount rate δ > 0 is exogenous. The problem of the social planner is to choose C and Q, so as to maximize:

$\begin{array}{ll}\{\begin{array}{l}\begin{array}{c}W=U(C,Q)\\ C,R,l_1\end{array}={\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-\delta t}(\frac{C^{1-\theta }-1}{1-\theta }-\frac{Q^{1+\omega }-1}{1+\omega })dt\\ s.t.\stackrel{•}{Q}=-\tau Q+\psi R\text{ and }Q(0)=Q_0,Q(t)\ge 0\\ \stackrel{•}{K}=Y-C\text{ and }K(0)=K_0,K(t)\ge 0\\ \stackrel{•}{A}=\xi (1-l_1)A\text{ and}A(0)=A_0,A(t)\ge 0\end{array}& (6)\end{array}$

The current-value Hamiltonian function is

$\begin{array}{l}H=\frac{C^{1-\theta }-1}{1-\theta }-\frac{Q^{1+\omega }-1}{1+\omega }-{\lambda }_1(-\tau Q+\psi R)\\ +{\lambda }_2\left[K^{{\alpha }_1}{(A{l}_1)}^{{\alpha }_2}{R}^{{\alpha }_3}-C\right]+{\lambda }_3\left[\xi (1-l_1)A\right]& (7)\end{array}$

where λ_i, i = 1, 2, 3 are the dynamic Hamilton multipliers of the stock variables. Note that we consider the shadow price of the carbon concentration λ₁ to be negative because that flow generates disutility.

The Optimal Balanced Growth Path

According to the optimal control theory (Pontryagin et al., 1962), necessary first-order conditions for an interior optimal solution with respect to the three control variables, C, R, and l_r, are:

$\begin{array}{ll}\frac{\partial H}{\partial C}=C^{-\theta }-{\lambda }_2=0.& (8)\end{array}$

$\begin{array}{ll}\frac{\partial H}{\partial R}=-{\lambda }_1\psi +{\lambda }_2{\alpha }_3\frac{Y}{R}=0.& (9)\end{array}$

$\begin{array}{ll}\frac{\partial H}{\partial l_1}=-{\lambda }_3\xi A+{\lambda }_2{\alpha }_2\frac{Y}{l_1}=0.& (10)\end{array}$

Then, from Euler Formula, we can obtain

$\begin{array}{ll}{\stackrel{•}{\lambda }}_1=-\frac{\partial H}{\partial Q}+\delta {\lambda }_1=Q^{\omega }+(\delta -\tau ){\lambda }_1.& (11)\end{array}$

$\begin{array}{ll}{\stackrel{•}{\lambda }}_2=-\frac{\partial H}{\partial K}+\delta {\lambda }_2=\delta {\lambda }_2-{\lambda }_2{\alpha }_1\frac{Y}{K}.& (12)\end{array}$

$\begin{array}{ll}{\stackrel{•}{\lambda }}_3=-\frac{\partial H}{\partial A}+\delta {\lambda }_3=\delta {\lambda }_3-{\lambda }_2{\alpha }_2\frac{Y}{A}-{\lambda }_3\xi (1-l_1).& (13)\end{array}$

λ_i(i = 1, 2, 3) are the shadow values of carbon concentration, physical capital, and human capital, respectively. An interior balanced-growth path that solves the problem of the social planner will fulfill the conditions (8)–(13) and the appropriate non-negativity and transversality conditions:

$\begin{array}{ll}Q(t)\ge 0,K(t)\ge 0,A(t)\ge 0& (14)\end{array}$

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}{e}^{-\delta t}{\lambda }_1(t)Q(t)=0& (15)\end{array}$

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}{e}^{-\delta t}{\lambda }_2(t)K(t)=0& (16)\end{array}$

$\begin{array}{ll}{\displaystyle \underset{t\to \infty }{lim}}{e}^{-\delta t}{\lambda }_3(t)A(t)=0& (17)\end{array}$

Here, it is assumed that all the conditions in Chiang (2015, p. 131), together with the concavity on the maximized Hamiltonian, are satisfied. The proof that the model describes a stable saddle point equilibrium path is given in Appendix C.

Along the balanced growth path, Y, K, and C must necessarily have the same growth rate (which we call, g). Otherwise, Equation (2) could not hold true for all time. If A grows with a constant rate, l₁ must be constant [from Equation (3)]. Also, if Q grows with a constant rate, Q and R must necessarily have the same growth [from Equation (4)]. Using these results, we obtained the steady-state growth rate of the final output (which is equal to the growth rate of capital and consumption). And growth rate for carbon concentration and the human capital was obtained as follows¹

$\begin{array}{ll}g=g_Y=g_C=g_K=\frac{{\alpha }_2(\xi -\delta )(1+\omega )}{({\alpha }_3+\theta {\alpha }_2)\omega +\theta ({\alpha }_2+{\alpha }_3)}& (18)\end{array}$

$\begin{array}{ll}{g}_Q=g_R=\frac{{\alpha }_2(\xi -\delta )(1-\theta )}{({\alpha }_3+\theta {\alpha }_2)\omega +\theta ({\alpha }_2+{\alpha }_3)}& (19)\end{array}$

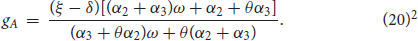
Later, the steady-state growth rate is impacted if the disutility of carbon emission is considered. And we obtained some propositions as follows.

Primary Results Analysis

Proposition 1: When carbon emission and its disutility are considered in the endogenous growth model, g_A and $g_Q(g_R)\{\begin{array}{c}>0if\theta <1\\ <0if\theta >1\end{array}$ in the steady state. In this way, g_A > g_Y(g_C) > g_Q(g_R) is always true as confirmed by Appendix B.

Proposition 1 shows that, if carbon concentration impacting the utility level of consumers is considered in the model, in the steady state, the growth rate of output (consumption), g_Y, and the growth rate of knowledge accumulation, g_A, are always greater than zero. But the sign of g_Q depends on the value of θ. If the elasticity of the marginal utility of consumption is lower than 1, which means people are not concerned with having a smooth consumption profile over time (θ is small), the growth rate of carbon concentration will be positive. The growth rate of output (consumption) is greater than the growth rate of the resource extraction (carbon concentration) all the time, and the growth rate of knowledge accumulation is always higher than the growth rate of the output. The result in this model shows that the economic growth depends more on the human capital input and less on the resource extraction when the disutility of the carbon concentration is considered. So, g_A is always greater than g_Y, and g_Q is always lower than g_Y. The conclusion made by Stiglitz (1974) and Scholz and Ziemes (1999) is different in the results obtained by both authors, which showed that g_A may be either smaller or larger than g_Y in conventional models.

Another issue that is worth considering is the impacts of the elasticity of the marginal utility with respect to carbon concentration and the balanced growth rate.

Proposition 2: In steady state, taking the partial derivative of g_Q, g_A, and g_Y with respect to ω results in $\frac{\partial g_A}{\partial \omega }<0$ all the time. The sign of $\frac{\partial g_Q}{\partial \omega }$ and $\frac{\partial g_Y}{\partial \omega }$ depends on the value of θ. The sign of the first-order condition is positive only if θ > 1 as shown in Appendix B.

Proposition 2 shows that, if θ > 1 (which means, g_Q < 0 according to proposition 1), a positive relationship exists between the growth rate of carbon concentration, g_Q, and the elasticity of the marginal utility with respect to carbon concentration ω. The increase of ω will bring two effects to the optimal path: raising the level of output (and consumption) to increase the positive utility (which will increase carbon concentration at the same time) and cutting down the recourse use to reduce the disutility level. If marginal utility with respect to consumption θ is big, the positive utility of g_Q will be bigger than the disutility level of it. So, g_Q (less than zero) will increase with the increase of ω and vice versa. The conclusion is the same with the analysis of g_Y. It was noticed that ∂g_A/∂ω < 0 holds all the time, which means that the increase of ω will bring a certain negative influence to the optimal steady-state growth rate of knowledge accumulation.

And then, taking the partial derivative of the growth rate of shadow prices with respect to ω, the next proposition was obtained as follows:

Proposition 3:

$\begin{array}{ll}\frac{\partial g_{{\lambda }_1}}{\partial \omega }\{\begin{array}{c}>0if\theta <1\\ <0if\theta >1\end{array},\frac{\partial g_{{\lambda }_2}}{\partial \omega }\{\begin{array}{c}>0if\theta <1\\ <0if\theta >1\end{array},\text{ and }\frac{\partial g_{{\lambda }_3}}{\partial \omega }=0& (21)\end{array}$

Proof. See Appendix B.

The shadow price λ₁ represents the sensitivity of the change of carbon concentration impacting the optimal utility level. The high growth rate of λ₁ means that high carbon concentrations will bring more negative effects to the optimal utility. Proposition 2 shows that if θ is relatively small (< 1), g_λ1 is less than zero, and g_λ1 will grow with the increase of the elasticity of the marginal utility with respect to carbon concentration ω. g_λ2 (which represents the growth rate of shadow price of physical capital) has the same conclusion with g_λ1, which means that, if θ is relatively small (< 1), the increase of ω will enhance the influence of physical capital to the optimal utility level. Note that g_λ3 would not be impacted by the change of ω.

The Extended Model Between the Two Economies

This section explored a two-economy system endogenous growth model based on the basic assumptions in section The Basic Model and Primary Results of One Economy. Consider two economies of M and N, which have different utility preferences, output elasticities, and efficiencies of knowledge accumulation. The social optimal problem for the two economy systems can be changed to Equation (22)

$\begin{array}{ll}\{\begin{array}{l}{W}^i=U(C^i,Q)=\underset{0}{\overset{\infty }{\int }}{e}^{-\delta t}(\frac{{C^i}^{(1-{\theta }^i)}-1}{1-{\theta }^i}-\frac{Q^{1+{\omega }^i}-1}{1+{\omega }^i})dt\\ s.t.\stackrel{•}{Q}=-\tau Q+{\psi }^i{R}^i+{\psi }^j{R}^j\text{ and }Q(0)=Q_0,Q(t)\ge 0\\ \stackrel{•}{K}i=Y^i-C^i\text{ and }{K}^i(0)=K_0^i,K^i(t)\ge 0\\ \stackrel{•}{A}i={\xi }^i(1-l_1^i)A^i\text{ and }{A}^i(0)=A_0^i,A^i(t)\ge 0\end{array},& (22)\end{array}$

where (i, j) ∈ {M, N} and i ≠ j. Note that the only thing that the two economies need to face together is the carbon concentration Q. According to the optimal control theory, necessary first-order conditions for an interior optimal solution and Euler formula from Equation (8) to Equation (13) still hold. So, this section will not cover those again. Along the balanced growth path, Q grows with a constant rate, Q and ψ^MR^M + ψ^NR^N should necessarily have the same growth³. It is easy to prove that⁴

$\begin{array}{ll}{g}_Q=g_{({\psi }^M{R}^M+{\psi }^N{R}^N)}\text{=}{g}_{R^M}+g_{R^N}& (23)\end{array}$

Equation (A9) can be rewritten

$\begin{array}{ll}{\omega }^i(g_{R^M}+g_{R^N})=(1-\theta )g_{Y^i}-g_{R^i}& (24)\end{array}$

Solving this system of Equations (A7), (A11), and (24) with respect to $g_{R^i}$ $g_{Y^i}$, and $g_{A^i}$, we obtained

$\begin{array}{ll}{g}^i=g_{Y^i}^{}=g_{C^i}^{}=g_{K^i}^{}=\frac{{\alpha }_2^i({\xi }^i-\delta )(1+{\omega }^i)-{\alpha }_3^i{\omega }^i{g}_{R^j}}{({\alpha }_3^i+{\theta }^i{\alpha }_2^i){\omega }^i+{\theta }^i({\alpha }_2^i+{\alpha }_3^i)}& (25)\end{array}$

$\begin{array}{ll}{g}_{R^i}=\frac{{\alpha }_2^i({\xi }^i-\delta )(1-{\theta }^i)-({\alpha }_3^i+{\theta }^i{\alpha }_2^i){\omega }^i{g}_{R^j}}{({\alpha }_3^i+{\theta }^i{\alpha }_2^i){\omega }^i+{\theta }^i({\alpha }_2^i+{\alpha }_3^i)}& (26)\end{array}$

$\begin{array}{ll}{g}_{A^i}=\frac{({\xi }^i-\delta )\left[({\alpha }_2^i+{\alpha }_3^i){\omega }^i+{\alpha }_2^i+{\theta }^i{\alpha }_3^i\right]-(1-{\theta }^i){\alpha }_3^i{\omega }^i{g}_{R^j}}{({\alpha }_3^i+{\theta }^i{\alpha }_2^i){\omega }^i+{\theta }^i({\alpha }_2^i+{\alpha }_3^i)}& (27)\end{array}$

From Equations (25) and (26), it is obvious that $\partial g^i/\partial g_{R^{j*}}<0$ and $g_{R^i}/\partial g_{R^{j*}}<0$ show that the economic activities of one economy will produce negative externality (carbon emission) to another economy at the same time. It will bring adverse impacts to other activities of the economies (Y, R) on the balanced path. Facing the global public goods (carbon concentration), multi-agent decisions often will cause the tragedy of the commons (Hardin, 1968). Both the implementer and sufferer will be punished (lower utility) by the environment. Also, from Equation (27), if θⁱ < 1, then $\partial g_{A^i}/\partial g_{R^{j*}}<0$ and if θⁱ > 1, then $\partial g_{A^i}/\partial g_{R^{j*}}>0$. It means that, if people are concerned with having a smooth consumption profile over time (θⁱ is bigger than 1), the increase in the rate of resource depletion of one economy will boost the growth rate of knowledge accumulation of another economy. That is because higher carbon concentrations caused by one economy's activities will stimulate the knowledge accumulation input of another economy to replace the resource depletion and reduce the growth rate of carbon emission when greater attention is paid to the consumption (θⁱ > 1). Conversely, the growth rate of knowledge accumulation of one economy will go down with the increase of resource depletion of another economy.

Using the symmetry of the optimal solution, we can obtain the optimal solutions of $g_{R^M}$ and $g_{R^N}$, respectively.

$\begin{array}{ll}{g}_{R^i}=\frac{\left[({\alpha }_3^j+{\theta }^j{\alpha }_2^j){\omega }^j+{\theta }^j({\alpha }_2^j+{\alpha }_3^j)\right]{\alpha }_2^i({\xi }^i-\delta )(1-{\theta }^i)-{\alpha }_2^j({\xi }^j-\delta )(1-{\theta }^j)({\alpha }_2^i{\theta }^i+{\alpha }_3^i){\omega }^i}{\left[({\alpha }_3^j+{\theta }^j{\alpha }_2^j){\omega }^j+{\theta }^j({\alpha }_2^j+{\alpha }_3^j)\right]{\theta }^i({\alpha }_2^i+{\alpha }_3^i)+{\theta }^j({\alpha }_2^j+{\alpha }_3^j)({\alpha }_2^i{\theta }^i+{\alpha }_3^i){\omega }^i},& (28)\end{array}$

where (i, j) ∈ {M, N} and i ≠ j, and $g_Q=g_{({\psi }^M{R}^M+{\psi }^N{R}^N)}\mathrm{\text{=}}{g}_{R^M}+g_{R^N}$ can be expressedx as

$\begin{array}{ll}{g}_Q=\frac{{\alpha }_2^M({\xi }^M-\delta )(1-{\theta }^M){\theta }^N({\alpha }_2^N+{\alpha }_3^N)+{\alpha }_2^N({\xi }^N-\delta )(1-{\theta }^N){\theta }^M({\alpha }_2^M+{\alpha }_3^M)}{\left[({\alpha }_3^N+{\theta }^N{\alpha }_2^N){\omega }^N+{\theta }^N({\alpha }_2^N+{\alpha }_3^N)\right]{\theta }^M({\alpha }_2^M+{\alpha }_3^M)+{\theta }^N({\alpha }_2^N+{\alpha }_3^N)({\alpha }_2^M{\theta }^M+{\alpha }_3^M){\omega }^M}.& (29)\end{array}$

It is obvious that $g_Q/{\omega }^i<0$⁵, which means that the increase of the elasticity of the marginal utility with respect to the carbon concentration of every economy will lower the growth rate of carbon concentration. Also note that the sign of $g_Q/{\xi }^i$ depends on the value of θⁱ⁶. If θⁱ > 1, the increase of the efficiency of knowledge accumulation will reduce the growth rate of carbon concentration. On the contrary, the increase of the efficiency of knowledge accumulation will speed up the growth rate of carbon concentration. The increase of the efficiency of knowledge accumulation will replace the resource input and decrease the carbon emission (which can be called substitution effect) and, on the other hand, promote economic growth and increase the carbon emission (which can be called growth effect). If θⁱ > 1, the substitution effect is bigger than the growth effect, and the growth rate of carbon concentration will decline with the increase of the efficiency of knowledge accumulation. Based on these results, the impacts of the parameters of one economy on the optimal balanced path of the other economy will be analyzed following the proposition below

Proposition 4: In the steady state, we have $\frac{\partial g_{R^i}}{\partial {\omega }^i}\{\begin{array}{c}>0if{g}_Q<0\\ <0if{g}_Q>0\end{array}$ and $\frac{\partial g_{R^i}}{\partial {\omega }^j}\{\begin{array}{c}>0if{g}_Q>0\\ <0if{g}_Q<0\end{array}$. What is more, we have $\frac{\partial g_{R^i}}{\partial {\xi }^i}\{\begin{array}{c}>0if{\theta }^i<1\\ <0if{\theta }^i>1\end{array}$ and $\frac{\partial g_{R^i}}{\partial {\xi }^j}\{\begin{array}{c}>0if{\theta }^j>1\\ <0if{\theta }^j<1\end{array}$.

Proof. See Appendix B.

Proposition 4 shows that the growth rate of resource exploitation of one economy will rise with the increase of the elasticity of the marginal utility with respect to the carbon concentration of another economy and with the decrease of its own elasticity of the marginal utility under the condition of g_Q > 0. If the people in one economy pay greater attention to carbon emission, the economy will lower its own resource input but increase the resource input of another economy simultaneously. It is similar to the real world, in that the public in some developed countries place a high value on carbon emission and force the government to reduce emissions but promote emissions imperceptibly of other countries. That is why the problem of carbon emission is one of the thorniest problems in the global governance.

Also, the efficiency of knowledge accumulation has a similar effect to the growth rate of resource exploitation. If the elasticity of the marginal utility with respect to the consumption of the two economies have θⁱ > 1 and θ^j > 1, the increase of ξⁱ will lower its own growth rate of resource exploitation and boost other economies' growth rate of resource exploitation. Further, we have the next corollary based on proposition 4.

Corollary 1: In the steady state, based on proposition 4, using Equation (26) and (27), we have $\frac{\partial g_{Y^i}}{\partial {\omega }^j}=\frac{\partial g_{Y^i}}{\partial g_{R^j}}\blacksquare \frac{\partial g_{R^j}}{\partial {\omega }^j}\{\begin{array}{c}<0if{g}_Q<0\\ >0if{g}_Q>0\end{array}$,$\frac{\partial g_{Y^i}}{\partial {\xi }^j}=\frac{\partial g_{Y^i}}{\partial g_{R^j}}\blacksquare \frac{\partial g_{R^j}}{\partial {\xi }^j}\{\begin{array}{c}<0if{\theta }^j<1\\ >0if{\theta }^j>1\end{array}$,$\frac{\partial g_{A^i}}{\partial {\omega }^j}=\frac{\partial g_{A^i}}{\partial g_{R^j}}\blacksquare \frac{\partial g_{R^j}}{\partial {\omega }^j}\{\begin{array}{c}>0if{g}_Q<0,{\theta }^i>1or{g}_Q>0,{\theta }^i<1\\ <0if{g}_Q>0,{\theta }^i>1or{g}_Q<0,{\theta }^i<1\end{array}$, and

$\begin{array}{l}\frac{\partial g_{A^i}}{\partial {\xi }^j}=\frac{\partial g_{A^i}}{\partial g_{R^j}}\blacksquare \frac{\partial g_{R^j}}{\partial {\xi }^j}\{\begin{array}{c}>0if{\theta }^i<1,{\theta }^j>1or{\theta }^i>1,{\theta }^j<1\\ <0if{\theta }^i>1,{\theta }^j>1or{\theta }^i<1,{\theta }^j<1\end{array}\end{array}$

Corollary 1 reflects that one economy's activities will exert influence on another economy through the changing fossil resource input and carbon emission. The increase of ω of one economy will have a positive influence on the economic growth of other economies when the balanced growth rate of carbon concentration is positive. If one economy has a higherθ, the increase of efficiency of knowledge accumulation will lower his own growth rate of resource exploitation and then promote the balanced growth rate of another economy.

The sign of first-order condition between $g_{A^i}$ and ω^j depends on both the values of g_Q and θⁱ. If g_Q and 1-θⁱ have the same positive or negative sign, there is a positive relationship between $g_{A^i}$ and ω^j. If the people in the two economies have the same preference degree (which means θⁱ − 1 and θ^j − 1 have the same sign), the increase of efficiency of knowledge accumulation of one economy will lower the balanced growth rate of knowledge accumulation of another economy.

Conclusions

The unity of opposites between economic development and environmental protection is an important proposition of environmental economics. At the present stage, the division of labor in economic development is becoming more and more detailed. Global production has already made the production links not only concentrated in a few countries. The differences in economic development between countries also bring about huge differences in the intensity of environmental regulation among countries. As a result, the research on environmental regulation with industries and enterprises as the main body is no longer applicable to the actual production practice, and the global environmental problems cannot be effectively solved. A natural resource that causes carbon emission is introduced into an endogenous growth model with human capital and is addressed in this study. If the carbon concentration impacting the utility level of consumers is considered in the model, in the steady state, the growth rate differs in several ways from usual models combining growth with environmental questions; the growth rate of output and knowledge accumulation is always greater than zero. If the elasticity of the marginal utility of consumption is lower than 1, which means people are not concerned with having a smooth consumption profile over time, and the growth rate of carbon concentration will be positive. The growth rate of output (consumption) is greater than the growth rate of resource extraction (carbon concentration) all the time. Economic growth depends more on the human capital input and less on resource extraction when the disutility of carbon concentration is considered.

Furthermore, the reaction of the two economies was considered in the model, as this is closer to the real world. In the two-economy system model, the activities of both economies will produce carbon compounds and reduce the utility of consumers. The economic activities of one economy will bring remarkable adverse impacts to the activities of other economies on the balanced path. Facing the global public goods (carbon concentration), the multi-agent decision will often cause the tragedy of the commons. Both the implementer and sufferer will be punished (lower utility) by the environment. The increase of the elasticity of the marginal utility with respect to carbon concentration of every economy will lower the growth rate of the carbon concentration. On the contrary, if the people in one economy pay more attention to the carbon emission environmental problem, the economy will lower its own resource input but increase another economy's resource input simultaneously. It is similar to the real world that the public in some developed countries put a high value on the carbon emission and force the government to reduce emission but promote the emission of other countries imperceptibly, making carbon emission one of the most difficult challenges in global governance.

Therefore, the cross-border and cross-industry characteristics of carbon emission problems make it difficult for the existing environmental regulation policies with the single country, industry, or enterprise as the main body to achieve the desired effect. The global environmental pollution control needs the help of the cross-regional governance mechanism. We should establish a global environmental regulation policy, so as to realize the clean technology progress of the global value chain under the condition of heterogeneity of environmental regulation, reduce the transfer of pollution links, practice the development concept of “community of human destiny,” walk out of the extensive economic development mode of “pollution before governance,” and realize green sustainable development.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

PS: framework construction and model processing. KZ: text sorting. SL: model analysis and verification. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (Project 71563008), High-level Talent Project of Hainan Provincial Natural Science Foundation (Project 720RC578), the Hainan Philosophy and Social Science Planning General Project [Project HNSK(YB)20-13], and the Hainan Natural Science Foundation High-level Talents Program in 2020.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.652832/full#supplementary-material

Footnotes

1. ^Solving the balanced growth path see Appendix A.

2. ^An interior pathimplies that labor time must be spent in both the education sector and the final output. So the growth rate of human capital must be positive, but less than the highest possible value, which is ξ (for l₁ = 0). We have 0 < g_A < ξ.

3. ^Other conditions in section The Basic Model and Primary Results of One Economy have remained the same.

4. ^For a similar explanation of Equation (23) see (Vita, 2005).

5. ^Note that ωⁱ only appears in the denominator of Equation (29).

6. ^Note that ξⁱ only appear in the numerator of Equation (29).

References

Afonso, O., and Afonso, A. C. (2015). Endogenous growth effects of environmental policies. Panoeconomicus 62, 607–629. doi: 10.2298/PAN1505607A

CrossRef Full Text | Google Scholar

Aronsson, T., and Löfgren, K. G. (1999). Pollution tax design and “Green” national accounting. Eur. Econ. Rev. 43, 1457–1474. doi: 10.1016/S0014-2921(98)00028-2

CrossRef Full Text | Google Scholar

Aznar-Márquez, J., and Ruiz-Tamarit, J. R. (2016). Environmental pollution, sustained growth, and sufficient conditions for sustainable development. Econ. Model. 54, 439–449. doi: 10.1016/j.econmod.2016.01.017

CrossRef Full Text | Google Scholar

Bianco, D. (2017). Environmental policy in an endogenous growth model with expanding variety. Rev. d'économiepolitique 127, 1013–1028. doi: 10.3917/redp.276.1013

CrossRef Full Text | Google Scholar

Bovenberg, A. L., and Smulders, S. (1995). Environmental quality and pollution-augmenting technological change in a two-sector endogenous growth model. J. Public Econ. 57, 369–391. doi: 10.1016/0047-2727(95)80002-Q

CrossRef Full Text | Google Scholar

Bovenberg, A. L., and Smulders, S. A. (1996). Transitional impacts of environmental policy in an endogenous growth model. Int. Econ. Rev. 37, 861–893. doi: 10.2307/2527315

CrossRef Full Text | Google Scholar

Byrne, M. M. (1997). Is growth a dirty word? Pollution, abatement and endogenous growth. J. Dev. Econ. 54, 261–284. doi: 10.1016/S0304-3878(97)00043-6

CrossRef Full Text | Google Scholar

Chiang, A. C. (2015). Elements of Dynamic Optimization. Beijing: China Renmin University Press.

Chu, H., and Lai, C. (2014). Abatement R&D, market imperfections, and environmental policy in an endogenous growth model. J. Econ. Dyn. Control. 41, 20–37. doi: 10.1016/j.jedc.2014.02.011

CrossRef Full Text | Google Scholar

Di Vita, G. (2006). Natural resources dynamics: exhaustible and renewable resources, and the rate of technical substitution. Res. Policy 31, 172–182. doi: 10.1016/j.resourpol.2007.01.003

CrossRef Full Text | Google Scholar

Di Vita, G. (2007). Exhaustible resources and secondary materials: a macroeconomic analysis. Ecol. Econ. 63, 138–148. doi: 10.1016/j.ecolecon.2006.10.004

CrossRef Full Text | Google Scholar

Dietz, S., and Stern, N. (2015). Endogenous growth, convexity of damage and climate risk: how Nordhaus' framework supports deep cuts in carbon emissions. Econ. J. 125, 574–620. doi: 10.1111/ecoj.12188

CrossRef Full Text | Google Scholar

Gradus, R., and Smulders, S. (1993). The trade-off between environmental care and long-term growth—pollution in three prototype growth models. J. Econ. 58, 25–51. doi: 10.1007/BF01234800

CrossRef Full Text | Google Scholar

Greiner, A. (2005). Fiscal policy in an endogenous growth model with public capital and pollution. Japan. Econ. Rev. 56, 67–84. doi: 10.1111/j.1468-5876.2005.00299.x

CrossRef Full Text | Google Scholar

Hardin, G. (1968). The tragedy of the commons. Science 162, 1243–1248. doi: 10.1126/science.162.3859.1243

CrossRef Full Text | Google Scholar

Jones, L. E., and Manuelli, R. E. (2001). Endogenous policy choice: the case of pollution and growth. Rev. Econ. Dyn. 4, 369–405. doi: 10.1006/redy.2000.0118

CrossRef Full Text | Google Scholar

Kamien, M. I., and Schwartz, N. L. (1978). Optimal exhaustible resource depletion with endogenous technical change. Rev. Econ. Stud. 45, 179–196. doi: 10.2307/2297093

CrossRef Full Text | Google Scholar

Kollenbach, G. (2015). Endogenous growth with a ceiling on the stock of pollution. Environ. Res. Econ. 62, 615–635. doi: 10.1007/s10640-014-9832-6

CrossRef Full Text | Google Scholar

Lorente, D. B., and Álvarez-Herranz, A. (2016). Economic growth and energy regulation in the environmental Kuznets curve. Environ. Sci. Pollut. Res. 23, 16478–16494. doi: 10.1007/s11356-016-6773-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Marsiglio, S. (2017). A simple endogenous growth model with endogenous fertility and environmental concern. Scott. J. Polit. Econ. 64, 263–282. doi: 10.1111/sjpe.12125

CrossRef Full Text | Google Scholar

Meadows, D. H., Randers, J., Meadows, D. L., and Behrens, D. D. (1972). The Limits to Growth. New York, NY: Universe Books.

Google Scholar

Michel, P., and Rotillon, G. (1995). Disutility of pollution and endogenous growth. Environ. Res. Econ. 6, 279–300.

Google Scholar

Pontryagin, L. S., Boltyanskii, V. G., Gamkrelidze, R. V., and Mishchenko, E. F. (1962). The Mathematical Theory of Optimal Processes, Translated From Russian by Triroyoff, K. N. New York, NY: Interscience.

Google Scholar

Reis, A. B. (2001). Endogenous growth and the possibility of eliminating pollution. J. Environ. Econ. Manage. 42, 360–373. doi: 10.1006/jeem.2000.1159

CrossRef Full Text | Google Scholar

Romer, P. M. (1990). Endogenous technological change. J. Polit. Econ. 98, 71–102. doi: 10.1086/261725

CrossRef Full Text | Google Scholar

Scholz, C. M., and Ziemes, G. (1999). Exhaustible resources, monopolistic competition, and endogenous growth. Environ. Res. Econ. 13, 169–185. doi: 10.1023/A:1008201811142

CrossRef Full Text | Google Scholar

Schou, P. (2000). Polluting non-renewable resources and growth. Environ. Res. Econ. 16, 211–227. doi: 10.1023/A:1008359225189

CrossRef Full Text | Google Scholar

Smith, V. L. (1972). Dynamics of waste accumulation: disposal versus recycling. Q. J. Econ. 86, 600–616. doi: 10.2307/1882044

CrossRef Full Text | Google Scholar

Stiglitz, J. (1974). Growth with exhaustible natural resources: efficient and optimal growth paths. Rev. Econ. Stud. 41, 123–137. doi: 10.2307/2296377

CrossRef Full Text | Google Scholar

Vita, G. D. (2005). Renewable resources and waste recycling. Environ. Model. Assessment 9, 159–167. doi: 10.1007/s10666-005-3798-2

CrossRef Full Text | Google Scholar

Withagen, C. (1995). Pollution, abatement and balanced growth. Environ. Res. Econ. 5, 1–8. doi: 10.1007/BF00691906

CrossRef Full Text | Google Scholar