Finite-Element Simulation of Residual Stresses During the Processing of Lumped Burnable Absorber Fuel

UO₂–Gd₂O₃ fuel is mostly used as a burnable absorber fuel in the form of a homogenous mixture of Gd₂O₃ and UO₂. More effective reactivity control can be achieved by lumping Gd₂O₃ within the UO₂ because this enhances the spatial self-shielding factor of the burnable absorber fuel. The fabrication of lumped burnable absorber fuel containing lumped Gd₂O₃ spherical particles or compacts has been experimentally demonstrated using yttrium-stabilized zirconia (YSZ) as a UO₂ fuel surrogate. Interfacial cracks or gaps forming under the interfacial stress that develops during the fabrication of the fuel can be eliminated by controlling the initial density of the lumped Gd₂O₃. In this study, this interfacial stress during the fabrication process was simulated using finite element methods. The effect of the size, shape, and initial density of the lumped Gd₂O₃ on the distribution and magnitude of the interfacial stress was investigated. The addition of Gd₂O₃ spherical particles resulted in a lower and more uniform interfacial stress distribution than the addition of cylindrical Gd₂O₃ compacts. The interfacial stress was increased with increasing Gd₂O₃ size and initial density. The calculated interfacial stress was compared with experimental results to estimate the threshold stress for crack development in a lumped burnable absorber fuel.

Introduction

The potential use of Gd as a burnable absorber was recognized many years ago, considering its extremely high thermal neutron absorption cross-section. Gd is usually used in the form of Gd₂O₃ uniformly mixed with UO₂ as a fuel matrix. Owing to the relatively high thermal neutron absorption cross-section, few fuel rods must contain Gd₂O₃. However, the main limitations of Gd₂O₃ are the significant end-of-cycle penalty due to the existence of Gd isotopes with higher thermal neutron absorption cross-sections (i.e., ¹⁵⁵Gd and ¹⁵⁷Gd) (Grossbeck et al., 2001) and the degradation of the fuel’s thermophysical properties (IAEA, 1995; Durazzo et al., 2013; Choe et al., 2016a). One possible way to overcome these limitations is changing the design of the UO₂–Gd₂O₃ mixed fuel.

Several burnable absorber fuel designs have been developed for small modular pressurized water reactors (SMPWRs) in order to eliminate the use of soluble boron and improve the reactor performance in terms of increasing the fuel cycle length while maintainig a flat power distribution. Choe et al. (2016b) have proposed the use of a thin-layer of Zr-¹⁶⁷Er (∼ 0.1–0.2 mm) on the inner side of the cladding as a new burnable absorber fuel design. A low burn-up swing of 548 pcm and cycle length of 26.5 months can be obtained for SMPWRs loaded with this burnable absorber fuel design. Another advanced burnable absorber fuel design integrated four azimuthally B₄C pads, with a thickness up to 90 μm and span up to 70^o, in the guide-thimble ring (Yahya and Kim, 2017a). This burnable absorber fuel design achieved a cycle length of about 53 months and a burnup swing between 634 and 800 pcm. Recently, a new design for burnable absorber fuel, called centrally shielded burnable absorber (CSBA), was developed (Nguyen et al., 2019). The CSBA comprises lumped Gd₂O₃ in the center of a UO₂ fuel pellet. The lumping of Gd₂O₃ results in a slower burn-out rate and longer suppression of the excess of reactivity due to spatial self-shielding effect (Galperin et al., 1986; Yahya and Kim, 2017b). It was found that the spherically lumped burnable absorber has a higher self-shielding factor than other lumped burnable absorber designs like cylindrical or slab due to the its higher volume-to-surface-area ratio (Fleming, 1982). Nguyen et al. (2019) studied the effect of the size and number of spherically lumped Gd₂O₃, and found that a more excess reactivity subression and flat power distribution can be obtained by increasing the Gd₂O₃ sphere radius from 1 mm to 1.3 mm or the number of Gd₂O₃ sphere (radius = 1 mm) from 1 to 3. They found that a low burn-up swing (∼1100 pcm), long cycle length (∼37 months), and higher burnup (∼30 GWd/tU) can be obtained for a small modular reactor loaded with one Gd₂O₃ sphere (radius = 1.69 mm) in the center, two Gd₂O₃ spheres (radius = 1.26 mm) in the intermediate region, three Gd₂O₃ spheres (radius = 0.7 mm) in the outer region (Nguyen et al., 2019). The fabrication of CSBA using yttria-stabilized zirconia (YSZ) as a surrogate for UO₂ and either lumped Gd₂O₃ pellets, spherical particles, or rods was recently demonstrated (Mistarihi et al., 2018).

One of the major challenges in CSBA fuel design is the formation of interfacial cracks that may form under the stress mismatch developed during the sintering or cooling processes. This may arise from mismatches in the densification and thermal expansion coefficients (TECs), as well as phase transformations, of the sintered materials (Sglavo and Bellettati, 2017). The existence of these interfacial cracks can increase the intensity of fuel cracking during reactor operation and eventually limit fuel performance. In our previous study (Mistarihi et al., 2018), we concluded that interfacial cracks were not formed in YSZ pellets containing lumped Gd₂O₃ because of the TEC mismatch or the phase transformation of Gd₂O₃. The TECs of YSZ and Gd₂O₃ are similar and interfacial cracks were absent from Gd₂O₃ mini-pellets pre-sintered at temperatures below the phase transformation temperature. Thus, interfacial cracks could be mainly attributed to the sintering stresses resulting from the shrinkage rate mismatch.

Several factors control the sintering stresses that develop during the processing of composites, including shrinkage rate mismatch, volume fraction, and the shape and size of inclusions (Davidge and Green, 1968). The results of our previous study (Mistarihi et al., 2018) showed that, in YSZ oxide pellets containing lumped Gd₂O₃ mini-pellets, interfacial cracks were formed only when using mini-pellets with high initial densities. However, no interfacial cracks were observed in the case of YSZ oxide pellets containing lumped Gd₂O₃ spherical particles with high initial densities. The fabricated Gd₂O₃ spherical particles and mini-pellets had similar relative densities, but they differed in size and shape. Therefore, the effect of the shape, size, and shrinkage rate of the lumped Gd₂O₃ on the formation of interfacial cracks during the manufacturing of YSZ oxide pellets containing lumped Gd₂O₃ is investigated in this study.

One method to investigate interfacial crack formation during the processing of composites is to determine the stress distribution. By determining the stress distribution, areas of high stress concentration can be located. These areas are important for the integrity of composites because failure, signified by the formation of interfacial cracks, begins in them (Agarwal, 1972). Several analytical studies based on the theory of elasticity have been performed to determine stress distributions in composites using simplified physical models such as spherical particles (Selsing, 1961) or fibers (Delale, 1988) distributed in infinite matrices. However, the behaviors of powder compacts during sintering are not elastic, and the relationship between the stress and deformation during the sintering process is complex. Nonetheless, the finite-element analysis (FEA) method allows the implementation of complex stress–deformation relationships and the analysis of complex geometries.

Because powder compacts exhibit viscoelastic behaviors, several phenomenological models have been developed to describe their behaviors during sintering. Riedel et al. (1993), using a simple 2D hexagonal grain structure with pores at the triple points, developed an isotropic linear viscous constitutive equation to describe sintering-dominated grain boundary diffusion. Olevsky (1998) developed a phenomenological model based on the continuum theory of sintering by determining the sintering parameters from the rheological behaviors of porous materials during sintering. This model was implemented in an FEA code (COMSOL) and used to study the sintering behavior of different powder compacts (Al₂O₃ and YSZ) processed by spark plasma sintering (Olevsky et al., 2012) and microwave sintering (Manière et al., 2017). In these studies (Olevsky et al., 2012; Manière et al., 2017), FEA was mostly used to predict the shrinkage rate and temperature distribution of the powders during sintering. Li et al. (2020) used the finite element software (ABAQUS) to study the stress distribution in the cladding of dispersed plate-type fuel as a function of irradiation time and temperatures by implementing nuclear fuel correlation as a subroutine.

In this study, the Olevsky model for sintering was implemented in the COMSOL Multiphysics code and used to understand the stress distribution formed during the manufacturing of YSZ oxide pellets containing lumped Gd₂O₃. In addition, the applicability of the CSBA to UO₂ was investigated, and the stress distribution in UO₂ containing lumped Gd₂O₃ was determined and compared with that of the YSZ-based pellets. The novelty of this study is to estimate the stress distribution and magnitude in the lumped burnable absorber fuel design during the fabrication process.

Materials and Methods

Governing Equations

Thermal, mechanical (linear elastic and sintering), and densification models were coupled by the FEA method (COMOSOL Multiphysics 5.4 code) and used to study the temperature, stress, and density distributions during the manufacturing of YSZ or UO₂ oxide pellets containing either lumped Gd₂O₃ spheres or mini-pellets. The heat-transfer model applied to the entire pellet is expressed by the following equation:

$$\mathrm{\rho }{C}_{\text{p}}\frac{\partial \text{T}}{\partial \text{t}}+\nabla .\left(-k\nabla \text{T}\right)=0(1)$$

where ρ is the material density (g.cm^–3), C_p is the heat capacity (J.kg^–1K^–1), T is the temperature (K), t is the time (s), and k is the thermal conductivity of the material (W.m^–1.K^–1).

The Gd₂O₃ spherical particle or mini-pellet was assumed to exhibit pure elastic behavior, wherein the relationship between the stress and deformation is expressed by Hooke’s law:

$${\mathrm{\sigma }}_{\text{ij}}=\text{C}{\stackrel{.}{\mathrm{\epsilon }}}_{\text{ij}}(2)$$

where σ_ij is the stress tensor (N.m^–2), ${\stackrel{.}{\epsilon }}_{\text{ij}}$ is the strain tensor (s^–1), and C is a fourth-order tensor that is a function of the shear modulus (G) and Young’s modulus (E) of the material.

The YSZ and UO₂ powder compact was assumed to exhibit a non-linear viscous behavior expressed by Olevsky (1998) phenomenological model (Eqs 3–6) based on the continuum theory of sintering:

$${\mathrm{\sigma }}_{\text{ij}}=\frac{1}{\mathrm{A}(\mathrm{T})}\left(\mathrm{\phi }{\stackrel{.}{\mathrm{\epsilon }}}_{\text{ij}}+\left(\mathrm{\psi }-\frac{1}{3}\mathrm{\phi }\right)\stackrel{.}{\text{e}}{\mathrm{\delta }}_{\text{ij}}\right)+\text{S}{\mathrm{\delta }}_{\text{ij}}(3)$$

$$\text{A}\left(\text{T}\right)=\frac{\text{A}}{\text{T}}{\text{e}}^{-\frac{\text{Q}}{\text{RT}}}(4)$$

$$\stackrel{.}{\text{e}}={\stackrel{.}{\mathrm{\epsilon }}}_{\text{x}}+{\stackrel{.}{\mathrm{\epsilon }}}_{\text{y}}+{\stackrel{.}{\mathrm{\epsilon }}}_{\text{z}}(5)$$

$$\mathrm{\phi }={(1-\text{P})}^2,\mathrm{\psi }=\frac{2}{3}\frac{{(1-\text{P})}^3}{\text{P}},\text{S}=\frac{3\mathrm{\alpha }}{\text{r}}{(1-\mathrm{P})}^2(6)$$

where A(T) is the creep rate factor having the form of an Arrhenius-type equation, Q is the activation energy for deformation, A is a pre-exponential factor, φ is the shear viscosity (Pa.s), Ψ is the bulk viscosity (Pa.s), $\stackrel{.}{\text{e}}$ is the shrinkage rate (s^–1), δ_ij is the identity tensor, S is the effective sintering stress (Pa), P is the porosity, α is the surface energy (J.m^–2), Q is the activation energy (J.mol^–1), R is the gas constant 8.314 (J.mol^–1.K^–1), and r is the average particle radius (m).

The densification of YSZ and UO₂ during the manufacturing process is expressed as the evolution of density during the fabrication process. The density can be related to porosity using the following expression:

$${\mathrm{\rho }}_{\text{eff}}={\mathrm{\rho }}_{\text{t}}(1-\text{P})(7)$$

where ρ_eff is the effective density of the material during the sintering process and ρ_t is the theoretical density of the material. Therefore, the densification of YSZ and UO₂ during the fabrication process can be calculated by the evolution of the porosity, which evolves according to the equation of mass conservation:

$$\stackrel{.}{\text{P}}+\stackrel{.}{\text{e}}\text{P}=\stackrel{.}{\text{e}}(8)$$

Materials Properties

For Gd₂O₃, the experimentally measured densities of the 1400 °C, 1500 °C, and 1600 °C pre-sintered Gd₂O₃ were obtained from our previous study (Mistarihi et al., 2018) and used in the simulation. These densities were approximately 6.29 ± 0.13, 7.10 ± 0.04, and 7.75 ± 0.0.6 g/cm³, corresponding to relative densities (RDs) of 75.5 ± 1.5, 85.2 ± 0.5, and 93.4 ± 0.8%, respectively. The RD equals to the experimentally measured density divided by the theoretical density.

The elastic and shear moduli of Gd₂O₃ as functions of temperature for samples with an RD of 96.75% were measured by Dole and Hunter (1976). Haglund and Hunter (1973) measured the elastic properties of polycrystalline Gd₂O₃ with different initial porosities ranging from 2.5% to 36.7% as functions of temperature. The elastic properties were found to decrease linearly with the initial porosity of the sintered samples. The initial porosity of the sintered samples was varied by changing the sintering temperature (Haglund and Hunter, 1973). The reported values of E and G of Gd₂O₃ as functions of T and RD were fitted to first-degree polynomials; the determined parameters of the fitting function are shown in Eqs 9 and 10.

$$\text{E}=0.00428\times \text{T}+265.30732\times \text{RD}-0.02349$$

$$\times \text{T}\times \text{RD}-117.14246(9)$$

$$\text{G}=0.00158\times \text{T}+104.39288\times \text{RD}+0.00584\times \text{T}$$

$$\times \text{RD}-46.46078(10)$$

Using the experimentally measured RDs of the 1400 °C, 1500 °C, and 1600 °C pre-sintered Gd₂O₃, E and G as functions of T were calculated using Eqs 9 and 10.

The thermal conductivity of the fully sintered Gd₂O₃ as a function of temperature was experimentally measured using the laser flash method, and the results are shown in Figure 1. The thermal conductivity of fully dense Gd₂O₃ at temperatures higher than 800 °C was extrapolated from the experimentally measured data.

FIGURE 1

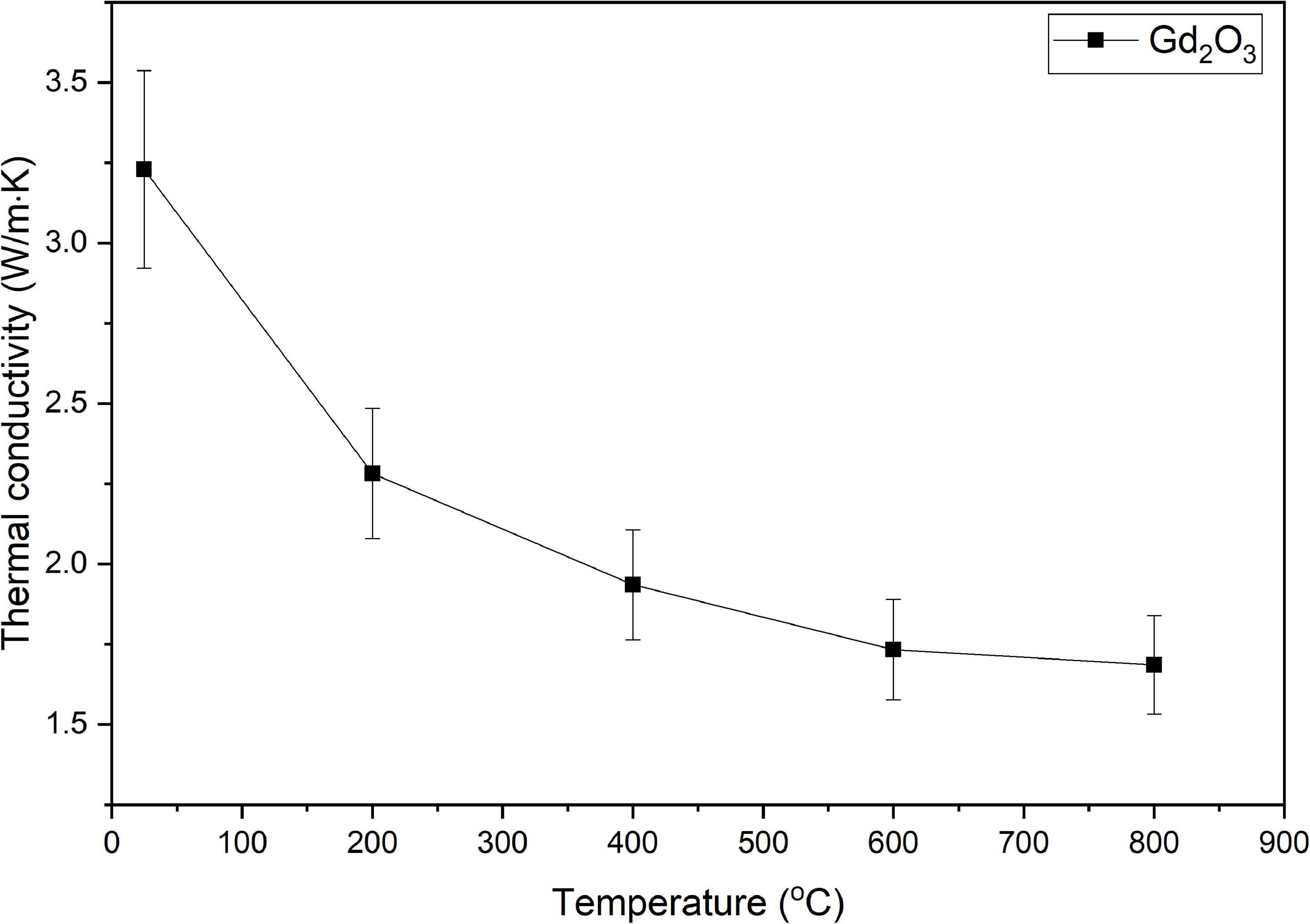
Figure 1. Thermal conductivity of fully dense Gd₂O₃ with increases in sintering temperature from 25 °C to 800 °C.

The thermal conductivities of the 1400 °C, 1500 °C, and 1600 °C pre-sintered Gd₂O₃ as functions of T were calculated from the thermal conductivity of the fully densified Gd₂O₃ using a modified Maxwell–Eucken correlation (Eq. 11):

$${\mathrm{K}}_{\mathrm{p}}=1.0789{\text{K}}_{100}\left(\frac{1-\text{P}}{1+0.5\text{P}}\right)(11)$$

where K₁₀₀ and K_p are the thermal conductivities of fully dense and porous Gd₂O₃, respectively.

For YSZ, the thermal conductivity and heat capacity as a function of T and density were provided by Manière et al. (2017) and used in the simulation (Eqs 12-13). The surface energy was provided by Tsoga and Nikolopoulos (1996) as given by Eq. 14. The density was calculated from the determined porosity. The average particle radius of 700 nm (Sigma Aldrich) was used in the simulation. The creep factor (Eq. 15) was determined by fitting the experimentally determined density of YSZ with those predicted by the FEA of YSZ oxide pellets without Gd₂O₃ spheres or mini-pellets. The density of YSZ was determined from the experimentally measured shrinkage of YSZ after correcting its TEC (9.75 × 10^–6 K^–1) (Song et al., 2011).

$$\text{k}=(1.96-2.32\times {10}^{-4}\text{T}+6.33\times {10}^{-7}{\text{T}}^2-1.91$$

$$\times {10}^{-10}{\text{T}}^3)(1-1.5\mathrm{P})(12)$$

$${\mathrm{C}}_{\mathrm{p}}=\{\begin{array}{c}(43+2.35\mathrm{T}-0.34\times {10}^{-3}{\mathrm{T}}^2+4.25\times {10}^{-6}{\mathrm{T}}^3-\hfill \\ 2.09\times {10}^{-9}{\mathrm{T}}^4+4.06\times {10}^{-13}{\mathrm{T}}^5)(1-1.5\mathrm{P}),\hfill \\ 273<\mathrm{T}(\mathrm{K})<1473\hfill \\ 638(1-1.5\mathrm{P}),1473<\mathrm{T}(\mathrm{K})<2200\hfill \end{array}(13)$$

$$\mathrm{\alpha }=1.927-0.428\times {10}^{-3}\text{T}(14)$$

$$A(T)=\{\begin{array}{c}\frac{0.12}{T}{e}^{-\frac{200000}{RT}},273<T(K)<1300\hfill \\ 23\times {10}^{-10}\left(1-\frac{1}{1+e^{\frac{T-1895.58}{63}}}\right),\hfill \\ 1300<T(K)<1800\hfill \end{array}(15)$$

For UO₂, the surface energy as a function of T from 273 to 3120 K was provided by Hall and Mortimer (1986). Fink (2000) summarized this reported data and provided a correlation for the mean value of the surface energy of UO₂ as a function of T (Eq. 16):

$$\mathrm{\alpha }=0.85-1.4\times {10}^{-4}\left(\text{T}-273.15\right)(16)$$

The heat capacity of the stoichiometric UO₂ was measured by Kerrisk and Clifton (1972) over the temperature range 483–3107 K. These data were summarized and fitted to Eq. 17 in MATPRO (Siefken et al., 2001):

$${\text{C}}_{\text{p}}=\frac{{\text{K}}_1{\text{M}}^2{\text{e}}^{\frac{\mathrm{\theta }}{\text{T}}}}{{\text{T}}^2{[{\text{e}}^{\frac{\text{M}}{\text{T}}}-1]}^2}+{\text{K}}_2\text{T}+\frac{{\text{YK}}_3{\text{E}}_{\text{D}}}{2\mathrm{R}{\text{T}}^2}{\text{e}}^{\frac{-{\text{E}}_{\text{D}}}{\text{RT}}}(17)$$

where Y is the oxygen-to-metal ratio (equal to 2), R is the universal gas constant (8.3143 J/mol⋅K), and M is the Einstein constant (535.285). The constants K₁, K₂, K₃, and E_D are equal to 296.7, 2.43 × 10^–2, 8.745 × 10⁷, and 1.577 × 10⁵.

Lucuta et al. (1996) summarized the thermal conductivity of non-irradiated and fully dense UO₂ and fitted the data to a function comprising a hyperbolic term for the lattice contribution through phonon–defect and phonon–phonon scattering processes and an exponential term for polaron contributions. The exponential term becomes dominant for high temperatures T > 1900 K.

$${\text{k}}_{\text{o}}=\frac{1}{0.0375+2.165\times {10}^{-4}\text{T}}+\frac{4.715\times {10}^9}{{\text{T}}^2}{\text{e}}^{\frac{-16361}{\text{T}}}(18)$$

The creep factor of UO₂ was generated in a similar way to that of YSZ and is expressed by Eq. 19.

$$A(T)=\{\begin{array}{c}\frac{0.12}{T}{e}^{-\frac{200000}{RT}},273<T(K)<1300\hfill \\ 30\times {10}^{-10}\left(1-\frac{1}{1+e^{\frac{T-1795.58}{100}}}\right),\hfill \\ 1300<T(K)<1800\hfill \end{array}(19)$$

An average particle radius of 2400 nm was used for the simulation of UO₂ (Yeo et al., 2013).

The shrinkage rates of the green YSZ, UO₂, and Gd₂O₃ compacts and the 1400 °C, 1500 °C, and 1600 °C pre-sintered pellets were measured by a dilatometer (DIL 402C) up to 1600 °C in an air atmosphere with a heating rate of 10 °C/min and a holding time of 3 h. The results are shown in Figure 2.

FIGURE 2

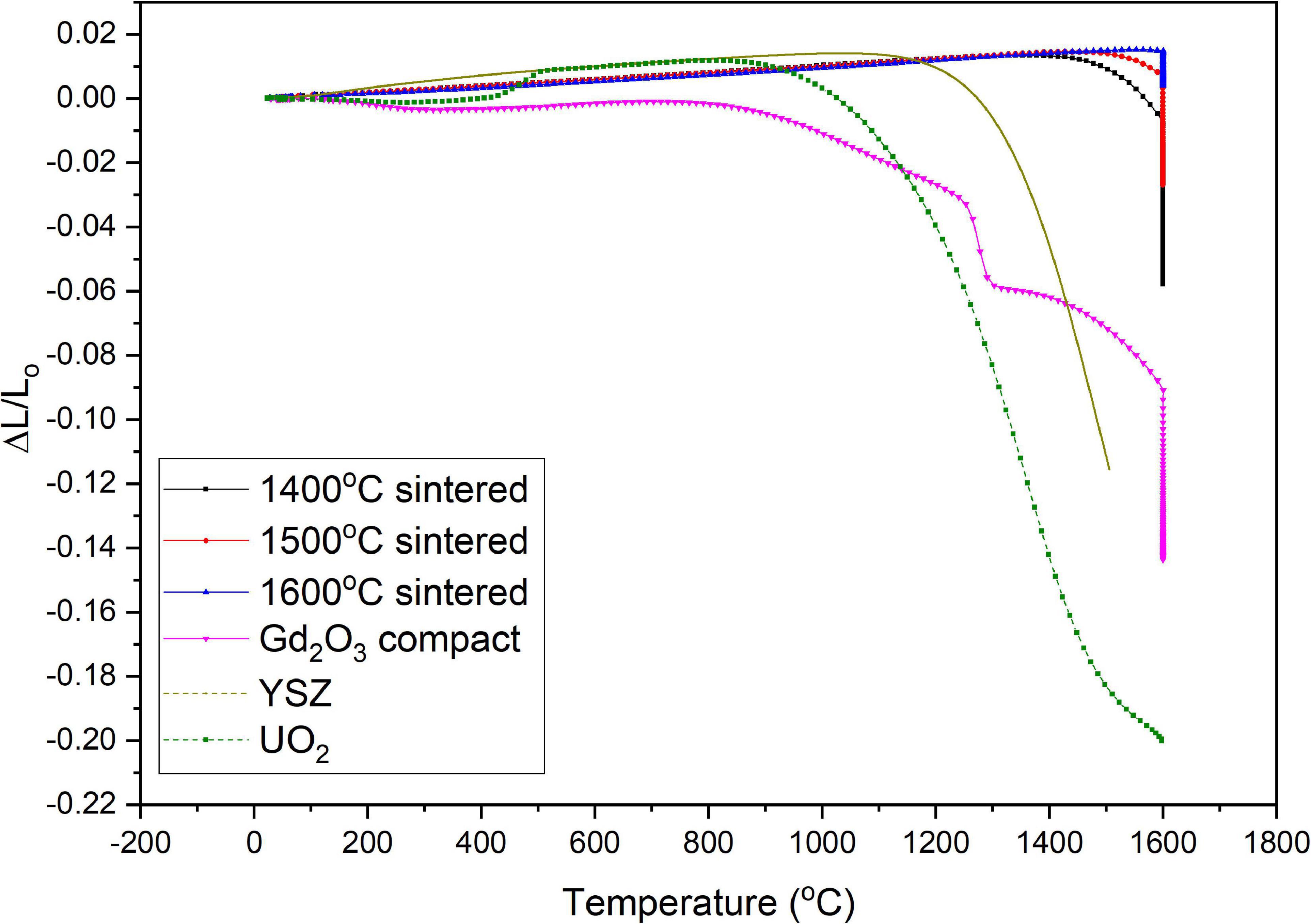
Figure 2. Shrinkage behaviors of Gd₂O₃ compact, sintered Gd₂O₃ pellet, YSZ compact, and UO₂ compact.

Geometric Models

2-D axisymmetric simulation models were developed to study the sintering stress distributions during the fabrication process of YSZ pellets containing lumped Gd₂O₃ mini-pellets or spherical particles. The geometrical models used in the FEA simulations are shown in Figure 3.

FIGURE 3

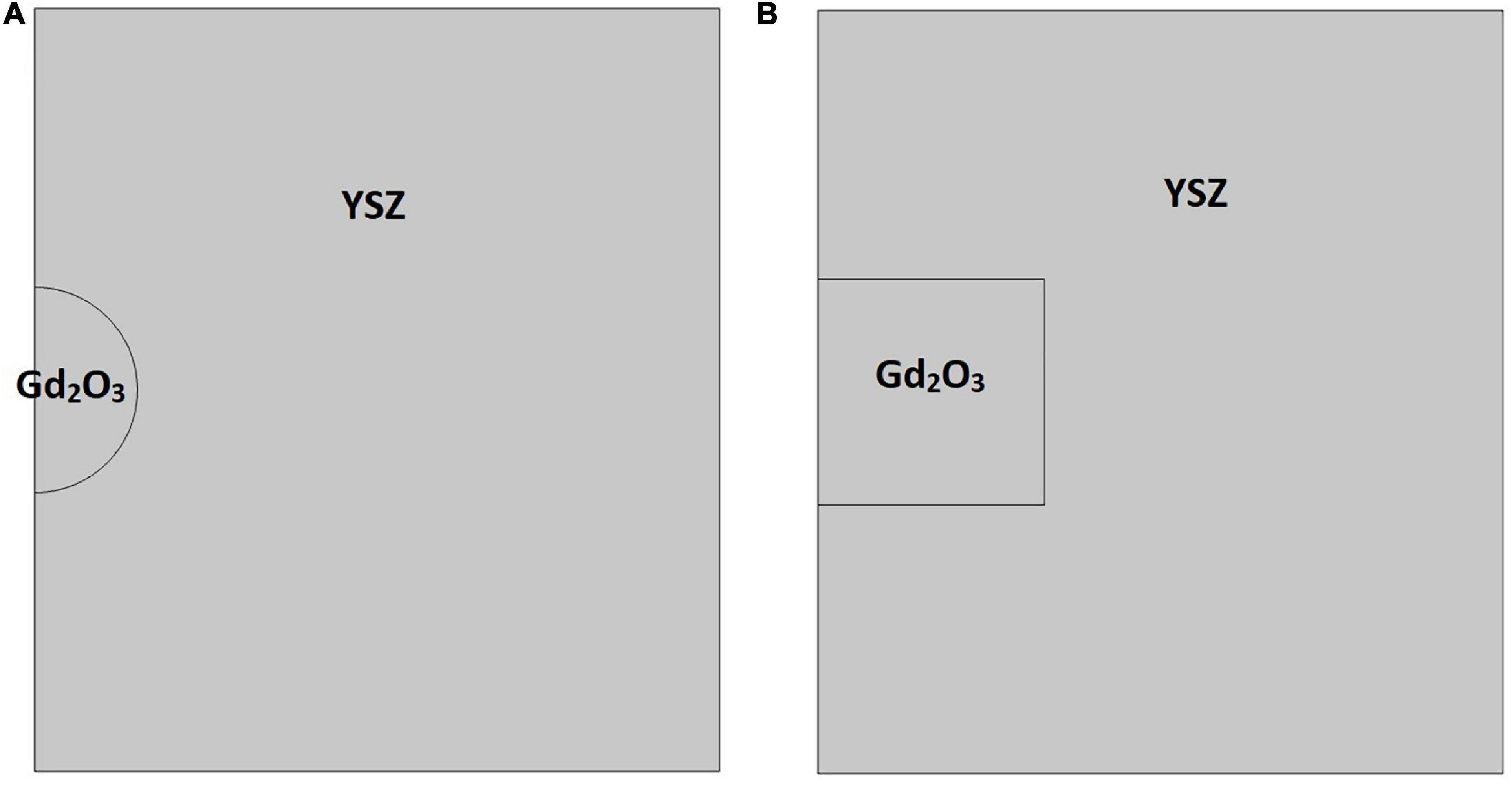
Figure 3. Geometrical models of YSZ oxide pellet containing (A) lumped Gd₂O₃ spherical particle and (B) mini-pellet.

In order to determine the critical sintering stress for cracking, simulation models of YSZ oxide pellets with a Gd₂O₃ mini-pellet pre-sintered at 1400 °C, 1500 °C, or 1600 °C having the average measured dimensions of the pre-sintered pellets (see Table 1) and the measured shrinkage rates of the pellets sintered at 1400, 1500, and 1600 °C (see Figure 2) were developed. Simulation models of YSZ oxide pellets containing either lumped Gd₂O₃ spherical particles or mini-pellets of the same size and the shrinkage rate of the 1400 °C pre-sintered pellets were also developed to understand the effect of the lumped Gd₂O₃ shape on the formation of interfacial cracks. In addition, simulation models of YSZ oxide pellets with lumped Gd₂O₃ spherical particles of 1.5, 2, or 3 mm in diameter and the shrinkage rate of the pellets pre-sintered at 1400 °C were developed to determine the critical size of the lumped Gd₂O₃ spherical particles. Finally, simulation models of YSZ oxide pellets with a Gd₂O₃ spherical particle having the shrinkage rate of the pellet at 1400 °C, 1500 °C, or 1600 °C and the size of 1.5 mm were developed to understand the effect of the shrinkage rate on the formation of interfacial cracks.

TABLE 1

Table 1. Dimensions of Gd₂O₃ mini-pellets after pre-sintering at different temperatures.

Initial and Boundary Conditions

The simulation models were assumed to have an initial temperature of 25 °C. The outer surfaces of the simulation models of the YSZ oxide pellets containing a lumped Gd₂O₃ sphere or mini-pellet were heated from 25 °C to 1500 °C or 1600 °C for the case of YSZ or UO₂ with a heating rate of 10 °C/min, in accordance with the experimental procedures.

Results and Discussion

YSZ pellet

Figure 4 shows the FEA simulation results for the maximum sintering stress in YSZ oxide pellets containing a lumped Gd₂O₃ mini-pellet pre-sintered at 1400 °C, 1500 °C, or 1600 °C during heating from 25 °C to 1500 °C.

FIGURE 4

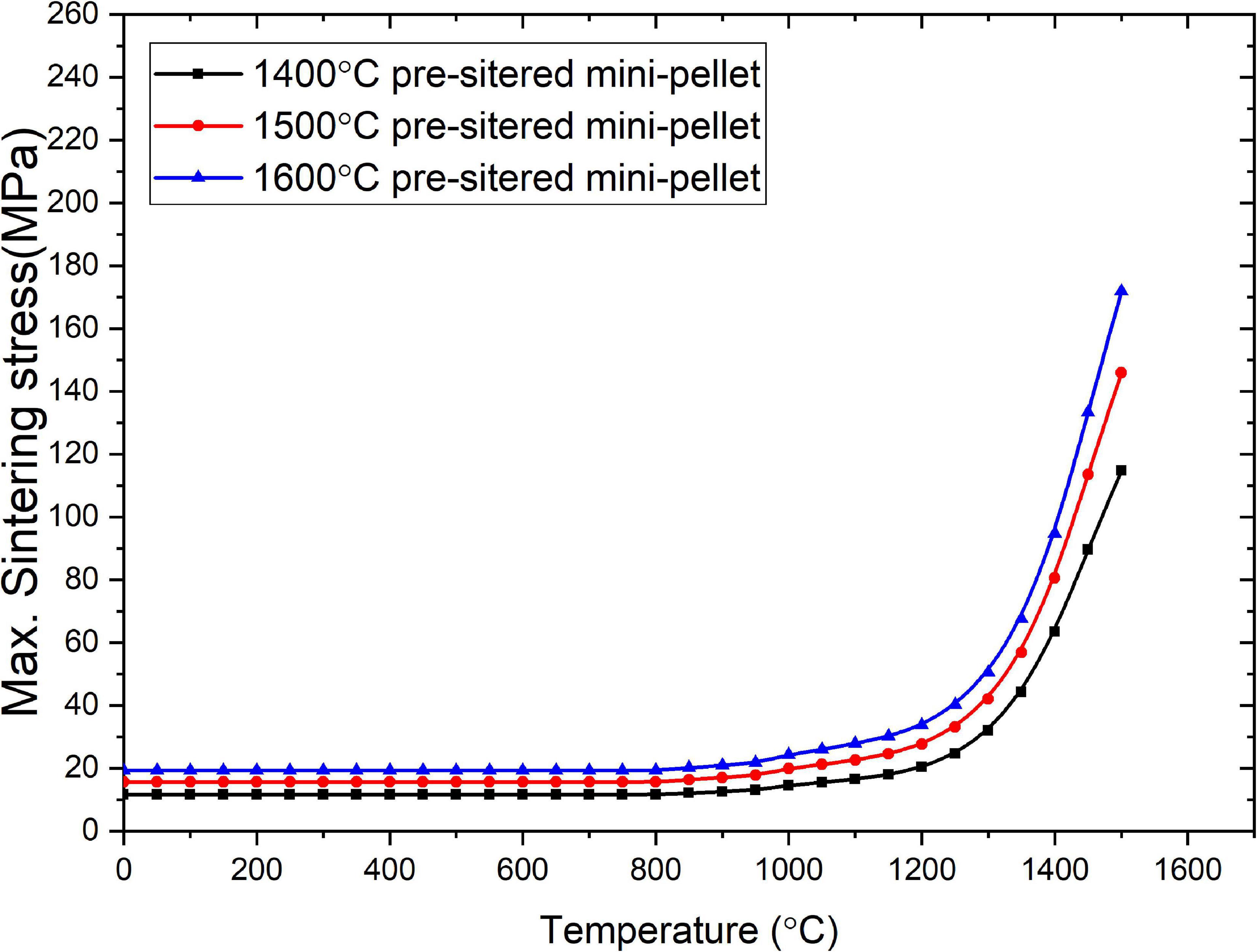
Figure 4. FEA-predicted maximum sintering stresses in YSZ oxide pellet containing a lumped Gd₂O₃ mini-pellet pre-sintered at 1400 °C, 1500 °C, or 1600 °C.

As shown in Figure 4, the maximum sintering stress in the YSZ oxide pellets containing a lumped Gd₂O₃ mini-pellet was almost constant in the temperature range 25–1100 °C and began increasing almost exponentially at approximately 1150 °C, corresponding to the temperature at which the YSZ pellet started to shrink (see Figure 2). As the pre-sintering temperature increased from 1400 °C to 1600 °C, the maximum sintering stress increased, which could be attributed to the increase in the shrinkage rate mismatch (see Figure 2). Previous experimental observations (Mistarihi et al., 2018) showed no interfacial cracks in YSZ pellets containing lumped Gd₂O₃ mini-pellets pre-sintered at 1400 °C, while cracks appeared in the YSZ oxide pellets containing lumped Gd₂O₃ mini-pellets pre-sintered at 1500 °C or higher. The maximum sintering stress in the YSZ oxide pellet containing a lumped Gd₂O₃ mini-pellet pre-sintered at 1400 °C during the fabrication process was calculated by FEA as approximately 120 MPa; that with the mini-pellets pre-sintered at 1500 °C was approximately 150 MPa. This indicates that sintering stresses in the range 120–150 MPa would result in the formation of interfacial cracks in the YSZ oxide pellet containing lumped Gd₂O₃. The flexural strength of the fully dense YSZ at room temperature is approximately 1000 MPa (Masaki, 1986) and it decreases almost linearly with increasing porosity to 170 MPa for YSZ with an RD of 40% (Gain et al., 2006). However, simulation studies of the residual stresses during the fabrication of ceramic composites have shown that residual stresses as low as 25 kPa (Schoenberg et al., 2006) or 90 MPa (DeHoff et al., 2008) can cause the formation of interfacial cracks in ceramic composites.

Figure 5 shows the stress distribution in the YSZ oxide pellet containing either a lumped Gd₂O₃ sphere (r = 0.75 mm) or mini-pellet (r = h = 0.83 mm) with the same volume of approximately 1.77 mm³ and the shrinkage rate of the 1400 °C pre-sintered Gd₂O₃ at a sintering temperature of 1300 °C.

FIGURE 5

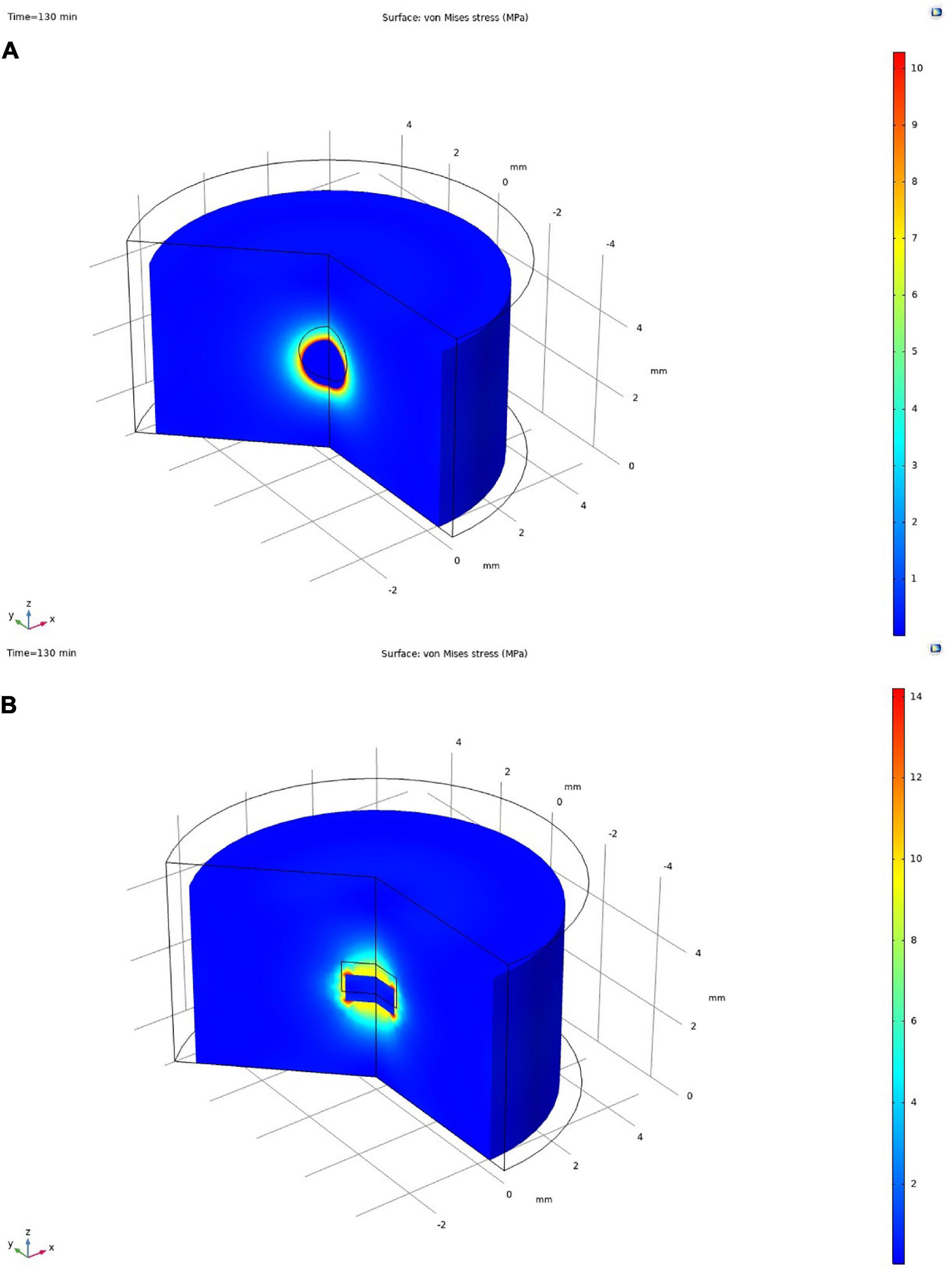
Figure 5. Stress distributions in YSZ oxide pellets containing lumped Gd₂O₃ (A) sphere (r = 0.75 mm) or (B) mini-pellet (r = h = 0.83 mm). (r is the radius of the sphere or mini-pellet and h is the height of the mini-pellet).

As shown in Figure 5, the addition of Gd₂O₃ spheres resulted in the formation of symmetric stresses around the interface. Meanwhile, the Gd₂O₃ mini-pellet caused the formation of localized stresses at the edges of the mini-pellet. The formation of these localized stresses indicates that cracks would form in these areas, which is in good agreement with the experimental observation presented in our previous study (Mistarihi et al., 2018), where interfacial cracks in YSZ pellets containing lumped Gd₂O₃ mini-pellets were observed at the mini-pellet edges.

The FEA-calculated maximum sintering stresses in YSZ oxide pellets containing either a lumped Gd₂O₃ sphere (r = 0.75 mm) or mini-pellet (r = h = 0.83 mm) with equal volume and shrinkage rates during the sintering process are shown in Figure 6. In order to investigate the effect of the dimensions of the Gd₂O₃ mini-pellets on the sintering stresses developed during the manufacturing of YSZ oxide pellets containing lumped Gd₂O₃ mini-pellets, simulation models were also developed with Gd₂O₃ mini-pellets of equal volume to the spheres but the reduced r/h ratio of 0.5. The maximum sintering stresses developed during the manufacturing of the YSZ oxide pellet containing a lumped Gd₂O₃ mini-pellet (r = 1/2h = 0.65 mm) as calculated by FEA are also shown in Figure 6.

FIGURE 6

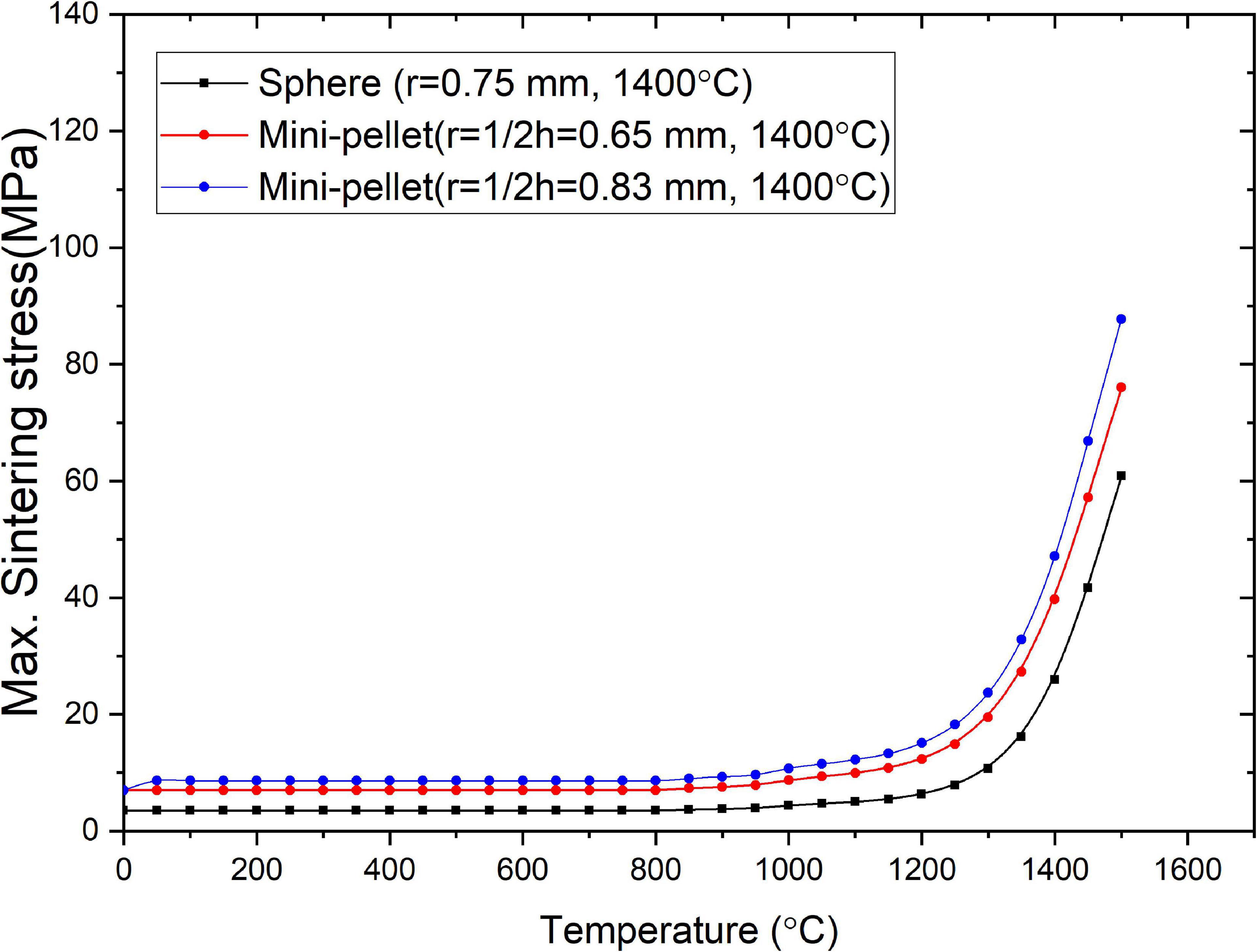
Figure 6. FEA-calculated maximum sintering stress in YSZ oxide pellets containing lumped Gd₂O₃ spheres and mini-pellets of the same volume and shrinkage rate.

The addition of mini-pellets yielded higher sintering stress over the entire temperature range, which can be attributed to the localized stresses at the edges of the mini-pellets. These higher localized sintering stresses are mainly caused by the outward bending of the Gd₂O₃ mini-pellet due to the shrinkage of the YSZ. The temperature gradient caused uniform shrinkage of the Gd₂O₃ spheres, yielding lower and symmetric sintering stresses in the YSZ oxide pellet containing a lumped Gd₂O₃ sphere. DeHoff et al. (2008) studied the stress distributions of bilayer open-ended cylindrical ceramics and spherical-core ceramics and found that the open-ended cylinder ceramics showed localized stresses at the upper edges of the cylinders, whereas the spherical-core ceramics had symmetric stress distributions around the core–shell interface. This indicates that the use of spherical Gd₂O₃ is better than that of mini-pellets to maintain the integrity of the CSBA fuel during fabrication. The localized stresses developed in the YSZ pellet containing a lumped Gd₂O₃ mini-pellet can be reduced by decreasing the aspect ratio of the mini-pellet because this diminishes the outward bending caused by the temperature gradient.

Figure 7 shows the FEA-calculated maximum sintering stress in YSZ oxide pellets containing lumped Gd₂O₃ spheres of equal size (r = 0.75 mm) but the shrinkage rates of Gd₂O₃ sintered at 1400 °C, 1500 °C, and 1600 °C. As shown in Figure 7, the maximum sintering stress during fabrication was increased with increases in the pre-sintering temperature of the lumped Gd₂O₃, which could be attributed to the increases in the shrinkage rate mismatch.

FIGURE 7

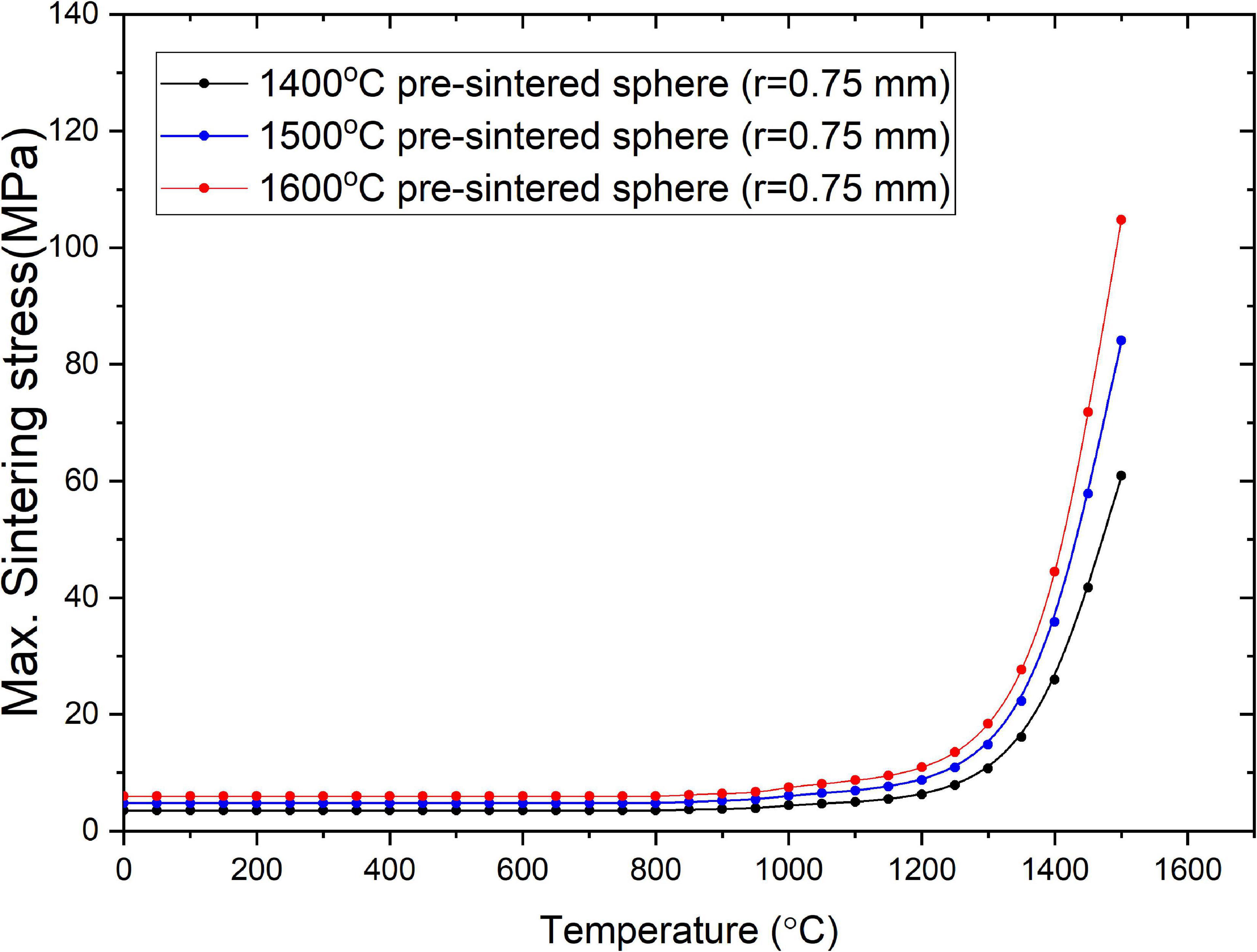
Figure 7. FEA-calculated maximum sintering stress in YSZ oxide pellets containing lumped Gd₂O₃ spheres of equal size (r = 0.75 mm) but different shrinkage rates.

According to the experimental observation in our previous study (Mistarihi et al., 2018), interfacial cracks were observed in YSZ oxide pellets containing lumped Gd₂O₃ mini-pellets pre-sintered at 1500 °C or higher, but not in YSZ containing lumped Gd₂O₃ spherical particles pre-sintered at 1600 °C. As can be seen from Figure 7, the calculated maximum sintering stress in the YSZ pellet containing a 0.75-mm-radius lumped Gd₂O₃ sphere pre-sintered at 1600 °C is approximately 105 MPa. The maximum calculated sintering stress in the YSZ pellet containing the 1500 °C pre-sintered mini-pellet was approximately 150 MPa (Figure 4). Therefore, the absence of interfacial cracks in the case of the YSZ pellet containing Gd₂O₃ spherical particles pre-sintered at 1600 °C could be attributed to the reduced symmetric sintering stress relating to their smaller sizes and spherical shapes, compared to those of the 1500 °C pre-sintered mini-pellet.

The effect of the Gd₂O₃ sphere size on the maximum sintering stress in YSZ oxide pellets containing lumped Gd₂O₃ spheres with the shrinkage rate of the 1400 °C sintered Gd₂O₃ during sintering is shown in Figure 8. As shown, the maximum sintering stress was increased with increases in the size of the Gd₂O₃ spheres. However, the increase was much smaller than that observed with increases in the Gd₂O₃ shrinkage rates. This indicates that the sintering stresses developed in the YSZ oxide pellets containing lumped Gd₂O₃ spheres are mostly controlled by the Gd₂O₃ shrinkage rate.

FIGURE 8

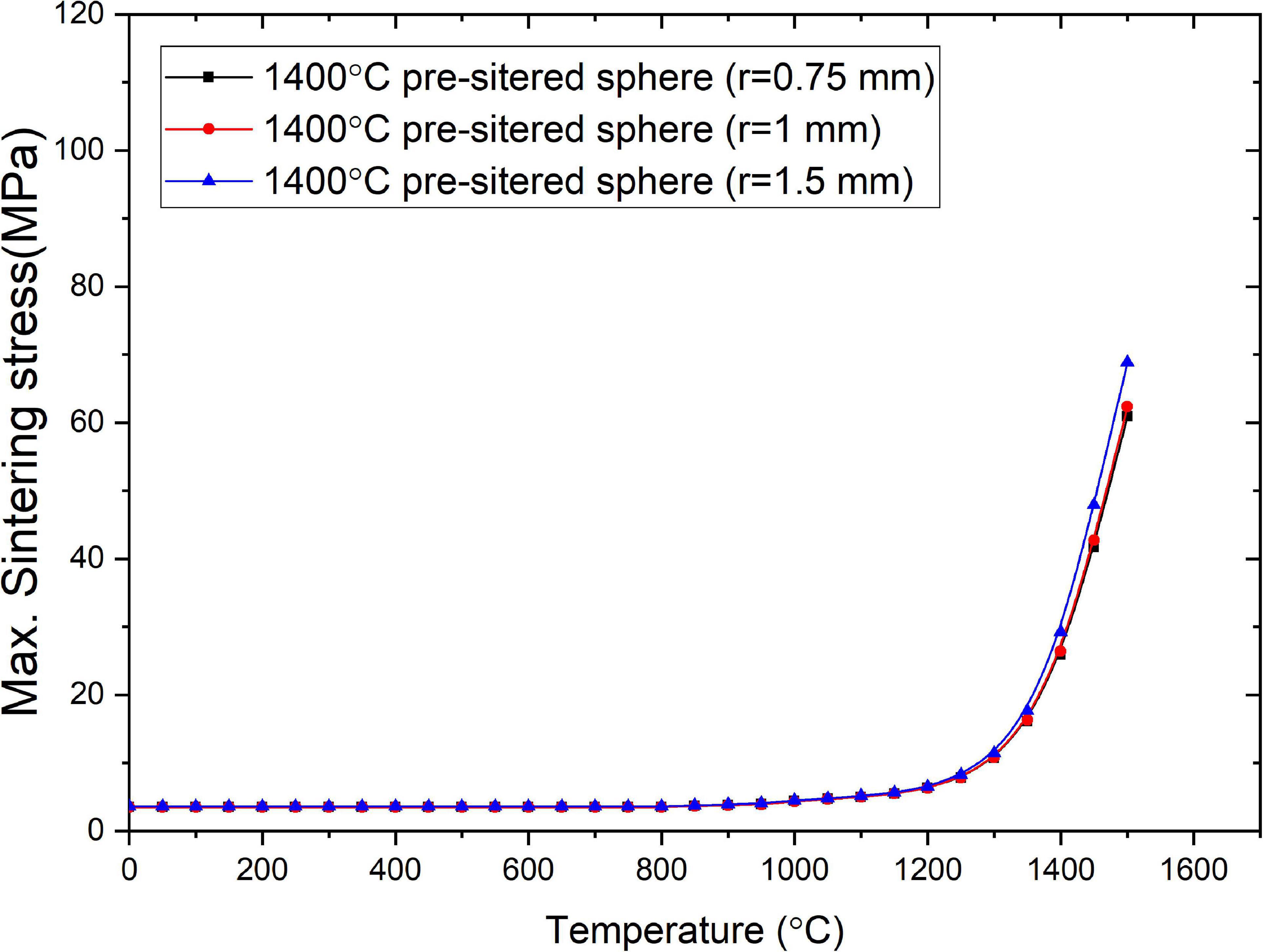
Figure 8. FEA-calculated maximum sintering stress in YSZ oxide pellets containing lumped Gd₂O₃ spheres of different sizes but equal shrinkage rates.

UO₂ Fuel Pellet

Experimental studies using UO₂ are expensive and present high levels of radiotoxicity. In an experimental demonstration (Mistarihi et al., 2018) of the fabrication of oxide pellets containing lumped Gd₂O₃ spherical particles, mini-pellets, or rods, YSZ was used as a surrogate for UO₂ because it has a similar crystal structure, high melting temperature, and sintering kinetics. However, for fabrication studies, the shrinkage rate and TEC of YSZ and UO₂ must be similar, as well as the diffusivity of Gd³⁺ in the YSZ and UO₂ matrices.

Figure 9 shows the FEA-calculated maximum sintering stress in UO₂ pellets containing a lumped Gd₂O₃ sphere with a shrinkage rate of 1400 °C pre-sintered Gd₂O₃ but different sizes (r = 0.75, 1, 1.5 mm). As shown in Figure 9, the maximum sintering stress during the fabrication process was increased with increases in the size of the lumped Gd₂O₃. However, the calculated maximum sintering stresses in the UO₂ fuel pellets were higher than those reported for YSZ pellets. The maximum sintering stresses in UO₂ containing lumped Gd₂O₃ sphere with a radius of 1.5 mm at 1300 °C, 1400 °C, and 1500 °C were about 45.2, 80.3, and 101 MPa, respectively, whereas the maximum sintering stresses determined in YSZ pellet containing the same Gd₂O₃ sphere and at the same sintering temperatures were about 11.4, 29.2, and 68.8 MPa, respectively (see Figure 8). This could be attributed to the greater mismatch in the shrinkage rates of UO₂ and Gd₂O₃ relative to that of YSZ and Gd₂O₃ (see Figure 2).

FIGURE 9

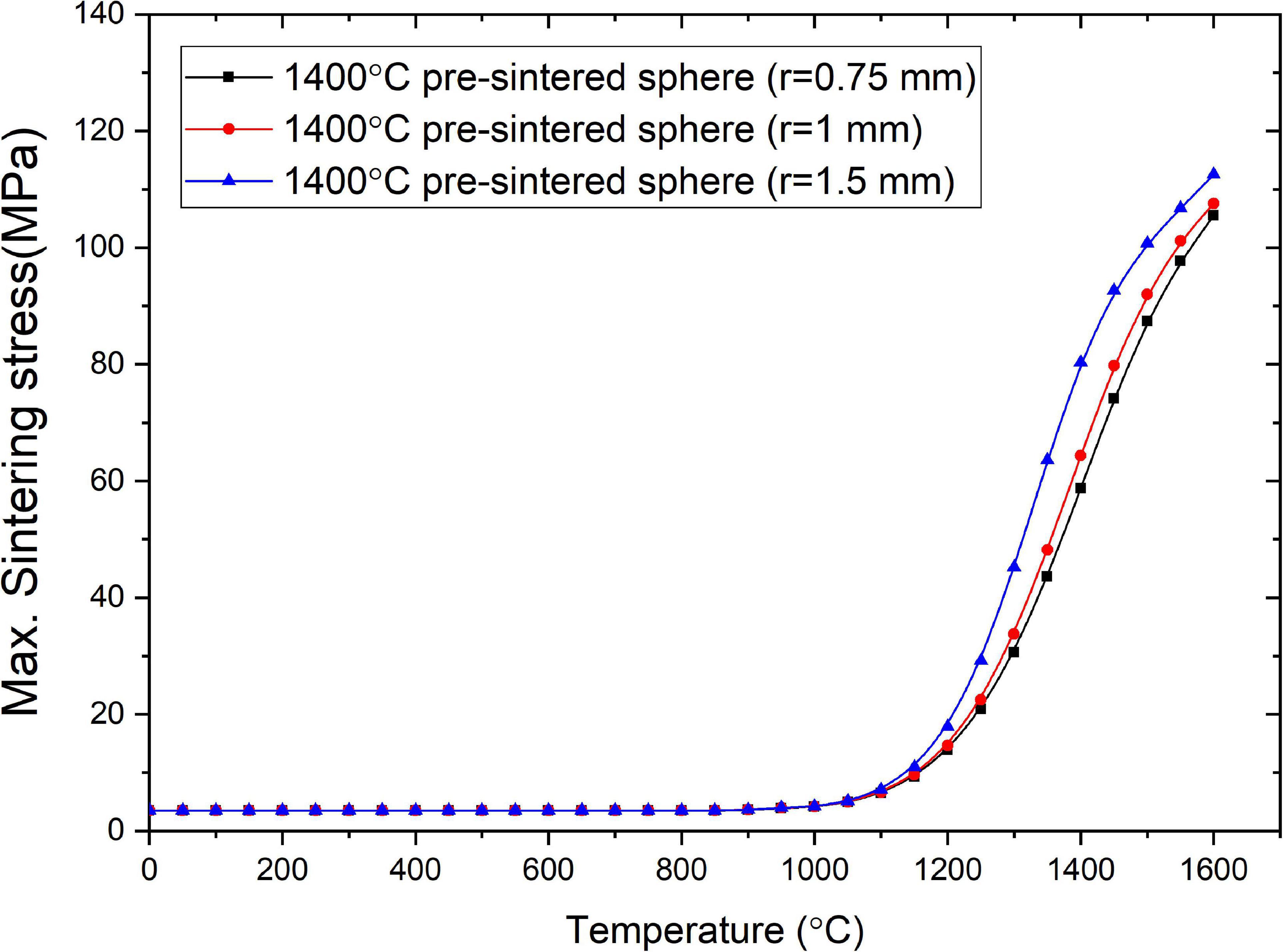
Figure 9. FEA-calculated maximum sintering stress in UO₂ pellets containing lumped Gd₂O₃ spheres of different sizes but equal shrinkage rates.

The stress distribution in the UO₂ pellet containing a lumped Gd₂O₃ sphere (r = 0.75 mm) with the shrinkage rate of 1400 °C pre-sintered Gd₂O₃ at the sintering temperature of 1300 °C is shown in Figure 10. The stress distribution was symmetric, similar to that in the YSZ pellet with the same conditions; however, the stress values were higher than those reported in YSZ, which can again be attributed to the higher shrinkage rate mismatch between UO₂ and Gd₂O₃ relative to that between YSZ and Gd₂O₃ (see Figure 2).

FIGURE 10

Figure 10. Stress distribution in UO₂ pellet containing a lumped Gd₂O₃ sphere (r = 0.75 mm).

Owing to the absence of sufficient experimental data for CSBA fuel using UO₂, it is difficult to set threshold stress values for the formation of interfacial cracks in UO₂-based CSBA. However, the fabrication of UO₂ oxide pellets containing lumped Gd₂O₃ spherical particles pre-sintered at 1400 °C was reported by Oh et al. (2017) using the conventional fabrication conditions for UO₂ of pressing under 3 ton/cm² followed by sintering at 1700 °C for 4 h in an H₂ atmosphere at approximately 5 °C/min. Similar results were observed regarding the absence of interfacial cracks and the formation of the gadolinium urinate phase at the interface between UO₂ and Gd₂O₃.

Conclusion

The sintering stresses developed in the YSZ oxide pellets containing either lumped Gd₂O₃ spheres or mini-pellets during fabrication from 25 °C to 1500 °C were simulated using the FEA method. Thermal and linear elastic models were used to simulate the sintering stresses in lumped Gd₂O₃, while thermal and sintering models based on the continuum theory of sintering were used to simulate those in the YSZ powder compact. These models were coupled and implemented using COMSOL Multiphysics code.

The critical sintering stresses for the formation of interfacial cracks in YSZ oxide pellets containing lumped Gd₂O₃ were determined by comparing the FEA-calculated stresses in YSZ oxide pellets containing lumped Gd₂O₃ mini-pellets with the shrinkage rates of 1400 °C, 1500 °C, and 1600 °C sintered Gd₂O₃ with experimental observations. It was found that sintering stresses in the range of 120–150 MPa could cause the formation of interfacial cracks in these pellets.

The effects of the shape, shrinkage rate, and size of lumped Gd₂O₃ on the formation of cracks during fabrication were studied. It was found that the addition of cylindrical Gd₂O₃ mini-pellets resulted in localized and higher stresses at the mini-pellet edges. In contrast, the addition of Gd₂O₃ spherical particles yielded symmetric and lower stresses at the interface between the Gd₂O₃ and YSZ. Increases in the shrinkage rate and size of Gd₂O₃ resulted in higher sintering stresses in the YSZ oxide pellets containing lumped Gd₂O₃.

The sintering stresses developed during the fabrication of UO₂ containing lumped Gd₂O₃ spheres were also estimated. Similar behaviors to those of YSZ were observed. However, the magnitude of the sintering stress was higher because of the higher shrinkage rate mismatch between UO₂ and Gd₂O₃ relative to that between YSZ and Gd₂O₃.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

QM did the finite element simulation and wrote the article. HR supervised and reviewed the written article. Both authors contributed to the article and approved the submitted version.

Funding

This study was supported by the KAI-NEET Institute of KAIST and the National Research Foundation (NRF) of Korea grant funded by the Korean Government (Ministry of Science, ICT and Future Planning) (NRF-2016R1A5A1013919, NRF-2018M2A8A1083889, and NRF-2019M2D1A1067210).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Agarwal, B. D. (1972). Micromechanics Analysis of Composite Materials Using Finite Element Methods. Ph.D. thesis, Illinois Institute of Technology, Chicago.

Google Scholar

Choe, J., Shin, H. C., and Lee, D. (2016a). New burnable absorber for long-cycle low boron operation of PWRs. Ann. Nucl. Energy 88, 272–279. doi: 10.1016/j.anucene.2015.11.011

CrossRef Full Text | Google Scholar

Choe, J., Zheng, Y., Lee, D., and Shin, H. C. (2016b). Boron-free small modular pressurized water reactor design with new burnable absorber. Int. J. Energy Res. 40, 2128–2135. doi: 10.1002/er

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidge, R. W., and Green, T. J. (1968). The strength of two-phase ceramic glass materials. J. Mater. Sci. 3, 629–634. doi: 10.1007/BF00757910

CrossRef Full Text | Google Scholar

DeHoff, P. H., Barrett, A. A., Lee, R. B., and Anusavice, K. J. (2008). Thermal compatibility of dental ceramic systems using cylindrical and spherical geometries. Dent. Mater. 24, 744–752. doi: 10.1016/j.dental.2007.08.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Delale, F. (1988). Critical fiber size for microcrack suppression in ceramic-fiber ceramic-matrix compoistes. Eng. Fract. Mech. 31, 145–155.

Google Scholar

Dole, S. L., and Hunter, O. (1976). Elastic properties of some Gd₂O₃-HfO₂ compositions. J. Nucl. Mater. 59, 207–214.

Google Scholar

Durazzo, M., Saliba-Silva, A. M., Urano De Carvalho, E. F., and Riella, H. G. (2013). Sintering behavior of UO₂-Gd₂O₃ fuel: pore formation mechanism. J. Nucl. Mater. 433, 334–340. doi: 10.1016/j.jnucmat.2012.09.033

CrossRef Full Text | Google Scholar

Fink, J. (2000). Thermophysical properties of uranium dioxide. J. Nucl. Mater. 279, 1–18. doi: 10.1016/S0022-3115(99)00273-1

CrossRef Full Text | Google Scholar

Fleming, R. F. (1982). Neutron self-shielding factors for simple geometrics. Int. J. Appl. Radiat. Isot. 33, 1263–1268. doi: 10.1016/0020-708X(82)90247-2

CrossRef Full Text | Google Scholar

Gain, A. K., Song, H. Y., and Lee, B. T. (2006). Microstructure and mechanical properties of porous yttria stabilized zirconia ceramic using poly methyl methacrylate powder. Scr. Mater. 54, 2081–2085. doi: 10.1016/j.scriptamat.2006.03.009

CrossRef Full Text | Google Scholar

Galperin, A., Segev, M., and Radkowsky, A. (1986). Substitution of the Soluble boron reactivity control system of a pressurized water reactor by gadolium burnable poisons. Nucl. Technol. 75, 127–133. doi: 10.13182/NT86-A33855

CrossRef Full Text | Google Scholar

Grossbeck, M. L., Renier, J.-P. A., and Grossbeck, M. L. (2001). Development of improved Burnable Poisons for Commercial Nuclear Power Reactors. Oak Ridge, TN: Oak Ridge National Laboratory.

Google Scholar

Haglund, J. A., and Hunter, O. (1973). Elastic properties of polycrystalline monoclinic Gd₂O₃. J. Am. Ceram. Soc. 56, 327–330. doi: 10.1111/j.1151-2916.1973.tb12506.x

CrossRef Full Text | Google Scholar

Hall, R. O. A., and Mortimer, M. J. (1986). A critical review of the surface energy of UO₂. J. Less Common Met. 121, 341–345. doi: 10.1097/00152193-198306000-00031

PubMed Abstract | CrossRef Full Text | Google Scholar

IAEA (1995). Characteristics and Use of Urania-Gadolinia Fuels. Vienna: IAEA.

Google Scholar

Kerrisk, J. F., and Clifton, D. G. (1972). Smoothed values of the enthalpy and heat capacity of UO₂. Nucl. Tech. 16, 531–535. doi: 10.13182/NT72-6

CrossRef Full Text | Google Scholar

Li, C., Wu, Y., Wang, Y., Wang, K., Wang, M., Tian, W., et al. (2020). Analysis on the behavior of dispersed plate-type fuel based on fluid-solid coupling method. Prog. Nucl. Energy 126:103398. doi: 10.1016/j.pnucene.2020.103398

CrossRef Full Text | Google Scholar

Lucuta, P. G., Matzke, H., and Hastings, I. J. (1996). A pragmatic approach to modelling thermal conductivity of irradiated UO₂ fuel: review and recommendations. J. Nucl. Mater. 232, 166–180. doi: 10.1016/S0022-3115(96)00404-7

CrossRef Full Text | Google Scholar

Manière, C., Zahrah, T., and Olevsky, E. A. (2017). Fully coupled electromagnetic-thermal-mechanical comparative simulation of direct vs hybrid microwave sintering of 3Y-ZrO₂. J. Am. Ceram. Soc. 100, 2439–2450. doi: 10.1111/jace.14762

CrossRef Full Text | Google Scholar

Masaki, T. (1986). Mechanical properties of toughened ZrO₂-Y₂O₃ ceramics. J. Am. Ceram. Soc. 69, 638–640. doi: 10.1111/j.1151-2916.1986.tb04823.x

CrossRef Full Text | Google Scholar

Mistarihi, Q. M., Park, W., Nam, K., Yahya, M.-S., Kim, Y., and Ryu, H. J. (2018). Fabrication of oxide pellets containing lumped Gd₂O₃ using Y₂O₃-stabilized ZrO₂ for burnable absorber fuel applications. Int. J. Energy Res 42, 2141–2151. doi10.1002/er.3995

Google Scholar

Nguyen, X. H., Kim, C. H., and Kim, Y. (2019). An advanced core design for a soluble-boron-free small modular reactor ATOM with centrally-shielded burnable absorber. Nucl. Eng. Technol. 51, 369–376. doi: 10.1016/j.net.2018.10.016

CrossRef Full Text | Google Scholar

Oh, J. S., Mistarihi, Q., Ryu, H. J., and Kim, D.-J. (2017). “Fabrication of Gadolinia-containing UO₂ fuel pellet,” in Proceedings of the 42nd International Conference and Expo on Advanced Ceramics and Composites, Daytona Beach, FL.

Google Scholar

Olevsky, E. A. (1998). Theory of sintering: from discrete to continuum. Mater. Sci. Eng. R Rep. 23, 41–100. doi: 10.1016/S0927-796X(98)00009-6

CrossRef Full Text | Google Scholar

Olevsky, E. A., Garcia-Cardona, C., Bradbury, W. L., Haines, C. D., Martin, D. G., and Kapoor, D. (2012). Fundamental aspects of spark plasma sintering: II. Finite element analysis of scalability. J. Am. Ceram. Soc. 95, 2414–2422. doi: 10.1111/j.1551-2916.2012.05096.x

CrossRef Full Text | Google Scholar

Riedel, H., Meyer, D., Svoboda, J., and Zipse, H. (1993). Numerical simulation of die pressing and sintering — development of constitutive equations. Int. J. Refract. Met. Hard Mater. 12, 55–60. doi: 10.1016/0263-4368(93)90016-9

CrossRef Full Text | Google Scholar

Schoenberg, S. E., Green, D. J., Segall, A. E., Messing, G. L., Grader, A. S., and Halleck, P. M. (2006). Stresses and distortion due to green density gradients during densification. J. Am. Ceram. Soc. 89, 3027–3033. doi: 10.1111/j.1551-2916.2006.01182.x

CrossRef Full Text | Google Scholar

Selsing, J. (1961). Internal stresses in ceramics. J. Am. Ceram. Soc. 44, 419–419. doi: 10.1111/j.1151-2916.1961.tb15475.x

CrossRef Full Text | Google Scholar

Sglavo, V. M., and Bellettati, N. (2017). Ceramic laminates with improved mechanical reliability by tailoring the porosity of the constituting layers. J. Eur. Ceram. Soc. 37, 1643–1650. doi: 10.1016/j.jeurceramsoc.2016.11.022

CrossRef Full Text | Google Scholar

Siefken, L. J., Coryell, E. W., Harvego, E. A., and Hohorst, J. K. (2001). MATPRO-A Library of Materials Properties for Light-Water-Reactor Accident Analysi. Idaho Falls, ID: Idaho National Engineering and Environmental Laboratory.

Google Scholar

Song, X., Lu, J., Zhang, T., and Ma, J. (2011). Two-stage master sintering curve approach to sintering kinetics of undoped and Al₂O₃-doped 8 Mol% yttria-stabilized cubic zirconia. J. Am. Ceram. Soc. 94, 1053–1059. doi: 10.1111/j.1551-2916.2010.04199.x

CrossRef Full Text | Google Scholar

Tsoga, A., and Nikolopoulos, P. (1996). Surface and grain-boundary energies in yttria-stabilized zirconia (YSZ-8 mol%). J. Mater. Sci. 31, 5409–5413. doi: 10.1007/BF01159310

CrossRef Full Text | Google Scholar

Yahya, M.-S., and Kim, Y. (2017a). An innovative core design for a soluble-boron-free small pressurized water reactor. Int. J. Energy Res. 41, 1–9. doi: 10.1002/er.3792

CrossRef Full Text | Google Scholar

Yahya, M.-S., and Kim, Y. (2017b). “Centrally-shielded burnable absorber for LWR fuel,” in Proceedings of the International Congress on Advances in Nuclear Power Plants (Fukui and Kyoto: American nuclear society).

Google Scholar

Yeo, S., McKenna, E., Baney, R., Subhash, G., and Tulenko, J. (2013). Enhanced thermal conductivity of uranium dioxide-silicon carbide composite fuel pellets prepared by Spark Plasma Sintering (SPS). J. Nucl. Mater. 433, 66–73. doi: 10.1016/j.jnucmat.2012.09.015

CrossRef Full Text | Google Scholar