Review on Coordinated Planning of Source-Network-Load-Storage for Integrated Energy Systems

Fan, Hong; Yu, Zichun; Xia, Shiwei; Li, Xuan

doi:10.3389/fenrg.2021.641158

REVIEW article

Front. Energy Res., 20 April 2021
Sec. Smart Grids
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.641158

Review on Coordinated Planning of Source-Network-Load-Storage for Integrated Energy Systems

Hong Fan^1,2

Zichun Yu²

Shiwei Xia¹^*

Xuan Li³

¹State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources, North China Electric Power University, Beijing, China
²Department of Electrical Engineering, Shanghai University of Electric Power, Shanghai, China
³State Grid Economic and Technological Research Institute Co., Ltd, Beijing, China

The integration of electricity, gas, and heat (cold) in the integrated energy system (IES) breaks the limitation of every single energy source, which is the development trend of future energy systems. To realize the coordinated planning of “source-network-load-storage,” the IES has to be conducive to improving energy efficiency, bringing economic and environmental benefit, and achieving sustainable development of energy. In this paper, the techniques and methods involved in IES planning are summarized. First, the structure and characteristics of the IES are briefly introduced. Second, the key findings of the IES planning are summarized from four perspectives: source, network, load, and storage. Then, the modeling methods of the IES collaborative planning are summarized, and the optimization methods for solving complex planning problems are analyzed. Compared with previous reviews, this paper focuses on the modeling of multi-energy coupling of each part of source-network-load-storage and modeling of the overall collaborative planning. Finally, the future research direction of IES planning is forecast.

Introduction

With the continuous development of the world economy, the demand for various forms of energy is also gradually increasing. The need for using energy efficiently, reducing environmental pollution, and achieving sustainable development of the whole society makes it necessary to explore a more efficient energy system. The integrated energy system (IES) provides a feasible framework for future energy development, and the overall planning of multiple energy sources can realize the optimal allocation of resources to a greater extent and improve the utilization efficiency of energy.

In recent years, much work on IES has been carried out by various countries and significant results have been achieved. According to their own needs, European countries have carried out a large number of research projects (Khanam et al., 2020) aiming at promoting the coordinated development of renewable energy and traditional energy. The United States has incorporated the construction of an IES into its national strategy. Building a clean, low-carbon, safe, and efficient modern energy system is the goal and requirement of the energy development plan of China. The structural characteristics (Cheng L. et al., 2019), unit modeling (Liu N. et al., 2019; Zhu et al., 2019), energy flow, and optimal planning (Pourakbari-Kasmaei et al., 2020; Yang W. et al., 2020) of IES have been analyzed and discussed in many studies. General modeling technology and comprehensive simulation method are tools for the study of IES, and multi-energy flow calculation is the basis for the analysis of IES. On this basis, relevant methods for planning energy stations and energy supply networks were proposed in (Zhang et al., 2018; Aldarajee et al., 2020). Energy hub (EH) (Liu T. et al., 2019) is the center of multi-energy coupling, and its mathematical model is the key to the modeling of IES. The current paper does not systematically summarize the modeling method of collaborative planning for “source-network-load-storage” in the IES, and its key technologies and relevant differences are not described in detail.

In combination with previous articles, this paper summarizes the optimization planning of the IES, mainly including the following contents: (1) the architecture and characteristics of the IES are briefly described; (2) the key findings of IES planning are analyzed from four perspectives: source, network, load, and storage; (3) the modeling method of IES coordinated planning is introduced and the different methods of solving the planning problem are discussed; (4) Based on the above contents, further research on “source-network-load-storage” coordinated planning of IES is forecast.

Structure And Characteristics Of An IES

An IES is a complex system with multi-energy coupling that integrates power systems, natural gas systems, and thermal systems. It has the links of energy production, transmission, transformation, storage, and consumption. Compared with a single energy system, the most important feature of the IES is that heterogeneous energy can be transformed through the coupling equipment and transmitted to the equipment terminal under the coordinated operation of all links. In this way, it can meet the differentiated demands of the whole society for electricity, gas, and heat; effectively solve the contradiction between supply and demand of heterogeneous energy in time and space; and achieve the goal of improving energy utilization rate, strengthening system robustness, and realizing the sustainable development of energy.

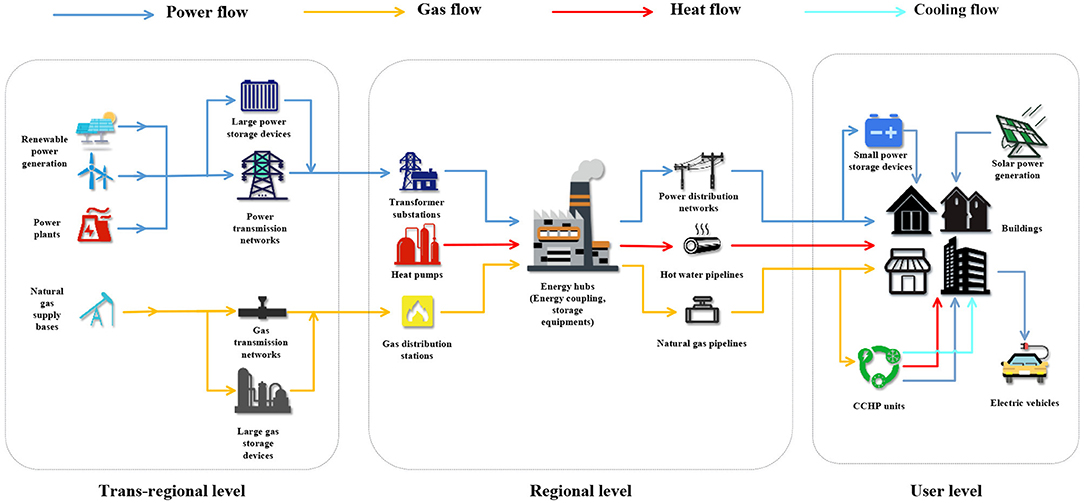
The IES can be divided from top to bottom into the trans-regional level system, the regional level system, and the user-level system. The trans-regional system involves the large-scale production, long-distance transmission, and large-capacity storage of multiple energy sources and plays the role of connecting energy sources and multiple areas with demand for energy. It is a wide-area energy interconnection system with large-scale power and gas transmission systems as backbone networks and large-scale energy conversion and storage systems as important components. The planning of the trans-regional system mainly involves the siting and sizing of energy production stations (new energy power stations, traditional power stations, and natural gas bases), large-scale energy storage and conversion equipment, and the optimal expansion of energy transmission networks (power transmission networks and gas transmission networks). The regional system mainly includes the near-distance transmission, transformation, and storage of various energy sources within the scope of the region (urban blocks, industrial zones, etc.) and it plays the role of being the connecting link in IES. It includes the power distribution system, natural gas system (middle and low pressure), and heating (cooling) system (Hao et al., 2020). Its planning model mainly involves the siting and sizing of energy conversion equipment [combined cooling heating and power (CCHP) units, gas-fired boilers, absorption refrigerators, etc.], energy storage equipment (electricity, gas, and heat storage), and the expansion of multi-energy distribution networks (power distribution network, natural gas pipeline, hot water pipeline, etc.). The user-level system is generally based on buildings and hospitals. It is a flexible and efficient micro-energy system with certain production and consumption capabilities, which is formed by considering the differentiated energy needs of different users. It mainly involves small-scale energy conversion, distribution, recovery, and storage. In its planning, intelligent power systems (including photovoltaic power generation equipment, and electric vehicle charging equipment), distributed/centralized gas, hot (cold) supply networks, small CCHP devices, and storage equipment are generally involved.

According to the regionalization characteristics of the IES structure, its basic physical framework is shown in Figure 1.

FIGURE 1

Figure 1. Structure of IES.

The complexity of the IES is reflected in many aspects. It is necessary to consider its flexibility in energy production, transmission, and consumption in the vertical direction, that is, the coordinated operation of energy stations, energy grids, demand side, and energy storage equipment. The diversity, multi-time scale, and coupling of energy in the system need to be considered horizontally. The equipment is no longer unique but belongs to different investors and operators, which leads to diversified ownership. In addition, considering the time dimension, the period of building an IES is relatively long, so the planned target is generally based on the year. Accurate and reasonable planning schemes need to go through multiple rolling optimizations, and the balance of short-term benefits and long-term returns needs to be considered at the same time along with the effects of certainty and uncertainty. Therefore, the planning of the IES must be a multi-objective, multi-constrained, non-linear, mixed-integer optimization problem with uncertain factors, and it is also a random and complex dynamic optimization process.

Key Findings of IES Planning

Electric energy, natural gas, and heat (cold) in traditional energy systems generally exist separately, and the potential advantages of these energy sources are not reflected. For example, the power system will be affected by large-scale new energy power generation and uncertain load fluctuations, and the natural gas system will be affected by regional temperature and other energy commodity prices. Systems without energy storage equipment will face greater operational difficulties. Only by coordinating and planning by incorporating the energy source, energy transmission network, flexible load, and energy storage device storage in the IES can the complementary advantages of multiple energy sources be brought into play to meet the comprehensive load demand of users in various regions and ensure the energy operators. At the same time, resources overflowing with production capacity can also be better absorbed.

Source of the IES

Source-side planning is used to solve the problem of energy demand in multiple areas in the long-term. It is necessary to comprehensively analyze the distribution of various resources in the planning area and the demand of the users for electricity, gas, heat, and other forms of energy. Although renewable energy, natural gas, and other resources have the advantages of low carbon and environmental protection, their volatility and randomness will make the adjustment ability of the entire system worse.

New energy: The power resources for the future are produced by new energy. In the face of a large-scale new energy grid connection, the efficient use and absorption of new energy and the power balance of the entire system depend on whether the system is properly planned, which requires that the source side, the energy storage side, and the load side be reasonably coordinated. Wind power is characterized by uncertainty and uncontrollability, and one of the best solutions is to combine the power storage system with wind farms. The uncertainty set of the probability distribution of the output power of the wind farm can also be effectively captured by the data-driven method (Dvorkin et al., 2016). The scene method is also used in many articles to fit the fluctuating characteristics of wind power. Solar energy is a low-carbon resource, and its carbon asset value (Olsen et al., 2018) is determined by the level of reduction in carbon emission, carbon price, and power generation. Focused solar power stations can increase their flexibility and improve intermittency by participating in the auxiliary service market. At the same time, the combination of solar energy and geothermal energy in power planning (He et al., 2016; Noorollahi et al., 2017) can make up for the shortcomings of the instability and high cost of solar energy as well as the shortcomings of low geothermal energy efficiency and insufficient energy grade. The formed solar-thermal dual-cycle power plant will increase the power generation greatly. Biogas, solar energy, and wind energy can also form a renewable energy system, which uses the combination, conversion, and storage of multiple energy sources to meet the different energy needs of users. In addition, ocean thermal energy and tidal energy (Jouanne and Brekken, 2017) are rich in reserves, but the relevant mining technology is not yet mature.

Gas and heat: The diversity of energy is the guarantee of the stability, reliability, and self-healing of the IES. Electricity can be produced from new energy sources and fossil fuels. Natural gas resources can be exploited and produced in conventional natural gas fields and oil and gas reservoirs. The planning of natural gas bases needs to be combined with the geographical distribution of gas resources and recoverable reserves (Conejo et al., 2020). Although there are abundant reserves of unconventional natural gas such as coal bed gas, shale gas, and natural gas hydrate, the high usage costs of the mining technology will lead to investment overruns. Heat energy is produced by geothermal sources, air sources, water sources, and other heat sources; however, it is only suitable for regional supply because of its large transmission loss (Wei et al., 2018). Regional shallow geothermal energy is affected by the amount of groundwater, water temperature, and stability of the water supply. Both geothermal cascade heating technology and composite central heating systems can reduce its impact. The middle and deep geothermal sources which have a high grade can be mined by heat pumps but the investment needed for the mining is relatively large. A variety of influencing factors need to be considered when planning the heat source.

Transmission and Distribution Network

The energy transmission network in the IES consists of a power and gas transmission network, and the energy distribution network consists of a power, gas, and heat distribution network. Electricity travels at a speed close to that of light (nanoseconds to milliseconds) while gas in a pipe travels at about the speed of sound (seconds or more), but heat flows more slowly. Therefore, the coordination between dynamic and delay characteristics should be fully considered when planning natural gas and heat networks.

Energy transmission network: At present, the IES is a multi-energy system with the power system as the center and other energy systems as the auxiliary. When planning the transmission network, it is necessary to consider not only the maximum bearing capacity of the network at the peak of power load but also the influence of the operation of energy coupling equipment on the voltage of the network. At the same time, the blocking effect becomes increasingly serious, and the no-load operation cost (Haghighat and Zeng, 2018), line breaking technology (Villumsen et al., 2013), and power grid operation efficiency will also have a certain impact on the planning of the transmission expansion. For the resource-rich long-distance offshore wind power and electric power in remote areas, high voltage direct current (HVDC) transmission lines (Apostolaki-Iosifidou et al., 2019) are the hot spots for future transmission network planning. The scale of the gas transmission network in the IES is gradually increasing. Power-to-gas (P2G) technology can transform water into artificial natural gas (CH₄) and input it into the natural gas network for large-scale transmission and storage. The dynamic characteristics of natural gas and the embedding of P2G and gas-to-power (G2P) increase the difficulty in modeling the gas transmission network. Compared with electricity, the time-ductility of gas is particularly evident in long-distance transmission. Transient and steady-state analysis of the whole natural gas is required when planning the actual large-scale natural gas network (Osiadacz and Chaczykowski, 2020). A dynamic gas network model was proposed in Reference (Zhou et al., 2017) but only the unidirectional gas flow was considered and dynamic factors such as compressors were ignored. Considering the difficulty of data interaction between the power grid and natural gas network, a static equivalent model of a natural gas network (Dai et al., 2020) was proposed, which laid a foundation for the cooperation between independent power and gas operators.

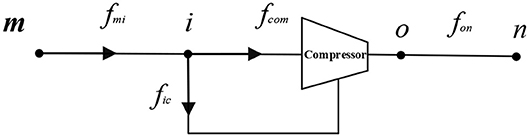
The general model of a gas transmission network containing a compressor (Figure 2) is shown in Equation (1).

\begin{array}{c} {\begin{array}{c} \begin{array}{c} f_{c o m} = f_{o n} = k_{o n} \sqrt{(p_{o}^{2} - p_{n}^{2})} \\ f_{i c} = \frac{k_{i c} f_{c o m} T_{g a s}}{q_{g a s}} (k_{i c}^{\frac{a - 1}{a}} - 1) \end{array} \\ \begin{array}{c} f_{m i} = f_{c o m} + f_{i c} \\ f_{m i} = k_{m i} \sqrt{(p_{m}^{2} - p_{i}^{2})} \end{array} \end{array} & (1) \end{array}

where m, o, i, and n are the nodes; f_mi and f_on are the flow of the compressor inlet and outlet pipelines, respectively; f_com is the flow through the compressor; f_ic is the amount of natural gas consumed by the compressor; k_mi and k_on are the pipeline constants; p_m, p_i, p_o, and p_n are the node pressures; k_ic is the compression ratio; T_gas is the temperature of natural gas; q_gas is the calorific value of natural gas; and a is the polytropic index.

FIGURE 2

Figure 2. Pipeline containing a compressor.

Energy distribution network: Energy stations, coupling equipment, and end-users in the regionally integrated energy system (RIES) interact with energy through the energy distribution network. The energy distribution network is composed of a distribution network, middle- and low-voltage natural gas network, and heating network. The coupling of a power distribution network and other energy networks is the foundation of the framework of RIES. In the planning of the energy distribution network, the comprehensive load demand of regional electricity, gas, and heat should be considered. In order to meet the constraints of energy supply and demand and power flow, the influence of urban layout on the arrangement of the pipe network should also be considered. The modeling method of the power and gas distribution network is similar to that of the power and gas transmission network, so it will not be described here. The heating network is an important part of the RIES, and the topological structure of the heat network (Xu et al., 2020), the equipment installation capacity, and the heat pipe transmission loss need to be considered in the expansion planning of the heat network. According to the dynamic characteristics of the regional heating network, its model can be equivalent to the one given in Yang J. et al. (2020). In addition, the heating network has a certain heat storage capacity (Li et al., 2016), which can improve the robustness of the IES.

A general model of the heating network is shown in Equation (2).

\begin{array}{l} {\begin{array}{c} \begin{matrix} A_{s} m = m_{q} \\ B_{h} h_{f} = 0 \end{matrix} \\ \begin{matrix} h_{f} = K m | m | \\ P = C_{w} m_{q} (T_{s} - T_{o}) \end{matrix} \\ \begin{matrix} T_{e d} = (T_{s t} - T_{a}) e^{- λ L / (C_{w} m)} + T_{a} \\ (\sum m_{o u t}) T_{o u t} = \sum (m_{i n} T_{i n}) \end{matrix} \end{array} & (2) \end{array}

where A_s is the node-branch incidence matrix of the heating network; m is the flow vector of the heat network pipeline; m_q is the water flow vector of the node injection load; B_h is the loop incidence matrix of the heating pipe network; h_f is the head loss vector; K is the pipeline resistance coefficient matrix; P is the load power; T_s and T_o are the water temperature of inflow and outflow loads, respectively; C_w is the specific heat capacity of water; T_st and T_ed are the water temperatures at the beginning and end of the pipeline, respectively; T_a is the external natural temperature; λ is the heat conduction coefficient of the pipeline; L is the length of the pipeline; m_in and m_out are the flow rates of node input and output pipelines, respectively; and T_in and T_out are the water temperatures of node input and output pipelines, respectively.

Integrated Load

The integrated load is a general term for electricity, natural gas, and thermal energy usage of the users. The demand response of the integrated load has a great influence on the planning of IES. Embedding the integrated demand response into the planning can improve the conservativeness of system planning, reduce the planning cost, and make the whole system more flexible and reliable. When one of the electricity, gas, and heat loads needed by the user reaches the peak value, the conversion between different loads can improve the peak-regulating situation.

Integrated demand response is an important technical measure for future planning and scheduling of IES. The demand response based on the incentive mechanism (Zheng et al., 2020) is considered a powerful tool to alleviate the imbalance of supply and demand in the power market. However, the integrated demand response of IES should also consider the energy substitution effect between different types of energy carriers and the coupling effect of consumer behavior. In addition to the incentive mechanism, a demand response strategy (Yan et al., 2019) based on the time-of-use electricity price is also an important measure. At the same time, joint planning of the demand-side response and the energy storage system can also greatly improve the reliability and economy of the whole system, especially when uncertainties such as renewable energy power generation and natural gas price are taken into consideration (Asensio et al., 2017; Xiao et al., 2018; Hamidpour et al., 2019). A method for determining the optimal proportion of interruptible load in the total load and the types and quantities of loads participating in the demand response in different scenarios needs to be studied further.

The basic model of the user demand response including electricity, gas, and heat can be expressed as follows:

\begin{array}{l} {\begin{matrix} p_{t} = p_{f i x, t} + p_{r p l, t} + \sum_{w_{1} = 1}^{W_{1}} p_{i n, t}^{w_{1}} - \sum_{w_{2} = 1}^{W_{2}} p_{o u t, t}^{w_{2}} \\ g_{t} = g_{f i x, t} + g_{r p l, t} + \sum_{w_{3} = 1}^{W_{3}} g_{i n, t}^{w_{3}} - \sum_{w_{4} = 1}^{W_{4}} g_{o u t, t}^{w_{4}} \\ h_{t} = h_{f i x, t} + h_{r p l, t} + \sum_{w_{5} = 1}^{W_{5}} h_{i n, t}^{w_{5}} - \sum_{w_{6} = 1}^{W_{6}} h_{o u t, t}^{w_{6}} \end{matrix} . & (3) \end{array}

Combined with the basic model of demand response, the model of integrated demand response can be expressed as follows:

\begin{array}{l} L_{t} = \sum_{i = 1}^{3} (l_{i, f i x, t} + l_{i, r p l, t} + l_{i, s f t, t} + l_{i, i n, t} - l_{i, o u t, t}) \\ + \sum_{w_{1} = 1}^{3} l_{i n, t}^{w_{1}} - \sum_{w_{2} = 1}^{3} l_{o u t, t}^{w_{2}}, & (4) \end{array}

where L_t is the integrated load, i.e., L_t = p_t + g_t + h_t; t is the response time; p_t is the electrical load power of t at the moment after the implementation of demand response; p_{fix, t} and p_{rpl, t} are the fixed load and transferrable load of users, respectively, at time t. $p_{i n, t}^{w_{1}}$ and $p_{o u t, t}^{w_{2}}$ represent, respectively, the electrical load replacing other energy sources by w₁ and that being replaced by other energy sources by w₂ at time t; W₁ is the set of w₁. The gas, heat, and integrated load are similar, and the constraints on energy conversion are not given.

Multi-Energy Storage

The energy storage system can not only compensate for the starting and stopping and climbing process of the unit but also can alleviate the contradiction between the energy supply and demand to make the load curve smoother. The power generation capacity of large-scale renewable energy exceeds the consumption capacity of the distribution network, which will lead to hazards such as counter-current and overvoltage. The energy storage system enables the energy in the IES to have two-way flow characteristics, providing greater flexibility for the system to absorb renewable energy. However, the cost of the energy storage system is relatively high, and blindly increasing the energy storage capacity to flatten the load curve and absorb excess renewable energy will yield lesser economic benefits.

Power storage: The location and capacity of energy storage units will significantly affect the results of the network operation, so regional energy networks need to be incorporated in the analysis of energy storage (Tenti and Caldognetto, 2019). The electric storage device not only needs to consider the capacity but also the impact of the charging and discharging process and control mode on the system (Deshun et al., 2018). Faced with the growth of electricity and natural gas demand and the uncertainty of supply and demand, the construction of infrastructure for electricity, natural gas, and thermal energy storage needs to be balanced by planning (Zhao et al., 2018). A large number of electric vehicles are connected to the power grid through vehicle-to-grid, which can also be regarded as an important energy storage unit to participate in the demand response strategy and will have an important impact on planning. At the same time, users and aggregators (Guo et al., 2020) will participate in the operation of the IES as the owners of energy storage devices, and their interests should also be considered in the configuration of power storage devices whose benefits are mainly realized through “storage at low price and generation at a high price.”

A general model of electric energy storage is shown in Equation (5).

\begin{array}{l} {\begin{matrix} \begin{matrix} E (t) = E (0) + \int_{0}^{t} [η_{c} P_{c} (t) - P_{d} (t) / η_{d}] \\ 0 \leq P_{c} (t) \leq P_{\max} 0 \leq P_{d} (t) \leq P_{\max} \end{matrix} \\ \begin{matrix} E_{\min} \leq E (t) \leq E_{\max} \\ P_{c} (t) P_{d} (t) = 0 \end{matrix} \end{matrix} & (5) \end{array}

where P_c(t) and P_d(t) are the charging and discharging power of the electric energy storage, respectively, at time t; E(t) is the remaining electric energy stored at time t; and η_c and η_d represent the charging and discharging efficiency of the electric energy storage, respectively. E(0) is the initial remaining amount of electric energy storage; P_max is the maximum charge-discharge power of the electric energy storage; E_min and E_max are the operating areas of the remaining power in the energy storage; P_c(t)P_d(t) = 0 is the constraint of electric energy storage, which restricts the unification of the energy storage state.

Gas storage: Compared with electricity, natural gas has better storage properties and is convenient for large-scale storage. Combining a natural gas storage system with a natural gas power plant has multiple advantages with regard to storage. Unconverted electric energy is stored in the form of gas to be transmitted to users when the price of natural gas is high and used to generate electricity when the price of electric power is high so that operators and power plants can get the best benefits. Therefore, when planning the natural gas storage system, corresponding strategies need to be adjusted according to the dynamic market prices of natural gas and electricity. At the same time, distributed natural gas storage (Wang et al., 2018) and seasonal storage technology (Clegg and Mancarella, 2016) can also smooth the natural gas demand curve and reduce operating costs. In addition, P2G technology can be used to convert excess renewable electricity into hydrogen/natural gas, which can be injected, transmitted, and stored in natural gas pipelines, providing an important and flexible choice for low-carbon energy systems.

A general model of gas storage is shown in Equation (6).

\begin{array}{l} {\begin{matrix} \begin{matrix} G_{1} = G_{0} + (Q_{c} μ_{c} - \frac{Q_{d}}{μ_{d}}) Δ t \\ G_{\min} \leq G \leq G_{\max} \end{matrix} \\ \begin{matrix} 0 \leq Q_{c} \leq Q_{c, \max} \\ 0 \leq Q_{d} \leq Q_{d, \max} \end{matrix} \end{matrix} & (6) \end{array}

where the charging and discharging power of the gas storage device is constant; G₀ and G₁ are respectively the energy stored by the gas storage equipment before and after charging or discharging; Q_c and Q_d respectively represent the energy charged and discharged by the energy storage device; μ_c and μ_d represent the efficiency of energy charging and discharging, respectively; G_max and G_min are the maximum and minimum values of stored energy, respectively; Q_{c, max} and Q_{d, max} are the maximum values of charge and discharge energy, respectively.

Heat storage: Sensible heat storage and phase change energy storage are the main heat storage methods used at present. Sensible heat storage costs are low, while phase change energy storage has a high heat storage density and a constant and controllable temperature during charge/discharge. In the planning, factors such as the charging and discharging process and dynamic characteristics of different heat storage modes should be considered, as well as the heat load demand and heat storage capacity of the heating network itself (Cheng et al., 2019b), which can reduce the capacity and cost of the device. The construction and operation cost of heat storage equipment is relatively high and it is difficult to be deployed on a large scale. Therefore, electric vehicles and heat storage in buildings can be regarded as virtual energy storage, and a RIES containing virtual energy storage methods (Zhu et al., 2019) can reduce the operation cost. Considering the collaborative planning of “source-storage,” a thermal power station system based on integrated energy storage for generation was proposed in Romanos et al. (2020). Under off-peak conditions, steam is extracted by high-pressure steam turbines and loaded into corresponding heat storage tanks at power stations, and when the thermal load of the system increases, these tanks can be used as the heat source of the secondary thermal power. The IES can be made more flexible and reliable by combining the heat storage device with the source-network-load planning.

The heat and cold storage models are similar in that they both have the following characteristic: there is energy dissipation during the charging and releasing of energy. Taking heat storage as an example, its general model can be expressed as follows.

\begin{array}{l} {\begin{cases} \begin{matrix} H (t) = ρ_{t} Y (t - 1) + ρ_{c} Y_{c} (t) - ρ_{d} / Y_{d} (t) \\ 0 \leq Y_{c} (t) \leq Y_{\max}, 0 \leq Y_{d} (t) \leq Y_{\max} \end{matrix} \\ \begin{matrix} 0 \leq H (t) \leq H_{\max} \\ Y_{c} (t) Y_{d} (t) = 0 \end{matrix} \end{cases} & (7) \end{array}

where H(t) is the residual heat of the heat storage device at time t; ρ_c and ρ_d are the heat storage and release efficiency of the heat storage device, respectively; ρ_t is the loss rate of the heat storage device after unit time; H_max is the maximum capacity of a heat storage device; Y_c(t) and Y_d(t) are, respectively, the heat storage and heat release power of the heat storage device at time t; and Y_max is the maximum heat storage and release power of the heat storage device.

In the IES, in order to facilitate the modeling and calculation of the complex system, the three energy storage units of electricity, heat, and gas storage can be uniformly expressed as a multi-energy storage model, as shown in Equation (8).

\begin{array}{l} {\begin{matrix} \begin{matrix} S_{t} = \sum_{i = 1}^{3} [S_{i, n, t - 1} + (η_{i}^{c h a r} P_{i, n, t}^{c h a r} - η_{i}^{d i s} P_{i, n, t}^{d i s})] \\ 0 \leq P_{i, n, t}^{c h a r} \leq P_{i, n, \max}^{c h a r}, 0 \leq P_{i, n, t}^{d i s} \leq P_{i, n, \max}^{d i s} \end{matrix} \\ \begin{matrix} 0 \leq S_{t} \leq S_{\max} \\ P_{i, n, t}^{c h a r} \times P_{i, n, t}^{d i s} = 0 \end{matrix} \end{matrix} & (8) \end{array}

where S_t is the residual energy of the multi-energy storage device at time t; i represents electricity, gas, and heat energy, which are 1, 2, and 3, respectively. $P_{i, n, t}^{c h a r}$ and $P_{i, n, t}^{d i s}$ are, respectively, the charging and discharging efficiency of Class i energy storage device n; S_max is the maximum capacity of the energy storage device; $P_{i, n, max}^{c h a r}$ and $P_{i, n, max}^{d i s}$ are the maximum charging power and discharging power of the energy storage device; $P_{i, n, t}^{c h a r} \times P_{i, n, t}^{d i s} = 0$ is the complementary constraint of energy storage, which restricts the unification of the charge and discharge state.

Coupling Device

Energy hub is a model proposed to solve the energy coupling problem in IES. Electricity, gas, and heat can be distributed to terminal equipment in a complementary form through EH coupling. The EH includes CCHP, gas-fired boiler, absorption refrigerator, electric heating boiler, air conditioning, and other coupling equipment, and its generalized model is shown in Figure 3.

FIGURE 3

Figure 3. Model of EH.

The vector P of the EH represents the energy input, and the vector L represents the energy output after the input energy has been transformed, stored, and transmitted. Each energy transformation in the EH can be represented by the coupling matrix C, which can be further represented by the distribution matrix N and the efficiency matrix η (Geng et al., 2020).

\begin{array}{l} L = C P = η N P & (9) \end{array}

The coupling matrix C changes with the change of coupling equipment in the EH. If various factors such as new energy grid connection, energy storage, and demand response are taken into comprehensive consideration in the EH modeling, the generalized model can be modified as follows:

\begin{array}{l} (L + T) = C (P + R) - S E + D L = [C S D] [\begin{matrix} P + R \\ - E \\ L \end{matrix}], & (10) \end{array}

where R is the input of new energy, T is the feedback residual energy, S is the coupling matrix of energy storage, D is the coupling matrix of demand response, and E is the storage capacity of energy. At present, the research on EHs is only limited to the simple linear distribution degree, without differential modeling for different energy sources with different time scales, and relevant uncertainty and dynamic models have not been embedded into the research on EHs.

Modeling and Solving Methods of Integrated Energy System Planning

Collaborative planning of IES refers to the investment planning of “source-network-load-storage” within the planning period, including generating sets, energy stations, natural gas pipelines, district heating pipelines, power lines, and coupling equipment. For IES, the planning problem should be established as a corresponding mathematical model; then, the objective function should be set up and the optimal planning scheme should be solved under the conditions of conformation to various constraints.

Objective Function

The coordinated planning of IES involves various links of energy generation, transmission, transformation, distribution, and consumption. It has an important influence on the development of a region, so at the beginning of planning, it is necessary to build the corresponding objective function according to specific policies and economic and social requirements, and its objective function can include indicators such as the economy, environmental protection, utilization efficiency, energy quality, and reliability.

At present, the economic index is the main decision variable in the modeling, and the objective of the coordinated planning of “source-network-load-storage” can be settled as the minimum investment cost as shown in Equation (11).

\begin{array}{l} C_{I N} = μ_{G} (\sum_{i \in Ω_{E G}} x_{i}^{E G} C_{i}^{E G} + \sum_{i \in Ω_{G G}} x_{i}^{G G} C_{i}^{G G} + \sum_{i \in Ω_{H G}} x_{i}^{H G} G_{i}^{H G}) \\ + μ_{L} (\sum_{j \in Ω_{E L}} x_{j}^{E L} C_{j}^{E L} + \sum_{j \in Ω_{G P}} x_{j}^{G P} C_{j}^{G P} + \sum_{j \in Ω_{H P}} x_{j}^{H P} C_{j}^{H P}) \\ + μ_{S} (\sum_{l \in Ω_{E S}} x_{l}^{E S} C_{l}^{E S} + \sum_{l \in Ω_{G S}} x_{l}^{G S} C_{l}^{G S} + \sum_{l \in Ω_{H S}} x_{l}^{H S} C_{l}^{H S}) \\ + μ_{E} \sum_{m \in Ω_{E H}} x_{m}^{E H} C_{m}^{E H}, & (11) \end{array}

where C_IN is the investment cost of “source-network-storage” of the IES; μ_G A is a decision variable indicating whether the system planning involves energy production; Ω_EG, Ω_GG, and Ω_HG are the sets of the candidate unit for power, gas, and thermal systems, respectively; $x_{i}^{E G}$ , $x_{i}^{G G}, a n d x_{i}^{H G}$ are the decision variables of each candidate unit for power, gas, and thermal systems, respectively; $C_{i}^{E G}$ , $C_{i}^{G G}$ , and $G_{i}^{H G}$ are the annual construction costs of each candidate unit of the power, gas, and thermal systems, respectively; μ_L is a decision variable indicating whether the system planning involves the transmission and distribution network; Ω_EL, Ω_GP, and Ω_HP are the sets of the candidate network and pipelines for the power, gas, and thermal systems, respectively; $x_{j}^{E L}$ , $x_{j}^{G P}$ , and $x_{j}^{H P}$ are the decision variables for each candidate network and pipeline of the power, gas, and thermal systems, respectively; $C_{j}^{E L}$ , $C_{j}^{G P}$ , and $C_{j}^{H P}$ are the annual construction costs of each candidate network of the power, gas, and thermal systems, respectively; μ_S is a decision variable indicating whether system planning is involved in an energy storage device; Ω_ES, Ω_GS, and Ω_HS are the sets of candidate energy storage devices for power, gas, and thermal system, respectively; $x_{l}^{E S}$ , $x_{l}^{G S}$ , and $x_{l}^{H S}$ are the decision variables of each candidate energy storage device in the power, gas, and thermal systems, respectively; $C_{l}^{E S}$ , $C_{l}^{G S}$ , and $C_{l}^{H S}$ are the annual construction costs of each candidate energy storage device of the power, gas, and thermal systems, respectively; μ_E is a decision variable indicating whether the system planning involves coupling equipment; Ω_EH contains energy converters including CCHP, gas-fired boiler, electric heating unit, heat pump, and absorption refrigerator; $x_{m}^{E H}$ is the decision variable of each energy converter; and $C_{m}^{E H}$ is the annual construction cost of each energy converter.

Planning is a problem with a large time scale, which requires considering not only the equipment investment and construction costs but also the operation and maintenance costs (Zhang N. et al., 2019). The model could be set as follows.

\begin{array}{l} C_{O P} = \sum_{t} (μ_{e} \sum_{i = Ω_{e s t}} P F_{i} + μ_{g} \sum_{i = Ω_{g s t}} G F_{i} + μ_{h} \sum_{i = Ω_{h s t}} H F_{i} \\ + μ_{d} \sum_{i = Ω_{d r}} D F_{i} + \sum_{i = Ω_{E H}} M T_{i}), & (12) \end{array}

where C_OP is the operating cost of IES; Ω_est,Ω_gst, and Ω_hst are the sets of the power substation, gas distribution station, and heat distribution station, respectively; PF_i, GF_i, and HF_i are, respectively, the energy output of substation, gas distribution station, and heat distribution station at time t; μ_e, μ_g, and μ_h are the purchase costs per unit of electricity, gas, and heat, respectively; Ω_dr is a set of demand response nodes; DF_i is the demand response over a period of time; μ_d is the compensation cost of demand response per unit; and MT_i is the operation and maintenance cost of each coupling device.

Constraints

When planning an IES, constraints at various levels need to be met as follows:

1) Supply-demand balance constraint, that is, the capacity on the energy side should meet the load demand on the user side within the planning years

2) Network constraints, including voltage/power constraints of the power grid, pressure/flow constraints of the gas network, and pressure/flow/temperature constraints of the heat network.

3) Equipment operation constraints, such as generator climbing constraints, charging and discharging constraints of the energy storage device, and maximum power constraints of the equipment

4) Other constraints, such as energy supply reliability constraints, carbon emissions constraints (Cheng Y. et al., 2019), equipment construction constraints, and environmental pollution constraints.

Solving Methods

Integrated energy system planning is a multi-dimensional, multi-variable, complex modeling and solution process (Cheng et al., 2019a), which can be solved by the mixed-integer programming method (Li G. et al., 2018). Its variables include integer and continuous variables. For this kind of complex programming problem, in order to accurately and quickly solve for the optimal solution, three perspectives should be considered: uncertainty optimization, model structure optimization, and algorithm optimization.

(1) From the perspective of uncertainty, when considering the actual uncertainty factors, such as wind and photovoltaic power and load demand, the IES planning problem is no longer a simple deterministic mathematical optimization problem, meaning it cannot be calculated to get the accurate optimal solution; usually, the stochastic programming (SP) method (Alharbi and Bhattacharya, 2018; Asensio et al., 2018) and the robust optimization (RO) method (Verástegui et al., 2019; Cao et al., 2020) are used to solve such problems.

Stochastic programming is an optimal programming method that involves adding random variables into the mathematical model while considering the probability distribution and correlation of the random variables in the modeling. The SP methods applied in the IES planning can be generally divided into three categories: expectancy method, chance constraint method, and multi-scene method.

The expectancy method replaces the actual value of the random variable with the expected value, and then the SP problem is transformed into a deterministic programming problem, but it often causes large errors because the distribution characteristics of the random variable cannot be considered. The chance constraint method (Zhang et al., 2021) uses the probability distribution of uncertain variables to transform correlation constraints into chance constraints, which need to meet a certain confidence level. This method balances the contradiction between the economy and security well, but obtaining its solution is very difficult. The multi-scenario method (Zhuo et al., 2020) samples the uncertain factors, takes the sampled scene as the deterministic boundary condition, and obtains the planning scheme that can be applied to all the scenarios. However, this method requires a large number of samples, and then typical scenes are selected. When the system scale is large, invalid scenes will affect the selection of typical scenes, and the amount of calculation will increase accordingly.

Robust optimization is used to solve the problem when the probability of a random variable is unknown but its fluctuation range is known. The objective function has a solution that strictly satisfies the constraint even for its worst case, and the optimal solution is less sensitive to changes in the parameters. When an IES runs, it will encounter uncertain parameter variables, extreme scenarios, etc., so it is necessary to consider variable fluctuations in planning and leave a certain margin, which makes the system more robust and more reliable. However, its conservatism will make the economy of the system planning worse, so when considering the uncertain factors, the indicators of economy and reliability need to be set reasonably.

(2) From the perspective of the model structure, most planning models can generally set a multi-objective optimization mathematical model (Melgar-Dominguez et al., 2019), that is, in the normal operation of the system, evaluating the economy, emissions, energy efficiency, and other indicators of the planning scheme. In a multi-objective problem, the objectives may conflict with one another, and there is no unique solution to make all indices reach the optimum. The Pareto solution set composed of the compromise solutions for each objective is the optimal solution obtained.

In addition, bilevel programming is also a commonly used model to solve the planning problem, and its solution is generally based on the idea of bilevel optimization (Xiao et al., 2018). For example, on the first level, the quantity and capacity of all kinds of equipment in the IES are optimized; on the second level, the operation of all equipment in the IES is optimized. Compared with the separate solution method of planning, configuration, and operation, bilevel optimization is more beneficial in that it avoids the local optimal solution.

A multi-stage planning method is needed when considering the long time scale of IES planning. This method is used to divide the planning cycle into several stages. With the continuous improvement in regional energy demands, the input of equipment should be increased at each planning stage to meet the growth of the load in the long-term planning cycle. The multi-stage decision-making process is used to make a decision at each stage, each decision depends on the current state, the solution of the subproblem in the first stage provides useful information for the next subproblem, and the solution of the final subproblem is the solution of the initial problem. The dynamic programming method (Lin et al., 2020) also uses a similar solution idea. The optimal scheme obtained through the multi-stage planning method is more in line with the load demand of the large-scale system in the operation cycle; it can reduce the depreciation cost of the equipment and avoid the problem of insufficient equipment capacity in the later periods of the system operation.

(3) From the perspective of the optimization algorithm, complex mixed-integer nonlinear programming problems can be simplified into linear problems that are easy to be solved first and then solved by mathematical optimization algorithms such as the branch-and-bound method, column generation method, and cut plane method (Dehghan and Amjady, 2016; Falke and Schnettler, 2016; Zhang L. et al., 2019). If the programming model is relatively complex, the programming model can be reasonably decoupled, and the large-scale problem can be decomposed into multiple sub-problems and then solved by alternating iteration of the main problem and sub-problems, such as in Benders decomposition (Fan et al., 2020). For the complex multi-objective problem in the programming model, many traditional optimization algorithms are difficult to solve for the optimal solution. A heuristic algorithm, such as the particle swarm optimization (PSO) algorithm, the genetic algorithm (GA), the ant colony algorithm, and the simulated annealing algorithm (Suhane et al., 2016; Hong et al., 2018; Li R. et al., 2018; Paul and Rather, 2019), can also be used to solve. Finally, a globally optimal solution can be found through these algorithms, but the local optimal situation should be avoided. However, the results obtained by the heuristic algorithm are inconsistent each time, and it is necessary to avoid falling into the local optimal situation, which requires the optimization of the limitations of the various algorithms, or the combination of the advantages of a variety of algorithms, to obtain the intelligent algorithm with a better solving performance. In addition, there are many solvers for convex optimization problems that can be used directly, such as Nairobi, Cplex, and Mosek, or in combination with toolkits, such as Yalmip (Sekhavatmanesh and Cherkaoui, 2019) and CVX.

Future Work Of Integrated Energy System Planning

Integrated energy system planning is a multi-variable, multi-objective problem, involving complicated power systems, natural gas systems, and thermal systems. Under the background of market-oriented reform, multi-energy coupling, and a low-carbon economy, detailed rules of planning and operation need to be explored in depth to establish a precise and reliable IES planning model. The challenges and opportunities for IES planning are as follows.

“Source-Network-Load-Storage” Coordinated Planning

The IES in the future is an integral part of the coordinated operation of source, network, load, and storage. It is necessary to embed the synchronous scheduling of source-network-load-storage into the planning of the IES to form an integrated model of planning and operation. The coupling degree of the current planning model is not high and the operation rules have not been considered comprehensively. It is necessary to further improve the programming model and adopt adaptive and distributed dynamic programming methods to make the IES planning scheme optimal.

Modeling With Dynamic Differences and Uncertainties

The scale of comprehensive energy is huge and complex, and the time scale and dynamic characteristics of electricity, gas, and heat are completely different. Therefore, it is very important to consider the differences of various energy sources and equipment comprehensively when modeling. At the same time, there are many uncertainties in the IES, so it is necessary to take the factors of uncertainty into full consideration and establish an appropriate model in the planning and operation.

Optimization Planning Considering Integrated Demand Response

The IES has not only the electric power system but also coupled natural gas and thermal systems. As the degree of multi-energy coupling deepens, the demand for natural gas and thermal energy will also change flexibly and subjectively with the establishment of energy transaction price and incentive mechanism. Therefore, the integrated demand response of electricity, gas, and heat also needs to be embedded into future planning.

Modeling Considering Energy Markets

With the reform of the energy market, the original integrated management model no longer exists. For example, the power generation and transmission rights belong to the power plant and the power grid, so their interest subjects have changed. At the same time, the addition of natural gas and heat systems will increase the number of participants in the IES, and each participant will participate in the energy market to maximize their own interests. Fluctuations in energy prices and investment strategies of various companies will fully affect the planning of the IES. Therefore, consideration of the influence of market factors in future planning will bring about savings in investment, coordination, and efficient utilization of energy.

The Application of Big Data Intelligent Algorithms

With the development of the Internet of Things, big data, and other technologies, the running state of the IES is presented by a large number of data resources. Therefore, data-driven intelligent algorithms (Cao et al., 2020; Zhang et al., 2020) will be increasingly applied widely in the planning and scheduling of the IES, such as deep learning. Data-driven intelligent algorithms can also fully mine historical data to construct uncertain sets, making the construction of uncertain sets more objective and accurate. Therefore, the application of big data intelligent algorithms in future IES planning is of great significance.

Conclusions

The IES is composed of four links: source, network, load, and storage. In each link, the site selection, layout, and sizing of the equipment have been carefully planned and various factors have been fully considered. Integrated energy system planning is the foundation of its economic and reliable operation. This paper firstly summarizes the definition and function of IES and then divides the whole system, from large- to small-scale, into the trans-regional level, the regional level, and the user level. Then, the diversity, multi-time scale, and the plurality of IES are also studied.

From the perspectives of source, network, load, and storage, the key technologies and differentiation characteristics of IES planning are discussed. Then, the transmission network model of electricity, gas, and heat; integrated demand response model; multi-energy storage model; and the energy hub model are summarized.

The methods of IES modeling and optimization are very important. Firstly, the objective function of “source-network-load-storage” coordinated planning is established according to different types of equipment in the IES. Then, constraints that need to be satisfied at all levels during planning are summarized, including supply-demand balance constraints, network constraints, and equipment operation constraints. Then, the optimal solution of the planning model is analyzed from the perspectives of uncertainty, model structure, and algorithm. The advantages and disadvantages of stochastic programming, robust optimization, multi-objective optimization,bilevel optimization, multi-stage programming, mathematical optimization algorithm, heuristic algorithm, and solver are introduced and discussed.

Finally, the direction of future research is forecast, including (1) “source-network-load-storage” coordinated planning; (2) modeling with dynamic differences and uncertainties; (3) optimization planning considering integrated demand response; (4) modeling considering energy markets; and (5) the application of big data intelligent algorithms.

Author Contributions

HF and ZY were responsible for the main writing of the paper, while SX and XL were responsible for the revision of the paper. All authors contributed to the article and approved the submitted version.

Funding

This work was supported partially by the National Natural Science Foundation of China (52077075), the Jiangsu Basic Research Project (BK20180284), and the Fundamental Research Fund for the Central Universities (2019MS007).

Conflict of Interest

XL was employed by company State Grid Economic and Technological Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors also thank the editor and the reviewer for their valuable comments.

References

Aldarajee, A. H. M., Hosseinian, S. H., Vahidi, B., and Dehghan, S. (2020). Security constrained multi-bjective bi-directional integrated electricity and natural gas co-expansion planning considering multiple uncertainties of wind energy and system demand. IET Renew. Power Generat. 14, 1395–1404. doi: 10.1049/iet-rpg.2019.1181

REVIEW article

Review on Coordinated Planning of Source-Network-Load-Storage for Integrated Energy Systems

Introduction

Structure And Characteristics Of An IES

Key Findings of IES Planning

Source of the IES

Transmission and Distribution Network

Integrated Load

Multi-Energy Storage

Coupling Device

Modeling and Solving Methods of Integrated Energy System Planning

Objective Function

Constraints

Solving Methods

Future Work Of Integrated Energy System Planning

“Source-Network-Load-Storage” Coordinated Planning

Modeling With Dynamic Differences and Uncertainties

Optimization Planning Considering Integrated Demand Response

Modeling Considering Energy Markets

The Application of Big Data Intelligent Algorithms

Conclusions

Author Contributions

Funding

Conflict of Interest

Acknowledgments

References

This article is part of the Research Topic

People also looked at