Evaluation Method of Wind Power Consumption Capacity Based on Multi-Fractal Theory

An analysis model of wind power consumption capacity is established with the multi-fractal theory. Firstly, the fluctuation characteristics of wind power are described through multi-fractal parameters, and the correlation between wind power fluctuation characteristics and consumption capacity are analyzed. Afterwards, the swinging door algorithm (SDA) is applied to divide the wind power curve in the evaluation period, and the fluctuation process with similar characteristics is clustered. Further, a functional analysis model to evaluate wind power consumption capacity is mentioned based on the fluctuation clustering results. Finally, the effectiveness of the method is verified by an example of a regional power grid in China, and the influence of adjustable parameters in the model on the consumption capacity is quantitatively analyzed.

Introduction

With the increase of power demands, the proportion of renewable energy in power grid is increasing, especially the wind power (Qazi et al., 2019). The installed capacity of wind power has reached 210 GW, accounting for 10.4% of the total in China by the end of 2019. The installed capacity is expected to reach 250 GW by the end of 2020, and the proportion of wind power in the energy supply system will increase year by year (Global Energy Interconnection Development and Cooperation Organization, 2020). However, the volatility and randomness of wind power bring severe challenges to the dispatching and operation of power system.

In recent years, the problem of “wind power curtailment” is becoming more and more serious, which has caused a waste of power generation resources and brought some economic losses. To ensure the safety and economy of power system, the reasonable wind power uncertainty model and unit commitment optimization method are established (Chen et al., 2019; Zhang et al., 2019a; Zhang et al., 2019b; Chen et al., 2020). In (Zhang et al., 2019a), the optimal unit commitment decision was obtained by considering the temporal and spatial correlation of wind load uncertainty prediction error. In (Zhang et al., 2019b), the time autocorrelation of wind power/load forecasting error and outage probability are considered in the unit commitment optimization method. These models not only reduce the operation cost of the optimization results, but also ensure the safe operation of the power system.

On the other hand, aiming at the problem of wind power curtailment, some literature focuses on how to improve the consumption capacity of wind power. In (Meena et al., 2017), a new bi-level optimization framework is proposed aim at the optimal configuration and operation management of wind power generation. To enhance the adaptability and load acceptance of wind power, Wu et al. (Wu and Jiang., 2019) considered the joint planning, which includes installed capacity and location of wind power, expansion of transmission network, and location and scale of energy storage system. With the increase of coupling among multi-energy systems, some scholars also try to increase the wind power consumption capacity from the perspective of integrated energy (Wang and Li., 2017; Mu et al., 2019; Ma et al., 2020). There are different methods to improve the consumption capacity. However, how to evaluate the wind power quickly and accurately is the precondition for achieving reasonable dispatching decision and planning. Only on the basis of accurate assessment of the consumption capacity, can those methods be more meaningful.

So far, most of the studies use mathematical optimization models to evaluate the wind power consumption capacity (Chen et al., 2017; Koutroumpezis and Safigianni., 2010; Xie, et al., 2016; Wang, et al., 2018; Wang et al., 2020). Usually, many kinds of security operation constraints (Abad et al., 2018; Fu et al., 2018; Torquato et al., 2018; Zhan and Liu., 2019) are considered and different optimization algorithms are used to obtain the optimal solution of the objective function. In (Nguyen and Mitra, 2016), the influence of wind power generation on frequency regulation ability under different penetration levels is explored. In (Sun et al., 2018), a multi-objective optimization method for power system coordination is established, which can be applied to evaluate the wind power consumption capacity. In (Xie et al., 2016), a wind power consumption optimization model with security constraints and flexible demand response is established. Xu et al. (Xu et al., 2016) calculated the wind power consumption capacity based on the multi-scenario method in which a variety of constraints were considered. In (Fu et al., 2018), the system peak shaving capacity constraints were considered, and the optimization model is established based on the statistical characteristics of wind power output. The mathematical optimization method is complex in modeling, with a large amount of calculation and limited application. In addition, most of the evaluation models in the above studies are for a certain moment, only considering the power grid’s consumption capacity at the extreme moment, but the wind power output also has strong volatility in other times. Therefore, the fluctuation characteristics of wind power in the whole period should be considered in the evaluation model.

On the basis of these studies, it is necessary to analyze the fluctuation characteristics of wind power from a long time scale, so as to improve the accuracy and adaptability of the assessment. Yang et al. (Yang et al., 2017) proposed an analysis method to divide and express the fluctuation process of wind power, but did not carry out quantitative analysis on the volatility of wind power. For the study of volatility, in (Shi et al., 2018), the fluctuation of wind power output data are analyzed by the probability density function (PDF) and discrete Fourier transform (DFT) in time and frequency domain. In (Zhang et al., 2017), fluctuating characters of the wind power are assumed to obey the versatile distribution. In (Lamsal et al., 2019; Li et al., 2019), the variation of the difference between the maximum and minimum power values within a certain time interval is used to describe the volatility of wind power.

Since the fluctuation of wind power varies with time, the fluctuation characteristics of wind power at different levels should be described by appropriate parameters. Multi-fractal theory (Harte and David, 2001) is an effective tool for studying the fluctuation characteristics of stochastic time series, and has been applied in many fields of power system. In (Teng et al., 2019), a multi-fractal spectrum is adopted to investigate wind speed characterizations. Liu et al. (Liu et al., 2014) examined the feasibility of applying the multi-fractal theory to analyse the electricity price fluctuation.

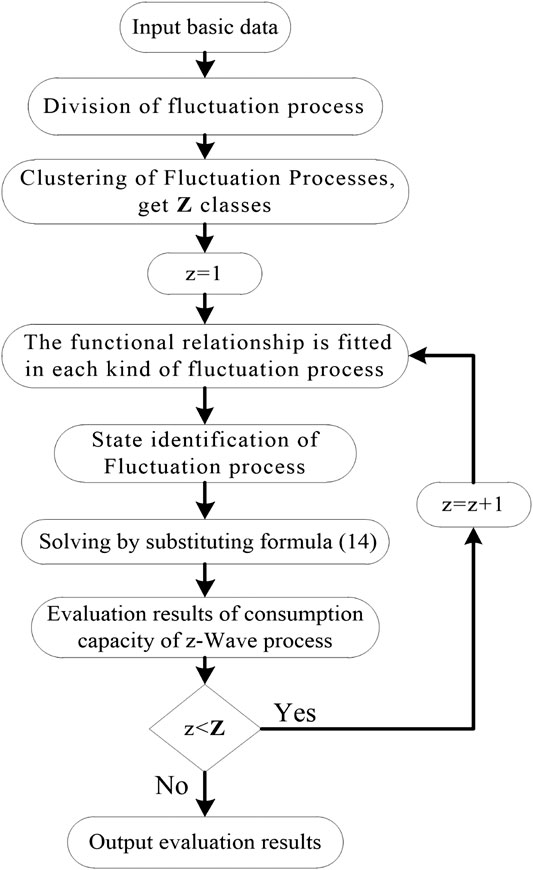
Thus, an evaluation method of wind power consumption capacity based on fluctuation characteristics analysis is carried out. Firstly, the singularity index of multi-fractal theory is adopted to describe the fluctuation characteristics of wind power. The matching degree between wind power and load curve is represented by the average Euclidean distance. The correlation between fluctuation parameters, average Euclidean distance and wind power consumption is verified based on historical data. On this basis, the fluctuation process is divided and clustered by the swinging door algorithm (SDA) and clustering algorithm, respectively. Finally, an evaluation model is established based on the fluctuation parameters. The method combines the fluctuation processes with the same fluctuation characteristics, greatly simplifies the calculation process. The consumption capacity of the power grid to a given wind power curve is analyzed, which is helpful for dispatchers to make reasonable decisions.

Key Influencing Factors

Fluctuation Degree of Wind Power Output

Multi-Fractal Theory

Multi-fractal is a kind of complex fractal structure which divides the non-uniform distribution area into multiple regions. It is composed of multiple non-uniform distribution sets with different singular indexes. The local characteristics of a system with complex fractals under different scales were described. Each scale can be represented by different parameters or dimensions. This series of parameters form a set, so that all different sets have different scales and fractal dimensions. Generally, the problems with fractal characteristics are described qualitatively and quantitatively by multi-fractal spectrum. The numerical value of each local detail and the probability distribution in the process of local detail change are calculated by Legendre transform.

The multi-fractal object is divided into $N$ regions. $x_i$ and $P_i$ be the scale size of each region and the probability of physical quantity respectively. The relationship between $x_i$ and $P_i$ in different regions is expressed by scale index ${\alpha }_i$:

${\mathrm{P}}_i={\mathrm{x}}_i^{{\alpha }_i}\left(\mathrm{i}=\mathrm{1,2,3},\dots N\right),(1)$

When $x_i\to 0$, Eq. 1 is changed into

$\alpha =\underset{x\to 0}{{\displaystyle \lim }}\frac{\ln P}{\ln x},(2)$

where $\alpha$ is the scaling index, which represents the fractal dimension of the local shape.

Fluctuation Degree

Based on multi-fractal theory, the local regularity of wind power output curve on different time scales is described by the singularity index. Wind power series $\left\{P_i\right\}$ with time length $T$, $i=\mathrm{1,2,3},\dots ,T$, $s$ is the time scale used to divide the series.

$p_j\left(s\right)=\frac{I_j\left(s\right)}{{\displaystyle \sum I_j\left(s\right)}}.(3)$

Here, $p_j\left(s\right)$ is the probability of wind power output in the $j^{th}$ interval. $I_j\left(s\right)$ is the wind power output of the $j^{th}$ interval. ${\displaystyle \sum I_j\left(s\right)}$ is the sum of wind power output of all sections.

The singularity of wind power fluctuation in the $j^{th}$ interval is characterized by local singularity index ${\alpha }_j$, which reflects the irregularity of wind power in this interval. It satisfies the following conditions in the scale-free interval.

$p_j\left(s\right)\propto s^{{\alpha }_j}(4)$

Since $s$ is smaller than 1 in multi-fractal calculation, ${\mathrm{\alpha }}_{\min }$ and ${\mathrm{\alpha }}_{\max }$ correspond to the maximum and minimum probability subsets respectively. The difference between the two probability is used to describe the fluctuation and stability of the sequence distribution. Variation of wind power output in a certain section can be expressed by $\Delta \alpha$. The larger the $\Delta \alpha$, the more uneven the wind power output distribution and the greater the volatility.

$\Delta \alpha ={\alpha }_{\max }-{\alpha }_{\min }\sim \frac{\ln p_{\min }}{\ln s}-\frac{\ln p_{\max }}{\ln s}=\frac{\ln \left(p_{\max }/p_{\min }\right)}{\ln \left(1/s\right)}.(5)$

Matching Degree of Wind Power Output and Load Demand

The consumption capacity is closely related to the fluctuation of the wind power curve if the unit parameters have been determined. Wind power will be curtailed if the fluctuation range of wind power exceeds the regulation capacity of the unit. However, wind power may fluctuate greatly at both high and low output, a single fluctuation parameter can not accurately reflect the wind power consumption capacity. The matching degree of wind power output and load demand is also a key factor, which is measured by the similarity between load and wind power curve. The higher the similarity, the greater the wind power consumption. To compare the wave processes of different time scales, the average value of Euclidean distance of all data points is reflected to the matching degree. The calculation formula is as follows:

$D_{av}=\frac{\sqrt{{\displaystyle {\sum }_{i=1}^N{\left(P_{W,i}-P_{L,i}\right)}^2}}}{N}.(6)$

Here, $N$ is the number of sampling points in the fluctuation duration. $P_{W,i}$, $P_{L,i}$ are the wind power and load power in the $i^{th}$ point.

Analysis on Fluctuation Characteristics of Wind Power Consumption

Correlation Analysis

Taking the data of a district in China in August 2019 as an example, the correlation between wind power consumption capacity and fluctuation characteristics is qualitatively analyzed by Pearson correlation coefficient (PCC). PCC is the most commonly used method to measure the correlation of series, and has many application examples in wind power output prediction (Vallée et al., 2011; Zhou et al., 2019; Wang and Zou, 2020). The correlation between any two variable sequences x and y can be calculated by Eq. 7.

$r\left(x,y\right)=\frac{\mathrm{cov}\left(x,y\right)}{{\sigma }_x{\sigma }_y}=\frac{E\left(xy\right)-E\left(x\right)E\left(y\right)}{\sqrt{E\left(x^2\right)-E^2\left(x\right)}\sqrt{E\left(y^2\right)-E^2\left(y\right)}},(7)$

where $r\left(x,y\right)$ is the correlation coefficient of x and y; $\mathrm{cov}(,)$ is the covariance operation; $E(\cdot )$ is the expected operation; ${\sigma }_x$ and ${\sigma }_y$ are the standard deviations of variables.

Figure 1 shows the calculation results of correlation analysis. With correlation coefficient $r_1=-0.7977$, which shows that fluctuation parameters have strong negative correlation with wind power consumption, that is, the greater the parameter value, the smaller the wind power consumption. With correlation coefficient $r_2=-0.8477$, similarly, there is a strong negative correlation between European distance and consumption.

FIGURE 1

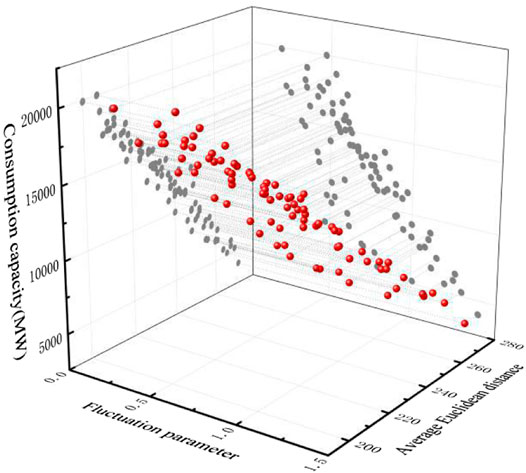
FIGURE 1. Correlation between volatility parameters, average Euclidean distance and wind power consumption.

Division of Fluctuation Process

The division of fluctuation process is the basis of studying the fluctuation characteristics of wind power output. The swinging door algorithm (SDA) proposed in (Florita et al., 2013) is applied to divide the fluctuation process. The principle is as follows:

$\{\begin{array}{c}{D}_u=\max \left(\frac{P\left(t\right)-P_0-\epsilon }{t}\right)\\ D_d=\min \left(\frac{P\left(t\right)-P_0+\epsilon }{t}\right)\end{array}t=\mathrm{1,2,3},\dots ,T.(8)$

Here, $D_u$ and $D_d$ are the up and down swinging door respectively. $\mathrm{\epsilon }$ is the window width. $P_0$ is the wind power at the initial time. $P\left(t\right)$ is the wind power at $t$ time. The up and down swinging door are calculated from $t=0$, and $t_m$ satisfying Eq. 9 is the end time of current fluctuation.

$\{\begin{array}{c}{t}_m=\min t,\\ s.t.D_u\ge D_d.\end{array}(9)$

According to the principle of swinging door algorithm, the next fluctuation process starts from $t_m$, the division is continued until the wind power data in the whole cycle is traversed. There may be an inflection point in a continuous and same trend fluctuation process, which will lead to the neglect of a data point and errors. Therefore, the traditional swinging door algorithm is improved.

The fluctuation trend before and after the termination point should be judged in the iterative process. That is, when each iteration process of fluctuation division is completed, it is necessary to judge the relationship between the change trend of the two fluctuation processes connected with the termination point. The termination condition of iteration division is changed from Eqs. 9, 10:

$\{\begin{array}{l}{t}_m=\min t,\\ s.t.D_u\ge D_d,\\ \left[P_W\left(t_m+1\right)-P_W\left(t_m\right)\right]\cdot \left[P_W\left(t_m\right)-P_W\left(t_m-1\right)\right]\ge 0,\end{array}(10)$

where $P_W\left(t_m\right)$, $P_W\left(t_{m+1}\right)$, $P_W\left(t_{m-1}\right)$ are the wind power at time $t_m$, the next sampling time and the last sampling time respectively.

In Eq. 8, the window width $\epsilon$ affects the identification of continuous and identical trend fluctuations. Most of the division results will be small fluctuations if the selection is too small. Instead, the results will be large fluctuations and small ones ignored.

Clustering of Fluctuation Processes

The consumption capacity is significantly associated with volatility parameters and average Euclidean distance. The fluctuation process of wind power is clustered based on $\Delta \alpha$ and $D_{av}$. Essentially, the same fluctuation process should have similar consumption capacity in the clustering results.

A clustering algorithm with breadth first search neighbors (BF-SN) (Xue et al., 2015) is applied to cluster the fluctuation process. It is not needed to determine the number of clusters in advance in the algorithm, and the optimal parameters are easy to set. The steps are as follows:

(1) Input fluctuation process set, and $\Delta \alpha$ is the abscissa of each fluctuation process and $D_{av}$ is the ordinate;

(2) Input the clustering parameters $r$ and $\lambda$. Where $r$ is the distance parameter to judge whether the two fluctuation processes are neighbors. Generally, the average distance between objects in the dissimilarity matrix can be taken as (Florita et al., 2013). $\lambda$ is the parameter to judge whether the fluctuation process can be clustered into one class. $\lambda \in \left[\mathrm{0,1}\right]$, that is, if the fluctuation is joined to a certain class, $\mathrm{X}$ must be neighbors with the original fluctuation process of $\lambda \%$ in this class;

(3) Solve the similarity matrix. The similarity degree matrix is a quantitative representation of the similarity of any two fluctuation processes. Its diagonal elements are 1, and the non diagonal elements $d\left(X_i,X_j\right)$ represent the similarity between the fluctuation processes $X_i$ and $X_j$;

(4) Search clustering. A new empty class is created and classified into this class from any fluctuation process $X$. All neighbors of $X$ are searched according to the parameter $r$ and whether they are classified into the class according to the parameter $\lambda$. When all the volatility processes except $X$ are traversed, the clustering is completed once;

(5) Repeat step 4)to complete the clustering of all fluctuation processes.

Evalution Model

Wind Power Output Model

According to Eqs. 3, 4, there is a one-to-one correspondence between wind power output $P_{W,i}$ and volatility parameters $\Delta {\alpha }_i$ in the $i^{th}$ fluctuation process.

$P_{Wi}=F\left(\Delta {\alpha }_i\right).(11)$

The functional relationship reflects the irregularity and distribution characteristics of wind power in the process of fluctuation.

Functional Analysis Model

State Space

The state of the system is judged according to the basic properties of the $i^{th}$ fluctuation stage. $Y$ represents the state set of the system in the whole evaluation period.

$\left\{Y=y_1,y_2,\dots ,y_k|y_1,y_2,\dots ,y_k\in \left(\mathrm{0,1}\right)\right\},(12)$

where $y_k$ indicates whether the system satisfy the $k^{th}$ constraint. If the system does not satisfy the constraint, $y_k=0$, otherwise, $y_k=1$.

The constraints are considered in the state space as follows:

Power Balance Constraints

$P_{L,i}=P_{G,i}+P_{W,i}+P_{\text{line},i}.(13)$

Power Output Constraints

$P_{G,\min }\le P_{G,i}\le P_{G,\max }.(14)$

Power Ramp Constraints

$\{\begin{array}{c}{P}_{G,i-1}-P_{G,i}\le \Delta T\cdot R_{\text{down}},\\ P_{G,i}-P_{G,i-1}\le \Delta T\cdot R_{\text{up}}.\end{array}(15)$

Tie Line Power Constraints

$0\le P_{\text{line},i}\le P_{\text{line},\max },(16)$

where $P_{L,i},P_{G,i},P_{W,i},P_{\text{line},i}$ are load demand, the unit output, wind power output and tie line power of the $i^{th}$ fluctuation process respectively; $P_{G,\min }$ and $P_{G,\max }$ are the minimum and maximum output of the unit; $P_{\text{line},\max }$ are the power limit of tie line; $R_{\text{down}}$ and $R_{\text{up}}$ are the climbing speed of the unit.

The proposed evaluation method is mainly used to calculate the wind power that the system can consume. If the system does not meet the power balance constraints, there may be two situations: excess power and power shortage. The former will lead to wind power being abandoned, and in the latter case, the system can consume all the wind power. However, the system will load shedding when the load demand can not be met. If the system satisfies the power balance constraints, y₁ will be 0; if the power is excessive, y₁ is one; if the power is insufficient, y₁ is –1.

Evaluation Model

For each kind of fluctuation process, a functional analysis model of consumption capacity evaluation is established according to the state set.

${\mathrm{Q}}_i=\{\begin{array}{c}{\displaystyle \int F\left(\Delta {\alpha }_i\right)\text{d}t,}\\ {\displaystyle \int \left[F\left(\Delta {\alpha }_i\right)-C_{1,i}\right]\text{d}t,Y=\left\{\mathrm{0,1,0,1}\right\},}\\ {\displaystyle \int C_{2,i}\text{d}t,Y=\left\{\mathrm{1,0,0,0}\right\},\left\{\mathrm{1,0,1,0}\right\},}\end{array}(17)$

$C_{1,i}=\Delta P_{W,i}-\Delta P_{L,i}-\Delta t\cdot R_{\text{down}},(18)$

$C_{2,i}=P_{L,i}-P_{G,\min }+P_{\text{line}\cdot \max }.(19)$

Here, $C_{1,i}$ is the wind power curtailment generated by the system due to insufficient climbing capacity of the unit. $C_{2,i}$ is the maximum consumption capacity of the wind power when the system has excess power. $\Delta t$ is the duration. The solution flow is shown in Figure 2.

FIGURE 2

FIGURE 2. Flow chart of wind power consumption capacity assessment.

Case Study

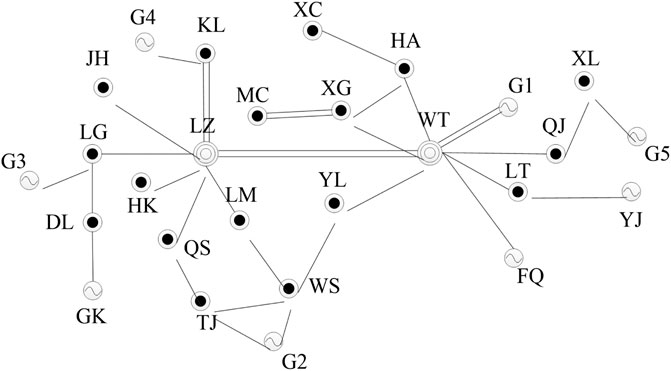
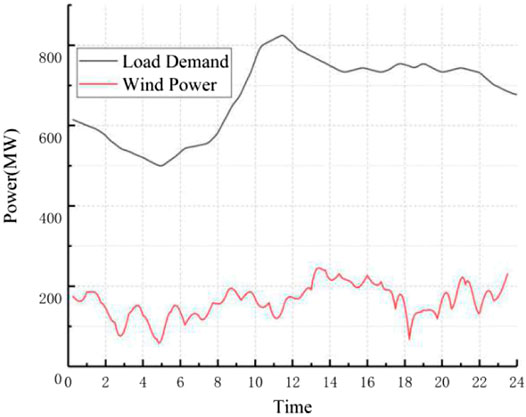
The effectiveness of the proposed method is verified by the actual power grid data. The grid structure is shown in Figure 3. There are three wind farms in the system with a total installed capacity of 350 MW, five thermal power units and the total installed capacity is 786 MW. The parameters of each generator set are shown in Table 1. Assuming that all units are in the starting state, the upper limit of tie line power is 50 MW. Load and wind power output curve are shown in Figure 4.

FIGURE 3

FIGURE 3. Grid structure diagram.

TABLE 1

TABLE 1. General parameters of generator set.

FIGURE 4

FIGURE 4. Load curve and wind power output curve.

Division and Clustering of Fluctuation Processes

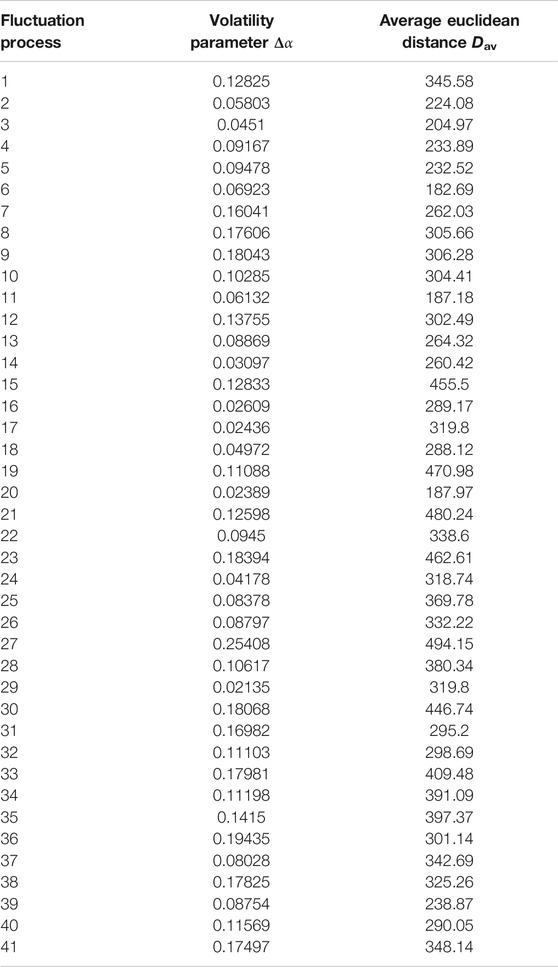
The fluctuation process of wind power is divided by SDA. Window width ε is taken as 5% of the installed capacity of wind power. A total of 41 fluctuation processes are obtained and numbered from left to right. The results of division are shown in Figure 5.

FIGURE 5

FIGURE 5. Division results of fluctuation process.

The volatility parameter $\Delta \alpha$ and average Euclidean distance $D_{av}$ of each fluctuation process are calculated. The results are shown in Table 2. According to the calculation results, the process is clustered by breadth first search neighbor algorithm. Clustering parameters $r$ and $\lambda$ are 0.8 and 1, respectively, and seven categories are obtained. The clustering results of each process are shown in Table 3.

TABLE 2

TABLE 2. Clustering parameters.

TABLE 3

TABLE 3. Clustering results of fluctuation process.

Calculation of Consumption Capacity

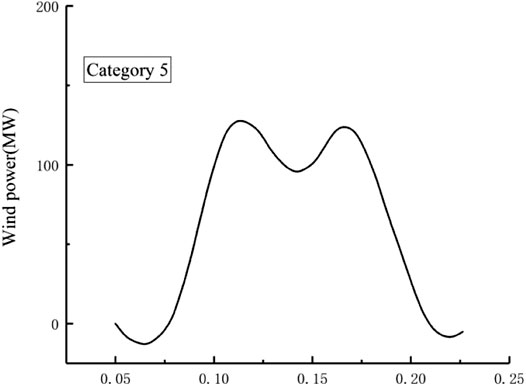
Function relationship between the wind power and singularity index in various wave stages is fitted. The wind power fitting function of 7 categories is replaced into the evaluation model, and the consumption capacity in the evaluation period is obtained. Take category 5 as an example to illustrate the calculation process. The results are shown in Figure 6.

$P_5\left(\Delta \alpha \right)=-1.281\times {10}^8\cdot \Delta {\alpha }^4+7.064\times {10}^7\cdot \Delta {\alpha }^3-\mathrm{1,428}\times {10}^7\cdot \Delta {\alpha }^2+1.251\times {10}^6\cdot \Delta \alpha -3.994\times {10}^4.$

FIGURE 6

FIGURE 6. Fitting results of wind power and singularity parameter.

The state of this kind of fluctuation is Y₅ = {1, 0, 1, 0} according to the basic data of each fluctuation process in Category 5. The power consumption is 253 MW·h, and the abandoned wind power is 64 MW·h. Similarly, the wind power consumption capacity of the whole grid is calculated.

To show the effectiveness of multi-fractal theory in describing the fluctuation degree of wind power, as a comparison, the volatility proposed in (Li et al., 2019) is used to describe the fluctuation degree. The method is recorded as Method 1, and the calculation formula is as follows:

${\alpha }^{\prime }=\frac{P_{t+1}-P_t}{P_C},(20)$

where $P_t$ denotes the output value at time $t$; $P_C$ denotes the rated capacity of a wind farm.

The consumption capacity of Method 1 is evaluated by using the same evaluation procedure proposed in this paper.

In addition, the evaluation method used in (Sun et al., 2018) is recorded as Method 2. Without considering the load regulation characteristics in different time scales, the wind power consumption was evaluated with the maximum consumption capacity as the optimization objective. The results are shown in Table 4.

TABLE 4

TABLE 4. Calculation results of consumption capacity.

The fluctuation degree of wind power in Method 1 is expressed by the change degree of a certain period of time, which depends on the size of the time interval used. This may lead to the irregularity of wind power fluctuations that can not be well described. By comparing Method 1 with the method proposed, the relative deviations between the results and the actual data are 12.54% and 3.16% respectively. The results show that the multi-fractal theory can reflect the fluctuation process better and make the evaluation results closer to the actual data.

The wind power consumption is calculated by the optimization problem in Method 2, the result is closest to the actual data, and the relative deviation is 1.12%. Compared with the optimization problem of long time scale, although there are errors between the proposed method and Method 2, the deviation between them is within the acceptable range of engineering application. The evaluation method proposed takes the fluctuation process as the unit for evaluation. Once the type of fluctuation process is determined, the current consumption can be evaluated according to the proposed functional model and the state space. It simplifies the calculation process of wind power energy consumption evaluation and reduces the amount of calculation, and has a wider applicability.

Analysis of Sensitive Factors of Consumption Capacity

Transmission Power Limit of Tie-Line

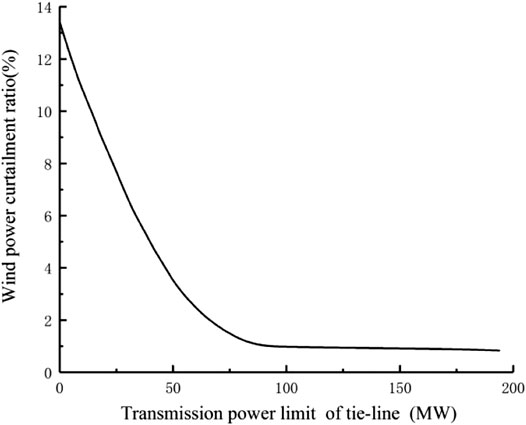
The results of wind power curtailment ratio of regional power grid are illustrated in Figure 7 when the output power of tie line is (0, 200) MW. If the limit of transmission power is less than 100 MW, the wind power curtailment ratio is negatively correlated with $P_{\text{line}}$. The increase of $P_{\text{line}}$ is equivalent to increasing the maximum consumption space of wind power, i.e. $P_L+P_{\text{line}}-P_{G\min }$, so that the system can consume the power curtailed at the low load. When $P_{\text{line}}$ is greater than 100 MW, the ratio basically remains unchanged, which is caused by the insufficient climbing capacity of the unit.

FIGURE 7

FIGURE 7. Wind power curtailment ratio with different transmission power limit of tie-line.

Peak Regulation Depth of Unit

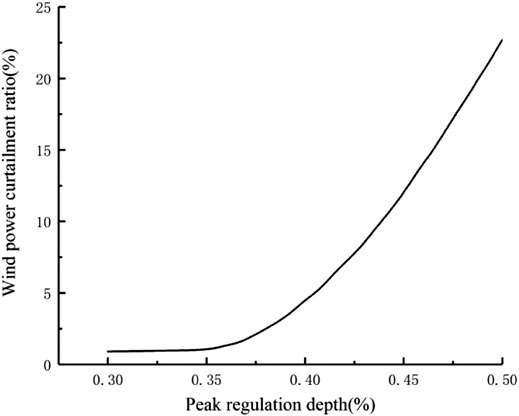
The calculation results of wind power curtailment ratio are shown in Figure 8 when the unit peak load regulation depth is (30, 50%). The curtailment ratio is positively correlated with the peak shaving depth. If the peak shaving depth is less than 35%, the curtailment ratio does not change, the wind power transmission is blocked due to the transmission power of tie line reaching the upper limit. The influence principle of unit peak regulation depth on the consumption capacity is the same as that of tie line power upper limit, both of which can improve the maximum consumption space of wind power.

FIGURE 8

FIGURE 8. Wind power curtailment ratio with different peak regulation depth.

Conclusion

To guide the development of new energy such as wind and reduce the abandonment risk of wind, a functional analysis model of wind power consumption capacity assessment is established, which takes the singularity parameters of wind power as independent variables, and simplifies the calculation process of wind power consumption assessment. Through the analysis of an example, the correctness and effectiveness of the refined consumption model proposed are proved. Moreover, the influence of the transmission power limit of tie-line and peak regulation depth of unit on wind power consumption capacity is analyzed quantitatively. The results show that the wind curtailment rate can be reduced to a certain extent by changing these two variables. Relevant research results can provide guidance for new energy development planning and construction.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript.

Conflict of Interest:

XZ was employed by the East China Electric Power Design Institute Co., Ltd, China Power Engineering Consulting Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abad, M. S. S., Ma, J., Zhang, D., Ahmadyar, A. S., and Marzooghi, H. (2018). Probabilistic assessment of hosting capacity in radial distribution systems. IEEE Trans. Sust. Energ. 9 (4), 1935–1947. doi:10.1109/TSTE.2018.2819201

CrossRef Full Text | Google Scholar

Chen, X., Wu, W. C., Zhang, B. M., and Lin, C. H. (2107). Data-driven DG capacity assessment method for active distribution networks. IEEE Trans. Power Syst. 32 (5), 3946–3957. doi:10.1109/TPWRS.2016.2633299

CrossRef Full Text | Google Scholar

Chen, Y. B., Zhang, Z., Chen, H., and Zheng, H. P. (2020). Robust UC model based on multi-band uncertainty set considering the temporal correlation of wind/load prediction errors. IET Gener, Transm. Dis. 14 (2), 180–190. doi:10.1049/iet-gtd.2019.1439

CrossRef Full Text | Google Scholar

Chen, Y. B., Zhang, Z., Liu, Z. Y., Zhang, P., Ding, Q., Liu, X. Y., et al. (2019). Robust N-k CCUC model considering the fault outage probability of units and transmission lines. IET Gener, Transm. Dis. 13 (17), 3782–3791. doi:10.1049/iet-gtd.2019.0780

CrossRef Full Text | Google Scholar

Florita, A., Hodge, B., and Orwig, K. (2013). “Identifying wind, solar ramping events,” in 2013 IEEE green technologies conference. Denver, CO, April 4–5, 2013 (Piscataway, NJ: IEEE), 147–152. doi:10.1109/GreenTech.2013.30

CrossRef Full Text | Google Scholar

Fu, K., Jia, Y., Han, X., Xiang, Y., and Wang, P. (2018). “Study on wind power consumption capacity of power grid considering risk and unit commitment,” in IEEE Power & Energy Society General Meeting (PESGM). Portland, OR, August 5–10, 2018 (Piscataway, NJ: IEEE), 1–5. doi:10.1109/PESGM.2018.8586402

CrossRef Full Text | Google Scholar

Global Energy Interconnection Development and Cooperation Organization (2020). Research on China’s ‘14th five year plan’ electric power development plan, Available at https://www.geidco.org/research/strategic/2020/2553.shtml (Accessed July 15, 2020).

Google Scholar

Harte, , and David, (2001). Multifractals: theory and applications. Boca Raton, FL: Chapman & Hall/CRC Imprint.

Koutroumpezis, G. N., and Safigianni, A. S. (2010). Optimum allocation of the maximum possible distributed generation penetration in a distribution network. Electric Power Syst. Res. 80 (12), 1421–1427. doi:10.1016/j.epsr.2010.06.005

CrossRef Full Text | Google Scholar

Lamsal, D., Sreeram, V., Mishra, Y., and Kumar, D. (2019). Smoothing control strategy of wind and photovoltaic output power fluctuation by considering the state of health of battery energy storage system. IET Renew. Power Genera. 13 (4), 578–586. doi:10.1049/iet-rpg.2018.5111

CrossRef Full Text | Google Scholar

Li, L., Wang, X., Zhang, L. N., Lei, X. H., Han, S., Liu, Y. Q., et al. (2019). Quantitative evaluation method for the complementarity of wind–solar–hydro power and optimization of wind-solar ratio. Appl. Energ. 189, 2019973–2019984. doi:10.1016/j.apenergy.2018.12.059

Google Scholar

Liu, W. J., Chung, C. Y., and Wen, F. S. (2014). Multifractal based return interval approach for short-term electricity price volatility risk estimation. Generation. Transm. Distribution, IET. 8 (9), 1550–1560. doi:10.1049/iet-gtd.2013.0680

CrossRef Full Text | Google Scholar

Ma, H., Xu, F., Chen, Q., Hu, K., Chen, L., Dai, Y. H., et al. (2020). Dispatch framework of power system with heat storage facilities in combined heat and power plants for wind power accommodation. IET Renew. Power Genera. 14 (3), 335–343. doi:10.1049/iet-rpg.2019.0595

CrossRef Full Text | Google Scholar

Meena, N. K., Swarnkar, A., Gupta, N., and Niazi, K. R. (2017). Optimal accommodation and management of high renewable penetration in distribution systems. J. Eng. 2017 (13), 1–7. doi:10.1049/joe.2017.0659

CrossRef Full Text | Google Scholar

Mu, Y. Q., Wang, C. S., Kang, G. Y., Wang, Z., Jiang, T., Li, J. F., et al. (2019). Research on sensitivity analysis of wind power consumption capability of integrated energy system based on unified optimal power flow model. J. Eng. 2019 (12), 8471–8476. doi:10.1049/joe.2019.0772

CrossRef Full Text | Google Scholar

Nguyen, N., and Mitra, J. (2016). An analysis of the effects and dependency of wind power penetration on system frequency regulation. IEEE Trans. Sust. Energ. 7 (1), 354–363. doi:10.1109/TSTE.2015.2496970

CrossRef Full Text | Google Scholar

Qazi, A., Hussain, F., Rahim, N. A. B. D., Hardaker, G., Alghazzawi, D., Shaban, K., et al. (2019). Towards sustainable energy: a systematic review of renewable energy sources, technologies, and public opinions. IEEE Access 9, 63837–63851. doi:10.1109/ACCESS.2019.2906402

CrossRef Full Text | Google Scholar

Shi, J., Lee, W. J., and Liu, X. F. (2018). Generation scheduling optimization of wind-energy storage system based on wind power output fluctuation features. IEEE Trans. Industry Appl. 54 (1), 10–17. doi:10.1109/TIA.2017.2754978

CrossRef Full Text | Google Scholar

Sun, F., Li, S. H., Ge, Y. Y., Fu, Y., Xie, C. J., Zhao, Q. S., et al. (2018). “Multi-objective optimization method for source-source coordination of power system considering wind power consumption” in 3rd international conference on smart city and systems engineering, Xiamen, China, December 29–30, 2018 (Piscataway, NJ: IEEE). doi:10.1109/ICSCSE.2018.00097

CrossRef Full Text | Google Scholar

Teng, J., Zhao, X., Qian, M., Men, Y., Yu, Z., and Hou, Y. (2019). “Short-term wind power forecasting based on variable time window and feature extraction” in IEEE Sustainable Power and Energy Conference, Beijing, China, November 21–23, 2019. doi:10.1109/iSPEC48194.2019.8974948

CrossRef Full Text | Google Scholar

Torquato, R., Salles, D., Oriente Pereira, C., Magalhaes Meira, P. C., and Freitas, W. (2018). A comprehensive assessment of PV hosting capacity on low-voltage distribution systems. IEEE Trans. Power Deliv. 33 (2), 1002–1012. doi:10.1109/TPWRD.2018.2798707

CrossRef Full Text | Google Scholar

Vallée, F., Brunieau, G., Pirlot, M., Deblecker, O., and Lobry, J. (2011). Optimal wind clustering methodology for adequacy evaluation in system generation studies using nonsequential Monte Carlo simulation. IEEE Trans. Power Syst. 26 (4), 2173–2184. doi:10.1109/TPWRS.2011.2138726

CrossRef Full Text | Google Scholar

Wang, C., Gong, Z., Liang, Y., Wei, W., and Bi, T. (2020). Data-driven wind generation admissibility assessment of integrated electric-heat systems: a dynamic convex hull-based approach. IEEE Trans. Smart Grid 11 (5), 4531–4543. doi:10.1109/TSG.2020.2993023

CrossRef Full Text | Google Scholar

Wang, G., Liu, Y., Chen, D., Yang, Z., Geng, H., Li, H., et al. (2018). “Basics non-time series production scale semantic wind power consumption evaluation method,” in 3rd international conference on Smart city and systems engineering. Xiamen, China, 6 May, 2019. doi:10.1109/ICSCSE.2018.00090

CrossRef Full Text | Google Scholar

Wang, H. T., and Zou, B. (2020). Probabilistic computational model for correlated wind speed, solar irradiation, and load using bayesian network. IEEE Access 8, 51653–51663. doi:10.1109/ACCESS.2020.2977727

CrossRef Full Text | Google Scholar

Wang, X. D., and Li, H. (2017). Multi-objectives combined electric heating dispatch model of wind power accommodation with heat storage device. J. Eng. 2017 (13), 1539–1545. doi:10.1049/joe.2017.0589

CrossRef Full Text | Google Scholar

Wu, X. S., and Jiang, Y. W. (2019). Source-network-storage joint planning considering energy storage systems and wind power integration. IEEE Access 7, 137330–137343. doi:10.1109/ACCESS.2019.2942134

CrossRef Full Text | Google Scholar

Xie, J., Wang, K., Feng, D. H., Zeng, D., Li, Y. P., and Yue, D. (2016). A security-constrained flexible demand scheduling strategy for wind power accommodation. Int. Trans. Electr. Energ. Syst. 26 (6), 1171–1183. doi:10.1002/etep.2123

CrossRef Full Text | Google Scholar

Xu, Q. Y., Kang, C. Q., Zhang, N., Ding, Y., Xia, Q., Sun, R. F., et al. (2016). A probabilistic method for determining grid-accommodable wind power capacity based on multiscenario system operation simulation. IEEE Trans. Smart Grid 7 (1), 400–409. doi:10.1109/TSG.2014.2381271

CrossRef Full Text | Google Scholar

Xue, Y., Sun, X. D., and Zhang, S. (2015). Modulation classification of communication signals based on broad first search neighbors clustering. Telecommunication Eng. 55 (1), 13–16. doi:10.3969/j.issn.1001-893x.2015.01.003

CrossRef Full Text | Google Scholar

Yang, S., Li, C., Li, X. F., Huang, Y. H., Liu, C., and Wang, W. S. (2017). Wind power fluctuation characteristics of Three North regions based on clustering algorithm. J. Eng. 2017 (13), 2266–2270. doi:10.1049/joe.2017.0734

CrossRef Full Text | Google Scholar

Zhan, X. Y., and Liu, C. (2019). Accommodation capability assessment of high-voltage direct current with a large-scale wind power integration system based on risk constraints of sub-synchronous oscillation. J. Eng. 2019 (16), 2131–2136. doi:10.1049/joe.2018.8710

CrossRef Full Text | Google Scholar

Zhang, X. S., Yuan, Y., Hua, L., Cao, Y., and Qian, K. J. (2017). On generation schedule tracking of wind farms with battery energy storage systems. IEEE Trans. Sust. Energ. 8 (1), 341–353. doi:10.1109/TSTE.2016.2598823

CrossRef Full Text | Google Scholar

Zhang, Z., Chen, Y. B., Liu, X. Y., and Wang, W. R. (2019a). Two-stage robust security-constrained unit commitment model considering time autocorrelation of wind/load prediction error and outage contingency probability of units. IEEE Access 7, 25398–25408. doi:10.1109/ACCESS.2019.2900254

CrossRef Full Text | Google Scholar

Zhang, Z., Chen, Y. B., Ma, J., Liu, X. Y., and Wang, W. R. (2019b). Two-stage robust security constrained unit commitment considering the spatiotemporal correlation of uncertainty prediction error. IEEE Access 7, 22891–22901. doi:10.1109/ACCESS.2019.2895625

CrossRef Full Text | Google Scholar

Zhou, S. Y., Zhao, Y., Gu, W., Wu, Z., Li, Y. P., Qian, Z. H., et al. (2019). Robust energy management in active distribution systems considering temporal and spatial correlation. IEEE Access 2019, 153635–153649. doi:10.1109/ACCESS.2019.2947415

CrossRef Full Text | Google Scholar