
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 13 May 2021
Sec. Nuclear Energy
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.620970
This article is part of the Research Topic Advanced Nuclear Fuel Technology View all 11 articles
For a water cooled reactor, the key thermal-hydraulic parameters span a wide range corresponding to different CHF regimes. Under accident conditions, due to the flow regime transition and interchannel mixing effect, the corresponding CHF can transition from the DO to DNB regime. In order to continuously and accurately predict DNB and DO regime CHF under wide parameter range for rod bundle channel, a comprehensive CHF mechanistic model covering the DNB and DO regime CHF prediction is established based on the rod bundle CHF-regime criterion. The DNB regime CHF mechanistic model of superheated liquid layer depletion under turbulence fluctuation bubbles and the mature DO regime CHF mechanistic model are combined to form the comprehensive CHF model. Furthermore, the comprehensive CHF model is assessed by 5 × 5 rod bundle CHF experimental data independently obtained by the Nuclear Power Institute of China (NPIC). The statistical evaluation and parametric trend analysis show that the maximum mean error of P/M is within ±22%, and the local pressure, mass flux, and quality do not have any effects on the average deviations of the predicted flux P from the measured flux M. This indicates that the comprehensive CHF mechanistic model can accurately and continuously predict the DNB and DO regime CHF in the rod bundle channel.
Critical heat flux (CHF) is an important thermal safety limit in the research and development of nuclear fuel assemblies and reactor thermal-hydraulic design and safety analysis. According to the different flow regimes and heat transfer characteristics corresponding to CHF, the flow boiling crisis in rod bundle channel can be divided into DNB regime and dryout (DO) regime (Tong, 1967).
For the pressurized water reactor (PWR), subcooled nucleate boiling occurs at the hot channel exit under normal operation conditions. Thus, the DNB regime CHF is the most likely to occur due to the low vapor quality in the channel. Under accident conditions, there are several kinds of flow regimes existing in the rod bundle channel. Moreover, due to the interchannel mixing mechanisms (Xiong et al., 2020) and the cross flow caused by the mixing vanes between adjacent open channels (Qu et al., 2019), the flow regime could transition from annular flow to bubble flow or slug flow. Accordingly, the corresponding CHF will also transition from the DO to DNB regime (Yang et al., 2019), as shown in Figure 1.
In addition, under the normal operation and accident conditions of PWR, the key thermal-hydraulic parameters span a wide range. For example, the pressure ranges from 2 to 17 MPa, the mass flux ranges from several hundred to nearly 5,000 kg/m2s, and the corresponding equilibrium quality ranges from −0.2 to 0.5. Obviously, such a wide range of thermal-hydraulic parameters may cover different CHF regimes (Groeneveld et al., 2018).
At present, due to the complex nature of two-phase flow with heat transfer in the rod bundle channel, the method for rod bundle CHF prediction is mainly CHF empirical correlation. In the development of CHF correlation, there is no classification for DNB and DO regime CHF conditions while all the CHF experimental data are put together to develop the CHF correlation (Chai et al., 2003). Moreover, once the application scope and original object of CHF empirical correlation are exceeded, the prediction accuracy will be significantly reduced. In addition, since the CHF empirical correlation usually depends on the specific correction factors, it has great uncertainty when it is extended to the condition lacking of CHF experimental data (Weisman and Pei, 1983).
Although extensive research has been carried out on CHF mechanisms and obtained several representative CHF mechanistic models with relatively high prediction accuracy (Zhang and Hewitt, 2016; Liu et al., 2020b), these CHF mechanistic models are all developed for a specific flow regime and often only applicable to DNB or DO regime CHF prediction. Obviously, the CHF prediction ability is limited to the flow or CHF regime. As Zeigarnik (Zeigarnik, 1996) pointed out, there is no universal flow boiling CHF mechanistic model that can predict CHF in the regimes of high subcooled, low subcooled, and saturated. Because there are different flow regimes and heat transfer modes in such a wide span range, only the main process can be modeled.
At present, different comprehensive CHF mechanistic models have been developed for prediction of DNB and DO regime CHF in round tubes (Kataoka et al., 1997; Kodama and Kataoka, 2002; Liu et al., 2019). However, the void fraction or quality is often used as the classification criterion for different CHF regimes in most of these comprehensive CHF mechanistic models. The accuracy and reliability of the CHF classification criterion still need further study.
Due to the complex nature of CHF phenomenon, the challenges of experimental measurement technology, and the characteristics of wide parameter range across different CHF regimes, the coexistence of various CHF mechanistic models at this stage seems reasonable and unchangeable.
In order to accurately and continuously predict the DNB and DO regime CHF in rod bundle channel under the wide parameter range, a feasible method is to classify the CHF conditions into different regimes and then establish the corresponding CHF mechanistic model based on the specific CHF-regime visualization phenomenon and mechanism hypothesis. Finally, different regimes of the CHF mechanistic model are combined to form the comprehensive CHF mechanistic model throughout the CHF-regime criterion.
In previous studies, the author has obtained the classification criterion for CHF conditions in the rod bundle channel with the dimensional analysis method (Liu et al., 2021a) and developed the DNB regime CHF mechanistic model of superheated liquid layer depletion under turbulence fluctuation bubbles (Liu et al., 2021b). In this study, a comprehensive CHF mechanistic model covering different regimes of CHF prediction will be established by using the existing research results and the mature DO regime CHF mechanistic model. The comprehensive CHF mechanistic model will be assessed by the 5 × 5 full-length rod bundle CHF experimental data independently obtained by the Nuclear Power Institute of China (NPIC), and the statistical evaluation and parametric trend analysis will be carried out by using statistical methods.
In order to correctly distinguish the rod bundle CHF regimes, a general dimensionless rod bundle CHF correlation is obtained based on the dimensional analysis method (Liu et al., 2021a). The real vapor quality, Katto number, and boiling length are introduced to establish the basic form of the dimensionless CHF correlation. According to the deep analysis of the distribution trend of typical CHF experimental data and the CHF characteristics of different CHF regimes, the CHF in rod bundle are separated into DO, DNB, and HP-DNB regimes. The dimensionless equations between the boundaries of each regime are established, and a clearly defined map of characteristic regimes of CHF in rod bundle is determined.
The equation of the dividing line between DO and DNB regimes is,
where
The equation of the dividing line between DNB and HP-DNB regimes is,
Figure 2 shows the dimensionless rod bundle CHF-regime map for
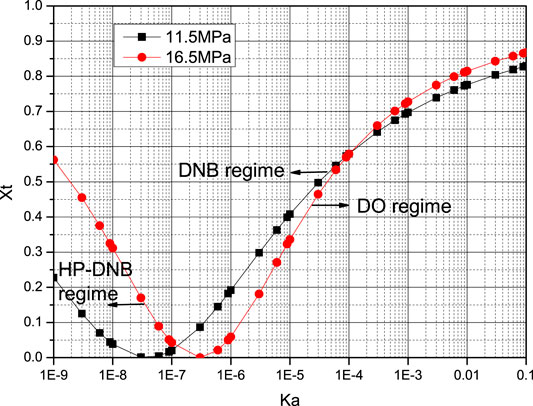
FIGURE 2. Dimensionless rod bundle CHF-regime map (Liu et al., 2021a).
It can be seen from Figure 2 that when the Katto number is large and real vapor quality is high, the CHF is corresponding to the DO regime. When the Katto number is small and real vapor quality is low, the CHF is corresponding to the DNB regime. The Katto number of the boundary point between DO and DNB regimes is about 10–7. With the increase of pressure, the boundary point moves right, and the boundary line between DNB and HP-DNB regimes moves up. Consequently, the HP-DNB regime is expanded.
The above research results provide a theoretical basis for the classification of rod bundle CHF conditions.
Under subcooled and low quality flow boiling conditions, a general CHF mechanistic model is essential to the thermal-hydraulic design and safety analysis. Based on the mechanism of superheated liquid layer depletion (Chun et al., 2000; Liu et al., 2021c), the net mass transfer from the bulk liquid to the superheated liquid layer caused by turbulent velocity fluctuations of flowing bubbles is determined, and a new calculation method of superheated liquid layer thickness is developed (Liu et al., 2021b). After matching with other constitutive equations, a novel CHF mechanistic model for subcooled and low quality flow boiling conditions has been developed, as shown in Figure 3.
For a fixed axial control volume Δz in the superheated liquid layer, the mass conservation equation is:
where
After simplification,
The radial net two-phase mass exchange rate from the bulk flow to the superheated liquid layer caused by turbulent velocity fluctuations (Liu et al., 2021b) is determined as
where
Then,
The calculation method of the superheated liquid layer thickness on the heating surface is proposed, as shown in Figure 4.
The superheated liquid layer thickness y* is obtained directly through thermal equilibrium temperature distribution in the rod bundle channel.
where Tw is the wall temperature, Pr is the Prandtl number of the liquid, and Q is a function of the local heat flux, liquid density, specific heat capacity, and friction velocity.
This DNB model is suitable for rod bundle CHF prediction under subcooled and low quality flow boiling conditions.
In annular flow, the dryout of liquid film is determined by a balance between the liquid film evaporation, liquid droplet entrainment, and deposition from the entrained core (Groeneveld, 2013), as shown in Figure 5.
In the steady state, the mass conservation equation for the liquid film is:
Several models have been proposed for solution of the mass conservation equation. The models differ in the constitutive correlations representing the mechanisms of entrainment and deposition.
In this study, the DO regime CHF mechanistic model for BWR fuel assembly developed by Lim and Weisman (Lim and Weisman, 1988) is used (see reference Lim and Weisman (1988) for the subchannel division and solution steps of this model).
In this section, the rod bundle CHF-regime criterion for DNB and DO regime CHF determined in Rod Bundle CHF-Regime Criterion is used to classify the CHF conditions. Then, the DNB regime CHF mechanistic model of superheated liquid layer depletion under turbulence fluctuation bubbles developed by the author is combined with the DO regime CHF mechanistic model of Lim and Weisman to form a comprehensive CHF mechanistic model covering the DNB and DO regime CHF prediction.
The detailed calculation process of the comprehensive CHF mechanistic model is shown in Figure 6.
First of all, input parameters such as pressure, mass flux, subcooling, and equivalent hydraulic diameter for subchannel code are needed to calculate local parameters in the current node. The initial heat flux is q and the corresponding physical properties xt and Katto number are calculated.
For xt > 0, the D-N criterion is used for judgment. If the current calculation condition belongs to DO regime, then the DO regime CHF model is used to calculate the liquid film flow rate. When the calculated liquid film flow rate is greater than the set value of 1 kg/m2s, it means that CHF has not occurred in the current node, then the next node I + 1 is calculated. If the liquid film flow rate of the last node is still greater than the set value, it means that CHF will not occur in the whole subchannel, then the corresponding heat flux is evaluated.
If the current calculation condition belongs to the DNB regime, the N-HP criterion is used for judgment, and the DNB regime CHF model is used to calculate CHF. When the calculated CHF qc does not meet the tolerance
It should be noted that the comprehensive CHF mechanistic model established in this study can automatically and accurately judge and classify the current calculation conditions. Then, the appropriate CHF model is called to calculate and the corresponding CHF is printed. This comprehensive CHF model can accurately and continuously predict the DNB and DO regime CHF in rod bundle channel under the wide parameter range.
Aiming at the development of advanced Chinese fuel assemblies, NPIC has independently carried out the CHF experiment of 5 × 5 rod bundle with axial uniform and nonuniform heating, taking into account the geometry structure of rod bundle and flow subchannel, heating length, different grid arrangements, rod radial peaking factors, and the guide tube effects (Qin et al., 2016). In this study, six CHF test series data are selected, and the database and its characteristics are shown in Table 1.
Table 2 shows the parameter range of CHF experimental data to assess the comprehensive CHF mechanistic model.
The local thermal-hydraulic parameters in the 5 × 5 rod bundle of each CHF test series are calculated with the subchannel code CORTH (Liu et al., 2017), which was developed in NPIC for thermal-hydraulic analysis of reactor cores and experimental facilities with heating rod bundles. The rod bundle specific effects such as heating length, mixing strength, cold wall, and axial nonuniform heating are considered to account properly for the calculation of rod bundle local parameters (Dong et al., 2018; Liu et al., 2020a).
Figure 7 shows the subchannel numbering in a 5 × 5 rod bundle.
First of all, the effects of heating length on CHF are validated by using the TEST 1, TEST 2, and TEST 5 experimental data. The distribution of P/M in these three series is shown in Figure 8.
It can be seen that the comprehensive CHF mechanistic model developed in this study can accurately and continuously predict the DNB and DO regime CHF in the rod bundle channel. All the P/M predicted by the comprehensive CHF mechanistic model are uniformly distributed in the vicinity of one within the mean error of ±22%.
The TEST 8 experimental data are used to validate the effect of spacer span (with intermediate mixing spacer grids to enhance the mixing strength) on CHF prediction. The distribution of P/M in this series is shown in Figure 9.
Similarly, all the P/M predicted by the comprehensive CHF mechanistic model are uniformly distributed near one within the mean error of ±12%.
The effect of cold wall is validated by TEST 7 experimental data. The distribution of P/M in this series is shown in Figure 10.
It can be seen that all the P/M predicted by the comprehensive CHF mechanistic model are uniformly distributed near one within the mean error of ±18%.
The TEST 9 experimental data are used to validate the effect of axial nonuniform heating. The distribution of P/M in this series is shown in Figure 11.
It can be seen that for the axial nonuniform heating CHF prediction, only one prediction comes up with mean error larger than 20%, and rest of the P/M are uniformly distributed near one within the mean error of ±13%.
For the axial nonuniform heating of TEST 9, the CHF may not occur at the channel exit. Figure 12 shows the comparison of the CHF mechanistic model–predicted locations with experimentally measured locations. It can be seen that the predicted CHF location is in good agreement with the experimentally measured location, and the deviation of some data points is only within one spacer span. This indicates that the comprehensive CHF mechanistic model can be used to predict the CHF location for the axial nonuniform heating condition.
Table 3 shows the mean and standard deviation of M/P predicted by the CHF mechanistic model and CF-DRW correlation (Liu W. et al., 2020) based on the CHF experimental data shown in CHF Experimental Data. It can be seen that the mean and standard deviation of M/P with these two prediction methods are quite identical.
Figures 13–15 show the distributions of M/P as a function of independent variables such as local pressure, mass flux, and quality, respectively. It can be seen that the distribution of M/P with local pressure, mass flux, and quality have no obvious systematic bias.
Figure 16 shows the flux predicted by the CHF mechanistic model, P, as a function of experimental measured flux M. It can be seen that the distribution of heat fluxes calculated with the comprehensive CHF mechanistic model is well distributed along the 45 line with measured CHF, and more than 95% experimental data are within the mean error of ±15%.
According to the statistical evaluation results, the comprehensive CHF mechanistic model is a promising candidate for rod bundle CHF prediction under the wide parameter range.
In this study, a comprehensive CHF mechanistic model covering DNB and DO regime CHF in a wide parameter range for the rod bundle channel is developed. This model is validated and statistically evaluated as a general CHF prediction method using the 5 × 5 rod bundle CHF experimental data. The important conclusions are as follows:
(1) The comprehensive CHF mechanistic model developed in this study covers the parameter range of PWR under normal operation and accident conditions and can accurately and continuously predict the DNB and DO regime CHF in the rod bundle channel.
(2) The mean and standard deviation of all M/P are 1.019 and 0.067, which are identical to the prediction accuracy of CF-DRW correlation. No specific correction factors such as heating length, cold wall, and axial nonuniform heating effect are needed anymore.
(3) The local pressure, mass flux, and quality do not have any effects on the average deviations of the predicted flux P from the measured flux M. This shows that the comprehensive CHF mechanistic model is a promising candidate for rod bundle CHF prediction under the wide parameter range.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
WL: Conceptualization, methodology, and writing—original draft preparation. SP: Supervision. GJ: Data curation and validation. YL: Software and writing—reviewing and editing. All authors read and contributed to the manuscript.
The authors express their appreciation to the Nuclear Power Institute of China for their financial support.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
CHF, critical heat flux; DNB, departure from nucleate boiling; DO, dryout; HP, high pressure; NPIC, Nuclear Power Institute of China; PWR, pressurized water reactor.
D channel diameter (m)/droplet deposition rate (kg/m2s)
De equivalent diameter (m)
E entrainment rate (kg/m2s)
G mass flux (kg/m2s)
hfg latent heat of vaporization (kJ/kg)
Ka Katto number
m mass flow rate (kg/s)
M measured CHF (MW/m2)
p pressure (MPa)
P predicted CHF (MW/m2)
Pr Prandtl number
q heat flux (MW/m2)
qc critical heat flux (MW/m2)
T temperature (°C)
v* net mass exchange rate (m/s)
V11 vapor generation rate (m/s)
x equilibrium quality
xt real vapor quality
y* distance from the wall (m)
z axial coordinate (m)
conv forced convection
evap evaporation
l liquid
turb turbulence fluctuations
v vapor
w wall
sat saturation condition
Chai, G. H., Wang, X. H., Chen, Z. L., and Tao, S. S. (2003). Review of Correlation FC-2000 for Critical Heat Flux Calculation. Nucl. Power Eng. S2 (6), 84–87.
Chun, T. H., Baek, W. P., and Chang, S. H. (2000). An Integral Equation Model for Critical Heat Flux at Subcooled and Low Quality Flow Boiling. Nucl. Eng. Des. 199, 13–29. doi:10.1016/s0029-5493(00)00224-7
Dong, S., Liu, W., Liu, Y., et al. (2018). Application of the Improved Spacer Grid Model in Subchannel Analysis Code. Nucl. Technol. 205 (1-2), 352–363. doi:10.1080/00295450.2018.1491182
Groeneveld, D. (2013). “The Critical Heat Flux Story,” in The 15th International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Pisa, Italy, May 12-17.
Groeneveld, D. C., Ireland, A., Kaizer, J., and Vasic, A. (2018). An Overview of Measurements, Data Compilations and Prediction Methods for the Critical Heat Flux in Water-Cooled Tubes. Nucl. Eng. Des. 331, 211–221. doi:10.1016/j.nucengdes.2018.02.031
Kataoka, I., Kodama, S., Tomiyama, A., and Serizawa, A. (1997). Study on Analytical Prediction of Forced Convective CHF Based on Multi-Fluid Model. Nucl. Eng. Des. 175, 107–117. doi:10.1016/s0029-5493(97)00167-2
Kodama, S., and Kataoka, I. (2002). “Study on Analytical Prediction of Forced Convective chf in the Wide Range of Quality,” in 10TH International Conference on Nuclear Engineering, Arlington, VA, USA, April 14-18. .
Lim, J. C., and Weisman, J. (1988). A Phenomenologically Based Prediction of Rod-Bundle Dryout. Nucl. Eng. Des. 105 (3), 363–371. doi:10.1016/0029-5493(88)90256-7
Liu, W., Peng, S., Jiang, G., and Liu, Y. (2021a). Analytical Investigation on Rod Bundle CHF-Regime Criterion Based on Dimensionless Groups. Int. J. Therm. Sci. 159, 106571. doi:10.1016/j.ijthermalsci.2020.106571
Liu, W., Peng, S., Jiang, G., and Liu, Y. (2021b). Development and Assessment of a New CHF Mechanistic Model for Subcooled and Low Quality Flow Boiling. Int. J. Heat Mass Transfer 165, 120641. doi:10.1016/j.ijheatmasstransfer.2020.120641
Liu, W., Peng, S., Jiang, G., Liu, Y., Du, S., Zhang, Y., et al. (2020). Development and Assessment of a New Rod-Bundle CHF Correlation for China Fuel Assemblies. Ann. Nucl. Energ. 138, 107175. doi:10.1016/j.anucene.2019.107175
Liu, W., Peng, S., Shan, J., Jiang, G., Liu, Y., Deng, J., et al. (2021c). Applicability Research of Round Tube CHF Mechanistic Model in Rod Bundle Channel. Nucl. Eng. Technol. 53, 439–445. doi:10.1016/j.net.2020.07.023
Liu, W., Shan, J., Peng, S., Jiang, G., and Liu, Y. (2019). The Study of Critical Heat Flux in Upflow Boiling Vertical Round Tube under High Pressure. Sci. Technol. Nucl. Installations 2019, 1–14. doi:10.1155/2019/3695685
Liu, Y., Dong, S., Shan, J., Zhang, B., Jiang, L., Liu, W., et al. (2020a). A Phenomenological CHF Model for Mixing-Vane Spacers in a Subchannel of a Rod Bundle. Ann. Nucl. Energ. 142, 107445. doi:10.1016/j.anucene.2020.107445
Liu, Y., Liu, W., Shan, J., Zhang, B., and Leung, L. K. H. (2020b). A Mechanistic Bubble Crowding Model for Predicting Critical Heat Flux in Subchannels of a Bundle. Ann. Nucl. Energ. 137, 107085. doi:10.1016/j.anucene.2019.107085
Liu, Y., Tan, C., Pan, J., et al. (2017). Development of Self-Reliant Subchannel Analysis Code CORTH. Nucl. Power Eng. 38 (6), 158–162.
Qin, S., Lang, X., Xie, S., Li, P., Zhuo, W., Liu, W., et al. (2016). Experimental Investigation on Repeatability of CHF in Rod Bundle with Non-uniform Axial Heat Flux Distribution. Prog. Nucl. Energ. 90, 151–154. doi:10.1016/j.pnucene.2016.03.015
Qu, W., Xiong, J., Chen, S., and Cheng, X. (2019). High-fidelity PIV Measurement of Cross Flow in 5 × 5 Rod Bundle with Mixing Vane Grids. Nucl. Eng. Des. 344, 131–143. doi:10.1016/j.nucengdes.2019.01.021
Tong, L. S. (1967). Heat Transfer in Water-Cooled Nuclear Reactors. Nucl. Eng. Des. 6 (4), 301–324. doi:10.1016/0029-5493(67)90111-2
Weisman, J., and Pei, B. S. (1983). Prediction of Critical Heat Flux in Flow Boiling at Low Qualities. Int. J. Heat Mass Transfer 26 (10), 1463–1477. doi:10.1016/s0017-9310(83)80047-7
Xiong, J., Qu, W., Zhang, T., Chai, X., Liu, X., and Yang, Y. (2020). Experimental Investigation on Split-Mixing-Vane Forced Mixing in Pressurized Water Reactor Fuel Assembly. Ann. Nucl. Energ. 143, 107450. doi:10.1016/j.anucene.2020.107450
Yang, B.-W., Han, B., Liu, A., and Wang, S. (2019). Recent Challenges in Subchannel Thermal-Hydraulics-CFD Modeling, Subchannel Analysis, CHF Experiments, and CHF Prediction. Nucl. Eng. Des. 354, 110236. doi:10.1016/j.nucengdes.2019.110236
Zeigarnik, Y. A. (1996). Universal Model of Critical Heat Flux of Subcooled Liquid Boiling in Channels. High temperature 34 (1), 48–52.
Keywords: departure from nucleate boiling, dryout, rod bundle channel, critical heat flux, mechanistic model
Citation: Liu W, Peng S, Jiang G and Liu Y (2021) Investigation on Rod Bundle CHF Mechanistic Model for DNB and DO Prediction Under Wide Parameter Range. Front. Energy Res. 9:620970. doi: 10.3389/fenrg.2021.620970
Received: 24 October 2020; Accepted: 23 April 2021;
Published: 13 May 2021.
Edited by:
Jinbiao Xiong, Shanghai Jiao Tong University, ChinaReviewed by:
Liangming Pan, Chongqing University, ChinaCopyright © 2021 Liu, Peng, Jiang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Liu, bGl1d2VpMDk1OEAxMjYuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.