- 1School of Electronic and Information Engineering, Suzhou University of Science and Technology, Suzhou, China
- 2The Suzhou Smart City Research Institute, Suzhou University of Science and Technology, Suzhou, China
This work presents an optimized probabilistic modeling methodology that facilitates the modeling of photovoltaic (PV) modules with measured data over a range of environmental conditions. The method applies cuckoo search to optimize kernel parameters, followed by electrical characteristics estimation via relevance vector machine. Unlike analytical modeling techniques, the proposed cuckoo search-relevance vector machine (CS-RVM) takes advantages of no required knowledge of internal PV parameters, more accurate estimation capability and less computational effort. A comparative study has been done among the electrical characteristics predicted by back-propagation neural network (BPNN), radial basis function neural network (RBFNN), support vector machine (SVM), Villalva's model, relevance vector machine (RVM), and the CS-RVM. Experimental results show that the proposed CS-RVM provides the best prediction in most scenarios.
1. Introduction
Recently an increasing interest in application of photovoltaic (PV) generation, together with related problems of power optimization, environmental impact, and grid stability, has led to a speedup of the research in this field (Di Piazza and Vitale, 2013). PV technology is largely applied into various areas. Such as solar still systems (Muthu Manokar et al., 2018a,b, 2020; Pounraj et al., 2018; Praveen Kumar et al., 2018; Kabeel et al., 2019; Balachandran et al., 2020; Sasikumar et al., 2020), self-powered room (Karthick et al., 2020), and etc.
Since the first PV cell was created, a variety of semiconductor materials has been used to develop PV cells. To suitably face the design issues, such as prediction of power generation, optimal choice of PV modules as well as design of power converter, a general performance estimation tool, known as PV model, is necessitated to estimate the electrical characteristics of these cells before installing.
Numerous modeling methods have been proposed to estimate the current-voltage (I-V) characteristics as well as the maximum power of PV modules. Mellit et al. (2013) classified these models into two types: explicit I = f(V) and implicit I = f(I, V) models. The former is basically a simple analytical expression predicting I in terms of V, and usually is less computational effort. On the other hand, the latter introduces more model parameters (e.g., series resistance Rs and shunt resistance Rp) and apply transcendental functions expressing the I-V relations. However, the parameters involved in implicit models, varied with different PV materials, are normally not provided by PV manufacturers. Although they can be obtained empirically, system designers often find difficulties in using the model (Massi Pavan et al., 2014).
Recently, a good number of artificial intelligence algorithms have been investigated in PV modeling. In 2004, AbdulHadi et al. (2004) first introduced neuro-fuzzy models to predict solar cell short-circuit current and open-circuit voltage, followed by coordinate translation of a measured I-V response. The simulation results matched measured data more accurately than four-parameter single-diode model, and required an order of magnitude fewer data to train than other neural-network models.
Mellit et al. (2013) developed artificial neural network (ANN) models for estimating the power produced. A comparative study showed that the ANN-models performed better than polynomial regression, multiple linear regression, analytical five-parameter single-diode models. In Mellit and Kalogirou (2011) and Bi et al. (2016), the authors used adaptive neuro-fuzzy inference scheme (ANFIS) in an expert configuration PV power supply system. The results showed that the ANFIS-based modeling method gave a good prediction accuracy of 98% and performed better than the ANN counterpart.
Celik (2011) applied a generalized regression neural network to predict the operating current of PV modules. The operating current were predicted from both neural network and five-parameter analytical model. The results showed that the ANN model provides a better prediction of the current than the analytical model.
A radial basis function neural network (RBFNN) based model of a PV module was developed by Bonanno et al. (2012) to improve the accuracy of the estimated output I-V and P-V (power-voltage) curves at different environmental conditions. The values of the computed I-V and P-V characteristics match closely to those obtained from the experimental data.
The main objective of this paper is to develop an accurate PV model, which offers the possibility to develop a new expert configuration of PV systems by implementing an cuckoo search-relevance vector machine (CS-RVM) in Matlab and through a PC with data acquisition system. The advantage of the proposed model is that they do not obtain additive model parameters or complicate calculations. A cuckoo search algorithm is applied to optimize the kernel parameter involved in relevance vector machine (RVM).
The rest of paper is organized as follows. In the next section, a general description of RVM is introduced. The proposed CS-RVM model for characterizing the behavior of PV modules, working at arbitrary environmental conditions, is presented in section 3. Section 4 demonstrates the simulation results and discussions. Finally, the conclusions are drawn in section 5.
2. Relevance Vector Machine (RVM)
Relevance vector machine (RVM) is a probabilistic model representing a Bayesian interpretation of a generalized linear model of identical functional form to support vector machine (Yuan et al., 2007).
Similar to the supervised learning, given a set of measurements at some training points , the function y(x, w) that needs to be predicted at some arbitrary point xi can be expressed as Equation (1).
where ε is the additive noise involved in target t. The y(x, w) can be formulated as Equation (2).
where w = [w1, w2, …, wN] is weight vectors and w0 is a bias. In practice, the w0 is usually incorporated into w. The y can be rewritten as Equation (3).
The K(x, xi) represents a kernel function and Φ is a matrix obtained by substituting into kernel function, namely Equation (4).
In this paper, the Gaussian data-centered basis function is chosen.
If the noise is with zero-mean Gaussian with variance σ2, the likelihood function of whole samples is expressed as Equation (5).
Maximum likelihood estimation of w and σ2 in Equation (5) often leads to over fitting (Caesarendra et al., 2010). To constrain complexity, Tipping (2001) recommended imposition of some prior constrains on the weights w. Typically, an explicit zero-mean Gaussian prior probability distribution over the weights w is defined as follows in Equation (6):
where α is a N × 1 vector of hyper parameters describing the inverse variance of each wi. On the basis of Bayes' rule, the posterior over all unknowns (w,σ2,α) could be computed via Equation (7).
The first part of Equation (7) P(w|t, α, σ2) satisfies Equation (8).
where the posterior covariance Σ = (σ−2ΦTΦ + A)−1, mean m = σ−2ΣΦTt. A is defined as A = diag(α0, α1, α2, ⋯ , αN).
In order to evaluate Σ and m, the α and σ−2 should be determined to maximize the second part of Equation (7) P(α, σ2|t), which is expressed as Equation (9).
Since uniform hyperpriors is assumed, P(α) and P(σ2) are ignored. The problem is to maximize the following equation (Equation 10).
The P(t|w, σ2) and P(w|α) obey following distributions as given in Equations (11) and (12).
Substituting Equations (11) and (12) into Equation (7), we get Equation (13).
Owing to and , the hyper parameters can be deduced by Equations (14), (15), and (16).
The values of hyper parameters can be iteratively adjusted to maximize the weigh of posterior distribution. Predictive results can be evaluated over t for a new input as given in Equation (17).
A new estimate of a target value t for a new input is given by Equation (18).
The confidence in prediction is the sum of variance associated with both the noise process and the uncertainty of the weight estimates as Equation (19).
In this optimization process, the vector from the training set that associates with the remaining non-zero weights is called the relevance vector (RV) (Yuan et al., 2007). The pseudocode of the summary the inference procedure of RVM is described in Algorithm 1.
3. CS-RVM Model Development
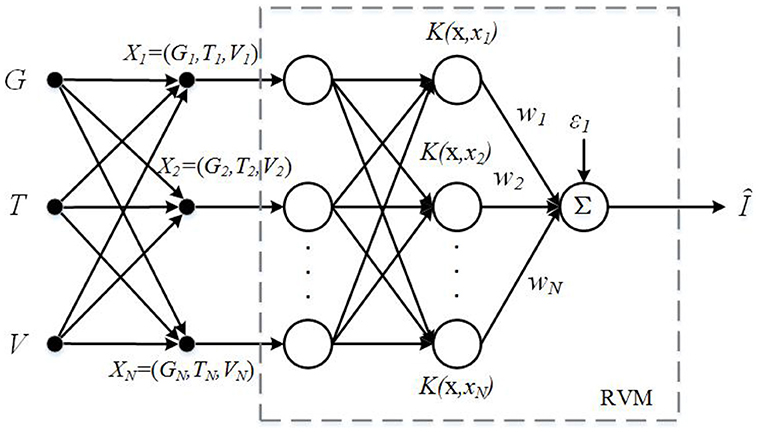
The electrical characteristics of PV modules are directly correlated to environmental factors. The RVM can be considered simply as a nonlinear input-output mapping as seen in Figure 1. It is able to find the desired relationships among the parameters, namely solar irradiance G, module temperature T, and terminal voltage V by approximating the function I = f(x), where x includes three dimensions: V, G, T.
Since the behavior of an RVM depends on the kernel parameter of Gaussian kernel Γ, practically, the RVM model can be improved by an optimization algorithm. The root mean square error (RMSE) of RVM models is suitable to be used as the fitness function for optimizations as expressed by Equation (20).
where I and Î denote measured and predicted current values of PV module, respectively. In this paper, cuckoo search (CS) (Yang and Deb, 2009, 2010) is used to determine the optimum kernel parameter in minimizing the RMSE. The CS is an optimization algorithm inspired from the obligate brood parasitic behavior of cuckoo species (Ma et al., 2013). In the CS, Lévy flights are used instead of simple random walks (i.e., the random numbers used for generation of new candidate solutions follows a Lévy distribution). The CS is a population-based algorithm. The jth nest at tth generation moves in terms of Lévy flights as Equation (21).
where α is the step size related to the scales of the problem. The product ⊕ means entry-wise multiplications. The consecutive random step of Lévy flights follows power-law step-length distribution with a heavy tail, given by Equation (22).
With the above walk around the best solution obtained so far will speed up the local search process. To avoid the search to be trapped in a local optimum, the CS generate replace the worst solutions by random walk with probability Pa.
The CS algorithm can be summarized in the following steps.
Step 1 Define stop criterion and Pa for the CS algorithm;
Step 2 Generate a random population of K host nests by Lévy flights, xi = {Gi, Ti, Vi}, i ∈ [1, N];
Step 3 Calculate fitness function via Equation (20);
Step 4 Select a nest randomly among the host nests, and replace it with new solution;
Step 5 Replace a fraction of Pa of the worst nest by generating new solutions using Lévy flights;
Step 6 Keep the current optimum nest, and go to Step 2 if the stop criterion is not fulfilled;
Step 7 Find the optimum Γ.
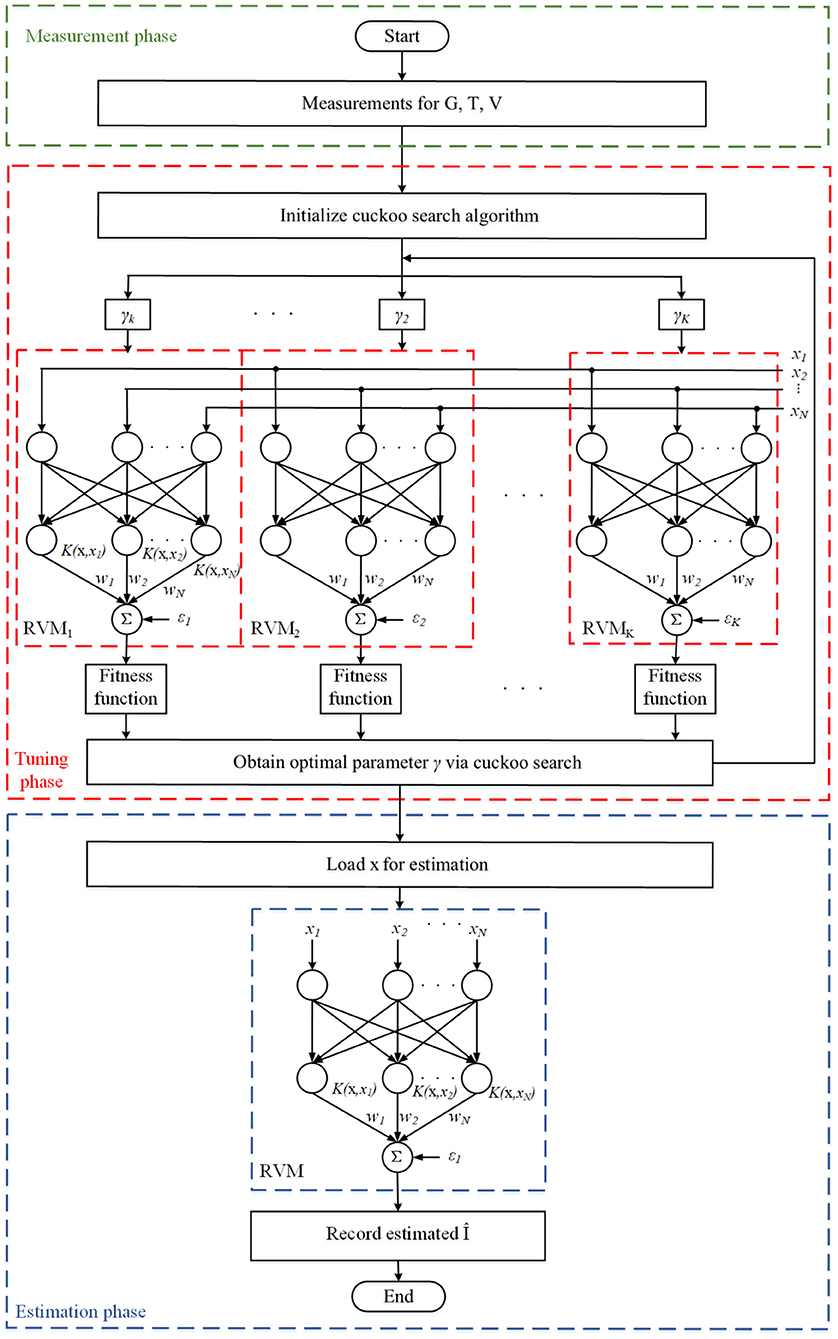
Figure 2 shows the block diagram of the complete optimized RVM PV model, which combines the CS algorithm with RVM models. The optimized RVM basically includes three procedures: experimental measurements, tuning phase, and estimation phase. The goal of tuning is to identify good Γ, the only one parameter involved in Gaussian kernels which attributes to the range [0, 1], so that the RVM model can accurately predict I-V relations. On the basis of experimental measurements on the applied PV modules, the parameter Γ can be easily tuned via cuckoo search. The hyper parameters of RVMs (α, γ, and σ2) are then determined by using Equations (14), (15), and (16), and the PV hyper-surface in the I−V−G−T working space is produced. The last stage is the estimation for terminal current. It can be simply done by substituting a set of measured data to Equation (18).
4. Results and Discussions
To objectively evaluate the performance of the proposed method, besides RMSE, mean absolute percentage error (MAPE), and coefficient of determination (R2), were also applied. The two statistical indicators are mathematically expressed as follows as Equations (23) and (24).
The formula for panel electrical efficiency is given in Equation (25).
where PMAX is the maximum power generated by the PV panel at the solar irradiance G. a is the area of the solar panel in meter squared.
Among the above statistical measures, RMSE was used as objective function in this study. It is a frequently used measure of the differences between values predicted by a model and the experimental data. MAPE makes use of all observations and has the smallest variability from sample to sample (Swanson et al., 2011). The R2 indicates how well data fit a statistical model (an R2 of 1 interprets that the statistical model perfectly fits the experimental data, while an R2 of 0 interprets that the statistical model does not fit the data at all).
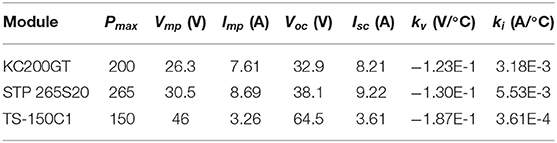
As shown in Figure 3, Gaobo GSMT-H-3A100 solar module tester was applied to measure the I-V experimental data of three different PV modules. These modules includes multicrystal “KYOCERA-Solar KC200GT” 200 W PV module, monocrystalline “SUNTECH STP 265S20” 265 W PV module, and thin film “TSMC-Solar TS-150C1” 150 W PV module. The module characteristics provided by manufacturers are listed in Table 1.
As discussed in section 3, the proposed CS-RVM approach has the capability of optimizing Γ, the only parameter involved in the kernel function of RVM model. Figure 4 depicts the median of RMSEs along the number of iterations in the 50 runs of a CS algorithm with 10 host nests. It can be seen that the CS algorithm converges within seven iterations, with the observed steady-state error to be <1.0E-4, which is relatively low and confirms the convergence performance.
Once the optimal Γ was determined, the CS-RVM was used to obtain the I-V curve of modules under various environmental conditions. The experimental data were collected by the solar module tester at different solar irradiation levels between 200 and 1,000 W/m2, every 200 W/m2. The tested temperature was varied from 25 to 50°C, every 5°C, controlled by an additional temperature controller. The voltage at each environment was collected evenly distributed throughout each module's valid voltage range. A comparative study has been done among the I-V curves predicted by back-propagation neural network (BPNN) (Gao, 2012), radial basis function neural network (RBFNN), support vector machine (SVM) (Shi et al., 2012), Villalva's model (Villalva et al., 2009), RVM and the proposed CS-RVM model (see Figure 5) with all tested PV experimental data. The BPNN and RBFNN are the most widely applied neural networks. SVM is a supervised learning model with associated learning algorithms that are used for regression and classification analysis. Villalva's model is a one of the most successful analytical PV models compromising simplicity and accuracy, and thus it was used for comparisons. Figure 5 illustrates the graphical output provided by this analysis. model outputs Î are plotted versus the measured data I as open circles. The perfect fit (I = Î) is indicated by a solid line. It is observed that many simulated current values deviate the best linear fit line for Villalva's model, indicating large errors in I-V characteristics estimation. The BPNN, RBFNN, and RVM show better fit, yet several open circulars can be found away from measured data. It is difficult to distinguish the predicted values of SVM and CS-RVM from the perfect fit line, suggesting the best estimation performance. The accuracy of these models can be quantified by RMSE, MAPE, and R2 values. The CS-RVM model obtains the minimum RMSE and MAPE. Compared to RVM, the CS-RVM model improves the MAPE by about 99.66%.
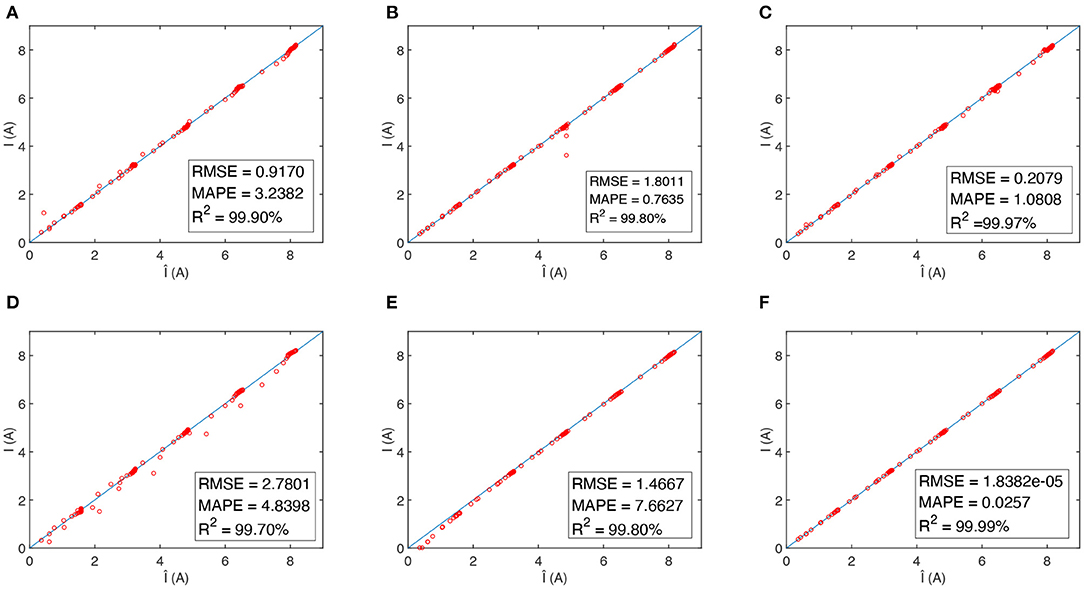
Figure 5. Median of the RMSE values along the number of function evaluations in the 50 runs of different models (A) BPNN, (B) RBFNN, (C) SVM, (D) Villalva's model, (E) RVM, and (F) CS-RVM.
Figure 6 depicts the superposition I-V curves between experimental data and predicted values via CS-RVM and Villalva's model for “KYOCERA-Solar KC200GT,” “SUNTECH STP 265S20,” and “TSMC-Solar TS-150C1” PV modules at the temperature of 25°C and different solar irradiances. As can be seen, the predicted values from CS-RVM are relatively close to the measured ones for the three modules produced by different process. The accuracy of Villalva's model is slightly lower than that of CS-RVM model. To assess the performance of the designed CS-RVM model, the RMSE, MAPE, and correlation coefficient between experimental data and predicted values were estimated in Table 2. It could be observed that the CS-RVM obtained the lower RMSE and MAPE values for “KYOCERA-Solar KC200GT,” “SUNTECH STP 265S20,” and “TSMC-Solar TS-150C1” PV modules, implying the more accurate estimation performance.
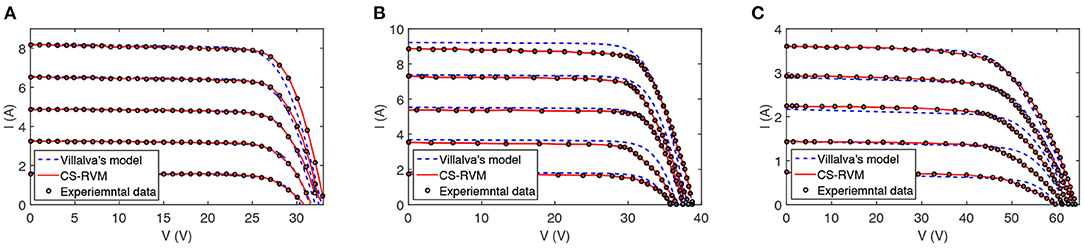
Figure 6. I-V curves obtained by CS-RVM and Villalva's model for various PV modules: (A) KC200GT (multicrystal), (B) STP 265S20 (monocrystalline), (C) TS-150C1 (thin film).
5. Conclusions
A simple and accurate CS-RVM probabilistic approach has been developed for modeling electrical characteristics of various PV modules. Owing to PV circuit models that require complicated calculations, with parameters not readily available, the proposed methodology estimates I-V characteristics curves associated with environmental conditions. The capability of the CS-RVM has been verified with reasonable statistical indicators such as RMSE. It has been demonstrated that the errors of RVM can be efficiently minimized by CS algorithm, and the CS-RVM model has been proven to be more beneficial than traditional explicit and implicit models in terms of accuracy. From the result comparison, we actually achieved significant improvements over the past works, with RMSE of 1.84 × 10-5. Others have RMSE of approximately 1.0. We conclude that the proposed CS-RVM to be a very efficient method in parameter estimation of PV modules. Consequently, the CS-RVM could be applied in the design stage, before PV system installation, providing a suitable performance estimation of PV modules. Hence, abundant solar energy could be harvested in a long run.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
JB wrote the manuscript. XP implemented the experiments. MG checked the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This research was supported in part by the National Natural Science Foundation of China under Grants 61372146 and 61702353, in part by the Natural Science Foundation of Suzhou University of Science and Technology under Grant XKQ201515, in part by the Open Foundation of the Suzhou Smart City Research Institute, Suzhou University of Science and Technology under Grant SZSCR2019015, and in part by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China under Grant 20KJB510026.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
AbdulHadi, M., Al-Ibrahim, A. M., and Virk, G. S. (2004). Neuro-fuzzy-based solar cell model. IEEE Trans. Energy Convers. 19, 619–624. doi: 10.1109/TEC.2004.827033
Balachandran, G. B., David, P. W., Vijayakumar, A. B. P., Kabeel, A. E., Athikesavan, M. M., and Sathyamurthy, R. (2020). Enhancement of PV/T-integrated single slope solar desalination still productivity using water film cooling and hybrid composite insulation. Environ. Sci. Pollut. Res. 27, 32179–32190. doi: 10.1007/s11356-019-06131-9
Bi, Z., Ma, J., Pan, X., Wang, J., and Shi, Y. (2016). ANFIS-based modeling for photovoltaic characteristics estimation. Symmetry 8:96. doi: 10.3390/sym8090096
Bonanno, F., Capizzi, G., Graditi, G., Napoli, C., and Tina, G. M. (2012). A radial basis function neural network based approach for the electrical characteristics estimation of a photovoltaic module. Appl. Energy 97, 956–961. doi: 10.1016/j.apenergy.2011.12.085
Caesarendra, W., Widodo, A., and Yang, B.-S. (2010). Application of relevance vector machine and logistic regression for machine degradation assessment. Mech. Syst. Signal Process. 24, 1161–1171. doi: 10.1016/j.ymssp.2009.10.011
Celik, A. N. (2011). Artificial neural network modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules. Sol. Energy 85, 2507–2517. doi: 10.1016/j.solener.2011.07.009
Di Piazza, M. C., and Vitale, G. (2013). Photovoltaic Sources: Modeling and Emulation. Springer. doi: 10.1007/978-1-4471-4378-9. Available online at: https://link.springer.com/book/10.1007%2F978-1-4471-4378-9
Gao, J. L. (2012). Modeling of photovoltaic cell based on BP neural networks improved by MEA. Appl. Mech. Mater. 217, 809–814. doi: 10.4028/www.scientific.net/AMM.217-219.809
Kabeel, A. E., Sathyamurthy, R., El-Agouz, S. A., Muthu Manokar, A., and El-Said, E. M. S. (2019). Experimental studies on inclined PV panel solar still with cover cooling and PCM. J. Therm. Anal. Calorimet. 138, 3987–3995. doi: 10.1007/s10973-019-08561-6
Karthick, A., Athikesavan, M., Pasupathi, M., Manoj Kumar, N., Chopra, S. S., and Ghosh, A. (2020). Investigation of inorganic phase change material for a semi-transparent photovoltaic (STPV) module. Energies 13:3582. doi: 10.3390/en13143582
Ma, J., Ting, T. O., Man, K. L., Zhang, N., Guan, S.-U., and Wong, P. W. H. (2013). Parameter estimation of photovoltaic models via cuckoo search. J. Appl. Math. 2013:362619. doi: 10.1155/2013/362619
Massi Pavan, A., Mellit, A., De Pieri, D., and Lughi, V. (2014). A study on the mismatch effect due to the use of different photovoltaic modules classes in large-scale solar parks. Prog. Photovolt. 22, 332–345. doi: 10.1002/pip.2266
Mellit, A., and Kalogirou, S. A. (2011). ANFIS-based modelling for photovoltaic power supply system: a case study. Renew. Energy 36, 250–258. doi: 10.1016/j.renene.2010.06.028
Mellit, A., Salam, S., and Kalogirou, S. A. (2013). Artificial neural network-based model for estimating the produced power of photovoltaic module. Renew. Energy 60, 71–78. doi: 10.1016/j.renene.2013.04.011
Muthu Manokar, A., Kabeel, A., Sathyamurthy, R., Mageshbabu, D., Madhu, B., Anand, P., et al. (2020). Effect of mass flow rate on fresh water improvement from inclined PV panel basin solar still. Mater. Today 32, 374–378. doi: 10.1016/j.matpr.2020.02.051
Muthu Manokar, A., Prince Winston, D., Kabeel, A., and Sathyamurthy, R. (2018a). Sustainable fresh water and power production by integrating PV panel in inclined solar still. J. Clean. Prod. 172, 2711–2719. doi: 10.1016/j.jclepro.2017.11.140
Muthu Manokar, A., Prince Winston, D., Mondol, J. D., Sathyamurthy, R., Kabeel, A., and Panchal, H. (2018b). Comparative study of an inclined solar panel basin solar still in passive and active mode. Sol. Energy 169, 206–216. doi: 10.1016/j.solener.2018.04.060
Pounraj, P., Prince Winston, D., Kabeel, A., Praveen Kumar, B., Muthu Manokar, A., Sathyamurthy, R., et al. (2018). Experimental investigation on peltier based hybrid pv/t active solar still for enhancing the overall performance. Energy Convers. Manage. 168, 371–381. doi: 10.1016/j.enconman.2018.05.011
Praveen Kumar, B., Prince Winston, D., Pounraj, P., Muthu Manokar, A., Sathyamurthy, R., and Kabeel, A. (2018). Experimental investigation on hybrid pv/t active solar still with effective heating and cover cooling method. Desalination 435, 140–151. doi: 10.1016/j.desal.2017.11.007
Sasikumar, C., Muthu Manokar, A., Vimala, M., Prince Winston, D., Kabeel, A. E., Sathyamurthy, R., et al. (2020). Experimental studies on passive inclined solar panel absorber solar still. J. Therm. Anal. Calorimet. 139, 3649–3660. doi: 10.1007/s10973-019-08770-z
Shi, J., Lee, W.-J., Liu, Y., Yang, Y., and Wang, P. (2012). Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Indus. Appl. 48, 1064–1069. doi: 10.1109/TIA.2012.2190816
Swanson, D. A., Tayman, J., and Bryan, T. (2011). MAPE-R: a rescaled measure of accuracy for cross-sectional subnational population forecasts. J. Popul. Res. 28, 225–243. doi: 10.1007/s12546-011-9054-5
Tipping, M. E. (2001). Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 1, 211–244. doi: 10.1162/15324430152748236
Villalva, M. G., Gazoli, J. R., and Filho, E. R. (2009). Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 24, 1198–1208. doi: 10.1109/TPEL.2009.2013862
Yang, X.-S., and Deb, S. (2009). “Cuckoo search via levy flights,” in 2009 World Congress on Nature Biologically Inspired Computing (NaBIC) (Coimbatore), 210–214. doi: 10.1109/NABIC.2009.5393690
Yang, X.-S., and Deb, S. (2010). Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 1, 330–343. doi: 10.1504/IJMMNO.2010.035430
Keywords: photovoltaic module, probabilistic model, relevance vector machine, cuckoo search, simulation
Citation: Ban J, Pan X and Gu M (2021) Electrical Characteristics Estimation of Photovoltaic Modules via Cuckoo Search—Relevant Vector Machine Probabilistic Model. Front. Energy Res. 9:610405. doi: 10.3389/fenrg.2021.610405
Received: 25 September 2020; Accepted: 02 March 2021;
Published: 31 March 2021.
Edited by:
Ka Lok Man, Baltic Institute of Advanced Technology, LithuaniaReviewed by:
Muthu Manokar A, B. S. Abdur Rahman Crescent Institute of Science and Technology, IndiaSen Li, Changzhou University, China
Copyright © 2021 Ban, Pan and Gu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xinyu Pan, cGFueHlAdXN0cy5lZHUuY24=
 Jianmin Ban1
Jianmin Ban1 Xinyu Pan
Xinyu Pan