Application of Rough Set and Neural Network in Water Energy Utilization

In water energy utilization, the damage of fault occurring in the power unit operational process to equipment directly affects the safety of the unit and efficiency of water power conversion and utilization, so fault diagnosis of water power unit equipment is especially important. This work combines a rough set and artificial neural network and uses it in fault diagnosis of hydraulic turbine conversion, puts forward rough set theory based on the tolerance relation and defines similarity relation between samples for the decision-making system whose attribute values are consecutive real numbers, and provides an attribute-reducing algorithm by making use of the condition that approximation classified quality will not change. The diagnostic rate of artificial neural networks based on a rough set is higher than that of the general three-layer back-propagation(BP) neural network, and the training time is also shortened. But, the network topology of an adaptive neural-fuzzy inference system is simpler than that of a neural network based on the rough set, the diagnostic accuracy is also higher, and the training time required under the same error condition is shorter. This algorithm processes consecutive failure data of the hydraulic turbine set, which has avoided data discretization, and this indicates that the algorithm is effective and reliable.

Introduction

With the continuous expansion in the scale of wind power, hydroelectric power, and other clean energy types, the hydraulic power generation system structure is also becoming increasingly complex, and the power generation unit of the hydropower station develops towards large scale and automation (Duy and Ozak, 2014; Liu and Packey, 2014). Hence, once a fault occurs, both power generation efficiency and unit safety will be affected, which will have harmful effects on the national economy and cause significant economic loss. The likelihood of malfunctions increases as the complexities of systems grow (Gokmen et al., 2013). The occasional occurrence of fault during the daily operation of hydropower units requires increasingly high reliability and safety of unit operation (Tang et al., 2010; Gao et al., 2016) The fault-diagnosis technology is also increasingly valued by people and has developed to be one comprehensive interdiscipline. Generally, the fault-diagnosis method consists of creating a real fault into the physical system and evaluating its effect on different measured variables (Attoui and Omeiri, 2014). In the current hydropower unit fault prediction and diagnosis, expert-system fault-diagnosis technology has been widely applied to the actual system, and excellent effects have been achieved (Lu et al., 2016a; Lu et al., 2016b). However, the inherent defect of the symbol information processing mechanism on which the expert system is based causes many traditional expert-system problems.

Scholars and engineering technicians put forward many technologies and methods of power system fault diagnosis to quickly and accurately recognize fault and judge the location and type of faulty components under various complicated conditions. The diagnoses are mainly including expert systems, optimization algorithms, fuzzy set theory, and multiagent technology (Pawlak, 1982; Chen et al., 2006; Clark et al., 2014; and Clark et al., 2015). Rough set theory has been widely applied in artificial intelligence, decision support, rule extraction, data mining, machine learning, etc., due to its strong capacity to handle uncertain information. In hydraulic power generation system fault diagnosis, to judge faulty components or areas based on actuating signal of protection and circuit breaker, it is possible to express the fault phenomenon and component state by pattern classification. It is appropriate to utilize the decision table method of rough set theory for this purpose (Pedrycz et al., 2008). However, in hydraulic power generation system fault diagnosis, fault-diagnosis rules of the power system correspond to attribute reduction of rough set theory. Therefore, in the case of a power system fault diagnosis with the rough set method, it is necessary to reduce the rough set decision table, which is an NP-complete problem (Wang et al., 2012). The work of Wang et al. (2013) and Cerrada et al. (2015) combine rough set theory and clone algorithm; the work of Foithog et al. (2012) and Hu et al. (2010) applied a self-adaptive genetic algorithm in attribute reduction of the rough set. The studies mentioned above mainly focus on rules extraction after using rough set theory; however, attribute reduction of the rough set itself is an NP problem.

This paper will utilize the rough set theory and neural network. The advantage of this methodology is to gain knowledge from data or input and output of living examples, and it does not require knowing the mathematical description of input and output. An artificial neural network is a model based on the human brain. It has a neuron system composed of many neurons, which has the advantages of massive parallelism, distributed processing, self-organization, and self-learning. Among these models, the BP neural network is currently the most popular neural network model in application. It has the universal advantages of all neural networks, self-learning and self-adaptive ability, nonlinear mapping ability, and high fault-tolerance rate (Yang et al., 2019). The BP algorithm’s main idea is to divide the learning process into two stages; the first stage is the forward propagation process. The given input information is to pass through the input layer and subject to the hidden layer node process and calculate the actual output value of every element. The second stage is a backward process; if the expected output value is not obtained at the output layer, it is necessary to carry out the recursive calculation of the difference between the actual output value and expected output value layer by layer to adjust the weight value based on the error.

This article establishes two kinds of neural network models under a rough set and fuzzy set. One model is the rough neural network, using a rough set to handle front-end data of neural network input and using rough set mining rules to replace the conventional adaptive-network-based fuzzy inference system (ANFIS). Utilizing this algorithm to handle the hydraulic power generation unit’s continuous fault data, ultimate results show the effectiveness of this algorithm.

Global Similarity Measurement and Attribute Reduction Algorithm

Improved General Discrimination of Attribute

Definition 1: a decision-making and information system S=(U,A,V,f) is given, where $A=C\cup \left\{d\right\},C$ refers to the condition attribute set, and d refers to the decision attribute. Ud = d1,d2,…,drd, ∀a∈C, and the general importance degree of attribute a is defined as

${\sigma }_g\left(a\right)=\{\begin{array}{cc}1-\frac{1}{C_{r\left(d\right)}^2}{\displaystyle {\sum }_{i,j=1}^{\begin{array}{l}r\left(d\right)\\ i\ne j\end{array}}\frac{a\left(d_i\right)\cap a\left(d_j\right)}{\mathit{max}cross\left[a\left(d\right)\right]}}& \text{other}\\ \forall \text{i,j},a\left(d_i\right)\cap a\left(d_j\right)=\Phi & \end{array},(1)$

where $C_{r\left(d\right)}^2$ refers to the combination with 2 taken out from r(d) numbers, $a\left(d_i\right)\cap a\left(d_j\right)\subset V$ represents the intersection between the subset of the attribute value of decision value d_i relevant to attribute a and subset of the attribute value of relevant decision value dj relevant thereto, and $\mathit{ maxcross}\left[\mathit{a}\left(\mathit{d}\right)\right]\subset \mathit{V }$ indicates the maximum interval encircled by all intersections of subsets of attribute values of two decision values relevant to attribute a, degree of general importance and measurement of the attribute. The general importance of the attribute measures indicates the global decision-making ability, rather than the impact of certain decision elements.

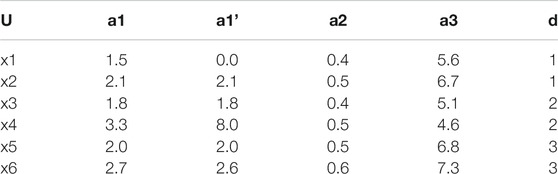
Suppose a decision table of absolute value, as shown in Table 1, with six objects.

$\text{U}/\text{d}=\left\{{\text{d}}_1{\text{,d}}_2{\text{,d}}_3\right\}=\left\{\left\{{\text{x}}_{1\text{,}}{\text{x}}_2\right\}\text{,}\left\{{\text{x}}_{3\text{,}}{\text{x}}_3\right\}\text{,}\left\{{\text{x}}_{5\text{,}}{\text{x}}_6\right\}\right\}.$

1) Subset interval of the attribute value of decision d_i relevant to attribute a₁ is [1.5,2.1], [1.8,3.3], and [2.0,2.7], respectively. The degree of importance of its general attribute calculated according to Eq. 1 is as follows:

${\sigma }_g\left(a_1\right)=1-\frac{1}{C_3^2}{\displaystyle \sum _{i\ne j}^3\frac{a\left(d_i\right)\cap a\left(d_j\right)}{\left[2.0,2.7\right]}}=1-\frac{1}{3}\left(\frac{\left[1.8,2.1\right]+\left[2.0,2.1\right]+\left[2.0,2.7\right]}{\left[2.0,2.7\right]}\right)=\mathrm{0.479.}$

2) Subset interval of the attribute value of decision d_i relevant to attribute a₁, is [0,2.1], [1.8,8], and [2.0,2.7], respectively, and the degree of importance of its general attribute is as follows:

${\sigma }_g\left({a^{\prime }}_1\right)=1-\frac{1}{C_3^2}{\displaystyle \sum _{i\ne j}^3\frac{a\left(d_i\right)\cap a\left(d_j\right)}{\left[2.0,2.7\right]}}=1-\frac{1}{3}\left(\frac{\left[1.8,2.1\right]+\left[2.0,2.1\right]+\left[2.0,2.7\right]}{\left[2.0,2.7\right]}\right)=\mathrm{0.479.}$

TABLE 1

TABLE 1. Decision table of absolute value.

Although, attribute $a_1$ and attribute ${a^{\prime }}_1$ are different in terms of subset interval of the attribute value of decision d_i, since

$\begin{array}{l}{a}_1\left(d_1\right)\cap a_1\left(d_2\right)={a^{\prime }}_1\left(d_1\right)\cap {a^{\prime }}_1\left(d_2\right)=0.3,\\ a_1\left(d_1\right)\cap a_1\left(d_3\right)={a^{\prime }}_1\left(d_1\right)\cap {a^{\prime }}_1\left(d_3\right)=0.2,\\ a_1\left(d_2\right)\cap a_1\left(d_3\right)={a^{\prime }}_1\left(d_2\right)\cap {a^{\prime }}_1\left(d_3\right)=0.9,\mathrm{and}\\ \mathit{max}cross\left[a_1\left(d\right)\right]=\mathit{max}cross\left[{a^{\prime }}_1\left(d\right)\right]=\mathrm{0.9.}\end{array}$

Therefore, they are identical in terms of the degree of importance of general attribute, namely, ${\sigma }_g\left(a_1\right)={\sigma }_g\left({a^{\prime }}_1\right)$. For attribute a₁, its degree of influence on $\frac{a_1\left(d_1\right)\cap a_1\left(d_2\right)}{\left[1.6,2.2\right]}=\frac{0.3}{0.6}=0.5$, and the degree of influence of $a_1$ on $d_1$ is $\frac{a_{1^{\prime }}\left(d_1\right)\cap a_{1^{\prime }}\left(d_2\right)}{\left[\mathrm{0,2.2}\right]}=\frac{0.3}{2.2}=0.136$.

Accordingly, for different subset intervals of the attribute value, the intersection between the subset of $d_i$ relevant to $a_1$ and ${a^{\prime }}_1$ and the subset $d_j$ relevant to it has different degrees of influence on the respective attribute subset interval.

Consequently, the concept about the degree of importance of improved general attribute is put forward, with the influence of intersection between subsets of attribute value on the respective attribute subset interval taken into consideration.

Definition 2: given the decision-making system $S=\left(U,C\cup d,V,f\right),U/d=\left\{d_1,d_2,\dots d_{r\left(d\right)}\right\},\forall a\in C$, an improved general discrimination of attribute a is defined as follows:

${\displaystyle {\sum }_g\left(a\right)}=\{\begin{array}{cc}1-\frac{1}{C_{r\left(d\right)}^2}{\displaystyle {\sum }_{i=1}^{r\left(d\right)}\frac{{\displaystyle {\sum }_{j=1}^{\begin{array}{l}r\left(d\right)\\ i\ne j\end{array}}{\phi }_1\left[a\left(d_i\right),a\left(d_j\right)\right]}}{\left|a\left(d_{i\mathit{max}}\right)-a\left(d_{\mathit{imin}}\right)\right|},}& \left(d_{i\mathit{max}}\right)\ne a\left(d_{\mathit{imin}}\right)\\ 1-\frac{1}{C_{r\left(d\right)}^2}{\displaystyle {\sum }_{i=1}^{r\left(d\right)}\frac{{\displaystyle {\sum }_{j=1}^{\begin{array}{l}r\left(d\right)\\ i\ne j\end{array}}{\phi }_2\left[a\left(d_i\right),a\left(d_j\right)\right]}}{\left|a\left(d_{i\mathit{max}}\right)\right|},}& \left(d_{i\mathit{max}}\right)=a\left(d_{\mathit{imin}}\right)\end{array},(2)$

where

$\begin{array}{l}{\phi }_1\left[a\left(d_i\right),a\left(d_j\right)\right]=\frac{a\left(d_i\right)\cap a\left(d_j\right)}{\left|r\left(d\right)-1\right|},\\ {\phi }_2\left[a\left(d_i\right),a\left(d_j\right)\right]=\{\begin{array}{cc}\frac{a\left(d_j\right)}{\left|r\left(d\right)-1\right|},& a\left(d_{\mathit{imax}}\right)\in a\left(d_j\right)\\ & a\left(d_{\mathit{imax}}\right)\notin a\left(d_j\right)\end{array}.\end{array}$

$C_{r\left(d\right)}^2$ represents the combination with 2 taken out from $r\left(d\right)$ numbers, $a\left(d_i\right)\cap a\left(d_j\right)\subset V$ refers to the intersection between the subset of the attribute value of decision value $d_i$ d_i relevant to attribute a and subset of the attribute value of decision value $d_j$ relevant thereto, and $a\left(d_{i\mathit{max}}\right)$ and $a\left(d_{i\mathit{min}}\right)$ are the maximum and minimum of decision value d_i relevant to attribute a, respectively. According to the calculation based on formula, ${\sigma }_g\left(a_1\right)=0.6827,{\sigma }_g\left({a^{\prime }}_1\right)=0.8171$.

Global Similarity Measurement of the Attribute

Definition 3: given a decision-making system $S=\left(U,A,V,f\right)\forall a\in A,x,y\in U$ , different similarity relations may be defined for different attributes, and this work defines the similarity of attribute a for objects x and y as follows:

$SIM\left(x,y\right)=1-\frac{\left|a\left(x\right)-a\left(y\right)\right|}{\left|a_{\max }-a_{\min }\right|},(3)$

where $a_{\max }$ and $a_{\min }$ are the maximum and minimum of attribute a, respectively.

Given a decision-making system $S=\left(U,A,V,f\right)$ for attribute subset $P\subseteq A,\forall x,y\in U$ in case that they satisfy the following formula:

$\frac{{\displaystyle {\sum }_{a\in P}k\ast SI{M}_a\left(x,y\right)}+\left(1-k\right)\ast {\sigma }_g\left(a\right)}{\left|P\right|}\ge \tau ,(4)$

where $k\in \left[0.5,1\right]$ and then $\left(x,y\right)\in SIM{\left(x,y\right)}_{p,\tau }$, which is the global similarity threshold. It gives the global similarity degree of the similarity class to take not only the similarity of the object but also the global decision-making ability of the attribute into consideration.

Definition 4: $SI{M}_{p,\tau }=\{y\in U|\left(x,y\right)\in SI{M}_{p,\tau }$ intolerance class.

Definition 5: tolerance class of object $x\in U$ and lower approximation $\left(P_{\tau }X\right)$ and upper approximation $\left({\overline{P}}_{\tau }X\right)$ of tolerance relation object set X are defined as follows:

${\underset{¯}{P}}_{\tau }X=\left\{x|SI{M}_{P,\tau }\left(x\right)\subseteq X\right\},$

${\overline{P}}_{\tau }X=\left\{x|SI{M}_{P,\tau }\left(x\right)\cap X\varnothing \right\}.$

They are referred to as the lower approximation of $SI{M}_{P,\tau }$ and upper approximation of $SI{M}_{P,\tau }$ of $X$, respectively.

Definition 6: if $P,Q\subseteq A$, then p (positive threshold) $PO{S}_p\left(Q\right)$ and the degree of dependence $k_{\tau }$ of Q are defined as follows:

$PO{S}_{P,\tau }\left(Q\right)=U_{x\subseteq U|Q}{\underset{¯}{P}}_{\tau }X,$

$k_{\tau }\left(Q\right)={\gamma }_{P,\tau }\left(Q\right)=\frac{\left|PO{S}_{P,\tau }\left(Q\right)\right|}{\left|U\right|}.(5)$

Attribute Reduction Algorithm Based on the Tolerance Relation

Attribute reduction of an information system often starts from the calculation of the attribute set to save much time (Min and Liu, 2009; Sun et al., 2017) since positive threshold change based on the global similarity relation is irregular; therefore, it is advisable to add the current foremost attribute from the empty set. The initial range of system threshold is $\left[\tau ,0.99\right]$ with threshold reduced by 0.01 from 0.99 every time to calculate the degree of dependence of the condition attribute set on the decision attribute set till the degree of dependence is unchanged (Sun et al., 2019).

Input: information system $S=\left(U,C\cup D,V,f\right)$, and the number of condition attributes is n

Output: reduced set of the attribute of S

Application Analysis

To analyze various performance indexes of hydropower unit operation at the hydropower station and monitor the state of the hydropower unit during the operation process, the power plant explores the dependency relationship between equipment in various unordered measured data by record and statistics of equipment operating data of the power generation unit. Knowledge discovery means the method of finding a dependency relationship between variables from these data and reporting the model found to the user in the form of a function or rule (Peng et al., 2011; Grbovic et al., 2012; Shang et al., 2017). Production rules are widely applied in knowledge representation because they are simple in form and are easy to understand by the user.

Haa and Xu (2001) provide water turbine fault-diagnosis data of a hydropower station, as shown in Supplementary Table SA1 in the appendix. Based on the fault-diagnosis system of the rough set, this work takes certain hydropower station data in western China as an example to carry out an experimental simulation study of fault diagnosis. Firstly, using the fuzzy membership function to disperse data with an equal-width discretization method, the membership function parameters generate automatically according to the given fuzzy membership grade. This method has good self-adaptability, and the fuzzification can be omitted in the ANFIS system (Tabakhi et al., 2014; Zhang and Min, 2016; Zhang et al., 2016). In this example, the membership grade is 4. Then, a rough set is utilized to prehandle data to obtain the core attribute, namely, the minimum attribute set {5, 6, 9}, determine the hidden node number of the BP network, repeat the training 10 times with consideration of network training time and the sum of squared errors (SSE), and get the average value of all training by giving the same training step.

With an increase in the hidden layer node number, network convergence error is reduced, but the training time is lengthened (Raileanu and Stoffel, 2004; Shi et al., 2015). The hidden node number is taken as 17 with comprehensive consideration of these two factors. When directly constructing a neural network without rough set handling, 12 input nodes are needed, and more hidden layer nodes are needed for network convergence. The same method is used to find the optimum hidden node number of original data free from dimensionality reduction.

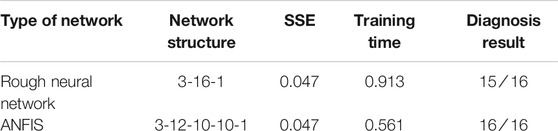
Table 2 compares the differences between the two kinds of networks (general neural network and rough neural network). As it is clear, the rough neural network has advantages over those of general neural networks. The two kinds of the network are respectively applied to bearing fault-diagnosis examples. The diagnosis data are shown in Supplementary Table SA2 in the appendix.

TABLE 2

TABLE 2. Diagnosis results of the two kinds of network.

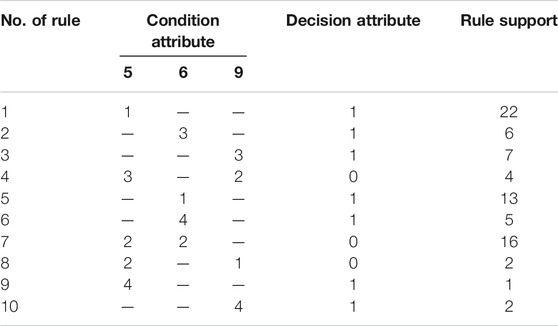
It can be seen from Table 2, that the rough neural network has advantages over the general neural networks from network structure, training time, and diagnosis results. But, the two kinds of diagnosis results are not complete in Table 2, and only relying on two reasons may cause the incompleteness through analysis. One reason may be that training samples exclude the “model” of tested samples, namely, that faulty reasoning is made about samples not tested. The other reason may be that the noise-resistance capacity of the neural network is not strong enough. More training samples are required for the former one to make a network cover sample space as much as possible (Klepaczko and Materka, 2010; Moradi and Rostami, 2015). But, in most cases, fault data information is pretty little, and normal formation is more, or in tests, it takes high risks to get fault data, so sometimes, an immune algorithm is adopted to diagnose the fault, namely, fault diagnosis by studying pretty much normal data to have immunity to abnormal data. For the latter one, it can be considered to utilize a fuzzy neural network to improve the corresponding noise-resistance capacity. The ANFIS diagnosis process is briefly introduced in the following part of this section. Rough set mining rules are utilized to obtain 10 rules, as shown in Table 3. The last item is rule support, namely, the rule repeatability rate in training samples: the higher the repeatability rate is, the more important the rule is.

TABLE 3

TABLE 3. Rule table of rough set mining.

The full connection method is adopted in general fuzzy neural network construction. For three-input and four-membership grade, 4³ = 64 nodes are needed for expression at the rule input layer. The ANFIS system in this work uses rough set mining rules to replace original rules, which reduces its connection weight, and it can be seen from the table that rules include irrelevant items. The complexity of this example with 13 connection weights and 10 nodes via this connection is greatly reduced when compared with the general network with 4⁴ = 256 connection weights and 64 nodes. Rules obtained with a rough set are used to replace the original rule represented by full connection by modifying the source code of the genfis function provided by the Matlab fuzzy logic toolbox (Aquil and Banerjee, 2008; Grzymala-Busse, 2008). Function anfis is utilized for training in the aspect of network training.

It can be seen from Table 4 that ANFIS based on a rough set further improves the accuracy of fault diagnosis. Under the same SSE conditions, the training time is shortened, which is attributed to the operation adopted in the intermediate layer. Also, certain noise-resistance capacity is possessed due to the adoption of the fuzzy method.

TABLE 4

TABLE 4. Diagnosis comparison of the rough neural network and ANFIS.

Conclusion

1) A rough neural network and self-adaptive neural-fuzzy inference system (ANFIS) are established by combining a rough set, neural network, and other methods to diagnose hydropower unit fault. The rough neural network has a simpler structure, shorter training time, and higher diagnostic accuracy than the general neural network by comparing their diagnosis results.

2) The hydropower unit fault-prediction and -diagnosis system during the hydroenergy conversion process based on rough set data overcome the problem of traditional expert-system knowledge acquisition bottleneck. In the rough set method, knowledge discovered is described directly, and it is very easy to convert the knowledge into useful rules.

3) A reduction algorithm based on rough classification rules is put forward, and good effects are achieved. Also, a hydropower unit fault-prediction and -diagnosis system based on rough set data mining is enabled. The system is capable of giving an output of high confidence, possesses strong fault-tolerance capability, and deserves a promotion.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

MW conceptualized the work, conducted formal analysis, and was responsible for the methodology; XB curated data and wrote the original draft; ZZ conducted investigation and obtained the resources; ZZ and JL were responsible for software; FT-H performed validation; and JL and FT-H reviewed and edited the manuscript.

Funding

This research was supported by the Research Center of Government Regulation and Public Policy, by Zhejiang province Funds for Distinguished Young Scientists (Grant No. LR15E090002), the National Social Science Foundation of Zhejiang Province (Grant No. 14YSXK02ZD), the Grant-in-Aid for Excellent Young Researcher of the Ministry of Education of Japan (MEXT) and the Youth Fund of Zhejiang Natural Science Foundation (Grant No. LQ18G010006)..

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.604660/full#supplementary-material.

References

Aquil, K., and Banerjee, M. (2008). Formal reasoning with rough sets in multiple-source approximation systems. Int. J. Approx. Reason 49 (2), 466–477. doi:10.1016/j.ijar.2008.04.005

CrossRef Full Text | Google Scholar

Attoui, I., and Omeiri, A. (2014). Modeling, control and fault diagnosis of an isolated wind energy conversion system with a self-excited induction generator subject to electrical faults. Energy Convers. Manag. 82, 11–26. doi:10.1016/j.enconman.2014.02.068

CrossRef Full Text | Google Scholar

Cerrada, M., Vinicio Sánchez, R., Cabrera, D., Zurita, G., and Li, C. (2015). Multi-stage feature selection by using genetic algorithms for fault diagnosis in gearboxes based on vibration signal. Sensors (Basel). 15, 23903–23926. doi:10.3390/s150923903

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, D. G., Zhang, W. X., Daniel, Y., and Tsang, E. C. C. (2006). Rough approximations on a complete completely distributive lattice with applications to generalized rough sets. Inf. Sci. 176, 1829–1848. doi:10.1016/j.ins.2005.05.009

CrossRef Full Text | Google Scholar

Clark, P. G., Grzymala-Busse, J. W., and Rzasa, W. (2014). Mining incomplete data with singleton, subset and concept probabilistic approximations. Inf. Sci. 280, 368–384. doi:10.1016/j.ins.2014.05.007

CrossRef Full Text | Google Scholar

Clark, P. G., Grzymala-Busse, J. W., and Rzasa, W. (2015). Consistency of incomplete data. Inf. Sci. 322, 197–222. doi:10.1016/j.ins.2015.06.011

CrossRef Full Text | Google Scholar

Duy, T. V. T., and Ozak, T. (2014). A decomposition method with minimum communication amount for parallelization of multi-dimensional FFTs[J]. Comput. Phys. Commun. 185 (1), 153–164. doi:10.1016/j.cpc.2013.08.028

CrossRef Full Text | Google Scholar

Foithong, S., Pinngern, O., and Attachoo, B. (2012). Feature subset selection wrapper based on mutual information and rough sets. Expert Syst. Appl. 39, 574–584. doi:10.1016/j.eswa.2011.07.048

CrossRef Full Text | Google Scholar

Gao, S., Mao, C., Wang, D., and Lu, J. (2016). Dynamic performance improvement of DFIG-based WT using NADRC current regulators. Int. J. Electr. Power Energy Syst. 82 (11), 363–372. doi:10.1016/j.ijepes.2016.03.026

CrossRef Full Text | Google Scholar

Gokmen, N., Karatepe, E., Silves tre, S., Celik, B., and Ortega, P. (2013). An efficient fault diagnosis method for PV systems based on operating voltage-window. Energy Convers. Manag. 73 (5), 350–360. doi:10.1016/j.enconman.2013.05.015

CrossRef Full Text | Google Scholar

Grbovic, M., Li, W., Xu, P., Usadi, A. K., Song, L., and Vucetic, S. (2012). Decentralized fault detection and diagnosis via sparse PCA based decomposition and Maximum Entropy decision fusion. J. Process Control. 22 (4), 738–750. doi:10.1016/j.jprocont.2012.02.003

CrossRef Full Text | Google Scholar

Grzymala-Busse, J. W. (2008). Three approaches to missing attribute values: a rough set perspective. Stud. Comput. Intell. 118, 139–152. doi:10.1007/978-3-540-78488-3_8

CrossRef Full Text | Google Scholar

Hao, L., and Xu, X. (2001). The application of rough set neural network system in fault diagnosis. Control Theory Appl. 5 (18), 681–685.

Google Scholar

Hu, Q., Yu, D., and Guo, M. (2010). Fuzzy preference based rough sets. Inf. Sci. 180, 2003–2022. doi:10.1016/j.ins.2010.01.015

CrossRef Full Text | Google Scholar

Klepaczko, A., and Materka, A. (2010). “Artifical intelligence and soft computing,” in 10th International Conference, Icaisc, Zakopane, Poland, June 13–17, 2010. (Berlin, Heidelberg: Springer Berlin Heidelberg).

Google Scholar

Liu, Y., and Packey, D. J. (2014). Combined-cycle hydropower systems - the potential of applying hydrokinetic turbines in the tailwaters of existing conventional hydropower stations. Renew. Energy. 66 (6), 228–231. doi:10.1016/j.renene.2013.12.007

CrossRef Full Text | Google Scholar

Lu, S., Wang, J., and Xue, Y. (2016a). Study on multi-fractal fault diagnosis based on EMD fusion in hydraulic engineering. Appl. Therm. Eng. 103, 798–806. doi:10.1016/j.applthermaleng.2016.04.036

CrossRef Full Text | Google Scholar

Lu, S., Zhang, X., Bao, H., and Skitmore, M. (2016b). Review of social water cycle research in a changing environment. Renew. Sust. Energy Rev. 63, 132–140. doi:10.1016/j.rser.2016.04.071

CrossRef Full Text | Google Scholar

Min, F., and Liu, Q. (2009). A hierarchical model for test-cost-sensitive decision systems. Inf. Sci. 179, 2442–2452. doi:10.1016/j.ins.2009.03.007

CrossRef Full Text | Google Scholar

Moradi, P., and Rostami, M. (2015). A graph theoretic approach for unsupervised feature selection. Eng. Appl. Artif. Intell. 44, 33–45. doi:10.1016/j.engappai.2015.05.005

CrossRef Full Text | Google Scholar

Pawlak, Z. a. (1982). Rough sets. Int. J. Comput. Inf. Sci. 11 (5), 341–356. doi:10.1007/bf01001956

CrossRef Full Text | Google Scholar

Pedrycz, W., Skowron, A., and Kreinovich, V. (2008). Handbook of granular computing. West Sussex, United Kingdom: John Wiley and Sons

Peng, F., Yu, D., and Luo, J. (2011). Sparse signal decomposition method based on multi-scale chirplet and its application to the fault diagnosis of gearboxes. Mech. Syst. Signal Process. 25 (2), 549–557. doi:10.1016/j.ymssp.2010.06.004

CrossRef Full Text | Google Scholar

Raileanu, L. E., and Stoffel, K. (2004). Theoretical comparison between the Gini index and information gain criteria. Ann. Math. Artif. Intell. 41, 77–93. doi:10.1023/b:amai.0000018580.96245.c6

CrossRef Full Text | Google Scholar

Shang, Y., Lu, S., Li, X., Hei, P., Lei, X., Gong, J., et al. (2017). Balancing development of major coal bases with available water resources in China through 2020. Appl. Energy 194, 735–750. doi:10.1016/j.apenergy.2016.07.002

CrossRef Full Text | Google Scholar

Shi, H., Li, Y., Han, Y., and Hu, Q. (2015). Cluster structure preserving unsupervised feature selection for multi-view tasks. Neurocomputing 175, 686–697. doi:10.1016/j.neucom.2015.11.001

CrossRef Full Text | Google Scholar

Sun, B., Ma, W., and Xiao, X. (2017). Three-way group decision making based on multigranulation fuzzy decision-theoretic rough set over two universes. Int. J. Approx. Reason. 81, 87–102. doi:10.1016/j.ijar.2016.11.001

CrossRef Full Text | Google Scholar

Sun, L., Zhang, X., Xu, J., and Zhang, S. (2019). An attribute reduction method using neighborhood entropy measures in neighborhood rough sets. Entropy (Basel). 21 (2), 155. doi:10.3390/e21020155

CrossRef Full Text | Google Scholar

Tabakhi, S., Moradi, P., and Akhlaghian, F. (2014). An unsupervised feature selection algorithm based on ant colony optimization. Eng. Appl. Artif. Intell. 32, 112–123. doi:10.1016/j.engappai.2014.03.007

CrossRef Full Text | Google Scholar

Tang, J., Shi, Y., Zhang, W., and Zhou, L. (2010). Nonlinear analog circuit fault diagnosis using wavelet leaders multifractal analysis method. J.Control Decis. 25 (4), 605–609.

Google Scholar

Wang, L., Yang, X., Yang, J., and Wu, C. (2012). Relationships among generalized rough sets in six coverings and pure reflexive neighborhood system. Inf. Sci. 207, 66–78. doi:10.1016/j.ins.2012.03.023

CrossRef Full Text | Google Scholar

Wang, S., Zhu, W., Zhu, Q., and Min, F. (2013). Four matroidal structures of covering and their relationships with rough sets. Int. J. Approx. Reason. 54, 1361–1372. doi:10.1016/j.ijar.2013.07.001

CrossRef Full Text | Google Scholar

Yang, C., Li, Z., Guo, X., Yu, W., Jin, J., and Zhu, L. (2019). Application of BP neural network model in risk evaluation of railway construction. Complexity 12, 1–12. doi:10.1155/2019/2946158

CrossRef Full Text | Google Scholar

Zhang, H.-R., and Min, F. (2016). Three-way recommender systems based on random forests. Knowl. Based Syst. 91, 275–286. doi:10.1016/j.knosys.2015.06.019

CrossRef Full Text | Google Scholar

Zhang, X., Miao, D., Liu, C., and Le, M. (2016). Constructive methods of rough approximation operators and multigranulation rough sets. Knowl. Based Syst. 91, 114–125. doi:10.1016/j.knosys.2015.09.036

CrossRef Full Text | Google Scholar