Activity and Stability of Oxides During Oxygen Evolution Reaction‐‐‐From Mechanistic Controversies Toward Relevant Electrocatalytic Descriptors

Plotting the roadmap of future “renewable energy highway” requires drastic technological advancement of devices like electrolyzers and fuel cells. Technological breakthrough is practically impossible without advanced fundamental understanding of interfacial energy conversion processes, including electrocatalytic water splitting. Particularly challenging is the oxygen evolution reaction which imposes high demands on the long-term activity of electrocatalysts and electrode support materials. To cross the “Rubicon” and in a deterministic manner claim that we developed principles of rational catalyst design, we need first to comprehend the determinants of electrocatalytic activity as well as character of their time evolution. How reliable are reported activity and stability trends, could we interrelate activity and stability, and how meaningful that relation really is are some of the important questions that have to be tackled in building of a more comprehensive view on critically important anodic oxygen evolution.

Introduction

Importance of Oxygen Evolution for Sustainable Energy Conversion and Storage

The need for clean and renewable energy sources is one of the most important challenges of modern societies (Lewis and Nocera, 2006). The possibility to store or convert energy from renewable sources (predominantly solar and wind) is of essential importance but conceals a scientific and technical complexity, which up-to-date has eluded definitive comprehension (Greeley and Markovic, 2012). Although considerable human and material resources have been recruited to resolve numerous issues related to renewable energy conversion and storage, the implementation of practical and scalable technologies still appears not to be economically feasible (Gasteiger and Markovic, 2009). One of the central challenges is the intermittent nature of renewable energy sources (Bockris, 2013). Namely, electricity generated by photovoltaics or wind turbines fluctuates with time in an unpredictable manner. A proper response to intermittency would be to store excess electricity in the form of chemical bonds and later, on demand, reconvert the stored chemical energy into electricity (Bockris, 1972). From a conceptual point of view, this necessitates the deployment of devices like electrolyzers and fuel cells that are capable of instantly or quickly responding to the oscillations of the power grid (Katsounaros et al., 2014). The possibility to generate liquid fuels (e.g., methanol) from CO₂, although very appealing, is still too far from practical efficiencies. A more realistic approach is to convert renewable electricity to hydrogen gas by means of electrolytic water splitting. Water electrolysis is a mature technology, which however is still not efficient enough to be recognized as a state-of-the-art solution for the storage of renewable electricity. In the past, alkaline water electrolysis was favored due to the possibility to use cheap electrode and electrolyte materials in such environments. Nowadays, acidic polymer electrolyte membrane (PEM) electolyzers are more attractive as they allow much higher current densities despite the necessity to use expensive and rare noble metals as components of the electrode materials. The two main reactions occurring in an acidic (pH = 0) electrolyzers are:

$2{\text{H}}^{+}+2{\text{e}}^{-} \rightleftharpoons {\text{H}}_2\text{E}°=0.00\text{ V vs}.\text{ SHE,}(1)$

$2{\text{H}}_2\text{O} \rightleftharpoons {\text{O}}_2+ 4{\text{H}}^{+}+4e^{-}\text{E}°=1.23\text{ V vs}.\text{ SHE}\text{.}(2)$

Similar equations can be written for alkaline (pH = 14) electrolyzers

$2{\text{H}}_2\text{O}+2{\text{e}}^{-} \rightleftharpoons {\text{H}}_2+2{\text{OH}}^{-}{\text{E}}^{\circ }=-0.800\text{ V vs}.\text{ SHE,}(3)$

$4{\text{OH}}^{-} \rightleftharpoons {\text{O}}_2+2{\text{H}}_2\text{O}+4e^{-}\text{E}°=0.403\text{ V vs}.\text{ SHE}\text{.}(4)$

Potentials are expressed on the SHE (standard hydrogen electrode) scale to clearly indicate the impact of pH value on the absolute potential scale (for an explanatory note of the absolute potential scale (Recommendations, 1986)). From the shown reactions (1–4), it is evident from the thermodynamic view point that it would be best to conduct hydrogen evolution (HER) in acidic media and oxygen evolution reaction (OER) in alkaline media in a system with two electrolytes and with a theoretical voltage of 0.4 V (Zeradjanin et al., 2014b). This system requires a bipolar membrane (Simons and Khanarian, 1978), and unavoidably, a catalyst that will accelerate water ionization (Oener et al., 2020). However, this kind of acido-alkaline system still suffers major instabilities (Zeradjanin et al., 2014b; Oener et al., 2020).

The HER, despite being very complex, is a relatively facile two-electron process involving only one intermediate (Zeradjanin et al., 2016). However, catalysis of the oxygen evolution reaction (OER) that requires the exchange of four electrons and four protons and the formation of at least two (probably three) intermediates (Dau et al., 2010) is even more challenging. Complexity and low intrinsic rate of OER as electrocatalytic process is actually at the very root of why widespread deployment of water electrolysis is still postponed. Therefore, in-depth understanding of electrocatalytic interfaces at relevant dynamic conditions, including the formation and mutual interaction of the intermediates, is one of the essential tasks that have to be fulfilled before we can come up with rational approaches of designing materials with superior electrocatalytic properties.

Reaction Pathway(s)

If we take into consideration the intermediates that participate in the OER, there are two distinct reaction pathways. Both of them are based on the assumption that under conditions of anodic polarization, water behaves as a Brönsted acid. The simplest pathway assumes partial oxidation of water in the first step, which comprises of electron transfer from physiosorbed water molecule to the electrode surface and deprotonation of water resulting in OH_ad formation (React. 5). Further, electron transfer and deprotonation of OH_ad in the second step and formation of O_ad (React. 6) as a prerequisite for chemical recombination of O_ad in the third step and formation of O₂ molecule (React. 7).

${\text{H}}_2\text{O} \rightleftarrows {\text{HO}}_{\text{ad}}+ {\text{H}}^{+}+{\text{e}}^{-},(5)$

${\text{HO}}_{\text{ad}} \rightleftarrows {\text{O}}_{\text{ad}}+ {\text{H}}^{+}+{\text{e}}^{-},(6)$

$2{\text{O}}_{\text{ad }}\rightleftarrows {\text{O}}_2.(7)$

This means that steps Eq. 5 and Eq.6 should happen at the same site, but it is also necessary to have the two sites next to each other to enable step Eq.7. Considering that in the lattice of the most active commercial electrocatalysts used for anodic oxidations (i.e., rutile RuO₂), the Ru–Ru distance in the tetragonal plane is 3.5 Å (McKeown et al., 1999) and that the distance between two oxygen atoms in the oxygen molecule is approximately 1.2 Å, it is necessary that the Ru–O bond involving oxygen adsorbed at coordinatively unsaturated site bends toward a neighboring Ru–O in the tetragonal plane. Both mentioned Ru–O bonds have a length of around 1.95 Å and mutual angle of 90°, implying that the Ru–O bond involving oxygen adsorbed at coordinatively unsaturated site would need to bend for approximately 1.5 Å. Energetically, this should probably not be favored due to existence of nonbonding electron pairs of oxygen as well as due to parallel dipoles of Ru–O which should repel each other. Worth to mention is that under in operando conditions where a wide range of potentials is applied including potentials sufficient for OER to commence, stretching of metal–oxygen bonds is almost negligible, fluctuating around 0.05 Å (Nong et al., 2018). DFT-based analysis also indicates skepticism about participance of recombination step Eq.7 at the RuO₂ surface; however, it cannot be excluded (Ma et al., 2018).

Besides the recombination pathway, a very intuitive pathway is the one usually considered in most computational models. Although discussed initially in the late 1960s (Damjanovic et al., 1966), it lends its popularity today to DFT studies (Rossmeisl et al., 2005, 2007). According to this pathway, the first two steps are like in the case of the recombination step (React. 5 and React. 6). In the third step, O_ad reacts with water to form HOO_ad together with transfer of a proton and electron (React. 8). Finally, in the fourth step, electron transfer from HOO_ad to the electrode surface together with release of a proton into the electrolyte is coupled with oxygen formation (React. 9).

${\text{O}}_{\text{ad}}+{\text{ H}}_2\text{O} \rightleftarrows {\text{HOO}}_{\text{ad}}+ {\text{H}}^{+}+{\text{e}}^{-},(8)$

${\text{HOO}}_{\text{ad}}\mathrm{\rightleftarrows }{\text{O}}_2\mathrm{+}{\text{H}}^{\mathrm{+}}\mathrm{+}{\mathrm{e}}^{\mathrm{-}}\mathrm{.}(9)$

In comparison to the mechanism in acidic electrolytes, a distinct feature of the reaction pathway in alkaline electrolytes is that it starts with an elementary step in which only one electron is exchanged (React. 10), in other words, there is no deprotonation. In this step, a hydroxyl ion from the electrolyte is getting adsorbed on the metal-center forming HO_ad with simultaneous transfer of an electron to the electrode. In the second step (React. 11), OH⁻ from the electrolyte deprotonates HO_ad forming a water molecule and O_ad while simultaneously transferring an electron to the electrode. The final step is recombination as proposed for the acidic media (React. 7)

${\text{OH}}^{-} \rightleftharpoons {\text{OH}}_{\text{ad}}+ e^{-},(10)$

${\text{HO}}_{\text{ad}} +{\text{ OH}}^{-} \rightleftarrows {\text{O}}_{\text{ad}}+ {\text{H}}_2\text{O}+{\text{e}}^{-}.(11)$

If we make the analogy between water electrolysis and gas-phase (de)hydrogenation, we can observe that in the case of OER, water is getting dehydrogenated. The released hydrogen atoms, electrons in the outer circuit and the solvated protons in the electrolyte, are transferred to the cathode to participate in hydrogenation. Concerted proton/electron transfer is possible; however, it is usually considered that electron transfer is much more facile in comparison to proton transfer. This leaves the open possibility, not only for a reaction pathway or mechanism with decoupled proton/electron transfer, especially at higher polarizations (overpotentials), but also for the existence of destabilized intermediates that are not identified by the usual schemes of reaction pathways. To further broaden this knowledge, the reader is directed to interesting discussions on other mechanistic pathways, including the bifunctional and binuclear mechanisms (Busch, 2018).

Origins of Electrocatalytic Performance and Existing Activity Trends

Due to the nature of the reaction, that is, decomposition of the solvent itself including strong acidification of the interfacial region during OER at high anodic potentials, every element from the periodic table used as electrocatalyst will be oxidized with time. Therefore, it is well accepted that metal oxides are the dominant class of chemical compounds that could survive the corrosive conditions of OER on a long term. From the reaction pathways shown above, it is straightforward that bond strengths of intermediates at the oxide surfaces are one of the essential parameters that determine kinetics of OER. Activity trends for OER were already observed in the 50s (Rüetschi and Delahay, 1955). In this important work, the M–OH bond strength was introduced as the first activity descriptor for OER. A linear relationship between the overpotential for OER in alkaline electrolyte and the M–OH bond strength was observed from which the computed M–OH bond strength was directly proportional to drop in the overpotential for OER, leading to the following activity trend for oxidized metals. Co > Fe > Cu > Ni > Pb > Ag > Cd > Pd > Pt > Au (Rüetschi and Delahay, 1955). From a semiquantitative point of view, the relationship in Figure 1A suggests that a change in adsorption energy of approximately 100 kJ/mol could change the overpotential by almost 1V, thus revealing great potential in enhancing kinetics of OER by tuning the M–OH adsorption energy. In this work, some important oxides are missing (those having less than seven d-electrons in the metallic state); however, it represents an important initial contribution toward understanding electrocatalysis of the OER. Later in the 1970s, more systematic studies of the OER on oxidized metals in acidic media were made, where the activity trend followed the order: Ir ∼ Ru > Pd > Rh > Pt > Au > Nb (Miles, 1976), as well as analysis of thermally prepared oxides in alkaline media with the activity trend following the order: Ru > Ir ∼ Pt ∼ Rh ∼ Pd ∼ Ni ∼ Os >> Co >> Fe (Miles, 1978). Evidently, the OER activity trends on these two sets of samples were different, although it was not clear whether that was due to the chemistry of the oxides or pH of the electrolyte.

FIGURE 1

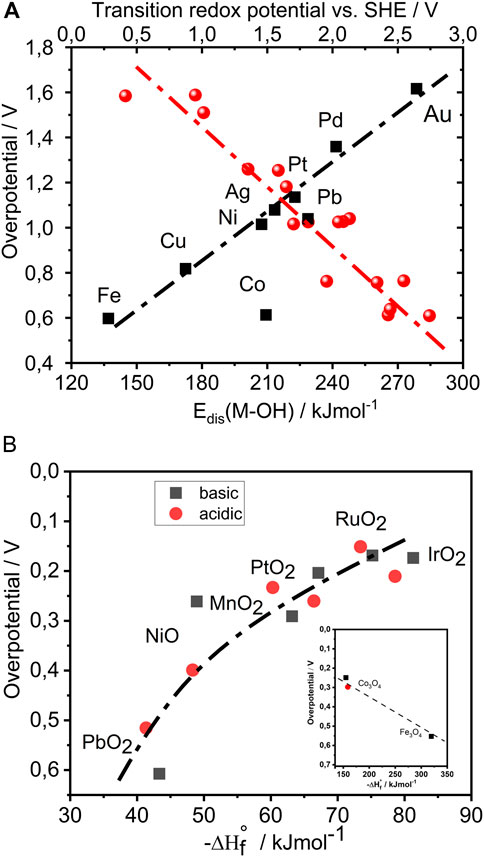
FIGURE 1. A) Measured OER overpotential for 9 metals in 1M KOH, at 25°C and 1 A/cm⁻², as a function of computed heat of M-OH formation (red circles). Replotted using data from Rüetschi and Delahay (1955). Measured overpotential for OER as a function of characteristic redox transitions from lower to higher oxidation state (black rectangular), in 5M KOH at temperature of 25°C and 1 A/cm⁻². Replotted using data from Rasiyah (1984). In the original reference, the computed M-OH formation heats were estimated using two or sometimes three methods. This is the reason why in the plot marked with red there is overall more than 9 points. (B) Illustration of activity trends for OER in acidic and alkaline media where overpotential is a function of bulk enthalpy of transition from lower to higher oxidation state of oxide. Replotted using data from (Trasatti, 1984). In the inset are shown two spinels removed from the original “volcano” plot.

In other words, either adsorption energies of intermediates like HO_ad strongly depend on pH or besides adsorption energy of intermediates we have additional governing factors which influence the kinetics of OER. In that context, important to notice is that anodic oxidation of water and/or adsorbed oxygen species originating from water requires previous transition of metal cation from lower to higher oxidation state. Higher oxidation state of cation will be more susceptible for the electron from adsorbed oxygen species. After the electron is transferred from the adsorbed oxygen species to the metal cation, the cation will get reduced and return to the initial oxidation state. In this way, a redox cycle is established for each elementary step. This requires an overlap of energy levels of the d-orbitals of the metal cation and energy levels of the p-orbitals of adsorbed oxygen species at the potential of redox transition. Redox transitions as descriptor were investigated in the 1980s where the dependence of reaction rate on redox transition is shown in Figure 1A (Rasiyah, 1984). The dependence predicts that for a drop in redox potential of 500 mV, the overpotential should drop by 250 mV. Considering the linear relation from Figure 1A, it seems formally that lower redox transitions relate to stronger OH adsorption; however, all the catalysts shown in these datasets were having seven or more d-electrons, which make the data incomplete. The question is what are in fact the most relevant redox transitions for the OER activity? More precisely, are the relevant redox transitions only those which overlap with OER onset or relevant or also those at much more negative potentials?

Trasatti in the 1980s systematically investigated thermally prepared oxides under acidic and alkaline conditions (Trasatti, 1984). Although the pH effect on kinetics could be clearly noticed, the general activity trends in acidic and alkaline media, interestingly, were very similar. Experiments indicate that RuO₂ is the most active oxide for OER. However, due to the low stability of RuO₂, the material of choice was typically IrO₂, which is less active than RuO₂, but very stable under the harsh oxidizing conditions of OER. It is very important to notice that RuO₂ and IrO₂ are among the very few electrocatalytically active oxides that exhibit metallic-type conductivity. The reason for this is the relatively small electronegativity difference between oxygen and metal (less than 1.3 units) that results in the absence of a band gap (Di Quarto et al., 1997). Illustration of activity trends for OER, based on experimental data gathered by Trasatti, is shown in the form of plot in Figure 1B. Overpotential is given as a function of enthalpy of transition from lower to higher oxidation state of the metal oxide, a bulk parameter related to difference in surface adsorption energy of two intermediates as well as related to characteristic redox transitions of oxides. Like in thermal chemistry, the high reaction rate was attributed to optimal bond strengths of one or more intermediates. Optimal bond strength is expressed by a qualitative rule “neither too strong nor too weak,” today’s widely accepted paradigm of catalysis known as Sabatier principle. If the binding of the intermediates is too strong, then the recombination of the intermediates should be inhibited. At the same time, if binding of the intermediate is too weak, the intermediate will desorb before the product is formed. Despite the importance of the Sabatier principle being recognized in electrocatalysis early on, old works (Rüetschi and Delahay, 1955; Miles, 1976) did not explain activity trends using the concept of the “volcano” plot. On the contrary, Trasatti’s model was taken as relevant, probably due to the fact that the descriptor he introduced was a bridge between adsorption energies and redox transitions, two essential parameters influencing OER kinetics. The “volcano” plot shown in the original reference (Trasatti, 1984) was perceived for decades as confirmation that the Sabatier principle also holds in OER electrocatalysis. A similar plot was obtained by computational chemists, several decades later. Namely, works of Rossmeisl and Norskov are showing similar trends with slight differences at the top of the “volcano” (Rossmeisl et al., 2007). Computationally obtained trends predicted Co₃O₄ to be the most active catalyst for OER, which does not correspond to the well-established experimental activity trends. Later, computational chemists revised their conclusions, including the so-called Hubbard correction into the analysis, and taking into consideration electrostatic repulsions coupled to the adsorption process, resulting in a consistency with the experimental trends. Also, besides individual adsorption energies, they used the difference in adsorption energies of two intermediates (ΔG_ad(O)–ΔG_ad(OH)) as a descriptor ((Man et al., 2011). In comparison to the individual adsorption energy, the differential descriptor was analogous to the previously mentioned bulk enthalpy of transition from lower to higher oxidation state of oxide. However, the data points in Figure 1B were obtained from the OER performances of oxides with two different crystal lattices, namely, the rutile-type and the spinel-type (inset). In particular, the weakly binding branch of Trasatti’s “volcano” plot contains rutile oxides, while the strongly adsorbing branch is based on spinel oxides (Co₃O₄ and Fe₃O₄). Therefore, the resulting dependence for the rutiles should be pseudo-linear where increase in the binding strength of the intermediates should be coupled with a drop in the overpotential for OER. In a semiquantitative manner, it seems that for a change in the enthalpy of transition from lower to higher oxidation state of about 50 kJ/mol, the overpotential would change by 500 mV, which is interestingly similar to what was predicted earlier (Rüetschi and Delahay, 1955). Besides the rutile and spinel oxides, perovskites have attracted the interests of researchers; however, their stability in acidic electrolytes is extremely low (Bockris, 1984). As a matter of fact, only rutile structures exhibit high practical stability under the harsh oxidizing conditions of water splitting in acidic media (Martelli et al., 1994). Worth also mentioning is that in the discussed literature (period 1950s–1980s), activity trends were usually analyzed at technically relevant conditions, meaning current density of 1 A cm⁻², usually concentrated electrolytes and temperatures of 80°C or higher. This is a probable reason why trends in older literature could deviate from the modern literature where experiments are done at 25°C and current densities of few tens of mA cm⁻² (McCrory et al., 2013; Frydendal et al., 2014). The free energy relations shown in Figure 1 are more qualitative than quantitative in nature; however, validity of the trends was widely accepted until today. At the same time, the shown trends were mostly explanatory in nature. The predictive power based on existing understanding of electrocatalysis was shown to be limited. In other words, there is no electrocatalyst that could really overcome the activity of RuO₂, and there is no known guiding principle of design thus far that could drive us in that direction.

Modern Catalytic Descriptors and Impact of Computational Chemistry

A catalytic descriptor is a relatively easily tunable property of a catalytic material or property of electrode/electrolyte interface that can be brought into direct relation with the reaction rate. A descriptor should have an explanatory role and predictive role. In other words, it has to shed light on activation processes and give a hint how to accelerate the reaction rate. In the last 10–15 years, intensive efforts were undertaken to discover new catalytic descriptors that could shed additional light on the origins of the electrocatalytic activity of OER, further contribute to building the theory of electrocatalysis as well as to advance rational catalyst design. Despite electrochemistry being a primarily experimental science, it is interesting that the most influential and authoritative descriptors and activity trends came from works of computational chemists (Nørskov et al., 2004; Rossmeisl et al., 2005). The school of Norskov and Rossmeisl extended the Anderson–Newns model for metal surfaces from 1960s (Newns, 1969) and computed adsorption energies of intermediates using the density functional theory (DFT). In a qualitative manner, parallel to metal surfaces can be deduced for oxides, where adsorbate bond strengths vary linearly with the relative position of the metal d-band center with respect to the Fermi level of the metal. In the case of oxides, what is relevant is the filling of bonding and antibonding orbitals created by hybridization of d-orbitals of the metal and O_2p orbitals of oxygen species in the oxide. After the interaction, d-orbitals are split into t_2g and e_g orbitals, whose filling determines the bond strengths of intermediates. For each of the reactions that describe the elementary steps, the corresponding change in free energy can be derived. The most endergonic elementary step (the so-called potential-determining step) defines what intermediate is the most difficult to obtain. Therefore, the introduced computational activity descriptor known as thermodynamic overpotential corresponds to the energy required to overcome the potential-determining step (PDS) per unit charge transfer. Importantly, Rossmeisl and Norskov showed that adsorption energies of typical OER intermediates are linearly related (Figure 2), constituting the so-called scaling relations (Man et al., 2011). This means that if we alter the bond strength of one intermediate, we alter the bond strength of the other intermediates, for example, by weakening HO_ad, we are also weakening HOO_ad and strengthening O_ad. In other words, for a reaction pathway based on reactions Eqs 5, 6, 8, and 9 and the corresponding changes in free energy of the elementary step, it is noticed universally that sum of change in free energies of Eq. 6 and Eq. 8 is always constant. Between HO_ad and HOO_ad, there is a constant energy difference of about 3 eV. Besides the theoretical overpotential originating from the potential-determining step, a more balanced thermodynamic descriptor is the electrochemical-step symmetry index (ESSI) (Govindarajan et al., 2018). Compared to theoretical overpotential, which relies on a single free-energy change, the ESSI takes all endergonic steps into account and practically represents the average/mean value of deviation from the reversible potential. Considering thermodynamic descriptors, today it seems that a rational strategy should be to first optimize catalyst(s) in the framework of scaling relations, then proceed toward catalyst optimization based on breaking of scaling relations. Scaling relations were considered a decisive limitation for rational catalyst design because it is not easy to decouple intermediates and tune their bond strengths individually. It was recently however shown that scaling relations can be overcome on more complex surfaces (Halck et al., 2014); nonetheless, it has been established that breaking the scaling relations is a necessary yet insufficient condition to attain enhanced electrocatalytic activity (Govindarajan et al., 2018).

FIGURE 2

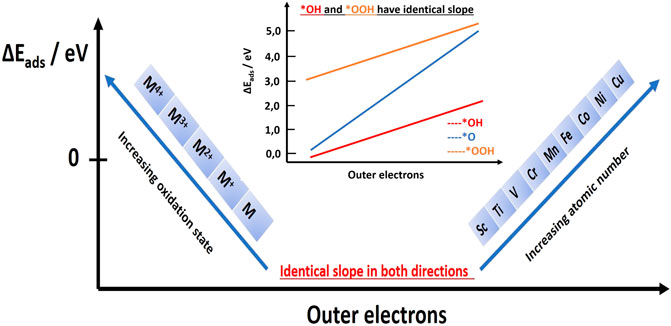
FIGURE 2. Illustration of how the adsorption energies change with the number of outer electrons for different metals and for various oxidation states of one metal. Replotted using information from Calle-Vallejo et al. (2013). In the inset is the illustration of scaling relations indicating that the change in the adsorption energy of one of the OER intermediates, due to change in electronic configuration (number of outer electrons), alters adsorption energies of the other two OER intermediates in the same manner. Importantly, adsorption energies of *OH and *OOH are also quantitatively changing in the same manner. Replotted using data from Calle-Vallejo et al. (2011).

The work of Shao-Horn et al. where filling of e_g orbitals was proposed as an activity descriptor for OER attracted significant attention, where the e_g orbital filling practically dictates the bond strength of intermediates (Suntivich et al., 2011). These authors found that for perovskites, the optimal e_g filling correlates with the potential at a predefined current density in the form of a “volcano.” This correlation practically means that the OER activity on perovskites relates to the optimal adsorption energy, confirming one more time the Sabatier principle as a universal rule in electrocatalysis. According to the authors, the proposed descriptor is fundamentally different from the number of 3d electrons (both e_g and t_2g electrons) proposed in the 1980s (Bockris and Otagawa, 1983), to which we partially agree. However, we could not find such a significant point of distinction from the concept published in 1970s (Matsumoto and Sato, 1979). Namely, in the work of Shao-Horn’s group, filling of the surface transition metal antibonding states of the e_g orbital is a more appropriate descriptor for catalysis because through the σ-bonding, the e_g orbital has a stronger overlap with the oxygen-related adsorbate than does the p-bonding with the t_2g orbital and can thus more directly promote electron transfer between surface cations and adsorbed reaction intermediates. Matsunoto’s work suggests that the degree of the overlap between the e_g orbital of the cation and the p_σ orbital of the oxygen atom in OH^– ion influences σ* antibonding band formation and consequently its electron filling, which is very similar to the concept described by the group of Shao-Horn.

The problem with the result of the group of Shao-Horn is that the compared oxides have significantly different chemistry despite of the perovskite-type crystal structure. A fair comparison should be made with oxides where only one cation is changing the number of valence electrons like in some previous experimental works on perovskites (Bockris and Otagawa, 1983; Bockris, 1984) or some previous computational analysis (Man et al., 2011). At the same time, from the results of Shao-Horn’s group, LaNiO₃, LaMnO_3, and LaCoO₃ have the same e_g orbital occupancy and different activity, which shows that the proposed descriptor conceals some drawback(s). The concept proposed by the group of Shao-Horn is a continuation of earlier work of Arikado dealing with electrocatalysis of a chlorine evolution reaction in the 1970s (Arikado et al., 1978). The chlorine evolution reaction, that is, a two-electron reaction, interestingly, exhibits identical trends on a significant number of oxides investigated for OER, that is, a four-electron reaction (Trasatti, 1984). At the same time, interpretation of the origins of electrocatalytic activity in the work of Arikado is different in some aspects. Namely, oxides with empty e_g and partially filled t_2g orbitals (e.g., RuO₂) have lower exchange current and higher Tafel slope than oxides with half or just filled t_2g and partially filled e_g orbitals (e.g., LaNiO₃). Importantly, the latter ones exhibit superior behavior only very close to equilibrium, while far away from equilibrium their Tafel slopes increase. Meanwhile, the former ones exhibit a constant Tafel slope in a larger range of potential. This highlights a general rule that activity trends are relative phenomena, dependent on overpotential. Very recently, a purely thermodynamic approach to computational electrochemistry was upgraded by using the applied overpotential of a reaction originating in rate-determining step, as indicator of free energy of intermediate formation in the potential-determining step (Exner, 2020a). To the best of our knowledge, this is the first approach that introduces kinetic effects into a framework of computational free-energy relations.

A recent summary on catalytic descriptors showed that the surface d-band center, work function, excess Bader charge on the adsorbates, integrated crystal orbital overlap population, and crystal orbital Hamilton populations are linear functions of the number of outer electrons (Su et al., 2016). Some of these quantities require complex computation; however, it is not trivial to notice that the number of outer electrons, that is, here an essential quantity, can be read directly from the periodic table (even if we do not know the exact electronic configuration of the valence level). Important to mention is that the number of outer electrons can be linearly related to the adsorption energies of characteristic OER intermediates on oxide surfaces as well as to various oxidation states of oxide, as shown in Figure 2 (Calle-Vallejo et al., 2013). Interestingly, the slope of graph of the number of outer electrons vs. adsorption energy is identical to the slope of graph of number of outer electrons vs. oxidation state of oxide but with opposite sign. This means that if we compare oxides whose cations have different atomic numbers, then higher the number of outer electrons, the more endergonic the adsorption process will be. At the same time, if we compare oxides whose cation has identical atomic number (i.e., originating from the same metal), then higher the oxidation state of the metal cation in the oxide is, the more endergonic the adsorption process will be. It seems that if the number of outer electrons in the metal oxide increases by one, the adsorption energy will become approximately 50 kJ/mol more endergonic, and the oxidation number of the corresponding metal in the oxide will be approximately one integer more negative. Important to note is the following: if we apply a sufficiently high anodic overpotential so that the oxidation state of the cation becomes more positive, then according to Figure 2, we should weaken the binding of the adsorbed oxygen species. This can be the case only if we remove an electron from the bonding orbital. This is a bit contradictory to the assumption that only filling of antibonding orbitals is relevant for understanding the activity of oxides.

The fact is that all the aforementioned descriptors broaden our view on electrocatalysis; however, they remain inside the conventional paradigm, that is, a conquest for optimal adsorption energies. All proposed descriptors correlated to outer electrons have a direct link to the adsorption energies of intermediates, routinely resulting in the “volcano”-type dependence, where the optimal value of the descriptor corresponds to the maximal reaction rate given at the top of “volcano.” What remains as a relevant question is how much further adsorption energies can be tuned to correspond to the very top of the “volcano” plot (or even above it) and whether there is any other way to enhance the intrinsic activity except by tuning adsorption energies of intermediates. It was predicted for ORR (oxygen reduction reaction) that the surface functional groups that could reversibly exchange protons with the electrolyte at redox potentials similar to the potential at which ORR proceeds could be an interesting solution to promote reactions (Busch et al., 2016). Similar reasoning could be adopted for OER. The question is how stable the functional groups under conditions of OER can be and how to control with synthesis the redox potential of the introduced functional group. Further, it is possible to introduce adsorbates (e.g., boron) which alter not only the slope of scaling relations but also exhibits negative scaling (Su et al., 2016), meaning that for the example of boron adsorbed on d-metals, the metal-boron bond strength drops as the number of outer electrons drops, completely opposite to oxygen-containing adsorbates. It is therefore evident that high covalency of the metal-adsorbate bond is important for breaking of scaling relations. Unfortunately, high covalency of metal-adsorbate bonds with the tendency to break scaling relations can be easily counterbalanced with the effect of solvation, especially if the solvent has a high dielectric constant (Calle-Vallejo et al., 2017). Further, a reasonable strategy to modify the OER activity of catalysts and avoid scaling relations is doping with cations that can activate proton donor–acceptor functionality on the conventionally inactive bridge surface sites (Halck et al., 2014). Probably the most popular approach today to tune catalyst activity is to introduce strain in the oxide lattice using a component(s) that can be easily leached out (Yao et al., 2019) or by interaction with the support (Zhou et al., 2019). Importantly, lattice strain has as a consequence a geometric effect in the form of lattice distortion and chemical effect in the form of change in oxygen nonstoichiometry (Wang et al., 2019). Therefore, for lattice distortions, an important descriptor could be the distance between metal centers in the lattice (Pittkowski et al., 2018), while oxygen nonstoichiometry can be analyzed in light of the relative position of the O_2p band center with respect to the Fermi level, an important descriptor that will be discussed in the section on electrocatalyst stability. Having all this in mind, it is important to distinguish catalyst optimization through the concept of tuning of adsorption energies (with the goal of approaching the top of the volcano) in the framework of scaling relations from scaling-free catalyst optimization (Govindarajan et al., 2019). Besides adsorption energies of intermediates and characteristic redox transitions, other descriptors (band structure, crystal/ligand field stabilization energy, effective Bohr magneton, etc…) relevant for electron transfer, surface restructuring, formation of radicals as well as magnetic properties of electrocatalytic materials were summarized in the past, offering much broader interpretation of activity (Matsumoto and Sato, 1986), than the descriptors introduced by contemporary leading groups. It seems that of essential importance on that road to designing new complex oxides is to dissect the rate law for OER by attributing, if possible, to every term in the equation for the rate law suitable properties of electrocatalyst materials or property of the property of electrocatalytic interface. In other words, parameters that define reaction rate, besides material descriptors, should be correlated with the structure and properties of the interface that are a result of the interaction of the electrocatalyst with the electrolyte, known as interfacial descriptors. Example of the interfacial descriptor is change of the work function of the metal upon the adsorption of the gas molecule through the water layer (Zeradjanin et al., 2017).

Some Controversial Issues Considering Activity Trends

DFT based OER activity trends on oxides (Man et al., 2011) seem to be very similar to the experimental trends (Bockris, 1984). This should be a straightforward example how theory and experiment complement each other. However, when comparing the abovementioned references, it is worth to observe the following: 1) the computational model analyzed well-defined single-crystal surfaces, while the experimental study was based on analysis of defect-rich polycrystalline materials where atom surroundings including coordination number vary in an unpredictable manner; 2) the descriptor used in the computational model was difference in surface adsorption energy of two intermediates, while the descriptor in the case of the experimental trends was bulk number of d-electrons easily readable from the periodic table; and 3) the values obtained by the computational model are estimated at equilibrium conditions, while results of the experimental model are measured at a specific current density. Having in mind that various crystal facets could exhibit different Tafel slopes (e.g., Tafel slope of poly-RuO₂ is lower than for any single-crystal constituent), and that the Tafel slope can change with overpotential at a point that it is difficult to predict, and that the surface is generally expected to have different features from those of the bulk, it is in fact very strange that the trends obtained on single crystal surfaces, at equilibrium conditions, using a surface catalytic descriptor, are almost identical to the trends obtained on polycrystalline materials, at far from equilibrium conditions using a bulk descriptor. This could be explained eventually by some unknown link between bulk and surface properties. An attempt to conceptualize that point of view was establishment of the intimate relationship between bulk thermochemistry and surface adsorption through outer electrons (Calle-Vallejo et al., 2015). However, oxides with different degrees of structural disorder caused by thermal treatment were shown to exhibit very similar catalytic properties, which indicated a negligible effect of the bulk phase on OER electrocatalysis (Gunkel et al., 2017). Perhaps, such similarity between experimental trends and computational trends for drastically different surfaces and applied conditions will be explained in the future by more realistic computational frameworks, like those reported recently that include experimental kinetic effects into a computational model (Exner, 2019; 2020b).

Stability Trends

Systematic studies on stability trends were initiated relatively recently. For example, in 2012 the Max-Planck-Institut für Eisenforschung (MPIE) reported an automated experimental setup dedicated for stability studies comprising a miniaturized electrochemical scanning flow cell coupled to a highly sensitive inductively coupled plasma mass spectrometer (SFC-ICPMS) (Topalov et al., 2012a). This setup allowed the recording of time-resolved potential-dependent catalyst dissolution profiles. For all analyzed metal oxides, dissolution was observed during both anodic and cathodic polarization. Despite the latter dominating, the former is more typical for conditions of OER. At the same time, dissolution can be continuous or transient, where transient dissolution is usually more intense for a short period of time, despite originating from the surface that has the tendency to passivate (Topalov et al., 2014). Some insights into stability/corrosion of electrocatalytic materials could be obtained from thermodynamic data given in Pourbaix diagrams; however, SFC-ICPMS allows measuring the dissolution rates at conditions far from equilibrium. Experimental results on catalyst stability from different groups are sometimes controversial. Importantly, the fundamental question about the existence and nature of a correlation between activity and stability remains open (Cherevko et al., 2014c). The first systematic quantitative activity–stability dataset appeared in 2014 (Danilovic et al., 2014), as shown in Figure 3A. In this work, it was found that the most active oxidized metals (Au ≪ Pt < Ir < Ru ≪ Os) are, in fact, the least stable (Au ≫ Pt > Ir > Ru ≫ Os). The relationship between activity and stability, according to Danilovic, is governed by the nature of metal cations as well as by the density of surface defects. The potential transformation of a stable metal cation with a valence state of n = +4 was assumed to end up with unstable metal cation with n > +4. The result of Danilovic was supported by thermodynamic analysis (Binninger et al., 2015), where OER universally proceeds partially via lattice oxygen. Importantly, kinetic reasoning is not included in the model of Binninger et al. Also, the appearance of metal cations in a higher oxidation state does not necessarily mean that these higher-valent cations are the active species for OER. Important to note is that for different groups that used ICP-MS, the electrochemical cells (including the mass transport conditions) were different. This could explain some differences in the reported data; however, the trends should generally be the same, which was not the case. A drastic difference between the group of Markovic and the group of Mayrhofer was the behavior of gold during water oxidation. Whereas for Markovic’s group, the gold anode was shown to be the most stable precursor for OER in perchloric acid (Danilovic et al., 2014); the group of Mayrhofer (Cherevko et al., 2014c) found that gold was among the most unstable precursors for OER in sulfuric acid. Although, the difference could be attributed to anions, the impact of anions was not further investigated in detail. The group of Mayrhofer could not find the inverse relation between activity (Ru > Ir > Rh > Pd > Pt > Au) and stability (Ru < Au < Ir < Rh < Pt < Pd) at stationary conditions; however, a clear correlation between technically relevant anodic dissolution rate and the Tafel slope in OER was found, as shown in Figure 3B. The trends differ at different current densities as stationary and nonstationary conditions also exhibit differences (Cherevko et al., 2014c), while trends at acidic pH in comparison to alkaline pH are surprisingly almost identical (Schalenbach et al., 2018).

FIGURE 3

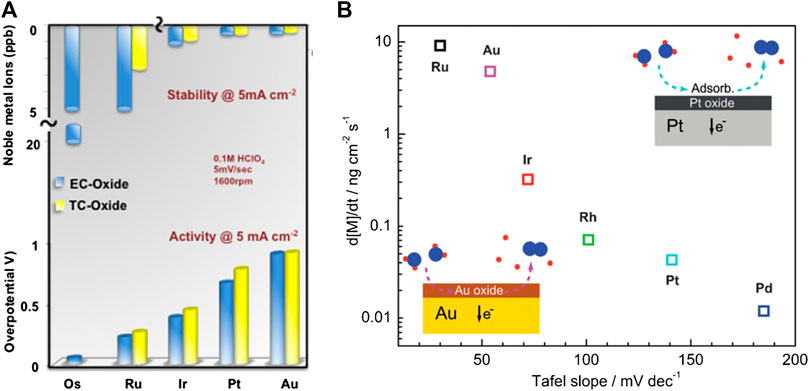
FIGURE 3. (A) Activity–stability relation for five oxidized noble metals and four thermally prepared oxides in 0.1 M HClO₄ used as electrolyte, at 1600 rotations per minute (rpm), at scan rate of 5 mV/sec at galvanostatic regime of 5 mA cm⁻². Overpotential is given in relation to the amount of dissolved metal ions. Reprinted from Ref. Danilovic et al. (2014), with permission from the American Chemical Society. (B) Dissolution rate as a function of the Tafel slope for OER, for six oxidized noble metals, in 0.1 M H₂SO₄ measured at galvanostatic regime of 5 mA cm⁻². Reprinted from Ref. Cherevko et al. (2014c), with permission from Wiley.

The Tafel slope is a kinetic parameter that indicates reaction pathway and sensitivity of the reaction barrier with respect to electrode potential. The lower the Tafel slope, the higher is the dissolution rate, and presumably, higher participation of lattice oxygen in the OER pathway. The relation given in Figure 3B is essentially different from the relation that could be derived from the Stern–Geary equation used in corrosion research. In the Stern–Geary equation, the corrosion current is increasing as the Tafel slope of the dissolution process increases, while in Figure 3B, corrosion current (rate of side anodic reaction) is dropping as the Tafel slope of OER (indicator of barrier of main anodic reaction) is increasing. It is important to stress that anodic dissolution during electrolytic OER cannot be observed as a classical corrosion process. Classical corrosion is a spontaneous process where chemical energy is transformed into electric energy, in which a case due to proximity of local anode and local cathode, electricity cannot be utilized through the external circuit. At a corroding surface, there is simultaneous coexistence of an anode where corrosion proceeds and cathode where oxygen reduction or hydrogen evolution (or some other reductive process) proceeds with electrons from the anode. As dissolution current and OER current cannot be combined into a direct relationship, there is hope for designing electrocatalytically highly active materials which could simultaneously survive for a long time in harsh environments. From existing literature data, there is no clear reason why activity and stability should be inversely related, as assumed by many. However, the relation between stability and Tafel slope for OER shown in Figure 3B seems more acceptable. A link between the dissolution rate and the Tafel slope for OER is the reaction pathway in which oxygen-containing species from the water and oxygen species from the crystal lattice compete for participance in formation of oxygen molecule. It was expected that oxides with high Tafel slope (Pt and Pd) will have low dissolution rate and negligible participance of lattice oxygen in generation of the oxygen molecule. The opposite to these should be oxides with low Tafel slope (Ru and Au) having high dissolution rate and significant participance of lattice oxygen in the generation of the oxygen molecule. The third group (Rh and Ir) is the case where the intermediate Tafel slope corresponds to intermediate dissolution rates and oxygen generated partially from the lattice. Taking into consideration Figure 3B and the relation between electronic configuration of the pure metal (i.e., number of unpaired d-electrons (Rao et al., 1963) or overall number of unpaired valence electrons) and coverage with adsorbed oxygen at equilibrium potential, one could conclude the following: 1) the larger the number of unpaired valence electrons, the larger will be equilibrium coverage with OH_ad and O_ad species; 2) the larger the equilibrium coverage with oxygen-containing species, the higher will be the probability to have more place exchange between surface Pt atoms and oxygen species per geometric unit of the surface, if anodic potential is applied; 3) more place exchange between surface Pt atoms and oxygen species per geometric unit of the surface at high anodic potentials will cause more intensive distortion of the crystal lattice of the oxide formed; 4) more defective oxide structure due to intensive place exchange will be more prone to dissolution under anodic polarizations or under conditions of oxide reduction; 5) more defective oxide will contain numerous defects which improve electronic conductivity and exhibit lower apparent Tafel slope, despite the OER pathway on all the analyzed oxides being the same. While electrochemical data are straightforward, lattice oxygen participation in OER kinetics was analyzed by various groups using differential electrochemical mass spectrometry (DEMS) or online electrochemical mass spectrometry (OLEMS), using isotope labeled experiments. In isotope labeled experiments, the oxide was built using source of O¹⁸, and then water electrolysis is performed together with analysis of mass fragments that could correspond to oxygen evolved from the lattice like O₂¹⁸. It was shown that oxygen originates significantly from the lattice on RuO_x (Wohlfahrt-Mehrens and Heitbaum, 1987) and Au_xO_y (Diaz-Morales et al., 2013), to a minor extent from IrO_y (Fierro et al., 2007) and practically no lattice oxygen evolved from PtO_x (Willsau et al., 1985), as predicted in Figure 3B. There are datasets that indicate that on RuO₂, no oxygen is evolved from the lattice (Stoerzinger et al., 2017), however, knowing that even in the case of IrO_x that is much more stable than RuO_x oxygen originates to a small extent from the lattice (Fierro et al., 2007), we believe that the absence of oxygen from the lattice in the case of RuO_x is not likely. Until now, no data on isotope-labeled experiments during OER on RhOx and PdO_x were found; nevertheless, existing data on other noble metals confirmed the perspective illustrated in Figure 3B. A widespread perception is that in situ or operando spectroscopic techniques will bring important clarifications regarding OER mechanism or at least supply new important information. If we focus on IrO_x as the most relevant OER catalyst in acidic media, ambient pressure X-ray photoelectron spectroscopy (APXPS) indicates that under OER conditions, iridium undergoes a transformation in oxidation state from Ir⁴⁺ to Ir⁵⁺ (Sanchez Casalongue et al., 2014), which is unexpected from the Pourbaix diagram. Higher oxidation states are more prone to solvation; so the possibility of existence of higher oxidation state Ir⁴⁺ suggests possible degradation mechanism. Results from OLEMS, besides oxidation state Ir⁵⁺, suggest formation of oxidation state of Ir⁶⁺ in the form of unstable IrO₃ that up to now has never been reported to have been isolated (Kasian et al., 2018). Recently, the formation of the Ir⁵⁺ oxidation state as an intermediate species was confirmed using in situ X-ray absorption (XAS), while Ir⁶⁺ was predicted by modeling to enable fast water nucleophilic attack as prerequisite for generation of oxygen molecule (Lebedev et al., 2020). Nevertheless, the point of view that IrO₂ goes to higher oxidation states during OER cannot explain the high stability of IrO₂ in acidic media in comparison to other oxides.

Crystalline vs. Amorphous Oxides

Rutile-type IrO₂ is used as a state-of-the-art OER catalyst in acidic water electrolysis due to its stability, although the reaction onset on this type of catalyst is around 1.6 V vs. SHE, suggesting that the practical reaction overpotential during electrolysis is at least 400 mV (Martelli et al., 1994). Amorphous IrO_x (additionally hydrated to different extents) exhibits at least 100 mV lower overpotential (Cherevko et al., 2016). Until now, no clear explanation has been given for this phenomenon. Amorphous oxides, due to the defective structure, could exhibit higher active surface area, but the intrinsic reasons why amorphous oxides are more active are still unknown. Interestingly, the stability of amorphous oxides was believed to be inferior in electrochemical environments in comparison to crystalline oxides. However, quantitative studies, which employed in situ dissolution diagnostics, showed that this issue is controversial. First, lower stability of amorphous hydrous oxide using SFC-ICPMS was reported (Geiger et al., 2016). By using a combination of SFC-ICPMS, TEM (transmission electron microscopy), and XAS (X-ray absorption spectroscopy), Jovanovič et al. observed quite the opposite (Jovanovič et al., 2017). This result suggested the existence of different types of amorphous IrO_x, some of which could maintain long-term high activity. Amorphous hydrated oxides are usually obtained electrochemically. Considering the significant number of stationary and nonstationary electrochemical procedures which can be used to generate amorphous hydrated IrO_x, the electrochemical synthesis and investigation of various types of amorphous hydrated IrO_x can be a reasonable platform for obtaining a multitude of different surfaces with different electrocatalytic properties. OLEMS data suggest that more probable generation of oxygen from the lattice is expected in the case of hydrated IrO_x, while rutile IrO₂ exhibits significantly more stable catalytic performance during OER (Kasian et al., 2019; Schweinar et al., 2020). The reasons for this were not really clarified. A widely spread perception is that anodic dissolution of oxides is linked with instability of their higher oxidation states. At the same time, one of the characteristics of amorphous hydrated oxides is lower average oxidation state and higher concentration of oxygen vacancies in comparison to the rutile structure. If higher oxidation states of oxides (e.g., IrO₃ or RuO₄) would be responsible for dissolution, then amorphous hydrated oxides, despite having initially lower average oxidation number of cations, could be more easily transformed to higher oxidation state (requiring lower overpotential). Increase in oxidation state generally is coupled with drop in radius of cation. Both phenomena enhance cation solvation. However, as shown previously, while oxidation state higher than 4+ is expected for Ru, it is not so probable for Ir.

Mixed (Ternary) Oxides

Besides the in-depth investigation of amorphous oxides including their electrocatalytic properties, an alternative strategy in obtaining more active, more stable, and less expensive OER catalysts is the design of mixed oxides (Trasatti, 1991). A realistic approach would be first to conduct comprehensive investigation of various ternary systems, where one of the components is known to be catalytically active (RuO_x or IrO_x). In the previous few decades, a lot of effort was devoted to building electrocatalytically active substitutional solid solutions. The following guiding principles were used: a) atomic radius of solvent and solute should not differ by more than 15%; b) crystal structures of solvent and solute should be similar; c) solvent and solute should have same valence or alternatively solute should have higher valence than solvent but not vice versa; and finally, d) solute and solvent should have similar electronegativity to avoid formation of intermetallic compounds. One illustrative example of a crystal lattice match/mismatch for various rutile-type of oxides is given in Figure 4 (Shannon, 1968).

FIGURE 4

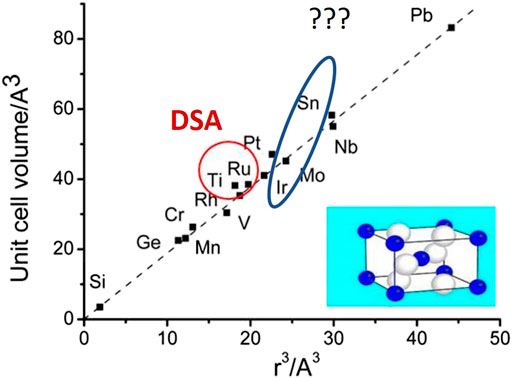
FIGURE 4. Unit cell volume as a function of effective ionic volume for several metal oxides with rutile structure, with indicated two distinct examples of mixed oxides intensively studied in literature (i.e. TiRu mixed oxide used as commercial dimensionally stable anode (DSA) and unstable SnIr mixed oxide). Replotted using data from Shannon (1968).

From Figure 4, it can be understood why, for example, commercially available dimensionally stable anodes (DSAs), often used in various industrial electrolytic processes, are actually mixed oxides (or more precisely substitutional solid solution) of Ru and Ti (Trasatti, 2000). Clearly, their crystal lattice parameters match to a large extent. Mixed TiRu oxide is also an excellent catalyst for OER, however, not sufficiently stable due to leaching of both Ti and Ru, which is one more example of the challenge of long-term catalyst stability in the case of OER. A very stable mixed oxide with solid electrocatalytic activity for OER is Ta₂O₅ + IrO₂ (Martelli et al., 1994). Very interesting is the behavior of the complex oxide RuO_x + IrO_x (Kötz and Stucki, 1986). Parameters of the crystal lattice of isolated oxides are very similar, as shown in Figure 4A. There was evidence for change in the characteristic redox transitions shown with cyclic voltammetry as well as chemical shift of the t_2g valence level (around 1 eV) revealed by XPS, suggesting d–d interactions. The Tafel slope of the catalyst is however mostly influenced by IrO₂. Despite of the charge transfer from Ir toward the Ru cation that probably reduces the oxidation state of RuO_2, the mixed oxide has lower activity than that of RuO₂, although even with a small percent of IrO₂ in the mixture, stability increases drastically. In other words, despite the change in stability being significant, the change in activity was minor. This behavior was unexpected, but at the same time, it showed yet another example that there is no direct correlation between activity and stability.

Nowadays, attempts to build electrocatalytically active interstitial solid solutions are relatively rare. In interstitial solid solutions, the solvent and the solute should also have similar electronegativity and valence; however, the atomic radius of the solute should be smaller than the interstitial sites in the solvent lattice. A highly active and stable interstitial solid solution, to our knowledge, was never reported in the literature, although it could be a very interesting direction of future research.

It seems that in the case of mixed oxides, changing the chemical composition results in various complex modifications like: change in the ratio between the oxidation states of the respective cations, formation of oxygen vacancies, inducing lattice strain via cation of particular radius or charge, enhancing d–d interaction or p–d hybridization, etc. All these modifications contribute in optimizing of frontier orbital filling/occupancy and tuning of characteristic redox transitions. A natural question to ask at this point is what else is relevant for intrinsic activity of OER?

Some Elements of Diagnostics of Reaction Mechanism

While the reaction pathway gives us the first information about reaction intermediates and number of elementary steps from reaction mechanism by using discriminatory criteria of electrode kinetics (partial orders of reaction, transfer coefficient, and stoichiometric number) and by using spectroscopic techniques, we learn much more including: what is the rate-determining step, does the generation of one molecule of the product require one or more active sites, the existence of coupled or decoupled electron and proton transfer, the coverage with intermediates, lateral interaction of intermediates, the formation and stabilization of radicals, etc. One of the key points relevant for understanding of the mechanism is the rate-determining step (RDS) that can only be investigated experimentally. This is a significant point of distinction between experimental and computational chemistry. Computational chemistry operates with potential-determining step (koper, 2013) (explained previously in the text) that is not accessible to experimentalists. Considering that the potential-determining step does not have to overlap with the rate-determining step, we accept the notion that experimental electrochemistry has definite priority in establishing activity trends and in building a picture of reaction mechanism. A desirable approach should be combined with computational/experimental studies like kinetic scaling relations where RDS is obtained from the free energy diagram as a function of the applied electrode potential (Exner and Over, 2019). In this approach, the free energy diagram was constructed from experimental Tafel plots and ab initio Pourbaix diagrams

One interesting experimental result is that the activation energy for OER on oxidized polycrystalline gold is around 55 kJ/mol, almost identical to the activation energy of oxidized gold dissolution (Cherevko et al., 2014b). Knowing that the reaction rate of OER on gold is much higher in comparison to the dissolution rate, equality of the activation energies of OER and gold dissolution processes suggests that dissolution happens with a very low frequency factor or in other words on very few active centers. This suggests that defects that are usually massively present on polycrystalline oxidized metal surfaces cannot be the explanation for the origins of dissolution/instability, contrary to what was usually assumed (Danilovic et al., 2014).

What we skipped intentionally in the above discussion on activity and stability descriptors is the relative position of O_2p orbitals with respect to d-orbitals and with respect to the Fermi level (Hong et al., 2015; Grimaud et al., 2017). This descriptor could shed more light on the mechanism and interrelation between activity and stability. Namely, when the O₂/H₂O redox potential aligns with the Fermi level of the oxide, OER can be triggered. Further, anodic polarization causes an average increase in oxidation state of cations which returns to the previous oxidation state by receiving the electron from oxygen-containing species from water. This is the catalytic cycle in which the metal cation evidently plays a major role by changing oxidation states and concomitantly the bond strengths of the intermediates accordingly. However, it is possible that electron(s) from lattice oxygen species is/are transferred to the cation, resulting in release of molecular oxygen, formation of oxygen vacancies, and possibly transition of the cation to a lower oxidation state. The reason for the oxidation of the lattice oxygen can be a shift of the Fermi level into the O_2p band of a highly covalent oxide at which the difference between the O_2p center and the d-band center is minimized. In that case, from electronic states that are substantially O_2p in character (Figure 5), the generation of oxygen from oxygen sites is probable. Evidently, this kind of mechanism does not imply a priori some destructive effects on the crystal lattice, despite of the general perception that the appearance of oxygen vacancies is linked to lattice instability under OER conditions (Hao et al., 2020). It is rather desirable because it “protects” the cation from higher oxidation states that are more prone to solvation/dissolution. From all that has been discussed until now, it would be essential to quantify isotope labeling measurements using DEMS or OLEMS and analyze the obtained data to conclude what is the actual ratio between species in higher oxidation states produced probably through disproportionation (e.g., RuO₄) and oxygen molecules originating from lattice fragments (e.g., O₂³⁶) and then correlate the data with in situ dissolution data (e.g., from ICP-MS). The issue here is that it is very questionable how sensitive and reliable DEMS or OLEMS setups are for quantitative analysis, as pointed out earlier (Grote et al., 2014).

FIGURE 5

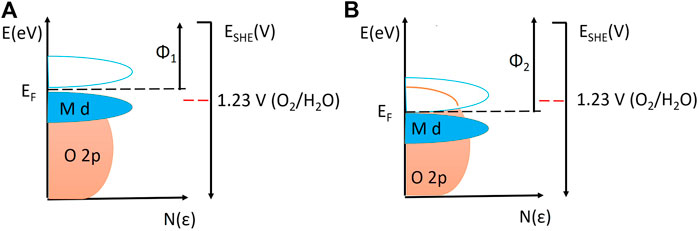
FIGURE 5. Density of states and relative positions of d band, O2p band, Fermi level, and work functions on the vacuum scale, in relation to OER reversible potential on the standard hydrogen redox potential scale. (A) Oxide with low work function and Fermi level positioned above OER reversible redox potential. (B) Oxide with high work function and Fermi level positioned below OER reversible redox potential and inside O2p band, allowing OER from the lattice. Replotted using information from (Hong et al., 2015).

An in-depth discussion on role of lattice oxygen in the OER reaction mechanism slightly shifts focus from the classical view that the metal cation is essential and/or the exclusive active site. Using a combination of synchrotron-based X-ray photoemission and absorption spectroscopies, ab initio calculations, and microcalorimetry suggests that holes in the O_2p states of IrO_x favor the formation of weakly bound oxygen that is extremely susceptible to nucleophilic attack of water (Pfeifer et al., 2016). Formation of an electrophilic oxygen species, O^I−, as a key OER intermediate, proceeds in the electrochemical step followed by a chemical step of molecular oxygen formation. This mechanism is occurring on both, amorphous and rutile Ir oxides, where the reaction rate is higher on former due to better flexibility of its surface (Saveleva et al., 2018).

Dynamic Character of Water Electrolysis

Industrial electrolytic processes, including water splitting, are conducted galvanostatically due to technical preferences which allow relatively straightforward current control, opposite to potential control. At the same time, the imposed current intensity is directly proportional to the mass of the product. It is a widely accepted point of view that water electrolysis is operated via stationary polarization; however, interfacial processes are rather complex and definitely time dependent. One of the important phenomena which influence the overall efficiency of water electrolysis is the formation of gas bubbles at industrially relevant current densities (Zeradjanin et al., 2014c). During the OER, the interfacial region is oversaturated with dissolved oxygen. When the oversaturation overcomes the barrier for the nucleation of a new phase, a gas bubble is formed. Gas bubbles periodically nucleate, grow, and finally detach from the surface. So the overall pseudo-stationary oxygen evolution process, occurring during galvanostatic polarization, is the sum of several time-dependent processes, where at different times the current passes through different fractions of the available/accessible active surface area (Zeradjanin et al., 2012b). Gas evolution kinetics strongly depend on: the hydrophilicity of the electrode surface (Chen et al., 2012), the morphological pattern (Zeradjanin et al., 2012a), as well as the spatial distribution of the morphological pattern (Zeradjanin et al., 2014a, 2018). It was shown that catalytic layers with specially designed morphology could achieve very facile gas evolution if the process of gas-bubble growth is limited at initial moments after nucleation (Zeradjanin et al., 2014c). The abovementioned available/accessible surface area is the one that is at the defined instance not covered by gas bubbles, and consequently, it is between the geometric surface area and “total/real” surface area. It is known as effective surface area and represents an essential quantity if one is to accurately estimate kinetic parameters (Calderon et al., 2009; Zeradjanin, 2018a). In the galvanostatic regime, if gas-bubble coverage is very high, the entire current passes through a small portion of the surface, causing locally high current densities as well as high local overpotentials that can damage the catalyst structure. Therefore, facile gas evolution is extremely important for catalyst stability (Zeradjanin et al., 2014c). Notably there are interesting attempts to accelerate gas evolution with external forces like centrifugal field, ultrasonic field, or magneto-hydrodynamic field (Taqieddin et al., 2017); however, they require additional components in the electrolyzer, which is at the moment not a desirable approach. Besides gas evolution phenomena, galvanostatic electrolysis is coupled with constant charging of the double layer. Double-layer charging is also a time-dependent process. The exact influence of double-layer charging on reaction kinetics, besides being perceived as a parasitic process, was never really understood. Finally, it is worth to stress that electricity originating from renewable sources will fluctuate, so to understand the behavior of electrocatalysts in a realistic manner; it is essential to conduct electrolysis at nonstationary conditions (e.g., galvanostatic pulses).

Challenges in Benchmarking Activity and Stability

One of the controversial aspects of electrocatalysis research is benchmarking the activity and stability of OER. The most accepted approach, probably due to simplicity, is where overpotential required to reach a current density of 10 mAcm⁻² is taken as figure of merit (McCrory et al., 2013). The approach proposed in this work to normalize surface area using cyclic voltammetry is oversimplification of a well-known method based on scan rate-dependent potential-controlled reversible exchange of protons between the electrolyte and oxide surface (Ardizzone et al., 1990). Despite there was some criticism related to absorption of protons in the oxide subsurface layers (Vogt, 1994), still no better method was proposed to date (Baronetto et al., 1994), especially having in mind that subsurface regions can actively participate in the reaction mechanism (Grimaud et al., 2017). Despite some fresh efforts to estimate the surface area (Watzele and Bandarenka, 2016; Watzele et al., 2019), still not much advancement was made since the IUPAC recommendation in 1991 (Trasatti and Petrii, 1991). A more relevant experimental protocol that includes data on catalyst stability was reported recently (Spanos et al., 2017). It is important to note that at technical conditions, the regime of current density and temperature is much more severe than in contemporary laboratory research. At the same time, it is extremely difficult to distinguish at technical conditions where energy losses are coming from (intrinsic kinetics, ohmic drops, diffusion limitations, gas-bubble effect, proton conductivity of the membrane, etc.), like it was done in the case of chlor-alkali electrolysis (Trasatti, 2000). In laboratory experiments, it is much easier to make a “dissection” of the energy losses. For obtaining of accurate kinetic data, besides ohmic drop correction (routinely using impedance spectroscopy at high frequencies), it is necessary to utilize a measurement cell with well-defined mass transport. The rotating disc electrode (RDE) is still the best tool to extract kinetic data, simply due to well-defined conditions of convective diffusion including well-defined value of diffusion-limited current. The validity of RDE implies a laminar flow that is assured only at flat surfaces or with very thin films << 100 µg cm⁻² (Gasteiger et al., 2005). Besides the classical measurement pitfalls (thick catalytic layers, using of the Ag/AgCl reference electrode, and glass-made electrochemical cell with alkaline electrolytes, etc.), one issue is still very problematic and that is the gas-bubble coverage and its influence on effective surface area (Zeradjanin, 2018a). An important aspect to add is that theoretical validity of the mathematical model of RDE (laminar flow) is up to 100,000 rotations/minute; however, due to roughness and inclinations of flat surface, it is considered that 10,000 rotation/minute is a more realistic upper limit. At that rotation rate, the size of the diffusion layer in aqueous electrolytes is around 5 μm, which suggests that nanobubbles or microbubbles with a diameter smaller than 5 µm will not be influenced by convection. In fact, gas bubbles inside the diffusion layer will block the active sites to an extent that it is difficult to estimate and that depends on the kinetics of the OER on a given material as well as on the hydrophilicity of the surface. Therefore, the challenge of reliably determining the effective surface area remains unsolved despite some commendable attempts to quantify the fraction of the surface accessible for reaction under dynamic conditions (Zeradjanin, 2018a). From the discussion above, one can conclude that extracting of overpotential at a predefined current density is prone to significant errors, especially due to issues with effective surface area, but also due to ohmic drop correction that can be problematic for gas evolving electrodes. In the past, it was more common to extract the Tafel slope as an intensive catalytic property (independent of surface area) (Trasatti, 1991); however, considering the existing challenges to ohmic drop correction as well as challenges related to effective surface area that are both overpotential dependent, one can say that extracting Tafel slopes as a kinetic parameter can conceal almost similar drawbacks. It remains a difficult task to search for specific reactions that can be used to reliably determine the number of active sites of a particular catalytic material. Active sites should be determined in relevant surroundings because the properties of the surroundings itself (coordination number, presence of defects in the lattice, etc.) are essential for the intrinsic activity. In other words, estimation of the activity of fragmented systems like the approaches used in single-entity electrochemistry can be used to understand the interplay of an individual entity and the assembly; however, the obtained results cannot be directly relevant for interpreting the behavior of an assembly of the entities (Baker, 2018).

Besides numerous recommendations for activity benchmarking in the last couple of years, catalyst stability benchmarking is becoming more spread and recognized as relevant. For stability benchmarking, it is necessary to have a setup that can measure in situ dissolution of metal species from metal oxide, for example, by means of SFC-ICPMS as previously mentioned (Topalov et al., 2014). Despite the fact that ICPMS works well in acidic electrolytes and with a low detection limit of 10 ppt (parts per trillion) (Topalov et al., 2012b) in alkaline media, it is difficult to calibrate the setup, especially if concentrations of alkaline electrolyte are above 0.05 mol/dm³ (Cherevko et al., 2014a). In that case, it is better to use ICPOES (inductively coupled plasma optical emission spectrometry), which has an order of magnitude lower detection limit than ICPMS; nonetheless, it can operate in more concentrated alkaline electrolytes with concentrations of up to 1 mol/dm³. Proper stability benchmarking requires, independent from the utilized electrochemical technique, that the dissolved amount of metal originating from the catalyst is normalized with the current corresponding to generated oxygen. The usefulness of this approach was first implicitly shown in a comparison of two RuO_x-based catalysts with almost identical chemistry but different morphology. Namely, the catalyst with a “cracked” morphology in comparison to a “crack-free” morphology showed two times higher current intensity and two times lower dissolution rate, indicating four times more effective surface of the “cracked” sample (Zeradjanin et al., 2014c). Later, similar logic was applied in the group of Markovic from Argonne National Laboratory, where the ratio between the amount of produced oxygen and the amount of dissolved metal species at a given overpotential named as activity–stability factor, was proposed as a unified activity–stability descriptor (Kim et al., 2017).

Instead of Conclusions (Remaining Fundamental Questions and Future Research Directions)

After decades of research on the electrocatalysis of OER, various aspects on the origins of activity and stability have been significantly clarified. However, as shown in this review, despite the progress of computational chemistry and spectroscopy, many aspects of the reaction mechanism remain elusive for comprehension. Therefore, we should be prudent with conclusions. To generate a more vivid picture about the complex interfacial transformations that result in the generation of the oxygen molecule, in the future more detailed work should be done in following areas:

1) Theory of charge transfer at interface oxide/electrolyte. Besides electron transfer, focus should be on proton transfer as well as on cation transfer during the dissolution process. Analysis should be done on conductive oxides as well as on semiconductors.

2) Complex compounds (i.e., intermetallics and/or alloys as precursors for surface mixed oxides…) based on the interaction of modestly active d-metals with metals out of d-block which have very low electronegativity, like recently reported Al₂Pt (Antonyshyn et al., 2020) that can give drastic enhancement in OER activity and stability. Similar is with metal–metalloid alloys (e.g., NiB) as precursors, where the metalloid influences the kinetics of water deprotonation and causes a shift in characteristic redox transitions of the catalytically active metal oxide (Masa et al., 2019), while a more intensive oxidation of the materials causes complex anion formation that remains in the double layer and could induce a self-healing effect on the catalyst surface (Masa and Schuhmann, 2019).

3) Role of external fields like electric field (Ghaani et al., 2020) or magnetic field (Garcés-Pineda et al., 2019) that can significantly enhance gas evolution, conductivity, or interfacial charge transfer.

4) Dynamic structural features of interfacial water layer should be investigated with various techniques (Zeradjanin et al., 2020) including sophisticated Terahertz spectroscopies as well as dynamic properties of the electrocatalyst surface layer should be probed with vibrational spectroscopies.

5) Role of impurities in the electrolyte like in the case of Fe cations from alkaline electrolytes interacting with Ni-based oxide or Co-based oxide (Spanos et al., 2019), assuring significant enhancement of the OER activity.

6) The compensation effect on various classes of oxides (e.g., rutiles) as is well known in heterogenous catalysis (Cremer, 1955; Bond et al., 2000; Bligaard et al., 2003) is practically uninvestigated in electrochemistry. It would be of major importance to experimentally determine adsorption energies and compare with computational models, investigate the quantitative relationship between activation energy and preexponential (frequency) factor, and enlarge the understanding of what are the contributors to the activation energy (Zeradjanin et al., 2021) and preexponential factor (proton tunneling, lattice vibrations, etc…) (Zeradjanin, 2018b).

7) Electrocatalysis of OER related to electron spin should be studied systematically (Bockris, 1984). Transition of the spin state from the spin singlet of OH⁻/H₂O reactant to the spin triplet O₂ molecule product imposes additional complexity on OER kinetics (Li et al., 2020). The rate of the chemical reaction will be extremely slow if the spin of the electronic wave function of the products differs from that of the reactants (Sun et al., 2020). Worth to mention is that the spin-related properties are: crystal field stabilization energy, coordination number, oxidation state, bonding, frontier orbital filling, conductivity, and magnetism.

8) A self-evident way to protect oxides from degradation is to reduce OER overpotential at working conditions. Consequently, the way to enhance stability is to improve the intrinsic OER activity of the catalyst. Therefore, we could say that finding new ways to improve the catalyst activity for OER, inside or outside the paradigm of the Sabatier principle, could be essential strategy to generally enhance catalyst performance.

Author Contributions

AZ concealed concept and wrote draft of the review. JM, IS, and RS helped shaping and writing of review.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Authors acknowledge Max Planck Society for granting open access of this work.

References

Antonyshyn, I., Barrios Jiménez, A. M., Sichevych, O., Burkhardt, U., Veremchuk, I., Schmidt, M., et al. (2020). Al 2 Pt for oxygen evolution in water splitting: a strategy for creating multifunctionality in electrocatalysis. Angew. Chem. Int. Ed. Engl., 59, 16770–16776, doi:10.1002/anie.202005445 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Ardizzone, S., Fregonara, G., and Trasatti, S. (1990). “Inner” and “outer” active surface of RuO₂ electrodes. Electrochim. Acta 35, 263–267. doi:10.1016/0013-4686(90)85068-X

CrossRef Full Text | Google Scholar

Arikado, T., Iwakura, C., and Tamura, H. (1978). Some oxide catalysts for the anodic evolution of chlorine: reaction mechanism and catalytic activity. Electrochim. Acta 23, 9–15. doi:10.1016/0013-4686(78)87026-1

CrossRef Full Text | Google Scholar

Baker, L. A. (2018). Perspective and prospectus on single-entity electrochemistry. J. Am. Chem. Soc. 140, 15549–15559. doi:10.1021/jacs.8b09747 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Baronetto, D., Krstajić, N., and Trasatti, S. (1994). Reply to “note on a method to interrelate inner and outer electrode areas” by H. Vogt. Electrochim. Acta 39, 2359–2362. doi:10.1016/0013-4686(94)E0158-K

CrossRef Full Text | Google Scholar

Binninger, T., Mohamed, R., Waltar, K., Fabbri, E., Levecque, P., Kötz, R., et al. (2015). Thermodynamic explanation of the universal correlation between oxygen evolution activity and corrosion of oxide catalysts. Sci. Rep. 5, 12167. doi:10.1038/srep12167 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, T., Honkala, K., Logadottir, A., Nørskov, J. K., Dahl, S., and Jacobsen, C. J. H. (2003). On the compensation effect in heterogeneous catalysis. J. Phys. Chem. B 107, 9325–9331. doi:10.1021/jp034447g

CrossRef Full Text | Google Scholar

Bockris, J. O., and Otagawa, T. (1983). Mechanism of oxygen evolution on perovskites. J. Phys. Chem. 87, 2960–2971. doi:10.1021/j100238a048

CrossRef Full Text | Google Scholar

Bockris, J. O. (1972). A hydrogen economy. Science 176, 1323. doi:10.1126/science.176.4041.1323 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Bockris, J. O. (1984). The electrocatalysis of oxygen evolution on perovskites. J. Electrochem. Soc. 131, 290. doi:10.1149/1.2115565

CrossRef Full Text | Google Scholar

Bockris, J. O. M. (2013). The hydrogen economy: its history. Int J Hydrogen Energ., 38, 2579–2588. doi:10.1016/j.ijhydene.2012.12.026

CrossRef Full Text | Google Scholar

Bond, G. C., Keane, M. A., Kral, H., and Lercher, J. A. (2000). Compensation phenomena in heterogeneous catalysis: general principles and a possible explanation. Catal. Rev. 42, 323–383. doi:10.1081/CR-100100264

CrossRef Full Text | Google Scholar

Busch, M., Halck, N. B., Kramm, U. I., Siahrostami, S., Krtil, P., and Rossmeisl, J. (2016). Beyond the top of the volcano?–a unified approach to electrocatalytic oxygen reduction and oxygen evolution. Nanomater. Energy 29, 126–135. doi:10.1016/j.nanoen.2016.04.011

CrossRef Full Text | Google Scholar

Busch, M. (2018). Water oxidation: from mechanisms to limitations. Current Opinion in Electrochemistry 9, 278–284. doi:10.1016/j.coelec.2018.06.007

CrossRef Full Text | Google Scholar

Calderon, E. H., Wüthrich, R., Mandin, P., Fóti, G., and Comninellis, C. (2009). Estimation of the effectiveness factor of an outer-sphere redox couple (Fe³⁺/Fe²⁺) using rotating disk Ti/IrO₂ electrodes of different loading. J. Appl. Electrochem. 39, 1379–1384. doi:10.1007/s10800-009-9813-6

CrossRef Full Text | Google Scholar

Calle-Vallejo, F., Martínez, J. I., and Rossmeisl, J. (2011). Density functional studies of functionalized graphitic materials with late transition metals for oxygen reduction reactions. Phys. Chem. Chem. Phys. 13, 15639. doi:10.1039/c1cp21228a |

PubMed Abstract | CrossRef Full Text | Google Scholar

Calle-Vallejo, F., Inoglu, N. G., Su, H.-Y., Martínez, J. I., Man, I. C., Koper, M. T. M., et al. (2013). Number of outer electrons as descriptor for adsorption processes on transition metals and their oxides. Chem. Sci. 4, 1245. doi:10.1039/c2sc21601a

CrossRef Full Text | Google Scholar

Calle-Vallejo, F., Díaz-Morales, O. A., Kolb, M. J., and Koper, M. T. M. (2015). Why is bulk thermochemistry a good descriptor for the electrocatalytic activity of transition metal oxides?. ACS Catal. 5, 869–873. doi:10.1021/cs5016657

CrossRef Full Text | Google Scholar

Calle-Vallejo, F., Krabbe, A., and García-Lastra, J. M. (2017). How covalence breaks adsorption-energy scaling relations and solvation restores them. Chem. Sci. 8, 124–130. doi:10.1039/C6SC02123A |

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, R., Trieu, V., Zeradjanin, A. R., Natter, H., Teschner, D., Kintrup, J., et al. (2012). Microstructural impact of anodic coatings on the electrochemical chlorine evolution reaction. Phys. Chem. Chem. Phys. 14, 7392. doi:10.1039/c2cp41163f |

PubMed Abstract | CrossRef Full Text | Google Scholar

Hempelmann, S., Zeradjanin, A. R., Keeley, G. P., and Mayrhofer, K. J. J. (2014a). A comparative study on gold and platinum dissolution in acidic and alkaline media. J. Electrochem. Soc. 161, H822–H830. doi:10.1149/2.0881412jes

CrossRef Full Text | Google Scholar

Cherevko, S., Zeradjanin, A. R., Topalov, A. A., Keeley, G. P., and Mayrhofer, K. J. J. (2014b). Effect of temperature on gold dissolution in acidic media. J. Electrochem. Soc. 161, H501–H507. doi:10.1149/2.0551409jes

CrossRef Full Text | Google Scholar

Cherevko, S., Zeradjanin, A. R., Topalov, A. A., Kulyk, N., Katsounaros, I., and Mayrhofer, K. J. J. (2014c). Dissolution of noble metals during oxygen evolution in acidic media. ChemCatChem 6, 2219–2223. doi:10.1002/cctc.201402194

CrossRef Full Text | Google Scholar

Cherevko, S., Geiger, S., Kasian, O., Kulyk, N., Grote, J.-P., Savan, A., et al. (2016). Oxygen and hydrogen evolution reactions on Ru, RuO 2 , Ir, and IrO 2 thin film electrodes in acidic and alkaline electrolytes: a comparative study on activity and stability. Catal. Today 262, 170–180. doi:10.1016/j.cattod.2015.08.014

CrossRef Full Text | Google Scholar

Cremer, E. (1955). “The compensation effect in heterogeneous catalysis,” in Advances in Catalysis. Amsterdam, Netherlands: Elsevier, 75–91. doi:10.1016/S0360-0564(08)60525-8

CrossRef Full Text | Google Scholar

Damjanovic, A., Dey, A., and Bockris, J. O. (1966). Kinetics of oxygen evolution and dissolution on platinum electrodes. Electrochim. Acta 11, 791–814. doi:10.1016/0013-4686(66)87056-1

CrossRef Full Text | Google Scholar

Danilovic, N., Subbaraman, R., Chang, K. C., Chang, S. H., Kang, Y. J., Snyder, J., et al. (2014). Activity–stability trends for the oxygen evolution reaction on monometallic oxides in acidic environments. J. Phys. Chem. Lett. 5, 2474–2478. doi:10.1021/jz501061n |

PubMed Abstract | CrossRef Full Text | Google Scholar

Markovic, H., Limberg, C., Reier, T., Risch, M., Roggan, S., and Strasser, P. (2010). The mechanism of water oxidation: from electrolysis via homogeneous to biological catalysis. ChemCatChem 2, 724–761. doi:10.1002/cctc.201000126

CrossRef Full Text | Google Scholar

Di Quarto, F., Sunseri, C., Piazza, S., and Romano, M. C. (1997). Semiempirical correlation between optical band gap values of oxides and the difference of electronegativity of the elements. Its importance for a quantitative use of photocurrent spectroscopy in corrosion studies. J. Phys. Chem. B 101, 2519–2525. doi:10.1021/jp970046n

CrossRef Full Text | Google Scholar

Diaz-Morales, O., Calle-Vallejo, F., De Munck, C., and Koper, M. T. M. (2013). Electrochemical water splitting by gold: evidence for an oxide decomposition mechanism. Chem. Sci. 4, 2334. doi:10.1039/c3sc50301a

CrossRef Full Text | Google Scholar

Exner, K. S., and Over, H. (2019). Beyond the rate-determining step in the oxygen evolution reaction over a single-crystalline IrO 2 (110) model electrode: kinetic scaling relations. ACS Catal. 9, 6755–6765. doi:10.1021/acscatal.9b01564

CrossRef Full Text | Google Scholar

Exner, K. S. (2019). Design criteria for oxygen evolution electrocatalysts from first principles: introduction of a unifying material-screening approach. ACS Appl. Energy Mater. 2, 7991–8001. doi:10.1021/acsaem.9b01480

CrossRef Full Text | Google Scholar

Exner, K. S. (2020a). A universal descriptor for the screening of electrode materials for multiple-electron processes: beyond the thermodynamic overpotential. ACS Catal. 10, 12607–12617. doi:10.1021/acscatal.0c03865

CrossRef Full Text | Google Scholar

Exner, K. S. (2020b). Recent progress in the development of screening methods to identify electrode materials for the oxygen evolution reaction. Adv. Funct. Mater. 30, 2005060. doi:10.1002/adfm.202005060

CrossRef Full Text | Google Scholar

Fierro, S., Nagel, T., Baltruschat, H., and Comninellis, C. (2007). Investigation of the oxygen evolution reaction on Ti/IrO₂ electrodes using isotope labelling and on-line mass spectrometry. Electrochem. Commun. 9, 1969–1974. doi:10.1016/j.elecom.2007.05.008

CrossRef Full Text | Google Scholar

Frydendal, R., Paoli, E. A., Knudsen, B. P., Wickman, B., Malacrida, P., Stephens, I. E. L., et al. (2014). Benchmarking the stability of oxygen evolution reaction catalysts: the importance of monitoring mass losses. ChemElectroChem 1, 2075. doi:10.1002/celc.201402262

CrossRef Full Text | Google Scholar

Garcés-Pineda, F. A., Blasco-Ahicart, M., Nieto-Castro, D., López, N., and Galán-Mascarós, J. R. (2019). Direct magnetic enhancement of electrocatalytic water oxidation in alkaline media. Nat Energy 4, 519–525. doi:10.1038/s41560-019-0404-4

CrossRef Full Text | Google Scholar

Gasteiger, H. A., and Marković, N. M. (2009). Chemistry. just a dream—Or future reality? Science 324, 48–49. doi:10.1126/science.1172083 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Gasteiger, H. A., Kocha, S. S., Sompalli, B., and Wagner, F. T. (2005). Activity benchmarks and requirements for Pt, Pt-alloy, and non-Pt oxygen reduction catalysts for PEMFCs. Appl. Catal. B Environ. 56, 9–35. doi:10.1016/j.apcatb.2004.06.021

CrossRef Full Text | Google Scholar

Geiger, S., Kasian, O., Shrestha, B. R., Mingers, A. M., Mayrhofer, K. J. J., and Cherevko, S. (2016). Activity and stability of electrochemically and thermally treated iridium for the oxygen evolution reaction. J. Electrochem. Soc. 163, F3132–F3138. doi:10.1149/2.0181611jes

CrossRef Full Text | Google Scholar

Ghaani, M. R., Kusalik, P. G., and English, N. J. (2020). Massive generation of metastable bulk nanobubbles in water by external electric fields. Sci. Adv. 6, eaaz0094. doi:10.1126/sciadv.aaz0094 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Govindarajan, N., García-Lastra, J. M., Meijer, E. J., and Calle-Vallejo, F. (2018). Does the breaking of adsorption-energy scaling relations guarantee enhanced electrocatalysis?. Current Opinion in Electrochemistry 8, 110–117. doi:10.1016/j.coelec.2018.03.025

CrossRef Full Text | Google Scholar

Govindarajan, N., Koper, M. T. M., Meijer, E. J., and Calle-Vallejo, F. (2019). Outlining the scaling-based and scaling-free optimization of electrocatalysts. ACS Catal. 9, 4218–4225. doi:10.1021/acscatal.9b00532

CrossRef Full Text | Google Scholar

Greeley, J., and Markovic, N. M. (2012). The road from animal electricity to green energy: combining experiment and theory in electrocatalysis. Energy Environ. Sci. 5, 9246. doi:10.1039/c2ee21754f

CrossRef Full Text | Google Scholar

Grimaud, A., Diaz-Morales, O., Han, B., Hong, W. T., Lee, Y. L., Giordano, L., et al. (2017). Activating lattice oxygen redox reactions in metal oxides to catalyse oxygen evolution. Nat. Chem. 9, 457–465. doi:10.1038/nchem.2695 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao-Horn, J. P., Zeradjanin, A. R., Cherevko, S., and Mayrhofer, K. J. (2014). Coupling of a scanning flow cell with online electrochemical mass spectrometry for screening of reaction selectivity. Rev. Sci. Instrum. 85, 104101. doi:10.1063/1.4896755 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunkel, F., Jin, L., Mueller, D. N., Hausner, C., Bick, D. S., Jia, C.-L., et al. (2017). Ordering and phase control in epitaxial double-perovskite catalysts for the oxygen evolution reaction. ACS Catal. 7, 7029–7037. doi:10.1021/acscatal.7b02036

CrossRef Full Text | Google Scholar

Halck, N. B., Petrykin, V., Krtil, P., and Rossmeisl, J. (2014). Beyond the volcano limitations in electrocatalysis--oxygen evolution reaction. Phys. Chem. Chem. Phys. 16, 13682–13688. doi:10.1039/C4CP00571F |

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, S., Liu, M., Pan, J., Liu, X., Tan, X., Xu, N., et al. (2020). Dopants fixation of ruthenium for boosting acidic oxygen evolution stability and activity. Nat. Commun. 11, 5368. doi:10.1038/s41467-020-19212-y |

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, W. T., Risch, M., Stoerzinger, K. A., Grimaud, A., Suntivich, J., and Shao-Horn, Y. (2015). Toward the rational design of non-precious transition metal oxides for oxygen electrocatalysis. Energy Environ. Sci. 8, 1404–1427. doi:10.1039/C4EE03869J |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Hodnik, N., Ruiz-Zepeda, F., Arčon, I., Jozinović, B., Zorko, M., et al. (2017). Electrochemical dissolution of iridium and iridium oxide particles in acidic media: transmission electron microscopy, electrochemical flow cell coupled to inductively coupled plasma mass spectrometry, and X-ray absorption spectroscopy study. J. Am. Chem. Soc. 139, 12837–12846. doi:10.1021/jacs.7b08071 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaberšček, O., Grote, J. P., Geiger, S., Cherevko, S., and Mayrhofer, K. J. J. (2018). The common intermediates of oxygen evolution and dissolution reactions during water electrolysis on iridium. Angew Chem. Int. Ed. Engl. 57, 2488–2491. doi:10.1002/anie.201709652 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasian, O., Geiger, S., Li, T., Grote, J.-P., Schweinar, K., Zhang, S., et al. (2019). Degradation of iridium oxides via oxygen evolution from the lattice: correlating atomic scale structure with reaction mechanisms. Energy Environ. Sci. 12, 3548–3555. doi:10.1039/C9EE01872G

CrossRef Full Text | Google Scholar

Katsounaros, I., Cherevko, S., Zeradjanin, A. R., and Mayrhofer, K. J. (2014). Oxygen electrochemistry as a cornerstone for sustainable energy conversion. Angew Chem. Int. Ed. Engl. 53, 102–121. doi:10.1002/anie.201306588 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y. T., Lopes, P. P., Park, S. A., Lee, A. Y., Lim, J., Lee, H., et al. (2017). Balancing activity, stability and conductivity of nanoporous core-shell iridium/iridium oxide oxygen evolution catalysts. Nat. Commun. 8, 1449. doi:10.1038/s41467-017-01734-7 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Kötz, R., and Stucki, S. (1986). Stabilization of RuO₂ by IrO₂ for anodic oxygen evolution in acid media. Electrochim. Acta 31, 1311–1316. doi:10.1016/0013-4686(86)80153-0

CrossRef Full Text | Google Scholar

Markovic, M. T. M. (2013). Analysis of electrocatalytic reaction schemes: distinction between rate-determining and potential-determining steps. J. Solid State Electrochem. 17, 339–344. doi:10.1007/s10008-012-1918-x

CrossRef Full Text | Google Scholar

Lebedev, D., Ezhov, R., Heras-Domingo, J., Comas-Vives, A., Kaeffer, N., Willinger, M., et al. (2020). Atomically dispersed iridium on indium tin oxide efficiently catalyzes water oxidation. ACS Cent. Sci.,6, 1189–1198. doi:10.1021/acscentsci.0c00604 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, N. S., and Nocera, D. G. (2006). Powering the planet: chemical challenges in solar energy utilization. Proc. Natl. Acad. Sci. USA. 103, 15729–15735. doi:10.1073/pnas.0603395103 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Cheng, Z., and Wang, X. (2020). Understanding the mechanism of oxygen evolution reaction (OER) with the consideration of spin. Available at: http://arxiv.org/abs/2004.05326

CrossRef Full Text | Google Scholar

Ma, Z., Zhang, Y., Liu, S., Xu, W., Wu, L., Hsieh, Y.-C., et al. (2018). Reaction mechanism for oxygen evolution on RuO₂, IrO₂, and RuO₂@IrO₂ core-shell nanocatalysts. J. Electroanal. Chem. 819, 296–305. doi:10.1016/j.jelechem.2017.10.062

CrossRef Full Text | Google Scholar

Man, I. C., Su, H.-Y., Calle-Vallejo, F., Hansen, H. A., Martínez, J. I., Inoglu, N. G., et al. (2011). Universality in oxygen evolution electrocatalysis on oxide surfaces. ChemCatChem 3, 1159–1165. doi:10.1002/cctc.201000397

CrossRef Full Text | Google Scholar

Martelli, G. N., Ornelas, R., and Faita, G. (1994). Deactivation mechanisms of oxygen evolving anodes at high current densities. Electrochim. Acta 39, 1551–1558. doi:10.1016/0013-4686(94)85134-4

CrossRef Full Text | Google Scholar

Masa, J., and Schuhmann, W. (2019). The role of non‐metallic and metalloid elements on the electrocatalytic activity of cobalt and nickel catalysts for the oxygen evolution reaction. ChemCatChem 11, 5842–5854. doi:10.1002/cctc.201901151

CrossRef Full Text | Google Scholar

Masa, J., Piontek, S., Wilde, P., Antoni, H., Eckhard, T., Chen, Y., et al. (2019). Ni‐metalloid (B, Si, P, as, and Te) alloys as water oxidation electrocatalysts. Adv. Energy Mater. 9, 33–39. doi:10.1002/aenm.201900796

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Sato, E. (1979). Oxygen evolution on La1−xSrxMnO₃ electrodes in alkaline solutions. Electrochim. Acta 24, 421–423. doi:10.1016/0013-4686(79)87030-9

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Sato, E. (1986). Electrocatalytic properties of transition metal oxides for oxygen evolution reaction. Mater. Chem. Phys. 14, 397–426. doi:10.1016/0254-0584(86)90045-3

CrossRef Full Text | Google Scholar

McCrory, C. C., Jung, S., Peters, J. C., and Jaramillo, T. F. (2013). Benchmarking heterogeneous electrocatalysts for the oxygen evolution reaction. J. Am. Chem. Soc. 135, 16977–16987. doi:10.1021/ja407115p |

PubMed Abstract | CrossRef Full Text | Google Scholar

McKeown, D. A., Hagans, P. L., Carette, L. P. L., Russell, A. E., Swider, K. E., and Rolison, D. R. (1999). Structure of hydrous ruthenium oxides: implications for charge storage. J. Phys. Chem. B 103, 4825–4832. doi:10.1021/jp990096n

CrossRef Full Text | Google Scholar

Miles, M. H. (1976). Periodic variations of overvoltages for water electrolysis in acid solutions from cyclic voltammetric studies. J. Electrochem. Soc. 123, 1459. doi:10.1149/1.2132619

CrossRef Full Text | Google Scholar

Miles, M. H. (1978). The oxygen electrode reaction in alkaline solutions on oxide electrodes prepared by the thermal decomposition method. J. Electrochem. Soc. 125, 1931. doi:10.1149/1.2131330

CrossRef Full Text | Google Scholar

Newns, D. M. (1969). Self-consistent model of hydrogen chemisorption. Phys. Rev. 178, 1123–1135. doi:10.1103/PhysRev.178.1123

CrossRef Full Text | Google Scholar

Nørskov, J. K., Rossmeisl, J., Logadottir, A., Lindqvist, L., Kitchin, J. R., Bligaard, T., et al. (2004). Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892. doi:10.1021/jp047349j

CrossRef Full Text | Google Scholar

Nong, H. N., Reier, T., Oh, H.-S., Gliech, M., Paciok, P., Vu, T. H. T., et al. (2018). A unique oxygen ligand environment facilitates water oxidation in hole-doped IrNiOx core–shell electrocatalysts. Nat Catal 1, 841–851. doi:10.1038/s41929-018-0153-y

CrossRef Full Text | Google Scholar

Oener, S. Z., Foster, M. J., and Boettcher, S. W. (2020). Accelerating water dissociation in bipolar membranes and for electrocatalysis. Science 369, 1099–1103. doi:10.1126/science.aaz1487 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Pfeifer, V., Jones, T. E., Wrabetz, S., Massué, C., Velasco Vélez, J. J., Arrigo, R., et al. (2016). Reactive oxygen species in iridium-based OER catalysts. Chem. Sci. 7, 6791–6795. doi:10.1039/C6SC01860B |

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlögl, R., Krtil, P., and Rossmeisl, J. (2018). Rationality in the new oxygen evolution catalyst development. Curr Opin Electrochem. 12, 218–224. doi:10.1016/j.coelec.2018.11.014

CrossRef Full Text | Google Scholar

Rao, M. L. B., Damjanovic, A., and Bockris, J. O. (1963). Oxygen adsorption related to the unpaired d-electrons in transition metals. J. Phys. Chem. 67, 2508–2509. doi:10.1021/j100805a520

CrossRef Full Text | Google Scholar

Rasiyah, P. (1984). The role of the lower metal oxide/higher metal oxide couple in oxygen evolution reactions. J. Electrochem. Soc. 131, 803. doi:10.1149/1.2115703

CrossRef Full Text | Google Scholar

Recommendations (1986). The absolute electrode potential: an explanatory note (Recommendations 1986). J. Electroanal. Chem. Interfacial Electrochem. 209, 417–428. doi:10.1016/0022-0728(86)80570-8

CrossRef Full Text | Google Scholar

Rossmeisl, J., Logadottir, A., and Nørskov, J. K. (2005). Electrolysis of water on (oxidized) metal surfaces. Chem. Phys. 319, 178–184. doi:10.1016/j.chemphys.2005.05.038

CrossRef Full Text | Google Scholar

Rossmeisl, J., Qu, Z.-W., Zhu, H., Kroes, G.-J., and Nørskov, J. K. (2007). Electrolysis of water on oxide surfaces. J. Electroanal. Chem. 607, 83–89. doi:10.1016/j.jelechem.2006.11.008

CrossRef Full Text | Google Scholar

Rüetschi, P., and Delahay, P. (1955). Influence of electrode material on oxygen overvoltage: a theoretical analysis. J. Chem. Phys. 23, 556–560. doi:10.1063/1.1742029

CrossRef Full Text | Google Scholar

Sanchez Casalongue, H. G., Ng, M. L., Kaya, S., Friebel, D., Ogasawara, H., and Nilsson, A. (2014). In Situ observation of surface species on iridium oxide nanoparticles during the oxygen evolution reaction. Angew Chem. Int. Ed. Engl. 53, 7169–7172. doi:10.1002/anie.201402311 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Saveleva, V. A., Wang, L., Teschner, D., Jones, T., Gago, A. S., Friedrich, K. A., et al. (2018). Operando evidence for a universal oxygen evolution mechanism on thermal and electrochemical iridium oxides. J. Phys. Chem. Lett. 9, 3154–3160. doi:10.1021/acs.jpclett.8b00810 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Savinova, M., Kasian, O., Ledendecker, M., Speck, F. D., Mingers, A. M., Mayrhofer, K. J. J., et al. (2018). The electrochemical dissolution of noble metals in alkaline media. Electrocatalysis 9, 153–161. doi:10.1007/s12678-017-0438-y

CrossRef Full Text | Google Scholar

Schweinar, K., Gault, B., Mouton, I., and Kasian, O. (2020). Lattice oxygen exchange in rutile IrO. J. Phys. Chem. Lett. 11, 5008–5014. doi:10.1021/acs.jpclett.0c01258 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Shannon, R. D. (1968). Synthesis and properties of two new members of the rutile family RhO₂ and PtO₂. Solid State Commun. 6, 139–143. doi:10.1016/0038-1098(68)90019-7

CrossRef Full Text | Google Scholar

Simons, R., and Khanarian, G. (1978). Water dissociation in bipolar membranes: experiments and theory. J. Membr. Biol. 38, 11–30. doi:10.1007/BF01875160

CrossRef Full Text | Google Scholar

Spanos, I., Auer, A. A., Neugebauer, S., Deng, X., Tüysüz, H., and Schlögl, R. (2017). Standardized benchmarking of water splitting catalysts in a combined electrochemical flow cell/inductively coupled plasma–optical emission spectrometry (ICP-oes) setup. ACS Catal 7, 3768–3778. doi:10.1021/acscatal.7b00632

CrossRef Full Text | Google Scholar

Spanos, I., Tesch, M. F., Yu, M., Tüysüz, H., Zhang, J., Feng, X., et al. (2019). Facile protocol for alkaline electrolyte purification and its influence on a Ni–Co oxide catalyst for the oxygen evolution reaction. ACS Catal 9, 8165–8170. doi:10.1021/acscatal.9b01940

CrossRef Full Text | Google Scholar

Stoerzinger, K. A., Diaz-Morales, O., Kolb, M., Rao, R. R., Frydendal, R., Qiao, L., et al. (2017). Orientation-dependent oxygen evolution on RuO 2 without lattice exchange. ACS Energy Lett. 2, 876–881. doi:10.1021/acsenergylett.7b00135

CrossRef Full Text | Google Scholar

Su, H.-Y., Sun, K., Wang, W.-Q., Zeng, Z., Calle-Vallejo, F., and Li, W.-X. (2016). Establishing and understanding adsorption–energy scaling relations with negative slopes. J. Phys. Chem. Lett. 7, 5302–5306. doi:10.1021/acs.jpclett.6b02430 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Y., Sun, S., Yang, H., Xi, S., Gracia, J., and Xu, Z. J. (2020). Spin‐related electron transfer and orbital interactions in oxygen electrocatalysis. Adv. Mater. 32. doi:10.1002/adma.202003297

CrossRef Full Text | Google Scholar

Suntivich, J., May, K. J., Gasteiger, H. A., Goodenough, J. B., and Shao-Horn, Y. (2011). A perovskite oxide optimized for oxygen evolution catalysis from molecular orbital principles. Science 334, 1383–1385. doi:10.1126/science.1212858 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Taqieddin, A., Nazari, R., Rajic, L., and Alshawabkeh, A. (2017). Review—physicochemical hydrodynamics of gas bubbles in two phase electrochemical systems. J. Electrochem. Soc. 164, E448–E459. doi:10.1149/2.1161713jes |

PubMed Abstract | CrossRef Full Text | Google Scholar

Topalov, A. A., Katsounaros, I., Auinger, M., Cherevko, S., Meier, J. C., Klemm, S. O., et al. (2012a). Dissolution of platinum: limits for the deployment of electrochemical energy conversion?. Angew. Chem. Int. Ed. 51, 12613–12615. doi:10.1002/anie.201207256 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Topalov, A. A., Katsounaros, I., Auinger, M., Cherevko, S., Meier, J. C., Klemm, S. O., et al. (2012b). Dissolution of platinum: limits for the deployment of electrochemical energy conversion?. Angew. Chem. Int. Ed. 51, 12613–12615. doi:10.1002/anie.201207256 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Topalov, A. A., Cherevko, S., Zeradjanin, A. R., Meier, J. C., Katsounaros, I., and Mayrhofer, K. J. J. (2014). Towards a comprehensive understanding of platinum dissolution in acidic media. Chem. Sci. 5, 631–638. doi:10.1039/C3SC52411F

CrossRef Full Text | Google Scholar

Trasatti, S., and Petrii, O. A. (1991). Real surface area measurements in electrochemistry. Pure Appl. Chem. 63, 711–734. doi:10.1351/pac199163050711

CrossRef Full Text | Google Scholar

Trasatti, S. (1984). Electrocatalysis in the anodic evolution of oxygen and chlorine. Electrochim. Acta 29, 1503–1512. doi:10.1016/0013-4686(84)85004-5

CrossRef Full Text | Google Scholar

Trasatti, S. (1991). Physical electrochemistry of ceramic oxides. Electrochim. Acta 36, 225–241. doi:10.1016/0013-4686(91)85244-2

CrossRef Full Text | Google Scholar

Trasatti, S. (2000a). Electrocatalysis: understanding the success of DSA®. Electrochim. Acta 45, 2377–2385. doi:10.1016/S0013-4686(00)00338-8

CrossRef Full Text | Google Scholar

Vogt, H. (1994). Note on a method to interrelate inner and outer electrode areas. Electrochim. Acta 39, 1981–1983. doi:10.1016/0013-4686(94)85077-1

CrossRef Full Text | Google Scholar

Wang, L., Stoerzinger, K. A., Chang, L., Yin, X., Li, Y., Tang, C. S., et al. (2019). Strain effect on oxygen evolution reaction activity of epitaxial NdNiO 3 thin films. ACS Appl. Mater. Interfaces 11, 12941–12947. doi:10.1021/acsami.8b21301 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Watzele, S., and Bandarenka, A. S. (2016). Quick determination of electroactive surface area of some oxide electrode materials. Electroanalysis 28, 2394–2399. doi:10.1002/elan.201600178

CrossRef Full Text | Google Scholar

Watzele, S., Hauenstein, P., Liang, Y., Xue, S., Fichtner, J., Garlyyev, B., et al. (2019). Determination of electroactive surface area of Ni-, Co-, Fe-, and Ir-based oxide electrocatalysts. ACS Catal 9, 9222–9230. doi:10.1021/acscatal.9b02006

CrossRef Full Text | Google Scholar

Willsau, J., Wolter, O., and Heitbaum, J. (1985). Does the oxide layer take part in the oxygen evolution reaction on platinum?. J. Electroanal. Chem. Interfacial Electrochem. 195, 299–306. doi:10.1016/0022-0728(85)80050-4

CrossRef Full Text | Google Scholar

Wohlfahrt-Mehrens, M., and Heitbaum, J. (1987). Oxygen evolution on Ru and RuO₂ electrodes studied using isotope labelling and on-line mass spectrometry. J. Electroanal. Chem. Interfacial Electrochem. 237, 251–260. doi:10.1016/0022-0728(87)85237-3

CrossRef Full Text | Google Scholar

Yao, Y., Hu, S., Chen, W., Huang, Z.-Q., Wei, W., Yao, T., et al. (2019). Engineering the electronic structure of single atom Ru sites via compressive strain boosts acidic water oxidation electrocatalysis. Nat Catal 2, 304–313. doi:10.1038/s41929-019-0246-2

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., La Mantia, F., Masa, J., and Schuhmann, W. (2012a). Utilization of the catalyst layer of dimensionally stable anodes—interplay of morphology and active surface area. Electrochim. Acta 82, 408–414. doi:10.1016/j.electacta.2012.04.101

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Ventosa, E., Bondarenko, A. S., and Schuhmann, W. (2012b). Evaluation of the catalytic performance of gas-evolving electrodes using local electrochemical noise measurements. ChemSusChem 5, 1905–1911. doi:10.1002/cssc.201200262 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Menzel, N., Schuhmann, W., and Strasser, P. (2014a). On the faradaic selectivity and the role of surface inhomogeneity during the chlorine evolution reaction on ternary Ti–Ru–Ir mixed metal oxide electrocatalysts. Phys. Chem. Chem. Phys. 16, 13741–13747. doi:10.1039/C4CP00896K |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Topalov, A. A., Cherevko, S., and Keeley, G. P. (2014b). Sustainable generation of hydrogen using chemicals with regional oversupply – feasibility of the electrolysis in acido-alkaline reactor. Int. J. Hydrogen Energy 39, 16275–16281. doi:10.1016/j.ijhydene.2014.08.026

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Topalov, A. A., Van Overmeere, Q., Cherevko, S., Chen, X., Ventosa, E., et al. (2014c). Rational design of the electrode morphology for oxygen evolution – enhancing the performance for catalytic water oxidation. RSC Adv. 4, 9579. doi:10.1039/c3ra45998e

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Grote, J.-P., Polymeros, G., and Mayrhofer, K. J. J. (2016). A critical review on hydrogen evolution electrocatalysis: re-exploring the volcano-relationship. Electroanalysis 28, 2256–2269. doi:10.1002/elan.201600270

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Vimalanandan, A., Polymeros, G., Topalov, A. A., Mayrhofer, K. J. J., and Rohwerder, M. (2017). Balanced work function as a driver for facile hydrogen evolution reaction–comprehension and experimental assessment of interfacial catalytic descriptor. Phys. Chem. Chem. Phys. 19, 17019–17027. doi:10.1039/C7CP03081A |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Ventosa, E., Masa, J., and Schuhmann, W. (2018). Utilization of the catalyst layer of dimensionally stable anodes. Part 2: impact of spatial current distribution on electrocatalytic performance. J. Electroanal. Chem. 828, 63–70. doi:10.1016/j.jelechem.2018.09.034

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Polymeros, G., Toparli, C., Ledendecker, M., Hodnik, N., Erbe, A., et al. (2020). What is the trigger for the hydrogen evolution reaction?–towards electrocatalysis beyond the sabatier principle. Phys. Chem. Chem. Phys. 22, 8768–8780. doi:10.1039/D0CP01108H |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Spanos, I., Masa, J., Rohwerder, M., and Schlögl, R. (2021). Perspective on experimental evaluation of adsorption energies at solid/liquid interfaces. J. Solid State Electrochem. 25, 33–42. doi:10.1007/s10008-020-04815-8

CrossRef Full Text | Google Scholar

Zeradjanin, A. R. (2018a). Frequent pitfalls in the characterization of electrodes designed for electrochemical energy conversion and storage. ChemSusChem 11, 1278–1284. doi:10.1002/cssc.201702287 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeradjanin, A. R. (2018b). Is a major breakthrough in the oxygen electrocatalysis possible?. Current Opinion in Electrochemistry 9, 214–223. doi:10.1016/j.coelec.2018.04.006

CrossRef Full Text | Google Scholar

Zhou, Z., Zaman, W. Q., Sun, W., Zhang, H., Tariq, M., Cao, L., et al. (2019). Effective strain engineering of IrO 2 toward improved oxygen evolution catalysis through a catalyst‐support system. ChemElectroChem 6, 4586–4594. doi:10.1002/celc.201901037

CrossRef Full Text | Google Scholar