Storage-Transmission Joint Planning Method to Deal with Insufficient Flexibility and Transmission Congestion

The insufficient power system flexibility and transmission congestion are two fundamental reasons for wind power curtailment. As the scale of the wind power in the power system is growing rapidly, the two factors of wind power curtailment events coexist and have a certain coupling relationship. The configuration of the energy storage system can not only increase the flexibility of the system but also alleviate transmission congestion. Therefore, the joint planning of energy storage and transmission grid that takes into account the flexibility of the system and the transmission congestion is of great significance to solve the wind curtailment. Hence, this paper first decouples the insufficient flexibility and transmission congestion wind power curtailment, and quantitatively analyzes the impact of transmission capacity on the coupling relationship between the two; second, reveals the principle of joint planning of energy storage system and transmission congestion, and constructs an optimization model, and proposes to set up the capacity of the wind power which connects the power network. The solution procedure, which deals with grid planning and the energy storage system optimization in turn, not only ensures the accuracy of the model, but also significantly reduces the calculation cost. Finally, a case study of a wind power base in Northeast China and an improved Garver-6 system are carried out to verify the effectiveness of the proposed method.

Introduction

Vigorously developing wind power is an important measure to promote the low-carbon transformation of energy and respond to the energy crisis and climate change. The development of wind power has increased rapidly in the past 10 years, from the installed capacity of 159.21 million kW in 2009 to 651 million kW in 2019, an increase of more than five times (GWEC, 2019). And countries all over the world have formulated a vision for the development of renewable energy in 2050 (Han et al., 2014; Price water house Coopers LLP et al., 2014). However, in the rapid development of wind power, the issue of wind power curtailment has not been effectively solved. For example, in China, the installed wind power capacity which was 210.05 million kW in 2019 is 8.1 times that of 25.805 million kW in 2009. During this period, the wind curtailment rate remained high, and the curtailment rate in 2015 and 2016 was as high as 15% and 17% respectively (NEA, 2016). Although the curtailment rate in 2019 reached 4%, there are still some areas with the curtailment rate as high as 14% (National Energy Administration, 2020). Therefore, analyzing the causes of wind curtailment and taking measures scientifically to alleviate or eliminate wind power curtailment is of vital importance to the healthy development of wind power in the future.

The main challenges for solving the wind power curtailment in the power system mainly includes two aspects: one is that the thermal power system lacks sufficiently available downward capacity due to its limitation of minimum technological output, which cannot guarantee effective wind power accommodation (Li et al., 2020; Wang et al., 2020). Another one is the wind power transmission congestion which is due to insufficient available transmission capacity. This normally results from that the construction of the power grid lags behind the development of wind power or the transmission capacity of the planned construction is inadequate (Jorgenson et al., 2017). In addition, in the system where the wind power base is far away from the load center and the proportion of thermal power units is large, the lack of flexibility and transmission congestion exist at the same time. If only considering the power supply side, the flexibility transformation of thermal power units (Zhou and Wang, 2017; Wang et al., 2019) and configuration of energy storage can increase the flexibility of the system. Although the problem of wind abandonment has been alleviated to a certain extent, there will still be wind curtailment caused by transmission congestion. Similarly, if only the transmission network expansion planning has carried out (Correa et al., 2016; Gan et al., 2016; Zhang et al., 2019), although the transmission congestion problem is solved, the wind curtailment caused by the lack of system flexibility still exists. Moreover, the downward regulation capacity of the system can be increased through the configuration of energy storage or flexible transformation of thermal power units at the power supply side. Simultaneously, the problem of transmission congestion can be solved by constructing more transmission lines from the power grid side. Although the above solutions can effectively overcome the wind power curtailment, they will result in the investment overlap, following the huge cost investment and low asset utilization rate.

The energy storage system is a high-quality and flexible resource with time migration ability of power and energy and flexible installation location. Large-scale energy storage system technology is considered as one of the key technical supports for the popularization of renewable energy (Li et al., 2019). The configuration of the energy storage system can not only increase the flexibility of the power supply side but also reduce the peak wind power to alleviate transmission congestion. Therefore, in the context of large-scale wind power grid integration, research on joint planning of energy storage and transmission grids to deal with insufficient flexibility and transmission congestion is of great significance to the overall economy of the system and reducing wind curtailment.

In recent years, many scholars have carried out a series of fruitful work to alleviate the wind curtailment problem, such as energy storage optimization configuration (Dicorato et al., 2012; Del Rosso and Eckroad, 2014; Zheng et al., 2015b; Lu et al., 2018; Masoumzadeh et al., 2018; Al Ahmad and Sirjani, 2020; Padhee et al., 2020), and joint planning of energy storage and transmission grids (Zheng et al., 2015a; Qiu et al., 2017; Bustos et al., 2018; Dvorkin et al., 2018; Jorgenson et al., 2018; Yacar et al., 2018; Zhang and Conejo, 2018; Nikoobakht and Aghaei, 2019; Sima et al., 2019; Wu and Jiang, 2019). In terms of energy storage optimization configuration, Padhee et al., (2020) proposed a hybrid energy storage optimization configuration method for the intermittency and uncertainty of renewable energy, while Al Ahmad and Sirjani (2020) combined the discretization method, multi-objective hybrid particle swarm algorithm and non-dominated sorting genetic algorithm. Zheng et al., (2015a) proposed a two-level planning model that considers the layout and operation of the energy storage system, and it has reached the goal of increasing the penetration rate of wind power. The poor predictability of wind power results in a large change in the actual power generation and the forecasted power in the power market. Dicorato et al., (2012) to meet the hourly electricity curve required by the day-ahead market, a joint planning and operation method for wind power and energy storage system is proposed. The fluctuation of renewable energy output brings about the problem of fluctuations in electricity prices. Masoumzadeh et al., (2018) using energy storage makes the electricity market price fluctuate at a certain level. Energy storage configuration can not only increase the flexibility of the system (Lu et al., 2018), but also delay the construction of transmission lines (Del Rosso and Eckroad, 2014), so the joint planning of energy storage and transmission grids has attracted extensive research interest. Yacar et al., (2018) explores the impact of transmission congestion, loss and different intermittent degree of wind power on energy storage layout and investment (Jorgenson et al., 2018). Comparatively analyzed the respective effects of the deployment of the energy storage system and the expansion plan of the transmission grid in reducing wind power curtailment and solar curtailment and gave the effect of mitigating wind power curtailment that the coordinated planning of the two is superior to their respective plans. Bustos et al., (2018) use of hourly energy requirements for coordinated planning of energy storage and transmission grid verified that the energy storage system is both a supplement to and a substitute for transmission lines. Alleviating transmission congestion can benefit the Energy storage situation. If the expansion of transmission lines will reduce or eliminate such benefits (Dvorkin et al., 2018), fully considered the benefits and return rates of the entire life cycle of the energy storage system, and constructed joint planning of energy storage system layout and transmission grid frame. The capacity of energy storage will decrease over time (Qiu et al., 2017), constructed a joint optimization plan for transmission grid and energy storage system that considers changes in energy storage capacity. Because of the uncertainty of renewable energy (Zhang and Conejo, 2018), from the perspective of system planners proposed an optimization model for the coordinated expansion planning of transmission and energy storage system that considers long-term and short-term uncertainties. Nikoobakht and Aghaei (2019) proposed a continuous-time model based on stochastic robust optimization technology to coordinate the planning model of transmission expansion and energy storage system. Zheng et al., (2015a), Sima et al., (2019), Wu and Jiang (2019) incorporated system operating and wind power curtailment costs into the joint planning of the energy storage system and transmission grid. Although it can improve the planning economy and reduce wind power curtailment, there is a problem of the excessive computational burden based on timing simulation.

The above references have carried out fruitful research on the optimal configuration of energy storage and the joint planning of energy storage and transmission network from different perspectives. However, there are few studies on the coupling relationship between wind curtailment caused by different reasons. During the joint planning of energy storage and transmission network, only the wind curtailment cost and energy storage operation cost are added into the planning model, and planning boundaries of wind power grid connection points are still calculated based on installed capacity. The joint planning does not make full use of analyzing the coupling relationship between energy storage efficiency and wind abandonment for different reasons and the principle of joint planning of transmission grid to reduce wind abandonment, and there is a problem that the calculation amount of the existing model solving method based on time series simulation is too large. To this end, this paper considers both system flexibility and transmission congestion. It constructs a joint planning method for the energy storage system and transmission grid to deal with insufficient system flexibility and transmission congestion. Firstly, decoupled the insufficient flexibility and the transmission congestion wind power curtailment, and analyzed the time-series coupling relationship between the two under different planning boundaries of the wind farm grid connection point; secondly, build a joint planning model of the energy storage system and transmission grid to deal with insufficient flexibility and transmission congestion on this basis; Finally, designed an iterative solution algorithm to optimize the configuration of energy storage after grid planning, that is, first set the grid-connected point capacity of the dynamic wind power to obtain the grid planning scheme, and obtain the total abandonment of the system under the grid planning topology, and then optimize between the energy storage system and the total system wind power curtailment, in the end, iterate the process repeatedly to arrive at an optimal plan for energy storage and transmission grid.

The main contributions of this paper are as follows:

1 By assuming sufficient power transmission capacity, the wind power curtailment caused by insufficient flexibility can be obtained, while assuming sufficient system flexibility, the wind power curtailment by transmission congestion can be obtained, and the decoupling is realized;

2 This article plans the boundary by changing the wind power grid connection point and the obstructed wind power curtailment is obtained at grid points under different planned boundary capacities and established the relationship between total curtailed wind power curtailment and grid-connected point capacity. Optimizing the configuration of energy storage system based on the total wind power curtailment can vastly reduce the difficulty of solving the joint planning model of the energy storage system and transmission grid, and also solve the double dilemma of the excessive shortage of capacity settings at wind power grid connection point;

3 The joint planning method of energy storage and transmission network is constructed to deal with the lack of flexibility and transmission congestion, which can fundamentally alleviate and solve the problem of wind power curtailment, and improve the utilization rate of energy storage and transmission network.

Analysis of the Coupling Relationship Between Insufficient Flexibility and Transmission Congestion

Large-scale grid integration of wind power puts higher requirements on the system's flexibility capacity and power transmission capacity. The occurrence of wind power curtailment is the main result of the combined effect of insufficient system flexibility and power transmission capacity. However, there is a certain coupling relationship between the abandonment wind of transmission congestion and the lack of flexibility in the unified system.

Quantitative Analysis of Wind Power Curtailment Caused by Insufficient System Flexibility

Assuming that the transmission capacity of the system is fully sufficient, analyze the relationship between the system flexibility and the wind power curtailment. Wind power consumption of the system is determined by flexibility (peak regulation depth) provided by conventional thermal power units. The "wind power feasible region" is defined as the daily dispatch time scale, and the difference between the load and the minimum technical output of the conventional units is the maximum wind power allowed by the system, and the formula is expressed as (1)

$P_{\text{FR}-i}\left(t\right)=P_{\text{D}-i}\left(t\right)-P_{\text{G}.\min -i}(1)$

In formula (1), P_FR-i(t) is the maximum wind power that the system can accept on dispatching day i; P_D-i(t) is the load value at time t on dispatching day i; P_{G. min-i} is the minimum technology for conventional units on dispatching day i contribute.

However, Windpower integration reduces the start-up capacity of conventional units. To ensure the reliability of power supply and consider the uncertainty of wind power output, the start-up capacity of conventional units after wind power is connected is (2)

$P_{\text{G}-i}=(P_{\text{D}.\max -i}-P_{\text{W}.\min -i})(1+k)(2)$

In formula (2), P_G-i, P_{D. max-i}, P_{W. min-i,} and k are the starting capacity, maximum load, minimum wind power, and standby coefficient of conventional units on dispatch day i, respectively.

After knowing the available wind power on the dispatch day i, the wind power beyond the feasible range of wind power will not be absorbed. The expression of wind power curtailment caused by insufficient flexibility system is (3)

$P_{\text{LG}-i}\left(t\right)=\{\begin{array}{ll}0,\hfill & P_{\text{W}-i}\left(t\right)<P_{\text{FR}-i}\left(t\right)\hfill \\ P_{\text{W}-i}\left(t\right)-P_{\text{FR}-i}\left(t\right),\hfill & P_{\text{W}-i}\left(t\right)\ge P_{\text{FR}-i}\left(t\right)\hfill \end{array}(3)$

In formula (3), P_LG-i(t) is the wind power curtailment caused by insufficient flexibility at time t within the scheduling day i. Figure 1 shows the feasible region and wind power curtailment in seven dispatch days.

FIGURE 1

FIGURE 1. Wind power consumption space and wind power curtailment.

Quantitative Analysis of Blockage and Abandonment Caused by Insufficient Transmission Capacity

Assuming that the system is sufficiently flexible, the relationship between transmission capacity and wind power curtailment is analyzed, that is the relationship between the planning of boundary wind power grid connection point and the abandoned wind congestion power. When the wind power P_W-i is greater than the transmission capacity P_line of the transmission grid, the phenomenon of wind-blocking and curtailment power occurs. The expression of blocked wind power is (4)

$P_{\text{LT}-i}\left(t\right)=\{\begin{array}{ll}0,\hfill & P_{\text{W}-i}\left(t\right)<P_{\text{line}}\hfill \\ P_{\text{W}-i}\left(t\right)-P_L,\hfill & P_{\text{W}-i}\left(t\right)\ge P_{\text{line}}\hfill \end{array}(4)$

In formula (4), P_LT-i(t) is the blocked wind power curtailment power generated at time t within the scheduling day i. Figure 2 shows the blocked abandonment power during seven dispatch days.

FIGURE 2

FIGURE 2. Transmission capacity and blocked wind power curtailment.

Coupling Relationship Between Two Factors Causing by Wind Power Curtailment

The total abandonment power is obtained by coupling the abandonment power caused by the above two factors. The formula is as (5).

$P_{LW-i}\left(t\right)=P_{LG-i}\left(t\right)\cup P_{LT-i}\left(t\right)(5)$

In formula (5), P_LW-i(t) is the total abandonment power at time t within the dispatch day i. Figure 3 shows the total abandonment, which is a result of the coupling of insufficient flexibility abandonment and blocking wind power curtailment in seven dispatch days.

FIGURE 3

FIGURE 3. The coupling of insufficient flexibility and blocked wind power curtailment.

Because the load is relatively stable with conventional units, the system's wind power absorption space is relatively stable, and the wind power curtailment caused by insufficient flexibility is relatively stable. However, when planning for the expansion of the transmission grid, the transmission capacity of wind power is different, and the generated wind power is also different. If the power transmission capacity of wind power curtailment power is sufficient, no obstruction or wind power curtailment will occur; if the transmission capacity of wind power is insufficient, wind power obstruction and curtailment will occur.

Taking the networking system of a wind power base in Northeast China as the analysis object, the installed capacity of wind power is 1900 MW, the maximum output per unit value is 0.77, and the system load is 3769 MW. Set up different transmission capacity P_line, then analyze the relationship between blocked wind power curtailment, insufficient flexibility curtailment, total wind power curtailment, and curtailment duration. Among them, ΔE₁ and T₁ are the power and duration caused by the transmission congestion throughout the year; ΔE₂ and T₂ are the power and duration of wind power curtailment guided by insufficient flexibility; ΔE and T are the total power and duration of wind power curtailment throughout the year, respectively.

It can be seen from Table 1:

1 When the transmission capacity is greater than the maximum wind power, the system wind power curtailment is determined by the power flexibility capacity, and the transmission capacity which is greater than the maximum wind power will not be used, resulting in excessive transmission investment;

2 When the transmission capacity is less than the maximum wind power, the blocked wind will be curtailed; when the transmission capacity decreases in steps of 0.1, the blocked wind power ΔE₁ and T₁ will increase accordingly, and the total power and duration of the system will be less than the sum of flexibility and insufficient wind power curtailment. Obstruction wind power curtailment shows that there is a certain overlap between the two wind power curtailment, as shown in Figure 3.

TABLE 1

TABLE 1. ΔP, ΔE and duration T under different Pline.

Principles of Coordinated Planning Between the Energy Storage System and Transmission

In the power system with a rapidly growing scale of wind power, insufficient flexibility wind power curtailment coexists. To completely solve or improve wind power curtailment, ensure that the system has sufficient flexibility and transmission capacity is necessary.

Based on the above analysis, there is a certain overlap between the two wind power curtailment events, and wind power generation has low energy density characteristics. The configuration of the energy storage system can increase the flexibility of the system, and it can also reduce the transmission demand for wind power at the same time. Therefore, in planning, the coordination and optimization of the energy storage system and transmission lines can significantly reduce wind power curtailment and increase the utilization rate of energy storage and transmission grid. On the one hand, it can increase system flexibility. On the other hand, it can reduce the nature of the storage-transmission joint planning to cope with insufficient flexibility and transmission congestion. The essence of the joint planning is to reduce wind power curtailment while achieving coordinated configuration between the energy storage system and transmission lines, and to minimize the comprehensive cost including transmission investment, energy storage system investment, power generation cost and wind power curtailment cost.

The specific planning principle is: the first step is to input wind power data and load data for the planning target year and give the initial grid topology and conventional power supply structure. In the second step, assuming sufficient power transmission capacity, a time-series simulation is performed to calculate the flexibility and wind power curtailment through the feasible region of wind power. The third step assumes that the flexibility capacity is sufficient, and the power flow is calculated based on a given power topology to get the blocking wind power curtailment. The fourth step is to couple the insufficient flexibility and the blocking wind power curtailment to obtain the system wind power curtailment. The fifth step is to configure energy storage system, and calculate the comprehensive costs including transmission investment, energy storage system investment, power generation cost, and wind power curtailment cost, and then modify the energy storage system configuration to repeatedly calculate the optimal configuration of energy storage system under the current grid topology. Revise the capacity of the wind power grid-connected point (that is, modify the planning boundary of the wind power grid-connected point), obtain a new grid topology through grid planning, and repeat the first step to the fifth step until the optimal plan for the coordinated planning of energy storage system and transmission lines is obtained. The specific principles are shown in Figure 4.

FIGURE 4

FIGURE 4. Principles of storage-transmission joint planning.

The Storage-Transmission Joint Optimization Planning Model

Planning Model

To achieve the goal of minimizing comprehensive costs such as transmission investment, energy storage investment and wind curtailment cost, this article comprehensively considers the coupling relationship between insufficient flexibility system and wind power curtailment and transmission congestion, and builds a storage-transmission joint optimization model to deal with insufficient flexibility and transmission congestion, and realizes coordination and optimization between energy storage system configuration and expansion of transmission lines. The objective function formula is as (6) (Wang et al., 2019):

$F=\min \left[I\left(P_{\text{line}}\right)+I(P_{\text{ess}},E_{\text{ess}})+L(P_{\text{line}},E_{\text{ess}})\right](6)$

In formula (6), I (P_line) is the cost of transmission lines expansion; I (P_ess, E_ess) is the investment cost of configuring energy storage system; L (P_line, E_ess) is the cost of wind power curtailment.

(1) Expansion cost of transmission lines: Transmission line expansion cost is the sum of all expansion line costs.

$I\left(P_{\text{line}}\right)={\displaystyle \sum _{i\in \Omega }{n}_i{C}_i{L}_i{Z}_i},C_i=K_l{P}_{l-i}(7)$

In formula (7), n_i is the number of construction times of the ith candidate line; C_i is the unit price per unit length of the ith candidate line, K_l is the unit power cost per unit length of the line, L_i is the length of the ith candidate line, and Z_i is the ith of the 0–1 decision variable for the investment of the line to be selected, P_l-i is the transmission capacity of the ith line to be selected; Ω is the set of lines to be selected.

(2) Energy storage system investment cost: Energy storage investment cost is the sum of energy storage power cost and energy storage capacity cost (Al Ahmad and Sirjani, 2020).

$I(P_{\text{ess}},E_{\text{ess}})=P_{\text{ess}}\times K_{\text{Pess}}+E_{\text{ess}}\times K_{\text{E}}(8)$

In formula (8), K_pess is the purchase cost per unit power converter; K_E is the purchase cost per unit capacity of the energy storage system.

(3) Loss cost of abandoned wind power

$L(P_{\text{line}},E_{\text{ess}})=K_{\text{W}}\times T_{\text{S}}\times {\displaystyle \sum _{i=1}^{365}\left({\displaystyle {\int }_0^{24}{P}_{LW-i}\left(t\right)\text{d}t-\Delta W_{\text{ess}-i}}\right)}(9)$

In formula (9), K_w is the penalty value of wind power curtailment per unit, T_s is the planning period, and ΔW_ess-i is the wind power curtailment absorbed by the energy storage on the ith dispatch day.

Constraints

(1) Transmission limit constraint of transmission lines: The power flow of the ith transmission line shall be less than its maximum power flow (Qiu et al., 2017).

$P_i^{\max }<n_i{P}_{l-i}{Z}_i(10)$

P_imax is the maximum flow of the i transmission line.

(2) Power balance constraint: The sum of thermal power units, wind power, energy storage and abandon wind power needs to keep balance with the load (Qiu et al., 2017; Zhang and Conejo, 2018).

${\displaystyle \sum _k{P}_{\text{gk}}\left(t\right)+P_{\text{w}}\left(t\right)+P_{\text{ess}}\left(t\right)+\Delta P_{\text{w}}\left(t\right)=P_{\text{l}}\left(t\right)}(11)$

Where is the output power of all thermal power units at time t; P_w(t) is the output power of the wind farm group at time t; P_ess(t) is the output power at time t of the energy storage system; ΔP_w(t) is the abandoned wind power at time t; P_l(t) is the total system load at time t.

(3) The state of charge of the energy storage system and Nissin constraints: The soc of the energy storage system is limited between the minimum SOC and the maximum SOC, and the SOC at the beginning and end of each day is the same (Nikoobakht and Aghaei, 2019; Wu and Jiang, 2019).

$\{\begin{array}{l}{\text{SOC}}_{\min }\le \text{SOC}\left(t\right)\le {\text{SOC}}_{\max }\\ \text{SOC}\left(0\right)=\text{SOC}\left(24\right)\end{array}(12)$

(4) The upper and lower limits of the output of thermal power units: The output limit of the thermal power unit is limited to the minimum output limit and rated capacity (Zheng et al., 2015a).

$P_{\text{g}k}^{\min }\le P_{\text{g}k}\left(t\right)\le P_{\text{g}k}^{\max }(13)$

(5) System and branch flow constraint (Zheng et al., 2015a)

$\text{B}\mathrm{\theta }=P_{\text{G}}+P_{\text{w}}+P_{\text{ess}}-P_{\text{L}}(14)$

In formula(13), B is the node admittance matrix; θ is the node voltage phase angle vector; P_G is the output power vector of the thermal power unit; P_w is the output power vector of the wind farm; P_ess is the output power vector of the energy storage system device; P_L is the load power vector.

(6) Electricity balance constraint: The sum of thermal power generation and wind power generation is not less than the sum of abandoned wind power and load power (Sima et al., 2019).

${\text{W}}_{\text{g}}+{\text{W}}_{\text{w}}-\Delta {\text{W}}_{\text{w}}\ge {\text{W}}_L(15)$

In formula (12), W_g, W_w, ΔW_w, W_L are the power of thermal power units, wind power generation, wind power generation, and load power respectively.

Case Studies

In order to verify the feasibility and effectivity of the proposed method, this paper analyzes a case of a wind power base in Northeast China and a modified Garver-6 node system, the relevant parameters of wind turbines are shown in Appendix Table A1. At the same time, the method in this paper and the traditional energy storage and transmission in literature (Sima et al., 2019), grid planning method without energy storage are contracted. Convenient for expression, the above method is named, and abbreviations:

(1) STJP, the method in this paper named: Storage-transmission joint planning method to deal with insufficient flexibility and transmission congestion, abbreviation: STJP

(2) STP, the traditional storage and coordinate grid planning method in literature (Sima et al., 2019), namely boundary according to the installed capacity for wind power grid planning, abbreviation: STP

(3) NSTP, without energy storage in the transmission planning method, abbreviation: NSTP

The given basic calculation conditions are:

(1) Unit comprehensive cost of 220 kV transmission project K_l = 10 thousand yuan/(km MW);

(2) Unit capacity cost of energy storage system K_E = 1.5 million yuan/MW h;

(3) The unit cost of converter K_Pess = 500,000 yuan/MW;

(4) Unit wind power curtailment penalty Kw = 0.083 million/MW h;

(5) Energy storage system life of 10 years;

(6) Planning period T_s = 20 years;

Testing System 1-Centralized Outward Transmission and Transmission Project of the Wind Power Base

The installed capacity of wind power in the centralized transmission system of a wind power base in Northeast China is 1900 MW, the maximum wind power is 1463 MW, the grid side load is 3769 MW, the total length of the transmission channel is 184 km, and the wind power base network topology is shown in Figure 5.

FIGURE 5

FIGURE 5. Wind farm cluster centralized grid.

To deeply analyze the interaction among transmission capacity, wind abandonment and energy storage in the planning process, based on the transmission capacity of the single-circuit transmission line, the outgoing transmission capacity of the wind power base is set as a continuous value, that is, the transmission capacity can change in 1 MW steps. Therefore, two examples of transmission capacity with continuous value and engineering value are shown.

(1) The transmission capacity as a continuous value

Use the storage-transmission joint optimization model proposed in this paper to deal with insufficient flexibility and transmission congestion. The optimization scheme obtained is shown in Table 2. When the wind power transmission channel capacity is 1253 MW, the energy storage system charge/discharge power is 178 MW, and the capacity is 358 MW h, the optimal total cost is 7.265 billion yuan.

TABLE 2

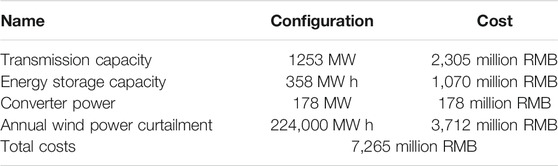
TABLE 2. Coordination and optimization results of energy storage and transmission channels (continuous value).

The centralized transmission capacity of wind power is reduced in steps of 100 MW. The relationship between the wind power congestion and the total wind power curtailment of the system is analyzed, as shown in Figure 6. It can be seen from the figure that when the transmission capacity is 1500 MW, the wind power curtailment of the system is insufficient for flexibility; when the transmission capacity continues to decrease, the blocked wind power curtailment starts to increase, and the total system wind power curtailment also increases, but the blocked wind power curtailment increases more than the total Wind power curtailment grows at a rapid rate. Eventually, wind power curtailment includes insufficient flexibility and wind power curtailment. The total wind power curtailment of the system coincides with the blocked.

FIGURE 6

FIGURE 6. Wind farm cluster centralized grid.

The changing trend of total costs in the process of coordination and optimization of the energy storage system and transmission capacity is shown in Figure 7A. The relationship between transmission capacity and total costs present a downward concave surface. In the process of increasing transmission capacity, the initial total costs are discarded. The total costs of wind are dominated, and the total costs of power transmission are dominated by the transmission investment cost when the optimal solution is reached. The optimal solution is marked with a yellow origin, and the horizontal and vertical directions of the optimal solution are the relationship between transmission capacity, energy storage system capacity and total costs, as shown in Figures 7B,C.

(2) Transmission lines capacity is engineering value

FIGURE 7

FIGURE 7. Windfarm cluster centralized grid.

After consulting relevant information, the transmission limit of a 220 kV transmission line of 184 km is 300 MW. Under these conditions, this paper compares the various performance of system parameters amount the proposed method STJP, STP (Sima et al., 2019) and NSTP. The comparison results of the above methods are shown in Table 3.

TABLE 3

TABLE 3. Comparison of planning schemes (engineering value).

As can be seen from Table 3, the proposed STJP can effectively reduce the annual wind power curtailment. To be more exact, it is reduced by 5 × 10³ MW h and 57 × 10³ MW h compared with the STJ method and NSTP method, respectively. In addition, the transmission capacity has dropped from 1800 to 1200 MW when using the proposed STJP. This improves the percentage of utilization of transmission assets. Although the energy storage capacity has increased by 31.7% compared with the STP, the total costs when using STJP method are much lower than the other two costs with STP and NSTP.

As is shown in Figure 8, the red line demonstrates the generated wind curtailment due to system’s lack of flexibility, whereas the blue one refers to the generated wind curtailment due to transmission congestion. In order the analyze the results of wind curtailment in different condition, the comparison has been made as below. Without consideration of transmission congestion, the summation of wind curtailment in each time period within one year is nearly 2.78 × 10⁵ MW h. However, the summation of wind curtailment in each time period within one year is nearly2.89 × 10⁵ MW h when the consideration is given to the lack of flexibility and transmission congestion. In addition, the sub-figure mainly illustrates the coupling relationship between the lack of flexibility and transmission congestion that lead to wind curtailment. During the period from 1,470 to 1715, there is an overlap of wind curtailment, which results from the above two reason. Therefore, when catcalling the summation of wind curtailment, the overlap part should be omitted. Further, the summation of wind curtailment should be less than the wind curtailment caused by lack of flexibility and transmission congestion respectively.

FIGURE 8

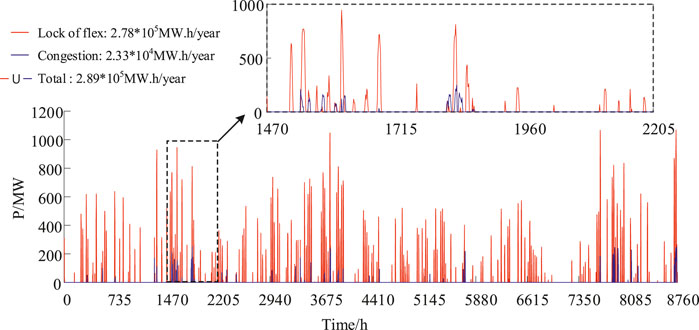
FIGURE 8. Coupling relationship of wind curtailment with an engineering value of transmission capacity.

In summary, the proposed method STJP can make full use of the coupling relationship between insufficient flexibility and wind power transmission congestion, which improves the transmission asset utilization and energy storage efficiency. It also achieves the most optimally economic planning schemes among the three methods.

Testing System 2-Garver6 System

In order to identify the universality of the proposed algorithm, the STJP algorithm is also applied in the cast study 5.2 of Garver6 System.

According to the original calculation example of the Garver-6 node system, the load of each node in the system matches the measured load and wind power data of a certain regional power grid in Northeast China. The total load is 763 MW, 6-node wind power installed capacity is 300 MW, and the maximum wind power is 261 MW. In the storage-transmission joint optimization using STJP of this article on this example system, the most important point here is to change the boundary of the 6-node wind power grid-connected planning during the optimization process (the rule is: the installed capacity is the benchmark, and the 0.1 installed capacity is used as the step size). Then get blocked wind curtailment, and coupled with insufficient flexibility to obtain the total wind curtailment of the system, and finally optimize the energy storage configuration and the wind curtailment loss. Finally, get the plan of the Garver6 system storage-transmission joint planning, the power grid planning scheme is shown in Figure 9.

FIGURE 9

FIGURE 9. Windfarm cluster centralized grid.

In Figure 9 of the overall optimization process, the yellow dot is the optimal solution position of the storage-storage joint planning. As the transmission lines increase or decrease according to the number of lines, the total cost of the wind power grid connection plan increases from small to small, and the total cost first decreases and then increases in a stepwise manner, and several grid-connected planning boundaries are corresponding to the same plan. In the process of energy storage configuration, the total cost is first reduced and then increased during the process of energy storage capacity reduction. The overall optimization process can reflect that the storage-transmission joint planning is effective to deal with insufficient flexibility and transmission congestion and abandonment of wind, which promotes wind power consumption and reduces transmission line investment.

At the same time, STP and NSTP are used for optimization planning. The planning scheme of each planning method is shown in Table 4, grid planning topology is shown in Figure 10, (a) Plan is for STJP, (b) Plan is for STP and NSTP.

TABLE 4

TABLE 4. Different planning methods of Garver6 system.

FIGURE 10

FIGURE 10. Power grid planning scheme.

Figure 11 is similar to Figure 8. In order the analyze the results of wind curtailment in different condition, the comparison has been made as below. Without consideration of transmission congestion, the summation of wind curtailment in each time period within one year is nearly 7.29 × 10⁴ MW h. However, the summation of wind curtailment in each time period within one year is nearly 7.74 × 10⁴ MW h when the consideration is given to the lack of flexibility and transmission congestion. In addition, the sub-figure mainly illustrates the coupling relationship between the lack of flexibility and transmission congestion that lead to wind curtailment. During the period from 1,470 to 1715, there is an overlap of wind curtailment, which results from the above two reason. Therefore, when catcalling the summation of wind curtailment, the overlap part should be omitted.

FIGURE 11

FIGURE 11. Coupling relationship of wind curtailment in Garver6 System.

As can be seen from Table 4, the proposed STJP can effectively reduce the annual wind power curtailment. To be more exact, it is reduced by 6330 MW h and 28,420 MW h compared with the STJ method and NSTP method, respectively. In addition, compared with STJ method and NSTP method, STJP reduces six transmission lines and saves 27 million dollars. In general, although the cost increase of STJP energy storage configuration increases by 72 million dollars, it brings about the decrease of annual wind power curtailment and transmission line investment, thus minimizing the total cost among the three methods.

Conclusion

To solve the wind curtailment caused by large-scale wind power grid integration, this paper first analyzes the coupling relationship between insufficient flexibility and wind abandonment events with power transmission congestion, then a joint planning model is constructed for energy storage and transmission grid to deal with insufficient flexibility and transmission congestion. Finally, a case study has been performed to identify the effectiveness of the proposed method by comparison with.

STP and NSTP methods. The main conclusions are as follows:

1 By applying the planning scheme STJP, the overall system achieve a much lower annual wind power curtailment compared with the other two traditional planning schemes, although it brings a relatively higher energy storage investment, cost of its total investment can be optimized to be far lower than any other planning performance. Taking a wind power base in Northeast China as an example, compared with the STP and NSTP methods, the annual curtailment of wind power is reduced by 2000 MW h and 57000 MW h, respectively, and the total system investment cost has been reduced by 11.3% and 11.8%.

2 During the optimization configuration of STJP, it gradually reduces the planning boundary of the wind power base grid connection point (rather than the installed capacity of the wind power base), and makes full use of the interaction between energy storage and transmission lines, the problem of low asset utilization of wind power transmission and transmission has been better solved. It is also the same case that the transmission capacity has dropped from 1800 to 1200 MW when applying the STJP with joint optimization of energy storage configuration and transmission capacity.

In summary, the method in this paper makes full use of the coupling relationship between insufficient flexibility and transmission congestion. The planning boundary of the grid connection point of the wind power base (below its installed capacity) was reduced, and the utilization rate of energy storage and transmission lines was greatly increased. Meanwhile, the proposed STJP overrides the STP and NSTP in terms of algorithm efficiency and complexity. With the continuous improvement of energy storage technology and the economy, an effective planning method is provided for the realization of a high proportion of renewable energy power system planning.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XY contributed to the conception of the study; GC performed the experiment; XL contributed significantly to analysis and manuscript preparation; MX performed the data analyses and wrote the manuscript; QG helped perform the analysis with constructive discussions.

Funding

This study was supported by the National Key Research and Development Program (2016YFB0900100).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Nomenclature

B The node admittance matrix

C_i The unit price per unit length of the ith candidate line

F Comprehensive cost

I(P_ess, E_ess) The investment cost of configuring energy storage system

I(P_line) The cost of transmission lines expansion

K The standby coefficient of conventional units on dispatch day i, respectively

K_E The purchase cost per unit capacity of the energy storage system

K_l The unit power cost per unit length of the line

K_pess The purchase cost per unit power converter

K_w The penalty value of wind power curtailment per unit

L(P_line, E_ess) The cost of wind power curtailment

L_i The length of the ith candidate line

n_i The number of construction times of the ith candidate line

NSTP The no-storage transmission planning method

P_D.max-i The maximum load of conventional units on dispatch day i, respectively

P_D-i(t) The load value at time t in dispatching day i

P_ess The output power vector of the energy storage system device

P_ess(t) The output power at time t of the energy storage system

P_FR-i(t) The maximum wind power that the system can accept on dispatching day i

P_G The output power vector of the thermal power unit

P_G.min-i The minimum technology for conventional units in dispatching day i contribute

P_G-i The starting capacity of conventional units on dispatch day i, respectively

P_gk(t) The output power of the thermal power unit at t time

P_gk^max The maximum output of thermal power units

P_gk^min The minimum output of thermal power units

P_i^max The maximum flow of the i transmission line

P_line Transmission capacity

P_L The load power vector

P_L(t) The total system load at time t.

P_LG-i(t) The wind power curtailment caused by insufficient flexibility at time t within the scheduling day i

P_l-i The transmission capacity of the ith line to be selected

P_LT-i(t) The blocked wind power curtailment power generated at time t within the scheduling day i.

P_LW-i(t) The total abandonment power at time t within the dispatch day i

P_w The output power vector of the wind farm

P_w(t) The output power of the wind farm group at time t

P_W.min-i The minimum wind power of conventional units on dispatch day i, respectively

SJP The traditional storage joint planning method

SOC(t) The state of charge of the energy storage system

SOC_max The maximum charge of energy storage system

SOC_min The minimum charge of energy storage system

STJP The method in this passage: Storage-transmission joint planning method

T The total duration of wind power curtailment throughout the year

T₁ The duration caused by the transmission congestion throughout the year

T₂ The duration of wind power curtailment guided by insufficient flexibility

T_s The planning period

W_g The power of thermal power units

W_L Load power respectively

W_w Wind power generation

Z_i The ith of the 0–1 decision variable for the investment of the line to be selected

ΔE The total power of wind power curtailment throughout the year

ΔE₁ The power caused by the transmission congestion throughout the year

ΔE₂ The power of wind power curtailment guided by insufficient flexibility

ΔP_w(t) The abandoned wind power at time t

ΔW_ess-i The wind power curtailment absorbed by the energy storage on the ith dispatch day

ΔW_w Wind power generation

θ The node voltage phase angle vector

Ω The set of lines to be selected

Appendix

TABLE A1

TABLE A1. 3 MW double-fed induction wind generator technical parameter.

References

Al Ahmad, A. K., and Sirjani, R. (2020). “Optimal allocation of energy storage system in transmission system considering wind power”, in 7th international conference on electrical and electronics engineering (New York: Institute of Electrical and Electronics Engineers Inc.), 181–187. doi:10.1109/ICEEE49618.2020.9102603

CrossRef Full Text | Google Scholar

Bustos, C., Sauma, E., De La Torre, S., Aguado, J. A., Contreras, J., and Pozo, D. (2018). Energy storage and transmission expansion planning: substitutes or complements?. IET Gener. Transm. Distrib. 12, 1738–1746. doi:10.1049/iet-gtd.2017.0997

CrossRef Full Text | Google Scholar

Correa, C., Sanchez, A., and Marulanda, G. (2016). Expansion of transmission networks considering large wind power penetration and demand uncertainty. IEEE Latin Am. Trans. 14, 1235–1244. doi:10.1109/TLA.2016.7459604

CrossRef Full Text | Google Scholar

Del Rosso, A. D., and Eckroad, S. W. (2014). Energy storage for relief of transmission congestion. IEEE Trans. Smart Grid. 5, 1138–1146. doi:10.1109/TSG.2013.2277411

CrossRef Full Text | Google Scholar

Dicorato, M., Forte, G., Pisani, M., and Trovato, M. (2012). Planning and operating combined wind-storage system in electricity market. IEEE Trans. Sustain. Energy. 3, 209–217. doi:10.1109/TSTE.2011.2179953

CrossRef Full Text | Google Scholar

Dvorkin, Y., Ricardo, F.-B., Wang, Y., Xu, B., Kirschen, D. S., Pandi, H., et al. (2018). Co-planning of investments in transmission and merchant energy storage. IEEE Trans. Power Syst. 33, 245–256. doi:10.1109/TPWRS.2017.2705187

CrossRef Full Text | Google Scholar

Gan, L., Li, G. Y., and Zhou, M. (2016). Coordinated planning of large-scale wind farm integration system and regional transmission network considering static voltage stability constraints. Electr. Power Syst. Res. 136, 298–308. doi:10.1016/j.epsr.2016.03.002

CrossRef Full Text | Google Scholar

GWEC (2019). Global Wind Report 2019 [Online]. Available online at: https://gwec.net/docs/global-wind-report-2019/.

Hand, M. M., Baldwin, S., and De Meo, E. (2014). Renewable electricity futures study. Colorado: National Renewable Energy Laboratory.

Jorgenson, J., Denholm, P., and Mai, T. (2018). Analyzing storage for wind integration in a transmission-constrained power system. Appl. Energy. 228, 122–129. doi:10.1016/j.apenergy.2018.06.046

CrossRef Full Text | Google Scholar

Jorgenson, J., Mai, T., and Brinkman, G. (2017). Reducing wind curtailment through transmission expansion in a wind vision future. NREL/TP-6A20-67240

Li, Y., Wang, C., Li, G., Wang, J., Zhao, D., and Chen, C. (2020). Improving operational flexibility of integrated energy system with uncertain renewable generations considering thermal inertia of buildings. Energy Convers. Manag. 207, 2526. doi:10.1016/j.enconman.2020.112526

CrossRef Full Text | Google Scholar

Li, Y., Yang, Z., Li, G. Q., Zhao, D. B., and Tian, W. (2019). Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties. IEEE Trans. Ind. Electron. 66, 1565–1575. doi:10.1109/TIE.2018.2840498

CrossRef Full Text | Google Scholar

Lu, Z., Li, H., and Qiao, Y. (2018). Probabilistic flexibility evaluation for power system planning considering its association with renewable power curtailment. IEEE Trans. Power Syst. 33, 3285–3295. doi:10.1109/TPWRS.2018.2810091

CrossRef Full Text | Google Scholar

Masoumzadeh, A., Nekouei, E., Alpcan, T., and Chattopadhyay, D. (2018). Impact of optimal storage allocation on price volatility in energy-only electricity markets. IEEE Trans. Power Syst. 33, 1903–1914. doi:10.1109/TPWRS.2017.2727075

CrossRef Full Text | Google Scholar

National Energy Administration (2020). Grid connected operation of wind power in 2019 (in Chinese) [Online]. Available online at: http://www.nea.gov.cn/2020-02/28/c_138827910.htm.

NEA (2016). Chinese wind curtailment hit 15% in 2015 on 33GW of new capacity [Online]. Available online at: http://www.rechargenews.com/wind/867893/chinese-wind-curtailment-hit-15-percent-in-2015-on-33gw-of-new-capacity-nea.

Nikoobakht, A., and Aghaei, J. (2019). Integrated transmission and storage systems investment planning hosting wind power generation: continuous-time hybrid stochastic/robust optimisation. IET Gener. Transm. Distrib. 13, 4870–4879. doi:10.1049/iet-gtd.2019.0257

CrossRef Full Text | Google Scholar

Padhee, M., Pal, A., Mishra, C., and Vance, K. A. (2020). A fixed-flexible BESS allocation scheme for transmission networks considering uncertainties. IEEE Trans. Sustain. Energy. 11, 1883–1897. doi:10.1109/TSTE.2019.2946133

CrossRef Full Text | Google Scholar

Price Water House Coopers LLP (PwC) (2014). Potsdam institute for climate impact research (PIK), and international institute for applied systems analysis (IIASA)% renewable electricity: a roadmap to 2050 for europe and North Africa.

Qiu, T., Xu, B., Wang, Y., Dvorkin, Y., and Kirschen, D. S. (2017). Stochastic multistage coplanning of transmission expansion and energy storage. IEEE Trans. Power Syst. 32, 643–651. doi:10.1109/TPWRS.2016.2553678

CrossRef Full Text | Google Scholar

Sima, C. A., Popescu, M. O., Popescu, C. L., and Lazaroiu, G. (2019). “Integrating energy storage systems and transmission expansion planning in renewable energy sources power systems”, in 54th international universities power engineering conference (New York: Institute of Electrical and Electronics Engineers Inc.). doi:10.1109/UPEC.2019.889348

CrossRef Full Text | Google Scholar

Wang, Y. C., Lou, S. H., Wu, Y. W., and Wang, S. R. (2020). Flexible operation of retrofitted coal-fired power plants to reduce wind curtailment considering thermal energy storage. IEEE Trans. Power Syst. 35, 1178–1187. doi:10.1109/TPWRS.2019.2940725

CrossRef Full Text | Google Scholar

Wang, Y., Lou, S., Wu, Y., Lv, M., and Wang, S. (2019). Coordinated planning of transmission expansion and coal-fired power plants flexibility retrofits to accommodate the high penetration of wind power. IET Gener. Transm. Distrib. 13, 4702–4711. doi:10.1049/iet-gtd.2018.5182

CrossRef Full Text | Google Scholar

Wu, X., and Jiang, Y. (2019). Source-network-storage joint planning considering energy storage systems and wind power integration. IEEE Access. 7, 137330–137343. doi:10.1109/ACCESS.2019.2942134

CrossRef Full Text | Google Scholar

Yacar, D., Tejada-Arango, D. A., and Wogrin, S. (2018). Storage allocation and investment optimisation for transmission-constrained networks considering losses and high renewable penetration. IET Renew. Power Gener. 12, 1949–1956. doi:10.1049/iet-rpg.2018.5472

CrossRef Full Text | Google Scholar

Zhang, H., Zhang, S., Cheng, H., Wang, Z., and Zhang, J. (2019). “Probabilistic transmission network expansion planning considering integration of wind power”, in IEEE PES innovative Smart grid technologies Asia. (New York: ISGTInstitute of Electrical and Electronics Engineers Inc.), 3194–3198. doi:10.1109/ISGT-Asia.2019.8881768

CrossRef Full Text | Google Scholar

Zhang, X., and Conejo, A. J. (2018). Coordinated investment in transmission and storage systems representing long- and short-term uncertainty. IEEE Trans. Power Syst. 33, 7143–7151. doi:10.1109/TPWRS.2018.2842045

CrossRef Full Text | Google Scholar

Zheng, J., Wen, F., Zhou, M., Hu, L., Xu, Q., and Lan, Z. (2015a). “Transmission planning with renewable generation and energy storage”, in 10th international conference on Advances in power system control, operation and management. (New York: Institution of Engineering and Technology). doi:10.1049/ic.2015.0224

CrossRef Full Text | Google Scholar

Zheng, L., Hu, W., Lu, Q., and Min, Y. (2015b). Optimal energy storage system allocation and operation for improving wind power penetration. IET Gener. Transm. Distrib. 9, 2672–2678. doi:10.1049/iet-gtd.2014.1168

CrossRef Full Text | Google Scholar

Zhou, Y. L., and Wang, D. (2017). An improved coordinated control technology for coal-fired boiler-turbine plant based on flexible steam extraction system. Appl. Therm. Eng. 125, 1047–1060. doi:10.1016/j.applthermaleng.2017.07.077

CrossRef Full Text | Google Scholar