Computational Screening of Doped Graphene Electrodes for Alkaline CO2 Reduction

The electrocatalytic CO₂ reduction reaction (CO₂RR) is considered as one of the most promising approaches to synthesizing carbonaceous fuels and chemicals without utilizing fossil resources. However, current technologies are still in the early phase focusing primarily on identifying optimal electrode materials and reaction conditions. Doped graphene-based materials are among the best CO₂RR electrocatalysts and in the present work we have performed a computational screening study to identify suitable graphene catalysts for CO₂RR to CO under alkaline conditions. Several types of modified-graphene frameworks doped with metallic and non-metallic elements were considered. After establishing thermodynamically stable electrodes, the electrochemical CO₂RR to CO is studied in the alkaline media. Both concerted proton-coupled electron transfer (PCET) and decoupled proton and electron transfer (ETPT) mechanisms were considered by developing and using a generalization of the computational hydrogen electrode approach. It is established that the CO₂ electrosorption and associated charge transfer along the ETPT pathway are of utmost importance and significantly impact the electrochemical thermodynamics of CO₂RR. Our study suggests an exceptional performance of metal-doped nitrogen-coordinated graphene electrodes, especially 3N-coordinated graphene electrodes.

1 Introduction

The extensive use of fossil resources has escalated the emission of green house gases, particularly CO₂, and disrupted the atmospheric carbon balance. An appealing approach for maintaining this balance is to utilize renewable energy resources but their intermittent nature presents a serious obstacle in the energy conversion and storage applications (Vasileff et al., 2017; Jia C. et al., 2019). In this regard, converting renewable electrical energy into chemical energy through the electrochemical CO₂ reduction reaction (CO₂RR) has been identified as an efficient solution (Tian et al., 2018; Jia C. et al., 2019). Recently, an integrated electrocatalytic CO₂RR process has drawn appreciable attention due to its extra-ordinary features in enabling atmospheric sequestration of CO₂ followed by ambient CO₂RR to synthesize chemicals or fuels (MacDowell et al., 2010; Vasileff et al., 2017; Jia C. et al., 2019). Further flexibility is obtained by using the electrode potential and reaction conditions (pH, electrolyte) to control reaction thermodynamics and kinetics as well as activity and selectivity.

However, achieving efficient CO₂RR is a challenging task and requires optimization of the electrode material as well as the reaction conditions. There are multiple reasons for this. Firstly, CO₂ is a highly stable molecule as reflected by its high negative reduction potential (−1.90 V vs. SHE) required to drive the first-electron transfer process. To circumvent this, active electrocatalysts need to be developed, where CO₂ can be converted to several different products through sequences of complex, multistep proton-coupled electron transfer (PCET) steps. In addition, as many CO₂ derived products have similar thermodynamic stability, the developed electrocatalyst has to be selective. Controlling selectivity while retaining high activity is the primary goal in CO₂RR electrocatalysis and requires exquisite control over the complex PCET chemistry, which depends sensitively on the electrode material, electrode potential, pH, and electrolyte. Therefore, optimizing the electrocatalytic performance presents a serious challenge to CO₂RR-based applications (Schneider et al., 2012; Jia C. et al., 2019).

In the search for ideal CO₂RR catalysts, numerous metallic electrodes have been thoroughly explored experimentally and computationally (Back et al., 2015a; Back et al., 2015b; Mistry et al., 2014; Peterson et al., 2010; Peterson and Nørskov, 2012; Shi et al., 2014; Zhu et al., 2014; Hori, 2008; DeWulf et al., 1989; Kim et al., 1988; Hori et al., 1986; Hori et al., 1989; Lu et al., 2014; Chen et al., 2012; Gattrell et al., 2006; Akhade et al., 2014; Bagger et al., 2019). However, most of them suffer from one or several of the following shortcomings: low faradic efficiency and selectivity, high overpotential, CO poisoning, high cost, and/or low abundance. The extended metal surfaces are also subject to the d-band center theory and intrinsic thermodynamic scaling relationships between the reaction energies of CO₂RR intermediates. These features together with the Sabatier principle set constraints on the achievable electrocatalytic performance of metallic CO₂RR catalysts and hampers the search for efficient electrode materials (Peterson and Nørskov, 2012; Hansen et al., 2013; Back et al., 2015b; Li et al., 2015).

To circumvent these inherent limitations of current CO₂RR electrocatalysts, several unorthodox or innovative CO₂RR electrocatalysts have been suggested recently (Qu et al., 2010; Wang et al., 2015; Lu and Jiao, 2016; Sun et al., 2017; Kibria et al., 2019; Nitopi et al., 2019). Carbon-based electrocatalysts and in particular doped graphene sheets, are among the most promising materials and have been widely investigated as potential CO₂RR electrodes. Graphene electrocatalysts have several attractive physical properties such as high surface area, high electron mobility, high thermal conductivity, high Young’s modulus etc. Furthermore, their geometrical flexibility and electronic structure have been suggested to enable escaping the scaling relationships (Kim et al., 2014; Li et al., 2015). While pure graphene can facilitate outer-sphere electron transfer reactions, edges or other defects are usually required for appreciable electrocatalytic activity (Brownson et al., 2012). Even higher activity and selectivity can be achieved by doping pristine or defected graphene with metal or non-metallic elements (Varela et al., 2018; Jia M. et al., 2019; Wu et al., 2019).

Given the promising CO₂RR performance of such graphene-based materials (Varela et al., 2018; Jia M. et al., 2019; Wu et al., 2019), several experimental and computational investigations have explored the origin of their electrocatalytic behavior and to search for new electrocatalysts. Most computational studies have focused on identifying the optimal reaction energies of the electrochemical PCET steps but the piling evidence (Ringe et al., 2019; Lee et al., 2020; Vijay et al., 2020) indicates that the non-PCET CO₂ adsorption step is limiting CO₂RR. The reason for calculations focusing on electrochemical PCET steps is that the computational hydrogen electrode (CHE) model (Nørskov et al., 2004), in its original form can only account for PCET steps. The importance of non-PCET steps, such as CO₂ adsorption, can be highlighted by comparing two recent CO₂RR studies (Li et al., 2019; Guo et al., 2020). Considering only the PCET steps, led to the conclusion that CO₂RR on a Fe_4N is thermodynamically facile and a potential as small as ∼0.1 V vs. RHE is sufficient to produce COOH (Guo et al., 2020). However, accounting for non-PCET steps led to a very different conclusion as the CO₂ adsorption itself is the potential limiting step that has a high thermodynamic barrier of ∼0.9 eV (Li et al., 2019).

In addition to considering the electrode material, it should be recognized that the electrocatalytic CO₂RR activity and selectivity are inherent properties of electrochemical interfaces. As the interfacial properties depend sensitively on the electrode material, the electrolyte, pH, and electrode potential (Lu and Jiao, 2016; Nitopi et al., 2019), they can be used for controlling the reaction environment and the electrocatalytic CO₂RR performance (Pérez-Gallent et al., 2017; Aljabour et al., 2018; Gao et al., 2018; Guo et al., 2018; Ringe et al., 2019). Recent studies have demonstrated that the CO₂ adsorption step is sensitive to these properties and it also determines the CO₂RR activity and selectivity (Ringe et al., 2019; Lee et al., 2020; Vijay et al., 2020). Furthermore, the faradaic efficiency of CO₂RR is higher in alkaline conditions where the competing hydrogen evolution reaction (HER) is suppressed. Utilizing highly alkaline conditions facilitates obtaining high current densities at lower overpotentials (Gabardo et al., 2018) and the issue of carbonate formation can be circumvented using gas diffusion electrodes (Malkhandi and Yeo, 2019). However, one has to consider both bulk and local pH which may differ as H⁺/OH⁻ are consumed or formed at the interface resulting in a pH gradient between the electrolyte and electrode interface (Bohra et al., 2019; Varela, 2020). Furthermore, these local pH changes are found to be sensitive to the used electrode potential and current density (Lu et al., 2020).

Given the advantages of pH control and highly alkaline conditions, it is surprising that previous computational CO₂RR studies have solely focused on the acidic CO₂RR. A crucial difference between acidic and alkaline CO₂RR is the proton donor: in acidic conditions, the proton is donated by the hydronium ion or some other acid, whereas, under alkaline conditions, the solvent (water) is more likely the hydrogen donor. This difference can introduce changes to the reaction mechanism: A fully coupled PCET mechanism is preferred in acidic conditions, whereas, under alkaline conditions, a decoupled transfer of an electron and a proton may become the dominant mechanism (Koper, 2013a). In order to understand alkaline CO₂RR, one has to examine the possibility of decoupled electron transfer/proton transfer (ETPT) steps but this requires going beyond the original CHE (Nørskov et al., 2004) model, which is applicable to coupled PCET reactions only. This limitation can be circumvented using more general approaches such as general grand canonical DFT methods (Mermin, 1965; Melander et al., 2019; Melander, 2020) and the decoupled CHE (Lindgren et al., 2020). While these methods are applicable to ETPT pathways as well, they are currently computationally too demanding for large scale computational screening studies and more tractable methods need to be developed.

In this study, we address the CO₂RR-to-CO on several graphene electrodes in alkaline conditions and account for both PCET and ETPT pathways. To enable this, the commonly applied computational hydrogen electrode method is extended to study the decoupled ETPT reactions. In particular, we consider the effect of partial ET and the potential-dependency of CO₂ adsorption. On this basis a computational screening approach is developed and applied to identify promising doped graphene electrocatalysts for alkaline CO₂RR. A four-level selection criteria is introduced to rank and select catalysts according to their thermodynamic stability, ability to bind and activate CO₂, electrosorption properties, and theoretical limiting and overpotentials. These principles allow us to identify thermodynamically stable doped graphene electrodes with low limiting and overpotentials in alkaline environments. Our study outlines that highly exergonic CO₂ adsorption associated with high degree of electron transfer is detrimental for catalytic performance. We find that N-coordinated Pt and Ru-doped electrodes are promising candidates as pH universal CO₂RR electrodes.

2 Methods

2.1 Modeling of Graphene Sheets

Pristine graphene is modeled using a simplified non-periodic structure with 42 carbon atoms forming a honeycomb structure with 14 benzene rings. The dangling carbon atoms at the edges of the sheet are terminated with hydrogen atoms (Verma et al., 2018). The flake-based graphene models have been previously shown to be perform well compared to their respective periodic models (Lazar et al., 2013; Verma et al., 2018; Shang et al., 2020). This is attributed to the accounts of non-clustering of carbon atoms and negligible edge effects due to hydrogen-terminations, which make the graphene-flake models trustworthy. In addition, terminating the dangling edge carbon atoms with hydrogen lead to uniform and delocalized distribution of charge and orbitals all over the catalyst surface (Tachikawa and Kawabata, 2011), which prevents any possible artificial localization effects. The graphene-flake models are computationally less expensive compared than extended models while providing a faithful description of graphene. Finally, the graphene-flake model allows us to carry out the large-scale screening studies at the hybrid functional DFT-level (see below for details), which is required to accurately capture the adsorption energies of the CO₂RR intermediates on doped graphene catalysts (Vijay et al., 2020).

Pristine graphene sheets are chemically inert, but their reactivity can be tuned with dopants and defects. The single vacancy is arguably the simplest point defect in graphene; however, larger point defects such as di- and tri-vacancies are also observed in experiments (Warner et al., 2012; He et al., 2014) forming after the coalescence of two or three neighboring mono-vacancies (Trevethan et al., 2014). Different vacancy and doping structures can be experimentally realized using, e.g., selective bombardment followed by ion deposition (Wang et al., 2012), or more refined chemical synthesis (Varela et al., 2018). These vacancies or defects can host a variety of dopants (Wang et al., 2012; He et al., 2014), which we modeled by introducing foreign atom(s) into the created vacancy. These atoms include platinum group metals (Rh, Pd, Pt, and Ru), coinage metals (Ag, Au, and Cu), base metals (Al, Fe, Ni, Mo, Co, Mn, Zn, and Cr), and non-metals (B and N). Structural information for all the studied systems is provided as a Supplementary Material set.

We consider three different vacancy structures: single-vacancy (SV), di-vacancy (DV), and tri-vacancy (TV), by removing one, two, and three central carbon atoms, respectively. Three SV systems are investigated namely, M_SV, M₂_SV, and MPt_SV (see Figures 1A–C). The M_SV structure results from the deposition of a single metal on a single-vacant structure and presents the simplest doped structure. In the case of M₂_SV and MPt_SV structures, homo- and heteroatom dimers are placed on SV as models for nucleated reaction centers (Ferrante et al., 2016). We also investigated an experimentally inspired M₂_2SV structure (He et al., 2014), where two neighboring single vacancies are both filled with identical atomic dopants, see Figure 1D. The M_DV structure, shown in Figure 1F has a single dopant in a di-vacancy. The trapping of dopant pairs over tri-vacant surface is energetically more favourable than a single metal dopant and have been observed experimentally (He et al., 2014), and for this reason the M₂_TV structure is considered as well (Figure 1H).

FIGURE 1

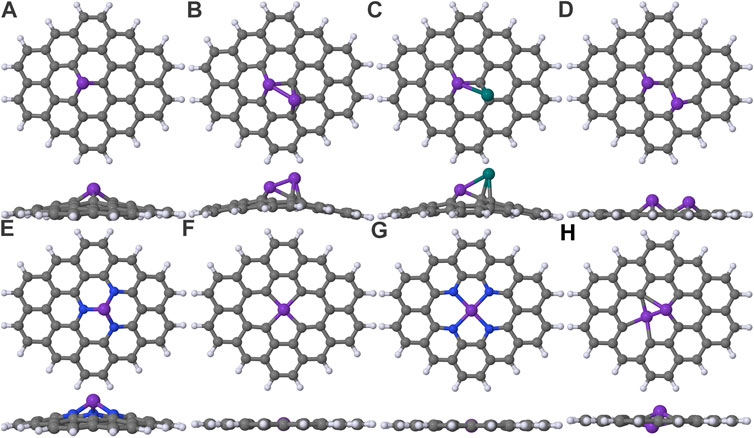
FIGURE 1. Various models of heteroatom doped graphene electrodes: (A) M_SV, (B) M₂_SV, (C) MPt_SV, (D) M₂_2SV, (E) M_3N, (F) M_DV, (G) M_4N, and (H) M₂_TV. The elements carbon, nitrogen and hydrogen are in gray, blue and lavender colors, respectively. The dopant atom is a model atom in purple color. The anchoring Pt atom in M₂_SV model is presented in teal color.

The N-coordinated, heteroatom-doped carbon frameworks are the most experimentally (Li et al., 2017; Cheng et al., 2019; Wang et al., 2019; Zhang et al., 2019; Koshy et al., 2020) and computationally (Tripkovic et al., 2013; Li et al., 2015; Ju et al., 2017; Pan et al., 2018; Varela et al., 2019) studied doped graphene electrodes for oxygen reduction reaction (ORR) and CO₂RR. In these N-coordinated structure, the reaction-center is modified by replacing the coordinating carbon atoms with nitrogens. Such modifications of the M_SV and M_DV structures lead to the M_3N and M_4N electrodes having either three or 4 N atoms (Figures 1E,G), respectively.

2.2 Density Functional Theory Methods

All density functional theory (DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) calculations were carried out using Gaussian 09 (RB.01) (Frisch et al., 2009) package with the help of the Gauss View 5 (Dennington et al., 2009) visualizer. Exchange-correlation effects were described using the B3PW91 (Perdew et al., 1991) functional with Grimme’s D3 (Grimme et al., 2010) dispersion corrections. The metallic atoms were treated within the effective core potential (ECP) formalism and the LANL2DZ (Hay and Wadt, 1985a; Hay and Wadt, 1985b; Wadt and Hay, 1985) basis set, while for all the other atoms (C, H, O, N, and B) the 6-31 + g (d,p) (Petersson et al., 1988; Petersson and Al-Laham, 1991) basis set was used. The atomic structures were relaxed until the maximum residual force reached below 0.02 eV Å⁻¹. The satisfactory performance of the adopted computational approach has been demonstrated previously for graphene (Verma et al., 2018) and metallic clusters (Verma and Kishore, 2017; Verma and Kishore, 2018; Verma and Kishore, 2019).

Both implicit and explicit solvent effects were mostly excluded from the present study. Considering explicit solvation would have been computationally intractable and the implicit solvent models do not markedly affect the adsorption properties of CO₂RR intermediates in constant charge calculations as, e.g., explicit hydrogen bonding cannot be captured with such models (Heenen et al., 2020). The exclusion of solvation effects from modeling the electrocatalytic reactions is a common approximation that has been shown to successfully describe a variety of electrocatalytic systems (Frydendal et al., 2015; Busch et al., 2016; Calle-Vallejo et al., 2017; Valter et al., 2018). However, we have checked the effect of implicit solvation for some of the consider structures. In particular, we addressed implicit solvent effects using the polarizable continuum model (PCM) (Scalmani and Frisch, 2010) for the best performing electrodes identified from the vacuum calculations. For this, we computed the overpotentials using Equation 6 with and without implicit solvent for the best performing catalysts, and the differences are at largest 0.16 V vs. RHE corresponding to 0.16 eV difference in reaction energies as shown in Table 1.

TABLE 1

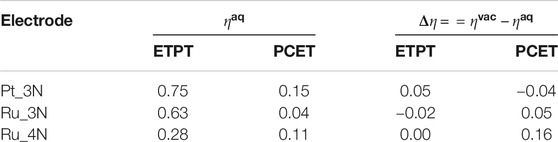
TABLE 1. Thermodynamic overpotentials in the presence of implicit solvation (${\eta }^{aq}$) (V vs. RHE) for the three promising ETPT and PCET electrocatalysts. Also, the magnitude of deviation ($\text{Δ}\eta$) from the vacuum phase (${\eta }^{vac}$) is indicated.

Metal-modified graphene structures are subject to spin-inversion and, therefore, spin-unrestricted DFT was used and a careful investigation of spin multiplicities was necessary to locate the lowest energy spin states. To ensure the correct spin-multiplicity, single point energies at different spin multiplicities were calculated followed by re-optimizations of the atomic structures at the correct spin-multiplicity. The Mulliken charge (q^M), magnetic moment (m), and the most stable spin multiplicity for each dopant in the considered graphene frameworks can be found in Supplementary Table S1. Note that all the formation and binding free energy calculations were performed using the most stable spin state structures and their energetics.

Vibrational frequency calculations were performed for all the optimized structures to confirm that they are true minima. The vibrational frequencies were computed to determine the vibrational entropy and zero-point energy contributions in the thermodynamics of CO₂RR. The thermodynamic parameters were calculated at 298.15 K temperature and 1 atm pressure. In the Supplementary Material, we present the methodology utilized to compute the thermodynamic entropy, enthalpy, and free energy. The charge analysis was based on the Mulliken scheme (Mulliken, 1955), which is assumed to be accurate enough for the comparison of similar models and similar basis sets.

2.3 Computation of Catalyst Stability

Electrode stability is a prerequisite for maintaining catalytic activity for extended operation time(Krasheninnikov et al., 2009; Wang et al., 2013; Back et al., 2017). In doped graphene electrodes, the deactivation is thought to take place through dopant dissolution (Shao et al., 2019). The dissolution will result in the formation of a graphene vacancy, while the dissolved atoms will likely form metallic nanoparticles or other stable products. Hence, the thermodynamic stability of the studied catalysts was evaluated against pristine graphene and the most stable (bulk) phase of the dopant. The catalyst stability was first referenced against gas-phase metal ions and subsequently against the dopant’s most stable bulk phase by utilizing experimental cohesive energies (Kittel, 2004). This way the formation energy is compared against the most stable bulk phase of a given dopant. Finally, the formation free energy (G_FE) is computed as:

$G_{FE}=1/N\left[G_{MGr}-\left(N\times G_M+N\times G_{vacantGr}\right)+N\times G_{coh}\right](1)$

where N is the number of dopant atoms, $G_{MGr}$ is the free energy of the doped graphene electrode, $G_M$ is the free energy of the metal atom in the gas-phase, $G_{vacantGr}$ is the free energy of the vacant graphene, and $G_{coh}$ is the cohesive energy of the dopant(s) (Kittel, 2004).

2.4 Computation of Reaction Free Energies

The CO₂ adsorption free energy ($G_{Ads}$) over the doped graphene electrodes was calculated using:

$G_{Ads}=\left[G_{MGr+C{O}_2}-\left(G_{MGr}+G_{C{O}_2}\right)\right](2)$

where $G_{MGr+C{O}_2}$ is the free energy of CO₂ adsorbed over modified-graphene, $G_{MGr}$ is the free energy of the bare modified-graphene, and $G_{C{O}_2}$ is the free energy of gas-phase CO₂.

To model alkaline conditions, we consider water as the hydrogen donor as commonly assumed for alkaline CO₂RR (Yin et al., 2019). In general, the reaction may take place either via a sequential ETPT or a concerted PCET mechanism (Dunwell et al., 2018). In the ETPT pathway, the first ET denotes partial charge transfer taking place during CO₂ adsorption on the graphene catalyst, which is followed by further partial ET and PT. For both the sequential and concerted pathways, the elementary steps for CO₂RR to CO are:

$\begin{array}{l}C{O}_2\left(aq\right)+\delta e^{-}+Gr\rightleftharpoons C{O}_2{\left(\text{*}\right)}^{\delta e-}\left(3\text{a}\right)\\ C{O}_2{\left(\text{*}\right)}^{\delta e-}+\left(1-\delta \right)e^{-}+H_{2}O\left(aq\right)\rightleftharpoons COOH\left(\text{*}\right)+O{H}^{-}\left(aq\right)\left(3\text{b}\right)\\ COOH\left(\text{*}\right)+e^{-}\rightleftharpoons CO\left(\text{*}\right)+O{H}^{-}\left(aq\right)\left(3\text{c}\right)\\ CO\left(\text{*}\right)+\rightleftharpoons CO\left(aq\right)+Gr\left(3\text{d}\right)\end{array}$

where Gr (also referred as “*”) is the graphene catalyst and δ denotes the partial charge. When Equations 3a,b, are separated, the mechanism is sequential (ETPT) whereas if they are summed the PCET mechanism is followed.

To compute the electrochemical CO₂RR thermodynamics along both the ETPT and PCET pathways in alkaline conditions, the CHE method was extended to include partial charge transfer and ETPT steps. Note that we are interested in ET taking place during adsorption, i.e., electrosorption, not outer-sphere ET to a dissolved CO₂ forming ${\text{CO}}_2^{-}$(aq). The crucial difference is that the solution phase ET to CO₂ can be considered as an outer-sphere ET reaction the thermodynamics of which are not affected by the electrode material. In that case, the tabulated (Bratsch, 1989) reduction potentials can simply be used for computing the thermodynamics of this outer-sphere ET reaction. For such outer-sphere reactions, the thermodynamics can also be accurately computed using standard approaches (Marenich et al., 2014). Here, we instead consider an inner-sphere ET taking place during adsorption, and in this case, the electrode cannot be neglected due to the strong interactions and hybridization between the electronic states of electrode and CO₂. For such reactions, the potential-dependent thermodynamics require going beyond standard approaches and methods such as grand canonical DFT are required (Hörmann et al., 2020). Grand canonical DFT as implemented presently is, however, too costly for large-scale screening studies and we propose a computationally feasible extension to CHE to enable addressing (partial) ET. The extension is motivated by the recent decoupled hydrogen electrode method (Lindgren et al., 2020), which combines the CHE with grand canonical DFT. We utilize a computationally more feasible approximation based on the electrosorption valency (Schmickler and Guidelli, 2014) to model the partial ET taking place during CO₂ adsorption to capture the potential-dependency of this step. By combining the electrosorption valency and CHE, the reaction thermodynamics for each elementary step can be calculated using:

$\begin{array}{c}\text{Δ}{G}_1\left(RHE\right)=G\left(C{O}_2^{\delta e-}\left(\text{*}\right)\right)-G\left(Gr\right)-G\left(C{O}_2\left(aq\right)\right)+\gamma U\left(RHE\right)\left(4\text{a}\right)\\ \text{Δ}{G}_2\left(RHE\right)=\text{Δ}{G}_w+\left(1-\gamma \right)U\left(RHE\right)+G\left(COOH\left(\text{*}\right)\right)\\ -\frac{1}{2}G\left(H_2\left(aq\right)\right)-G\left(C{O}_2^{\delta e-}\left(\text{*}\right)\right)\left(4\text{b}\right)\\ \text{Δ}{G}_3\left(RHE\right)=\text{Δ}{G}_w+U\left(RHE\right)+G\left(CO\left(\text{*}\right)\right)+G\left(H_{2}O\left(aq\right)\right)\\ -\frac{1}{2}G\left(H_2\left(aq\right)\right)-G\left(COOH\left(\text{*}\right)\right)\left(4\text{c}\right)\\ \text{Δ}{G}_4=G\left(CO\left(aq\right)\right)+G\left(Gr\right)-G\left(CO\left(\text{*}\right)\right)\left(4\text{d}\right)\end{array}$

A complete derivation of Equation 4 is presented in the Supplementary Material. Here $\text{Δ}{G}_w={\tilde{\mu }}_{H^{+}}+{\tilde{\mu }}_{O{H}^{-}}-{\mu }_{H_{2}O}$ is the water dissociation free energy (0.83 eV at pH = 14) (Bratsch, 1989) Equations 4a,b are written for the ETPT pathway and when added together, the reaction free energy for the concerted PCET step is obtained, i.e., $\text{Δ}{G}_{1+2}\left(RHE\right)=\text{Δ}{G}_1\left(RHE\right)+\text{Δ}{G}_2\left(RHE\right)$. $\gamma =\left(\partial \text{Δ}{G}^{ads}\left(U\right)/\partial U\right)$ is the electrosorption valency (Schmickler and Guidelli, 2014), which changes the adsorption energy as $\text{ΔΔ}{G}^{ads}\left(U\right)=\gamma \text{Δ}U$. Note that $\gamma \le \delta$ and the partial charge transfer upon adsorption do not directly change the Gibbs free energy. As discussed in the SM, γ is a potential-dependent quantity and could be obtained from experiments or using potential-dependent grand canonical DFT, (Melander et al., 2019; Hörmann et al., 2020) but such data is not available for the catalysts studied here. Therefore, we assume that the electrosorption valency is independent of the potential ($\gamma \left(U\right)\approx \gamma$), which is a good approximation at potentials close to the reference potential but breaks down as $\left|U\right|\gg \left|U_{ref}\right|$. This is seen as unphysically large equilibrium potential values for CO₂ adsorption steps–the true upper bound for the CO₂→CO₂⁻ should be close to its thermodynamic reduction potential of −1.9 V vs. SHE (Bratsch, 1989). Here, we approximate the electrosorption valency using the fitting approach (Schmickler and Guidelli, 2014), which gives:

$\gamma \approx \delta \left[0.84+0.16\times \text{exp}\left(-3{\left({\chi }^{Gr}-{\chi }^{C{O}_2}\right)}^2\right)\right](5)$

where χs are Pauling electronegativities. ${\chi }^{Gr}\approx 2.5$ for all metal-doped graphene electrodes. ${\chi }^{C{O}_2}\approx 1.5$ is computed using the experimental (NIST database, 2020) CO₂ electron affinity and ionization energies for computing its Mulliken electronegativity (Mulliken, 1934). The Mulliken electronegativity is then converted to the Pauling scale using the linear correlation (Herrick, 2005) between the two scales.

To compare and analyze the electrochemical thermodynamics, we also define the thermodynamic equilibrium potential ($U_{eq}$), the thermodynamic limiting potential ($U_L$), and overpotential (η) (Durand et al., 2011) as further discussed in the SM. However, our definition will take into account the ETPT steps with partial charge transfer in terms of the electrosorption valency.

$\begin{array}{l}{U}_{Eq}\left(RHE\right)=\left[{\displaystyle \sum }_i\text{Δ}{G}_i(U=0vs.RHE)\right]/n_{e,tot}\left(6\text{a}\right)\\ U_L\left(ETPT\right)=-\text{max}\{\text{Δ}{G}_1(U=0)/\gamma ,\text{Δ}{G}_2(U=0)/(1-\gamma ),\text{Δ}{G}_3(U=0)\}\left(6\text{b}\right)\\ U_L\left(PCET\right)=-\text{max}\{\text{Δ}{G}_{1+2}(U=0),\text{Δ}{G}_3(U=0)\}\left(6\text{c}\right)\\ {\eta }_{PCET/ETPT}=|U_{eq}-U_L\left(PCET/ETPT\right)|\left(6\text{d}\right)\end{array}$

where $n_{e,tot}=2$ is the total number of electrons transferred in the CO₂RR to CO.

3 Results

3.1 Structures and Stabilities

Thermodynamic stability against dissolution is a key material property mandatory for maintaining electrocatalytic activity and, therefore, we first addressed the stability of our graphene model electrodes against pristine graphene and the thermodynamically most stable (bulk) phase of the dopant. Figure 2 summarizes the Gibbs free energies for formation, computed according to Equation 1. Additional data on formation thermodynamics with numerical values, zero-point energy corrections, and formation enthalpies are reported in the Supplementary Tables S2–S5. We found that majority of the studied dimers (M₂_SV and MPt_SV) in single vacancies are thermodynamically unstable and these results are therefore presented and discussed solely in the SM. For other systems, the findings of Figure 2 are discussed in more detail below.

FIGURE 2

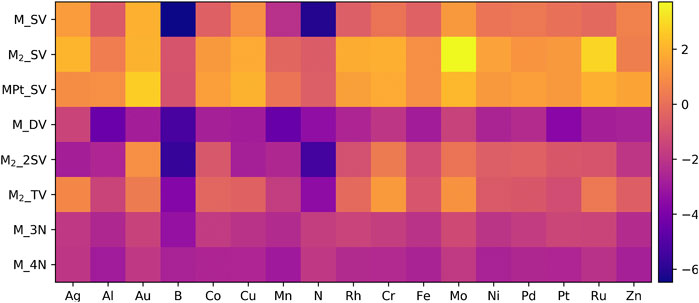
FIGURE 2. Formation free energies (eV) of various heteroatom doped graphene models. Increasing negative energetics denote stronger formation stability of dopant(s) to the vacant site(s).

3.1.1 Single and Two Mono-Vacant Graphene

The M_SV graphenes are the simplest doped graphene structures (see Figure 1A). Calculations showed that all metal atoms exhibit slight protrusion out of the graphene plane upon bonding with the dangling carbon atoms, and the vertical distance between a metal atom and graphene plane varies from 0.73 Å to 1.19 Å in good agreement with previous computational studies (Li et al., 2015; Verma et al., 2018; Zhao et al., 2019). About half of the M_SV systems are thermodynamically stable as can be seen from Figure 2. The free energy of formation ranges from −0.19 to −6.47 eV; however, doping with coinage metals and a few of base and platinum group metals is thermodynamically unfavorable (see Supplementary Table S5). The formation free energies of B- and N-doped graphene are above −6 eV, which demonstrates their extremely strong interaction with the graphene single vacancy.

In the case of M₂_2SV, the metal dopants are also elevated out of the graphene plane similar to M_SV. Almost all M₂_2SV systems are symmetric with the dopants occupying two vacancies. The formation free energy of stable M₂_2SV electrodes ranges from −0.42 eV to −5.70 eV. Doping by non-metallic B and N atoms is extremely exergonic (∼−5.5 eV). We found that, upon structural optimization, the Ag, Al, and Cu dopants spontaneously drift away from the vacancy to form dimers, therefore, they are excluded from electrochemical thermodynamics studies.

3.1.2 Di- and Tri-vacant Graphene

In the M_DV graphene, dopant atoms are bound to four nearest undercoordinated C atoms and remain in the basal plane due to the large size of the double vacancy compared to the dopant’s atomic radius. The considered non-metallic elements B and N feature benzene-like hexagons with two out of the four undercoordinated carbon atoms. According to the formation free energy analysis, all M_DV graphene structures are highly stable with formation energies ranging from −1.43 eV to −5.28 eV.

The tri-vacancy of M₂_TV models can accommodate the dopant pair in two different orientations: 1) both dopant atoms above the tri-vacancy (Supplementary Figure S4A) and 2) one atom above and one below the tri-vacancy (Supplementary Figure S4B). We found that the latter geometry is more stable (see Supplementary Figure S4C) and was selected for further studies. In the M₂_TV structure, the dopant atoms are bound to the three nearest undercoordinated carbon atoms. Non-metallic B and N dimers break down during structural optimization to form benzene-like structures, and the resulting structures mimic mono-vacant graphenes. The computed formation free energies show that non-metallic dopants in the M₂_TV structure are highly stable, while metallic M₂_TV electrodes are at best modestly stable, and Ag-, Au-, Cr-, Mo-, and Ru-doped graphenes are unstable.

3.1.3 N-Coordinated Graphene

All the optimized M_3N and M_4N structures are highly symmetric and show no buckling behavior. We find that the average M-N bond distances along with other geometrical features of both N-coordinated structures are similar to their carbon coordinated counterparts (M_SV and M_DV) (Zhao et al., 2019; Kattel et al., 2012). Our calculations suggest that the incorporation of three nitrogen atoms enhances the dopant’s stability as can be inferred from the formation free energies ranging from −1.22 eV to −3.28 eV, which are more exergonic than their M_SV counterparts. The formation free energies of M_4N structures vary from −1.84 eV to −2.99 eV and are comparable to the values computed for M_DV models. However, it is evident that the non-metallic dopants prefer 4C-coordination as their formation free energies (see Figure 2) are much more exergonic than in the 4N-coordination environment. Therefore, the 4N-coordination environment does not enhance the stability of metallic dopants compared to 4C-coordination in agreement with previous computational results (Zhao et al., 2019).

In general, the geometric and energetic stabilities of modified-graphene sheets depend strongly on the dopant and vacancy but some overall trends are observed. The Ag-, Au-, Cr-, and Mo-doped carbon-coordinated graphene structures are always unstable irrespective of the type of vacancy whereas all the considered dopants in 3N- and 4N-environments are highly stable, which is in line with previous studies (Tripkovic et al., 2013; Li et al., 2015; Ju et al., 2017; Pan et al., 2018; Varela et al., 2019; Wang et al., 2019; Zhang et al., 2019; Koshy et al., 2020).

3.2 CO₂ Adsorption

As discussed in the Introduction, CO₂ adsorption and activation are crucial steps for CO₂RR in alkaline conditions as the adsorption is often thermodynamically unfavorable and limits CO₂RR activity (Jones et al., 2014; Gauthier et al., 2019; Yu et al., 2019; Vijay et al., 2020). Furthermore (partial) charge transfer during CO₂ adsorption may take place and this process is sensitive to the electrode potential but formally independent of solution pH. CO₂ may also be activated upon adsorption, which is seen as the deviation of the O–C–O angle from 180^o. Under alkaline conditions, where only weak proton donors (water) are present, the CO₂ adsorption and an accompanied ET step are important contrary to pure PCET steps. Therefore, we closely monitor the CO₂ adsorption geometry and energy over all of the considered electrodes, regardless of electrode stability. Figure 3 displays CO₂ binding geometries on the stable M_SV, M₂_2SV, M_3N, M_DV, and M_4N electrodes whereas binding geometries on stable M₂_SV, MPt_SV, and M₂_TV structures are illustrated in Supplementary Figure S5. Electronic structure information such as magnetic moments and stable spin multiplicities are supplied in Supplementary Table S6 for each system, and numerical values for adsorption energies, enthalpies, and free energies are provided in the Supplementary Tables S7–S10.

FIGURE 3

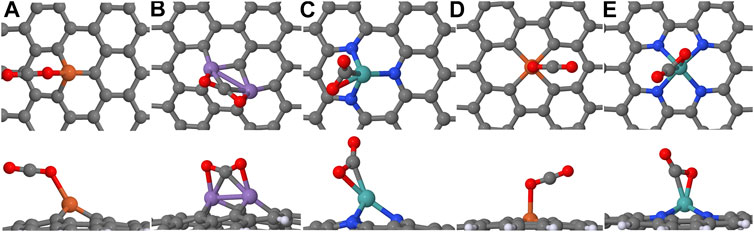
FIGURE 3. The optimized binding geometries of CO₂ over considered electrodes: (A) Fe_SV, (B) Mn₂_2SV, (C) Mo_3N, (D) Fe_DV, and (E) Mo_4N. The elements carbon, oxygen, and nitrogen are in gray, red, and blue colors, respectively.

Among the M_SV electrodes, CO₂ adsorption is exergonic only on Fe_SV (−0.12 eV). In this case, CO₂ remains linear upon adsorption (see Figure 3A) and the oxygen atom interacts weakly with the metal site having Fe–O distance 2.16 Å and small electron transfer from CO₂ (0.22 e). A similar pattern is observed for the M_DV electrodes as well. The CO₂ adsorption is exergonic only on Fe_DV (see Figure 3D) with similar binding configuration and free energy as observed for Fe_SV; however, the charge transfer (0.47 e) from CO₂ is rather high compared to Fe_SV. On the B- and N-doped SV sheets, CO₂ merely physisorbs as seen from the long B-C and N-C distances, which are over 3.1 Å. This is similar to the CO₂ adsorption on the pristine graphene (Rad and Foukolaei, 2015). The activation of CO₂, i.e., non-linear CO₂ structure, occurs only on Mn_SV and Cr- and Mo-based SV and DV structures but the CO₂ adsorption is thermodynamically unfavorable. Note that the formation of Cr- and Mo-doped SV electrodes are thermodynamically unstable as well.

Figure 3B illustrates the adsorption geometry of CO₂ on Mn₂_2SV. The adsorption geometry is similar on all the CO₂-activating M₂_2SV structures. CO₂ adsorption is exergonic on B-, Co-, Mn-, and N-based 2SV structures with adsorption free energies varying from −0.18 eV to −0.68 eV. However, only Co₂_2SV and Mn₂_2SV are able to activate CO₂ and facilitate modest electron transfer to the molecule. While Fe₂_2SV and Ru₂_2SV structures can also activate CO₂, they exhibit thermoneutral adsorption. On the other hand, upon structural optimization, the coinage and a few base metal (Al, Ni, and Zn) dopants stem out of the vacancies and form CO₂-dimer complex above graphene structure, and hence these systems were excluded from further studies.

Apart from Ag- and Cu-doped M_3N models, the majority of M_3N structures exhibit promising CO₂ adsorption characteristics as CO₂ both adsorbs and becomes activated with the O–C–O angle varying between 127.9^o to 150.4^o. The molecule interacts with the metal dopant via the carbon atom and one oxygen in a bidentate conformation shown in Figure 3C for the Mo_3N structure. In the case of non-metallic dopants, CO₂ favors a monodentate adsorption configuration. The free energies of adsorption range from −0.24 eV to −0.74 eV being comparable to the values found for the M₂_2SV structures. CO₂ adsorption on 4N-coordinated electrodes is surprisingly unfavorable: roughly half of the M_4N structures can activate CO₂ but only Mo_4N (see Figure 3E) exhibits exergonic adsorption free energy (−0.89 eV) with exceptionally large charge transfer (−0.67 e). Similar to M_3N graphenes, CO₂ favors a bidentate adsorption geometry on Mo_4N with O–C–O angle of 130.7^o. Given the experimentally proven performance of 4N catalysts, it is unexpected to observe rather high endergonic adsorption energies on these electrodes. Possible reasons for the observed weak adsorption include, e.g., the neglected axial ligands and dipolar interactions as further elucidated in the Discussion section, or the deformation of the electrode structure upon adsorption. To test the latter, we computed the deformation energy for Fe_4N in the same way as in ref (Nykänen and Honkala, 2011). but the contribution from structural deformation is very small and therefore unfavourable adsorption energies cannot be attributed to structural deformations.

3.3 Selection Criteria

After analyzing the electrode stabilities and CO₂ adsorption, we develop the selection criteria for identifying the most promising modified graphene CO₂RR electrocatalysts from a large pool of materials. For instance, the doping of heteroatom to the graphene electrode should be highly stable to avoid any possible dissolution. The binding of CO₂ to the electrode material should be strong enough to avoid being the limiting step at industrially relevant current densities/potentials. Furthermore, at high pH conditions, Tafel slopes approach 120 mV/dec (Gabardo et al., 2018), which is indicative of electron-transfer (ET) step being the limiting step (Dunwell et al., 2018). Therefore, CO₂ should be activated upon adsorption, become negatively charged, and bind strongly: these features are ranked based on O-C-O angle, negative charge transfer, and negative G_Ads values.

To rank and identify prospective CO₂RR electrocatalysts, we introduce a four-level selection criteria (see the flow chart in Supplementary Figure S6). First, we screen all bare electrodes and select the ones with negative formation free energy but disregard the systems with geometric instability. The electrodes fulfilling the first criterion are subjected to CO₂ adsorption energy screening. Catalysts, over which the adsorption free energy is below or equal to 0.15 eV (i.e., more adsorbing) are selected. Third, after passing the screening of binding free energies, the next step is CO₂ activation for which we set the threshold value of 150^o for O–C–O angle. Fourth, after previous three criteria, we consider the net charge transfer due to the binding of CO₂ to the electrode as another criteria. In this section, the systems demonstrating net charge transfer below or equal to 0.15 are selected. The upper range of 0.15 eV in the binding free energies of CO₂ and in the net charge transfer is considered to account for any possible number sensitivity due to the DFT methods (Gauthier et al., 2020). This is an acceptable condition considering the fact that the electronic structure results often deviate by 0.1 eV due to different DFT functionals or basis sets.

A combined plot of three key selection parameters, i.e., adsorption free energy (G_Ads), O–C–O angle, and charge transfer (q) for each of the electrode categories, namely, M_SV, M_DV, M₂_2SV, M₂_TV, M_3N, and M_4N, is supplied in Supplementary Figure S7. Based on the selection criteria, the qualified systems to study the electrochemical thermodynamics are: M₂_2SV (Co, Mn, Rh, Fe, and Ru), M₂_TV (Al, Cu, and Zn), M_3N (Al, N, Rh, Cr, Fe, Mo, Pd, Pt, and Ru), and M_4N (Mo and Ru). Thus, a total of 19 electrodes are selected for further study. Note that none of M_SV and M_DV electrodes qualify the present selection criteria.

3.4 COOH and CO Binding: Scaling Relations

CO and COOH adsorption energies typically exhibit scaling relations and are therefore often taken as CO₂RR activity and selectivity descriptors (Peterson and Nørskov, 2012; Koper, 2013a; Kuhl et al., 2014; Nitopi et al., 2019). However, there are indications (Kim et al., 2014; Li et al., 2015; Back et al., 2017) that the CO/COOH scaling relations and descriptors are not valid for graphene-based electrodes. To study whether scaling relations can be established among the materials studied here, we attempt to find correlations between the CO₂, COOH, and CO adsorption free energies. This analysis is carried out for the M_3N and M₂_2SV electrodes only as M_4N and M₂_TV electrodes contain too few data points. The binding energies are presented in the Supplementary Table S11 and are utilized in the next section to study the electrochemical thermodynamics.

From Supplementary Figures S8, S9, it is evident that a poor correlation exists between the binding free energies of COOH and CO₂ over M_3N (R² = 0.07) and M₂_2SV (R² = 0.24) electrodes. Similar results are observed for COOH/CO scaling relationships on M_3N (R² = 0.29) and M₂_2SV (R² = 0.08) electrodes as well. These poor scaling relations are in agreement with previous studies on graphene-based electrodes (Li et al., 2015; Back et al., 2017; Li et al., 2019; Guo et al., 2020), which indicates that graphene electrodes may break scaling relationships making these materials an interesting class of CO₂RR electrocatalysts. However, it needs to be recognized that the number of materials subjected to the scaling relation studies is small and too far-reaching conclusions on breaking scaling should be avoided. Yet, it has been shown that even slight modifications to N-doped graphene electrodes lead to different scaling relations (Guo et al., 2020).

3.5 Electrochemical Thermodynamics

To address the electrochemical performance of the qualified electrodes, electrochemical thermodynamics for CO₂ reduction to CO were computed using Equations 4, 6. While Figure 4 displays the thermodynamic profiles for selected materials with varying behavior along the PCET and ETPT pathways, the limiting potentials and overpotentials are illustrated in Figure 5. For other materials, not shown here, the potential energy surfaces are displayed in Supplementary Figure S10 and the explicit potential values are collected in Supplementary Table S12.

FIGURE 4

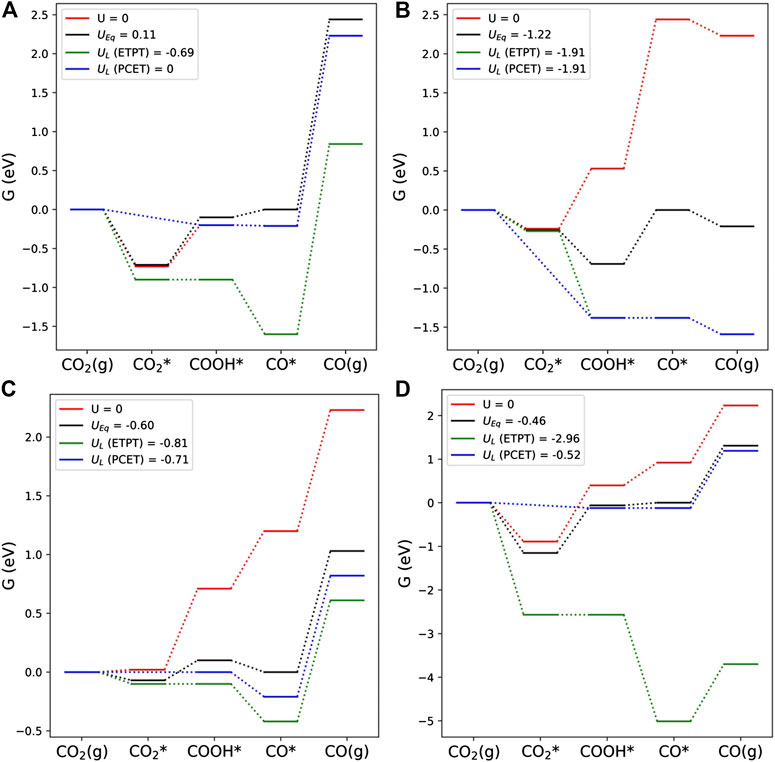
FIGURE 4. Electrochemical thermodynamics of CO₂ reduction reaction using PCET and ETPT mechanisms over four selected electrodes: (A) Pt_3N, (B) Al_3N, (C) Ru₂_2SV, and (D) Mo_4N.

FIGURE 5

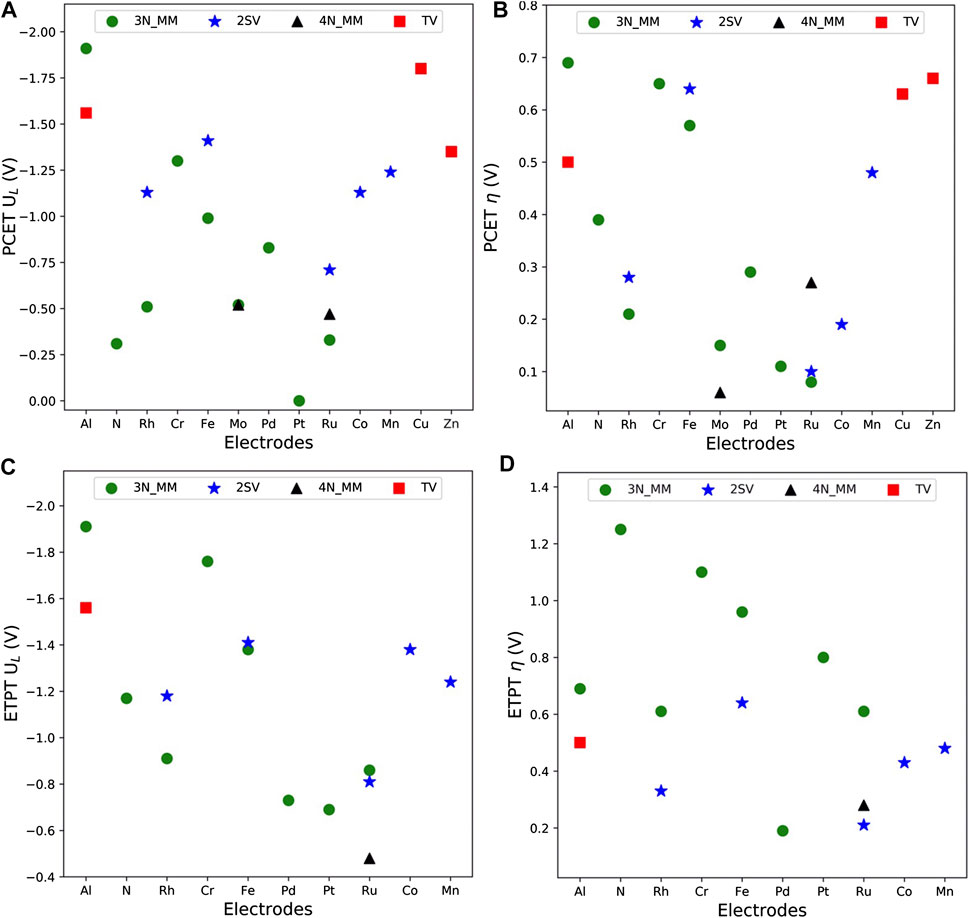
FIGURE 5. Calculated theoretical limiting ((A,C), 0 to −2.0 V vs. RHE) and overpotential ((B,D),0–1.5 V vs. RHE) of electrocatalytic CO₂RR process via PCET (A,B) and ETPT (C,D) mechanisms.

As displayed in Figure 4A, a large potential difference (0.69 V) between the ETPT and PCET pathways is observed for the Pt_3N catalyst. We attribute this difference to the inclusion of the CO₂ binding in the former mechanism. The CO₂ adsorption step itself is rather exergonic and associated with a modest charge transfer (∼−0.3 e) from the electrode. Along the PCET pathway, COOH and CO formation steps are mildly exergonic at zero potential resulting in positive equilibrium potential. This observation suggests that PCET pathway on Pt_3N is nearly thermodynamically ideal and requires zero limiting potential (blue PES). On the other hand, the ETPT mechanism is far from ideal and a large negative limiting potential is required due to the highly endergonic CO₂→COOH step and the significant partial charge transfer (∼0.7 e) in this step.

CO₂RR thermodynamics on the Al_3N catalysts, shown in Figure 4B, provides an example where both the ETPT and PCET pathways attain same limiting potential. Herein, CO₂ adsorption energy is modestly exergonic and features insignificant charge transfer. Furthermore, CO formation is highly unfavourable compared to COOH and is therefore identified as the potential-determining step. As the reaction free energy for CO formation (see Equation 4c) is same for both PCET and ETPT pathways, the resulting thermodynamic potentials are also equal.

In Figure 4C, the Ru₂_2SV electrode is considered. CO₂ adsorption is almost thermoneutral at zero potential (red line) associated with a small charge transfer (∼−0.2 e) from the electrode. The formation of COOH is identified as the limiting step owing to its high endergonicity. Altogether these factors make ETPT and PCET limiting potentials rather similar, which in turn implies that this material is a promising candidate for both ETPT and PCET pathways, i.e., for both alkaline and acid conditions. However, the CO adsorption free energy (∼−1 eV) on the electrode is too strong, which makes it susceptible to catalyzing further reduction or poisoning.

The last example, given in Figure 4D, features very different limiting potentials for the ETPT and PCET pathways on the Mo_4N electrode. In this case, CO₂ adsorbs strongly, significant charge transfer (∼−0.7 e) to the molecule takes place, and the COOH formation is quite endergonic at zero potential (red line). Together these factors result in a large negative limiting potential along the ETPT pathway, while the PCET exhibits a fairly modest overpotential. Similar behavior is seen for the Mo_3N electrode as well and we conclude that the N-Mo-modified graphene catalysts are unsuitable for a ETPT mechanism but could work for the PCET pathway.

Comparison of the ETPT potential energy profiles given in Figure 4 shows that CO₂ adsorption and associated charge transfer are pivotal for this mechanism to be operational, but they are absent from PCET due to the assumption of simultaneous electron and proton transfer. Overall, these differences modify the reaction thermodynamics, and we observed that the charge transfer during adsorption has a profound effect on the electrocatalytic thermodynamics as manifested by the limiting potentials shown in Figures 4, 5. We found that the slightly exergnonic CO₂ adsorption is beneficial as it enables the formation of a stable CO₂-catalyst complex and prevents excessively endergonic COOH formation. Furthermore, charge transfer associated with CO₂ adsorption should be as low as possible: if the COOH formation requires only a very small degree of charge transfer, a very high reductive potential is needed to make this step thermodynamically favorable as shown in, e.g., Figure 4D. In a case where no charge transfer takes place during ${\text{CO}}_2^{\mathrm{-}}$ + H⁺ → COOH, the COOH formation step is fully chemical and cannot be controlled by the electrode potential. The very large limiting potentials along the ETPT pathways are likely an artifact of the simple charge transfer and electrosorption model adopted herein, but we believe that the present model enables qualitatively correct comparison of thermodynamics between ETPT and PCET processes.

The thermodynamic potentials are extensively used for ranking or comparing the expected performance of different catalysts, and limiting potentials and overpotentials should be close to zero for the best performing catalysts. Figure 5 presents both potentials for the PCET and ETPT pathways. For all the qualified electrodes, the overpotentials are within 0.7 V (vs. RHE) for PCET pathways. The best-performing electrodes include Ru, Rh, and Mo-doped 3N graphene and Ru and Mo-doped 4N graphene for which the limiting potentials vary from 0 to −0.52 V vs. RHE and overpotentials range from 0.06 to 0.21 V vs. RHE. For the ETPT mechanism, the best-performing electrodes contain Pd_3N, Ru_3N, Pt_3N, Ru₂_2SV, and Ru_4N with limiting potentials between −0.48 and −0.86 V vs. RHE and overpotentials varying from 0.28 to 0.8 V vs. RHE. The limiting potentials found for the studied structures are either comparable or even smaller than those previously computed for 4N and 3N catalysts (Guo et al., 2020; Pan et al., 2020), non-metallic defected graphene (Siahrostami et al., 2017), and single-atom doped metal catalysts (Lim et al., 2014). Overall, the ETPT mechanism leads to higher overpotentials and limiting potentials than the PCET pathway, which we take to indicate that pure ET steps are detrimental for the reaction thermodynamics as commonly suggested (Koper, 2013b). Interestingly, we find that three of the studied materials–Ru_3N, Pt_3N, and Ru_4N–exhibit very promising electrochemical thermodynamics along both the ETPT and PCET pathways making these materials promising candidates for CO₂RR under both acidic (PCET) and alkaline (ETPT) conditions.

Next, we simulated the three promising ETPT and PCET electrocatalysts (Ru_3N, Pt_3N, and Ru_4N) using the PCM model (Scalmani and Frisch, 2010) for water to check the solvation effects on the overpotentials, and their deviations from the vacuum phase thermodynamics. The adsorption free energies of CO₂ in the aqueous medium are lower (G_Ads(aq)^Pt_3N = −0.49 eV; G_Ads(aq)^Ru_3N = −0.08 eV; and G_Ads(aq)^Ru_4N = 0.02 eV) than those of computed for the vacuum phase, but charge transfer from electrodes to the CO₂ in the solution phase is significantly higher (−0.5 e to −0.6 e). The aqueous phase PCET and ETPT limiting potentials of Pt_3N and Ru_3N are slightly lower compared to vacuum phase, whereas, slightly higher limiting potentials are observed for Ru_4N. As shown in Table 1, including solvation introduces only small changes to overpotentials. The largest change is observed for Ru_4N ($\text{Δ}\eta$ = 0.16 V), which is still relatively small given typical DFT inaccuracies. We ascribe the observed difference to slightly more stable adsorption of COOH* in the solution phase compared to vacuum phase. Finally, it can be concluded that the implicit solvation framework does not significantly change the thermodynamics computed in gas-phase, and thus the conclusions remain largely unaffected by the implicit solvation.

4 Discussion

Our computational predictions show that the CO₂RR activity and selectivity on a given graphene-based electrode depend on the mechanism, i.e., whether the PCET or ETPT pathway is followed. For conditions favoring the PCET mechanism, the N-coordinated graphene electrodes demonstrate the best performance among the studied models. The aforementioned holds true also when ETPT is operational but this typically leads to larger limiting potentials. Pd_3N is an exception to this rule and is the only electrode for which a lower overpotential along the ETPT than the PCET pathway is observed. This anomaly is caused by the slightly positive CO₂ binding energy and minor charge transfer. In general, we find that the coupled PCET is thermodynamically more favorable but for kinetic reasons the ETPT pathway may be preferred (Koper, 2013b).

The obtained results show that the ETPT pathway is highly sensitive to the CO₂ electrosorption energy and charge transfer. Ignoring these important features from mechanistic consideration and focusing solely on the PCET mechanism, often leads to a different potential-determining step, and underestimation of thermodynamic potentials. For example, the current and previous computational studies (Li et al., 2019; Vijay et al., 2020) on Fe_4N show that the CO₂ binding itself introduces a thermodynamic barrier of ∼0.9 eV, whereas, the PCET pathway (Guo et al., 2020) presents a quite small (∼0.1 eV) thermodynamic barrier for producing COOH. These results demonstrate that CO₂ adsorption directly affects the CO₂RR elementary thermodynamics and should therefore be considered. The adsorption process and its potential-dependency are particularly important under alkaline conditions where the coupled PCET becomes less likely, and at high current densities where mass transfer and adsorption are the limiting processes. We identified that slightly exergonic CO₂ adsorption associated with minor charge transfer is a desirable feature for promising catalysts. The conclusions from a large number of studies (see Introduction) neglecting the adsorption step and focusing only on PCET steps are limited to acidic conditions or to the electrodes that cannot catalyze the ETPT pathway.

The importance of the adsorption step can be further illustrated by the widely studied Fe_4N electrode. Our results suggest that the Fe_4N electrode (Zhang et al., 2018; Li et al., 2019; Vijay et al., 2020) does not belong to the best performing CO₂RR materials. We attribute this to the thermodynamically unfavorable CO₂ adsorption step, which agrees with the recent finding that the adsorption step on Fe_4N is thermodynamically uphill even under high electrode potentials and field strengths (Vijay et al., 2020). Therefore, CO₂RR on Fe_4N is limited by CO₂ adsorption and mass transfer at industrially relevant current densities (Vijay et al., 2020). Even though our decoupled pathway and CO₂RR analyses are based on a relatively simple and ideal electrosorption valency concept, the identification of CO₂ adsorption as a crucial step is expected to be rather general. In particular, our approach provides a fast approach to identify a catalyst, where ET during adsorption is an important feature.

In addition to accounting for ETPT and electrosorption, future studies should also consider the role of “innocent” ligands introduced by the pH or the supporting electrolyte. A recent joint experimental and computational work (Li et al., 2019) has shown that axial ligands are important in determining the CO₂RR to CO performance on M_4N-type materials. While the experimental results exhibit a high current density and Faradaic efficiency toward CO at applied potentials of −0.5 and −0.6 V vs. RHE, the calculations predict a significant thermodynamic barrier of ∼0.9 eV for CO₂ adsorption in agreement with our results. As the initial computational results were not in line with the experimental findings, the effect of axial adsorption of H₂O and OH was considered. While the adsorption energy was found to be further destabilized with axial OH adsorption, the axially adsorbed H₂O stabilized CO₂ adsorption on Fe_4N by ∼0.3 eV. Including the axial H₂O ligand in the computational Fe_4N model resulted in a better agreement with experiments as the CO₂ adsorption posed only a small thermodynamic barrier (0.06 eV) at −0.6 V vs. RHE. Furthermore, the simulated Pourbaix diagrams (Li et al., 2019) confirmed that Fe_4N electrode may bind axial ligands on both sides. While the kinetic role of the axial ligands was not considered for CO₂RR, the oxygen reduction reaction kinetics were shown to be very sensitive to the presence of “innocent” axial ligands (Rebarchik et al., 2020).

Previous studies (Peterson and Nørskov, 2012; Kuhl et al., 2014; Nitopi et al., 2019) suggested that CO binding strength is a descriptor that determines the CO₂RR product distribution. Materials with strong CO adsorption are either poisoned or produce C₁- or C₂-species or form hydrogen via the competing HER. On the contrary, electrodes binding CO weakly yield CO as the major product due to favourable CO desorption kinetics. Apart from Al-, Cr-, and Pd-dopants, the majority of 3N-coordinated electrodes bind CO quite strongly suggesting that they might be poisoned by CO. The CO adsorption on Al_3N (${\eta }_{ETPT/PCET}$ = 0.69 V) is weak and leads to facile CO desorption. Intermediate CO adsorption energies on Cr_3N and Pd_3N suggest that these two materials are promising electrocatalysts for producing C₁- or C₂-molecules; however, the former suffers from rather high limiting potential making Pd_3N the only 3N-graphene electrode suitable for further CO reduction. With the exception of Ru₂_2SV, all the other 2SV electrodes exhibit CO binding strength within ∼−0.7 eV indicating that they will primarily produce CO. The M₂_2SV electrodes show low overpotentials but feature high negative limiting potentials (above −1V) except for Ru₂_2SV, which is identified as the most promising M₂_2SV structure. Both M_4N and M₂_TV electrodes suffer from either strong CO binding or high limiting potentials, and are therefore unsuitable for CO production.

5 Conclusion

In this work, we identified promising modified graphene electrodes for CO₂RR to CO under alkaline conditions. Robust selection criteria based on thermodynamic stability, CO₂ adsorption thermodynamics, and potential-dependent reaction free energies were devised and applied. The computational hydrogen electrode concept was extended to treat decoupled PCET steps at electrode surfaces to account for the possible decoupled ETPT mechanism in alkaline conditions. We utilized this development to evaluate the effect of pure charge transfer during adsorption, i.e., electrosorption, and found that a high degree of partial charge transfer during CO₂ is detrimental to electrocatalyst performance and that moderately strong CO₂ adsorption energy without charge transfer leads to promising electrode materials. We identified metal sites coordinated to three nitrogen atoms (M_3N) and two single vacancy metal (M₂_2SV) electrodes as highly promising materials for CO₂RR following either the coupled or decoupled pathways. N-coordinated Ru and Pt electrodes exhibit promising characteristics for both coupled and decoupled pathways making these materials interesting candidates as pH-universal CO₂RR electrodes and call for further experimental and computational studies.

Data Availability Statement

The datasets presented in this study can be accessed at https://gitlab.com/ 1341 compcatjyu/co2rr-on-graphene-electrodes.

Author Contributions

AV performed the calculations and analysed the data. MM developed the thermodynamic model and oversaw the analysis. KH oversaw the calculations and analysis. All authors contributed to conceptualising the work and writing the manuscript.

Funding

MM was supported by the Academy of Finland grants 307853 and 317739. AV and KH were supported by the Academy of Finland grant 317739.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The computational resources were provided by the CSC–IT Center for Science, Espoo, Finland (https://www.csc.fi/en/) and the FGCI–Finnish Grid and Cloud Infrastructure.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.606742/full#supplementary-material.

References

Akhade, S. A., Luo, W., Nie, X., Bernstein, N. J., Asthagiri, A., and Janik, M. J. (2014). Poisoning effect of adsorbed CO during CO electroreduction on late transition metals. Phys. Chem. Chem. Phys. 16, 20429–20435. doi:10.1039/C4CP03340J

PubMed Abstract | CrossRef Full Text | Google Scholar

Aljabour, A., Coskun, H., Apaydin, D. H., Ozel, F., Hassel, A. W., Stadler, P., et al. (2018). Nanofibrous cobalt oxide for electrocatalysis of CO reduction to carbon monoxide and formate in an acetonitrile-water electrolyte solution. Appl. Catal. B. 229, 163–170. doi:10.1016/j.apcatb.2018.02.017

CrossRef Full Text | Google Scholar

Back, S., Kim, H., and Jung, Y. (2015a). Selective heterogeneous CO electroreduction to methanol. ACS Catal. 5, 965–971. doi:10.1021/cs501600x

CrossRef Full Text | Google Scholar

Back, S., Yeom, M. S., and Jung, Y. (2015b). Active sites of Au and Ag nanoparticle catalysts for CO electroreduction to CO. ACS Catal. 5, 5089–5096. doi:10.1021/acscatal.5b00462

CrossRef Full Text | Google Scholar

Back, S., Lim, J., Kim, N.-Y., Kim, Y.-H., and Jung, Y. (2017). Single-atom catalysts for CO electroreduction with significant activity and selectivity improvements. Chem. Sci. 8, 1090–1096. doi:10.1039/C6SC03911A

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagger, A., Ju, W., Varela, A. S., Strasser, P., and Rossmeisl, J. (2019). Electrochemical CO reduction: classifying Cu facets. ACS Catal. 9, 7894–7899. doi:10.1021/acscatal.9b01899

CrossRef Full Text | Google Scholar

Bohra, D., Chaudhry, J. H., Burdyny, T., Pidko, E. A., and Smith, W. A. (2019). Modeling the electrical double layer to understand the reaction environment in a CO electrocatalytic system. Energy Environ. Sci. 12, 3380–3389. doi:10.1039/C9EE02485A

CrossRef Full Text | Google Scholar

Bratsch, S. G. (1989). Standard electrode potentials and temperature coefficients in water at 298.15 K. J. Phys. Chem. Ref. Data 18, 1–21. doi:10.1063/1.555839

CrossRef Full Text | Google Scholar

Brownson, D. A. C., Kampouris, D. K., and Banks, C. E. (2012). Graphene electrochemistry: fundamental concepts through to prominent applications. Chem. Soc. Rev. 41, 6944–6976. doi:10.1039/C2CS35105F

PubMed Abstract | CrossRef Full Text | Google Scholar

Busch, M., Halck, N. B., Kramm, U. I., Siahrostami, S., Krtil, P., and Rossmeisl, J. (2016). Beyond the top of the volcano? – a unified approach to electrocatalytic oxygen reduction and oxygen evolution. Nano. Energy 29, 126–135. doi:10.1016/j.nanoen.2016.04.011

CrossRef Full Text | Google Scholar

Calle-Vallejo, F., Krabbe, A., and García-Lastra, J. M. (2017). How covalence breaks adsorption-energy scaling relations and solvation restores them. Chem. Sci. 8, 124–130. doi:10.1039/C6SC02123A

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Li, C. W., and Kanan, M. W. (2012). Aqueous CO reduction at very low overpotential on oxide-derived Au nanoparticles. J. Am. Chem. Soc. 134, 19969–19972. doi:10.1021/ja309317u

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, Y., Yang, S., Jiang, S. P., and Wang, S. (2019). Supported single atoms as new class of catalysts for electrochemical reduction of carbon dioxide. Small Methods 3, 1800440. doi:10.1002/smtd.201800440

CrossRef Full Text | Google Scholar

Dennington, R., Keith, T. A., and Millam, J. M. (2009). Gaussview Version 5. Semichem Inc. Shawnee Mission KS.

DeWulf, D. W., Jin, T., and Bard, A. J. (1989). Electrochemical and surface studies of carbon dioxide reduction to methane and ethylene at copper electrodes in aqueous solutions. J. Electrochem. Soc. 136, 1686. doi:10.1149/1.2096993

CrossRef Full Text | Google Scholar

Dunwell, M., Luc, W., Yan, Y., Jiao, F., and Xu, B. (2018). Understanding surface-mediated electrochemical reactions: CO reduction and beyond. ACS Catal. 8, 8121–8129. doi:10.1021/acscatal.8b02181

CrossRef Full Text | Google Scholar

Durand, W. J., Peterson, A. A., Studt, F., Abild-Pedersen, F., and Nørskov, J. K. (2011). Structure effects on the energetics of the electrochemical reduction of CO by copper surfaces. Surf. Sci. 605, 1354–1359. doi:10.1016/j.susc.2011.04.028

CrossRef Full Text | Google Scholar

Ferrante, F., Prestianni, A., Cortese, R., Schimmenti, R., and Duca, D. (2016). Density functional theory investigation on the nucleation of homo-and heteronuclear metal clusters on defective graphene. J. Phys. Chem. C. 120, 12022–12031. doi:10.1021/acs.jpcc.6b02833

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian˜09 revision B.01. Wallingford CT: Gaussian Inc.

Frydendal, R., Busch, M., Halck, N. B., Paoli, E. A., Krtil, P., Chorkendorff, I., et al. (2015). Enhancing activity for the oxygen evolution reaction: the beneficial interaction of gold with manganese and cobalt oxides. ChemCatChem. 7, 149–154. doi:10.1002/cctc.201402756

CrossRef Full Text | Google Scholar

Gabardo, C. M., Seifitokaldani, A., Edwards, J. P., Dinh, C.-T., Burdyny, T., Kibria, M. G., et al. (2018). Combined high alkalinity and pressurization enable efficient CO electroreduction to CO. Energy Environ. Sci. 11, 2531–2539. doi:10.1039/C8EE01684D

CrossRef Full Text | Google Scholar

Gao, D., McCrum, I. T., Deo, S., Choi, Y.-W., Scholten, F., Wan, W., et al. (2018). Activity and selectivity control in CO electroreduction to multicarbon products over CuO_x catalysts via electrolyte design. ACS Catal. 8, 10012–10020. doi:10.1021/acscatal.8b0258

CrossRef Full Text | Google Scholar

Gattrell, M., Gupta, N., and Co, A. (2006). A review of the aqueous electrochemical reduction of CO to hydrocarbons at copper. J. Electroanal. Chem. 594, 1–19. doi:10.1016/j.jelechem.2006.05.013

CrossRef Full Text | Google Scholar

Gauthier, J. A., Chen, L. D., Bajdich, M., and Chan, K. (2020). Implications of the fractional charge of hydroxide at the electrochemical interface. Phys. Chem. Chem. Phys. 22, 6964–6969. doi:10.1039/C9CP05952K

PubMed Abstract | CrossRef Full Text | Google Scholar

Gauthier, J. A., Fields, M., Bajdich, M., Chen, L. D., Sandberg, R. B., Chan, K., et al. (2019). Facile electron transfer to CO during adsorption at the metal— solution interface. J. Phys. Chem. C. 123, 29278–29283. doi:10.1021/acs.jpcc.9b10205

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, C., Zhang, T., Liang, X., Deng, X., Guo, W., Wang, Z., et al. (2020). Single transition metal atoms on nitrogen-doped carbon for CO electrocatalytic reduction: CO production or further CO reduction? Appl. Surf. Sci. 533, 147466. doi:10.1016/j.apsusc.2020.147466

CrossRef Full Text | Google Scholar

Guo, S.-X., Li, F., Chen, L., MacFarlane, D. R., and Zhang, J. (2018). Polyoxometalate-promoted electrocatalytic CO reduction at nanostructured silver in dimethylformamide. ACS Appl. Mater. Interfaces 10, 12690–12697. doi:10.1021/acsami.8b01042

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, H. A., Varley, J. B., Peterson, A. A., and Nørskov, J. K. (2013). Understanding trends in the electrocatalytic activity of metals and enzymes for CO reduction to CO. J. Phys. Chem. Lett. 4, 388–392. doi:10.1021/jz3021155

PubMed Abstract | CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985a). Ab initio effective core potentials for molecular calculations. potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 82, 299–310. doi:10.1063/1.448975

CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985b). Ab initio effective core potentials for molecular calculations. potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 82, 270–283. doi:10.1063/1.448799

CrossRef Full Text | Google Scholar

He, Z., He, K., Robertson, A. W., Kirkland, A. I., Kim, D., Ihm, J., et al. (2014). Atomic structure and dynamics of metal dopant pairs in graphene. Nano Lett. 14, 3766–3772. doi:10.1021/nl500682j

PubMed Abstract | CrossRef Full Text | Google Scholar

Heenen, H. H., Gauthier, J. A., Kristoffersen, H. H., Ludwig, T., and Chan, K. (2020). Solvation at metal/water interfaces: an ab initio molecular dynamics benchmark of common computational approaches. J. Chem. Phys. 152, 144703. doi:10.1063/1.5144912

PubMed Abstract | CrossRef Full Text | Google Scholar

Herrick, D. R. (2005). Connecting pauling and mulliken electronegativities. J. Chem. Theor. Comput. 1, 255–260. doi:10.1021/ct049942a

CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864. doi:10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

Hori, Y. i. (2008). “Electrochemical CO reduction on metal electrodes,” in Modern aspects of electrochemistry (New York, NY: Springer), 89–189.

Google Scholar

Hori, Y., Kikuchi, K., Murata, A., and Suzuki, S. (1986). Production of methane and ethylene in electrochemical reduction of carbon dioxide at copper electrode in aqueous hydrogencarbonate solution. Chem. Lett. 15, 897–898. doi:10.1246/cl.1986.897

CrossRef Full Text | Google Scholar

Hori, Y., Murata, A., and Takahashi, R. (1989). Formation of hydrocarbons in the electrochemical reduction of carbon dioxide at a copper electrode in aqueous solution. J. Chem. Soc. Faraday Trans. 1 85, 2309–2326. doi:10.1039/F19898502309

CrossRef Full Text | Google Scholar

Hörmann, N. G., Marzari, N., and Reuter, K. (2020). Electrosorption at metal surfaces from first principles. Npj Comput. Mater. 6, 136. doi:10.1038/s41524-020-00394-4

CrossRef Full Text | Google Scholar

Jia, C., Dastafkan, K., Ren, W., Yang, W., and Zhao, C. (2019). Carbon-based catalysts for electrochemical CO reduction. Sust. Energy Fuels 3, 2890–2906. doi:10.1039/C9SE00527G

CrossRef Full Text | Google Scholar

Jia, M., Fan, Q., Liu, S., Qiu, J., and Sun, Z. (2019). Single-atom catalysis for electrochemical CO reduction. Curr. Opin. Green Sustain. Chem. 16, 1–6. doi:10.1016/j.cogsc.2018.11.002

CrossRef Full Text | Google Scholar

Jones, J.-P., Prakash, G. S., and Olah, G. A. (2014). Electrochemical CO reduction: recent advances and current trends. Isr. J. Chem. 54, 1451–1466. doi:10.1002/ijch.201400081

CrossRef Full Text | Google Scholar

Ju, W., Bagger, A., Hao, G.-P., Varela, A. S., Sinev, I., Bon, V., et al. (2017). Understanding activity and selectivity of metal-nitrogen-doped carbon catalysts for electrochemical reduction of CO. Nat. Commun. 8, 1–9. doi:10.1038/s41467-017-01035-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Kattel, S., Atanassov, P., and Kiefer, B. (2012). Stability, electronic and magnetic properties of in-plane defects in graphene: a first-principles study. J. Phys. Chem. C. 116, 8161–8166. doi:10.1021/jp2121609

CrossRef Full Text | Google Scholar

Kibria, M. G., Edwards, J. P., Gabardo, C. M., Dinh, C.-T., Seifitokaldani, A., Sinton, D., et al. (2019). Electrochemical CO reduction into chemical feedstocks: from mechanistic electrocatalysis models to system design. Adv. Mater. 31, 1807166. doi:10.1002/adma.201807166

CrossRef Full Text | Google Scholar

Kim, D., Resasco, J., Yu, Y., Asiri, A. M., and Yang, P. (2014). Synergistic geometric and electronic effects for electrochemical reduction of carbon dioxide using gold–copper bimetallic nanoparticles. Nat. Commun. 5, 1–8. doi:10.1038/ncomms5948

CrossRef Full Text | Google Scholar

Kim, J., Summers, D., and Frese, K. (1988). Reduction of CO and CO to methane on Cu foil electrodes. J. Electroanal. Chem. Interfacial Electrochem. 245, 223–244. doi:10.1016/0022-0728(88)80071-8

CrossRef Full Text | Google Scholar

Kittel, C. (2004). Introduction to solid state physics. New York, NY: Wiley.

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133. doi:10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

Koper, M. T. M. (2013a). Theory of multiple proton-electron transfer reactions and its implications for electrocatalysis. Chem. Sci. 4, 2710–2723. doi:10.1039/C3SC50205H

CrossRef Full Text | Google Scholar

Koper, M. T. M. (2013b). Theory of the transition from sequential to concerted electrochemical proton–electron transfer. Phys. Chem. Chem. Phys. 15, 1399–1407. doi:10.1039/C2CP42369C

PubMed Abstract | CrossRef Full Text | Google Scholar

Koshy, D. M., Chen, S., Lee, D. U., Stevens, M. B., Abdellah, A. M., Dull, S. M., et al. (2020). Understanding the origin of highly selective CO electroreduction to CO on Ni, N-doped carbon catalysts. Angew. Chem. Int. Ed. 132, 4072–4079. doi:10.1002/anie.201912857

CrossRef Full Text | Google Scholar

Krasheninnikov, A., Lehtinen, P., Foster, A. S., Pyykkö, P., and Nieminen, R. M. (2009). Embedding transition-metal atoms in graphene: structure, bonding, and magnetism. Phys. Rev. Lett. 102, 126807. doi:10.1103/physrevlett.102.126807

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuhl, K. P., Hatsukade, T., Cave, E. R., Abram, D. N., Kibsgaard, J., and Jaramillo, T. F. (2014). Electrocatalytic conversion of carbon dioxide to methane and methanol on transition metal surfaces. J. Am. Chem. Soc. 136, 14107–14113. doi:10.1021/ja505791r

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazar, P., Karlickỳ, F., Jurečka, P., Kocman, M., Otyepková, E., Šafářová, K., et al. (2013). Adsorption of small organic molecules on graphene. J. Am. Chem. Soc. 135, 6372–6377. doi:10.1021/ja403162r

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, M.-Y., Ringe, S., Kim, H., Kang, S., and Kwon, Y. (2020). Electric field mediated selectivity switching of electrochemical CO reduction from formate to CO on carbon supported Sn. ACS Energy Lett. 5, 2987–2994. doi:10.1021/acsenergylett.0c01387

CrossRef Full Text | Google Scholar

Li, J., Pršlja, P., Shinagawa, T., Martín Fernández, A. J., Krumeich, F., Artyushkova, K., et al. (2019). Volcano trend in electrocatalytic CO reduction activity over atomically dispersed metal sites on nitrogen-doped carbon. ACS Catal. 9, 10426–10439. doi:10.1021/acscatal.9b02594

CrossRef Full Text | Google Scholar

Li, X., Bi, W., Chen, M., Sun, Y., Ju, H., Yan, W., et al. (2017). Exclusive Ni–N sites realize near-unity CO selectivity for electrochemical CO reduction. J. Am. Chem. Soc. 139, 14889–14892. doi:10.1021/jacs.7b09074

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Su, H., Chan, S. H., and Sun, Q. (2015). CO electroreduction performance of transition metal dimers supported on graphene: a theoretical study. ACS Catal. 5, 6658–6664. doi:10.1021/acscatal.5b01165

CrossRef Full Text | Google Scholar

Lim, H.-K., Shin, H., Goddard, W. A., Hwang, Y. J., Min, B. K., and Kim, H. (2014). Embedding covalency into metal catalysts for efficient electrochemical conversion of CO. J. Am. Chem. Soc. 136, 11355–11361. doi:10.1021/ja503782w

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindgren, P., Kastlunger, G., and Peterson, A. A. (2020). A challenge to the G 0 interpretation of hydrogen evolution. ACS Catal. 10, 121–128. doi:10.1021/acscatal.9b02799

CrossRef Full Text | Google Scholar

Lu, Q., and Jiao, F. (2016). Electrochemical CO reduction: electrocatalyst, reaction mechanism, and process engineering. Nano. Energy 29, 439–456. doi:10.1016/j.nanoen.2016.04.009

CrossRef Full Text | Google Scholar

Lu, Q., Rosen, J., Zhou, Y., Hutchings, G. S., Kimmel, Y. C., Chen, J. G., et al. (2014). A selective and efficient electrocatalyst for carbon dioxide reduction. Nat. Commun. 5, 1–6. doi:10.1038/ncomms4242

CrossRef Full Text | Google Scholar

Lu, X., Zhu, C., Wu, Z., Xuan, J., Francisco, J. S., and Wang, H. (2020). In situ observation of the pH gradient near the gas diffusion electrode of CO reduction in alkaline electrolyte. J. Am. Chem. Soc. 142, 15438–15444. doi:10.1021/jacs.0c06779

PubMed Abstract | CrossRef Full Text | Google Scholar

MacDowell, N., Florin, N., Buchard, A., Hallett, J., Galindo, A., Jackson, G., et al. (2010). An overview of CO capture technologies. Energy Environ. Sci. 3, 1645–1669. doi:10.1039/C004106H

CrossRef Full Text | Google Scholar

Malkhandi, S., and Yeo, B. S. (2019). Electrochemical conversion of carbon dioxide to high value chemicals using gas-diffusion electrodes. Curr. Opin. Chem. Eng. 26, 112–121. doi:10.1016/j.coche.2019.09.008

CrossRef Full Text | Google Scholar

Marenich, A. V., Ho, J., Coote, M. L., Cramer, C. J., and Truhlar, D. G. (2014). Computational electrochemistry: prediction of liquid-phase reduction potentials. Phys. Chem. Chem. Phys. 16, 15068–15106. doi:10.1039/C4CP01572J

PubMed Abstract | CrossRef Full Text | Google Scholar

Melander, M. M. (2020). Grand canonical rate theory for electrochemical and electrocatalytic systems I: general formulation and proton-coupled electron transfer reactions. J. Electrochem. Soc. 167, 116518. doi:10.1149/1945-7111/aba54b

CrossRef Full Text | Google Scholar

Melander, M. M., Kuisma, M. J., Christensen, T. E. K., and Honkala, K. (2019). Grand-canonical approach to density functional theory of electrocatalytic systems: thermodynamics of solid-liquid interfaces at constant ion and electrode potentials. J. Chem. Phys. 150, 041706. doi:10.1063/1.5047829

PubMed Abstract | CrossRef Full Text | Google Scholar

Mermin, N. D. (1965). Thermal properties of the inhomogeneous electron gas. Phys. Rev. 137, A1441–A1443. doi:10.1103/PhysRev.137.A1441

CrossRef Full Text | Google Scholar

Mistry, H., Reske, R., Zeng, Z., Zhao, Z.-J., Greeley, J., Strasser, P., et al. (2014). Exceptional size-dependent activity enhancement in the electroreduction of CO over Au nanoparticles. J. Am. Chem. Soc. 136, 16473–16476. doi:10.1021/ja309317u

PubMed Abstract | CrossRef Full Text | Google Scholar

Mulliken, R. S. (1934). A new electroaffinity scale; Together with data on valence states and on valence ionization potentials and electron affinities. J. Chem. Phys. 2, 782–793. doi:10.1063/1.1749394

CrossRef Full Text | Google Scholar

Mulliken, R. S. (1955). Electronic population analysis on LCAO-MO molecular wave functions. I. J. Chem. Phys. 23, 1833–1840. doi:10.1063/1.1740588

CrossRef Full Text | Google Scholar

NIST database (2020). Nist webbook. Available at: https://webbook.nist.gov/cgi/cbook.cgi?ID=C124389.

Google Scholar

Nitopi, S., Bertheussen, E., Scott, S. B., Liu, X., Engstfeld, A. K., Horch, S., et al. (2019). Progress and perspectives of electrochemical CO reduction on copper in aqueous electrolyte. Chem. Rev. 119, 7610–7672. doi:10.1021/acs.chemrev.8b00705

PubMed Abstract | CrossRef Full Text | Google Scholar

Nørskov, J. K., Rossmeisl, J., Logadottir, A., Lindqvist, L., Kitchin, J. R., Bligaard, T., et al. (2004). Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B. 108, 17886–17892. doi:10.1021/jp047349j

CrossRef Full Text | Google Scholar

Nykänen, L., and Honkala, K. (2011). Density functional theory study on propane and propene adsorption on Pt(111) and PtSn alloy surfaces. J. Phys. Chem. C. 115, 9578–9586. doi:10.1021/jp1121799

CrossRef Full Text | Google Scholar

Pan, F., Li, B., Sarnello, E., Fei, Y., Feng, X., Gang, Y., et al. (2020). Pore-edge tailoring of single atomic iron-nitrogen sites on graphene for enhanced CO reduction. ACS Catal. 10, 10803–10811. doi:10.1021/acscatal.0c02499

CrossRef Full Text | Google Scholar

Pan, F., Zhang, H., Liu, K., Cullen, D., More, K., Wang, M., et al. (2018). Unveiling active sites of CO reduction on nitrogen-coordinated and atomically dispersed iron and cobalt catalysts. ACS Catal. 8, 3116–3122. doi:10.1021/acscatal.8b00398

CrossRef Full Text | Google Scholar

Perdew, J. P., Ziesche, P., and Eschrig, H. (1991). Electronic structure of solids’91. Berlin: Akademie Verlag.

Pérez-Gallent, E., Marcandalli, G., Figueiredo, M. C., Calle-Vallejo, F., and Koper, M. T. (2017). Structure-and potential-dependent cation effects on CO reduction at copper single-crystal electrodes. J. Am. Chem. Soc. 139, 16412–16419. doi:10.1021/jacs.7b10142

PubMed Abstract | CrossRef Full Text | Google Scholar

Peterson, A. A., Abild-Pedersen, F., Studt, F., Rossmeisl, J., and Nørskov, J. K. (2010). How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels. Energy Environ. Sci. 3, 1311–1315. doi:10.1039/C0EE00071J

CrossRef Full Text | Google Scholar

Peterson, A. A., and Nørskov, J. K. (2012). Activity descriptors for CO electroreduction to methane on transition-metal catalysts. J. Phys. Chem. Lett. 3, 251–258. doi:10.1021/jz201461p

CrossRef Full Text | Google Scholar

Petersson, a., Bennett, A., Tensfeldt, T. G., Al-Laham, M. A., Shirley, W. A., and Mantzaris, J. (1988). A complete basis set model chemistry. I. the total energies of closed-shell atoms and hydrides of the first-row elements. J. Chem. Phys. 89, 2193–2218. doi:10.1063/1.455064

CrossRef Full Text | Google Scholar

Petersson, G., and Al-Laham, M. A. (1991). A complete basis set model chemistry. II. open-shell systems and the total energies of the first-row atoms. J. Chem. Phys. 94, 6081–6090. doi:10.1063/1.460447

CrossRef Full Text | Google Scholar

Qu, L., Liu, Y., Baek, J.-B., and Dai, L. (2010). Nitrogen-doped graphene as efficient metal-free electrocatalyst for oxygen reduction in fuel cells. ACS Nano. 4, 1321–1326. doi:10.1021/nn901850u.PMID:20155972

PubMed Abstract | CrossRef Full Text | Google Scholar

Rad, A. S., and Foukolaei, V. P. (2015). Density functional study of Al-doped graphene nanostructure towards adsorption of CO, CO and HO. Synth. Met. 210, 171–178. doi:10.1016/j.synthmet.2015.09.026

CrossRef Full Text | Google Scholar

Rebarchik, M., Bhandari, S., Kropp, T., and Mavrikakis, M. (2020). How noninnocent spectator species improve the oxygen reduction activity of single-atom catalysts: microkinetic models from first-principles calculations. ACS Catal. 10, 9129–9135. doi:10.1021/acscatal.0c01642

CrossRef Full Text | Google Scholar

Ringe, S., Clark, E. L., Resasco, J., Walton, A., Seger, B., Bell, A. T., et al. (2019). Understanding cation effects in electrochemical CO reduction. Energy Environ. Sci. 12, 3001–3014. doi:10.1039/C9EE01341E

CrossRef Full Text | Google Scholar

Scalmani, G., and Frisch, M. J. (2010). Continuous surface charge polarizable continuum models of solvation. i. general formalism. J. Chem. Phys. 132, 114110. doi:10.1063/1.3359469

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmickler, W., and Guidelli, R. (2014). The partial charge transfer. Electrochim. Acta. 127, 489–505. doi:10.1016/j.electacta.2014.02.057

CrossRef Full Text | Google Scholar

Schneider, J., Jia, H., Muckerman, J. T., and Fujita, E. (2012). Thermodynamics and kinetics of CO, CO, and H binding to the metal centre of CO reduction catalysts. Chem. Soc. Rev. 41, 2036–2051. doi:10.1039/C1CS15278E

PubMed Abstract | CrossRef Full Text | Google Scholar

Shang, R., Steinmann, S. N., Xu, B.-Q., and Sautet, P. (2020). Mononuclear Fe in N-doped carbon: computational elucidation of active sites for electrochemical oxygen reduction and oxygen evolution reactions. Cat. Sci. Tech. 10, 1006–1014. doi:10.1039/C9CY01935A

CrossRef Full Text | Google Scholar

Shao, Y., Dodelet, J.-P., Wu, G., and Zelenay, P. (2019). PGM-free cathode catalysts for PEM fuel cells: a mini-review on stability challenges. Adv. Mater. 31, 1807615. doi:10.1002/adma.201807615

CrossRef Full Text | Google Scholar

Shi, C., Hansen, H. A., Lausche, A. C., and Nørskov, J. K. (2014). Trends in electrochemical CO reduction activity for open and close-packed metal surfaces. Phys. Chem. Chem. Phys. 16, 4720–4727. doi:10.1039/C3CP54822H

PubMed Abstract | CrossRef Full Text | Google Scholar

Siahrostami, S., Jiang, K., Karamad, M., Chan, K., Wang, H., and Nørskov, J. (2017). Theoretical investigations into defected graphene for electrochemical reduction of CO. ACS Sustain. Chem. Eng. 5, 11080–11085. doi:10.1021/acssuschemeng.7b03031

CrossRef Full Text | Google Scholar

Sun, Z., Ma, T., Tao, H., Fan, Q., and Han, B. (2017). Fundamentals and challenges of electrochemical CO reduction using two-dimensional materials. Inside Chem. 3, 560–587. doi:10.1016/j.chempr.2017.09.009

CrossRef Full Text | Google Scholar

Tachikawa, H., and Kawabata, H. (2011). Ground and low-lying excited electronic states of graphene flakes: a density functional theory study. J. Phys. B Atom. Mol. Opt. Phys. 44, 205105. doi:10.1088/0953-4075/44/20/205105

CrossRef Full Text | Google Scholar

Tian, Z., Priest, C., and Chen, L. (2018). Recent progress in the theoretical investigation of electrocatalytic reduction of CO. Adv. Theory Simul. 1, 1800004. doi:10.1002/adts.201800004

CrossRef Full Text | Google Scholar

Trevethan, T., Latham, C. D., Heggie, M. I., Briddon, P. R., and Rayson, M. J. (2014). Vacancy diffusion and coalescence in graphene directed by defect strain fields. Nanoscale 6, 2978–2986. doi:10.1039/c3nr06222h

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripkovic, V., Vanin, M., Karamad, M., Björketun, M. E., Jacobsen, K. W., Thygesen, K. S., et al. (2013). Electrochemical CO and CO reduction on metal-functionalized porphyrin-like graphene. J. Phys. Chem. C. 117, 9187–9195. doi:10.1021/jp306172k

CrossRef Full Text | Google Scholar

Valter, M., Busch, M., Wickman, B., Grönbeck, H., Baltrusaitis, J., and Hellman, A. (2018). Electrooxidation of glycerol on gold in acidic medium: a combined experimental and DFT study. J. Phys. Chem. C. 122, 10489–10494. doi:10.1021/acs.jpcc.8b02685

CrossRef Full Text | Google Scholar

Varela, A. S., Ju, W., and Strasser, P. (2018). Molecular nitrogen-carbon catalysts, solid metal organic framework catalysts, and solid metal/nitrogen-doped carbon (MNC) catalysts for the electrochemical CO reduction. Adv. Energy Mater. 8, 1703614. doi:10.1002/aenm.201703614

CrossRef Full Text | Google Scholar

Varela, A. S., Ju, W., Bagger, A., Franco, P., Rossmeisl, J., and Strasser, P. (2019). Electrochemical reduction of CO on metal-nitrogen-doped carbon catalysts. ACS Catal. 9, 7270–7284. doi:10.1021/acscatal.9b01405

CrossRef Full Text | Google Scholar

Varela, A. S. (2020). The importance of pH in controlling the selectivity of the electrochemical CO reduction. Curr. Opin. Green Sustain. Chem. 26, 100371. doi:10.1016/j.cogsc.2020.100371

CrossRef Full Text | Google Scholar

Vasileff, A., Zheng, Y., and Qiao, S. Z. (2017). Carbon solving carbon’s problems: recent progress of nanostructured carbon-based catalysts for the electrochemical reduction of CO. Adv. Energy Mater. 7, 1700759. doi:10.1002/aenm.201700759

CrossRef Full Text | Google Scholar

Verma, A. M., Agrawal, K., and Kishore, N. (2018). Binding of phenolic model compounds with noble metal doped graphene sheets. Comp. Theo. Chem. 1134, 37–46. doi:10.1016/j.comptc.2018.05.001

CrossRef Full Text | Google Scholar

Verma, A. M., and Kishore, N. (2019). First-principles study on the gas-phase decomposition of bio-oil oxygenated compounds over the palladium catalyst surface. Phys. Chem. Chem. Phys. 21, 22320–22330. doi:10.1039/C9CP04858H

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, A. M., and Kishore, N. (2018). Molecular modeling approach to elucidate gas phase hydrodeoxygenation of guaiacol over a Pd (111) catalyst within DFT framework. J. Mol. Model 24, 254. doi:10.1007/s00894-018-3803-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, A. M., and Kishore, N. (2017). Molecular simulations of palladium catalysed hydrodeoxygenation of 2-hydroxybenzaldehyde using density functional theory. Phys. Chem. Chem. Phys. 19, 25582–25597. doi:10.1039/C7CP05113A

PubMed Abstract | CrossRef Full Text | Google Scholar

Vijay, S., Gauthier, J. A., Heenen, H. H., Bukas, V. J., Kristoffersen, H. H., and Chan, K. (2020). Dipole-field interactions determine the CO reduction activity of 2D Fe-N-C single-atom catalysts. ACS Catal. 10, 7826–7835. doi:10.1021/acscatal.0c01375

CrossRef Full Text | Google Scholar

Wadt, W. R., and Hay, P. J. (1985). Ab initio effective core potentials for molecular calculations. potentials for main group elements Na to Bi. J. Chem. Phys. 82, 284–298. doi:10.1063/1.448800

CrossRef Full Text | Google Scholar

Wang, H., Wang, Q., Cheng, Y., Li, K., Yao, Y., Zhang, Q., et al. (2012). Doping monolayer graphene with single atom substitutions. Nano Lett. 12, 141–144. doi:10.1021/nl2031629

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Feng, Q., Cheng, Y., Yao, Y., Wang, Q., Li, K., et al. (2013). Atomic bonding between metal and graphene. J. Phys. Chem. C. 117, 4632–4638. doi:10.1021/jp311658m

CrossRef Full Text | Google Scholar

Wang, W.-H., Himeda, Y., Muckerman, J. T., Manbeck, G. F., and Fujita, E. (2015). CO hydrogenation to formate and methanol as an alternative to photo-and electrochemical CO reduction. Chem. Rev. 115, 12936–12973. doi:10.1021/acs.chemrev.5b00197

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Zhao, Q., Yang, B., Li, Z., Bo, Z., Lam, K. H., et al. (2019). Emerging nanostructured carbon-based non-precious metal electrocatalysts for selective electrochemical CO reduction to CO. J. Math. Chem. A. 7, 25191–25202. doi:10.1039/C9TA09681G

CrossRef Full Text | Google Scholar

Warner, J. H., Margine, E. R., Mukai, M., Robertson, A. W., Giustino, F., and Kirkland, A. I. (2012). Dislocation-driven deformations in graphene. Science 337, 209–212. doi:10.1126/science.1217529

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, J., Sharifi, T., Gao, Y., Zhang, T., and Ajayan, P. M. (2019). Emerging carbon-based heterogeneous catalysts for electrochemical reduction of carbon dioxide into value-added chemicals. Adv. Mater. 31, 1804257. doi:10.1002/adma.201804257

CrossRef Full Text | Google Scholar

Yin, Z., Peng, H., Wei, X., Zhou, H., Gong, J., Huai, M., et al. (2019). An alkaline polymer electrolyte CO electrolyzer operated with pure water. Energy Environ. Sci. 12, 2455–2462. doi:10.1039/C9EE01204D

CrossRef Full Text | Google Scholar

Yu, F., Wei, P., Yang, Y., Chen, Y., Guo, L., and Peng, Z. (2019). Material design at nano and atomic scale for electrocatalytic CO reduction. Nano Mater. Sci. 1, 60–69. doi:10.1016/j.nanoms.2019.03.006

CrossRef Full Text | Google Scholar

Zhang, B., Zhang, J., Shi, J., Tan, D., Liu, L., Zhang, F., et al. (2019). Manganese acting as a high-performance heterogeneous electrocatalyst in carbon dioxide reduction. Nat. Commun. 10, 1–8. doi:10.1038/s41467-019-10854-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Yang, S., Wu, J., Liu, M., Yazdi, S., Ren, M., et al. (2018). Electrochemical CO reduction with atomic iron-dispersed on nitrogen-doped graphene. Adv. Energy Mater. 8, 1703487. doi:10.1002/aenm.201703487

CrossRef Full Text | Google Scholar

Zhao, T., Tian, Y., Wang, Y., Yan, L., and Su, Z. (2019). Mechanistic insight into electroreduction of carbon dioxide on FeN_x (x= 0–4) embedded graphene. Phys. Chem. Chem. Phys. 21, 23638–23644. doi:10.1039/C9CP03370J

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, W., Zhang, Y.-J., Zhang, H., Lv, H., Li, Q., Michalsky, R., et al. (2014). Active and selective conversion of CO to CO on ultrathin Au nanowires. J. Am. Chem. Soc. 136, 16132–16135. doi:10.1021/ja5095099

PubMed Abstract | CrossRef Full Text | Google Scholar