- 1School of Nuclear Science and Technology, University of South China, Hunan, China
- 2Research Center for Digital Nuclear Reactor Engineering and Technology of Hunan Province, University of South China, Hunan, China
- 3Reactor Engineering Technology Research Division, China Institute of Atomic Energy, Beijing, China
- 4School of Resource Environment and Safety Engineering, University of South China, Hunan, China
In this study, the dynamic characteristics of accelerator-driven subcritical reactor (ADSR) under beam transients with high heterogeneity of neutron flux in time-space are investigated. Multi-mode core few-group constants are generated by three kinds of neutron fluxes: steady state of ADSR, λ-eigenvalue fundamental wave, and α-eigenvalue fundamental wave. The proposed few-group constants overcome the limitation of single few-group constant generated by two-step method that cannot consider the variation in neutron flux density and neutron energy spectrum with time and space. Compared to the existing few-group constants generated by two-step method under different operating conditions, the self-adapting multi-mode core few-group constants exhibit higher accuracy in the case of following two modes: steady-state mode of ADSR in the starting process and λ-eigenvalue mode in the beam trip condition. Overall, this research provides useful insights on neutron kinetics and can boost the development of ADSRs.
Introduction
With the increasing utilization of nuclear power, the disposal of accumulated nuclear waste has become a critical issue globally. The minor actinides (MA) and long-lived fission products (LLFP) in the spent fuel discharged from nuclear power plants are highly radioactive with long half-lives. Accelerator-driven subcritical reactors (ADSRs) have a high neutron redundancy and subcritical safety, they could be powerful tools for transmuting MA and LLFP (Li et al., 2011; Zhan and Xu, 2012; Zhou et al., 2013). ADSR is driven by a high-power proton accelerator (HPPA) to generate continuous wave proton beams of Giga-electron volts (GeV) energy that bombard heavy metal targets and generate spallation neutrons. Beam transients cause rapid changes in the intensity of spallation neutron sources, leading to a drastic variation in the power of ADSR (Yu, 2005). The resulting shock is a key factor that affects the safety and reliability of ADSR (Hayancri et al., 2009).
Traditional neutron kinetics analysis mainly focuses on the breeding system of non-external neutron source that is not far from the critical point, and the dynamic characteristics are only related to the inherent properties of the system. Further, since it is not far from the critical point, the neutron flux of the breeding system is not much different from that of the critical system. It is approximately based on the λ-eigenvalue fundamental wave of neutron flux.
ADSR is a high-energy and strong external source-driven deep subcritical system. The dynamic characteristics are not only affected by the inherent system properties but also by high-energy spallation neutrons. During beam transients, the characteristics of external source change rapidly, and the fundamental and harmonic neutron fluxes are perturbated. Due to their different temporal characteristics, the neutron flux and the neutron energy spectrum at different positions are not consistent with each other over time, resulting in strong time-space heterogeneity of the neutron flux (Shen and Wang, 2011; Wang and Shen, 2011).
Due to the strong time-space heterogeneity of the neutron flux, it is difficult to apply traditional neutron kinetics models and analysis methods for investigating the dynamic characteristics of ADSR with beam transients.
The dynamic characteristics of some ADSRs including YALINA (Persson et al., 2008), MUSE (Soule et al., 2004), KUCA (Masao et al., 2017; Pyeon et al., 2017), VENUS 1# (Cao et al., 2005; Xie, 2011), and VENUS II (Jiang et al., 2018; Liang et al., 2018; Liu et al., 2018) have been studied earlier. However, these experimental studies were primarily based on the measurement of sub-criticality, reactivity, and effective fraction of delayed neutron.
The existing studies on the dynamic characteristics of ADSRs under beam transients are mainly based on numerical simulation. In the existing neutron kinetics models and analysis methods for ADSR under beam transients, the core few-group cross sections are generated by the traditional two-step method. The strong time-space heterogeneity of neutron flux during beam transients leads to a complex evolution of the core few-group cross sections over time and space. Therefore, these cross sections based on the two-step method cannot be used to describe the strong time-space heterogeneity of the neutron flux in ADSRs under beam transients (Akio and seiji, 2003; Shen and Wang, 2011; Yu et al., 2014). Therefore, further investigations are needed for core few-group cross sections.
To overcome the limitations of the existing models, in this study, the multi-mode core few-group constants with beam transients and time-space heterogeneity were generated by three kinds of neutron fluxes: steady state of ADSR, fundamental wave with eigenvalue λ, and fundamental wave with eigenvalue α. This resolves the issue in the existing few-group constants based on two-step method that cannot describe the variation in neutron flux and neutron energy spectrum over time and space. Based on the proposed quasi-static model with multi-mode core few-group constants, we establish a neutron kinetics model for strong time-space heterogeneity in ADSR under beam transients. Finally, the dynamic characteristics of ADSR are revealed under various sub-criticalities and beam transients. Overall, this study potentially improves the understanding of neutron kinetics and promotes the development of ADSRs.
The rest of the paper is organized as follows. Analysis of Neutron Dynamics describes the analysis of neutron dynamics. In Calculation Model and Generation of Self-Adapting Multi-Mode Core few-Group Constants of ADSR, we introduce the calculation model and the generation of multi-mode core few-group constants of ADSR. Dynamic Characteristics of ADSR Under Beam Transients presents the dynamic characteristics of ADSR under beam transients. Finally, the study is concluded in Conclusion.
Analysis of Neutron Dynamics
Presently, the time-space dynamic model under the improved quasi-static (IQS) framework is generally used to examine neutron kinetics (Rineiski et al., 2002; Song et al., 2017; Hou et al., 2018). This model employs factorization to decompose the neutron flux density that changes with time and space into the product of the amplitude and shape functions. Further, it describes the change in the amplitude function by an accurate point reactor kinetic equation. The employment of different shape functions can affect the results of neutron dynamics.
Therefore, the investigation of the selection and effect of shape function is crucial to understand the dynamic characteristics of neutrons in ADSR and can improve the calculation accuracy of neutron kinetics methods.
Improved Quasi-Static Method
The time-space dynamics equation of ADSR with consideration of delayed and external neutrons can be expressed as follows:
where
where
Assuming that the neutron flux density
Substituting Eq.4 into Eq.1, the equation of amplitude function
where
Equation 5 describing the amplitude function is also called the accurate point reactor dynamic equation, which is directly derived from the neutron space-time dynamic equation. The amplitude function can be obtained by solving this equation using the Gear method (Huang, 2007). In the IQS method, the shape function at a time t can be obtained by the first-order difference Eq.14, i.e.,
where
Selection of Initial Shape Function
To simulate the neutron kinetics during the starting process of ADSR, the neutron flux density at the initial time is 0, which causes the shape function at the initial time to have a certain “arbitrariness” while calculating the IQS. Thus, in this study, in addition to the influence of the weight function, three initial shape functions are considered for the simulation of starting process of ADSR: neutron flux density
The neutron flux density of λ fundamental wave is the most commonly employed shape function in traditional analysis of neutron kinetics. The prompt α eigenvalue is a natural eigenvalue, which describes the neutron multiplication characteristics of a reactor that deviates from critical condition. In principle, prompt α eigenvalue has the advantage of describing the time evolution of neutron kinetics of ADSRs. The steady-state neutron flux density of ADSR incorporates the effect of external neutron sources on the steady-state distribution of neutron flux. The initial shape function is obtained from the neutron flux density at the beam loss condition.
When IQS simulation is performed on ADSR, neutron flux density of λ fundamental wave, neutron flux density of prompt α fundamental wave, and steady-state neutron flux density of ADSR are selected as the shape functions, which are called λ mode, prompt α mode, and fixed source mode, respectively.
Calculation Model and Generation of Self-Adapting Multi-Mode Core few-Group Constants of ADSR
Calculation Model
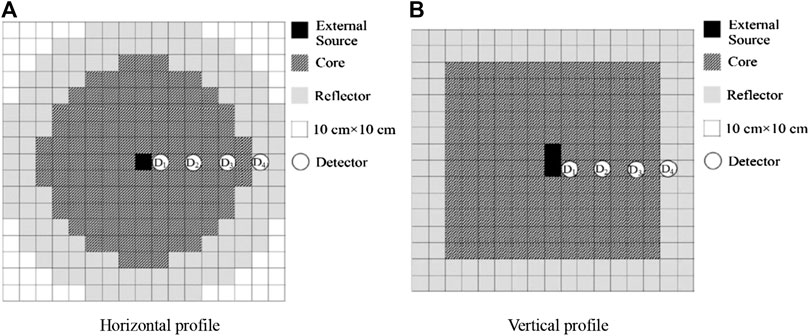
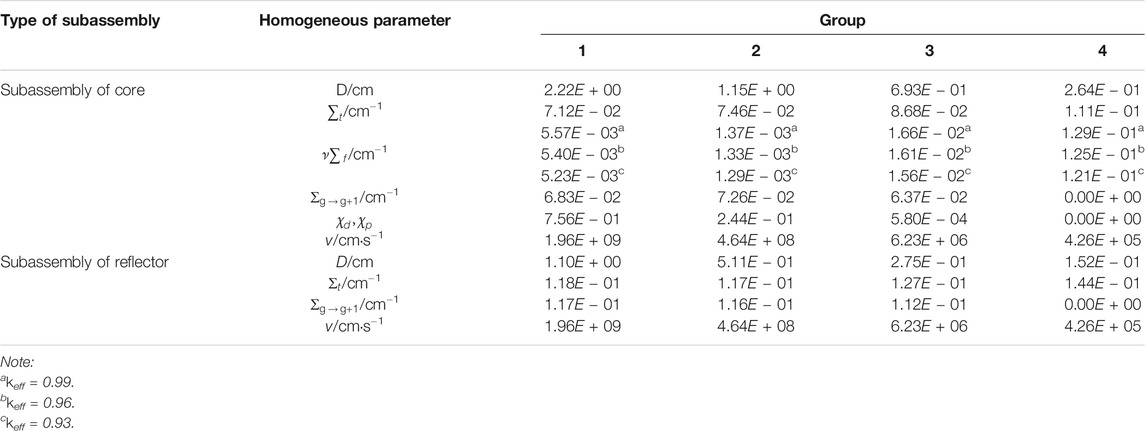
The core of the ADSR considered in this study has a three-dimensional cylindrical structure (Cao, 2008; Xie, 2016), as shown in Figure 1. Both fuel and reflector are square assemblies with the size of 10 × 10 cm2. An isotropic external neutron source is placed at the center of the core with a height of 20 cm. Detectors are arranged at D1, D2, D3, and D4 to measure the core power distribution.
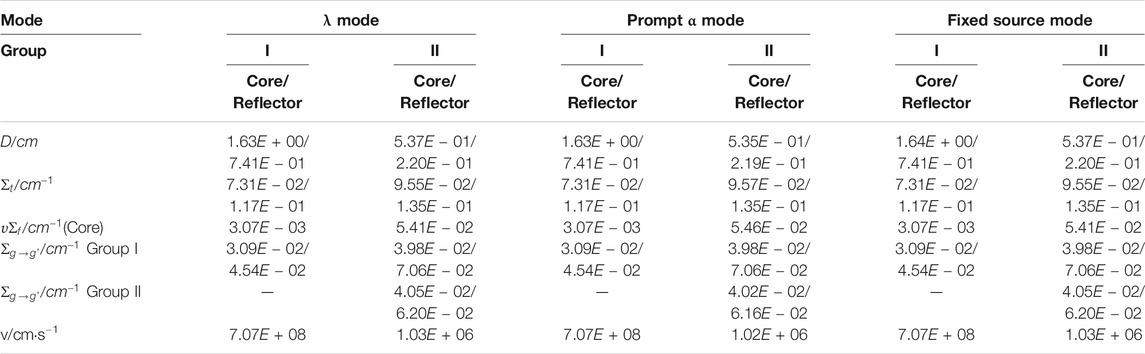
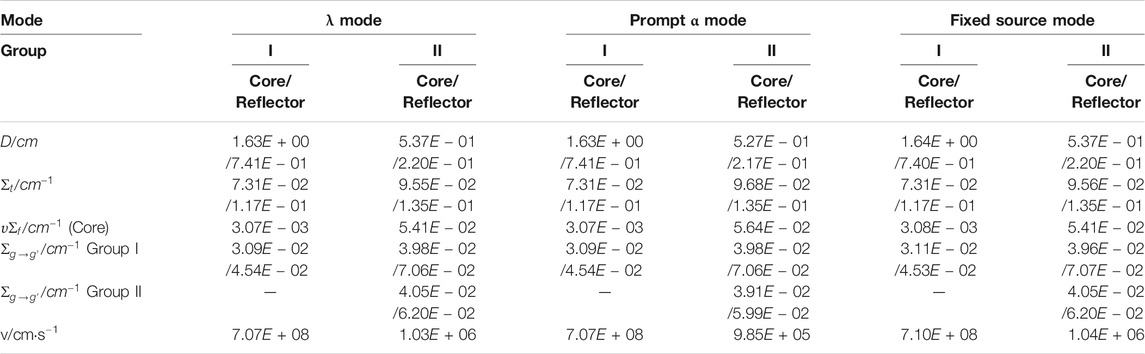
For the diffusion calculation of ADSR, four-group homogenized constants are used, and the initial cross sections are obtained from reference (Cao, 2008). For investigating the dynamic characteristics of neutrons at different sub-criticalities, the core fission neutron cross section υΣf is adjusted, and then three kinds of sub-criticalities (keff = 0.99, 0.96, and 0.93) are considered using the diffusion code DONJON (Alain et al., 2018). The adjusted four-group homogenized cross sections of the ADSR are shown in Table 1 (Xie, 2016; Hou et al., 2018).
The intensity of the steady-state external neutron source set in the reactor is 1 × 107/(cm3·s), and the initial energy falls in the first energy group.
Generation of Core few-Group Constants
ADSR under beam transients has a strong time-space heterogeneity of the neutron flux. When the beam is stable, the core few-group constants are only related to space. In the absence of beam state, these constants change with time and space. The two different states of core few-group constants can be combined to form the multi-mode core few-group constants that accurately characterize the strong time-space heterogeneity of the neutron flux. It can improve the existing quasi-static model with few-group constants based on two-step method.
As a preliminary study, we considered the four-group homogenized cross sections of the ADSR (Table 1) as the initial cross sections to perform multi-mode energy group condensation. According to the conservation of the reaction rate, the first and second groups of the four-group cross sections in Table 1 are collapsed as group I, and the third and fourth groups are collapsed as group II.
The energy group condensation formula for the total cross section of group I is as follows:
The energy group condensation formula for the diffusion coefficient of group I is as follows:
The energy group condensation formula for the fission cross section of group I is as follows:
The energy group condensation method of group II is the same as that of group I. The condensation formulas for transfer cross sections of group I and group II are as follows:
The condensation formulas for speed are as follows:
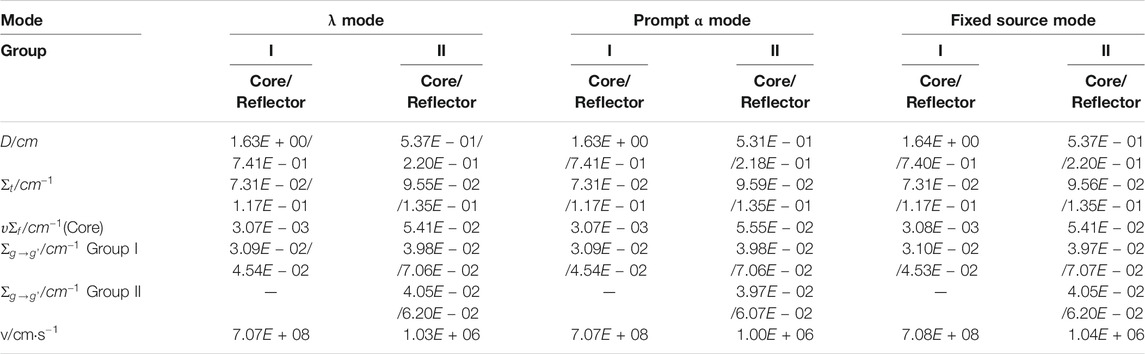
The four-group cross sections of the reference ADSR core and reflector assemblies (Table 1) are collapsed to form two-group constants, where the three modes (λ mode, prompt α mode, and fixed source mode) are considered. The results of condensation for the ADSR core and reflector assemblies corresponding to keff = 0.99, keff = 0.96, and keff = 0.93 are shown in Tables 2–4, respectively. It is clear the results of condensation for core and reflector of the three modes are different, and the discrepancies become larger with the increase in the sub-criticality, which is because diverse neutron energy spectrum is calculated by different modes and the influence of the external neutron source becomes stronger.
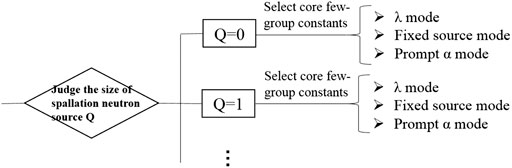
The three kinds core few-group constants (λ mode, prompt α mode, and fixed source mode) generated in this study can be adapted to the beam transient conditions to establish the self-adapting multi-mode core few-group constants (Figure 2). Figure 2 shows that different core few-group constants can be selected by judging the size of the spallation neutron source (according to various beam transient conditions).
The three modes: λ mode, prompt α mode, and fixed source mode, of few-group constants obtained above are linked and correspond to the quasi-static core diffusion code for neutron kinetics of under beam transients. This helps in establishing a method for the analysis of neutron kinetics of ADSR with self-adapting multi-mode core few-group constants for arbitrary beam transient conditions.
Dynamic Characteristics of ADSR Under Beam Transients
In this section, we discuss the results of neutron kinetics obtained using multi-mode core few-group constants and IQS methods under various sub-criticalities, locations, and beam transient conditions. Further, compared to the direct solutions of time-space dynamic equations (referred to as reference values) (Hou et al., 2018), the dynamic characteristics of ADSR under beam transients are analyzed. For a clear comparison, the number of core neutrons is considered as the physical quantity governing neutron kinetics.
In this study, the results obtained using self-adapting multi-mode core few-group constants (multi-mode s_α and multi-mode s_λ) are compared with those obtained using the existing few-group constants based on single two-step method (λ mode or S mode). Table 5 shows the few-group constants used in several modes. Due to the different operating conditions considered, according to a previous study (Hou et al., 2018) on the weighting functions for the starting process and the beam trip conditions, the adjoint λ fundamental neutron flux density is uniformly used as the weighting function of various modes.
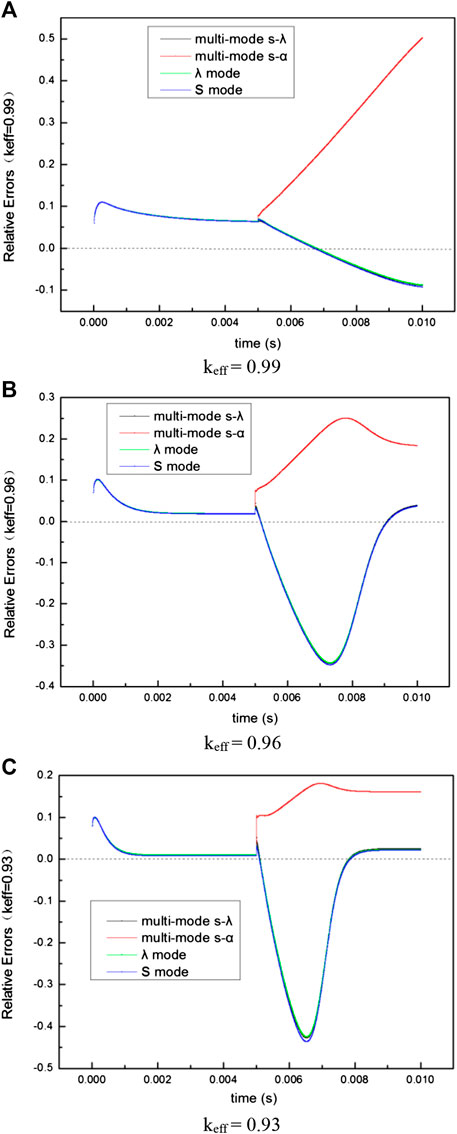
Here, we studied the beam transients by considering the starting process and the beam trip conditions. Since the errors between the different quasi-static dynamic results and the reference value is concentrated in a very short time after the external source changes (Hou et al., 2018), we set the simulation time of both operating conditions to 0.005 s. Figures 3A–C shows the relative errors of the core neutron number and the reference value for the four modes under the conditions of keff = 0.99, 0.96 and 0.93, respectively.
The following inferences can be drawn from Figure 3:
1. For the starting process: the results of four modes are similar, and the relative error increases first, then decreases, and finally stabilizes.
2. For the beam trip conditions: the results of λ mode, S mode, and multi-mode s_λ are similar. The relative error of multi-mode s_α is relatively larger and its variation trend with time is different from that of the other three modes. When keff = 0.99, the relative errors of λ mode, S mode, and multi-mode s_λ decrease first and then increase, while that of multi-mode s_α keeps increasing. When keff = 0.96 and 0.93, the relative errors of λ mode, S mode, and multi-mode s_λ increase first, then decrease, then increase, and finally stabilize, while that of multi-mode s_α first increases, then decreases, and finally stabilizes.
3. As the sub-criticality increases, the difference in dynamics between the four modes also increases.
Under the beam trip conditions, the multi-mode s_α behaves differently from the other modes, which can be attributed to the following two reasons:
1. Delayed neutrons and prompt neutrons are distinguished in the prompt α mode but not in the other two modes.
2. When the beam is stable, the delayed neutron source term is small and can be ignored. Mathematically, the source term of the prompt α mode is smaller.
As the sub-criticality increases, the influence of the external neutron source becomes stronger. Hence, the dynamic parameter difference of different modes increases, which causes the difference between the results of different modes to become larger.
To measure the deviation of IQS dynamics in several modes during the entire beam transients, we summed the absolute values of the relative errors at various time points to quantify the accuracy of each mode (Table 6) (Hou et al., 2018). Table 6 indicates that under various sub-criticalities, the relative magnitudes of the accumulated errors of the four modes under the entire beam transients are basically the same.
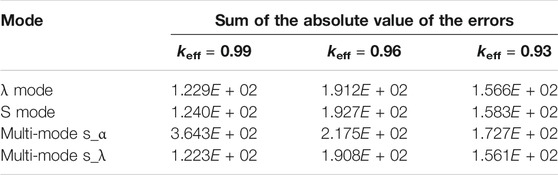
TABLE 6. Sum of the deviations between the IQS and reference results during the entire beam transients.
Overall, the error of the multi-mode s_λ based on S mode for the starting process and λ mode for the beam trip conditions is the smallest.
To study the space effect, we considered the relative errors of neutron number in four typical positions of the core in four modes (Figure 4). Figures 4–C show the relative errors between the number of neutrons and the reference values at the positions D1, D2, D3, and D4 of core for keff = 0.99, 0.96, and 0.93, respectively.
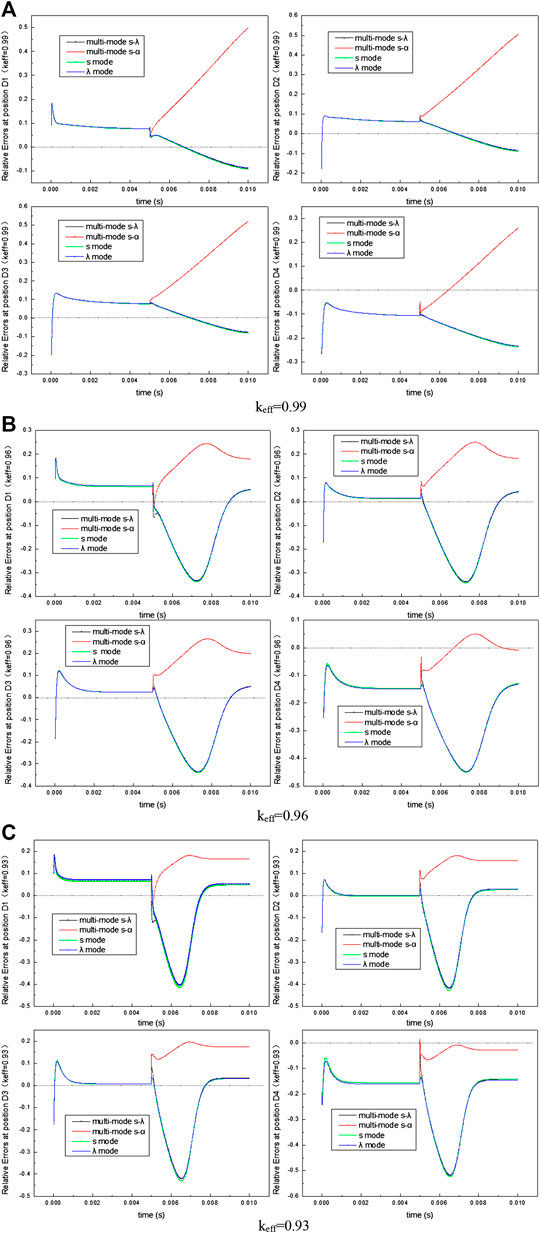
FIGURE 4. Relative errors for the results of neutron kinetics at different positions under various sub-criticalities and beam transient conditions.
Figure 4 indicates that at the four positions D1, D2, D3, and D4, the variation trend of relative errors of the IQS results for the four modes is roughly consistent with that of the total neutron number of core. For the starting process, the error of the neutron kinetics at D4 is the largest, and that at D2 is the smallest. For the beam trip conditions, the error of the neutron kinetics results at the D4 position is the largest, and that at the D1 and D2 positions is relatively small. As the sub-criticality increases, the difference between the IQS results of the four modes also increases.
In general, by comparing the relative errors of neutron kinetics results at various positions, it can be inferred that the relative error of multi-mode s_λ is the smallest under the beam transient conditions.
Conclusion
In this study, the multi-mode core few-group constants of ADSR with beam transients and time-space heterogeneity of neutron flux were generated by three kinds of neutron fluxes: steady state of ADSR, λ-eigenvalue fundamental wave, and α-eigenvalue fundamental wave. We established a method for analyzing the dynamic characteristics of ADSR under beam transients with the generated self-adapting few-group constants. Further, the influence of core few-group constants on the dynamic characteristics of the ADSR under beam transients was examined. The results obtained using self-adapting multi-mode core few-group constants (multi-mode s_α and multi-mode s_λ)were compared with those obtained using the existing few-group constants based on two-step method (λ mode and S mode). The results revealed that under various sub-criticalities and high heterogeneity of neutron flux in time-space, the multi-mode s_λ was the most accurate, which was comprised of the following two modes: steady-state mode of ADSR in the starting process and λ-eigenvalue mode in the beam trip conditions. This research provides useful insights on neutron kinetics and can boost the development of ADSRs. In the future, more beam transient conditions will be considered to verify the multi-mode method.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
ND developed the code and performed simulations, analyzed data, and drafted or provided the revision of the paper. JX, CH, and WZ developed the code and performed simulations, analyzed data, and co-wrote the paper. ZC, PZ, ZL, CX, and QX have given some advice about the article. TY supervised the research and resolved appropriately, provided the revision of the paper, and approved of the final version to be published. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the National Natural Science Foundation of China (No. 11875162).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Akio, Y., and Seiji, S. (2003). Study on neutronics design of accelerator driven subcritical reactor as future neutron source, part 2: kinetic characteristics. Ann. Nucl. Energy 30, 1425–1435. doi:10.1016/S0306-4549(03)00078-1
Alain, H., Sekki, D., and Richard, C. (2018). Technical Report IGE-344. A user guide for DONJON Version5. Montréal: École Polytechnique de Montréal.
Cao, J., Shi, Y. Q., Xia, P., Zhu, Q. F., Zhang, W., Luo, H. D., et al. (2005). Annual Report for China Institute of Atomic Energy. Research progress of VENUS 1# subcritical neutron dynamic experiment, 67–68.
Cao, Y. (2008). Space-time kinetics and time-eigenfunctions. PhD thesis. Ann Arbor, MI: University of Michigan.
Hayancri, T., Kenji, N., and Kazufumi, T. (2009). “Estimation of acceptable beam trip frequencies of accelerators for ADS and comparison with experimental data of accelerators,” International topical meeting on nuclear research applications and utilization of accelerators, Vienna, Austria, May 4–May 8, 2009 (Vienna, Austria: IAEA).
Hou, C., Yu, T., Xie, J. S., Zeng, W. J., Chen, Z. P., Xie, Q., et al. (2018). The effects of the shape function and weighting function on the kinetics of the ADS sub-critical reactor. Nuclear Techniques 41 (09), 77–86. doi:10.11889/j.0253-3219.2018.hjs.41.090602
Huang, Z. Q. (2007). Fundamentals of nuclear reactor dynamics. 2nd Edn. Beijing, China: Peking University Press.
Jiang, W., Gu, L., Zhu, Q. F., Zhou, Q., Chen, L., Liu, X., et al. (2018). Experiment and simulation study for fuel rod worth of VENUS-II light Water Reactor. Atomic Energy Sci. Technol. 52 (09), 1665–1670. doi:10.7538/yzk.2017.youxian.0793
Li, Z. X., Liu, X. P., Zhu, X. L., Huang, L. G., and Leng, F. H. (2011). International development trend analysis of accelerator-driven sub-critical system. Science Focus 6 (3), 32–43.
Liang, S. H., Zhu, Q. F., Shi, Y. Q., Zhou, Q., and Luo, H. D. (2018). Sub-critical reactivity and dynamic characteristic measured by source-jerk method on VENUS-II. Atomic Energy Sci. Technol. 52 (02), 302–306. doi:10.7538/yzk.2017.youxian.0259
Liu, Y., Zhou, Q., Zhu, Q. F., Zhang, W., Liu, D. H., Chen, L., et al. (2018). Reactivity measurement of solid spallation target in VENUS-II by period method. Atomic Energy Sci. Technol. 52 (10), 1769–1773. doi:10.7538/yzk.2018.youxian.0054
Masao, Y., Song, H. K., and Cheol, H. P. (2017). “Measurement of effective delayed neutron fraction in accelerator-driven system with 100 MeV protons and solid targets,” Proceedings of the reactor physics asia, Chengdu, China, August 24–August 25, 2017.
Persson, C. M., Fokau, A., Serafimovich, I., Bournos, V., Fokov, Y., Routkovskaia, C., et al. (2008). Pulsed neutron source measurements in the subcritical ADS experiment YALINA-Booster. Ann. Nucl. Energy 35 (12), 2357–2364. doi:10.1016/j.anucene.2008.07.011
Pyeon, C. H., Yamanaka, M., Endo, T., Rooijen, W. F. G., and Chiba, G. (2017). Experimental benchmarks on kinetic parameters in accelerator-driven system with 100 MeV protons at Kyoto University Critical Assembly. Ann. Nucl. Energy 105, 346–354. doi:10.1016/j.anucene.2017.03.030
Rineiski, A., Maschek, W., and Rimpault, G. (2002). Performance of neutron kinetics models for ADS transient analyses. Reno, NV: Accapp/adtta.
Shen, F., and Wang, S. (2011). Point kinetic equation of ADS sub-critical reactor. Atomic Energy Sci. Technol. 45 (11), 1300–1304.
Song, Y. M., Gao, Q. Y., Xu, Y. C., Wang, K., Yang, Y. W., Zhang, L., et al. (2017). Simulation analysis of neutron time-space kinetics for ADS sub-critical reactor based on IQS/MC method. Atomic Energy Sci. Technol. 51(3): 450–456. doi:10.7538/yzk.2017.51.03.0450
Soule, R., Assal, W., Chaussonnet, P., Destouches, C., Domergue, C., Jammes, C., et al. (2004). Neutronic studies in support of accelerator-driven systems: the MUSE experiments in the MASURCA facility. Nucl. Sci. Eng. 148, 124–152. doi:10.13182/NSE01-13C
Wang, S., and Shen, F. (2011). Adjoint equation of ADS sub-critical reactor. Atomic Energy Sci. Technol. 45 (7): 775–779. doi:10.1007/s12264-011-1035-3
Xie, J. S. (2011). Study on the criticality extrapolation neutron space effect in VENUS 1#. Master’s thesis. Hunan, China: University of South China.
Xie, J. S. (2016). A study on neutronics of ADS sub-critical reactor based on harmonics expansion method. PhD thesis. Beijing, China: China Institute of Atomic Energy.
Yu, T. (2005). Computer simulation on transient response of beam transients in accelerator driven sub critical system. PhD thesis. Beijing, China: China Institute of Atomic Energy.
Yu, T., Xie, J. S., and Liu, Z. J. (2014). “Some considerations on the analysis method of the dynamic characteristics of the accelerator beam transients ADS subcritical reactor,” The 15th conference on numerical calculation and particle transport of reactors and the 2014 conference on reactor physics, Chengdu, China. 25–27.
Zhan, W. L., and Xu, H. S. (2012). Advanced fission energy program—ADS transmutation system. Bull. Chin. Acad. Sci. 27 (3), 375–381.
Keywords: accelerator-driven subcritical system, multi-mode core few-group constants, improved quasi-static method, dynamic characteristics analysis, beam transients
Citation: Deng N, Xie J, Hou C, Zeng W, Chen Z, Yu T, Zhao P, Liu Z, Xie C and Xie Q (2021) Dynamic Characteristics of Accelerator-Driven Subcritical Reactor With Self-Adapting Multi-Mode Core Few-Group Constants. Front. Energy Res. 8:603084. doi: 10.3389/fenrg.2020.603084
Received: 05 September 2020; Accepted: 30 November 2020;
Published: 13 January 2021.
Edited by:
Mingjun Wang, Xi’an Jiaotong University, ChinaReviewed by:
Qian Zhang, Harbin Engineering University, ChinaJiankai Yu, Massachusetts Institute of Technology, United States
Copyright © 2021 Deng, Xie, Hou, Zeng, Chen, Yu, Zhao, Liu, Xie and Xie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tao Yu, eXV0YW8yOUBzaW5hLmNvbQ==
 Nianbiao Deng
Nianbiao Deng Jinsen Xie1,2
Jinsen Xie1,2