Mixed-Integer Linear Programming (MILP) Approach for the Synthesis of Efficient Power-to-Syngas Processes

Introduction

It is generally agreed that immediate large-scale actions are required worldwide to cease further CO₂ emissions and to reduce its current concentration in the atmosphere (IPCC, 2013). To achieve this goal, a shift from fossil fuels toward renewable energy carriers is necessary. Products, intermediates, and raw materials that contribute to high CO₂ emissions must be identified alongside suitable technologies for the conversion of CO₂ and biological feedstocks into useful chemicals and fuel. This can be achieved by Power-to-X technologies, which are capable of transforming renewable electricity and sustainable feedstock into useful components such as syngas.

Synthesis gas (syngas), a mixture of H₂ and CO in variable proportions, is an important intermediate and precursor necessary for the production of a wide range of products. Its worldwide production requires approximately 2% of the global primary energy demand (El-Nagar and Ghanem, 2019). However, since most of the syngas production is based on fossil fuels, it entails large, positive CO₂ emissions. Therefore, the sustainable production of syngas offers high potential for the reduction of CO₂ emissions. Furthermore, its intermediate location within the overall production chain, from feedstocks to chemicals or fuels, allows for existing downstream processes to be run without any substantial modifications and, simultaneously, to benefit from a sustainable feed stream. Due to the fact that syngas can be readily converted into liquid fuels, i.e., via Fischer-Tropsch synthesis (Gruber et al., 2019), it plays a crucial role in decarbonizing the transportation system.

In recent years, Power-to-Syngas related processes have been an object of interest in the scientific community on different scales. Detailed catalytic studies were performed on the reaction steps. Abdullah et al. (2017) and Arora and Prasad (2016) proposed an extensive review of the role of Ni-based catalysts in dry-reforming of methane, effective in terms of the efficient, direct utilization of biogas, although negatively affected by its endothermic nature. Rh-based catalysts were studied in the context of oxygen-enhanced dry-reforming (oxy-dry reforming): oxygen debottlenecks the dry reforming process by reducing coking effects (Moral et al., 2018). Singha et al. (2016) characterized nanocrystalline Ni-ZrO₂ catalysts for tri-reforming, particularly suited to accept flue gases without the need for previous separation. In the context of partial oxidation, a study by Pantaleo et al. (2016) proposes the use of CeO₂-supported nickel catalysts: the catalyst activity and stability are revealed to be deeply affected by the crystallite size and interaction between nickel oxide and ceria. Furthermore, high conversion and selectivity were obtained. The analysis of a synergistic combination of partial oxidation and dry reforming of methane was explored by Kang et al. (2018): a non-stoichiometric dry reforming feed-stream (excess methane over carbon dioxide) is fed to a fixed bed reactor previously oxidized by air. The subsequent oxidation of methane accompanies the endothermic dry reforming, with a resulting decrease in energy demand. Chemical looping was also dealt with by Wenzel et al. (2018) in the context of the reverse water-gas shift reaction. The author simulated and compared fixed-bed and fluidized-bed reactors filled with iron oxide and ceria oxygen-storage material (OSM) with a novel reaction kinetic. The study concluded that fixed-bed outperforms fluidized-bed with respect to OSM and carbon monoxide concentration in the outlets.

Methodological advancements were achieved in terms of process networks by Schack et al. (2016), who combined several renewable-to-chemical processes within the same optimization framework by means of large linear models. In this context, process pathways were identified via linear programming and with respect to the cost of resources. More recently, Liesche et al. (2019) and Schack et al. (2020) proposed an optimization technique based on the linearization of the states for process and unit optimization (FluxMax). The benefits of implementing linear programming techniques combines the guarantee for global optimality with the advancement achieved by the underlying algorithms, capable of exploring large scenarios with little computational effort, thus making them suitable for large-scale analyses.

In the present contribution, a superstructure optimization approach is used to identify which reaction and separation steps should be chosen to produce syngas with a minimum overall energy demand. Special emphasis is put on differentiating between energy inputs in the form of heat and electricity. Biogas from anaerobic digestion, water, and CO₂ from direct air-capture are considered as renewable raw materials. Essentially, biogas is a carbon-neutral resource, and it does therefore not contribute significantly to the increase in atmospheric CO₂ levels (Paolini et al., 2018). As chemical reaction steps, water electrolysis, methane steam reforming, dry reforming, partial oxidation, tri-reforming, and reverse water-gas shift are considered and possible synergies allowed. For the subsequent separation of the mixtures, both state-of-the-art as well as new and emerging technologies are considered. The aim is to highlight most promising flowsheets for current and future implementation, for the downstream applications reported in Table 1. The overall idea is sketched in Figure 1. An analysis of costs is omitted in this contribution for two reasons: (1) reliable cost estimates are not readily available for all unit operations, especially for emerging technologies, and (2) the analysis should not be biased toward existing, commercially available technologies but should reflect a wide range of opportunities to identify possible future research needs.

TABLE 1

Table 1. Syngas downstream applications, molar ratios, temperature, and pressure requirements.

FIGURE 1

Figure 1. General representation of the syngas production framework.

Methods

System Description

Syngas is produced by chemical conversion steps followed by separation and conditioning of the molar H₂/CO ratio. Figure 2 represents a simplified flowsheet of the system described in this section. Purified biogas (BG) from anaerobic digestion and CO₂ from direct air-capture are the candidate carbon sources. Several reactors generate raw syngas from the feedstocks. Biogas purification steps are not included in the analysis. Nevertheless, a 2-to-3 CO₂/CH₄ biogas mixture can be fed directly to dry-reforming (DR) or tri-reforming (TRI), or separated into its components CO₂ and CH₄, reactants for reverse water-gas-shift (RWGS), methane steam-reforming (SR), and methane partial oxidation (POX). CO₂ from direct air capture can be fed to the RWGS reaction. With the exception of DR, the other chemical reactors require H₂O, O₂, or H₂. Consequently, a make-up stream of H₂O is also allowed, which either feeds SR and TRI or is split into pure H₂ and O₂ via an electrolyzer (EL). The raw syngas is composed of unreacted components and side products. Recycle and outlet streams are therefore introduced. Excess O₂ can be utilized for power generation by oxy-combustion of excess CH₄, or released into the atmosphere. Unreacted CO₂ is also released into the atmosphere. However, such emissions are biogenic due to the selected carbon sources for the process. Excess H₂ is pressurized and stored at 300 bar (Di Profio et al., 2009). EL can provide green H₂ directly into the outlet syngas stream, bypassing the battery of reactors.

FIGURE 2

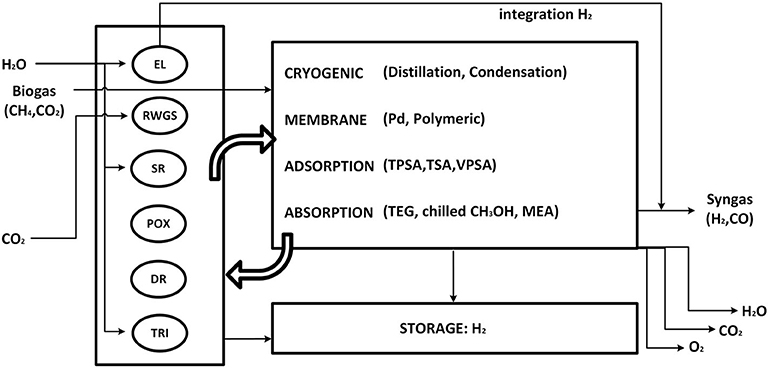
Figure 2. Simplified process flowsheet. EL, electrolyzer; RWGS, reverse water-gas-shift reactor; SR, methane steam reforming; POX, methane partial oxidation; DR, dry reforming of methane; TRI, tri-reforming of methane; TPSA,TSA,VPSA, temperature/pressure/vacuum swing adsorption; TEG, ethylene glycol absorption; MEA, mono-ethanol amine.

The product separation can be accomplished by a number of state-of-the-art or emerging technologies. For a single separation task, e.g., separation of component A from an initial mixture ABC, the superstructure comprises one or more separation methods. As an example, the task of separating H₂ from CO₂, CO and CH₄ can be accomplished by three competing methods: layered bed pressure-swing adsorption, polymeric membrane and palladium membranes. This contribution is intended to provide a conservative energy analysis of the system. Electricity is therefore not recovered by expansion and cooling utility consumption not accounted for. The power required for pumping cooling water is assumed to be negligible compared to the major energy contributions in the system.

General Modeling Assumptions for Reactors and Separators

The underlying modeling assumptions for reactors are the following:

- Reactor temperature, pressure, and feed composition are assigned prior to optimization;

- RWGS, SR, DR, and POX are modeled as Gibbs reactors, and a stoichiometric feed is assigned. Their outlet composition is calculated prior to optimization;

- Side reactions occurring in SR, DR, and POX are considered;

- Due to the intrinsic system complexity, representative temperature, pressure, and inlet and outlet composition for TRI are retrieved from literature (Song and Pan, 2004);

- Water conversion at EL is 100%;

- Each reactor is associated with a single set of temperature, pressure, feed, and outlet composition.

All reactors specifications are reported in Table 2.

TABLE 2

Table 2. Parameters for the description of reactors.

For separators, the following most general assumptions are applied:

- Sharp-split separators;

- The generic separator is decomposed into operation and regeneration steps;

- Typical temperature and pressure levels are assigned prior to optimization;

- Unit-specific calculations are embedded if required;

- The components in gas phase obey the ideal gas law;

- Compression and expansion steps are adiabatic;

Scope of the contribution is to underline dominant process paths in a topological perspective. For this reason, the optimization of the operating conditions of each process element is not part of this study.

Modeling of Reactors

The complete set of parameters implemented at a reactor-level is reported in Table 2. The current section discusses the rationale behind its identification.

Mass Balances

When a non-adiabatic system is at thermodynamic equilibrium, it is sufficient to define the molar composition by the following set of algebraic equations for each given independent stoichiometric relation j:

$\begin{array}{ll}{f}_j(T,p,\lambda )=0,\forall j\in J,& (1)\end{array}$

where f is a function of the system temperature, pressure, and the extent of reaction λ. Hence, for the RWGS reactor, J = {j | j = {RWGS}}; for SR J = {j | j = {SR, WGS}}, and for DR J = {j | j = {DR, RWGS}}, where WGS denotes the water gas shift reaction. The outlet composition can thus be determined. Given that (T, p) are fixed and that the feed to the reactor is stoichiometric, the ratio between outlet and inlet flowrates remains constant for any given inlet flowrate. As a result, the outlet molar flowrate is linearly proportional to the feed flowrate, and the compositions are fixed for all streams.

POX is run within an adiabatic reactor with irreversible reactions of partial and total oxidation:

$\begin{array}{ll}2{CH}_4+O_2\to 2CO+4H_2& (2)\end{array}$

$\begin{array}{ll}{CH}_4+2O_2\to 2H_{2}O+{CO}_2.& (3)\end{array}$

As a consequence, Equation set (1) is not sufficient to characterize the equilibrium. For this process-step, T is the temperature after adiabatic reaction, which is calculated from the following energy balance

$\begin{array}{ll}{H}_{in}^{◦}(T_{in})-H^{◦}(T)=0,& (4)\end{array}$

which expresses the conservation of energy in terms of total enthalpy change. Furthermore, atomic balances for the elements saturate the degrees of freedom, leading to the set of equations

$\begin{array}{ll}{f}_j(\text{n})=0,\forall j\in J:=\left\{\text{DR},\text{SR}\right\},& (5)\end{array}$

$\begin{array}{ll}{H}^{◦}(T_{in},\text{n})-H^{◦}(T)=0,& (6)\end{array}$

$\begin{array}{ll}{n}_{i,in}-n_i=0,\forall i\in I:=\left\{\text{C},\text{O},\text{H}\right\},& (7)\end{array}$

which is solved for T and n (vector of molar outlet flowrates). Here, C, O, and H belong to set I and denote the chemical elements carbon, oxygen, and hydrogen, respectively. As for RWGS, SR, and DR, feed composition, temperature, and pressure are fixed, and the outlet composition and reactor temperature can be calculated.

The ratio between outlet and inlet mole flowrate is calculated accounting for the conversion of methane and the outlet composition.

Energy Balances

The process system includes endothermic reactors (RWGS, SR, DR, and TRI) and an adiabatic reactor (POX). In all the cases, preconditioning of the feed streams to the reactors is performed by compression and pre-heating, thus enabling the internal energy of reactants to reach the requirements for chemical conversion.

Each endothermic reactor requires a thermal power input, expressed by a linear combination such as

$\begin{array}{ll}{\displaystyle \sum _{j\in J}}{\lambda }_j\Delta H_j^{◦}(T)=n_{in}{\displaystyle \sum _{j\in J}}{\theta }_j\Delta H_j^{◦}(T),& (8)\end{array}$

where θ_j is the constant ratio between the extent of reaction j and n_in the feed flowrate. POX is adiabatic and requires no modeling of excess heat. For TRI, the summation appearing in the right-hand side of Equation (8) is determined from the standard reaction enthalpy of the main reactions—dry, steam reforming, and partial oxidation of methane—and from their extent of reaction, estimated from Song and Pan (2004).

The electrolyzer requires power in the form of electrical input. As reported in Bensmann et al. (2013), the Gibbs free energy of reaction provides a reasonable estimation for the reversible power requirement, which is divided by an efficiency factor of 72% to obtain the real demand. As for the reactors, EL requires feed preconditioning to reach the operative temperature at atmospheric pressure.

Modeling of Separators

An extensive literature survey was conducted to identify unit-specific calculations. The energy requirements are therefore characterized for each specific case, resulting in linear gray-box models. The superstructure embeds the following families of separation methods: adsorption (temperature- and pressure-swing), absorption (glycol, amine, and methanol), membrane separation (polymeric and palladium), and cryogenic operations (chilled methanol and cryogenic distillation). Table 3 introduces the set of separators allowed within the control volume and their parameters selection.

TABLE 3

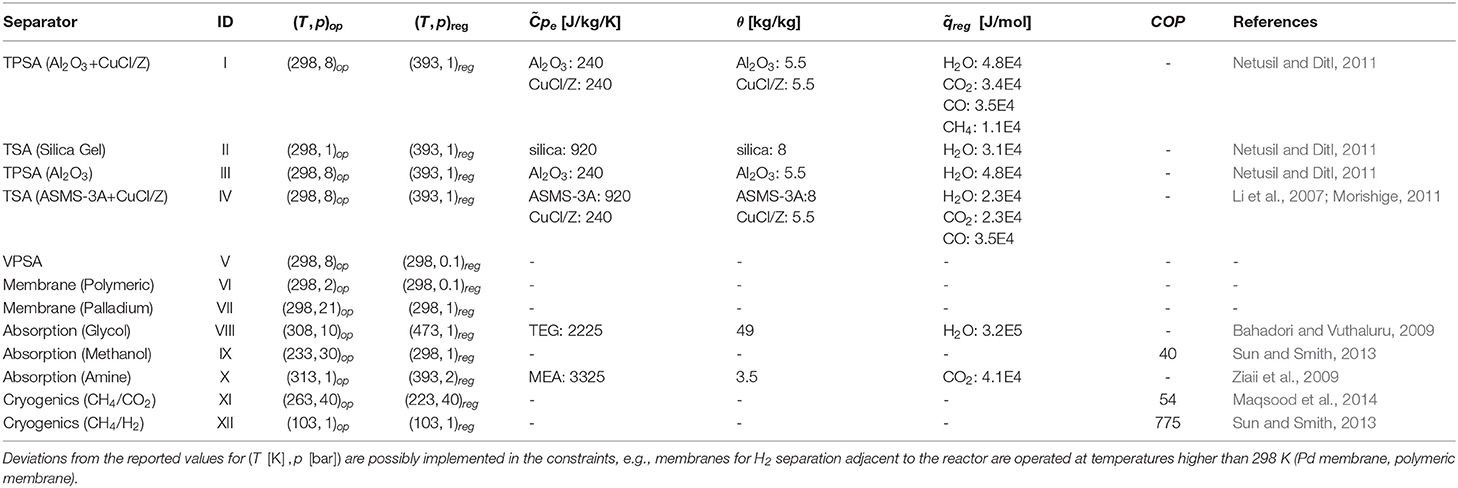
Table 3. Separation methods and identifier adopted in Table 4.

Mass Balances

The sharp-split assumption allows for a linear mathematical description only if the composition at the beginning of the separation train is fixed. For this reason, the modeling choice of fixing temperature and pressure at the Gibbs reactors introduced in section (2.2) is justified. This approach has been adopted in literature (Biegler et al., 1997) for the screening of distillation sequences, while the current contribution extends the method to a wider choice of separators. The underlying mathematical formulation reads

$\begin{array}{ll}{n}_A=n_{(A,B,C)}\frac{x_A}{x_A+x_B+x_C}=n_{(A,B,C)}{\xi }_{A/(B,C)},& (9)\end{array}$

where a generic component A is ideally separated out of a mixture (A, B, and C), and the split factor ξ is given by the ratio of the mole fractions x at the outlet stream of the reactor. The splits modeled in the framework are listed in Table 4 together with the corresponding feasible separation methods and literature references. It is here stressed that not all the separation techniques are at high readiness level. A few separators are considered feasible for specific separation tasks if characteristic properties, such as kinetic diameter, relative permeability, dew points, etc., suggest so. Nevertheless, most of the separators are state-of-the-art technologies in industry or in laboratory-scale applications.

TABLE 4

Table 4. Numbered list of splits allowed in the superstructure and available separation methods.

Energy Balances

The generic separator is divided into an operation and regeneration step. A membrane separates the permeate from the retentate stream, a gas-liquid absorption process is followed by stripping, and an adsorption step via VPSA/TSA is periodically switched into regeneration mode by vacuum generation or heating, respectively. Each method is therefore associated with two distinct (T, p) values for operation (T, p)_ops and regeneration (T, p)_reg, respectively: the feed stream, as well as the outlet from the operation-step, are at (T, p)_ops. In order to model the adjustment of the internal energy between consecutive separators, heating or cooling, compression or expansion are considered. For thermal-power calculations, the heat capacity $\tilde{C}p$ is calculated as a weighted average for pure components, accounting for the actual mixture composition and the initial and final temperature.

As formerly stated in section (2.1), power recovery by expansion and cooling are not considered as long as they occur above the atmospheric conditions (T = 298K, p = 1 bar). Nevertheless, the expansion of gas may require inter-heating steps. Similarly, compression may require cooling. The temperature attained after isentropic transformation is calculated as

$\begin{array}{ll}{T}_{2,id}=T_1{\left(\frac{p_2}{p_1}\right)}^{\frac{R}{\tilde{C}p}},& (10)\end{array}$

where R is the universal gas constant. The real temperature is calculated assuming an efficiency factor of T = 80%. In agreement with the conservative framework, the power requirement for compression is over-estimated by a single, isentropic step as well as the temperature out of compression and expansion. As an example, whenever a process stream delivers gas to higher (T, p) values, the pressurization can be deployed to partly satisfy the need for thermal power input. For an adiabatic compression step, the specific molar electrical work is estimated as

$\begin{array}{ll}\tilde{w}=\frac{\gamma }{(\gamma -1)}R{T}_1\left({\left(\frac{p_2}{p_1}\right)}^{\frac{\gamma -1}{\gamma }}-1\right)\frac{1}{\eta },& (11)\end{array}$

$\begin{array}{ll}\gamma =\frac{\tilde{C}p}{\tilde{C}v}& (12)\end{array}$

where η = 0.8 is the efficiency, and γ is the ratio of specific heats at constant pressure and constant volume (see Grande and Rodrigues, 2007). Equation (11) defines a coefficient which multiplies the gas flowrate, i.e., the mathematical description is linear. The same formula is adopted to model vacuum operations as in Grande and Rodrigues (2007), e.g., vacuum normalization in VPSA or membrane separators. For the latter, the pressure in the retentate is assumed to be 20 times higher than in the permeate side, set at p = 0.1 bar is assumed (Huang et al., 2014). In order to describe the energy demand of each separator, additional and method-specific calculations are included.

Cryogenic separator

The non-ideal coefficient of performance (COP) describes the ratio between the thermal power absorbed by the refrigerant and the real electrical power required at the compressor in a cryogenic loop. The definition of COP reads

$\begin{array}{ll}CO{P}_{real}=CO{P}_{id}\eta =\frac{Q}{W_{id}}\eta =\frac{T_{ev}^R}{T_{cond}^R-T_{ev}^R}\eta ,& (13)\end{array}$

where W_id is the ideal electrical power requirement. In an ideal case, it corresponds to a reverse Carnot cycle between the cryogenic evaporation temperature of the refrigerant, $T_{ev}^R$ and the temperature at which the refrigerant releases its internal energy by condensation, $T_{cond}^R$. The ideal COP is corrected by a thermodynamic efficiency factor η of 60% (Smith, 2005). Q is the thermal power acquired by the refrigerant during cryogenic evaporation and is lost by the cooling process fluid in order to reach the required cryogenic temperature. A proportionality coefficient for the estimation of the power requirement in cryogenic operations is derived by rearranging Equation (13):

$\begin{array}{ll}\tilde{w}=\frac{1}{CO{P}_{id}\eta }Q=\frac{1}{\eta }\frac{T_{cond}^R-T_{ev}^R}{T_{ev}^R}\tilde{C}p\left(T_{amb}-T_{cryo}\right).& (14)\end{array}$

In Equation (14), a distinction is made between the cryogenic temperatures T_cryo and $T_{ev}^R$, the former being 15K higher than the latter, thus ensuring the heat transfer.

Temperature-swing adsorption: TSA

TSA operations consist of cyclic switch between operation and regeneration at high temperature of the adsorbent bed. Consequently, the relevant contributions for regenerations are the heat of desorption for the entrained components Q_des and the heat input to raise the bed temperature Q_bed:

$\begin{array}{ll}{Q}_{TSA}=Q_{bed}+Q_{des}=\left({\tilde{q}}_{des}+{\tilde{q}}_{bed}\right)n_{feed}& (15)\end{array}$

$\begin{array}{ll}{\tilde{q}}_{bed}=\left(T_{reg}-T_{op}\right){\displaystyle \sum _{k\subset K}}\left(\frac{1}{{\theta }_i}\widehat{C}{p}_{bed,l}M{W}_i{x}_i\right),& (16)\end{array}$

$\begin{array}{ll}{\tilde{q}}_{des}={\displaystyle \sum _{k\subset K}}\left({\tilde{q}}_{des,i}^{*}{x}_i\right).& (17)\end{array}$

For Equations (16) and (17), sets k and K are introduced:

$\begin{array}{l}k\subset K,\\ k=\{i,l\mid i=\{\text{components adsorbed by adsorbent-type }l\},\\ l=\left\{\text{adsorbent-type }l\right\}\}.& (18)\end{array}$

In Equation (16), ${\theta }_i^{-1}M{W}_i$ is the molar mass of adsorbent required to adsorb component i, which is multiplied by the specific heat per unit of mass of adsorbent $\widehat{C}$p. Furthermore, MW_i is the molecular weight. In Equation (17), ${\tilde{q}}_{des,i}^{*}$ is the molar heat of desorption for component i.

Layered beds are also considered, which necessitates the subscript l and the summation operator in Equations (16) and (17).

Absorption in glycol, amines, or chilled methanol

The gas-liquid absorption processes require high-temperature regeneration. It is often the case that the absorption operation is performed in pressurized vessels. Unit-specific calculations must account for the change of the internal energy of the fluid sent to regeneration. The specific thermal power input reads

$\begin{array}{ll}{\tilde{q}}_{rec}={\theta }_{rec}\tilde{C}{p}_{entrainer}(T_{reg}-T_{op}),& (19)\end{array}$

where θ_rec is the ratio between the flowrate of entrainer required per unit of entrained key component (circulation rate). The description of amine and glycol absorption resort to Equation (19). The absorption of CO₂ in methanol occurs at cryogenic conditions, whereas the regeneration is operated at ambient temperature. As a consequence, this specific separator is described by the relations already introduced for cryogenic systems in section (2.4.2).

Modeling of Interconnections

This section discusses the conceptual structures that enable to build the final set of problem constraints in a linear form.

Mixture

For a given mixture ϕ, there are two sets of mass balances:

$\begin{array}{ll}{\xi }_i^{\varphi }{n}_i-{\displaystyle \sum _j}{n}_{ji}=0\forall i\in I,& (20)\end{array}$

$\begin{array}{ll}{n}_j-{\displaystyle \sum _i}{n}_{ji}=0\forall j\in J.& (21)\end{array}$

Sets I and J in Equations (20) and (21) incorporate the feed streams to the separators that generate and accept ϕ, respectively. Furthermore, n_i and n_j are the feed flowrates to the separators, while n_ji represents the flowrate of the connecting stream from separator i to j; ${\xi }_i^{\varphi }$ is the split factor associated with separator i and its outlet mixture ϕ. Coefficients of molar thermal energy and work (see section Modeling of Separators) are multiplied by the corresponding flowrates n_ji. The linear description of the change in (T, p) between consecutive separators is formulated as

$\begin{array}{ll}{Q}_{ji}-{\tilde{q}}_{ji}{n}_{ji}=0,& (22)\end{array}$

$\begin{array}{ll}{W}_{ji}-{\tilde{w}}_{ji}{n}_{ji}=0,& (23)\end{array}$

where Q and W denote the thermal and electrical power, respectively.

Set Φ is introduced. It groups Equations (20, 21, 22, 23), related to the specified mixture ϕ.

Separation Train

Each stream j, belonging to set Φ₁ (see nomenclature in section Mixture), is associated with two streams i belonging to Φ₂ and Φ₃, respectively. Therefore, two equations describing the connectivity between equations sets Φ₁ and Φ₂, and Φ₁ and Φ₃, can be formulated:

$\begin{array}{ll}{n}_{j,{\Phi }_1}-n_{i,{\Phi }_2}=0,& (24)\end{array}$

$\begin{array}{ll}{n}_{j,{\Phi }_1}-n_{i,{\Phi }_3}=0,& (25)\end{array}$

indicating that stream j in set Φ₁ coincides with i in Φ₂ and Φ₃, respectively. Such concatenation constraints make sure that the mass balances downstream of each conversion technology are fulfilled.

Substance Nodes

Each component is associated with 1 + N nodes, where N is the number of reactors it is fed to, belonging to set J (reference to Figure 3). The first node balance reads

$\begin{array}{ll}{n}_{i,ext}-{\displaystyle \sum _{j\in J}}{n}_{i,j}^{makeup}=0,& (26)\end{array}$

indicating that component i, provided from an external source, can be delivered to any j^th reactor ∈ J, “make-up” stream. For each reactor feed in set J, a constraint is imposed with respect to i:

$\begin{array}{ll}{n}_{i,j}^{makeup}+{\displaystyle \sum _{k\in K}}{n}_{i,j,k}^{recycle}-n_{i,j}^{feed}=0,& (27)\end{array}$

where K is the set of process units which produce a stream of pure i. Equation (27) binds the component flowrate of i in the reactor feed to the make-up stream for the same reactor as well as to all the relevant recycles within the plant.

FIGURE 3

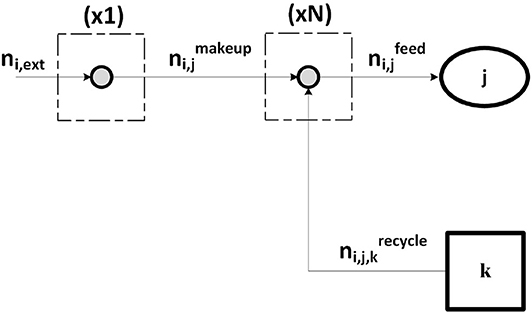
Figure 3. Substance-node balances associated to component i fed to the plant. Stream n_i,ext is split into N streams $n_{i,j}^{makeup}$, each contributing to the reactor feed $n_{i,j}^{feed}$ together with other streams $n_{i,j,k}^{recycle}$ from the plant.

Outlet and Syngas Nodes

As previously discussed in section (2.1), excess H₂ and CH₄ can leave the plant after pressurization, as excess CO₂ and H₂O can be released into the environment, whereas O₂ can be used in oxy-combustion for heat generation. For each component leaving the plant, a node balance is introduced:

$\begin{array}{ll}{\displaystyle \sum _{j\in J}}{n}_{i,j}-n_{i,out}=0,& (28)\end{array}$

where J is the set of process-units which produce or separate component i, leaving the battery limit. Similarly, the following syngas node balances are required:

$\begin{array}{ll}{\displaystyle \sum _{j\in J}}{n}_{\text{CO},j}-n_{\text{CO},syngas}=0,& (29)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{k\in K}}{n}_{{\text{H}}_2,k}-n_{{\text{H}}_2,syngas}=0,& (30)\end{array}$

$\begin{array}{ll}{n}_{{\text{H}}_2,syngas}-\psi n_{\text{CO},syngas}=0,& (31)\end{array}$

Equation (31) sets the syngas ratio to the desired value for downstream applications.

Logical Constraints

Logical constraints are imposed such that at most one separation method per task is active. Binary variables support such logical conditions:

$\begin{array}{ll}{\displaystyle \sum _{i\in I}}{y}_i-1=0,& (32)\end{array}$

$\begin{array}{ll}{n}_i-M{y}_i\le 0,\forall i\in I.& (33)\end{array}$

When the binary operator y_i in Equations (32) and (33) is zero, the feed flowrate n_i to separator i belonging to the set I of methods accomplishing the given task is also zero. On the contrary, if y_i = 1 the separator is active. M is a constant whose value is big enough but possibly of the same order of magnitude. The selected value for implementation is four times the specified syngas productivity. If the value of M exceeds the value of the underlying flowrate for several orders of magnitude, numerical issues might be encountered, and the condition of mutual exclusivity among separators is violated.

Each reactor has an associated separation sequence. Even though RWGS, SR, POX, DR, and TRI could share the same separators, five distinct separation-trains are implemented, which allows for linearity to be preserved. In case the selected route for separation strongly depends on the outlet composition from the reactor, redundancies may occur if more reactors are simultaneously operated. For instance, membrane and adsorption technologies may entrain the same key component out of a given mixture in the downstream of two distinct reactors. The optimal separation sequence can therefore be homogenized by introducing complexity-reduction constraints. For each separator shared among N different separation-trains, an inequality is implemented:

$\begin{array}{ll}\frac{1}{N}{\displaystyle \sum _{i\in I}}{y}_i-y^{CC}\le 0.& (34)\end{array}$

The new binary variable y^CC appears in the final inequality which sets the maximum number of units allowed within the plant N_max as

$\begin{array}{ll}{\displaystyle \sum _{j\in J}}{y}_j^{CC}+{\displaystyle \sum _{k\in K}}{y}_k-N_{max}\le 0.& (35)\end{array}$

Inequality (35) combines the binary variables associated to the possibly redundant units, set J, with the binaries of unique units, set K, i.e., reactors and non-redundant separators. For N_max = +∞, unitary binaries can be paired with zero-flow units. In case the maximum number of units allowed is less than the number generated by MILP in the unconstrained case, N_max ≤ N_{unconstrained} the plant is forced toward higher power requirements. Each binary variable therefore assumes unitary value only if the corresponding unit operation is active and N_max coincides with the actual number of operating units.

Objective Function

The general formulation of the objective function reads

$\begin{array}{ll}{\displaystyle \underset{n,y}{\text{min}}}(Q+\omega W),& (36)\end{array}$

where a pseudo-price ω ∈ [0, 1] is introduced. The process is optimized with respect to the molar flowrates, in vector n, and of binary variables, in vector y. The objective penalizes the electrical power demand, W, added to the thermal power demand Q. The values of ω, spanning within its boundaries, generates a Pareto front with respect to the power consumption. For decreasing values of ω, less relevance is given to the electricity demand. This reflects a transition toward plant layouts favoring the use of sustainable, carbon-neutral sources of electricity.

In this contribution, topological results and total power consumption are explored at the boundaries of the pseudo-price domain, namely ω = 1, objective (A):

$\begin{array}{ll}{\displaystyle \underset{n,y}{\text{min}}}(Q+W),& (37)\end{array}$

and ω = 0, objective (B):

$\begin{array}{ll}{\displaystyle \underset{n,y}{\text{min }}}Q.& (38)\end{array}$

Objectives and constraints are linear, and decision variables are either continuous or integer. The resulting MILP problems are solved in MATLAB^® 2018b using the function intlinprog. The algorithm solves and tightens LP relaxations before implementing heuristics and branch-and-bound strategies.

Results and Discussion

The aim of this section is to introduce and discuss the optimization results resulting from the enforcement of objective (A) and (B).

Firstly, biogas is considered as feedstock for unconstrained plant complexity. Thereafter, redundancies are removed by application of Equation (35). Total, thermal, and electrical power demands are reported for the resulting plant topologies and compared with the respective requirements after heat integration (pinch analysis, minimum ΔT = 15K). Subsequently, the feed is limited to CO₂ from DAC. The power contributions are expressed per molar flow of syngas.

Feedstock: Biogas

Plant topologies obtained for objective (A) and (B) and unconstrained plant complexity are reported in Tables 5A,B. The number of units account for possible redundancies. As an example, for objective (A) and phosgene synthesis, the optimizer identifies an interaction between RWGS and DR and a plant comprising 10 units. The quinary outlet gas from DR shares 4 components with the outlet from RWGS, including the components of the biogas feed stream: CO₂ and CH₄. At most, therefore, three separators can be shared between DR and RWGS, one of which splits the biogas stream into pure CO₂ and CH₄. As a matter of fact, four separators and two reactors are sufficient to perform the production, and four units are redundant. Interactions among reactors are not deemed redundant.

TABLE 5

Table 5. Topological results for unconstrained plant complexity.

Results show that for unconstrained complexity, redundancies always occur. These results are therefore not representative of implementable solutions in terms of downstream operations. Nevertheless, relevant general features of the resulting configurations can be observed:

- POX is never part of the solution with objective (A) but is always selected with (B);

- DR results from all syngas applications with objective (A);

- The pair TRI-EL is selected for high syngas ratios with (A) while RWGS is for low syngas ratios;

- None of the separation trains allows for absorption-based methods;

- Cryogenics is selected by enforcement of objective (B) and for any downstream application, i.e., separation of CH₄ from H₂ (method VII).

Redundancies are thus removed in the setting $N_{max}=n_{Units}^{◦}-n_{Redundancies}^{◦}$ in Equation (35). In case redundancies are still present after reduction, e.g., if a lower number of reactors is selected, N_max is updated and the procedure reiterated. The Tables 6A,B include the plant configurations thus obtained. Reactor-wise, they reflect the same pattern discussed for the case of unconstrained complexity in Table 5: EL and POX come with objective (B), whereas POX does not activate with (A). In (A), DR is the only reactor active for low syngas ratios, whereas combinations of TRI, EL, and SR are better suited for higher ratios. Separator-wise, the predominance of adsorption and membranes over absorption methods is confirmed, whereas cryogenics with objective (B) is not due to the restriction imposed on the number of units: if biogas has to be split, the binary mixture to be separated in the biogas train is necessarily (CH₄/CO₂), split 22 in Table 4 and is thus shared with the downstream of POX. The only cryogenic method available for this task is distillation, conducted at pressure higher than POX reactor—Table 3. The thermal power input to adjust the temperature of CH₄ to the reactor level is therefore far higher than the input required from the selected separator, the polymeric membrane, which can decrease this thermal duty by adiabatic temperature increase after vacuum normalization and pressurization (adiabatic temperature increase). Palladium membrane for the separation of H₂ is the result if the electrical power is not penalized.

TABLE 6

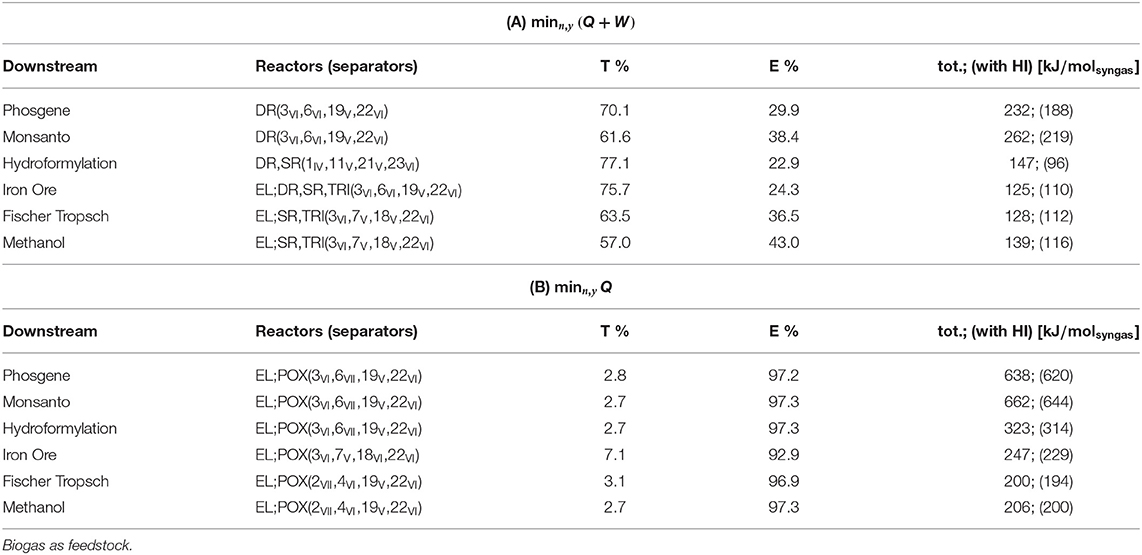
Table 6. Plant topology and power consumption, divided into thermal percent (T%), electrical percent (E%), and total power (tot.) and compared with total power required after heat integration via pinch (HI).

In objective (A), the predominant power contribution is thermal, whereas most of the power required with objective (B) is electrical. Partial contributions to the total power without heat integration are represented in Figures 4, 5. The sum of reactor and preconditioning gives the total reactor power input, the former being associated with the chemical reaction in the reactor only, while the latter accounts for the pressure and temperature adjustment to bring the reactants to feed conditions. Adjustment denotes the power input to meet the (T, p) level at which syngas is required for its further downstream applications; storage is associated with the power for pressurization of surplus H₂, while separation comprises the remaining contributions.

FIGURE 4

Figure 4. Contributions to the total power requirements for ${\text{min}}_{n,y}(Q+W)$, biogas as feedstock.

FIGURE 5

Figure 5. Contributions to the total power requirements for ${\text{min}}_{n,y}Q$, biogas as feedstock.

With both objectives (A) and (B), the reactors dominate the total power demand and exhibit a decreasing trend with H₂/CO. The high power requirement for storage with objective (B) is determined by the large H₂ surplus, accompanying the large O₂ demand at the POX reactor to sustain the CO production (see Table 2 for POX stoichiometry).

Within the context of objective (A), the pinch analysis determines a substantial recovery of heat within the separation train and complete recovery in the context of (B). Nevertheless, all the reactors in (A) are heat sinks at high temperatures. Consequently, they cannot benefit from heat integration. As highlighted by the energy contributions in Figure 4, the power requirement at the reactors dominates over the other contributions, which justifies the modest reduction in total power demand reported in Table 6. Moreover, if heat integration is beneficial in terms of utility minimization, it neglects the effect of poor overall heat transfer coefficients typical of gas-gas economizers. Excluding the phase transition required for water to adjust to SR and TRI reactor conditions and a liquid make-up stream for EL, the process system encompasses gas streams only. The overall heat transfer coefficients are normally greatly improved in presence of phase-changing fluids, typically condensing steam, which can justify the more conservative approach of sequential optimization and heat integration.

Biogas is totally or partially separated into its components and utilized as a reactant. Nevertheless, surplus bio-CH₄ could be used to generate carbon-neutral hot and electrical utilities by combustion. Figure 6 depicts the net total power demand, or demand for possibly fossil-based power, in terms of hot utility after heat integration and with objectives (A) and (B). It is assumed that

I Electricity is generated by a gas-fired power plant (worst-case scenario) with an efficiency of 60%: Q_E = W/0.6;

II The hot utility at the syngas and power plant is provided directly by the combustion of CH₄ (low heating value LHV = 785kJ/mol);

III The heat generated by combustion of surplus bio-CH₄ can be directly transferred to the process or the power plant, thus neglecting the generation of steam and the irreversibilities.

FIGURE 6

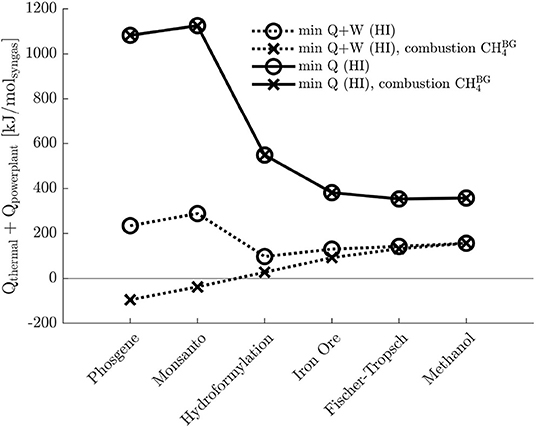
Figure 6. Comparison among total power demands after heat integration (HI) for the two objectives, ${\text{min}}_{n,y}(Q+W)$ and ${\text{min}}_{n,y}Q$, for biogas as feedstock, with and without surplus bio-CH₄ utilization. The electrical power is generated by gas-fired power plant of 60% efficiency, Q_powerplant = W/0.6.

Assumption III necessarily outlines the most optimistic scenario, which is to be benchmarked against the demand which does not account for bio-CH₄ utilization: the actual power demand is expected to fall between these boundaries. As indicated by Figure 6, plant configurations resulting with objective (A) can greatly benefit from the utilization of surplus bio-CH₄, especially for low syngas ratios. On the contrary, with objective (B), bio-CH₄ is entirely converted, as CH₄ is the only feedstock for POX.

Feedstock: CO₂ From DAC

Direct air capture (DAC) provides pure CO₂ to the plant and substitutes biogas as a source of carbon for the system. In this system, low temperature (LT) solid sorbent performs DAC with a thermal and electrical power input of 277 and 39kJ/mol_CO2, respectively. The values are adapted from Fasihi et al. (2019). Table 7 shows that the combination of EL and RWGS, the only technology available for the feedstock, is followed by combinations of membranes (polymeric and Pd) and VPSA operations. The contributions to the total power, similar between objectives (A) and (B), are shifted toward electricity and proportional to the syngas ratio. Compared with the corresponding values in Table 6, the power demands are conspicuously higher due to the presence of DAC, the latter spanning between 19 and 37% of the required total input.

TABLE 7

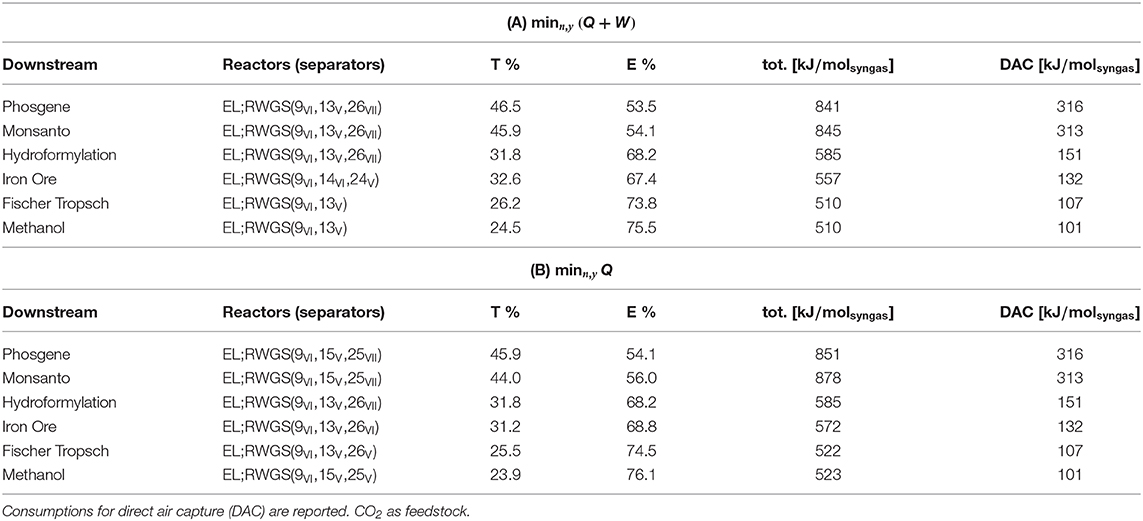
Table 7. Plant topology and power consumption, divided into thermal percent (T%), electrical percent (E%), and total power (tot.).

Conclusions

Candidate process topologies for Power-to-Syngas applications are embedded within a superstructure. Mixed-integer, linear constraints are set for alternative feedstock scenarios: biogas and CO₂ from DAC (LT-solid sorbent). A general objective-function formulation combines thermal and electrical power input linearly. The electrical power contribution is weighted by a pseudo price ω ∈ [0, 1]. For ω → 1, electricity is penalized, e.g., purchased from fossil-based power plant facilities, whereas ω → 0 assumes carbon-free in-house electricity production. The resulting MILP problems are solved for extreme-value scenarios: objective (A) for ω = 1 and objective (B) for ω = 0. Results show that the higher total power demand with (B) with respect to (A) is compensated by the predominance of electricity demand, up to 97%, possibly increasing after heat integration. Furthermore, topological configurations with (B) include two reactors for any syngas application, EL and POX, whereas interaction among EL, SR, TRI, and DR result in (A). Forcing the plant complexity toward a single reactor would therefore increase the total energy values. Surplus bio-CH₄ can relieve the demand for external fossil-based fuel, especially for downstream applications requiring low syngas ratios.

Membranes and adsorption-based separators prevail over absorption and scrubbing methods. Cryogenics possibly result with (B). For CO₂ as feedstock, the combination of EL, RWGS, and DAC enhances the total power requirements even though the electricity demand prevails over thermal inputs.

Assuming that proper storage strategies to face the intermittent nature of renewable resources are available, such as batteries for electricity and biogas buffer tanks, process configuration favoring electricity over thermal inputs are preferable for applications requiring high syngas ratios, suggesting the implementation of POX in conjunction with EL. On the contrary, for low ratios, surplus bio-CH₄ can be utilized to mitigate the thermal power requirements for DR, resulting with (A). Nevertheless, in case the effect of coking in DR were mitigated by introduction of oxygen (oxy-DR), the energy demand is expected to increase substantially due to the introduction of EL.

The possibility of a severe drop in biogas availability over the long-term suggests the implementation of reverse water-gas-shift to allow for operations based on CO₂ as feedstock.

Data Availability Statement

The raw data supporting the conclusions of this article can be made available by the authors upon request, without undue reservation.

Author Contributions

KS conceived of the general framework: the application of superstructure optimization for the Power-to-Syngas processes. AM identified the specific system elements of interest, developed the underlying theory, and produced the numerical results. AM interpreted the results and generated the manuscript. MW supervised AM through his work, providing suggestions concerning the theoretical background and the interpretation of results. Furthermore, MW also contributed to the generation of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge their Partners within the context of P2Chem, a project financially supported by the Federal Ministry of Education and Research of Germany (support code: 05M18OCB). Johanna Klüsener and Stefan Bube are gratefully acknowledged for providing icons for Figure 1 used in the manuscript.

References

Abdullah, B., Ghani, N. A. A., and Vo, D.-V. N. (2017). Recent advances in dry reforming of methane over Ni-based catalysts. J. Clean. Product. 162, 170–185. doi: 10.1016/j.jclepro.2017.05.176

CrossRef Full Text | Google Scholar

Agarwal, A., Biegler, L. T., and Zitney, S. E. (2010). A superstructure-based optimal synthesis of PSA cycles for post-combustion CO2 capture. AIChE J. 56, 1813–1828. doi: 10.1002/aic.12107

CrossRef Full Text | Google Scholar

Arora, S., and Prasad, R. (2016). An overview on dry reforming of methane: strategies to reduce carbonaceous deactivation of catalysts. RSC Adv. 6, 108668–108688. doi: 10.1039/C6RA20450C

CrossRef Full Text | Google Scholar

Bahadori, A., and Vuthaluru, H. B. (2009). Simple methodology for sizing of absorbers for TEG (Triethylene Glycol) gas dehydration systems. Energy 34, 1910–1916. doi: 10.1016/j.energy.2009.07.047

CrossRef Full Text | Google Scholar

Battrum, M., and Thomas, W. (1991). Carbon monoxide recovery by pressure swing adsorption. Chem. Eng. Res. Design 69, 119–129.

Google Scholar

Bensmann, B., Hanke-Rauschenbach, R., Arias, I. P., and Sundmacher, K. (2013). Energetic evaluation of high pressure PEM electrolyzer systems for intermediate storage of renewable energies. Electrochim. Acta 110, 570–580. doi: 10.1016/j.electacta.2013.05.102

CrossRef Full Text | Google Scholar

Biegler, L. T., Grossmann, I. E., and Westerberg, A. W. (1997). Systematic Methods for Chemical Process Design. Old Tappan, NJ: Prentice Hall.

Google Scholar

Burr, B., and Lyddon, L. (2008). “A comparison of physical solvents for acid gas removal,” in 87th Annual Convention of the Gas Processors Association (Red Hook, NY: Curran).

Google Scholar

Delgado, J. A., Águeda, V., Uguina, M., Sotelo, J., Brea, P., and Grande, C. A. (2014). Adsorption and diffusion of H2, CO, CH4, and CO2 in BPL activated carbon and 13X zeolite: evaluation of performance in pressure swing adsorption hydrogen purification by simulation. Indus. Eng. Chem. Res. 53, 15414–15426. doi: 10.1021/ie403744u

CrossRef Full Text | Google Scholar

Di Profio, P., Arca, S., Rossi, F., and Filipponi, M. (2009). Comparison of hydrogen hydrates with existing hydrogen storage technologies: energetic and economic evaluations. Int. J. Hydrogen Energy 34, 9173–9180. doi: 10.1016/j.ijhydene.2009.09.056

CrossRef Full Text | Google Scholar

DiMartino, S., Glazer, J., Houston, C., and Schott, M. (1988). Hydrogen/carbon monoxide separation with cellulose acetate membranes. Gas Separat. Purif. 2, 120–125. doi: 10.1016/0950-4214(88)80027-6

CrossRef Full Text | Google Scholar

Dutta, N., and Patil, G. (1995). Developments in CO separation. Gas Separat. Purif. 9, 277–283. doi: 10.1016/0950-4214(95)00011-Y

CrossRef Full Text | Google Scholar

El-Nagar, R. A., and Ghanem, A. A. (2019). “Syngas production, properties, and its importance,” in Sustainable Alternative Syngas Fuel, eds C. Ghenai and A. Inayat (Rijeka: IntechOpen), 1–408.

Google Scholar

Fasihi, M., Efimova, O., and Breyer, C. (2019). Techno-economic assessment of CO2 direct air capture plants. J. Clean. Product. 224, 957–980. doi: 10.1016/j.jclepro.2019.03.086

CrossRef Full Text | Google Scholar

Gao, F., Wang, S., Wang, W., Duan, J., Dong, J., and Chen, G. (2018). Adsorption separation of CO from syngas with CuCl@ AC adsorbent by a VPSA process. RSC Adv. 8, 39362–39370. doi: 10.1039/C8RA08578A

CrossRef Full Text | Google Scholar

Gao, F., Wang, Y., Wang, X., and Wang, S. (2016). Selective CO adsorbent CuCl/AC prepared using CuCl 2 as a precursor by a facile method. RSC Adv. 6, 34439–34446. doi: 10.1039/C6RA03116A

CrossRef Full Text | Google Scholar

Grande, C. A., Blom, R., Andreassen, K. A., and Stensrød, R. E. (2017). Experimental results of pressure swing adsorption (PSA) for pre-combustion CO2 capture with metal organic frameworks. Energy Proc. 114, 2265–2270. doi: 10.1016/j.egypro.2017.03.1364

CrossRef Full Text | Google Scholar

Grande, C. A., and Rodrigues, A. E. (2007). Layered vacuum pressure-swing adsorption for biogas upgrading. Indus. Eng. Chem. Res. 46, 7844–7848. doi: 10.1021/ie070942d

CrossRef Full Text | Google Scholar

Gruber, H., Groß, P., Rauch, R., Reichhold, A., Zweiler, R., Aichernig, C., et al. (2019). Fischer-Tropsch products from biomass-derived syngas and renewable hydrogen. Biomass Conv. Bioref . doi: 10.1007/s13399-019-00459-5

CrossRef Full Text | Google Scholar

Han, C., Zahid, U., An, J., Kim, K., and Kim, C. (2015). CO2 transport: design considerations and project outlook. Curr. Opin. Chem. Eng. 10, 42–48. doi: 10.1016/j.coche.2015.08.001

CrossRef Full Text | Google Scholar

Häussinger, P., Lohmüller, R., and Watson, A. M. (2011). Hydrogen, 3. Purification. Weinheim: American Cancer Society. doi: 10.1002/14356007.o13_o04

CrossRef Full Text | Google Scholar

Hochgesand, G. (1970). Rectisol and purisol. Indus. Eng. Chem. 62, 37–43. doi: 10.1021/ie50727a007

CrossRef Full Text | Google Scholar

Huang, Y., Merkel, T. C., and Baker, R. W. (2014). Pressure ratio and its impact on membrane gas separation processes. J. Memb. Sci. 463, 33–40. doi: 10.1016/j.memsci.2014.03.016

CrossRef Full Text | Google Scholar

IPCC (2013). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, UK; New York, NY: Cambridge University Press.

Google Scholar

Jang, S.-C., Yang, S.-I., Oh, S.-G., and Choi, D.-K. (2011). Adsorption dynamics and effects of carbon to zeolite ratio of layered beds for multicomponent gas adsorption. Korean J. Chem. Eng. 28, 583–590. doi: 10.1007/s11814-010-0399-9

CrossRef Full Text | Google Scholar

Kang, D., Lim, H. S., Lee, M., and Lee, J. W. (2018). Syngas production on a Ni-enhanced Fe2O3/Al2O3 oxygen carrier via chemical looping partial oxidation with dry reforming of methane. Appl. Energy 211, 174–186. doi: 10.1016/j.apenergy.2017.11.018

CrossRef Full Text | Google Scholar

Kim, H. W., Yoon, H. W., Yoon, S.-M., Yoo, B. M., Ahn, B. K., Cho, Y. H., et al. (2013). Selective gas transport through few-layered graphene and graphene oxide membranes. Science 342, 91–95. doi: 10.1126/science.1236098

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, A., Liang, W., and Hughes, R. (2000). The effect of carbon monoxide and steam on the hydrogen permeability of a Pd/stainless steel membrane. J. Memb. Sci. 165, 135–141. doi: 10.1016/S0376-7388(99)00223-9

CrossRef Full Text | Google Scholar

Li, X., Li, Z., Xia, Q., and Xi, H. (2007). Effects of pore sizes of porous silica gels on desorption activation energy of water vapour. Appl. Thermal Eng. 27, 869–876. doi: 10.1016/j.applthermaleng.2006.09.010

CrossRef Full Text | Google Scholar

Liesche, G., Schack, D., and Sundmacher, K. (2019). The FluxMax approach for simultaneous process synthesis and heat integration: production of hydrogen cyanide. AIChE J. 65:e16554. doi: 10.1002/aic.16554

CrossRef Full Text | Google Scholar

Lin, H., Thompson, S. M., Serbanescu-Martin, A., Wijmans, J. G., Amo, K. D., Lokhandwala, K. A., et al. (2012). Dehydration of natural gas using membranes. Part I: composite membranes. J. Memb. Sci. 413, 70–81. doi: 10.1016/j.memsci.2012.04.009

CrossRef Full Text | Google Scholar

Maqsood, K., Mullick, A., Ali, A., Kargupta, K., and Ganguly, S. (2014). Cryogenic carbon dioxide separation from natural gas: a review based on conventional and novel emerging technologies. Rev. Chem. Eng. 30, 453–477. doi: 10.1515/revce-2014-0009

CrossRef Full Text | Google Scholar

Merel, J., Clausse, M., and Meunier, F. (2008). Experimental investigation on CO2 post- combustion capture by indirect thermal swing adsorption using 13X and 5A zeolites. Indus. Eng. Chem. Res. 47, 209–215. doi: 10.1021/ie071012x

CrossRef Full Text | Google Scholar

Merkel, T., Gupta, R., Turk, B., and Freeman, B. D. (2001). Mixed-gas permeation of syngas components in poly (dimethylsiloxane) and poly (1-trimethylsilyl-1-propyne) at elevated temperatures. J. Memb. Sci. 191, 85–94. doi: 10.1016/S0376-7388(01)00452-5

CrossRef Full Text | Google Scholar

Metz, S. J., Van de Ven, W., Potreck, J., Mulder, M., and Wessling, M. (2005). Transport of water vapor and inert gas mixtures through highly selective and highly permeable polymer membranes. J. Memb. Sci. 251, 29–41. doi: 10.1016/j.memsci.2004.08.036

CrossRef Full Text | Google Scholar

Mondal, M. K., Balsora, H. K., and Varshney, P. (2012). Progress and trends in CO2 capture/separation technologies: a review. Energy 46, 431–441. doi: 10.1016/j.energy.2012.08.006

CrossRef Full Text | Google Scholar

Moral, A., Reyero, I., Alfaro, C., Bimbela, F., and Gandia, L. M. (2018). Syngas production by means of biogas catalytic partial oxidation and dry reforming using Rh-based catalysts. Catalysis Tdy 299, 280–288. doi: 10.1016/j.cattod.2017.03.049

CrossRef Full Text | Google Scholar

Morishige, K. (2011). Adsorption and separation of CO2/CH4 on amorphous silica molecular sieve. J. Phys. Chem. C 115, 9713–9718. doi: 10.1021/jp202572w

CrossRef Full Text | Google Scholar

Mulgundmath, V., and Tezel, F. H. (2010). Optimisation of carbon dioxide recovery from flue gas in a TPSA system. Adsorption 16, 587–598. doi: 10.1007/s10450-010-9255-9

CrossRef Full Text | Google Scholar

Netusil, M., and Ditl, P. (2011). Comparison of three methods for natural gas dehydration. J. Nat. Gas Chem. 20, 471–476. doi: 10.1016/S1003-9953(10)60218-6

CrossRef Full Text | Google Scholar

Pantaleo, G., La Parola, V., Deganello, F., Singha, R., Bal, R., and Venezia, A. (2016). Ni/CeO2 catalysts for methane partial oxidation: synthesis driven structural and catalytic effects. Appl. Catal. Environ. 189, 233–241. doi: 10.1016/j.apcatb.2016.02.064

CrossRef Full Text | Google Scholar

Paolini, V., Petracchini, F., Segreto, M., Tomassetti, L., Naja, N., and Cecinato, A. (2018). Environmental impact of biogas: a short review of current knowledge. J. Environ. Sci. Health A 53, 899–906. doi: 10.1080/10934529.2018.1459076

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J.-H., Kim, J.-N., and Cho, S.-H. (2000). Performance analysis of four-bed H2 PSA process using layered beds. AIChE J. 46, 790–802. doi: 10.1002/aic.690460413

CrossRef Full Text | Google Scholar

Poudel, J., Choi, J. H., and Oh, S. C. (2019). Process design characteristics of syngas (CO/H2) separation using composite membrane. Sustainability 11:703. doi: 10.3390/su11030703

CrossRef Full Text | Google Scholar

Reimert, R., Marschner, F., Renner, H.-J., Boll, W., Supp, E., Brejc, M., et al. (2015). “Ullmann's energy: resources, processes, products,” in Gas Production, 2 Processes: Natural Gas, ed Wiley-VCH (Weinheim: Wiley-VCH).

Ritter, J. A., and Ebner, A. D. (2007). State-of-the-art adsorption and membrane separation processes for hydrogen production in the chemical and petrochemical industries. Separat. Sci. Technol. 42, 1123–1193. doi: 10.1080/01496390701242194

CrossRef Full Text | Google Scholar

Schack, D., Liesche, G., and Sundmacher, K. (2020). The FluxMax approach: simultaneous flux optimization and heat integration by discretization of thermodynamic state space illustrated on methanol synthesis process. Chem. Eng. Sci. 215:115382. doi: 10.1016/j.ces.2019.115382

CrossRef Full Text | Google Scholar

Schack, D., Rihko-Struckmann, L., and Sundmacher, K. (2016). “Structure optimization of power-to-chemicals (P2C) networks by linear programming for the economic utilization of renewable surplus energy,” in Computer Aided Chemical Engineering, Vol. 38, eds Z. Kravanja and M. Bogataj (Elsevier), 1551–1556. doi: 10.1016/B978-0-444-63428-3.50263-0

CrossRef Full Text | Google Scholar

Scholes, C. A., Bacus, J., Chen, G. Q., Tao, W. X., Li, G., Qader, A., et al. (2012). Pilot plant performance of rubbery polymeric membranes for carbon dioxide separation from syngas. J. Memb. Sci. 389, 470–477. doi: 10.1016/j.memsci.2011.11.011

CrossRef Full Text | Google Scholar

SGC (2012). Basic Data on Biogas.

Sijbesma, H., Nymeijer, K., van Marwijk, R., Heijboer, R., Potreck, J., and Wessling, M. (2008). Flue gas dehydration using polymer membranes. J. Memb. Sci. 313, 263–276. doi: 10.1016/j.memsci.2008.01.024

CrossRef Full Text | Google Scholar

Singha, R. K., Shukla, A., Yadav, A., Adak, S., Iqbal, Z., Siddiqui, N., et al. (2016). Energy efficient methane tri-reforming for synthesis gas production over highly coke resistant nanocrystalline Ni/ZrO2 catalyst. Appl. Energy 178, 110–125. doi: 10.1016/j.apenergy.2016.06.043

CrossRef Full Text | Google Scholar

Sircar, S., and Golden, T. (2000). Purification of hydrogen by pressure swing adsorption. Separat. Sci. Technol. 35, 667–687. doi: 10.1081/SS-100100183

CrossRef Full Text | Google Scholar

Smith, R. (2005). Chemical Process: Design and Integration. West Sussex: John Wiley & Sons.

Google Scholar

Song, C., and Pan, W. (2004). Tri-reforming of methane: a novel concept for catalytic production of industrially useful synthesis gas with desired H2/CO ratios. Catalysis Tdy 98, 463–484. doi: 10.1016/j.cattod.2004.09.054

CrossRef Full Text | Google Scholar

Sun, L., and Smith, R. (2013). Rectisol wash process simulation and analysis. J. Clean. Product. 39, 321–328. doi: 10.1016/j.jclepro.2012.05.049

CrossRef Full Text | Google Scholar

Uebbing, J., Rihko-Struckmann, L. K., and Sundmacher, K. (2019). Exergetic assessment of CO2 methanation processes for the chemical storage of renewable energies. Appl. Energy 233, 271–282. doi: 10.1016/j.apenergy.2018.10.014

CrossRef Full Text | Google Scholar

Wang, B., Cote, A. P., Furukawa, H., O'Keeffe, M., and Yaghi, O. M. (2008). Colossal cages in zeolitic imidazolate frameworks as selective carbon dioxide reservoirs. Nature 453, 207–211. doi: 10.1038/nature06900

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., and LeVan, M. D. (2009). Adsorption equilibrium of carbon dioxide and water vapor on zeolites 5A and 13X and silica gel: pure components. J. Chem. Eng. Data 54, 2839–2844. doi: 10.1021/je800900a

CrossRef Full Text | Google Scholar

Wenzel, M., Rihko-Struckmann, L., and Sundmacher, K. (2017). Thermodynamic analysis and optimization of RWGS processes for solar syngas production from CO2. AIChE J. 63, 15–22. doi: 10.1002/aic.15445

CrossRef Full Text | Google Scholar

Wenzel, M., Rihko-Struckmann, L., and Sundmacher, K. (2018). Continuous production of CO from CO2 by RWGS chemical looping in fixed and fluidized bed reactors. Chem. Eng. J. 336, 278–296. doi: 10.1016/j.cej.2017.12.031

CrossRef Full Text | Google Scholar

Wurzbacher, J. A., Gebald, C., Piatkowski, N., and Steinfeld, A. (2012). Concurrent separation of CO2 and H2O from air by a temperature-vacuum swing adsorption/desorption cycle. Environ. Sci. Technol. 46, 9191–9198. doi: 10.1021/es301953k

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Lee, C.-H., and Chang, J.-W. (1997). Separation of hydrogen mixtures by a two-bed pressure swing adsorption process using zeolite 5A. Indus. Eng. Chem. Res. 36, 2789–2798. doi: 10.1021/ie960728h

CrossRef Full Text | Google Scholar

Ziaii, S., Cohen, S., Rochelle, G. T., Edgar, T. F., and Webber, M. E. (2009). Dynamic operation of amine scrubbing in response to electricity demand and pricing. Energy Proc. 1, 4047–4053. doi: 10.1016/j.egypro.2009.02.211

CrossRef Full Text | Google Scholar