
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 07 July 2020
Sec. Nuclear Energy
Volume 8 - 2020 | https://doi.org/10.3389/fenrg.2020.00124
This article is part of the Research Topic Advances in Nuclear Power Engineering View all 20 articles
The Graphics Processing Units (GPUs) are increasingly becoming the primary computational platform in the scientific fields, due to its cost-effectiveness and massively parallel processing capability. On the other hand, the coarse mesh finite difference (CMFD) method has been one of the most popular techniques to accelerate the neutron transport calculation. The GPU is employed into the method of characteristics (MOC) accelerated by two-level CMFD to solve the neutron transport equation. In this work, the Jacobi method, the successive over-relaxation (SOR) method with red-black ordering, and the preconditioned generalized minimum residual (PGMRES) method are applied to solve the linear system under the framework of CMFD. The performance of these linear system solvers is characterized on both CPU (Central Processing Unit) and GPU. The two-dimensional (2-D) C5G7 benchmark problem and an extended mock quarter-core problem are tested to verify the accuracy and efficiency of the algorithm with double precision, as well as the feasibility of massive parallelization. Numerical results demonstrate that the desired accuracy is maintained. Moreover, the results show that the few-group CMFD acceleration is effective to accelerate the multi-group CMFD calculation. The PGMRES method shows remarkable convergence characteristics compared to the Jacobi and the SOR methods. However, the SOR method shows better performance on GPU for solving the linear system of CMFD calculation, which reaches about 2,400x speedup on GPU with two-level CMFD acceleration compared to the CPU-based MOC calculation.
Significant advances in high-performance computing (HPC) systems enable the computational feasibility of high-fidelity, three-dimensional (3-D) whole-core neutron transport calculation. Several applications have been developed and deployed on the HPC systems based on the method of characteristics (MOC) (Askew, 1972). These applications employ the MOC as their routine 2-D or 3-D neutron transport method for practical whole-core simulations. The MOC code nTRACER (Jung et al., 2013) was developed as direct whole-core simulator by Seoul National University. Meanwhile, the University of Michigan developed the MPACT code (Kochunas et al., 2013) to perform the 3-D neutron simulation. And then followed by OpenMOC (Boyd et al., 2014) and NECP-X (Chen et al., 2018). However, many researches show that the MOC suffers from the slow convergence rate especially for the large heterogeneous whole-core simulation. Hence, various numerical acceleration techniques and parallel algorithms have been employed to accelerate the MOC calculation.
Considerable research has been performed to accelerate the convergence of MOC neutron transport calculation. The non-linear acceleration technique is appropriate when considering that the steady-state problem of interest for a reactor is an eigenvalue problem. The coarse mesh finite difference (CMFD) method (Smith, 1984), has been widely used with pronounced success for reactor analysis for the last several decades. As a low-order acceleration scheme, CMFD solves the diffusion-like equation on a coarse mesh and it is very effective at accelerating the MOC calculation (Liu et al., 2011; Kochunas et al., 2013). However, CMFD can introduce numerical instabilities in optically thick regions which results in a degradation in performance or even a failure to convergence. As a result, several specific techniques such as the partial-current CMFD (pCMFD) method (Cho et al., 2003), the odCMFD method (Zhu et al., 2016) and lpCMFD method (Wang and Xiao, 2018) have been studied for stabilizing CMFD acceleration of neutron transport problems.
Moreover, massively parallel computing has been applied successfully to whole-core analysis based on the HPC systems which deploys CPU as their computational units (Kochunas et al., 2013; Godfrey et al., 2016). However, the cost of high-fidelity whole-core simulation is still unacceptable, even the large scale, parallel computing hardware is used (Kochunas et al., 2015; Ryu et al., 2015). Recently, CPUs/GPUs heterogeneous computing systems have increasingly come to the forefront of state-of-the-art supercomputers. As reported by the top supercomputer rankings in June 2019, 122 heterogeneous systems equips the NVIDIA GPUs are their main computing resources (TOP500 official site, 2019).
Massively parallel architecture of GPUs allows more powerful, more energy-efficient and higher throughput than CPUs. Therefore, the inclusion of GPU and heterogeneous computing in the neutron transport calculation is increasingly explored. Boyd et al. (2013) and Han et al. (2014) developed the GPU-accelerated 2-D MOC code which shows that the GPU is suitable to accelerate the MOC neutron transport calculation. Also Tramm et al. (2016) implemented a formulation of 3-D MOC neutron transport simulation. In our former research, a GPU-accelerated 2-D MOC parallel algorithm was implemented and the performance of the algorithm is investigated by a performance analysis model (Song et al., 2019). Meanwhile, efforts have been focused on implementing the MOC neutron transport calculation on multi-GPUs. The ray parallel scheme was introduced into the 3-D MOC simulation with intra-node multi-GPUs parallelization by Zhang et al. (2013). A CPU-GPU hybrid parallel MOC neutron transport calculation was implemented with a dynamic workload assignment (Liang et al., 2020; Song et al., 2020).
Since the feasibility of GPU acceleration of MOC calculation had been explored, the GPU-accelerated CMFD calculation is required to keep up with the enhanced performance of GPU-based MOC. Several researches has been conducted to accelerate the CMFD calculation on GPU. Kang and Joo, 2018) implemented the GPU-based preconditioned BiConjugate Gradient Stabilized solver (pBiCGSTAB) in nTRACER. Furthermore, the performance of several linear system solvers on GPU under the CMFD framework has been studied based on the nTRACER code (Choi et al., 2018). Since the core work of CMFD calculation is solving the linear system which is conducted by the CMFD equation, the researched and experience of solving linear systems on GPU can be used as reference to deploy the CMFD calculation on GPU. Li and Saad (2012) developed the high-performance iterative linear solvers on GPU. They speeded up the sparse matrix-vector product (SpMV) operations and discussed the suitable preconditioning methods. Jong et al. (2017) presented the GPU-accelerated RRB-solver, which is a PCG-type solver based on the Repeated Red-Black (RRB) method and the incomplete Cholesky factorization. And it shown good performance on GPU for solving 5-/9-point stencils problems.
In this work, for the solution of the large sparse linear system involved in the CMFD formulation, the performance of the Jacobi method, the successive over-relaxation (SOR) method, and the preconditioned generalized minimum residual (PGMRES) method are implemented on GPU. Especially, the numerical performance of these linear system solvers on both CPU and GPU under the CMFD framework is compared. Afterward, the effectiveness of the CMFD is examined.
The rest of the paper is organized as follows. Section Background gives the required background about the MOC and the CMFD framework. Then the parallelization of MOC and several liner system solvers on GPU are introduced in section Implementation on GPU. Section Numerical resultsshows the numerical tests and related analysis. Then the conclusions and discussions are presented in section Conclusion.
The method of characteristics is a general mathematical technique for solving the partial differential equations. The characteristic form of the multi-group neutron transport equation in steady-state is given by Equation (1):
where s is the coordinate which represents both the reference position and the flight direction of the neutron, φg(s), Σt,g(s) represent the angular neutron flux, and total cross-section, respectively. Qg(s) is the source term. And g represents the index of energy group.
With the isotropic scattering approximation and the flat source region approximation, the source term Qg(s) includes the fission and scattering sources and it can be expressed in terms of scalar neutron flux ϕg:
Σ denotes the cross-section, and the subscript f and s represent different reaction types, which are fission and scattering, respectively. χg is the normalized fission spectrum, and keff represents the effective neutron multiplication factor or eigenvalue of the system.
Equation (1) can be integrated along the characteristic line within a flat source region. And the angular flux along the characteristic line can be expressed as Equation (3). The average angular flux along a specific segment is calculated by Equation (4).
where and are the incoming and outgoing angular neutron flux of segment, respectively. represents the average angular neutron flux, and ls is the length of current segment along s. The subscript g is omitted for simplicity in Equation (3) and Equation (4).
For a given direction, a set of characteristic rays must be tracked through a discretized spatial domain and the transport sweep is performed along with those rays during the calculation. Then the scalar flux is integrated over discretized angles, as expressed in Equation (5).
where the quadrature weights ωp are introduced for each of the quadrature points Ωp. dp is the ray spacing in Ωp direction.
In order to obtain the scalar flux distribution over the space and all energy groups, an iteration scheme is applied to solve the source in Equation (2) and finally the scalar flux in Equation (5). The quadrature proposed by Yamamoto et al. (2007) is used for the polar angles and weights by default. Another well-known optimization of MOC calculation is to tabulate the exponential function or more specifically, , which is actually time-consuming in Equation (3). For the evaluation of the exponential function, the table with linear interpolation is used in this work.
The MOC provides a framework for solving the neutron transport equation in heterogeneous geometries. However, challenges arise when whole-core problems are encountered. To reduce this computational burden, numerous acceleration methods are developed. The coarse mesh finite difference method (CMFD) is a popular method for accelerating the neutron transport calculation.
CMFD defines a diffusion equation on a coarse mesh with a correction to the diffusion coefficient that preserves the current between the cells from the transport solution. The neutron balance equation on coarse-mesh is derived as:
where i is the index of the coarse-mesh cell, is is the index of the surface of cell i, G represents the CMFD group index. represents the surface-averaged net current across the surface is. is the area of surface is and Vi is the volume of cell i, is the cell-averaged scalar flux on the coarse mesh. And the coarse-mesh cross-sections are generated by energy-condensation and area-averaging from the MOC fine-mesh cross-sections. The homogenized cross-section for cell i is
In order to conserve the neutron balance between the CMFD and MOC problems, a non-linear diffusion coefficient term is introduced to correct the difference between the inter-cell current calculated by the transport solution and approximated by the Fick's Law. The net current across the surface is is expressed as:
where is is the surface between cell i and cell i + 1. is the actual net current produced from the MOC solution. The parameter is the coupling coefficient determined by the ordinary finite difference method and expressed in Equation (9-a), and is the non-linear diffusion coefficient correction factor as shown in Equation (9-b)
where is the diffusion coefficient of cell i, and is the thickness of cell i along the surface is.
Going back to Equation (6) and inserting the surface net current illustrated in Equation (8), the finite difference form of the CMFD diffusion equation can be condensed down matrix form to get the generalized eigenvalue problem:
where M represents neutron migration by diffusion and scattering. F represents the neutron generation by fission. The CMFD equations in 2-D form a five-stripe sparse linear system which is usually solved using the iterative methods.
Then the multi-group CMFD can be solved numerically. Upon convergence of the CMFD eigenvalue problem, a prolongation is performed by scaling the scalar flux of MOC fine mesh and the angular fluxes at the core boundaries with the ratio of the converged scalar flux to the scalar flux which is generated from the MOC solution:
where is the boundary angular flux of track l.
For large scale problems, the multi-group CMFD is still time-consuming. As a result, the few-group based CMFD (FG CMFD) formulation has been successfully applied to accelerate the multi-group CMFD calculation (Cho et al., 2002; Joo et al., 2004). Hence, the multi-group MOC calculation can be accelerated by the two-level CMFD technique. The multi-group CMFD (MG CMFD) calculation is directly accelerated by the few-group CMFD (FG CMFD) calculation. The FG CMFD is the group-condensed CMFD which has the same coarse mesh geometry as MG CMFD.
The FG CMFD has a similar formulation as illustrated in Equation (6) and the few-group constants are simply calculated using multi-group constants and multi-group spectra as:
where FG is the energy group index in the FG CMFD equation.
In order to obtain the non-linear diffusion coefficient correction factor, condensed few-group surface currents are calculated as:
Here, the multi-group currents are calculated using the MG CMFD solution and Equation (8). Then the coupling coefficient and the nonlinear diffusion coefficient correction factor of FG CMFD can be calculated by Equation (9) in which the multi-group quantities are replaced by that of few-group.
With the group-condensed constants, FG CMFD calculation which is also an eigenvalue problem as shown in Equation (10) can be performed. Once the desired FG CMFD solution is obtained, an additional update is needed for the MG CMFD scalar flux before the subsequent MG CMFD calculation. The multi-group scalar flux prolongation can be achieved simply by multiplying the ratio of the converged few-group scalar flux to the few-group scalar flux generated by the MG CMFD solution:
The iteration algorithm of MOC neutron transport calculation with two-level CMFD acceleration is illustrated in Figure 1. First, the homogenized multi-group constants for all cells and all the cell surfaces are calculated. The few-group constants are determined from the multi-group constants. The CMFD calculation begins from the few-group calculation and moves to the multi-group calculation if FG CMFD converges or the number of iterations meets the user setting. Then the multi-group scalar fluxes are updated by the converged few-group scalar flux, as shown in Equation (14). The multi-group iteration continues until the MG CMFD converges or the maximum number of iterations is reached. After the multi-group CMFD calculation is completed, the scalar fluxes of MOC fine mesh and the angular fluxes at the domain boundaries need to be scaled using the MG CMFD solution. Then the MOC neutron transport calculation is performed after the evaluation of the total source. When the MOC neutron transport calculation is finished, the overall convergence is checked using the keff and the MOC scalar flux.
The GPU is designed to perform the compute-intensive and highly parallel computations. Hence, the basic idea of GPU programming is transferring the compute-intensive parts of the application to the GPU, and the sophisticated flow control parts still remain at CPU. For the MOC neutron transport calculation, there is an enormous amount of parallel rays tracing across the computational domain. These relatively independent rays quite suitable for massive parallelization. Therefore, the ray parallelization is involved to implement the MOC neutron transport calculation on GPU.
Figure 2 illustrates the flowchart of the GPU-based MOC neutron transport calculation. The initialization which includes the preparation of cross-section and track information is performed on the CPU. Then those information is copied to the GPU global memory. Then the total source which including the fission source and scattering source is evaluated on GPU. And each of the GPU threads handles the source evaluation of one energy group for one fine-mesh. After the source evaluation, the transport sweep is performed. In order to reach the optimal performance on GPU, our former research (Song et al., 2019) recommends to deploy the loop over rays and the loop over energy groups onto the GPU threads, as illustrated in Figure 2.
As shown in Figure 1, the group constants condensation, the linear system construction and linear system solving are three main parts which can be parallelized on GPU for CMFD calculation. It is quite direct to parallelize the group constants condensation, the evaluation of group constants of coarse mesh i and CMFD group G is assigned to a GPU thread. Hence the groups constants for all coarse meshes and all CMFD groups are evaluated simultaneously and independently. As for the linear system which is constructed explicitly, the generation of elements in each row of matrix M and vector F is assigned to each GPU thread.
The third main part is to solve the sparse linear system, as shown in Equation (10). And the power iteration is used in this study for obtaining the eigenvalue and its corresponding normalized eigenvectors. However, for the problems we are primarily interested in, solving the linear system directly is prohibitively costly, since the directed inversion of matrix M is expensive. Hence, it is replaced by solving the linear system using the iterative method:
where n is the power iteration index.
The goal of a linear system solver is to solve for x in the linear system:
Here, x,b ∈ ℝn, A ∈ ℝn×n.
In this study, we applied three methods to solve the linear system iteratively: the Jacobi method, the successive over-relaxation (SOR) method, and the preconditioned generalized minimum residual (PGMRES) method. These three linear system solvers are implemented on both CPU and GPU, and the performance of these solvers are compared and analyzed.
For the linear system of equations described by Equation (16), the diagonal elements, aii, of A are all non-zero. It starts with the decomposition of matrix A.
where, D=diag(a11, ···, ann) is the diagonal matrix containing the diagonal elements of A, L is the strict lower part, and U is the strict upper part.
Then the Jacobi method can be organized as following matrix form:
where the superscript indicates the iteration number.
The parallelization of the Jacobi method on GPU is straightforward because the Jacobi scheme is naturally parallelizable. As a result, n GPU threads are invoked and each of the threads performs the calculation of one x in vector x, namely:
The successive over-relaxation (SOR) method is one of the well-known iterative methods. The SOR formulation can be defined by introducing the over-relaxation factor ω:
A necessary condition for the SOR method to be convergent is that 0 < ω < 2. Choosing ω < 1 results in under-relaxation, which can help stabilize a divergent of this method. Choosing ω > 1 results in over-relaxation, which can accelerate the convergence in certain situations.
For the parallelization of SOR, a red-black ordering strategy is used. In Equation (10), the solution estimated at iteration (k + 1) of cell i is only depends on the solution of its six immediate neighbors at iteration (k). If all the cells in a computational domain are colored in a checkerboard-like manner, then, during the calculation, the red cells only need data from the black cells. Thus, red-black SOR is a high parallelizable algorithm. At a given step, half of the cells can be updated simultaneously.
The preconditioned generalized minimum residual (PGMRES) method (Saad and Schultz, 1986) is one of the most popular Krylov methods for solving the non-symmetric linear system. The basic idea of PGMRES is to produce a n × n Hessenberg matrix and the corresponding basis V, then the approximate solution x(n) is found by minimizing the residual norm . The methodology and fundamental properties of PGMRES method can be found in many literatures (Van der Vorst and Vuik, 1993).
The performance of the GMRES method is usually improved significantly via preconditioning. A preconditioner M whose inverse satisfies M−1≈A−1 in some sense should be relatively inexpensive to apply. The preconditioner is designed to improve the spectral properties of A, making the system converge faster. In this study, the left preconditioning technique is utilized in the GMRES method, which is based on solving the linear system as M−1Ax=M−1b. A preconditioner applied to Algorithm 1 would appear in lines 1 and 4. The preconditioner investigated in this work is the Jacobi preconditioner. The Jacobi preconditioner is the diagonal matrix which contains the diagonal elements of the sparse matrix A. The inversion of the Jacobi preconditioner can be easily performed done with a small computation burden.
The main computational components in the PGMRES method are: (1) Sparse matrix-vector product; (2) Vector operations; (3) Preconditioning operation; (4) Solving the least-square problem. The implementation of these four parts on GPU is discussed as follows.
In this study, the sparse matrix A and the preconditioner M are stored with the compressed sparse row (CSR) format which is widely used as a general-purpose sparse matrix storage format. As illustrated in Algorithm 1, the sparse matrix-vector product (SpMV) is one of the major components which are highly parallelizable in the PGMRES method. To parallel the SpMV for a matrix with the CSR format, the multiplication of one row of the matrix with the vector is simply assigned to one thread. As a result, the computation of all threads is independent.
There exist several other GPU-friendly operations in the PGMRES method, such as the vector addition, dot production of two vectors, and vector scaling. These procedures can be easily parallelized by assigning the operation of elements of vectors to the GPU threads. The reduction is involved when calculating the 2-norm of the vector and performing the dot product of two vectors. The reduction operation is also performed on GPU by utilizing the shared memory. The parallel reduction is performed to sum up all partial results which are saved into the shared memory by the GPU threads.
One important aspect of the PGMRES method is the preconditioning operation. The incomplete-LU preconditioning technique is implemented to provide an incomplete factorization of the coefficient matrix. It requires a solution of lower and upper triangular linear system in every iteration of PGMRES method. In order to implement the preconditioning operation, the sparse triangular solve implemented in the cuSPARSE library (NVIDIA cu SPARSE Library) is used.
The least-square problem is solved by the QR factorization of the Hessenberg matrix. Since this procedure is naturally serial, a series of Givens rotation is performed to solve the least-square problem on GPU with serial execution.
The numerical tests were conducted on a workstation with Intel Core i9-7900X Processor (3.30 GHz, 10-core) and an NVIDIA GeForce GTX 1080Ti (1.5 GHz, 3584 CUDA cores, 11GB memory) running 64-bit Linux systems. All tests are performed with double-precision arithmetic.
The 2-D C5G7 benchmark (Lewis et al., 2003) is usually used to verify the accuracy of the algorithm. Figures 3A–C illustrate the assembly and core configuration of this benchmark with the boundary conditions. The fuel assembly is constructed with 17 by 17 of square pins. And the geometry of fuel pin is shown in Figure 3B. Seven-group macroscopic cross-sections are specified. For spatial discretization, the whole computing domain is divided into 51 by 51 pins. Each pin is subdivided into 5 radial subdivision and 8 azimuthal divisions, as illustrated in Figure 3B. All tests are performed with the 0.03 cm ray spacing and 56 azimuthal angles. Tabuchi-Yamamoto (Yamamoto et al., 2007) polar quadrature sets are used. The stopping criteria for convergence are εkeff <10−6 and εflux <10−5.
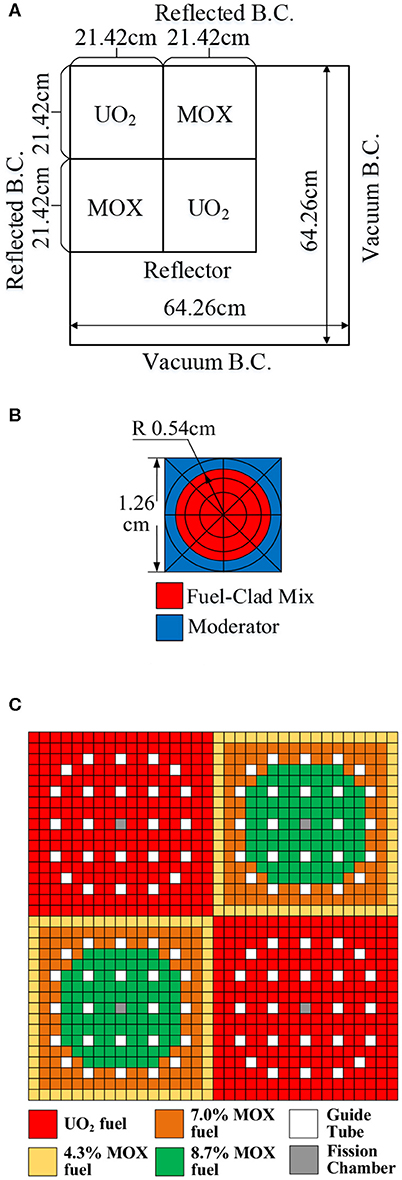
Figure 3. (A) Core configuration for the 2-D C5G7 benchmark problem. (B) Fuel pin layout. (C) Benchmark fuel pin compositions.
The computations are performed with and without two-level CMFD acceleration. Table 1 shows the eigenvalue and power distribution of the benchmark, along with the reference Monte Carlo solution. Compared to the reference results, the absolute difference of eigenvalue is 6 pcm which is under the stochastic uncertainty of the reference. The power distribution shows good agreement. And the maximum relative pin power error is <1.4%. The results demonstrate desired agreement for both eigenvalue and the power distribution. Moreover, the CMFD acceleration maintains the desired accuracy compared to the MOC calculation.
In this section, the overall performance of two-level CMFD and GPU acceleration is studied. In order to exploit the full computing power of GPU, a series of cases are performed with a fictitious quarter-core problem. The quarter core contains 21 UO2 fuel assemblies and 20 MOX fuel assemblies from the 2-D C5G7 benchmark problem. Those assemblies are aligned in a checkerboard pattern as illustrated in Figure 4. The mesh division and computing parameters maintain the same as the aforementioned 2-D C5G7 benchmark problem, except the overall convergence criterion of flux which is set to be 10−4. The convergence criteria for keff and flux of MG CMFD calculation are εkeff <5 × 10−7 and εflux <5 × 10−5. And the related convergence criteria of FG CMFD are εkeff <2.5 × 10−7 and εflux <2.5 × 10−5.
In order to characterize the convergence performance of different linear system solvers, Three cases are executed with MG CMFD acceleration on GPU. Based on a series of tests, the maximum number of iterations of MG CMFD and the maximum number of linear iterations per CMFD calculation are both set to be 30. The Krylov subspace dimension of the PGMRES solvers is set to 2. Then Figure 5 illustrates the overall convergence history of the keff with the Jacobi, SOR, and PGMRES solvers. As shown in Figure 5, the PGMRES solver shows a better convergence rate. Moreover, the SOR solver has a medium rate of convergence, and it needs more iterations to achieve convergence when the Jacobi solver is involved.
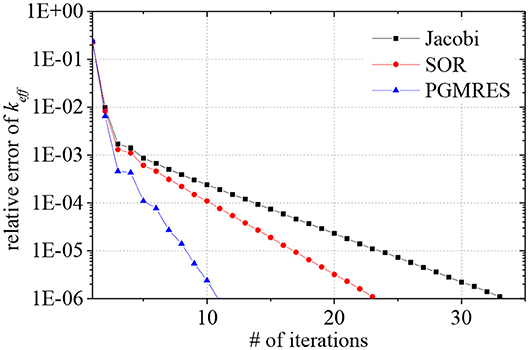
Figure 5. Convergence history of keff of the different linear system solvers for the mock quarter-core problem.
A series of runs are performed to evaluate the overall performance of two-level CMFD and GPU acceleration. The sensitivity study has been performed with varied upper limits of the number of CMFD iterations and the number of linear solver iterations. Moreover, the impact of different Krylov subspace dimensions to the overall performance is also examined and it is set to 2. After the sensitivity study, the best results for each execution are listed in Table 2.
From Table 2, the following observations can be made based on the numerical results:
(1) The GPU shows great performance advantages compared to the CPU. The comparison of the case (0a) and case (0b) shows that the GPU-based MOC calculation achieves about 25x speedup compared to the serial CPU-based calculation. This observation is consistent with the results drawn in our former research (Song et al., 2019).
(2) The CMFD acceleration can significantly reduce the number of iterations. For both CPU-based and GPU-based calculation, about 100x speedup is provided by two-level CMFD acceleration. Moreover, the GPU acceleration for CMFD calculation is about 13x [case (1d) vs. case (2d) and case (1e) vs. case (2e)] for cases using Jacobi solver and SOR solver. While the GPU acceleration for CMFD calculation is about 5.8x [case (1f) vs. case (2f)] when PGMRES solver is used. Compared to the serial CPU-based MOC calculation (case (0a)], the overall speedup of case (2e) is contributed by 3 aspects: (1) the speedup provided by the CMFD acceleration which can significantly reduce the number of iterations (about 100x), (2) GPU acceleration on MOC neutron transport calculation (about 25x), (3) GPU acceleration on CMFD calculation (about 13x). And in case (2e), the CMFD calculation contributes about 7% of overall runtime. As a result, over 2,400x [case (0a) vs. case (2e)] speedup is obtained when the two-level CMFD and GPU accelerations are applied simultaneously.
(3) Although the Jacobi method has the maximum degree of parallelism on GPU, a relatively large number of CMFD iterations is needed because of the poor convergence performance of the Jacobi method, as illustrated in Figure 5. However, the SOR method can maintain the desired parallelism by adopting the red-black ordering strategy. On the other hand, it also can keep the relative high convergence rate compared to the Jacobi method, which results in a reduction in the number of CMFD iterations. Hence, the SOR-based calculations show better performance than the Jacobi-based calculations. The number of CMFD iterations is relatively reduced when the PGMRES solver is involved. And the overall performance of PGMRES-based calculations on CPU is comparable to the Jacobi-based and SOR-based calculations. Nevertheless, the performance degradation of PGMRES-based calculations is observed on GPU. The detailed analysis is discussed in the following sections. As a result, the SOR-based calculations show better performance compared against other cases with the Jacobi and PGMRES solver in the same group [such as the comparison of the cases (1a), (1b), and (1c)].
(4) The FG CMFD is effective to accelerate the CMFD calculation. Compared to the cases with MG CMFD calculations, over 50% improvement in 2 L CMFD calculations is observed by comparing the execution time of CMFD calculations.
The execution time of CMFD calculation is contributed by three parts, (1) cross-sections generation (xs_gene), (2) linear system construction (linSys_cons), (3) linear system solving (Ax = b). Figure 6 shows the execution time of different partitions of CMFD calculation for the cases listed in Table 2. As shown, for CPU calculation, the generation of multi-group cross-sections contributes a considerable part to the overall CMFD calculation, especially for the two-level CMFD calculation. However, since the xs_gene procedure is performed with thread parallelization on GPU, the execution time of xs_gene is significantly reduced to <0.2 s on GPU. For all cases, the execution time for constructing the linear system is <0.1 s. Moreover, Figure 6 indicates that the FG CMFD acceleration can significantly reduce the execution time of solving the linear system in 2 L CMFD calculation. When applying the PGMRES method on GPU, the performance improvement for linear system solving is about 3.7 x which is relatively small compared to the other two methods. The detailed performance analysis of the linear solvers will be performed in future work.
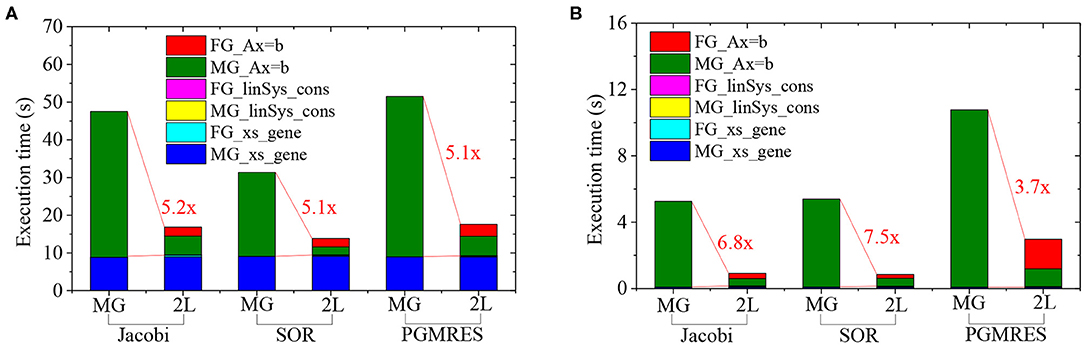
Figure 6. (A) Time break down of CMFD calculations on CPU. (B) Time break down of CMFD calculations on GPU.
Current work is focused on the 2-D CMFD calculation on GPU. However, simulation of practical problem is usually focused on 3-D calculations. The CMFD equations in 2-D form a five-stripe sparse linear system, while it is a seven-stripe sparse linear system on the 3-D geometry. Since the iterative methods applied in this work are general methods for solving the CMFD linear systems. Hence, the related linear system solvers can be directly applied to solve the 3-D CMFD problems. And the performance is supposed to be consistent in 3-D cases.
In addition, the large-scale problems usually need to be solved with parallel strategy such as spatial domain decomposition. The scalability and efficiency to computing the large-scale problems with multiple GPUs need to be examined.
As for the further performance optimization, the MOC calculation contributes the majority of runtime for the simulation of 2-D neutron transport calculations on GPU. This observation is supposed to be consistent in 3-D simulations. Hence, in order to improving the overall performance, more efforts should be focused on the optimization of GPU-based MOC calculation in 3-D situation. In addition, when the spatial domain decomposition and multiple GPUs are involved, the performance of 3-D CMFD calculation may be impacted by the communication between decomposed domains. And it may further impact the overall performance.
In this work, a two-level CMFD acceleration technique was implemented on both CPU and GPU to accelerate the 2-D MOC neutron transport calculation. In the two-level CMFD scheme, a few-group CMFD problem is used as a lower-order accelerator to the standard pinwise multi-group CMFD problem. Several linear system solvers, i.e., Jacobi solver, SOR solver with red-black ordering, and the PGMRES solver, are applied and the performance was examined under the CMFD framework. The overall performance of CMFD acceleration on both CPU and GPU is compared to evaluate the effectiveness of CMFD and GPU acceleration.
The numerical calculations are performed with 2-D C5G7 benchmark problem and an extended 2-D mock quarter-core problem and the following conclusions can be drown:
(1) For the 2-D C5G7 benchmark, the difference of eigenvalue is 6 pcm and the power distribution shows good agreement compared against the reference solution. The results of calculations with and without two-level CMFD acceleration provide desired accuracy in both eigenvalue and power distribution.
(2) As a linear system solver, the PGMRES solver shows a better convergence rate with minimum number of iterations. While the number of iterations of Jacobi solver is tripled compared to the PGMRES solver at the same convergence level. And the SOR solver has a medium rate of convergence.
(3) It appears that SOR is a suitable method for solving the linear system under the CMFD framework on both CPU and GPU. For CPU-based CMFD calculation, the PGMRES method has comparable performance to the SOR method, because the arithmetic complexity of the PGMRES method can be counteracted by its remarkable convergence characteristics. However, since the Jacobi method and SOR method can reach a relatively high degree of parallelism on GPU, the performance of these two methods is better than the PGMRES method. When the two-level CMFD and GPU accelerations are applied simultaneously, the overall speedup is contributed by 3 aspects: 1) the CMFD acceleration which can significantly reduce the number of iterations (about 100x), 2) GPU acceleration on MOC neutron transport calculation (about 25x), 3) GPU acceleration on CMFD calculation (about 13x for SOR method). As a result, it reaches about 2,400x speedup on GPU with two-level CMFD acceleration compared to the CPU-based MOC calculation.
(4) The CMFD calculation contributes about 7% (for cases with Jacobi and SOR solver) and 17% (for cases with PGMRES solver) of the overall runtime. The procedure for solving the linear system contributes to the majority of the runtime of the CMFD calculation. Moreover, the results show that the FG CMFD acceleration is effective to accelerate the MG CMFD execution.
This work demonstrates the high potential of the two-level CMFD technique and GPUs to accelerate the practical whole-core neutron transport calculation. Based on the numerical results, GPUs provide a high-performance advantage for accelerating both MOC and CMFD calculations. Since the PGMRES method is still preferred in that it can solve various linear systems with a wide range of numerical properties, more efforts need to be concentrated on the performance optimization of the PGMRES method on GPU. Moreover, the main purpose is to perform the 3-D whole-core MOC neutron transport simulation on GPU under CMFD framework. Hence, in the future, more efforts will be focused on the 3-D CMFD calculation on GPU with the detailed performance analysis. In addition, the efficiency comparison of different solvers and the study of the parallelization will be included with practical computational cases. Furthermore, the scalability to computing the large-scale problems on large-scale parallel machines also needs to be examined in the future.
All datasets generated for this study are included in the article/supplementary material.
PS, ZZ, and LL contributed to the ideas and designs of this study. PS implemented the algorithm through programming and wrote the first draft of the manuscript. ZZ helped to design and organize the cases for validating the algorithm. LL helped to perform the numerical analysis and organize the database. QZhang and QZhao explained the details of linear algebra used in this work and provided technical support during programming. All authors helped to revise the manuscript and approve the submitted version.
This work is supported by the funds provided by the following sources: Science and Technology on Reactor System Design Technology Laboratory, Heilongjiang Province Science Foundation for Youths [QC2018003], Nuclear Power Technology Innovation Center, Fundamental Research Funds for the Central Universities [grant number GK2150260178], the Research on Key Technology of Numerical Reactor Engineering [J121217001], and the National Key R&D Program of China [2018YFE0180900].
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Askew, J. R. (1972). A characteristics formulation of the neutron transport equation in complicated geometries. AEEWM 38:1108.
Boyd, W., Shaner, S., Li, L., Forget, B., and Smith, K. (2014). The OpenMOC method of characteristics neutral particle transport code. Ann. Nucl. Energy 68, 43–52.
Boyd, W. R., Smith, K., and Forget, B. (2013). “A massively parallel method of characteristics neutral particle transport code for GPUs,” in Proceedings of the International conference on Mathematics and Computational Method Applied To Nuclear Science and Engineering (M&C 2013), (Sun Valley).
Chen, J., Liu, Z., Zhao, C., He, Q., Zu, T., Cao, L., et al. (2018). A new high-fidelity neutronics code NECP-X. Ann. Nucl. Energy 116, 417–428. doi: 10.1016/j.anucene.2018.02.049
Cho, J. Y., Joo, H. G., Kim, K. S., and Zee, S. Q. (2002). Cell based CMFD formulation for acceleration of whole-core method of characteristics calculations. J. Korean Nucl. Soc. 34, 250–258.
Cho, N., Lee, G. S., and Park, C. J. (2003). Partial current-based CMFD acceleration of the 2D/1D fusion method for 3D whole-core transport calculations. Trans. Am. Nucl. Soc. 88:594.
Choi, N., Kang, J., and Joo, H. G. (2018). “Performance comparison of linear system solvers for CMFD acceleration on GPU architectures,” in Transactions of the Korean Nuclear Society Spring Meeting (Jeju).
Godfrey, A., Collins, B., Kim, K. S., Lee, R., Powers, J., Salko, R., et al. (2016). VERA benchmark results for Watts Bar nuclear plant unit 1 cycle 1-12,” in The Physics Reactor Conference (PHYSOR 2016) (Sun Valley).
Han, Y., Jiang, X., and Wang, D. (2014). CMFD and GPU acceleration on method of characteristics for hexagonal cores. Nucl. Eng. Des. 280, 210–222. doi: 10.1016/j.nucengdes.2014.09.038
Jong, M. D., Ploeg, A. V. D., Ditzel, A., and Vulk, K. (2017). Fine-grain parallel RRB-solver for 5-/9-point stencil problems suitable for GPU-type processors. Electron Transc Numer Ana. 46, 375–393.
Joo, H. G., Cho, J. Y., Kim, K. S., Lee, C. C., and Zee, S. Q. (2004). “Methods and performance of a threedimensional whole-core transport code DeCART,” in Proceedings of the PHYSOR2004 (Chicago).
Jung, Y. S., Shim, C. B., Lim, C. H., and Joo, H. G. (2013). Practical numerical reactor employing direct whole core neutron transport and subchannel thermal/hydraulic solvers. Ann. Nucl. Energy 62, 357–374. doi: 10.1016/j.anucene.2013.06.031
Kang, J., and Joo, H. G. (2018). “GPU-based parallel krylov linear system solver for CMFD calculation in nTRACER,” in Transactions of the Korean Nuclear Society Spring Meeting (Jeju).
Kochunas, B., Collins, B., Jabaay, D., Downar, T. J., and Martin, W. R. (2013). “Overview of development and design of MPACT: Michigan parallel characteristics transport code,” in International Conference on Mathematics & Computational Methods Applied To Nuclear Science & Technology (Sun Valley).
Kochunas, B., Collins, B., Jabaay, D., Stimpson, S., Salko, R., Graham, A., et al. (2015). “VERA core simulator methodology for PWR cycle depletion,” in Joint International Conference on Mathematics and Computation (M&C), Supercomputing in Nuclear Applications (SNA) and the Monte Carlo (MC) Method (Nashville).
Lewis, E. E., Palmiotti, G., Taiwo, T. A., Blomquist, R. N., Smith, M. A., and Tsoulfanidis, N. (2003). Benchmark Specifications for Deterministic MOX Fuel Assembly Transport Calculations without Spatial Homogenization. (Organization for Economic Co-operation and Development's Nuclear Energy Agency).
Li, R., and Saad, Y. (2012). GPU-accelerated preconditioned iterative linear solvers. J Supercomput. 63, 443–466. doi: 10.1007/s11227-012-0825-3
Liang, L., Zhang, Q., Song, P., Zhang, Z., Zhao, Q., Wu, H., et al. (2020). Overlapping communication and computation of GPU/CPU heterogeneous parallel spatial domain decomposition MOC method. Ann. Nucl. Energy 135:106988. doi: 10.1016/j.anucene.2019.106988
Liu, Z., Wu, H., Chen, Q., Cao, L., and Li, Y. (2011). A new three-dimensional method of characteristics for the neutron transport calculation. Ann. Nucl. Energy 38, 447–454. doi: 10.1016/j.anucene.2010.09.021
NVIDIA cu SPARSE Library (2019). Avaliable online at: https://docs.nvidia.com/cuda/cusparse/index.html (accessed May 01, 2020).
Ryu, M., Jung, Y. S., Cho, H. H., and Joo, H. G. (2015). Solution of the BEAVRS benchmark using the nTRACER direct whole core calculation code. J Nuclear Sci Technol. 52, 961–969. doi: 10.1080/00223131.2015.1038664
Saad, Y., and Schultz, M. H. (1986). GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869. doi: 10.1137/0907058
Smith, K. S. (1984). Nodal method storage reduction by non-linear iteration. Transac. Am. Nuclear Soc. 44:265.
Song, P., Zhang, Z., Liang, L., Zhang, Q., and Zhao, Q. (2019). Implementation and performance analysis of the massively parallel method of characteristics based on GPU. Ann. Nucl. Energy. 131, 257–272. doi: 10.1016/j.anucene.2019.02.026
Song, P., Zhang, Z., and Zhang, Q. (2020). Implementation of the CPU/GPU hybrid parallel method of characteristics neutron transport calculation using the heterogeneous cluster with dynamic workload assignment. Ann. Nucl. Energy. 135:106957. doi: 10.1016/j.anucene.2019.106957
TOP500 official site (2019). Avaliable online at: https://www.top500.org/> (accessed May 11, 2019).
Tramm, J. R., Gunow, G., He, T., Smith, K. S., Forget, B., and Siegel, A. R. (2016). A task-based parallelism and vectorized approach to 3D Method of Characteristics (MOC) reactor simulation for high performance computing architectures. Comput. Phys. Commun. 202, 141–150. doi: 10.1016/j.cpc.2016.01.007
Van der Vorst, H. A., and Vuik, C. (1993). The superlinear convergence behaviour of GMRES. J. Comput. Appl. Math. 48, 327–341.
Wang, D., and Xiao, S. (2018). A linear prolongation approach to stabilizing CMFD. Nucl. Sci. Eng. 190, 45–44. doi: 10.1080/00295639.2017.1417347
Yamamoto, A., Tabuchi, M., Sugimura, N., Ushio, T., and Mori, M. (2007). Derivation of optimum polar angle quadrature set for the method of characteristics based on approximation error for the Bickley function. J. Nucl. Sci. Eng. 44, 129–136. doi: 10.1080/18811248.2007.9711266
Zhang, Z., Wang, K., and Li, Q. (2013). Accelerating a three-dimensional MOC calculation using GPU with CUDA and two-level GCMFD method. Ann. Nucl. Energy 62, 445–451. doi: 10.1016/j.anucene.2013.06.039
Keywords: MOC, GPU, CUDA, CMFD acceleration, PGMRES
Citation: Song P, Zhang Q, Liang L, Zhang Z and Zhao Q (2020) GPU Based Two-Level CMFD Accelerating Two-Dimensional MOC Neutron Transport Calculation. Front. Energy Res. 8:124. doi: 10.3389/fenrg.2020.00124
Received: 22 November 2019; Accepted: 25 May 2020;
Published: 07 July 2020.
Edited by:
Jun Wang, University of Wisconsin-Madison, United StatesReviewed by:
Kees Vuik, Delft University of Technology, NetherlandsCopyright © 2020 Song, Zhang, Liang, Zhang and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qian Zhang, cWlhbnpoYW5nQGhyYmV1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.