
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 06 March 2020
Sec. Process and Energy Systems Engineering
Volume 8 - 2020 | https://doi.org/10.3389/fenrg.2020.00032
This article is part of the Research Topic Energy and Chemical Engineering - Outcomes from the EFCE Energy Section in the 12th European Congress on Chemical Engineering (ECCE12) View all 15 articles
The purpose of the work is to develop an analytical method for calculating the effective ranges of structural parameters of the throttle part of the axial valve with the external location of the locking shell based on the proposed stochastic models of bubble formation at the initial stage of hydrodynamic cavitation. In contrast to the well-known engineering methods for choosing the conditional bore diameter for the designed control device constructed using the Pi-Buckingham theorem, this calculation method relies not only on gyrodynamic similarity criteria, but also on functional dependences for the laws of distribution of cavitation bubbles according to various characteristics (specific size bubbles, the degree of opening of the node “separator-external locking shell”). This takes into account a wide range of design and operating parameters, including the required valve capacity, as well as the physical and mechanical characteristics of the working medium. A block diagram of the calculation of the node “separator-external locking shell” for the specified axial valve is proposed. The influence of a set of design parameters for the “separator-external locking shell” assembly from the rational ranges of their variation obtained using the proposed analytical calculation algorithm on the size of cavitation bubbles is investigated. It has been established that when using the latest results in comparison with the values of parameters from irrational ranges of change, there is a tendency to reduce the ensemble average value of the diameter of the cavitation bubble by 1.95 times, when switching to a mode from 20% of the degree of separation of the separator to 80% of the opening of the throttle holes, the nominal valve capacity increases by 10.7 times. The results obtained illustrate the possibility of preventing an increase in the intensity of formation of cavities in the flow part of the control device already at the initial stage of the occurrence of cavitation.
Improving engineering methods for calculating valves is a pressing issue in the field of pipeline fittings design. The use of valves (Emerson, 2020; Flowserve, 2020; Mokveld, 2020; Rust, 2020; Talis, 2020) in various branches of the chemical and oil and gas industry continues to expand. At the same time, the requirements for the main indicators of fluid transportation, such as throughput and expenditure characteristic of the valve, are constantly becoming tougher. The task of reducing the intensity of cavitation effects (Knapp et al., 1970; Franc and Michel, 2005; Xu et al., 2015) in the flow part of the valve can be successfully solved by throttling fluid flows in designs (Emerson, 2020; Flowserve, 2020; Mokveld, 2020; Rust, 2020; Talis, 2020), which differ, for example, according to a number of characteristics: the shape of the throttle body, the number of throttle stages, the shape of throttle openings, the type of throttle channels, etc. Axial valves (Weevers, 1982; Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019; Ziegler, 2019) provide a straight-line flow of fluid with minimal resistance when opened. Note that this type of valve is actively used in controlling flows, both liquid (Weevers, 1982; Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019; Ziegler, 2019; Emerson, 2020; Flowserve, 2020; Mokveld, 2020; Rust, 2020; Talis, 2020) and gaseous media (Bian et al., 2019a,b; Cao and Bian, 2019; Emerson, 2020; Flowserve, 2020; Mokveld, 2020; Rust, 2020; Talis, 2020). Moreover, the system “perforated separator—internal piston” (Weevers, 1982; Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019), in particular, with one (Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019) or several throttle stages (Weevers, 1982) of throttling, when the internal piston, as a rule, is most widely used as a locking and regulating element. driven by rack and pinion (Preston, 2018; Canjuga, 2019) or crank mechanism. On the one hand, the shut-off and control system in the indicated design (Weevers, 1982; Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019) allows separation of the fluid flows due to the formation of radial jets in the direction of the central axis of the valve, which contributes to the radial displacement of the cavitation bubbles formed in the central part of the separator and their accelerated removal from him. Thus, in the central part of the separator with one (Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019) or several stages (Weevers, 1982) of throttling, the region of the working medium is displaced, which is subsequently subjected to the developed stage of cavitation, which prevents the collapse of bubbles near the inner surface of the cylindrical separator, and, consequently, its erosion. However, on the other hand, the internal arrangement of the locking element, in particular in the form of a piston (Weevers, 1982; Peterman and Keithahn, 1987; Esveldt, 2012; Preston, 2018; Canjuga, 2019), complicates the design of the sealing assembly, increases the energy costs of the drive and contributes to additional turbulization of the medium flow due to the location of the piston rod and spacers in the cavitation area. In Weevers (1982), another design version of the locking and regulating system in the form of a hollow cylindrical sleeve covering the separator was used. However, this design (Weevers, 1982) turned out to be quite complex and did not solve the problem of cavitation at small stages of valve opening. Note that the active use of various nozzle designs and the principle of swirling the working fluid flow are observed in Mokveld products (Mokveld, 2020), and similar technical solutions are used for gas liquefaction (Bian et al., 2019a,b; Cao and Bian, 2019). In particular, the analysis of design features of axial valves was performed in Lebedev et al. (2016, 2017a).
Regarding the methods for calculating the effective ranges of the design parameters of control valves, two approaches are most widespread: analytical estimation (Arzumanov, 1971, 1985; Blagov, 1990) using the Pi-Buckingham theorem (Buckingham, 1915; Misic et al., 2010) or numerical modeling for gaseous (Bian et al., 2019a,b; Cao and Bian, 2019) and liquid (Qu et al., 2015; Hou et al., 2017; Rudolf et al., 2017; Qiu et al., 2019; Tang et al., 2019) environments using ready-made software products (Ansys Inc, 2013, 2017). Moreover, the first approach requires a wide experimental base, and the second requires a long adaptation of the software product to the main factors influencing the course of the studied processes, including cavitation (Knapp et al., 1970; Franc and Michel, 2005; Xu et al., 2015), in a specific design. The formation of the theoretical base for the development of an engineering methodology for the analytical calculation of the desired parameters of control valves in this work is carried out on the basis of the stochastic approach by the energy method (Klimontovich, 2014). This choice (Kapranova et al., 2016c) from a variety of methods for describing the cavitation phenomenon, which include deterministic (Besant, 1859; Baron Rayleigh, 1911–1919; Plesset and Chapman, 1971; Chahine, 1994), stochastic (Volmer and Weber, 1926; Frenkel, 1946; Hsu, 1962; Lienhard and Karimi, 1981; Shin and Jones, 1993; Kwak and Kim, 1998; Ellas and Chambre, 2000) and combined Sokolichin et al., 1997; Koch et al., 2012; Seung and Kwak, 2017 approaches, is explained by the possibility of modeling differential functions of the distribution of the number of cavitation bubbles according to the characteristic features of the studied process (specific size of the bubbles, the degree of opening of the valve) depending on the structural, operational parameters of the regulating device and the physico-mechanical properties of the working medium (Weevers, 1982).
Usually the stochastic approach (Volmer and Weber, 1926; Frenkel, 1946; Hsu, 1962; Lienhard and Karimi, 1981; Shin and Jones, 1993; Kwak and Kim, 1998; Ellas and Chambre, 2000) [as models of homogeneous nucleation (Volmer and Weber, 1926; Frenkel, 1946; Lienhard and Karimi, 1981), their modifications with the introduction of the heterogeneity factor (Kwak and Kim, 1998; Ellas and Chambre, 2000), or heterogeneous nucleation (Hsu, 1962; Shin and Jones, 1993)] and combined one (Sokolichin et al., 1997; Koch et al., 2012; Seung and Kwak, 2017) suggest the use of the postulation of the differential distribution functions of cavitation nuclei by their size based on experimental dependences. Note that the deterministic approach (Besant, 1859; Baron Rayleigh, 1911–1919; Plesset and Chapman, 1971; Chahine, 1994) is usually implemented either when describing the behavior of a single bubble of variable radius, or in modified models taking into account additional factors of inertial, thermal, and diffusion nature. However, the latter approach is most relevant when applied to the estimation of the velocity regimes of growth of cavitation bubbles near the wall, including during numerical simulation (Qian et al., 2016).
The team of authors analyzed the design features of direct-flow type control valves (Lebedev et al., 2016, 2017a,b), methods for modeling the cavitation phenomenon (Kapranova et al., 2016c) and calculation of the main indicators of this process (Kapranova et al., 2016d,e), and also performed theoretical (Kapranova et al., 2016a,b, 2017, 2018a,b; Kapranova, 2018; Kapranova and Miadonye, 2019) and experimental (Esveldt, 2012; Lebedev et al., 2017a,b; Preston, 2018) studies of the initial stage of hydrodynamic cavitation with axisymmetric throttling of fluid flows, which made it possible to obtain a theoretical justification and experimental confirmation (Kapranova and Miadonye, 2019) of the possibility of reducing the intensity of formation of cavitation bubbles and the use of external locking shell. As a result of these studies, the authors proposed the design of an axial valve (Arzumanov, 1985; Lebedev et al., 2018) with a locking and regulating system “perforated separator—external locking cylinder-conical shell.” The specified design (Arzumanov, 1985; Lebedev et al., 2018) involves a coaxial arrangement of the separator and the movable external locking member, which has the form of hollow cylindrical shell (Figure 1). Thus, the throttle round holes of the fixed separator overlap when the cylindrical shell obeys along its outer cylinder-conical surface. This shell can be set in motion as a rack and a crank mechanism.
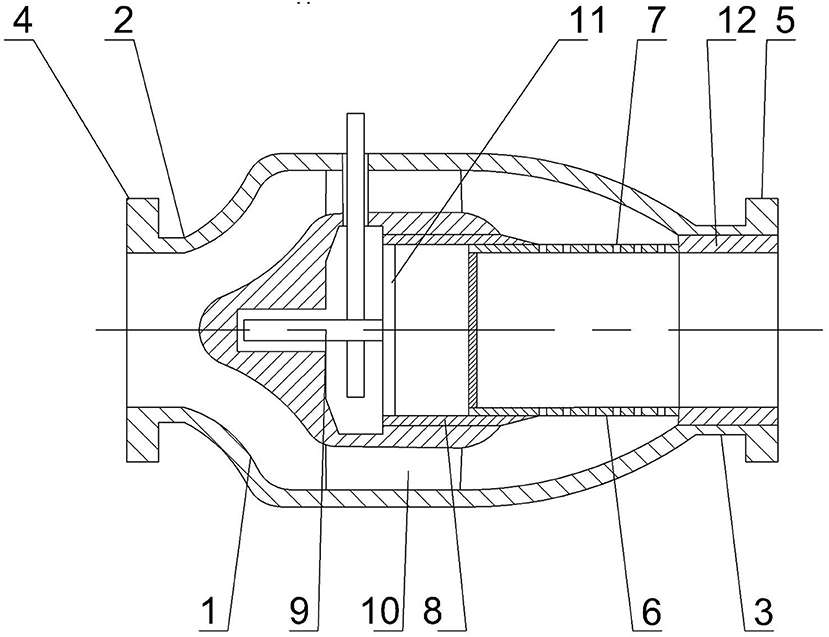
Figure 1. Schematic diagram of an axial valve with an external positioning of the locking member: 1–outer case, 2 and 3–inlet and outlet nozzles, 4 and 5–flanges, 6–separator, 7–throttle holes, 8–cylindrical conical (external locking shell), 9–rack and pinion mechanism, 10–cavity of the inner housing, 11–radial partitions, 12–expansion sleeve.
Thus, after solving a number of problems in developing stochastic models for the formation of cavitation bubbles in an axial valve separator by their size (Kapranova et al., 2016a, 2017, 2018a) and the degree of its opening (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019), after performing a series of comparative analysis (Kapranova and Miadonye, 2019) of the theoretical (Kapranova et al., 2016a, 2017, 2018a,b; Kapranova, 2018; Kapranova and Miadonye, 2019) and experimental results (Lebedev et al., 2017a,b) the next goal of studies of axisymmetric throttling of fluid flows is the development of engineering methods for calculating operational and design parameters of the separator-locking shell assembly.
To ensure the effective operation of an axial valve with an external position of the locking member, an engineering procedure has been proposed for calculating a separator with round throttle holes. The purpose of the work is to develop a scientifically based method for calculating the effective ranges of the design parameters of the throttle part of the axial valve. Currently, the design of equipment (Hou et al., 2017; Qiu et al., 2019) subject to the effect of cavitation, as a rule, is based on the active use of ready-made software products (Tang et al., 2019), and as a result, has a numerical representation of the results (Rudolf et al., 2017) of their application in graphical or tabular form. Visualization of the studied process (Qu et al., 2015), performed by this method, has a high degree of visibility for a particular device, however, this requires the preliminary implementation of labor-intensive experimental validation (Qu et al., 2015). Such an approach often puts the designer in a dependent position on the level of development of numerical methods, on the completeness of taking into account in the finished software package the main factors of influence on the studied physical phenomena, requires a long adaptation of this software package to the specific regulatory requirements of the customer of control valves. In this presentation, preference is given to constructing an engineering methodology for calculating the main assembly of the valve using estimated analytical dependencies that allow us to analyze the mechanics of the behavior of the system of forming bubbles in the process of throttling the fluid flow. The theoretical basis for this calculation is stochastic modeling of the bubble formation process in the separator at the initial stage of hydrodynamic cavitation (Klimontovich, 2014; Kapranova et al., 2016a,b). Earlier, the authors used the stochastic approach with the equilibrium representation of the states of the energetically closed macrosystem (Klimontovich, 2014; Tang et al., 2019) within the framework of the Ornstein-Uhlenbeck random process (Kapranova et al., 2016b) to form the model of this process the bubble formation process in the separator at the initial stage of hydrodynamic cavitation. The proposed stochastic models (Kapranova et al., 2016a, 2017, 2018a,b; Kapranova, 2018; Kapranova and Miadonye, 2019) allowed us to obtain differential distribution functions of the number of cavitation bubbles formed during the initial stage of the evolution of hydrodynamic cavitation, according to their size (Kapranova et al., 2016a, 2017, 2018a) and the degree of opening of the axial valve (Arzumanov, 1971; Lebedev et al., 2017a,b). The performed experimental studies (Lebedev et al., 2017a,b) confirmed the possibility of reducing the intensity of hydrodynamic cavitation at its initial stage when using the modernized part of “separator-locking shell” of axial valve. In this case, a comparative analysis (Kapranova and Miadonye, 2019) of the obtained theoretical (Kapranova et al., 2016a, 2017, 2018a,b; Kapranova, 2018; Kapranova and Miadonye, 2019) and experimental (Lebedev et al., 2017a,b) results for the dependence of the differential distribution function of the number of bubbles fz(z) at the initial stage of hydrodynamic cavitation with a separator with round holes depending on the degree of their opening with using an external locking shell showed satisfactory convergence with a relative error not exceeding 13%. Note that the value of z is determined by the ratio of the given position z′ for the movable shutter (external locking shell) along its axis to the conditional position L corresponding to the length of the perforated part of the separator. The well-known classical method for calculating some rational parameters of a control valve (Arzumanov, 1971, 1985), which is actively used in various interpretations, including numerical ones, does not imply the use of functional dependencies for the laws of distribution of cavitation bubbles according to various characteristics, but it contains a reliable algorithm for the designer's actions when choosing the type regulatory device, depending on the regulatory data of the customer. In this case, the basis of the calculation is a set of empirical dependences for the diameter of the nominal bore, the valve throughput on a number of operating parameters characterizing the movement of the fluid flow (maximum achievable fluid flow, pressure drop, etc.) and the main hydrodynamic similarity criterion (critical Reynolds number). An empirical analysis of the conditions for achieving a critical value of the cavitation coefficient as a doubled criterion of Euler similarity plays a decisive role in the choice of type of control device (Knapp et al., 1970; Franc and Michel, 2005; Xu et al., 2015; Kapranova et al., 2016e). The last operation is performed according to the critical value of the hydraulic resistance coefficient using graphical experimental material (Arzumanov, 1971, 1985; Blagov, 1990) at the stage of estimating the maximum value of the valve throughput in comparison with the routine. Thus, the application of the classical method for choosing the type of control device is associated with the application of the Pi-Buckingham theorem (Buckingham, 1915; Misic et al., 2010) in solving the scaling problem and reducing the number of constant parameters describing the process under study. As a result of the model (Kapranova et al., 2016a,b), the integral characteristics of the cavitation bubble were calculated. The expression obtained using model (Kapranova et al., 2016a) for calculating the average over the ensemble of the diameter Dcb for the macrosystem of cavitation bubbles (Kapranova et al., 2017; Kapranova, 2018) takes into account the physical and mechanical properties of the working medium, as well as the main design and operating parameters of the axial valve. In particular, the analysis of graphic material for the functional dependence of Dcb = Dcb(Dy, Kvy) on the conditional diameter Dy and the corresponding throughput ability of the Kvy valve is presented in Kapranova A. B. et al. (2019). Another model (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019) made it possible to establish a connection between the critical value of the Reynolds number Recr in the case of a complete opening of the valve and its design parameters. So, these expressions for Dcb (Kapranova et al., 2017, 2018a) and Recr based on (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019), as well as the obtained expressions for the energy parameter of the stochastic model (Kapranova et al., 2018b) and the hydraulic resistance coefficient (Kapranova et al., 2018c) are used in the proposed engineering method for calculating the separator and constitute the main difference from the known approach (Arzumanov, 1971, 1985). Note that in practice, the identification of the cavitation region in the flow part of the control device is associated with the analysis of the dependence of the hydraulic resistance coefficient for the conditional flow area on the cavitation number kC, which is also reflected in this work.
We divide the whole set of parameters of the studied process of throttling the fluid flow into several sets: for design parameters q, for mode parameters τ, for additional φ. In particular, the main structural parameters of the axial valve with the design of an external movable locking device (Lebedev et al., 2018) (Figure 1) include: for the separator, external shells and corresponding parts of the housing: the diameter of the round throttle holes d0, the arc distance between the holes in the same row Sφ1, the distance between the rows of these holes l0, the thickness of the separator h, the number of holes for one row u1, the number of these rows u2, respectively, the inner and outer diameters separator Dout and Dc, the length of its perforator of the left part L, the bevel angle for the cylindrical part of the shell α, the inner diameter for the cylindrical part of the outer casing Dcas2, the outer diameter of the inner valve body Dch2, the wall thickness of the inner and outer casing δ2. Thus, the explicit representation of the set {qk2 = const} has the form
Set (1) is conveniently divided into three subsets for the main parameters of the separator , for the outer locking shell , and for the body
Specified operating parameters are the maximum attainable expenditure Q1max (m3/h) of the liquid through the regulating device at a given value of the medium temperature t1 (°C), the minimum pressure drop ΔPmin, the maximum pressure in the center of the bubble Pmax, which corresponds to the minimum value of its radius rmin, the saturated vapor pressure of the medium ps, the velocity of the fluid in the pipeline w then for {τk2 = const} we have
The following additional parameters are taken into account:
describing the physical and mechanical properties of the medium: respectively, the density of the liquid ρL, gas ρg and vapor ρs; kinematic viscosity of the liquid ν1 at a given value of its temperature t1 (°C), surface tension coefficient σ, volumetric weight of the medium γ, adiabatic exponent k.
We make a selection of input and output parameters for the process of regulating fluid flows in the flow part of the axial valve
where the set x1 is a subset of the operational parameters τ from (2); are limits for Δpmin; is required valve throughput.
When describing the block diagram (Figures 2, 3) for calculating the design parameters of the “separator-external locking shell” assembly of the axial valve, from the listed sets (2)–(8), it is necessary to select the following parameters:
• for input data input: sets φ, x1, x2, respectively, from (6) to (8); the set of initial values of a number of parameters from the subset for the set from (1)
as well as the subset for the set of regime parameters τ from (5)
• to search for the limits of change of parameters from q-set (1) in the form of the set of desired design parameters for the designed axial valve elements (Figure 1) according to sets (2)–(4): for the separator , for the external locking shell and for the body .
The proposed block diagram (Kapranova et al., 2019b) (Figures 2, 3) consists of 25 main blocks for calculating 13 effective values of the design parameters of the axial valve separator tested in calculating the example in Kapranova et al. (2020).
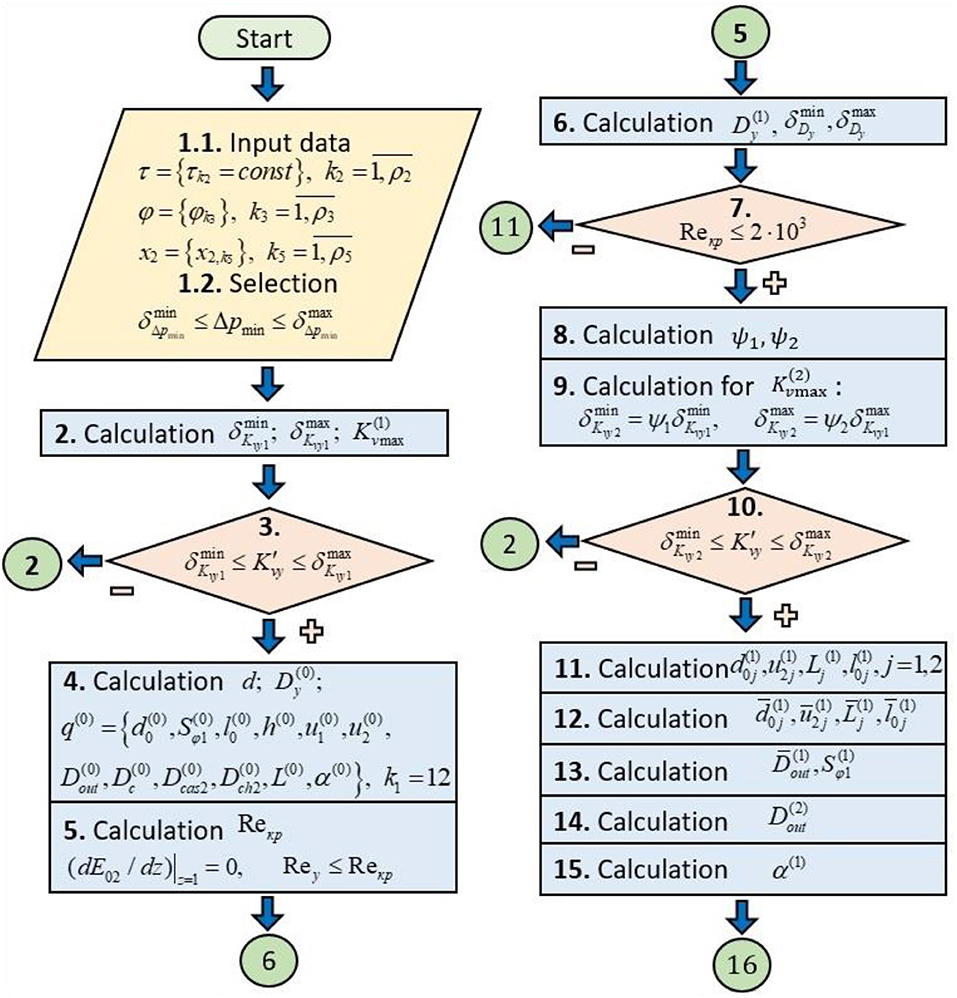
Figure 2. Conventional block diagram of the calculation of the design parameters of the axial valve separator with the external location of the locking member (Part 1).
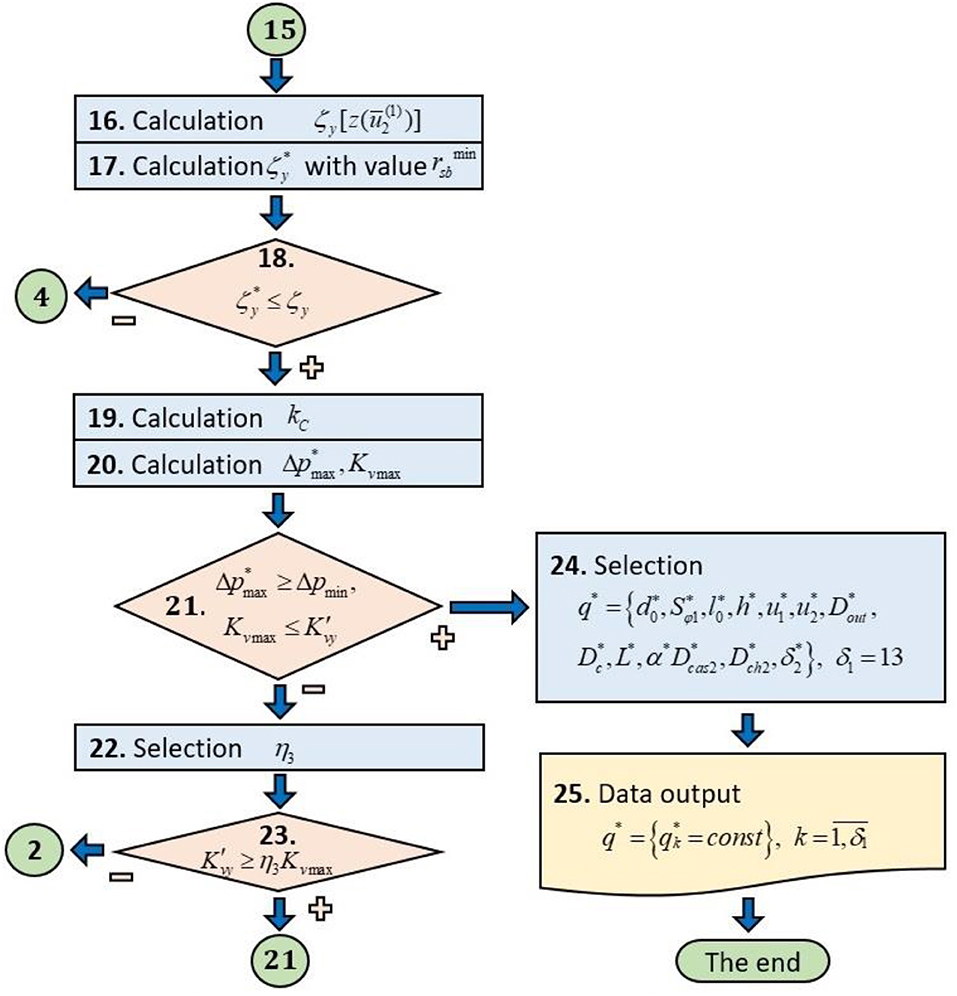
Figure 3. Conventional block diagram of the calculation of the design parameters of the axial valve separator with the external location of the locking member (Part 2).
Block 1 (Figure 2) includes the introduction of the parameters listed above: regime from (5), including the input set x1-set from (7); additional characteristics reflecting the physicomechanical properties of the working medium and the gas-vapor system inside the bubble from (6); weekend x2 from (8). In particular, according to the x1-set from (7), the variation limits and are set for the minimum pressure drop Δpmin from (7) for a fixed value of the medium temperature t1 (°C)
Block 2 (Figure 2) calculates the interval of variation in the maximum flow capacity of the valve for given values of and from (11) taking into account the dependence Kvmax(Δpmin) (Arzumanov, 1971), also used in (Kapranova et al., 2020)
where Q1max (m3/h) is the maximum attainable flow rate of the fluid through the valve; γ (g × c/cm3) is the bulk density of the liquid; η1 and η2 are safety factors in the range of at least 10–20% of the calculated value for the maximum throughput Kvmax according to Arzumanov (1971), for example, η1 = 1.1 and η2 = 1.2 (Kapranova et al., 2020); dimension for and is Pa.
Using conditional block 3 (Figure 2), the condition of belonging of the required value of throughput for the valve to the obtained range of values is checked
If inequality (13) is satisfied, the transition to block 4 follows; otherwise, it returns to block 2 (Figure 2) with the change of the safety factors η1 and η2 by 10–20%, respectively.
In block 4 (Figure 2) initial values are set:
• diameter of conditional passage (m), as the nearest integer to the larger side ⌈d⌉ (“ceiling” d)
• for the diameter of the pipeline d (m) according to Bian et al. (2019a)
where the fluid velocity w, for example, is usually taken for a water supply system w = 1.0 m/s, when supplied to a centrifugal pump w = 2.0 m/s, during transportation w = 3.0 m/s;
• for the design parameters described in sets (1), (9)
using the following expressions (Kapranova, 2018; Kapranova et al., 2020): ; ; ; ; ; ; ; ; ; ; α(0) = π/4 taking into account the value of the conditional diameter from (14) and the condition h = Dc − Dout with a checkerboard arrangement of the throttle holes of the cylindrical separator. Note that when determining the values , the right-hand sides of the corresponding expressions contain the integer parts of the indicated relations of quantities.
In block 5 (Figure 2), the critical value of the Reynolds number Recr is determined when, when the inequality
cavitation-free flow of liquid in the valve is observed at a conditional value of the Reynolds number Rey. In this case, the extremum condition is used
for the energy parameter E02(z) with the value of the phase variable z(u2) = 1, i.e., with full valve opening for a stochastic model of bubble formation at an early stage of hydrodynamic cavitation (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019). Here z is the phase variable corresponding to the number of the throttle bore of the separator . The parameter E02(z) is determined by the expression for the energy E02(ξ, η, z) of the cavitation bubble at the moment of its stochastization (when the trajectories of the formed bubbles acquire a random character), where ξ and, η are the conditional values of the diameter of the cavitacin bubble and the velocity of its center of mass. Condition (18) implies the approximation
which can be used as an algebraic equation for the value Recr from (Kapranova, 2018; Kapranova et al., 2020)
Condition (19) contains the error function erf(μ) with argument μ. In the expressions (19), (20) it is indicated: rm, vL are the characteristic values of the radius of the bubble and the velocity of the fluid, respectively; ψ10(z) = rm[τ11(1)+ς12(z)τ12(1)] according to Kapranova and Miadonye (2019); ς12(z) is the dependence of the hydraulic resistance coefficient on the phase variable z for the transition region of the fluid flow (10 < Re < 104), obtained in (Kapranova et al., 2018c)
In (21) it is indicated: ε(z) is the modified compression ratio of the jet from Kapranova et al. (2016a) with parameters U0 = 0.57; U1 = 0.043; U0 = 1.1 from Arzumanov (1971); the coefficients τ11(1), τ12(1), s0, s3, due to Kapranova et al. (2018c) depend on the design parameters of the valve and the characteristics of the liquid-gas-vapor system, in particular a1 = 2π(αgρg + αsρs)/3 Using expressions (14), (21) and the values described in block 4 (Figure 2) for the initial approximations of the design parameters for the set q01 from (19), the following expression of the relationship between the design parameters is accepted
The physical and mechanical characteristics of the working medium ρL, ρg, ρs from (25) correspond to the set from (6). Expression (27) corresponds to the initial approximation for the hydraulic resistance function ς12(z) on the phase variable z from (21) (Kapranova et al., 2018c), taking into account the dependence of the degree of valve opening z(u2) on parameter u2 with the equality of argument according to the accepted value in block 4.
Block 6 (Figure 2) sets the 1st approximation for the conditional diameter (m) using the empirical formula from (Arzumanov, 1971)
where the values of Q1max (m3/h) and ν1 (cm2/c) are determined by the set (5); Recr is the critical value of the Reynolds number from (20). The limits of change for the value of (m) from (28)
are established taking into account (12) for , in the form
where the value is calculated using (27). The expressions in (30) were obtained using the well-known empirical relationship between the coefficients of the transmission capacity of the regulating device and hydraulic resistance (Arzumanov, 1985; Blagov, 1990) at the value of the coefficient m0 = 5.04.
Service block 7 (Figure 2) compares the calculated critical value of the Reynolds number Recr from (20) with the characteristic value of this criterion for liquid flow in cavitation-free mode according to the recommendations from Arzumanov (1971) (if which is not met, go to block 11, Figure 2) . If this inequality is true, in block 8 (Figure 2), correction coefficients ψ1, ψ2 for the viscosity of the working medium are calculated similarly to the recommendations from Arzumanov (1971) for the limits of the valve throughput taking into account (12), (28), (20) for the values , Recr, as well as the values of initial approximations adopted in block 4 (Figure 2) for the design parameters , in the form
The expressions in (31) contain the value of the conditional section area (m2) depending on the degree of valve opening z according to the parameter values accepted in block 4 (Figure 2). Therefore, in block 9 (Figure 2), taking into account (12), (31), a new range of variation in the valve throughput can be determined .
The conditional block 10 (Figure 2) checks the condition that the required valve throughput belongs to a new range of values using the following inequality similar to (13). If the last inequality is true, the transition to the block 11 (Figure 2) is carried out, in case of its injustice—return to block 2 with a change in the values n1 and n2 of the safety factors and, accordingly, by 10–20%.
In block 11 (Figure 2), the values of the first approximations are estimated for the limits of variation of the following design parameters of the separator according to the inequalities: , using a system of equations including:
• the expression , which reflects the condition for linear profiling of the dependence σ(z) of the throughput characteristic of the control device on the degree of its opening according to the definition of σ[z(n2)] = Kvy[z(n2)]/Kvy[z(u2)], ;
• extremum condition for the hydraulic resistance coefficient ς12(z) from (21) with respect to the parameter when the valve is fully open when the condition z(u2) = 1 is satisfied, in the form
• two geometric relations between the sought parameters taking into account the checkerboard arrangement of the throttle holes on cylindrical surface of the separator
The solution of system (32), (33) is accompanied by the expansion of the first two equations from those listed in the Maclaurin series with respect to unknowns corresponding to the parameter values u2, d0 to terms of order , then the values take
where correspond to the formula (24); parameters –to the expressions adopted in block 4 (Figure 2), taking into account –the limits of change of the value (m) from (29). Note that the right-hand side of (34) contains an integer value from the corresponding relation.
In the next block 12 (Figure 2), the calculation is carried out of the required parameters d0, u2, L, l0 as averaged values from the obtained boundary expressions (34)–(36):
Note that in (37) for only the integer value of the obtained right-hand side is also taken.
Block 13 (Figure 2) is designed to estimate the value of the first approximation of the parameter using the formula , where the inner diameter of the separator according to (35) and the accepted approximations in blocks 4, 6 (Figure 2) is determined by the limits of change for the value , then .
Block 14 (Figure 2) includes the calculation of the second approximation for the inner diameter of the separator using the corollary from the extremum condition (18) for the energy parameter E02(z) from the stochastic model of bubble formation at an early stage of hydrodynamic cavitation (Kapranova et al., 2016b, 2018a) in the form
Given the form of the function ψ10(z) described in block 5 (Figure 2), for the desired parameter value, condition (38) yields the value of the desired structural parameter
where according to the expressions adopted in blocks 4, 5, 12 (Figure 2) for as well as the expressions (33), (36), (37) for are indicated: , , , , , ,, ,
In block 15 (Figure 2), to determine the first approximation of the bevel angle for the cylindrical part of the shell α(1), we also apply the corollary from the extremum condition (18) for E02(z) from the stochastic model of bubble formation at an early stage of hydrodynamic cavitation (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019) in form
Therefore, according to (42), the value of the desired structural parameter is determined by the expression , where they are calculated according to the expressions adopted in blocks 12, 14 (Figure 2), taking into account the notation
To calculate the values in (43)–(45), the formulas are used, which are contained in blocks 4, 5 (Figure 2), as well as expressions (27), (40), (41). In conclusion, we determine the first approximation of the following parameters:
In block 16 (Figure 3), the value for the hydraulic resistance coefficient is calculated according to (21) and the formulas from (Kapranova et al., 2018c)
where the compression ratio of the jet, in contrast to (26), is equal to
and the constants correspond to the expressions from block 14 (Figure 2).
In block 17 (Figure 3) calculates the critical value for the coefficient of hydraulic resistance from the condition of achieving the minimum value for the ensemble average diameter of the cavitation bubble Dcb according to Kapranova et al. (2017, 2018a,c); Kapranova A. B. et al. (2019), which corresponds to the following condition
In condition (48), the coefficients E01, C4, τ11(1) from the stochastic model (Kapranova et al., 2016a), which describes the process of formation of a bubble system at the initial stage of hydrodynamic cavitation in a control device, depend on the physical and mechanical properties of the working medium (including the density of the liquid, gas and vapor, and kinematic viscosity fluid at a given value of its temperature, surface tension coefficient, volumetric weight of the medium, adiabatic index) and the desired value , then where indicated: , , , , , , m0≡5.04, .
In conditional block 18 (Figure 3), a possible manifestation of a cavitation effect in the flow part of the valve is checked. Fulfillment of the following condition leads to a graphical estimation of the cavitation coefficient kC in block 19 (Figure 3) from empirical reference data (Arzumanov, 1971) for the critical value of the coefficient of hydraulic resistance obtained in block 17 (Figure 3). Otherwise, when the inequality holds, it returns to block 4 (Figure 2), associated with setting the critical value of the Reynolds number Recr and changing the value of in (14).
In the next block 20 (Figure 3), the calculation is performed:
• critical (maximum permissible) pressure drop during the regime of fluid movement with a critical value of kCmax for the cavitation coefficient kC, where p1 (kgf/cm2) is the absolute fluid pressure to the control valve at its maximum flow rate; pH1 (kgf/cm2) is absolute pressure of saturated steam at temperature t1 (°C);
• valve capacity in cavitation operation according to the well-known formula (Arzumanov, 1971, 1985) with a safety factor of η12;
Conditional block 21 (Figure 3) checks one of two inequalities:
• for differential pressure ;
• for valve capacity Kvmax and the required value when .
If these inequalities are true, the calculation can be completed with the transition to blocks 24 and 25 (Figure 3) to select and display the desired parameters of the separator. Otherwise, it is required to select a value in the subsequent block 22 (Figure 3) in order to n3 fulfill the condition for the conditional throughput from block 23 (Figure 3) according to the inequality , where n3 is the safety factor within at least 10–20% of maximum value, i.e., in the range (1.1–1.2) units, and then return to block 2 (Figure 2).
Thus, in block 25 (Figure 3), the desired structural parameters of the designed axial valve separator are output in the form of the set according to the set , from (1) when choosing the desired parameters, performed in block 24 (Figure 3)
Moreover, in the set (49) the following approximations are used: then
for the diameter of the radial throttle holes; the diameter of the round throttle holes d0, the arc distance between the holes in the same row Sφ, the distance between the rows of these holes l0, the thickness of the separator h, the number of holes for one row u1, the number of these rows u2, respectively, the inner and outer diameters separator Dout and Dc, the length of its perforator of the left part L, the bevel angle for the cylindrical part of the shell α, the inner diameter for the cylindrical part of the outer casing Dcas2, the outer diameter of the inner valve body Dch2, the wall thickness of the inner and outer casing δ2.
From a practical point of view, of particular interest is the analysis of the influence of the desired set of design parameters from rational ranges of their change for the “separator-external locking shell” unit on the size of cavitation bubbles, as a reflection of the result of an engineering calculation on the nature of the course of the initial stage of hydrodynamic cavitation in the flow part of the designed control device.
The described engineering methodology from sections Selection of the Main Parameters of the Liquid Throttling Process in an Axial Valve With an External Locking Shell, Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell was tested in Kapranova et al. (2020) using the example of the calculation of the “separator-external locking shell” assembly of an axial valve with a regulated value of the valve throughput m3/h when choosing water as the working medium and the following parameters of the throttling process: Q1max = 0.5 m3/h; Δpmin = 0.90 kPa; kg/m3; t1 = 30°C; cm2/s; σ = 7.28 ×10−4 H/m; w = 0.43 m/s; m; κΠa; Pa; ρg = 1.205 kg/m3; kg/m3 and adiabatic index k = 1.3. According to the calculation example performed in Kapranova et al. (2020) based on the engineering method (Kapranova et al., 2019b) described in this paper, with m3/h; Recr = 5209, 58; obtained rational ranges of changes of the desired parameters, in particular, the average value of d0 from the specified range is m with a separator outlet diameter of m and the length of its perforated part m with the number of rows of throttle holes for pieces in each and the distance between these rows m. Moreover, additional design parameters of the separator-external locking shell assembly correspond to the following effective values: separator thickness h(1) = 2.11 ×10−3 m; its outer diameter m; inner diameter for the cylindrical part of the outer casing m; the outer diameter of the inner valve body m; wall thickness of the inner and outer shell m; bevel angle for the cylindrical part of the shell α(1) = 44, 840. The indicated values for the set of sought-for structural parameters from expressions (49) and (50) allow, by analogy with the approach from Kapranova A. B. et al. (2019), based on (Kapranova et al., 2017, 2018a) to analyze the dependence Dcb = Dcb(Dy, Kvy) between the ensemble average value of the diameter Dcb for the macro-system of cavitation bubbles, the conditional diameter Dy and the corresponding throughput of the Kvy valve for its opening degree z (Figures 4A,B).
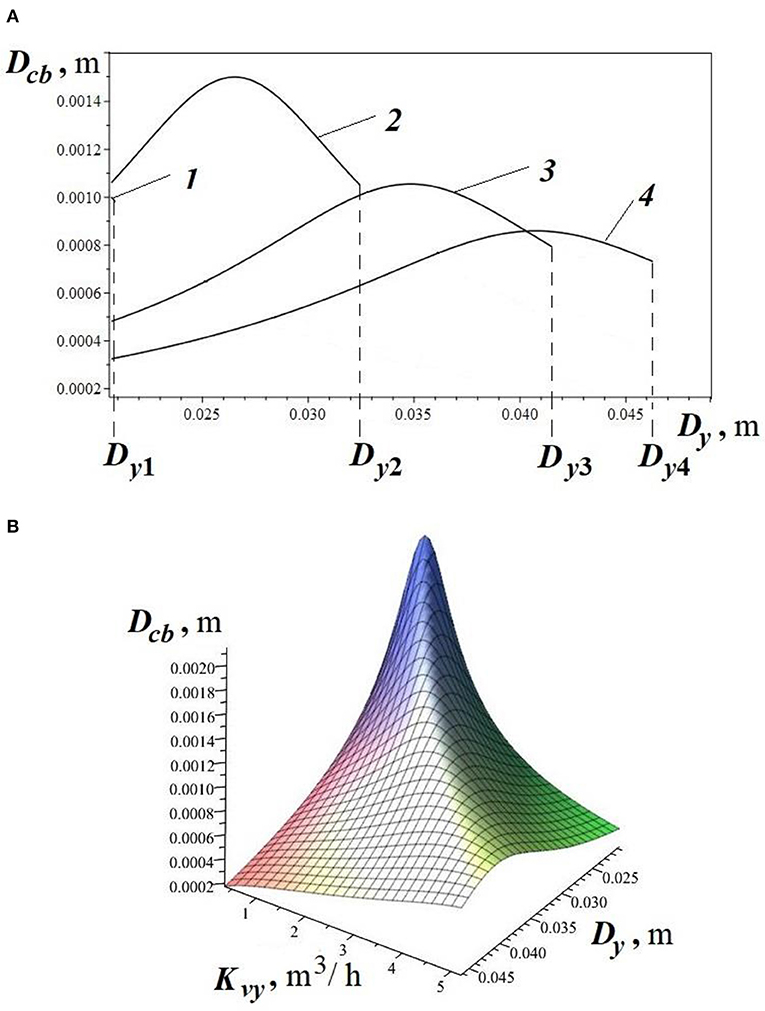
Figure 4. The influence of the main indicators of the process of throttling the working medium in the node “separator-external locking shell” on the value of the ensemble average diameter of the cavitation bubble by the example of the dependencies: (A) Dcb(Dy); 1 – z = 0.2; m; m3/h; 2 – z = 0.5; m; Kvy2 = 2.200 m3/h; 3 – z = 0.8; m; Kvy3 = 3.799 m3/h; 4 – z = 1.0; m; Kvy4 = 5, 205 m3/h; (B) Dcb(Dy, Kvy).
The values of for the ensemble-average diameter of cavitation bubbles for various indicators of the degree of opening of the separator z = {0.2;0.5;0.8;1.0} are determined by the position of the end points of the lines for graphs 1–4 according to Figure 4A. Additionally, as a more comprehensive three-dimensional illustration, the dependence Dcb(Dy, Kvy) in Figure 4B is presented. An analysis of the results showed that the transition from mode 1 of the separator with a degree of opening of 20% to mode 3 with 80% opening of the throttle openings is accompanied by an increase in the conditional throughput of the Kvy valve by 10.7 times (as the ratio Kvy3/Kvy1), and in the case of the transition from mode 3 to full opening (mode 4), the ratio Kvy4/Kvy3 = 1, 4. For comparison, we note that the case considered in Kapranova A. B. et al. (2019) for other values of the design parameters of the separator-external locking shell assembly that are not related to the rational ranges of their changes leads to the following relations Kvy3/Kvy1 = 2.1 and Kvy4/Kvy3 = 1.4. In addition, according to Figure 4A, a decrease in the size of the resulting bubbles is noted in Dcb1/Dcb4 = 1.35 times from the range of the ensemble average diameter of the cavitation bubble m against the case from Kapranova A. B. et al. (2019), when Dcb1/Dcb4 = 1.12 from the range m. Moreover, a comparison of the results presented in Figure 4A and in Kapranova A. B. et al. (2019) showed that there is a tendency to decrease the Dcb value by 1.95 times when taking into account the rational ranges of changes in the desired design parameters obtained in this article.
The proposed block diagram consists of 25 main blocks for calculating 13 effective values of the design parameters of an axial valve separator. For example, the required parameters include: diameter of round throttle holes d0, arc distance between the holes in one row, distance between rows of these holes, separator thickness, number of holes for one row, number of these rows, diameter of the outlet of the separator, its perforated part length, bevel angle for the cylindrical part of the shell, etc. Specified operating parameters are the maximum attainable fluid flow through the regulating device at a given value of the medium temperature, the minimum pressure drop, the maximum pressure in the center of the bubble, which corresponds to the minimum value of its radius, the saturated vapor pressure of the medium, the velocity of the fluid in the pipeline. The input parameters for the calculation are the maximum attainable flow rate of the medium, the temperature of the medium, the limits of variation of the minimum pressure drop and the velocity of the fluid in the pipeline. The output parameter is the required valve capacity . The block diagram (Figures 2, 3) proposes a phased calculation of various approximations of the desired design parameters depending on the selected intervals for changing the maximum value of the valve capacity. The indicated intervals are refined three times when taking into account the required value of throughput with the choice of safety factors. The first time this is done at specified intervals for changing the minimum pressure drop, the second after calculating Recr based on (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019) to determine the correction factors for the viscosity of the medium, the third after evaluating the hydraulic resistance coefficient (Kapranova et al., 2018c) from the minimum condition values of Dcb (Kapranova et al., 2017, 2018a, 2019a). Note that the calculation of the conditional flow area for the control valve separator depends on the configuration of the throttle holes, which significantly affects the application of the expressions proposed in the method according to the models (Kapranova et al., 2018a,b,c; Kapranova and Miadonye, 2019). For example, this is reflected when using expressions (20)–(28) in blocks 5, 6 (Figure 2) for the critical value of the Reynolds number Recr, when choosing the first approximation for the conditional diameter , and therefore, when calculating the value of the hydraulic resistance coefficient, including the critical (blocks 17 and 18, Figure 3), etc. An analysis of the obtained critical value of the Reynolds number in comparison with the characteristic value from Kapranova et al. (2020) allows us to assess the need for additional consideration of the viscosity of the working medium using correction factors and to clarify the limits of change of the device throughput coefficient when setting the next approximation of the valve design parameters to ensure its effective operation according to the regulatory value . The work of the proposed engineering calculation method (sections Selection of the Main Parameters of the Liquid Throttling Process in an Axial Valve With an External Locking Shell, Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell) is illustrated by the example of comparative analysis (section The Influence of a Set of Design Parameters From the Rational Ranges of Their Change for the Node “Separator-Locking Shell” on the Size of Cavitation Bubbles) for the ensemble average diameter of the cavitation bubbles formed in the “separator-external locking shell” assembly with the external arrangement of the latter in the design of the control valve, depending on taking into account the values of design parameters from rational and irrational ranges of their change.
Thus, summarizing the results of this study leads to the following main conclusions and results:
• In the presented engineering method for calculating the main structural parameters (sections Selection of the Main Parameters of the Liquid Throttling Process in an Axial Valve With an External Locking Shell, Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell) for the direct-flow type apparatus (Lebedev et al., 2018), the following facts received their practical application:
(1) Analysis of the design features of direct-flow type control valves (Lebedev et al., 2016, 2017a,b), methods for modeling the cavitation phenomenon (Kapranova et al., 2016c) and calculation of the main indicators of this process (Kapranova et al., 2016d,e);
(2) Stochastic models (Kapranova et al., 2016a,b, 2017, 2018a,b; Kapranova, 2018; Kapranova A. B. et al., 2019; Kapranova and Miadonye, 2019) for the process of bubble formation in the initial stage of hydrodynamic cavitation, the results of which are in satisfactory agreement (Kapranova and Miadonye, 2019) with the experimental data (Lebedev et al., 2017a,b) and justify the possibility of reducing the cavitation intensity in the node “separator-external locking shell.”
• The proposed engineering methodology for calculating the main structural parameters of the node “separator-external locking shell” uses two approaches:
(1) Application of the Pi-Buckingham theorem (Buckingham, 1915; Misic et al., 2010) in solving the problem of scaling and lowering the number of constant parameters describing the process under study, within the framework of the well-known classical algorithm for choosing the type of control device (Arzumanov, 1971, 1985) based on the experimental relationships between the main process indicators (blocks 2 and 6, expressions (12) and (30), section Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell), as well as an empirical analysis of the conditions for attaining critical values of hydrodynamic similarity criteria: a) the Reynolds number (block 6, expression (28), section Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell); b) the cavitation coefficient as a doubled Euler number (Knapp et al., 1970; Franc and Michel, 2005; Xu et al., 2015; Kapranova et al., 2016e) (blocks 18 and 20, section Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell);
(2) Using for calculating the set of sought-for structural parameters functional dependencies obtained from models (Kapranova et al., 2016a,b, 2017, 2018a,b; Kapranova, 2018; Kapranova and Miadonye, 2019) and reflecting the conditions for the minimum size of the cavitation bubbles formed (block 17, expression (48), section Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell), hydraulic resistance (blocks 11 and 16, expressions (32) and (46), section Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell), energy parameters of the cavitation bubble system (blocks 14 and 15, expressions (38) and (42), section Description of the Work Flowchart of the Engineering Methodology for Calculating the Parameters of These System of the Separator-External Locking Shell), etc.
• When assessing the impact of the design parameters of the separator-external locking shell assembly on the nature of cavitation bubble formation, a comparative analysis (section The Influence of a Set of Design Parameters From the Rational Ranges of Their Change for the Node “Separator-Locking Shell” on the Size of Cavitation Bubbles) of the application of parameters from rational (Kapranova et al., 2020 according to the present methodology) and irrational (Kapranova A. B. et al., 2019) ranges of their change which showed that when using the results of Kapranova et al. (2020), there is a tendency to reduce the value between the ensemble average diameter value Dcb by 1.95 times, while the transition from a mode from 20% for the degree of the opening of the separator to 80% for the opening of it's throttle openings and the last operation is accompanied by an increase in the value of the conditional throughput of the Kvy valve by 10.7 times.
Let us briefly dwell on the main directions of further improvement of the proposed engineering methodology for calculating the parameters of the separator-external locking shell unit, as an object of research of various nature (hydrodynamic, vibro-acoustic, managerial, etc.) that go beyond the scope of the tasks posed in this work. As already noted in section Methods, the relative error of theoretical calculations (Kapranova, 2018; Kapranova et al., 2018b; Kapranova and Miadonye, 2019) in comparison with experimental data (Lebedev et al., 2017a,b) in estimating the distribution of bubbles by the degree of opening of the axial valve with an external locking shell did not exceed 13% according to Kapranova and Miadonye (2019). This fact is reflected in the results of applying the engineering methodology described in section Results and Discussion, due to the use of the results of stochastic models (Kapranova, 2018; Kapranova et al., 2018b; Kapranova A. B. et al., 2019; Kapranova and Miadonye, 2019) for the process of bubble formation in the initial stage of hydrodynamic cavitation. However, these models do not take into account the consequences of the evolution of the cavitation phenomenon in the flow part of the valve, for example, the possible process of combining bubbles, the growth of their diameters and subsequent collapse. The emphasis in the proposed models and the corresponding engineering methodology for calculating the design parameters of the designed unit “separator-external locking shell” is made on the possibility of preventing an increase in the intensity of formation of cavities in the flow part of the regulating device already at the initial stage of the occurrence of cavitation. In addition, there are a number of difficulties that a designer may encounter in practice when implementing the described methodology. Additionally, it should be investigated: the conditions for reducing noise effects during the implementation of high-speed flow regimes of the working medium, and, therefore, vibro-acoustic characteristics; force factors in the movable elements of the device in order to calculate the hydrodynamic balance of the control valve; quality issues of the process of managing the static and dynamic characteristics of this unit, etc.
An analytical method has been developed for calculating the effective ranges of the structural parameters of the locking-regulating system “perforated separator—external locking cylinder-conical shell” based on the proposed stochastic models of bubble formation at the initial stage of hydrodynamic cavitation. In particular, in addition to the gyrodynamic similarity criteria, the following were used: differential distribution functions of the bubble distribution density at the initial stage of hydrodynamic cavitation in two phase variables—the conditional diameter of the cavitation bubble (Kapranova et al., 2018a) and the degree of valve opening (Kapranova and Miadonye, 2019). In addition, the proposed block diagram of the calculation of the node “separator-external locking shell” uses estimated analytical expressions: for the value of the coefficient of hydraulic resistance (Kapranova et al., 2018c); for the average ensemble diameter of the cavitation bubble from the indicated works (Kapranova et al., 2016c); for the critical value of the Reynolds criterion depending on the desired design parameters (Kapranova, 2018).
When studying the influence of a set of design parameters for the “separator-external locking shell” assembly from certain rational ranges of their change, a tendency is found to reduce the ensemble average value of the diameter of the cavitation bubble by almost 2 times compared with the values of the parameters from irrational limits. It is shown that for these comparative cases, a change in the degree of opening of the throttle holes of the separator from 20 to 80% is able to change the valve throughput by more than 10 times.
The proposed methodology for the engineering calculation of the design parameters of an axial valve with an external location of the locking body is of interest to designers of control valves in the chemical and oil refining industries, and can be expanded when designing axial valves of other structures on a theoretical basis using a stochastic approach (Kapranova et al., 2019a).
All datasets generated for this study are included in the article/supplementary material.
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
This work was supported by JSC Regulator (Yaroslavl, Russia). The funder was not involved in the study design, collection, analysis, and interpretation of data, the writing of the article or the decision to submit for publication.
SN, AM, and DV were employed by the company JSC Regulator (Yaroslavl, Russia).
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Ansys Inc (2013). ANSYS Fluent UDF Manual. Available online at: http://www.pmt.usp.br/academic/martoran/NotasModelosGrad/ANSYS%20Fluent%20UDF%20Manual.pdf (accessed February 13, 2020).
Ansys Inc (2017). ANSYS Fluent User's Guide. Available online at: https://archive.org/details/ANSYSFluentUsersGuide/mode/2up (accessed February 13, 2020).
Arzumanov, E. S. (1971). Calculation and Selection of the Regulatory Bodies of Automatic Systems. Moscow: Energy.
Arzumanov, E. S. (1985). Hydraulic Regulatory Bodies of Automated Control Systems. [Gidravlicheskiye reguliruyushchiye organy sistem avtomatizirovannogo upravleniya]. Moscow: Engineering [Mashinostroyeniye].
Baron Rayleigh, J. W. S. (1911–1919). Scientific Papers, Vol. 6: 1911–1919. Cambridge: Cambridge University Press, 1899–1920.
Bian, J., Cao, X., Teng, L., Sun, Yu., and Gao, S. (2019a). Effects of inlet parameters on the supersonic condensation and swirling characteristics of binary natural gas mixture. Energy 188:116082. doi: 10.1016/j.energy.2019.116082
Bian, J., Cao, X., Yang, W., Song, X., Xiang, C., and Gao, S. (2019b). Condensation characteristics of natural gas in the supersonic liquefaction process. Energy 168, 99–110. doi: 10.1016/j.energy.2018.11.102
Blagov, E. E. (1990). Throttle and Control Valves of Thermal Power Plants and Nuclear Power Plants. [Drossel'no-reguliruyushchaya armatura TES i AES]. Moscow: Energoatomizdat. [Energoatomizdat].
Canjuga, S. (2019). Axial Valve of the Modular Concept of Construction. Patent WO2019220153A2, F16K 37/00, F16K 27/02. Zagreb: World Intellectual Property Organization (WIPO).
Cao, X., and Bian, J. (2019). Supersonic separation technology for natural gas processing: a review. Chem. Eng. Process. 136, 138–151. doi: 10.1016/j.cep.2019.01.007
Chahine, G. L. (1994). Strong Interactions Bubble/Bubble and Bubble/Flow. Dordrecht: Kluwer Academic Publishers; Springer. 195–206. doi: 10.1007/978-94-011-0938-3_18
Ellas, E., and Chambre, P. L. (2000). Bubble transport in flashing flow. Int J. Multiphase Flow 26, 191–206. doi: 10.1016/S0301-9322(99)00011-7
Emerson, F. (2020). Available online at: https://www.emerson.com/en-us/automation/fisher (accessed January 26, 2020).
Esveldt, V. (2012). Throttle Valve. Patent US8297315B2. F16K 47/08. Werkendam: United States Patent and Trademark Office (USPTO).
Flowserve (2020). Linear Control Valves. Available online at: https://www.flowserve.com/en/products/valves/linear-control-valves (accessed January 26, 2020).
Franc, J.-P., and Michel, J.-M. (2005). “Fluid mechanics and its applications,” in Fundamentals of Cavitation, Vol. 76 (Springer Science + Business Media), 306. doi: 10.1007/1-4020-2233-6
Frenkel, J. (1946). Kinetic Theory of Liquids. International Series of Monographs on Physics. London: Oxford University Press.
Hou, C.-W., Qian, J., Chen, F., Jiang, W., and Jin, Z. (2017). Parametric analysis on throttling components of multi-stage high pressure reducing valve. Appl. Thermal Eng. 128, 1238–1248. doi: 10.1016/j.applthermaleng.2017.09.081
Hsu, Y. Y. (1962). On the size range of active nucleation cavities on a heating surface. J. Heat Transf. 94, 207–212. doi: 10.1115/1.3684339
Kapranova, A. (2018). On the influence of the degree of opening of the regulator valve separator on the process of formation of cavitation bubbles. J. Chem. Eng. Process Technol. 9:36. doi: 10.4172/2157-7048-C3-016
Kapranova, A., Lebedev, A., and Meltser, A. (2017). The definition of the integral characteristics of the process of formation of cavitation bubbles when operating the control valve. J. Chem. Eng. Process Technol. 8:58. doi: 10.4172/2157-7048-C1-009
Kapranova, A., Lebedev, A., Meltser, A., and Neklyudov, S. (2018a). Determination of the average parameters of cavitation bubbles in the flowing part of the control valves. Int. J. Mech. Eng. Technol. 9, 25–31.
Kapranova, A., and Miadonye, A. (2019). Stochastic simulation of cavitation bubbles formation in the axial valve separator influenced by degree of opening. J Oil Gas Petrochem. Sci. 2, 70–75. doi: 10.30881/jogps.00026
Kapranova, A., Miadonye, A., Lebedev, A. E., and Meltser, A. M. (2019a). “Formation of a general approach to stochastic modeling of the initial stage of hydrodynamic cavitation in a control valve,” in Proceedings of the International Conference on Innovative Applied Energy–IAPE'19 (Oxford), 38. Available online at: http://www.iape-conference.org/Downloads~/Proceedings/Proceedings%20of%20IAPE'19.pdf
Kapranova, A., Neklyudov, S., Lebedev, A., and Meltser, A. (2018b). Investigation of the energy of the stochastic motion of cavitation bubbles in the separator of the axial valve, depending on the degree of its opening. Int. J. Mech. Eng. Technol. 9, 160–166.
Kapranova, A., Neklyudov, S., Lebedev, A., and Meltser, A. (2018c). Qualitative evaluation of the coefficient of hydraulic resistance in the area of the divider of the fluid flow of the axial valve. Int. J. Mech. Eng. Technol. 9, 153–159.
Kapranova, A., Neklyudov, S., Lebedev, A., Meltser, A., and Voronin, D. (2019b). “Engineering method for calculating of an axial valve separator with an external location of the locking part,” in Bridging Science With Technology: 12th European Congress of Chemical Engineering/5th European Congress of Applied Biotechnology–ECCE12/ECAB5 (Florence), 660–663.
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., and Neklyudov, S. V. (2016a). Stochastic model of process of formation of cavitation bubbles in the flow path of control valve. Vestn. IGEY Her IGEY. 4, 24–29. doi: 10.17588/2072-2672.2016.4.024-029
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., and Neklyudov, S. V. (2019). The ensemble-averaged characteristics of the bubble system during cavitation in the separator. E3s Web Conf. 140:06005. doi: 10.1051/e3sconf/201914006005
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., and Neklyudov, S. V. (2020). “About formation of elements of a cyber-physical system for efficient throttling of fluid in an axial valve,” in Cyber-Physical Systems: Advances in Design & Modelling. Studies in Systems, Decision and Control, Vol. 259, eds A. Kravets, A. Bolshakov, and M. Shcherbakov (Cham: Springer), 109–119. doi: 10.1007/978-3-030-32579-4_9
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., and Solopov, S. A. (2016b). The application process of the Ornstein-Ulenbek to the formation of cavitation bubbles. Czas. Tech. Mech. 113, 136–144. doi: 10.4467/2353737XCT.16.101.5500
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., Solopov, S. A., and Neklyudov, S. V. (2016d). About methods for calculating hydraulic resistance regulatory authorities during transportation single component media. Fundam. Res. 4, 52–60.
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., Solopov, S. A., and Serov, E. M. (2016c). Methods of modeling the developmental stages of hydrodynamic cavitation. Fundam. Res. 3, 268–273.
Kapranova, A. B., Lebedev, A. E., Meltser, A. M., Solopov, S. A., and Serov, E. M. (2016e). On the way to assess critical parameters cavitation in transport regulators in the working environment. Fundam. Res. 3, 488–494.
Klimontovich, Y. L. (2014). Turbulent Motion and Chaos Structure: A New Approach to the Statistical Theory of Open Systems. Moscow: LENAND.
Koch, S., Garen, W., Hegedus, F., Neu, W., Reuter, R., and Teubner, U. (2012). Time-resolved measurements of shock induced cavitation bubbles in liquids. Appl. Phys. 108, 345–351. doi: 10.1007/s00340-012-5070-1
Kwak, H.-Y., and Kim, Y. W. (1998). Homogeneous nucleation and macroscopic growth of gas bubble in organic solutions. Int. J. Heat Mass Transf. 41, 757–767. doi: 10.1016/S0017-9310(97)00182-8
Lebedev, A. E., Kapranova, A. B., Meltser, A. M., Neklyudov, S. V., Serov, E. M., and Voronin, D. V. (2017a). Design Features of the New Control Valves Direct-Flow Type. Rostov-on-Don: Engineering Herald of Don (Inzhenernyy vestnik Dona). Available online at: http://www.ivdon.ru/uploads/article/pdf/IVD_31_lebedevN.pdf_64daa310a4.pdf (accessed February 28, 2020).
Lebedev, A. E., Kapranova, A. B., Meltser, A. M., Neklyudov, S. V., Serov, E. M., and Voronin, D. V. (2017b). Development of the design of a direct-flow control valve with an upper position of the locking organ. Mod. High Tech. 9, 48–52.
Lebedev, A. E., Kapranova, A. B., Meltser, A. M., Solopov, S. A., and Neklyudov, S. V. (2016). Analysis of devices for reducing pressure in control valves. Mod. High Techn. 8, 68–71.
Lebedev, A. E., Kapranova, A. B., Meltser, A. M., Solopov, S. A., Voronin, D. V., and Neklyudov, S. V. (2018). Direct-Acting Control Valve. Patent on the model 175446 Russian Federation, IPC F16K 1/12, F16K 47/14, F16K 3/24. Yaroslavl: Federal Service for Intellectual Property (Rospatent).
Lienhard, J. H., and Karimi, A. (1981). Homogeneous nucleation and the spinodal line. J. Heat Transf. 103, 61–64. doi: 10.1115/1.3244431
Misic, T., Najdanovic-Lukic, M., and Nesic, L. (2010). Dimensional analysis in physics and the Buckingham theorem. Eur. J. Phys. 31, 893–906. doi: 10.1088/0143-0807/31/4/019
Mokveld (2020). Axial Flow Valves. Available online at: https://mokveld.com/en/home (accessed January 26, 2020).
Peterman, C. P., and Keithahn, J. D. (1987). Flow Control Apparatus. Patent US 4635678. F16K 3/00, F16K 31/528, F16K 31/52, F16K 3/26, F16K 001/36; F16K 031/528. Houston, TX: United States Patent and Trademark Office (USPTO).
Plesset, M. S., and Chapman, R. B. (1971). Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 47, 283–290. doi: 10.1017/S0022112071001058
Preston, T. J. (2018). Valve. KR20180055897A, F16K 3/26, F16K 3/26, F16K 3/314. Staffordshire: Korea Intellectual Property Office (KR).
Qian, J., Liu, B., Jin, Z., Zhang, H., and Lu, A. (2016). Numerical analysis of flow and cavitation characteristics in a pilot-control globe valve with different valve core displacements. J. Zhejiang Univ. Sci. A 17, 54–64. doi: 10.1631/jzus.A1500228
Qiu, C., Jiang, C.-H., Zhang, H., Wu, J.-Y., and Jin, Z. (2019). Pressure drop and cavitation analysis on sleeve regulating valve. Processes 7:829. doi: 10.3390/pr7110829
Qu, W., Tan, L., Cao, S., Xu, Y., Huang, J., and Xu, Q. (2015). Experiment and numerical simulation of cavitation performance on a pressure-regulating valve with different openings. IOP Conf. Ser. Mater. Sci. Eng. 4:72. doi: 10.1088/1757-899X/72/4/042035
Rudolf, P., Kubina, D., Kozák, J., Hudec, M., and Pochylý, F. (2017). Dynamics of the cavitating flow downstream of the orifice plate. AIP Conf. Proc. 1:1889. doi: 10.1063/1.5004367
Rust (2020). Axial Valves. Available online at: http://www.roost.ru/katalog/klapany/osevie_klapan/ (accessed January 26, 2020).
Seung, S., and Kwak, HY. (2017). Shock wave propagation in bubbly liquids at small gas volume fractions. J. Mech. Sci. Technol. 31, 1223–1231. doi: 10.1007/s12206-017-0221-2
Shin, T. S., and Jones, O. C. (1993). Nucleation and flashing in nozzles-1. A distributed nucleation model. Int. J. Multiphase Flow 19, 943–964. doi: 10.1016/0301-9322(93)90071-2
Sokolichin, A., Eigenberger, G., Lapin, A., and Lubbert, A. (1997). Dynamic numerical simulation of gas-liquid two-phase flows: Euler/Eler versus Euler/Lagrange. Chem. Eng. Sci. 52, 611–626. doi: 10.1016/S0009-2509(96)00425-3
Talis, E. (2020). Available at: https://www.talis-group.com/brands/erhard.html (accessed January 26, 2020).
Tang, T. F., Gao, L., Li, B., Liao, L., Xi, Y., and Yang, G. (2019). Cavitation optimization of a throttle orifice plate based on three-dimensional genetic algorithm and topology optimization. Struct. Multidiscipl. Optimiz. 60, 1227–1244. doi: 10.1007/s00158-019-02249-z
Volmer, V., and Weber, A. (1926). Keimbildung in uebersaetigen Daempfen. Z. Phys. Chem. 119, 277–301. doi: 10.1515/zpch-1926-11927
Weevers, H. H. (1982). Control Valve. Patent US4327757. F16K 47/14. Gouda: United States Patent and Trademark Office (USPTO).
Keywords: valve, separator, hydrodynamic cavitation, engineering method, parameter, stochastic model
Citation: Kapranova A, Neklyudov S, Lebedev A, Meltser A and Voronin D (2020) Engineering Method for Calculating of an Axial Valve Separator With an External Location of the Locking Part. Front. Energy Res. 8:32. doi: 10.3389/fenrg.2020.00032
Received: 05 December 2019; Accepted: 19 February 2020;
Published: 06 March 2020.
Edited by:
Theodoros Damartzis, Federal Institute of Technology in Lausanne, SwitzerlandReviewed by:
Hadi Taghavifar, Malayer University, IranCopyright © 2020 Kapranova, Neklyudov, Lebedev, Meltser and Voronin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anna Kapranova, a2FwcmFub3ZhX2FubmFAbWFpbC5ydQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.