- Clean Energy Processes (CEP) Laboratory, Department of Chemical Engineering, Imperial College London, London, United Kingdom
The suitability of organic Rankine cycle (ORC) technology for the conversion of low- and medium-grade heat sources to useful power has established this as a promising option in geothermal power-generation applications. Despite extensive research in this field, most of which has focused on parametric analyses and thermodynamic performance evaluations, there is still a lack of understanding concerning the comparative performance of different plant configurations from both thermodynamic and economic perspectives. This study seeks to investigate the thermo-economic performance of subcritical and transcritical geothermal ORC power-plants, while considering a range of working fluids and the use of superheating and/or recuperation. A specific case study based on the exploitation of a medium-temperature geothermal heat source (180 °C, 40 kg/s) is conducted. Multi-objective optimization is performed to maximize the power/exergy efficiency (i.e., resource use) and to minimize the payback period. Different optimized configurations are compared and the influence on system performance of superheating, recuperation, and subcritical vs. transcritical operation are evaluated. The results reveal that superheating is preferable for working fluids with low critical temperatures, but hinders the performance of fluids whose critical temperature is higher. Recuperation is not attractive under most operating conditions, since the thermodynamic performance improvement and cooling water saving cannot compensate the cost associated with the installation of the additional heat exchanger. Finally, transcritical ORC systems are favored thanks to the better thermal match between the heat source and the working fluid in these configurations. A more generalized geothermal heat source is then considered to explore the optimal configuration over a range of heat sources, which indicates that non-recuperated transcritical-cycle systems with working fluids whose critical temperature is close to the heat-source temperature are generally favorable.
Introduction
Accelerated fossil fuel consumption and consequent environmental concerns have led to increasing importance of exploitation of renewable energy sources, such as solar, wind, and geothermal energy. One of the main advantages of geothermal energy in comparison to other renewables is the reliability for continuous base-load power production. The total installed capacity of geothermal plants reaches 14,100 MW worldwide and it is forecasted to be up to 21,400 MW by 2020 (Moya et al., 2018; EXERGY, 2019). In general, the high-temperature geothermal resources (>220 °C) are the most suitable for commercial electricity production via dry steam and flash steam systems (Liu et al., 2016). However, the largest availability of geothermal reservoirs is between 100 to 220 °C, known as medium-temperature geothermal resources (Hettiarachchi et al., 2007). Binary plants are currently considered as appropriate solutions to the geothermal energy utilization within this temperature range, including Kalina cycle and organic Rankine cycle (ORC) (Anderson and Rezaie, 2019).
The ORC has been proven to be an effective heat-to-power conversion technology (Markides, 2015; White and Sayma, 2019) and it is acknowledged as a promising option to extract useful energy in a wide range of applications such as solar (Freeman et al., 2017; Ramos et al., 2018), biomass (Drescher and Brüggemann, 2007; Pantaleo et al., 2018), waste heat recovery (Song et al., 2015; Castelli et al., 2019) and also geothermal (Rodríguez et al., 2012; Shokati et al., 2015). ORC systems offer an attractive option for geothermal energy exploitation and extensive research in this field is available, including working fluid selection, component design, cycle optimization, and economic evaluation. Zhai et al. (2014) studied the influence of working fluid properties on the performance of geothermal ORC systems. The results indicated that the optimized evaporation temperatures were almost the same for the selected working fluids and those with double bonds or cyclic structure delivered higher thermal efficiencies. By using zeotropic working fluids in geothermal ORC system, Heberle et al. (2012) found that the thermal efficiency was increased by up to 15% compared to pure fluids, and other authors have confirmed such gains while also highlighting cost increases (Oyewunmi and Markides, 2016). Imran et al. (2015) conducted multi-objective optimization of the evaporator in a geothermal ORC system and the Pareto front solutions were obtained to indicate the trade-off between pressure drop and cost. Sauret and Rowlands (2011) presented the rationale for using radial-inflow turbines in geothermal ORC systems. The preliminary designs showed similar efficiencies of 77% but significant differences in dimensions of rotor diameter (139–289 mm). Walraven et al. (2015) compared the performances of ORC systems with different cooling technologies for low-temperature geothermal applications and found that the mechanical-draft wet cooling towers showed better economics. Astolfi et al. (2014a,b) carried out both thermodynamic and economic assessment of binary ORC power plants for medium- and low-temperature geothermal sources, and the main conclusions suggested that working fluids with critical temperature close to the heat source temperature were optimal for subcritical configurations, superheating was not profitable and supercritical configurations performed better from the economic point of view.
A basic subcritical ORC system consists of a pump, an evaporator, an expander and a condenser, derived from which various configurations, such as superheated system and recuperated system, can be presented. Superheater is included in ORC systems to maintain the working fluid in the superheated region after heat absorption and to prevent liquid droplet formation in the expander; this is of great importance when wet fluids are exploited. Roy et al. (2011) presented an analysis of non-recuperative ORC with superheating process using R12, R123, R134a, and R717 as working fluids, and the results revealed that system with R123 was the best choice for converting low-grade heat to power. Algieri and Morrone (2012) evaluated the influence of superheating and a 2-fold behavior in the system performance was observed. A positive effect on thermal efficiency was demonstrated in the recuperated system, due to the higher fluid energy at the turbine outlet; while a decrease from the saturation condition was noted without recuperation. Recuperator is used to preheat the working fluid at the pump outlet by recovering part of the heat released during desuperheating at the expander outlet, which could reduce the amount of heat required in the evaporator and increase the thermal efficiency. Ventura and Rowlands (2015) investigated the performance of recuperated ORC systems with various working fluids for different heat sources. The inclusion of a recuperator could generally enhance the performance by increasing the specific power production, however, there was a threshold pressure, above which the recuperator had no positive influence on the ORC system.
Switching the operation from subcritical to transcritical is another modification on the cycle configuration. Transcritical operation can improve systems' thermodynamic performance as it can achieve a better thermal match between the working fluid and the heat source, and hence reducing the exergy losses in the heat exchange processes. Though thermodynamic efficiency can be increased, studies have shown that transcritical ORC system suffered from a worse economics (Oyewunmi et al., 2017). This was further strengthened through the work by Lecompte et al. (2015), which indicated that transcritical ORC system resulted in an improvement of 31.5% on the net power output but suffered an increment of 72.8% on specific investment cost (SIC) for waste heat recovery applications.
Comparisons of different ORC configurations for geothermal applications has attracted increasing attention. Zare (2015) evaluated the thermodynamic and exergoeconomic performance of a simple ORC system, a regenerative ORC system and an ORC system with an internal heat exchanger (IHE). The results indicated that the system with IHE was superior from the thermodynamic point of view while simple system showed the best economic performance. Walraven et al. (2013) presented the comparison results of subcritical/transcritical cycles with one or more pressure levels, indicating that the transcritical and multi-pressure subcritical cycles were the best options with exergy efficiency of up to 50%. Zhang et al. (2011) carried out comparison of subcritical and transcritical ORC systems with different working fluids, which revealed that subcritical ORC with R123 yielded the highest exergy efficiency of 54% and transcritical ORC with R125 provided the lowest levelized electricity cost (LEC) of 0.056 $/(kWh). Similar work was conducted by Vetter et al. (2013) and their results demonstrated that transcritical ORC with propane achieved a thermal efficiency of 10%, which was higher than that of subcritical cycles. Although these studies have presented some comparison results, mainly parametric analyses, and performance assessments, of different cycle configurations and working fluids, the thermo-economic optimization seems to be incomplete.
Therefore, despite the numerous studies on ORC systems in geothermal applications, there is still a lack of understanding on the potential benefit of different configurations from both thermodynamic and economic perspectives. The aim of this study is to explore the thermo-economic optimization of a variety of available ORC configurations (saturated and superheated, non-recuperated and recuperated, subcritical and transcritical), operating with different working fluids (R1234yf, R134a, isobutane, R245fa, R1233zd, and isopentane), for the exploitation of a medium-temperature geothermal heat source (180 °C and 40 kg/s). Pareto fronts of different cycle configurations and working fluids that indicate the maximum exergy efficiency and minimum payback period are compared. The influence on thermodynamic and economic plant performance of the superheater and recuperator, as well as subcritical and transcritical ORC system operations are evaluated. In addition, the optimal configuration as well as the working fluid are also explored by implementing thermo-economic optimization in this work over a range of conditions on a generalized geothermal heat source.
Methodology
Cycle Configurations
Six ORC configurations are considered in this study. Specifically, four different subcritical-cycle combinations can be achieved, with/without a recuperator and/or superheater, along with two additional transcritical cycles, recuperated, and non-recuperated.
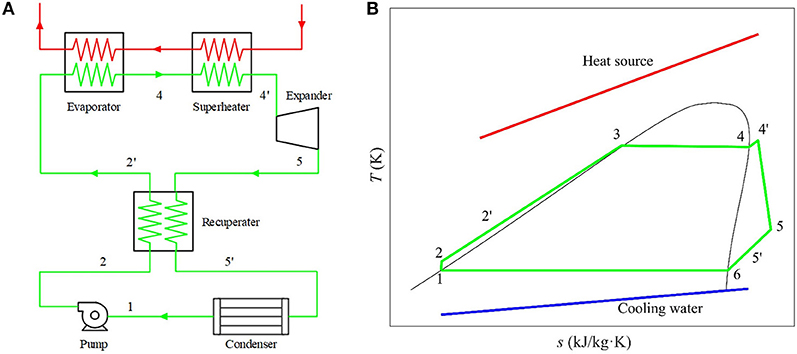
Figure 1 shows a schematic diagram and corresponding T-s diagram of a recuperated, superheated subcritical ORC, and defines the notation that will be used in the present analysis. This power-cycle system consists of a pump, a series of heat exchangers (recuperator, evaporator, superheater, and condenser), and an expander/turbine. For saturated cycle configurations, the superheater is removed and State Point 4′ coincides with State Point 4, while for non-recuperated cycle configurations, the recuperator is detached and State Points 2′ and 5′ simply overlap with State Points 2 and 5, respectively. Furthermore, for transcritical cycles, the working fluid is pressurized to a pressure that is higher than its critical pressure by the pump and then heated to a temperature higher than the critical temperature. In other words, State Points 3 and 4 will merge with State Point 4′ and it will be raised to a higher temperature and pressure state in the supercritical region.
Heat-Source Conditions and Working Fluid Selection
Located near the Pacific Rim, Indonesia has one of the greatest potentials for geothermal energy utilization. It has been estimated that around 29 GW of thermal energy is available in total for use, while only 4% is being exploited currently (Nasruddin et al., 2016). The selected heat source in this study is a medium-temperature geothermal heat-source at the Wayang Windu Geothermal Field, which discharges geothermal brine at 180 °C and 1.02 MPa, with a mass-flow rate of 40 kg/s (Suyanto et al., 2010; Prananto et al., 2018).
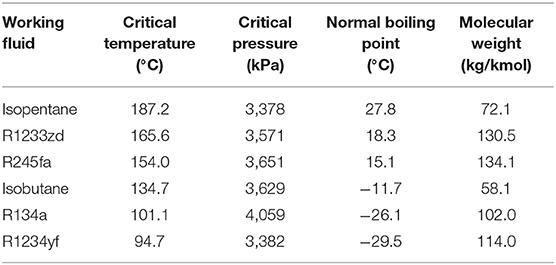
The selection of the optimal cycle configuration is strictly related to the selected working fluid. Currently, refrigerants and short-chained alkanes are most commonly used in commercial ORC systems. Table 1 reports the working-fluid candidates considered in this study (NIST, 2016). Four of the candidates, R1234yf, R134a, isobutane, and R245fa, are adopted in transcritical cycle configurations, as they have critical temperatures that are below the heat-source temperature. Amongst all of the working-fluid candidates, R134a is a wet fluid, while the others are all dry or isentropic. Therefore, R134a is not considered in saturated, subcritical ORCs so as to avoid significant liquid-phase formation in the turbine; the other dry/isentropic working fluids are exploited over a range of superheating degrees to evaluate the influence of this process on overall system performance.
Thermodynamic Modeling
The present modeling is based on the first and second laws. Working fluid properties are obtained from REFPROP (NIST, 2016) and energy balances are carried out across all the components. It should be highlighted that thermodynamic performance of the ORC system in this study is measured by the overall exergy efficiency instead of thermal efficiency, since the latter can be raised often with the cost of decreasing the heat recovery ratio (by increasing the heat source outlet temperature), which makes this parameter only useful for the interpretation of cycle calculation but cannot be selected as the optimization objective, especially in geothermal plants (and also in waste-heat recovery cases). The exergy efficiency, ηex, is defined as the ratio of the net power generated (Ẇn) to the total exergy input to the ORC system, which can be calculated from:
where ṁHS, cp, HS and THS, in are the heat source mass flow rate, specific heat capacity and inlet temperature, respectively, and T0 is the reference temperature, which is set to be 25 °C in this study. It is noted that the denominator of Equation (1) is constant as it depends on the heat source, so for a given heat source the exergy efficiency is also proportional to the generated power.
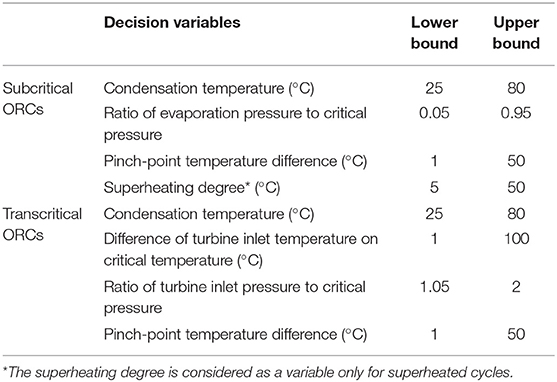
In the cycle calculations, the condensation temperature, evaporation pressure, pinch-point temperature differences in all heat exchangers (recuperator, evaporator, and condenser) and superheating degree are selected as optimization variables and are optimized simultaneously to achieve the optimal operating conditions. Several assumptions and other conditions employed in this study are listed below:
(1) All processes are modeled as being in steady state.
(2) The heat losses and pressure drops in the heat exchangers and pipes are neglected.
(3) The isentropic efficiencies of the pumps and turbines are both set to be 0.80.
(4) The electrical generator efficiency is set to be 0.95.
(5) The maximum evaporation pressure in subcritical ORC systems is set to be 0.95 Pcrit.
(6) The minimum superheating degree in superheated ORC systems is set to be 5 °C.
(7) The maximum turbine inlet temperature and pressure in transcritical ORC system are set to be 100 °C higher than the critical temperature and 2 Pcrit, respectively.
(8) The cooling water temperature is set to be 20 °C.
Economic Modeling
Component Sizing the Costing
The pump, turbine, and generator are sized based on their power consumption or power output, which will also be used as component capacity index in the cost estimation below. In addition, the total heat exchanger (HEX) area, A, is needed for costing these components, which is given by:
where is the thermal duty, ΔT is the log mean temperature difference (LMTD) between the hot and cold side of the HEX, and U is the overall heat transfer coefficient (HTC), which is determined by the HTCs on both the shell and tube sides, and the thermal resistance of the solid HEX material.
It is common practice to have the fluid with higher fouling propensity on the tube side of HEX as it is easier to clean the interior than the exterior of tubes (Cao, 2010). In this study, working fluid have higher fouling factors thus it flows on the tube side while geothermal brine and cooling water flow on the shell side. The correlations used in this study to calculate the HTCs on shell side and tube side are summarized below (Chen et al., 2015; Chatzopoulou et al., 2019; van Kleef et al., 2019).
Shell side:
where αi denotes the ideal crossflow HTC, μs and μw are the viscosity at bulk mean temperature and wall temperature, and j is a correction factor accounting for combined effects of baffle cut and spacing, for baffle leakage effects, for bundle bypass flow, for variable baffle spacing in the inlet and outlet sections, and for adverse temperature gradient build-up in laminar flow.
Tube side:
(1) Single phase:
where λ is the thermal conductivity and d is the diameter of the tube.
(2) Two phase (boiling):
where αNB is the nucleate boiling heat transfer coefficient, SChen and FChen are multiplication factors used for the forced convection and nucleate boiling contributions to overall heat transfer, respectively.
(3) Two phase (condensation):
(4) Supercritical:
The module costing technique is used to calculate the bare module cost (CBM) of each component, with chemical engineering plant cost index (CEPCI) used to obtain the purchased cost (Turton et al., 2008):
where j denotes the components in the ORC system, i.e., pump, heat exchangers, turbine, and generator, and X is the corresponding component capacity index, which has been defined and calculated above (power/hear exchange area). Coefficients for cost calculation of each component are listed in Table 2, and we have used CEPCI2001 = 397.0 and CEPCI2017 = 567.5 (Chemical Engineering Index, 2018) to convert to present cost values in Equation (11), which are dimensionless numbers employed to updating capital cost required to erect a power-cycle system from a past date to a later time.
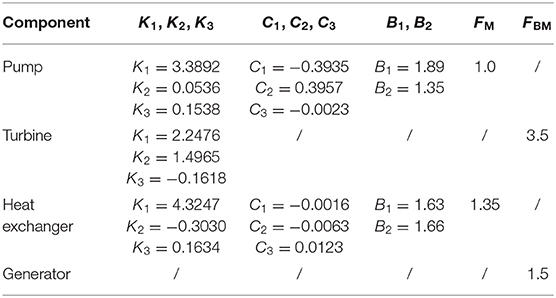
Table 2. Coefficients used in cost models for each ORC system component (Turton et al., 2008).
As for the generator, the cost is estimated by Toffolo et al. (2014):
where P is the power output of the generator.
In the specific case of the organic working fluids that we are considering in this study, it is known from the literature and our own prior experience in purchasing such chemicals that the cost of the fluid is small relative to the cost of the other key components in the system that are including in our costing, i.e., the heat exchangers, pump, expander, and generator. For this reason, in our approach, which is similar in this regard to the majority of publications in the literature that address the economic modeling of ORC systems, we do not account for the cost of the working fluid. Actually our own experience in establishing an ORC testing facility in our laboratory (Unamba et al., 2019) confirms that the cost of the working fluid is small compared to the total system costs. Therefore, we are confident that the influence of the working fluid cost can be neglected in our early-stage analyses.
Turton's method has been used here for the economic evaluation of all system configurations, following many ORC studies in the literature (e.g., Shu et al., 2014; Lecompte et al., 2015; Li et al., 2019), which have shown that its results correlate well with known costs of larger-scale plants (van Kleef et al., 2019).
Economic Indicator
The payback period (PBP) is selected as the indicator to evaluate the ORC systems from economic perspective and also for economic optimization (Shu et al., 2014), which can be calculated by:
where i is the discount rate (set to be 5% in this paper Shu et al., 2014), Costtot represents the total initial investment cost of the power plant and profit represents the annual cash flow in the lifetime.
The total initial investment cost of the ORC system is calculated by summing the purchased cost of the components (pump, heat exchangers, turbine, and generator) shown above, and also taking costs of installation and construction into consideration. Cash flow of the geothermal plant is the revenue obtained by selling the generated electricity at a price of 0.0836 $/kWh (Infrastructure Asia Online, 2018) (industrial tariff) while subtracting variable costs including the operation and maintenance costs, in addition to the cooling water costs with a price at 0.08 $/ton. In this study, the geothermal ORC plants are assumed to operate for 8,000 hours per year under design conditions, which is a commonly applied assumption in geothermal system analysis (Rodríguez et al., 2012; Zhao and Wang, 2016; Seyfouri et al., 2018). Typical capacity factors of geothermal power plants can be up to ~80% (Independent Statistics and Analysis, 2019), which is high compared to other ORC applications, e.g., waste heat or solar energy.
Optimization Strategy
The thermodynamic and economic models of the geothermal ORC systems were developed in MATLAB. As mentioned above, the exergy efficiency and payback period are selected as objective functions, while condensation temperature, evaporation pressure, superheating degree, and pinch-point temperature differences of heat exchangers are considered as decision variables. Due to the trade-off between the two objective functions, a single optimal solution does not exist. Instead, there exists a set of non-dominated solutions that makes up a Pareto optimal front. The Non-Dominated Sorting Genetic Algorithm II (NSGA-II) is implemented in this work to perform the optimization, as it performs better in finding a diverse set of solutions and in converging near the true Pareto-optimal set when compared to the other multi-objective evolutionary algorithms, such as Pareto-archived evolution strategy (PAES) and strength-Pareto EA (SPEA) (Mathworks, 2018). NSGA-II is one of the most popular multi-objective optimization algorithms with three special characteristics: fast non-dominated sorting approach, fast crowded distance estimation procedure, and simple crowded comparison operator (Deb et al., 2002). NSGA-II works by initializing random individuals subjected to a set of constraints. The fitness function of each individual is then calculated, evaluated and ranked, and only the non-dominated individuals survive to the next generation. A non-dominated solution is finally achieved, where there exists no other solution that outperforms it in both objective functions. The range of the decision variables of different cycle configurations are summarized in Table 3. It should be stated that the pinch-point temperature difference of different heat exchangers (i.e., evaporator, recuperator, and condenser) are optimized individually. Therefore, for example, there would be six decision variables in the recuperated, superheated subcritical ORC systems, i.e., condensation temperature, evaporation pressure, superheating degree, and pinch-point temperature differences in the heat exchangers. Other parameters of the ORC system can be calculated once all these decision variables are determined.
Results and Discussion
Saturated and Superheated Cycles
Saturated and superheated ORC systems are compared to evaluate the influence of superheater on the system performance. Figure 2A shows the Pareto fronts from the thermo-economic optimization for saturated, non-recuperated ORC system with different working fluids. It should be stated that R134a listed in Table 1 is not considered here in the saturated system due to the possibility of liquid formation in the expansion process, which would potentially damage the organic turbine. The bottom right-hand side corner in the figure is favorable as it provides a system with both a higher exergy efficiency (net power output as well, see Equation 1) and a shorter payback period. R245fa and isobutane stand out among all the working fluid candidates due to the moderate critical temperatures as compared to the heat source temperature (180 °C), which results in an adequate evaporation temperature and reduces the exergy loss in the heat exchange process. Selecting the ORC system's exergy efficiency to be 0.60 as an example, which corresponds to a net power output of 3.19 MW according to Equation (1), the payback period of the geothermal plant with R245fa and isobutane are 4.7 and 6.8 years, respectively. On the contrary, R1234yf delivers considerably worse performance, of which the exergy efficiency is limited to be lower than 0.38 however the payback period is always longer than 11.6 years. This is because the evaporation temperature of R1234yf cannot go beyond the working fluid critical temperature (94.7 °C) in subcritical operation. As a consequence, the exergy loss in the evaporator would be relatively larger. The thermal match plays a vital role in the ORC system performance. Figure 3 shows the T-s diagrams of ORC systems of these two cases, namely working fluids with moderate and low critical temperature (as compared with heat source temperature), which could clearly reveal the deviation in exergy loss in the heat exchange process.
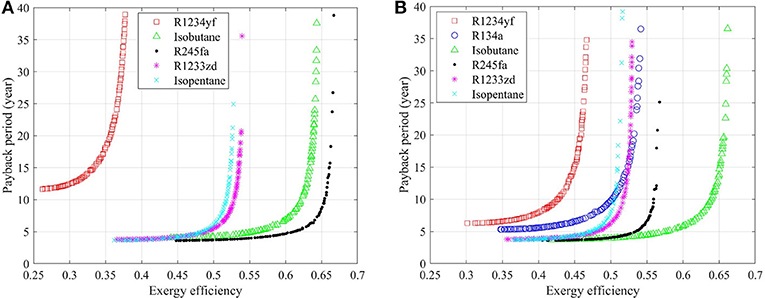
Figure 2. Thermo-economic optimization of: (A) saturated, non-recuperated ORC systems, and (B) supercritical, non-recuperated ORC systems.
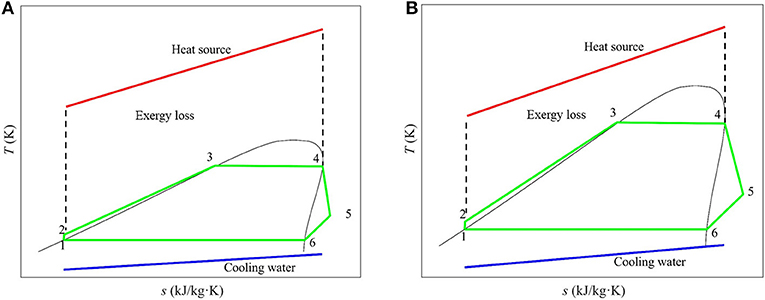
Figure 3. T-s diagram of ORC systems with: (A) moderate critical temperature working fluid, and (B) low critical temperature working fluid (relative to heat-source temperature).
Thermo-economic optimization results of superheated ORC system are shown in Figure 2B. R134a is considered here since the liquid formation in the expansion process can be prevented by involving the superheater. It is noted that the Pareto front of R1234yf is pushed to a region with higher exergy efficiency and shorter payback period, indicating a significant performance improvement with comparison to the saturated case (see Figure 2A). This can be explained by the better thermal match between the heat source and the working fluid that is attained when involving the superheater, which reduces the aforementioned exergy loss in the heat addition process. Similarly, the superheating process is also preferable in ORC systems with isobutane as the Pareto front marginally stretches to the right-hand side, which reveals that the payback period of the ORC system could be reduced for the same exergy efficiency. More precisely, taking the system with an exergy efficiency of 0.60 as an example, the payback period decreases from 6.8 to 5.7 years when an additional superheater is involved. Isobutane even outperforms all the other working fluids in the superheated ORC systems.
On the other hand, performance of ORC system with R245fa is hindered when the superheater is included. It can be seen that the exergy efficiency decreases from 0.61 to 0.53 when the payback period is set to be 5 years. The evaporation temperature in the superheated system decreases since an amount of heat is required for superheating, which would extend the cycle profile in the (isothermal) phase change region hence increasing exergy loss in the evaporator. While for R1233zd and isopentane, Figures 2A,B indicate that the optimization results are quite similar in saturated and superheated cases. In other words, the influence of superheating on the ORC system thermo-economic performance is slight with these two working fluids.
Thermo-economic optimization results of saturated and superheated, recuperated ORC systems are shown in Figure 4, and similar conclusions can be noted with those from Figure 2. R245fa outperforms in saturated system while isobutane yields the best performance in superheated system. R1234yf is not suitable for exploitation in saturated ORC systems, while the superheating process can significantly enhance the system performance, which is the same with that in the non-recuperated case. With the recuperator included, only a slight change in performance is obtained for isobutane through the addition of a superheater; however, significant performance deterioration is still suffered in the ORC system with R245fa as the Pareto front is pushed to the left hand side and the maximum exergy efficiency decreases from 0.66 to 0.56. The superheater has only a slight influence on the thermo-economic performance of recuperated ORC systems with R1233zd and isopentane.
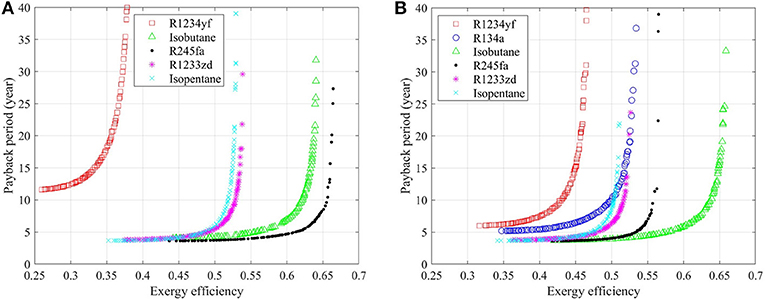
Figure 4. Thermo-economic optimization of: (A) saturated, recuperated ORC system, and (B) superheated, recuperated ORC systems.
A geothermal plant with a payback period <25 years is considered as feasible from the economic perspective in this study. The overlap of the Pareto fronts below this value of both saturated and superheated systems is used to compare the deviation and evaluate the influence of superheater on the ORC system performance. Detailed change (increment/decrement) in payback period of the superheated ORC system relative to the saturated system is shown in Figure 5, for both non-recuperated and recuperated cases. It would be beneficial to involve a superheater if the change is negative, proving that the payback period for the same exergy efficiency (net power output) would be reduced through the addition of a superheater. Figure 5A demonstrates that superheater is desirable in ORC system with R1234yf, which can reduce the payback period by up to 50–73% in the overlapped operation range of saturated and superheated systems. Isobutane is another working fluid that favors superheating, since its critical temperature is also much lower than the heat source temperature. The temperature glide in the superheating process allows a better thermal match with the heat source than the (isothermal) evaporation process. The trend of decrease in the payback period goes much steeper when the exergy efficiency is higher, and the maximum decrement in the payback period reaches 60%. However, a significant increment on the payback period is revealed when the superheater is included in the ORC system with R245fa as working fluid. A payback period that is up to 60% longer would be suffered if the superheated system needs to achieve the same exergy efficiency of 0.54 with the saturated system. Superheating is also not preferable when using R1233zd and isopentane, with a corresponding maximum increase on the payback period of such systems is 23 and 33%.
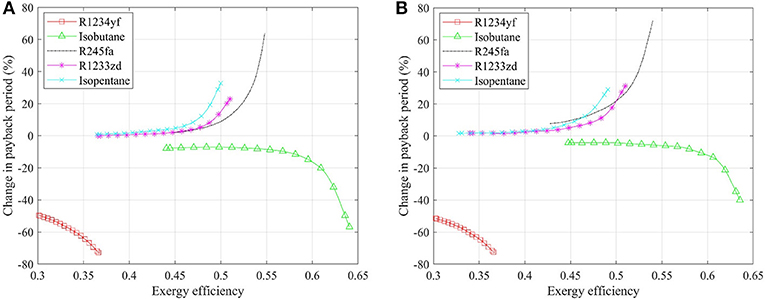
Figure 5. Change in payback period of superheated relative to saturated ORC systems: (A) non-recuperated case, and (B) recuperated case.
Figure 5B shows the change in the payback period of a superheated system relative to a saturated system with recuperation, which is similar with the results of non-recuperated cases. Working fluids with lower critical temperatures, i.e., R1234yf and isobutane, favor the configuration featuring a superheated cycle, while the payback period would increase if the superheater is included in the recuperated ORC system with the other working fluids. In addition, the increment on payback period, of the ORC system with R245fa, R1233zd, and isobutane, increases with increasing exergy efficiency, indicating that superheating should not be considered if the thermodynamic performance is the priority for system design and optimization. The maximum increment reaches 32, 30, and 40% for these three working fluids. On the contrary, when adopting R1234yf and isobutane in the ORC system, a larger decrease in the payback period is achieved with a higher exergy efficiency. Therefore, it is essential to install a superheater when the system is expanded to a larger scale (higher exergy efficiency and power output), in both non-recuperated and recuperated cases.
Non-recuperated and Recuperated Cycles
Thermo-economic optimization results of recuperated and non-recuperated subcritical ORC systems have already been shown in Figures 2, 4, of which Figures 2A, 4A can be compared to evaluate the influence of the recuperator on the saturated ORC systems, while Figures 2B, 4B could reveal the performance difference of superheated systems.
Figures 6A,B works similarly to those in Figure 5, which show the change in payback period of recuperated systems relative to non-recuperated systems. The negative value indicates the recuperator is preferred in the ORC system and could reduce the payback period while maintaining the exergy efficiency (net power output) at the same level. Figure 6A indicates that the influence of recuperation on the payback period of saturated ORC systems with R1234yf, R1233zd, and isopentane is relatively slight, with changes <1%. While system with isobutane and R245fa would experience an increment on the payback period up to 3 and 4%, respectively; it is also noted that the increment would be larger when the system exergy efficiency is higher. Therefore, the non-recuperated configuration is favored in the saturated case. Figure 6B shows the change in payback period of recuperated system as compared to a non-recuperated system in superheated conditions. With R1234yf and R134a as the working fluid, operating range with a low exergy efficiency favors the recuperator, within which the payback period could be reduced by 6 and 3% at most. However, the recuperator becomes not preferable in systems with higher exergy efficiency, with a maximum increase in the payback period that can reach 8 and 7%, for R1234yf and R134a, respectively. As for the other working fluids, the payback period of the system would be longer when the recuperator is involved in the system. All the increment increases with the system exergy efficiency and the individual increment would be larger for the working fluid with a higher critical temperature. The maximum change in payback period of the ORC system with isobutane, R245fa, R1233zd, and isopentane reach 3, 5, 8, and 8%, respectively.
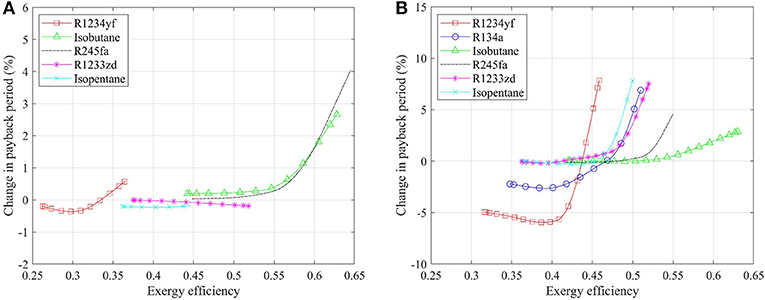
Figure 6. Change in payback period of recuperated relative to non-recuperated ORC systems: (A) saturated case, and (B) superheated case.
Although the recuperation process could improve the thermodynamic performance of the ORC system by extracting the thermal energy of the hot working fluid stream from the turbine, and at the same time, reduce the cooling demand as well as the cost of cooling water, it seems that these two factors still cannot compensate for the additional cost for the recuperator, which makes the recuperated system not attractive, in most cases.
The influence of recuperation on the system's performance has also been evaluated for transcritical ORCs, with thermo-economic optimization results shown in Figure 7 and the effect on the payback period shown in Figure 8, respectively. Working fluids with lower critical temperatures (R1234yf, R134a, isobutene, and R245fa) are considered as candidates in transcritical systems. Figure 7A shows that the trends of the Pareto front of different working fluids are similar, and system with R245fa, whose critical temperature is close to the heat source temperature, outperforms of the four working fluids. While working fluid with a lower critical temperature delivers worse thermo-economic performance. More precisely, selecting the payback period to be 5 years, the maximum exergy efficiency of the ORC system with R245fa, isobutane, R134a, and R1234yf are 0.74, 0.68, 0.57, and 0.50, respectively. Figure 7B shows the thermo-economic optimization results of recuperated transcritical ORC systems, which is similar with those of non-recuperated case, revealing that the recuperator has a slight effect on the thermo-economic performance of transcritical ORC system for this geothermal application.
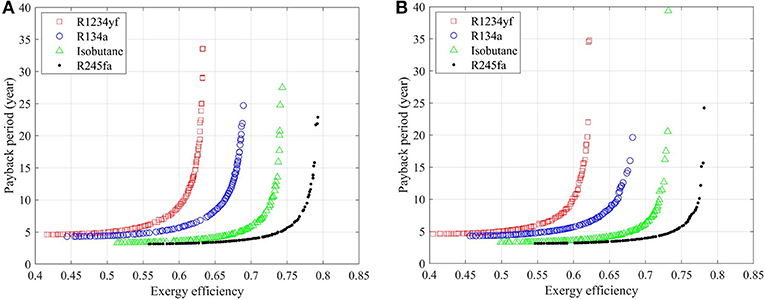
Figure 7. Thermo-economic optimization of: (A) non-recuperated transcritical ORC systems, and (B) recuperated transcritical ORC systems.
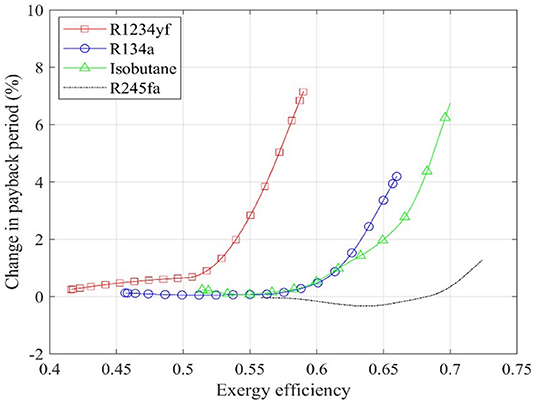
Figure 8. Change in payback period of recuperated relative to non-recuperated transcritical ORC systems.
Figure 8 shows the change in payback period of recuperated transcritical system relative to non-recuperated transcritical system. Despite the slight reduction in the payback period obtained in the system with R245fa within the range of exergy efficiency from 0.56 to 0.67, it is noted that the recuperator is not favorable in most cases. On the other hand, the increment on payback period is within 8%, indicating the influence of recuperation on the thermo-economic performance of transcritical ORC system is negative but slight, which is different from the situation of subcritical systems as shown in Figure 6. The aforementioned two advantages offered by the recuperation process, namely the thermodynamic performance improvement and the cooling water saving, could nearly recompense the cost increment by involving the recuperator.
Subcritical and Transcritical Cycles
A comparison of subcritical or transcritical ORC systems is implemented in this section. It is noted that in the subcritical systems considered here the superheating degree is selected as a decision variable that varies from 0 to 50 °C, which is optimized with other variables including the condensation temperature, the evaporation pressure and the pinch-point temperature differences in the heat exchangers.
The change in payback period of transcritical systems relative to subcritical systems are shown in Figure 9. Negative values are obtained for all the working fluids in both non-recuperated and recuperated cases, thus the advantage of selecting the configuration featuring a transcritical cycle could be envisioned. Moreover, a larger decrease in payback period can be achieved with a higher exergy efficiency of the ORC system. The transcritical cycles consequently appear to be more attractive in large-scale (high exergy efficiency as well as power output) systems for the geothermal application studied here. A reduction of up to 90% can be achieved in the payback period by switching from subcritical to transcritical ORC systems.
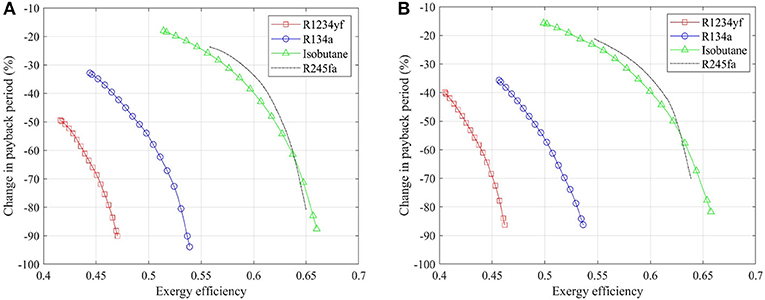
Figure 9. Change in payback period of transcritical relative to subcritical ORC systems: (A) non-recuperated case, and (B) recuperated case.
Comprehensive Comparison of Configurations
A screening on the values of decision variables that are associated with the optimal systems and lie on the Pareto fronts is implemented, which spans a number of working fluids and different configurations. For subcritical systems, the condensation temperature decreases as the system exergy efficiency increases and also as the payback period increases, while the pinch-point temperature difference in the evaporator also decreases at higher system exergy efficiencies and higher payback periods; the ratio of evaporation pressure to critical pressure and the pinch-point temperature difference in the condenser and superheater, stay approximately constant over the same range of optimal exergy efficiencies and payback periods; while the pinch-point temperature difference in the recuperator varies significantly. Results of transcritical systems are similar, of which the condensation temperature and the pinch-point temperature in the main heater decrease, the pinch-point temperature difference in the recuperator also varies, and the other decision variables, i.e., ratio of the turbine inlet pressure to critical pressure, the temperature difference in the critical temperature and the pinch-point temperature difference in the condenser, nearly stay constant, with the increment of system exergy efficiency and payback period.
This section performs a comprehensive comparison of the mentioned configurations in this study based on the thermo-economic optimization results above. A fixed payback period of 10 years is set as an example for all the 6 architectures, and the optimal working fluid and the corresponding optimal operating parameters can be determined, which could achieve the optimization point that locates on the Pareto fronts. Under a fixed payback period, a higher net power output indicates the ORC geothermal plant could achieve a higher profit in the long-term operation. The maximum net power output as well as the working fluid are summarized in Table 4. R245fa is the most suitable working fluid for saturated subcritical and transcritical ORC systems, and isobutane could yield the highest net power output in superheated (subcritical) systems. In both non-recuperated and recuperated cases, the superheated configuration delivers a worse thermodynamic performance than the saturated one (3 and 4% lower in the maximum net power output), making the superheater unattractive to be considered; while the maximum net power output of the configuration featuring a transcritical cycle is nearly 20% higher than the saturated case. On the other hand, the recuperator seems also unfavorable in the ORC system for this geothermal application from the thermodynamic perspective, as the maximum net power output would decrease by 0.6, 2.5, and 0.7%, in saturated, superheated and transcritical cases, respectively, when the recuperator is included. This is because the heat source outlet temperature (after transferring energy to the ORC system) would be higher when the recuperation process is involved and the total thermal energy absorbed by the ORC system would be reduced.
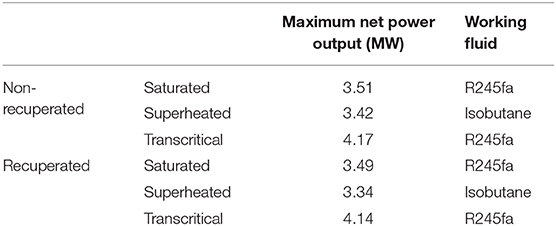
Table 4. Maximum net power output and the corresponding working fluid of various cycle configurations for a payback period of 10 years.
Identifying the distribution of the total cost can help in determining the focus for further component optimization and system development. Figure 10A shows the cost composition of each component in different configurations with maximum net power output (corresponding to the results in Table 4). Turbine accounts for a large fraction of the total cost of the ORC system of all the configurations, while that of pump and generator is relatively small. In general, the evaporator accounts for the largest cost amongst the heat exchangers, followed by the condenser; one exception to this conclusion is the case of saturated, recuperated cycles, in which the recuperator is associated with a similar cost to the evaporator but a higher cost than the condenser. The cost of superheater is considerably small, indicating a small superheating degree in the optimal system and hence it is not attractive to be considered. It also indicates that the total cost of the transcritical system is higher than that of the subcritical system, which is determined by the high operation pressure and the high power output (see Table 4).
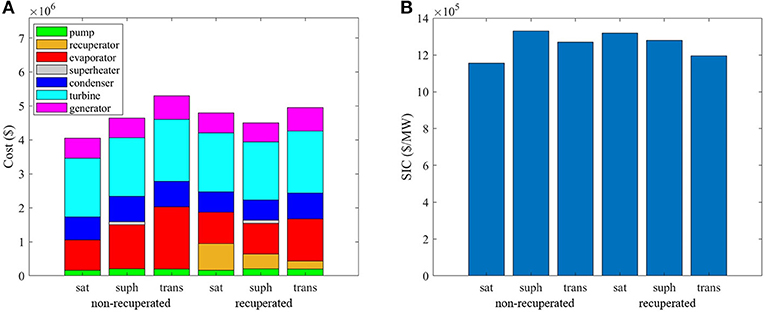
Figure 10. (A) Cost composition of each component, and (B) SIC of various cycle configurations for a payback period of 10 years (R245fa is selected for saturated and transcritical-cycle systems, and isobutane is selected for superheated systems).
Figure 10B shows the corresponding SIC of different configurations. In the non-recuperated case, the saturated configuration provides the lowest SIC of 1,155,000 $/MW, which is 9 and 13% lower than that of the superheated and transcritical configurations. While in the recuperated case, SIC of the transcritical configuration is 9 and 7% lower than the other two configurations. The recuperator is preferred in the superheated system and transcritical-cycle system, as the SIC is decreased by 4 and 6%, respectively. While in the saturated system, an increment of 14% on the SIC is observed.
Further Discussion—Analysis of a Generalized Heat Source
All previous results relate to a specific geothermal application, with a heat-source temperature of 180 °C. In this section, we present thermo-economic optimization results from a more generalized heat-source with a temperature ranging from 140 to 200 °C, while the mass flow rate is still set to 40 kg/s. The electricity price is selected to be 0.098 $/kWh according to an average assessment of the prices in the UK, US, China, Germany, and France (China Electricity Price, 2019; Energy Prices and Costs in Europe, 2019; Industrial Price Comparison, 2019), which is used to evaluate the general potential of exploiting geothermal energy through ORC technology in various global regions. A fixed payback period of 10 years is also set to explore the optimal configuration, which could deliver the maximum net power output and gain more profit in long-term operation.
The results of the generalized heat-source temperature analysis, including the optimal configuration and the corresponding working fluid, are shown in Figure 11 which reveals that the non-recuperated transcritical configuration with a working fluid whose critical temperature is close to the heat-source temperature is preferable (the critical temperatures of R134a, isobutane, R245fa, and R1233zd are 101.1, 134.7, 154.0, and 165.6 °C, respectively). The maximum net power output increases from 2.16 MW to 5.21 MW, while the corresponding SIC decreases from 1,961,000 to 967,000 $/MW, when the heat source temperature increases from 140 to 200 °C. In our future work, it will be of interest to expand this insight to consider the thermo-economic performance of geothermal plants for over a wider range of temperatures but also over a range of mass flow rates, and to compile performance maps relating to the operation and capabilities of relevant plants in different regions.
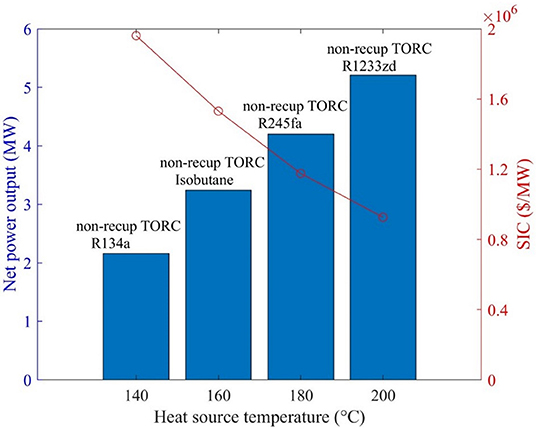
Figure 11. Net power output and SIC of optimal configuration for a geothermal heat-source temperature ranging from 140 to 200 °C and a payback period of 10 years.
Conclusions
In this study, thermo-economic optimization was implemented on a range of ORC power-generation system configurations, namely: saturated and superheated; non-recuperated and recuperated; subcritical and transcritical, while considering six working fluids (R1233yf, R134a, isobutane, R245fa, R1233zd, and isopentane) for the exploitation of geothermal heat in a specific case study with a heat-source temperature of 180 °C and mass flow rate of 40 kg/s. The exergy efficiency (i.e., resource use) and payback period were selected as optimization objective functions, and Pareto fronts were generated for each scenario and compared in order to evaluate the influence of superheating, recuperation and subcritical vs. transcritical operation on the thermo-economic performance of these systems. The thermo-economic optimization results can be considered as a useful tool for configuration comparison and selection in the early stages of ORC system design in geothermal energy unitization applications.
The results revealed that superheating can improve the system performance with R1234yf and isobutane, whose critical temperature is relatively low; the maximum decrease in payback period reach 73 and 60%. However, a deterioration in thermo-economic performance was observed for working fluids with higher critical temperatures, e.g., R245fa, R1233zd, and isopentane (examined in this study), with the maximum increment on the payback period of 32, 33, and 60%, respectively. Furthermore, although recuperation presents advantages such as thermal-efficiency enhancements and cooling water savings, these did not compensate the costs associated with the installation of the additional heat exchanger, which consequently makes recuperation less favorable in most cases. The comparison results indicated that an increment up to 8% on the payback period was observed when the recuperator was included in the system. A significant decrease in the payback period, up to a maximum of 90%, was achieved by switching from subcritical to transcritical ORC systems. Therefore, transcritical ORC systems offer a promising option for power generation in geothermal applications.
Under a fixed payback period, a higher net power output indicates the ORC geothermal plant could achieve a higher profit in the long-term operation. After selecting a system payback period of 10 years as an example, it was found that R245fa outperforms the working fluids in saturated (subcritical) and transcritical ORC systems, while isobutane is the most suitable fluid for superheated (subcritical) systems. The recuperator emerged as unattractive in this application, as it was shown that its inclusion resulted in reductions in the maximum power output by 0.6, 2.5, and 0.7%, in saturated, superheated and transcritical cases, respectively, relative to non-recuperated cycles systems. While from the perspective of SIC, recuperator is favored in superheated and transcritical configurations, in which decrease of 4 and 6% were observed, but it should not be considered in the saturated-cycle system as the SIC was increased by 14%. It was shown that this application favors ORC configurations based on transcritical cycles, which provide a power output that is nearly 20% higher than equivalent subcritical systems; in addition, lower SICs (by 9 and 7%, respectively) can be achieved by recuperated cycles relative to saturated and superheated systems.
Finally, a more generalized geothermal heat-source with a temperature ranging from 140 to 200 °C was considered to further explore optimal plant configurations in this application. The results from this exercise indicate that non-recuperated transcritical-cycle systems with a working fluid whose critical temperature is close to the heat-source temperature typically deliver the maximum power output under a fixed payback period, which suggests that these configurations have the potential to offer more profit in long-term operation of the ORC geothermal plant, following project payback.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
JS conducted the case study, analyzed the data, and wrote an initial draft of this paper. PL and JT conceived and developed the methodology, conducted the case study, and assisted in the preparation of the manuscript. CM provided advice and suggestions throughout the development of this research and also on the preparation of the paper, and was responsible for proofreading and revising the paper before submission.
Funding
This work was supported by the UK Engineering and Physical Sciences Research Council [grant number EP/P004709/1].
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank the Zijing Scholarship from Tsinghua University that supported JS for this research. The authors would also like to thank Oyeniyi A. Oyewunmi for his help on developing the heat exchanger models and Xiaoya Li for her help on developing the economic models used to perform the present research. Data supporting this publication can be obtained on request from Y2VwLWxhYkBpbXBlcmlhbC5hYy51aw==.
References
Algieri, A., and Morrone, P. (2012). Comparative energetic analysis of high-temperature subcritical and transcritical organic Rankine cycle (ORC). A biomass application in the Sibari district. Appl. Therm. Eng. 36, 236–244. doi: 10.1016/j.applthermaleng.2011.12.021
Anderson, A., and Rezaie, B. (2019). Geothermal technology: trends and potential role in a sustainable future. Appl. Energy 248, 18–34. doi: 10.1016/j.apenergy.2019.04.102
Astolfi, M., Romano, M. C., Bombarda, P., and Macchi, E. (2014a). Binary ORC (organic Rankine cycles) power plants for the exploitation of medium–low temperature geothermal sources–Part A: thermodynamic optimization. Energy 66, 423–434. doi: 10.1016/j.energy.2013.11.056
Astolfi, M., Romano, M. C., Bombarda, P., and Macchi, E. (2014b). Binary ORC (organic Rankine cycles) power plants for the exploitation of medium–low temperature geothermal sources–Part B: techno-economic optimization. Energy 66, 435–446. doi: 10.1016/j.energy.2013.11.057
Castelli, A. F., Elsido, C., Scaccabarozzi, R., Nord, L. O., and Martelli, E. (2019). Optimization of organic Rankine cycles for waste heat recovery from aluminum production plants. Front. Energy Res. 7:44. doi: 10.3389/fenrg.2019.00044
Chatzopoulou, M. A., Simpson, M., Sapin, P., and Markides, C. N. (2019). Off-design optimisation of organic Rankine cycle (ORC) engines with piston expanders for medium-scale combined heat and power applications. Appl. Energy 238, 1211–1236. doi: 10.1016/j.apenergy.2018.12.086
Chemical Engineering Index (2018). Available online at: www.chemengonline.com/cepci-updates-january-2018-prelim-and-december-2017-final (accessed January 6, 2019).
Chen, W., Fang, X., Xu, Y., and Su, X. (2015). An assessment of correlations of forced convection heat transfer to water at supercritical pressure. Ann. Nucl. Energy 76, 451–460. doi: 10.1016/j.anucene.2014.10.027
China Electricity Price (2019). Available online at: https://www.ceicdata.com/en/china/electricity-price (accessed July 6, 2019).
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. A. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197. doi: 10.1109/4235.996017
Drescher, U., and Brüggemann, D. (2007). Fluid selection for the organic Rankine cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 27, 223–228. doi: 10.1016/j.applthermaleng.2006.04.024
Energy Prices Costs in Europe (2019). Available online at: https://www.businesselectricityprices.org.uk/europe (accessed July 6, 2019).
EXERGY (2019). Available online at: http://exergy-orc.com/application/geothermal (accessed April 17, 2019).
Freeman, J., Hellgardt, K., and Markides, C. N. (2017). Working fluid selection and electrical performance optimisation of a domestic solar-ORC combined heat and power system for year-round operation in the UK. Appl. Energy 186, 291–303. doi: 10.1016/j.apenergy.2016.04.041
Heberle, F., Preißinger, M., and Brüggemann, D. (2012). Zeotropic mixtures as working fluids in organic Rankine cycles for low-enthalpy geothermal resources. Renew. Energy 37, 364–370. doi: 10.1016/j.renene.2011.06.044
Hettiarachchi, H. M., Golubovic, M., Worek, W. M., and Ikegami, Y. (2007). Optimum design criteria for an organic Rankine cycle using low-temperature geothermal heat sources. Energy 32, 1698–1706. doi: 10.1016/j.energy.2007.01.005
Imran, M., Usman, M., Park, B. S., Kim, H. J., and Lee, D. H. (2015). Multi-objective optimization of evaporator of organic Rankine cycle (ORC) for low temperature geothermal heat source. Appl. Therm. Eng. 80, 1–9. doi: 10.1016/j.applthermaleng.2015.01.034
Independent Statistics Analysis (2019). Available online at: https://www.eia.gov/electricity/monthly/epm_table_grapher.php?t=epmt_6_07_b (accessed January 7, 2020)
Industrial Price Comparison (2019). Available online at: https://www.rockymountainpower.net (accessed July 6, 2019).
Infrastructure Asia Online (2018). Available online at: www.infrastructureasiaonline.com/government/indonesia-electricity-tariff-still-competitive-asean-region (accessed January 6, 2019).
Lecompte, S., Lemmens, S., Huisseune, H., Van den Broek, M., and De Paepe, M. (2015). Multi-objective thermo-economic optimization strategy for ORCs applied to subcritical and transcritical cycles for waste heat recovery. Energies 8, 2714–2741. doi: 10.3390/en8042714
Li, X., Song, J., Yu, G., Liang, Y., Tian, H., Shu, G., et al. (2019). Organic Rankine cycle systems for engine waste-heat recovery: heat exchanger design in space-constrained applications. Energy Convers. Manage. 199:111968. doi: 10.1016/j.enconman.2019.111968
Liu, C., Gao, T., Zhu, J., and Xu, J. (2016). “Performance optimization and economic analysis of geothermal power generation by subcritical and supercritical organic Rankine cycles,” in Proceedings of the ASME 2016 Turbomachinary Technical Conference and Exposition (Seoul).
Markides, C. N. (2015). Low-concentration solar-power systems based on organic Rankine cycles for distributed-scale applications: overview and further developments. Front. Energy Res. 47, 1–16. doi: 10.3389/fenrg.2015.00047
Mathworks (2018). Available online at: uk.mathworks.com/help/matlab/index.html (accessed February 19, 2019).
Moya, D., Aldás, C., and Kaparaju, P. (2018). Geothermal energy: power plant technology and direct heat applications. Renew. Sust. Energy Rev. 94, 889–901. doi: 10.1016/j.rser.2018.06.047
Nasruddin, Idrus Alhamid., M., Daud, Y., Surachman, A., Sugiyono, A., Aditya, H. B., et al. (2016). Potential of geothermal energy for electricity generation in Indonesia: a review. Renew. Sust. Energy Rev. 53, 733–740. doi: 10.1016/j.rser.2015.09.032
NIST (2016). Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) (Gaithersburg).
Oyewunmi, O. A., Ferré-Serres, S., Lecompte, S., van den Broek, M., De Paepe, M., and Markides, C. N. (2017). An assessment of subcritical and trans-critical organic Rankine cycles for waste-heat recovery. Energy Procedia 105, 1870–1876. doi: 10.1016/j.egypro.2017.03.548
Oyewunmi, O. A., and Markides, C. N. (2016). Thermo-economic and heat transfer optimization of working-fluid mixtures in a low-temperature organic Rankine cycle system. Energies 9:448. doi: 10.3390/en9060448
Pantaleo, A. M., Camporeale, S. M., Sorrentino, A., Miliozzi, A., Shah, N., and Markides, C. N. (2018). Hybrid solar-biomass combined Brayton/organic Rankine-cycle plants integrated with thermal storage: techno-economic feasibility in selected Mediterranean areas. Renew. Energy 147, 2913–2931. doi: 10.1016/j.renene.2018.08.022
Prananto, L. A., Zaini, I. N., Mahendranata, B. I., Juangsa, F. B., Aziz, M., and Soelaiman, T. A. (2018). Use of the Kalina cycle as a bottoming cycle in a geothermal power plant: Case study of the Wayang Windu geothermal power plant. Appl. Therm. Eng. 132, 686–696. doi: 10.1016/j.applthermaleng.2018.01.003
Ramos, A., Chatzopoulou, M. A., Freeman, J., and Markides, C. N. (2018). Optimisation of a high-efficiency solar-driven organic Rankine cycle for applications in the built environment. Appl. Energy 228, 755–765. doi: 10.1016/j.apenergy.2018.06.059
Rodríguez, C. E., Palacio, J. C., Venturini, O. J., Lora, E. E., Cobas, V. M., dos Santos, D. M., et al. (2012). Exergetic and economic comparison of ORC and Kalina cycle for low temperature enhanced geothermal system in Brazil. Appl. Therm. Eng. 52, 109–119. doi: 10.1016/j.applthermaleng.2012.11.012
Roy, J. P., Mishra, M. K., and Misra, A. (2011). Performance analysis of an organic Rankine cycle with superheating under different heat source temperature conditions. Appl. Energy 88, 2995–3004. doi: 10.1016/j.apenergy.2011.02.042
Sauret, E., and Rowlands, A. S. (2011). Candidate radial-inflow turbines and high-density working fluids for geothermal power systems. Energy 36, 4460–4467. doi: 10.1016/j.energy.2011.03.076
Seyfouri, Z., Ameri, M., and Mehrabian, M. A. (2018). Exergo-economic analysis of a low-temperature geothermal-fed combined cooling and power system. Appl. Therm. Eng. 145, 528–540. doi: 10.1016/j.applthermaleng.2018.09.072
Shokati, N., Ranjbar, F., and Yari, M. (2015). Exergoeconomic analysis and optimization of basic, dual-pressure and dual-fluid ORCs and Kalina geothermal power plants: a comparative study. Renew. Energy 83, 527–542. doi: 10.1016/j.renene.2015.04.069
Shu, G., Yu, G., Tian, H., Wei, H., and Liang, X. (2014). A multi-approach evaluation system (MA-ES) of organic Rankine cycle (ORC) used in waste heat utilization. Appl. Energy 132, 325–338. doi: 10.1016/j.apenergy.2014.07.007
Song, J., Song, Y., and Gu, C. (2015). Thermodynamic analysis and performance optimization of an organic Rankine cycle (ORC) waste heat recovery system for marine diesel engines. Energy 82, 976–985. doi: 10.1016/j.energy.2015.01.108
Suyanto, T. S., Atmojo, J. P., and Prasetyo, B. T. (2010). “Design of a geothermal energy dryer for tea withering and drying in Wayang Windu geothermal field,” in Proceedings of World Geothermal Congress (Bali).
Toffolo, A., Lazzaretto, A., Manente, G., and Paci, M. (2014). A multi-criteria approach for the optimal selection of working fluid and design parameters in organic Rankine cycle systems. Appl. Energy 121, 219–232. doi: 10.1016/j.apenergy.2014.01.089
Turton, R., Bailie, R. C., Whiting, W. B., and Shaeiwitz, J. A. (2008). Analysis, Synthesis and Design of Chemical Processes. London: Pearson Education.
Unamba, C. K., Sapin, P., Li, X., Song, J., Wang, K., Shu, G., et al. (2019). Operational optimisation of a non-recuperative 1-kWe organic rankine cycle engine prototype. Appl. Sci. 9:3024. doi: 10.3390/app9153024
van Kleef, L. M., Oyewunmi, O. A., and Markides, C. N. (2019). Multi-objective thermo-economic optimization of organic Rankine cycle (ORC) power systems in waste-heat recovery applications using computer-aided molecular design techniques. Appl. Energy 251:112513. doi: 10.1016/j.apenergy.2019.01.071
Ventura, C. A., and Rowlands, A. S. (2015). Recuperated power cycle analysis model: investigation and optimisation of low-to-moderate resource temperature organic Rankine cycles. Energy 93:484–494. doi: 10.1016/j.energy.2015.09.055
Vetter, C., Wiemer, H. J., and Kuhn, D. (2013). Comparison of sub-and supercritical Organic Rankine Cycles for power generation from low-temperature/low-enthalpy geothermal wells, considering specific net power output and efficiency. Appl. Therm. Eng. 51, 871–879. doi: 10.1016/j.applthermaleng.2012.10.042
Walraven, D., Laenen, B., and D'haeseleer, W. (2013). Comparison of thermodynamic cycles for power production from low-temperature geothermal heat sources. Energy Convers. Manage. 66, 220–233. doi: 10.1016/j.enconman.2012.10.003
Walraven, D., Laenen, B., and D'haeseleer, W. (2015). Minimizing the levelized cost of electricity production from low-temperature geothermal heat sources with ORCs: water or air cooled? Appl. Energy 142, 144–153. doi: 10.1016/j.apenergy.2014.12.078
White, M. T., and Sayma, A. I. (2019). Simultaneous cycle optimisation and fluid selection for ORC systems accounting for the effect of the operating conditions on turbine efficiency. Front. Energy Res. 7:50. doi: 10.3389/fenrg.2019.00050
Zare, V. (2015). A comparative exergoeconomic analysis of different ORC configurations for binary geothermal power plants. Energy Convers. Manage. 105, 127–138. doi: 10.1016/j.enconman.2015.07.073
Zhai, H., Shi, L., and An, Q. (2014). Influence of working fluid properties on system performance and screen evaluation indicators for geothermal ORC (organic Rankine cycle) system. Energy 74, 2–11. doi: 10.1016/j.energy.2013.12.030
Zhang, S., Wang, H., and Guo, T. (2011). Performance comparison and parametric optimization of subcritical organic Rankine cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 88, 2740–2754. doi: 10.1016/j.apenergy.2011.02.034
Keywords: geothermal, optimization, ORC, power generation, thermo-economic, configuration
Citation: Song J, Loo P, Teo J and Markides CN (2020) Thermo-Economic Optimization of Organic Rankine Cycle (ORC) Systems for Geothermal Power Generation: A Comparative Study of System Configurations. Front. Energy Res. 8:6. doi: 10.3389/fenrg.2020.00006
Received: 26 July 2019; Accepted: 10 January 2020;
Published: 07 February 2020.
Edited by:
Rangan Banerjee, Indian Institute of Technology Bombay, IndiaReviewed by:
Jacob Brouwer, University of California, Irvine, United StatesXiao Feng, Xi'an Jiaotong University (XJTU), China
Copyright © 2020 Song, Loo, Teo and Markides. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christos N. Markides, Yy5tYXJraWRlc0BpbXBlcmlhbC5hYy51aw==
 Jian Song
Jian Song Ping Loo
Ping Loo Jaime Teo
Jaime Teo Christos N. Markides
Christos N. Markides